Irrelevant matches in round-robin tournaments

Abstract

We consider tournaments played by a set of players in order to establish a ranking among them. We introduce the notion of irrelevant match, as a match that does not influence the ultimate ranking of the involved parties. After discussing the basic properties of this notion, we seek out tournaments that have no irrelevant matches, focusing on the class of tournaments where each player challenges each other exactly once. We prove that tournaments with a static schedule and at least five players always include irrelevant matches. Conversely, dynamic schedules for an arbitrary number of players can be devised that avoid irrelevant matches, at least for one of the players involved in each match. Finally, we prove by computational means that there exist tournaments where all matches are relevant to both players, at least up to eight players.

1 Introduction

Tournaments consist of pairwise matches aimed at establishing a ranking among a set of participants. Sport competitions are often organized in tournaments that attract significant popular interest and financial resources. Depending on the type of tournament and on the ranking rule, there may be matches that are known to have no effect on the ultimate ranking of the two contestants, regardless of their outcome. Clearly, such irrelevant matches are undesirable, as they lack the incentive to win that is the very essence of any contest.

For instance, the last round of the preliminary stage of the UEFA Champions League 2014 (Group H) consisted in the matches Porto vs Shakhtar Donetsk and Athletic Bilbao vs BATE Borisov. The scoreboard before the round was: Porto was on top of the group with 13 points, Shakhtar Donetsk was second with 8 points, whereas Athletic Bilbao and BATE Borisov had 3 points each. Since in football tournaments winning a match yields 3 points, Shakhtar Donetsk had no chance of overtaking Porto and, conversely, neither Athletic Bilbao nor BATE Borisov could have overtaken Shakhtar Donetsk. Consequently, any possible outcome of the match Porto vs Shakhtar Donetsk would not have changed the final ranking of both the involved teams. Incidentally, the match ended in an unexciting 1–1 tie.

More recently, in Group F of the UEFA Champions League 2018, Manchester City was challenging Shakhtar Donetsk in the last round. The scoreboard before the match was: Manchester City on top with 15 points, Shakhtar Donetsk in second position with 9 points, Napoli 6 points, and finally Feyenoord with 0 points. With respect to the previous example, this case presents an asymmetric situation where Manchester City is not interested in the result of the match because it will be on top of the ranking in any case, whereas Shakhtar Donetsk is interested because, if it loses the match and Napoli wins against Feyenoord, its score would be reached by Napoli. Also this kind of matches is troublesome since it can unfairly skew the incentives.

In order to avoid the previous situations, the second stage of the UEFA Champions League is a knock-out tournament organized in rounds, where the team losing a match is immediately eliminated. Clearly, knock-out tournaments trivially ensure that each match is relevant for the involved teams, however they also have significant drawbacks. First, the number of teams has to be a power of 2. Secondly, they implicitly enforce a sort of transitivity condition such that whenever a beats b and b beats c, then a is evaluated as stronger than c, even if they never played against each other. However, in many sports the result of a match cannot be reduced to an absolute value measuring the strength of the two challengers, but it contextually depends on their abilities and tactics. Indeed, no treatment of round-robin tournaments forces the transitivity of match outcomes [4, 27, 31].

In this paper, we formalize the notion of relevant and irrelevant matches and we tackle the problem of designing round-robin tournaments that contain no irrelevant matches. The very definition of relevance is not trivial. We start from the intuition that a match is relevant for one of the involved agents if the future ranking of that agent depends on its outcome. If the future ranking is uniquely determined by the outcome of the present match (say that we are analysing the last match in the tournament), then establishing the relevance of a match is relatively simple: we only need to compare two rankings from the point of view of the involved agents. However, in general, the future ranking is not uniquely determined by the outcome of the present match. Other matches may follow, possibly influencing the ultimate ranking. We resolve the uncertainty on the future matches via a probabilistic setting, in which players hold prior beliefs about the probability that any future match ends in either way, as in the classical Bradley-Terry model [3].

The paper is organized as follows. In Sect. 2, the basic concepts concerning matches, rankings, and tournaments are formalized. In particular, we assume for simplicity that a match between a and b can only end in two possible ways: a wins or b wins. Moreover, in common tournaments, the sequence of matches is fixed a-priori, regardless of the outcomes. We call these static tournaments. We also consider the more general class of dynamic tournaments, in which the sequence of matches adapts according to past outcomes.

Section 3 recalls the notion of score vector [27], and proves some related properties, used extensively in the following sections. Section 4 introduces the notion of relevant match for a given player, as a match where one outcome stochastically dominates the other [17, 30], from the point of view of that player. Such probabilistic setting is based on the assumption that players hold beliefs about the likelihood of different outcomes for all future matches. In sport tournaments, these beliefs are not unlike the odds that the betting venues routinely publish as part of their business. We also prove two equivalent non-probabilistic characterizations of relevance, applicable to point-based round-robin tournaments [28]. For this class of tournaments, we show that relevance is essentially a local property of a match, that can be checked based on past matches only.

Relevance of a match ultimately depends on how the players compare different rankings according to a preference relation. Hence, in Sect. 5, we postulate a set of admissibility conditions over preferences, modelling the fact that players aim at outdoing the others.

Once the basic definitions have been laid out, in Sect. 6 we study the circumstances under which relevant (point-based round-robin) tournaments exist. Briefly, we obtain the following main results:

• 1. All tournaments with a static schedule and at least five players include a match that is irrelevant for both of the involved agents (Theorem 12).

• 2. For all numbers of players, there is a tournament with a dynamic schedule where all matches are relevant for at least one of the involved players (Theorem 13). Moreover, up to eight players, we algorithmically synthesize a dynamic tournament where matches are relevant for both the players.

• 3. All tournaments where all players are called to play with approximately equal frequency (called balanced tournaments) with at least six players include a match that is irrelevant for one of the involved players (Theorem 14).

In the conclusions, Fig. 6 provides an overview of the main results.

Related work

In graph theory, a tournament is a complete and asymmetric directed graph [27]. Nodes represent agents and an edge from a to b indicates that a won the match against b. In common terms, such a tournament is in fact an outcome of a round-robin (real-world) tournament. Hence, graph-theoretic tournaments ignore the temporal aspects and only focus on the ultimate outcome of all the matches. On the other hand, a match may be relevant if played at the beginning of a tournament and irrelevant if played towards the end. So, in this paper we explicitly model the temporal ordering of the matches.

Designing tournament schedules that optimize certain measures of interest is a topic that has been attracting an increasing amount of literature [2, 9, 19, 29]. Typical objectives include balancing home and away matches, harmonizing referee assignments to teams and venues, minimizing the distance travelled by the teams, and balancing the sequence of adversaries to limit the so-called carry-over effect.¹ Goossens and Spieksma provide an overview of European soccer schedules, observing in particular that the canonical schedule adopted in 2008 by several national championships presents a high incidence of the carry-over effect [15].

Scarf et al. explicitly mention match relevance as a success factor in tournament design [32]. Using random sampling, they compare a collection of standard tournament designs on the basis of different metrics, including the rate of irrelevant matches. In this paper, our aim is not to measure the prevalence of irrelevant matches w.r.t. some fixed tournament design, but rather to investigate the existence of tournament designs where irrelevant matches do not occur.

A measure of relevance has been investigated in [31, 33] for static round-robin tournaments. Roughly speaking, in those papers the relevance of a match is the increase in probability of achieving a parametric goal (e.g., coming in first) when winning that match (w.r.t. losing it). On the other hand, our notion of relevance is not parameterized by a goal, instead we postulate a preference framework shared by all players where any swap in the final ranking matters. In addition, as mentioned above, we also consider dynamic tournaments.

In a recent paper [8], the authors propose a new dynamic tournament scheme, called a reaper tournament, with the objective of satisfying ranking precision and competitiveness development, the latter being a semi-formal analogue of our notion of relevance. Regarding round-robin tournaments, the authors merely point out examples where competitiveness development is violated.

Gotzes and Hoppmann [16] use integer programming to address the following problem: at any point of a tournament, what are the lowest and highest final ranks a certain team can ultimately achieve? The authors focus on the Bundesliga, Germany’s primary football division, but their approach is directly applicable to other national football league systems. The final rank problem has some connection with our notion of relevance (roughly, a match is irrelevant for a team if its lowest and highest attainable final ranks are equal). Other than that, the two problems show substantial differences. First, their problem depends only on which matches are left, but not on their order. Secondly, determining the lowest/highest final rank requires to search the possible outcomes of the remaining matches. We show, instead, that deciding whether a match is relevant for a team does not require to consider future courses but it can be easily computed on the basis of the current situation only.

The problem of ranking the participants to a tournament has been studied in the literature, with the two most prominent approaches being the maximum likelihood method and the points system [22, 28]. In this paper, we focus on the points system, as it is commonly used in real-world tournaments.

Tournament rankings are special cases of rank aggregation problems, widely studied in machine learning [7, 35]. The common objectives in that area are orthogonal to ours, mainly concerning accuracy (i.e., obtaining a ranking that is close to some model of ground truth) and efficiency (i.e., obtaining a ranking from few comparisons).

In computational social choice, tournaments can be used to represent pairwise comparisons among different alternatives. In this perspective, each player represents a possible alternative and a match corresponds to a preference judgment (e.g., a majority voting) between two alternatives. Eventually, a tournament is identified with a complete and asymmetric directed graph [27]. If an alternative beats all the others, it is unquestionably the best choice. In the other cases, it is not straightforward how to filter a set of “winners” as result of a tournament. In the literature, several solutions have been proposed and evaluated w.r.t. different admissibility criteria (monotonicity, stability, strategyproofness, etc.) [4]. Laffond et al., for example, propose a solution correspondence, called the bipartisan set, based on Nash equilibrium [14]. More specifically, they considered a two-players zero-sum game over a tournament where each player chooses an alternative, a player wins the game if its alternative beats in the tournament the one chosen by the opponent. They proved that such a game has a unique equilibrium in mixed strategies. Then, all the alternatives that are not in support of the equilibrium are strategically rejected whereas the remaining ones constitute the bipartisan set. Moulin proposed a single-valued selection correspondence based on multi-stage elimination trees [23]. On the positive side, the selected winner is Pareto-optimal and refines other well known solution concepts such as the top cycle and the uncovered set.² On the negative side, this methodology does not satisfy neutrality, i.e., it is not invariant under permutation of the alternatives.

Finally, the Economics literature discusses tournament design with the objective of maximizing profit for the organizers [10, 34]. The inquiry that is most related to ours finds strong correlation between match attendance and importance for either team, where the latter is measured by an ad-hoc formula based on the possibility that the team will win the championship and the number of remaining matches [18]. Another recent work focuses on multi-tournament scenarios in which it is convenient for a team to lose rather than win a match [6].

Relation to our previous works. The present work is based on [12] and extends it in several ways. First, the notion of relevance and its properties were based on a single preference relation over rankings, namely the lexicographic preference. Here, we consider an entire class of admissible preferences (Sect. 5) which includes all preferences based on linear utility (the lexicographic preference is a particular case thereof).

Secondly, we present a novel result reducing the relevance of a match in a tournament to a local property, based on the number of remaining matches of the involved players and the score differences with the other players (Theorem 5). Using this local characterization, one can recognize an irrelevant match without enumerating all possible futures, which are exponentially many in the number of remaining matches. The local characterization also induces some conditions which, roughly speaking, predict the presence of an irrelevant match at an earlier stage of the tournament. We use these conditions as an optimization technique in a search algorithm which decides whether there exists a strongly relevant tournament for a given number of players. This search algorithm allows us to present here the first positive results on strongly relevant tournaments, described in Sect. 6.4.

Finally, Sect. 4.3 provides a novel lower bound to the stage at which an irrelevant match may occur.

2 Preliminaries

Informally, by tournament we mean a plan of matches among multiple players which eventually produces a scoreboard, according to the outcomes of the single matches. More specifically, in this paper we focus on tournaments that are ordinal in the sense that what really matters is the mutual placement of players rather than their absolute scores. Moreover, as in [1, 24, 30], a scoreboard can in principle fail to distinguish two agents. For these reasons, we assume that the final outcome of a tournament is a weak order, representing a ranking among players, including ties.

In the following, unless differently specified, we assume a fixed set of players ${A} = \{1,\ldots ,n\}$. A ranking is a weak order on ${A}$, i.e., a total, reflexive, and transitive relation, $\preceq \,\subseteq {A} \times {A}$. As usual, by $\sim$ and $\prec$ we denote the symmetric and asymmetric parts of $\preceq$, respectively. Intuitively, $a\prec b$ means that player b has a better placement than a, whereas $a\sim b$ means that they are ranked the same (a.k.a. a tie).

We call match an unordered pair $\{a,b\}$ of distinct players. Generally speaking, a match may have multiple outcomes. In this work, we focus on binary tournaments, whose matches can have one of two possible outcomes: a wins (and b loses) or vice versa. We represent the outcome of a match via an ordered pair of players, where the first component indicates who won the match; for instance (a, b) means that a prevailed in a match against b. We call such pairs events.

Then, a tournament $\mathcal {T}$ is a labelled full binary tree where: (i) each internal node x is labelled with a match $\{a,b\}$; (ii) its two outgoing arcs are labelled with a and b, respectively; (iii) each leaf is labelled with a ranking. Intuitively, given an internal node x labelled with a match $\{a,b\}$, the outgoing a-arc corresponds to a having won the match (and therefore, b having lost it). Analogously, the outgoing b-arc corresponds to b having won the match. Thereafter, internal nodes will also be called match nodes.

Fig. 1

Two tournaments among three players

A path ${\pi } =(x_1,\ldots , x_m)$ in a tournament is a sequence of nodes such that $x_{i+1}$ is a child of $x_i$. If the final node of ${\pi }$ is a leaf, then ${\pi }$ is called a terminal path and the ranking labeling the leaf is denoted by $\preceq _{\pi }$. A full path is a terminal path whose first node is the root of $\mathcal {T}$.

Given a path ${\pi } =(x_1,\ldots , x_m)$, we denote by $\langle {\pi } \rangle =(e_1,\ldots , e_{m-1})$ the sequence of associated events where, for each $1\le i\le m-1$, $e_i$ is the pair (a, b) such that $\{a,b\}$ is the match associated to $x_i$ and the arc $(x_i, x_{i+1})$ is labelled with a. In what follows let $\mathsf {won} (a, {\pi })$ be the number of matches won by a in $\pi$, that is the number of events $(a,\cdot )$ in $\langle \pi \rangle$. Similarly, $\mathsf {lost} (a, {\pi })$ is the number of matches lost by a in ${\pi }$. Finally, if $\langle \pi \rangle$ is a permutation of $\langle \pi '\rangle$, then we say that the paths $\pi$ and $\pi '$ are homologous.

Remark

In some popular tournaments, as national football leagues, a match can possibly end with a tie. Here, we do not consider ties to make our model as simple as possible. However, this assumption encompasses many real-world situations. For example, all sports where a match ends when one of the contenders gets a predetermined number of points (e.g., tennis, table tennis, volley, fencing) do not admit ties.³ In other sports like basket if the score is tied after regular time, then an overtime period is held to break the tie.

Types of tournaments.

We distinguish the following families of tournaments:

• A tournament is static if it is a complete tree and all its internal nodes at a given level are labeled with the same match. In other words, the sequence of matches is the same on all full paths.

• A round-robin tournament is a tournament where in all full paths each player challenges each other exactly once. Notice that each full path in a round-robin tournament with n players comprises $\left( {\begin{array}{c}n\\ 2\end{array}}\right) = \frac{n(n-1)}{2}$ match nodes.

  Furthermore, a round-robin tournament is balanced if n is even and for all full paths $\pi = (x_1,\ldots , x_m,z)$, with $m=\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ and all $0\le i\le n-2$, the set of $\frac{n}{2}$ match nodes

  $$\begin{aligned} \left\{ x_j \,\big |\, j = i \frac{n}{2} +1, \, i\frac{n}{2}+2, \, \ldots , \, (i+1)\frac{n}{2} \right\} \end{aligned}$$

  involves all players. In other words, balanced tournaments are organized into $n-1$ rounds. Every player plays one match in each round.

• A tournament is point-based if players accrue points corresponding to winning or losing each match, and the final ranking is based on such points.

  Formally, let

  $$\begin{aligned} \mathsf {score} (c,{\pi }, {p} _\mathsf {w}, {p} _\mathsf {l}) = \mathsf {won} (c,{\pi }) {p} _\mathsf {w} + \mathsf {lost} (c,{\pi }) {p} _\mathsf {l} \, , \end{aligned}$$

  where c is a player, ${\pi }$ is a full path, and ${p} _\mathsf {w}, {p} _\mathsf {l}$ are real numbers. We say that a tournament is point-based if there exist ${p} _\mathsf {l} < {p} _\mathsf {w}$ such that for all full paths ${\pi }$ and players a and b, $a\preceq _{\pi } b$ iff $\mathsf {score} (a,{\pi },{p} _\mathsf {w},{p} _\mathsf {l}) \le \mathsf {score} (b,{\pi },{p} _\mathsf {w},{p} _\mathsf {l})$.

Example 1

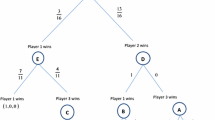
Figure 1 shows two tournaments $\mathcal {T} _1$ and $\mathcal {T} _2$ among the players a, b, and c.

In $\mathcal {T} _1$ all full paths share the same sequence of matches and each player challenges the other ones exactly once. Therefore, $\mathcal {T} _1$ is a static round-robin tournament. Moreover, the placement of a player at the end of a full path ${\pi }$ depends on the number of matches it won, i.e., $t_1 \preceq t_2$ iff $\mathsf {won} (t_1, \pi ) \le \mathsf {won} (t_2, \pi )$. Then, since $\mathsf {won} (\cdot , {\pi })$ corresponds to the score function where ${p} _\mathsf {l} =0$ and ${p} _\mathsf {w} =1$, we have that $\mathcal {T} _1$ is point-based.

The second tournament $\mathcal {T} _2$ is also round-robin and point-based. However, if player a wins the first match than the order of the reamaning matches is the same as in $\mathcal {T} _1$, otherwise the order is the opposite. This means that the schedule of matches dynamically changes depending on the outcomes of the previous matches. So, $\mathcal {T} _2$ is a dynamic round-robin point-based tournament.

Similarly to utility functions in Decision Theory [25], the following theorem shows that the score function associated to a point-based tournament is invariant under linear transformations.

Theorem 1

Let $\mathcal {T}$ be a point-based round-robin tournament and let ${p} _\mathsf {l}$ and ${p} _\mathsf {w}$ be two real values such that ${p} _\mathsf {l} < {p} _\mathsf {w}$. Then, for each full path ${\pi }$, we have that $a\preceq _{\pi } b$ iff $\mathsf {score} (a,\pi ,{p} _\mathsf {w},{p} _\mathsf {l}) \le \mathsf {score} (b,\pi ,{p} _\mathsf {w},{p} _\mathsf {l})$.

Proof

From $\mathcal {T}$ being point-based, there exist some ${p} '_\mathsf {l} < {p} '_\mathsf {w}$ such that, for each full path ${\pi }$, the score function $\mathsf {score} (\cdot ,\pi ,{p} '_\mathsf {w},{p} '_\mathsf {l})$ is monotonic w.r.t. the ranking $\preceq _{\pi }$. Moreover, from $\mathcal {T}$ being round-robin, it holds that $\mathsf {lost} (a, {\pi }) = (n-1) - \mathsf {won} (a, {\pi })$. Then, we have that

$$\begin{aligned} \mathsf {score} (\cdot ,\pi ,{p} _\mathsf {w},{p} _\mathsf {l})= & {} \mathsf {won} (\cdot ,\pi ) {p} _\mathsf {w} + \mathsf {lost} (\cdot ,\pi ) {p} _\mathsf {l} \\= & {} \mathsf {won} (\cdot ,\pi ) {p} _\mathsf {w} + ((n-1)-\mathsf {won} (\cdot ,\pi )) {p} _\mathsf {l} \\= & {} \mathsf {won} (\cdot ,\pi )({p} _\mathsf {w}-{p} _\mathsf {l})+ (n-1) {p} _\mathsf {l} \, . \end{aligned}$$

Similarly, $\mathsf {score} (\cdot ,\pi ,{p} '_\mathsf {w},{p} '_\mathsf {l}) = \mathsf {won} (\cdot ,\pi )({p} '_\mathsf {w}-{p} '_\mathsf {l})+ (n-1) {p} '_\mathsf {l}$. Then, it is straightforward to see that $\mathsf {score} (\cdot ,\pi ,{p} _\mathsf {w},{p} _\mathsf {l}) = \alpha \mathsf {score} (\cdot ,\pi ,{p} '_\mathsf {w},{p} '_\mathsf {l}) +\beta$, where

$$\begin{aligned} \alpha =\frac{{p} _\mathsf {w}-{p} _\mathsf {l}}{{p} '_\mathsf {w}-{p} '_\mathsf {l}}\qquad \text {and}\qquad \beta =(n-1)\left( {p} _\mathsf {l}-\frac{{p} _\mathsf {w}-{p} _\mathsf {l}}{{p} '_\mathsf {w}-{p} '_\mathsf {l}}\,{p} '_\mathsf {l} \right) \, . \end{aligned}$$

Since $\alpha >0$, then $\mathsf {score} (\cdot ,\pi ,{p} _\mathsf {w},{p} _\mathsf {l})$ and $\mathsf {score} (\cdot ,\pi ,{p} '_\mathsf {w},{p} '_\mathsf {l})$ are co-monotonic and hence the thesis. $\square$

Roughly speaking, Theorem 1 says that the score function representing a point-based round-robin tournament does not depend on which weights ${p} _\mathsf {l} < {p} _\mathsf {w}$ we choose. Therefore, w.l.o.g. we will always assume that ${p} _\mathsf {l} =0$ and ${p} _\mathsf {w} =1$, that is, $\mathsf {score} (a,\pi )=\mathsf {won} (a,\pi )$.

3 Score vectors

The score vector $v _\pi$ of a full path $\pi$ is the sequence of scores $\{ \mathsf {won} (a, \pi ) \}_{a \in {A}}$, ordered by increasing value [27]. We say that a vector u of integers is a round-robin score vector if there exist a round-robin tournament $\mathcal {T}$ and a full path $\pi$ in $\mathcal {T}$ such that u is the score vector of $\pi$. We recall the following classical result, known as Landau’s theorem.

Theorem 2

([20]) A vector $(u_1,\ldots ,u_n) \in \mathbb {N} ^n$ is a round-robin score vector if and only if, for all $k = 1, \ldots , n-1$,

$$\begin{aligned} \sum _{i=1}^{k} u_i \ge \left( {\begin{array}{c}k\\ 2\end{array}}\right) \qquad \text {and}\qquad \sum _{i=1}^{n} u_i = \left( {\begin{array}{c}n\\ 2\end{array}}\right) \, . \end{aligned}$$

Consider a node $x$ in a round-robin tournament $\mathcal {T}$ and its children $x'$ and $x''$. It is straightforward to see that the homology relation induces a bijection between the terminal paths starting from $x'$ and those starting from $x''$. In particular, if $\mathcal {T}$ is also static, then two homologous paths $\pi _1$ and $\pi _2$ induce the same sequence of events, i.e., $\langle \pi _1\rangle =\langle \pi _2\rangle$.

Example 2

Consider again the tournament $\mathcal {T} _1$ in Fig. 1 and the paths ${\pi } _1$ and ${\pi } _2$ highlighted in bold. Since both $\langle {\pi } _1\rangle$ and $\langle {\pi } _2\rangle$ are equal to ((c, a), (b, c)), these paths are clearly homologous. In $\mathcal {T} _2$, the analogous paths ${\pi } _3$ and ${\pi } _4$ highlighted in bold do not satisfy the property $\langle {\pi } _3\rangle =\langle {\pi } _4\rangle$. However, $\langle {\pi } _4\rangle =((b,c),(c,a))$ is a permutation of $\langle {\pi } _3\rangle =((c,a), (b,c))$ and hence also ${\pi } _3$ and ${\pi } _4$ are homologous.

The following two lemmas will be used in Sect. 6.⁴ The first one states that, once we fix the number of players, all possible round-robin score vectors satisfying Theorem 2 occur in all point-based round-robin tournaments.

Lemma 1

Let $\mathcal {T}$ be a point-based round-robin tournament with n players and let u be a round-robin score vector with n players. Then, there exists a full path $\pi$ in $\mathcal {T}$ such that $u = v _\pi$.

In the following, given a score vector $(s_1,\ldots ,s_n)$, we say that the vector $(\delta _0,\ldots ,\delta _{n-1})$ is the corresponding score difference vector, where $\delta _0=s_1$ and $\delta _i = s_{i+1} - s_i$ for all $i=1,\ldots ,n-1$. We refer to a zero-valued score difference $\delta _i$ as a plateau. The second lemma states that, whenever a score difference $\delta _i$ is higher than 1, there are at least $\delta _i$ plateaus. In other words, the number of plateaus is at least as large as the greatest score difference, provided the latter is greater than 1.

Lemma 2

For all score vectors s, let $\delta$ be its score difference vector. For all i s.t. $\delta _i > 1$ it holds $|\{ j \mid \delta _j = 0\}| \ge \delta _i$.

4 Notions of relevance

We would like each match in a tournament to be relevant to both players involved. Intuitively, a match is relevant for a player if its future ranking depends in a significant way on the outcome of that match. To define exactly what changes in ranking are significant for a given player, we need to make assumptions on the way in which players compare rankings. Clearly, players prefer to be as high as possible in the ranking. But do they care about which players are above and below them? And are they interested in how many other players share their own position in the ranking?⁵

We restrict the space of all possible preferences among rankings to a family of so-called admissible preferences. Such a family is general enough to encompass most practical scenarios, while providing the basic properties needed by our results. The breadth and the limits of the family of admissible preferences are further discussed in Sect. 5.

First, for a given player a we define two flavors of dominance on rankings: weak dominance and dominance. For all pairs of rankings $\preceq _1$ and $\preceq _2$, it holds ${WDom}_{a}(\preceq _1,\preceq _2)$ ($\preceq _2$ weakly dominates $\preceq _1$) iff for all players b (i) if $a\sim _1 b$, then $b\preceq _2 a$, and (ii) if $b\prec _1 a$, then $b\prec _2 a$. Moreover, ${Dom}_{a}(\preceq _1,\preceq _2)$ ($\preceq _2$ strongly dominates $\preceq _1$, or simply dominates) iff ${WDom}_{a}(\preceq _1,\preceq _2)$ and there exists a player b such that either (i) $a\prec _1 b$ and $b\preceq _2 a$, or (ii) $a\sim _1 b$ and $b\prec _2 a$. Roughly speaking, weak dominance indicates that one ranking is at least as good as another, from the point of view of the given player a. If additionally the placement of a w.r.t. another player b is strictly better, we are in the presence of (strong) dominance.

Notice that ${WDom} _{a}$ and ${Dom} _{a}$ are a preorder and a strict partial order, respectively, whereas preferences are required to be weak orders. Then, an admissible a-preference $\mathcal {P}_{a}$ over rankings is a weak order refining ${WDom} _a$ and whose asymmetric part refines ${Dom} _a$. Formally,

• 1. if ${WDom}_{a}(\preceq _1,\preceq _2)$, then $\mathcal {P}_{a}(\preceq _1,\preceq _2)$;

• 2. if ${Dom}_{a}(\preceq _1,\preceq _2)$, then $\mathcal {P}_{a}(\preceq _1,\preceq _2)$ and not $\mathcal {P}_{a}(\preceq _2,\preceq _1)$.

Thereafter, we assume that any player a has a fixed admissible preference relation $\mathcal {P}_{a}$. We write $[\preceq ]_{{a}}$ to denote the class of rankings $\preceq '$ that are a-equivalent to $\preceq$, i.e., $\mathcal {P}_{a}(\preceq ,\preceq ')$ and $\mathcal {P}_{a}(\preceq ',\preceq )$. Since the number of possible rankings is finite, $\mathcal {P}_{a}$ induces a finite number $\mathcal {C} ^a_1,\ldots , \mathcal {C} ^a_m$ of a-equivalent classes, linearly ordered by $\mathcal {P}_{a}$.

We can now proceed to define when a match in a tournament is relevant to a given player. As anticipated in the introduction, we adopt a probabilistic view: we assume that each player is equipped with a belief about the likelihood of different outcomes for all future matches. We assume that players are never absolutely certain about the outcome of future matches, so that the likelihood of a given outcome lies in the open interval (0, 1).

In the following, we fix a tournament $\mathcal {T}$ and omit it from the notation. A belief is a function $\beta : A\times A \rightarrow (0,1)$ assigning probabilities to the outcomes of every possible match. Since matches are zero-sum games where one player wins and one player loses, it also holds that $\beta (a,b) + \beta (b,a)=1$, for all players $a,b\in A$.

The probability of any path $\pi = (x_1,\ldots , x_m)$ is obtained by combining the beliefs of the corresponding events, treated as stochastically independent:

$$\begin{aligned} {Pr}_\beta (\pi )=\prod _{i=1}^{m-1} \beta (e_i) \, . \end{aligned}$$

(1)

where $\langle \pi \rangle =(e_1,\ldots ,e_{m-1})$. Note that homologous paths have the same probability to occur according to any belief.

For a player a, let $R_a$ be the random variable assigning to each terminal path $\pi$ the a-equivalence class of the ranking $\preceq _\pi$, i.e., $R_a(\pi ) = [\preceq _\pi ]_{a}$. We denote by $\gamma (R_a, x,\beta )$ the distribution of $R_a$ over all terminal paths starting from $x$. More precisely, given an internal node $x$ and an a-equivalence class $\mathcal {C} ^a_j$, with $1\le j\le m$, let $\mathsf {Paths} (x,a,j)$ be set of all terminal paths starting from $x$ whose final ranking belongs to $\mathcal {C} ^a_j$. Then, $\gamma (R_a, x,\beta )$ associates to the class $\mathcal {C} ^a_j$ the probability

$$\begin{aligned} \sum _{\pi \in \mathsf {Paths} (x,a,j)}{Pr}_\beta (\pi ). \end{aligned}$$

Example 3

Consider again the tournament $\mathcal {T} _1$ in Fig. 1 and assume that a bookmaker estimates the following odds $\beta$: player a has a probability 0.7 of beating b and a probability 0.5 of beating player c; player b has a probability 0.4 of beating c.

According to the final rankings, each player $t\in \{a,b,c\}$ has four different equivalence classes $\mathcal {C} ^t_1,\ldots ,\mathcal {C} ^t_4$, where $\mathcal {C} ^t_1$ is the set of all rankings where t comes in last, $\mathcal {C} ^t_2$ means that t is in the second position, $\mathcal {C} ^t_3$ is the case where all the players tie, and finally in $\mathcal {C} ^t_4$ t takes the first position with no ties.

Thus, the class $\mathcal {C} ^a_4$ corresponds in Fig. 1 to the two leftmost paths. Let $x$ be the root of the tree, $\gamma (R_a, x,\beta )$ assigns probability $0.7*0.5 = 0.35$ to $\mathcal {C} ^a_4$. Similarly, the paths where player b takes the second position are the leftmost and the rightmost ones, hence $\mathcal {C} ^b_2$ has probability $0.14+0.09=0.23$.

Now, we formalize when player a prefers an internal node $x_1$ to another node $x_2$, based on the corresponding distributions $\gamma _1 = \gamma (R_a, x_1,\beta )$ and $\gamma _2=\gamma (R_a, x_2, \beta )$. This notion is based on stochastic dominance between two distributions taking values over a linearly ordered set [17]. In our case, the linear order is the set $\mathcal {C} ^a_1,\ldots , \mathcal {C} ^a_m$ of a-equivalence classes ordered by $\mathcal {P}_{a}$. Let $\varGamma _1$ and $\varGamma _2$ be the cumulative probabilities of $\gamma _1$ and $\gamma _2$, respectively:

$$\begin{aligned} \varGamma _i(\mathcal {C} ^a_k) = \sum _{j=1}^k \gamma _i(\mathcal {C} ^a_j) \, , \end{aligned}$$

with $i=1,2$. Then, $\gamma _2$ stochastically dominates $\gamma _1$ if and only if, for all $1\le k\le m$, $\varGamma _2(\mathcal {C} ^a_k)\le \varGamma _1(\mathcal {C} ^a_k)$, with a strict inequality for at least one value of k.

Stochastic dominance is a well-known and robust notion to lift qualitative preference relations over distributions. In particular, it holds that $\gamma _2$ stochastically dominates $\gamma _1$ iff for all utility functions over rankings conforming with $\mathcal {P}_{a}$, the expected utility of $\gamma _2$ is greater than the one of $\gamma _1$.

Definition 1

A node $x$ labelled with a match $\{a,b\}$ is c-relevant, with $c\in \{a,b\}$, iff, for all beliefs $\beta$, $\gamma (R_c, x_a, \beta )$ stochastically dominates $\gamma (R_c, x_b, \beta )$ or vice versa. A tournament is strongly (resp., weakly) relevant iff all internal nodes are relevant for both (resp., at least one of the) involved players.

Fig. 2

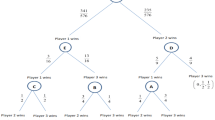
A fragment of a 5-player tournament (see Example 4). Each leaf is decorated underneath by its score vector. Players that tie in a final ranking are grouped in set notation

Example 4

Consider a static point-based round-robin tournament among five players a, b, c, d, and e and let $x$ be a node where the intermediate scores are:

$$\begin{aligned} \begin{array}{ccccc} a &{} b &{} c &{} d &{} e \\ \hline 1 &{} 3 &{} 1 &{} 1 &{} 2\\ \end{array} \end{aligned}$$

and only the two matches $\{b,c\}$ and $\{a,d\}$ are left. Such a node occurs as the result of the following sequence of events:

$$\begin{aligned} (b,a),\, (b,d),\, (b,e),\, (a,c),\, (e,a),\, (c,d),\, (e,c),\, (d,e) \,. \end{aligned}$$

Figure 2 shows the subtree rooted in $x$.

Given a generic belief $\beta$, since at this point player b will surely take first place with no ties, the admissibility of $\mathcal {P}_{b}$ (precisely, condition 1 of admissibility) ensures that both distributions $\gamma (R_b, x_b, \beta )$ and $\gamma (R_b, x_c, \beta )$ assign probability 1 to the same $\mathcal {P}_{b}$-equivalence class, and zero to all the other classes. Consequently, none of the distributions stochastically dominates the other and $x$ is b-irrelevant.

Remark

Notice that weakly relevant matches are not more desirable than irrelevant matches, the adjective “weakly” has a pure mathematical flavor. Consider for example the match of UEFA Champions League 2018 described in the introduction (Machester City vs Shakhtar Donetsk). Machester City, which was ranked first in any case, had a notably turnover of its first-string players to make them repose. Then, against the odds, Shakhtar Donetsk won the match and Napoli was inexorably ruled out. The fact that only one contender is interested in winning can affect the result of a weakly relevant match and unfairly distort the final ranking.

4.1 Getting rid of probabilities

For round-robin tournaments, we now develop a characterization of relevance that avoids any reference to the probabilistic setting. We say that an internal node $x$ labelled with $\{a,b\}$ is c-important, with $c\in \{a,b\}$, if there exists a terminal path from $x_a$ whose ranking is not c-equivalent to the ranking of the homologous path starting from $x_b$. The following theorem states that, in round-robin tournaments, relevance implies importance.

Theorem 3

For all nodes $x$ in a round-robin tournament and all players c, if $x$ is c-relevant, then it is c-important.

Proof

Assume that node $x$ labelled with a match $\{a,b\}$ is c-relevant. Recall that for all beliefs $\beta$ and all pairs of homologous paths $\pi _1$ and $\pi _2$, $\beta$ assigns the same probability to them, i.e., ${Pr}_\beta (\pi _1) = {Pr}_\beta (\pi _2)$.

Assume by contradiction that $x$ is not c-important. As usual, denote by $x_a$ and $x_b$ the children of $x$. By definition, it follows that all pairs of homologous paths starting from $x_a$ and $x_b$, respectively, end with c-equivalent rankings. Hence, the two distributions $\gamma (R_c,x_a,\beta )$ and $\gamma (R_c,x_b,\beta )$ are equal, and so neither one stochastically dominates the other, contradicting our initial assumption that $x$ is c-relevant. $\square$

Next, we prove that if the tournament is additionally point-based, relevance is equivalent to importance.

Theorem 4

For all point-based round-robin tournaments, a node labelled with match $\{a,b\}$ is c-relevant, with $c \in \{a, b\}$, iff it is c-important.

Proof

Theorem 3 implies the “only if” direction, so we are left to prove the “if” implication.

Assume that $x$ is c-important, it follows that there exist two homologous terminal paths $\pi _a$ and $\pi _b$ starting from $x_a$ and $x_b$, respectively, such that $\preceq _{\pi _a}$ and $\preceq _{\pi _b}$ are not c-equivalent.

Assume w.l.o.g. that $c = a$. As the tournament is point-based, the score of a at the end of $\pi _a$ is equal to the score at the end of $\pi _b$ plus one. The scores of all other players in $\pi _a$ are less or equal than in $\pi _b$. Consequently, $\preceq _{\pi _a}$ weakly dominates $\preceq _{\pi _b}$ from the point of view of player a and hence $\mathcal {P}_{a}(\preceq _{\pi _b},\preceq _{\pi _a})$. Finally, since $\preceq _{\pi _a}$ and $\preceq _{\pi _b}$ are not a-equivalent, then a strictly prefers $\preceq _{\pi _a}$ to $\preceq _{\pi _b}$, i.e., $\mathcal {P}_{a}(\preceq _{\pi _b},\preceq _{\pi _a})$ and not $\mathcal {P}_{a}(\preceq _{\pi _a},\preceq _{\pi _b})$.

Let $\mathcal {C} ^a_1,\ldots , \mathcal {C} ^a_m$ be the a-equivalence classes of rankings, ordered by $\mathcal {P}_{a}$. Let $\beta$ be any belief and let $\varGamma _a$ (resp., $\varGamma _b$) be the cumulative distribution of $\gamma (R_a,x_a,\beta )$ (resp., $\gamma (R_a,x_b,\beta )$). For all homologous paths $\pi '_a$ and $\pi '_b$ starting from $x_a$ and $x_b$, respectively, it holds by the same argument as before that ${WDom}_{a}(\preceq _{\pi '_b},\preceq _{\pi '_a})$ and hence $\mathcal {P}_{a}(\preceq _{\pi '_b},\preceq _{\pi '_a})$. This means that if $\preceq _{\pi '_a}$ belongs to the class $\mathcal {C} ^a_i$, then $\preceq _{\pi '_b}$ belongs to a class $\mathcal {C} ^a_j$ with $j \ge i$. As a consequence, we have that $\varGamma _a(\mathcal {C} ^a_i) \le \varGamma _b(\mathcal {C} ^a_i)$ for all $i=1,\ldots ,m$.

In order to prove stochastic dominance, it remains to show that there exists an $1\le i\le m$ such that the above inequality is strict. Let $\mathcal {C} ^a_k$ be the least preferred class in that linear order such that there exist two homologous paths $\pi ''_a$ and $\pi ''_b$ starting from $x_a$ and $x_b$, respectively, with $\pi ''_b$ ending in $\mathcal {C} ^a_k$ and $\pi ''_a$ ending in a different, and hence strictly preferred, class. Such a class is guaranteed to exist, due to the pair of paths $\pi _a$ and $\pi _b$. Let $p = {Pr}_\beta (\pi ''_a) = {Pr}_\beta (\pi ''_b)$, we have that $p > 0$.

It follows that

$$\begin{aligned} \gamma (R_a,x_a,\beta )(\mathcal {C} ^a_i) = \gamma (R_a,x_b,\beta )(\mathcal {C} ^a_i) \end{aligned}$$

for all $i=1,\ldots ,k-1$, and

$$\begin{aligned} \gamma (R_a,x_a,\beta )(\mathcal {C} ^a_k) \le \gamma (R_a,x_b,\beta )(\mathcal {C} ^a_k) - p < \gamma (R_a,x_b,\beta )(\mathcal {C} ^a_k). \end{aligned}$$

Hence, $\varGamma _a(\mathcal {C} ^a_k) < \varGamma _b(\mathcal {C} ^a_k)$, and our thesis. $\square$

Fig. 3

A fragment of a 3-player tournament that is not point-based. The root x of the fragment is c-important but not c-relevant

Example 5

Consider again Fig. 2. Let $x$ be the root and $\preceq _1,\ldots ,\preceq _4$ be the final rankings from left to right. Consider the two rankings $\preceq _1$ and $\preceq _3$. Since in the former c takes third place whereas in the latter c comes in second, by admissibility we have that c strictly prefers $\preceq _3$ over $\preceq _1$, i.e., $\mathcal {P}_{c} (\preceq _1, \preceq _3)$ and not $\mathcal {P}_{c} (\preceq _3, \preceq _1)$. Now, those rankings appear at the end of the two homologous paths $\langle x_b, \preceq _1\rangle$ and $\langle x_c, \preceq _3\rangle$. Consequently, by definition $x$ is c-important and, by Theorem 4, also c-relevant.

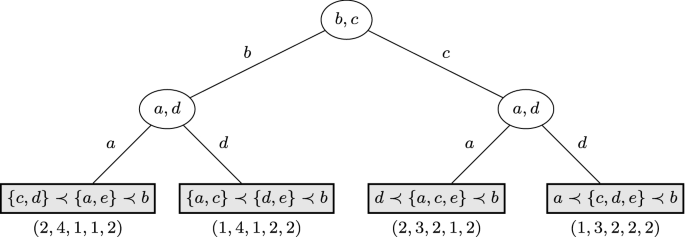
Being point-based is necessary for Theorem 4 to hold. In particular, consider Fig. 3, which depicts a fragment of a 3-player round-robin tournament. Notice that the tournament is not point-based. To see this, call $\preceq _1,\ldots ,\preceq _4$ the four final rankings, left to right. In the path leading to $\preceq _3$, a (resp., c) has won one more match (resp., one fewer match) compared to the path leading to $\preceq _4$. This contradicts the fact that $a \prec _3 c$ and $c \prec _4 a$. In fact, the ranking $\prec _4$ is intentionally unrealistic, in order to violate the equivalence in Theorem 4.

Now, let $x$ be the root of the fragment, and $x_b$ and $x_c$ be its left and right children, respectively. Observe that $x$ is c-important but not c-relevant. Importance follows from comparing the two homologous paths starting from $x_b$ and $x_c$ and leading to $\preceq _1$ and $\preceq _3$, respectively. Then, consider the belief $\beta$ that assigns equal probabilities to either player winning the match $\{ a,c \}$. According to $\beta$, in both $x_b$ and $x_c$ player c has probability $\frac{1}{2}$ of being second and probability $\frac{1}{2}$ of being third (i.e., $\gamma (R_c, x_b, \beta ) = \gamma (R_c, x_c, \beta )$). So, neither distribution stochastically dominates the other and therefore $x$ is not c-relevant.

4.2 Getting rid of the future

Theorem 4 provides an effective procedure to check in round-robin point-based tournaments whether a match $x$ is irrelevant for one of the involved players. However, since the number of homologous terminal paths descending from the children of $x$ is exponential in the number of remaining matches, the notion of importance is not computationally tractable and hence it cannot be used in practice as such. Fortunately, we show that there exist more efficient ways to check the importance of a node that do not require to look at its possible futures. It simply suffices to compare some quantities that can be derived locally.

Furthermore, we also show that in some cases it is possible to foresee the presence of an irrelevant node at an earlier stage of the tournament. This will be used in Sect. 6.4 to speed up a procedure that checks whether a strongly relevant dynamic tournament exists for a given number of participants.

Given a node $x$ of a round-robin point-based tournament $\mathcal {T}$, let $r_i$ be the number of matches that player i has not played yet, including the match associated to $x$ in case i is one of the involved players, and let $s_i$ be its current score — that is $s_i= \mathsf {won} (\pi ,i)$, where $\pi$ is the path from the root to $x$. Then, let ${Abv}_i$ (resp. ${Blw}_i$) be the set of players $j\ne i$ such that $s_j\ge s_i$ (resp. $s_j\le s_i$). Note that, if ${Abv}_i\cap {Blw}_i\ne \emptyset$, then i ties with another player. Instead, ${Abv}_i=\emptyset$ (resp. ${Blw}_i=\emptyset$) means that player i ranks first (resp. last), with no ties.

Now, let h and k be two players such that, in $x$, $s_h\le s_k$. We denote by $d_{hk}=r_h+ s_h-s_k$ the score difference between h and k assuming that h wins all its remaining matches and, conversely, k loses all remaining matches. Finally, for each player h, let $\theta _h$ and $\lambda _h$ be defined as follows:

$$\begin{aligned} \theta _h= & {} \left\{ \begin{array}{l} r_h+s_h- \min _{k\in {Abv}_h} s_k \quad \text{ if } {} {Abv}_h\ne \emptyset \\ -1 \quad \text{ otherwise } \end{array} \right. \\ \lambda _h= & {} \left\{ \begin{array}{l} \max _{k\in {Blw}_h}(r_k+s_k) - s_h \text{ if } {Blw}_h\ne \emptyset \\ -1 \text{ otherwise } \end{array} \right. \end{aligned}$$

Notice that, in case ${Abv}_h\ne \emptyset$, $\theta _h$ is the maximum $d_{hk}$ for $k\in {Abv}_h$, so it intuitively represents how many chances player h has of catching up with an opponent having a better score (if h does not tie with any other player) or overcoming a player with the same score. In case h has the highest score with no ties, i.e. ${Abv}_h=\emptyset$, we assign the conventional value $-1$ which, roughly speaking, represents the fact that currently h cannot improve its ranking (since it is already first with no ties).

Similarly, $\lambda _h$ represents the number of chances to be reached or overcome by a player with a lower or equal score. As before, we use $-1$ in case h ranks last with no ties, i.e. ${Blw}_h=\emptyset$.

The following theorem establishes that a node is important for one of the involved players c if and only if c has some chance to reach a player with a better score or a player with a lower score than c can reach c. Let $\mu _h$ be the maximum between $\theta _h$ and $\lambda _h$.

Theorem 5

Let $x$ be a node of a round-robin point-based tournament $\mathcal {T}$, labeled with a match $\{a,b\}$. Then, $x$ is c-important, with $c\in \{a,b\}$, iff $\mu _c\ge 0$.

Proof

Since it does not make any difference in the proof, for the sake of simplicity let c be the player a.

For the “if” direction, $\mu _a\ge 0$ means that either $\theta _a\ge 0$ or $\lambda _a\ge 0$. We will show that $x$ is a-important in both cases. Assume first that $\theta _a\ge 0$. By definition, there exists a player k with $s_k\ge s_a$ such that $r_a\ge s_k-s_a$. We distinguish two cases, $s_k=s_a$ and $s_k > s_a$.

Let $s_k=s_a$ and consider two homologous paths $\pi$ and $\pi '$ starting from $x_a$ and $x_b$, respectively, where a loses all its matches and k wins only against a (in case the match $\{a,k\}$ occurs in the paths). Notice that the final score of a is $s_k+1$ in $\pi$, and $s_k$ in $\pi '$, whereas the score of b can be: $s_k$ in both $\pi$ and $\pi '$; $s_k+1$ in both $\pi$ and $\pi '$; or $s_k$ in $\pi$ and $s_k+1$ in $\pi '$ (in case $k=b$). Therefore, since $\pi$ and $\pi '$ are homologous, we have that: (i) for all other players h, if $a \preceq _{\pi } h$, then $a \preceq _{\pi '} h$, and (ii) either $a \prec _{\pi '} k$ and $a \sim _{\pi } k$, or $a \sim _{\pi '} k$ and $a \succ _{\pi } k$. Then, in all cases ${Dom}_{a}(\preceq _\pi ',\preceq _\pi )$ holds and hence $x$ is a-important.

Then, assume $s_k>s_a$. This time we let k lose all its matches in $\pi$ and $\pi '$, and we let a win $s_k-s_a$ matches, if $r_a>s_k-s_a$, and all the remaining $s_k-s_a-1$ matches otherwise (if $r_a=s_k-s_a$). Then, the final scores of a and k can be the pairs (i) $(s_k, s_k)$ in $\pi$ and $(s_k-1, s_k)$ in $\pi '$, (ii) $(s_k+1, s_k)$ in $\pi$ and $(s_k, s_k)$ in $\pi '$, or (iii) $(s_k, s_k)$ in $\pi$ and $(s_k, s_k+1)$ in $\pi '$ (this last situation occurs in case $k=b$). Consequently, ${Dom}_{a}(\preceq _\pi ',\preceq _\pi )$ holds in all cases and hence $x$ is a-important.

Next, assume that $\lambda _a\ge 0$, which means that $s_k\le s_a$ and $r_k\ge s_a-s_k$, for some player k. As before, consider two homologous paths $\pi$ and $\pi '$ from $x_a$ and $x_b$, respectively. Now, if $s_k=s_a$, we let a lose all its remaining matches and k win only against a, if that match is yet to be played. Conversely, if $s_k<s_a$, then a loses every time and k wins $s_a-s_k$ matches, if $k\ne b$, or $s_a-s_k-1$ matches otherwise. Similarly to the previous case, in both cases ${Dom}_{a}(\preceq _\pi ',\preceq _\pi )$ holds.

For the “only if” direction, we will show the contrapositive. Assume that $\mu _a<0$; this means that both $\theta _a$ and $\lambda _a$ are negative. Let $\pi$ and $\pi '$ be two homologous paths starting from $x_a$ and $x_b$, respectively. In $\pi$, the final score of a ranges from $s_a+1$ to $s_a+r_a$. In $\pi '$ the only difference is that a has one point less, because it lost the match in $x$, so its final score ranges from $s_a$ to $s_a+r_a-1$. We consider three different cases.

First, let ${Abv}_a\ne \emptyset$ and ${Blw}_a\ne \emptyset$. Since $\theta _a< 0$ and $\lambda _a< 0$, then each $k\in {Abv}_a$ has in both $\pi$ and $\pi '$ a final score greater than $s_a+r_a$ and analogously the score of each $k\in {Blw}_a$ will be less than $s_a$. This means that for all other players h: (i) neither $a \sim _\pi h$ nor $a \sim _{\pi '} h$ holds, and (ii) $a\prec _\pi h$ (resp. $h \prec _{\pi } a$) iff $a\prec _{\pi '} h$ (resp. $h \prec _{\pi '} a$). Then, it is straightforward to see that ${WDom}_{a}(\preceq _\pi ,\preceq _{\pi '})$ and ${WDom}_{a}(\preceq _{\pi '},\preceq _{\pi })$. Therefore, $\preceq _\pi$ and $\preceq _{\pi '}$ are a-equivalent. Being $\pi$ and $\pi '$ two arbitrary homologous paths, $x$ is not a-important.

Then, assume that ${Abv}_a\ne \emptyset$ and ${Blw}_a=\emptyset$. ${Blw}_a=\emptyset$ means that in $x$ a ranks last with no ties, so $x$ is a-important only if winning gives to a the chance to reach some opponent. However, as before, the maximal score that a can attain is $s_a+r_a$ and, since $\theta _a< 0$, all the other players have a greater score. So, it is immediate to see that $\preceq _\pi$ and $\preceq _{\pi '}$ weakly dominate each other. Consequently, $x$ is not a-important. Finally, assume ${Abv}_a=\emptyset$ and ${Blw}_a\ne \emptyset$. Contrary to the previous case, a ranks first with no ties, and hence $x$ is a-important only if winning could prevent some other player from reaching the score of a. However, $\lambda _a< 0$ implies that no player can achieve that objective. So, for all other players h, it holds that $h \prec _{\pi } a$ and $h \prec _{\pi '} a$. Therefore, as before $\preceq _\pi$ and $\preceq _{\pi '}$ weakly dominate each other and hence $x$ is not a-important. $\square$

So far, for the sake of simplicity, we have omitted the node $x$ from the notation. In the next sections, when we need to compare different nodes, we will use a functional notation to make it explicit. For example, $r_a(x)$ and $s_a(x)$ denote the number of remaining matches and the current score of player a at node $x$, respectively.

Finally, we show some local properties that, if satisfied by a node $x$, ensure the presence of a non-strongly-relevant node in the sub-tree rooted in $x$. First we prove that, along a path, $\mu _a$ cannot switch from a negative to a positive value.

Lemma 3

Let ${\pi } =(x_1,\ldots , x_m)$ be a path in a round-robin tournament. For each player $a \in {A}$, if $\mu _a(x_1)< 0$, then $\mu _a(x_m)< 0$.

The next theorem shows three conditions predicting the presence of a non-strongly-relevant node in a sub-tree of a tournament, depending only on local properties of the root of the sub-tree. The first condition strengthens Theorem 5 on the basis of Lemma 3. The other two conditions are variants that, roughly speaking, directly check whether the last match of a player is relevant assuming that it wins (resp. it loses) all the other remaining matches.

Theorem 6

Let $\mathcal {T}$ be a round-robin point-based tournament, a be a player, and $x$ be a node in $\mathcal {T}$. Moreover, assume that $r_a(x)>0$ and at least one of the following conditions holds:

• 1. $\mu _a(x)< 0$;

• 2. $\lambda _a(x)< 0$ and $r_a(x)-\theta _a(x)\ge 2$;

• 3. $r_a(x)+s_a(x)> 1+ r_j(x)+s_j(x)$, for all $j\in {A} \setminus \{a\}$.

Then, $\mathcal {T}$ is not strongly relevant.

Proof

Assume that the first condition holds. Since $r_a(x)>0$, player a has to challenge at least one other player, say b. Then, there exists a path from $x$ to a node $x'$ which is labelled with the match $\{a,b\}$. By Lemma 3, $\mu _a(x') <0$ and hence, by Theorems 4 and 5 , $\mathcal {T}$ is not strongly relevant because $x'$ is not a-relevant.

Assume that the second condition holds. Consider a path ${\pi }$ from $x$ to a node $x'$ where a has lost all the $r_a(x)-1$ remaining matches except the last one which is the label of $x'$. This means that $r_a(x')=1$ and $s_a(x)=s_a(x')$. From $r_a(x)-\theta _a(x)\ge 2$ we have that each player j in ${Abv}_a(x)$ has a score $s_j(x)$ which is at least $s_a(x)+2$. Then, since $s_j(x)\le s_j(x')$, we have that $r_a(x')+s_a(x')-s_j(x')<0$. Moreover, from $\lambda _a(x)< 0$ we know that all the players in ${Blw}_a(x)$, if any, have no chance to reach the score of a at $x'$. Consequently, ${Abv}_a(x)={Abv}_a(x')$ and ${Blw}_a(x)={Blw}_a(x')$. Then, as before, we have that $\theta _a(x')< 0$ and $\lambda _a(x')< 0$ and hence $\mathcal {T}$ is not strongly relevant because $x'$ is not a-relevant.

Finally, assume that condition 3 above holds and consider a path from $x$ to a node $x'$ where, symmetrically to the previous case, a has won $r_a(x)-1$ matches except the last one which is the label of $x'$. Then, for all $j\in {A} \setminus \{a\}$, we have that

$$\begin{aligned} s_a(x')=r_a(x)+s_a(x)-1\ge 1+r_j(x)+s_j(x)>r_j(x')+s_j(x')\, . \end{aligned}$$

It follows that $\lambda _a(x')<0$ and $\theta _a(x')$ is $-1$. Similarly to the previous cases, we conclude that $\mathcal {T}$ is not strongly relevant. $\square$

Thereafter, we say that x is doomed whenever it satisfies one of the three conditions in Theorem 6 for some player a. Note that if a node is not doomed, then by Theorem 5 that node is strongly relevant.

4.3 The earliest non-strongly-relevant match

Intuitively, the first matches of tournament are more likely to be relevant due to the large number of different possible futures. This rises the following natural question: when is the earliest possible round at which a non-strongly-relevant match can occur? The following theorem provides a lower bound to this question.

Theorem 7

Let $\mathcal {T}$ be a point-based round-robin tournament of $n\ge 5$ players and ${\pi } =(x_1,\ldots , x_m)$ be a path such that $x_m$ is not strongly relevant. Then, $m> 2(n-1)$.

Proof

Let $(s_1,\ldots ,s_n)$ be the score vector at $x_m$. For each player j, let $r_j$ the number of remaining matches and $l_j$ the number of lost matches. By definition, it holds that $s_j+r_j+l_j=n-1$. Moreover, since $m-1$ matches have been completed at node $x_m$, we have that

$$\begin{aligned} m-1=\sum _{h=1}^{n} s_h=\sum _{h=1}^{n} l_h\, . \end{aligned}$$

(2)

Since by assumption $x_m$ is not relevant, by Theorems 4 and 5 there exists a player i involved in the match of $x_m$ such that $\mu _i<0$. This implies that (i) $r_i>0$, (ii) $s_i+r_i< s_k$, for all $k>i$, and (iii) $s_i>s_h+r_h$, for all $h<i$.

By (2), we have that

$$\begin{aligned} m-1&\ge \sum _{h=1}^{i-1} l_h \end{aligned}$$

(3)

$$\begin{aligned} m-1&\ge s_i+\sum _{k=i+1}^{n} s_k\, . \end{aligned}$$

(4)

Notice that condition (iii) implies that $l_h = (n-1) - (s_h + r_h) \ge (n-1) - (s_i -1 )$,

for all $h<i$. Consequently, from (3) we have that:

$$\begin{aligned} m-1&\ge (i-1) \left[ (n-1) - (s_i -1 )\right] \, . \end{aligned}$$

(5)

Moreover, assuming $i>1$, (5) implies that

$$\begin{aligned} s_i&\ge n-\frac{m-1}{i-1}\, . \end{aligned}$$

(6)

Similarly, conditions (i) and (ii) imply that $s_k\ge s_i+2$, for all $k>i$. Consequently, (4) implies:

$$\begin{aligned} m -1 \ge s_i+(n-i)(s_i+2) =(n-i+1)s_i+2(n-i)\, . \end{aligned}$$

(7)

We now prove our thesis by showing that $m-1>2(n-1)-1$, whoever is player $i\in \{1,\ldots , n\}$. We distinguish the following cases:

Case $i=1$. The thesis directly derives from (7) and $s_i\ge 0$. In particular, we do not need (6), which does not apply to $i=1$.

Case $i=n$. Since $r_n>0$ by condition (i), we have that $s_n$ is at most $n-2$. Replacing i with n and $s_n$ with $n-2$ in (5) yields $m-1\ge 2(n-1)$ and hence the thesis.

Case $i=2$. By condition (iii) we have that $s_2>s_1+r_1$ which means that $s_2\ge 1$. Then, from (7) we obtain that

$$\begin{aligned} m-1\ge 3n -5\, . \end{aligned}$$

Since $3n -5> 2(n-1)-1$ for all $n\ge 3$, we have the thesis.

Case $i=n-1$. By condition (ii), it holds that $s_{n-1}+r_{n-1}< s_n$. Moreover, since $r_{n-1}>0$ and $s_n$ is at most $n-1$, it follows that $s_{n-1}$ is at most $n-3$, which means that the inequality (5) yields $m-1\ge 3n-6$. Then, the thesis derives from the fact that $3n-6> 2(n-1)-1$ for all $n \ge 4$.

Case $3\le i\le n-2$. First, we have from (6) and (7) that

$$\begin{aligned} m -1 \ge (n-i+1)\left[ n-\frac{m-1}{i-1}\right] +2(n-i)\, . \end{aligned}$$

After some algebra, we obtain

$$\begin{aligned} (m -1) \frac{n}{i-1}&\ge n (n-i+1) +2(n-i) \, , \nonumber \\ m -1&\ge -\left( 1+\frac{2}{n} \right) i^2+ \left( n+4+\frac{2}{n}\right) i - (n+3)\, . \end{aligned}$$

(8)

Let f(i) be the left-hand side of (8), where i is upgraded to real values. Since f(i) is a convex parabolic function, for any three values $x<y<z$, f(y) is greater than the minimum of f(x) and f(z). Therefore, if f(3) and $f(n-2)$ are greater than $2(n-1)-1$, then so is f(i), for all $3\le i\le n-2$. It is straightforward to see that both the conditions $f(3)>2(n-1)-1$ and $f(n-2)>2(n-1)-1$ hold for all $n\ge 5$. Hence, the thesis. $\square$

5 Admissible preferences

The main results in the previous section rely on the assumption that preferences are admissible. This naturally raises the question: how general is such a notion? In this section, we address this issue by presenting a large class of admissible preferences that are based on linear utilities. On the other hand, we also emphasize the limits of such a notion by showing a rather simple preference that is not admissible.

Thereafter, $\mathsf {B}_{a}(\preceq ) =\{b\in {A} \mid a\prec b\}$ is the set of players that have a better placement than a in the ranking $\preceq$, $\mathsf {S}_{a}(\preceq ) =\{b\in {A} \mid a\sim b\}$ is the set of players having the same placement as a (including a itself), and $\mathsf {W}_{a}(\preceq ) =\{b\in {A} \mid b\prec a\}$ is the set of players with a worse placement than a. Moreover, let $U^B$, $U^S$, and $U^W$ be three functions from ${A}$ to real values subject to the constraint that $U^B(b)<U^S(b)<U^W(b)$, for each player b. Intuitively, $U^B(b)$ is the utility associated to b having a better placement than a. In normal circumstances $U^B(b)$ is likely to be negative. Similarly, $U^S(b)$ is the utility of having b ranked the same as a and finally $U^W(b)$ applies when b is ranked worse than a; normally it is a positive value. A linear utility $U_a$ over rankings is then defined as follows

$$\begin{aligned} U_a(\preceq )=\sum _{b\in \mathsf {B}_{a}(\preceq )} U^B(b)+ \sum _{b\in \mathsf {S}_{a}(\preceq )} U^S(b)+ \sum _{b\in \mathsf {W}_{a}(\preceq )} U^W(b)\, . \end{aligned}$$

We say that the linear utility $U_a$ induces the preference relation $\mathcal {P}^\mathrm {lin} _a$ defined by $\mathcal {P}^\mathrm {lin} _{a}(\preceq _1,\preceq _2)$ iff $U_a(\preceq _1)\le U_a(\preceq _2)$.

Example 6

Consider a round-robin point-based tournament between players a, b, and c where a has more rivalry with c than with b. More precisely, the preference of player a is represented by a linear utility $U_a$ with $U^W(b)=1$, $U^W(c)=2$, $U^B(b)=-1$, $U^B(c)=-2$, and S equals to the constant function 0.

Then, $U_a$ induces five equivalence classes shown in the following table:

$$\begin{aligned} \begin{array}{|c|c|c|c|c|} \hline \mathcal {C} ^a_1 &{} \mathcal {C} ^a_2 &{} \mathcal {C} ^a_3 &{} \mathcal {C} ^a_4 &{} \mathcal {C} ^a_5\\ \hline a\prec b \prec c &{} b\prec a\prec c &{} a\sim b\sim c &{} c\prec a\prec b &{} b\prec c\prec a\\ a\prec c\prec b &{} &{} &{} &{} c\prec b\prec a\\ \hline \end{array} \end{aligned}$$

where the utility values of $\mathcal {C} ^a_1$ – $\mathcal {C} ^a_5$ are respectively $-3$, $-1$, 0, $+1$, and 3.

Theorem 8

All preference relations induced by linear utilities are admissible.

Proof

Let $\mathcal {P}^\mathrm {lin} _a$ be a preference relation induced by a linear utility $U_a$.

We show that $\mathcal {P}^\mathrm {lin} _a$ refines ${WDom} _a$ and its asymmetric part refines ${Dom} _a$. Assume that $\preceq _1$ and $\preceq _2$ are two rankings such that ${WDom}_{a}(\preceq _1,\preceq _2)$ holds. By definition, the following inclusions hold:

$$\begin{aligned} \mathsf {S}_{a}(\preceq _1)&\subseteq \mathsf {S}_{a}(\preceq _2) \cup \mathsf {W}_{a}(\preceq _2) \end{aligned}$$

(9)

$$\begin{aligned} \mathsf {W}_{a}(\preceq _1)&\subseteq \mathsf {W}_{a}(\preceq _2). \end{aligned}$$

(10)

Let b be a player, we show that its contribution to the utility $U_a(\preceq _2)$ is at least as large as its contribution to $U_a(\preceq _1)$. If $b \in \mathsf {W}_{a}(\preceq _1)$, by (10) we have that $b \in \mathsf {W}_{a}(\preceq _2)$ and hence its contribution $U^S(b)$ is exactly the same in the two utilities. If instead $b \in \mathsf {S}_{a}(\preceq _1)$, by (9) we have that b is either in $\mathsf {S}_{a}(\preceq _2)$ or in $\mathsf {W}_{a}(\preceq _2)$, and since $U^W(b) > U^S(b)$ its contribution to $U_a(\preceq _2)$ is greater than or equal to the one to $U_a(\preceq _1)$. Finally, if $b \in \mathsf {B}_{a}(\preceq _1)$, considering that $U^B(b)$ is the least possible utility for player b, its contribution can only increase when moving to $U_a(\preceq _2)$. Since this argument holds for all players b, we obtain that $U_a(\preceq _1) \le U_a(\preceq _2)$ and hence $\mathcal {P}^\mathrm {lin} _{a}(\preceq _1,\preceq _2)$.

Next, assume that ${Dom}_{a}(\preceq _1,\preceq _2)$ holds. By definition, ${WDom}_{a}(\preceq _1,\preceq _2)$ also holds, and by the above argument $U_a(\preceq _1) \le U_a(\preceq _2)$. It remains to prove that the above inequality is strict. We follow the two cases in the definition of ${Dom}$. First, assume there is a player b such that $a\prec _1 b$ and $b\preceq _2 a$. In other words, $b \in \mathsf {B}_{a}(\preceq _1)$ and $b \in \mathsf {S}_{a}(\preceq _2) \cup \mathsf {W}_{a}(\preceq _2)$. So, its contribution to $U_a(\preceq _2)$ is strictly greater than its contribution to $U_a(\preceq _1)$, which proves our thesis. The argument for the other case (namely, $a\preceq _1 b$ and $b\prec _2 a$) is analogous. $\square$

Example 7

A notable preference relation that is induced by a linear utility is the lexicographic preference: player a prefers $\preceq _2$ to $\preceq _1$ if there are fewer players above a in the former ranking or, those being equal, the number of ties is smaller. More formally, a prefers $\preceq _2$ to $\preceq _1$, written $\mathcal {P}^\mathrm {lex} _{a}(\preceq _1,\preceq _2)$, iff:

• (i) $\vert \mathsf {B}_{a}(\preceq _2) \vert < \vert \mathsf {B}_{a}(\preceq _1) \vert$, or

• (ii) $\vert \mathsf {B}_{a}(\preceq _2) \vert = \vert \mathsf {B}_{a}(\preceq _1) \vert$ and $\vert \mathsf {S}_{a}(\preceq _2) \vert \le \vert \mathsf {S}_{a}(\preceq _1) \vert$.

Let n be the number of players, it is straightforward to see that $\mathcal {P}^\mathrm {lex} _a$ is induced by the utility function $U^{\mathrm {lex}}_a$ where $U^B$, $U^S$, and $U^W$ are constant functions yielding respectively $-n$, $-1$, and 0.

Linear utilities provide a large class of admissible preferences, however as we show in the next theorem they do not fully capture the notion of admissibility.

Theorem 9

There exists an admissible preference that is not induced by any linear utility.

Proof

Consider a round-robin point-based tournament $\mathcal {T}$ among five players $\{a,b,c,d,e\}$. Since (0, 1, 2, 3, 4) is a possible score vector, by symmetry each linear order among the players is the label of some leaf. Hence, the following four rankings can be found in some of the leaves from $\mathcal {T}$:

$$\begin{aligned}&a\prec _1 b\prec _1 c\prec _1 d \prec _1 e\\&a\prec _2 d\prec _2 c\prec _2 b \prec _2 e\\&e\prec _3 d\prec _3 c\prec _3 b \prec _3 a\\&e\prec _4 b\prec _4 c\prec _4 d \prec _4 a\, . \end{aligned}$$

We prove that there exists an admissible preference $\mathcal {P}_{c}$ such that $\mathcal {P}_{c}(\preceq _1,\preceq _2)$ and $\mathcal {P}_{c}(\preceq _3,\preceq _4)$. First, consider any linear utility that puts in the same class $\mathcal {C} _{2,c,2}$ all and only the rankings where two players are lower than c and two players are above c. For example, by choosing $U^W(\cdot ) = 10$, $U^S(\cdot ) = 0$, and $U^B(\cdot ) = -1$, we obtain $\mathcal {C} _{2,c,2}$ as the class whose utility value is 18. By Theorem 8, the resulting preference $\mathcal {P}_{}$ is admissible.

Now, modify $\mathcal {P}_{}$ so that it is still a weak order, but it partitions class $\mathcal {C} _{2,c,2}$ into two adjacent levels in the weak order (two equivalence classes): in the lower class $\mathcal {C} _ {low}$, the two players below c are either a and b or e and d; the upper class $\mathcal {C} _ {upp}$ contains the remaining rankings. In particular, $\preceq _1$ and $\preceq _3$ belong to the lower class and $\preceq _2$ and $\preceq _4$ belong to the upper class. Let $\mathcal {P}_{c}$ be the modified preference, it remains to prove that it is still admissible. This follows from the fact that, for each pair of rankings $\preceq$, $\preceq '$ in the lower and upper class, respectively, there is no dominance relation between them; that is, neither ${WDom}_{c}(\preceq ,\preceq ')$ nor ${WDom}_{c}(\preceq ',\preceq )$ holds.

Next, assume by contradiction that $\mathcal {P}_{c}$ is induced by a linear utility. Then, from $\mathcal {P}_{c}(\preceq _1,\preceq _2)$ and $\mathcal {P}_{c}(\preceq _3,\preceq _4)$ it follows that there exist three real-valued functions $U^W$, $U^S$, and $U^B$ such that

$$\begin{aligned}&U^W(a)+U^W(b)+U^S(c)+U^B(d)+U^B(e)< \\&U^W(a)+U^W(d)+U^S(c)+U^B(b)+U^B(e) U^W(e)+U^W(d)+U^S(c)+U^B(b)+U^B(a) < \\&U^W(e)+U^W(b)+U^S(c)+U^B(d)+U^B(a)\,. \end{aligned}$$

From the first inequality we have that $U^W(b)+U^B(d)<U^W(d)+U^B(b)$, whereas the second inequality implies that $U^W(b)+U^B(d)>U^W(d)+U^B(b)$, a contradiction. $\square$

Both Theorems 8 and 9 advocate the generality of our notion of admissibility. However, not all the preferences that can be reasonably adopted by a player are admissible. Consider, for instance, the preference $\mathcal {P}^\mathrm {pos}$ which relaxes $\mathcal {P}^\mathrm {lex} _a$ by ignoring ties. Formally, player a prefers $\preceq _2$ to $\preceq _1$, denoted by $\mathcal {P}^\mathrm {pos} _{a}(\preceq _1,\preceq _2)$, iff $\vert \mathsf {B}_{a}(\preceq _2) \vert \le \vert \mathsf {B}_{a}(\preceq _1) \vert$.

Theorem 10

The preference $\mathcal {P}^\mathrm {pos}$ is not admissible.

Proof

Consider again a round-robin point-based tournament of five players (a, b, c, d, and e) and the following two score vectors:

$$\begin{aligned} \begin{array}{ccccc} a &{} b &{} c &{} d &{} e \\ \hline 0 &{} 2 &{} 2 &{} 3 &{} 3 \\ 0 &{} 1 &{} 2 &{} 3 &{} 4 \\ \end{array} \end{aligned}$$

The first score vector induces the ranking $a\prec _1 b\sim _1 c\prec _1 d\sim _1 e$ whereas the second one corresponds to $a\prec _2 b\prec _2 c\prec _2 d\prec _2 e$. Notice that $\mathsf {B}_{e}(\preceq _1) = \mathsf {B}_{e}(\preceq _2) =\emptyset$ and hence, according to $\mathcal {P}^\mathrm {pos} _e$, $\preceq _1$ and $\preceq _2$ are equivalent. However, by definition ${Dom}_{e}(\preceq _1,\preceq _2)$ holds. Consequently, all admissible preferences for player e consider $\preceq _2$ strictly better than $\preceq _1$. $\square$

6 Existence of relevant tournaments

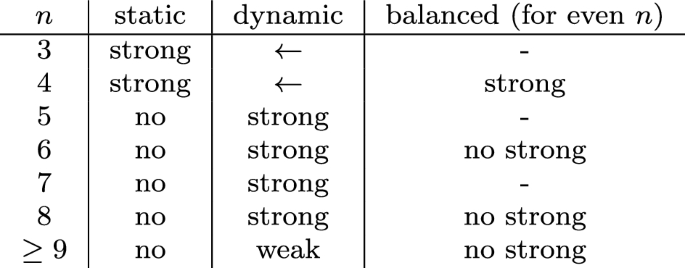
In this section we investigate the possibility to design point-based round-robin tournaments which promote relevance. First, we prove that, in static tournaments, relevance is unfeasible quite soon ($n\ge 5$). Then, we consider dynamic tournaments and show that it is possible to avoid irrelevant matches. Unfortunately, the proposed method is not balanced. Finally, we prove that balanced strongly relevant tournaments exist only for $n=4$.

Remark

In many team sports, like football or basket, tournaments last for an entire season and matches are disputed in huge stadium across the country. Clearly, for economic and logistic reasons, this kind of tournament requires a fixed calendar to be settled beforehand. Nevertheless, many individual sports (e.g., fencing or e-sports), are typically held in a single venue and last for 1–2 days. In these cases there is no practical obstacle to implementing dynamic point-based round-robin tournaments.

6.1 Static tournaments

First, we show that if $n\le 4$, then there exists a static point-based round-robin tournament that is balanced and strongly relevant.

Theorem 11

If $n\le 4$, then there exists a static point-based round-robin tournament $\mathcal {T}$ that is strongly relevant. Moreover, in case $n=4$, $\mathcal {T}$ is also balanced.

Proof

For $n=3$, it is straightforward to see that all six possible static tournaments are strongly relevant.

Let $n=4$ and consider the static tournament $\mathcal {T}$ given by the sequence of the following matches: $\{a,b\}$, $\{c,d\}$, $\{a,d\}$, $\{b,c\}$, $\{a,c\}$, $\{b,d\}$. Then, it can be proved by inspection that $\mathcal {T}$ is strongly relevant. Notice that $\mathcal {T}$ is also balanced.$\square$

The following theorem states that, in every round-robin tournament for at least 5 players that is static and point-based, there is a match that is irrelevant for both of the involved players.

Theorem 12

For all $n\ge 5$, there is no point-based round-robin tournament that is static and weakly relevant.

Proof

Then, let $n\ge 5$. Since the tournament is static, there is a match, say (i, j), that is played last in all paths. Consider a path, starting from the root, in which i wins all matches, j loses all matches, and the other $n-2$ players win approximately half of their games, leading to a node x, where only the match (i, j) remains to be played. At x, player i has score $n-2$, player j has score 0, and the other players have score approximately equal to $\frac{n-1}{2}$. Precisely, if n is odd then all other players have score $\frac{n-1}{2}$, otherwise some of them have score $\lfloor \frac{n-1}{2}\rfloor$ and some have score $\lceil \frac{n-1}{2}\rceil$. It is easy to prove that this is indeed a valid scenario. ⁶ We prove that neither i nor j can change their ranking in their last game. Since $n \ge 5$, $\lfloor \frac{n-1}{2}\rfloor \ge 2$, so even if player j wins the last match, its ranking will still be the the last of all. Dually, $\lceil \frac{n-1}{2}\rceil \le n-3$, so even if player i loses the last match, its ranking will be the first of all. Notice that the latter argument does not hold for $n\le 4$. $\square$

Example 8

For $n=5$, the scenario described in Theorem 12 leads to the score vector $(s_1,\ldots ,s_5) = (0, 2, 2, 2, 3)$, where the last match is between players 1 and 5. Clearly, those players cannot modify their ranking as a consequence of their last match.

6.2 Weakly relevant dynamic tournaments

We describe a family T(n) of dynamic round-robin point-based tournaments that are weakly relevant, for all numbers n of players. In the following, for a score vector $(s_1,\ldots ,s_n)$, we say that the vector $(\delta _0,\ldots ,\delta _{n-1})$ is the corresponding score difference vector, where $\delta _0=s_1$ and $\delta _i = s_{i+1} - s_i$ for all $i=1,\ldots ,n-1$.

Let T(2) be the trivial round-robin tournament between 2 players, $T(n+1)$ is recursively defined as follows. First, players $1,\ldots ,n$ play T(n) (first phase), resulting in a score vector $(s_1,\ldots ,s_n)$ and score differences $(\delta _0, \ldots , \delta _{n-1})$. We partition the players into two sets:

• $\varDelta _0 = \{ i = 1, \ldots , n-1 \mid \delta _i = 0 \}$;

• $\varDelta _+ = \{ i = 1, \ldots , n-1 \mid \delta _i \ge 1 \} \cup \{ n \}$.

The second phase of the tournament consists in all matches involving player $n+1$. First, we let $n+1$ play against all players in $\varDelta _+$, in any order. Then, we schedule the remaining matches, in any order.

Example 9

Let T(5) be a recursive tournament among the players $\{a,b,c,d,e\}$ where the first phase consists in a tournament T(4) among the first four players. Then, consider as possible outcomes of the first phase the score vectors $u=(0,2,2,2)$ and $v=(1,1,2,2)$, where scores are assigned, from left to right, to a, b, c, and d. By construction, in the first case $\varDelta _0=\{b,c\}$ and $\varDelta _+=\{a,d\}$, whereas in the second case $\varDelta _0=\{a,c\}$ and $\varDelta _+=\{b,d\}$. Consequently, in the first case the match (a, e) will precede the match (b, e) whereas in the second case the opposite holds.

This shows that different outcomes of T(4) dynamically induce different schedules in the second phase. In particular, a possible schedule for the second case (score vector v) requires e to challenge the other players in the following order: b, d, c, and a. If we used such a schedule in the first case (where T(4) ends with the score vector u) and e beat b, d, and c, then the scores before the last match (e, a) would be:

$$\begin{aligned} \begin{array}{ccccc} a &{} b &{} c &{} d &{} e \\ \hline 0 &{} 2 &{} 2 &{} 2 &{} 3\\ \end{array} \end{aligned}$$

and hence the last match would be irrelevant for both a and e.

The intuition behind the recursive tournament $T(n+1)$ is the following. Players in $\varDelta _0$ are “safe” in the sense that, when they will play against $n+1$, the match will be relevant for them. The other players are “unsafe” in the same sense. Hence, we first schedule the unsafe matches, because they are certainly relevant for $n+1$ (as a consequence of the next Lemma 4). Then, we schedule the remaining matches, that will be relevant for the other player.

Lemma 4

Assume that the sub-tournament T(n) ends with a score vector $(u_1,\ldots ,u_n)$ and a maximum score difference $\delta ^\mathrm {max}$. For all $i = 0,\ldots ,n-1$ such that $i \le u_n$ and $(n-i) > \delta ^\mathrm {max}$, the $(i+1)$-th match of the second phase is relevant for player $n+1$.

We can now prove the main result of this section.

Theorem 13

The recursive tournament scheme $T(n+1)$ is weakly relevant, for all $n\ge 1$.

Proof

Assume by induction that the sub-tournament T(n) is weakly relevant.

First, we prove that the nodes in T(n) are still weakly relevant when considered as nodes in the first phase of $T(n+1)$. Consider a node x in T(n) labeled with (a, b) and assume that x is t-relevant in T(n), for $t \in \{a, b\}$. By Theorem 4, x is t-important in T(n). Hence, there is a path $\pi _\mathsf {w}$ from $x_\mathsf {w}$ in T(n) whose ranking is not t-equivalent to the ranking of the homologous path $\pi _\mathsf {l}$ starting from $x_\mathsf {l}$. Now, both $\pi _\mathsf {w}$ and $\pi _\mathsf {l}$ can be prolonged assuming that agent $n+1$ wins all matches in the second phase of $T(n+1)$. Notice that the two prolonged paths are homologous. Moreover, at the end of the two prolonged paths, all agents except $n+1$ have the same points that they had at the end of $\pi _\mathsf {w}$ and $\pi _\mathsf {l}$, respectively. Therefore, x is t-important and weakly relevant in $T(n+1)$.

Next, we prove that the matches in the second phase are also weakly relevant. Assume that the sub-tournament T(n) ends with score vector $(s_1,\ldots ,s_n)$ and score differences $(\delta _0, \ldots , \delta _{n-1})$. Partition the agents into $\varDelta _0$ and $\varDelta _+$, as explained earlier. The second phase first performs all matches between agent $n+1$ and each agent in $\varDelta _+$.

Notice that the maximum i satisfying Lemma 4 is ${\hat{\imath }} = \min \{ s_n, n -\delta ^\mathrm {max}-1 \}$. That lemma ensures that the first ${\hat{\imath }}+1$ matches in the second phase are relevant for agent $n+1$. Let $r = {\hat{\imath }} + 1 = \min \{ s_n +1 , n -\delta ^\mathrm {max}\}$, we prove that r is at least equal to the number $|\varDelta _+|$ of unsafe agents.

First case: $r = s_n +1$. Write $s_n$ as $s_1 + \sum _{i=1}^{n-1} \delta _i$. Notice that each agent j in $\varDelta _+$ has $\delta _j \ge 1$, so

$$\begin{aligned} |\varDelta _+| \le \sum _{j\in \varDelta _+\setminus \{n\}} \delta _j + 1 \le \sum _{i=1}^{n-1} \delta _i +1 \le s_n + 1 = r. \end{aligned}$$

Second case: $r = n - \delta ^\mathrm {max}$. By Lemma 2 applied to $\delta ^\mathrm {max}$, we have that $|\varDelta _0| \ge \delta ^\mathrm {max}$. Hence, $|\varDelta _+| = n - |\varDelta _0| \le n - \delta ^\mathrm {max}= r$ and we are done. It follows that all matches between $n+1$ and one of the agents in $\varDelta _+$ are relevant for $n+1$.

Since $r\ge |\varDelta _+|$, all matches of agent $n+1$ with an agent of $\varDelta _+$ will be relevant for $n+1$. It remains to evaluate the matches between agent $n+1$ and the agents in $\varDelta _0$. Let $x$ be a node corresponding to such a match, involving agents $n+1$ and $a \in \varDelta _0$, and let $u_j$ be the score of a at the end of T(n). Since $a \in \varDelta _0$, there exists at least one other agent b having at the end of T(n) the same score $u_j$. Note that in $x$ $s_b(x)$ is either $u_j$ or $u_j+1$. Since $r_a(x)=1$, we have that $\theta _a(x)\ge 1+u_j-u_j-1\ge 0$ and hence $x$ is relevant for a. In conclusion, the whole tournament is weakly relevant. $\square$

It is an open problem whether there exist strongly relevant round-robin point-based tournaments for arbitrarily large n.

6.3 Balanced tournaments

The tournament described in Sect. 6.2 is poorly balanced, in the sense that a player may be put on hold for a long time, and then be asked to play all of its matches in a row. Clearly, this may be undesirable since that player would be physically and cognitively stressed in a short time span.⁷ Conversely, we would like all players to play equally often, or at least approximately so.

Recall from Sect. 2 that a round-robin balanced tournament with n players is organized into $n-1$ rounds, during which each player is involved in a single match. This structure is reminiscent of team tournaments that follow a regular, often weekly, schedule, with each team challenging another team every week. Unfortunately, the following result states that being balanced in this sense is incompatible with being strongly relevant.

Theorem 14

For all even $n\ge 6$, there is no round-robin point-based balanced tournament that is strongly relevant.

Proof

Let u be the score vector $(0, \frac{n}{2}, \frac{n}{2},\ldots ,\frac{n}{2})$. It is straightforward to prove that this is a valid score vector according to Theorem 2. Consider an arbitrary round-robin point-based balanced tournament $\mathcal {T}$. By Lemma 1, there is a full path $\pi$ in $\mathcal {T}$ such that u is its score vector. Let i be the player having score 0 at the end of $\pi$. Consider the last event involving player i in $\pi$, and let x be the corresponding node. We know that i loses the match at x, because it will end up with score 0. We prove that the score vector at x is of the type $(0, \frac{n}{2}-1, \ldots )$. First, player i has score 0 at x because scores are non-decreasing in time. Then, by definition of balanced tournament, x is one of the last $\frac{n}{2}$ nodes in $\pi$. Consequently, between x and the end of $\pi$ each player plays at most one match. So, the score of each player at x is either equal to its final score, or to its final score minus one. In particular, the opponent of i at x is one of the players whose score increases by one. This implies that the lowest non-zero score at x is $\frac{n}{2} -1$.

To prove that x is not i-relevant, it is sufficient to observe that, no matter whether i wins or loses at x, in all leaves i ends up with score at most 1, corresponding to minimum rank. $\square$

Remark

In some real-world situations, each round in a tournament consists of multiple matches that are disputed in parallel. Typically, for n even, we have $n-1$ rounds of $\frac{n}{2}$ simultaneous matches. Notice that this kind of tournaments are inherently balanced and, since score vectors do not depend on how tournaments are scheduled, each parallel tournament can possibly end with the score vector $(0, \frac{n}{2}, \frac{n}{2},\ldots ,\frac{n}{2})$. Then, the proof of Theorem 14 can be repeated without any substantial change. In particular, in the last round there will be a player with score 0 that challenges a player with score greater than or equal to $\frac{n}{2} -1$. Consequently, no point-based round-robin parallel tournament with $n\ge 6$ is strongly relevant.

6.4 Strongly relevant dynamic tournaments

Section 6.2 provides a general schema for a weakly relevant tournament with any number of participants. On the other hand, we do not know whether strongly relevant tournaments always exist. Thus, in this section we focus on small numbers of participants, at most eight, and search for strongly relevant tournaments algorithmically.

Since the number of different round-robin tournaments for n players is finite, we could exhaustively generate all of them, until a strongly relevant one is found, if any. However, the number of different dynamic tournaments for n players is

$$\begin{aligned} \left( {\begin{array}{c}n\\ 2\end{array}}\right) \cdot \left( \left( {\begin{array}{c}n\\ 2\end{array}}\right) -1 \right) ^2 \cdot \left( \left( {\begin{array}{c}n\\ 2\end{array}}\right) -2 \right) ^4 \cdot \; \ldots \;\cdot 1= \prod _{i=0}^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) -1}\left( \left( {\begin{array}{c}n\\ 2\end{array}}\right) -i \right) ^{2^i}\ge 2^{\left( 2^{\left( \left( {\begin{array}{c}n\\ 2\end{array}}\right) -1\right) }-1\right) } \end{aligned}$$

and hence, roughly speaking, it is doubly exponential in n squared. For example, for 7 players we have more than $10^{10^5}$ tournaments. Even checking 1 billion tournaments per second, it would take more than the age of the universe to check them all. Moreover, even with the help of Theorem 5, checking whether a single tournament $\mathcal {T}$ is strongly relevant requires to compute the $\mu _a$ values at each internal node and hence it is exponential in the depth of $\mathcal {T}$. Clearly, such a naive approach is infeasible even for small values of n.

We generate tournaments incrementally by choosing at each node one of the remaining matches and testing whether the resulting children are strongly relevant or not, a process that we call expanding a tournament. When a non-strongly-relevant node is found, we do not discard all nodes built so far; instead, we backtrack to its ancestors until a different match can be chosen. Clearly, the search benefits from any criterion capable of predicting in advance the presence of non-strongly-relevant nodes. Indeed, we use the three conditions in Theorem 6 to backtrack as soon as possible and hence reduce the number of generated nodes.

For the sake of readability, we first provide in Algorithm 1 an abstract description of our searching procedure. $\mathtt {StronglyRel}$ is a recursive procedure that takes as input a node x and returns $\mathsf {true}$ if a strongly relevant tournament rooted at x is found, and $\mathsf {false}$ otherwise. At the implementation level, a node x is a compound structure that records: (i) the current score vector, (ii) the $\theta$ and $\lambda$ values and the number of remaining matches of each player, (iii) the set of unplayed matches, and (iv) the level of x in the tournament.

If x is a final node, that is the number of remaining matches is 0 for all players, then $\mathtt {StronglyRel}$ returns $\mathsf {true}$ (line 2). Otherwise, $\mathtt {StronglyRel}$ scans the set of unplayed matches $x.{unplayed}$ for a next match (lines 3–12). In lines 4–6, an unplayed match $\{a,b\}$ is extracted and the algorithm generates the representations of the two children of x, corresponding to a (resp. b) having won the current match. Then, line 7 checks the assumptions of Theorem 6. If one of $x_a$ and $x_b$ is doomed (that is, it satisfies one of the three conditions in Theorem 6) we know that the match $\{a,b\}$ leads to a non-strongly-relevant node. Then, $\mathtt {StronglyRel}$ moves on to another unplayed match without expanding $x_a$ or $x_b$ further (aka local backtrack). If neither $x_a$ nor $x_b$ is doomed, Theorem 5 ensures that both of those nodes are strongly relevant and hence need to be expanded by recursively invoking $\mathtt {StronglyRel}$ on them. If both calls return $\mathsf {true}$, the algorithm reports success to the caller. If none of the unplayed matches succeeds, the algorithm reports failure (aka non-local backtrack).

6.4.1 Optimizations

We then exploit several techniques to further speed up the search, leading to a positive answer within a reasonable amount of time for all $n \le 8$ (see Fig. 4).

Symmetry. Since at the beginning all players have zero points and $n-1$ matches to carry out against all the other players, by symmetry the choice of the first match and of its outcome are inconsequential. Hence, $\mathtt {StronglyRel}$ is called on an initial node where the first match and its outcome are set with arbitrary values. Note that fixing the players involved in the first match reduces the number of tournaments to be considered by $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$. Moreover, fixing the outcome of the first match halves the number of nodes to be generated, because only half of each tournament needs to be explored.

Parallelism. First of all, the tree structure of a tournament ensures that if two nodes $x$ and $x'$ are not on the same path, then $\mathtt {StronglyRel} (x)$ and $\mathtt {StronglyRel} (x')$ are independent computations which can be executed in parallel. Therefore, the recursive calls in $\mathtt {StronglyRel}$ are executed by separate threads, up to a given level of the tournament. Tuning this threshold allows us to choose a desired degree of parallelism. In our experiments, due to the architectural specifications, we set the threshold to 3 and hence the maximum number of parallel threads to 8. Multi-threading allows $\mathtt {StronglyRel}$ to run three times faster.

First-match heuristic. To speed up generation of new nodes and save memory, we ordered matches lexicographically and represent the set of available matches, $x.{unplayed}$, by a bit vector. We also adopted a specific heuristic while extracting a match from $x.{unplayed}$. Intuitively, if a match is a good choice for a node x then it would be probably a good choice for neighbouring nodes at the same level. More specifically, when $\mathtt {StronglyRel}$ is called on a node at level l and one of the unplayed matches m succeeds (that is, it passes both checks in lines 7 and 8), then before returning $\mathsf {true}$ $\mathtt {StronglyRel}$ associates m to l in a per-thread mapping ${lvl\_heur\_choice}$. Consequently, ${lvl\_heur\_choice}$ maintains the last successful match (if any) for each level. Then, the next call to $\mathtt {StronglyRel}$ on a node at level l will check whether m is unplayed at that node, and if so it will choose m as the first match to be extracted.

Fail-fast match evaluation. Furthermore, since the conditions in Theorem 6 can be checked player by player, we merged in a single procedure the children generation in lines 5–6 and the admissibility check in line 7. More specifically, the score vector of a child is computed first, then starting the values of $\theta$ and $\lambda$ are computed one player at a time and simultaneously the three conditions in Theorem 6 are checked. As soon as a player satisfies one of these conditions, $\mathtt {StronglyRel}$ stops updating the remaining players and jumps to the next match in $x.{unplayed}$. In this way, the combined generation-and-test phase can be performed in linear time in the number of players.

6.4.2 Experimental results

Fig. 4

Experimental results of $\mathtt {StronglyRel}$: running time, number of generated nodes and ratio between the number of generated nodes and the optimal number of nodes

Fig. 5

Number of local and non-local backtracks in $\mathtt {StronglyRel}$ with 7 players

We run the resulting algorithm $\mathtt {StronglyRel}$ on a PC based on AMD Ryzen 7 2700X CPU (8 cores/16 threads) clocked at 3.7 GHz with 16 GB of RAM.

When the number of players ranges from 5 to 8 the algorithm finds a strongly relevant tournament. The first two rows in Fig. 4 show the execution time and the total number of generated nodes for each choice of player number. Both grow by several orders of magnitude for each extra player. Indeed, with 9 players the algorithm does not terminate within a reasonable amount of time (more than 14 days).

The third row in Fig. 4 reports the ratio between the number of generated nodes and the optimal number of nodes. The latter is equal to $2^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }-1$, corresponding to the case where a strongly relevant tournament is found right away with no backtracking.⁸ For example, for 5 players the optimal number of nodes is 1023; meaning that $\mathtt {StronglyRel}$ generates, approximately, only 100 additional nodes—hence, backtracking is limited to few cases. This ratio is relatively stable for 6 and 7 players, but jumps by an order of magnitude for 8 players.

Figure 5 shows, level by level, the number of local and non-local backtracks for 7 players (and hence 21 matches). Up to level 12, no backtracking occurs. On level 13 the number of backtracks is 40; fortunately they are all detected locally so they do not notably burden the performances. From level 14, non-local backtracks constantly increase (with the obvious exception of level 21); however they are always fewer than the local ones. The total number of generated nodes is about 2.7 million nodes.

Concerning local backtracks, we have considered a simpler check in line 7, verifying the first condition of Theorem 6 only. Doing so, the number of generated nodes grows to 37 millions. This shows that the second and third conditions in Theorem 6 occur frequently enough to positively impact on performances.

7 Conclusions

In this paper we investigate the problem of designing point-based round-robin tournaments where irrelevant matches never occur. In particular, we introduced two different notions of relevance, depending on whether at least one of the players involved in a match is motivated to win (weak relevance) or both of them (strong relevance). We also consider four different classes of tournaments, which differ on whether the scheduling process is established a-priori (static) or depends on past events (dynamic), and whether the matches involving a certain player are adequately balanced over the entire sequence of matches. Figure 6 gives a quick overview of the positive and negative results. Static tournaments cannot prevent the presence of irrelevant matches even in the case of 5 participants. For balanced dynamic tournaments, strong relevance fails starting with 6 participants, whereas weak relevance can be assured by unbalanced dynamic tournaments no matter how many players are participating. It is still unknown whether the previous result can be extended to balanced dynamic tournaments. Moreover, we algorithmically verified the existence of strongly relevant tournaments for up to 8 players. However, it is an open issue whether such result holds for arbitrarily large numbers of players, although we know that, if strongly relevant tournaments exist, they cannot be balanced (Theorem 14).

Fig. 6

Summary of results concerning relevance for round-robin point-based tournaments. “No” = there is no weakly relevant tournament; “weak” = there is a weakly relevant tournament; “strong” = there is a strongly relevant tournament; “no strong” = there is no strongly relevant tournament (but there might be a weakly relevant one)

Even in the scope of negative results, future refined analyses may be able to quantify the amount (or likelihood) of relevant matches, and suggest ways to maximize them. This could be useful in case of popular team sports where only static tournaments can be implemented in practice.

The present model can be extended in various directions. For instance, it would be interesting to accommodate more than two possible outcomes for each match, as sport matches often have multiple outcomes. The simplest addition would be the “tie” outcome. In that case, negative results based on the irrelevance of the last match, such as Theorem 12, should easily carry over to the extended model.

An orthogonal extension is to tournaments with simultaneous matches. In particular, a common occurrence in practice is the type of tournaments where every week all players play against each other simultaneously. Interestingly, simultaneity induces two opposing consequences on match relevance. On the one hand, it restricts the number and type of schedules available, which can in principle hinder relevance. On the other hand, if two matches x and y are played simultaneously, when proving the relevance of x we can freely choose the outcome of y, and vice versa. We have shown in Sect. 6.3 that this ability does not guarantee strong relevance (for $n\ge 6$). However, it could facilitate weak relevance.

Finally, we did not specifically consider the class of double round-robin tournaments, in which every player challenges each other twice. This class has special practical relevance, as it is employed in a vast majority of team sports. Some results can easily be extended to this class. For instance, it is easy to prove, along the lines of Theorem 12, that for at least three players no static double round-robin tournament is strongly relevant.

Appendix

Lemma 2

Let $\mathcal {T}$ be a point-based round-robin tournament with n players and let u be a round-robin score vector with n players. Then, there exists a full path $\pi$ in $\mathcal {T}$ such that $u = v _\pi$.

Proof

By definition, u is induced by a full path $\pi _u$ from a round-robin tournament $\mathcal {T} _u$. Consider the full path $\pi$ in $\mathcal {T}$ that is homologous to $\pi _u$. Such a path exists because all full paths in all round-robin tournaments with n players contain the same matches, only in a different order. As the events in $\pi$ are a permutation of the events in $\pi _u$, every player wins the same number of matches in $\pi$ as in $\pi _u$. Hence, u is the score vector of $\pi$. $\square$

Lemma 3

For all score vectors s, let $\delta$ be its score difference vector. For all i s.t. $\delta _i > 1$ it holds $|\{ j \mid \delta _j = 0\}| \ge \delta _i$.

Proof

Let s be a score vector, $\delta$ be its score difference vector, and $\varDelta _0 = \{ i \mid \delta _i = 0\}$ be the set of (indices of) plateaus. Assume that i is an index s.t. $\delta _i > 1$. For all $1 \le j \le k \le n$, let $S_{j,k} = \sum _{l=j}^k s_l$. We have $S_{1,n} = S_{1,i} + S_{i+1,n} = \left( {\begin{array}{c}n\\ 2\end{array}}\right)$. We can write $S_{i+1,n}$ as $s_i (n-i) + h$. By Landau’s theorem, $S_{1,i} \ge \left( {\begin{array}{c}i\\ 2\end{array}}\right)$. It follows that

$$\begin{aligned} \begin{aligned} h&= S_{i+1,n} - s_i(n-i) \\&= S_{1,n} - S_{1,i} - s_i(n-1) \\&\le \left( {\begin{array}{c}n\\ 2\end{array}}\right) - \left( {\begin{array}{c}i\\ 2\end{array}}\right) - s_i(n-i). \end{aligned} \end{aligned}$$

(11)

We distinguish two cases.

Fig. 7

Case 1 of Lemma 2: $s_i \ge i-1$. The score vector is (0, 1, 2, 4, 6, 6, 6, 6, 7, 7), with $i=4$. We have $\delta _i = 2$ and four plateaus, all occurring after position i

Fig. 8

Case 2 of Lemma 2: $s_i< i-1$. The score vector is (0, 3, 3, 3, 3, 3, 7, 7, 8, 8), with $i=6$. We have $\delta _i = 4$, four plateaus before position i and two more plateaus after it

First, assume that $s_i \ge i-1$ (see Fig. 7 for an illustration). By (11), $h \le \left( {\begin{array}{c}n\\ 2\end{array}}\right) - \left( {\begin{array}{c}i\\ 2\end{array}}\right) - (i-1)(n-i) = \left( {\begin{array}{c}n-i+1\\ 2\end{array}}\right) = \sum _{j=1}^{n-i} j$. On the other hand,

$$\begin{aligned} h&= \delta _i (n-i) + \delta _{i+1}(n-i-1) + \ldots + \delta _{n-1} \\&\le (n-i) + (n-i-1) + \ldots + 1. \end{aligned}$$

Hence,

$$\begin{aligned} (\delta _i-1) (n-i) + \sum _{j=i+1}^{n-1} (\delta _j -1)(n-j) \le 0. \end{aligned}$$

(12)

Assume by contradiction that $|\varDelta _0| < \delta _i$, and let $\varDelta _0'$ be the intersection between $\varDelta _0$ and the range $\{i+1, \ldots , n-1\}$. Then,

$$\begin{aligned}&(\delta _i-1) (n-i) + \sum _{j=i+1}^{n-1} (\delta _j -1)(n-j) \\ \ge&(\delta _i-1) (n-i) + \sum _{j \in \varDelta _0'} (0 -1)(n-j) \\ \ge&(\delta _i-1) (n-i) - \sum _{j \in \varDelta _0'} (n-i-1) \\ =&(\delta _i-1) (n-i) - |\varDelta _0'| (n-i-1) \\ \ge&(\delta _i-1) (n-i) - (\delta _i-1) (n-i-1) \\ =&\delta _i-1. \end{aligned}$$

From the above and (12), it follows $\delta _i-1 \le 0$, which contradicts the assumption $\delta _i>1$.

As second case, assume that $s_i < i-1$ and let $\alpha = i-1-s_i > 0$ (see Fig. 8 for an illustration). First, we show that there are at least $\alpha$ plateaus before index i. Since $s_i = s_1 + \sum _{j=1}^{i-1} \delta _j$, and both $s_1$ and the $\delta _j$’s are non-negative integers, at most $s_i$ different $\delta _j$’s are positive. The remaining $(i-1)-s_i$ must be zero, hence the number of plateaus before index i is at least $\alpha$, and in particular $|\varDelta _0| \ge \alpha$. If $\delta _i \le \alpha$, we are done. Otherwise, let $\beta = \delta _i - \alpha > 0$. We can write $S_{i+1,n}$ as $(s_i+\alpha ) (n-i) + h$. As in the previous case, $h \le \left( {\begin{array}{c}n-i+1\\ 2\end{array}}\right)$. On the other hand, $h = \beta (n-i) + \delta _{i+1}(n-i-1) + \ldots + \delta _{n-1}$. With an argument similar to the previous case, we obtain that the number of plateaus between $i+1$ and n is at least $\beta$. In conclusion, the total number of plateaus is at least $\alpha + \beta = \delta _i$. $\square$

Lemma 4

Let ${\pi } =(x_1,\ldots , x_m)$ be a path in a round-robin tournament. For each player $a \in {A}$, if $\mu _a(x_1)< 0$, then $\mu _a(x_m)< 0$.

Proof

Note that every time that a player c is involved in a match the number of remaining matches $r_c(\cdot )$ always decreases by one, whereas the current score $s_c(\cdot )$ increases by one only if c wins the match. This implies that along a path the sum of $r_c$ and $s_c$ is monotonically non-increasing. Thus, for all $c \in {A}$, we have that

$$\begin{aligned}&s_c(x_1)\le s_c(x_m) \end{aligned}$$

(13)

$$\begin{aligned}&r_c(x_m)+s_c(x_m)\le r_c(x_1)+s_c(x_1)\, . \end{aligned}$$

(14)

Now, let a be a player such that $\mu _a(x_1)< 0$. By definition, it follows that $\theta _a(x_1)<0$ and $\lambda _a(x_1)<0$. From $\theta _a(x_1)< 0$ we have that for each $j\in {Abv}_a(x_1)$, if any, $r_a(x_1)+s_a(x_1)<s_j(x_1)$. Then, by (13) and (14), we have that

$r_a(x_m)+s_a(x_m)< s_j(x_m)$. In particular, it holds that ${Abv}_a(x_1)\subseteq {Abv}_a(x_m)$. Analogously, $\lambda _a(x_1)< 0$ means that for each $j\in {Blw}_a(x_1)$, if any, $s_a(x_1)>r_j(x_1)+s_j(x_1)$. Again, by (13) and (14), it follows that for each $j\in {Blw}_a(x_1)$, $r_j(x_m)+s_j(x_m)<s_a(x_m)$ and hence ${Blw}_a(x_1)\subseteq {Blw}_a(x_m)$. Finally, since ${Abv}_a(x_1)\cap {Blw}_a(x_1)=\emptyset$ and ${Abv}_a(x_1)\cup {Blw}_a(x_1)$ and ${Abv}_a(x_m)\cup {Blw}_a(x_m)$ are both equal to ${A} \setminus \{a\}$, it follows that ${Blw}_a(x_m)= {Blw}_a(x_1)$ and ${Abv}_a(x_m)= {Abv}_a(x_1)$. Consequently, both $\theta _a(x_m)$ and $\lambda _a(x_m)$ are negative and hence $\mu _a(x_m)<0$. $\square$

Lemma 5

Assume that the sub-tournament T(n) ends with a score vector $(u_1,\ldots ,u_n)$ and a maximum score difference $\delta ^\mathrm {max}$. For all $i = 0,\ldots ,n-1$ such that $i \le u_n$ and $(n-i) > \delta ^\mathrm {max}$, the $(i+1)$-th match of the second phase is relevant for player $n+1$.

Proof

Call x a node in the tournament corresponding to the $(i+1)$-th match of the second phase. At that point, player $n+1$ has played i matches, so its current score $s_{n+1}(x)$ is at most i and hence it is smaller than or equal to $u_n$. Since $i \le u_n$, if we add a virtual player 0 with score $u_0=0$, there is an index $j\in \{0,\ldots ,n-1\}$ such that $u_j \le s_{n+1}(x) \le u_{j+1}$. Notice that $u_{j+1} - u_j$ is at most $\delta ^\mathrm {max}$.

Let a be a player having the score $u_{j+1}$ at the end of phase one, its score at x is either $u_{j+1}$ or $u_{j+1}+1$, because it may have played at most one match during phase two. Hence, $s_{a}(x) - s_{n+1}(x)$ is at most $\delta ^\mathrm {max}+ 1$.

By definition, this implies $a \in P_{n+1} \ne \emptyset$ and the following holds:

$$\begin{aligned} \theta _{n+1}(x)&\ge r_{n+1}(x) + s_{n+1}(x) - s_a(x) \\&= (n-i) - (s_a(x) - s_{n+1}(x)) \\&\ge (\delta ^\mathrm {max}+ 1) - (\delta ^\mathrm {max}+1 ) \\&= 0. \end{aligned}$$

By Theorems 4 and 5 , x is relevant for agent $n+1$. $\square$