Skip to main content
SpringerLink
Log in

First-mover advantage in round-robin tournaments

  • Original Paper
  • Published:
Social Choice and Welfare Aims and scope Submit manuscript

Abstract

We study round-robin tournaments with either three or four symmetric players whose values of winning are common knowledge. With three players there are three rounds, each of which includes one pair-wise game such that each player competes in two rounds only. The player who wins two games wins the tournament. We characterize the subgame perfect equilibrium and show that each player’s expected payoff and probability of winning is maximized when he competes in the first and the last rounds. With four players there are three rounds, each of which includes two sequential pair-wise games where each player plays against a different opponent in every round. We again characterize the subgame perfect equilibrium and show that a player who plays in the first game of each of the first two rounds has a first-mover advantage as reflected by a significantly higher winning probability as well as by a significantly higher expected payoff than his opponents.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. The case when each player plays against all the other players twice is known as a double round-robin tournament.

  2. The main reason that the games are played sequentially is that the profit of the organizers from broadcasting the games will be much higher than when the games are played simultaneously.

  3. See also Glenn (1960) and Searles (1963) for early contributions.

  4. The uniqueness of the equilibrium in our model is derived from the uniqueness of the equilibrium in a two-player one-stage all-pay auction (Baye et al. 1996).

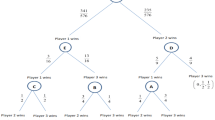
  5. The probability of winning of each of the players who plays in the first round is equal to 0.35 while the probability of the player who start playing in the second round is 0.3. The mathematical analysis is available upon request.

References

  • Baye M, Kovenock D, de Vries C (1996) The all-pay auction with complete information. Econ Theory 8:291–305

    Article  Google Scholar 

  • Becker G (1983) A theory of competition among pressure groups for political influence. Q J Econ 98(3):371–400

    Article  Google Scholar 

  • Dasgupta P (1986) The theory of technological competition. In: Stiglitz JE, Mathewson GF (eds) New developments in the analysis of market structure. MIT Press, Cambridge, pp 519–547

    Chapter  Google Scholar 

  • David H (1959) Tournaments and paired comparisons. Biometrika 46:139–149

    Article  Google Scholar 

  • Glenn W (1960) A comparison of the effectiveness of tournaments. Biometrika 47:253–262

    Article  Google Scholar 

  • Gradstein M, Konrad K (1999) Orchestrating rent seeking contests. Econ J 109:536–545

    Article  Google Scholar 

  • Groh C, Moldovanu B, Sela A, Sunde U (2012) Optimal seedings in elimination tournaments. Econ Theory 49:59–80

    Article  Google Scholar 

  • Hillman A, Riley J (1989) Politically contestable rents and transfers. Econ Polit 1:17–39

    Article  Google Scholar 

  • Konrad K, Leininger W (2007) The generalized Stackelberg equilibrium of the all-pay auction with complete information. Rev Econ Design 11(2):165–174

    Article  Google Scholar 

  • Kovenock D, Roberson B (2009) Is the 50-state strategy optimal? J Theor Polit 21(2):213–236

    Article  Google Scholar 

  • Rosen S (1986) Prizes and incentives in elimination tournaments. Am Econ Rev 74:701–715

    Google Scholar 

  • Searles D (1963) On the probability of winning with different tournament procedures. J Am Stat Assoc 58:1064–1081

    Article  Google Scholar 

  • Wright B (1983) The economics of invention incentives: patents, prizes, and research contracts. Am Econ Rev 73(4):691–707

Download references

Author information

Authors and Affiliations

  1. Swiss Institute for Empirical Economic Research (SEW), University of St. Gallen, 9000, St. Gallen, Switzerland

    Alex Krumer

  2. Department of Applied Economics and Department of Managing Human Resources, Sapir Academic College, 79165, M.P. Hof Ashkelon, Israel

    Reut Megidish

  3. Department of Economics, Ben-Gurion University of the Negev, 84105, Beer-Sheva, Israel

    Aner Sela

Authors
  1. Alex Krumer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reut Megidish
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aner Sela
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aner Sela.

Appendices

Appendix A

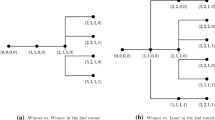
We present in Figs. 2, 3, 4 and 5 the game tree of the round-robin tournaments for the two possible allocations of players in the round-robin tournament with four symmetric players (Case A and Case B). Each game tree describes all the possible paths in the round-robin tournament. Since there are 55 possible games (vertexes) in the tournament with four players, each game tree is exceedingly large and we have to divide it into two parts.

Fig. 2
figure 2

Part I of the game tree in Case A of the round-robin tournament with four symmetric players

Full size image
Fig. 3
figure 3

Part II of the game tree in Case A of the round-robin tournament with four symmetric players

Full size image
Fig. 4
figure 4

Part I of the game tree in Case B of the round-robin tournament with four symmetric players

Full size image
Fig. 5
figure 5

Part II of the game tree in Case B of the round-robin tournament with four symmetric players

Full size image

Appendix B

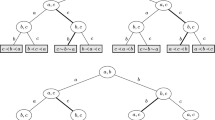
In the following, we provide in every possible vertex (game) the players’ mixed-strategies, their expected payoffs and their probabilities of winning. These results are summarized in Table 1 (Case A) and Table 2 (Case B) each of which includes 55 vertexes. We provide first the expected payoffs and winning probabilities of Case A by Table 1 and then of Case B in Table 2.

Table 1 Players’ expected payoffs and winning probabilities in vertexes 1–55 of Figs. 2 and 3
Full size table
Table 2 Players’ expected payoffs and winning probabilities in vertexes 1–55 of Figs. 4 and 5
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Krumer, A., Megidish, R. & Sela, A. First-mover advantage in round-robin tournaments. Soc Choice Welf 48, 633–658 (2017). https://doi.org/10.1007/s00355-017-1027-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00355-017-1027-y

Search

Navigation