Abstract
We study the optimal design of round-robin tournaments with three symmetric players. We characterize the subgame-perfect equilibrium in these tournaments with either one or two prizes. Our results show that the players who wish to maximize their expected payoffs or their probabilities of winning have different preferences about the order of games under tournaments with one or two prizes. We analyze the optimal allocations of players for a designer who wishes to maximize the players’ expected total effort in the tournaments with one and two prizes, and by comparing between them, it is demonstrated that in order to maximize the players’ expected total effort the designer should allocate only one prize.






Similar content being viewed by others
Notes
Applications of the all-pay contest have been made to rent-seeking and lobbying in organizations, R&D races, political contests, promotions in labor markets, trade wars, military and biological wars of attrition (see, for example, Hillman and Riley 1989; Baye et al. 1993; Amman and Leininger 1996; Krishna and Morgan 1997; Che and Gale 1998; Siegel 2009).
In each match, the probability of a tie in our model is zero, since each player’s strategy set is infinite. Note that it has been suggested that for the FIFA football tournaments starting from 2026 there will be no draws, and group matches that end in draws will be decided by penalty shootouts (https://www.ibtimes.co.uk/how-48-team-world-cup-2026-will-work-what-left-be-decided-1600342).
In real life, there are many kinds of three-player games. For example, Leagues A and B of the 2018 UEFA Nations League consist of three teams (https://en.wikipedia.org/wiki/2018%E2%80%9319_UEFA_Nations_League#League_A). Other examples can be found in tennis tournaments between nations, such as men’s Davis Cup and women’s Fed Cup. For instance, in 2015 three pools of Group 3 of the European Zone of Davis Cup consisted of three teams (https://www.daviscup.com/en/draws-results/group-iii/europe/2015.aspx). The same structure also appeared in two pools of the 2018 Fed Cup European Zone (https://www.fedcup.com/en/draws-results/group-i/europe-africa/2018.aspx).
References
Amman, E., & Leininger, W. (1996). Asymmetric all-pay auctions with incomplete information: The two-player case. Games and Economic Behavior,14, 1–18.
Ashraf, N., Camerer, C. F., & Loewenstein, G. (2005). Adam Smith, behavioral economist. The Journal of Economic Perspectives,19(3), 131–145.
Bartsch, A., Drexl, A., & Kroger, S. (2006). Scheduling the professional soccer leagues of Austria and Germany. Computers & Operations Research,33(7), 1907–1937.
Barut, Y., & Kovenock, D. (1998). The symmetric multiple prize all-pay auction with complete information. European Journal of Political Economy,14, 627–644.
Baye, M. R., Kovenock, D., & de Vries, C. (1993). Rigging the lobbying process: An application of the all-pay auction. American Economic Review,83, 289–294.
Baye, M. R., Kovenock, D., & De Vries, C. G. (1996). The all-pay auction with complete information. Economic Theory,8(2), 291–305.
Che, Y.-K., & Gale, I. (1998). Caps on political lobbying. American Economic Review,88, 643–651.
Cohen, C., & Sela, A. (2008). Allocation of prizes in asymmetric all-pay auctions. European Journal of Political Economy,24, 123–132.
Fleurent, C., & Ferland, J. A. (1993). Allocating games for the NHL using integer programming. Operations Research,41(4), 649–654.
Gill, D., & Stone, R. (2010). Fairness and desert in tournaments. Games and Economic Behavior,69(2), 346–364.
Goosens, D., & Spieksma, F. (2009). Scheduling the Belgian soccer league. Interfaces,39(2), 109–118.
Groh, C., Moldovanu, B., Sela, A., & Sunde, U. (2012). Optimal seedings in elimination tournaments. Economic Theory,49(1), 59–80.
Henz, M., Muller, T., & Thiel, S. (2004). Global constraints for round robin tournaments scheduling. European Journal of Operations Research,153, 92–101.
Hillman, A., & Riley, J. (1989). Politically contestable rents and transfers. Economics and Politics,1, 17–39.
Krishna, V., & Morgan, J. (1997). An analysis of the war of attrition and the all-pay Auction. Journal of Economic Theory,72(2), 343–362.
Krumer, A., & Lechner, M. (2017). First in first win: Evidence on schedule effects in round-robin tournaments in mega-events. European Economic Review,100, 412–427.
Krumer, A., Megidish, R., & Sela, A. (2017). First-mover advantage in round-robin tournaments. Social Choice and Welfare,48(3), 633–658.
Moldovanu, B., & Sela, A. (2001). The optimal allocation of prizes in contests. American Economic Review,91(3), 542–558.
Moldovanu, B., & Sela, A. (2006). Contest architecture. Journal of Economic Theory,126(1), 70–96.
Nemhauser, G. L., & Trick, M. A. (1998). Scheduling a major college basketball conference. Operations Research,46, 1–8.
Rasmussen, R. V. (2007). A Benders approach for constrained minimum break problem. European Journal of Operations Research,177(1), 198–213.
Rasmussen, R. V., & Trick, M. A. (2008). Round robin scheduling—A survey. European Journal of Operations Research,188(3), 617–636.
Rosen, S. (1986). Prizes and incentives in elimination tournaments. American Economic Review,74, 701–715.
Russel, R. A., & Leung, J. M. Y. (1994). Devising a cost effective schedule for a baseball league. Operations Research,42(4), 614–625.
Siegel, R. (2009). All-pay contests. Econometrica,77(1), 71–92.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix A: A random allocation of players in the round-robin tournament with three players and two prizes
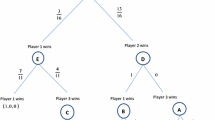
In the following, we provide in every possible vertex (game) of Figure 1, the players’ mixed strategies, their expected payoffs and their probabilities of winning. These results are summarized in Table 6. The complete analysis can be found in Online-Appendix A.
The players’ expected payoffs
The players’ probabilities of winning
Player 1’s probability to win a prize is
Player 2’s probability to win a prize is
And, player 3’s probability to win a prize is
The players’ expected total effort
The expected total effort in the tournament is
The length of the tournament
The probability that the winners of the tournament will be determined before the last round is
Appendix B: The winner of the first round competes in the second round of the round-robin tournament with three players and two prizes
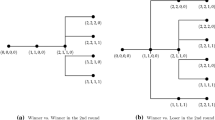
In the following, we provide in every possible vertex (game) of Figure 2, the players’ mixed strategies, their expected payoffs and their probabilities of winning. These results are summarized in Table 7. The complete analysis can be found in Online-Appendix B.
The players’ expected payoffs
The players’ probabilities of winning
Player 1’s probability to win a prize is
Player 2’s probability to win a prize is
And, player 3’s probability to win a prize is
The players’ expected total effort
The expected total effort in the tournament is
The length of the tournament
The probability that the winners of the tournament will be determined before the last round is equal to zero since there is no possibility that one of the players lost twice in the first two rounds.
Appendix C: The winner of the first round competes in the third round of the round-robin tournament with three players and two prizes
In the following, we provide in every possible vertex (game) of Figure 3, the players’ mixed strategies, their expected payoffs and their probabilities of winning. These results are summarized in Table 8. The complete analysis can be found in Online-Appendix C.
The players’ expected payoffs
The players’ probabilities of winning
Player 1’s probability to win a prize is
Player 2’s probability to win a prize is
And, player 3’s probability to win a prize is
The players’ expected total effort
The expected total effort in the tournament is
The length of the tournament
The probability that the winners of the tournament will be determined before the last round is
Appendix D: A random allocation of players in the round-robin tournament with three players and one prize
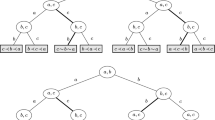
This case which is presented in Figure 4 was already analyzed by Krumer et al. (2017). In the following, we summarize the main results.
The players’ expected payoffs
The players’ probabilities of winning
The players’ expected total effort
The expected total effort in the tournament is
The length of the tournament
The probability that the winner of the tournament will be determined before the last round is
Appendix E: The winner of the first round competes in the second round of the round-robin tournament with three players and one prize
In the following, we provide in every possible vertex (game) of Figure 5, the players’ mixed strategies, their expected payoffs and their probabilities of winning. These results are summarized in Table 9. The complete analysis can be found in Online-Appendix E.
The players’ expected payoffs
The players’ probabilities of winning
Player 1’s probability to win the prize is
Player 2’s probability to win the prize is
And, player 3’s probability to win the prize is
The players’ expected total effort
The expected total effort in the tournament is
The length of the tournament
The probability that the winner of the tournament will be determined before the last round is
Appendix F: The winner of the first round competes in the third round of the round-robin tournament with three players and one prize
In the following, we provide in every possible vertex (game) of Figure 6, the players’ mixed strategies, their expected payoffs and their probabilities of winning. These results are summarized in Table 10. The complete analysis can be found in Online-Appendix F.
The players’ expected payoffs
The players’ probabilities of winning
Player 1’s probability to win the prize is
Player 2’s probability to win the prize is
And, player 3’s probability to win the prize is
The players’ expected total effort
The expected total effort in the tournament is
The length of the tournament
The probability that the winner of the tournament will be determined before the last round is equal to zero since there is no possibility that one of the players won twice in the first two rounds.
Rights and permissions
About this article
Cite this article
Krumer, A., Megidish, R. & Sela, A. The optimal design of round-robin tournaments with three players. J Sched 23, 379–396 (2020). https://doi.org/10.1007/s10951-019-00624-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10951-019-00624-8
Keywords
- Multi-stage contests
- All-pay auctions
- First-mover advantage
- Second-mover advantage
- Round-robin tournaments