1 Introduction

Airborne pollen dispersion is part of plant phenology, following yearly seasonal cycles with the aim of successful reproduction. While elementary for the ecosystem, pollen grains are known to be a trigger for allergic reactions in sensitized individuals (Sofiev and Bergmann, 2013). The current prevalence of allergic diseases worldwide remains high, ranging from 15 to 25% (Passali et al. 2018), with industrialized countries affected more by this negative trend (Pawankar 2014). The ongoing increase in air temperature and the overall effect of climate change have been increasing steadily the abundances of airborne pollen across the globe and, at the same time, have been shifting earlier the pollen seasons for several allergenic taxa (Ziska et al. 2019). The World Allergy Organization has warned that, because of climate change, plants will be stressed to flower and pollinate earlier within the year and in higher amounts, thus increasing the natural pollen exposure of sensitized individuals and, consequently, increasing the severity of associated symptoms (Pawankar 2014).

Being mostly not a life-threatening condition, pollen allergic symptoms can significantly reduce health-related quality of life and workplace productivity of people concerned because of profound physical and psychological complications (Blaiss et al. 2018; Devillier et al. 2016; Haanpää et al. 2018). Allergic individuals have several possibilities to control allergic symptoms, with allergen avoidance being one of the most effective measures (Glacy et al. 2013). However, since severity of occurring symptoms significantly depends on the current concentration of aeroallergens in the ambient environment (Bastl et al. 2013), to be effective, allergen avoidance strategies make sense only if performed when concentration of airborne allergenic pollen is high. Consequently, pollen information provided for example via pollen applications to the target population of allergic individuals might become an important aid in avoiding exposure to allergenic pollen, and in planning medication and outdoor activities (Kmenta et al. 2014). As airborne pollen has been identified as a biological weather parameter, a network of nearly 400 Hirst-type pollen traps is currently monitoring the airborne pollen in Europe (Berger et al. 2013). However, for pollen information to be useful for allergy management, it has to be delivered on time, shortly after the measurement took place, to reflect the actual pollen abundance. Therefore, in order to provide up-to-date information on pollen concentration, a more rapid, and preferably instantaneous technique in pollen monitoring than a conventional pollen trap of Hirst-type is needed. Automated pollen monitoring in real time might be a solution covering this urgent need.

Such novel approaches have been implemented very rarely, as by Chappuis et al. (2020), who used data deriving from an automatic pollen monitoring system. The importance of integrating hourly resolution pollen measurements to forecasting models and, even more, using real-time data from novel, automatic monitoring devices has been suggested and discussed by Sofiev (2019), highlighting that such an approach could boost the predictive power of future models. To be fair, it is also pointed out (and we agree, as our current results also show) that there is still a way to reach operational predictions for everyday practice. Toward the same direction, Geller-Bernstein and Portnoy (2019) reviewed that automatic, real-time pollen monitoring information would be valuable for short-term operational forecasts for allergic individuals, which, otherwise, is currently provided via daily predictive models with no detailed information on the intradiurnal variation for everyday activities and planning.

For this reason, the Bavaria State in south Germany has developed a network based on the automatic pollen monitoring devices of BAA500 type (Bio Aerosol Analyzer 500) (Oteros et al. 2019), as described in more technical detail in (Oteros et al. 2015). The BAA 500 is an automatic system for air particle collection (among others, pollen and fungal spores), analysis, and automatic data transmission to a data bank, with pollen information available three hours after observation. Automatic pollen monitoring is a promising tool in pollen season monitoring, as it provides pollen information nearly up-to-date with a high sampling rate of up to 8 pollen measurements per day. The BAA 500 operated in Munich, Germany, was reported to be a functional pollen monitoring device with 93.3% of pollen automatically classified by that device to be correctly identified (Oteros et al. 2015). Automatic pollen monitoring is a new technique, which is yet not widely used. At the moment, only few countries stand out developing innovative monitoring sites. Among those are Japan (Kawashima et al. 2017), the USA (Buters et al. 2018), Switzerland (Crouzy et al. 2016), and Germany, the latter of which has been operating automatic pollen monitors for the last half decade.

The circadian pathophysiology of pollen allergy is well documented already (Nakao et al. 2015), with symptoms worsening over night or in the early morning. Because of the lack of real-time, high-resolution (hourly) pollen measurements, this phenomenon remains poorly researched. Most commonly, aerobiologists work on daily data, predicting the pollen concentration for the next day or several days ahead. The novel automatic pollen monitoring devices, with the near-real-time pollen data, allow to go beyond the current state-of-the-art and to develop reliable short-term pollen predictions. Pollen forecasting at this scale can be the cornerstone of operational diurnal allergy risk alerts for allergic individuals.

To achieve such operational forecasts, apart from the real-time, high-resolution pollen data, sophisticated mathematical and statistical tools need to be employed. Scientific works examining the diurnal pollen variation in the air only seldom apply deterministic predictive models, narrowing their efforts down to descriptive methods and correlation analysis (Chappuis et al. 2020; Fernández-Rodríguez et al. 2014; Ščevková et al. 2015). The most common predictive techniques used so far are linear or nonlinear regressions, with significant steps having been made the last few years (Nowosad et al. 2018; Piotrowska, 2012; Ritenberga et al. 2016), and time-series analysis, based on Box–Jenkins methods (García-Mozo et al. 2014; Ocana-Peinado et al. 2008; Valencia et al. 2019). Also, variables like meteorological factors are frequently considered, as they have been proven as significant predictors of airborne pollen concentrations. Meteorological factors, such as solar radiation (Iglesias-Otero et al. 2015; Nowosad et al. 2018), sunshine duration (Myszkowska & Majewska, 2014; Rodríguez-Rajo et al. 2006), and air temperature (Howard & Levetin, 2014; Nowosad et al. 2018; Ščevková et al. 2015), are positively correlated with airborne pollen concentrations, whereas variables like relative humidity (Ščevková et al. 2015; Makra et al. 2011), and precipitation (Piotrowska, 2012; Rodríguez-Rajo et al. 2006) show a negative association with airborne pollen abundances. Some articles examined the relationship with wind vectors and found them to be of significant influence (Astray et al. 2010).

Nowadays, novel and more sophisticated forecasting techniques are starting to be employed, as in the case of machine learning, which is increasingly gaining scientific interest. Several aerobiological studies have implemented machine learning algorithms, at various scales of analysis, such as artificial neural networks (Iglesias-Otero et al. 2015; Puc, 2012; Valencia et al. 2019), random forests (Nowosad et al. 2018; Zewdie et al. 2019), and support vector machines (Zewdie et al. 2019).

Each pollen forecasting technique exhibits pros and cons, and their selection is based on the research question per case and on data availability and quality. Therefore, regression analysis allows for inclusion of co-factors, but neglects the serial autocorrelation of all variables. On the contrary, Box–Jenkins models consider the autocorrelation of the dependent variable, but neglect the effect of other potential co-factors. Dynamic regression, albeit a statistical approach using the advantages of both above-mentioned forecasting techniques (Pankratz, 2012), has been seldom adopted in airborne pollen forecasting (Ocana-Peinado et al. 2008). Overall, forecasting of pollen concentrations is challenging due to the data complexity, intense seasonality with numerous ‘out of season’ zero values, high skewness and level of irregularity and extreme outliers. The above are mixed in a double-periodic pattern, within-day and within-year, with different factors influencing each periodicity and pollen distribution. The relationships are often nonlinear and the affecting co-factors usually collinear and sometimes confounding. This challenge could be answered by machine learning algorithms, like artificial neural networks, as they have a high ability to assess complex relationships (Twomey & Smith, 1995). To ensure the sound interpretation of the acquired results produced by the artificial neural network, it then makes sense to cross-validate the model output with that of ‘conventional’ forecasting techniques, as time series analysis and dynamic regression.

The aim of the present study was to assess and forecast the diurnal variability of airborne pollen concentrations and the development of short-term predictive models using near-real-time 3-hourly Betula and Poaceae pollen data. Both pollen taxa were selected because of their high atmospheric abundance in Bavaria (Oteros et al. 2019), and of their high prevalence in sensitization rates among the study area population (Muzalyova et al. 2019). To our best of knowledge, there is very limited research focusing on forecasting of diurnal pollen concentrations based on data provided by automatic pollen measurement systems. Therefore, this is the first paper using a 3-h sampling frequency of airborne pollen detected by an automatic pollen monitoring to develop and compare different predictive models. Knowledge of variation of pollen quantity on hourly scale is very important for people suffering from pollen allergies, as it can help them to avoid exposure to allergenic pollen. Incorporating real-time, automatic pollen measurements in airborne pollen forecasts is expected to dramatically improve the efficiency of allergy management.

2 Materials and methods

2.1 Data

Pollen data for Betula and Poaceae were acquired by use of an automatic pollen monitoring device BAA500, located in Augsburg, Germany. The automatic pollen monitor was situated at the Bavarian State Office for the Environment (Bayerisches Landesamt für Umwelt—LFU Bayern) (coordinates 48°32′ 60.29′′N, 10°90′30.77′′E), located in a suburban environment in Augsburg, Germany. The pollen data were collected in 3-h intervals for the years 2016–2019. Accordingly, each day (24-h period) encompasses 8 data points beginning with the first pollen measurement performed at midnight (0.p.m), and the last performed at 9 p.m. Pollen concentrations are expressed in grains per m3 with a time step n corresponding to a 3-h interval. Missing data (8.4% Betula and 7.8% Poaceae) were imputed based on regression analysis using 5 data points of the corresponding time period before and after the data gap. Scattered missing points were imputed by averaging closest measurement before and after the data gap. The normal distribution of the data was tested using the Kolmogorov–Smirnov and Shapiro–Wilk tests, where it was concluded that the hourly data did not follow a normal distribution being extremely right-skewed (Table 1).

Table 1 Descriptive statistics of the pollen measurements of examined taxa (grains per m3)
Full size table

Meteorological data were retrieved from the German Weather Institute (Deutscher Wetterdienst—DWD, https://opendata.dwd.de/climate_environment/CDC/), recorded at the airport of Augsburg (coordinates 48°21′57.564′′ N, 10°53′ 34.944′′ E), located approximately 11 km north of LFU. The following meteorological parameters were available for data analysis: air temperature [°C], relative humidity [%], air pressure [hPA], precipitation [mm], sunshine duration [min], solar radiation [J/cm2], and wind speed [m/s]. A Spearman correlation test was used to analyze associations between the examined meteorological variables. The statistical analysis included the 3-hourly data set from March to September (main pollen season of Betula and Poaceae) and was performed with the SPSS 25.0 statistical package.

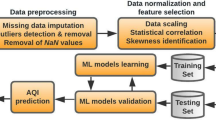
The analysis of the diurnal distribution of pollen concentrations and development of predictive models was performed based on pollen data of the main pollen season for each pollen taxa and each year. Accordingly, the following phenological features were determined for each available study year: Pollen Season Start (PSS), Pollen Season Peak (PSP), Pollen Season End (PSE), Pollen Season Duration (PSD), and the annual Pollen Integral (PI) in line with (Galan et al. 2017). The PSS was defined in line with European Aeroallergen Network pollen season definition. Due to this, the PSS was the first day achieving 5% of the cumulative daily pollen concentrations over the whole year. The PSE was determined as a day reaching 95% of the accumulated daily pollen concentrations throughout the whole pollen season (Bastl et al. 2018). The PI was specified as the sum of the daily average pollen concentrations per cubic meter over the whole year. The PSP was defined as the day with the highest daily pollen concentration. The overview of the data used and the development of the forecasting models is given in Fig. 1.

Fig. 1
figure 1

Process flowchart of the forecasting model development based on 3-hourly data

Full size image

2.2 Autoregressive integrated moving average (ARIMA)

ARMA or ARIMA (also known as Box–Jenkins model) represent a combination of autoregressive and moving average models (Box et al. 2016). For modeling of seasonal time series, ARIMA (p, d, q)(P, D, Q)ω is known as multiplicative ARIMA model (Cowpertwait & Metcalfe, 2009). Due to this, six parameters, namely p, d, q, P, D, and Q, have to be determined to be included in the forecasting model. This step was performed based on the analysis of the Partial Auto-Correlation Function (PACF) and Auto-Correlation Function (ACF). The Akaike Information Criteria (AIC) and the Bayesian Information Criterion (BIC) were the adjustment criteria used for selection of the best model for each examined pollen species. Additional confidence in the best fitting model was gained by deliberately overfitting the model by including further parameters and observing increase in the AIC and BIC. After the best fitting model was found, the correlogram of the residuals was verified as white noise.

2.3 Dynamic regression (DR)

A dynamic regression is an extension of a regression model allowing errors from the regression to contain autocorrelations (Pankratz, 2012). A dynamic regression uses advantages of the Box–Jenkins method modeling the autoregression between successive observations of the time series and allows for the inclusion of the external influencing variables like a conventional regression. Additionally, dynamic regression can be applied to seasonal data (Harvey & Scott, 1994) and also allows for lagged effect of the predictors (Pankratz, 2012). In the present study, the order of the autoregressive and moving average components for the dynamic regression modeling was determined based on the evaluation of the PACF and ACF. The external predictors were selected based on backward elimination using Julian day, and 16 lags (two days) of each available meteorological variable. Similar to ARIMA, AIC and BIC were used as adjustment criteria for the best fitting model along with the significance of the selected parameters.

2.4 Artificial neural network (ANN)

Artificial neural networks are forecasting methods based on a simple mathematical model inspired by information flow in the human brain. A neural network consists of a system of artificial neurons organized in layers. A common neural network incorporates an input, an output layer, as well as one or several intermediate layers containing so-called hidden neurons. A network can incorporate one to many hidden layers, and one to many neurons in each. The number of input neurons is defined by the number of used input features, and the number of output neurons is defined by the number of required output. The idea of a neural network is to model the response variable, representing the output, based on nonlinear combination of several input variables. A neuron receives information from other neuron or from an external influencing variable and computes a function f based on the weighted sum of the inputs (Goodfellow et al. 2016). The output of a neural network structure having three neurons in the hidden layer shown in Fig. 2 where \(x_{j}\) represents the input, \(w_{ij }\) is the weight from neuron j to neuron i, and b denotes bias. The function f represents an activation function which determines the output activity of the neuron. Through the activation function, the neuron and, thus, the model maps from a linear input to a nonlinear output. Neural network development requires a big implementation of models with different number of neurons in the hidden layer. Designing an optimal schema involves finding the structure with the smallest size network (parsimonious network), which produces optimal errors for trained as well as untrained cases (Astray et al. 2016). During the training phase of the model development, bias values and weights are modified to minimize the error between outputs produced by the model and target values using Mean Squared Error Loss function for linear problems, as given in the preset study.

Fig. 2
figure 2

Neural network structure with three hidden neurons

Full size image

In the present study, the Julian day of the measurement and available meteorological variables with up to 16 lags of each (up to two-day delay-effect) was used as input variables for the neural networks developed. As the pollen data are usually strongly autocorrelated, the pollen concentrations detected in the previous time periods reflect this time series and were included as influencing variables in order to improve the prediction capacity of the neural network. Since measurements of available input parameters were made on different scales, the parameter were normalized to lie between 0 and 1 before being imputed to the neural network.

2.5 Neural network autoregression (NNAR)

Neural network autoregression has a similar theoretical foundation as the ANN explained above. However, this type of an artificial neural network was specifically developed for autoregressive time series and represents a hybrid architecture comprising an ARIMA model and a neural network (Hyndman & Athanasopoulos, 2018). Those combined methods are argued to give better forecasts by taking advantage of each model’s capability (Taskaya-Temizel & Casey, 2005). Due to its neural network part of architecture, it is capable of estimating nonlinear relationships, and due to its underlying ARIMA part, the algorithm explicitly uses lagged values of the time series as inputs.

A neural network autoregression is denoted as NNAR (p, P, k) with p indicating the number of lagged inputs, P indicating the number of seasonal lagged inputs, and k representing nodes in the hidden layer. For example, an NNAR (2, 1, 3)8 uses inputs \(y_{t - 1}\), \(y_{t - 2}\), and \(y_{t - 8}\), has three neuron in the hidden layer and is complementary to ARIMA (2,0,0)(1,0,0)8 but without the restriction on the parameters that ensure stationarity.

In the present pollen study, the order of p and P was determined based on the PACF analysis with Julian day and meteorological variables used as external influencing variables similar to the deployment of the ANN. The number of neurons in hidden layer was established similar to the ANN by a trial and error process based on the prediction accuracy of several tested models.

2.6 Model validation

It is a common practice in the data modeling to test the predictive power of the established forecasting models on unknown data, not deployed for the fitting process (Goodfellow et al. 2016). For this purpose, the available pollen dataset was split into a training and test datasets as following: the dataset representing the main pollen season in the last year, 2019, was used for the test of the developed predictive models, and the remaining three years of pollen data were applied for the model fitting and training. The predictive accuracy and validity of each established forecasting model was determined based on the comparison of predicted and observed pollen concentration values. Two accuracy metrics, namely mean absolute error (MAE) and root mean squared error (RMSE), were used as criteria for evaluation of the performance of the established forecasting models:

$${\text{MAE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left| {\hat{y}_{i} - y_{i } } \right|}}{N}$$
$${\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\hat{y}_{i} - y_{i } } \right)^{2} }}{N}}$$

Generally, the RMSE stronger punishes deviation between predicted value \(\hat{y}_{n}\) and observed variable \(y_{n }\) due to squaring the difference. It is therefore better suited for modeling on data with strong peak and outliers (Twomey & Smith, 1995).

As both introduced accuracy metrics are based only on error term \(e_{t}\), they are therefore scale-dependent and allow to make comparison between time series that involve different units. In order to compare the performance of predictive models based on pollen data of Betula and Poaceae, the coefficient of determination \(\left( {R^{2} } \right)\) was used. \(R^{2}\) describes the proportion of variance explained by the model to the total variance in the data and can be defined using the following formula:

$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - \overline{y}} \right)^{2} }}$$

All forecasting techniques were implemented in RStudio, version 1.0.143 using tseries, fpp2, lmtest, neuralnet libraries.

3 Results

The characteristics of the examined pollen seasons are outlined in Table 2. The main pollen season of Betula average started by the end of March (from 15/03 to 8/04), and lasted on average 38 days (SD = 10.2). The main pollen season of Poaceae average started by the end of April (from 20/04 to 12/05) and had a comparably longer duration of 95 days (SD = 12.9). Considering Betula, the PD of the pollen season usually occurred shortly after the PSS on the 13th day of the main pollen season (from 04/04 to 14/04), whereas the PD of Poaceae was situated closer to the middle of the main pollen season and occurred on the 40th day (from 03/06 to 09/06) of the main pollen season. Furthermore, Betula usually had one well-defined peak, whereas Poaceae was characterized by several peaks of variable amplitude within the main pollen season. Generally, the pollen release of Betula was more intensive in absolute terms, peak values and also average pollen concentration per time period, compared to that of Poaceae.

Table 2 Descriptive statistics of the examined pollen seasons
Full size table

Regarding inter-annual variability, the pollen season of the year 2018, interestingly, stands out among analyzed pollen seasons due to the earlier PSS and PSE for both investigated allergenic species (Table 2). In particular, the main pollen season of Betula started already by the beginning of April and lasted for more than fifty days. The PSS of Poaceae occurred 10 days earlier of the average date and ended by the middle of July. Furthermore, the intensity of the Poaceae pollen seasons was continuously decreasing across examined years, with 2019 exhibiting the lowest pollen abundance of all years (Fig. 3).

Fig. 3
figure 3

Boxplots of averaged annual concentrations of Betula and Poaceae pollen, where the horizontal line denotes the median of all concentrations throughout the year, while the box and vertical lines signify the quartiles 25–75%

Full size image

The diurnal distribution of pollen concentrations of both taxa is depicted in Fig. 4. The pollen load of Betula was relatively constant during the day with the highest levels occurring at 3 p.m. Kruskal–Wallis-Test revealed a significant difference between time periods (H (7) = 28.590, p < 0.01). However, due to high standard deviation and none well-defined diurnal patterns a post hoc test (Dunn–Bonferroni) revealed only difference between 12 a.m. and 3 p.m. to be significant (z =  − 3.137, p = 0.048), whereas all other differences of pollen concentration between considered time periods were non-significant. On the contrary, the pollen concentration of Poaceae was noticeably peaking twice a day at 9 a.m. and 3 p.m., with relatively low abundance during the night hours. The Kruskal–Wallis Test revealed a significant difference between groups [H (7) = 317.982, p < 0.01], and a pairwise comparison showed significant differences between pollen concentrations measured between the night hours and early morning (9 p.m.–6 a.m.) and those observed beginning with morning until evening (9 a.m.–6 p.m.). As pollen concentration of Poaceae is higher during the warmer parts of the day, it suggests a stronger relationship between airborne pollen concentrations of this allergenic species and heat-related meteorological variables like air temperature, sunshine duration, and solar radiation.

Fig. 4
figure 4

3-hourly average distribution of Betula and Poaceae pollen concentrations over 24 h

Full size image

Correlogram analysis (Fig. 5) of Betula pollen concentrations showed a steady decrease with no well-defined peaks at daily cycle (at 8th lags), concluding that a seasonal term has to be included in the model. Inspection of the PACF-correlogram suggested that choosing one non-seasonal, and none seasonal autoregressive and moving average parameters were sufficient. However, due to rising significant correlation between 5 and 8th lags in the PACF, up to seven non-seasonal autoregressive and moving average parameters were tested. Correlogram of the Poaceae pollen data depicts a tendency similar to Betula’s, including a well-defined seasonality of the data at 8th lags; however, the decrease across the lags occurs considerably slower in comparison with Betula, presumably due to the shorter main pollen season duration. Inspection of the partial autocorrelation function showed a high significant correlation at lag one. According to this analysis one non-seasonal, as well as, up to two seasonal autoregressive and moving average parameters might be sufficient for the ARIMA model. However, in order to estimate the effect of overfitting up to seven, both, autoregressive and moving average parameters, and one seasonal autoregressive and moving average parameters were tested. The best fitting model for each pollen species was chosen based on the lowest AIC and BIC statistics.

Fig. 5
figure 5

ACF (autocorrelation function) and PACF (autocorrelation function) for Betula (a) and Poaceae (b) pollen data

Full size image

It is not possible to mention all relevant results of tested ARIMA model structures in this paper; therefore, the structures related singly to the best-fitted models are presented in Table 4. Thus, the best ARIMA model of Betula pollen concentration corresponded to ARIMA (7,1,3)(1,1,1)[8] and contained seven non-seasonal autoregressive and three moving average parameter, and one of each seasonal autoregressive and moving average parameter. Regarding Poaceae, the best fitting model was given by ARIMA (1,1,2)(1,0,1)[8] and consisted of one non-seasonal autoregressive parameters, two non-seasonal moving average parameter, and one of each seasonal autoregressive and moving average parameter.

Descriptive analysis of the meteorological variables (Fig. 6) reviled a significant difference between the years used in the training data set and the year 2019 representing the test data set. Of particular note, the year 2019 was significantly drier in comparison with all other considered pollen seasons.

Fig. 6
figure 6

Boxplots of averaged annual values of different meteorological factors, where the horizontal line denotes the median of all measurements throughout the year, while the box and vertical lines signify the quartiles 25–75%

Full size image

The Spearman’s correlation analysis was used preliminary to DR development in order to discover relationships between pollen concentrations and available meteorological parameters. The results of correlation analysis are given in Table 3. Generally, correlations were significant in a large number of cases. As expected, Poaceae pollen concentrations were strongly related to air temperature, sunshine, and solar radiation in comparison with Betula pollen counts. The air pressure was found to be significantly correlated only to Betula, whereas precipitation and humidity were negatively related to the pollen concentrations of both pollen taxa. No significant relationship between wind speed and pollen concentrations was detected.

Table 3 Correlation coefficients of pollen concentrations and meteorological variables (only training dataset)
Full size table

The order of autoregressive and moving average parameters in DR was determined based on ACF and PCF analysis, however, with regard to previous ARIMA modeling. All available weather data were imputed in the dynamic regression using up to 16 lagged values representing two days as well as Julian day of the measurement and tested for significance. A step-by-step procedure was followed, and a backward stepwise removal of all non-significant influencing variables was processed, beginning with the highest p-value. The best fitting model was determined using AIC and BIC values along with significance of the certain influencing variables. The final result depicting the best fitting model for both pollen taxa can be taken out of Table 4.

Table 4 Coefficients obtained for ARIMA and DR models
Full size table

Similar to correlation analysis, air temperature had a positive significant effect on the airborne pollen concentrations for both examined pollen species, with regression coefficient being higher for Betula. However, multiple lagged time periods of temperature measurement were found significant for Poaceae, suggesting airborne pollen concentration of this species to be more sensitive to air temperature. Precipitation had a substantially greater impact on pollen abundance for both examined species reflected in higher calculated parameters with this effect lasting up to 6 h. Interestingly, the effect of rain occurred immediately on Betula airborne pollen concentration and with a delay of three hours on Poaceae. The air pressure was a significant predictor but only for airborne Betula pollen. Furthermore, only examined meteorological variables representing at most 8th lag were determined as significant predictors of the airborne pollen concentration, suggesting that only most current values have an influence on the pollen levels in the air.

Generally, extension of ARIMA model by meteorological variables has improved the performance of the predictive models in terms of higher coefficient of determination (R2); however, this effect was small despite highly significant relationships.

Statistical results obtained from the ARIMA and DR analysis were used as a starting point for the setup of the both neural networks. Particularly, the best fitting order of the autoregressive parameters served as a starting framework for definition of the NNAR structure. Accordingly, for Betula NNAR structure was defined as NNAR (7,1,k)[8], and NNAR (1,1,k)[8] for Poaceae. Lagged pollen counts corresponding to the p and q order of the ARIMA model were also employed as input features in the ANN. All available meteorological variables including its lagged values were deployed as influencing variables in NNAR and ANN, as well as Julian day of the measurement. The number of neurons in the hidden layer k for each neural network was determined iteratively by testing different neuron schemas. After the trial-and-error process, structures providing better results in terms of the model accuracy were obtained for each of examined allergenic species, and each neural network used for data modeling. The final neuron structures, as well as, goodness-of-fit criteria can be taken out from Table 5. Interestingly, the best NAAR structure for predicting Betula airborne pollen counts was given by one autoregressive non-seasonal component in comparison with ARIMA and DR having the order of 7. The most important meteorological variables for NNAR and ANN were Julian day, air temperature, precipitation, and solar radiation, whereas the NNAR prediction of Poaceae pollen levels was dominated singly by precipitation. It is also remarkable that neural networks predicting Betula pollen counts achieved substantially higher \(R^{2}\) coefficients in training process in comparison with Poaceae.

Table 5 Neural networks schemas of fitted models
Full size table

The predictive models fitted to the training data set were applied on the test data set in order to determine their predictive accuracy. Overall, the ARIMA and DR could achieve higher coefficients of determination in the test run in comparison with the training of the models. Furthermore, ARIMA and DR performed almost equally well; thus, the deployment of additional meteorological parameters has not changed the predictive accuracy significantly.

On the contrary, the high coefficient of determination achieved when fitting neural networks using training data were only partly reproduced in the independent test. The goodness-of-fit of the independent model test can be seen in Table 6. The NNAR produced better predictions for Betula, whereas simple seasonal ARIMA outperformed all other predictive methods in forecasting airborne Poaceae pollen concentrations. Furthermore, DR exhibited low predictive power for Poaceae pollen levels. Despite substantially higher values of RMSE and MAE, forecasting models predicting Betula pollen concentrations performed better, achieving \(R^{2}\) in the range between 0.13 and 0.62. On the contrary, predictive models of Poaceae achieved coefficients of determination between 0.03 and 0.55. The high RMSE and MAE for Betula pollen concentrations were predetermined by higher intensity of airborne pollen levels in comparison with Poaceae.

Table 6 Prediction capacity of four models with a one-day forecast horizon on a 3-hourly resolution
Full size table

Figure 7 shows the comparison of predicted values based on four applied modeling techniques and observed Betula pollen concentrations. The test prediction was made using roughly 25% of the available data and, in total, consisted of 200 data points. The figure depicts predictions provided by each of the tested forecasting models. The black line shows the observed pollen counts for considered data points, and the other lines depict prediction made by ARIMA, DR, NNAR, and ANN. As can be seen, for the hold-out year 2019, Betula had no single well-defined peak in this test data set, and the highest pollen level was achieved closer to the middle of the pollen season. The salient finding was that in terms of pollen season occurrence, ARIMA, DR, and NNAR performed remarkably well; however, they consistently underestimated the pollen abundances. Practically, all models’ overall performances were lower than expected, because of not ever managing to predict the highest peak of the season. Noticeably, the test year, 2019, was the driest one of all examined years (Fig. 6) and, potentially for this reason with the highest annual pollen integral of Betula pollen compared to all years in the study period (Fig. 3). The ANN exhibited the highest irregularities, by underestimating the first peak in the overall cluster and overestimating the second peak, whereas it performed quite well in the lower concentrations. Furthermore, it is noticeable that ANN tended either to strongly overestimate, or miss several peaks inside the season, whereas the NNAR generally captured this pollen behavior but underestimated it. Additionally, the DR also showed a tendency to slightly overestimate the airborne pollen concentrations.

Fig. 7
figure 7

Results of independent test for Betula pollen data (3-hourly sequence) using 4 forecasting techniques

Full size image

The test of the established predictive models for Poaceae pollen concentrations was performed using the main pollen season 2019 representing roughly one fourth of the data and contained in total 872 data points. Figure 8 depicts a representative section of the observed pollen counts beginning with the start of the considered pollen season and predicted values using four forecasting techniques. As shown in the graphical representation, the observed peaking behavior of pollen counts was overestimated by all applied forecasting techniques except for ARIMA. Additionally, DR showed a tendency to strongly overestimate the variability of the airborne pollen concentrations, whereas both neural networks predict values clearly above the actually observed pollen concentrations, however, capturing the pollen behavior in terms of its amplitude. This result can be traced back to the lowest intensity of the Poaceae pollen season among all examined pollen seasons. ARIMA describes well the pollen behavior of low pollen concentrations of low pollen levels, and the ANN outperformed in forecasting the peaking behavior beginning with the time period 161.

Fig. 8
figure 8

Results of independent test for Poaceae pollen data (3-hourly sequence) using 4 forecasting techniques

Full size image

4 Discussion

In the present study, we elaborated novel, automated, near-real-time pollen data, on a 3-hourly time resolution, attempting to predict pollen concentrations on a diurnal horizon. In contrast to the current tendency to forecast the start, peak and end of the main pollen season, here we attempted to define the pollen concentration after the start of and within the main pollen season, so as to potentially provide real-time, operational allergy risk alerts. To achieve this, we used a variety of statistical techniques, among which time series analysis and machine learning. Most forecasting attempts have been using much simpler tools or less fine time resolution. From an operational and clinical point of view, allergic patients and their practitioners actually need the diurnal distribution of air pollen abundances every day so as to plan their daily activities, including exposing (or not) themselves to expected airborne pollen concentrations and receiving the appropriate medication.

Considering that sensitization rates to airborne pollen account up to 25% worldwide (Passali et al. 2018), and pollen allergies comprise according to the World Allergy Organization one of the emerging diseases of the century (Pawankar 2014), the above-mentioned information will undoubtedly be the cornerstone for the pollen allergen avoidance on a regular basis, if disseminated operationally. Specifically in the study area’s country, Germany, almost 15% of adult population are suffering from at least one allergic disorder (Bergmann et al. 2016), and allergic individuals account for about 12.6% among German children (Schmitz et al. 2014). This additionally highlights the necessity for the elaboration of such prophylaxis and management toolkits.

This study employed advanced statistical methods, namely ARIMA, dynamic regression, and machine learning, such as neural autoregression and artificial neural network, to predict pollen concentrations of Betula and Poaceae in Augsburg, Germany. The mathematical modeling techniques were used by integrating meteorological factors and past pollen observations. Such approaches are quite common in this research area, but not on such a fine, 3-hourly, timescale.

Among the statistical forecasting techniques employed in the present study, dynamic regression considered autocorrelations both with the dependent pollen data and the values of meteorological variables and performed better in pollen prediction based on the training dataset. This finding agrees with Sanchez et al. (2005), who showed the combination of meteorological factors and previous pollen data to yield better results in pollen forecasting, than using alone pollen data or meteorological variables (Sánchez Mesa et al. 2005). In the present study, two meteorological variables, namely air temperature and precipitation, were determined as significant predictors in DR modeling for both examined pollen species, with precipitation having a stronger effect on the airborne pollen concentration. In the current aerobiological research, the most of pollen forecasting studies apply some meteorological variables as input parameters. Among them, air temperature is one of the most studied meteorological factors which is discovered to have a significant effect on airborne pollen concentrations across different pollen taxa (García-Mozo et al. 2014; Ziello et al. 2012). For example, Howard and Levetin (2014) used air temperature and precipitation to predict pollen concentrations too (Howard & Levetin, 2014), discovering that temperature was one of the most significant repressor. Iglesias-Otero et al. (2015) employed precipitation, sunshine duration, and humidity, with rainfall being the most sensitive variable in the predictive model (Iglesias-Otero et al. 2015). These findings agree with our result, showing the precipitation to have an even stronger impact on airborne pollen levels. That suggests that rainfall simply washes out the pollen grains from the air with this effect lasting for several hours. It is worth pointing out here that different meteorological and climatic indices would provide variable predictive capacity to our developed models, and this is highly relying on the timescale examined. It is well known, as documented, i.e., by Damialis et al. (2005) that even by conventional Hirst-type monitoring techniques, wind vectors and precipitation are the leading determining factors, with the effects lasting for at least four hours (Damialis et al. 2005). In the present study, although an extension of the simple ARIMA model by meteorological variables provided better results in the training, the predictive power of ARIMA and DR models were similar for Betula pollen counts, whereas DR failed in predicting airborne pollen concentration of Poaceae, achieving coefficient of determination of only \(R^{2}\) = 0.03. Furthermore, considering Poaceae pollen concentrations, the simplest among applied forecasting techniques, namely ARIMA, clearly outperformed all other models.

Regarding the two machine learning techniques used for the development of predictive models, neural autoregression substantially outperformed the artificial neural network, for Betula pollen data, and delivered the best predictive power in terms of \(R^{2}\) of all applied forecasting techniques. On the contrary, Poaceae was better predicted by ANN. In general, the forecasting model developed for Betula pollen performed better in terms of obtained coefficient of determination R2 in independent test, despite higher variation in the data. Possibly, it can be explained by a shorter main pollen season for Betula and a clearer pattern of pollen behavior consisting of only one well-defined peak. Furthermore, it is worth mentioning, that intensity of the Poaceae pollen season was decreasing across examined years with 2019 having the lowest pollen abundance. Also, 2019 was the driest year, especially in the pollen season of Poaceae, both in terms of precipitation and relative humidity, which contributed to it being also the longest pollen season. Consequently, both applied machine learning techniques were constantly overestimating observed airborne pollen counts, especially in the weakly abundant beginning of the pollen season. An additional inclusion of a parameter reflecting expected intensity of the pollen season might have an essential effect on the accuracy of the predictive models. Consequently, more historical pollen data are obviously needed to more thoroughly investigate the intensity of the Poaceae pollen seasons.

Overall, a good predictive performance of simple seasonal ARIMA model in comparison with advanced forecasting techniques suggests that the phenology of the plants, reflected by the lagged pollen concentrations, is the most relevant predictor for the observed airborne pollen concentration. This insight is also supported by diurnal pollen concentration patterns discovered in the present study, especially for Poaceae, showing significant differences in airborne pollen concentrations depending on the time period of the measurement. This finding highlights the importance of the further, scrupulous investigation of the diurnal variation of the airborne pollen concentration and its influencing factors. Investigation of airborne pollen concentrations on hourly scales represents a promising research direction, since it accommodates one of the most urgent/important objectives, namely that of the delivery of pollen information to people suffering from pollen-induced allergies. Given that under ongoing climate change conditions, increasing and more intense extreme weather events influence the abundance and seasonality and circadian periodicity of airborne pollen, developing accurate short-term forecasts is a real challenge. In our results, this is highlighted by the fact that the significantly drier year 2019 led to reduced predictive capacity of most models and signified past pollen records as the most reliable, in this dataset, predictor of future, on an hourly scale, pollen concentrations. It is anticipated that unexpected and extreme weather incidents may be already causing unpredictable pollen seasons and diurnal distribution, which is worth to be investigated more thoroughly.

When developing a forecasting model to notify the pollen allergic individuals about expected airborne pollen levels for supporting their pollen allergy management, one has to keep in mind the needs of the target population. Allergic individuals might be hardly interested in pollen forecasting expressed in absolute values. On the contrary, they might be interested in notifications of critical pollen values, or expected symptom severity induced by the airborne pollen levels. Firstly, this consideration can also affect the definition of the main pollen, taking into account pollen thresholds inducing allergic reaction of different severity in sensitized individuals (Karatzas et al. 2019). Secondly, there are several studies focusing on prediction of certain levels of airborne pollen concentration (Brighetti et al. 2014; Castellano-Méndez et al. 2005) or even expected season severity (Sánchez Mesa et al. 2005). Pollen level inducing an allergic reaction of a certain severity in allergic individuals might be variable for different locations due to different climatic conditions (Weger et al. 2013). The forecasting of critical values might be very useful for allergic individuals. However, so far, it lacks scientific efforts in this direction in Germany, and, thus, it lacks knowledge of pollen thresholds triggering allergic symptoms in sensitive individuals.

Overall, after comparing the performance of the four models used here with the actual observed pollen concentrations, it is concluded that all models had a satisfactory capacity to predict the timing of pollen occurrence on a 3-hourly scale, but most of them were not as well-performing when they had to forecast highly peaked pollen concentrations. Given the avowedly short length of the overall examined time series, as well as the weather peculiarities in the hold-out year 2019, we consider all models exhibiting adequate forecasting performance. In similar statistical approaches on a 2-hourly timescale, only few researchers, like Chappuis et al. (2020), reported some significant correlations between hourly pollen concentrations and hourly weather variables, most frequently weaker than the ones presented in our work. Noticeably, Chappuis et al. (2020) also used data deriving from an automatic pollen monitoring system, even though from a different manufacturer. Some other studies that attempted to predict pollen concentrations with weather variables on a diurnal level were those by Simoleit et al. (2016), also in Germany (Berlin), who found by rule weaker relationships with most meteorological factors. Likewise, Ríos et al. (2016) in Mexico, and Alba et al. (2000) in Spain also detected much weaker predictions, almost by rule.

An important limiting factor of the present study is the volume of the available pollen data. As BAA500 has been operating in Augsburg for only half a decade, only four complete pollen seasons were available for the data analysis. Environmental data are known to be very complex to model due to underlying inter-relations (Zewdie et al. 2019); hence, the time-series available for the present research might be too short to determine the seasonal phenology of examined species or to identify and characterize anomalous pollen seasons. In order to realize and to calibrate forecasting models, long historical series of pollen and meteorological data are necessary. Furthermore, it is worth pointing out that the predictive models presented in this study are based on data provided by an innovative fully automated pollen monitor, which, being a novel device, is still undergoing improvements. Although the pollen monitoring has been reported to show a high accuracy of pollen determination (Oteros et al. 2015), it has been documented already that a further improvement of the recognition algorithm is possible and that, consequently, there is still a lot of room for increasing the accuracy of pollen identification in near future (Schiele et al. 2019). Therefore, we conclude that the key for reliable, short-term pollen predictions, does not necessarily lie on the complexity and how sophisticated the applied statistical techniques are, but on the completeness of the toolkit used toward this purpose, as suggested below:

  • good quality of data (reliability)

  • long datasets (consistency)

  • considerations of the whole multi-factorial design

    • pollen autocorrelations

    • interaction effects with weather and climatic parameters

    • trends and multi-periodicities (within season and within the day).