Abstract
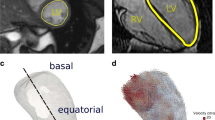
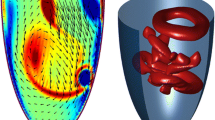
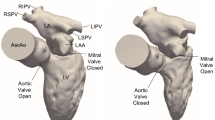
Intra-cardiac flow has been explored for decades but there is still no consensus on whether or not healthy left ventricles (LV) may harbour turbulent-like flow despite its potential physiological and clinical relevance. The purpose of this study is to elucidate if a healthy LV could harbour flow instabilities, using image-based computational fluid dynamics (CFD). 35 cardiac cycles were simulated in a patient-specific left heart model obtained from cardiovascular magnetic resonance (CMR). The model includes the valves, atrium, ventricle, papillary muscles and ascending aorta. We computed phase-averaged flow patterns, fluctuating kinetic energy (FKE) and associated frequency components. The LV harbours disturbed flow during diastole with cycle-to-cycle variations. However, phase-averaged velocity fields much resemble those of CMR measurements and usually reported CFD results. The peak FKE value occurs during the E wave deceleration and reaches 25% of the maximum phase-averaged flow kinetic energy. Highest FKE values are predominantly located in the basal region and their frequency content reach more than 200 Hz. This study suggests that high-frequency flow fluctuations in normal LV may be common, implying deficiencies in the hypothesis usually made when computing cardiac flows and highlighting biases when deriving quantities from velocity fields measured with CMR.








Similar content being viewed by others
References
Barré, D., M. Kraushaar, G. Staffelbach, V. Moureau, and L. Y. M. Gicquel. Compressible and low Mach number LES of a swirl experimental burner. Comptes Rendus Mécanique 341:277–287, 2013.
Baya Toda, H., O. Cabrit, K. Truffin, G. Bruneaux, and F. Nicoud. Assessment of subgrid-scale models with a large-eddy simulation-dedicated experimental database: the pulsatile impinging jet in turbulent cross-flow. Phys. Fluids 26:075108, 2014.
Carlsson, M., E. Heiberg, J. Toger, and H. Arheden. Quantification of left and right ventricular kinetic energy using four-dimensional intracardiac magnetic resonance imaging flow measurements. AJP Hear. Circ. Physiol. 302:H893–H900, 2012.
Celik, I. B., Z. N. Cehreli, and I. Yavuz. Index of resolution quality for large eddy simulations. J. Fluids Eng. 127:949, 2005.
Charonko, J. J., R. Kumar, K. Stewart, W. C. Little, and P. P. Vlachos. Vortices formed on the mitral valve tips aid normal left ventricular filling. Ann. Biomed. Eng. 41:1049–1061, 2013.
Cheng, C. P., D. Parker, and C. A. Taylor. Quantification of Wall shear stress in large blood vessels using Lagrangian interpolation functions with cine phase-contrast magnetic resonance imaging. Ann. Biomed. Eng. 30:1020–1032, 2002.
Chien, S. Shear dependence of effective cell volume as a determinant of blood viscosity. Science (80-) 168:977–979, 1970.
Chnafa, C. Using image-based large-eddy simulations to investigate the intracardiac flow and its turbulent nature. Montpellier: University of Montpellier, 2014.
Chnafa, C., S. Mendez, R. Moreno, and F. Nicoud. Using image-based CFD to investigate the intracardiac turbulence. In: Modeling the Heart and the Circulatory System, edited by A. Quarteroni. New-York: Springer, 2015, pp. 97–117.
Chnafa, C., S. Mendez, and F. Nicoud. Image-based large-eddy simulation in a realistic left heart. Comput. Fluids 94:173–187, 2014.
Collins, S. P., P. Arand, C. J. Lindsell, W. F. Peacock, and A. B. Storrow. Prevalence of the third and fourth heart sound in asymptomatic adults. Congest. Hear. Fail. 11:242–247, 2005.
Davies, P. F., A. Remuzzi, E. J. Gordon, C. F. Dewey, and M. A. Gimbrone. Turbulent fluid shear stress induces vascular endothelial cell turnover in vitro. Proc. Natl. Acad. Sci. USA 83:2114–2117, 1986.
Domenichini, F., G. Pedrizzetti, and B. Baccani. Three-dimensional filling flow into a model left ventricle. J. Fluid Mech. 539:179, 2005.
Domenichini, F., G. Querzoli, A. Cenedese, and G. Pedrizzetti. Combined experimental and numerical analysis of the flow structure into the left ventricle. J. Biomech. 40:1988–1994, 2007.
Dyverfeldt, P., M. Bissell, A. J. Barker, A. F. Bolger, C.-J. Carlhäll, T. Ebbers, C. J. Francios, A. Frydrychowicz, J. Geiger, D. Giese, M. D. Hope, P. J. Kilner, S. Kozerke, S. Myerson, S. Neubauer, O. Wieben, and M. Markl. 4D flow cardiovascular magnetic resonance consensus statement. J. Cardiovasc. Magn. Reson. 17:72, 2015.
Dyverfeldt, P., M. D. Hope, E. E. Tseng, and D. Saloner. Magnetic resonance measurement of turbulent kinetic energy for the estimation of irreversible pressure loss in aortic stenosis. JACC Cardiovasc. Imaging 6:64–71, 2013.
Dyverfeldt, P., J.-P. E. Kvitting, C. J. Carlhäll, G. Boano, A. Sigfridsson, U. Hermansson, A. F. Bolger, J. Engvall, and T. Ebbers. Hemodynamic aspects of mitral regurgitation assessed by generalized phase-contrast MRI. J. Magn. Reson. Imaging 33:582–588, 2011.
Dyverfeldt, P., J. P. E. Kvitting, A. Sigfridsson, J. Engvall, A. F. Bolger, and T. Ebbers. Assessment of fluctuating velocities in disturbed cardiovascular blood flow: in vivo feasibility of generalized phase-contrast MRI. J. Magn. Reson. Imaging 28:655–663, 2008.
Falahatpisheh, A., and A. Kheradvar. High-speed particle image velocimetry to assess cardiac fluid dynamics in vitro: from performance to validation. Eur. J. Mech. B/Fluids 35:2–8, 2012.
Glower, D. D., R. L. Murrah, C. O. Olsen, J. W. Davis, and J. S. Rankin. Mechanical correlates of the third heart sound. J. Am. Coll. Cardiol. 19:450–457, 1992.
Hendabadi, S., J. Bermejo, Y. Benito, R. Yotti, F. Fernández-Avilés, J. C. Del Álamo, and S. C. Shadden. Topology of blood transport in the human left ventricle by novel processing of doppler echocardiography. Ann. Biomed. Eng. 41:2603–2616, 2013.
Hult, P., T. Fjällbrant, B. Wranne, and P. Ask. Detection of the third heart sound using a tailored wavelet approach. Med. Biol. Eng. Comput. 42:253–258, 2004.
Kanski, M., P. M. Arvidsson, J. Töger, R. Borgquist, E. Heiberg, M. Carlsson, and H. Arheden. Left ventricular fluid kinetic energy time curves in heart failure from cardiovascular magnetic resonance 4D flow data. J. Cardiovasc. Magn. Reson. 17:111, 2015.
Khalafvand, S. S., E. Y. K. Ng, L. Zhong, and T. K. Hung. Fluid-dynamics modelling of the human left ventricle with dynamic mesh for normal and myocardial infarction: preliminary study. Comput. Biol. Med. 42:863–870, 2012.
Kheradvar, A., and M. Gharib. On mitral valve dynamics and its connection to early diastolic flow. Ann. Biomed. Eng. 37:1–13, 2009.
Kilner, P. J., G. Z. Yang, A. J. Wilkes, R. H. Mohiaddin, D. N. Firmin, and M. H. Yacoub. Asymmetric redirection of flow through the heart. Nature 404:759–761, 2000.
Kono, T., H. Rosman, M. Alam, P. D. Stein, H. N. Sabbah, D. Stein, and N. Wbbah. Hemodynamic correlates of the third heart sound during the evolution of chronic heart failure. Am. J. Med. 21:419–423, 1992.
Le, T. B., and F. Sotiropoulos. On the three-dimensional vortical structure of early diastolic flow in a patient-specific left ventricle. Eur. J. Mech. B/Fluids 35:20–24, 2012.
Long, Q., R. Merrifield, X. Y. Xu, P. Kilner, D. N. Firmin, and G.-Z. Yang. Subject-specific computational simulation of left ventricular flow based on magnetic resonance imaging. Proc. Inst. Mech. Eng. H 222:475–485, 2008.
Lu, P. C., H. C. Lai, and J. S. Liu. A reevaluation and discussion on the threshold limit for hemolysis in a turbulent shear flow. J. Biomech. 34:1361–1364, 2001.
Mann, D. L., D. P. Zipes, P. Libby, and R. O. Bonow. Braunwald’s Heart Disease: A Textbook of Cardiovascular Medicine. Philadelphia: Elsevier, p. 2136, 2014.
Markl, M., P. J. Kilner, and T. Ebbers. Comprehensive 4D velocity mapping of the heart and great vessels by cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 13:7, 2011.
Mendez, S., E. Gibaud, and F. Nicoud. An unstructured solver for simulations of deformable particles in flows at arbitrary Reynolds numbers. J. Comput. Phys. 256:465–483, 2014.
Mihalef, V., R. I. Ionasec, P. Sharma, B. Georgescu, I. Voigt, M. Suehling, and D. Comaniciu. Patient-specific modelling of whole heart anatomy, dynamics and haemodynamics from four-dimensional cardiac CT images. Interface Focus 1:286–296, 2011.
Nicoud, F., H. B. Toda, O. Cabrit, S. Bose, and J. Lee. Using singular values to build a subgrid-scale model for large eddy simulations. Phys. Fluids 23:1–35, 2011.
Olesen, S. P., D. E. Clapham, and P. F. Davies. Haemodynamic shear stress activates a K+ current in vascular endothelial cells. Nature 331:168–170, 1988.
Pasipoularides, A. Diastolic filling vortex forces and cardiac adaptations: probing the epigenetic nexus. Hell. J. Cardiol. 53:458–469, 2012.
Pasipoularides, A. Mechanotransduction mechanisms for intraventricular diastolic vortex forces and myocardial deformations: part 1. J. Cardiovasc. Transl. Res. 8:76–87, 2015.
Pedrizzetti, G., and F. Domenichini. Left ventricular fluid mechanics: the long way from theoretical models to clinical applications. Ann. Biomed. Eng. 43:26–40, 2015.
Pedrizzetti, G., F. Domenichini, and G. Tonti. On the left ventricular vortex reversal after mitral valve replacement. Ann. Biomed. Eng. 38:769–773, 2010.
Pedrizzetti, G., G. La Canna, O. Alfieri, and G. Tonti. The vortex—an early predictor of cardiovascular outcome? Nat. Rev. Cardiol. 11:545–553, 2014.
Pham, D. L., C. Xu, and J. L. Prince. Current methods in medical image segmentation. Annu. Rev. Biomed. Eng. 2:315–337, 2000.
Pope, S. B. Turbulent Flows. Cambridge: Cambridge University Press, 2000. doi:10.1088/0957-0233/12/11/705.
Pope, S. B. Ten questions concerning the large-eddy simulation of turbulent flows. N. J. Phys. 6:35, 2004.
Querzoli, G., S. Fortini, and A. Cenedese. Effect of the prosthetic mitral valve on vortex dynamics and turbulence of the left ventricular flow. Phys. Fluids 22:1–10, 2010.
Sabbah, H. N., and P. D. Stein. Turbulent blood flow in humans: its primary role in the production of ejection murmurs. Circ. Res. 38:513–525, 1976.
Saber, N. R., N. B. Wood, A. D. Gosman, R. D. Merrifield, G. Z. Yang, C. L. Charrier, P. D. Gatehouse, and D. N. Firmin. Progress towards patient-specific computational flow modeling of the left heart via combination of magnetic resonance imaging with computational fluid dynamics. Ann. Biomed. Eng. 31:42–52, 2003.
Schenkel, T., M. Malve, M. Reik, M. Markl, B. Jung, and H. Oertel. MRI-Based CFD analysis of flow in a human left ventricle: methodology and application to a healthy heart. Ann. Biomed. Eng. 37:503–515, 2009.
Töger, J., M. Kanski, M. Carlsson, S. J. Kovács, G. Söderlind, H. Arheden, and E. Heiberg. Vortex ring formation in the left ventricle of the heart: analysis by 4D Flow MRI and Lagrangian Coherent Structures. Ann. Biomed. Eng. 2012. doi:10.1007/s10439-012-0615-3.
Valen-Sendstad, K., and D. A. Steinman. Mind the gap: impact of computational fluid dynamics solution strategy on prediction of intracranial aneurysm hemodynamics and rupture status indicators. Am. J. Neuroradiol. 35:536–543, 2014.
Vedula, V., J.-H. Seo, A. C. Lardo, and R. Mittal. Effect of trabeculae and papillary muscles on the hemodynamics of the left ventricle. Theor. Comput. Fluid Dyn. 2015. doi:10.1007/s00162-015-0349-6.
Watanabe, H., S. Sugiura, and T. Hisada. The looped heart does not save energy by maintaining the momentum of blood flowing in the ventricle. Am. J. Physiol. Heart Circ. Physiol. 294:H2191–H2196, 2008.
Zajac, J., J. Eriksson, P. Dyverfeldt, A. F. Bolger, T. Ebbers, and C.-J. Carlhäll. Turbulent kinetic energy in normal and myopathic left ventricles. J. Magn. Reson. Imaging 41:1021–1029, 2015.
Acknowledgments
The authors would like to express their gratitude to MD Dr. D. Coisne for many fruitful discussions. Dr. R. Moreno from the Rangueil University Hospital, Toulouse (France) is acknowledged for the CMR exams. Dr. V. Moureau and Dr. G. Lartigue from the CORIA lab, and the SUCCESS scientific group are acknowledged for providing the YALES2 code, which served as a basis for the development of YALES2BIO. This work was performed using HPC resources from GENCI-CINES (Grants 2014- and 2015-c2014037194).
Author information
Authors and Affiliations
Corresponding author
Additional information
Associate Editor Umberto Morbiducci oversaw the review of this article.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Chnafa, C., Mendez, S. & Nicoud, F. Image-Based Simulations Show Important Flow Fluctuations in a Normal Left Ventricle: What Could be the Implications?. Ann Biomed Eng 44, 3346–3358 (2016). https://doi.org/10.1007/s10439-016-1614-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10439-016-1614-6