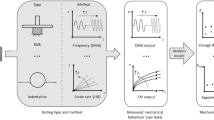
Abstract
Measurement the viscoelastic properties is important for studying the developmental and pathological behavior of soft biological tissues. Magnetic resonance elastography (MRE) is a non-invasive method for in vivo measurement of tissue viscoelasticity. As a flexible method capable of testing small samples, indentation has been widely used for characterizing soft tissues. Using 2nd-order Prony series and dimensional analysis, we analyzed and compared the model parameters estimated from both indentation and MRE. Conversions of the model parameters estimated from the two methods were established. We found that the indention test is better at capturing the dynamic response of tissues at a frequency less than 10 Hz, while MRE is better for describing the frequency responses at a relatively higher range. The results provided helpful information for testing soft tissues using indentation and MRE. The models analyzed are also helpful for quantifying the frequency response of viscoelastic tissues.
Graphic Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Biomechanical measurement of soft tissues in vivo plays an important role in diagnostics and treatment of diseases [1, 2]. Quantitative measurement of the viscoelastic properties provides insights into the development and pathology of tissues. The measured viscoelastic parameters could help construct theoretical models for the prognosis of diseases in organs such as brain and liver [3,4,5,6].
Traditionally, viscoelastic properties were measured using indentation or rotational rheometry [7, 8]. Magnetic resonance elastography (MRE) has been clinically used for in vivo measurement of viscoelasticity [9, 10]. To verify the in vivo measurement, many studies have compared the measurement results from rheometry and MRE [3, 11, 12]. Besides rotational rheometry, different forms of dynamic mechanical tests were also used for comparison and validation [13].
The indentation test is a widely used technique for quantification of mechanical properties in both macro and nanoscales [14,15,16,17]. It has also been modified to combine with rheometry for a wide range of frequency test [18]. Due to its capability to measure small-sized samples, indentation has been used for measuring the viscoelastic properties of many soft tissues [19,20,21]. However, few studies have quantified the viscoelastic measurement between the indentation and MRE methods.
The selection of viscoelastic models is crucial for analyzing results from ex vivo and in vivo measurements. Klatt et al. [22] were among the earliest to study the frequency responses of the soft tissues using rotational rheometry and MRE. By using multi-frequency MRE, they found that a 3-parameter Zener model provided the best fit for the dynamic response of shear moduli. Weickenmeier et al. [23] used a standard linear solid model to analyze the frequency response of brain tissue. However, a model that can be used for viscoelastic characterization for both indentation and MRE tests is still needed.
In this study, we first analyzed and explained the physical meanings of the parameters from the Prony series. Then, viscoelastic properties measured using indentation and MRE were compared and analyzed. The analytical responses of the model based on indentation and MRE were also compared. Finally, we made quantitative comparisons of the two tests using phantom and animal experiment data.
2 Viscoelastic model
The deformation of soft tissues is usually small in MRE and indentation tests. For example, displacements of shear wave propagation in MRE were in the magnitude of micrometers [24, 25]. Therefore, small strain deformation was assumed, and the linear viscoelastic material model was adopted for the analysis.
2.1 Linear viscoelastic models and Prony series
Linear viscoelastic models have been widely used for characterizing the soft biological tissues [26,27,28,29,30]. A general form of the constitutive equation of the linear viscoelastic material is [31]
The Laplace transform form of Eq. (1) is usually used for analysis:
where \(P\left(s\right)=\sum_{k=0}^{m}{p}_{k}{s}^{k}\) and \(Q\left(s\right)=\sum_{k=0}^{n}{q}_{k}{s}^{k}\). Typically, a ramp-hold displacement is usually applied to the sample in an indentation test, inducing a stress relaxation response. If a step function is \(u(t)\), the ramp-hold indentation input can be written as \(\varepsilon \left(t\right)={\varepsilon }_{0}u(t)\). The corresponding stress response can be solved by substituting \(\stackrel{-}{\varepsilon }\left(\mathrm{s}\right)={\varepsilon }_{0}/s\) into Eq. (2)
where \(E\left(s\right)\) is the Young’s modulus in the Laplace plane. The time-dependent relaxation of stress is
where \(Y\left(t\right)={\mathcal{L}}^{-1}\left\{E(s)\right\}\) is the relaxation modulus. If an incompressible condition is assumed for the tissue, where the Poisson’s ratio \(\nu \) is 0.5, a relaxation shear modulus could also be defined as \(G\left(t\right)=Y\left(t\right)/3\). In indentation tests, the relaxation process can be approximated using Prony series. Therefore, the relaxation shear modulus can be written in a series form:
where \({C}_{i}\) and \({\tau }_{i}\) are constants that could be determined by fitting experiment curves.
For most biological tissues, a 2nd-order approximation could provide a reasonable approximation of the relaxation process. Therefore with \(l=2\),
2.2 Physical interpretation of the 2nd-order Prony series
The physical interpretation of the 2nd-order Prony series can be illustrated using a standard spring-dashpot Maxwell model (Fig. 1). \({E}_{i}\) and \({F}_{i}\) represent the spring and dashpot constants, respectively. The corresponding Laplacian transformation of the time-dependent elastic modulus \(E(t)\) is
Once the relaxation shear modulus was determined from Eq. (6), the spring and dashpot parameters can be determined:
In fact, this constitutive equation is equivalent to a 5-parameter Kelvin model.
2.3 Dynamic shear modulus
For dynamic response of the linear viscoelastic material, a harmonic vibration is usually applied. In MRE, for example, a vibration with a fixed frequency is applied to generate shear wave in soft tissues. If a harmonic vibration of strain \(\varepsilon \left(t\right)={\varepsilon }_{0}{\mathrm{e}}^{\mathrm{i}\omega t}\) is applied, with Eq. (1), the stress response is
For steady-state response \(\sigma \left(t\right)={\sigma }_{0}{\mathrm{e}}^{\mathrm{i}\omega t}\), we have
If we define the dynamic Young’s modulus as \(E(\mathrm{i}\omega )=\frac{Q(\mathrm{i}\omega )}{P(\mathrm{i}\omega )}\), for incompressible material, the dynamic shear modulus is \(G\left(\mathrm{i}\omega \right)=E(\mathrm{i}\omega )/3\). For the 2nd-order Prony series,
By comparing with Eq. (7), the parameters written in terms of the physical parameters are
By substituting Eq. (8), the parameters can be expressed in terms of the fitting constants:
Using Eqs. (11) and (13), a conversion is established between the dynamic shear modulus and the parameters of the Prony series.
2.4 Dimensional analysis
For experimental measurement, indentation tests can be carried out in scales from nanometers [32] to millimeters [30]. However, the measured displacement using MRE is usually on the scale of micrometers. Despite the different measurement scales, the equation that describes the relationship between the physical quantities should remain the same regardless of the unit. Therefore, if we compare tests in millimeter and micrometer scales, dimensional analysis is needed for a conversion.
For a flat-top indentation [29], the general form of the reaction force \(F\) is
where \(R\) is the radius of the indenter, \(V\) is the indentation velocity, \(C\) is the shear modulus of the tested material, and \(\tau \) is the relaxation time constant. The dimensions of the variables are
Therefore, the dimensionless independent variables are
The dimensionless dependent variable is
Based on the Pi theorem [33], Eq. (14) can be transformed to \({\Pi }_{0}=\stackrel{\sim }{f}({\Pi }_{1},{\Pi }_{2})\).
Using the similarity principle [33], a conversion between different measurement scales could be achieved by keeping the dimensionless variables the same. Considering \(C\) is the intrinsic properties of the material, if we keep the same indentation velocity, the unit of \(\tau \) would be inversely proportional to the unit of \(R\). For example, if the indentation is in the scale of millimeters, and the measured relaxation time constant is in seconds, the converted measurement of the relaxation time constant should be in milliseconds corresponding to an indentation in micrometers.
Similar dimensional analysis has been used for indentation studies. Using the Pi theorem, Cao et al. [34] found the normalized relaxation modulus depends only on the indentation loads, independent of the indenter geometry. The dimensional analysis has also been used for characterizing hyperelastic materials [35].
3 Analysis of stress relaxation
In this section, we compared different procedures of fitting parameters in the indentation test. As a demonstration, we used brain tissues of female mice (Balb/c, 8 weeks old, 16 g, SPF grade, certificate No. SCXK 2018-0006) for all the analyses in this section. The indentation region of interest (ROI) was the right cortex. The indentation strain and velocity were 8% and 0.6 mm/s, respectively. Each sample slice had a thickness of about 3 mm. The detailed experiment protocol has been reported in previous studies [36]. The results validated the selection of the 2nd-order Prony series and provided helpful guidelines for the indentation experiment.
3.1 Comparisons of different fitting schemes
A typical relaxation test has a ramp section and a relaxation section. To find the best parameter estimation, we used a ramp section only, a relaxation section only, and both sections for fitting (Fig. 2). We observed that the model fitted with a ramp section only could not describe the relaxation behavior (Fig. 2a). It indicated that the ramp section could capture the elastic response of the tissue but provided no viscoelastic information. By fitting the relaxation section only, we observed that the model could not describe the ramp behavior, thus losing the elastic information (Fig. 2b). The collective fitting of both sections captures both the ramp and relaxation responses (Fig. 2c).
In addition, we also compared the frequency responses of the viscoelastic model using Eqs. (11) and (13) (Fig. 3). We observed no frequency-dependent response with the model fitted with the ramp section only. This is consistent with our previous observation that only elastic information was included in the ramp section. The shear moduli were higher for the model fitted with both sections. This again suggested a loss of elastic component when fitted for the relaxation section only. Therefore, the analysis of both ramp and relaxation sections is a necessity for accurate measurement of viscoelastic behavior.
3.2 Selection of relaxation time
Since the relaxation section provides curial information of the viscoelastic behavior, we compared the frequency responses of the model estimated from fitting different relaxation time. Although a longer relaxation time would provide a better estimation of the viscoelastic parameters, practical issues such as tissue dehydration and measurement efficiency constrained the selection of longer relaxation time. We took a relaxation time of 60 s, 80 s, 120 s, 180 s for analysis [37,38,39], where no significant differences in the estimated shear moduli were observed. We observed a similar frequency response except for the low-frequency section (< 1 Hz). However, since most of the dynamic measurements of the viscoelastic properties were in the larger frequency range (> 1 Hz), the relaxation time does not play a significant role in characterizing the viscoelastic behavior (Fig. 4).
3.3 Order of the Prony series
Although higher orders of the Prony series can improve the fitting accuracy, it will complicate the parameter analysis and the computational implementation for simulations. Studies have shown that the 2nd-order Prony series could fit the experiment curve with enough accuracy [30, 40, 41]. We analyzed the frequency response of the Prony series with three different orders. Considering the poor performance of the 1st-order Prony series (Fig. 5), we focused on comparing the 2nd- and 3rd-order Prony series. For the 3rd-order Prony series, the patterns of \({G}_{2}\) and \(\phi \) values appeared to deviate from that of the 1st- and 2nd-order results at the lower frequency range (< 1 Hz). This is probably because the 3rd-order Prony series not only captured the fine details of the relaxation curve but also experimental noise. Therefore, the 2nd-order Prony series could provide the best trade-off between accuracy and model complexity (Fig. 6).
4 Analysis of dynamic response from phantom and tissue
Based on the previous analysis, we used the 2nd-order Prony series to characterize the viscoelastic properties of a gel phantom and analyzed the corresponding dynamic frequency response. The dynamic shear moduli were compared with that measured from MRE. We also carried out similar analysis using mouse brain data from literature and discussed the differences between ex vivo and in vivo measurements.
4.1 Phantom test
We made a tissue-mimicking gelatin phantom [24, 42] for both indentation and MRE tests. Viscoelastic properties were measured using a custom-built indentation tester [36]. The sample was indented with 8% of its thickness and relaxed for 180 s (Fig. 7a).
A custom-built magnetic resonance elastography system was used for measuring the dynamic moduli of the phantom [24]. The experiments were Shanghai, China). The actuator and the phantom were placed in a 24-channel head coil (Fig. 7b). The frequency of actuation was set to 50, 60, 70, 80, 90, and 100 Hz. A spin-echo based echo-planar imaging MRE sequence was used for imaging, a matrix size of 127 × 127, and a slice thickness of 5 mm.
Viscoelastic properties were estimated by fitting the 2nd-order Prony series to both the ramp and relaxation sections (Fig. 7c). Dynamic shear moduli from MRE were estimated by both local frequency estimation (LFE) and direction inversion (DI) method [43]. LFE method estimates the local wave length \(\lambda \) and the corresponding shear modulus is
where \(\rho \) is the tissue density and \(\omega \) is the vibration frequency. For DI method,
where \(\rho \) is the tissue density, \(\omega \) is the vibration frequency, \(\Delta \) is the Laplacian operator, and \({U}_{1}\) is the Fourier fundamental component of the displacement field [44].
In the frequency range of 50–100 Hz, we observed an apparent frequency-dependent behavior by MRE (Fig. 8). The shear moduli increased monotonically with the vibration frequency. However, in the same frequency range, no apparent frequency-dependent behavior was observed based on the indentation test. Both tests showed the loss moduli were lower than the storage moduli, which indicated that the gel phantom is more of a solid.
With \(E\left(\mathrm{i}\omega \right)=\frac{Q(\mathrm{i}\omega )}{P(\mathrm{i}\omega )}\) and relaxation modulus \(Y\left(t\right)={\mathcal{L}}^{-1}\left\{E(s)\right\}={\mathcal{L}}^{-1}\{\frac{Q\left(s\right)}{sP\left(s\right)}\}\), we define \(E\left(\mathrm{i}\omega \right)\) as
Taking the form of the 2nd-order Prony series of Eq. (7), \(E\left(\mathrm{i}\omega \right)\) can be rewritten as
For incompressible material, \(G\left(\mathrm{i}\omega \right)=E\left(\mathrm{i}\omega \right)/3.\) With Eq. (8), the storage modulus \({G}_{1}\left(\mathrm{i}\omega \right)\) is
By fitting the frequency response data from the MRE test with Eq. (22), we obtained the corresponding Prony series parameters: \({C}_{0}\) = 1.46 kPa, \({C}_{1}\) = 3.72 kPa, \({C}_{2}\) = 1.77 kPa, \({\tau }_{1}\) = 2.01 ms, \({\tau }_{2}\)= 28.65 ms. Assuming the same ramp velocity and indentation depth, a pseudo indentation curve can be plotted (Fig. 9). We observed that the peak ramp force from the pseudo indentation curve was smaller due to the small relaxation coefficient \({\tau }_{1}\) and \({\tau }_{2}\). Therefore, the shear modulus attenuated to \({C}_{0}\) in a very short time, resulting in a lower ramp force.
Our results are consistent with the dynamic compressive mechanical test, where the frequency response was observable only in a frequency range larger than 30 Hz [45]. This also implies that the dynamic response of viscoelastic materials can be predicted using a ramp-hold indentation test. A direct comparison between the dynamic mechanical test and the MRE test using gel phantom showed a close match of the measured shear moduli [13]. A linear correlation was also observed for the shear moduli measured using rotational rheometry and MRE [3]. However, the differences in the frequency response between the rheometry and indentation tests indicated that boundary and loading conditions may have considerable influences. Besides, the differences of the dynamic \(E\) and \(G\) values implied that the Poisson’s ratio could be frequency-dependent too.
4.2 Comparison of brain tissue test
We took two indentation tests of mouse brain tissue for analysis, one in the micron-scale [46] and the other in the millimeter scale [30]. The viscoelastic parameters of the cortex using 2nd-order Prony series are summarized in Table 1. The displacement in MRE is in microns [47] and the velocities of both indentation and MRE are on the same scale (mm/s). Therefore, the corresponding relaxation time must be converted from seconds to milliseconds, as discussed in Sect. 2.4. A similar pattern with different amplitude showed a clear frequency-dependent response of the mouse brain tissue (Fig. 10).
By comparing results from MRE test (Fig. 11), we observed the \({G}_{1}\) and \(|{G}^{*}|\) values measured by MRE are mostly in the range from 4 to 8 kPa. The \({G}_{1}\) value measured by MacManus et al. [46] is 6.5 kPa, while by Qiu et al. [30] is 1.73 kPa. Besides the differences in frequency response of the two methods, the results also quantify the differences between in vivo and ex vivo measurements. Because of the low \({G}_{2}\) values from the indentation tests, we observed the small difference between \({G}_{1}\) and \(|{G}^{*}|\) values. Compared with indentation, the phase angles measured by MRE were between 0.3 and 0.7 radians. These results indicated the mouse brain demonstrated a more of a solid behavior in vivo. The large discrepancy of the estimated shear moduli between in vivo MRE and ex vivo indentation showed that the testing condition and inversion algorithm greatly influenced the results.
Comparisons of a storage modulus, b loss modulus, c shear modulus amplitude, and d phase angle of mouse brain measured using indentation and MRE [30, 46, 48,49,50,51,52,53,54]. SN: substantia nigra; CTR: the mouse type (C57BL/6 J) in the control group; APP23: a mouse model used for studying Alzheimer’s disease
5 Conclusions
In this study, we analyzed and compared the viscoelastic parameters estimated from indentation and MRE. A summary of the main findings is:
-
1.
The 2nd-order Prony series provided a good trade-off between the fitting accuracy and model complexity to describe the viscoelastic behavior of soft tissues.
-
2.
To compare the parameters estimated from indentation and MRE at different scales, we used dimensional analysis to convert the parameters between the two measurements.
-
3.
Both Indentation and MRE tests can be used to measure the dynamic response of viscoelastic soft tissues. The former is more prone to capture the low-frequency range response (less than 10 Hz), while the latter is better for describing the response at a relatively higher frequency range.
By comparing the gel phantom and brain tissue tests, we have illustrated the differences between in vivo and ex vivo tests. The results could provide helpful information for the ex vivo and in vivo measurements of soft tissues.
References
Streitberger, K.J., Lilaj, L., Schrank, F., et al.: How tissue fluidity influences brain tumor progression. Proc. Natl. Acad. Sci. USA 117, 128–134 (2020). https://doi.org/10.1073/pnas.1913511116
Chaudhuri, O., Cooper-White, J., Janmey, P.A., et al.: Effects of extracellular matrix viscoelasticity on cellular behaviour. Nature 584, 535–546 (2020). https://doi.org/10.1038/s41586-020-2612-2
Klatt, D., Friedrich, C., Korth, Y., et al.: Viscoelastic properties of liver measured by oscillatory rheometry and multifrequency magnetic resonance elastography. Biorheology 47, 133–141 (2010). https://doi.org/10.3233/BIR-2010-0565
Comellas, E., Budday, S., Pelteret, J.P., et al.: Modeling the porous and viscous responses of human brain tissue behavior. Comput. Methods Appl. Mech. Eng. 369, 113128 (2020). https://doi.org/10.1016/j.cma.2020.113128
Li, X., Zhou, Z., Kleiven, S.: An anatomically detailed and personalizable head injury model: significance of brain and white matter tract morphological variability on strain. Biomech. Model. Mechanobiol. (2020), in press. https://doi.org/10.1007/s10237-020-01391-8
Wang, J., Yu, Q.Y., Li, W., et al.: Influence of clamping stress and duration on the trauma of liver tissue during surgery operation. Clin. Biomech. 43, 58–66 (2017). https://doi.org/10.1016/j.clinbiomech.2017.02.005
Cirka, H.A., Koehler, S.A., Farr, W.W., et al.: Eccentric rheometry for viscoelastic characterization of small, soft, anisotropic, and irregularly shaped biopolymer gels and tissue biopsies. Ann. Biomed. Eng. 40, 1654–1665 (2012). https://doi.org/10.1007/s10439-012-0532-5
Li, Y., Deng, J., Zhou, J., et al.: Elastic and viscoelastic mechanical properties of brain tissues on the implanting trajectory of sub-thalamic nucleus stimulation. J. Mater. Sci. Mater. Med. 27, 163 (2016). https://doi.org/10.1007/s10856-016-5775-5
Bunevicius, A., Schregel, K., Sinkus, R., et al.: REVIEW: MR elastography of brain tumors. Neuroimage Clin. 25, 102109 (2020). https://doi.org/10.1016/j.nicl.2019.102109
Garteiser, P., Doblas, S., Van Beers, B.E.: Magnetic resonance elastography of liver and spleen: methods and applications. Nmr Biomed. 31, e3891 (2018). https://doi.org/10.1002/nbm.3891
Dittmann, F., Hirsch, S., Tzschatzsch, H., et al.: In vivo wideband multifrequency MR elastography of the human brain and liver. Magn. Reson. Med. 76, 1116–1126 (2016). https://doi.org/10.1002/mrm.26006
Vappou, J., Breton, E., Choquet, P., et al.: Magnetic resonance elastography compared with rotational rheometry for in vitro brain tissue viscoelasticity measurement. MAGMA. 20, 273–278 (2007). https://doi.org/10.1007/s10334-007-0098-7
Arunachalam, S.P., Rossman, P.J., Arani, A., et al.: Quantitative 3D magnetic resonance elastography: comparison with dynamic mechanical analysis. Magn. Reson. Med. 77, 1184–1192 (2017). https://doi.org/10.1002/mrm.26207
Sakai, M., Shimizu, S.: Indentation rheometry for glass-forming materials. J. Non-Cryst. Solids 282, 236–247 (2001). https://doi.org/10.1016/S0022-3093(01)00316-7
Wang, G.F., Niu, X.R.: Nanoindentation of soft solids by a flat punch. Acta Mech. Sin. 31, 531–535 (2015). https://doi.org/10.1007/s10409-015-0440-7
Li, M., Zhang, H.X., Zhao, Z.L., et al.: Surface effects on cylindrical indentation of a soft layer on a rigid substrate. Acta Mech. Sin. 36, 422–429 (2020). https://doi.org/10.1007/s10409-020-00941-8
Wei, Y., Wang, X., Zhao, M., et al.: Size effect and geometrical effect of solids in micro-indentation test. Acta Mech. Sin. 19, 59–70 (2003). https://doi.org/10.1007/BF02487454
Rolley, E., Snoeijer, J.H., Andreotti, B.: A flexible rheometer design to measure the visco-elastic response of soft solids over a wide range of frequency. Rev. Sci. Instrum. 90, 023906 (2019). https://doi.org/10.1063/1.5064599
Zhang, H., Guo, Y., Zhou, Y., et al.: Fluidity and elasticity form a concise set of viscoelastic biomarkers for breast cancer diagnosis based on Kelvin-Voigt fractional derivative modeling. Biomech. Model. Mechanobiol. 19, 2163–2177 (2020). https://doi.org/10.1007/s10237-020-01330-7
MacManus, D.B., Maillet, M., O’Gorman, S., et al.: Sex- and age-specific mechanical properties of liver tissue under dynamic loading conditions. J. Mech. Behav. Biomed. Mater. 99, 240–246 (2019). https://doi.org/10.1016/j.jmbbm.2019.07.028
Kihan, P., Lonsberry, G.E., Gearing, M., et al.: Viscoelastic properties of human autopsy brain tissues as biomarkers for alzheimer’s diseases. IEEE Trans. Biomed. Eng. 66, 1705–1713 (2019). https://doi.org/10.1109/TBME.2018.2878555
Klatt, D., Hamhaber, U., Asbach, P., et al.: Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: a study of brain and liver viscoelasticity. Phys. Med. Biol. 52, 7281–7294 (2007). https://doi.org/10.1088/0031-9155/52/24/006
Weickenmeier, J., Kurt, M., Ozkaya, E., et al.: Magnetic resonance elastography of the brain: a comparison between pigs and humans. J. Mech. Behav. Biomed. 77, 702–710 (2018). https://doi.org/10.1016/j.jmbbm.2017.08.029
Feng, Y., Zhu, M., Qiu, S., et al.: A multi-purpose electromagnetic actuator for magnetic resonance elastography. Magn. Reson. Imaging 51, 29–34 (2018). https://doi.org/10.1016/j.mri.2018.04.008
Murphy, M.C., Huston, J., Ehman, R.L.: MR elastography of the brain and its application in neurological diseases. NeuroImage 187, 176–183 (2019). https://doi.org/10.1016/j.neuroimage.2017.10.008
Qiang, B., Greenleaf, J., Oyen, M., et al.: Estimating material elasticity by spherical indentation load-relaxation tests on viscoelastic samples of finite thickness. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58, 1418–1429 (2011). https://doi.org/10.1109/TUFFC.2011.1961
Samadi-Dooki, A., Voyiadjis, G.Z., Stout, R.W.: A combined experimental, modeling, and computational approach to interpret the viscoelastic response of the white matter brain tissue during indentation. J. Mech. Behav. Biomed. Mater. 77, 24–33 (2018). https://doi.org/10.1016/j.jmbbm.2017.08.037
Finan, J.D., Sundaresh, S.N., Elkin, B.S., et al.: Regional mechanical properties of human brain tissue for computational models of traumatic brain injury. Acta Biomater. 55, 333–339 (2017). https://doi.org/10.1016/j.actbio.2017.03.037
Qiu, S., Zhao, X., Chen, J., et al.: Characterizing viscoelastic properties of breast cancer tissue in a mouse model using indentation. J. Biomech. 69, 81–89 (2018). https://doi.org/10.1016/j.jbiomech.2018.01.007
Qiu, S., Jiang, W., Alam, M.S., et al.: Viscoelastic characterization of injured brain tissue after controlled cortical impact (CCI) using a mouse model. J. Neurosci. Methods 330, 108463 (2020). https://doi.org/10.1016/j.jneumeth.2019.108463
Christensen, R.M.: Theory of Viscoelasticity. Dover, Mineola, NY (2003)
Hu, J., Chen, S., Huang, D., et al.: Global mapping of live cell mechanical features using PeakForce QNM AFM. Biophys. Rep. 6, 9–18 (2020). https://doi.org/10.1007/s41048-019-00103-9
Gibbings, J.C.: Dimensional Analysis. Springer, London (2011)
Cao, Y.P., Ji, X.Y., Feng, X.Q.: Geometry independence of the normalized relaxation functions of viscoelastic materials in indentation. Philos. Mag. (Abingdon) 90, 1639–1655 (2010). https://doi.org/10.1080/14786430903439826
Zhang, M.G., Cao, Y.P., Li, G.Y., et al.: Spherical indentation method for determining the constitutive parameters of hyperelastic soft materials. Biomech. Model. Mechanobiol. 13, 1–11 (2014). https://doi.org/10.1007/s10237-013-0481-4
Chen, Y., Qiu, S., Wang, C., et al.: Measurement of viscoelastic properties of injured mouse brain after controlled cortical impact. Biophys. Rep. 6, 137–145 (2020). https://doi.org/10.1007/s41048-020-00110-1
Antonovaite, N., Beekmans, S.V., Hol, E.M., et al.: Regional variations in stiffness in live mouse brain tissue determined by depth-controlled indentation mapping. Sci. Rep. 8, 12517 (2018). https://doi.org/10.1038/s41598-018-31035-y
Chen, F., Zhou, J., Li, Y., et al.: Mechanical properties of porcine brain tissue in the coronal plane: interregional variations of the corona radiata. Ann. Biomed. Eng. 43, 2903–2910 (2015). https://doi.org/10.1007/s10439-015-1350-3
Elkin, B.S., Morrison, B.: Viscoelastic properties of the P17 and adult rat brain from indentation in the coronal plane. J. Biomech. Eng. 135, 114507 (2013). https://doi.org/10.1115/1.4025386
Qian, L., Zhao, H., Guo, Y., et al.: Influence of strain rate on indentation response of porcine brain. J. Mech. Behav. Biomed. Mater. 82, 210–217 (2018). https://doi.org/10.1016/j.jmbbm.2018.03.031
Tönük, E., Silver-Thorn, M.B.: Nonlinear viscoelastic material property estimation of lower extremity residual limb tissues. J. Biomech. Eng. 126, 289–300 (2004). https://doi.org/10.1115/1.1695575
Feng, Y.: Dynamic deformation and mechanical properties of brain tissue. All Theses and Dissertations (ETDs). 1003 (2012). https://doi.org/10.7936/K7DB7ZW9
Fovargue, D., Nordsletten, D., Sinkus, R.: Stiffness reconstruction methods for MR elastography. Nmr. Biomed. 31, e3935 (2018). https://doi.org/10.1002/nbm.3935
Feng, Y., Clayton, E.H., Okamoto, R.J., et al.: A longitudinal magnetic resonance elastography study of murine brain tumors following radiation therapy. Phys. Med. Biol. 61, 6121–6131 (2016). https://doi.org/10.1088/0031-9155/61/16/6121
Bartlett, R.D., Eleftheriadou, D., Evans, R., et al.: Mechanical properties of the spinal cord and brain: Comparison with clinical-grade biomaterials for tissue engineering and regenerative medicine. Biomaterials 258, 120303 (2020). https://doi.org/10.1016/j.biomaterials.2020.120303
MacManus, D.B., Pierrat, B., Murphy, J.G., et al.: A viscoelastic analysis of the P56 mouse brain under large-deformation dynamic indentation. Acta Biomater. 48, 309–318 (2017). https://doi.org/10.1016/j.actbio.2016.10.029
Bertalan, G., Guo, J., Tzschätzsch, H., et al.: Fast tomoelastography of the mouse brain by multifrequency single-shot MR elastography. Magn. Reson. Med. 81, 2676–2687 (2019). https://doi.org/10.1002/mrm.27586
Boulet, T., Kelso, M.L., Othman, S.F.: Long-term in vivo imaging of viscoelastic properties of the mouse brain after controlled cortical impact. J. Neurotrauma 30, 1512–1520 (2013). https://doi.org/10.1089/neu.2012.2788
Hain, E.G., Klein, C., Munder, T., et al.: Dopaminergic neurodegeneration in the mouse is associated with decrease of viscoelasticity of substantia nigra tissue. PLoS ONE 11, e0161179 (2016). https://doi.org/10.1371/journal.pone.0161179
Jamin, Y., Boult, J.K.R., Li, J., et al.: Exploring the biomechanical properties of brain malignancies and their pathologic determinants in vivo with magnetic resonance elastography. Cancer Res. 75, 1216–1224 (2015). https://doi.org/10.1158/0008-5472.CAN-14-1997
Klein, C., Hain, E.G., Braun, J., et al.: Enhanced adult neurogenesis increases brain stiffness: in vivo magnetic resonance elastography in a mouse model of dopamine depletion. PLoS ONE 9, e92582 (2014). https://doi.org/10.1371/journal.pone.0092582
Riek, K., Millward, J.M., Hamann, I., et al.: Magnetic resonance elastography reveals altered brain viscoelasticity in experimental autoimmune encephalomyelitis. Neuroimage Clin. 1, 81–90 (2012). https://doi.org/10.1016/j.nicl.2012.09.003
Clayton, E.H., Garbow, J.R., Bayly, P.V.: Frequency-dependent viscoelastic parameters of mouse brain tissue estimated by MR elastography. Phys. Med. Biol. 56, 2391–2406 (2011). https://doi.org/10.1088/0031-9155/56/8/005
Munder, T., Pfeffer, A., Schreyer, S., et al.: MR elastography detection of early viscoelastic response of the murine hippocampus to amyloid beta accumulation and neuronal cell loss due to Alzheimer’s disease. J. Magn. Reson. Imaging 47, 105–114 (2018). https://doi.org/10.1002/jmri.25741
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant 31870941) and Shanghai Science and Technology Committee (Grant 1944190700). We thank the technical support from Jiayu Zhu, Xiaomao Gong, Cong Zhang, Xiaodong Zhou, and Qiang He from United Imaging Healthcare, Shanghai.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Executive Editor: Xi-Qiao Feng
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, Y., Qiu, S., He, Z. et al. Comparative analysis of indentation and magnetic resonance elastography for measuring viscoelastic properties. Acta Mech. Sin. 37, 527–536 (2021). https://doi.org/10.1007/s10409-020-01042-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10409-020-01042-2