Abstract
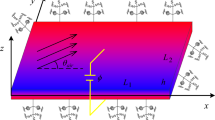
Using Reddy’s high-order shear theory for laminated plates and Hamilton’s principle, a nonlinear partial differential equation for the dynamics of a deploying cantilevered piezoelectric laminated composite plate, under the combined action of aerodynamic load and piezoelectric excitation, is introduced. Two-degree of freedom (DOF) nonlinear dynamic models for the time-varying coefficients describing the transverse vibration of the deploying laminate under the combined actions of a first-order aerodynamic force and piezoelectric excitation were obtained by selecting a suitable time-dependent modal function satisfying the displacement boundary conditions and applying second-order discretization using the Galerkin method. Using a numerical method, the time history curves of the deploying laminate were obtained, and its nonlinear dynamic characteristics, including extension speed and different piezoelectric excitations, were studied. The results suggest that the piezoelectric excitation has a clear effect on the change of the nonlinear dynamic characteristics of such piezoelectric laminated composite plates. The nonlinear vibration of the deploying cantilevered laminate can be effectively suppressed by choosing a suitable voltage and polarity.











Similar content being viewed by others
References
Lee, B.H.K., Price, S.J., Wong, Y.S.: Nonlinear aeroelastic analysis of airfoil: bifurcation and chaos. Prog. Aerospace Sci. 35, 205–334 (1999)
Arrison, M., Birocco, K., Gaylord, C., et al.: 2002–2003 AE/ME morphing wing design. Virginia Tech Aerospace Engineering Senior Design Project Spring Semester Final Report. (2003)
Tabarrok, B., Leech, C.M., Kim, Y.I.: On the dynamics of an axially moving beam. J. Frankl. Inst. 297, 201–220 (1974)
Taleb, I.A., Misra, A.K.: Dynamics of an axially moving beam submerged in a fluid. J. Hydronaut. 15, 62–66 (1981)
Wang, P.K.C., Wei, J.D.: Vibration in a moving flexible robot arm. J. Sound Vib. 116, 149–160 (1987)
Behdinan, K., Stylianou, M., Tabarrok, B.: Dynamics of flexible sliding beams non-linear analysis. Part I: formulation. J. Sound Vib. 208, 517–539 (1997)
Deng, Z.C., Zheng, H.J., Zhao, Y.L., et al.: On computation of dynamic properties for deploying cantilever beam based on precision integration method. J. Astronaut. 22, 110–113 (2001). (in Chinese)
Zhu, W.D., Zheng, N.A.: Exact response of a translating string with arbitrarily varying length under general excitation. J. Appl. Mech. 75, 519–525 (2008)
Gosselin, F., Paidoussis, M.P., Misra, A.K.: Stability of a deploying/deploying beam in dense fluid. J. Sound Vib. 299, 124–142 (2007)
Wang, L., Ni, Q.: Vibration and stability of an axially moving beam immersed in fluid. Int. J. Solids Struct. 45, 1445–1457 (2008)
Zhang, W., Sun, L., Yang, X.D., et al.: Nonlinear dynamic behaviors of a deploying-and-retreating wing with varying velocity. J. Sound Vib. 332, 6785–6797 (2013)
Huang, R., Qiu, Z.P.: Transient aeroelastic responses and flutter analysis of a variable-span wing during the morphing process. Chin. J. Aeronaut. 26, 1430–1438 (2013)
Wang, L.H., Hu, Z.D., Zhong, Z.: Dynamic analysis of an axially translating plate with time-variant length. Acta Mech. 215, 9–23 (2010)
Zhang, W., Lu, S.F., Yang, X.D.: Analysis on nonlinear dynamics of a deploying cantilever laminated composite plate. Nonlinear Dyn. 76, 69–93 (2014)
Yang, X.D., Zhang, W., Chen, L.Q., et al.: Dynamical analysis of axially moving plate by finite difference method. Nonlinear Dyn. 67, 997–1006 (2012)
Ding, H., Chen, L.Q.: Nonlinear dynamics of axially accelerating viscoelatic beams based on differential quadrature. Acta Mechanica Solida Sinica 22, 267–275 (2009)
Matsuzaki, Y., Torii, H., Toyama, M.: Vibration of a cantilevered beam during deployment and retrieval: analysis and experiment. Smart Mater. Struct. 4, 334–339 (1995)
Liu, K.F., Deng, L.Y.: Experimental verification of an algorithm for identification of linear time-varying systems. J. Sound Vib. 279, 1170–1180 (2005)
Liu, K.F., Deng, L.Y.: Identification of pseudo-natural frequencies of an axially moving cantilever beam using a subspace-based algorithm. Mech. Syst. Signal Process. 20, 94–113 (2006)
Fuller, C.R., Elliott, S.J., Nelson, P.A.: Active Control of Vibration. Academic Press, San Diego (1996)
Reddy, J.N., Mitchell, J.A.: On refined nonlinear theories of laminated composite structures with piezoelectric laminae. Sadhana 20, 721–747 (1995)
Rafiee, M., Mohammadi, M., Sobhani Aragh, B., et al.: Nonlinear free and forced thermo-electro-aero-elastic vibration and dynamic response of piezoelectric functionally graded laminated composite shells, Part I: Theory and analytical solutions. Compos. Struct. 103, 179–187 (2013)
Fu, Y.M., Wang, X.Q., Yang, J.H.: Nonlinear dynamic response of piezoelastic laminated plates considering damage effects. Compos. Struct. 81, 353–361 (2007)
Huang, X.L., Shen, H.S.: Nonlinear free and forced vibration of simply supported shear deformable laminated plates with piezoelectric actuators. Int. J. Mech. Sci. 47, 187–208 (2005)
Dash, P., Singh, B.N.: Nonlinear free vibration of piezoelectric laminated composite plate. Finite Elem. Anal. Des. 45, 686–694 (2009)
Wang, Y., Hao, Y.X., Wang, J.H.: Nonlinear vibration of a cantilever FGM Rectangular plate with piezoelectric layers based on third- order plate theory. Adv. Mater. Res. 415–417, 2151–2155 (2012)
Zhang, W., Yao, Z.G., Yao, M.H.: Periodic and chaotic dynamics of laminated composite plated piezoelectric rectangular plate with one-to-two internal resonance. Sci. China Ser. E Technol. Sci. 52, 731–742 (2009)
Zhang, H.Y., Shen, Y.P.: Vibration suppression of laminated plates with 1–3 piezoelectric fiber-reinforced composite layers equipped with interdigitated electrodes. Compos. Struct. 79, 220–228 (2007)
Wang, S.Y., Quek, S.T., Ang, K.K.: Vibration control of smart piezoelectric composite plates. Smart Mater. Struct. 10, 637–644 (2001)
Ray, M.C., Reddy, J.N.: Active control of laminated cylindrical shells using piezoelectric fiber reinforced composites. Compos. Sci. Technol. 65, 1226–1236 (2005)
Qiu, Z.C., Zhang, X.M., Wu, H.X., et al.: Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate. J. Sound Vib. 301, 521–543 (2007)
Dong, X.J., Meng, G., Peng, J.C.: Vibration control of piezoelectric smart structures based on system identification technique: Numerical simulation and experimental study. J. Sound Vib. 297, 680–693 (2006)
Reddy, J.N.: Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. CRC Press LLC, Boca Raton (2004)
Ashley, H., Zartarian, G.: Piston theory-a new aerodynamic tool for the aeroelastician. J. Aeronaut. Sci. 23, 1109–1118 (1956)
Acknowledgements
The project was supported by the National Natural Science Foundation of China (Grants 11402126, 11502122, and 11290152) and the Scientific Research Foundation of the Inner Mongolia University of Technology (Grant ZD201410).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lu, S.F., Zhang, W. & Song, X.J. Time-varying nonlinear dynamics of a deploying piezoelectric laminated composite plate under aerodynamic force. Acta Mech. Sin. 34, 303–314 (2018). https://doi.org/10.1007/s10409-017-0705-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10409-017-0705-4