Skip to main content
SpringerLink
Log in

Aeroelastic-electric flutter characteristics of functionally graded piezoelectric material plates in supersonic airflow

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

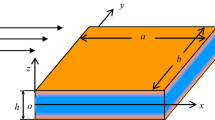
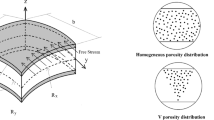
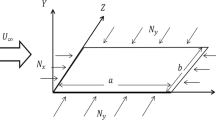
Excellent mechanical and electric properties enable the piezoelectric materials to be widely and dynamic aero-mechanical-electric coupling properties of the piezoelectric plate structures can significantly affect performance of aircrafts flying in high speed. This paper is focused on the flutter behaviors of the functionally graded piezoelectric material (FGPM) plate in supersonic airflow. The first-order shear deformation theory (FSDT) is employed to formulate the energy functional of the FGPM plate with general boundary conditions. The supersonic air flow is taken into account using the supersonic piston theory. The governing equations for the aero-mechanical-electric coupling system are deduced on basis of the Hamilton’s principle. To address the limitation of intricate boundary conditions to the admissible functions, a modified Fourier series is introduced to yield the unified solutions of the FGPM plate subject to supersonic airflow and with arbitrary boundary conditions. Flutter properties of series of FGPM plates are investigated to demonstrate robust ability of the proposed method to accurately yet consistency include the aero-elastic-electric coupling, inhomogeneous material and arbitrary boundary conditions. The influences of the boundary condition, material constituent, external voltage and yawed flow angle on the vibration, and flutter behaviors of the FGPM plate are examined. Adjusting corresponding parameters accordingly can significantly improve the stability of the plate structures subject to supersonic airflow, which provides physical insights into dynamic optimal design of the plate structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Babuscu Yesil, U., Yahnioglu, N.: Free vibration of simply supported piezoelectric plates containing a cylindrical cavity. Arch. Appl. Mech. 92, 2665–2678 (2022)

    Article  Google Scholar 

  2. Thai, L.M., Luat, D.T., Phung, V.B., Minh, P.V., Thom, D.V.: Finite element modeling of mechanical behaviors of piezoelectric nanoplates with flexoelectric effects. Arch. Appl. Mech. 92, 163–182 (2022)

    Article  Google Scholar 

  3. Wu, C.P., Chiu, K.H., Wang, Y.M.: A review on the three-dimensional analytical approaches of multilayered and functionally graded piezoelectric plates and shells. Comput. Mater. Contin. 8(2), 93–132 (2008)

    Google Scholar 

  4. Li, L., Ren, Y.: On impact process of FGPM plate with the damaged interlayer: piezoelectricity-based interaction effect analysis and stress field prediction using BPNN. Eng. Struct. 291, 116447 (2023)

    Article  Google Scholar 

  5. Xue, Y., Li, J., Wang, Y., Song, Z., Krushynska, A.O.: Widely tunable magnetorheological metamaterials with nonlinear amplification mechanism. Int. J. Mech. Sci. 264, 108830 (2024)

    Article  Google Scholar 

  6. Li, J., Xue, Y., Li, F.: Active band gap control of magnetorheological meta-plate using frequency feedback control law. J. Sound Vib. 567, 118076 (2023)

    Article  Google Scholar 

  7. Lu, S.F., Li, H.J., Zhang, W., Song, X.J.: Vibration reduction of FG-CNTR piezoelectric laminated composite cantilever plate under aerodynamic load using full-dimensional stat observer. Eng. Struct. 255, 113942 (2022)

    Article  Google Scholar 

  8. Li, Y., Shi, Z.: Free vibration of a functionally graded piezoelectric beam via state-space based differential quadrature. Compos. Struct. 87(3), 257–264 (2009)

    Article  Google Scholar 

  9. Doroushi, A., Eslami, M.R., Komeili, A.: Vibration analysis and transient response of an FGPM beam under thermo-electro-mechanical loads using higher-order shear deformation theory. J. Intell. Mater. Syst. Struct. 22(3), 231–243 (2011)

    Article  Google Scholar 

  10. Behjat, B., Salehi, M., Sadighi, M., Armin, A., Abbasi, M.: Static, dynamic, and free vibration analysis of functionally graded piezoelectric panels using finite element method. J. Intell. Mater. Syst. Struct. 20(13), 1635–1646 (2009)

    Article  Google Scholar 

  11. Sheng, G.G., Wang, X.: Thermoelastic vibration and buckling analysis of functionally graded piezoelectric cylindrical shells. Appl. Math. Model. 34(9), 2630–2643 (2010)

    Article  MathSciNet  Google Scholar 

  12. Bodaghi, M., Shakeri, M.: An analytical approach for free vibration and transient response of functionally graded piezoelectric cylindrical panels subjected to impulsive loads. Compos. Struct. 94(5), 1721–1735 (2012)

    Article  Google Scholar 

  13. Su, Z., Jin, G., Ye, T.: Electro-mechanical vibration characteristics of functionally graded piezoelectric plates with general boundary conditions. Int. J. Mech. Sci. 138, 42–53 (2018)

    Article  Google Scholar 

  14. Wang, Q., Zhong, R., Qin, B., Yu, H.: Dynamic analysis of stepped functionally graded piezoelectric plate with general boundary conditions. Smart Mater. Struct. 29(3), 035022 (2020)

    Article  Google Scholar 

  15. Barati, M.R., Zenkour, A.M.: Electro-thermoelastic vibration of plates made of porous functionally graded piezoelectric materials under various boundary conditions. J. Vib. Control 24(10), 1910–1926 (2018)

    Article  MathSciNet  Google Scholar 

  16. Nguyen, L.B., Thai, C.H., Zenkour, A.M., Nguyen-Xuan, H.: An isogeometric Bézier finite element method for vibration analysis of functionally graded piezoelectric material porous plates. Int. J. Mech. Sci. 157, 165–183 (2019)

    Article  Google Scholar 

  17. Wang, Y.Q., Zu, J.W.: Porosity-dependent nonlinear forced vibration analysis of functionally graded piezoelectric smart material plates. Smart Mater. Struct. 26(10), 105014 (2017)

    Article  Google Scholar 

  18. Wang, Y.Q.: Electro-mechanical vibration analysis of functionally graded piezoelectric porous plates in the translation state. Acta Astronaut. 143, 263–271 (2018)

    Article  Google Scholar 

  19. Su, J., Qu, Y., Zhang, K., Zhang, Q., Tian, Y.: Vibration analysis of functionally graded porous piezoelectric deep curved beams resting on discrete elastic supports. Thin-Walled Struct. 164, 107838 (2021)

    Article  Google Scholar 

  20. Fakhari, V., Ohadi, A.: Nonlinear vibration control of functionally graded plate with piezoelectric layers in thermal environment. J. Vib. Control 17(3), 449–469 (2011)

    Article  MathSciNet  Google Scholar 

  21. Li, J., Xue, Y., Li, F., Narita, Y.: Active vibration control of functionally graded piezoelectric material plate. Compos. Struct. 207, 509–518 (2019)

    Article  Google Scholar 

  22. Sharma, A.: Effect of porosity on active vibration control of smart structure using porous functionally graded piezoelectric material. Compos. Struct. 280, 114815 (2022)

    Article  Google Scholar 

  23. Li, F.M., Song, Z.G.: Aeroelastic flutter analysis for 2D Kirchhoff and Mindlin panels with different boundary conditions in supersonic airflow. Acta Mech. 225(12), 3339–3351 (2014)

    Article  MathSciNet  Google Scholar 

  24. Sun, Q., Xing, Y.F.: Exact eigensolutions for flutter of two-dimensional symmetric cross-ply composite laminates at high supersonic speeds. Compos. Struct. 183(1), 358–370 (2018)

    Article  Google Scholar 

  25. Muc, A., Flis, J.: Closed form solutions–analysis and optimal design of supersonic composite laminated flat plates considering mechanical and thermal effects. Compos. Struct. 230, 111491 (2019)

    Article  Google Scholar 

  26. Li, F.M., Song, Z.G.: Flutter and thermal buckling control for composite laminated panels in supersonic flow. J. Sound Vib. 332(22), 5678–5695 (2013)

    Article  Google Scholar 

  27. Guimarães, T.A.M., Marques, F.D., Ferreira, A.J.M.: On the modeling of nonlinear supersonic flutter of multibay composite panels. Compos. Struct. 232, 111522 (2020)

    Article  Google Scholar 

  28. Song, Z.G., Li, F.M.: Active aeroelastic flutter analysis and vibration control of supersonic composite laminated plate. Compos. Struct. 94(2), 702–713 (2012)

    Article  Google Scholar 

  29. Song, Z.G., Li, F.M.: Investigations on the flutter properties of supersonic panels with different boundary conditions. Int. J. Dyn. Cont. 2(3), 346–353 (2014)

    Article  Google Scholar 

  30. Dowell, E.H.: Nonlinear oscillations of a fluttering plate. AIAA J. 4(7), 1267–1275 (1966)

    Article  Google Scholar 

  31. Shitov, S., Vedeneev, V.: Flutter of rectangular simply supported plates at low supersonic speeds. J. Fluid. Struct. 69, 154–173 (2017)

    Article  Google Scholar 

  32. Navazi, H.M., Haddadpour, H.: Nonlinear aero-thermoelastic analysis of homogeneous and functionally graded plates in supersonic airflow using coupled models. Compos. Struct. 93(10), 2554–2565 (2011)

    Article  Google Scholar 

  33. Zhao, H., Cao, D.: Supersonic flutter of laminated composite panel in coupled multi-fields. Aerosp. Sci. Technol. 47, 75–85 (2015)

    Article  Google Scholar 

  34. Prakash, T., Ganapathi, M.: Supersonic flutter characteristics of functionally graded flat panels including thermal effects. Compos. Struct. 72(1), 10–18 (2006)

    Article  Google Scholar 

  35. Ibrahim, H.H., Yoo, H.H., Lee, K.S.: Supersonic flutter of functionally graded panels subject to acoustic and thermal loads. J. Aircraft. 46(2), 593–600 (2009)

    Article  Google Scholar 

  36. Grover, N., Singh, B.N., Maiti, D.K.: An inverse trigonometric shear deformation theory for supersonic flutter characteristics of multilayered composite plates. Aerosp. Sci. Technol. 52, 41–51 (2016)

    Article  Google Scholar 

  37. Zheng, Y., Wang, Y., Huang, J., Tan, Z.: Flutter stability analysis of composite corrugated plates in supersonic flow. Arch. Appl. Mech. 94(4), 1079–1098 (2024)

    Article  Google Scholar 

  38. Torabi, K., Afshari, H., Aboutalebi, F.H.: Vibration and flutter analyses of cantilever trapezoidal honeycomb sandwich plates. J. Sandw. Struct. Mater. 21(8), 2887–2920 (2017)

    Article  Google Scholar 

  39. Farsadi, T., Asadi, D., Kurtaran, H.: Nonlinear flutter response of a composite plate applying curvilinear fiber paths. Acta Mech. 231(2), 715–731 (2020)

    Article  MathSciNet  Google Scholar 

  40. Yazdi, A.A.: Nonlinear flutter of laminated composite plates resting on nonlinear elastic foundations using homotopy perturbation method. Int. J. Struct. Stab. Dyn. 15(05), 1450072 (2015)

    Article  MathSciNet  Google Scholar 

  41. Khalafi, V., Fazilati, J.: Supersonic panel flutter of variable stiffness composite laminated skew panels subjected to yawed flow by using NURBS-based isogeometric approach. J. Fluids Struct. 82, 198–214 (2018)

    Article  Google Scholar 

  42. An, X., Wang, Y.: Nonlinear flutter analysis of composite panels. Mod. Phys. Lett. B 32(12), 1840043 (2018)

    Article  Google Scholar 

  43. Liew, K.M., Wang, C.M., Xiang, Y., Kitipornchai, S.: Vibration of Mindlin Plates: Programming the p-Version Ritz Method. Elsevier, Oxford (1998)

    Google Scholar 

  44. Zhou, K., Su, J., Hua, H.: Aero-thermo-elastic flutter analysis of supersonic moderately thick orthotropic plates with general boundary conditions. Int. J. Mech. Sci. 141, 46–57 (2018)

    Article  Google Scholar 

  45. Ilanko, S., Monterrubio, L., Mochida, Y.: The Rayleigh-Ritz method for structural analysis. Wiley, Hoboken (2014)

    Book  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (Nos. 52374158, 52204143 and 52234005).

Funding

This study was funded by the National Natural Science Foundation of China (52374158, 52204143, 52234005).

Author information

Authors and Affiliations

  1. Shandong University of Science and Technology, Qianwangang Road 579, Qingdao, 266590, China

    Jinpeng Su, Shoubo Jiang & Qiang Zhang

  2. Wuhan Second Ship Design and Research Institute, Wuhan, 43000, China

    Jianhui Wei

  3. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Dongchuan Road 800, Shanghai, 200240, China

    Jinpeng Su

Authors
  1. Jinpeng Su
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianhui Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shoubo Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qiang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Jinpeng Su proposed the conceptualization, derived the methodology, prepared riginal draft and acquired funding. Jianhui Wei was responsible for programing, formal analysis and data curation. Shoubo Jiang validated the proposed method, improved the figures and acquired funding. Qiang Zhang improved the table, checked and revised the programs and acquired funding. All authors revised and reviewed the manuscript.

Corresponding author

Correspondence to Shoubo Jiang.

Ethics declarations

Conflict of interest

There is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

The displacement fields of the FGPM plate are given by follows, where H denotes the trial functions and ql (l = 1, 2,…, 6) represents the unknown coefficient eigenvector.

$$\begin{gathered} u(x,y) = {\varvec{Hq}}_{1} \hfill \\ v(x,y) = {\varvec{Hq}}_{{2}} \hfill \\ w(x,y) = {\varvec{Hq}}_{{3}} \hfill \\ \theta_{x} (x,y) = {\varvec{Hq}}_{{4}} \hfill \\ \theta_{y} (x,y) = {\varvec{Hq}}_{{5}} \hfill \\ \phi_{0} (x,y) = {\varvec{Hq}}_{6} \hfill \\ \end{gathered}$$
(A1)

The trial functions of the FGPM plate are written as

$${\varvec{H}} = \left[ {\varphi_{{1}} (x)\psi_{{1}} (y), \ldots ,\varphi_{{\text{m}}} (x)\psi_{{\text{n}}} (y), \ldots ,\varphi_{{\text{M}}} (x)\psi_{{\text{N}}} (y)} \right]$$
(A2)

The unknown coefficient eigenvectors are given by

$${\varvec{q}}_{1} = [A_{{{11}}} , \ldots ,A_{{{\text{mn}}}} , \ldots ,A_{{{\text{MN}}}} ]$$
(A3)
$${\varvec{q}}_{2} = [B_{{{11}}} , \ldots ,B_{{{\text{mn}}}} , \ldots ,B_{{{\text{MN}}}} ]$$
(A4)
$${\varvec{q}}_{3} = [C_{{{11}}} , \ldots ,C_{{{\text{mn}}}} , \ldots ,C_{{{\text{MN}}}} ]$$
(A5)
$${\varvec{q}}_{4} = [D_{{{11}}} , \ldots ,D_{{{\text{mn}}}} , \ldots ,D_{{{\text{MN}}}} ]$$
(A6)
$${\varvec{q}}_{5} = [E_{{{11}}} , \ldots ,E_{{{\text{mn}}}} , \ldots ,E_{{{\text{MN}}}} ]$$
(A7)
$${\varvec{q}}_{{6}} = [F_{{{11}}} , \ldots ,F_{{{\text{mn}}}} , \ldots ,F_{{{\text{MN}}}} ]$$
(A8)

Appendix B

The detailed expressions in the stiffness, mass and damping matrices of the FGPM plate are written as

$${\varvec{K}} = \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{{{\text{uu}}}} } & {{\varvec{K}}_{{{\text{uv}}}} } & {\varvec{0}} & {{\varvec{K}}_{{{\text{ux}}}} } & {{\varvec{K}}_{{{\text{uy}}}} } \\ {{\varvec{K}}_{{{\text{uv}}}}^{{\text{T}}} } & {{\varvec{K}}_{{{\text{vv}}}} } & {\varvec{0}} & {{\varvec{K}}_{{{\text{vx}}}} } & {{\varvec{K}}_{{{\text{vy}}}} } \\ {\varvec{0}} & {\varvec{0}} & {{\varvec{K}}_{{{\text{ww}}}} } & {{\varvec{K}}_{{{\text{wx}}}} } & {{\varvec{K}}_{{{\text{wy}}}} } \\ {{\varvec{K}}_{{{\text{ux}}}}^{{\text{T}}} } & {{\varvec{K}}_{{{\text{vx}}}}^{{\text{T}}} } & {{\varvec{K}}_{{{\text{wx}}}}^{{\text{T}}} } & {{\varvec{K}}_{{{\text{xx}}}} } & {{\varvec{K}}_{{{\text{xy}}}} } \\ {{\varvec{K}}_{{{\text{uy}}}}^{{\text{T}}} } & {{\varvec{K}}_{{{\text{vy}}}}^{{\text{T}}} } & {{\varvec{K}}_{{{\text{wy}}}}^{{\text{T}}} } & {{\varvec{K}}_{{{\text{xy}}}}^{{\text{T}}} } & {{\varvec{K}}_{{{\text{yy}}}} } \\ \end{array} } \right]$$
(B1)
$${\varvec{K}}_{{{\text{cou}}}} = \left[ \begin{gathered} {\varvec{K}}_{{{\text{ue}}}} \hfill \\ {\varvec{K}}_{{{\text{ve}}}} \hfill \\ {\varvec{K}}_{{{\text{we}}}} \hfill \\ {\varvec{K}}_{{{\text{xe}}}} \hfill \\ {\varvec{K}}_{{{\text{ye}}}} \hfill \\ \end{gathered} \right]$$
(B2)
$$\begin{gathered} {\varvec{K}}_{{{\text{uu}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {A_{11} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right) + A_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)} \right]} } dxdy \hfill \\ \quad \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{{{\text{uy}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = 0}} + \left. {k_{{{\text{uy}}L_{2} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = L_{2} }} } \right)} dx + \int_{0}^{{L_{2} }} {\left( {\left. {k_{{{\text{ux}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = 0}} + \left. {k_{{{\text{uxL}}_{1} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = L_{1} }} } \right)} dy \hfill \\ \end{gathered}$$
(B3)
$${\varvec{K}}_{{{\text{uv}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {A_{12} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) + A_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)} \right]} } dxdy$$
(B4)
$${\varvec{K}}_{{{\text{ux}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {B_{11} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right) + B_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)} \right]} } dxdy$$
(B5)
$${\varvec{K}}_{{{\text{uy}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {B_{12} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) + B_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)} \right]} } dxdy$$
(B6)
$$\begin{gathered} {\varvec{K}}_{{{\text{vv}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {A_{22} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) + A_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)} \right]} } dxdy \hfill \\ \quad \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{{{\text{vy}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = 0}} + \left. {k_{{{\text{vy}}L_{2} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = L_{2} }} } \right)} dx + \int_{0}^{{L_{2} }} {\left( {\left. {k_{{{\text{vx}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = 0}} + \left. {k_{{{\text{vx}}L_{1} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = L_{1} }} } \right)} dy \hfill \\ \end{gathered}$$
(B7)
$${\varvec{K}}_{{{\text{vx}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {B_{12} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right) + B_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)} \right]} } dxdy$$
(B8)
$${\varvec{K}}_{{{\text{vy}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {B_{22} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) + B_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)} \right]} } dxdy$$
(B9)
$$\begin{gathered} {\varvec{K}}_{{{\text{ww}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ \begin{gathered} K_{{\text{s}}} A_{44} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) + K_{{\text{s}}} A_{55} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right) + K_{{\text{s}}} A_{45} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) \hfill \\ + K_{{\text{s}}} A_{45} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right) \hfill \\ \end{gathered} \right]} } dxdy \hfill \\ + \int_{0}^{{L_{1} }} {\left( {\left. {k_{{{\text{wy}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = 0}} + \left. {k_{{{\text{wy}}L_{2} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = L_{2} }} } \right)} dx + \int_{0}^{{L_{2} }} {\left( {\left. {k_{{{\text{wx}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = 0}} + \left. {k_{{{\text{wx}}L_{1} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = L_{1} }} } \right)} dy \hfill \\ + \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {\frac{{\lambda D_{{\text{c}}} }}{{L_{1}^{3} }}\left( {{\varvec{H}}^{{\text{T}}} \frac{{\partial {\varvec{H}}}}{\partial x}{\text{cos}}\theta_{{{\text{air}}}} + {\varvec{H}}^{{\text{T}}} \frac{{\partial {\varvec{H}}}}{\partial y}{\text{sin}}\theta_{{{\text{air}}}} } \right)} \right]} } dxdy \hfill \\ \end{gathered}$$
(B10)
$${\varvec{K}}_{{{\text{wx}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {K_{{\text{s}}} A_{55} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} ({\varvec{H}}) + K_{{\text{s}}} A_{45} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} ({\varvec{H}})} \right]} } dxdy$$
(B11)
$${\varvec{K}}_{{{\text{wy}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {K_{{\text{s}}} A_{44} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} ({\varvec{H}}) + K_{{\text{s}}} A_{45} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} ({\varvec{H}})} \right]} } dxdy$$
(B12)
$$\begin{gathered} {\varvec{K}}_{{{\text{xx}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {K_{{\text{s}}} A_{55} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}}) + D_{11} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right) + D_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)} \right]} } dxdy \hfill \\ \quad \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{{{\text{xy}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = 0}} + \left. {k_{{{\text{xy}}L_{2} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = L_{2} }} } \right)} dx + \int_{0}^{{L_{2} }} {\left( {\left. {k_{{{\text{xx}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = 0}} + \left. {k_{{{\text{xx}}L_{1} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = L_{1} }} } \right)} dy \hfill \\ \end{gathered}$$
(B13)
$${\varvec{K}}_{{{\text{xy}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {K_{s} A_{45} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}}) + D_{12} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) + D_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)} \right]} } dxdy$$
(B14)
$$\begin{gathered} {\varvec{K}}_{{{\text{yy}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {K_{s} A_{44} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}}) + D_{22} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) + D_{66} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)} \right]} } dxdy \hfill \\ \quad \quad + \int_{0}^{{L_{1} }} {\left( {\left. {k_{yy0} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{y = 0} + \left. {k_{{yyL_{2} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{y = L_{2} }} } \right)} dx + \int_{0}^{{L_{2} }} {\left( {\left. {k_{yx0} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{x = 0} + \left. {k_{{yxL_{1} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{x = L_{1} }} } \right)} dy \hfill \\ \end{gathered}$$
(B15)
$${\varvec{K}}_{{{\text{ue}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {E_{31} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} ({\varvec{H}})} \right]} } dxdy$$
(B16)
$${\varvec{K}}_{{{\text{ve}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {E_{32} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} ({\varvec{H}})} \right]} } dxdy$$
(B17)
$${\varvec{K}}_{{{\text{we}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {E_{15} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right) + E_{24} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)} \right]} } dxdy$$
(B18)
$${\varvec{K}}_{{{\text{xe}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {E_{{31{\text{z}}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} ({\varvec{H}}) + E_{15} ({\varvec{H}})^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)} \right]} } dxdy$$
(B19)
$${\varvec{K}}_{{{\text{ye}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {E_{{32{\text{z}}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} ({\varvec{H}}) + E_{24} ({\varvec{H}})^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)} \right]} } dxdy$$
(B20)
$$\begin{gathered} {\varvec{K}}_{e} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\left[ {G_{11} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial x}} \right) + G_{22} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{H}}}}{\partial y}} \right) + G_{33} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} \right]} } dxdy \hfill \\ + \int_{0}^{{L_{1} }} {\left( {\left. {k_{{\phi {\text{y}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = 0}} + \left. {k_{{\phi {\text{y}}L_{2} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{y}} = L_{2} }} } \right)} dx + \int_{0}^{{L_{2} }} {\left( {\left. {k_{{\phi {\text{x}}0}} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = 0}} + \left. {k_{{\phi {\text{x}}L_{1} }} {\varvec{H}}^{{\text{T}}} {\varvec{H}}} \right|_{{{\text{x}} = L_{1} }} } \right)} dy \hfill \\ \end{gathered}$$
(B21)
$${\varvec{M}} = \left[ {\begin{array}{*{20}c} {{\varvec{M}}_{{{\text{uu}}}} } & {\varvec{0}} & {\varvec{0}} & {{\varvec{M}}_{{{\text{ux}}}} } & {\varvec{0}} \\ {\varvec{0}} & {{\varvec{M}}_{{{\text{vv}}}} } & {\varvec{0}} & {\varvec{0}} & {{\varvec{M}}_{{{\text{vy}}}} } \\ {\varvec{0}} & {\varvec{0}} & {{\varvec{M}}_{{{\text{ww}}}} } & {\varvec{0}} & {\varvec{0}} \\ {{\varvec{M}}_{{{\text{ux}}}}^{{\text{T}}} } & {\varvec{0}} & {\varvec{0}} & {{\varvec{M}}_{{{\text{xx}}}} } & {\varvec{0}} \\ {\varvec{0}} & {{\varvec{M}}_{{{\text{vy}}}}^{{\text{T}}} } & {\varvec{0}} & {\varvec{0}} & {{\varvec{M}}_{{{\text{yy}}}} } \\ \end{array} } \right]$$
(B22)
$${\varvec{M}}_{{{\text{uu}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{0} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} } dxdy$$
(B23)
$${\varvec{M}}_{{{\text{ux}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{1} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} } dxdy$$
(B24)
$${\varvec{M}}_{{{\text{vv}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{0} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} } dxdy$$
(B25)
$${\varvec{M}}_{{{\text{vy}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{1} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} } dxdy$$
(B26)
$${\varvec{M}}_{{{\text{ww}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{0} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} } dxdy$$
(B27)
$${\varvec{M}}_{{{\text{xx}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{2} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} } dxdy$$
(B28)
$${\varvec{M}}_{{{\text{yy}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {I_{2} ({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} } dxdy$$
(B29)
$${\varvec{C}} = \left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {{\varvec{C}}_{{{\text{ww}}}} } & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ \end{array} } \right]$$
(B30)
$${\varvec{C}}_{{{\text{ww}}}} = \int_{0}^{{L_{1} }} {\int_{0}^{{L_{2} }} {\frac{{\sqrt {\mu \lambda \rho^{{\text{u}}} hD_{{\text{c}}} /M_{\infty } } }}{{L_{1}^{2} }}({\varvec{H}})^{{\text{T}}} ({\varvec{H}})} } dxdy$$
(B31)

where

$$\left( {A_{{{\text{ij}}}} ,{\kern 1pt} {\kern 1pt} B_{{{\text{ij}}}} ,{\kern 1pt} {\kern 1pt} D_{{{\text{ij}}}} } \right) = \int_{ - h/2}^{h/2} {\overline{C}_{{{\text{ij}}}} \left( {1,z,z^{2} } \right){\kern 1pt} dz}$$
$$\left( {E_{31} ,{\kern 1pt} E_{{31{\text{z}}}} } \right) = \int_{ - h/2}^{h/2} {\left( {\frac{dg}{{dz}},z\frac{dg}{{dz}}} \right){\kern 1pt} e_{31} dz}$$
$$\left( {E_{{3{2}}} ,{\kern 1pt} E_{{3{2}z}} } \right) = \int_{ - h/2}^{h/2} {\left( {\frac{dg}{{dz}},z\frac{dg}{{dz}}} \right){\kern 1pt} e_{{3{2}}} dz}$$
(B32)
$$\left( {E_{{{24}}} ,{\kern 1pt} E_{{{15}}} } \right) = \frac{{{1 + }K_{s} }}{{2}}\int_{ - h/2}^{h/2} {(e_{24} ,e_{15} ){\kern 1pt} gdz}$$
$$\left( {G_{{{11}}} ,{\kern 1pt} G_{22} ,{\kern 1pt} G_{33} {\kern 1pt} } \right) = \int_{ - h/2}^{h/2} {\left( {gg,gg,{\kern 1pt} {\kern 1pt} \frac{dg}{{dz}}\frac{dg}{{dz}}} \right){\kern 1pt} \overline{\kappa }_{{{\text{ii}}}} dz}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Su, J., Wei, J., Jiang, S. et al. Aeroelastic-electric flutter characteristics of functionally graded piezoelectric material plates in supersonic airflow. Arch Appl Mech (2024). https://doi.org/10.1007/s00419-024-02603-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00419-024-02603-8

Keywords

Search

Navigation