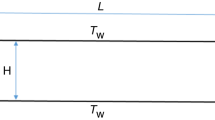
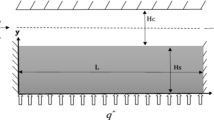
Abstract
The lattice Boltzmann method (LBM) modeling shows its powerful capability in the numerical prediction of thermal gaseous fluid flow. However, the LBM simulation of gaseous microflow with complex boundaries is still challenging, in which the uniform Cartesian lattices are adopted in the numerical model. In this work, a new curved boundary treatment for LBM modeling of thermal gaseous microflow in slip regime is proposed, which is a combination of the non-equilibrium extrapolation method for curved boundary and the counter-extrapolation method for the gas velocity/temperature on the curved wall. The proposed treatment considers the effect of the offset between the physical boundary and the closest grid line and involves no specific gas–wall interaction parameters, which is proved to be more accurate and applicable. The new curved boundary treatment is utilized with the multiple-relaxation-time model and then validated for several benchmark cases, which shows its superiority in slip flow and heat transfer prediction compared with the current curved boundary schemes for gaseous microflow.












Similar content being viewed by others
Abbreviations
- A :
-
Area [m2]
- c :
-
Velocity [m s−1]
- c s :
-
Pseudo sound speed [m s−1]
- D :
-
Diameter [m]
- e :
-
Particle velocity, [m s−1]
- f :
-
Particle distribution function of density
- F :
-
External forcing term
- g :
-
Particle distribution function of temperature
- G :
-
External force [N]
- k :
-
Specific heat ratio
- Kn :
-
Knudsen number
- L :
-
Characteristic length [m]
- H :
-
Height [m]
- Ma :
-
Mach number
- n :
-
Unit normal vector
- P :
-
Pressure [N m−2]
- r :
-
Radius or radial distance [m]
- R :
-
Gas constant [J mol−1 K−1] or radius [m]
- Re :
-
Reynolds number
- t :
-
Time [s]
- T :
-
Temperature [K]
- u :
-
Velocity [m s−1]
- u τ :
-
Tangential velocity [m s−1]
- u :
-
Velocity in x direction [m s−1]
- v :
-
Velocity in y direction [m s−1]
- x,y :
-
Cartesian coordinates [m]
- x :
-
Position = (x,y) [m]
- δ t :
-
Time step [s]
- δ x :
-
Lattice spacing [m]
- θ :
-
Angle [°]
- λ :
-
Gas molecule mean free path [m]
- μ :
-
Dynamic viscosity [kg m−1 s−1]
- ρ :
-
Density [kg m−3]
- σ T :
-
Temperature accommodation coefficient
- σ v :
-
Velocity accommodation coefficient
- τ g :
-
Dimensionless relaxation time of temperature
- τ s :
-
Dimensionless relaxation time of velocity
- ν :
-
Viscosity [Pa s]
- ω :
-
Weight coefficient or angular velocity [rad s−1]
- \(\Omega\) :
-
Collision operator
- eq:
-
Equilibrium
- neq:
-
Non-equilibrium
- f:
-
Fluid
- g:
-
Gas or temperature
- int:
-
Interface
- s:
-
Solid
- slip:
-
Slip
- T:
-
Temperature
- w:
-
Wall
References
Ansumali S, Karlin IV (2002) Kinetic boundary conditions in the lattice Boltzmann method. Phys Rev E 66:026311. https://doi.org/10.1103/PhysRevE.66.026311
Baaaolu H, Carrola JT, Freitas CJ, Baaaolu B, Succi S (2015) Lattice Boltzmann simulations of vortex entrapment of particles in a microchannel with curved or flat edges. Microfluid Nanofluidics 18:1165–1175. https://doi.org/10.1007/s10404-014-1509-5
Cai C, Sun Q (2015) Near continuum flows over a sphere. Comput Fluids 111:62–68. https://doi.org/10.1016/j.compfluid.2015.01.004
Chai Z, Guo Z, Zheng L, Shi B (2008) Lattice Boltzmann simulation of surface roughness effect on gaseous flow in a microchannel. J Appl Phys 104:014902. https://doi.org/10.1063/1.2949273
Choi YJ, Kwon OJ (2015) Numerical study of effects of accommodation coefficients on slip phenomena. J Mech Sci Technol 29:1883–1888. https://doi.org/10.1007/s12206-015-0409-2
Djoko J, Koko J (2016) Numerical methods for the Stokes and Navier–Stokes equations driven by threshold slip boundary conditions. Comput Methods Appl Mech Eng 305:936–958. https://doi.org/10.1016/j.cma.2016.03.026
Ebrahimi A, Roohi E (2017) DSMC investigation of rarefied gas flow through diverging micro- and nanochannels. Microfluid Nanofluidics. https://doi.org/10.1007/s10404-017-1855-1
Gad-el-Hak M (1999) Fluid mechanics of microdevices—the freeman scholar lecture. J Fluids Eng Trans ASME 121:5–33. https://doi.org/10.1115/1.2822013
Gokaltun S, Dulikravich GS (2014) Lattice Boltzmann method for rarefied channel flows with heat transfer. Int J Heat Mass Transf 78:796–804. https://doi.org/10.1016/j.ijheatmasstransfer.2014.07.018
Guo Z-L, Zheng C-G, Shi B-C (2002) Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin Phys 11:366–374. https://doi.org/10.1088/1009-1963/11/4/310
Guo Z, Shi B, Zhao TS, Zheng C (2007) Discrete effects on boundary conditions for the lattice Boltzmann equation in simulating microscale gas flows. Phys Rev E 76:056704. https://doi.org/10.1103/PhysRevE.76.056704
Guo Z, Shi B, Zheng C (2011) Velocity inversion of micro cylindrical Couette flow: a lattice Boltzmann study. Comput Math Appl 61:3519–3527. https://doi.org/10.1016/j.camwa.2010.01.022
Hampson SM, Rowe W, Christie SDR, Platt M (2018) 3D printed microfluidic device with integrated optical sensing for particle analysis. Sens Actuators B Chem 256:1030–1037. https://doi.org/10.1016/j.snb.2017.10.041
Kempe T, Lennartz M, Schwarz S, Fröhlich J (2015) Imposing the free-slip condition with a continuous forcing immersed boundary method. J Comput Phys 282:183–209. https://doi.org/10.1016/j.jcp.2014.11.015
Lallemand P, Luo L-S (2000) Theory of the lattice Boltzmann method: dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys Rev E 61:6546–6562. https://doi.org/10.1103/PhysRevE.61.6546
Le G, Oulaid O, Zhang J (2015) Counter-extrapolation method for conjugate interfaces in computational heat and mass transfer. Phys Rev E 91:033306. https://doi.org/10.1103/PhysRevE.91.033306
Lee T, Lin C-L (2005) Rarefaction and compressibility effects of the lattice-Boltzmann-equation method in a gas microchannel. Phys Rev E 71:046706. https://doi.org/10.1103/PhysRevE.71.046706
Li Q, He YL, Tang GH, Tao WQ (2011) Lattice Boltzmann modeling of microchannel flows in the transition flow regime. Microfluid Nanofluidics 10:607–618. https://doi.org/10.1007/s10404-010-0693-1
Lim CY, Shu C, Niu XD, Chew YT (2002) Application of lattice Boltzmann method to simulate microchannel flows. Phys Fluids 14:2299–2308. https://doi.org/10.1063/1.1483841
Liu Z, Wu H (2016) Pore-scale study on flow and heat transfer in 3D reconstructed porous media using micro-tomography images. Appl Therm Eng 100:602–610. https://doi.org/10.1016/j.applthermaleng.2016.02.057
Morinishi K (2006) Numerical simulation for gas microflows using Boltzmann equation. Comput Fluids 35:978–985. https://doi.org/10.1016/j.compfluid.2005.04.012
Nie X, Doolen GD, Chen S (2002) Lattice-Boltzmann simulations of fluid flows in MEMS. J Stat Phys 107:279–289. https://doi.org/10.1023/a:1014523007427
Niu XD, Shu C, Chew YT (2007) A thermal lattice Boltzmann model with diffuse scattering boundary condition for micro thermal flows. Comput Fluids 36:273–281. https://doi.org/10.1016/j.compfluid.2005.11.007
Sarkar S, Ganguly S, Chakraborty S (2017) Influence of combined electromagnetohydrodynamics on microchannel flow with electrokinetic effect and interfacial slip. Microfluid Nanofluidics. https://doi.org/10.1007/s10404-017-1894-7
Sen S, Mittal S, Biswas G (2009) Steady separated flow past a circular cylinder at low Reynolds numbers. J Fluid Mech 620:89–119. https://doi.org/10.1017/s0022112008004904
Shimokuri D, Hara T, Matsumoto R (2015) Development of a small-scale power system with meso-scale vortex combustor and thermo-electric device. J Micromech Microeng 25:104004. https://doi.org/10.1088/0960-1317/25/10/104004
Sofonea V, Sekerka RF (2005) Diffuse-reflection boundary conditions for a thermal lattice Boltzmann model in two dimensions: evidence of temperature jump and slip velocity in microchannels. Phys Rev E 71:066709. https://doi.org/10.1103/PhysRevE.71.066709
Succi S (2002) Mesoscopic modeling of slip motion at fluid-solid interfaces with heterogeneous catalysis. Phys Rev Lett 89:064502. https://doi.org/10.1103/PhysRevLett.89.064502
Suga K (2013) Lattice Boltzmann methods for complex micro-flows: applicability and limitations for practical applications. Fluid Dyn Res 45:034501. https://doi.org/10.1088/0169-5983/45/3/034501
Szalmás L (2007) Slip on curved boundaries in the lattice Boltzmann model. Int J Mod Phys C 18:15–24 https://doi.org/10.1142/s0129183107010358
Tang GH, Tao WQ, He YL (2005) Lattice Boltzmann method for gaseous microflows using kinetic theory boundary conditions. Phys Fluids 17:058101. https://doi.org/10.1063/1.1897010
Tao S, Guo Z (2015) Boundary condition for lattice Boltzmann modeling of microscale gas flows with curved walls in the slip regime. Phys Rev E 91:043305. https://doi.org/10.1103/PhysRevE.91.043305
Tian ZW, Zou C, Liu HJ, Guo ZL, Liu ZH, Zheng CG (2007) Lattice Boltzmann scheme for simulating thermal micro-flow. Phys A Stat Mech Appl 385:59–68. https://doi.org/10.1016/j.physa.2007.01.021
Tritton DJ (1959) Experiments on the flow past a circular cylinder at low Reynolds numbers. J Fluid Mech 6:547–567. https://doi.org/10.1017/s0022112059000829
Verhaeghe F, Luo L-S, Blanpain B (2009) Lattice Boltzmann modeling of microchannel flow in slip flow regime. J Comput Phys 228:147–157. https://doi.org/10.1016/j.jcp.2008.09.004
Wang CH, Yang R (2006) A numerical study for slip flow heat transfer. Appl Math Comput 173:1246–1264. https://doi.org/10.1016/j.amc.2005.04.068
Zhang W-M, Meng G, Wei X (2012) A review on slip models for gas microflows. Microfluid Nanofluidics 13:845–882. https://doi.org/10.1007/s10404-012-1012-9
Zheng L, Guo ZL, Shi BC (2008) Discrete effects on thermal boundary conditions for the thermal lattice Boltzmann method in simulating microscale gas flows. EPL 82:44002. https://doi.org/10.1209/0295-5075/82/44002
Acknowledgements
This work was supported by the National Natural Science Foundation of China through Grant nos. 51536005, 51676124 and 51820105009; Shanghai International Science and Technology Cooperation Project through Grant no. 18160743900.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Liu, Z., Mu, Z. & Wu, H. A new curved boundary treatment for LBM modeling of thermal gaseous microflow in the slip regime. Microfluid Nanofluid 23, 27 (2019). https://doi.org/10.1007/s10404-019-2192-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10404-019-2192-3