Introduction

The response of slopes to the action of strong ground shaking, such as the propagation of seismic waves generated by a large earthquake, can result in ground deformations and failures. Responses fall into two main categories: primary coseismic effects, e.g., when morphological changes associated with the earthquake (i.e., permanent deformations, faulting, and fracturing) are visible on the surface, and secondary coseismic effects, such as liquefaction and gravitational movements (Fan et al. 2019).

The CEDIT database, a comprehensive inventory of earthquake-induced ground failures in Italy, contains data on ground cracks, surface faulting, and landslides for events with Mercalli intensity MI > VIII, which have occurred in the last millennium (Martino et al. 2014). Caprari et al. (2018) reveals that ground effects are mainly rockfalls and earth/rockslides (45 %), followed by ground cracks (32 %) and liquefaction (18 %). The literature on earthquake-induced landslides is conspicuous; a classic review (Keefer 1984) shows that rockfalls are among the most threatening type of landslide to human life.

Relevant, well-known examples are the Niigata Ken Chuetsu earthquake in 2004 (Mw 6.6), which triggered a vast number of landslides (Kieffer et al. 2006). The Northridge earthquake in 1994 (Mw 6.7), which induced thousands of landslides in a radius of about 25 km from the epicenter (Stewart et al. 1995); the Wenchuan earthquake of 2008 (Mw 7.9), China, which induced numerous landslides, including shallow and deep-seated rockslides, rockfalls, debris slides, and debris flows (Chigira et al. 2010); and the Gorkha Earthquake of 2015 (Mw 7.8), Nepal, which triggered more than 25,000 landslides (Roback et al. 2018; Pokharel et al. 2021; Alvioli et al. 2022b). Additional examples are in Tanyaş et al. (2017) and references therein.

Earthquake-induced instability of natural slopes manifests in the form of (i) first-time landslides, characterized by ruptures induced by shear or traction stress along newly formed surfaces coinciding, in whole or in part, with stratigraphic discontinuities or levels of lower competence in inhomogeneous formations; (ii) reactivation of quiescent landslides, with movement along pre-existing fracture surfaces; and (iii) resumption or acceleration of active landslides, along pre-existing discontinuities as well.

The response of a slope under ground shaking depends on many factors. For example, variability in the geological materials not only controls rock mass resistance, but it might also modify ground motion. Site-specific geometry and slope height are also relevant (Massey et al. 2017), providing mass potential energy and affecting rockfall trajectories. Nonetheless, knowledge of geology, topography, and properties of the rock mass, although accurate, does not guarantee a full understanding of the mechanisms controlling the detachment of rock blocks from a slope, nor the accurate prediction of their origin location and evolution. A probabilistic framework for modeling earthquake-induced rockfall scenarios is a valid alternative. In one such framework, the location of sources, the trigger, and the propagation components of falling blocks are modeled statistically, with parameters tuned on the basis of observations.

Based on a world collection of earthquake-induced landslides (Tanyaş et al. 2017), statistical approaches proved successful in accounting for the different predisposing factors and using ground motion as dynamical factors to determine the spatial likelihood of earthquake-induced landslides (Nowicki Jessee et al. 2018; Tanyaş et al. 2019a, b), their magnitude (Tanyaş et al. 2019b), and the spatial distribution described by accurate inventories prepared after an earthquake event (Dai et al. 2011; Harp et al. 2011; Tanyaş and Lombardo 2020; Pokharel et al. 2021).

In this study, we propose a method for preparing rockfall scenarios induced by specific seismic events with a combination of statistical methods and a physical model. The method includes a few independent steps: (i) a probabilistic morphometric determination of potential rockfall sources (Alvioli et al. 2021; ii) an empirical estimate of ground motion using the ShakeMap software (Worden et al. 2020) to produce realistic ground motion maps (Akkar and Bommer 2007; Mori et al. 2022; iii) a novel approach to triggering of rockfall sources by ground shaking, previously applied with return-time scenarios (Alvioli et al. 2022a, 2023); and (iv) a physical model to simulate rockfall trajectories.

We used the three-dimensional program STONE (Guzzetti et al. 2002) to simulate block trajectories. We calibrated the model using data from the Friuli Venezia Giulia region (hereinafter FVG), Northern Italy, and particularly from the landslide inventory compiled by Govi (1977) after the 1976 Friuli earthquake (Ml 6.5). We show that, within the framework outlined above and summarized in the flowchart of Fig. 1, one can use heterogeneous data and combine techniques for earthquake ground shaking estimation and landslide numerical modeling to obtain probabilistic maps for seismically-induced rockfall runout. The proposed approach is thus suitable for rapid impact evaluation in civil protection applications, as it can be readily implemented after the occurrence of any major earthquake in almost real time, similarly to existing examples of near-real-time damage estimation to infrastructure (Tamaro et al. 2018; Poggi et al. 2021). A comparable implementation was proposed by Valagussa et al. (2014), who used the model Hy-STONE in the same study area using frequency of occurrence and magnitude relative-frequency relations obtained from field data, with the aim of assessing the long-term rockfall hazard (rather than for post-event rapid impact evaluation).

The paper is organized as follows: the “Test–bed area and data” section lists and describes the data used in this work, including details of the 1976 earthquake in FVG. The “Methods” section describes the ideas behind the identification of rockfall sources on a digital topography and of the proposed seismic triggering mechanism. Results are shown in the “Results” section and discussed in the “Discussion” section. The “Conclusions” section draws conclusions of this study and gives hints for future work.

Test-bed area and data

Italy is earthquake-prone, with many examples of landslides triggered by earthquakes. Keefer (2002) explicitly mentions the 1973 earthquake swarm in Calabria. Other relevant and well-documented events are Friuli (1976, Mw 6.4\(-\)6.1), with a prevalence of rock collapses and, secondarily, debris avalanches (Govi 1977; Civita et al. 1985); Irpinia (1980, Mw 6.9), with collapses and overturns in rock but also many of triggered or reactivated flows, flows and complex landslides (D’Elia 2018); Umbria–Marche (1997, Mw 5.5\(-\)5.8), with a prevalence of collapses but numerous sliding phenomena, almost all reactivated ancient landslides (Prestininzi and Romeo 2000); the 2016 central Apennines earthquake sequence (Amatrice and Norcia Earthquakes 2016), with numerous triggered rockfalls (Caprari et al. 2018; Santangelo et al. 2019, 2020).

This work focuses on the Friuli event, which occurred between May and September 1976, and consisted of a seismic sequence with two major earthquakes. The first event occurred on May 6th, with an intensity-derived magnitude MI 6.5 (Fig. 2), followed by thousands of aftershocks, including two major shocks on September 11th (MI 5.5) and September 15th (MI 6.0). The sequence caused almost 1000 casualties and was responsible for about 1000 landslides, mainly rockfalls (about 90 %), for a total mobilized volume of about 100,000 m\(^3\), documented in the landslide inventory by Govi (1977) (see Fig. 2). Other instability phenomena, such as slides or debris flow, were observed in small numbers (Govi 1977; Civita et al. 1985).

We assumed that the documented rockfalls from the Govi inventory are related to the occurrence of the main shock, and thus we analyzed them statistically as a whole for model calibration. This might lead to some overestimation of the initial seismically triggered events, but it is conservative enough for the purpose of direct application to civil protection, already intrinsically accounting for the effects of possible aftershocks in the short term. Govi (1977) shows that the most important factors influencing the landslides at the same distance from the epicenter were weakening of the rocks by intense tectonic fracturing and slope steepness, controlled by structure and lithology.

The FVG region has a rich geological and geomorphological setting, dominated by sedimentary rocks (cf. Table 1). The results of metamorphic actions of a low degree are subordinated, only of interest in some Paleozoic formations. Among the sedimentary deposits, terrigenous rocks (sandstones, argillites, siltstones, conglomerates, etc.) and carbonate rocks (limestones, dolomites) predominate. Evaporite rocks (gypsum, dolomitic breccias, carious dolomites, etc.) are subordinate, even if widespread in local belts. Evaporite are also relevant for the structural geomorphology and instability of the areas. Intrusive rocks are absent.

The region is characterized by a compressional seismotectonic regime, with E-W trending thrust systems, mostly south dipping, with a subordinate strike-slip component to the east. Seismicity, spatial, and kinematic characteristics of main seismogenic sources of the area are summarized in Slejko et al. (1999), Bressan et al. (2018), and Aoudia et al. (2000).

The epicenter of the May 6th earthquake is as reported in the parametric catalog of Italian earthquakes, CPTI15 (Rovida et al. 2019), although its location is debated (e.g., Aoudia et al. (2000); cf. Fig. 2). The associated seismogenic fault trace was likely oriented E-W, as evidenced by the orientation of the nodal planes from focal mechanism solutions and agrees with the general orientation of active tectonic structures of the region. A southward dipping fault plane is in accordance with a blind thrust derived from seismic profiles and from the distribution of aftershocks (Peruzza et al. 2002; Poli et al. 2008; Galadini et al. 2005).

Data used in this work were the following:

  • Digital elevation model (DEM) at 10-m resolution, TINITALY (Tarquini et al. 2007);

  • Slope unit map extracted from the national map of Alvioli et al. (2020);

  • National landslide inventory map IFFI (Trigila et al. 2010; ISPRA 2018). Here, we extracted the subset of the national IFFI inventory within the FVG region and further selected the features in the vector layer labeled as “falls.” These features helped in partially validating the results of simulations or rockfall runout with STONE in FVG. Figure 2 shows the inventory, with landslide polygons in red. We refer to Loche et al. (2022) for a description of the inventory.

  • Landslide inventory map containing polygons of rockfalls triggered by the May–September sequence in 1976 (Govi 1977). Figure 2 shows the inventory, with landslide polygons in blue, prepared using photointerpretation supplemented by field surveys. The inventory is a key input to the method presented here: it served as calibration data to select the best dynamic (i.e., dependent on a specific earthquake event) localization method of rockfall sources.

  • Geo-mechanical information based on a lithological map of Italy, scale 1:100,000 (Bucci et al. 2022). The map served to assign terrain parameters required by the software STONE. Table 1 lists the numerical values of such parameters, also used by Alvioli et al. (2021).

  • Peak ground acceleration map corresponding to the 1976 earthquake in FVG generated using ShakeMap (Worden et al. 2020).

  • Location of the epicenter of the earthquake of May 6th, 1976 (Rovida et al. 2019).

  • Roads and railways data extracted from OpenStreetMap (https://www.openstreetmap.org; Accessed September 22, 2022). Licensed Data are released under the Open Data Commons Open Database License (ODbL) by the OpenStreetMap Foundation (OSMF).

Methods

Data-driven selection of sources

They key input of simulations with STONE requires identification of grid cells representing rockfall sources, in which the program sets initial points of three-dimensional trajectories. The overlap of all the simulated trajectories results in the overall runout, the key output we are interested in here. Source selection is a non-trivial step, and, in principle, it can be carried out by visual interpretation of orthophotos and manual mapping of potential sources. This approach is time-consuming, especially over large areas, and subjective (Guzzetti et al. 2004; Santangelo et al. 2019; Santangelo et al. 2020).

The traditional, straightforward way of selecting source areas for the model STONE, and similar physically-based approaches, is to set a slope-angle threshold and consider as potential sources all of the grid cells with slope angles larger than the thresholds (Guzzetti et al. 2002; Matas et al. 2017; Torsello et al. 2022). This approach has limitations in that (i) different geomorphological settings and/or DEM resolutions may require different thresholds; (ii) it does not provide a probability of each grid cell to actually trigger a rockfall; (iii) it does not consider additional variables other than slope; and (iv) it neglects the different possible triggers.

The approach introduced by Alvioli et al. (2021), adopted here, addresses points (i) and (ii) above, while it does not yet include variables other than slope (Alvioli et al. 2022a; Pokharel et al. 2023). Alternative approaches exist (Rossi et al. 2021), which we did not adopt here. Point (iv), instead, is the object of the next section. Here, we briefly describe the method of Alvioli et al. (2021) to both locate sources and assign a probability of failure in a homogeneous way over a large area, on the 10 m-resolution DEM of Italy TINITALY (Tarquini et al. 2007). Expert geomorphologists mapped potential sources in a conservative way to select locations where rockfalls may occur, mapping polygons where there is a combination of steep slope, bare rock, substantial curvature, and—where possible—apparent macroscopic fracturing state.

The method is data-driven in that it uses information from expert mapping of potential rockfall sources by photo interpretation in a few selected, representative slope units (Alvioli et al. 2020) in the area of interest. In each slope unit, expert mapping was carried over in a complete manner: geomorphologists mapped each and every potential source. Analysis of the distribution of slope angle values underneath the mapped polygons, with respect to slope angle distribution within the whole corresponding slope unit, provides a probability of presence for sources as a function of slope. Statistical generalization with a quantile regression procedure allows determination of the probability as a function of slope, which was taken of the following form:

$$P_{static}(S)\,=\,c\,\left( \frac{S}{90}\right) ^4,$$
(1)

where S is a grid cell slope angle and c a parameter. The procedure was applied in 29 physiographic units in Italy (Guzzetti and Reichenbach 1994); in this work, we used the result of Alvioli et al. (2021) in two units overlapping with the FVG study area (values of the parameter c in Eq. (1)).

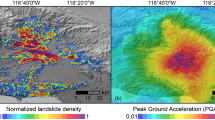
The physiographic units used here and in Alvioli et al. (2021) were slightly modified with respect to the original ones; Alvioli et al. (2020) show the modified map. The units relevant to this work are Central-Eastern Alps and Carso, containing the epicenter, and Veneto Plain, south from the epicenter (cf. Fig. 2). Figure 3 shows the probabilistic curves, corresponding to the selected physiographic units, with corresponding values of the parameter c in Eq. (1) (c = 4.32 for Central-Eastern Alps and Carso and c = 5.54 for Veneto Plain). Calculation of the function in Eq. (1) as a function of slope angle, using these parameters, provides a probabilistic map of potential rockfall sources in FVG (Figure 4). The map is “static” in that it is only dependent on topography, and it is considered here as the starting point to obtain a map of sources as a function of a specific seismic trigger, as described in the following.

Ground shaking model

The spatial distribution of ground motion associated with the May 6th, 1976 event was assessed using an empirical ground motion prediction—the ShakeMap software (Worden et al. 2020). The tool allows for rapid assessment of the shaking distribution (either in terms of peak ground acceleration, peak ground velocity, 5 % damped response spectral acceleration at 0.1 and 0.3 s, and Arias intensity) over a large area, and it can also account for the effects of local geology (using V\(_{s30}\) from physiographic slope (Allen and Wald 2009) and existing ground motion observations, where available). This last feature makes ShakeMap particularly suitable for rapid earthquake impact evaluation and in combination with seismological monitoring networks, e.g., the SMINO Seismological Monitoring Infrastructure of North-Eastern Italy managed by the Italian National Institute of Oceanography and Applied Geophysics (OGS; see Fig. 1) (Bragato et al. 2021). SMINO provides in almost real-time magnitude, hypocenter location, and ground motion estimates of any detected event (Poggi et al. 2021).

For this simulation, we selected the robust empirical ground motion prediction equation (GMPE) model of Akkar and Bommer (2007), which accounts for source geometry through the Joyner and Boore distance metrics (RJB). Figure 4 shows the spatial distribution of peak ground accelerations (PGA) in the epicenter area. This ground shaking map is used throughout this work to infer selective activation of subsets of previously obtained static rockfall sources using a triggering model described in the next section.

Earthquake trigger for rockfalls in STONE

In this section, we describe a probabilistic approach to localize possible rockfall sources triggered by a specific earthquake. We assume the probabilistic, “static” map of potential rockfall sources as a starting point (Eq. (1)). We introduce a simple mechanism to activate each grid cell with non-zero probability of failing, assuming that the probability of activation is a function of PGA generated by seismic shaking. The proposed mechanism assumes that cells where PGA is null have zero probability of activation, and probability increases up to a maximum value, corresponding to the point with maximum value of PGA.

The latter intuitive assumption is supported by the simple analysis in Fig. 5a, showing the distribution of PGA values in the area of interest. The figure contains three histograms, namely, (i) the distribution of PGA values (grid cells) in the entire area (blue); (ii) the distribution of PGA values within the bounding box containing all of the landslide (rockfall) polygons in the inventory from Govi (1977) (yellow); the distribution of PGA values restricted to the landslide polygons (red). This suggests that the presence of landslides is strongly dependent on PGA values, with an increasing number of landslide cells for increasing values of PGA, supporting the approach adopted here.

The activation mechanism is implemented multiplying the static probability \(P_{static}(S)\) of Eq. (1) by a factor F varying in the interval [0, 1] and depending on the value of PGA in each grid cell. For the factor F, we propose two different functional dependencies on PGA, namely, a linear dependence:

$$\begin{aligned} F_L(PGA)\,=\,\frac{PGA\,-\,PGA_{min}}{PGA_{max}\,-\,PGA_{min}}\,, \end{aligned}$$
(2)

and a non-linear dependence, using a functional form known as normalized tunable sigmoid function (NTSF), as follows:

$$F_{NTSF}(PGA)\,=\,\frac{1}{2}\,+\,\frac{1}{2}\frac{PGA^\prime\,-\,k\,PGA^\prime}{k\,-\,2\,k\,\left|PGA^\prime\right|+1}\,,$$
(3)

where k is a parameter and PGA\(^\prime\) is itself a linear transformation of the PGA values into the interval [0, 1], defined as follows:

$$PGA^\prime\,=\,2\,\frac{PGA\,-\,PGA_{cut}}{PGA_{max}\,-\,PGA_{cut}}\,-\,1\,.$$
(4)

Both Eqs. (2) and (3) map values of PGA in the [0, 1] interval. The free parameter \(PGA_{cut} > PGA_{min}\) in Eq. (4) introduces a minimum activation threshold (different from the observed \({PGA}_{min}\)), below which failure probability is forced to null. In this study, we selected a single value \(k = -0.5\) and investigated three different values of PGA cutoffs (see Fig. 5b), namely, the actual minimum value \(PGA_{min}\) = 2.7 found in the area (labeled NTFS I in Fig. 5b), \((PGA_{max}-PGA_{min})/4\) = 9.25 (NTSF II), and \((PGA_{max}-PGA_{min})/2\) = 15.67 (NTSF III). Values of PGA are given as percent of g, Earth’s acceleration of gravity.

The final, dynamic probability \(P_{dynamic}\) of a grid cell to represent a rockfall source is the product of the static probability and of the event-dependent activation factor \(F_\alpha (PGA)\), where \(\alpha\) stands either for L Eq. (2) or for NTSF Eq. (3) (Alvioli et al. 2022a, 2023). As a result, \(P_{dynamic}\) depends on both S and PGA as follows:

$$\begin{aligned} P_{dynamic}(S,PGA)\,=\,P_{static}(S)\,F_\alpha (PGA)\,. \end{aligned}$$
(5)

Curves for \(F_\alpha (PGA)\) corresponding to Eqs. (2) and (3), for the values of PGA that occurred during the Friuli Earthquake in 1976, are in Fig. 5b. The curve labeled as NTSF I reduces the relative probability of smaller values of PGA and enhances the probability of larger values, with respect to the linear function. On the other hand, using NTSF II or NTSF III would set to null the probability for PGA values below 9.25 % of g and 15.67 % of g, respectively.

Given that no robust physical justification exists to support neither the linear nor one of the three proposed NTSF functional models, we selected the most suitable option a posteriori, based on the fit between their prediction and data from the Govi (1977) inventory. Four independent rockfall runout calculations were performed using the software STONE, and the results were compared with observed rockfall runout using different classification methods (see “Results”).

We stress that \(P_{dynamic}(S,PGA)\) in Eq. (5) represents a model for the possibility of source presence. The model can be applied in any area in Italy or elsewhere for any seismic event for which the PGA map is known and calibration data exist. We expect the calibration procedure to be specific of the study area and less related to a specific event. This allows, in principle, to run a simulation with STONE a few hours after an earthquake takes place.

Rockfall runout calculation

The software STONE is a three-dimensional modeling tool for simulating rockfall trajectories (Guzzetti et al. 2002). It assumes point-like boulders and calculates individual trajectories starting from user-defined source points. Trajectories describe the paths of boulders, and simulation includes free falling, bouncing, and rolling on the ground, during which the falling mass loses kinetic energy. The end point of each trajectory is obtained when the velocity of a falling boulder reaches a value close to zero.

Inputs to the software, in addition to a digital elevation model needed to constrain the three-dimensional topography, are source points location and maps of numerical coefficients (Table 2), used to describe energy loss during bounces and rolling. During the simulation, STONE randomly samples the possible value of model parameters, such as the detachment angle, friction, and normal and tangential restitution, in a ±10 % range of the tabulated central value for each lithological intersected class, thus producing different trajectories along different paths for each simulation.

Outputs from the software are raster maps, containing the count of trajectories, maximum height, and maximum velocity and blocks, for each DEM grid cell; in this work, we only considered the first output. Values of the rockfall count usually vary wildly; for this reason, a classification method of the output raster is a crucial step to evaluate model predictions. For the sake of transparency, in this work, we considered different classification methods, namely, percentiles, head/tail breaks, and decades of values in the output maps. Results are presented as a function of the different classification methods.

We ascribe a probabilistic meaning to the different values in the raster map of sources in input to the model. Different values in the source map (up to 100, herein) correspond to a different number of simulated trajectories, initiated from each source grid cell. Each trajectory evolves into a different path, thanks to the random generation of different parameters in the STONE code, namely, the detachment angle, friction, and normal and tangential restitution parameters. Each such parameter is changed up to 10 % from its nominal value listed in Table 2 as a function of lithology. That, eventually, results in a higher probability of trajectories crossing locations downhill from sources with higher probability of detachment and lower probability otherwise.

Impact evaluation

Earthquake-induced landslides can cause up to 11 % of fatalities caused by earthquakes (Daniell et al. 2017). Aside from direct damage, landslides and rockfalls can significantly impact the transportation networks (Xie et al. 2017; Alvioli et al. 2021; Pokharel et al. 2023), thus affecting commercial viability, disrupting traffic, and limiting access to emergency operators in the aftermath of an earthquake (Robinson et al. 2018). This leads to additional human and economic losses and exacerbate the impacts on affected population by isolating small but vulnerable villages. Nowicki Jessee et al. (2018) and Tanyaş et al. (2019a, b) proposed assessment of expected earthquake-induced landslides casualties at global scale based on empirical data and available ground shaking scenarios. An extension of that approach to assess expected damages for specific scenarios requires locally calibrated vulnerability curves for the main exposed assets (e.g., buildings, transportation infrastructures, bridges). Agliardi et al. (2009) proposed a method to obtain physical vulnerability functions for buildings based on empirical data. In the case of transportation corridors, the European project SYNER-G project (Systemic Seismic Vulnerability and Risk Analysis for Buildings, Lifeline Networks and Infrastructures Safety Gain; https://cordis.europa.eu/project/id/244061) collects existing vulnerability curves which account for expected ground shaking and secondary effects Argyroudis and Kaynia (2015). In many near real-time applications, vulnerability/fragility is assumed to be maximum, in order to produce rapid and conservative results (Corominas et al. 2014). Following this approach, (Guzzetti et al. 2004) investigates the occurrence of potential rockfall damages on transportation corridors based on the simulation of rockfall trajectories. Robinson et al. (2018) proposed a near real-time damage assessment method based on a rapid but simplified approach and demonstrated the relevance of this information in the emergency response phase. However, the simulation of rockfall trajectories has not yet been applied to near real-time damage assessment of seismic-induced landslides. In this section, we propose an approach to support rapid assessment of earthquake-induced rockfall damages to infrastructure.

In this study, as in Alvioli et al. (2022a), potential damage is estimated combining the proposed dynamic trajectory mapping and the locations of exposed assets. For the purpose, rockfall trajectory count is first reclassified into 5 classes (ranging from very low to very high occurrence frequency), while exposure data are extracted from OpenStreetMap, which provides georeferenced layers of buildings footprints and road paths. The exposure spatial resolution is comparable with the one of the trajectory count (10 m). Then, by overlapping the rockfall trajectory count layer and the exposure layer, we can identify those assets potentially in the rockfall path, assuming that each exposed asset is impacted by at least one rockfall trajectory.

Results

In this section, we present results of rockfall runout simulated using the three-dimensional model STONE with both “static” sources \(P_{static}(S)\), independent of any specific trigger, Eq. (1), and “dynamic” sources \(F_{dynamic}(S,PGA)\), depending on an earthquake trigger and obtained from the approximations for the PGA-probability mapping functions, Eq. (5).

Simulations with static sources

Figure 4 shows results from different approximations of the source map of rockfalls triggered by the earthquake of 1976 in FVG. This is the key input of the model STONE and can only be evaluated subjectively—we have no observed counterpart. The lack of it is one of the main obstacles we want to overcome. On the other hand, results of simulations with STONE, represented by rockfall runout corresponding to the different approximations for sources, can be compared with observed rockfalls. Available observations are of two kinds, shown in Fig. 2. A geomorphological inventory of rockfalls in FVG, extracted from the IFFI inventory (“falls”), and the event inventory compiled after the 1976 earthquake.

In the static case, the comparison is between IFFI polygons and the modeled runout obtained from static sources. This is the map of sources obtained from statistical generalization of expert-mapped potential sources, i.e., independent of any trigger; Fig. 6 shows the corresponding results of STONE. Even if this is not the main focus of this work, we still list a few numerical results from the comparison with IFFI. The polygonal inventory contains 666 rockfalls in FVG, of which 604 overlap with the predicted runout, and 62 do not. Percentages of overlap between IFFI and STONE predicted trajectories are listed in Table 2. For the sake of completeness, we calculated percentages for the overlap of runout from static sources and the earthquake-induced rockfalls of Govi (1977); results are listed in Table 3. In this case, misses (i.e., false negatives) are substantially larger than in the IFFI comparison.

Results in Tables 3 and 4 are given for three different runout classification methods: “decades” refers to five classes delimited by powers of 10; “head/tail breaks” corresponds to this well-known classification method; “percentiles” corresponds to classes delimited by the 20th, 40th, 60th, and 80th percentiles of the distribution of values in each map. We stress that the head/tail breaks method is particularly suited for highly asymmetrical distributions, as the ones we are dealing with, here, given that maps of trajectories contain the vast majority of very small values and an increasingly smaller number of grid cells with many occurrences (number of simulated trajectories crossing the cell).

Simulations with dynamic sources

The earthquake-induced landslide inventory from Govi (1977) should be linked to the PGA map for that event. Comparison of the inventory and the runout results obtained from the different approximations allows to determine which one produces a better trigger for activating static sources; in other words, a satisfactory model \(P_{dynamic}(S,PGA)\) Eq. (5) for a dynamic trigger for earthquake-induced rockfalls.

The model \(P_{dynamic}(S,PGA)\) allowed preparing different source maps, using a damping function \(F_\alpha (PGA)\) either in linear form Eq. (2) or in the form of a sigmoid with different parameters k and PGA\(_{min}\) Eq. (3). The corresponding source maps are in Fig. 7a–d. The figures suggest a dependence of the suppression factor upon PGA; the static source map, previously shown in Fig. 4, is now vanishing for values of PGA approaching zero. The values of the dynamic sources peak at PGA\(_{max}\), for all of the approximations, by construction.

The “counter” maps resulting from simulations, i.e., raster maps whose values report the number of trajectories crossing each grid cells, are in Figs. 8a–d and 9a–d, in areas at different distance from the epicenter, and at two different zoom levels. As in the case for the sources in the previous figure, the different dependence of rockfall runout upon the values of PGA, in the four different approximations, is manifest from a visual perspective.

Numerical results about the comparison of the inventory from the event in 1976 and different approximations for the dynamic sources are listed in Table 4. The table lists results for two different runout classification methods, namely, the head/tail breaks and percentile methods. We used these two methods as they provided extreme cases, in previous comparisons with observations (Tables 2 and 3). Results suggest that for decreasing spatial extent of the source map (maximum for linear and minimum for NTSF III), the overlap between observed landslides and simulated runout decrease, consistently for both classification methods. Further comments are in the “Discussion” section.

Example of impact evaluation

In this section, we describe results obtained by overlapping the rockfall trajectory count layer and the exposure layer (cf. “Impact evaluation”). The application of the proposed methodology to the 1976 FVG earthquake scenario highlights that such an event, on the current transportation network, would potentially disrupt more than 150 km of roads and 12 km of railway, while damaging more than 5000 buildings (Table 5). Under the considered scenario, both the Alpe Adria highway and the primary road SS13 would be affected by many rockfalls in the upper Tagliamento Valley. The potential disruption of highway and primary roads is particularly relevant and can affect the activities of emergency managers and local communities. In addition, damages may occur to many buildings and secondary or tertiary roads located in mountain areas. On top of that, buildings might be hit by rockfalls in villages with documented damages caused by the 1976 earthquake (e.g., Vito D’Asio) or with known rockfall hazard concerns (e.g., Portis, relocated after the 1976 seismic sequence).

Discussion

The rockfall source maps used for this work were defined as “static” Eq. (1) and “dynamic” Eq. (5). The former is simply an extension to the whole of Italy of the data-driven method by Alvioli et al. (2021), while the latter is new to this work and aims at introducing an existing event trigger. A similar approach was introduced by Alvioli et al. (2022a) and applied all over Italy by Alvioli et al. (2023); in that case, though, only Eq. (2) was used (and non-linear factors were not considered, as in Eq. (3)). Moreover, Alvioli et al. (2023) calibrated the the limits PGA\(_{min}\) and PGA\(_{max}\) against scenarios with specific return times, unlike in here. The source maps developed herein link a specific event to a specific STONE output. Optimization of the model of Eq. (5) is new to this work and represents a further step for the rapid assessment of earthquake-induced rockfall hazard.

We first initialized STONE using full “static” sources and investigated different classification strategies for the results. In fact, the values in the main raster map produced by the model are the number of trajectories crossing a given grid cell; more precisely, they report about the locations in which the trajectories hit the ground—by bouncing or rolling. Figure 6 shows the output of this run. Values in the output maps have a huge variation range, because we simulated up to a hundred trajectories from each source. This results in trajectory counts ranging from unity to a few tens of thousands, with a distribution skewed towards small values. The results summarized in Table 2 show the difference in classification using different methods, considering the IFFI inventory for rockfalls in FVG. Classes based on head/tail breaks and percentiles show two extreme cases; in the former, most grid cells in IFFI polygons are in the very low class, while in the latter, the very high class contains most. The “decades” method produced an intermediate picture, where most of the values were in the medium class. Table 3 shows corresponding results for the inventory compiled after the 1976 earthquake; comments are practically the same, though the percentage of misses (false negatives) is double that in the case of IFFI.

Given the large differences between results using the three classification methods shown in the tables, we examined more in depth the distributions of trajectory count values for one specific case. We considered the count map resulting from STONE using the “static” map of sources. The map contains 10,028,244 non-null cells, with maximum value 40,746; 9 % of the cells have value 1, and 25 % of them have values smaller than 10. The inset in Fig. 10 shows a histogram of the normalized frequency values, spanning seven order of magnitudes. The main plot in the figure, instead, shows boxplots as follows. The black whiskers correspond to the same distribution of the inset, with outliers removed, for they would make the figure unreadable as they represent the vast majority of values. This is also true for the remaining whiskers, which show distributions within each class (1–5), for the three classification methods described herein. One should appreciate that the percentile method is not a satisfactory one, nor is the decades method, for a distribution so skewed as shown in the inset. In fact, all of the five whiskers for the percentiles method show similar content; in the case of the decades method, this is still true for the first three classes. Whiskers for the head/tail method, instead, show that the five classes are well distinguished from each other. We suggest that this classification is better suited for a skewed distribution. We do not show maps colorized with the three methods because they are not really informative and it would be difficult to visually show the effect discussed here.

Figure 6b shows a detail of the results for the static case in a small area. This was chosen in an area with few records in the IFFI inventory. The figure shows that most of areas predicted with non-null, and even high and very high susceptibility, do not find correspondence in the inventory. Besides the fact that the inventory may not be complete in that area (Loche et al. 2022), or that new rockfalls can still occur where they had not occurred before, we stress a trivial but important fact here. The model STONE initiated with sources based on morphometric arguments but otherwise independent of any trigger may substantially overestimate rockfall susceptibility in specific areas. Such sources result from extrapolation of observations (morphometric properties) in a few spots to a substantially larger area. Figure 6 shows that enhancing/damping static sources using specific triggers, as the seismic trigger introduced in this work, could provide much more reliable predictions. On the other hand, observed landslides that have no match in the predicted susceptibility map cannot be improved using a specific trigger; the dynamic source map is always a spatial subset of the static map, though with different probability values.

Optimization of dynamic sources requires assessment of the agreement between simulated STONE runout and rockfalls observed after the earthquake under investigation (Govi 1977). Considering different approximations for the \(F_\alpha (PGA)\) function, Eqs. (2) and (3) plotted in Fig. 5b, we obtained results shown in Fig. 7 (sources) and Figs. 8 and 9 (details of the runout). In the figures, contours show PGA values, and a star shows the quake’s epicenter. By inference, sources are null where PGA values approach zero; the damping factor is less important for increasing values, up to the maximum where \(F_\alpha (PGA) = 1\) and the model earthquake-induced sources are identical to the static sources. The damping is different in the linear and non-linear approximations; the figures suggest that the observed rockfalls have different degrees of agreement with the model runout in the four cases. Agreement is quantified in Table 4; the values in the table should allow one to single out the best approximation for the \(F_\alpha (PGA)\) damping factor.

One may use different strategies to select a good match, though. First, Table 4 lists results for two classification methods, given the large differences, as discussed above; we considered only the two extreme cases, head/tail breaks and percentiles. Analyzing the numerical results, one may follow different strategies to select the dynamic sources providing better match. The number of misses increases consistently from Linear to NTSF III—again, by inference, because the source map “shrinks” as we move left to right in the table. The percent variation of “non-null” from left to right is smaller between linear and NTSF I (0.37 %) than other changes (static to linear: 2.86%; NTSF I to NTSF II: 3.82 %; NTSF II to NTSF III: 1.03 %), which could suggest NTSF I as best match. Looking at the content of individual classes, as already noted, the percentiles classification method accommodates most of the values in class 5, VH, and the opposite for head/tail breaks. However, moving from left (static/linear) to right (NTSF III), the trend is not always monotonic. In fact, in the head/tail breaks method, there is a maximum in NTSF I for classes 3 and 4, in linear for classes 2 and 5, and in static for class 1. In the percentiles method, the maximum is always for static, except for linear being the class 5 maximum; because of this behavior, we deem this classification method ineffective. We believe the NTSF I provides an overall better match, with smallest true positives percentage variation from linear and the largest true positives percentage variation going to NTSF II. Moreover, individual classes also seem to provide a more consistent split of the distribution of true positives.

An alternative/additional way to determine a good match may be to consider a full confusion matrix determination of observed/predicted positives/negatives. However, we note that the large number of false positives and true negatives (of the order of many millions, in contrast with a few thousands for false negatives and true positives) could unbalance the confusion matrix, and we preferred not to follow that strategy. Nevertheless, for the sake of completeness, we report results of a standard training/validation procedure.

We split the landslides data into a training sample (70 % of the landslides, selected randomly) and a validation sample (the remaining 30 %), repeating the random selection ten times. For each selection, we calculated the true positive rate, TPR = TP/(TP + FN), and true negative rate, TNR = TN/(TN + FP), where T, F, P, and N stand for true, false, positives and negatives, respectively. For all of the selections, and within the numerical variability across different selections, we found monotonic decrease (increase) of TPR (of TNR) going from the linear to the NTSF I–III. The large numbers representing TN and FP values make TNR less relevant in our case. In this view, the best result would be the linear approximation, and validation consists in calculating TPR and TNR for the only linear approximation, using the 30 % landslides that did not enter the previous analysis, for each random selection. Numerical results are in Table 6. As this analysis does not distinguish classes, the classification strategy is irrelevant here. We still consider this procedure less informative than the assessment of Table 4.

Eventually, we stress that we did not aim at a finer determination of the parameters of the NTSF approximation, nor to experiment with different functional forms. A finer determination would probably require more than one example of an earthquake inducing rockfalls to obtain a more robust result, and that may be performed elsewhere for historical events in Italy and for additional scenarios.

Conclusions

This work implemented an event-based earthquake trigger for seismically induced rockfalls within a three-dimensional physically based models. The traditional method, common to different existing models (Guzzetti et al. 2002; Frattini et al. 2008; Matas et al. 2017; Dorren et al. 2022), considers a given set of locations as possible block detachment points and calculates the geometrical extent of rockfall trajectories on the downslope topography.

The typical input source map is a static one; simulations initiated with such input data provide a spatially distributed likelihood of rockfall occurrence. A full assessment of rockfall hazard requires the joint knowledge of the magnitude of rockfalls and temporal frequency, return times, or explicit dependence on specific triggering events. Previous work, by a few of us, considered different spatial probabilities for the source map, instead of a uniform probability (Alvioli et al. 2021); recent developments using the same 3D model include a seismic trigger, considering scenario-like shake maps with different return times (Alvioli et al. 2023).

Here, we introduced fully dynamic source maps by calibrating a triggering mechanism on both the shake map and the observed rockfalls. Calibration concerned the parameters of a function used to map peak ground acceleration values into a damping factor for morphological, static sources. The damping function was either a linear mapping or a parametric sigmoid. An in-depth investigation and calibration of the damping function may also consider more refined estimates of the seismic ground shaking, which should account for topography and soil type, among the others, and can be a matter for future research.

Results of simulations with STONE, a three-dimensional rockfall runout model, support the following conclusions for the simulations in the area of 1976 earthquake, in the FVG region, North-Eastern Italy:

  • Rockfall runout obtained with static sources showed a reasonable match (8.9 % false negatives) with the relevant subset of the national polygonal inventory IFFI, restricted to “falls”; match with the inventory prepared after the 1976 earthquake event was poorer (16.2 % false negatives).

  • We deem the head/tail breaks method as the most suitable classification method for the trajectory count output of the model STONE.

  • Introduction of a dynamic trigger, driven by the peak ground acceleration associated with a specific seismic event, effectively linked the event to a specific set of sources and corresponding simulated runout.

  • Simulations with different functional forms of a damping function, \(F_\alpha (PGA)\), allowed calibration of the parameters of the function itself against observed rockfalls; our analysis favored the NTSF I version, with \(PGA_{min}\) corresponding to the minimum existing PGA and k = -0.5 (cf. Eq. (3) and Table 4).

The conclusions above deserve a few additional remarks. Results from the dynamic map cannot be better than those from the static map—the number of false negatives does not decrease—because the triggering factor of Eq. (5) only damps the static sources, but no new sources are introduced. On the other hand, the balance between different classes is changed, due to different values of probability in corresponding static and the active dynamic grid cells. This calls for further improvements of the static probabilistic map, here motivated only by morphometric arguments, though based on statistical generalization of expert mapping.

We stress that our approach does not consider the expected magnitude of the rockfalls, necessary for a full assessment of hazard; this would amount to implementing blocks of different sizes in the code. We are working on an effective method to cope with different sizes, without the need to modify the code, as we did here for the triggering mechanism. Nevertheless, we considered an example impact assessment, calculating the overlap between the existing infrastructure and the model output, in the simulated scenario. This is a preliminary example of the outcome one would obtain in a real-time application of the framework proposed here.

The automation of this framework in almost real time would support the rapid assessment of expected damages caused by rockfalls induced by a seismic event in a study area, which is paramount for first respondents and emergency managers after a seismic event. The potential implications for emergency management will be explored in future work using more sophisticated approaches for both landslides and exposure modeling, such as traffic and social exposure data.

Table 1 Numerical values of parameters used in STONE. “ID” and “Lithological Class” refer to classes L1–L19 identified by Bucci et al. (2022). The program performs a random sampling of the values in a ± 10 % range around the values shown here. The interested reader can find a figure of the lithological map in Alvioli et al. (2021) and Bucci et al. (2022), not shown here
Full size table
Table 2 Comparison between counts of trajectories obtained by the method of Alvioli et al. (2021) on the whole FVG region and rockfalls in the IFFI catalog (Trigila et al. 2010; ISPRA 2018). We used three classifications of the counter raster map. “Decades”: 1–10; 11–100; 101–1000; 1001–10,000; more than 10,000; “head/tail breaks” refer to the well-known classification method; “percentiles” are 0 %–20 %–40 %–60 %–80 %–100 % classes
Full size table
Table 3 Comparison between counts of trajectories obtained by the method of Alvioli et al. (2021) on the whole FVG region and rockfalls in the Govi (1977) inventory. “Decades,” “head/tail breaks,” and “percentiles” as in Table 2
Full size table
Table 4 Comparison between counts of trajectories and rockfalls in the Govi (1977) inventory. Sources were selected by either the method of Alvioli et al. (2021) Eq. (1) for “static” sources or with the “dynamic” method introduced here by Eq. (5) with a dependence on peak ground acceleration. Different approximations for \(F_\alpha (PGA)\) are linear dependence Eq. (2), and three different parameterizations for a normalized tunable sigmoid function (NTSF, Eq. (3) also shown in Fig. 5). Classes correspond to head/tail breaks for the upper part of the table, as in the second column of Tables 2 and 3, and to 0–20–40–60–80–100 percentiles of each map in the lower part of the table, as in the third column of Tables 2 and 3
Full size table
Table 5 Impact assessment of rockfalls on infrastructure, based on the scenario simulated in this work, the 1976 earthquake. Figures for buildings represent a count; any other result represents a length in kilometers. The classification of roads is from OpenStreetMap. For road bridges, the total affected length refers to the overall length on the different road types
Full size table
Table 6 A simulation of training/validation procedure, considering landslide data as truth and the full model runout in the four approximations discussed in this work. The negligible variation in TNR is given by the large numbers representing TN and FP cases
Full size table
Fig. 1
figure 1

Summary of the proposed rapid assessment of earthquake-induced rockfalls. The seismic trigger can be coupled with an actual earthquake alert system (e.g., from the OGS seismic network) or any earthquake scenario, as in this work. Output impact evaluation is designed to be readily used in civil protection

Full size image
Fig. 2
figure 2

A shaded relief of the Friuli Venezia Giulia region, North-East of Italy. Blue polygons show the landslide (rockfall) inventory prepared by Govi (1977) (a yellow star shows the location of the epicenter of May 6, 1976); red polygons are a subset of the national IFFI catalog (Trigila et al. 2010; ISPRA 2018) showing only rockfall features. Size of the polygons is exaggerated to allow resolving the smaller ones. The areas delimited by black lines are physiographic units from Guzzetti and Reichenbach (1994), namely, Central-Eastern Alps and Carso, containing the epicenter, and Veneto Plain, south from the epicenter (cf. Alvioli et al. 2020, 2021)

Full size image
Fig. 3
figure 3

Analysis of the properties of expert mapped rockfall source areas, represented by green dots. NLQR 90 % is the method introduced by Alvioli et al. (2021) and adopted in this work. The two red curves Eq. (1) are obtained with the values c = 4.32 (a) and c = 5.54 (b), corresponding to the two different physiographic areas in FVG region, shown in Fig. 2

Full size image
Fig. 4
figure 4

The “static” rockfall source map, obtained only from morphometric properties in the whole FVG region, using Eq. (1). The contour lines in a show the values of PGA corresponding to the earthquake considered throughout this work, expressed in percent of the acceleration of gravity. In b, the detail within the dashed rectangle in a, one can resolve different values of probabilities, obtained from the red curves in Fig. 3, colorized with different shades of blue. Values in the raster map represent the number of simulated trajectories originating from each grid cell

Full size image
Fig. 5
figure 5

a Normalized histograms of PGA values on the whole study area (light blue) and restricted either to the rectangular region including landslides from the Govi (1977) inventory (BBox; yellow) or to the only grid cells with landslides (red). b Different methods used in this work to modulate the probability of each grid cell to represent a source of a simulated rockfall trajectory (Alvioli et al. 2021); Linear refers to a simple min-max rescaling of the PGA values to the [0, 1] interval Eq. (2) and NTSF I–II–III to different non-linear mappings Eq. (3)

Full size image
Fig. 6
figure 6

Rockfall runout simulated with STONE, using the “static” rockfall source map, of Fig. 4, classified with the head/tail breaks algorithm. It represents a susceptibility map in that it does not describe magnitude, nor it contains indications on the trigger and its expected temporal occurrence. Black polygons, filled in a and empty in the detail b, show the location of polygons classified as “falls” in the national inventory IFFI (Trigila et al. 2010; ISPRA 2018)

Full size image
Fig. 7
figure 7

The different approximations for event-dependent rockfall source maps, proposed in this work, obtained from Eq. (5), where \(\alpha\) stands either for L (linear, a) Eq. (2) or for NTSF (b–d) Eq. (3). The raster of the sources (white), as well as the observed rockfalls (blue), were slightly exaggerated for better visibility. The corresponding runout simulated with STONE is shown in Fig. 8, within the area in the blue dashed rectangle, and in Fig. 9, for the red rectangle

Full size image
Fig. 8
figure 8

Rockfall runout simulated with STONE initialized with the different approximations for sources, \(P_{dynamic}(S,PGA)\), shown in Fig. 7. Here, we show details in the area within the rectangle of the previous figure. Blue polygons represent the inventory prepared by Govi (1977) after the earthquake corresponding to the PGA contours shown in the figure. Numerical values describing the agreement between simulations and observed rockfalls are listed in Table 4

Full size image
Fig. 9
figure 9

As in Fig. 8, but for the area delimited by the red rectangle in Fig. 7

Full size image
Fig. 10
figure 10

The distribution of rockfall trajectory count values in the map obtained from “static” sources and used for the comparison in Table 2. The inset shows the normalized frequency. The black whisker in the boxplot also refers to the distribution in the inset (outliers always removed). The colored whisker corresponds in each class (1–5) to the distributions obtained in the three classification methods considered in this work

Full size image