Introduction

Debris flows are one of the most hazardous types of landslides in Norway and other parts of the world and become more frequent due to an increase of precipitations from climate change. Its steep topography makes Norway susceptible to debris flow events. The events are often accompanied by significant bed entrainment (e.g. Breien et al. 2008). The initial debris flow volume is typically rather small, but the volume can extensively increase by entraining or accumulating soil, rocks, fluid and vegetation along the flow path (Hungr et al. 2005). The Centre for Research-based Innovation, Klima 2050 (Solheim et al. 2021), was created with the aim of reducing the risks associated with climate change and protecting critical infrastructures from landslides. A typical debris flow landslide took place in Hunnedalen (Norway) on 2nd June 2016 after a period of intense rainfall (Fig. 1a). The initial landslide volume was only about 2000 m3, but following entrainment, it increased to 20,000 m3 (Vicari et al. 2021b) and buried a regional road, FV 45, remarkably without causing injuries. Figure 1b shows a detail of the eroded flow channel (field survey in June 2019), with entrainment depths of more than 2 m.

Fig. 1
figure 1

Hunnedalen (Norway) debris flow on 2nd June 2016: (a) aerial photo after the event (courtesy: Multiconsult and Norwegian Public Roads Administration NPRA) (b) details of the eroded channel

Full size image

To study the entrainment process and mitigation solutions, large-scale flume tests have been conducted (Vicari et al. 2021a) in a unique facility located in Hong Kong (Ng et al. 2019). The 28-m-long flume was designed to reduce scaling effects typical for debris flows (Iverson 2015). The experimental study of Vicari et al. (2021a) showed that an upstream flexible barrier (i.e. placed upstream of the erodible bed) can effectively reduce both entrainment and the impact on a terminal barrier. The experimental results will be briefly summarized in this paper. To gain more insights regarding the entrainment mechanisms and the impact on the barrier, a numerical study was suggested to back-calculate the experimental results. Among the several numerical methods described in the literature, an appropriate model should be selected to simulate both the interaction with the barrier and the entrainment. Typically, depth-averaged models are used to simulate the debris flow runout and entrainment (e.g. Medina et al. 2008; Pirulli and Pastor 2012; Pastor et al. 2014; Frank et al. 2015). However, depth-averaged numerical models cannot capture the vertical momentum redirection (Ng et al. 2020), which is typical of the interaction of a debris flow with a structure. Three-dimensional models have been successfully applied for this purpose (e.g. Kwan et al. 2015; Koo et al. 2018; Zhao et al. 2020; Cuomo et al. 2021; Lam and Wong 2021). However, only a few study entrainment using a three-dimensional model (Lee and Jeong 2018; Lee et al. 2019; Nikooei and Manzari 2020). Previous research has not focused on simulating both the entrainment of an erodible bed and the impact on a flexible barrier using the same numerical tool.

Gravity driven mass flows can entrain an erodible by two mechanisms: (i) transmission of basal stresses from the flow on to the erodible bed (Hungr et al. 2005), possibly followed by (ii) shear resistance decrease in the erodible bed by development of excess pore pressures (Sassa 1985). Concerning the first, the flow can transmit two types of basal stresses onto the erodible bed: a basal shear stress acting on a surface parallel to the flow direction, and a ploughing stress, which in principle is a normal stress acting on a surface perpendicular to the flow direction. Analytical solutions and models have previously been derived considering the transmission of shear stresses at the base (Iverson 2012; Issler 2014), but not ploughing stresses. Iverson (2012) obtained a formulation to evaluate the entrainment rate for a two-layer model (Fig. 2a). The upper layer (in red) represents the flow and the lower layer (in yellow) represents the erodible bed, resting on a rigid base. A Cartesian coordinate system is oriented with the x-direction along the flow direction and the z-direction orthogonal to the base of the bed. A thin cross-hatched element of the bed with thickness \(\Delta {z}_{\mathrm{b}}\) is about to be entrained in the flow. The stresses acting on the element are the upper contact shear stress from the debris flow onto the element (\({\tau }_{\mathrm{f}-\mathrm{b}}\)) while the bed resisting shear stress (\({\tau }_{\mathrm{b}}\)) acts from below. This bed resisting shear stress can be modelled to decrease as a consequence of the development of excess pore pressures. By considering momentum conservation for the (cross-hatched) entrained bed layer (Fig. 2b), the entrainment rate can be expressed as:

$$E\cong \frac{\Delta {z}_{\mathrm{b}}}{\Delta t}=\frac{{\tau }_{\mathrm{f-b}}-{\tau }_{\mathrm{b}}+{\rho }_{\mathrm{b}}g\Delta {z}_{\mathrm{b}}\;\mathrm {sin}\;\theta }{{\rho }_{\mathrm{b}}{v}_{\mathrm{f}}({z}_{\mathrm{b}})}$$
(1)

where \(E\) is the entrainment rate, t is time, \({z}_{\mathrm{b}}\) is the distance from the rigid bed to the top of the boundary layer, \({\rho }_{\mathrm{b}}\) is the erodible bed density, \(\theta\) is the slope angle, \(g\) is the acceleration due to gravity and \({v}_{\mathrm{f}}({z}_{\mathrm{b}})\) is the flow velocity at \({z}_{\mathrm{b}}\). Compared to Iverson (2012) formulation, Eq. (1) also includes the slope-parallel gravitational term \({\rho }_{\mathrm{b}}g\Delta {z}_{\mathrm{b}}sin\theta\), to account for a finite thickness of the entrained bed layer \(\Delta {z}_{\mathrm{b}}\).

Fig. 2
figure 2

Schematic of two-layer entrainment model: (a) vertical section of a debris flow travelling over an erodible bed (b) details of the entrained bed layer

Full size image

Equation (1) only models the shear stress (\({\tau }_{\mathrm{f}-\mathrm{b}}\)) acting on the planar x-parallel boundary of the entrained bed layer \(\Delta {z}_{\mathrm{b}}\), neglecting the ploughing basal stresses. On the other hand, three-dimensional models (hereon, this term is used to distinguish from depth-averaged models) can capture both basal shear stress and ploughing stress (Nikooei and Manzari 2020) and take complex and non-regular geometrical boundaries into account. In a three-dimensional model, the entrainment simply happens as a consequence of bed failure and the subsequent transport by flow. Bed failure needs to be controlled by an adequate constitutive model. For instance, Nikooei and Manzari (2020) considered an elasto-plastic behaviour with a Mohr–Coulomb criterion. In their study, however, a dry bed with constant friction was considered, which is quite inconsistent with the case of rainfall induced debris flows. A wet bed, instead, is expected to develop excess pore pressures as a consequence of the action of the debris flow (Sassa 1985; Hungr et al. 2005; Iverson et al. 2011; Iverson 2012), leading to strength reduction and ultimately to entrainment. Lee and Jeong (2018) and Lee et al. (2019) introduced a shear strength reduction law to allow the bed material to transform from a solid behaviour to a viscous one. Experiments carried out by Vicari et al. (2021a) pointed towards a frictional-type debris flow (Iverson 1997). An appropriate constitutive model to account for frictional shear strength reduction of the bed will therefore be introduced in this work to study the mechanisms leading to entrainment. The constitutive model is implemented into the generalized interpolation material point method (MPM) because of its ability to simulate large deformations, the coupled soil-structure interaction (e.g. impact on barriers) and the entrainment. The MPM was coded in the open-source Uintah computational framework. MPM in Uintah has previously been validated by simulations of penetration problems (Tran et al. 2017a), the quickness tests (Tran et al. 2017b), sensitive clay landslides (Tran and Sołowski 2019) and flow impact on rigid barrier (Seyedan and Solowski 2017) all compared with experimental results in laboratory or field. In this study, we model the debris flow experiments almost as a plane strain problem (a narrow 3D model to save computational cost) and the flexible barrier as a curved rigid barrier. A model to capture entrainment from a wet erodible bed is implemented in MPM inspired by field measurements of pore pressures and behaviouristic observations.

Physical and numerical model

Description of the large-scale flume tests

Large-scale flume experiments were conducted by Vicari et al. (2021a) to study the entrainment process by a debris flow and the impact on barriers. Figure 3 shows the 28-m-long flume (Ng et al. 2019) that was used to perform the two tests addressed herein with an initial volume of 6 m3. The flume is 2 m wide and is delimited by two 1-m-tall lateral walls. The debris flow is released by mechanically opening the 1-m-tall door of the storage container, which is inclined at 30°. The debris can then flow over a 15-m-long channel, which is inclined at 20°. An upper 9-m-long fixed bed section ends in a very gentle wedge-shaped 2-m-long transition zone (denoted platform in Fig. 3a) which sends the flow on to the erodible bed. The wet, partly saturated erodible bed has a thickness of 120 mm and was prepared over the last 6 m of the 20° inclined channel. A steel grid provides high friction under the 120-mm erodible bed. An upper flexible barrier is installed 4.3 m from the release gate in one of two tests presented. The flowing mass is finally retained by a terminal flexible barrier, which is positioned at the end of a 4.4-m-long horizontal runout section. The debris material comprises 36% gravel, 61% sand and 3% fines and has a solid concentration of 70% by volume. The erodible bed comprises of 33% of fine gravel, 63% of sand and 4% fines and has an initial gravimetric water content of 15% in a loose state.

Fig. 3
figure 3

Flume model: (a) cross-section with instrumentation layout (U refers to ultrasonic sensor; E refers to the erosion column; Cell 1 measures flow basal normal and shear stresses; and Cell 2 measures normal stress and pore pressure at the base of the bed) (b) aerial photo of the flume

Full size image

In each test, an ultrasonic sensor was mounted at location U1 (3.4 m from the gate) to measure the flow depth. An unmanned aerial vehicle was used to track the position of the flow front and calculate the frontal flow velocity. Furthermore, a load cell was installed at the base of the flume at U1 to simultaneously measure the flow basal normal stress and shear stress (Cell 1). Another load cell (Cell 2) was placed at the base of the flume at 12.5 m from the gate, measuring the normal stress and pore pressures under the erodible bed. Finally, a novel technique, called ‘erosion columns’, was developed to measure entrainment depths along the erodible bed section and distinguish them from deposition. Some key measurements of flow depth, flow velocity, entrainment depth, basal stress and pore pressure will be presented together with the calibration of the numerical model. The interested reader is referred to Vicari et al. (2021a) for additional information on the flume experiments.

Table 1 shows a summary of the two flume experiments each with an initial volume of 6 m3. In the first experiment (V6-B1), the primary aim is to study the entrainment process, and therefore only a terminal barrier (height of 1.5 m) was installed at the end of the channel to stop and retain the debris flow. In the second test (V6-B2), an additional upstream flexible barrier (height of 0.6 m) was installed at 4.3 m from the gate in order to study the impact process on the flexible barrier for a well-defined flow, not disturbed by entrainment. The present work aims at back-calculating these two experiments using MPM, with a particular focus on interaction with the upstream barrier and on entrainment. First, measured flow in the upper section of the channel as well as the observed behaviour during impact is used to calibrate the parameters of the debris flow material in the MPM model. With these parameters locked the entrainment with no upstream barrier is then studied separately. During simulations of the entrainment, the focus is on identifying properties and parameters for the erodible bed.

Table 1 Test program, key flow characteristics and key parameters addressed by numerical modelling
Full size table

Description of the MPM model

The material point method (MPM) based on continuum mechanics is well-suited to solve dynamic large deformation problems. Compared to the finite element method in which the integration points are fixed in the deformed mesh, the MPM allows the integration points, or namely material points, to move freely in the background mesh (Fig. 4). This provides the capability to model the large deformation of solid mechanics for history-dependent materials. Later, Bardenhagen and Kober (2004) proposed the generalized interpolation material point method (GIMP), which greatly improves the robustness and the accuracy of the original MPM. In this paper, GIMP version of material point method is used exclusively as coded in the open-source Uintah computational framework. All the numerical implementations can be found at the open-source platform GitHub (github.com/QuocAnh90/Uintah_NTNU) to replicate the numerical simulations in this paper.

Fig. 4
figure 4

Comparison of FEM and MPM methods

Full size image

To model the frictional-type debris flow of the flume tests (Vicari et al. 2021a), an elasto-plastic model, with a Mohr–Coulomb yield criterion, is selected both for the flowing debris material and erodible bed. In general, the Mohr–Coulomb criterion can be expressed as:

$$\tau =c+\left(\sigma -{p}_{\mathrm{w}}\right)\;\mathrm{tan}\;{\varphi }^{\mathrm{^{\prime}}}=c+\sigma \left(1-\lambda \right)\;\mathrm{tan}\;{\varphi }^{\mathrm{^{\prime}}}=c+\sigma \;\mathrm{tan}\;\varphi$$
(2)

where \(\tau\) is the shear stress, \(\sigma\) is the normal stress, \({p}_{\mathrm{w}}\) is the pore pressure, \(c\) is the cohesion, \({\varphi }^{^{\prime}}\) is the effective friction angle and \(\lambda ={p}_{\mathrm{w}}/\sigma\) is defined as the pore pressure ratio (Iverson and Denlinger 2001). Stresses are positive in compression. \(\varphi\) is the apparent friction angle (Pirulli and Pastor 2012; Kwan et al. 2019) defined by Eq. (2) as:

$$\;\mathrm{tan}\;\varphi =\left(1-\lambda \right)\;\mathrm{tan}\;{\varphi }^{^{\prime}}$$
(3)

In the present work, the flow and erodible bed materials are modelled as one-phase materials, which corresponds to using apparent friction in Eq. (2). This implies that the apparent friction angle implicitly accounts for the effect of pore pressures, if \(\uplambda >0\) is used. The one-phase approach is the state of the art for debris flow numerical modelling (Kwan et al. 2015, 2019; Koo et al. 2018; Zhao et al. 2020; Lam and Wong 2021) and is the most commonly used in engineering practice (e.g. Frank et al. 2015). The dilatancy angle is set to zero in the simulations.

The yield criterion for the debris flow (f) material is expressed with the following notation:

$${\tau }_{\mathrm{f}}={c}_{\mathrm{f}}+\sigma \;\mathrm{tan}\;{\varphi }_{\mathrm{f}}$$
(4)

where \({c}_{\mathrm{f}}\) is the internal cohesion and \({\varphi }_{\mathrm{f}}\) is the internal apparent friction angle of the flowing debris. Since the pore pressure evolution in the flow cannot be computed explicitly, \({\varphi }_{\mathrm{f}}\) needs to be calibrated to simulate the observed debris flow mobility (Koo et al. 2018; Zhao et al. 2020; Lam and Wong 2021) and impact kinematics with the barrier (Kwan et al. 2015, 2019; Lam and Wong 2021).

The contact shear stresses between the debris flow (f) and the flume base (b) are also modelled using Mohr–Coulomb’s law:

$${\tau }_{\mathrm{f-b}}=\sigma \;\mathrm{tan}\;{\varphi }_{\mathrm{f-b}}$$
(5)

where \({\varphi }_{\mathrm{f}-\mathrm{b}}\) is the flow basal apparent friction angle between the debris flow and the flume base. The contact algorithm described by Bardenhagen et al. (2001) has been implemented to model the contact stresses. For simplicity, Eq. (5) is also pragmatically used to model the contact shear stress between the debris flow (f) and the erodible bed (b), where (b) then refers to bed rather than base. This simplification may be made since the yield criterion of erodible bed will control the behaviour if entrainment takes place during a slide.

The yield criterion of the erodible bed (b) is expressed as:

$${\tau }_{\mathrm{b}}={c}_{\mathrm{b}}+\sigma \;{\mathrm{tan}}\;{\varphi }_{\mathrm{b}}$$
(6)

where \({c}_{\mathrm{b}}\) is the internal cohesion and \({\varphi }_{\mathrm{b}}\) is the internal apparent friction angle of the erodible bed. The bed pore pressures and therefore the apparent friction angle of the bed are expected to change in time in function of the shearing imposed by the debris flow (Iverson 2012). A softening model is used in this study (Fig. 5) to simulate the shear resistance reduction resulting from increase in pore pressures for increasing distortional strain (Iverson 2012; George and Iverson 2014). This is inspired by the field observations reported in Vicari et al. (2021a). Simplifying to plane strain and incompressible bed material, the increment of distortional strain in the bed can be expressed as:

$$\delta {\varepsilon }_{\mathrm{d}}=\frac{1}{\surd 3}\sqrt{4{\delta \varepsilon }_{\mathrm{z}}^{2}+{\delta \gamma }_{\mathrm{xz}}^{2}}$$
(7)

where \({\delta \varepsilon }_{\mathrm{z}}\) is the normal strain increment in the z-direction and \({\delta \gamma }_{\mathrm{xz}}\) is the shear strain increment. The bed is initially considered to be in a solid state, with zero pore pressures: the effective friction angle (\({\varphi }_{\mathrm{b}}^{^{\prime}}\)) is therefore implemented, remaining constant until the accumulated distortional strain in the erodible bed reaches a threshold value defined by \({\varepsilon }_{\mathrm{d}0}\). The friction coefficient is thereafter reduced linearly from an initial value \(\mathrm{tan}\;{\varphi }_{\mathrm{b}}^{^{\prime}}\) to a final value \(\mathrm{tan}\;{\varphi }_{\mathrm{bR}}\) (where \({\varphi }_{\mathrm{bR}}\) is the bed residual apparent friction angle). The residual value of \({\varphi }_{\mathrm{bR}}\) is reached at \({\varepsilon }_{\mathrm{dR}}\) and kept for distortional strains larger than \({\varepsilon }_{\mathrm{dR}}\). The correspondent bed pore pressure ratio can be calculated according to Eq. (3) providing the red dashed line in Fig. 5. The bed pore pressure is zero for \({\varepsilon }_{\mathrm{d}}<{\varepsilon }_{\mathrm{d}0}\); it then increases linearly until \({\varepsilon }_{\mathrm{dR}}\) and remains constant at the final value \({\lambda }_{\mathrm{bR}}=1-\frac{\mathrm{tan}\;{\varphi }_{\mathrm{bR}}}{\mathrm{tan}\;{\varphi }_{\mathrm{b}}^{^{\prime}}}\) for \({\varepsilon }_{\mathrm{d}}>{\varepsilon }_{\mathrm{dR}}\). By using this softening model, the erodible bed is therefore stable prior to the arrival of the debris flow, but it will yield and move significantly if the apparent friction angle of the bed becomes sufficiently low.

Fig. 5
figure 5

Softening model for the erodible bed: bed apparent friction coefficient (solid black) and correspondent bed pore pressure ratio (dotted red)

Full size image

Calibration of the numerical model

Flume model, test setup and calibration procedure

Figure 6 shows the 2D model used for the simulations with MPM to simulate tests V6-B1 and V6-B2. The flume base is for convenience modelled as horizontal and therefore the gravity is tilted 20° to the vertical direction. We focus only on what happens along a longitudinal cross-section downward along the centreline of the real flume, i.e. in a way a plane strain problem is considered. The plane strain model is actually a narrow 3D model, made narrow to reduce the computational cost. The mesh size of 0.02 m in any direction is sufficiently low to guarantee the numerical convergence of the computations. This corresponds to the total number of the mesh elements equal to 192,033 and the total number of the material points is equal to 768,132. Numerical simulations have been performed using a high-performance computer (Sigma2 Betzy) using 8 nodes and a total of 1024 CPUs running in parallel. With these parameters, the simulation of 10 s of flow required about 7 h of computation time.

Fig. 6
figure 6

Geometry of the model in MPM, materials and contacts (f refers to the debris flow material, b refers to the erodible bed, f-b refers to the base of the flow)

Full size image

The numerical model is calibrated with regard to the observed flow behaviour, the impact dynamics on the upstream barrier and the entrainment. Table 2 shows a summary of the debris and bed parameters used for the calibration. The debris and bed materials, as defined by Eqs. (4), (5) and (6), are shown in Fig. 6. The calibration is performed in two steps: (i) the debris flow parameters (\({c}_{\mathrm{f}}\), \({\varphi }_{\mathrm{f}}\), \({\varphi }_{\mathrm{f}-\mathrm{b}}\)) are calibrated based on measured data from the flume test and on the impact on the upstream flexible barrier; (ii) the erodible bed parameters (\({\varphi }_{\mathrm{bR}}\), \({\varepsilon }_{\mathrm{d}0}\), \({\varepsilon }_{\mathrm{dR}}\)) are calibrated to simulate the measured entrainment. The selection and discussion of the parameters values in Table 2 and detailed calibration results are provided in the next sections.

Table 2 Summary of the debris and bed material parameters
Full size table

Modelling the debris flow behaviour

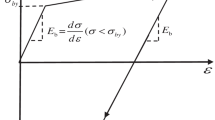
In this section, the debris material (f) parameters (Table 2) are discussed and calibrated. The flow density of 2155 kg/m3 was calculated from the debris flow mixture used in the experiments. A low value of the elastic shear modulus (0.2 MPa) together with a Poisson’s ratio of 0.49 was selected to consider the high-water content of the flow. These stiffness parameters were found to have a negligible influence on the flow behaviour, since the flow rapidly reaches large deformations, in which the plastic behaviour from the Mohr–Coulomb yield criterion dominates over the elastic behaviour.

The flow basal apparent friction angle (\({\varphi }_{\mathrm{f}-\mathrm{b}}\)) was calculated and selected based on the measurements from Cell 1 of the basal normal (\(\sigma\)) and shear (\({\tau }_{\mathrm{f}-\mathrm{b}}\)) stresses in Test V6-B1, as shown in Fig. 7 (the flow depth is also shown for comparison with the normal stress). As the flow depth increases, the normal stress also increases almost proportionally. The flow basal shear stress is actually not directly proportional to the normal stress, as a result of different magnitudes of pore pressures along the flow (Vicari et al. 2021a). Correspondingly, the flow basal apparent friction angle from Eq. (5) (Fig. 8), \({\varphi }_{\mathrm{f}-\mathrm{b}}\), decreases in time from approximately 35° to 5°. The result is consistent with a typical distribution of pore pressures in a debris flow (Iverson et al. 2010). The debris flow front is unsaturated and carries lower pore pressures, which increases the basal shear resistance and therefore the apparent friction angle. The flow body behind the front is observed to be liquefied, and therefore carrying higher pore pressures, which results in a much lower basal shear stress and friction angle. From Fig. 8, the average value of the basal apparent friction angle versus time is calculated equal to 9°, which is the value assumed for the numerical simulations. The influence of choosing a constant friction angle in time will be discussed later.

Fig. 7
figure 7

Measured flow depth and basal shear and normal stress at 3.4 m from the gate for experiment V6-B1 (no upstream barrier)

Full size image
Fig. 8
figure 8

Calculated flow basal apparent friction angle at 3.4 m from the gate for experiment V6-B1 (no upstream barrier) and the constant average value \({\varphi }_{\mathrm{f}-\mathrm{b}}\) used in simulations

Full size image

The flow internal apparent friction angle (\({\varphi }_{\mathrm{f}}\)) and cohesion (\({c}_{\mathrm{f}}\)) are the two parameters that need to be calibrated to simulate the debris flow behaviour, in terms of velocity and flow depth (e.g. Koo et al. 2018; Zhao et al. 2020). Based on the sensitivity analysis, the parameters \({c}_{\mathrm{f}}=500 Pa\) and \({\varphi }_{\mathrm{f}}=15^\circ\) were selected as they provide a good agreement in terms of flow velocity. Figure 9 shows the measured frontal flow velocity in test V6-B1 compared to the computed one with the selected flow parameters from Table 2. The debris flow front is observed to accelerate over the fixed bed section because of the conversion of potential energy into kinetic energy. The measured debris flow front is then observed to decelerate at the beginning of the erodible bed area and to move steadily over the final part of the erodible bed. The deceleration may be due to the higher friction of the entrained bed material (we will discuss the calibration of the erodible bed parameters in more detail later). The numerical simulations can capture the trend and magnitude of the flow velocity well.

Fig. 9
figure 9

Frontal flow velocity for test V6-B1 (no upstream barrier) and comparison with the numerical simulation

Full size image

Figure 10 shows the comparison of the measured flow depth at 3.4 m from the gate (U1) with the simulation using the parameters in Table 2. The result from the numerical simulation differs from the measurement: the computed flow duration is longer, and the computed maximum flow depth of 0.3 m is lower compared to measured 0.4 m. All the simulations performed, changing the values of \({c}_{\mathrm{f}}\), \({\varphi }_{\mathrm{f}}\), \({\varphi }_{\mathrm{f}-\mathrm{b}}\) and the stiffness parameters, did not have significant influence on the flow duration and on the maximum flow depth. The difference between simulated and measured flow depth may be due to modelling an instantaneous release of the debris flow, without considering a finite time for opening the gate (George and Iverson 2014). Furthermore, the assumption of a constant flow basal apparent friction may affect the debris flow duration. This will be addressed in the ‘Discussion’ section.

Fig. 10
figure 10

Measured flow depth at 3.4 m from the gate for test V6-B1 (no upstream barrier) and comparison with the numerical simulation

Full size image

Modelling the debris flow impact kinematics on the upstream flexible barrier

Since a 2D model is used in this study to reduce the computational cost, an exhaustive model of the flexible barrier—i.e. considering the deformability of the cables and net (e.g. Leonardi et al. 2016; Kwan et al. 2019; Li et al. 2020; Zhao et al. 2020)—cannot be implemented. Instead, the upstream flexible barrier (test V6-B2) in this numerical study is simplified to a rigid constraint. However, to capture the fundamental effect of the deformability of a flexible barrier on flow redirection (Wendeler et al. 2019; Vicari et al. 2021a), the barrier is modelled with a curvature corresponding to its final deformed shape (deflection of 0.1 m, Fig. 6).

Figure 11a shows the impact run-up mechanism on the upstream flexible barrier observed in the experiment V6-B2, where a dead zone formed behind the barrier and the flow was redirected upwards reaching a maximum run-up height of 1.5 m orthogonal to the channel (Vicari et al. 2021a) (video from the experiment shown in Online Resource 1). Figure 11b shows the run-up mechanism for the numerical simulation using \({c}_{\mathrm{f}}=500 Pa\) and \({\varphi }_{\mathrm{f}}=15^\circ\) (video shown in Online Resource 2), while Fig. 11c shows the numerical simulation using \({c}_{\mathrm{f}}=500 Pa\) and \({\varphi }_{\mathrm{f}}=30^\circ\) (video shown in Online Resource 3). Both simulations exhibit a run-up mechanism which overpasses the barrier height. However, the maximum run-up height is significantly different: the simulation with \({\varphi }_{\mathrm{f}}=15^\circ\) results in a run-up of 1.5 m, which is similar to that observed in the experiment, while the simulation with \({\varphi }_{\mathrm{f}}=30^\circ\) underestimates the jet height (1.2 m). The frictional dissipation during the run-up happens on the surface indicated in Fig. 11b (dot red line), which separates the stationary debris material leaning towards the barrier (on the right, with almost nil velocity), namely the dead zone, to the debris material flowing upwards (on the left). Interestingly, the volume of the dead zone is higher for the simulation with \({\varphi }_{\mathrm{f}}=30^\circ\) (Fig. 11c), which shows that frictional energy dissipation and velocity reduction are the factors limiting the run-up height, as also observed by Kwan et al. (2019).

Fig. 11
figure 11

Comparison of run-up mechanism on the upstream barrier in test V6-B2: (a) observed impact mechanism in test V6-B2 (with upstream barrier) (b) numerical simulation with \({\varphi }_{\mathrm{f}}=15^\circ\) using a curved barrier (c) numerical simulation with \({\varphi }_{\mathrm{f}}=30^\circ\) using a curved barrier (d) numerical simulation with \({\varphi }_{\mathrm{f}}=15^\circ\) using a rectilinear barrier

Full size image

For comparison, a simulation has also been performed using a straight rigid barrier (Fig. 11d) and the parameters \({c}_{\mathrm{f}}=500\ {Pa}\) and \({\varphi }_{\mathrm{f}}=15^\circ\) (video shown in Online Resource 4). In this case, the rectilinear barrier cannot redirect the flow backwards as observed in the experiment and the run-up height is overestimated (1.9 m). Therefore, it can be concluded that the curved barrier implemented in the 2D model is a more satisfactory approximation of a flexible barrier to simulate the kinematics of the flow-barrier interaction. Such 2D model may be very useful to perform faster simulations compared to a 3D geometrical model. Furthermore, it can be observed that the curvature effect of a flexible barrier is a favourable feature to limit the run-up height and overflow.

Given the similarity between the numerical simulation of the impact mechanism with the observed one, \({c}_{\mathrm{f}}=500 Pa\), \({\varphi }_{\mathrm{f}}=15^\circ\) and \({\varphi }_{\mathrm{f}-\mathrm{b}}=9^\circ\) are considered to be the best-fit parameters to simulate the debris flow behaviour. The values are quite similar to the ones calibrated by Lam and Wong (2021) (\({\varphi }_{\mathrm{f}}=12^\circ\) and \({\varphi }_{\mathrm{f}-\mathrm{b}}=10^\circ\)) to simulate debris flows, with a slightly lower solid concentration of 60%, in the same flume model considered in this study. This similarity confirms the validity of our back-calculation for the flow behaviour and impact with the upstream barrier. Therefore, these calibrated debris flow parameters (Table 2) will be used consistently in the next sections, which focus on the calibration of the erodible bed parameters for the back-calculation of entrainment.

Modelling the entrainment volume

In this section, the erodible bed material (b) parameters (Table 2) are back-calculated to simulate entrainment measured in test V6-B1 (no upstream barrier) (an aerial video from the experiment is shown in Online Resource 5). The bed density was calculated from the bed composition equal to 1920 kg/m3. The elastic shear modulus is chosen equal to 15 MPa, corresponding to a moderately compacted, thin loose sand and gravel layer. The Poisson’s ratio is chosen equal to 0.49 to model the fast entrainment phenomenon, which is likely to produce undrained conditions (Iverson et al. 2011). The contact apparent friction angle between the debris flow and the erodible bed (\({\varphi }_{\mathrm{f}-\mathrm{b}}\)) is fixed to 9°, corresponding to the average estimate obtained from Cell 1 (Fig. 8). A low value of the bed cohesion (\({c}_{\mathrm{b}}\)) of 100 Pa is assigned to limit the bed deformation prior to entrainment. The internal apparent friction angle of the erodible bed (\({\varphi }_{\mathrm{b}}\)) is modelled according to the softening model presented in Fig. 5. Initially, the apparent friction angle is set equal to the bed effective friction angle of 42° (measured through direct shear test), which represents the partly saturated bed lacking positive pore pressures. As shearing of the bed occurs, the apparent friction angle is decreased to a final value of \({\varphi }_{\mathrm{bR}}\). A parametric study is carried out to study the influence of \({\varphi }_{\mathrm{bR}}\), \({\varepsilon }_{\mathrm{d}0}\) and \({\varepsilon }_{\mathrm{dR}}\) on the entrainment volume. The angle \({\varphi }_{\mathrm{bR}}\) is varied between 6.5° and 42°. The distortional strain \({\varepsilon }_{\mathrm{d}0}\) is varied between 0.033 and 0.067 and \({\varepsilon }_{\mathrm{dR}}\) between 0.067 and 0.133, which represent typical values (Lee et al. 2019).

Figure 12 shows the measured entrainment volume in test V6-B1 (0.9 m3) and the results of the numerical simulations, with different values of \({\varphi }_{\mathrm{bR}}\), \({\varepsilon }_{\mathrm{d}0}\) and \({\varepsilon }_{\mathrm{dR}}\). The bed residual pore pressure ratio, \({\lambda }_{\mathrm{bR}}\), is obtained from Eq. (3) and shown on the top horizontal axis. The entrainment volume increases for decreasing values of \({\varphi }_{\mathrm{bR}}\), or equivalently for increasing values of \({\lambda }_{\mathrm{bR}}\), which illustrates how bed shear strength reduction, due to pore pressure generation, increases entrainment (Iverson et al. 2011; Iverson 2012). It can also be observed that the entrainment volume is inversely proportional to \({\varepsilon }_{\mathrm{d}0}\) and \({\varepsilon }_{\mathrm{dR}}\), which have a retarding effect on the onset of entrainment. However, the influence of \({\varepsilon }_{\mathrm{d}0}\) and \({\varepsilon }_{\mathrm{dR}}\) on the entrainment volume is lower compared to the parameter \({\varphi }_{\mathrm{bR}}\).

Fig. 12
figure 12

Measured and computed entrainment volumes for test V6-B1 (no upstream barrier). See Fig. 5 for explanation of the parameters varied

Full size image

The grid size affects the accuracy of the MPM simulations. Therefore, we performed a sensitivity analysis of the grid size presented in Fig. 12 (Fig. 13). The simulations with a grid size of 0.01 m compute a slightly smaller entrainment volume than the simulations with a grid size of 0.02 m. The minimum erodible thickness in a MPM simulation is equal to half the grid size, or one material point (cf. Figure 4). Therefore, in the simulations with the 0.02 m grid size, the entrainment of an additional 0.01-m-thick layer would result in a higher entrainment than the simulations with the 0.01-m grid size. In general, the simulations with a grid size of 0.02 m produced quite similar results compared to the simulations with a 0.01-m grid size. The back-calculated value of the bed residual apparent friction angle would be similar using the two grid sizes. A simulation with a grid size of 0.01 m required approximately 40 h of computation. Therefore, a grid size of 0.02 m was selected in this study for the sake of the computational cost. By using the 0.02-m grid size, the minimum erodible thickness (0.01 m) is still small compared to the high entrainment measured in test V6-B1. Li et al. (2021) showed that a 0.5 m grid size was sufficiently small to model in MPM a real snow avalanche event, where entrainment was neglected. However, if entrainment should also be modelled in MPM, the grid size should be sufficiently small compared to the expected entrainment depth in the field. Hence, a quite small grid size may be needed to simulate entrainment, even in real-scale debris flows, at the cost of very high computation time.

Fig. 13
figure 13

Computed entrainment volumes for test V6-B1 using different grid sizes

Full size image

Using a grid size of 0.02 m, the set of parameters \({\varphi }_{\mathrm{bR}}=22.5^\circ\), \({\varepsilon }_{\mathrm{d}0}=0.033\) and \({\varepsilon }_{\mathrm{dR}}=0.100\) provides the best fit with the measured entrainment volume (Fig. 12). The video of this numerical simulation is shown in Online Resource 6. The measured (test V6-B1) and computed spatial entrainment depth profiles are compared in Fig. 14. The measured entrainment depth is higher at the beginning of the erodible bed (x < 11 m) and it decreases downstream, which is probably due to the stability effect given by the soil wedge leaning on the horizontal runout section. Furthermore, the fixed height of the platform may have caused the flow to plough the erodible bed at x < 11 m, as shown by the video in Online Resource 7. The numerical simulation can capture the spatial variations of entrainment depth and shows a good agreement with the experimental observation. The capability of the three-dimensional model used in this study to compute the internal mechanics and stability of the whole erodible bed is clearly an advantage compared to depth-averaged models, where entrainment would be calculated only based on the boundary shear stresses (cf. Eq. (1)).

Fig. 14
figure 14

Entrainment profile measured in test V6-B1 (no upstream barrier) and computed (\({\varphi }_{\mathrm{bR}}=22.5^\circ\), \({\varepsilon }_{\mathrm{d0}}=0.033\) and \({\varepsilon }_{\mathrm{dR}}=0.100\))

Full size image

Figure 15a shows a detail of the entrainment process for the simulation with the best-fit parameters. When the debris material flows over the erodible bed, it exerts a shear stress on the planar bed surface parallel to the x-axis. Since entrainment had already happened in some parts of the bed upstream, but less further down, the flow can also impact the bed by a normal stress in the direction of the x-axis. The entrainment process therefore is a combination of basal shear, on the planar surface parallel to the x-axis, and ploughing, roughly on the surface parallel to the z-axis. The stresses that are acting on the bed layer are exemplified in Fig. 15b. In addition to the shear stresses \({\tau }_{\mathrm{f}-\mathrm{b}}\) and \({\tau }_{\mathrm{b}}\) discussed in Fig. 2, the flow transmits a normal stress \({\sigma }_{\mathrm{f}-\mathrm{b}}\) (referred as ploughing stress) at the boundary between flow and bed on the surface parallel to the z-axis, while the normal stress \({\sigma }_{\mathrm{b}}\) is the reaction inside the erodible bed. The stress \({\sigma }_{\mathrm{f}-\mathrm{b}}\) is a dynamic loading from the debris flow, while the stress \({\sigma }_{\mathrm{b}}\) is a passive static pressure. It can be expected that the resulting stress from \({\sigma }_{\mathrm{f}-\mathrm{b}}\) and \({\sigma }_{\mathrm{b}}\) is positive in the x-direction, which increases the destabilizing effect on the erodible bed layer and erosion by ploughing may occur.

Fig. 15
figure 15

Details of the entrainment process: (a) simulation with \({\varphi }_{\mathrm{bR}}=22.5^\circ\), \({\varepsilon }_{\mathrm{d0}}=0.033\) and \({\varepsilon }_{\mathrm{dR}}=0.100\), observed at x≈10 m, 2 s after the flow front arrival (b) schematics of the eroded bed layer and stresses acting on it

Full size image

The existence of the additional ploughing stress by the debris flow implies that the back-calculated value of the bed residual apparent friction angle in MPM (\({\varphi }_{\mathrm{bR}}=22.5^\circ\)) is different compared to the back-calculation using the analytical solution which considers basal shear stress only (Eq. (1)). Indeed, Eq. (1) requires, for entrainment to happen, that the flow basal apparent friction angle (\({\varphi }_{\mathrm{f}-\mathrm{b}}\)) from the flow on to the bed is higher than the bed residual apparent friction angle (\({\varphi }_{\mathrm{bR}}\)). The application of Eq. (1) would lead to \({\varphi }_{\mathrm{bR}}=6.5^\circ\). However, we show that the entrainment volume computed in MPM with \({\varphi }_{\mathrm{bR}}=6.5^\circ\) would be too high compared to the measured entrainment volume, because of the existence of the ploughing stresses. In general, the analytical solution of Eq. (1) (only basal shear \({\tau }_{\mathrm{f}-\mathrm{b}}\)) may still be valid when the topography of the bed remains approximately uniform and planar and therefore the ploughing stresses may be neglected. However, the three-dimensional MPM model, which also considers ploughing, becomes especially important if the topography of the bed changes significantly from the initial planar topography, as for example observed in the initial part of the erodible bed (x < 11 m).

Estimation of the pore pressures in the erodible bed

By using Eq. (3), the back-calculated bed residual apparent friction angle, \({\varphi }_{\mathrm{bR}}=22.5^\circ\), corresponds to a pore pressure ratio \({\lambda }_{\mathrm{bR}}=0.5\) in correspondence of the evolving entrainment layer (approximately 0.01–0.02 m below the evolving upper surface of the erodible bed). Since this pore pressure ratio is higher than 0, it is suggested that the development of excess pore pressures at the bed-flow interface was a fundamental mechanism for entrainment to happen. In comparison, the simulation with \({\varphi }_{\mathrm{bR}}={\varphi }_{\mathrm{b}}^{^{\prime}}=42^\circ\), i.e. without pore pressures generated in the bed (\({\lambda }_{\mathrm{bR}}=0\)), shows a too low entrainment volume.

To gain more insights into the mechanisms of pore pressure development in the erodible bed, the measurements of the normal stress and pore pressure, in test V6-B1 at the base of the erodible bed (Cell 2), are shown in Fig. 16. Prior to entrainment (t < 1 s), the vertical normal stress is approximately 2.8 kPa, corresponding to the static weight of the erodible bed, while pore pressure is 0 kPa because the bed is initially unsaturated. When the debris material flows over the erodible bed, the normal stress increases to a maximum value of approximately 9 kPa and pore pressure increases to a maximum value of 1.5 kPa. The normal stress then decreases (t > 4 s) to 4.6 kPa, which is higher than the initial value of 2.8 kPa simply because significant debris material is deposited. Pore pressures remained approximately constant, which is likely due to limited dissipation in undrained conditions.

Fig. 16
figure 16

Measured normal stress and pore pressure at the base of the erodible bed at 12.5 m downstream from the gate (Cell 2) for test V6-B1 (no upstream barrier)

Full size image

The bed pore pressure ratio \({\lambda }_{\mathrm{b}}\) at the base of the bed can be calculated as the ratio between the measured pore pressure and the normal stress (Fig. 17). The ratio \({\lambda }_{\mathrm{b}}\) increases from 0 to a maximum value of 0.25 (continuous blue line). This implies that, at the base of the erodible bed, the soil material, which has not been entrained, develops a lower pore pressure ratio, without reaching the residual state (\({\lambda }_{\mathrm{bR}}=0.5\)). This result may be understood considering the field observations from Mccoy et al. (2012) who only recorded an increase in pore pressure when the entrainment front was at a distance lower than 0.05 m from the pore pressure sensor. The limited transmission of pore pressures along the depth of the erodible bed shows that pore pressure generation in an initially unsaturated erodible bed may be mainly due to a shearing effect, which qualitatively confirms the validity of Fig. 5 to model pore pressure ratio increase as a function of the cumulated distortional strain.

Fig. 17
figure 17

Calculated and computed pore pressure ratio at the base of the erodible bed at 12.5 m downstream from the gate (Cell 2) for test V6-B1 (no upstream barrier)

Full size image

Figure 17 also shows the computed \({\lambda }_{\mathrm{b}}\) using Eq. (3) at the base of the bed, for the numerical simulations with \({\varphi }_{\mathrm{bR}}=22.5^\circ\) and for different combinations of \({\varepsilon }_{\mathrm{d}0}\) and \({\varepsilon }_{\mathrm{dR}}\). \({\lambda }_{\mathrm{b}}\) is inversely proportional to \({\varepsilon }_{\mathrm{d}0}\) and \({\varepsilon }_{\mathrm{dR}}\). Using \({\varepsilon }_{\mathrm{d}0}=0.067\) would even result in null pore pressures at the base of the bed. The best fit is obtained using \({\varepsilon }_{\mathrm{d}0}=0.033\) and \({\varepsilon }_{\mathrm{dR}}=0.100\). The parameters \({\varepsilon }_{\mathrm{d}0}\) and \({\varepsilon }_{\mathrm{dR}}\) of the proposed model therefore control how deep and how fast friction reduction (i.e. pore pressure increase) is transmitted into the erodible bed.

Discussion

Two entrainment behaviours

It appears from the numerical simulations and experimental observations that entrainment resulted from the following succession of mechanisms: (i) the debris flow overrides the erodible bed transmitting a basal shear stress (i.e. \({\tau }_{\mathrm{f}-\mathrm{b}}\)), which (ii) causes the development of excess pore pressures, which in turn (iii) lead to a shear strength (i.e. \({\tau }_{\mathrm{b}}\)) reduction of the bed layer; (iv) at the same time, the debris flow exerts basal shear (\({\tau }_{\mathrm{f}-\mathrm{b}}\)) and ploughing stress (\({\sigma }_{\mathrm{f}-\mathrm{b}}\)) on the bed which destabilize it and promote entrainment. In other words, entrainment is caused by a combination of stresses from the debris flow and bed shear strength reduction. Based on whether bed shear strength loss or transmission of flow basal stresses is dominant, it is reasonable to distinguish between two types of entrainment behaviours (Fig. 12):

  1. (a)

    We suggest calling the first one a self-propelled entrainment. In this behaviour type, the strength reduction (event iii) dominates and the entrainment accelerates when the current apparent friction angle of the bed (\({\varphi }_{\mathrm{bR}}\)) is reduced to the slope angle (\(\theta\)) or less. At this stage, the whole softened bed is unstable and moves downslope simply due to gravity. The movement is further accelerated by the contact stresses from the debris on top. The reduction in strength is considered to be an effect of pore pressure build up. This type of entrainment behaviour catches large volumes and causes a very fast motion, as observed in the case of very wet beds by Iverson et al. (2011).

  2. (b)

    The second may be denoted ploughing-enabled entrainment. If the reduction of the bed shear strength (event iii) is less significant, a ploughing-enabled behaviour may dominate. In this case, the residual apparent friction angle of the bed is larger than the slope angle, \({\varphi }_{\mathrm{bR}}>\theta\). The bed is then stable under gravity alone and entrainment can only happen if sufficiently high ploughing stresses are transmitted by the debris flow on to the bed below to destabilize it (event iv). Such ploughing-enabled entrainment has been reported for high values of the apparent friction angle of the bed. Entrainment is for instance observed experimentally in the case of dry beds which do not develop excess pore pressures (Mangeney et al. 2010; de Haas and van Woerkom 2016). This entrainment is definitely caused by the stresses from the debris flow. The high shear strength of the erodible bed leads to lower entrainment depths and lower velocities are observed for ploughing-enabled entrainment.

Some additional comments are appropriate regarding the curve in Fig. 12. In the ploughing-enabled entrainment zone of the plot, a small variation in the residual apparent bed friction, \({\varphi }_{\mathrm{bR}}\), makes a huge difference in entrainment volume. The entrainment volume increases almost exponentially as the residual apparent bed friction approaches the slope angle \(\theta\). For a residual apparent bed friction less than the slope angle, the whole bed layer may become unstable (if sufficiently sheared by the debris flow). In the latter case, the entrainment volume is determined by how much volume passes into the residual state, which is controlled by the parameters \({\varepsilon }_{\mathrm{d}0}\) and \({\varepsilon }_{\mathrm{dR}}\). If the entire bed liquifies by reaching the residual state, the volume in our test would be 1.48 m3 (i.e. the total volume of bed material placed in the flume). We observe that we approach this limiting condition for low residual apparent friction.

Limitations of the one-phase model

A one-phase model has been used in this study to model the debris flow, and conventionally this implies that the flow apparent friction angle is constant, as the pore pressure ratio \(\lambda\) is assumed constant in time and space. This assumption is also made herein. However, debris flows are usually characterized by evolving magnitude of pore pressures, which has a significant influence on the basal friction, as shown in Fig. 8. The debris flow front is usually carrying lower pore pressures and is followed by a more liquefied body (McArdell et al. 2007; Iverson et al. 2010). The decreasing basal friction from the front to the tail of the flow may have an influence on the flow depth and velocity (Iverson 1997): a higher frictional resistance at the debris flow front may create a ‘moving dam’ pushed by the more liquefied flow body (Iverson et al. 2010). Therefore, the real debris flow duration is expected to be shorter compared to a debris flow with constant friction, since the tail of the flow can in reality move faster compared to the flow front. However, in the numerical simulations using a constant basal friction, the flow front and tail have the same basal resistance and therefore the flow duration is longer, and the maximum flow depth is smaller compared to the measurements (Fig. 10). In recent years, two-phase numerical models have been developed (e.g. George and Iverson 2014; Cuomo et al. 2021; Tayyebi et al. 2021), which allow to model the evolution of pore pressure in space and time and its effect on the flow mobility. Future developments of our MPM simulations should involve implementing a two-phase flow. By better capturing the pore pressure distribution in the flow, the flow dynamics (in terms of flow depth and velocity) could be improved.

It may be particularly important to use a two-phase model to simulate the flow interaction with the flexible barrier. Indeed, a flexible barrier may allow the fluid part to pass through the permeable mesh. At the same time, the permeability of the flexible barrier would impose a zero-pore pressure boundary condition on the static dead zone impounding against the flexible barrier, which could alter the run-up process. On the other hand, the airborne jet generated from the run-up may result in an increase in porosity (Cuomo et al. 2021), which could lead to a faster dissipation of excess pore pressures. The collision of the jet at landing may also cause a porosity increase and fast dissipation of excess pore pressures. Depending on which mechanism is dominant, either fluid passing through the mesh or dissipation of excess pore pressures during overflow, the debris flow downstream of the flexible barrier may be characterized by respectively lower or higher shear resistance than the original debris flow before impact on the barrier. For instance, in test V6-B2 (Vicari et al. 2021a), the debris flow was observed to significantly decelerate downstream of the flexible barrier, which is likely due to pore pressure dissipation. The one-phase model used in this study failed in modelling the flow behaviour downstream of the flexible barrier for test V6-B2: in this case, a two-phase model would be needed.

The pore pressure distribution within the debris flow may also affect the entrainment process. Lower pore pressures at the flow front followed by the more liquefied body may have consequences for entrainment. Indeed, the flow front may transmit higher shear stress to the erodible bed at the front, increasing entrainment, while the flow body and tail may transmit lower shear stress, with a reduced entrainment (Vicari et al. 2021a). On the other hand, regarding the erodible bed, despite being modelled as a one-phase material, the softening model introduced in Fig. 5 allows to mimic the evolution of pore pressures due to bed shearing. Thus, despite this model being semi-empirical and requiring the calibration of the bed parameters, it allows to effectively simulate bed entrainment and to estimate the magnitude of the bed pore pressure ratio involved during the entrainment process.

Conclusions

The large-scale flume experiments by Vicari et al. (2021a) were back-calculated using a three-dimensional MPM numerical model to simulate the debris flow behaviour, impact on a flexible barrier and entrainment of a wet erodible bed. A narrow 3D longitudinal cross-section along the slope of the flume was modelled in the MPM, in order to reduce the computational time. The debris flow and bed were modelled as one-phase materials with an elasto-plastic model and a Mohr–Coulomb yield criterion. The apparent friction angle of the flow was calibrated to back-calculate the flow velocity and run-up impact dynamics on the upstream flexible barrier. We simplified the complexity of the flexible barrier to a rigid constraint, to be able to simulate the flexible barrier in a 2D geometrical model. The barrier is drawn with a curved shape, correspondent to the final curvature of the barrier. We observe that the run-up impact mechanism on the barrier can be well captured. We confirm that flexible barriers allow to reduce the run-up height compared to rigid rectilinear barriers, and that they may be beneficial to reduce the debris volume flowing downstream.

A softening model was implemented to model the friction reduction of the erodible bed, due to the increase in pore pressures, by coupling pore pressure increase to the distortional strain development. The introduced model is based on three parameters: the bed residual apparent friction angle, mainly controlling the total entrainment volume, and two thresholds for the distortional strain, which regulate the depth and speed of the pore pressure increase in the bed (or, equivalently, the shear strength reduction). We show that entrainment can happen because of bed shear strength reduction and due to the basal stresses transmitted by the flow. Our MPM model can account for both shear and ploughing basal stresses exerted by the debris flow on the erodible bed. In particular, the capability of MPM to also model the ploughing stresses, which have often been neglected in previous entrainment models, finally allows to explain why beds which are stronger than the flow can be entrained. The resulting entrainment behaviour for this type of flows and beds is referred as ploughing-enabled. This behaviour seems to be characterized by limited entrainment depths. On the other hand, if the bed pore pressure increase is high, the shear strength of the bed may become sufficiently low for the bed to fail under gravity alone. The additional shear and ploughing stresses transmitted by the debris flow then cause rapid and large entrainment. We suggest referring to this second behaviour as self-propelled entrainment.

The three-dimensional MPM model and the bed softening model introduced in this work were proved to be effective in simulating the debris flow entrainment. The introduced model may be particularly suited to analyse the complexity of natural debris flow events, where ploughing may especially occur for a non-uniform bed topography with concave and convex inflexions and varying geometry sideways. Furthermore, the boulders which are transported by the flow may in further MPM developments be incorporated to simulate how boulders may collide the bed and plough it. Finally, the three-dimensional model may allow to model secondary entrainment processes such as the instability of the channel banks. Depth-averaged models clearly cannot capture all these complex phenomena. A three-dimensional model is needed. The entrainment model introduced in this paper uses principles that have a potential towards a more holistic simulation of the entrainment process as seen in natural debris flow events.