Introduction

Landslides are among the most common and dangerous natural hazards in mountainous regions (Domakinis et al. 2008; Huang et al. 2007; Petley 2012). According to Petley (2012), between 2004 and 2010, 2620 fatal landslides were recorded globally, resulting in a total death toll of at least 32,322. In Taiwan alone, between 1971 and 2000, rock falls, landslides, and debris flows caused 595, 182, and 185 casualties, respectively (Lin 2004). Government agencies around the world have developed various measures to mitigate and prevent the losses due to landslides, including building engineering structures, planning evacuation routes, and issuing early warnings. However, all of these measures depend on knowing where landslides are likely to occur.

The most common approach to landslide susceptibility model (LSM) is to compute a composite score or index (i.e., landslide susceptibility index, LSI) at each cell (or pixel) of gridded raster data that indicates the susceptibility based on preparatory factors (e.g., slope, aspect, and lithology; see p-165 in Lee and Jones 2004) weighted according to importance. The factors or parameters used in such approaches, however, are mostly cell-based local parameters and do not consider the influence of neighboring cells. For example, a particular cell may be considered stable according to its local factors, but if its neighboring cells are unstable, then it may also be susceptible to landslides. For this reason, the accuracy of cell-based LSMs is limited.

LSMs commonly apply region-based factors to take into account the influence of neighboring cells. For example, the proximity to a drainage pattern has been considered as a contributing factor to landslide occurrence, as streams can adversely affect the stability of the adjacent slope by eroding the toe and/or saturating the slope (Gökceoglu and Aksoy 1996). The drainage distance factor, DD, expressed as concentric multi-ringed buffer zones based on the distance of each cell from the main stream, has thus been utilized to capture this effect in LSM (Fourniadis et al. 2007; van Westen et al. 2003). However, using DD buffers implies that all cells within the same buffer zone have the same landslide susceptibility. In reality, cells within the same DD buffer zone may experience a different total flux of water, and thus different amount of erosion or saturation, as lower-order streams may have joined the main stream along the way. Thus, DD may not be an accurate factor to represent the influence of neighboring cells, as it may not properly represent the flux of water, likely responsible for the failure of slopes adjacent to streams.

This paper proposes a region-based factor, namely, total flux (TF), which takes into account the topography and hydrology conditions in the neighboring and upstream of each cell. Based on a detailed landslide inventory in Taiwan, derived from the annual composite of Formosat-2 imagery acquired from 2005 to 2013 (Lin et al. 2013; Liu 2015), we employ a standard LSM to quantitatively assess the effectiveness of DD and TF as preparatory factors. The results show that landslide occurrence is strongly associated with TF (rather than DD) and serves as a good preparatory factor that can significantly improve the performance of LSM in Taiwan, with potential applications elsewhere in the world.

Region-based factor of total flux

The concept of total flux is derived from flow accumulation in hydrologic modeling, which reflects how much water would flow through each cell from upstream areas. It is represented by the number of upstream cells that would contribute to the cell under consideration (O’Callaghan and Mark 1984). However, flow accumulation in hydrology and GIS is usually calculated by routing water along the steepest descent path, and thus water from each cell can only flow to one of its eight neighbors. The shortcomings of this routing algorithm have been well documented in the literature (e.g., Tarboton 1997; Wilson et al. 2008 and references therein), and the problem is especially prominent in flat terrain areas. Some of the multi-directional flow routing algorithms are complicated (e.g. Tarboton 1997), so here we propose a simple multiple direction routing algorithm using slope as weight, somewhat similar to Quinn et al. (1991), to capture the relative magnitude of total water flux.

The total amount of water in a grid cell (m, n) Q m,n can be calculated as the summation of precipitation P m,n from the sky and runoff water R m,n from the adjacent cells without considering any infiltration along the way

$$ {Q}_{m,n}={P}_{m,n}+{R}_{m,n}. $$
(1)

This amount of runoff water would be distributed to eight surrounding cells (i, j) by a factor F m,n→i,j , which is based on the topography conditions in the vicinity of each cell:

$$ {R}_{m,n\to i,j}={Q}_{m,n}\times {F}_{m,n\to i,j} $$
(2)

where F m,n→i,j is proportional to the gradient G m,n→i,j

$$ {F}_{m,n\to i,j}\equiv \frac{G_{m,n\to i,j}}{{\displaystyle \sum {G}_{m,n\to i,j}}}, $$
(3)

and

$$ {G}_{m,n\to i,j}\equiv \frac{H_{m,n}-{H}_{i,j}}{D_{m,n\to i,j}},\mathrm{where}\begin{array}{c}\hfill i=m-1,m,m+1\hfill \\ {}\hfill j=n-1,n,n+1\hfill \end{array}. $$
(4)

H m,n and H i,j are elevations at cell (m, n) and cell (i, j), respectively. D m,n→i,j is the distance between cell (m, n) and cell (i, j):

$$ {D}_{m,n\to i,j}=\left\{\begin{array}{ll}1\hfill & \mathrm{if}\ i=m\ \mathrm{or}\ j=n\hfill \\ {}\sqrt{2}\hfill & \mathrm{if}\ i\ne m\ \mathrm{and}\ j\ne n\hfill \end{array}\right. $$
(5)

Note that TF is not meant to be the absolute amount of water of each cell, which should be obtained by running more sophisticated hydrological models fed with more thorough and detailed measurements, such as surface roughness, soil types, and associated infiltration rates. Although the role of groundwater is not considered directly, the areas that are more likely to have high groundwater discharge and saturation are generally consistent with the areas of high surface flow accumulation. For the purpose of LSM, a relative measure of the water flux is sufficient, since we are only comparing the relative potential for landslide among the cells. TF is thus intended to serve as a region-based factor that is able to provide the relative measure of water flux by taking into account the topography and hydrology in the vicinity and upstream of each cell.

The calculation is started from the cell with the highest elevation and then moved to the cells with the second highest elevation, and so on, to ensure that H m,n is no less than H i,j and G m,n→i,j is always positive. One unit of precipitation is provided at each cell and distributed to adjacent cells based on the relationships specified by Eqs. (1)–(5) without considering any infiltration along the way. This calculation is repeated until all precipitated waters are routed to the boundary of the study area. The accumulated Q m,n is the value of TF for cell (m, n).

Selection of preparatory factors for LSM in the study area

Koukis and Ziourkas (1991) made a comprehensive review and discussion of more than 64 factors that have been used by various LSMs. They reported that some factors are not independent with each other; some factors can be parameterized, yet some factors cannot be quantitatively measured everywhere. To develop a practical model of landslide susceptibility, Liu et al. (2004) suggested that the preparatory factors should be obtainable and applicable anywhere. From a review of 145 studies spanning the period from 1986 to 2007, Süzen and Kaya (2011) concluded that the most influential natural factors were lithology, slope, land use/land cover, DD, and aspect as causative environmental parameters. Since the existing land use/land cover database already has a category of landslide that is highly correlated with our landslide inventory, an apparent bias would be introduced if the parameter of land use/land cover is included in our LSM. Therefore, we selected slope, aspect, lithology, and DD as the four major preparatory factors to build up a standard LSM, namely, LSM DD . The DD factor was then replaced by the region-based factor TF to build up a new LSM, namely, LSM TF . Note that a plane is fitted to a 3 × 3 kernel centered over each pixel to calculate the slope and aspect of the plane. The slope is measured in degrees, from 0 to 90. Aspect angle is measured with 0° to the north with increasing angles in a clockwise direction.

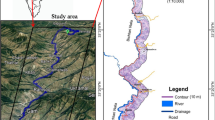
I-Lan is located in the northeastern part of Taiwan (Fig. 1), where the elevation rises significantly from the I-Lan plain in the northeast (~10–100 m above sea level (a.s.l)) to the Central Mountain in the southwest (~2000 m a.s.l), over a distance of just 30 km. Typhoons affect the southern part of Taiwan during the autumn. Their counterclockwise winds converge and are further intensified by the northeasterly monsoon. Extreme precipitation is often observed on the windward side, and many landslides have been triggered in this area as a result. To gain insights into the mechanisms and the long-term trends of landslides, the Forestry Bureau of Taiwan funded two multi-year projects to generate a detailed landslide inventory of the entire country, using the annual composite of Formosat-2 imagery acquired from 2005 to 2013 (Lin et al. 2013) and processed by the Formosat-2 automatic image processing system (F-2 AIPS) (Liu 2006). With this long-term and detailed inventory of landslides, we are able to evaluate each preparatory factor by relating its values with the occurrence of landslides from 2005 to 2013 (Fig. 1b). A digital elevation model (DEM) of I-Lan area with a resolution of 5 m was made available by the Ministry of Interior Affairs of Taiwan. With this DEM, we calculated two cell-based factors, slope (Fig. 2a) and aspect (Fig. 2b), and two region-based factors, DD (Fig. 2c) and TF (Fig. 2d). The lithology map of the study area is provided by the Central Geological Survey of Taiwan at the scale of 1/50,000 (Fig. 2e).

Fig. 1
figure 1

a True color image of the study area, I-Lan, taken by Formosat-2 on March 28, 2013. b The detailed landslide inventory of I-Lan prepared from the annual composite of Formosat-2 imagery acquired from 2005 to 2013

Full size image
Fig. 2
figure 2figure 2

Maps (left panels) and bar charts (right panels) of AR pf(i) (green bars) and W pf(i) (red bars) for each preparatory factor: a slope, b aspect, c drainage distance DD, d total flux TF, and e lithology

Full size image

Choosing the parameters for LSM

The preparatory factors are weighted by the landslide inventory compiled from 2005 to 2013 (Fig. 1b) using a frequency ratio method, which has been commonly employed in the literature (e.g., Lee et al. 2002; Lee and Pradhan 2007; Lee and Sambath 2006; Nguyen and Liu 2014). Note that this method assumes that the landslide inventory is comprehensive enough to cover all kinds of landslide events; thus, the frequency can be represented as an area ratio. For each preparatory factor pf, a fixed number of intervals (zones) n is specified, and the area ratio of each interval AR pf(i) is defined as

$$ A{R}_{pf(i)}\equiv \frac{A_{pf(i)}}{A_t}=\frac{A_{pf(i)}}{{\displaystyle \sum_{i=1}^n{A}_{pf(i)}}}, $$
(6)

where A pf(i) is the area of preparatory factor pf at interval i, and A t is the total area of the study area. To give an example, a fixed number of intervals (n = 90) is specified for the preparatory factor Slope. Then, the area ratio of each interval AR Slope(i) is calculated at interval of 1°. The landslide ratio of each interval LR pf(i) is defined as

$$ L{R}_{pf(i)}\equiv \frac{L_{pf(i)}}{L_t}=\frac{L_{pf(i)}}{{\displaystyle \sum_{i=1}^n{L}_{pf(i)}}}, $$
(7)

where L pf(i) is the landslide area of preparatory factor pf at interval i, and L t is the total landslide area. The weight of preparatory factor pf at interval i is defined as the frequency ratio

$$ {W}_{pf(i)}\equiv \frac{L{R}_{pf(i)}}{A{R}_{pf(i)}}. $$
(8)

Take the interval 40 (39° ~ 40°) for the preparatory factor Slope as an example, L Slope(40) is the area of landslides that occurred in 40° slopes. The landslide ratio and the area ratio of this interval are LR Slope(40) and AR Slope(40), respectively. Equation (8) gives the weight of Slope at interval 40 W Slope(40), which is 1.175 (see the bar chart of Fig. 2a).

The right panel of Fig. 2 gives the bar charts of AR pf (green bars) and W pf (red bars) for each preparatory factor. Note that a large number of intervals is specified (every 1° for slope, every 4° for aspect, and every 25 m for DD), to increase the resolution and avoid the ambiguity raised by averaging the contribution over a broader range in one single interval.

For the preparatory factor of slope shown in Fig. 2a, AR Slope (green bars) exhibits a clear pattern of a normal distribution, with a peak at about 36° (angle of repose of the surface material). The corresponding W Slope (red bars) increases monotonically as the slope increases from 10° to 57°, and maintains high values for those regions with slopes higher than 57°. Only a small fraction (1 %) of the study area has slopes higher than 57°, yet these regions account for a relatively large proportion of landslide occurrence (29 % of W Slope ), indicating a higher probability of landslides for steep slopes. This is consistent with the expectation that, in general, steeper slopes are more susceptible to landslides. Therefore, slope serves as a good preparatory factor for landslides.

Note that in those regions with slopes lower than 10° (approximately 3 % of the study area), the trend of W Slope is slightly reversed (Fig. 2a). This is because some landslide materials fall into valleys with very gentle slopes, and thus these gentle slope areas are included in the landslide inventory. This could be improved by carefully masking these areas out in the future. However, these regions only account for a relatively small proportion of landslide inventory (6 % of W Slope ) and thus do not detract from the overall effectiveness of slope as a good preparatory factory.

Likewise, for the preparatory factor of aspect (Fig. 2b), AR aspect (green bars) shows a clear pattern with lower values between 135° and 225° (south direction), while the corresponding W aspect (red bars) is comparatively high within this range. This phenomenon reflects the prevailing direction of monsoons: landslides tend to occur in south facing directions (135°–225°), and more regions with these aspects collapsed. For example, 7.5 % of the study area has aspects between 212° and 244°, and these regions account for 14 % of W Slope , indicating a higher probability of landslide occurrence for these aspects.

For the preparatory factor of DD, W DD should be inversely related to DD, as most landslides are expected to occur near main streams. However, Fig. 2c (right panel) shows a trend consistent with this expectation only up to about 200 m, which is then reversed and becomes stochastic when DD is larger than 200 m. About 8 % of the study area is 200 to 300 m away from the main stream and thus should be less likely to experience landslides, yet these regions account for a considerable amount of landslide occurrence (18 % of W DD ). Furthermore, a similar trend was also reported for the Central Mountain Range of Taiwan (see Table 8 in Su et al. 2009), and thus this is not a coincidence. Neither is this an artifact of how the intervals are divided, since the same reversal trend is also observed when a 5-m interval is used (not shown). The inconsistent reversal trend can be clarified by taking slope into consideration. As we move more than 200 m away from the main stream, it is very likely that we are already in areas of the mountains where the slope is usually steep. This will not be a problem if only three intervals of DD (<25, 25–50, and >50 m) are used, such as in van Westen et al. (2003). But, if a large number of intervals are specified to increase the resolution of DD, we would see that the region with larger DD would also have a steeper slope. Therefore, DD is not a good preparatory factor of LSM.

By contrast, for the preparatory factor TF (Fig. 2d), AR TF (green bars) shows a Gaussian distribution with a peak at about e 2.7 and two troughs toward the two ends of the high and low slopes. The corresponding W TF (red bars) shows another Gaussian distribution with a peak at about e 8.6. Note that both AR TF and W TF are plotted against ln(TF), because TF changes significantly. Carefully examining the TF map of I-Lan area (Fig. 2d) using Eq. (1)–(5), the network shown in blue matches the ridgeline very well, because all the water in this region is basically from precipitation. This water is then distributed immediately to the adjacent cells. By contrast, the regions showed in yellow or red are the cells that receive water from upstream areas. These regions would have a higher susceptibility to landslides, yet they are not always within the main stream. Only a small fraction (1 %) of the study area has ln(TF) larger than 7.1, yet these regions account for 57 % of W TF . This example demonstrates that TF is strongly associated with the occurrence of landslides and can serve as a good preparatory factor of them. Note that another comparison between TF and DD will be illustrated later in Fig. 4.

Lithology is a nominal property rather than a continuous value. There are 11 major types of lithology in I-Lan area, as denoted in the legend of Fig. 2e. In the I-Lan area, landslides tend to occur at regions composed of weathered slate. For example, slate (type G) occupies 4.2 % of study area but accounts for a relatively large proportion of landslide occurrence (30.9 % of W Lithology ); argillite with metamorphic sandstone (type D) occupies 23.5 % of study area and accounts for 21.4 % of W Lithology , and slate with metamorphic sandstone (type A) occupies 44.0 % of study area and accounts for 21.2 % of W Lithology .

After selecting the preparatory factors, two types of multivariate models are usually employed to calculate LSI for each cell j, i.e., the arithmetic mean model (Lee and Talib 2005; Yilmaz 2009)

$$ LSI(j)=\frac{1}{m}{\displaystyle \sum_{k=1}^m{W}_{p{f}_k\left({i}_k\right)}}, $$
(9)

and the geometric mean model (Fourniadis et al. 2007; Nguyen and Liu 2014)

$$ LSI(j)={\left({\displaystyle \prod_{k=1}^m{W}_{p{f}_k\left({i}_k\right)}}\right)}^{\frac{1}{m}}, $$
(10)

where m is the number of pf considered in LSI. For one particular pf k , i k is the corresponding interval of pf k at that cell j. For example, the slope at one particular cell is 15.7°, which falls in the 16th interval, and thus the value for W Slope(16) will be used as the weight for the slope factor at that cell. The merits of the geometric mean model in integrating preparatory factors for the regional assessment of landslide hazard were discussed by Liu et al. (2004). We follow their suggestion and build up two LSMs using the geometric mean model.

Results and discussion

The percentage of landslide occurrence (POLO) and its cumulative (CPOLO) are commonly used as a good indicator to measure the performance of LSM: The steeper the CPOLO curve, the better the capability of LSM to predict landslides and to validate LSMs (e.g., Chung and Fabbri 2003; Frattini et al. 2010; Mezughi et al. 2011; Oh and Lee 2011). We follow this procedure to derive a success rate curve by calculating the LSM of all cells using Eq. (10), and dividing them into 100 equal classes, ranging from high (large LSI value) to low (small LSI value) susceptibility. The POLO value in each susceptible class is determined from the landslide inventory compiled from 2005 to 2013 (Fig. 1b), and CPOLO as shown in Fig. 3. For the case of LSM DD (dashed line), the top 1 % highly susceptible area includes 6 % of the total landslide area, the top 10 % highly susceptible area includes 42 % of the total landslide area, and the top 20 % highly susceptible area covers more than 62 % of the total landslide area. For the case of LSM TF (solid line), the top 1 % highly susceptible area includes 9 % of the total landslide area, the top 10 % highly susceptible area includes 47 % of the total landslide area, and the top 20 % highly susceptible area covers more than 66 % of the total landslide area. To give a quantitative assessment of improvement, we defined the percentage of improvement ρ as shown below and illustrated in Fig. 3:

Fig. 3
figure 3

Cumulative percentage of landslide occurrence (CPOLO) based on LSM TF (solid line) and LSM DD (dashed line). The percentage of improvement ρ is plotted as a dotted line

Full size image
$$ \rho \equiv \frac{CPOL{O}_{TF}- CPOL{O}_{DD}}{CPOL{O}_{DD}}, $$
(11)

By replacing DD with TF, the performance of LSM is significantly improved by ρ = 44 % for the top 1 % highly susceptible area, and gradually decreases by ρ = 13 % for the top 10 % highly susceptible area, and ρ = 7 % for the top 20 % highly susceptible area. Since the association between landslides and TF (Fig. 2d) is much better than the one between landslides and DD (Fig. 2c), the improvement in the LSM is direct and clear: The higher the LSI value, the better the capability of LSM to predict landslides. LSM usually determines whether a landslide has occurred or not based on a threshold value of LSI. The ideal case is to have a distribution of LSI with two extreme values, high (occurence of landslide) and low (no landslide), which correspond to the occurrence of landslide: yes or no, respectively. In the real world, however, LSI values change gradually. Using TF instead of DD is equivalent to enhancing the contrast of LSI values. The improvement in accuracy in these high-risk areas is critical for preventing and mitigating the economic and human losses due to landslides.

To gain a better understanding of why and where LSM TF performs better than LSM DD , one Formosat-2 image taken in 2012 (Fig. 4a), as well as the maps of DD (Fig. 4b) and TF (Fig. 4c), is overlaid onto the DEM and zoomed into one landslide location (denoted as a red polygon), where the spatial distribution of DD is very different from the spatial distribution of TF. This site is far away from the main stream. Consequently, according to the definition of DD, this site has low weighting values for DD and, hence, low values of LSI. However, the corresponding TF values are rather high, since most of the surrounding waters tend to converge and flow through these locations. Such a mechanism cannot be described appropriately by DD: All cells within the same buffer zone would have the same susceptibility to landslide, despite the fact that various orders of stream might have merged, and the amount of flux would be rather different in the same buffer zone. As discussed earlier, only a small fraction (1 %) of the study area has ln(TF) larger than 7.1 (green color), yet these regions account for 57 % of W TF . This site indeed covers a few regions with ln(TF) larger than 7.1 (green color), which serves as a good indicator of landslide susceptibility.

Fig. 4
figure 4

Example illustrating the improvement of the LSM TF method compared to LSM DD . a Formosat-2 image taken in 2012, b maps of LSM DD , and c LSM TF overlaid onto DEM and zoomed on a landslide (denoted as a red polygon). Colors nearer the red-end of the color scale in (b) and (c) indicate a higher rank of susceptibility to landslides

Full size image

Concluding remarks

Current landslide susceptibility models (LSMs) are mostly based on conditions represented by the data contained within each gridded cell. Although drainage distance (DD) has been used to account for landslides occurring on slopes adjacent to main streams, we demonstrate, based on a detailed landslide inventory data derived from remote sensing in the I-Lan region in Taiwan, that DD is not the best region-based preparatory factor, because the cells in the same DD buffer zone may experience different total water flux as tributaries join the main stream when water flows downstream. A new region-based preparatory factor total flux (TF) is presented, which takes into account the topography and hydrology conditions in the vicinity and upstream of each cell. TF better represents the total flux of water in the stream. The results obtained using the landslide frequency ratio method show that TF is strongly associated with the occurrence of landslides and serves as a good preparatory factor for them. Using TF instead of DD in I-Lan region shows significant improvements in the accuracy in terms of cumulative percentage of landslide occurrence (CPOLO), with 44, 14, and 7 % improvements for the top 1, 10, and 20 % susceptible areas, respectively. An LSM intrinsically is a statistic model that describes the spatial relationship among landslides and various preparatory factors. It has a limitation of accuracy, and the uncertainty comes from the measurement of each preparatory factor, as well as the method of analysis. With exactly the same LSM and the same preparatory factors, except for using TF instead of DD, improvements of CPOLO are 44, 14, and 7 % for the top 1, 10, and 20 % susceptible areas, respectively. This significant improvement in accuracy in these high-risk areas is critical for preventing and mitigating the economic and human losses due to landslides. A code to calculate TF, written in Interactive Data Language (IDL), is available under request to the corresponding author.