Abstract
Annual growth, fibre and wood properties of Norway spruce are all under strong influence from genetics, age and weather. They change dynamically, particularly at young ages. Most genetic research and tree improvement programs are based on data from this most dynamic phase of the life of trees, affected by differences in weather among sites and years. In the work presented, influences of age and weather were investigated and modelled at the detail of annual rings and at the sub-tree ring level of earlywood, transitionwood and latewood. The data used were analysed from increment cores sampled at age 21 years from almost 6000 Norway spruce trees of known genetic origin, grown on two sites in southern Sweden. The traits under investigation were radial growth, cell widths, cell numbers, cell wall thickness and coarseness as a measure of biomass allocation at cell level. General additive mixed models (GAMMs) were fitted to model the influences of age, local temperature and precipitation. The best models were obtained for number of tracheids formed per year, ring width, average radial tracheid width in earlywood, and ring averages for tangential tracheid width and coarseness. Considering the many sources behind the huge variation, the explained part of the variability was high. For all traits, models were developed using both total tree age and cambial age (ring number) to express age. Comparisons indicate that the number of cell divisions and ring width are under stronger control of tree age, but the other traits under stronger control of cambial age. The models provide a basis to refine data prior to genetic evaluations by compensating for estimated differences between sites and years related to age and weather rather than genetics. Other expected applications are to predict performance of genotypes in relation to site or climate and simulation of climate change scenarios.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Motivation
Norway spruce (Picea abies (L.) Karst.) is one of the economically most important tree species in Europe and constitutes a forest resource that is of crucial value for the environment, society and industry (Bergh et al. 2005). It is of increasing importance for sustainable production of new forest-based products, as well as a carbon sink. Therefore, initiatives to improve tree performance through breeding are on the rise, addressing aspects like biomass increment and properties important for traditional solid wood and fibre-based products, as well as emerging products such as new bio-based materials, fuels and chemicals (Bennich and Belyazid 2017). Thus, it is essential to know more about the factors controlling wood formation, defining volume growth, biomass growth and wood properties. Of particular interest is the differentiation of intrinsic effects related to tree age and genetics, and extrinsic effects related to site, management and weather, which is expected to change with climate in the future. The magnitudes and patterns of reaction to these factors are likewise relevant and strongly connected with the processes of wood formation.
For efficiency in tree breeding, final selection for the next generation shall be done rather early (12–16 years), which is about 20% of rotation period (Westin and Haapanen 2013). During the time span from planting to these ages, growth and properties are in a phase of rapid change and the variations at breast height reflect the major part of the successive transition from the most juvenile wood of inner annual rings towards the later formed mature wood dominating the stem of the adult tree. This has been shown for many species, also in heritability studies based on the same trees here used for modelling by Chen et al. (2014, 2016). The character and rate of transition from juvenile to mature wood differ between properties. For tracheid dimensions, such as widths, wall thickness and length, the typical patterns are initial rapid increases, followed by successively decreasing changes towards mature levels. For wood density, the larger pattern is similar, but for some species an initial decrease during the first years may be observed. For microfibril angle, however, the typical pattern is totally different, with high values in the most juvenile wood followed by a rapid transition toward a lower stable level, which for Norway spruce typically happens within the time span given above. Due to these different patterns, it is crucial to state the property referred to when using the concept of juvenile wood. Also, it is important to consider that the concepts of juvenile and mature wood do not represent two wood types separated by obvious features in wood. The transitions are rather characterised by a gradual change which continues to fair ages. Harris and Cown (1991) state that for several conifer species, the most damaging features for sawn timber occur in the first 3–5 annual rings, often related to pronounced juvenility, while all wood properties including density may not have stabilised until after the 25–30th ring. Not seldom, the concept of juvenile wood is used in an intuitive way without presentation of precise criteria. In this work, the first part of the transition with the most dynamic change is studied, and all analysed wood is juvenile.
Despite some scientific contributions that specifically addressed also the development of wood properties at this young growing stage of Norway spruce (Olesen 1977; Lewark 1981; Lindström 1998), the early dynamics of tracheid development have gained too little attention. This is astonishing considering the fact that a large part of the research in tree improvement and genetics is built on data from young trees in this growing stage.
Annual but also intra-annual environmental changes have been reported to influence growth and wood anatomical properties (Fonti et al. 2010). Effects in this context of intrinsic and extrinsic growth factors can be revealed through studies on the formation of wood and its tracheids, which involves several steps (Plomion et al. 2001; Vaganov et al. 2006; Rathgeber et al. 2016):
-
(a)
Formation of cells through cell division and differentiation at the vascular cambium. Most of the cells become vertically oriented tracheids. Cell division is most intense in the earlier parts of the growth season,
-
(b)
Expansion of the cells, at this stage with a thin plastic primary wall, to its final exterior dimension. Expansion happens during a limited but varying time after the cell is formed, and with varying rate, generally decreasing over the growth season, and
-
(c)
Allocation of further biomass to thicken the cell wall, creating a secondary layer inside the primary wall, and stiffening the cells through lignification in walls and between. This allocation can be described with the coarseness (biomass/length unit) of the cell. After this, most cells die.
As new cells are formed during most of the growth season, cell division, expansion and wall thickening will happen in parallel for different cells, each process influenced by the weather variations from formation to death of the cell. Variations in the impacts of intrinsic and extrinsic factors will thus define the within-ring variations in cell and wood properties, and eventually the widths and properties of annual rings and the stem cross-section. The band of wide and thin-walled fibres formed early in the growing season is a result of intense cell division, ample time for cell expansion and little wall thickening, resulting in low wood density. The thin band of cells at the outer part of the ring is constituted by cells formed later in the growth season with low division activity in the cambium, less intense cell expansion, and eventually the most intense wall thickening, resulting in high wood density. Between these parts of rather stable properties is a transition part of varying width and character.
Traditionally, within-ring variations have been described by dividing the rings into two parts, earlywood (EW) and latewood (LW), and presented with data on the widths and average properties of the two. The most commonly used definition of EW and LW was presented by Mork (1928), setting a transition point where the tracheid double wall thickness equals the lumen diameter. Such a description of the within-ring variation with two parts will, however, not provide high-quality information about the relatively stable properties of the innermost and outermost parts of each ring, which are supposed to be under stronger genetic control. The information on both these stable parts will be influenced by the transition phase in between, which often extends over a considerable part of the ring. The width and properties of this phase are strongly influenced by weather variations during the season of wood formation. Therefore, a third compartment of transitionwood (TW), reflecting the most weather-dependent part of the ring, was introduced by Olsson et al. (1998). Alternative definitions of the term have later been used by others (Park and Spiecker 2005; Cuny and Rathgeber 2016).
Previous work on models of growth and properties
There is a long history of growth models and a multitude of mainly empirical models for estimation of volume and biomass growth for trees and forest stands of Norway spruce, addressing various levels of detail (see Pretzsch et al. 2007 for a review). Most management models address the assessment of resources, optimisation of harvesting from a forest owner perspective, and raw material allocation for industrial value. Some efforts were spent on integrating wood properties into these forest management models (see Mäkelä et al. 2010 for a review). Most models were built to represent full rotation periods, and the younger growth phases are often not well represented in the calibration data.
Considering the commercial importance of Norway spruce, it is little surprising that models addressing stem, wood and fibre properties and their variations within stems have been presented at different levels of detail, ranging from the stem shape and taper to specific fibre properties. Prominent examples are the models for external tree properties such as branchiness (Moberg 1999; Seifert and Pretzsch 2004; Seifert 2003; Hein et al. 2007), models for spiral grain and inner defects such as resin pockets (Gjerdrum and Bernabei 2009; Seifert et al. 2010), and the models from the joint works of Wilhelmsson et al. (2002) on wood properties and Lundqvist et al. (2002) on fibre properties, estimating property variations radially and longitudinally in stems of trees at different ages, latitudes and growth conditions, modelled from data on the same large set of trees from across Sweden. These models were developed for optimisation of wood use from an industrial perspective, based on data from pith to bark at different heights of trees ready for thinning or final cut, spanning ages from 30 to 150 years. Similar models based on data from several European countries were presented in Lundqvist et al. (2011), models comparing properties of Norway spruce, Sitka spruce, Scots pine and loblolly pine in Lundqvist et al. (2005a) and on loblolly pine in the US in Lundqvist et al. (2005b). These models provide estimates also for the most juvenile wood, but the fitting of the innermost rings was not prioritised as they represent a very small fraction of the feedstock on industrial use. Similar models for within stem variations also on the level of EW, TW and LW were developed by Lundqvist et al. (2008) for the estimation of statistical distributions of fibre ensembles used to simulate fibre structures in sheets of paper. Franchescini et al. (2012) modelled within stem variations in fibre widths for EW, TW and LW at latitudes from France to southern Norway on trees of ages common for harvesting. In this work, the innermost eight annual rings were excluded due to their small contribution as raw material, but also because better models could be obtained for the major volume of the stem if this part of most dynamic change was excluded.
The models above were developed from an industrial perspective but are interesting also in the context of tree breeding, as they describe the continued change from young to mature trees. However, there is also a need for models emphasising the dynamics of the very young trees, also incorporating influences of weather. All models mentioned above are empiric and regression-based and are dominantly used for the simulation of growth and properties. Another track is the application of models based on ecophysiological processes, which were also developed to simulate the wood formation of several species (Deleuze and Houllier 1998; Fritts et al. 1999; Deckmyn et al. 2006; Hölttä et al. 2010; Drew et al. 2010).
On tree improvement, selection of suitable candidates for propagation and the next breeding generation is done early, to reduce breeding time and ensure an earlier return of investment. In this, access to models describing typical changes in growth and properties also for very young trees would be useful, going back to wood formation processes and incorporating weather influences.
Objectives
This article emphasises the development of young Norway spruce from the age when reaching breast height to an age of 21 years. This is the most dynamic growth phase of the life of the trees, which also often determines the competitive status a tree will reach within an even-aged stand. The work was based on data from almost 6000 Norway spruce trees from a total of 524 mother trees of documented origin. The samples were analysed with SilviScan (Evans et al. 1994, 2006) at Innventia (Stockholm, Sweden), now part of RISE Bioeconomy, providing high-resolution information on between and within annual ring variations, which was combined with meteorological data on weather variations across the same years.
Aims of this study were to shed light on how growth and anatomical wood were influenced by tree age and weather during different parts of the growing season. For this purpose, various wood anatomical traits were modelled statistically as averages of annual rings and their parts of earlywood (EW), transitionwood (TW) and latewood (LW). The analyses focus on radial increment and xylogenetic parameters of tracheids, such as numbers formed, cross-sectional extensions, coarseness (biomass allocated) and wall thickness. The models should allow for a use in further investigations of genetic influence on growth and properties. One objective was to estimate the effects of the weather during specific years at different experimental sites, followed by harmonisation of data from the locations with regard to variations between sites and years, resulting in improved information on effects of genes, soil and other environmental factors.
Correlations between growth, tracheid and wood properties are a core issue in tree improvement and have been investigated in numerous studies, also based on the same data material as we used for modelling (Chen et al. 2014, 2016). In the current work, we have instead applied a bottom-up approach starting with modelling processes of wood formation behind these properties and growth, processes which influence them in parallel, thereby contributing to the correlations between the traits.
Materials and methods
Material
Geographic location and trial design
The plant material originated from 5618 Norway spruce trees sampled from two experimental sites in Southern Sweden: Höreda (longitude 15°04′E, latitude 57°60′N, elevation 225 m) and Erikstorp (longitude 13°90′E, latitude 56º80′N, elevation 155 m). The sites were established by Skogforsk in spring of 1990 as a randomised incomplete block design with single tree plots planted in a homogenous spacing of 1.4 × 1.4 m.
Site conditions
Both sites show similar soil types of sandy-silty moraine typical for Norway spruce forests in southern Sweden. The southern site, Erikstorp, has a slightly higher site index due to better water availability, higher fertility and longer vegetation period. Major determinants for growth on the sampled sites are certainly temperature and access to water. Solar radiation forms a third important growth factor. However, radiation is strongly controlled by the spatial position of trees and their individual competition within the crown space. Since limited information was available on sizes of surrounding trees, within stand competition could not be used as a variable in the modelling. It was, however, assumed that ranking on family level can be performed based on analysis of residuals, due to the randomised design and same spacing of the experiments. Monthly temperature and precipitation values of the two sites were retrieved from the Swedish Meteorological and Hydrological Institute (SMHI 2016). Figure 1 illustrates to the left averages from 1990 to 2010. The vegetation period is significantly shorter at Höreda which is on a higher elevation, on average 160 days from 4/5 to 1/10 (Fig. 1a), compared to 174 days from 30/4 to 21/10 for Erikstorp (Fig. 1b), criteria for start and cessation given below. To the right, the temperature and precipitation sums across each annual vegetation period are shown (Fig. 1c). Further details about the trial sites can be found in Chen et al. (2014).
Genetic origin and silvicultural treatment
The trees represented 524 open-pollinated half-sib families from seeds harvested from plus trees originating from provenances across southern Sweden. All 524 mother clones exist as grafts in clonal archives. Six trees per family and trial were sampled randomly among healthy trees which were not suppressed according to an earlier diameter assessment. In 2010, two 12-mm increment cores were sampled at breast height (1.3 m) from the northern side of the stem. With some losses along the chain from sampling to ready data, this finally resulted in data on an average of 5.4 trees per family and site for wood property analysis. The genetic origin ranges from Swedish proveniences to Baltic, Russian and German origin. Precommercial thinning was conducted in Höreda and Erikstorp in 2010 and 2008, respectively. Strongly suppressed trees, which were judged not to reach commercial dimensions at the first thinning, were cut down. Most of these were less than 50 mm diameter at breast height. The thinning was assumed not to have affected the growth or properties of the remaining trees and was considered of minor importance for this study. The material and sampling are described in more details in Chen et al. (2014).
Methods
Measurement of response variables
Silviscan measurements of tracheid numbers and widths, density, coarseness and biomass
From one core of each tree, 2-mm-thick radial sample strips from pith to bark were cut and analysed with SilviScan for radial variations in various properties of growth, wood and tracheids, providing averages for consecutive intervals of 25 µm. SilviScan has been developed for rapid analysis on the annual ring and within-ring level, using automated and integrated X-ray and microscopy measurements, image and data analyses (Evans 1994, 2006). The high efficiency of the analysis makes it possible to investigate large numbers of samples, which are needed for sound statistics in projects on tree improvement and genetics. The instrument at Innventia has been used since 2004 on many species worldwide, addressing both fundamental research issues and industrial development. SilviScan has previously been successfully used in a wide span of studies. Examples are, on different softwoods (Lindström et al. 1998, Downes et al. 2002; Lundgren 2004a; Havimo et al. 2007; Kostiainen et al. 2009; McLean et al. 2010; Piispanen et al. 2013; Fries et al. 2014) and on hardwoods (Kostiainen et al. 2014; Lundqvist et al. 2017). Examples of previous work on modelling have been presented by Wilhelmsson et al.2002; Lundqvist et al. 2005a; Franchescini et al. 2012; Auty et al. 2014.
In this study, the 5618 spruce sample strips were scanned to automatically record microscopy images of tracheid cross-sections extending from pith to bark of each sample. Image analysis was applied to determine the radial variations in the numbers and widths of tracheids in radial and tangential direction of the wood matrix. Tracheid lengths in longitudinal direction can, however, not be determined from these cross-sectional images. Next, the strips were scanned with X-ray transmission for synchronised information on the radial variations in wood density with the same radial resolution, followed by calculation of corresponding data for tracheid coarseness, wall thickness and biomass. Coarseness is defined as the dry mass per length unit of the tracheid (µg/m). The strips were also scanned with X-ray diffraction, providing information for estimation of microfibril angle and wood stiffness. On measurement, the wood was in equilibrium with the atmosphere of the conditioned laboratory, with a moisture content of about 8%. It is important to mention that the coarseness obtained represents tracheids in situ in wood, rather than for chemically liberated tracheids from which a considerable part of the substance has been dissolved, resulting in much lower values.
Definition of annual rings and their parts
The locations of all annual rings and their parts of EW, TW and LW were determined from the radial variations in wood density, altogether for about 300,000 rings and parts. The ring boundaries were set algorithmically at the steep density drops at the interface between each LW band and the EW of the next year. After that, a “20–80” density threshold definition was applied for separating three compartments within each ring. For each ring, the span from minimum to maximum density was determined. The part from 0 to 20% of the span was defined as EW, the part from 80 to 100% as LW, and the part in between as TW, see Fig. 2. This method was introduced by Olsson et al.(1998), initially as “20–50”, to allow better descriptions of variations in the statistical distribution of wood and fibre property variations for pulp and paper applications but has become commonly used also in wood-related science (Kostiainen et al. 2009; Franchescini et al. 2012; Fries et al. 2014; Hong et al. 2014).
Next, the widths and arithmetic mean values of all properties were calculated for the rings and all compartments. This article focuses on diameter growth and anatomical traits related to processes of wood formation, more specifically the widths of rings and their EW, TW and LW, as well as the average numbers, widths, wall thickness and coarseness values of the tracheids in rings and their parts.
Calculation of independent variables
The independent variables were split into intrinsic and extrinsic variables, the first determined by the tree internal growth rhythm, the latter externally driven by the weather. Genetic effects were at this stage not explicitly modelled as fixed effects but taken into account as random effects.
Age-related variables
Most often, variations in growth and properties of trees with age and over time are studied from materials sampled at breast height (1.3 m) and investigated with reference to the tree ring number, expressing cambial age (e.g. Lenz et al. 2010; Franceschini et al. 2013; Ivković et al. 2013). This is obviously not the full age of the tree, as the tree first must reach breast height, driven by the development of the apical meristem, which determines the height growth and shoot extension. The apical meristem already has a certain age when reaching breast height. The second component of growth is the vascular cambium, which is formed by the apical meristem and invokes the radial growth of stem and shoots. For a more detailed explanation of the interactions of apical and vascular cambium and the involved hormonal control, the reader is referred to the excellent publications of Iqbal (1990) and Larson (1994). As a consequence of the formation of the cambial meristems, the apical meristem is naturally more related to the total physical tree age (TA), while the cambial age (CA) varies with height along the tree stem and relates to the tree age when the vascular cambium was formed. To look into the differences for young trees, we tested both age variables for their influence.
Weather-related variables
Due to the lack of phenological data and data on the onset and cessation of stem diameter growth in the experimental areas the vegetation period had to be estimated. They can be estimated with different approaches of varying complexity (e.g. Rötzer et al. 2004; Korpela et al. 2008). A simple temperature-based approach was chosen. The start of the growing period was defined at growing degree day (GDD) of 70, an average value calculated based on the reported values by Kallioski et al. (2013, Table 5) to trigger stem diameter growth in Norway spruce. Growing degree days were determined according to McMaster and Wilhelm (1997), which used Eq. 1 to determine GDD:
where Tmax and Tmin are the maximum and minimum daily temperature and Tbase base was chosen at 5 °C, according to earlier phenological studies of Schmitt et al. (2004) and Gruber et al. (2009) as proposed by Prislan et al. (2013).
The end of the vegetation period was defined as the day when the mean daily temperature reached 5 °C. Only days after the calendar day 150 were allowed to limit the vegetation period to avoid that cold spells in spring would terminate the modelled vegetation period too early. This way, temperature GDDs across the annual vegetation periods were calculated for use as one of the candidate independent variable. As alternative candidates, temperature sums were calculated also for parts of different lengths of the vegetation periods.
The calculated precipitation sums were also constrained to the previously defined vegetation period, assuming that after the winter there would be a sufficient available water reservoir in the soil for the trees to grow.
Further, an index integrating precipitation and temperature, the de Martonne index (DMI) was calculated (de Martonne 1926). The equation used is DMI = MAP/(MAT + 10), where MAP and MAT represent the mean annual precipitation and mean annual temperature, respectively.
Models based on various mutations of weather variables were compared for selection of model structures best meeting the objectives, such as annual sums of GDD and precipitation, DMI, as well as sums of them across 1, 2, 3 and 4 weeks. As a further aggregate, the vegetation length of each year was split in four quarters and the quarterly sums were added to the tested candidate variables. To cater for different starts and cessations of the vegetation periods, the periodical sums were calculated from the start to the end of each vegetation period, and not on calendar basis.
Statistical modelling
The modelling employed was mainly aimed at identifying biologically/physically meaningful influence variables rather than attempting to fit a model with the highest degree of predictive value. Thus, a generic modelling approach was applied that made it possible to compare the effects of a set of identified meaningful influence variables on the defined response variables.
Data preparation
Closest to the pith, the wood matrix shows a radial organisation with strongly curved rings. Thus, it is not possible to derive sound information on property variations in radial and tangential direction of the wood matrix with X-ray beams through the 2-mm-thick sample strip, nor to precisely localise and calculate averages for rings and their parts. Therefore, after ring boundaries and ages had been determined, the tree rings within a radius of 2 mm around the pith were excluded from the further analysis. Also the last tree ring formed in 2010 was excluded from the analysis, since not all samples had been taken at the same time of the year, with the result that for some samples the formation of latewood of 2010 was incomplete.
Modelling process
A mixed generalised additive model (GAMM) was used to model the relationships between tree age and weather with the response variables of the tree at ring and intra-ring level. The model development was done in two steps. First, the relevant fixed variables were identified. To select the most correlated variables, a partial correlation analysis was performed. Traditional multiple linear regressions with automatic variable selection were used to filter for a reasonable set of variables and select the ones that showed a generic behaviour for most response variables, while avoiding joint use of variables with strong intercorrelation.
In a second step, these variables were introduced into a generalised additive model (GAM), which was developed without a random component at the beginning. Akaike’s information criterion (AIC), degree of determination (R2) and deviance were used to select the models. Residual plots were used to identify outliers and check for a potential bias in the models. All models were selected for significant total model performance and significant variable contribution. Cubic regression splines were used for smoothing. They were generally constrained to a maximum degree of freedom of three, in order to reveal the general reaction pattern without providing too much flexibility for the spline.
After the variables contributing to the fixed effects had been finally selected, a random model part was added as a hierarchical (nested) model in a third step. This random model part included the individual tree’s identifier nested in family, which represented the genetic mother of each tree. This way the within and between tree variabilities were modelled, and the clustered data structure was accounted for. An autoregressive covariance structure (AR1) was introduced to cater for serial autocorrelations between the years. It provided better models than a simple identity structure. Trees with standardised residuals outside ±10 were removed as outliers before refitting the models.
All modelling was done with the GAM and the GAMM function of the mgcv package (Wood 2017) of the R statistical language (R Core Development Team 2017). The regressions were fitted based on maximum likelihood estimation to provide meaningful possibilities for the use of AIC and maximum likelihood tests to compare the models.
Modelling strategy
As stated before, the main ambition was to obtain best possible information about the influences of age and weather, rather than the best possible fit to growth and property data. Therefore, as a result from the process above, only age, GDD and precipitation during the four parts of the growth season were included in the fixed part of the model. The resulting generalised additive mixed model (GAMM) with cubic regression spline functions, a hierarchical random part with tree (i) within family (j) and an AR1 autoregressive element in the random part is provided in Eq. 2.
where the residual variance εji are zero mean normal random variables, with correlation given by
and where β0 denotes for the intercept, βj and βji for regression coefficients, f1 to f6 are cubic regression spline smoothers, age for age (either cambial age or tree age), GDD for the growing degree days in the total vegetation period, whereas PQ1 to PQ4 denote for the precipitation in the four quarters of the vegetation period.
The estimates presented and discussed below are the sums of the intercept value (β0), named baseline value below, and the set of spline functions f1 to f6, while the terms βj + βji + εji in this article are treated as a combined residual, expressed with the R2 values. The parts of the residuals related to families (βj) and individual trees within families (βji) will be exploited in genetic studies to follow.
Site was not included explicitly as a variable, despite the expectation that it might have improved fit values of the models, which tests indicated. Site effects were excluded since they might have interfered with weather effects at the site level, considering that only two sites, differing in average GDD and precipitation sums, were represented in the data. This would have carried the risk of taking away much of the generic character of the models. Non-weather-related site effects were instead investigated through a second step correlation analysis of residuals.
Results
Dynamics and variability of response variables
The data on growth and properties show a considerable variability of different origin. This is illustrated in Fig. 3 with means for growth ring width plotted versus cambial age with data from 24 trees: From each site, 6 trees of a slow-growing family and 6 of a fast-growing family. The dynamic variation related to age is evident. There are clear differences between the two families (related to genetics and the suitability of the families to perform on the sampled sites). Also, clear site differences were observed caused by factors such as local climate and soil fertility. However, there are also very large differences among individual trees of the same family and same site, reflecting large variation not related to age or site, but to individual environmental conditions of each tree.
Figure 3 also illustrates effects of the differences among the trees in longitudinal growth mentioned above, resulting in different cambial ages of the last ring formed inside the bark at the time of sampling. Frequency distributions for cambial age at breast height of all the sampled trees are shown in Fig. 4 for both sites. At sampling age (21 years) the number of annual rings at breast height ranged from 6 to 18, a considerable variability among trees planted the same year, meaning that the ages at which the trees reached breast height ranged from 3 to 15 years. Thus, wood of rings with the same cambial age has been formed during different growth seasons with different weather. The trees of Trial 1147 Erikstorp generally reached breast height earlier than those of Trial 1146 Höreda. More than 90% of the trees reached breast height at ages from 4 to 8 years, with the highest frequency for age 5 and 6 years, resulting in 14 and 15 annual rings, respectively.
The fact that trees with slower height growth are not represented at the higher cambial ages makes cambial age not necessarily the best independent variable for modelling age and weather effects, in particular if the trees are young, showing rapid changes with age. To elucidate this, the trees were classified based on the year when they reached breast height. Averages were calculated for all cambial ages within each tree class and plotted versus both cambial age (CA) and total tree age (TA) for comparison. The results show clearly different patterns depending on the use of cambial age or tree age. In Fig. 5a, this is illustrated with plots of the average widths of rings and their EW, TW and LW bands for the five most frequent classes of trees reaching breast height 1994 to 1998, respectively, presented with colours in the following order: magenta (1994), blue, green, yellow green, brown (1998). In its upper part, the averages are plotted versus cambial age, separately for the two trials. In its lower part, the same data are plotted versus the year of wood formation which equals the tree age, if the year of planting (1990) is subtracted. It should be noted that the latewood widths are shown in 10-fold scale of the y-axis.
Curves for annual averages of trees reaching breast height 1994–1998, respectively, plotted versus both cambial age and total tree age, for comparison. The colours represent years of reaching breast height, in the following order: magenta (1994), blue, green, yellow green, brown (1998): a widths of rings and their compartments, mm. Age as cambial age and total tree age, b radial tracheid widths, μm. Age as cambial age and total tree age and c coarseness of tracheids, μm/m. Age as cambial age and total tree age. Observe that for the width of LW is magnified with a factor 10 in the plots to make the variations clearly visible
Several distinct patterns were observed, related to influences of intrinsic or extrinsic control of growth traits. A first pattern is that the year-to-year variations of the ring width curves as expected synchronise obviously better when plotted against tree age (Fig. 5a lower plots) compared to cambial age (Fig. 5a upper plots), for which the wood of the tree classes was formed under different years and weather conditions. This extrinsic effect is also consistent for the different parts of the tree ring and on both sites. A second pattern, less expected, is the good agreement between the developments of widths versus total tree age among the tree classes, from the extremely juvenile wood towards maturity. The average ring widths for the tree classes decreased from 5 to 6 mm close to the pith of trees reaching breast height around age 5 years to 2–3 mm at age 20, in relative terms equalling 50–60%. The curves representing trees reaching breast height later successively lined up. This means that trees with slow height growth, reaching breast height late, will not only fall behind in competition for light and resources. They will also miss the opportunity to form the widest rings close to the pith and start with narrower rings, decreasing outwards. The trees with higher longitudinal growth are thus prone to also have higher radial growth, which is expressed by a positive correlation of R2 = 0.67 between family averages of diameter at breast height and tree height at age 7 years on both sites. Very similar patterns were observed for cell numbers in radial direction in the rings and their parts.
The corresponding plots for radial tracheid width in Fig. 5b show a third pattern differing from that for the tree ring widths. When plotted versus cambial age, the curves for the development of ring and EW means representing the different tree classes followed each other closely up to cambial age of 8 years (upper graphs), a very dynamic phase, indicating cambial age control. Thereafter, the average curves of the different tree classes successively entered a more moderate phase. These shifts seem related to the total tree age according to the lower graphs. This indicates that, on average, the trees which grew faster in height and also radially will experience more years of initial increase before entering the more moderate phase, forming wider tracheids in radial direction at higher tree ages than those of slower grown trees. This is in line with observations from old trees of Norway spruce (Lundqvist et al. 2005a; Franchescini et al. 2012). The results thus indicate a stronger intrinsic control of tracheid width during the most dynamic phase, combined with control related to tree age of the time when the more moderate phase is entered. The compartments show a very clear cambial age control of radial tracheid width in EW, less so for TW, and radial fibre widths in LW, which seems more related to total age (and annual weather), and further, little influence from annual weather variations on the radial cell expansion in EW, some in LW, but strong influence in TW. The overall effect on the total ring level indicates that the year-to-year variations during the early years are dominated by cambial control, while during the following period of moderate change they become dominated by weather effects and are strongly related to the variations in TW, and with differentiated controlled by growth rate and total age.
For tangential fibre width (not shown), the variations showed a similar character as for radial width, with the exception that the differences were smaller between EW, TW and LW, and so were the annual variations. This is expected as the fibres are organised in files, and their widths cannot vary freely.
Figure 5c shows the corresponding graphs for tracheid coarseness, allocated biomass per length unit of the tracheids, indicating stronger cambial control age than that of total tree age. The graphs representing the average developments with age of the different tree classes line up well when plotted versus cambial age, expect for disturbances from extreme weather conditions during 2004, which occur at different cambial ages. Adversely, the graphs plotted versus tree age are well synchronised regarding the annual variations, while showing bias between the tree classes, reflecting the stronger cambial control. The radial development of coarseness was still in a more dynamic phase at the time of sampling, indicating a slower maturation of the biomass allocation process than for the radial tracheid expansion process.
Capabilities of the models and contributions from age and weather-related factors
Against the backdrop of the idiosyncratic patterns described above, models were developed from combining total tree age or cambial age, respectively, with temperature sum across growth season (GDD) and precipitation sums for the four quarters of the growth seasons. Table 1 presents the degrees of determination R2 of models for means of rings and their parts. The first two data columns to the left show this for models with age only in their fixed parts, age expressed with cambial age and total tree age, respectively, the following two columns illustrate the same for models including also the temperature and precipitation parts, showing the change in R2 when adding weather variables to the age factors in absolute terms. Values in bold indicate if a specific age variable provided a substantially higher degree of determination than the other for the trait (R2 difference ≥ 0.01). The two next columns show the gains in R2 when adding the weather factors, in relative terms. Models benefitting more than 4%, and then reaching R2 values > 0.15, are indicated in italics. To the far left, the baseline (intercept) values of the models are presented.
To facilitate comparisons, the R2 values of model estimation the traits representing the three fundamental processes of wood formation are shown graphically in Fig. 6. Each set of four bars shows the two CA-based models to the left with dashed contours and the two TA-based models to the right with solid contours, models based on age only with white bars and those using also weather input in grey. It should be mentioned that this study focuses on the ages of most dynamic change. At higher ages with smaller age-related changes, the differences between the residuals when using CA or TA are expected to be smaller, and the effects of genetics and environmental factors larger in a relative but not necessarily in an absolute sense.
Degree of determination (R2) values of models estimating averages for rings and their parts of the traits closest related to the wood formation processes. Each group of four bars show the two CA-based models to the left with dashed contours of bars and the two TA-based models to the right with solid contours. White bars represent models based on age only, grey bars models including both age and weather factors
Cell divisions: Number of radial tracheids
The best models of all were obtained for the number of tracheids formed per year in radial direction. Using total tree age alone gave an R2 value as high as 0.49, as mentioned before, reflecting the large relative decrease in the intensity of cell division across this very dynamic phase in the life of trees. When adding the weather-related parts, R2 increased for 7% to 0.53, indicating substantial influences from the temperature sum and the precipitation sums. It should be pointed out here that these sums reflect not only the levels of temperature and precipitation, but also the lengths of the seasons. Use of tree age combined with the weather parts gave the best degrees of determination also for the radial numbers of tracheids in the ring compartments: high for EW (0.41 → 0.48) and TW (0.29 → 0.35), but very low for LW (0.03 → 0.07) with its small overall variation.
Thus, the R2 values for the compartments were lower than that for the ring level, but their relative improvements when adding the weather factors were larger for the compartments than on the ring level: 18% for EW, 20% for TW, and as high as 155% for LW.
This can be understood as follows: While each cell division is solely governed by the current and previous weather, the final identity of the tracheid as part of EW, TW or LW is also influenced by the weather during the time of cell expansion and biomass allocation/wall thickening to follow, which will eventually affect if a tracheid will grow to a EW or TW tracheid and, if later formed, to a TW or LW tracheid. From this perspective, it is expected that the influences of weather are relatively stronger on the parts of the rings than on the total ring, as well as the substantial increase in R2 for radial number of tracheids in TW when adding weather factors, as TW is defined to capture the most weather-dependent part of the wood.
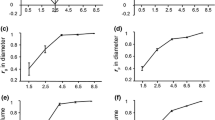
Cell expansion: Radial and tangential tracheid widths
The model with the second highest R2 value was obtained for tracheid widths in for EW (R2 = 0.44) based on cambial age, which was reached already with use of the age factor only. For all models estimating tracheid widths, cambial age provided higher R2 values than tree age. The marginal gain in degree of determination for EW from adding the weather factors may reflect that the expansion of these tracheids first formed is mainly influenced by conditions during the initial phase of the vegetation period, to a large extent predetermined by factors such as the reserve state of the tree, which is in turn largely determined by previous growth periods. In contrast, the R2 values obtained for TW and LW were low, but with large relative increases when adding the weather factors: for TW 0.06 → 0.16 and for LW with its very small overall variation 0.02 → 0.10. The LW band contained on average only 11 tracheids, less than 10% of the average number for rings. As EW and TW thus stand for more than 90% of the tracheids, it is reasonable that the capability of the model for average tracheid width of the full ring was in between those of EW and TW, rising from 0.17 to 0.23 on adding the weather-related part.
For the tangential widths of tracheids, the models for means of rings and their EW and TW all showed R2 values of about 0.35 and 0.25 for LW. The gains when adding the weather parts were small, most likely reflecting that the tracheids are arranged in radial files, leaving limited freedom for variation in tangential tracheid width.
Widths of rings and their parts
The relative capabilities of the models for widths of rings and their parts are similar to those for number of tracheids formed in radial direction. The obvious explanation is that the ring width is a product of the number and the width of tracheids radially, combined with the fact that the relative variation of the numbers is much larger than that of the widths. This also implies that total tree age provides better models than cambial age, and also a similar particularly large relative increase in R2 for TW models when the weather part is added (also for LW but at much lower levels of R2). However, the degrees of determination are generally lower than for the number of tracheids radially, most likely since the widths of rings and their parts are products of two variables, both influences by many factors, meaning that its variability has a more complex background.
Biomass allocation: Coarseness and wall thickness of tracheids
For the allocation of biomass at cell level, measured as tracheid coarseness, the cambial age-related part of the model explained 0.39 of the overall variances from all sources for the average coarseness of rings, just above 0.30 for EW and TW and 0.21 for LW. When adding the weather-related parts, these R2 values increased to 0.42, 0.34, 0.37 and 0.30, respectively, again remarkable increases for TW and LW.
The wall thickness of a tracheid is related to its coarseness and its radial and tangential tracheid widths (also of the tracheid wall density, but this shows little variation). Wall thickness is thus another complex property under multiple influences. Therefore, it is reasonable that its models show lower R2 values than those for coarseness.
Developments with age and effects of temperature and precipitation
Influences presented with spline functions and differences between cambial and total age
The developments with age and weather factors are described with spline functions showing changes across the span of variation of each factor in relation to baseline values, given in Table 1. These baseline values differ among traits and also among the averages for rings, EW, TW and LW. Generally, these values are close to the calculated averages for the trait across all trees and rings and the spline function is a model for the average development related to each trait across all trees of the two sites. This is illustrated in Fig. 7 for influences of age on number of tracheids formed annually (left) and their mean coarseness on ring level (right). The plots superimpose the spline functions of the models based on tree age (TA, black curves) and cambial age (CA, red dotted curves) together, shifted in time for the best match of curves.
Spline functions expressing the influences of age on a number of tracheids formed radially per year and b their coarseness, and their baseline values (approximately the means on ring level across all trees of different families on both sites), splines for models bases on total tree age (TA) with black curves, on and cambial age (CA) with red dotted curves
Shifted like that, the TA and the CA splines become very similar at the lower end of the age span, but they differ considerably at the higher end. This is obviously related to the differences in height growth of the trees. With use of TA, the models are based on more trees with increasing age, in fact all trees for the last 6 annual rings, see Fig. 4. But with use of CA, the models at the highest cambial ages will be based solely on the trees with the fastest longitudinal growth. The negative but decreasing slope of the TA spline function for number of tracheids, combined with the upturn of the CA splines at high ages, and the adverse developments for coarseness, suggests that with age: (1) fewer tracheids were formed but that these had higher coarseness, on average across all trees, and that (2) the more fast-grown trees had more tracheids with somewhat lower coarseness compared to the averages at these ages. The fact that only trees with a fast height growth are represented at higher CA values is the reason of the upturn of cell numbers with the higher cambial age and the downturn for coarseness. Similar effects are seen also for radial tracheid width, where the more fast-grown trees have wider than average tracheids as noticed from Fig. 5b. Such differences in relation to the averages will be studied in later steps of these investigations.
Thus, the comparison of models based on TA and CA, respectively, shows that for CA, the model for a trait may be distorted at high cambial ages due to an over-representation of trees with faster height growth, with the consequence that it will not reflect the average development of the trait. This is, however, not the case for models based on TA. Therefore, the choice was made to present spline functions only for models based on tree age. The splines for influences of weather factors were however as expected similar on use of both age types.
Models based on age and weather
Figure 8 illustrates the full sets of spline functions for all the traits modelled and presented in this article: Influences of age to the left, then of GDD, and to the right of that the four precipitation sums of quarters of the vegetation period. Splines are provided for effects on the ring level (solid black) and for EW, TW and LW (dashed curves in green, red and blue), all along a common zero line representing their baseline values provided in Table 1. The absolute value of each estimation is thus the sum of the specific baseline value and the contributions from age, GGD and the precipitation sums.
Effects of tree age, temperature sum and precipitation during different parts of the growth season as expressed by the models in different colours: ring (black), EW (green), TW (red) and LW (blue). a Mean number of tracheids radially in rings and their parts, b mean radial tracheid width in rings and their parts, c mean tangential tracheid width in rings and their parts, d mean widths of rings and their parts, e mean coarseness of tracheids in rings and their parts, f mean wall thickness of tracheids in rings and their parts
The splines showed three major patterns: an increase, a decrease or a humpback shape pattern with a maximum. In all plots of spline functions related to weather effects, three vertical lines have been introduced. The middle vertical line indicates the median annual weather in the data set, the outer ones the 10% and 90% quantiles. Effects indicated outside these lines should only be interpreted with care. In the following sections, temperature and precipitation sums inside but close to the outer lines will be referred to as low and high, and values closer to the median as on the low or high side. For all weather-related factors, the splines indicate that the influences of the median values of the factors were close to zero, meaning that median weather would result in spline values close to the baseline.
Numbers of cell divisions at cambium across the years and of tracheids in EW, TW and LW
Part a of Fig. 8 presents the models obtained for number of tracheids formed in radial direction across the year, together with the numbers of tracheids in EW, TW and LW. The baseline numbers for rings, EW, TW and LW were 120, 60, 47 and 11 (cf. last column of Table 1). According to the age-related graphs, these base values occur at a total tree age of about 12 years, where the curve crosses the zero line. The ring level model tells that the trees having reached breast height at age 5 years had formed on average 125 tracheids more than this average, thus 245 in total. The radial number of cells then decreased linearly down to on average about 30 above the average at age 10 years. At age 15, a level of about 40 cells below the baseline was reached, meaning on average 80 tracheids formed radially per year. The models indicate that the radial number of tracheids in EW continues to decrease at all investigated ages, while for TW the decrease stops at about age 14. This would entail an increasing proportion of TW tracheids during the last years investigated.
The model indicates a positive GDD effect from about − 15 to + 15 tracheids across the span of GDDs observed, the 10% most extreme events at both ends excluded. At low GDD, the decrease in tracheid numbers was divided about equally between EW and TW, but at high GDD, the increase was mostly reflected in the TW. Further, the splines for precipitation sums indicate similar positive influence of high precipitation during the second quarter of the vegetation period (Q2 = major parts of June and July), also here mostly reflected in TW, while dry conditions during this period impacted negatively. The precipitation sum during Q3 did not affect the annual radial number of tracheids much, but in dry weather conditions, more of them got EW character and equally less TW character. A similar but weaker antagonistic behaviour was expressed at median precipitation sum during Q1.
Widths of tracheids in rings and parts, and comparison of models based on cambial and tree age
Part b of Fig. 8 illustrates the corresponding effects on the radial tracheid widths in rings, EW, TW and LW, in relation to their baseline widths of 29, 32, 27 and 20 µm, respectively. The modelled radial tracheid widths of trees which had reached breast height at age 5 years were on average 5 µm slimmer than the baseline value, while those formed at age 14 were 1.2 µm broader than the baseline value of 29 µm. At higher ages, the estimated age effect on ring means started to decrease slightly. The age effects on the tracheids in the EW were larger than this, but smaller for those in the TW. The radial widths of the radially slim LW tracheids increased only slightly in absolute terms across the ages.
Radial extension (widening) of tracheids is according to the models for ring means favoured by low GDD (small effect), precipitation on the high side during Q1, high during Q2 and Q4, but low during Q3. Just as for the influences from age, several of these weather conditions affects the number and size of the tracheids adversely. For tracheids in TW, the weather splines indicate that high precipitation during the 2nd and on high side in the 3rd quarters favours larger widths of TW tracheids, which makes them in this respect more similar to those in EW.
In Fig. 8c, the influences on tangential cell widths are illustrated. The baseline values in Table 1 show that the average widths are quite similar for ring, EW, TW and LW, and the dynamics with age are so, too. The variations related to the weather variables are also small. This strengthens the assumption that their freedom of variation is limited due to the organisation of the tracheids in radial cell files.
Widths of rings and their parts
Part d of Fig. 8 illustrates the average effects on widths of rings and their parts, in relation to the baseline values for the ring 3.4 mm, EW 1.9 mm, TW 1.3 mm and LW 0.2 mm. All spline functions are very similar to those for number of tracheids radially.
The trees which have reached breast height at age 5 years had then on average about 2.7 mm broader rings than baseline, resulting in an average ring width of 6.1 mm. Following a close to linear slope, the rings were at age 10 years on average only about 0.5 mm broader than the baseline value, 3.9 mm, and at age 15 years after continued but retarding decline they were about 1 mm thinner than this value, 2.4 mm. Further, the model indicates that the average age effects on EW and TW first are on average rather similar, but that the proportion of TW increases toward the end of the age range investigated. The width of the LW band is very thin, and the changes due to age are barely visible in the figure.
Continuing to weather-related effects, the model results indicate that low GDD is negative for ring width, decreasing its average with up to about 0.5 mm, while at high GDD about 0.4 mm of radial increment is added, extremes excluded. The graphs indicate that both thinner EW and TW bands are the cause of the narrower ring widths at low GDD, with the strongest effect from EW, possibly reflecting a late start of the growth season. The same pattern reveals broader bands of EW and TW at higher GDDs, contributing to the broader rings. The influences from the weather factors on ring widths were generally quite similar to those observed on radial number of tracheids. According to the models, the effects on radial growth of the variations in GDD and in precipitation during Q2 corresponded to ± 0.3 to ± 0.4 mm per year, each.
The results also suggest that widths of EW and TW often show a certain competitive behaviour. As commented after the description of the definition of TW: Fibres at the interphase between the two compartments may end up in either of the classes, depending on how the weather a certain year influences the expansion of the cells.
Tracheid coarseness and wall thickness
Part e of Fig. 8 shows the corresponding spline functions for tracheid coarseness. The baseline values for averages of the ring, EW, TW and LW were 318, 274, 358 and 428 µg/m, respectively (Table 1). The modelled average age-related developments were rather similar for ring, EW, TW and LW, starting in the innermost rings from coarseness values 80–120 µg/m below their respective baselines, with LW and TW at the lower end, then converging almost linearly to reach the baseline at the same tree age of 12 years. Above this age, the spline functions start to diverge: the spline for EW tracheids levels off at values about 20 µg/m above the baseline, the LW spline continues to add biomass, reaching the double at tree age 19, while the splines for ring and TW averages develop in between. These increases in coarseness will be linked with increasing thickness of the tracheid walls, and as the perimeters of the tracheids in TW are smaller than those of EW, and even more so in LW, the increase in wall thickness with age will be largest in LW, smallest in EW, and with TW and ring averages in between (Fig. 8f).
The weather factors showed smaller influences than age in this age span. The average influence of GDD shows the same development for means of rings, EW and TW: for coarseness a linear decrease from + 15 µg/m at low GDD to − 15 µg/m at high GDD, and a similar development for wall thickness. At higher temperature sums, the biomass is thus distributed to more tracheids (Fig. 8a) with smaller radial width (Fig. 8b), lower coarseness (Fig. 8e) and thinner walls (Fig. 8f). The most evident precipitation effects are indicated for the LW, for which the coarseness and wall thickness splines show reducing values on increasing precipitation during Q2 and Q3.
Example: Combined weather effects of ring width
The use of GAMMs makes it possible to simply add up the influences of different variables. A simulation was done to exemplify the effects of different scenarios of annual weather, including extreme scenarios for radial growth. For this, we used different combinations of medium, low and high GDD and precipitation sums, defined by the median and 10% and 90% quantile values of the weather variables. The effects of these different levels of the weather variables were assumed to be the values of the respective spline functions at these levels in Fig. 8d. In Table 2, all individual effects of the five weather factors are compiled and added to estimate the full annual effect of each scenario.
With a baseline value of 3.4 mm and age effects of about + 2.0 at age 7 and − 1.0 at 19 years, an average tree would according to the simulations on ideal weather show a decrease in ring width from age 7 to age 19 years of 6.1 to 4.1 mm and of 3.1 to 1.1 mm on worst weather conditions.
Residual analysis
The residuals were checked for influences related to the different independent variables. In Fig. 9, the results are illustrated for the model of ring width against tree age, and the outcomes are similar for the other properties modelled. Figure 9a shows the original data for all tree ages from 5 to 19 years including the trees from both sites based on a box plot. The central lines of each box plot indicate the median values, and the vertical widths of the boxes the 0.25 and 0.75 quantiles of the distributions. In Fig. 9b, the residuals are shown in the same manner. Subtraction of the modelled age- and weather-related variation resulted in a substantial reduction of the variance. Some systematic deviations may however be observed in the residual plot, such as a sequence of positive residuals (under-estimation) at ages 9–12 coinciding with a period of four warmer than average years on both sites, and negative residuals (over-estimation) at ages 5 and 7 coinciding with two cold years.
Discussion
Influences of age and weather on wood formation have been investigated for very young Norway spruce trees. The results have been expressed by numbers and cross-sectional extensions of tracheids, the resulting radial growth, and the biomass allocated to the tracheids. Models have been developed for the changes of these traits with age and differences in temperature and precipitation between and within vegetation seasons. The models estimate averages of rings and their EW, TW and LW parts. In the following, the methods used and interpretations of the results are motivated and discussed.
Transitionwood
Within-ring variations are often described with proportions and properties of two compartments: EW and LW. The concept of a third intermediate compartment of TW using the “20–80” density definition was introduced to allow better judgements of the potential of wood raw materials for different industrial uses. Normally, the rather stable parts of pronounced EW and LW represent the wood with the minimum and maximum property levels in raw materials, or vice versa. The wood and tracheid properties of these parts may be particularly beneficial or detrimental depending on the product, in cases even in small amounts. Therefore, there was a need to know their levels for properties critical to products, as well as their percentages. However, such information on the minimum and maximum levels could not be obtained from the conventionally used averages of two compartments only. Then, the considerable part of wood of the transition between the pronounced EW and LW is split and defined as parts of EW and LW, respectively, in proportions depending on the character of the transition, resulting in averages which are more moderate than the those for pronounced EW and LW of interest. This was solved with the introduction of the TW concept as a third compartment, initially for industrially related research, but already then, the usefulness of sharp information on pronounced EW and LW in studies of wood formation and genetics was clear. The definition has since then been regularly applied for refinement of SilviScan data in numerous types of projects. Most examples are found for industrial studies of wood effects on product quality, such as in Downes et al. (2002), McLean et al. (2010) and Lundqvist et al. (2008, 2011). It was for instance concluded that density of earlywood is a strong determinant of mechanical strength of Sitka spruce. Compartment data have also been exploited in studies of climate effects (Kostiainen et al. 2009). Recent examples within tree improvement are Donnelly et al. (2017) and Hayatgheibi el al. (2017). There is also another definition of a third transitional compartment used preferably by quantitative wood anatomists and in the xylogenesis research (e.g. Park and Spiecker 2005; Cuny and Rathgeber 2016) who relate the definition of TW to Mork’s definition of cell dimension and cell wall thickness. Application of Mork’s definition to our data showed that the larger part of what we classified as TW would become part of the EW, moderating its value.
The TW represents the wood with relationships between cell expansion and biomass allocation, expressed as wood density, in a span between those of EW and LW. This relationship is largely controlled by environmental factors, including weather. This is not to say that the amount of TW formed, and its character, cannot be under genetic influence, nor that it is without biological or technical importance. It is shown to influence vulnerability to drought (Dalla-Salda et al. 2014) and mechanical properties (Donnelly et al. 2017), in which also differences among clones of Sitka spruce grown on the same locations were shown.
Short time series, many trees
The material used in this study covers a short chrono-sequence compared to other studies of climate-growth relationships, but on the other hand with its data comprising of close to 6000 trees, it is a unique data set covering a substantial genetic pool. Typical methods used such as dose–response functions, transfer functions or moving response functions (Briffa and Cook 1990; Biondi 1997; Miina 2000; Oberhuber et al. 2008) require longer chrono-sequences and were thus not applicable. The modelling approach to be applied had to be adapted to this circumstance. A generalised additive mixed model (GAMM) approach with restricted cubic regression splines was chosen and proved to be advantageous compared to the traditional stepwise regression modelling with ordinary least squares fits. The latter typically works in a two-step approach, implying first a tree individual detrending for age-related effects and then a modelling on the residuals or a growth index in a second step (Cook et al. 1990). The GAMM approach in contrast enabled us to amalgamate these steps in one model and to ensure that age-related and weather-related effects were tested in the same model simultaneously. Similar approaches based on generalised additive models have been successfully applied, for example, by Cuny et al. (2013, 2016) in studies of wood formation. The clustered data structure inherent to the analysis of successive tree rings and trees belonging to families required use of mixed models (Pinheiro and Bates 2000).
When we optimised the structure of the models, we found as expected that using splines with larger flexibility, such as k values of 5 rather than 3, provided somewhat higher R2 values, and residual plots indicated very high conformity. However, the resulting splines showed unrealistic features, indicating that these models had too high degrees of freedom. Therefore, a conservative approach was chosen. This need for restriction of the flexibility of the spline functions may be a result of the limited number of “weather events” caused by the short chrono-sequence.
It may be possible to reach even better models and a deeper understanding of differences in properties between fast- and slow-growing trees in the future by developing a more sophisticated modelling approach based on the indicated dual control mechanisms of apical and vascular cambial control. Their interaction is described by Iqbal (1990) and Larson (1994). Our results suggest that initially the age of the cambium governs the expansion of the cells, while the time when this expansion turns into a moderate phase is more related to the total age. This might be one point of departure for hypothesis building and model improvement.
Model selection and model fit
An important decision in modelling of data with more than one variable of interest is the question of whether to use the best model for each dependent variable or rather opt for a generic approach and select the independent variables in order to enable a comparison of the influence of independent variables across dependent variables. In this study, we chose the second option since not the predictive capacity but rather the explanatory value of the model was in the focus. The best way of model selection still is an open debate. A constructive criticism of the best model approach can be found in Burnham and Anderson (1998) and Zuur et al. (2011).
Another specific issue of spline modelling is to find the best adjustment of the spline smoothing terms. In this study, rather rigid splines were chosen to reflect the central tendency and to avoid overly flexible splines, which might also greedily take up explanation value from other variables. We followed the suggestion of Beck and Jackman (1998) that describe significant disadvantages by an automated determination of the degrees of freedom of smoothing terms and thus strongly argue for a hypothesis driven approach. Thus, biologic interpretability guided our way in an iterative approach.
Juvenile wood
Our work is based on 21-year-old trees, most of them with 14 to 18 annual rings at breast height. In tree breeding studies, trees of this age are normally not considered as very juvenile, and according to Chen et al. (2014) it is possible for Norway spruce to efficiently select for wood quality traits as early as based on data from cambial age 6–7 years, with ring 15 as the reference. But that does not mean that the wood has reached properties of mature wood. The concepts of juvenile and mature wood are unfortunately without precise definition as indicated in the introduction and data for different traits stabilize at different tree ages (Lindström 2002). Different definitions are commented in Lindström (2002). Harris and Cown (1991) state, as referred to in the introduction, that for several conifer species, most damaging features for sawn timber occur in the first 3–5 annual rings, while all wood properties including density may not have stabilised until after the 25–30th ring. Similar results were obtained by Lundqvist et al. (2005a) by fitting models based on exponential functions to data of Norway spruce trees well over 100 years of age. This resulted in time constants (τ) for both fibre length and wood density of 25–30 years. Such time constants could be used as a reasonable definition of transition ages from juvenility to maturity. In related research, rings 1–30 were defined as juvenile, and rings 1–15 as pronounced juvenile when addressing Norway spruce. For microfibril angle of Norway spruce, maturity is often reached at cambial age around 10 or somewhat higher, and later for wood stiffness (Lindström et al. 1998). However, also effects of site fertility may influence the maturation of wood with regards to microfibril angle (Lundgren 2004b).
Longitudinal growth and the influence of cambial age versus tree age
The study showed significant differences between the use of cambial age and tree age as variables for expression of age, indicating different underlying control of the developments of the traits. Typically, diameter growth and anatomical wood properties are investigated from samples at breast height (1.3 m) and traits are related to annual ring number, that is cambial age at breast height. Examples for Norway spruce addressing trait variation and modelling are Lindström (1998), Wilhelmsson et al. (2002), Lundqvist et al. (2002, 2005a). Examples addressing tree improvement can be found in Hannrup el al. (2004), Gerendiain et al. (2008), Chen et al. (2014, 2016). The results obtained in this study elucidate that the application of cambial age as a descriptor in very young trees might be problematic as trees reach breast height at different ages, resulting in different numbers of rings from pith to bark among trees. This in turn causes wood of same cambial age being formed in different years, under influence of different weather conditions. Also, the appearance of the average developments of traits over cambial age may be distorted at the highest cambial ages where the fast-growing trees are over-represented, as illustrated in Fig. 7, with the effect that the annual averages for these highest cambial ages may deflect from the typical development of averages at these ages and in the years to come. These problems are reduced at increasing age when the age-related changes become less pronounced.
A practical way of dealing with the lack of matching between cambial age and year of wood formation is to number the rings from the bark and inwards and calculate averages, thereby grouping together rings with wood formed in the same years. Effects of year-to-year weather variations can then be reduced by averaging across several rings. This approach has shown efficient despite differences in cambial age among trees, at least for trees of ages around 20 years according to Chen et al. (2014). It can, however, be problematic for very young trees for certain traits, as the procedure instead brings cambial age out of phase.
Models and interpretation
Overall development of traits with age and weather factors
All spline functions expressing the average development with age across all the trees show initially close to linear patterns. The rates of change of the different spline functions start to decrease at a total tree age of about 10 years. The radial number of tracheids formed per year decreases, in the rings, and in their EW, TW and LW. In parallel, the widths of these tracheids increase, both radially and tangentially, as well as their wall thickness and coarseness. These patterns have been previously described for Norway spruce (Lundqvist et al. 2005a, 2011) and other tree species (Lundqvist et al. 2005a, b, 2017). It is also important to consider the relative variation of each trait, i.e. to take into account also the baseline value the change relates to. The largest relative variation is observed for the number of cells in radial direction and, as a consequence, ring width is the trait with the second largest relative change.
Regarding weather effects, Mäkinen et al. (2003) showed with microscopic analyses of weekly drawn micro cores from Norway spruce trees in Southern Finland that tracheid formation started in mid-June and that only very few were formed after end of July, while the increase in stem radius observed in April and May was rather related to hydraulics and swelling. They also found strong correlation between daily temperature and tracheid formation. This relates well to our findings that the strongest weather effects on tracheid formation were caused by precipitation between on average 13/6 and 25/7 and temperature sum, especially when considering that the trees studied in Finland grew at somewhat higher latitudes.
In our study, fewer tracheids were formed with increasing age, but they were on average broader both radially and tangentially, thus with larger perimeter. They also had on average thicker cell walls and a higher coarseness. In summary: Less tracheids, individually larger and with more biomass. Superimposed on this were positive correlations of tracheid width and coarseness with growth rate (Fig. 5), but these effects are not included in the models presented here. Analogous effects were observed in relation to GDD, temperature sum across the vegetation season: at high GDDs on average more tracheids were formed, each one with lower radial width, wall thickness and coarseness, however resulting in larger ring width. This conforms with the findings of Miina (2000) on longer time series, who showed a positive impact of current years temperature on EW, LW and ring width development. Precipitation effects are not as easily summarised, but according to the model results, factors related to broad growth ring width were favoured by higher than average precipitation during the second quarter of the vegetation season.
Cambial age or tree age control of traits
Analogous models were developed with age represented by total tree age and cambial age, respectively. The results indicate that the number of radial cell divisions is under stronger control of total tree age than cambial age. The contrary effect was observed for radial and tangential widths of the fibres. As the width of the annual ring is a product of the radial number and the radial widths of its tracheids, and the relative variation in tracheid numbers is much larger than that of widths, the stronger control of the total tree age transferred to ring width. Also coarseness was under stronger cambial age control if judged from the R2 values of the models. For wall thickness, it was less obvious what type of age provides the best description. This dual control from total tree age and cambial age on intensity of cell division and expansion indicates influences from both apical meristem and maturity of the vascular cambium, which is discussed in Sirviö and Kärenlampi (2001). Relationships between growth and properties on the one side and various aspects of age have previously also been investigated and presented in Lindström (1998).
Influences on properties of rings and their parts
For an overview of the changes with age, a comparison of properties and growth at age 5 (in the early juvenile phase) and age 15 (later during the transition towards mature wood) is very revealing. During the very first juvenile years, the trees added huge numbers of tracheids in radial direction: on average approximately factor 3 more at age 5 years (for the vigorous trees which had reached breast height at that age) than at age 15 years (all trees). The tracheids formed at age 5 were slimmer in radial and tangential directions compared to those formed at age 15 (factor 0.8), had thinner walls (factor 0.75) and lower coarseness (factor 0.65). The combination of many more but somewhat slimmer tracheids in radial direction resulted in much broader annual rings at age 5 than at age 15 (reflected by the product of the factors of change in radial tracheid number and width).
During these early years, the radius of the stem is small, and thus also the numbers of tracheids to add around the perimeter for each annual increment. Further, the load by the crown is still comparatively low and therefore the need for mechanical strength of the wood is lower than for the larger tree. From this perspective, the pattern seems rational: First the tree develops many light elements to efficiently build radius and conductive area, while reducing risk of embolism which would result from large lumina. Then, the pattern shifts towards stronger elements with thicker cell walls along the periphery of the stem to support the growing tree mechanically, and wider lumina for more efficient water conductance.
The temperature sum effects showed some resemblance with this pattern: higher GDD resulted in formation of more tracheids radially with smaller radial widths, with the consequence of broader annual increments, lower coarseness and wall thickness. High precipitation sum across June and July increased both the number and radial width of the tracheids, consequently also radial growth.
On the compartment level, the patters of influence were generally similar to those on the ring level, but not always of the same magnitude. However, the radial width of the EW tracheids showed limited influence from the year’s weather and was probably largely predetermined from stored resources. Additionally, antagonistic responses were observed for EW and TW, which was expected. Tracheids which would develop wide tracheids with thin walls and thus wide lumina under certain weather conditions across the vegetation seasons, typical for EW, may become radially slimmer under other conditions, or still stay wide but with thicker walls, and then no longer show that typical EW character but become part of the TW.
Allocation of biomass and wall thickening
Wood formation is commonly divided into cell division, expansion and wall thickening as indicated in the Introduction. In this work, we added coarseness, i.e. biomass allocated per length unit of the tracheids as an alternative to wall thickness for description of this third stage of wood formation. The wall thickness is obviously influenced by the biomass allocated to the tracheid, as well as by its perimeter (its radial and tangential widths). This makes wall thickness a rather complex trait, subjected to many influences. Most previous studies have emphasised on wall thickness (Mäkinen et al. 2002; Lundgren 2004a), even though coarseness has also been addressed (Gerendiain et al. 2008; Kostiainen et al. 2009). The reason for this preference is probably that data have been acquired with commonly available light microscopes. When comparing results on coarseness from different studies, it is important to consider the state of the tracheids when the analysis is performed. In this study, it was done on tracheids in solid wood. Other studies analyse coarseness after their chemical liberation from the wood matrix, which is not comparable since a substantial part of their mass then has been lost in the chemical process. Our ambition was to elucidate whether coarseness as a less complex trait might better express the fundamentals of biomass allocation and can be expected to be tighter related to genetic data. The higher R2 values obtained when modelling coarseness compared to wall thickness, and the more homogeneous pictures these models provide for ring, EW, TW and LW averages, indicate that coarseness is an interesting alternative in genetic studies.
Application of the models
Evaluations for tree improvement and within genetic research often start with allocation of the variability in traits to various sources (e.g. Ivković et al. 2013; Chen et al. 2014, 2016). The parts of the variability which are expected to be related to measurable factors but not linked to genetics are modelled with a fixed part. The resulting residuals are correlated with other known factors, including the genetic backgrounds of the trees. One reason to cover genetics in the random model part is that it cannot be assumed that the full population of interest was sampled. Another reason is to avoid pseudo-replication in clustered data (Bolker et al. 2009). Genotypes are ranked according to traits and judged as more or less adapted to environmental conditions at different sites. In this context, the novel GAMM models presented in this study, formulating the average influences of age and weather across all trees, may support such evaluations by estimating the variations in growth and properties related to known differences in age and weather between sites and years. This has a potential to improve the information value of the residuals for investigation of genotype and environment interaction. Average influence shall in this case more be understood more precisely as the influence of a weather event on an individual tree based on the assumption that all trees react in the predictive way.
The models may bring several opportunities, such as:
-
Harmonisation of data originating from experimental sites with systematic differences in temperature and precipitation or in age.
-
Refinement of data by removal of estimated effects of year-to-year weather variations.
-
Establishment of traits expressing suitability of trees on sites with different weather, and with different responses to foreseen climate change, such as seasonal drought.
-
Taking today’s studies of genotype x environment interaction a step forward by splitting this traditional site effect into a weather-related part and a more fundamentally site-related part, allowing investigation of more specific site factors in studies based on data from several field experiments.
-
Another ambition is to use the models to estimate effects of different climate change scenarios on genotypes of average weather responses as well as on selected families with different response profiles.
A major aim of the presented work was to create such opportunities for use in traditional genetic analyses as well as for Quantitative Trait Locus (QRL) analysis and other methods. The scope was not to develop the best fitting models to describe the variations in the data set, but to elucidate relationships and influences, and formulate them in models for research. The estimations can be further improved by inclusion of further independent variables and by using more of the available information about sites, families and trees in the random parts of mixed models. This could, however, reduce the usefulness of the models for the main aim application, but is addressed in ongoing studies with other objectives.
Conclusions
-
During the investigated age span, growth and properties of the trees were in a very dynamic phase. The total variability in the data was large and originated from a multitude of intrinsic and extrinsic sources. This study focused on the influences of age-related and weather-related factors. Additionally, large differences between trees in longitudinal stem growth contributed to the observed variability with the consequence that rings with same cambial age represented wood formed during different years with different weather.
-
The radial numbers of cells formed every year and the annual ring widths were more related to the total tree age than to cambial age, while the contrary was valid for tracheid widths. This duality may indicate different genetic controls.
-
The best models were obtained for number of radial cell divisions per year and ring width, for which about half of the total variation was accounted for, using age (tree age or cambial age), temperature sum across ring the growth season and precipitation sums for four equal parts of the growth season as independent variables. Age contributed the most to the variation of all traits. Temperature and precipitation gave smaller but significant contributions.
-
The results may indicate that the number of tracheids formed annually, radial width of tracheids in EW, coarseness and early longitudinal growth rate, all closely related to processes of wood formation, are traits under less complex genetic control, and particularly interesting targets for search of candidate genes.
-
Expected applications of the models are refinement of data for tree improvement, establishment of new traits expressing weather responses and simulation of weather scenarios.
References
Auty D, Achim A, Macdonald E, Cameron AD, Gardiner BA (2014) Models for predicting wood density variation in Scots pine. Forestry 87(3):449–458
Beck N, Jackman S (1998) Beyond linearity by default: generalized additive models. Am J Polit Sci 42:596–627
Bennich T, Belyazid S (2017) The route to sustainability—prospects and challenges of the bio-based economy. Sustainability 9:887
Bergh J, Linder S, Bergström J (2005) Potential production of Norway spruce in Sweden. For Ecol Manag 204:1–10
Biondi F (1997) Evolutionary and moving response functions in dendroclimatology. Dendrochronologia 15:139–150
Bolker BM, Brooks ME, Clark CJ, White J-SS (2009) Generalized linear mixed models: a practical guide for ecology and evolution. Trends Ecol Evol 24:127–135
Briffa KR, Cook ER (1990) Methods of response function analysis. In: Cook ER, Kairiukstis L (eds) Methods of dendrochronology. Kluwer Academic Publishers, Dordrecht, pp 165–178
Burnham KP, Anderson DR (1998) Model selection and multimodel inference: a practical information-theoretic approach. Springer, New York
Chen Z-Q, García-Gil MR, Karlsson B, Lundqvist S-O, Olsson L, Wu HX (2014) Inheritance of growth and solid wood quality traits in a large Norway spruce population tested at two locations in southern Sweden. Tree Genet Genomes 10(5):1291–1303. https://doi.org/10.1007/s11295-014-0761-x
Chen Z-Q, Karlsson B, Mörling T, Olsson L, Mellerowicz MJ, Wu HX, Lundqvist S-O, García-Gil MR (2016) Genetic analysis of fiber dimensions and their correlation with stem diameter and solid-wood properties in Norway spruce. Tree Genet Genomes 12:123. https://doi.org/10.1007/s11295-016-1065-0
Cook ER, Briffa KR, Shiyatov SG, Mazepa VS (1990) Tree-ring standardization and growth-trend estimation. In: Cook ER, Kairiukstis LA (eds) Methods of dendrochronology. Kluwer, Dordrecht, pp 104–123
Cuny HE, Rathgeber CBK (2016) Xylogenesis: coniferous trees of temperate forests are listening to the climate tale during the growing season but only remember the last words! Plant Physiol 171:306–317
Cuny HE, Rathgeber CBK, Senga Kiesse T, Hartmann FP, Barbeito I, Fournier M (2013) Generalized additive models reveal the intrinsic complexity of wood formation dynamics. J Exp Bot 64:1983–1994
Dalla-Salda G, Fernández ME, Sergent AS, Rozenberg P, Badel E, Martinez Meier A (2014) Dynamics of cavitation in a Douglas-fir tree-ring: transition-wood, the lord of the ring? J Plant Hydraul. https://doi.org/10.20870/jph.2014.e005
de Martonne E (1926) Aréisme et indice d’aridité. C R Acad Sci 182:1395–1398
Deckmyn G, Evans SP, Randle TJ (2006) Refined pipe theory for mechanistic modelling of wood development. Tree Physiol 26:703–717
Deleuze C, Houllier F (1998) A simple process-based xylem growth model for describing wood microdensitometric profiles. J Theor Biol 193:99–113
Donnelly L, Lundqvist S-O, O’Reilly C (2017) Inter- and intra-annual wood property variation in juvenile wood between six Sitka spruce clones. Silva Fenn 51(4):14. https://doi.org/10.14214/sf.7728 (article id 7728)
Downes GM, Nyakuengama JG, Evans R, Northway R, Blakemore P, Dickson RL, Lausberg M (2002) Relationship between wood density, microfibril angle and stiffness in thinned and fertilized Pinus radiata. IAWA J 23:253–266
Drew DM, Downes GM, Battaglia M (2010) CAMBIUM, a process based model of daily xylem development in Eucalyptus. J Theor Biol 264:395–406
Evans R (1994) Rapid measurement of the transverse dimensions of tracheids in radial wood sections from Pinus Radiata. Holzforschung 48:168–172
Evans R (2006) Wood stiffness by X-ray diffractometry. In: Stokke DD, Groom HL (eds) Characterization of the cellulosic cell wall. Wiley, Hoboken, pp 138–146
Fonti P, von Arx G, García-González I, Eilmann B, Sass-Klaassen U, Gärtner H, Eckstein D (2010) Studying global change through investigation of the plastic responses of xylem anatomy in tree rings. New Phytol 185(1):42–53
Franceschini T, Lundqvist S-O, Bontemps J-D, Grahn T, Olsson L, Evans R, Leban J-M (2012) Empirical models for radial and tangential fibre width in tree rings of Norway spruce in north-western Europe. Holzforschung 66:219–230
Franceschini T, Longuetaud F, Bontemps J-D, Bouriaud O, Caritey B-D, Leban J-M (2013) Effect of ring width, cambial age, and climatic variables on the within-ring wood density profile of Norway spruce Picea abies (L.) Karst. Trees 27(4):913–925. https://doi.org/10.1007/s00468-013-0844-6
Fries A, Ulvcrona T, Wu HX (2014) Kroon J (2014) Stem damage of lodgepole pine clonal cuttings in relation to wood and fiber traits, acoustic velocity, and spiral grain. Scand J For Res 29(8):764–776
Fritts HC, Shashkin A, Downes GM (1999) TreeRing 3: a simulation model of conifer ring growth and cell structure. In: Wimmer R, Vetter RE (eds) Tree ring analysis: biological, methodological and environmental aspects. CAB International, Oxford, pp 3–32
Gerendiain AZ, Peltola H, Pulkkinen P, Jaatinen R, Pappinen A (2008) Differences in fibre properties in cloned Norway spruce (Picea abies). Can J For Res 38:1071–1082
Gjerdrum P, Bernabei M (2009) Three-dimensional spiral grain pattern in five large Norway spruce stems. Silva Fenn 43(3):457–464
Gruber A, Baumgartner D, Zimmermann J (2009) Temporal dynamic of wood formation in Pinus cembra along the alpine treeline ecotone and the effect of climate variables. Trees 23(3):623–635
Hannrup B, Cahalan C, Chantre G, Grabner M, Karlsson B, Le Bayon I, Jones GL, Muller U, Pereira H, Rodrigues JC, Rosner S, Rozenberg P, Wilhelmsson L, Wimmer R (2004) Genetic parameters of growth and wood quality traits in Picea abies. Scand J For Res 19:14–29. https://doi.org/10.1080/02827580310019536
Harris JM, Cown DJ (1991) Basic wood properties. In: Kininmoth JM, Whithouse LJ (eds) Properties and uses of New Zealand radiata pine, chapter 6. Ministry of Forestry, Wellington, pp 1–28
Havimo M, Rikala J, Sirviö J, Sipi M (2007) Distributions of tracheid cross-sectional dimensions in different parts of Norway spruce stems. Silva Fenn 42(1):89–99
Hayatgheibi H, Fries A, Kroon J (2017) Wu HX (2017) Genetic analysis of lodgepole pine (Pinus contorta) solid-wood quality traits. Can J For Res 47:1303–1313. https://doi.org/10.1139/cjfr-2017-0152
Hein S, Mäkinen H, Yue C, Kohnle U (2007) Modelling branch characteristics of Norway spruce from wide spacings in Germany. For Ecol Manag 242(2–3):155–164
Hölttä T, Mäkinen H, Nöjd P, Mäkelä A, Nikinmaa E (2010) A physiological model of softwood cambial growth. Tree Physiol 30:1235–1252
Hong Z, Fries A, Wu HX (2014) High negative genetic correlations between growth traits and wood properties suggest incorporating multiple traits selection including economic weights for the future Scots pine breeding programs. Ann For Sci 71(4):463–472. https://doi.org/10.1007/s13595-014-0359-3
Iqbal M (ed) (1990) The vascular cambium. Research Studies Press, Taunton
Ivković M, Gapare W, Wu H, Espinoza S, Rozenberg P (2013) Influence of cambial age and climate on ring width and wood density in Pinus radiata families. Ann For Sci 70(5):525–534
Kallioski T, Mäkinen H, Jyske T, Nöjd P, Linder S (2013) Effects of nutrient optimization on intra-annual wood formation in Norway spruce. Tree Physiol 33:1145–1155
Korpela M, Mäkinen H, Sulkava M, Nöjd P, Hollmen K (2008) Smoothed prediction of the onset of tree stem radius increase based on temperature patterns. In: Boulicaut J-F, Berthold MR, Horvàth T (eds) 11 international conference on discovery science, Budapest. Springer, Heidelberg, pp 100–111
Kostiainen K, Kaakinen S, Saranpää P, Sigurdsson BD, Lundqvist S-O, Linder S, Vapaavuori E (2009) Stem wood properties of mature Norway spruce after 3 years of continuous exposure to elevated [CO2] and temperature. Glob Change Biol 15:368–379
Kostiainen K, Saranpää P, Lundqvist S-O, Kubiske ME, Vapaavuori E (2014) Wood properties of Populus and Betula in long-term exposure to elevated CO2 and O3. Plant Cell Environ 37(6):1452–1463. https://doi.org/10.1111/pce.12261
Larson PR (1994) In: Timell, T. (Ed.), The Vascular Cambium: Development and Structure. Springer Series in Wood Science. Springer, Berlin, pp 725
Lenz P, Cloutier A, MacKay J, Beaulieu J (2010) Genetic control of wood properties in Picea glauca: an analysis of trends with cambial age. Can J For Res 40(4):703–715
Lewark S (1981) Untersuchungen von Holzmerkmalen junger Fichten (Picea abies [L.] Karst.). PhD Thesis Georg-August-Universität Göttingen. 193 p. [in German]
Lindström H (2002) Intra-tree models of juvenile wood in Norway spruce as an input to simulation software. Silva Fennica 36(2):521–534
Lindström H, Evans JW, Verrill SP (1998) Influence of cambial age and growth conditions on microfibril angle in young Norway spruce. Holzforschung 52:573–581
Lundgren C (2004a) Cell wall thickness and tangential and radial cell diameter of fertilized and irrigated Norway spruce. Silva Fenn 38(1):95–106
Lundgren C (2004b) Microfibril angle and density patterns of fertilized and irrigated Norway spruce. Silva Fenn 38(1):107–117
Lundqvist S-O, Ekenstedt F, Grahn T, Wilhelmsson L (2002) A system of models for fiber properties in Norway spruce and Scots pine and tools for simulation. In: Proceedings of the 4th workshop on “Connection between forest resources and wood quality: Modelling approaches and simulation software”, IUFRO Working Party 5.01.04, Harrison Hot Springs, Canada, pp 8–15
Lundqvist S-O, Grahn T, Hedenberg Ö (2005a) Models for fibre dimensions in different softwood species. Simulation and comparison of within and between tree variations for Norway and Sitka spruce, Scots and Loblolly pine. In: 5th workshop on “Wood quality modelling”, IUFRO Working Party 5.01.04, Auckland, New Zealand, Nov 22–27 2005. STFI-Packforsk Report ART 05/54
Lundqvist S-O, Ekenstedt F, Hedenberg Ö, Twaddle A (2005b) Wood and fibre properties of Loblolly pine in southeast USA. Variations and prediction models. In: 5th workshop on “Wood quality modelling”, IUFRO Working Party 5.01.04, Auckland, New Zealand, Nov 22–27 2005. STFI-Packforsk Report ART 05/53
Lundqvist S-O, Grahn T, Olsson L, Thomson L (2008) Modelling and simulation of properties of forest resources and along the paper value chain. In: Proceedings of 6th workshop “Connection between forest resources and wood quality: modelling approaches and simulation software”, IUFRO Working Party 5.01.04, Koli National Park, Joensuu, Finland, pp 31–35
Lundqvist S-O, Grahn T, Olsson L, Wilhelmsson L, Arlinger J, Valinger E, Brüchert F, Müller M, Sauter UH, Gardiner B, Pizzirani S, Fonweban J (2011) Mapping of properties in forest resources and models used—results from EFORWOOD case studies in Västerbotten (North Sweden), Baden-Württemberg (Germany) and South Scotland. EFI technical report 73, 2011
Lundqvist S-O, Grahn T, Olsson L, Seifert T (2017) Comparison of wood, fibre and vessel properties of drought-tolerant eucalypts in South Africa. South For J For Sci 79:215–225. https://doi.org/10.2989/20702620.2016.1254910
Mäkelä A, Grace JC, Deckmyn G, Kantola A, Campioli M (2010) Simulating wood quality in forest management models. For Syst 19:48–68
Mäkinen H, Saranpää P, Linder S (2002) Wood-density variation of Norway spruce in relation to nutrient optimization and fibre dimensions. Can J For Res 32(2):185–194
Mäkinen H, Nöjd P, Saranpåå P (2003) Seasonal changes in stem radius and production of new tracheids in Norway spruce. Tree Physiol 23:959–968
McLean JP, Evans R, Moore JR (2010) Predicting the longitudinal modulus of elasticity of Sitka spruce from cellulose orientation and abundance. Holzforschung 64:495–500
McMaster GS, Wilhelm WW (1997) Growing degree-days: one equation, two interpretations. Agric For Meteorol 87:291–300
Miina J (2000) Dependence of tree-ring, earlywood and latewood indices of Scots pine and Norway spruce on climatic factors in eastern Finland. Ecol Model 132(3):259–273
Moberg L (1999) Models of knot properties for Norway spruce and Scots pine. Doctoral thesis, Silvestria 121, Swedish University of Agricultural Sciences. Faculty of Forestry, Uppsala, Sweden, p 24. ISBN 91-576-5855-2
Mork E (1928) Die Qualität des Fichtenholzes unter besonderer Rücksichtnahme auf Schleif- und Papierholz. Pap Fabr 23:741–747
Oberhuber W, Kofler W, Pfeifer K, Seeber A, Gruber A, Wieser G (2008) Long-term changes in tree-ring—climate relationships at Mt. Patscherkofel (Tyrol, Austria) since the mid 1980s. Trees 22(1):31–40
Olesen PO (1977) The variation of the basic density level and tracheid width within the juvenile and mature wood of Norway spruce. Forest tree improvement, Arboretet, Hørsholm, vol 12, p 21. ISBN 87-500-1780-2
Olsson L, Hedenberg Ö, Lundqvist S-O (1998) Measurements of growth ring patterns—comparisons of methods. STFI-Rapport TF111. Stockholm (in Swedish with abstract and captions in English)
Park YI, Spiecker H (2005) Variations in the tree-ring structure of Norway spruce (Picea abies) under contrasting climates. Dendrochronologia 23:93–104
Piispanen RM, Heinonen J, Valkonen S, Mäkinen H, Lundqvist S-O, Saranpää P (2013) Wood density of Norway spruce in uneven-aged stands. Can J For Res 44(2):136–144
Pinheiro JC, Bates DM (2000) Mixed-effects models in S and S-PLUS. Springer, New York
Plomion C, Leprovost G, Stokes A (2001) Wood formation in trees. Plant Physiol 127:1513–1523
Pretzsch H, Grote R, Reineking B, Rötzer T, Seifert S (2007) Models for forest ecosystem management: a European perspective. Ann Bot 101(8):1065–1087
Prislan P, Gričar J, de Luis M, Smith KT, Čufar K (2013) Phenological variation in xylem and phloem formation in Fagus sylvatica from two contrasting sites. Agric For Meteorol 180(15):142–151
Rathgeber CBK, Cuny HE, Fonti P (2016) Biological basis of tree-ring formation: a crash course. Front Plant Sci 7:734
Rötzer T, Grote R, Pretzsch H (2004) The timing of bud burst and its effect on tree growth. Int J Biometeorol 48(3):109–118
R Core Team (2017) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. ISBN 3-900051-07-0, http://www.R-project.org/
Schmitt U, Jalkanen R, Eckstein D (2004) Cambium dynamics of Pinus sylvestris and Betula spp. in the northern boreal forest in Finland. Silva Fenn 38(2):167–178
Seifert T (2003) Integration of wood quality, bucking and sorting. PhD thesis, Technische Universität München, p 314 (in German with extended English summary)
Seifert T, Pretzsch H (2004) Modeling growth and quality of Norway spruce (Picea abies Karst.) with the growth simulator SILVA. In: Proceedings of the 4th workshop “Connection between forest resources and wood quality: modelling approaches and simulation software”, IUFRO Working Party S5.01.04, Harrison Hotsprings, Canada, pp 562–574
Seifert T, Breibeck J, Seifert S, Biber P (2010) Resin pocket occurrence in Norway spruce depending on tree and climate variables. For Ecol Manag 260:302–312
Sirviö J, Kärenlampi P (2001) The effect of maturity and growth rate on the properties of spruce wood tracheids. Wood Sci Technol 35:541–554
Vaganov EA, Hughes MK, Shashkin AV (2006) Growth dynamics of conifer tree rings. Springer, New York, p 354
Westin J, Haapanen M (2013) Norway spruce—Picea abies (L.) Karst. In: Mullin TJ, Lee SJ (eds) Best practice for tree breeding in Europe. Skogforsk, Uppsala, pp 29–47. https://www.skogforsk.se/english/news/2014/best-practice-for-tree-breeding/
Wilhelmsson L, Arlinger J, Spångberg K, Lundqvist S-O, Grahn T, Hedenberg Ö, Olsson L (2002) Models for predicting wood properties in stems of Picea abies and Pinus sylvestris in Sweden. Scand J For Res 17:330–350. https://doi.org/10.1080/02827580260138080
Wood S (2017) Generalized additive models: an introduction with R, 2nd edn. Chapman-Hall, London. ISBN 9781498728331
Zuur A, Ieno EN, Smith GM (2011) Analysing ecological data. Springer Science & Business Media, Berlin
Acknowledgements
The work was performed within the Swedish Strategic Research Program Bio4Energy. Johan Malm and coworkers at Skogforsk are acknowledged for their contributions on sampling, Åke Hansson and Thomas Trost at Innventia (now part of RISE Bioeconomy) for skilful sample preparation and characterisation of the thousands of samples, and Erich Seifert for help with the illustrations. Thomas and Stefan Seifert also thank the EU RISE project “Care4C” for providing an excellent platform for scientific discussion.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Communicated by Martina Meincken.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lundqvist, SO., Seifert, S., Grahn, T. et al. Age and weather effects on between and within ring variations of number, width and coarseness of tracheids and radial growth of young Norway spruce. Eur J Forest Res 137, 719–743 (2018). https://doi.org/10.1007/s10342-018-1136-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10342-018-1136-x