Linear and Nonlinear Formulation of Phase Field Model with Generalized Polynomial Degradation Functions for Brittle Fractures

Abstract

The classical phase field model has wide applications for brittle materials, but nonlinearity and inelasticity are found in its stress–strain curve. The degradation function in the classical phase field model makes it a linear formulation of phase field and computationally attractive, but stiffness reduction happens even at low strain. In this paper, generalized polynomial degradation functions are investigated to solve this problem. The first derivative of degradation function at zero phase is added as an extra constraint, which renders higher-order polynomial degradation function and nonlinear formulation of phase field. Compared with other degradation functions (like algebraic fraction function, exponential function, and trigonometric function), this polynomial degradation function enables phase in [0, 1] (should still avoid the first derivative of degradation function at zero phase to be 0), so there is no $\Gamma$ convergence problem. The good and meaningful finding is that, under the same fracture strength, the proposed phase field model has a larger length scale, which means larger element size and better computational efficiency. This proposed phase field model is implemented in LS-DYNA user-defined element and user-defined material and solved by the Newton–Raphson method. A tensile test shows that the first derivative of degradation function at zero phase does impact stress–strain curve. Mode I, mode II, and mixed-mode examples show the feasibility of the proposed phase field model in simulating brittle fracture.

1 Introduction

Over the last several decades, phase field model has been used widely in static and dynamic simulations with brittle materials [1,2,3,4]. The major advantage of phase field model is that arbitrary nucleation, propagation, branching and merging can be modeled in a single standard-alone framework, with no need for any ad hoc criterion or extrinsic tracking algorithm [5]. Francfort and Marigo [6] used minimization of total energy in phase field model, where the potential energy includes strain energy and fracture energy. To provide a feasible numerical method for difficult free-discontinuity problem, Bourdin et al. [7] regularized the fracture energy as an elliptic functional of the displacement field and an auxiliary field called phase field. This regularized energy functional was characterized by a length scale which controls the width of crack band [8]. The main idea is the transformation from line integral and surface integral to volume integral for fracture surface calculation, which then could be coupled with other energies with volume integral, like kinetic energy, internal energy, and external work. By doing so, the solid domain with crack can be described by displacement field and phase field together. Refer to Wu et al. [9] for a comprehensive review of phase field modeling of fracture.

According to the variational formulation of Griffith’s theory [6], phase field model of quasi-static brittle fracture was implemented for the first time by Bourdin et al. [7]. More recently, a quasi-static phase field formulation aligned with thermodynamic arguments was proposed by Miehe et al. [2]. Phase field model has also been widely used in dynamic brittle fracture simulations [3, 10]. Liu et al. [11] investigated quasi-static and dynamic fracture and solved the model using staggered and monolithic schemes. In 2014, Miehe and Schänzel [12] extended the phase field model to plastic materials with large strain. Different methods to derive the governing equations have also been presented in papers. Based on the first and second laws of thermodynamics, Wu [13] derived the governing equations from the variation of energy dissipation. Based on the energy method—Hamilton’s principle, Borden et al. [3] obtained the governing equations from the minimization of energy (including kinetic energy and internal energy) using the Euler–Lagrange equation. Refer to [14] for more information about Hamilton’s principle.

Even though phase field model has been used widely, some aspects of it are still under investigation. The first is the split of strain energy to depict the degradation of material. A directional split method was introduced, analyzed, and compared with the two classical formulations (spectral split and volumetric-deviatoric split) in [15]. An orthogonal split to tensile and compressive strains was implemented to mimic unilateral contact conditions in [16]. A methodology to split strain energy was proposed in [17] that can be applied to a large variety of polyconvex energies. Several existing approaches were reviewed to account for the tension–compression asymmetry of materials’ fracture behavior in [18]. After the phase field problem is fully defined, the next is about how to solve it. Common ways to solve phase field model include staggered algorithm and monolithic algorithm [19, 20]. An improved staggered iteration scheme was proposed in [21] where nonlinear subproblems are solved by a one-pass procedure. Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm was proposed in [22] to solve the system of coupled governing equations in a monolithic manner. Γ convergence is still a hot topic in phase field model to make sure the fracture surface and fracture energy results are correct. Theoretical proofs about Γ convergence can be found in [23, 24]. However, in practical setting, error has been reported in numerical solutions regarding the approximated fracture surface and dissipated energy [25]. The approximation of fracture energy in phase field model was studied in [26].

Nonlinearity and inelasticity are inherent problems in the classical phase field model, and different methods have been attempted to solve them. Miehe et al. [27] set a minimum strain energy threshold to keep the stiffness constant before reaching fracture strength. This strain energy threshold was also used in [28, 29] to avoid stiffness reduction. Another way to solve this is from degradation function. Bourdin et al. [7] introduced cubic and quartic functions to obtain more brittle behavior. To consider the different behaviors of materials, Wu [13] proposed an algebraic fraction degradation function with several parameters to adjust degradation function, and made the phase field model a length-scale-insensitive model. Arriaga and Waisman [30] used cubic function with a parameter to adjust degradation function, which can give more options for the behavior of material. Yin et al. [31] tried a sinusoidal form of degradation function to investigate strain-rate-dependent fracture toughness. Even though the degradation function can be set more and more complex, it loses some good properties like phase in [0, 1]. Zhang et al. [32] used the degradation function in [13], but an extra phase constraint function is needed to let phase in [0, 1]. What’s worse, analytical homogeneous solution is not available for some special degradation functions, which makes it difficult to investigate some basic features of phase field model based on homogeneous solution.

In this paper, nonlinear formulation of phase field is investigated through generalized polynomial degradation functions to enable linear elastic behavior for brittle materials, and good properties of the proposed degradation function include phase in [0, 1] and better computational efficiency. This paper is constructed as follows. In Sect. 2, fracture surface density function, fracture energy, and governing equations of phase field model using generalized degradation function are derived according to Hamilton’s principle. In Sect. 3, different degradation functions used in publications are summarized first, and then the focus is on the comparison between linear and nonlinear formulations of phase field. Analytical solutions (homogeneous and nonhomogeneous solutions) and FEM formulation of these two kinds of models are presented and compared, and stress–strain curve obtained from a tensile test shows that the proposed phase field model handles linear elastic behavior better. In Sect. 4, mode I, mode II, and mixed-mode examples show the feasibility of the proposed phase field model in simulating brittle fracture. In Sect. 5, conclusions are made.

2 Governing Equations of Phase Field Model

Much attention has been paid to computational fracture mechanics using phase field model after the work of Miehe et al. [2], and this classical phase field model (linear formulation of phase field) is also followed in this paper. Since both linear and nonlinear phase field formulations have similar strong forms, it is convenient to show this derivation first.

2.1 Fracture Surface Density Function and Fracture Energy

Griffith’s theory states that a crack propagates when the reduction of potential energy due to crack growth is equal to or greater than the increase of surface energy due to the creation of new free surfaces. The difficulty that limits the numerical application of this theory is how to calculate fracture length or fracture area. To bypass this difficulty, the transformation from line integral and surface integral to volume integral has been utilized in the classical phase field model [2, 7]. For the one-dimensional case in [2], fracture surface $\Gamma$ is expressed as

$$ {\Gamma = \mathop \int \limits_{\Omega }^{{}} \frac{1}{2l}\alpha \left( \varphi \right) + \frac{l}{2}\left( {\varphi^{\prime}} \right)^{2} {\text{d}}V = \mathop \int \limits_{\Omega }^{{}} \frac{1}{2l}\varphi^{2} + \frac{l}{2}\left( {\varphi^{\prime}} \right)^{2} {\text{d}}V}$$

(1)

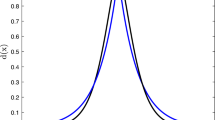
where, $l$ is length scale to adjust the crack band; ${\alpha \left(\varphi \right)=\varphi }^{2}$ is called geometric function in [9, 13]; ${\varphi }{\prime}$ is spatial derivative of phase. Note that the phase function $\varphi \left(x\right)=\text{e}^{-|x|/l}$ is defined over the entire domain $x\in [-\infty ,+\infty ]$ and $\varphi \left(x\right)\in [0,1]$. For a visualization of a situation that fracture occurs only at location $x=0$, non-smooth phase field and diffusive phase field obtained from the classical phase field model is shown in Fig. 1.

Fig. 1

a Non-smooth phase field; b diffusive phase field with length scale $l$

The integrand in Eq. (1) is known as fracture surface density function, $\gamma$. This one-dimensional case can be extended to two-dimensional and three-dimensional cases as

$$\gamma =\frac{1}{2l}\alpha \left(\varphi \right)+\frac{l}{2}{\left|\nabla \varphi \right|}^{2}$$

(2)

where, $\nabla \varphi$ is $\left(\frac{\partial \varphi }{\partial x}, \frac{ \partial \varphi }{\partial y}\right)$ or $\left(\frac{\partial \varphi }{\partial x}, \frac{ \partial \varphi }{\partial y}, \frac{ \partial \varphi }{\partial z}\right)$. See [2] for the detailed derivation of this fracture surface density function. According to Griffith’s theory, fracture energy ${\Psi }_{c}$ is therefore expressed as

$${\Psi }_{c}={G}_{c}\Gamma ={G}_{c}\int_{\Omega }\text{d}A\approx {G}_{c}\int_{\Omega }\gamma \text{d}V$$

(3)

where, ${G}_{c}$ is critical energy release rate with unit N/mm.

2.2 Derivation of the Governing Equations of Phase Field Model

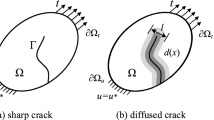
Since fracture energy is defined, governing equations of phase field model can be derived. Consider an arbitrary body $\Omega \subset {\mathbb{R}}^{dim}$ ($dim=1, 2, 3$) with external boundary $\partial \Omega \subset {\mathbb{R}}^{dim-1}$ and sharp crack set $\Gamma \subset {\mathbb{R}}^{dim-1}$. During the interested time interval $[0,T]$, displacement at position ${\varvec{x}}$ and time $t$ is denoted by ${\varvec{u}}({\varvec{x}},t)$. The external boundary is divided into time-dependent Dirichlet boundary $\partial {\Omega }_{u}$ and time-dependent Neumann boundary $\partial {\Omega }_{t}$ with outward normal vector ${\varvec{n}}$. Prescribed time-dependent displacement ${{\varvec{u}}}^{p}$ and surface force ${{\varvec{t}}}^{p}$ are applied on $\partial {\Omega }_{u}$ and $\partial {\Omega }_{t}$, respectively, i.e., ${\varvec{u}}({\varvec{x}},t)={{\varvec{u}}}^{p}({\varvec{x}},t)$ on $\partial {\Omega }_{u}$ and ${\varvec{\sigma}}\cdot {\varvec{n}}={{\varvec{t}}}^{p}({\varvec{x}},t)$ on $\partial {\Omega }_{t}$, where ${\varvec{\sigma}}$ is symmetric Cauchy stress tensor. For simplicity, $\partial {\Omega }_{u}$ and $\partial {\Omega }_{t}$ satisfy $\partial {\Omega }_{u}\cup \partial {\Omega }_{t}=\partial \Omega$ and $\partial {\Omega }_{u}\cap \partial {\Omega }_{t}=\varnothing$. The sharp crack has outward normal vector ${{\varvec{n}}}_{c}$. Body force ${\varvec{b}}$ is distributed in the entire body $\Omega$. For small deformation, the body is described by its displacement field ${\varvec{u}}({\varvec{x}},t)$ and strain field ${\varvec{\varepsilon}}\left({\varvec{x}},t\right)={\nabla }^\text{sym}{\varvec{u}}({\varvec{x}},t)$, where symmetric gradient operator ${\nabla }^\text{sym}$ maps displacement field to strain field. For phase field, time-dependent Dirichlet boundary is $\varphi \left({\varvec{x}},t\right)=1$ on $\partial {\Omega }_{\Gamma }$, where $\partial {\Omega }_{\Gamma }$ is fracture surface, and time-dependent Neumann boundary is the flux of phase through the external boundary equal to 0, i.e., $\nabla \varphi \cdot {\varvec{n}}=0$ (Fig. 2).

Fig. 2

Representation of a crack in domain $\Omega$: a displacement field; b phase field

The variational principle used for dynamic problems is called Hamilton’s principle. According to this principle, the variation of the energy functional is taken with respect to time as

$$\delta \int_{{t}_{1}}^{{t}_{2}}\left({\Psi }_{\text{kin}}-{\Psi }_{\text{int}}+{\Psi }_{\text{ext}}\right)\text{d}t=0$$

(4)

where, kinetic energy, internal energy, and external work in the time interval $[{t}_{1},{t}_{2}]$ are expressed as

$${\Psi }_{\text{kin}}\left(\dot{{\varvec{u}},}\dot{\varphi }\right)=\int_{\Omega }\frac{1}{2}\rho \dot{{\varvec{u}}}\cdot \dot{{\varvec{u}}}\text{d}V+\int_{\Omega }\frac{1}{2}\varrho \dot{\varphi }\dot{\varphi }\text{d}V$$

(5)

$${\Psi }_{\text{int}}\left({\varvec{u}},\Gamma \right)=\int_{\Omega }{\psi }_{s}\text{d}V+\int_{\Omega }{G}_{c}\gamma \text{d}V$$

(6)

$${\Psi }_{\text{ext}}\left({\varvec{u}}\right)=\int_{\partial \Omega }{\varvec{t}}\cdot {\varvec{u}}\text{d}A+\int_{\Omega }{\varvec{b}}\cdot {\varvec{u}}\text{d}V$$

(7)

respectively. Note that a generalized kinetic energy is presented here, and density $\varrho$ with unit kg/m is used to describe the kinetic energy from phase field [9]. The Euler–Lagrange equation $L$ is expressed as

$${L=\Psi }_{\text{kin}}-{\Psi }_{\text{int}}+{\Psi }_{\text{ext}}$$

(8)

and the minimization of this Euler–Lagrange equation $L$ gives the unknowns wanted, i.e.,

$$\left({\varvec{u}},\varphi \right)=\text{ArgInf}\left\{L\right\}$$

(9)

To consider the degradation of material with the increase of phase, strain energy ${\psi }_{s}^{0}$ is multiplied by a degradation function $g\left(\varphi \right)$,

$${\psi }_{s}=g\left(\varphi \right){\psi }_{s}^{0}$$

(10)

where, superscript 0 in ${\psi }_{s}^{0}$ is used to differentiate undegraded and degraded strain energy. However, it is also found that a degradation function applied on the overall strain energy cannot avoid fracture under compressive load [16]. To solve this issue, usually, the strain energy is split into two parts, and only one part is influenced by degradation function. In this paper, tensile and compressive strain energy split is used,

$${\psi }_{s}=g\left(\varphi \right){\psi }_{s}^{0+}+{\psi }_{s}^{0-}$$

(11)

Based on the definition of positive and negative parts of strain energy from the spectral decomposition of strain tensor, strain matrix at position ${\varvec{x}}$ and time $t$ is expressed as its eigen value ${\varepsilon }_{i}$ and eigen vector ${{\varvec{n}}}_{i}$,

$$ {\varepsilon \left( {{\varvec{x}},t} \right) = \nabla^{{{\text{sym}}}} u\left( {{\varvec{x}},t} \right) = \mathop \sum \limits_{i = 1}^{3} \varepsilon_{i} {\varvec{n}}_{i} \otimes {\varvec{n}}_{i} } $$

(12)

where, ⊗ is tensor product of vectors. The strain energy and its tensile and compressive parts are expressed as

$${\psi }_{s}^{0}=\frac{1}{2}{\sigma }_{ij}^{0}{\varepsilon }_{ij}=\frac{\lambda }{2}{\left({\varepsilon }_{1}+{\varepsilon }_{2}+{\varepsilon }_{3}\right)}^{2}+\mu \left({\varepsilon }_{1}^{2}+{\varepsilon }_{2}^{2}+{\varepsilon }_{3}^{2}\right)$$

(13)

$$ \begin{aligned} {\psi }_{s}^{0\pm }=&\,\frac{1}{2}{\sigma }_{ij}^{0\pm }{\varepsilon }_{ij}^{\pm }=\frac{\lambda }{2}{\langle {\varepsilon }_{1}+{\varepsilon }_{2}+{\varepsilon }_{3}\rangle }_{\pm }^{2}\\ &+\mu \left({\langle {\varepsilon }_{1}\rangle }_{\pm }^{2}+{\langle {\varepsilon }_{2}\rangle }_{\pm }^{2}+{\langle {\varepsilon }_{3}\rangle }_{\pm }^{2}\right)\end{aligned}$$

(14)

where, $\lambda$ and $\mu$ are elastic constants; Macaulay brackets $\left\langle \cdot \right\rangle_{ + }$ and $\left\langle \cdot \right\rangle_{ - }$ mean

$${\langle {\varepsilon }_{i}\rangle }_{+}=\left\{\begin{array}{ll}0,&\quad {\varepsilon }_{i}\le 0\\ {\varepsilon }_{i},&\quad {\varepsilon }_{i}>0\end{array}\right.$$

(15)

$${\langle {\varepsilon }_{i}\rangle }_{-}=\left\{\begin{array}{ll}{\varepsilon }_{i},&\quad {\varepsilon }_{i}\le 0\\ 0,&\quad {\varepsilon }_{i}>0\end{array}\right.$$

(16)

respectively.

Combining Eqs. (5–8) gives the Euler–Lagrange equation

$$\begin{aligned} L&= \int_{\Omega }\frac{1}{2}\rho \dot{{\varvec{u}}}\cdot \dot{{\varvec{u}}}\text{d}V+\int_{\Omega }\frac{1}{2}\varrho \dot{\varphi }\dot{\varphi }\text{d}V\\ &\quad-\int_{\Omega }\left[g\left(\varphi \right){\psi }_{s}^{0+}+{\psi }_{s}^{0-}\right]\text{d}V\\ &\quad-\int_{\Omega }{G}_{c}\left[\frac{1}{2l}{\varphi }^{2}+\frac{l}{2}{\left|\nabla \varphi \right|}^{2}\right]\text{d}V\\ &\quad+\int_{\partial \Omega }{\varvec{t}}\cdot {\varvec{u}}\text{d}A+\int_{\Omega }{\varvec{b}}\cdot {\varvec{u}}\text{d}V\end{aligned}$$

(17)

This Euler–Lagrange equation $L$ has several functions ($u, v, w,\varphi$) of several variables ($x, y, z,t$) and their first derivative as

$$\begin{aligned} L= &\,L\left(x, y, z,t, u, v, w,\varphi , \frac{ \partial u}{\partial x}, \frac{ \partial u}{\partial y}, \frac{ \partial u}{\partial z},\frac{ \partial u}{\partial t}, \frac{ \partial v}{\partial x}, \frac{ \partial v}{\partial y}, \right.\\ &\left.\frac{ \partial v}{\partial z}, \frac{ \partial v}{\partial t},\frac{ \partial w}{\partial x},\frac{ \partial w}{\partial y}, \frac{ \partial w}{\partial z}, \frac{ \partial w}{\partial t},\frac{ \partial \varphi }{\partial x}, \frac{ \partial \varphi }{\partial y}, \frac{ \partial \varphi }{\partial z},\frac{ \partial \varphi }{\partial t}\right)\end{aligned}$$

(18)

For the several functions of several variables with first derivatives, a stationary point exists when Eq. (19) is satisfied,

$$\frac{\partial L}{\partial {f}_{i}}-\sum_{j=1}^{n}\frac{1}{\partial {x}_{j}}\frac{\partial L}{\partial {f}_{i,j}}=0 [33]$$

(19)

Based on Eq. (19), the governing equations of phase field model can be obtained as

$$\left\{\begin{array}{l}g\left(\varphi \right){\sigma }_{ij,j}^{0+}+{\sigma }_{ij,j}^{0-}+{b}_{i}=\rho {\ddot{u}}_{i}\\ {-g}{\prime}\left(\varphi \right){\psi }_{s}^{0+}-\frac{{G}_{c}}{l}\varphi +l{G}_{c}\Delta \varphi =\varrho \ddot{\psi }\end{array}\right.$$

(20)

Here, we show a generalized strong form of phase field with kinematic term from phase field, but the focus of this paper will be on the case with $\varrho =0$. More research is still needed for ϱ ≠ 0. In Eq. (20), ${\psi }_{s}^{0+}$ is usually replaced by maximum history strain energy $H$ (so, $\dot{H}\ge 0$) to consider the irreversibility of fracture propagation $\dot{\varphi }\ge 0$. And the governing equations are subject to time-dependent Dirichlet boundary conditions and time-dependent Neumann boundary conditions for displacement field and phase field as

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}l} {{\varvec{u}} = {\varvec{u}}^{p} ,{ }} \hfill & {{\text{on}}\, \partial \Omega_{u} \times \left[ {0,T} \right]} \hfill \\ {{\varvec{\sigma}}\cdot{\varvec{n}} = {\varvec{t}}^{p} ,{ }} \hfill & {{\text{on}}\, \partial \Omega_{t} \times \left[ {0,T} \right]} \hfill \\ {\varphi = 1,{ }} \hfill & {{\text{on}}\, \partial \Omega_{{\Gamma }} \times \left[ {0,T} \right]} \hfill \\ {\nabla \varphi \cdot{\varvec{n}} = 0,{ }} \hfill & {{\text{on}}\, \partial \Omega \times \left[ {0,T} \right]} \hfill \\ \end{array} } \right.} \\ \end{array} $$

(21)

2.3 Requirements of Degradation Function

The above-mentioned degradation function $g\left(\varphi \right)$ has to satisfy some basic requirements, like decreasing from 1 to 0 when phase increases from 0 to 1, and its first derivative should be in a small range to limit the driving force to a small value when phase reaches 1 [2], as shown below

$$\left\{\begin{array}{l} g\left(\varphi =0\right)=1\\ g\left(\varphi =1\right)=0\\ {g}{\prime}\left(\varphi =1\right)=0\end{array}\right.$$

(22)

For brittle materials, a good degradation function should not only provide linear elastic behavior, but also guarantee $\Gamma$ convergence. Even though many different degradation functions based on Eq. (22) have been proposed to obtain different stress–strain curves, $\Gamma$ convergence is destroyed and ignored by some of them. More discussion about the influence of degradation function on phase field model will be shown in Sect. 3.

3 Different Phase Field Models Obtained from Different Degradation Functions

The classical phase field model with degradation function ${g\left(\varphi \right)=\left(1-\varphi \right)}^{2}$ has problem to recreate linear elastic behavior for brittle materials. To better understand the influence of this degradation function on stress–strain curve, the relation between stress and phase is shown as

$$ \begin{array}{*{20}c} {\sigma_{ij} = g\left( \varphi \right)\sigma_{ij}^{0 + } + \sigma_{ij}^{0 - } = g\left( \varphi \right)E\varepsilon_{ij}^{ + } + E\varepsilon_{ij}^{ - } } \\ \end{array} $$

(23)

From the above equation, stiffness $E$ is only controlled by degradation function $g\left(\varphi \right)$, so this degradation function is the deep reason for stiffness reduction. Figure 3 shows the degradation function in the classical phase field model. From this figure, it is easy to see that degradation function decreases fast at zero phase. However, for an “ideal” degradation function, its value should be almost 1 for a certain strain range to enable linearity of stress–strain curve. In this paper, the first derivative of degradation function at zero phase will be used to describe how fast degradation function decreases.

Fig. 3

The relation between degradation function and phase

Some degradation functions used in publications are summarized and analyzed first, as shown in Table 1, where the first derivative at zero phase is calculated. The first function in Table 1 is used in classical phase field model. The second, third and last functions in Table 1 are only dependent on phase, which means a fixed degradation function and a fixed stress–strain curve. The analytical homogenous solution for the last is not available, which makes it difficult to further investigate properties based on homogeneous solution. The fourth function in Table 1 is a good degradation function, but its application is limited to only second-order and third-order terms. The fifth and sixth functions in Table 1 are more complicated, but they could lead to phases outside of [0, 1], making it difficult to achieve a homogeneous solution. The disadvantage of the sixth function is that its first derivative at zero phase can only be in [$-\infty , -1$].

Table 1 Some degradation functions used in publications

Zhang et al. [32] used the degradation function in [13] with $p=2$ and a quadratic polynomial function $Q\left(\varphi \right)=210\varphi (1-0.5\varphi )$, but also an extra phase constraint function to get a successful simulation. All five numerical homogenous solutions of this degradation function are shown in Fig. 4. For a correct solution, its real part should increase from 0 to 1 with the increase of strain, while the imaginary part should be 0. From this point, it can be seen that this degradation function does not make phase in [0, 1].

Fig. 4

Five homogenous solutions obtained from the degradation function used in [32]: a real part; b imaginary part

Based on the analysis above, generalized polynomial degradation functions are investigated to cover more stress–strain curves in one model. To check the influence of the first derivative of degradation function at zero phase, several different degradation functions are considered. First, following the form of the classical phase field model, a third-order and a fourth-order degradation functions are considered, which have the first derivatives at zero phase equal to − 3 and − 4, respectively,

$$ \left\{ {\begin{array}{*{20}l} {g\left( \varphi \right) = \left( {1 - \varphi } \right)^{2} ,} \hfill & {{\text{case }}1} \hfill \\ {g\left( \varphi \right) = \left( {1 - \varphi } \right)^{3} ,} \hfill & {{\text{case }}2} \hfill \\ {g\left( \varphi \right) = \left( {1 - \varphi } \right)^{4} ,} \hfill & {{\text{case }}3} \hfill \\ \end{array} } \right. $$

(24)

Next, to better control the rate of the decrease of degradation function at zero phase, one more constraint is considered as the first derivative of degradation function at zero phase, i.e.,

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}l} {g\left( {\varphi = 0} \right) = 1} \hfill \\ {g\left( {\varphi = 1} \right) = 0} \hfill \\ {g^{\prime}\left( {\varphi = 1} \right) = 0} \hfill \\ {g^{\prime}\left( {\varphi = 0} \right) = c1} \hfill \\ \end{array} } \right.} \\ \end{array} $$

(25)

Four constraints give a third-order polynomial degradation function. By setting a different $c1$ value in Eq. (25), four more degradation functions are obtained as

$$ \left\{ {\begin{array}{*{20}l} {g\left( \varphi \right) = 1 - \varphi - \varphi^{2} + \varphi^{3} ,{ }} \hfill & {{\text{case }}4} \hfill \\ {g\left( \varphi \right) = 1 - 0.5\varphi - 2\varphi^{2} + 1.5\varphi^{3} ,} \hfill & {{\text{case }}5} \hfill \\ {g\left( \varphi \right) = 1 - 0.1\varphi - 2.8\varphi^{2} + 1.9\varphi^{3} ,} \hfill & {{\text{case }}6} \hfill \\ {g\left( \varphi \right) = 1 - 3\varphi^{2} + 2\varphi^{3} ,} \hfill & {{\text{case }}7} \hfill \\ \end{array} } \right. $$

(26)

These seven cases are selected so that the constant $c1$ in Eq. (25) for case 1 to case 7 is − 2, − 3, − 4, − 1, − 0.5, − 0.1, and 0, respectively. Figure 5 shows that degradation function decreases slower if this first derivative of degradation function at zero phase is closer to 0. Even though the constant $c1$ in case 6 is − 0.1, it is still very close to case 7 with constant $c1$ equal to 0. A higher-order degradation function makes the phase field model a nonlinear problem, and the Newton–Raphson method will be used to solve this nonlinear problem. In the rest of this paper, case 1 will be called linear formulation of phase field, while case 2 to case 7 will be called nonlinear formulation of phase field.

Fig. 5

The relations between degradation function and phase for the seven cases

3.1 Analytical Solutions of the Linear Formulation of Phase Field

Following the idea in Borden et al. [3], homogeneous solutions mean solutions obtained from the governing equations when spatial derivative of φ is ignored (i.e., $\Delta \varphi =0$), while nonhomogeneous solutions mean solutions obtained from the entire governing equations, i.e., $\Delta \varphi$ is considered in the solutions.

3.1.1 Homogeneous Solution of the Linear Formulation of Phase Field

In this paper, the special case with ϱ = 0 is considered (i.e., $\varrho \ddot{\psi }=0$), which has been used in many publications. For the homogeneous solutions of the linear formulation of phase field in this paper (or ${g}{\prime}\left(\varphi \right)=-2\left(1-\varphi \right)$), spatial derivative of φ is ignored (i.e., $l{G}_{c}\Delta \varphi =0$), and the strong form of Eq. (20 ~ 2) is reduced to

$$2\left(1-\varphi \right)H-\frac{{G}_{c}}{l}\varphi =0$$

(27)

Considering the difference between loading and unloading conditions, $\varphi$ can be calculated for these two conditions. Here, loading condition is expressed as strain, ${\psi }_{s}^{0+}=E{\varepsilon }^{2}/2$,

$$ \begin{array}{*{20}c} {\varphi = \left\{ {\begin{array}{*{20}l} {\frac{2H}{{2H + G_{c} /l}},} \hfill & {\psi_{s}^{0 + } \le H} \hfill \\ {\frac{{E\varepsilon^{2} }}{{E\varepsilon^{2} + G_{c} /l}},} \hfill & {\psi_{s}^{0 + } > H} \hfill \\ \end{array} } \right.} \\ \end{array} $$

(28)

Note that $\sigma ={\left(1-\varphi \right)}^{2}E\varepsilon$, then the stress–strain curve in loading condition can be obtained as

$$\sigma ={\left(\frac{{G}_{c}/l}{E{\varepsilon }^{2}+{G}_{c}/l}\right)}^{2}E\varepsilon $$

(29)

Figure 6 plots the relation of phase and stress with respect to strain from Eqs. (28 ~ 2) and (29). Material parameters used include Young’s modulus E of 41,000 MPa and critical energy release rate ${G}_{c}$ of 0.05 N/mm. As shown in these two figures, with the increase of strain, phase keeps monotonically increasing from 0 to 1. A larger length scale $l$ leads to a faster increase in phase, a smaller range of stress–strain curve and a lower fracture strength. The stiffness reduction can be seen from Fig. 6a, where at any non-zero strain, there is a phase larger than 0 and a degradation function value less than 1, or from Fig. 6b where stiffness is much less than Young’s modulus right before reaching the fracture strength.

Fig. 6

Homogeneous solutions of the linear formulation of phase field: a phase versus strain; b stress versus strain

It is easy to obtain the fracture strength and strain from the derivative of Eq. (29), as shown in Eqs. (30) and (31). Note that the phase is a fixed number (0.25) in Fig. 6b at the fracture strength for different length scale $l$. According to Eq. (30), length scale $l$ is not a randomly picked parameter, but a parameter that can be determined from Young’s modulus, fracture strength and critical energy release rate [34].

$${\sigma }_{c}=\frac{9}{16}\sqrt{E{G}_{c}/6l}$$

(30)

$${\varepsilon }_{c}=\sqrt{{G}_{c}/6lE}$$

(31)

3.1.2 Nonhomogeneous Solution of the Linear Formulation of Phase Field

For the nonhomogeneous solution of the linear formulation of phase field (or ${g}{\prime}\left(\varphi \right)=-2\left(1-\varphi \right)$), spatial derivative of $\varphi$ is remained and loading condition is expressed as stress, ${\psi }_{s}^{0+}={\sigma }^{2}/2E$. With these changes, the strong form of Eq. (20 ~ 2) is rewritten as

$$\frac{{\sigma }^{2}}{E}\left(1-\varphi \right)-\frac{{G}_{c}}{l}\varphi +l{G}_{c}{\varphi }^{{\prime}{\prime}}=0$$

(32)

Since this equation is equal to 0, its integration with respect to phase is also equal to 0,

$$\int_{\Omega }\left[\frac{{\sigma }^{2}}{E}\left(1-\varphi \right)-\frac{{G}_{c}}{l}\varphi +l{G}_{c}{\varphi }^{{\prime}{\prime}}\right]\text{d}\varphi =0$$

(33)

After the integration, it is further rewritten as

$$-\frac{{\sigma }^{2}}{2E}{\left(1-\varphi \right)}^{2}-\frac{{G}_{c}}{2l}{\varphi }^{2}+\frac{l{G}_{c}}{2}{\left({\varphi }{\prime}\right)}^{2}=0$$

(34)

Then, the first spatial derivative of $\varphi$ can be obtained as

$${\varphi }{\prime}=\frac{\text{d}\varphi }{\text{d}x}=\pm \sqrt{\frac{2}{l{G}_{c}}\left[\frac{{\sigma }^{2}}{2E}{\left(1-\varphi \right)}^{2}+\frac{{G}_{c}}{2l}{\varphi }^{2}-{c}^{*}\right]}$$

(35)

Here, the boundary condition ${\varphi }{\prime}\left(\infty \right)=0$ is considered, and the constant ${c}^{*}$ can be determined as

$${c}^{*}=\frac{{\sigma }_{\infty }^{2}}{2E}{\left(1-{\varphi }_{\infty }\right)}^{2}+\frac{{G}_{c}}{2l}{\varphi }_{\infty }^{2}$$

(36)

where, ${\sigma }_{\infty }$ and ${\varphi }_{\infty }$ are the stress and phase at infinite position, respectively. For the nonhomogeneous solution, the relation between phase and position is obtained as

$$\text{d}x=\pm \frac{1}{\sqrt{\frac{2}{l{G}_{c}}\left[\frac{{\sigma }^{2}}{2E}{\left(1-\varphi \right)}^{2}+\frac{{G}_{c}}{2l}{\varphi }^{2}-{c}^{*}\right]}}\text{d}\varphi $$

(37)

$$x=\pm \int_{\varphi \left(x\right)}^{\varphi \left(0\right)}\frac{1}{\sqrt{\frac{2}{l{G}_{c}}\left[\frac{{\sigma }^{2}}{2E}{\left(1-\varphi \right)}^{2}+\frac{{G}_{c}}{2l}{\varphi }^{2}-{c}^{*}\right]}}\text{d}\varphi $$

(38)

where, $\varphi \left(0\right)$ is assumed to be the maximum phase, which could be 1 or less than 1. For any other phase not at the origin, its position can be found from Eq. (38), which then gives the relation between phase and position, as shown in Fig. 7.

Fig. 7

Nonhomogeneous solution of the linear formulation of phase field, phase versus position

3.2 Linear Formulation of Phase Field

The FEM formulation of displacement field has been well investigated in publications, so it is not presented here. After the displacement field is solved, phase field can be solved based on displacement, strain, and strain energy. For the strong form in Eq. (20 ~ 2), without considering the kinetic energy from phase field, its weak form is expressed as

$$\int_{\Omega }\vartheta \left[2H\left(1-\varphi \right)-\frac{{G}_{c}}{l}\varphi +l{G}_{c}\Delta \varphi \right]\text{d}V=0$$

(39)

where, $\vartheta$ is weighing function. Galerkin’s method is used in this paper, so the weighing function $\vartheta$ is set as shape function ${{\varvec{N}}}_{i}^{\text{T}}$,

$$\int_{\Omega }{{\varvec{N}}}_{i}^{\text{T}}\left[2H-2H\varphi -\frac{{G}_{c}}{l}\varphi +l{G}_{c}\Delta \varphi \right]\text{d}V=0$$

(40)

By applying integration by parts and Gauss’s divergence theorem, and also considering the boundary condition of Eq. (21 ~ 4) ($\nabla \varphi \cdot {\varvec{n}}=0$), the order of the last term on the left-hand side of Eq. (40) is decreased from two to one as

$$\begin{aligned}\int_{\Omega }{{\varvec{N}}}_{i}^{\text{T}}l{G}_{c}\Delta \varphi \text{d}V&= \int_{\partial \Omega }{{\varvec{N}}}_{i}^{\text{T}}l{G}_{c}\nabla \varphi \cdot {\varvec{n}}\text{d}A\\ &\quad-\int_{\Omega }{{\varvec{B}}}_{i}^{\text{T}}l{G}_{c}\nabla \varphi \text{d}V\\ &= -\int_{\Omega }{{\varvec{B}}}_{i}^{\text{T}}l{G}_{c}\nabla \varphi \text{d}V\end{aligned}$$

(41)

$\varphi$ and $\nabla \varphi$ can be expressed by shape function matrix, strain–displacement matrix, and phase unknows, $\varphi ={{\varvec{N}}}_{j}{\boldsymbol{\varphi }}_{j}$, $\nabla \varphi ={{\varvec{B}}}_{j}{\boldsymbol{\varphi }}_{j}$,

$$\begin{aligned}&\int_{\Omega }\left[{{\varvec{N}}}_{i}^{\text{T}}2H-{{\varvec{N}}}_{i}^{\text{T}}2H{{\varvec{N}}}_{j}{\boldsymbol{\varphi }}_{j}-{{\varvec{N}}}_{i}^{\text{T}}\frac{{G}_{c}}{l}{{\varvec{N}}}_{j}{\boldsymbol{\varphi }}_{j}\right.\\ &\qquad\left.-{{\varvec{B}}}_{i}^{\text{T}}l{G}_{c}{{\varvec{B}}}_{j}{\boldsymbol{\varphi }}_{j}\right]\text{d}V=0\end{aligned}$$

(42)

By using iso-parametric element, $\text{d}V$ is mapped into natural coordinate system as $\text{d}V=\left|{\varvec{J}}\right|\text{d}\xi \text{d}\eta \text{d}\varsigma$. The weak form is further updated as

$$\begin{aligned} &\int_{\Omega }\left[{{\varvec{N}}}_{i}^{\text{T}}2H-{{\varvec{N}}}_{i}^{\text{T}}2H{{\varvec{N}}}_{j}{\boldsymbol{\varphi }}_{j}-{{\varvec{N}}}_{i}^{\text{T}}\frac{{G}_{c}}{l}{{\varvec{N}}}_{j}{\boldsymbol{\varphi }}_{j}\right.\\ &\qquad\left.-{{\varvec{B}}}_{i}^{\text{T}}l{G}_{c}{{\varvec{B}}}_{j}{\boldsymbol{\varphi }}_{j}\right]\left|{\varvec{J}}\right|\text{d}\xi \text{d}\eta \text{d}\varsigma =0\end{aligned}$$

(43)

Then, stiffness matrix and force vector can be obtained as

$$\begin{aligned}& {{\varvec{K}}}_{ij}=\int_{\Omega }\left({{\varvec{N}}}_{i}^{\text{T}}2H\left|{\varvec{J}}\right|{{\varvec{N}}}_{j}+{{\varvec{N}}}_{i}^{\text{T}}\frac{{G}_{c}}{l}\left|{\varvec{J}}\right|{{\varvec{N}}}_{j}\right.\\ &\left.\qquad+{{\varvec{B}}}_{i}^{\text{T}}l{G}_{c}\left|{\varvec{J}}\right|{{\varvec{B}}}_{j}\right)\text{d}\xi \text{d}\eta \text{d}\varsigma \end{aligned}$$

(44)

$${{\varvec{F}}}_{i}=\int_{\Omega }{{\varvec{N}}}_{i}^{\text{T}}2H\left|{\varvec{J}}\right|\text{d}\xi \text{d}\eta \text{d}\varsigma $$

(45)

where, $\left|{\varvec{J}}\right|$ is the determinant of Jacobian matrix. Since this is a linear FEM problem, the phase unknows can be directly calculated by solving a system of linear equations as

$$K\varphi =F$$

(46)

The staggered method is used in this paper to solve the displacement-phase coupled problem for its robustness. The basic idea of this method is that the displacement field and phase field in Eq. (20) can be solved independently and in turn, as shown in Fig. 8, and both implicit and explicit schemes can be used in this calculation [11]. An explicit scheme is used in this paper.

Fig. 8

Staggered method for displacement-phase coupled problem

3.3 Analytical Solutions of the Nonlinear Formulation of Phase Field

3.3.1 Homogeneous Solution of the Nonlinear Formulation of Phase Field

For the homogeneous solutions of case 2 to case 7, spatial derivative of $\varphi$ is ignored, and the strong form of Eq. (20 ~ 2) is reduced to

$${-g}{\prime}\left(\varphi \right){\psi }_{s}^{0+}-\frac{{G}_{c}}{l}\varphi =0$$

(47)

The first derivative of degradation function for the six cases are obtained as

$$ \begin{array}{*{20}c} {g^{\prime}\left( \varphi \right) = \left\{ {\begin{array}{*{20}l} { - 3\left( {1 - \varphi } \right)^{2} ,} \hfill & {{\text{case }}2} \hfill \\ { - 4\left( {1 - \varphi } \right)^{3} ,} \hfill & {{\text{case }}3} \hfill \\ { - 1 - 2\varphi + 3\varphi^{2} ,{ }} \hfill & {{\text{case }}4} \hfill \\ { - 0.5 - 4\varphi + 4.5\varphi^{2} ,} \hfill & {{\text{case }}5} \hfill \\ { - 0.1 - 5.6\varphi + 5.7\varphi^{2} ,} \hfill & {{\text{case }}6} \hfill \\ { - 6\varphi + 6\varphi^{2} ,} \hfill & {{\text{case }}7} \hfill \\ \end{array} } \right.} \\ \end{array} $$

(48)

By substituting Eq. (48) into Eq. (47) and considering loading condition as strain, ${\psi }_{s}^{0+}=E{\varepsilon }^{2}/2$, $\varphi$ can be calculated for these six cases. Depending on the order of degradation function, two or three solutions can be obtained for each case. For case 3, its analytical complex results are not shown because of its complexity, and only analytical real result is shown here. For case 2,

$$\varphi =\left\{\begin{array}{l}1+\frac{{G}_{c}}{3El{\varepsilon }^{2}}+\sqrt{{\left(1+\frac{{G}_{c}}{3El{\varepsilon }^{2}}\right)}^{2}-1}\\ 1+\frac{{G}_{c}}{3El{\varepsilon }^{2}}-\sqrt{{\left(1+\frac{{G}_{c}}{3El{\varepsilon }^{2}}\right)}^{2}-1}\end{array}\right.$$

(49)

for case 3,

$$\varphi =\sqrt[3]{\sqrt[2]{\frac{{a}^{3}}{27}+\frac{{a}^{2}}{4}}-\frac{a}{2}}-\frac{1}{3}\frac{a}{\sqrt[3]{\sqrt[2]{\frac{{a}^{3}}{27}+\frac{{a}^{2}}{4}}-\frac{a}{2}}}+1, a=\frac{{G}_{c}}{2El{\varepsilon }^{2}}$$

(50)

for case 4,

$$\varphi =\left\{\begin{array}{l}\frac{1}{3}-\frac{{G}_{c}}{3El{\varepsilon }^{2}}+\sqrt{{\left(\frac{1}{13}-\frac{{G}_{c}}{13El{\varepsilon }^{2}}\right)}^{2}-\frac{1}{3}}\\ \frac{1}{3}-\frac{{G}_{c}}{3El{\varepsilon }^{2}}-\sqrt{{\left(\frac{1}{13}-\frac{{G}_{c}}{13El{\varepsilon }^{2}}\right)}^{2}-\frac{1}{3}}\end{array}\right.$$

(51)

for case 5,

$$\varphi =\left\{\begin{array}{c}\frac{4}{9}-\frac{2{G}_{c}}{9El{\varepsilon }^{2}}+\sqrt{{\left(\frac{2}{81}-\frac{{G}_{c}}{81El{\varepsilon }^{2}}\right)}^{2}-\frac{1}{9}}\\ \frac{4}{9}-\frac{2{G}_{c}}{9El{\varepsilon }^{2}}-\sqrt{{\left(\frac{2}{81}-\frac{{G}_{c}}{81El{\varepsilon }^{2}}\right)}^{2}-\frac{1}{9}}\end{array}\right.$$

(52)

for case 6,

$$\varphi =\left\{\begin{array}{c}\frac{28}{57}-\frac{10{G}_{c}}{57El{\varepsilon }^{2}}+\sqrt{{\left(\frac{140}{3249}-\frac{50{G}_{c}}{3249El{\varepsilon }^{2}}\right)}^{2}+\frac{1}{57}}\\ \frac{28}{57}-\frac{10{G}_{c}}{57El{\varepsilon }^{2}}-\sqrt{{\left(\frac{140}{3249}-\frac{50{G}_{c}}{3249El{\varepsilon }^{2}}\right)}^{2}+\frac{1}{57}}\end{array}\right.$$

(53)

and for case 7,

$$\varphi =\left\{\begin{array}{c}1-\frac{{G}_{c}}{3El{\varepsilon }^{2}}\\ 0\end{array}\right.$$

(54)

The homogeneous solutions of these six nonlinear formulations of phase field are plotted in Fig. 9. Considering that a phase in [0, 1] is the desired one, only solution 1 in these figures is used to describe stress–strain curve later. For Fig. 9b of case 3, solution 2 and solution 3 are complex numbers that are not desired; their absolute values are calculated and plotted here. From these figures, if the first derivative of degradation function at zero phase is closer to 0, phase result has a relatively larger strain range with almost 0 value. And from Fig. 9c–f, with the first derivative of degradation function at zero phase closer to 0, the two solutions get closer, and these two solutions intersect with each other when the first derivative is 0.

Fig. 9

Homogenous solution: a case 2: ${g}{\prime}\left(0\right)=-3$; b case 3: ${g}{\prime}\left(0\right)=-4$; c case 4: ${g}{\prime}\left(0\right)=-1$; d case 5: ${g}{\prime}\left(0\right)=-0.5$; e case 6: ${g}{\prime}\left(0\right)=-0.1$; f case 7: ${g}{\prime}\left(0\right)=0$

For Fig. 9f of case 7, if negative phase is forced to be zero, there is no stiffness reduction for a certain strain range, which could give a “perfect” linear relation between stress and strain. The phase versus strain, and degradation function versus strain for these seven cases are shown in Fig. 10. As we can see, if the first derivative of degradation function at zero phase is closer to 0, degradation function decreases slower, which leads to slower decrease of stiffness in stress–strain curve at a certain range of strain.

Fig. 10

a Phase versus strain; b degradation function versus strain

It is widely known that bilinear cohesive law can handle linear elastic behavior very well, and the damage factor used in [35, 36] is shown in Fig. 11a, where damage factor is 0 before stress reaches fracture strength, and then damage factor increases to 1 with the increase of separation. Figure 11b plots the $1-g\left(\varphi \right)$ for phase field model case 3 and case 6. Case 6 agrees with the damage factor found in bilinear cohesive law much better than case 3. From this comparison, it is clear that by changing degradation function, a better degradation function can be obtained for describing linear elastic behavior.

Fig. 11

a Damage factor in bilinear cohesive law; b degradation function in phase field model

Figure 12 shows the relation between stress and strain. It is found that a larger first derivative (or closer to 0) has less stiffness reduction before stress reaches fracture strength, which agrees with the findings from the degradation function. One more thing to mention is that the length scale is adjusted to get the same fracture strength. With a larger first derivative, the length scale is also larger. Case 1 has a length scale equal to 1, and case 6 could have a length scale as large as 3.0250 to get the same fracture strength. What’s more, according to the investigation in [2], it is suggested that $l/h$ should be larger than 2 ($h$ represents element size here). From these two points, the practical significance of this finding is that, compared with the classical phase field model, linear elastic behavior can be obtained even with larger element size for case 6.

Fig. 12

Stress–strain curve for the seven cases

Even though phase zeroing is used for case 7 to get homogeneous and nonhomogeneous solutions, it does not mean that phase zeroing is totally correct, or it does not mean ${g}{\prime}\left(0\right)=0$ is good to use in phase field model. For case 7, the range of phase from $\varphi \left(x\right)=\text{e}^{-\left|x\right|/l}$ (according to crack surface derivation) over the entire $x$ domain $x\in [-\infty ,+\infty ]$ is $[0, 1]$, but the range of phase from $\varphi \left(\varepsilon \right)=1-{G}_{c}/3El{\varepsilon }^{2}$ (according to homogenous solution) over the entire strain domain $\varepsilon \in [-\infty ,+\infty ]$ is $[-\infty , 1]$. In this situation, phase zeroing on $\varphi \left(\varepsilon \right)$ would definitely decrease the limits of integration for fracture surface calculation that should be over the entire $x$ domain $x\in [-\infty ,+\infty ]$, and then problem could happen with $\Gamma$ convergence. However, this kind of degradation function is used in [7, 30], see Table 1. To avoid this $\Gamma$ convergence issue, case 6 will be our choice for later simulations in Sect. 4, instead of case 7.

3.3.2 Nonhomogeneous Solution of the Nonlinear Formulation of Phase Field

Nonhomogeneous solution can be obtained following the procedure in Sect. 3.1.2, but it does not provide too much useful information compared with homogeneous solution. Because phase profile $\varphi \left(x\right)$ is derived from fracture surface density function [2], which has nothing to do with degradation function, the nonhomogeneous solution should be identical for the seven cases. Here, only the fracture situation with maximum phase equal to 1 is plotted, as shown in Fig. 13.

Fig. 13

Nonhomogeneous solutions for the seven cases

3.4 Nonlinear FEM Formulation of Phase Field

Similar to Sect. 3.2, only the FEM formulation of phase field is presented here. For the strong form in Eq. (20 ~ 2), without considering kinetic energy from phase field, it can be rewritten as

$$\Delta \varphi -\frac{1}{l{G}_{c}}\left[{g}{\prime}\left(\varphi \right)H+\frac{{G}_{c}}{l}\varphi \right]=0$$

(55)

Since this equation is a nonlinear FEM problem now, phase cannot be directly solved like the linear formulation of phase field, but delta phase can be solved by using the Newton–Raphson method. For the convenience of presenting this derivation, the second term on the left-hand side of Eq. (55) is expressed as $F(\varphi )$, i.e., $F\left(\varphi \right)=-\frac{1}{l{G}_{c}}\left[{g}{\prime}\left(\varphi \right)H+\frac{{G}_{c}}{l}\varphi \right]$, so

$$\Delta \varphi +F\left(\varphi \right)=0$$

(56)

The Galerkin method is also used to construct the weak form of this equation as

$$\int_{\Omega }{N}_{i}^{\text{T}}\left[\Delta \varphi +F\left(\varphi \right)\right]\text{d}V=0$$

(57)

Consider the first-order Taylor series, $\Delta \varphi$ and $F\left(\varphi \right)$ can be expressed as

$$\Delta \varphi =\Delta {\varphi }_{0}+\Delta \left(\varphi -{\varphi }_{0}\right)=\Delta {\varphi }_{0}+\Delta \delta \varphi $$

(58)

$$F\left(\varphi \right)=F\left({\varphi }_{0}\right)+{F}^{\prime}\left({\varphi }_{0}\right)\left(\varphi -{\varphi }_{0}\right)=F\left({\varphi }_{0}\right)+{F}^{\prime}\left({\varphi }_{0}\right)\delta \varphi $$

(59)

where, ${\varphi }_{0}$ is the phase result obtained from previous time step. By substituting Eqs. (58) and (59) back into Eq. (57), the weak form can be updated as

$$\int_{\Omega }{N}_{i}^{\text{T}}\left[\Delta {\varphi }_{0}+\Delta \delta \varphi +F\left({\varphi }_{0}\right)+{F}^{\prime}\left({\varphi }_{0}\right)\delta \varphi \right]\text{d}V=0$$

(60)

Rearranging the delta phase to the left-hand side and all the other terms to the right-hand side gives

$$\int_{\Omega }{N}_{i}^{\text{T}}\left[\Delta \delta \varphi +{F}^{\prime}\left({\varphi }_{0}\right)\delta \varphi \right]\text{d}V=-\int_{\Omega }{N}_{i}^{\text{T}}\left[\Delta {\varphi }_{0}+F\left({\varphi }_{0}\right)\right]\text{d}V$$

(61)

For the two terms ${N}_{i}^{\text{T}}\Delta \delta \varphi$ and ${N}_{i}^{\text{T}}\Delta {\varphi }_{0}$, using integration by parts, divergence theorem, and considering the boundary condition in Eq. (21 ~ 4) ($\nabla \varphi \cdot {\varvec{n}}=0$) gives

$$\int_{\Omega }{N}_{i}^{\text{T}}\Delta \delta \varphi \text{d}V=\int_{\partial \Omega }{N}_{i}^{\text{T}}\nabla \delta \varphi \cdot {\varvec{n}}\text{d}A-\int_{\Omega }{B}_{i}^{\text{T}}\nabla \delta \varphi \text{d}V=-\int_{\Omega }{B}_{i}^{\text{T}}\nabla \delta \varphi \text{d}V$$

(62)

$$\int_{\Omega }{N}_{i}^{\text{T}}\Delta {\varphi }_{0}\text{d}V=\int_{\partial \Omega }{N}_{i}^{\text{T}}\nabla {\varphi }_{0}\cdot {\varvec{n}}\text{d}A-\int_{\Omega }{B}_{i}^{\text{T}}\nabla {\varphi }_{0}\text{d}V=-\int_{\Omega }{B}_{i}^{\text{T}}\nabla {\varphi }_{0}\text{d}V$$

(63)

Substituting Eqs. (62) and (63) back into Eq. (61) gives

$$\int_{\Omega }{[B}_{i}^{\text{T}}\nabla \delta \varphi -{F}^{\prime}\left({\varphi }_{0}\right){N}_{i}^{\text{T}}\delta \varphi ]\text{d}V=\int_{\Omega }\left[{{N}_{i}^{\text{T}}F\left({\varphi }_{0}\right)-B}_{i}^{\text{T}}\nabla {\varphi }_{0}\right]\text{d}V$$

(64)

By using the finite element expression of phase and phase gradient,

$$\left\{\begin{array}{c}\nabla \delta \varphi ={B}_{j}\delta {\varphi }_{j}\\ \delta \varphi ={N}_{j}{\delta \varphi }_{j}\\ \nabla {\varphi }_{0}={B}_{j}{\varphi }_{0j}\end{array}\right.$$

(65)

Equation (68) is further updated as

$$\int_{\Omega }{[B}_{i}^{\text{T}}{B}_{j}-{F}^{\prime}\left({\varphi }_{0}\right){N}_{i}^{\text{T}}{N}_{j}]\delta {\varphi }_{j}\text{d}V=\int_{\Omega }\left[{N}_{i}^{\text{T}}F\left({\varphi }_{0}\right)-{B}_{i}^{\text{T}}{B}_{j}{\varphi }_{0j}\right]\text{d}V$$

(66)

According to isoperimetric element and numerical integration, the tangent stiffness matrix and unbalanced force vector are obtained as

$${{\varvec{K}}}_{ij}^{t}=\int_{\Omega }{[B}_{i}^{\text{T}}{B}_{j}-{F}^{\prime}\left({\varphi }_{0}\right){N}_{i}^{\text{T}}{N}_{j}]\left|{\varvec{J}}\right|\text{d}\xi \text{d}\eta \text{d}\varsigma $$

(67)

$${{\varvec{F}}}_{i}^{u}=\int_{\Omega }\left[{N}_{i}^{\text{T}}F\left({\varphi }_{0}\right)-{B}_{i}^{\text{T}}{B}_{j}{\varphi }_{0j}\right]\left|{\varvec{J}}\right|\text{d}\xi \text{d}\eta \text{d}\varsigma $$

(68)

Then the unknow delta phase can be solved by

$${{\varvec{K}}}^{{\varvec{t}}}\delta \varphi ={{\varvec{F}}}^{u}$$

(69)

The new phase at the next time step is obtained by adding the delta phase to the phase in the previous time step as

$$\varphi ={\boldsymbol{\varphi }}_{0}+\delta \varphi $$

(70)

Usually, one iteration does not make the solution convergent. To solve this, ${L}_{2}$ norm of delta phase is calculated as ${L}_{2}=\left|\delta \boldsymbol{\varphi }\right|/n$, and only if the condition Eq. (71) is satisfied, the calculation will move to the next time step.

$${L}_{2}=\frac{\left|\delta \boldsymbol{\varphi }\right|}{n}\le 0.01$$

(71)

3.5 Tensile Test of Different Phase Field Model

A tensile test is used to show the difference between these phase field models. Dimensions, boundary condition and load of this tensile test are shown in Fig. 14. Hexahedron element with 0.1 mm size and full integration method for both displacement field and phase field are used in the simulation. To let fracture develop at the center of the bar, a small cross-section reduction is made at the center.

Fig. 14

Dimensions, boundary condition and load of the tensile test, unit [mm]

Two simulations are conducted to check the properties of linear formulation of phase field for case 1. The first one is about the linearity of brittle materials. Three different length scales $l$ 0.5, 1.0 and 2.0 mm are used in the simulation up to the fracture of the bar. The displacement load and stress–strain curve results for this simulation are shown in Figs. 15a and 16a, respectively. As shown in Fig. 16a, a clear stiffness reduction happens before the bar breaks, which conflicts with the linearity property of brittle materials. However, with the decrease of length scale $l$, fracture strength increases, and linearity property gets better, which makes sense because damaged area is smaller now.

Fig. 15

Displacement load at the right end: a no unloading to fracture; b with unloading to fracture

Fig. 16

Stress–strain curves for linear formulation of phase field: a no unloading to fracture (nonlinear); b with unloading to fracture (inelastic)

The second one is about the elasticity of brittle materials. A process with loading, unloading, and reloading is used to check this. The displacement load and stress–strain curve results for this simulation are shown in Figs. 15b and 16b, respectively. As shown in Fig. 16b, even though the linearity is found during unloading and reloading, this unloading does not follow the original stress–strain curve, which means elasticity is not followed in this model.

To verify the correctness of the nonlinear FEM formulation and the correctness of the use of Newton–Raphson method in LS-DYNA, the linear formulation of phase field is also solved by the Newton–Raphson method. The obtained stress–strain curves from the non-iterative method and iterative method (Newton–Raphson method) are shown in Fig. 17, and the two solutions are almost the same, with only a small difference after the bar breaks. This comparison indicates that the Newton–Raphson method works well in this paper.

Fig. 17

Stress–strain curves obtained from non-iterative method and iterative method

Linearity is also investigated for the nonlinear formulation of phase field from case 2 to case 7. For the simplicity of this tensile test, length scale equal to 1.0 mm is used in all the seven cases, and stress–strain curves obtained are shown in Fig. 18. It is clear to see that a larger first derivative (or closer to 0) gives a stress–strain curve closer to brittle material and a higher fracture strength, which agrees with the finding about length scale from homogeneous solution. Compared with case 1, case 6 is more suitable for brittle materials, and a larger fracture strength for case 6 means that larger element can be used and more computationally efficient.

Fig. 18

Stress–strain curves obtained from the seven cases

From the investigation in [2], it is suggested that $l/h$ should be larger than 2. This empirical formula is also investigated here. Length scale $l=1.0$ for both case 3 and case 6 are simulated with element size 0.1, 0.2, and 0.5 mm, which gives $l/h$ 10, 5, and 2, respectively. From Fig. 19, the results obtained from $l/h$ equal to 10, 5 and 2 are almost the same, which means the empirical formula is good in this simulation. It is also found that by using a larger length scale $l=2.0$, case 6 has a smaller fracture strength. From this comparison, case 6 can still capture the linear elastic behavior even with larger length scale, which could mean larger element size and better computational efficiency in some large-scale simulations.

Fig. 19

The investigation of the relation between length scale and element size

Following the same idea, if a degradation function decreases slowly at an even larger phase range, it would be more suitable for brittle materials and have a higher fracture strength under the same length scale. Apart from the constrains in Eq. (22), three more higher-order degradation functions can be obtained by considering extra constrains as follow,

$$\left\{g\left(\varphi ={\varphi }^{*}\right)=c2,\text{ fourth order}\right.$$

(72)

$$\left\{\begin{array}{c}g{\prime}{\prime}\left(\varphi =0\right)=0\\ g\left(\varphi ={\varphi }^{*}\right)=c2\end{array},\text{ fifth order}\right.$$

(73)

$$\left\{\begin{array}{c}g{\prime}{\prime}\left(\varphi =0\right)=0\\ g{\prime}{\prime}{\prime}\left(\varphi =0\right)=0\\ g\left(\varphi ={\varphi }^{*}\right)=c2\end{array},\text{ sixth order}\right.$$

(74)

where, ${\varphi }^{*}$ is a number between 0 and 1. $g\left(\varphi ={\varphi }^{*}\right)=c2$ can be used in fine tuning for a desired degradation.

The three higher-order degradation functions versus phase are plotted in Fig. 20a. It is clear to see that these three higher-order degradation functions decrease much slower compared with the previous case 3 and case 6. And these degradation functions are also applied in the same tensile test again. Fifth order and sixth order do not break in the simulation because of the high fracture strength. The fourth order breaks with a much higher fracture strength, and the linearity is perfectly kept in its stress–strain curve.

Fig. 20

a Higher-order polynomial degradation function; b comparison of stress–strain curves obtained from different degradation functions

4 Numerical Verification

To further investigate this nonlinear formulation of phase field for simulating brittle fracture, three more representative numerical examples are presented here, including mode I, mode II, and mixed-mode tests.

4.1 Mode I Failure of Single-Edge Notched Beam

First, the single-edge notched beam test conducted by Hoover et al. [37] is considered, which has been used for verification in many papers [38, 39]. A comprehensive set of experimental data based on three-point bending of single-edge notched beam is presented in [37]. The specimen has a rectangular shape with dimensions of 223 mm × 93 mm × 40 mm, which is simply-supported at both sides 11 mm away from the edge. A vertical notch is made up to 14 mm from the middle bottom of the specimen. Vertical force is applied at the top center of the specimen. The detailed dimensions, boundary condition and load are shown in Fig. 21. The material parameters used are Young’s modulus $E=$ 41,000 MPa, Poison’s ratio $\upsilon =$ 0.17, fracture strength ${\sigma }_{f}=$ 3.5 MPa, and critical energy release rate ${G}_{c}=$ 0.07 N/mm. Force and displacement data are recorded during the simulation.

Fig. 21

Dimensions, boundary condition and load of the single-edge notched beam test, unit [mm]

Hexahedron element is used to mesh the specimen. Local refinement with about 1-mm element along the fracture path is used, but larger element is used at other positions. To show the difference caused by degradation function, case 3 and case 6 are compared here. Because same length scale leads to different fracture strength for these two cases, length scale is adjusted separately for these two cases, case 3 with $l$ equal to 2.0 and case 6 with $l$ equal to 3.4. The phase field results obtained for these two cases are shown in Fig. 22. It is clear that case 3 with higher nonlinearity in stress–strain curve has a larger crack area. However, the crack area for case 6 is more localized along the crack path, which is true for brittle materials that have smaller damage zone near the crack tip.

Fig. 22

Phase field results obtained from different cases: a case 3; b case 6

The force–displacement curves obtained for the two cases are shown in Fig. 23. Even though both models agree somehow with experiment data, case 6 is closer to experiment data. One clear difference happens before reaching peak force. Case 6 almost has no stiffness reduction, but clear stiffness reduction happens in case 3 before the peak force. After the peak force, the force in case 6 drops fast, but case 3 drops slowly, which could be attributed to the larger damage zone in case 3. Another thing is peak force, even with the smallest allowable length scale for case 3 (2.0 used in simulation), it still has a peak force lower than experimental result. To solve this issue, a smaller element and a smaller length scale should be used, which could give a higher fracture strength and higher peak force, but also more computational costs.

Fig. 23

Force–displacement curves obtained from different cases: a case 3; b case 6

4.2 Mode II Failure of Shear Test

Second, a shear test simulation is conducted to check the impact of degradation function on shear failure. This test is originally investigated in [2]. The specimen has dimensions of 1 mm × 1 mm, and a 0.5-mm initial crack is made at the center left, see Fig. 24. A prescribed horizontal displacement is applied at the top of the specimen. Materials properties are Young’s modulus of 210,000 MPa, Poisson’s ratio of 0.3, length scale of 0.015 mm, and critical energy release rate of 2.7 N/mm. The lower right part of the plate is meshed with 0.003-mm element to satisfy grid convergence, where fracture propagates in that portion. Force and displacement data are recorded during the simulation.

Fig. 24

Dimensions, boundary condition and load of the shear test, unit [mm]

To show the difference caused by degradation function, case 3 (${g}{\prime}\left(0\right)=-4$), case 1 (${g}{\prime}\left(0\right)=-2$), and case 5 (${g}{\prime}\left(0\right)=-0.5$) are compared here. The focus of this simulation is the different response, not the exact peak loading, so the same length scale is used in all cases. Figure 25 shows phase field results obtained for these three cases. First, all three cases can capture the curved shear crack in this simulation. However, a similar finding to Sect. 4.1 is that, clearly, from Fig. 25a–c, a narrower crack band is found when the first derivative of degradation function is closer to 0.

Fig. 25

Phase field results obtained from different cases: a case 3: ${g}{\prime}\left(0\right)=-4$; b case 1: ${g}{\prime}\left(0\right)=-2$; c case 5: ${g}{\prime}\left(0\right)=-0.5$

Figure 26a shows the force–displacement curves of the three cases above. Case 1 in this paper agrees with the results from Miehe et al. [2] very well (both having the first derivative of degradation function ${g}{\prime}\left(0\right)=-2$), where a kind of hardening in the force–displacement curve is found. However, case 3 with ${g}{\prime}\left(0\right)=-4$ behaves like a softer material, where stiffness decreases very clear before reaching the peak force. Case 5 with ${g}{\prime}\left(0\right)=-0.5$ behaves more like a stiffer and brittle material, where there is no stiffness reduction before the peak loading, and also the force drops faster after the fracture starts to propagate. Figure 26b shows the comparison with other studies where the first derivative of degradation function is − 1 [30] and $- \pi /2$ [31]. Basically, this comparison still agrees with the finding in this paper, and when the first derivative of degradation function at zero phase is closer to 0, the phase field model gives a higher peak force and also behaves more like a brittle material. According to the analysis at the end of Sect. 3.3.1, the degradation function with ${g}{\prime}\left(0\right)=0$ is not considered here because of possible Γ convergence issue.

Fig. 26

Phase field results obtained from different cases: a comparison with the model in this paper; b comparison with the models in publications

4.3 Mixed-Mode Failure of Single-Edge Notched Plate

Third, the single-edge notched plate test conducted by Ambati et al. [40] is considered. The specimen is a notched plate, with a rectangular shape of dimensions 65 mm × 120 mm. The specimen is fixed at the lower pin, and load is applied at the top pin, and a hole offset from the center is used to induce mixed-mode fracture. A horizontal 10-mm notch is made 55 mm away from the top. The detailed dimensions, boundary condition and load are shown in Fig. 27. The material parameters used are Young’s modulus $E=$ 41,000 MPa, Poison’s ratio $\upsilon =$ 0.22, and critical energy release rate ${G}_{c}=$ 2.28 N/mm. Force and displacement data are recorded during the simulation.

Fig. 27

Dimensions, boundary condition and load of the notched plate with hole test, unit [mm]

Hexahedron element is also used to mesh the specimen. Local refinement with about 0.5-mm element along the fracture path is used, but larger element is used at other positions. By using the minimum length scale $l=1.0$ in this simulation, phase field results obtained from case 3 and case 6 are shown in Fig. 28. For case 3, there is no clear fracture like that in experiment, and the high phase is spread out over a large area. However, for case 6, the fracture path is almost the same as experiment results.

Fig. 28

Phase field results obtained from different cases: a experiment [40]; b case 3; c case 6

The force–displacement curve is obtained for these two cases, as shown in Fig. 29. For this simulation, a fixed length scale $l=1.0$ is used for both cases. Because no fracture occurs in case 3, there is no force drop in its force–displacement curve, which is totally different from the experiment. The stiffness reduction is very clear for case 3 in this simulation. Case 6 almost has no stiffness reduction before the peak force, and force drops fast after it breaks. The peak force in case 6 is a little lower than experiment, and this could also be solved by using a smaller element and a smaller length scale. Compared with $l=0.25$ used in [41], a relatively larger length scale $l=1.0$ for case 6 in this paper can still capture the force–displacement curve well.

Fig. 29

Force–displacement curves obtained from different cases: a case 3; b case 6

5 Conclusions

In this paper, generalized polynomial degradation functions are proposed to solve the nonlinearity and inelasticity problem in the classical phase field model, and nonlinear formulation of phase field has been solved successfully by using the Newton–Raphson method. The conclusions obtained are as follows:

• For the classical phase field model, the stress–strain curve obtained from its homogeneous solution appears suitable for brittle materials, but the real stress–strain curve obtained from a tensile test shows nonlinearity and inelasticity problems. Even so, the homogeneous solution can still provide some general and inherent information of the model.

• The degradation function is a key part in phase field model. Different stress–strain curves are obtained by adjusting the first derivative of degradation function at zero phase. And a better linear elastic behavior is obtained if this first derivative is closer to 0. For the proposed degradation function, its relation between phase and strain has similar shape to the damage factor used in bilinear cohesive law, which verifies the correctness of the proposed degradation function for brittle materials from another point of view.

• By adjusting the proposed degradation function, different fracture strengths can be obtained while keeping the linearity of the stress–strain curve, which makes the proposed nonlinear formulation of phase field a length-scale-insensitive phase filed model.

• Compared with the classical degradation function, the proposed degradation function leads to a larger fracture strength with the same length scale. This has great practical significance, because a larger length scale and element size can be used in simulations, and it could be more computationally efficient.