Introduction

The motion of artificial satellites and keeping proper orbital parameters are of crucial importance in the wide field of satellite geodesy and the maintenance of satellite constellations. In this study, we focus uniquely on the principal dynamic properties of Global Navigation Satellite System (GNSS; Teunissen and Montenbruck 2017) satellite orbits of GPS, GLONASS, and Galileo — how the orbital parameters evolve and what the main orbit perturbing forces are that introduce changes observed in Keplerian parameters.

Different types of orbit perturbations can be distinguished in the Keplerian parameters. The short-term orbit perturbations denote the perturbations equal to the satellite revolution period or its harmonics and the so-called m-daily perturbations which repeat every day or within its fraction. Thus, short-periodic perturbations are related to the satellite revolution and the Earth rotation. Secular perturbations denote continuous changes of the Keplerian parameters which are not periodic, e.g., the secular change of the ascending node caused by Earth’s oblateness or by the Lense-Thirring effect. Long-periodic perturbations imply periodic changes of the Keplerian parameters longer than one day. These perturbations result from the revolution of celestial bodies and derivative effects, such as solid Earth tides, the draconitic perturbations caused by the solar radiation pressure (SRP) which depends on the specific Sun elevation angles above the orbital plane, as well as the very long-periodic perturbations, such as the nutation period of 18.6 years or the full revolution of GNSS orbital plane obliquity with respect to the ecliptic, which may last up to 40 years for MEO GNSS. Short-periodic perturbations are typically characterized by large amplitudes and affect most of the Keplerian elements, therefore, deriving mean Keplerian parameters is needed to assess which Keplerian parameters are actually affected by long-term and secular perturbations. Please note, however, that the aliasing effects of the short-periodic orbit perturbations and the Earth rotation or the repeatability of the GNSS constellation with respect to the ground stations may result in perturbations that are observed as periods longer than one day, e.g., 2.5, 3.4, and 10 days for Galileo or 2.6, 3.9, and 7.9 days for GLONASS or the tidal aliasing signals resulting in the spurious signals of 14.2 and 14.8 days (Zajdel et al., 2020).

Keplerian orbits and perturbations

The satellite orbit is uniquely identified by orbital elements or a state vector. Following the classical Keplerian system, the geometry of a satellite’s orbit can be explained using two elements: the semi-major axis (a) and eccentricity (e); Additionally, three other Keplerian elements depict the orientation of the orbital planes in three-dimensional space: the argument of perigee (\(\omega\)), the right ascension of the ascending node (\(\varOmega\)), and the inclination (i); As a final element, the true anomaly (ν) or argument of latitude (u), which is the sum of the true anomaly and the argument of perigee, are used interchangeably to define the position of a satellite moving along a Keplerian orbit.

A particular solution of the equation of motion (Beutler 2005) consists of a satellite state vector. Using the formulas of the two-body problem it is possible to assign one set of orbital elements to each epoch t to the state vector, i.e., satellite position \(\mathbf{r}(t)\) and satellite velocity \(\mathbf{\dot{r}}(t)\):

$$\:t:\:\left\{\mathbf{r}(t),\mathbf{\dot{r}}(t)\right\}\leftrightarrow\:\left\{a(t),e(t),i(t),\varOmega(t),\omega(t),u_{0}(t)\right\}.$$
(1)

These orbital elements, known as osculating elements, represent the instantaneous unperturbed (Keplerian) orbit of a satellite (Der and Danchick 1996). The osculating orbit aligns with the state vector of the true orbit only at epoch t. However, from that point forward, the osculating orbit does not adhere to the laws of the two-body problem due to the orbit perturbations. Time series of osculating elements visualize therefore the impact of the perturbing forces on the Keplerian elements and are better suited to gain insight into the orbital motion over a few orbital periods. For studying the evolution of orbits over long time periods, i.e., over many orbit revolutions, one seeks for mean orbital elements. These are driven by averaging the osculating elements over a number of full revolutions (Beutler 2005). Mean orbital elements do not accurately depict the true position and velocity vectors of a satellite, but they characterize orbit behavior over time. An orbit described by a set of mean orbital elements is considered perturbed or non-Keplerian (Der and Danchick 1996). A mean element \(\:\stackrel{-}{I}\left(t\right)\) (Eq. 2) at the epoch 𝑡 is expressed as:

$$\:\stackrel{-}{I}(t)\in\:\left\{\widehat{a(t)},\:\widehat{e(t)},\widehat{i(t)},\widehat{\varOmega(t)},\widehat{\omega(t)},\widehat{u_{0}(t)}\right\},$$
(2)
$$\:\:\stackrel{-}{I}\left(t;\varDelta\:t\left(t\right)\right)=\frac{1}{\varDelta\:t}{\int\:}_{t-\frac{\varDelta\:t}{2}}^{t+\frac{\varDelta\:t}{2}}\:I\left({t}^{{\prime\:}}\right)d{t}^{{\prime\:}},$$
(3)

where \(\:\varDelta\:t\left(t\right)\:\)corresponds to the averaging time interval covering an entire number of revolution periods. The singularities of small eccentricity, small inclination or critical inclination do not exist in the conversion of osculating elements to mean elements (Der and Danchick 1996). The mean elements do not capture short-period perturbations, given that the averaging period ∆t considerably exceeds all short periods, or if it perfectly aligns with multiples of all short periods (Beutler 2005). This is often difficult due to the variability of constant periods, in perturbed problems, such as revolution or draconitic periods (Rodriguez-Solano et al. 2014; Zajdel et al. 2022). In this study, ∆t(t) varies as a function of a revolution period and is computed for each day from \(\mathbf{r}(t)\) and \(\mathbf{\dot{r}}(t)\) at time t.

Conversion of the osculating elements into mean elements have been studied by (Brouwer 1959; Walter 1967; Zhong and Gurfil 2013; Ely 2015; Arnas 2023) to name only a few. The analysis of long-term variations of the orbital elements were used for the optimal design of the broadcast ephemeris parameters (Fu and Wu 2012; Choi et al. 2020). Mean orbital elements are fed into satellite guidance and orbit control systems (Zhong and Gurfil 2013). Cojocaru et al. (2009) used mean orbital elements of GNSS satellites to assess the magnitude of perturbations affecting the motion of different GNSS. Ait-Lakbir et al. (2023) focused on the long-term orbital dynamics of the four available constellations, including GPS, GLONASS, Galileo and BeiDou, and evaluated their impact on the coloured noise of station position series.

In this study, we examine the long-term changes of mean Keplerian parameters for GPS, GLONASS, Galileo, as well as Galileo in eccentric orbits with an explanation of main perturbing forces changing specific orbital parameters. We concentrate on secular and long-periodic effects occurring in Keplerian parameters due to gravitational, non-gravitational, and general relativistic effects observed in the mean Keplerian parameters. The aim of this study is to understand the reasons for the long-term and secular perturbations of GNSS orbits distinguishing between particular Keplerian parameters and GNSS satellite systems and types. Short-term orbit perturbations affect most of the Keplerian parameters and cause high-frequency variations of large amplitudes of hundreds of meters within one GNSS revolution period due to the Earth’s gravity field. Therefore, mean Keplerian parameters must be derived to separate the long-periodic and secular perturbations which are characterized by much smaller magnitudes than short-periodic perturbations and are present only for selected orbital parameters depending on the nature of the perturbing acceleration.

The next section provides analyses of the orbital mean elements for a selected set of GNSS satellites. In this study, we consider three GNSS, i.e., GPS, GLONASS, and Galileo, which were used for the latest realization of the International Terrestrial Reference Frame (ITRF2020; Altamimi et al. 2023). Table 1; Fig. 1 provide the main differences in selected characteristics of GPS, GLONASS and Galileo constellations specified separately for different orbital planes. One should note that the Galileo constellation has been split into two subgroups of satellites as the two Galileo satellites were launched into eccentric orbits in 2014 (Sośnica et al. 2018, 2021; Delva et al. 2018; Herrmann et al. 2018). Therefore, the fourth orbital plane denoted E-X has been specified besides the nominal three. The draconitic year denotes the period of two consecutive passes of the Sun in the same direction through the orbital plane. The draconitic year corresponds to the repeatability period of the satellite-Earth-Sun geometry and lasts about 351–356 days for GNSS satellites (see Table 1). Due to the obliquity of the ecliptic, there is a second period characterizing the relative geometry of the satellite and the Sun during which the \(\beta\)-angle, i.e., the elevation of the Sun above the orbital plane, outlines a full revolution. The full \(\beta\)-cycle is equal to full node revolution (\(\:{T}_{\varOmega\:}\)) and takes from 25 to 39 years, which is more than the nominal lifetime of GNSS satellites (see Table 1).

Table 1 Selected characteristics of the GPS, GLONASS, and Galileo constellations. a – semi-major axis; e – eccentricity; i – inclination; \(\:\dot{\:{\Omega\:}}\) – ascending node drift; \(\:\dot{\omega\:}\) - perigee drift; Drac. Year – draconitic year; Rev. – satellite revolution period; \(\:{\text{T}}_{{\Omega\:}}\) – full ascending node revolution; \(\:{\text{T}}_{{\upomega\:}}\:\--\) full perigee revolution
Full size table
Fig. 1
figure 1

Distribution of GPS (blue), GLONASS (red) and Galileo (green) satellites as a function of (a) the satellite altitude ranges and the argument of latitude; (b) the right ascension of ascending node and argument of latitude (as of 10.01.2019)

Full size image

Methods

Mean elements are computed using a modified version of the Bernese GNSS Software (Dach et al. 2015) program ORBbit GENeration (ORBGEN). In the program, the averaging time interval \(\:\varDelta\:t\left(t\right)\) is of one revolution period for each GNSS expressed based on the Kepler’s third law as:

$$\:\text{T}=2\pi\:\sqrt{\left(\frac{a^{3}}{\mu}\right)}=2\pi\:/n,$$
(4)

where \(\:\mu\:=GM\) is a standard gravitational parameter and n denotes the mean motion. The investigation of long-term evolution of Keplerian elements by averaging the osculating elements over a number of full revolutions needs the time series of homogeneously processed precise orbits. In 2021, the International GNSS Service (IGS, Johnston et al. 2017) presented the results of the most recent reprocessing effort (IGS Repro3, Rebischung et al. 2024) following the latest models and standards resulting in combined GNSS orbits (Zajdel et al. 2023). The IGS Repro3 products constitute the GNSS contribution to the realization of the International Terrestrial Reference Frame 2020 (ITRF, Altamimi et al. 2023). The contributors to IGS Repro3 have consistently processed time series of geodetic parameters, including satellite orbits, Earth rotation parameters, clocks, geocenter coordinates, and station coordinates. This marks the first instance where Galileo has been integrated into the processing workflow of most analysis centers. As a result, the new GNSS reference frame, IGSR3, has been established, featuring an ITRF-independent scale based on Galileo. In 2019, the IGS Analysis Center Coordinator initiated an experimental multi-GNSS orbit combination service, adapting the longstanding combination software previously used for GPS and GLONASS combinations within IGS. Subsequently, in 2020, Geoscience Australia (GA) together with Massachusetts Institute of Technology (MIT) released experimental multi-GNSS combined orbits based on individual products generated by IGS and multi-GNSS Pilot Project analysis centers (Sośnica et al. 2020). In this study, we used IGS Repro3 combined orbits delivered by GA&MIT based on individual products generated by IGS Repro3 contributors (Zajdel et al. 2023). The time of analyses covers up to 8 years of GNSS orbits from 2013 to 2021.

Results

This section discusses the evolution of the mean Keplerian elements of selected satellites in the form of time series and spectral analysis. We selected nine satellites identified with Satellite Vehicle Number (SVN)/Pseudo Random Noise (PRN) 62/G25, 45/G21, 61/G02, 50/G05, 103/E19, 201/E18, 205/E24, 855/R21, and 720/R19, which represent the GPS-IIF, IIR-A, IIR-B, IIR-M, Galileo In-Orbit-Validation (IOV), Galileo Full-Operational-Capability (FOC) in circular and eccentric orbits (FOC*), GLONASS-M +, and GLONASS-M satellite types. The behavior of the satellites, as described in the following subsections, is consistent within the identified groups, so for simplicity, only the representatives have been identified and discussed.

Semi-major axis

Figure 2 shows the semi-major axis time series for selected satellites from three GNSS constellations. Grey lines indicate the absolute elevation of the Sun above the orbital plane (\(\beta\)). The black dashed lines indicate the empirical fit of the draconitic and semi-draconitic signals, as well as the trend fitted into the values. The jumps and spikes have been removed beforehand. The most frequent discontinuities occur for GPS, for which, the strong 2:1 resonance of the GPS orbits and Earth gravity field cause large drift of the semi-major axis, thus, GPS satellites need to be regularly repositioned (Hugentobler et al. 2003). For the other GNSS, the resonance is milder than for GPS and equals 17:8 and 17:10 for GLONASS and Galileo, respectively.

Fig. 2
figure 2

Time series of the semi-major axis evolution for selected satellites. Grey dash-dotted lines indicate the absolute elevation of the Sun above the orbital plane (\(\beta\)) (right y-axis). The black dashed lines indicate the empirical fit of the draconitic and semi-draconitic signals, as well as the trend fitted into the values. The value of the fitted trend is shown on the right above each graph

Full size image

Hugentobler (1998) studied the secular changes of the GPS semi-major axis and found that the J32 gravity field coefficient is responsible for most of the observed secular rates of the semi-major axis. These rates are, in fact, very long-term perturbations. Amongst the resonant terms for GPS, J32, J22, and J44 result in secular rates up to 6, 1.8, and 2.5 m/day, respectively, depending on the initial value of a, e, and i, which slightly differ for GPS satellites. However, the sum of all resonant terms up to degree and order 6 is up to 6.5 m/day because some terms amplify and some attenuate the total effect. The effect can be both negative and positive resulting in opposite trends observed in the semi-major axis. The rates for the GPS semi-major axis in Fig. 2 fit well within the range expected from the main J32, J22, and J44 resonant terms.

Figure 2 shows that the Galileo and GLONASS satellites do not demonstrate any significant resonant perturbations, however, their periodical variations depend on the phase of the draconitic year and the elevation of the Sun above the orbital plane (\(\beta\)). The SRP does not induce any long-periodic or secular rates of the semi-major axis. However, the Y-bias, i.e., the force acting perpendicular to the Sun direction causes drifts or long-periodic perturbations in the semi-major axis. The effect on the semi-major axis change reads as (Hugentobler 1998):

$$\:\frac{da}{dt}=\frac{2}{n}{Y}_{bias}\frac{\text{sin}\beta\:}{\sqrt{{\text{s}\text{i}\text{n}}^{2}\beta\:+{\text{c}\text{o}\text{s}}^{2}\beta\:{\text{s}\text{i}\text{n}}^{2}(u-\omega\:)}},$$
(5)

and after solving this equation for the secular part:

$$\eqalign{{\left( {{{da} \over {dt}}} \right)_{sec}} & = {4 \over {n\pi \>}}{Y_{bias}}\mathop {\mathop {\int \> }\limits^{{{\pi \>} \over 2}} }\limits_0 {{{\rm{sin}}\beta \>du} \over {\sqrt {1 - {\rm{co}}{{\rm{s}}^2}\beta \>{\rm{si}}{{\rm{n}}^2}\left( {u - \omega \>} \right)} }} \cr & = {4 \over {n\pi \>}}{Y_{bias}}K\left( {{\rm{co}}{{\rm{s}}^2}\beta \>} \right){\rm{sin}}\beta \>, \cr}$$
(6)

where K is the complete elliptic integral of the first kind. For high \(\beta\) angles, the Y-bias has a large along-track component, which increases the impact of the change of the semi-major axis. For low \(\beta\) angles (\(\sin\beta \approx 0\), i.e., eclipsing periods), the daily rate is the smallest, however, the accumulated effect results in local extrema of the periodic variations (see Fig. 2). The Y-bias of 1.10−9 m/s2 corresponds to the semi-major axis change of about 1.2 m/day at the GPS height, which gives about the amplitude of 105 m in the period of a half draconitic year. Galileo IOV satellites have a very small Y-bias, whereas the Y-bias is about − 6.10−10 and − 7.10−10 m/s2 for Galileo FOC in circular and eccentric orbits, respectively (Bury et al. 2020), which explains the largest periodical variations of the semi-major axis for Galileo FOC/FOC* satellites.

The Y-bias for Galileo FOC is caused by asymmetric radiators distributed on one Y-side of the satellite bus, whereas in the old GPS blocks, the Y-bias was typically explained by a small misalignment of the solar panels with respect to the Sun’s direction.

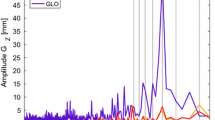
Besides the Earth’s gravity field and the Y-bias, the semi-major axis is affected by the gravitational attraction of the Moon and the Sun with the periods corresponding to tidal constituents and the revolution of the constellation with respect to the rotating Earth (Zajdel et al. 2021) (see Fig. 3). The primary orbital features associated with Galileo exhibit periods of 2.5 days, 2.9 days, and approximately 3.4 days. For Galileo satellites in eccentric orbits (SVN201), the primary orbital periods are 6.6, 4.5, 3.3, and 2.7 days. These periods differ from those of the nominal Galileo constellation, as indicated in Table 1. Likewise, the corresponding signals for GLONASS are observed with periods of 4 days, and around 8 days, e.g., 7.8, 8.0, 8.2 days (Abraha et al. 2017).

Fig. 3
figure 3

Amplitude spectra of the semi-major axis evolution for selected satellites. The left periodogram corresponds to periods from 1 to 50 days, while the right subplot corresponds to periods from 50 to 1000 days. Please note the difference in scale between the left and right subplots. The vertical gray lines denote the harmonics of a year

Full size image

Secular drifts and periodic variations of Ω and ω

The development of the mean right ascension of the ascending node is dominated by the almost linear regression of the node (see Fig. 4). This effect is mainly due to the oblateness of the Earth (J2/C20) with a minor contribution from other even-degree zonal spherical harmonics. Based on the theoretical consideration given by Beutler (2005), the secular drift of the right ascension of the ascending node due to the oblateness of the Earth (assuming C20 ≈ 1.082 · 10− 3) equals to:

Fig. 4
figure 4

Time series of the satellite right ascension of the ascending node evolution for selected satellites. Grey dash-dotted lines indicate the absolute elevation of the Sun above the orbital plane (\(\beta\)) (right y-axis). The black dashed lines indicate the empirical fit of the draconitic and semi-draconitic signals, as well as the trend fitted into the values. The value of the fitted trend is shown on the right above each graph. The theoretical trend as calculated using Eq. 7 is shown on the left above each graph

Full size image
$$\:\stackrel{\_}{\dot{{\Omega\:}}}\left[^\circ\:/\text{day}\right]=\frac{3\cdot\:180}{2\pi\:}\sqrt{\frac{GM}{{a}_{e}^{3}}}{\left(\frac{{{a}_{e}}}{a}\right)}^{\frac{7}{2}}{C}_{20}\text{cos}i=-\frac{{10.0}^{\circ\:}\text{cos}i}{{\left(\frac{a}{{a}_{e}}\right)}^{\frac{7}{2}}{\left(1-{e}^{2}\right)}^{2}},$$
(7)

where \(\it {a}_{e}\) – Earth radius. The drift is −14.5, −10.0, −14.6, and −12.5 °∕year for GPS, GAL-IOV&FOC, FOC*, and GLONASS-M+, respectively. Small secular rates of Ω are caused by J4, J6, J8, etc., and two relativistic effects: the Lense-Thirring and the De Sitter effects. The effect of these latter two is 0.0084 and 0.0556 mas/day for GPS satellites, respectively (Sośnica et al. 2021) whereas the main relativistic effect – Schwarzschild – does not cause any secular rates of the ascending node. Long-term orbit perturbations of Ω are caused by Earth’s gravity field, tidal forces, and gravitational attraction of third celestial bodies, especially the Moon and the Sun (see Fig. 5).

The changes of the ascending node due to the direct SRP read as (Krivov et al. 1996):

Fig. 5
figure 5

Amplitude spectra of the right ascension of the ascending node evolution for selected satellites. The left periodogram corresponds to periods from 1 to 50 days, while the right subplot corresponds to periods from 50 to 1000 days. Please note the difference in scale between the left and right subplots. The vertical gray lines denote the harmonics of a year

Full size image
$$\:\frac{d\varOmega\:}{dt}=-\frac{3a\gamma\:}{2}\sqrt{\frac{a}{GM}}\frac{{e}^{2}}{\sqrt{1-{e}^{2}}}\text{sin}\omega\:\text{s}\text{i}\text{n}(\varOmega\:-{\nu\:}_{s})\:,$$
(8)

with the periodic perturbations:

$$\:{\left(\frac{d\varOmega\:}{dt}\right)}_{l\_per}=-\frac{3\pi\:\gamma\:}{n}\frac{{e}^{2}}{\sqrt{1-{e}^{2}}}\text{sin}\omega\:\text{cos}\left(\varOmega\:-{\nu\:}_{s}\right),$$
(9)

where \(\:\gamma\:=\frac{C}{2}\frac{A}{m}\frac{S}{c}\) with A – area of the satellite cross-section, m – satellite mass, S – solar constant rescaled by the instantaneous Earth-Sun distance during the synodic year, c – speed of light, C – satellite surface coefficient, \(\it {\nu}_{s}\)\(\:\--\:\)true anomaly w.r.t. the Sun, \(\it {a}_{e}\) – Earth radius. These perturbations are very small because they strongly depend on \(\:{e}^{2}\). Even for Galileo in eccentric orbits the expected periodical variations of the ascending node due to SRP are of the order of 0.005º. Therefore, SRP does not cause any significant changes of the ascending node, when compared to other orbit perturbing forces.

The long-term change of the argument of perigee is also characterized by almost linear regression (see Fig. 6). Based on the theoretical consideration given by Beutler (2005), the secular drift due to C20 can be expressed as:

$$\eqalign {\overline{\dot{\omega}}\left[\frac{^\circ}{d a y}\right] & =\frac{3 \cdot 180 \cdot 86400}{4 \pi} C_{20} \sqrt{\frac{G M}{a_e^3}} \frac{1-5 \cos ^2 i}{\left(\frac{a}{a_e}\right)^{\frac{7}{2}}\left(1-e^2\right)^2} \cr &=+\frac{5.0^{\circ} \cdot\left(5 \cos ^2 i-1\right)}{\left(\frac{a}{a_e}\right)^{\frac{7}{2}}\left(1-e^2\right)^2}, \cr}$$
(10)

The drift equals 4, 7, 12.5, −2°∕year for GPS, GAL-IOV&FOC, FOC*, and GLONASS-M+, respectively. GLONASS satellites are close to the critical inclination of 63.4° where C20 does not cause any secular rates of the perigee, which explains the very small rate of perigee. For Galileo in near-circular orbit, the position of the perigee is ill-defined and affected by large errors up to hundreds of meters, as opposed to Galileo FOC E18 (SVN 201) and E14 (SVN 202), for which the position of the perigee can be well determined with the accuracy corresponding to centimeter level (see Fig. 6). For Galileo E14, the mean formal error of perigee determination is 0.2232 mas from 1-day solutions, whereas for E08 in near-circular orbit, the perigee error is 95.4684 mas (Bury et al. 2020).

Other even zonal spherical harmonics of the Earth potential also cause secular rates of perigee, whereas the odd zonal, tesseral, and sectorial harmonics cause long and short-periodic perturbations. The perigee is also perturbed by the gravitational attraction of the Moon and the Sun, as well as by all three general relativity effects, including Schwarzschild, Lense-Thirring, and De Sitter.

The dominating periodical changes in the argument of perigee from Fig. 7 correspond to half of the draconitic year. The SRP perturbations can be expressed as (Krivov et al. 1996; Lantukh et al. 2015):

$$\begin{aligned} \frac{d \omega}{d t} =&-\frac{3 a e \gamma}{2} \sqrt{\frac{a}{G M}} \frac{1}{e \sqrt{1-e^2}} \cr & \left[\left(1-e^2\right) \cos \omega \cos \left(\Omega-\nu_s\right)-\sin \omega \sin \left(\Omega-\nu_s\right) \cos i\right] .\end{aligned}$$
(11)

For Galileo FOC, \(\:\gamma\:\approx1.1\cdot\:{10}^{-7}\)m/s2 when considering the sum of the solar panel cross-section and the mean cross-section of the satellite bus. After integrating the equation, we obtain the long-periodic perturbation:

$$\eqalign {\left(\frac{d \omega}{d t}\right)_{l\_per} = & \frac{3 \pi \gamma}{n} \frac{1}{\sqrt{1-e^2}} \cr & \left[\left(1-e^2\right) \cos \omega \sin \left(\Omega-\nu_s\right)+\sin \omega \cos \left(\Omega-\nu_s\right) \cos i\right]\cr}$$
(12)

which corresponds to maximum range of periodic perturbations of about 0.4º or the amplitude of 0.2º which agrees well with the results from Fig. 7.

Fig. 6
figure 6

Time series of the argument of perigee evolution for Galileo FOC in eccentric orbits. Grey dash-dotted lines indicate the absolute elevation of the Sun above the orbital plane (\(\beta\)) (right y-axis). The black dashed lines indicate the empirical fit of the draconitic and semi-draconitic signals, as well as trend into the values. The value of the fitted trend is shown on the right above each graph. The theoretical trend as calculated using Eq. 10 is shown on the left above each graph

Full size image
Fig. 7
figure 7

Amplitude spectra of the argument of perigee evolution for Galileo FOC in eccentric orbits. The left periodogram corresponds to periods from 1 to 50 days, while the right subplot corresponds to periods from 50 to 1000 days. Please note the difference in scale between the left and right subplots. The vertical gray lines denote the harmonics of a year

Full size image

Inclination and eccentricity

Orbital eccentricity is perturbed by the direct SRP, as well as the gravitational attraction of the Moon – to the greatest extent. Smaller perturbations emerge from Earth’s gravity field and the Sun, whereas the relativistic effects do not cause any secular rates nor long-periodic perturbations of the eccentricity (Sośnica et al. 2022).

The impact of the SRP on satellite eccentricity can be derived as:

$$\eqalign {\frac{d e}{d t} = & -\frac{3 a e \gamma}{2} \sqrt{\frac{a}{G M}} \frac{1}{\sqrt{1-e^2}} \cr & \left[\sin \omega \cos \left(\Omega-\nu_s\right)-\cos \omega \sin \left(\Omega-\nu_s\right) \cos i\right],\cr}$$
(13)

and after solving for long-periodic perturbations:

$$\left(\frac{d e}{d t}\right)_{l\_per}=\frac{3 \pi \gamma}{n} \frac{e}{\sqrt{1-e^2}}\left[\sin \omega \sin \left(\Omega-\nu_s\right)+\cos \omega \cos \left(\Omega-\nu_s\right) \cos i\right] .$$
(14)

The satellites with large eccentricities show the most prominent perturbations due to SRP.

Figure 8 shows that the eccentricity of Galileo FOC E18 (SVN 201) changed from 0.155 to 0.165. For satellites in near-circular orbits, Galileo IOV, FOC, and GLONASS, the value of e shows periodic variations with two main periods corresponding to the draconitic year and its first harmonic. For GPS and Galileo in eccentric orbits, long-periodic perturbations dominate with the periods corresponding to the full maximum \(\beta\)-cycle (about 26 years for Galileo in eccentric orbits and 37 years for Galileo in circular orbits, see Table 1), i.e., \(\beta\)max period ranging from |\(\:i-\epsilon\:\)| through |\(\:i+\epsilon\:\)| to |\(\:i-\epsilon\:\)|, where \(\epsilon\) is the obliquity of the ecliptic (Sośnica et al. 2021). Inclination angles show secular-like perturbations, which are in fact long-periodic perturbations with periods of 26–40 years depending on the orbital plane (see Table 1).

Fig. 8
figure 8

Time series of the satellite orbit eccentricity (left) and inclination (right) for selected satellites. Grey dash-dotted lines indicate the absolute elevation of the Sun above the orbital plane (\(\beta\)) (right y-axis). The black dashed lines indicate the empirical fit of the trend, draconitic and semi-draconitic signals, as well as the long-periodic signal (Eq. 14 and Eq. 16 for e and i, respectively). The value of the fitted trend is shown on the right above each graph

Full size image
Fig. 9
figure 9

Amplitude spectra of the satellite orbit eccentricity (left) and inclination (right) evolution for selected satellites. The left periodogram corresponds to periods from 1 to 50 days, while the right subplot corresponds to periods from 50 to 1000 days. Please note the difference in scale between the left and right subplots. The vertical gray lines denote the harmonics of a year

Full size image

The inclination is mostly affected by gravitational perturbations due to the Earth, Moon, and Sun’s gravity field with a very small contribution from the De Sitter effect (Sośnica et al. 2021). Oppositely, Schwarzschild and Lense-Thirring do not cause any secular nor long-periodic perturbations of the inclination angles, whereas the direct SRP introduces minor variations.

SRP does not introduce any once-per-revolution perturbations in cross-track for circular orbits which are needed to change the orbital inclination. Therefore, for near-circular orbits, inclination is not affected by SRP. However, for eccentric orbits, a very small SRP effect proportional to \(\:{e}^{2}\:\)may occur due to variable satellite velocity:

$$\:\frac{di}{dt}=-\frac{3a\gamma\:}{2}\sqrt{\frac{a}{GM}}\frac{{e}^{2}\text{sin}i}{\sqrt{1-{e}^{2}}}\text{sin}\omega\:\text{c}\text{o}\text{s}(\varOmega\:-{\nu\:}_{s})\:,$$
(15)

with the periodic perturbations of:

$$\:{\left(\frac{di}{dt}\right)}_{l\_per}=\frac{3\pi\:\gamma\:}{n}\frac{{e}^{2}\text{sin}i}{\sqrt{1-{e}^{2}}}\text{sin}\omega\:\text{sin}\left(\varOmega\:-{\nu\:}_{s}\right).$$
(16)

The long-term evolution of the eccentricity and inclination shows a clear long-term oscillation. The inclination parameter exhibits similar perturbation periods to the right ascension of the ascending node, while the eccentricity – similar to the argument of perigee (Beutler 2005). This can be explained by the Gaussian perturbation equations - cross-track perturbations may change the inclination and ascending node; along-track and radial perturbations may change the semi-major axis and eccentricity; whereas the argument of perigee can be perturbed by accelerations in any direction.

Knowing the annual regression of the right ascension of the ascending node (Eq. 7) and the argument of perigee (Eq. 10), we can conclude how long it takes for the satellite orbital planes to carry out one entire revolution in the inertial system. The empirical fit of the signals with periods as discussed above matches well the observed evolution of the eccentricity and inclination with the same periods as perigee and node revolution, respectively (see Table 1).

From Fig. 8, the oscillation of the inclination has its maximum when the elevation angle of the Sun above the orbital plane (\(\beta\) angle) reaches its minimum. The eccentricity comes to its minimum along with the β angle. However, the origin of these perturbations is different, while non-gravitational SRP affects mostly the eccentricity, the observed perturbations in the inclination angle should be assigned to the gravitational perturbations.

Figure 8 shows that for GPS satellites, the value of eccentricity changed in 8 years from 0.006 to 0.020, for SVN62 (block IIF) and SVN61 (block IIR-B), respectively. Such changes correspond to a perigee change of about 150–500 km. The inclination angle of Galileo FOC 205 changed by 1.5º in 5 years, which shows how difficult the maintenance of the nominal orbit constellation is even in the absence of deep orbital resonance with the Earth’s rotation.

Tidal signals

The perturbations with the periods related to tides, i.e., 13.6 days (Mf) and 27.3 days (Mm) are visible in the series of e, i, \(\varOmega\), and ω (see, Figs. 5, 7 and 9). As these parameters describe the shape (e) and the angular orientation of the orbit, which may accumulate some effects arising from the lunar attraction, solid Earth tides, ocean tides, and Earth rotation, all of which slightly change the satellite revolution period with respect to rotating Earth. Furthermore, 24 h orbit sampling causes subdaily tidal model errors to alias at fortnightly periods, e.g. 13.6, 14.2, 14.8 days (Griffiths and Ray 2013).

Annual and semi-annual signals

All the Keplerian elements are perturbed with the annual and semi-annual oscillation or close to their draconitic and semi-draconitic periods. These are mostly caused by SRP or the gravitational attraction of the Sun (draconitic signals, Griffiths and Ray 2013; Rodriguez-Solano et al. 2014) or can originate from the Earth’s gravity field and its processes (annual signals), e.g., tidal forces, oceanic, atmospheric and hydrological loadings, thermal expansion of ground and monuments, varying tropospheric delays, multi-path variations (Klos et al. 2017). Figure 10 provides a comparison of the amplitude of the signals with periods of annual and semi-annual oscillations in the series of mean elements. These periods cannot be undoubtedly distinguished from draconitic signals for 8-year analysis, thus, they are discussed together. For the semi-major axis, the annual signal dominates and is the largest for Galileo FOC and GPS IIR-M, IIR-A and IIR-B reaching 50–75 m in amplitude, compared to only a few meters for GLONASS, Galileo IOV and GPS IIF. These perturbations can be explained by the Y-bias, which is the largest for GPS IIR and Galileo FOC.

For the eccentricity, the annual signal is also dominant for the satellites in the circular orbit (mostly due to gravitational attraction); However, the amplitude of the semi-annual signal equates to the annual signal only for the Galileo FOC 201/202 in eccentric orbits (see Fig. 10). The SRP perturbations acting on the eccentricity are proportional to the initial value of e, explaining semi-annual signals for Galileo in eccentric orbits. The semi-annual signal due to the gravitational perturbations is also the main visible in the evolution of inclination for all the satellites. The amplitude of the annual and semi-annual signals for the ascending node and the argument of perigee differ between satellites. However, for near-circular orbits, the amplitudes of perigee perturbations are unrealistic and overestimated. Interestingly, most of the GNSS satellites with prominent annual variations in the ascending node also show annual variations in the inclination angle (see Fig. 10); whereas satellites without distinct annual signals in the ascending node, have only semi-annual with no annual signal in the inclination angle.

Fig. 10
figure 10

Comparison of the amplitude of the signals with periods of the annual (1cpdy) and semi-annual (2cpdy) oscillations in the series of mean elements

Full size image

Summary and conclusions

Table 2 summarizes the main orbit perturbations of GNSS satellites causing long-periodic and secular variations of Keplerian parameters. Please note, however, that almost all of the listed forces cause short-periodic perturbations, as well. Nevertheless, we concentrate on perturbations causing secular changes of orbital elements and the major long-periodic perturbations that can be derived from the analysis of mean elements.

Even zonal harmonics of the Earth’s gravity field cause secular rates of ω and \(\varOmega\) and short-periodic terms in other Keplerian parameters. GPS resonant harmonics cause rates of the semi-major axis which are hardly distinguishable from secular rates due to their very long periods. However, the secular change of the semi-major axis implies the energy change which would violate the energy conservation law, therefore, the observed perturbations caused by resonant terms are, in fact, long-term variations. Other spherical harmonics of Earth’s potential cause short-periodic (m-daily, nth-per-revolution) and long-periodic variations of Keplerian parameters which can be analyzed using, e.g., Kaula parameterization (Kaula 1966).

Direct SRP causes once-per-revolution perturbations in the radial and along-track components and constant perturbations in cross-track (Meindl et al. 2013). Such perturbations cannot change the ascending node and inclination. However, for the orbits with large eccentricities, such as the first Galileo FOC satellites and some GPS satellites, the SRP impact on the inclination and ascending node becomes fully detectable due to variable satellite velocities. SRP remarkably affects eccentricity and the argument of perigee because these two parameters are sensitive to once-per-revolution perturbations acting in radial and along-track directions. Direct SRP does not change the semi-major axis, however, the Y-bias which can emerge from the misalignment of the solar panels or thermal effects, introduces semi-major perturbations with the largest impact for maximum β angles.

Navigation antenna thrust is the only perturbing force that does not cause any periodic variations (for circular orbits, Bury et al. 2020). Antenna thrust introduces a constant acceleration in the radial direction causing a constant radial offset and a small change in satellite mean motion. However, for satellites in eccentric orbits, antenna thrust may also cause short-periodic perturbations (Bury et al. 2019, 2020).

The gravitational attraction of the Moon and Sun causes perturbations in all Keplerian parameters in the form of long-periodic perturbations (see Table 2). Different tidal-like periods can be found in the spectral analysis of Keplerian parameters. The impact of the Sun on satellite eccentricity for near-circular orbits is minor when compared to other orbit-perturbing sources. Some perturbations repeat with a very long period of several years (see Table 1) due to the very long β-cycle and full revolution of the inclination angle with respect to the ecliptic plane.

Table 2 Main orbit perturbing sources and their effects on Keplerian parameters; s denotes secular effect, lp denotes main long-periodic perturbations, s* denotes a long-term resonant perturbation undistinguishable from secular rates, e* applies to the orbits with large eccentricities with long-term perturbations, - denotes only short-periodic variations (m-daily or nth-per-revolution) or long-periodic perturbations of minor impact. E and R denote Galileo and GLONASS, respectively
Full size table

The main relativistic effect due to Earth-induced spacetime curvature – Schwarzschild – introduces perturbations for the radial component in the case of circular orbits or radial and along-track components for eccentric orbits. Such perturbations do not affect inclination and ascending node, however, they imply short-periodic variations of the semi-major axis and eccentricity especially for eccentric orbits (Sośnica et al. 2022). Schwarzschild effect also causes secular rates of the perigee which was proven for Mercury’s orbit underlying the whole theory of general relativity. The Lense-Thirring relativistic effect is due to the angular momentum of the rotating Earth. This effect causes secular rates of the ascending node and perigee. Lense-Thirring may also cause short-periodic variations of the eccentricity and inclination of a very small amplitude (Sośnica et al. 2022). De Sitter caused by spacetime curved by the Sun along which the Earth moves with its satellites, introduces secular rates of the ascending node and perigee, long-periodic variations of the inclination, and short-periodic eccentricity perturbations. However, the impact of De Sitter depends on satellite inclination and the phase of the β-cycle, i.e., the actual satellite-Earth-Sun geometry (Sośnica et al. 2022).

Please note that the perturbations due to the relativistic effects are small when compared to gravitational and non-gravitational perturbations. However, they become detectable with the current accuracy of satellite measurements, e.g., the mean secular rate of the ascending node due to the De Sitter effect corresponds to 19.185 mas/y which gives a drift of 7.2 mm/day at the Galileo heights after 1 day or 2.6 m after one year. Nevertheless, the observed changes in Keplerian parameters are typically dominated by the main perturbations, whereas the extraction of minor effects requires special computational procedures or orbital constellations, such as the butterfly configuration.