Abstract
In ionospheric modeling, the differential code biases (DCBs) are a non-negligible error source, which are routinely estimated by the different analysis centers of the International GNSS Service (IGS) as a by-product of their global ionospheric analysis. These are, however, estimated only for the IGS station receivers and for all the satellites of the different GNSS constellations. A technique is proposed for estimating the receiver and satellites DCBs in a global or regional network by first estimating the DCB of one receiver set as reference. This receiver DCB is then used as a ‘known’ parameter to constrain the global ionospheric solution, where the receiver and satellite DCBs are estimated for the entire network. This is in contrast to the constraint used by the IGS, which assumes that the involved satellites DCBs have a zero mean. The ‘known’ receiver DCB is obtained by simulating signals that are free of the ionospheric, tropospheric and other group delays using a hardware signal simulator. When applying the proposed technique for Global Positioning System legacy signals, mean offsets in the order of 3 ns for satellites and receivers were found to exist between the estimated DCBs and the IGS published DCBs. It was shown that these estimated DCBs are fairly stable in time, especially for the legacy signals. When the proposed technique is applied for the DCBs estimation using the newer Galileo signals, an agreement at the level of 1–2 ns was found between the estimated DCBs and the manufacturer’s measured DCBs, as published by the European Space Agency, for the three still operational Galileo in-orbit validation satellites.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
In the last few decades, specialized Global Navigation Satellite System (GNSS) Ionospheric Scintillation Monitor Receivers (ISMRs), such as the NovAtel/AJ Systems GSV4004 and the Septentrio PolaRxS Pro, have been developed with a view to support continuous ionospheric modeling by estimating total electron content (TEC) and different scintillation parameters. However, it is not a straightforward task to derive accurate TEC information from these specialized receivers because the recorded code-based pseudorange measurements are contaminated by instrumental biases, the so-called differential code biases (DCBs), existing between the code observations from different frequencies, at both the satellite and receiver ends (Wilson and Mannucci 1993). Considering these existing hardware delays to be stable for reasonable periods of time, the recorded TEC measurements have been used quite successfully on a relative basis in a number of experiments. Yet, to enable the calculation of absolute TEC for ionospheric monitoring, these receivers must be calibrated to account for their respective DCBs. Ignoring the satellite and receiver DCBs when computing TEC may result in an error of up to 20 TECU (or 7 ns) for satellites and 40 TECU (or 14 ns) for receivers, and their cumulative effect can reach as much as 100 TECU (or 35 ns) in extreme cases (Sardón et al. 1994). If not accounted for, these can also sometimes lead to non-physical negative TEC values (Ma and Maruyama 2003; Mylnikova et al. 2015). This could become even worse for the more recent new GNSS signals and hence cannot be ignored (Montenbruck et al. 2014; Wang et al. 2016).
With the advent of modernized GPS, GLONASS and the new Galileo and Beidou signals in addition to the legacy GPS and GLONASS signals, a variety of signal pairs is available to compute TEC. However, the associated DCBs and different available tracking modes, such as pilot only and combined, make the accurate TEC computation even more challenging.
Van Dierendonck (1999) and Van Dierendonck and Hua (2001) defined a calibration procedure for GSV4004 monitors, by comparing their estimated TEC data with a ‘reference’ TEC, such as that generated by the International GNSS Service (IGS) or a space-based augmentation system (SBAS), an approach attempted in Dodson et al. (2001). Additionally, different algorithms for computing these DCBs have also been proposed in the past. For single station receiver DCB estimate, these can be roughly categorized in two groups (Arikan et al. 2008; Komjathy et al. 2005; Li et al. 2014, 2016). The first group models vertical TEC (VTEC) as a polynomial that is a function of ionospheric pierce point coordinates in a coordinate system referenced to the earth–sun axis. Both the satellite and receiver DCBs are considered as unknowns along with other coefficients and are solved for in a least squares (LSQ) solution (Lanyi and Roth 1988; Sardón et al. 1994; Jakowski et al. 1996; Lin 2001; Otsuka et al. 2002, Rao 2007; Yuan et al. 2007; Mayer et al. 2011; Durmaz and Karslioglu 2015). The second group uses the method of minimization of the standard deviation of VTEC using different receiver trial biases and the one that minimizes the standard deviation of computed VTEC is chosen as the receiver bias for that particular station (Ma and Maruyama 2003; Zhang et al. 2003; Komjathy et al. 2005; Arikan et al. 2008, Montenbruck et al. 2014).
The published DCB products are routinely estimated by different analysis centers (ACs) of the IGS as a by-product of their local or global ionospheric analyses for almost all the available satellites in different constellations and a selected number of IGS or Multi-GNSS Experiment (MGEX) stations. A linear geometric combination of code-based pseudoranges is employed by the ACs to derive the DCBs on a daily basis along with a set of ionospheric coefficients. However, this is a rank deficient system and an external constraint must be employed to break the rank deficiency and separate the satellite DCBs from the receiver DCBs. This is normally achieved by constraining the mean of the satellites DCBs to zero, in a so-called ‘zero mean constraint.’ Consequently, with the routine changes carried out in the satellite constellations, frequent jumps can be observed in the estimated DCBs (Zhong et al. 2015). On the other hand, the problem of rank deficiency can also be resolved by constraining the solution to a known receiver DCB in the network instead. The advantage of using this approach is that a more realistic and stable set of satellite and receiver DCBs are estimated.
For global TEC monitoring and other related applications, it would be straightforward to carry out the analysis provided the receiver with the known DCB is part of the IGS/MGEX network. However, as in a general situation this receiver will not be part of the network, its DCB must be obtained from the manufacturer or otherwise carefully estimated through a technique that can ensure that it is consistent with the available set of satellite DCBs. We hereby introduce a technique for satellite and receiver DCB estimation by first estimating the DCB of an available receiver through simulation and afterward ‘inserting’ this receiver in a global network for processing. For carrying out this technique, a Septentrio PolaRxS Pro ISMR, referred to hereafter as ‘SEPT,’ was used in conjunction with the Spirent GSS8000 hardware simulator, in a simulation where the state of the ionosphere, troposphere and the other group delays could be controlled, as demonstrated in Ammar (2011). Once the receiver DCB has been estimated, it is then used to constrain the solution in a global network of stations following the strategy implemented by the Centre of Orbit Determination in Europe (CODE), to ultimately estimate the DCBs of the satellites and all the other receivers involved in the network (Schaer 1999). The final results should produce a consistent set of stable DCBs, which are now closer to their physical values and therefore more representative to be employed in any TEC monitoring application. For validation purposes, another Septentrio PolaRxS Pro ISMR and a Javad Triumph-I receiver are also involved. These are referred to hereafter as ‘SEP2’ and ‘JAVD,’ respectively. Moreover, the idea of working with an ISMR as a primary receiver was originally conceived because of the specific feature of this receiver to estimate TEC for ionospheric monitoring purposes, where the estimation of DCBs is desirable so that absolute and calibrated TEC can be obtained. Nevertheless, the proposed technique can be applied to any conventional multi-frequency, multi-constellation receiver, as long as its capabilities can be reflected in the GNSS simulator.
It is important to remember that the calibrated DCBs obtained via simulators can vary between simulators based on their ability to generate high quality signals and on their intrinsic hardware delays. Further complications can arise from the fact that there may exist differences between live and simulated signals depending on correlator spacing and multipath mitigation techniques (Hauschild and Montenbruck 2016). This would not be a problem in TEC monitoring due to relative time independence of the satellites and receivers DCBs, but for other precise operations such as time transfer, this must be given due consideration.
DCB in the context of TEC estimation
For a specific GNSS constellation, the difference of two code-based pseudorange measurements obtained from two signals, in linear units, equals the sum of the differential ionospheric path delays and the respective satellite and receiver DCBs. If both signals share the same frequency, as in the case of C1 and P1, the combined satellite and receiver DCB equals the average difference of the respective code measurements (Montenbruck and Hauschild 2013). This can be written as follows:
Here, the superscript ‘s’ and the subscript ‘r’ are used to refer to satellite and receiver, respectively. The subscripts ‘i’ and ‘j’ can be 1, 2 or 5 depending upon the carrier frequency in use. Also, \(P_{{i,{\text{r}}}}^{\text{s}}\) and \(P_{{j,{\text{r}}}}^{\text{s}}\) are the code pseudorange observables on carrier frequencies L i and L j with corresponding ionospheric delays as \(I_{i}\) and \(I_{j}\), respectively. The frequency-dependent ionospheric delay (in meter) can be further written in the generalized form as follows:
\(f_{L}\) refers to the frequency (in Hz) of the signal L, and \({\text{STEC}}\) is the Slant TEC (in meter) between the satellite transmitter and the receiver antenna.
Working with GPS, the correction parameter for the satellite DCB between P1 and P2 pseudoranges on GPS L1 and L2 signals (or \({\text{DCB}}_{P1 - P2}^{{ {\text{s}}}}\)) is referred to as the estimated group delay differential or TGD and this is provided to the users through the broadcast message. The relation between satellite \({\text{DCB}}_{P1 - P2}^{{ {\text{s}}}}\) and TGD is given as follows (IS-GPS-200H 2014):
where for GPS L1 and L2 frequencies,
Using (2)–(4) and the definition of 1 TEC Unit (TECU) which is equal to 1016 electrons/m2, the standard equation that can be used in any dual frequency receiver generating P1 and P2 to compute STEC in TECU can be written as follows:
Similarly, working with Galileo E1 and E5a code observables, the STEC equation can take the following form:
where \({\text{DCB}}_{{{\text{r}},E1 - E5a}}\) is the differential code bias between Galileo E1 and E5a signals and \(B_{\text{GD}}\), i.e., the broadcast group delay is the correction parameter for \({\text{DCB}}_{E1 - E5a}^{\text{s}}\) as transmitted in the navigation message by the Galileo satellites.
For either (5) or (6), if the terms STEC, TGD and BGD are controlled in simulation by setting them to 0, then the DCB of the receiver can directly be estimated from the observations. Here we assume that the simulator DCB is negligible and can be ignored.
M_DCB software
Jin et al. (2012) developed an open-source M_DCB software package in MATLAB to estimate the global or regional receivers and GPS satellites DCBs. This is based on the CODE’s global ionospheric analysis strategy in which the VTEC is expressed as a spherical harmonic expansion of a degree and order 15. Differences of less than 0.7 ns and an RMS of less than 0.4 ns were found to exist between the M_DCB software and IGS ACs products (e.g., JPL, CODE and IGS combined). We modify this software to not only handle the external constraint of known receiver DCB but also to handle the newer GPS L5 and Galileo E1 and E5a signals, which were not covered in the original package. Hereafter, the revised version of the M_DCB software with the external constraint of zero mean condition on the satellites DCBs is referred to as the ‘DCB_ZM,’ whereas with the external constraint of known receiver DCB, it is referred to as the ‘DCB_FIX.’
Receiver DCB estimation using simulation (methodology)
The approach that was followed to estimate the receiver DCB was to use the Spirent GSS8000 hardware signal simulator to generate all possible GNSS signals without ionospheric and tropospheric delays, as well as eliminating simulated satellite signal delays such as TGD and BGD by setting them to 0. The Septentrio PolaRxS (SEPT) receiver was set to track these simulated signals under default tracking loop parameters with no multipath mitigation as presented in Table 1. From the recorded RINEX observations, the STEC was computed based on (5) for GPS and (6) for Galileo depending upon the signal combination, using all the available satellites. The mean of the computed STEC for all the satellites essentially gave the DCB of the receiver for a particular signal combination. The same methodology was followed for the DCB estimation of SEP2 and JAVD receivers, and the different tracking parameters applied to these receivers are also presented in Table 1.
Cable DCB
The antenna cable is commonly considered a non-dispersive medium (Defraigne et al. 2014). However, Dyrud et al. (2008) showed that a small constant variation of 0.004 m or approximately 13 ps (picoseconds) can exist in the absolute DCB of the receiver system while working with different cable lengths. Working on a similar strategy with different lengths of the RG213 coaxial cables ranging from 1 to 30 m, Ammar (2011) also showed variations of up to 35 ps in the estimated DCB between P1 and P2 pseudoranges using simulated data. These small variations in the absolute DCB of the receiver system with varying cable lengths can be explained on the basis of the additional noise that the longer cables introduce in the pseudorange measurements in comparison to the shorter ones. To rule out any minor effect coming from the cable, the same antenna cable of 20 m length was used with the SEPT receiver both to connect it with the simulator and to connect it with the antenna for open sky data collection. On the other hand, the same was not possible for the other two receivers, SEP2 and JAVD, because of the difficulty in taking existing routed cables out of the building fixtures. Therefore, to keep the noise level to a minimum, the smallest available 1-m cable was used to connect them to the simulator during the estimation of their respective DCBs.
Antenna DCB
The antenna DCB (also referred to as the differential group delay) should also be given due importance because in an open sky situation it obviously forms part of the overall DCB of the data recording system comprising the antenna, the cable and the receiver itself.
For the specific NovAtel GPS 702GG antenna that was used initially with the SEPT receiver, the DCB of − 2.7 ns was provided by the manufacturer between L1 and L2. It was measured at 23 °C and with 4.53 V power supply (NovAtel 2016).
For the Leica AR10 antennas that were used initially with the SEP2 and JAVD receivers, the DCB value of 3 ns between L1 and L2 was provided (Leica 2016). This is not antenna specific and is just the maximum DCB value as estimated by the manufacturer at 22 °C for all the Leica AR10 antennas. More recently, to accommodate the newer GPS L5 and Galileo signals, the antenna used with the SEPT receiver has been upgraded to the NovAtel GPS 703GGG. For this particular antenna, the DCBs between L1 and L2 and between L1 and L5, as computed by the manufacturer at 25 °C and with 4.5 V power supply, are 2.2 and 1.3 ns, respectively (NovAtel 2016). SEP2 antenna has also been upgraded to Septentrio choke ring antenna, but no differential group delay value has been provided by the manufacturer.
Satellites and receivers DCBs estimation from real data (methodology)
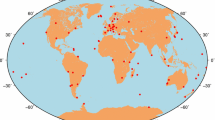
Initially ‘Network A’ of 96 stations, comprising of 93 IGS stations and 3 additional stations, namely SEPT, SEP2 and JAVD that were set up at the Nottingham Geospatial Institute (NGI), was chosen to be part of the global ionospheric analysis using the DCB_FIX software. These stations are represented by red dots in Fig. 1. For consistency and compatibility with the original M_DCB software, these stations were specifically selected to consist of GPS P1, P2 receiver types only. The estimated DCBs from the DCB_FIX software are later compared with the IGS published daily DCB estimates given in IONEX format. The estimated ionospheric coefficients as part of the LSQ processing are not analyzed in any way for the generation of global ionospheric maps (GIMs).
To incorporate the modernized GPS L5 signal and the newer Galileo E1 and E5a signals, a new network of 41 stations comprising of 39 IGS or MGEX stations and 2 NGI stations, i.e., SEPT and SEP2, was chosen to be part of the DCB estimation using the DCB_FIX software. This network is referred to as ‘Network B,’ and the corresponding stations are represented by green dots in Fig. 1. Also, this network selection was dictated by the fact that the SEPT receiver incorporates a pilot only tracking technique and limited receivers in the IGS or MGEX network are currently available with the same tracking technique. While Li et al. (2016) were able to use a network of 100 plus stations tracking Galileo based on their localized ionospheric modeling, it can still be a problem for the research groups working with a global ionospheric model to obtain a good spread of stations worldwide. Finally, the blue dots in Fig. 1 are the stations that are common in both the networks.
Results for estimated receivers DCBs using simulation
To estimate the DCB of the SEPT receiver, data from three 26-h simulations was captured, where the ionosphere, troposphere and the group delays are set to 0. The simulated signals are recorded by the SEPT receiver using a 20 m RG213 coaxial cable. The first two hours of the simulations are discarded to allow for the simulator and receiver hardware to reach stable operating temperatures. The DCBs for the desired signal combinations are computed independently from the code-based pseudoranges as recorded in the RINEX files.
Figures 2 and 3 show the estimated DCBs for the SEPT receiver between GPS P1/P2, C1/P1, C1/P2, C1/C5 and Galileo E1/E5a. The mean and one sigma standard deviation of these DCBs (in ns) across the three simulations were found to be − 1.70 ± 0.53, 0.03 ± 0.09, − 1.67 ± 0.52, − 4.97 ± 0.44 and − 5.21 ± 0.26, respectively. The consistency between these estimates was confirmed by verifying the following relation:
Following the same methodology, Figs. 4 and 5 show the DCB estimates for SEP2 and JAVD receivers, respectively, for only the GPS P1/P2 code combination. The mean and one sigma standard deviation of these DCBs (in ns) across the three simulations were found to be − 1.90 ± 0.31 and 6.83 ± 1.35, respectively.
From Figs. 2 to 5, it can be seen that the ISMRs present a lower noise level than the JAVD receiver even without the application of carrier phase smoothing. However, keeping in mind that the ISMRs are working under different tracking parameters (Table 1), a fair comparison would only be possible by using a consistent set of tracking parameters for all the three receivers.
Results for estimated satellites and receivers DCBs using Network A (GPS P1/P2 only)
Using the DCB_FIX software with the archived RINEX data of 96 stations (Network A) from March 17 to April 7, 2016 (22 days), and the spherical harmonics of degree and order 15, the processing was run on a day to day basis with the solution constrained to the known DCB value of the SEPT receiver system. A known DCB value of − 4.41 ns was used for the SEPT receiver system which is the sum of the antenna DCB (see the section on antenna DCB) and the mean receiver DCB as computed in the previous section. Also, the selection of these 22 days was made on the basis that two additional receivers, i.e., SEP2 and JAVD, were available during that time to validate the results along with their antenna DCBs.
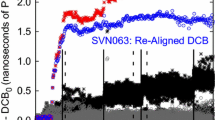
In Figs. 6 and 7, the red curves show the mean DCBs as estimated by the IGS, whereas the blue curves show the mean DCBs as estimated by the DCB_FIX software. Note that the mean DCB for both the satellites and receivers is computed over a period of 22 days. Also, in Fig. 6, the GPS satellites are grouped together as per the different family blocks to which they belong. It can be observed that a similar pattern exists between the IGS computed DCBs and the DCBs estimated through the DCB_FIX software. However, stable mean offsets of − 3.47 ns for satellites and + 3.54 ns for receivers were found to exist between the estimated DCBs and the IGS published DCBs. A possible explanation is that the zero mean satellite DCB constraint, although effective to break the rank deficiency, imposes an artificial shift on the estimated DCBs. By using a more realistic constraint in the form of a properly estimated receiver DCB, the resulting DCBs are closer to their actual values. The more accurate the known DCB used to constrain the solution, the more accurate the estimated DCBs for the other receivers and satellites.
The DCB estimates for SEP2 and JAVD receiver systems from the DCB_FIX software and the DCB_ZM software are investigated as per in Table 2:
Since the maximum DCB value of 3 ns for Leica AR10 antenna has been used to compute the overall known DCB of the two receiver systems as discussed in the earlier section on antenna DCB, it is quite remarkable that the DCB_FIX software has been able to estimate the DCBs for the two receiver systems within few tenths of a nanosecond. The accuracy of the DCB estimated by the DCB_FIX is also independent of the fact that the SEP2 receiver is of a relatively higher quality in comparison with the geodetic grade JAVD receiver. When constrained by the zero mean condition, the DCB_ZM software produces DCB estimates comparable to the IGS DCB solution and it can be seen from Table 2 that the latter are over estimated by about 3.5 ns. On the other hand, the satellite DCBs estimated by IGS are under estimated by approximately the same amount when compared to those estimated by the DCB_FIX software (Fig. 6).
It can also be seen from Fig. 6 that the satellite DCBs for the newer generation of GPS block IIF satellites are lower than the previous generation of satellites. One possible explanation can be that with the advancement in technology, the newer satellites are better equipped in terms of quality of hardware to handle in-orbit temperatures and hence possess lower DCBs. The temperature sensitivity for signals transmitted by satellites in orbit is discussed in Coco et al. (1991).
Stability of estimated DCBs (GPS P1/P2 only)
To investigate the stability of the estimated DCBs using the DCB_FIX software, the standard deviations of both the satellites and the receivers DCBs are plotted in Figs. 8 and 9 respectively. The estimated DCBs are generally stable over time for both the satellites and the receivers. The average standard deviations of the estimated satellite and receiver DCBs are found to be 0.15 and 0.45 ns, respectively. Sudden jumps in standard deviations may indicate a possible replacement of the satellite or receiver or any part of the receiver system, such as antennas and cables. In some cases, it can also indicate potential hardware issues within the receiver or receiver architecture. These are, however, difficult to investigate because of the independent working of the IGS and MGEX stations. In Fig. 9, a peak can be observed in the standard deviation of ‘PALV’ receiver system DCB—this is because the receiver was changed on the March 29, 2016, as published in the station log file (https://igscb.jpl.nasa.gov/igscb/station/log/ palv20160329.log) and the replacement receiver has a significantly different DCB. As receivers from the same brand have relatively similar DCBs, it can be difficult to identify their replacement based on the standard deviations’ figures only.
In all the above data processing with DCB_FIX or DCB_ZM software, the quality of the LSQ solution is analyzed based on the a posteriori unit variance or the standard error of observation, which is generally found to be independent of the external constraints, whether artificial or real. Therefore, the quality of the LSQ solution can only be improved by using a more refined model in the global ionospheric analysis.
Results for estimated satellites and receivers DCBs using Network B (Galileo E 1/E 5a only)
Using the DCB_FIX software with the archived RINEX data of 41 stations (Network B) from October 4, 2016, up to November 15, 2016 (43 days), and a degree and order of 15 for the spherical harmonics, the processing was run on a day to day basis, constrained by the known DCB value between Galileo E1 (C1C) and E5a (C5Q) signals for the SEPT receiver system. This value was estimated in simulation using the previously explained strategy as − 3.91 ns.
From the estimated satellite and receiver DCBs, the results with a relatively higher average standard deviation of 0.54 and 1.24 ns, respectively, have been observed. Also, the DCB estimates of some of the stations and the Galileo E24 satellite have been ignored in the computation of these standard deviations because abnormally high DCBs were estimated on some days of the processing. One possible explanation for these abnormalities and relatively higher standard deviations is that the hardware technology that is currently in place to transmit and process these newer signals is still under test phase and in the process of refinement. For the sake of conciseness, the figures showing the estimated satellites and receivers DCBs are not presented. Table 3 compares for three Galileo IOV (in-orbit validation) satellites, the DCBs estimated using the DCB_FIX software with the manufacturer measured DCBs that have recently been published by the European Space Agency (ESA) on its website (Galileo 2016). Note that these published values for IOVs are based on absolute calibration carried out on ground against a payload verification system.
It can be seen from Table 3 that the DCB estimates from the DCB_FIX software agree with the manufacturer measured on ground DCBs at the level of 1 to 2 ns. The results obtained by the DCB_FIX software are expected to improve further once the simulator DCB is accounted for in this processing strategy. Minor improvements have also been observed in the DCB estimation by increasing the degree and order of the spherical harmonics in the global VTEC expression.
Results for estimated STEC using different calibration strategies (GPS P1/P2 only)
Based on Eq. (5) and using daily RINEX datasets, the STEC is estimated for different co-located receivers in the network, with the purpose of comparing the different STEC estimation strategies. The uncalibrated STEC refers to the case where no DCBs were applied and the calibrated STEC refers to the case where either IGS published DCBs or DCB_FIX estimated DCBs were applied.
Figure 10 shows the STEC plots constructed on the basis of different calibration strategies for PRN 24, as observed by the three NGI receivers, i.e., SEPT, SEP2 and JAVD, on the ionospherically quiet day of March 26, 2016. The improvement and consistency in the estimated STEC as observed by three different receivers can be clearly seen from these plots between uncalibrated and calibrated solutions. It is also apparent that, in comparison with the highly specialized ISMRs such as SEPT and SEP2, the geodetic grade receiver, the Javad Triumph − 1, can also be used to generate almost similar STEC, if receiver and satellite DCBs can be properly estimated. Here, one minor concern would be the increased noise level in the JAVD’s TEC measurements even after the application of smoothing. However, as previously stated, a fair comparison would only be possible by using a consistent set of tracking parameters for all three receivers. Note that all three receivers are connected separately to three different antennas and were operating under different tracking parameters, as presented in Table 1.
From Fig. 10, it can also be observed that there is a good agreement between IGS (or DCB_ZM) calibrated and DCB_FIX calibrated STEC plots. This demonstrates that for all practical purposes of ionospheric modeling, using the ‘known’ receiver DCB as an external constraint in comparison to the IGS strategy represents a perfectly valid way of resolving the rank deficiency problem.
Estimation of simulator DCB (For GPS P1/P2 Only)
As contrary to our earlier assumption of negligible simulator DCB, a strategy was devised to estimate the contribution of the simulator in the DCB estimation by involving the IGS AMC2 station. From the log file of AMC2 station (https://igscb.jpl.nasa.gov/igscb/station/log/amc2_20140915.log), it can be seen that the individual hardware delays existing between different components of the system such as antenna, antenna cable, antenna splitter, receiver, etc., have already been measured and applied to the raw code-based pseudoranges. Although not knowing exactly how these individual delays are measured, it is considered here that the measurements are done accurately enough. Based on that assumption, one can expect to get a DCB value close to 0 for this station when estimating DCBs using a ‘known’ receiver DCB, provided that the ionosphere has been correctly modeled. As shown in Fig. 7, by using the DCB_FIX software, a mean DCB value of + 1.62 ns was estimated for this station, implying therefore that a value of − 1.62 ns with some uncertainty can be interpreted to represent the DCB of the simulator itself existing between GPS P1 and P2 signals. Hence, it can be inferred that the simulator DCB for a certain signal combination can be measured by exploiting the proposed strategy in conjunction with a station receiver with accurately known hardware delays and this would further push the estimated DCBs toward their physical values.
Conclusions
-
1.
A hardware signal simulator such as the Spirent GSS8000 can be effectively used to estimate a consistent set of DCBs between different signal combinations for any multi-frequency, multi-constellation receiver. The proposed technique can be improved further by accounting for the simulator delays as well.
-
2.
The receiver DCB is often mistaken as a function of the receiver hardware only. This is in fact not true because in an open sky situation, the receiver DCB refers to the DCB of the entire ‘system’ comprising of antenna, cable and the receiver itself. Therefore, it should be ensured that if a receiver DCB is to be used to estimate the satellites and receivers DCBs in a regional or global network, the DCB of the whole system is used to constrain the solution; otherwise, one can expect variations in the estimated DCBs with the changing system components such as antenna, cable, splitter.
-
3.
Since the IGS is generating DCBs for only a selected number of terrestrial stations, the technique proposed offers an alternative way of locally estimating the DCB of any receiver—satellite system using the DCB_FIX software. The advantage would be that the changes in the constellation will not affect the DCB estimation, unlike when any other constraint is used.
-
4.
A good agreement at the level of 1 to 2 ns was found to exist between the estimated DCBs from the DCB_FIX software and the manufacturer measured on ground absolute DCBs for the 3 Galileo IOVs satellite as published by the ESA.
-
5.
The comparison between calibrated and uncalibrated STEC estimation clearly shows the improvement and consistency in the estimated STEC techniques between the different receiver types. Relative to highly specialized ionospheric scintillation monitor receivers, a geodetic grade receiver like Javad Triumph − 1 can also be used to compute STEC provided that the receiver and satellite DCBs are properly estimated and applied.
-
6.
A good agreement between the IGS (or DCB_ZM) and DCB_FIX calibrated STEC plots was demonstrated. This also demonstrates that for all practical purposes of ionospheric modeling, using the ‘known’ receiver DCB as an external constraint is a demonstrated valid way of resolving the rank deficiency problem that arises when computing DCB estimations for receiver/satellite network.
References
Ammar M (2011) Calibration of ionospheric scintillation and total electron content monitor receivers. M.Sc. Dissertation, University of Nottingham
Arikan F, Nayir H, Sezen U, Arikan O (2008) Estimation of single station interfrequency receiver bias using GPS-TEC. Radio Sci. https://doi.org/10.1029/2007RS003785
Coco DS, Coker C, Dahlke SR, Clynch JR (1991) Variability of GPS satellite differential group delay biases. IEEE Trans Aerosp Electron Syst 27(6):931–938
Defraigne P, Aerts W, Cerretto G, Cantoni E, Sleewaegen JM (2014) Calibration of Galileo signals for time metrology. IEEE Trans Ultrason Ferroelectr Freq Control 61(12):1967–1975
Dodson AH, Moore T, Aquino MH, Waugh S (2001) Ionospheric scintillation monitoring in northern Europe. In: Proceedings of ION ITM. Institute of Navigation, Salt Lake City, UT, Sept 11–14, pp 2490–2498
Durmaz M, Karslioglu MO (2015) Regional vertical total electron content (VTEC) modeling together with satellite and receiver differential code biases (DCBs) using semi-parametric multivariate adaptive regression B-splines (SP-BMARS). J Geod 89(4):347–360. https://doi.org/10.1007/s00190-014-0779-8
Dyrud L, Jovancevic A, Brown A, Wilson D, Ganguly S (2008) Ionospheric measurement with GPS: receiver techniques and methods. Radio Sci. https://doi.org/10.1029/2007rs003770
Galileo (2016) Galileo IOV satellite metadata. https://www.gsc-europa.eu/support-to-developers/galileo-iov-satellite-metadata
Hauschild A, Montenbruck O (2016) A study on the dependency of GNSS pseudorange biases on correlator spacing. GPS Solut 20(2):159–171. https://doi.org/10.1007/s10291-014-0426-0
IS-GPS-200H (2014) Navstar GPS space segment/navigation user interface control document. http://www.gps.gov/technical/icwg/IS-GPS-200H.pdf
Jakowski N, Sardon E, Engler E, Jungstand A, Klaehn D (1996) Relationships between GPS-signal propagation errors and EISCAT observations. Ann Geophys 14(12):1429–1436
Jin R, Jin SG, Feng G (2012) M_DCB: matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solut 16(4):541–548
Komjathy A, Sparks L, Wilson BD, Mannucci AJ (2005) Automated daily processing of more than 1000 ground-based GPS receivers for studying intense ionospheric storms. Radio Sci. https://doi.org/10.1029/2005RS003279
Lanyi G, Roth T (1988) A comparison of mapped and measured total ionospheric electron content using global positioning system and beacon satellite observations. Radio Sci 23(4):483–492
Leica Support Team – Personal Communication (email) (2016)
Li Z, Yuan Y, Fan L, Huo X, Hsu H (2014) Determination of the differential code bias for current BDS satellites. IEEE Trans Geosci Remote Sens 52(7):3968–3979. https://doi.org/10.1109/TGRS.2013.2278545
Li M, Yuan Y, Wang N, Li Z, Li Y, Huo X (2016) Estimation and analysis of Galileo differential code biases. J Geodesy 91(3):279–293. https://doi.org/10.1007/s00190-016-0962-1
Lin LS (2001) Remote sensing of ionosphere using GPS measurements. In: Proceedings of 22nd Asian conference on remote sensing, vol 1. Singapore, pp 69–74
Ma G, Maruyama T (2003) Derivation of TEC and estimation of instrumental biases from GEONET Japan. Ann Geophys 21(10):2083–2093
Mayer C, Becker C, Jakowski N, Meurer M (2011) Ionosphere monitoring and inter-frequency bias determination using Galileo: first results and future prospects. Adv Space Res 47(5):859–866
Montenbruck O, Hauschild A (2013) Code biases in multi-GNSS point positioning. In: Proceedings of ION ITM. Institute of Navigation, San Diego, California, Jan 29–27, pp 616–628
Montenbruck O, Hauschild A, Steigenberger P (2014) Differential code bias estimation using multi-GNSS observations and global ionosphere maps. Navigation 61(3):191–201
Mylnikova AA, Yasyukevich YuV, Kunitsyn VE, Padokhin AM (2015) Variability of GPS/GLONASS differential code biases. Results Phys 5:9–10
NovAtel Support Team – Personal Communication (email) (2016)
Otsuka Y, Ogawa T, Saito A, Tsugawa T, Fukao S, Miyasaky S (2002) A new technique for mapping of total electron content using GPS in Japan. Earth Planets Space 54(1):63–70
Rao GS (2007) GPS satellite and receiver instrumental biases estimation using least squares method for accurate ionosphere modelling. J Earth Syst Sci 116(5):407–411. https://doi.org/10.1007/s12040-007-0039-x
Sardón E, Rius A, Zarraoa N (1994) Estimation of the transmitter and receiver differential biases and the ionospheric total electron content from Global Positioning System observations. Radio Sci 29(3):577–586
Schaer S (1999) Mapping and predicting the Earth’s ionosphere using the Global Positioning System. Ph.D. thesis, University of Bern
Van Dierendonck AJ (1999) Eye on the ionosphere: measuring ionospheric scintillation events from GPS signals. GPS Solut 2(4):60–63. https://doi.org/10.1007/PL00012769
Van Dierendonck AJ, Hua Q (2001) Measuring ionospheric scintillation effects from GPS signals. In: Proceedings of ION 57th annual meeting. Institute of Navigation, Albuquerque, NM, June 11–13, pp 391–396
Wang N, Yuan Y, Li Z, Montenbruck O, Tan B (2016) Determination of differential code biases with multi-GNSS observations. J Geod 90(3):209–228
Wilson BD, Mannucci AJ (1993) Instrumental biases in ionospheric measurements derived from GPS data. In: Proceedings of ION GPS 1993. Institute of Navigation, Salt Lake City, UT, Sept 22–24, pp 1343–1351
Yuan YB, Huo XL, Ou JK (2007) Models and methods for precise determination of ionospheric delay using GPS. Prog Natl Sci 17(2):187–196
Zhang Y, Wu F, Kubo N, Yasuda A (2003) TEC measurement by single dual-frequency GPS receiver. In: Proceedings of international symposium on GPS/GNSS. Tokyo, 351–358
Zhong J, Lei J, Dou X, Yue X (2015) Is the long-term variation of the estimated GPS differential code biases associated with ionospheric variability? GPS Solut 20(3):313–319
Acknowledgements
M. Ammar is grateful to the National University of Sciences and Technology (NUST), Pakistan, and to the Faculty of Engineering at the University of Nottingham for sponsoring this research. This work was supported by the Engineering and Physical Sciences Research Council (Grant No. EP/H003479/1). The authors would also like to thank the International GNSS Service, the Multi-GNSS Experiment Service, NovAtel Inc., Spirent Communications plc and Leica Geosystems AG for supporting this research work. A special acknowledgement is given to Septentrio and, in particular, to Jean-Marie Sleewaegen for providing us with invaluable support during the entire research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ammar, M., Aquino, M., Vadakke Veettil, S. et al. Estimation and analysis of multi-GNSS differential code biases using a hardware signal simulator. GPS Solut 22, 32 (2018). https://doi.org/10.1007/s10291-018-0700-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-018-0700-7