Direct and inverse identification of constitutive parameters from the structure of soft tissues. Part 1: micro- and nanostructure of collagen fibers

Abstract

Soft tissues are characterized by a nonlinear mechanical response, highly affected by the multiscale structure of collagen fibers. The effectiveness and the calibration of constitutive models play a major role on the reliability and the applicability of computational models in biomechanics. This paper presents a procedure for the identification of the relationship between collagen-related structural features in soft tissues with model parameters of classical polynomial- and exponential-based constitutive models. Histological features at microscale, as well as biochemical and biophysical properties at nanoscale, are addressed by employing a multiscale structural description of soft tissue mechanics as benchmark data set. Both the direct (from structure to parameters) and the inverse (from parameters to structure) problem are addressed. Suitable optimization problems are introduced for accurate numerical and approximated analytical direct relationships. The inverse identification has been addressed by providing also a measure of the reliability of the computed estimates. Results show the effectiveness of the proposed strategies and allow to discuss the fitting capabilities of classical constitutive approaches in terms of parameters identification.

Appendices

A Multiscale structural approach: collagen mechanics

The benchmark data set $\sigma = \sigma (\lambda ,\mathcal {S})$ is obtained by employing a multiscale structural approach for the description of collagen nonlinearities, in the formulation presented by Marino and Wriggers (2017) and Marino et al. (2017a), whose governing equations are here reported for the sake of completeness. This approach allows to introduce the explicit dependence of the stress function on the set $\mathcal {S}$ of structural features in Eq. (10). For the sake of compactness, other parameters governing the multiscale structural approach are briefly summarized in Table 7, where the values employed in all numerical simulations (in agreement with experimental measurements) are also reported.

Since present work focuses on collagen contribution, the matrix-related isotropic contribution ${\varPsi }_{iso}$ is introduced by following a phenomenological Mooney–Rivlin approach as in Eq. (3a). The strain-energy term ${\varPsi }_{ani}$ in Eq. (2) associated with collagen fibers is defined as:

$$\begin{aligned} {\varPsi }_{ani}(\mathbf{C},\mathbf{M}_o)= \int _{1}^{1+\langle \lambda _4 -1 \rangle } \int _{1}^{1+ \langle \xi - 1 \rangle } E_F(\eta ) \mathrm{d}\eta \mathrm{d}\xi , \end{aligned}$$

(A.1)

where $\lambda _4 = \sqrt{I_4}$ [see Eq. (4)] and $E_F=E_F(\lambda _4)$ is the equivalent tangent modulus of crimped collagen fibers. The latter is defined as $E_F(\lambda _4) =C_F(\lambda _4)/\lambda _4$, with $C_F$ being the along-the-chord tangent modulus of Euler–Bernoulli curvilinear beams whose geometry corresponds to the one of fibers, defined as (dependences omitted):

$$\begin{aligned} C_F = E_f \frac{\ell _F^2+H_F^2}{\sqrt{\ell _{F,o}^2+H_{F,o}^2}} \left[ \ell _F + \frac{4 H_F^2}{3 r_F^2\, \ell _F} \left( \ell _F^2+ H_F^2\right) \right] ^{-1}.\nonumber \\ \end{aligned}$$

(A.2)

Here, $\ell _F = \ell _F(\lambda _4)$ and $H_F=H_F(\lambda _4)$ are fiber quarter-of-period and amplitude in the current configuration. As a modeling choice, it is defined $\ell _F(\lambda _4)=\lambda _4 \ell _{F,o}$ with $\ell _{F,o}=L_{F,o}/4$ being fiber reference quarter-of-period, while $H_F(\lambda _4)$ is obtained from the solution of the geometry evolution Eq.:

$$\begin{aligned}&\frac{d H_F}{d \lambda _4}= - \frac{\ell _F H_F \left[ 4\left( \ell _F^2+H_F^2\right) - 3 r_F^2\right] }{\lambda _4 \left[ 4H_F^2\left( \ell _F^2 + H_F^2\right) +3 \ell _F^2 r_F^2\right] } , \end{aligned}$$

(A.3)

with $H_F(1) = H_{F,o}$, which gives the evolution of crimp amplitude upon fiber deformation. Moreover, $E_f$ in Eq. (A.2) represents the tangent modulus of fiber material, that is of collagen fibrils, depending on entropy-related $\lambda _m^s$ and energy-related $\lambda _m^h$ molecular stretches. Hence, it results $E_f=E_f(\lambda _m^s,\lambda _m^h)$ where:

$$\begin{aligned}&E_f\left( \lambda _m^s,\lambda _m^h\right) = \frac{E_m\left( \lambda _m^s,\lambda _m^h\right) \, {\varLambda }_c \, k_{c}\, \ell _{m,o}}{\left[ {\varLambda }_c \, k_{c} \,\ell _{m,o}+ A_m \, E_m\left( \lambda _m^s,\lambda _m^h\right) \right] } , \end{aligned}$$

(A.4a)

with molecular tangent modulus $E_m$ equal to:

$$\begin{aligned}&E_m\left( \lambda _m^s,\lambda _m^h\right) =\frac{E^s_m\left( \lambda ^s_m\right) \, E^h_m\left( \lambda ^h_m\right) }{E^s_m \left( \lambda ^s_m\right) +E^h_m\left( \lambda ^h_m\right) }\, , \end{aligned}$$

(A.4b)

depending on entropy-related $E_m^s$ and energetic-related $E_m^h$ stiffnesses:

$$\begin{aligned}&E^s_m\left( \lambda ^s_m\right) =\frac{k_B\, T \, \ell _{m,o}}{\ell _p\, \ell _c \, A_m}\left[ \frac{\ell _{c}^3}{2\left( \ell _c-\ell _{m,o}\lambda _m^s\right) ^3}+1\right] \, , \end{aligned}$$

(A.4c)

$$\begin{aligned}&E^h_m\left( \lambda ^h_m\right) \nonumber \\&=\frac{\ell _{m,o}}{\ell _c} \left\{ \frac{\hat{E}}{1+\text {exp}\left\{ -\eta \left[ \ell _{m,o}\left( \lambda ^h_m-1\right) /\ell _c - \varepsilon ^h_o\right] \right\} }+\hat{E}_o \right\} . \end{aligned}$$

(A.4d)

In agreement with integrations in Eq. (A.1), the functional dependences $\lambda _m^s =\lambda _m^s(\lambda _4)$ and $\lambda _m^h =\lambda _m^h(\lambda _4)$ are obtained via the interscale compatibility relationships:

$$\begin{aligned}&\frac{d \lambda _m^s}{d\lambda _4}= {\varPhi }_{ms}\left( \lambda _m^s,\lambda _m^h\right) {\varPhi }_{fm}\left( \lambda _m^s,\lambda _m^h\right) {\varPhi }_{f}(\lambda _4,H_F) , \end{aligned}$$

(A.5a)

$$\begin{aligned}&\frac{d \lambda _m^h}{d \lambda _4}= {\varPhi }_{mh}\left( \lambda _m^s,\lambda _m^h\right) {\varPhi }_{fm}\left( \lambda _m^s,\lambda _m^h\right) {\varPhi }_{f}(\lambda _4,H_F) \, , \end{aligned}$$

(A.5b)

with $\lambda _m^s(1) = \lambda _m^h(1) = 1$, depending on the following interscale relationships derived from equilibrium and compatibility conditions:

$$\begin{aligned}&{\varPhi }_{f}(\lambda _4,H_F) = \frac{d\lambda _f}{d \lambda _4} = \frac{\lambda _4 \ell _{F,o}^2 + H_F \frac{d H_F}{d \lambda _4}}{\sqrt{\left( \lambda _F^2\ell _{F,o}^2+H_F^2\right) \left( \ell _{F,o}^2+H_{F,o}^2\right) }}\, , \end{aligned}$$

(A.6a)

$$\begin{aligned}&{\varPhi }_{fm}\left( \lambda _m^s,\lambda _m^h\right) = \frac{d \lambda _m}{d \lambda _f}= \frac{E_f\left( \lambda _m^s,\lambda _m^h\right) }{ E_m\left( \lambda _m^s,\lambda _m^h\right) } , \end{aligned}$$

(A.6b)

$$\begin{aligned}&{\varPhi }_{ms}\left( \lambda _m^s,\lambda _m^h\right) = \frac{d \lambda ^s_m}{d\lambda _m}= \frac{E_m\left( \lambda _m^s,\lambda _m^h\right) }{E^s_m(\lambda ^s_m)}\, , \end{aligned}$$

(A.6c)

$$\begin{aligned}&{\varPhi }_{mh}\left( \lambda _m^s,\lambda _m^h\right) = \frac{d \lambda ^h_m}{d\lambda _m} = \frac{E_m\left( \lambda _m^s,\lambda _m^h\right) }{E^h_m(\lambda ^h_m)}\, , \end{aligned}$$

(A.6d)

where $dH_F/d\lambda _4$ in Eq. (A.6a) can be found in Eq. (A.3).

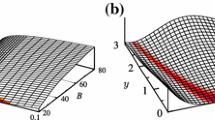
B Additional plots for functions $\kappa _P(\mathcal {S})$

Functions $\kappa _P(\mathcal {S})$, as well as the corresponding objective functions at optimum $f_{obj}^{P}(\kappa _{P}(\mathcal {S}),\mathcal {S},0.5)$, are reported here for the polynomial and exponential strain-energy terms in Eq. (10), i.e., with $P=pol$ and exp. Employing indexes i, j in $\{1, \ldots , n_s\}$ with $i \ne j$, planes $\mathbb {S}^{(ij)}$ are introduced in the space of structural features $\mathcal {S}$. Within $\mathbb {S}^{(ij)}$, couples $s_i,s_j \in \mathcal {S}$ vary, while other features $s_v \ne s_i,s_j$ are kept equal to reference values $\bar{\mathcal {S}}$ in Table 1, namely

$$\begin{aligned}&\mathbb {S}^{(ij)} = \{s_i /\bar{s}_i , s_j/ \bar{s}_j \in [0.5, 2] , \nonumber \\&\quad s_v = \bar{s}_v, \; v = 1,\ldots ,n_s \text { with } v \ne i, j\} . \end{aligned}$$

(B.1)

Addressing the polynomial law in Eq. (5a), function $\kappa _{pol}(\mathcal {S})$ is reported in Figs. 16,  17 and 18 for $k_1$, $k_2$ and $k_3$, respectively. Fitting capabilities are evaluated in Fig. 19 where the value of the objective function at optimum $f_{obj}^{pol}(\kappa _{pol}(\mathcal {S}),\mathcal {S},0.5)$ is shown.

Function $\kappa _{exp}(\mathcal {S})$ for the exponential strain-energy term in Eq. (5b) is shown in Figs. 20,  21 and 22 for $k_1$, $k_2$ and $k_3$, respectively. Figure 23 reports the value of the corresponding objective function at optimum $f_{obj}^{exp}(\kappa _{exp}(\mathcal {S}),\mathcal {S},0.5)$.

Fig. 16

Polynomial strain-energy term [see Eq. (5a)]. Trace of function $k_1 \in \kappa _{pol}(\mathcal {S})$, see Sect. 2.3, on planes $\mathbb {S}^{(12)}$ (top left), $\mathbb {S}^{(13)}$ (top right) $\mathbb {S}^{(14)}$, (middle left), $\mathbb {S}^{(23)}$ (middle right), $\mathbb {S}^{(24)}$ (bottom left), and $\mathbb {S}^{(34)}$ (bottom right) in the space of structural features [see Eq. (B.1)]. Scatter data represent the computed discrete values $\kappa _P(\mathcal {S}_g)$ for $\mathcal {S}_g \in \mathbb {S}^{(ij)}$

Fig. 17

Polynomial strain-energy term [see Eq. (5a)]. Trace of function $k_2 \in \kappa _{pol}(\mathcal {S})$, see Sect. 2.3, on planes $\mathbb {S}^{(12)}$ (top left), $\mathbb {S}^{(13)}$ (top right) $\mathbb {S}^{(14)}$, (middle left), $\mathbb {S}^{(23)}$ (middle right), $\mathbb {S}^{(24)}$ (bottom left), and $\mathbb {S}^{(34)}$ (bottom right) in the space of structural features [see Eq. (B.1)]. Scatter data represent the computed discrete values $\kappa _P(\mathcal {S}_g)$ for $\mathcal {S}_g \in \mathbb {S}^{(ij)}$

Fig. 18

Polynomial strain-energy term [see Eq. (5a)]. Trace of function $k_3 \in \kappa _{pol}(\mathcal {S})$, see Sect. 2.3, on planes $\mathbb {S}^{(12)}$ (top left), $\mathbb {S}^{(13)}$ (top right) $\mathbb {S}^{(14)}$, (middle left), $\mathbb {S}^{(23)}$ (middle right), $\mathbb {S}^{(24)}$ (bottom left), and $\mathbb {S}^{(34)}$ (bottom right) in the space of structural features [see Eq. (B.1)]. Scatter data represent the computed discrete values $\kappa _P(\mathcal {S}_g)$ for $\mathcal {S}_g \in \mathbb {S}^{(ij)}$

Fig. 19

Polynomial strain-energy term [see Eq. (5a)]. Trace of the objective function at optimum $f_{obj}^{pol}(\kappa _{pol}(\mathcal {S}),\mathcal {S},0.5)$ on planes $\mathbb {S}^{(12)}$ (top left), $\mathbb {S}^{(13)}$ (top right) $\mathbb {S}^{(14)}$, (middle left), $\mathbb {S}^{(23)}$ (middle right), $\mathbb {S}^{(24)}$ (bottom left), and $\mathbb {P}^{(34)}$ (bottom right) in the space of structural features [see Eq. (B.1)]. Scatter data represent the computed discrete values corresponding to $\kappa _P(\mathcal {S}_g)$ for $\mathcal {S}_g \in \mathbb {S}^{(ij)}$

Fig. 20

Exponential strain-energy term [see Eq. (5b)]. Trace of function $k_1 \in \kappa _{exp}(\mathcal {S})$, see Sect. 2.3, on planes $\mathbb {S}^{(12)}$ (top left), $\mathbb {S}^{(13)}$ (top right) $\mathbb {S}^{(14)}$, (middle left), $\mathbb {S}^{(23)}$ (middle right), $\mathbb {S}^{(24)}$ (bottom left), and $\mathbb {S}^{(34)}$ (bottom right) in the space of structural features [see Eq. (B.1)]. Scatter data represent the computed discrete values $\kappa _P(\mathcal {S}_g)$ for $\mathcal {S}_g \in \mathbb {S}^{(ij)}$

Fig. 21

Exponential strain-energy term [see Eq. (5b)]. Trace of function $k_2 \in \kappa _{exp}(\mathcal {S})$, see Sect. 2.3, on planes $\mathbb {S}^{(12)}$ (top left), $\mathbb {S}^{(13)}$ (top right) $\mathbb {S}^{(14)}$, (middle left), $\mathbb {S}^{(23)}$ (middle right), $\mathbb {S}^{(24)}$ (bottom left), and $\mathbb {S}^{(34)}$ (bottom right) in the space of structural features [see Eq. (B.1)]. Scatter data represent the computed discrete values $\kappa _P(\mathcal {S}_g)$ for $\mathcal {S}_g \in \mathbb {S}^{(ij)}$

Fig. 22

Exponential strain-energy term [see Eq. (5b)]. Trace of function $k_3 \in \kappa _{exp}(\mathcal {S})$, see Sect. 2.3, on planes $\mathbb {S}^{(12)}$ (top left), $\mathbb {S}^{(13)}$ (top right) $\mathbb {S}^{(14)}$, (middle left), $\mathbb {S}^{(23)}$ (middle right), $\mathbb {S}^{(24)}$ (bottom left), and $\mathbb {S}^{(34)}$ (bottom right) in the space of structural features [see Eq. (B.1)]. Scatter data represent the computed discrete values $\kappa _P(\mathcal {S}_g)$ for $\mathcal {S}_g \in \mathbb {S}^{(ij)}$

Fig. 23

Exponential strain-energy term [see Eq. (5b)]. Trace of the objective function at optimum $f_{obj}^{exp}(\kappa _{exp}(\mathcal {S}),\mathcal {S},0.5)$ on planes $\mathbb {S}^{(12)}$ (top left), $\mathbb {S}^{(13)}$ (top right) $\mathbb {S}^{(14)}$, (middle left), $\mathbb {S}^{(23)}$ (middle right), $\mathbb {S}^{(24)}$ (bottom left), and $\mathbb {S}^{(34)}$ (bottom right) in the space of structural features [see Eq. (B.1)]. Scatter data represent the computed discrete values corresponding to $\kappa _P(\mathcal {S}_g)$ for $\mathcal {S}_g \in \mathbb {S}^{(ij)}$