Abstract
Most soft tissues possess an oriented architecture of collagen fiber bundles, conferring both anisotropy and nonlinearity to their elastic behavior. Transverse isotropy has often been assumed for a subset of these tissues that have a single macroscopically-identifiable preferred fiber direction. Micro-structural studies, however, suggest that, in some tissues, collagen fibers are approximately normally distributed about a mean preferred fiber direction. Structural constitutive equations that account for this dispersion of fibers have been shown to capture the mechanical complexity of these tissues quite well. Such descriptions, however, are computationally cumbersome for two-dimensional (2D) fiber distributions, let alone for fully three-dimensional (3D) fiber populations. In this paper, we develop a new constitutive law for such tissues, based on a novel invariant theory for dispersed transverse isotropy. The invariant theory is derived from a novel closed-form ‘splay invariant’ that can easily handle 3D fiber populations, and that only requires a single parameter in the 2D case. The model fits biaxial data for aortic valve tissue as accurately as the standard structural model. Modification of the fiber stress–strain law requires no reformulation of the constitutive tangent matrix, making the model flexible for different types of soft tissues. Most importantly, the model is computationally expedient in a finite-element analysis, demonstrated by modeling a bioprosthetic heart valve.








Similar content being viewed by others
Notes
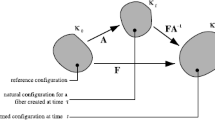
Tensors \(\hbox{\text {B}} = \hbox{\text {FF}}^{\rm T} = \hbox{\rm V}^{2}\) and \(\hbox{\rm C} = \hbox{\rm F}^{\rm T} \hbox{\rm F} = \hbox{\rm U}^2\) are often referred to as the left and right Cauchy–Green deformation tensors, respectively, because V and U are called the left- and right-stretch tensors, so named because of the polar decomposition F = VR = RU wherein RRT=I. We prefer to call B and C the left- and right-deformation tensors. Historically, Cauchy (1827, pp 60–69), used B−1 (sometimes expressed as c) and Green (1841) used C, while Finger (1894) introduced their duals, B (sometimes expressed as b) and C−1. Therefore, naming these fields after Cauchy and Green seems an injustice to Finger, especially since Finger introduced B into the literature.
The following well-known tensor derivatives are useful in the derivation of constitutive formulae:
$$ \frac{\partial \; \hbox{tr Z}}{\partial \hbox{Z}} =\hbox{l}, \quad \frac{\partial \; \hbox{tr}\;\hbox{Z}^{-1}} {\partial \hbox{Z}} = -\hbox{Z}^ {-{\rm T}} \hbox{Z}^{-{\rm T}}, \quad \frac{\partial \det \hbox{Z}}{\partial \hbox{Z}} = \det (\hbox{Z}) \hbox{Z}^{-{\rm T}} , \quad \det\, \hbox{Z} \neq 0. $$\(\partial^2 {\widetilde{\mathcal W}} / {\partial \Theta}^{2} = \frac{1}{2} \kappa ( 1 + \Theta^{-2} ) > 0\), as Θ>0 due to the conservation of mass
\(e = \ln \,\det\, \hbox{F} \approx \frac{1}{2} (\det\, \hbox{F} - \det\, \hbox{F}^{-1})\)
These tensor gradients are useful when deriving the subsequent tangent moduli:
$$ \frac{\partial \hbox{Z}}{\partial \hbox{Z}} = \hbox{I} \odot \hbox{I} , \quad \frac{\partial \hbox{Z}^{-1}}{\partial \hbox{Z}} = -\hbox{Z}^{-1} \odot \hbox{Z}^{-1} , \quad \hbox{Z} = \hbox{Z}^{\rm T} , \quad \det{\hbox{Z}} \neq 0 , $$where \((\hbox{Z}^{-1} \!\odot \hbox{Z}^{-1})_{ijk\ell} = \frac{1}{2} \bigl( Z^{-1}_{ik} Z^{-1}_{j\ell} + Z^{-1}_{i\ell} Z^{-1}_{jk} \bigr)\) in the notation of Holzapfel (2000, p. 254).
The outer-dyadic tensor product \((\hbox{A} \otimes \hbox{B} )_{ijk\ell} = A_{ij} B_{k\ell},\) and the inner-dyadic tensor product \(( \hbox{A} \boxtimes \hbox{B} )_{ijk\ell} = \frac{1}{4} ( A_{ik} B_{j\ell} + A_{i\ell} B_{jk} + A_{jk} B_{i\ell} + A_{j\ell} B_{ik} ),\) are established in Appendix 4. Whenever A and B are the same tensor field—say, A—then the inner-dyadic product \(\hbox{A} \boxtimes \hbox{A}\) simplifies to \(\hbox{A} \odot \hbox{A},\)i.e., \(\hbox{A} \boxtimes \hbox{A} = \hbox{A} \odot \hbox{A}.\)
References
Belytschko T, Liu WK, Moran B (2000) Nonlinear finite elements for continua and structures. Wiley, Chichester
Billiar KL, Sacks MS (2000a) Biaxial mechanical properties of the natural and glutaraldehyde-treated aortic valve cusp—Part I: experimental results. ASME J Biomech Eng 122:23–30
Billiar KL, Sacks MS (2000b) Biaxial mechanical properties of the natural and glutaraldehyde-treated aortic valve cusp—Part II: a structural constitutive model. ASME J Biomech Eng 122:327–335
Cauchy A-L (1827) Exercices de Mathématiques, vol 2. de Bure Frères, Paris
Criscione JC, Douglas AS, Hunter WC (2001) Physically based strain invariant set for materials exhibiting transversely isotropic behavior. J Mech Phys Solids 49:871–897
Doehring TC, Carew EO, Vesely I (2004) The effect of strain rate on the viscoelastic response of aortic valve tissue: a direct-fit approach. Ann Biomed Eng 32:223–232
Einstein DR (2002) Nonlinear acoustic analysis of the mitral valve. PhD thesis, University of Washington, Seattle
Finger J (1894) Über die allgemeinsten Beziehungen zwischen endlichen Deformationen und den zugehörigen Spannungen in aeolotropen und isotropen Substanzen. Sitzungsberichte der Akademie der Wissenschaften Wien 103:1073–1100
Flory PJ (1961) Thermodynamic relations for high elastic materials. Trans Faraday Soc 57:829–838
Freed AD, (2004) Transverse-isotropic elastic and viscoelastic solids. ASME J Eng Mater Technol 126:38–44
Freed AD, Doehring TC (2005) Elastic model for crimped collagen fibrils. ASME J Biomech Eng (in press)
Green G (1841) On the propagation of light in crystallized media. Trans Cambridge Phil Soc 7:121–140
Hartmann S, Neff P (2003) Polyconvexity of generalized polynomial-type hyperelastic strain energy functions for near-incompressibility. Int J Solids Struct 40:2767–2791
Hencky H (1928) Über die Form des Elastizitätsgesetzes bei ideal elastischen Stoffen. Z Tech Phys 9:215–220
Holzapfel GA (2000) Nonlinear solid mechanics: a continuum approach for engineering. Wiley, Chichester
Holzapfel GA, Gasser TC, Stadler M (2002) A structural model for the viscoelastic behavior of arterial walls: continuum formulation and finite element analysis. Eur J Mech A Solids 21:441–463
Holzapfel GA, Weizsäcker HW (1998) Biomechanical behavior of the arterial wall and its numerical characterization. Comput Biol Med 28:377–392
Horowitz A, Lanir Y, Yin FC, Perl M, Sheinman I, Strumpf RK (1988) Structural three-dimensional constitutive law for the passive myocardium. ASME J Biomech Eng 110:200–207
Hurschler C, Loitz-Ramage B, Vanderby R Jr (1997) A structurally based stress-stretch relationship for tendon and ligament. ASME J Biomech Eng 119:392–399
Lanir Y (1983) Constitutive equations for fibrous connective tissues. J Biomech 16:1–12
Leonov AI (2000) On the conditions of potentiality in finite elasticity and hypo-elasticity. Int J Solids Struct 37:2565–2576
Lodge AS (1974) Body tensor fields in continuum mechanics: with applications to polymer rheology. Academic, New York
Malkus DS, Hughes TJR (1978) Mixed finite element methods—reduced and selective integration techniques: a unification of concepts. Comput Meth Appl Mech Eng 15:63–81
Mijailovich A, Stamenovic D, Fredberg JJ (1993) Toward a kinetic theory of connective tissue micromechanics. J Appl Physiol 74:665–681
Mooney M (1940) A theory of large elastic deformations. J Appl Phys 11:582–592
Sacks MS (2000) Biaxial mechanical evaluation of planar biological materials. J Elasticity 61:199–246
Sacks MS (2003) Incorporation of experimentally-derived fiber orientation into a structural consitutive model for planar collagenous tissues. ASME J Biomech Eng 125:280–287
Simo JC, Hughes TJR (1998) Computational inelasticity, vol 7 of Interdisiplinary applied mathematics. Springer, Berlin Heidelberg New York
Simo JC, Taylor RL (1991) Quasi-incompressible finite elasticity in principal stretches. Continuum basis and numerical algorithms. Comp Meth Appl Mech Eng 85:273–310
Spencer AJM (1972) Deformations of fibre-reinforced materials. Clarendon, Oxford
Sussman T, Bathe K-J (1987) A finite element formulation for nonlinear incompressible elastic and inelastic analysis. Comput Struct 26:357–409
Wuyts FL, Vanhuyse VJ, Langewouters GJ, Decraemer WF, Raman ER, Buyle S (1995) Elastic properties of human aortas in relation to age and atherosclerosis: a structural model. Phys Med Biol 40:1577–1597
Zioupos P, Barbenel JC (1994) Mechanics of native bovine pericardium: I. The multiangular behavior of strength and stiffness of the tissue. Biomaterials 15:366–373
Acknowledgements
The authors take this opportunity to thank Prof. Michael Sacks at the University of Pittsburgh for providing us with his experimental data, and to Dr. Todd Doehring at the Cleveland Clinic and Mr. Dimitri Deserranno at the National Center for Microgravity Research for many delightful discussions on this and related topics. Research partially funded by the US DOD via Award No. DAMD17-01-1-0673 to the Cleveland Clinic Foundation and Children’s Hospital Los Angeles.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
The primary reason for adopting a Gaussian distribution to describe fiber splay is that the corresponding stiffness matrix \({\varvec \kappa}\) can be computed analytically. Alternatively, Hurschler et al (1997) have employed a von Mises distribution for splay in conjunction with a Weibull distribution for crimp that they collectively solve numerically.
1. A two-dimensional splay
We recall that our local coordinate system was chosen so that
and as such
which leads to an expression for Eq. 16 that can be solved analytically; it being,
where the two non-zero stiffness components have values of
and
wherein \(i = \sqrt{-1}\) is the unit imaginary number. The sum of two error functions whose arguments are complex conjugates, i.e., erf(x + i y) + erf(x−i y), produces a real result, and as such, κ11 and κ22 are both real numbers.
2. Three-dimensional splay
Here, the formulation is somewhat different; specifically,
and as such
which leads to an expression for Eq. 17 that can be solved analytically; it being,
where the two non-zero stiffness components have values of
which is the same as Eq. 49, and
where this value for κ22 is exactly half that of the 2D case (Eq. 50, wherein κ33=0) but here \(\kappa_{33} = \kappa_{22}.\)
3. Collagen model
A micro-structural model based on the physiology of crimped collagen fibers was recently derived by Freed and Doehring (2005) that we have altered to meet our needs (see Algorithm 1); specifically, given a fiber stretch λ, this model returns the engineering stress σ / λ and tangent modulus dσ / dλ of the fiber. There are four physiological parameters (material constants defined at the top of the algorithm) that the user must supply; three if failure is not to be considered.
A typical pair of response curves are plotted in Fig. 9. The discontinuity observed in the dσ/dλ curve indicates that the model presented in Algorithm 1 predicts a stress σ response that is continuous and differentiable in stretch λ up to fiber failure, which is not depicted in this figure. The values assigned to the model to obtain these curves were \(H_0/r_0 = 27.5,\) \(R_0/r_0 = 2,\) and E f =45 MPa, which results in a transitional stretch Λ of 1.1. This is but one example of a fiber stress/stretch model.
Algorithm 1
Given H0/r0, E f and λ u , where H0 is the initial wavelength of crimp, R0 is the initial amplitude of crimp, r0 is the initial fibril radius, E f is the elastic modulus of the fiber in the linear region, and λ u is its ultimate stretch, then:
Set r0=1 so that H0≡ H0/r0 & R0≡ R0/r0
Compute the constant parameters: \(L_0 =\bigl( ( 2 \pi R_0 )^2 + H_0^2 \bigr)^{1/2}, \qquad \Lambda = L_0 / H_0 < \lambda_u,\) \(E_s = E_f H_0 / \{ H_0 + [ 1 + 37/6\pi^2 + 2 ( L_0 / \pi r_0 )^2 ] ( L_0 - H_0 ) \},\)
where L0 is the chord length of helix over one wavelength, while Λ is the stretch and E s is the secant modulus at the transition between the toe and linear regions.
If λ ≤ Λ Then
Else If Λ ≤ λ ≤ λ u Then
Else Fibril Failure
Return σ / λ and dσ / dλ.
4. Voigt notation for dyadic products of tensors
Because the Lagrangian fields for stress S ij and strain E ij , i,j=1,2,3, are symmetric tensors, it is customary to express their components as six-dimensional arrays Sα and Eα, α=1,2,...,6 (Belytschko et al. 2000, pp 615–618). These arrays are not vector fields in the sense that they do not obey the tensor-transformation law; nevertheless, they have proven to be very useful in the employ of finite elements.
A linear approximation for stress increment dS ij relates to the strain increment \(\hbox{d}E_{ij} = \frac{1}{2} \hbox{d}C_{ij}\) in the Lagrangian frame through
where the tangent modulus \({\mathbb{C}}\) has a Voigt representation of
with \({\mathbb{C}}_{\alpha\beta} \neq {\mathbb{C}}_{\beta\alpha}\) unless the \({\mathbb{C}}_{ijk\ell}\) possess major symmetry \({\mathbb{C}}_{ijk\ell} = {\mathbb{C}}_{k\ell ij}.\) The tangent modulus always possesses minor symmetries \({\mathbb{C}}_{ijk\ell} = {\mathbb{C}}_{ij\ell k} = {\mathbb{C}}_{jik\ell} = {\mathbb{C}}_{ji\ell k}\) because of the inherent symmetries in S ij and C ij . Major symmetry follows automatically if stress S ij is given by some potential function F such that \(S_{ij} = \partial F / \partial E_{ij},\)as in hyperelasticity.
Three dyadic products of tensor fields arise naturally when deriving tangent moduli, in the sense of Eqs. D1 and D2. Of these three, there are two fundamental dyadic products that we denote as \(\hbox{A} \otimes \hbox{B}\) and \(\hbox{A} \boxtimes \hbox{B};\) we call them the outer- and inner-dyadic products, respectively, or the circle- and box-products for short, wherein A and B are taken to be symmetric fields. The third dyadic product, denoted as \(\hbox{A} \odot \hbox{A},\) is a special case of the inner-dyadic product \(\hbox{A} \boxtimes \hbox{A}\) wherein both arguments are the same tensor field—in this case, A. We know of no publication where \(\hbox{A} \boxtimes \hbox{B}\) has been defined as we use it, which is the main reason for writing this appendix.
The circle product \(\hbox{A} \otimes \hbox{B}\) is well known and has components
which reduce down to the simple expression \(( \hbox{A} \otimes \hbox{B} )_{ijk\ell} = A_{ij} B_{k\ell}\) as a consequence of A and B being symmetric. This dyadic product has the simple Voigt notation of
Matrix \(( \hbox{A} \otimes \hbox{B} )_{\alpha\beta}\) is not symmetric unless A = B; however, \(( \hbox{A} \otimes \hbox{B} ) + ( \hbox{B} \otimes \hbox{A} )\) does yield a symmetric matrix in Voigt notation. This is because \(\hbox{A} \otimes \hbox{B}\) possesses minor symmetry, but not major symmetry, therefore \(( \hbox{A} \otimes \hbox{B} )_{\alpha\beta} \neq ( \hbox{A} \otimes \hbox{B} )_{\beta\alpha},\) in general. The box product \(\hbox{A} \boxtimes \hbox{B}\) is a new dyadic product that we define by the sum
and possesses minor and major symmetries, therefore \(( \hbox{A} \boxtimes \hbox{B} )_{\alpha\beta} = ( \hbox{A} \boxtimes \hbox{B} )_{\beta\alpha};\) consequently, the box product commutes, viz., \(\hbox{A} \boxtimes \hbox{B} = \hbox{B} \boxtimes \hbox{A}.\) A special case that arises frequently in practice is when both tensor arguments of this product are the same. This dyadic product is well known and has its own notation of \(\hbox{A} \odot \hbox{A}\) (cf., Holzapfel (2000, pg. 254)) with components
The Voigt representation of \(( \hbox{A} \boxtimes \hbox{B} )_{\alpha\beta}\) has the following symmetric matrix components:
while the Voigt representation of \(( \hbox{A} \odot \hbox{A})_{\alpha\beta}\) has symmetric matrix components:
wherein terms on the right-hand side are tensor components while those on the left-hand side are the Voigt components. Obviously, \(\odot\) and \(\boxtimes\) are different products.
6.1 Example
The theory of linear elasticity has stress components
and as such, its tangent modulus is readily determined to be
wherein λ and μ are the elastic moduli, and where
The \(\frac{1}{2}\)’s in \((\hbox{I} \odot \hbox{I})_{\alpha\beta}\) are offset by the 2’s present in Eβ.
Rights and permissions
About this article
Cite this article
Freed, A.D., Einstein, D.R. & Vesely, I. Invariant formulation for dispersed transverse isotropy in aortic heart valves. Biomech Model Mechanobiol 4, 100–117 (2005). https://doi.org/10.1007/s10237-005-0069-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10237-005-0069-8