Abstract
Despite its climatic and ecosystemic significance, the coastal upwelling that takes place off Oman is not well understood. A primitive-equation, regional model forced by climatological wind stress is used to investigate its dynamics and to compare it with the better-known Eastern Boundary Upwellings (EBUs). The solution compares favorably with existing observations, simulating well the seasonal cycles of thermal structure, surface circulation (mean and turbulent), and sea-surface temperature (SST). There is a 1.5-month lag between the maximum of the upwelling-favorable wind-stress-curl forcing and the oceanic response (minima in sea-surface height and SST), which we attribute to onshore-propagating Rossby waves. A southwestward-flowing undercurrent (opposite to the direction of the near-surface flow) is also simulated with a core depth of 1000 m, much deeper than found in EBUs (150–200 m). An EKE budget reveals that, in contrast to EBUs, the upwelling jet is more prone to barotropic than baroclinic instability and the contribution of locally-generated instabilities to EKE is higher by an order of magnitude. Advection and redistribution of EKE by standing mesoscale features also play a significant role in EKE budget.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coastal upwelling can occur wherever the wind has an alongshore component that drives offshore Ekman drift. Regions of sustained upwelling exist on both eastern- and western-ocean boundaries. The four major Eastern-Boundary Upwellings (EBUs) occur along the west coasts of North and South America and North and South Africa. Western-boundary upwelling regions include southeastern Australia (Marchesiello et al. 2000), Brasil (Azevedo et al. 2012), and eastern Africa/northern Arabian seas (McCreary and Kundu 1985).
EBUs have received considerable attention, owing to their biological productivity over a large area of the coastal ocean. EBUs coexist with turbulent activity associated with mesoscale, and to a lesser extent submesoscale, eddies, that are primarily generated by the baroclinic instability of coastal currents (Marchesiello et al. 2003). Eddy Kinetic Energy (EKE) in EBUs is consequently modulated by the seasonal cycle of upwelling winds (Kelly et al. 1998). Once generated, surface-intensified EKE propagates offshore at roughly the speed of long-wavelength baroclinic Rossby waves (Kelly et al. 1998; Marchesiello et al. 2003). EKE is also redistributed vertically as part of the barotropization tendency of balanced turbulence, thereby energizing the subsurface ocean (Haney et al. 2001).
Western-boundary upwellings are comparatively less studied than EBUs, although they also cover vast areas of coastal areas, e.g., in the Arabian Sea. In the Arabian Sea, currents are primarily driven by monsoonal winds (Lee et al. 2000; Schott and McCreary 2001). In response to the semiannual reversal of the monsoonal winds, the surface boundary currents also reverse. During the summer monsoon, strong upwelling occurs in the western Arabian Sea, offshore of Somalia and Oman (Elliott and Savidge 1990; McCreary et al. 1993). A notable observational program in the region was the Arabian-Sea Process Study program conducted during 1994–1995, which was designed to investigate the interaction of biological activity and ocean dynamics in the region (Lee et al. 1998; Morrison et al. 1998; Shi et al. 1999). Among other things, it was found that mesoscale variability efficiently redistributes nutrients offshore from Oman during the upwelling season. Whether the eddies were locally generated by coastal instabilities or remotely generated in the eastern/interior Arabian Sea was not determined.
Coastal dynamics differ significantly between eastern- and western-boundary systems. McCreary and Kundu (1985) explored the large-scale coastal dynamics along western boundaries, both theoretically and with the use of simple numerical models, comparing their solutions to their counterparts in eastern boundaries. They explained the different structures of their solutions through the propagation direction of Rossby waves with respect to the coast, which is offshore (onshore) at eastern-boundary (western-boundary) coasts, respectively. A key result of McCreary and Kundu (1985) is that undercurrents at western boundaries can not be driven by alongshore winds alone. However, western-boundary undercurrents can be driven by offshore wind stress curl. McCreary et al. (1993) further discuss how onshore propagating Rossby waves generate coastal currents in the western Arabian Sea. Another specific feature of western boundaries is that they are influenced by remotely-generated, mesoscale turbulence and waves that propagate westward under the β effect (Chelton et al. 2011). However, the interaction of onshore-propagating eddies and waves with locally generated turbulence has not been explored.
In this study, we seek to clarify the dynamics that impact the ocean offshore of Oman during the upwelling season. To address this goal, we obtain solutions to a regional numerical model with sufficiently high resolution (Δx = 2 km) to represent mesoscale eddies completely and to partially account for smaller-scale (sub-mesoscale) features (Capet et al. 2008b; Marchesiello et al. 2011). Throughout the text, we also offer comparisons with EBUs to highlight specificities of western-boundary systems.
Key results are the following. There is a significant lag between the peaks in upwelling-favorable winds and the corresponding lows in coastal sea-surface height (SSH) and sea-surface temperature (SST), which we interpret to result from the onshore propagation of Rossby waves. Although not dynamically explained, a southward-flowing undercurrent also develops during the upwelling season, with its core at 1000 m, significantly deeper than in EBUs (150–200 m). As demonstrated by an EKE budget analysis, levels of barotropic and baroclinic instabilities of the upwelling jet are considerably higher compared to their levels in EBUs. Standing mesoscale features play a role in the EKE budget in redistributing EKE offshore. More generally, our study offers additional insights into the dynamical differences between western- and eastern-boundary upwelling regions.
The outline of the paper is as follows. The model configuration is presented in Section 2 and an extensive characterization of the upwelling follows in Section 3. An EKE budget is performed in Section 4. Finally, our conclusions are summarized in Section 5.
2 Regional ocean model
The ocean model used here is a version of the Regional Oceanic Modeling System (ROMS, Shchepetkin and McWilliams. 2005) set up in a one-way, nested configuration, consisting of two regions: an inner region offshore from Oman with a 2-km horizontal resolution; and an outer (“parent”) region with a 6.6-km resolution, which supplies boundary conditions for the inner region (procedure follows Mason et al. 2010). The parent simulation is extensively described in Vic et al. (2014). The inner domain and topography are shown in the right panel in Fig. 1. The topography is from the Shuttle Radar Topography Mission dataset at 30 ′ of resolution (SRTM30-plus, Becker et al. 2009). Atmospheric forcing is from monthly climatologies, which simplifies our investigation of basic upwelling dynamics by removing interannual and externally-forced, intraseasonal variability. Wind stress is from the Scatterometer Climatology of Ocean Winds (SCOW, Risien and Chelton 2008) and heat and freshwater fluxes are from the International Comprehensive Ocean Atmosphere Dataset (ICOADS, Worley et al. 2005)Footnote 1.
a Snapshot of sea surface temperature during an upwelling event off the Oman coast. Thick black lines are isobaths 100, 200, and 1000 m. The blue rectangle is the area where variables in Fig. 2 are averaged. Thin parallel black lines limit the upwelling region. The (x,y)arrows represent the coordinate system used to plot sections and hovmoller diagrams. The inset map on the right shows the nested domain (orange rectangle) and isobaths 1000, 2000, 3000, and 4000 m (black lines). ROMS fields: b Mean SSH 〈η〉, c surface geostrophic currents (g/f)||∇〈η〉||, and d EKE during the upwelling season. e–g Same fields from Aviso absolute dynamics topography (ADT, Rio et al. 2011). ROMS SSH has been low-pass filtered at 30 km (Gaussian filter) to be comparable to Aviso ADT (same technique is used in Capet et al. 2008a), and both field means have been set to zero to exhibit the same range of variation. Currents in ROMS have also been filtered to compute EKE
Turbulent vertical mixing is parameterized by the K-profile parameterization (KPP, Large et al. 1994) for the surface and bottom boundary layers. Mixed-layer thickness is diagnosed by comparing a bulk Richardson number to a critical value. Below the mixed layer, the interior mixing scheme takes into account three processes: static instability (convection), vertical shear, and internal wave breaking (for details on interior and boundary layer mixing, see the appendix in Jullien et al. 2012). Bottom stress is linear with a drag coefficient C d = 3 × 10−4 m s −1. Additional information is in Vic et al. (2015).
3 Modeled circulation and evaluation
In this section, we describe the general characteristics of the circulation and hydrography off Oman, and evaluate the ability of our ROMS solution to reproduce them.
3.1 Seasonality
Climatologies of the model’s surface atmospheric forcing fields averaged over the blue box in Fig. 1 are presented in Fig. 2, showing alongshore wind stress τ a (positive northeastward), wind stress curl ∇× τ, and net heat flux Q. The figure also illustrates the model’s response, plotting similar time series of SST and SSH. The atmospheric forcings exhibit a dominant annual cycle, characteristic of the monsoon seasonality in the Arabian Sea (e.g., Schott and McCreary 2001). Wind stress τ a lies approximately in the direction of the dominant monsoonal winds in this region, blowing northeastward during the summer monsoon (mid-May to mid-September) and southwestward during the winter monsoon (mid-November to March). The winds are stronger during the summer monsoon, when the Findlater Jet (in the τ a direction) is established and blows almost parallel to the Arabian Peninsula (Findlater 1969).
Time series of a alongshore wind stress, b wind stress curl, c atmospheric net heat flux, d sea surface temperature (SST), and (e) sea surface height (SSH). All variables are averaged in the blue rectangle in Fig. 1. SST and SSH are averaged over the 4 years of simulations and dark gray shaded areas represent one standard deviation on each part of the mean (biased estimator). Light gray area in (c) defines the upwelling season
Onshore of the jet axis, there is strong positive wind-stress curl, extending more than 200 km offshore from the Omani coast (e.g., Fig. 1c in Vic et al. 2014). Thus, both τ a and ∇× τ provide upwelling-favorable forcing during the summer monsoon (Manghnani et al. 1998). They respectively force Ekman divergence from the coast and Ekman pumping offshore (e.g., Bakun and Nelson. 1991). They both drive the upwelling that cools SST from mid-May to mid-October (Fig. 2d). According to Fig. 2d, the upwelling season occurs from June to September (4 months), when SST is significantly lower (by more than 0.5 ∘C) than the semiannual maxima.
A notable feature of the annual cycle of SSH and SST is a ∼1.5-month lag between the maximum of the upwelling forcing (τ a and ∇× τ) and the ocean’s response (SST and SSH minima). Such phase differences have been noticed in satellite observations (Manghnani et al. 1998) but have so far been unexplained. The lag is in contrast with EBUs dynamics where wind forcing and SSH/SST are generally in phase (Wang 1997) or lag by no more than a few days (Desbiolles et al. 2014). Following a suggestion by J. McCreary in his review of an initial version of this manuscript, we propose that the lag results from the onshore propagation of long-wavelength, upwelling-favorable, Rossby waves. Rossby waves propagate at the zonal group velocity \(c_{g}=\beta (k^{2}-R_{d}^{-2})/(k^{2}+R_{d}^{-2})\), where k is the zonal wavenumber, β is the meridional derivative of the Coriolis parameter, R d is an estimate of the Rossby radius of deformation for the first baroclinic mode, and for simplicity we neglect their meridional propagation. In the long-wavelength approximation (2π/k ≫ R d ), the group velocity simplifies to \(c_{g}^{lw}=-\beta {R_{d}^{2}}\) (positive eastward). Using β = 2.2 × 10−11 m −1 s −1 and R d = 60 km in the region, \(c_{g}^{lw}=-7.9\mathrm {\:cm\:s^{-1}}\). The wind stress curl maximum is situated 200–300 km offshore from the Omani coast. Assuming the Rossby waves are generated there, they would take 29–44 days to reach the coast, similar to the ∼45-day lag between the maxima of the wind stress curl (Fig. 2b) and the oceanic response.
3.2 Surface circulation
Figure 1b,e shows the mean SSH during the upwelling season 〈η〉 and Fig. 1c, f shows the amplitude of the surface geostrophic current derived from 〈η〉, both for ROMS and for Aviso’s absolute dynamic topography gridded at a resolution of 1/4 ∘ (Rio et al. 2011). The magnitude of the geostrophic current is determined by (g/f)||∇〈η〉||, where g is the acceleration of gravity and f is the local Coriolis frequency). Note that the amplitudes of 〈η〉 from ROMS and Aviso are comparable in the domain, the larger discrepancies nearshore are at horizontal scales where Aviso is known to have limitations (Vignudelli et al. 2005).
The nearshore flow is directed northeastward in response to the offshore Ekman flow and low coastal SSH (Fig. 1b, e). The path of the current reaches the peninsula’s easternmost cape (Ras al Hadd, Fig. 1a), where farther north it detaches from the coast to generate the Ras al Hadd Jet (not shown; Böhm et al. 1999). Both fields display a persistent anticyclonic structure offshore Ras Madraka, although their positions differ slightly in the model and observations. We see this feature as an analog of the quasi-standing meanders observed in EBUs. Such meanders are the manifestation of topographic steering on the unstable current system (Marchesiello et al. 2003; Centurioni et al. 2008).
Given the similarity of their SSH fields, the intensity of the northeastward current is also comparable in ROMS and in Aviso (Fig. 1c,f), with peak velocities of 0.5 m s −1. Although current maxima are not exactly colocated, they are both located where the circulation is intensified by the standing anticyclone. Seasonal EKE also compares well (Fig. 1d, g) although ROMS is slightly more energetic even after filtering the currents. Interestingly, both fields display a local increase of EKE downstream of the current intensification by the standing anticyclone noted above. Notice that the annual EKE over the whole domain is higher in ROMS than in Aviso by ∼ 20% (Fig. 3 in Vic et al. 2015).
3.3 Thermal structure
The convoluted coastline and shelf break, and relatively small upwelling area (Fig. 1) complicate the analysis compared to usual situation along EBUs, for which typical coastlines are longer and relatively straight (> 1000 km in the California and Peru-Chile coasts for instance). Alongshore (y) and cross-shore (x) directions are defined in Fig. 1a. For a variable q, \(\overline {q}\) denotes an alongshore average in the upwelling area (490 km long between thin parallel black lines in Fig. 1). The most inshore point is taken as the coastline in Fig. 3.
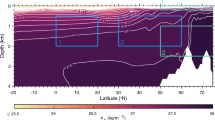
Alongshore and time averaged temperature \(\langle \overline {T}\rangle \) during the upwelling season in (left) GDEM (Teague et al. 1990) and (right) ROMS
Alongshore-averaged temperature sections are shown in Fig. 3, for both the model and data (Generalized Digital Environment Model, GDEM, Teague et a. 1990). Briefly, GDEM is a climatology based only on in-situ observations that better preserves gradients and intra-annual variability than the Levitus climatology (Levitus and Boyer 1994; Levitus et al. 1994). There is a good overall agreement between both fields, albeit with a model warm bias near the surface (∼1 ∘C) and a small cold bias below the main thermocline (0.5–1 ∘C). The surface warm bias may be linked to the surface heat flux Q being too strongFootnote 2, whereas the cold bias is likely fed by the parent solution. Isotherms tilt upward when approaching shore as expected in this upwelling context. The tilting is present down to 300 m, in agreement with the synoptic measurements described in Elliott and Savidge (1990). This vertical extent is much deeper than in EBUs, where upward tilting is confined to the upper 150 m in the Peru-Chile current system (Colas et al. 2012) and to the upper 100 m in the California Current System (CCS, Capet et al. 2008b). The deeper extent is consistent with the westward propagation of Rossby waves (see Figs. 5 and 9 in McCreary and Kundu. 1985).
3.4 Current vertical structure
Figure 4 shows mean alongshore \(\langle \overline {v}\rangle \) and across-shore \(\langle \overline {u}\rangle \) currents, both averaged in the alongshore direction. We focus on the region deeper than the shelf break at the 300-m isobath, as the shelf area (shallower than the 300-m isobath) has strong spatial heterogeneities due to the convoluted coastline.
Sections of time and alongshore averaged (a, b) alongshore velocity \(\langle \overline {v}\rangle \) and (c, d) cross-shore velocity \(\langle \overline {u}\rangle \). Left panels are zoomed in on right panels. Black thin lines on panels (a, b) are the time and alongshore averaged temperature \(\langle \overline {T}\rangle \). Notice that color bars are different for \(\langle \overline {v}\rangle \) and \(\langle \overline {u}\rangle \). Because of the shelf indentation heterogeneities, areas where h > 200 m are masked
The standing mesoscale patterns described in Section 3.2 present affect the offshore part of the cross-sections. Specifically, the standing anticyclone visible in Fig. 1b explains the dipolar structure of \(\langle \overline {v}\rangle \) in the upper 200 m. The lateral structure of \(\langle \overline {v}\rangle \) within about 200 km of the shore is similar to that found in EBUs with a surface intensified current flowing in the downwind direction (geostrophically balanced by the SSH low at the coast), and a weaker undercurrent in the opposite direction. Consistent with the deep-isotherm tilt, the upper-ocean poleward current reaches ∼250 m, deeper than in EBUs (50 m, Colas et al. 2012).
An undercurrent flowing in the opposite direction of the surface jet is present in the depth range 500–1500 m, and it exists only during summer. Its core depth is ∼1000 m, much deeper than found in EBUs (∼150–200 m). Similar deep undercurrents, although not seasonal, are found in other western-boundary-current systems. For instance, in the Brazil Current system, a deep undercurrent is located at 800 m (Da Silveira et al. 2004), similar to the undercurrents of the Agulhas (Beal and Bryden 1997; Beal 2009) and East Australian (Mata et al. 2000) current systems. In contrast to EBUs, alongshore winds in western-boundary current systems do not generate undercurrents (McCreary and Kundu 1985). Thus, western-boundary undercurrents require a different forcing mechanism than their eastern-boundary counterparts (McCreary and Kundu 1985), and hence are not expected to have similar structures.
The cross-shore velocity field \(\langle \overline {u}\rangle \) (Fig. 4c,d) mainly consists of offshore flow in the surface Ekman layer (upper 50 m), and so its depth range is similar to that for EBUs. Note that there is no indication of onshore return flow. Examination of nearshore vertical velocities indicates that a large fraction of subsurface waters are injected onto the continental shelves between Ras Marbat and Ras Sharbatat, where the shelf break abruptly changes orientation (not shown).
4 Eddy kinetic energy
The analysis in Section 3 suggests our model solution is close enough to reality to warrant an in-depth investigation of EKE in the Oman current system. In particular, we seek to examine the validity of Manghnani et al.’s 1998 hypothesis that Oman upwelling waters are stirred and exported offshore by a remotely-generated, mesoscale eddy field. Our simulation offers a more complex picture in which local generation of mixed baroclinic-barotropic instabilities is also important.
To set the context, we present Hovmoller diagrams for alongshore-averaged sea level and surface EKE (Fig. 5). Sea level \(\overline {\eta }\) exhibits a strong seasonal cycle within 100 km of the shore (Fig. 5a), with a marked negative anomaly during the upwelling season. This anomaly is the geostrophic signature of the northeastward-flowing East Arabian Current (Schott and McCreary 2001). The locally forced, seasonal signal coexists with remotely-generated, westward-propagating structures, which are particularly noticeable at ∼200 km and farther offshore. Similar remote features occur in EKE, with westward-propagating features that extend over 400–500 km (visible in Fig. 5b). The westward intensification of EKE within ∼200 km of the shore, as well as significant year-to-year variability, complicate the interpretation of the coastal response as compared to the situation for EBUs (Fig. 12 in Marchesiello et al. 2003; Kelly et al. 1998).
To investigate the processes that determine the EKE distribution, we analyze the budget,
Marchesiello et al. (2003). In the following definitions of terms, brackets denote an average over the upwelling season (June–September) during the last 3 years of simulation, primed quantities are deviations from time-mean fields. In Eq. 1, then, \(\text {EKE}=\frac {1}{2}(\langle u^{\prime 2}+v^{\prime 2}\rangle )\), the advection of EKE is
and the wind-work input into the oceanic perturbations is
where \((u_{s}^{\prime },v_{s}^{\prime })\) is the horizontal eddy velocity in the surface layer, \((\tau _{sx}^{\prime },\tau _{sy}^{\prime })\) is the eddy wind stress and ρ 0 is the reference Boussinesq density. Conversion from mean to eddy kinetic energy is
where
and
are contributions from the horizontal and vertical Reynolds stress, respectively (e.g., Gula et al. 2015). The baroclinic conversion term, which transfers eddy potential energy to eddy kinetic energy through a vertical buoyancy flux, is given by
where b ′ = −g ρ ′/ρ 0 is the local buoyancy anomaly. Eddy dissipation by friction at the ocean bottom is given by
where \((u_{b}^{\prime },v_{b}^{\prime })\) is the horizontal eddy velocity in the bottom layer and \((\tau _{bx}^{\prime },\tau _{by}^{\prime })\) is the eddy bottom stress. Finally, the pressure term PRS, which represents contributions from the pressure work by eddies and waves, is determined as the residual of the other terms in Eq. 1.
Figure 6 shows vertical integrations of the terms of Eq. 1. First, note that ∂EKE/∂ t (Fig. 6i) is weak compared to the other terms, indicating that mesoscale turbulence is close to an equilibrium state during the upwelling season. The dominant sources of EKE are barotropic (HRS) and baroclinic (PeKe) instabilities (Fig. 6b, d, respectively). The HRS and PeKe terms are dominantly positive along the path of the jet. Hotspots of EKE generation are situated near capes, similar to the CCS (Marchesiello et al. 2003), although capes are not necessary to trigger instabilities in EBUs (McCreary et al. 1991; Fukamachi et al. 1995). Locally, HRS and PeKe reach O(10) cm 3 s −3, one order of magnitude higher than in the CCS. Interestingly, opposite to EBUs, HRS is higher than PeKe. This difference is a consequence of the amplitude of horizontal shear in the upwelling jet being stronger than in EBUs (0.3 ms −1/100 km vs. 0.1 ms −1/100 km in Chatterjee et al. 2012). It is consistent with results of Chatterjee et al. (2013), who find that HRS dominates in the Somali Current system farther to the south. Note also that HRS is also very strong at the edge of the anticyclonic structure, where the shear is enhanced. The overall contribution of these terms in the area (Fig. 6a) is one order of magnitude higher than in the CCS (Marchesiello et al. 2003), reflecting intensified instabilities of western-boundary currents. The third source of EKE by oceanic instability, VRS, quantifying Kelvin-Helmoltz instabilities, is negligible compared to HRS and PeKe (Fig. 6c).
b–i Time averaged and vertically integrated terms of the EKE equation and (a) averaged terms in the black rectangle area in panel (b). b Horizontal Reynolds Stress (HRS, horizontal shear—i.e., barotropic—instability EKE production), c Vertical Reynolds Stress (VRS, vertical shear instability), d eddy-potential to eddy-kinetic energy (PeKe, baroclinic instability), e advection of EKE (ADV), f wind work (F e K e ), g dissipation by bottom friction (De), h pressure work (PRS), and i temporal variation of EKE during the upwelling season ∂EKE/∂ t. Thin black lines are isolines of mean SSH 〈η〉
The advection term plays an important role in the EKE budget (Fig. 6e), primarily by redistributing energy from nearshore to offshore. This redistribution is particularly evident in the vicinity of standing mesoscale features, which are thus instrumental in the offshore export of EKE. This mesoscale structure advects EKE from the jet vicinity (where it is generated) offshore. This mechanism leads to negative patterns of ADV along the jet path and positive patterns offshore. A similar behavior is found in the Somali Current sytem during the summer monsoon as demonstrated in Chatterjee et al. (2013). They show that EKE is generated by instabilities of the Somali Current and then is advected offshore by the Southern Gyre.
Pressure work is generally positive nearshore and negative offshore, with meso- and finer-scale details that mirror to some extent those in ADV (Fig. 6h). This might not be coincidental but we presently do not understand the underlying reasons. On the other hand, horizontally averaged pressure work is a factor of 3 to 5 smaller than the dominant terms and does not affect the energy budget to leading order.
The wind work (FeKe, Fig. 6f) and bottom dissipation (D e , Fig. 6g) bring small contributions to the EKE budget. The wind work creates EKE in the nearshore band, where the wind is in the direction of the upwelling jet (the Findlater Jet blows northeastward). It is negative offshore where the wind opposes the circulation. On average, it brings a negative contribution to the EKE budget (Fig. 6a). Bottom dissipation is maximum nearshore where currents drag on the shelf slope.
The vertical structures of EKE and PeKe are shown in Fig. 7. PeKe is maximum in the core of the upwelling jet, where the vertical shear of velocity is maximum. This is also where the vertical tilting of isotherms is maximum and where baroclinic instability is therefore most likely to occur. Colas et al. (2013) provide similar plots for the California and Peru-Chile current systems (their Figs. 3 and 4). Consistent with the deeper extent of the upwelling jet off Oman than in EBUs, significant PeKe values reach down to a greater depth (200 vs. 100 m). Their magnitude is also larger by an order of magnitude, a consequence of the more sharply tilted isopycnals associated with the western-boundary upwelling. As previously noted, EKE is significantly larger, and reaches deeper levels.
Time and alongshore averaged vertical sections of a \(\langle \overline {\mathrm {E}\mathrm {K}\mathrm {E}}\rangle \) and b baroclinic conversion term \(\langle \overline {\mathrm {P}_{\mathrm {e}}\mathrm {K}_{\mathrm {e}}}\rangle \). The black lines are the alongshore velocity \(\langle \overline {v}\rangle \) with CI = 5 cm s −1 (negative values are dashed). The white lines are isotherms 15, 20, and 25 ∘C
The ratio between EKE values and the amplitude of PeKe and HRS provides a replenishment time scale τ p for the mesoscale eddy activity, i.e., the time is takes for some baroclinic/barotropic instability to produce the observed level of EKE. Using vertically integrated values, we find τ p ∼10–20 days. Thus, since our budget is performed over a 4-month period of upwelling, it should be balanced. However, the magnitude of the sink of EKE through bottom friction (De) is an order of magnitude less than that of its sources (PeKe and KmKe). The balanced budget therefore implies the loss of EKE through advective and possibly wave fluxes. Since our alongshore average is carried out on a rather small distance (490 km), EKE leakage in the alongshore direction cannot be neglected.
Finally, this EKE budget potentially offers an alternative scenario from the one of Manghnani et al. (1998) to explain the lateral export of upwelled waters. Mesoscale eddies, resulting from barotropic and baroclinic instabilities of the jet, play a role in stirring upwelled waters away from coast. Stirring is thus performed by both the locally and remotely generated eddy field.
5 Summary
The seasonal cycle of upwelling dynamics off Oman is analyzed using a realistic regional numerical simulation that compares favorably with observations. A lag of ∼1.5 month is found between the maximum of the wind stress curl and the maximum of the response (SST and SSH lows). Our interpretation of this lag underscores an important property of western boundary systems: In contrast to EBUs, positive wind-stress curl located offshore generates upwelling-favorable Rossby waves that propagates onshore; these waves have a profound influence on coastal-upwelling dynamics, which among other things produces a delayed upwelling due to their slow propagation speed. In the context of the Oman region, the time scale for the propagation time, infered from Rossby wave propagation speed and the distance of the offshore forcing to the coast, is compatible with the modeled 1.5-month delay.
The vertical structure of the upwelling is found to contrast with that in EBUs: The upward tilt of isotherms toward the coast extends deeper (300 vs. 100–150 m), as does the associated surface jet in thermal wind balance. Our model solution produces a southwestward-flowing undercurrent whose core is also much deeper than in EBUs (1000 vs. 150–200 m). In addition, to demonstrate that coastal alongshore winds cannot produce a western-boundary undercurrent, McCreary and Kundu (1985) showed that forcing by offshore wind curl could do so. The depth of their undercurrent, however, was much shallower than the one in our model. So, a dynamical explanation for the forcing of this undercurrent remains unknown.
Overall, our EKE budget analysis reveals that the Oman upwelling region is significantly influenced by locally generated mesoscale activity. Barotropic instabilities dominate (as is does in the Somali Current, Chatterjee et al. 2013), which contrasts with EBUs where baroclinic instabilities are more prominent. Significant spatial redistribution of EKE is also observed in relation with standing mesoscale patterns, as also found in EBUs.
This work illustrates fundamental differences between eastern- and western-boundary current systems. These differences can be broadly explained by Rossby waves propagation offshore and onshore, respectively. The coexistence of locally-generated turbulence and onshore-propagating signals, both in the form of Rossby waves and mesoscale eddies, makes western-boundary upwelling systems more complex than their eastern-boundary counterparts. Our study highlights dynamical processes from a climatologically-forced ocean model and we expect these processes to typically occur every year. Nonetheless, their timing and strength at interannual time scales—related to basin-scale ocean dynamics and interactions with the atmosphere—remain to be investigated.
Notes
In the model, the wind stress is directly prescribed but the net heat flux is adjusted to better simulate SST, following the procedure in Barnier et al. (1995). Notice that the adjustment is limited and the net heat flux received by the model is essentially identical to ICOADS observations.
Uncertainty in the net heat flux in this region is large. We compared short wave radiations from ICOADS (Worley et al. 2005), the Common Ocean-Ice Reference Experiment dataset (CORE2, Large and Yeager 2009) and the Clouds and Earth’s Radiant Energy System dataset (CERES, Kato et al. 2013) and found local discrepancies of up to 80 W m −2.
References
Azevedo JLLd, Nof D, Mata MM (2012) Eddy train encounters with a continental boundary: a South Atlantic case study. J Phys Oceanogr 42(9):1548–1565. doi:10.1175/JPO-D-11-027.1
Bakun A, Nelson CS (1991) The seasonal cycle of wind-stress curl in subtropical eastern boundary current regions. J Phys Oceanogr 21(12):1815–1834. doi:10.1175/1520-0485(1991)021<1815:TSCOWS>2.0.CO;2
Barnier B, Siefridt L, Marchesiello P (1995) Thermal forcing for a global ocean circulation model using a three-year climatology of ECMWF analyses. J Mar Syst 6(4):363–380
Beal LM (2009) A time series of Agulhas Undercurrent transport. J Phys Oceanogr 39(10):2436–2450. doi:10.1175/2009JPO4195.1
Beal LM, Bryden HL (1997) Observations of an Agulhas undercurrent. Deep Sea Res 44(9):1715–1724. doi:10.1016/S0967-0637(97)00033-2
Becker J, Sandwell D, Smith W, Braud J, Binder B, Depner J, Fabre D, Factor J, Ingalls S, Kim S et al (2009) Global bathymetry and elevation data at 30 arc seconds resolution: SRTM30_PLUS. Marine Geodesy 32(4):355–371. doi:10.1080/01490410903297766
Böhm E, Morrison J, Manghnani V, Kim H, Flagg C (1999) The Ras al Hadd Jet: remotely sensed and acoustic Doppler current profiler observations in 1994–1995. Deep Sea Res 46(8):1531–1549. doi:10.1016/S0967-0645(99)00034-X
Capet X, Colas F, McWilliams J, Penven P, Marchesiello P (2008a) Eddies in eastern boundary subtropical upwelling systems. Ocean Modeling in an Eddying Regime pp 131–147, 10.1029/177GM10
Capet X, McWilliams J, Molemaker M, Shchepetkin A (2008b) Mesoscale to submesoscale transition in the California Current System. part i: Flow structure, eddy flux, and observational tests. J Phys Oceanogr 38 (1):29–43. doi:10.1175/2007JPO3671.1
Centurioni L, Ohlmann J, Niiler PP (2008) Permanent meanders in the California Current System. J Phys Oceanogr 38(8):1690–1710. doi:10.1175/2008JPO3746.1
Chatterjee A, Shankar D, McCreary J, Vinayachandran P (2013) Yanai waves in the western equatorial Indian Ocean. J Geophys Res Oceans 118(3):1556–1570. doi:10.1002/jgrc.20121
Chelton DB, Schlax MG, Samelson RM (2011) Global observations of nonlinear mesoscale eddies. Prog Oceanogr 91(2):167–216. doi:10.1016/j.pocean.2011.01.002
Colas F, McWilliams JC, Capet X, Kurian J (2012) Heat balance and eddies in the Peru-Chile current system. Climate Dyn 39(1-2):509–529. doi:10.1007/s00382-011-1170-6
Colas F, Capet X, McWilliams JC, Li Z (2013) Mesoscale eddy buoyancy flux and eddy-induced circulation in Eastern Boundary Currents. J Phys Oceanogr 43(6):1073–1095. doi:10.1175/JPO-D-11-0241.1
Da Silveira I, Calado L, Castro B, Cirano M, Lima J, Mascarenhas AdS (2004) On the baroclinic structure of the Brazil Current–Intermediate Western Boundary Current system at 22–23 S. Geophys Res Lett 31 (14). doi:10.1029/2004GL020036
Desbiolles F, Blanke B, Bentamy A (2014) Short-term upwelling events at the western African coast related to synoptic atmospheric structures as derived from satellite observations. J Geophys Res 119. doi:10.1002/2013JC009278
Elliott AJ, Savidge G (1990) Some features of the upwelling off Oman. J Mar Res 48(2):319–333
Findlater J (1969) A major low-level air current near the Indian Ocean during the northern summer. Quart J Roy Meteor Soc 95(404):362–380
Fukamachi Y, McCreary JP, Proehl JA (1995) Instability of density fronts in layer and continuously stratified models. J Geophys Res 100(C2):2559–2577
Gula J, Molemaker MJ, McWilliams JC (2015) Gulf Stream dynamics along the Southeastern US Seaboard. J Phys Oceanogr 45(3):690–715. doi:10.1175/JPO-D-14-0154.1
Haney RL, Hale RA, Dietrich DE (2001) Offshore propagation of eddy kinetic energy in the California Current. J Geophys Res 106(C6):11,709–11,717. doi:10.1029/2000JC000433
Jullien S, Menkes CE, Marchesiello P, Jourdain NC, Lengaigne M, Koch-Larrouy A, Lefevre J, Vincent EM, Faure V (2012) Impact of tropical cyclones on the heat budget of the South Pacific Ocean. J Phys Oceanogr 42(11):1882–1906. doi:10.1175/JPO-D-11-0133.1
Kato S, Loeb NG, Rose FG, Doelling DR, Rutan DA, Caldwell TE, Yu L, Weller RA (2013) Surface irradiances consistent with CERES- derived top-of-atmosphere shortwave and longwave irradiances. J Clim 26(9):2719–2740. doi:10.1175/JCLI-D-12-00436.1
Kelly KA, Beardsley RC, Limeburner R, Brink KH, Paduan JD, Chereskin TK (1998) Variability of the near-surface eddy kinetic energy in the California Current based on altimetric, drifter, and moored current data. J Geophys Res 103(C6):13,067–13,083. doi:10.1029/97JC03760
Large W, Yeager S (2009) The global climatology of an interannually varying air–sea flux data set. Climate Dyn 33(2-3):341–364. doi:10.1007/s00382-008-0441-3
Large W, McWilliams J, Doney S (1994) Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev Geophys 32(4):363–403. doi:10.1029/94RG01872
Lee C, Murray D, Barber R, Buesseler K, Dymond J, Hedges J, Honjo S, Manganini S, Marra J, Moser C et al (1998) Particulate organic carbon fluxes: compilation of results from the 1995 US JGOFS Arabian Sea process study: By the Arabian Sea carbon flux group. Deep Sea Res Part II 45(10):2489–2501
Lee C, Jones B, Brink K, Fischer A (2000) The upper-ocean response to monsoonal forcing in the Arabian Sea: seasonal and spatial variability. Deep Sea Res 47(7):1177–1226. doi:10.1016/S0967-0645(99)00141-1
Levitus S, Boyer TP (1994) World Ocean Atlas 1994, vol 4. Temperature. Technical report, National Environmental Satellite, Data, and Information Service, DC, USA
Levitus S, Burgett R, Boyer TP (1994) World Ocean Atlas 1994, vol 3. Salinity. Technical report, National Environmental Satellite, Data, and Information Service, DC, USA
Manghnani V, Morrison JM, Hopkins TS, Böhm E (1998) Advection of upwelled waters in the form of plumes off Oman during the Southwest Monsoon. Deep Sea Res 45(10):2027–2052. doi:10.1016/S0967-0645(98)00062-9
Marchesiello P, Gibbs MT, Middleton JH (2000) Simulations of coastal upwelling on the Sydney continental shelf. Mar Freshwater Res 51(6):577–588. doi:10.1071/MF99046
Marchesiello P, McWilliams J, Shchepetkin A (2003) Equilibrium structure and dynamics of the California Current System. J Phys Oceanogr 33(4):753–783. doi:10.1175/1520-0485(2003)33<753:ESADOT>2.0.CO;2
Marchesiello P, Capet X, Menkes C, Kennan SC (2011) Submesoscale dynamics in tropical instability waves. Ocean Modell 39(1):31–46. doi:10.1016/j.ocemod.2011.04.011
Mason E, Molemaker J, Shchepetkin AF, Colas F, McWilliams JC, Sangrà P (2010) Procedures for offline grid nesting in regional ocean models. Ocean Modell 35(1):1–15. doi:10.1016/j.ocemod.2010.05.007
Mata MM, Tomczak M, Wijffels S, Church JA (2000) East Australian Current volume transports at 30 S: Estimates from the World Ocean Circulation Experiment hydrographic sections PR11/P6 and the PCM3 current meter array. J Geophys Res 105(C12):28,509–28,526. doi:10.1029/1999JC000121
McCreary J, Kundu P (1985) Western boundary circulation driven by an alongshore wind: With application to the SoMali Current system. J Mar Res 43(3):493–516
McCreary J, Kundu P, Molinari R (1993) A numerical investigation of dynamics, thermodynamics and mixed-layer processes in the Indian Ocean. Prog Oceanogr 31(3):181–244. doi:10.1016/0079-6611(93)90002-U
McCreary JP, Fukamachi Y, Kundu PK (1991) A numerical investigation of jets and eddies near an eastern ocean boundary. J Geophys Res 96(C2):2515–2534
Morrison JM, Codispoti L, Gaurin S, Jones B, Manghnani V, Zheng Z (1998) Seasonal variation of hydrographic and nutrient fields during the US JGOFS Arabian Sea Process Study. Deep Sea Res Part II 45 (10):2053–2101. doi:10.1016/S0967-0645(98)00063-0
Rio M, Guinehut S, Larnicol G (2011) New CNES-CLS09 global mean dynamic topography computed from the combination of GRACE data, altimetry, and in situ measurements. J Geophys Res 116(C7). doi:10.1029/2010JC006505
Risien C, Chelton D (2008) A global climatology of surface wind and wind stress fields from eight years of QuikSCAT scatterometer data. J Phys Oceanogr 38(11):2379–2413. doi:10.1175/2008JPO3881.1
Schott F, McCreary J (2001) The monsoon circulation of the Indian Ocean. Prog Oceanogr 51(1):1–123. doi:10.1016/S0079-6611(01)00083-0
Shchepetkin A, McWilliams J (2005) The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Modell 9(4):347–404. doi:10.1016/j.ocemod.2004.08.002
Shi W, Morrison JM, Böhm E, Manghnani V (1999) Remotely sensed features in the US JGOFS Arabian Sea Process Study. Deep Sea Res Part II 46(8):1551–1575. doi:10.1016/S0967-0645(99)00035-1
Teague WJ, Carron MJ, Hogan PJ (1990) A comparison between the Generalized Digital Environmental Model and Levitus climatologies. J Geophys Res 95(C5):7167–7183. doi:10.1029/JC095iC05p07167
Vic C, Roullet G, Carton X, Capet X (2014) Mesoscale dynamics in the Arabian Sea and a focus on the Great Whirl life cycle : a numerical investigation using ROMS. J Geophys Res 119(9):6422–6443. doi:10.1002/2014JC009857
Vic C, Roullet G, Capet X, Carton X, Molemaker MJ, Gula J (2015) Eddy-topography interactions and the fate of the Persian Gulf Outflow. J Geophys Res 120(10):6700–6717. doi:10.1002/2015JC011033
Vignudelli S, Cipollini P, Roblou L, Lyard F, Gasparini G, Manzella G, Astraldi M (2005) Improved satellite altimetry in coastal systems: Case study of the Corsica Channel (Mediterranean Sea). Geophys Res Lett 32(7). doi:10.1029/2005GL022602
Wang DP (1997) Effects of small-scale wind on coastal upwelling with application to Point Conception. J Geophys Res 102(C7):15,555–15,566
Worley S, Woodruff S, Reynolds R, Lubker S, Lott N (2005) ICOADS release 2.1 data and products. Int J Climatol 25(7):823–842. doi:10.1002/joc.1166
Acknowledgments
The altimeter products were produced by Ssalto/Duacs and distributed by Aviso, with support from Cnes (http://www.aviso.altimetry.fr/duacs/). CV was supported by the Direction Générale de l’Armement (DGA) and the Région Bretagne in the form of a PhD scolarship. We thank Antoine Hochet (UBO, Brest) for fruitful discussions and Jérôme Vialard (LOCEAN, Paris) for valuable comments on the manuscript. This manuscript has benefitted considerably from the thorough comments of two reviewers, in particular J. McCreary. We also thank D. G. Evans (NOCS, UK) for improving the writing.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Roger Proctor
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Vic, C., Capet, X., Roullet, G. et al. Western boundary upwelling dynamics off Oman. Ocean Dynamics 67, 585–595 (2017). https://doi.org/10.1007/s10236-017-1044-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10236-017-1044-5