Maintenance of the mean kinetic energy in the global ocean by the barotropic and baroclinic energy routes: the roles of JEBAR and Ekman dynamics

Abstract

In order to determine the maintenance mechanisms of the currents of the global ocean, this study investigates the budget of the annual mean kinetic energy (KE) in a high-resolution (0.1° × 0.1°) semi-global ocean simulation. The analysis is based on a separation of the mean KE using the barotropic (i.e., depth-averaged) and baroclinic (the residual) components of velocity. The barotropic and baroclinic KEs dominate in higher and lower latitudes, respectively, with their global average being comparable to each other. The working rates of wind forcing on the barotropic and baroclinic circulations in the global ocean are 243 and 747 gigawatts, respectively. This study presents at least three new results for the budget of the barotropic KE. Firstly, an energy diagram is rederived to show that the work of the barotropic component of the horizontal pressure gradient (HPG) is connected to the work related to the joint effect of baroclinicity and bottom relief (JEBAR), and then to the budget of potential energy (PE). Secondly, the model analysis shows that the globally averaged work of the barotropic HPG (which is connected to the work related to JEBAR and then to the budget of the PE) is nearly zero. This indicates that the wind- and buoyancy-induced barotropic circulations in the global ocean are of the same strength with opposite sign. Thirdly, it is found that the work of the wind forcing on the barotropic component of the simulated Antarctic Circumpolar Current (ACC) is canceled by the combined effect, in equal measure, of the work of the barotropic HPG and the work of dissipative processes for mean KE. This result makes a significant contribution to the discussion on the depth-integrated momentum balance of the ACC. The barotropic KE is dissipated by the effects of bottom frictional stress, lateral frictional stress, and the Reynolds stress, of which more than half is attributed to an unexpectedly large contribution from biharmonic horizontal friction. Future studies should pay more attention to the role of biharmonic friction used in high-resolution numerical models.

1 Introduction

Characterizing the geography of sources, sinks, and conversions of kinetic energy (KE) in the global ocean remains one of the outstanding issues in physical oceanography (cf. Ferrari and Wunsch 2009). This study investigates the budget of the annual mean KE in a high-resolution semi-global numerical simulation, and identifies the dominant equilibrium in the energy balance in a number of important regions. The focus on the mean-field energy (rather than total-field energy) is intended to revisit existing hypotheses for the momentum and vorticity balances in general circulation theories, and also suggest what kind of a KE budget should be represented by coarse-resolution ocean models used in climate studies.

In this study, the mean KE is separated into that associated with the barotropic (i.e., depth-averaged) and baroclinic (i.e., the residual) components of velocity. Such a separation has been adopted in previous studies for wave KE and eddy KE concerning topographic generation of tidal internal waves or barotropization of geostrophic turbulence (cf. Cummins and Oey 1997; Holloway 1986). On the other hand, the separation of the mean KE in this study gives insight into the mechanisms maintaining the ocean currents, and in particular allows the relative importance of the frictional and pressure effects of bottom topography to be determined.

The pressure effect associated with bottom topography has attracted significant attention in previous studies of the depth-integrated momentum balance of the Antarctic Circumpolar Current (ACC). Munk and Palmen (1951) (MP51) and Johnson and Bryden (1989) (JB89) presented an inviscid theory for the dynamics of the ACC. They considered the presence of only a bottom slope and a horizontally inhomogeneous density distribution, leading to a hypothesis that the eastward wind stress over the Southern Ocean must be canceled by the difference of pressure upstream and downstream of a bottom ridge (Appendix A). The steady-state depth-integrated balance of momentum is written as,

$$\label{btwek} \rho_0 \mathbf{f}\times \int^0_{-H} \overline{\mathbf{V}}~{\rm d}z \simeq - \int^0_{-H} \nabla \overline{p}~{\rm d}z + \overline{\boldsymbol{\tau}}^\mathbf{wind}, $$

(1)

where ρ ₀ is reference density, f is the Coriolis parameter f multiplied by a unit vector z in the vertical direction, V is the horizontal velocity vector, $\nabla$ is the horizontal gradient operator, $p \equiv p^s + \int_{z}^0 g \rho~{\rm d}z$ is the sum of sea surface pressure p ^s and the hydrostatic pressure with g and ρ being the gravitational acceleration and in situ density of seawater, respectively, and $\boldsymbol{\tau}^\mathbf{wind}$ is the wind stress vector. The sea surface is located at z = 0 and assumed to be rigid, with H ( > 0) being the bottom depth. Equation 1 represents a statistically steady state of the ACC with the overbar denoting an Eulerian time mean (or a low-pass temporal filter at fixed height). See Table 1 for an explanation of symbols used in the present paper.

Table 1 List of symbols, where A(x,y,z,t) is an arbitrary quantity

An equation for barotropic KE can be derived from either of Eqs. 1 and 47, whose spatial integral in the band δΨ between two barotropic streamlines circling Antarctica or in the global domain Ω becomes (Holland 1975; Treguier 1992; Ivchenko et al. 1997),

$$ \label{btke1} 0 \simeq -\int_{\delta \Psi, \Omega} \mathcal{TPE} \frac{\overline{\mathbf{V}}^\mathbf{bt}\cdot\nabla H}{H} + \int_{\delta \Psi, \Omega} \overline{\mathbf{V}}^\mathbf{bt} \cdot \overline{\boldsymbol{\tau}}^\mathbf{wind} ~{\rm d}^2x, $$

(2)

where $\mathcal{TPE} \equiv \int^0_{-H} g \overline{\rho} z~{\rm d}z$ is total (mean plus eddy) potential energy (PE) in each vertical column, and $\overline{\mathbf{V}}^\mathbf{bt} \equiv \int^0_{-H} \overline{\mathbf{V}}~{\rm d}z/H$ is the barotropic (i.e., depth-averaged) component of $\overline{\mathbf{V}}$.

The first term of Eq. 2 is the expression¹ derived by Ivchenko et al. (1997), and has two interesting characteristics: (1) it does not contain the sea surface pressure $\overline{p}^s$ and (2) it vanishes when the contours of $\mathcal{TPE}$ and H are parallel ($\nabla \mathcal{TPE} \times \nabla H = 0)$, the latter of which is proved by the present study. These characteristics are the same as that of the joint effect of baroclinicity and bottom relief (JEBAR) (Sarkisyan and Ivanov 1971) term in the barotropic vorticity Eq. 47, except that Eq. 2 is in an integrated form. Although JEBAR is a concept that was originally developed from the vorticity equation, we use the term of JEBAR in a general sense and call the first term of Eq. 2 the working rate of JEBAR.

There remain several important questions concerning Eq. 2: (1) whether the work of JEBAR is connected to the PE equation or the baroclinic KE equation, (2) which of the barotropic KE balance (Eq. 2) and its baroclinic counterpart is more effective in the ocean, and (3) whether the work of JEBAR prevails over the contributions of bottom frictional stress, lateral frictional stress, and the Reynolds stress in the ACC. In order to examine these questions, this paper presents the set of mathematical, physical, and numerical investigations in Sections 2, 3, and 4, respectively. In Section 2, we derive an energy diagram which is used in the rest of the present paper. In Section 3, we investigate the relationship between the role of JEBAR and Ekman dynamics. Section 4 presents a comprehensive analysis of the annual mean KE in a high-resolution semi-global simulation. Section 5 presents a summary.

2 Mathematical investigation

This section derives a version of Holland’s (1975) energy diagram by focusing on the general circulation. We show that the integrated work of JEBAR—the first term of Eq. 2—is connected to the budget of PE. We also show that the work of JEBAR vanishes when the contours of $\mathcal{TPE}$ and H are parallel ($\nabla \mathcal{TPE} \times \nabla H = 0)$.

2.1 Time-mean momentum equations

The momentum and continuity equations for an incompressible hydrostatic rotating Boussinesq fluid that are used in eddy-resolving ocean general circulation models (OGCMs) are

$$ \begin{array}{rll} &&\rho_0 [\mathbf{V}_t + \nabla\cdot(\mathbf{V}\, \mathbf{V}) + (w\mathbf{V})_z + \mathbf{f}\times \mathbf{V} ] \\&&= - \nabla p + \mathbf{B} + \mathbf{\boldsymbol{\tau}}_z,\label{me} \end{array}$$

(3)

$$ p_z = - \rho g, \label{hse} $$

(4)

$$ \nabla \cdot \mathbf{V} + w_z = 0, \label{ce} $$

(5)

where w is the vertical component of velocity, subscript z is the vertical derivative operator, B is the subgrid-scale horizontal mixing term, and $\boldsymbol{\tau}_z$ is the subgrid-scale vertical mixing term. In this paper, the sea surface is assumed to be rigid to simplify the equations used in the analysis (the fact that the model we use for our analysis has a free surface does not compromise our results). The momentum flux of vertical mixing or shear stress $\boldsymbol{\tau}$ is defined at all depths with boundary conditions of $\boldsymbol{\tau}|_{z=0} \equiv \boldsymbol{\tau}^\mathbf{wind}$ (wind stress) and $\boldsymbol{\tau}|_{z=-H} \equiv \boldsymbol{\tau}^\mathbf{btm}$ (bottom-frictional stress). All equations in the present study are expressed in z coordinates.

The present study focuses on the dynamics of the general circulation (i.e., mean field rather than perturbation field) which can be described by applying a low-pass temporal filter. Momentum Eq. 3 and continuity Eq. 5 become,

$$\begin{array}{rll}\label{mme} &&\rho_0 \left[\overline{\mathbf{V}}_t + \nabla\cdot(\overline{\mathbf{V}}\, \overline{\mathbf{V}}) + (\overline{w}\overline{\mathbf{V}})_z + \mathbf{f}\times\overline{\mathbf{V}} \right] \nonumber\\ &&= - \nabla \overline{p} + \mathbf{R} + \overline{\mathbf{B}} + \overline{\mathbf{\boldsymbol{\tau}}}_z , \end{array}$$

(6)

$$ \label{mce} \nabla \cdot \overline{\mathbf{V}} + \overline{w}_z = 0, $$

(7)

which allow a slow variation of the general circulation. The vector $\mathbf{R} \equiv - \rho_0 [\nabla\cdot(\overline{\mathbf{V}'\mathbf{V}'}) + (\overline{w'\mathbf{V}'})_z]$ is the Reynolds stress divergence with prime denoting deviation from the Eulerian time mean.

2.2 Mean and eddy KEs

The total (mean plus eddy) field equations for KE and pressure-flux divergence can be derived from Eqs. 3–5:

$$ \begin{array}{rll} && \frac{\rho_0}{2} \left[\overline{|\mathbf{V}|^2}_t + \nabla\cdot(\overline{\mathbf{V} |\mathbf{V}|^2}) + (\overline{w | \mathbf{V}|^2})_z \right]\nonumber\\ && = - \overline{\mathbf{V} \cdot \nabla p} + \overline{\mathbf{V}\cdot \mathbf{B}} + \overline{\mathbf{V}\cdot \boldsymbol{\tau}_z}, \label{tke} \end{array}$$

(8)

$$ \nabla\cdot (\overline{\mathbf{V}p}) + (\overline{w p})_z = \overline{\mathbf{V}\cdot \nabla p} +\overline{wp_z}. $$

(9)

The mean-field equations for KE and pressure-flux divergence can be derived from Eqs. 6 and 7:

$$ \begin{array}{rll} \label{mke} &&\frac{\rho_0}{2} \left[|\overline{\mathbf{V}}|^2_t + \nabla\cdot(\overline{\mathbf{V}} |\overline{\mathbf{V}}|^2) + (\overline{w} |\overline{\mathbf{V}}|^2)_z \right] \nonumber \\ && = \overline{\mathbf{V}} \cdot (-\nabla \overline{p}+\mathbf{R}+\overline{\mathbf{B}} +\overline{\boldsymbol{\tau}}_z), \end{array}$$

(10)

$$ \label{mpf} \nabla\cdot (\overline{\mathbf{V}}\ \overline{p}) + (\overline{w}\ \overline{p})_z = \overline{\mathbf{V}}\cdot\nabla\overline{p} + \overline{w}\ \overline{p}_z. $$

(11)

The volume integrals of Eqs. 8–11 in the global domain Ω yield,

$$ \label{imke} \frac{d}{{\rm d}t} \int_{\Omega} \frac{\rho_0}{2} |\overline{\mathbf{V}}|^2 ~{\rm d}^3x = \int_{\Omega} \overline{\mathbf{V}}\cdot (- \nabla \overline{p}+ \mathbf{R}+ \overline{\mathbf{B}}+\overline{\boldsymbol{\tau}}_z) ~{\rm d}^3x, $$

(12)

$$ \begin{array}{rll} && \label{impf} {\kern-6pt}0 = \int_{\Omega}(\overline{\mathbf{V}}\cdot\nabla\overline{p}+\overline{w}\ \overline{p}_z)~{\rm d}^3x, \\&& {\kern-6pt} \frac{d}{{\rm d} t}\int_{\Omega}\frac{\rho_0}{2}\overline{|\mathbf{V}'|^2}~{\rm d}^3x \end{array}$$

(13)

$$ \label{ieke}= \int_{\Omega} [ \overline{\mathbf{V}' \cdot (-\nabla p'+\mathbf{B}'+\boldsymbol{\tau}'_z)} - \overline{\mathbf{V}}\cdot \mathbf{R} ]~{\rm d}^3x, $$

(14)

$$ \label{iepf} 0 = \int_{\Omega} ( \overline{\mathbf{V}'\cdot \nabla p'} +\overline{w'p'_z}) ~{\rm d}^3x, $$

(15)

where $\int_\Omega~{\rm d}^3 x = \int_\Omega\int^0_{-H}~{\rm d}z{\rm d}^2 x$. Equations 12 and 13 are for the mean field, while Eqs. 14 and 15 are for the eddy field.

2.3 Barotropic component of mean KE

Holland (1975) derived a prototype of the barotropic KE (Eq. 2). He separated KE in each vertical column into that associated with the barotropic and baroclinic components of velocity. His approach is applied here to the mean KE, to focus on the general circulation, rather than (the unaveraged) total KE,

$$\label{holl} \frac{\rho_0}{2} \int^0_{-H} |\overline{\mathbf{V}}|^2~{\rm d}z = \frac{\rho_0}{2} H|\overline{\mathbf{V}}^\mathbf{bt}|^2 + \frac{\rho_0}{2} \int^0_{-H} |\overline{\mathbf{V}}^\mathbf{bc}|^2~{\rm d}z, $$

(16)

where $\overline{\mathbf{V}}^\mathbf{bc} \equiv \overline{\mathbf{V}} - \overline{\mathbf{V}}^\mathbf{bt}$ is the baroclinic component of velocity: $\int^0_{-H} \overline{\mathbf{V}}^\mathbf{bc} {\rm d}z = 0$. This separation is essential for formulating the energetics of JEBAR. In sharp contrast to a vertical mode decomposition in a linear theory assuming no bottom slope, each of the barotropic and baroclinic components of velocity in the present study satisfies a no-normal-flow boundary condition at the top and bottom of the ocean even if the bottom is steeply sloped, as will be shown below.

The time evolution of the barotropic velocity is governed by the depth integrals of momentum and continuity Eqs. 6 and 7,

$$ \begin{array}{rll} \label{btmom} &&\rho_0 \left[H\overline{\mathbf{V}}^\mathbf{bt}_t + \nabla\cdot\left(H\overline{\mathbf{V}}^\mathbf{bt}\overline{\mathbf{V}}^\mathbf{bt}\right) + \mathbf{f}\times H\overline{\mathbf{V}}^\mathbf{bt} \right]\nonumber\\ && = \int^0_{-H} (-\nabla \overline{p}+\mathbf{F}+\mathbf{D})~{\rm d}z + \mathbf{N},\end{array}$$

(17)

$$ \label{btcon} {\kern-6pt}\nabla \cdot (H \overline{\mathbf{V}}^\mathbf{bt}) = 0, $$

(18)

where $\mathbf{F} \equiv S_\mathbf{srf} \overline{\boldsymbol{\tau}}_z$ is the wind forcing vector with S _s rf(z) being a step function which becomes unity in the surface Ekman layer and zero underneath. The vector $\mathbf{D} \equiv S_\mathbf{btm}\overline{\boldsymbol{\tau}}_{z} + \overline{\mathbf{B}} + \mathbf{R}$ is the sum of bottom friction, horizontal mixing, and the Reynolds stress divergence terms, with S _b tm(z) being a step function which becomes unity in the bottom Ekman layer and zero above. Introduction of the two separate vectors F and D simplifies our presentation. The vector D is hereafter called the sum of dissipative processes for convenience². It may also be called the sum of turbulent drag forces.

The vector $\mathbf{N} \equiv - \rho_0 \nabla\cdot\int^0_{-H} \overline{\mathbf{V}}^\mathbf{bc}\overline{\mathbf{V}}^\mathbf{bc}{\rm d}z$ represents an advective (nonlinear) interaction between barotropic and baroclinic modes. The advective terms in Eq. 17 are transformed from those in Eq. 6 by using,

$$ \begin{array}{rll} &&\int_{-H}^0 \left[\nabla \cdot( \overline{\mathbf{V}}\,\overline{\mathbf{V}}) +(\overline{w}\overline{\mathbf{V}})_z\right]~{\rm d}z \nonumber\\ &&{\kern6pt} =\nabla \cdot \int_{-H}^0 \overline{\mathbf{V}}\,\overline{\mathbf{V}}~{\rm d}z -(\overline{\mathbf{V}}\,\overline{\mathbf{V}})|_{z=-H}\cdot\nabla H + \left[\overline{w}\overline{\mathbf{V}}\right]^{z=0}_{z=-H} \nonumber\\ &&{\kern6pt} =\nabla \cdot \int_{-H}^0 \left( \overline{\mathbf{V}}^\mathbf{bt}\,\overline{\mathbf{V}}^\mathbf{bt} + \overline{\mathbf{V}}^\mathbf{bc}\,\overline{\mathbf{V}}^\mathbf{bc} \right)~{\rm d}z, \end{array}$$

(19)

where a no-normal-flow boundary condition of the mean velocity has been applied. Namely, $\overline{w}|_{z=0} = 0$ and $\overline{w}|_{z=-H} = - \overline{\mathbf{V}}|_{z=-H}\cdot\nabla H$ at the top and bottom of the ocean, respectively.

Using Eqs. 17 and 18 we derive equations for the barotropic part of the mean KE and mean pressure-flux divergence,

$$ \begin{array}{rll} \label{btmke} && \frac{\rho_0}{2} \left[H |\overline{\mathbf{V}}^\mathbf{bt}|^2 _t + \nabla\cdot\left(H\overline{\mathbf{V}}^\mathbf{bt} |\overline{\mathbf{V}}^\mathbf{bt}|^2\right)\right]\nonumber\\ [-2pt] && = \overline{\mathbf{V}}^\mathbf{bt}\cdot \left[ \mbox{$\displaystyle\int^0_{-H}$} (-\nabla \overline{p}+\mathbf{F}+\mathbf{D})~{\rm d}z + \mathbf{N} \right], \end{array}$$

(20)

$$ \begin{array}{rll} \label{btmpf} && \nabla\cdot \left( \overline{\mathbf{V}}^\mathbf{bt} \mbox{$\displaystyle\int^0_{-H}$} \overline{p}~{\rm d}z \right) \\ &&= \overline{\mathbf{V}}^\mathbf{bt} \cdot \mbox{$\displaystyle\int^0_{-H}$} \nabla \overline{p}~{\rm d}z + \mbox{$\displaystyle\int^0_{-H}$} \overline{w}^\mathbf{bt} \overline{p}_z ~{\rm d}z, \end{array}$$

(21)

where $\overline{w}^\mathbf{bt}$ is the vertical component of barotropic velocity:

$$ \label{btw} \overline{w}^\mathbf{bt} \equiv (z/H) \overline{\mathbf{V}}^{\mathbf{bt}}\cdot \nabla H. $$

(22)

This vertical component of velocity satisfies the boundary conditions at the top and bottom of the ocean even if the bottom is steeply sloped (Fig. 1). The utility of Eq. 22 has been little explored in previous studies for JEBAR or bottom form stress. Use of Eqs. 18 and 22 shows that the barotropic velocity $(\overline{\mathbf{V}}^\mathbf{bt},\overline{w}^\mathbf{bt})$ is three-dimensionally nondivergent: $\nabla \cdot \overline{\mathbf{V}}^\mathbf{bt} = - (1/H) \overline{\mathbf{V}}^\mathbf{bt} \cdot\nabla H \equiv - \overline{w}^\mathbf{bt}_z$.

Fig. 1

Illustration of the vertical component of velocity which is induced by the horizontal component of barotropic velocity over a sloping bottom, as defined in Eq. 22

We consider the volume budgets of both mean barotropic Eq. 20 and pressure-flux divergence Eq. 21,

$$ \begin{array}{rll} \label{ibtmke} && \frac{\rm d}{{\rm d}t} \int_{\delta\Psi,\Omega} \frac{\rho_0}{2} H |\overline{\mathbf{V}}^\mathbf{bt}|^2 ~{\rm d}^2x =\int_{\delta\Psi,\Omega} \overline{\mathbf{V}}^\mathbf{bt}\cdot \mathbf{N} ~{\rm d}^2x\\&& + \int_{\delta\Psi,\Omega} \overline{\mathbf{V}}^\mathbf{bt} {\kern10pt} \cdot \mbox{$\mbox{$\displaystyle\int^0_{-H}$}$} (-\nabla \overline{p}+\mathbf{F}+\mathbf{D})~dz ~{\rm d}^2x, \end{array}$$

(23)

$$ \label{ibtmpf} 0 = \int_{\delta \Psi, \Omega}\left( \overline{\mathbf{V}}^\mathbf{bt} \cdot \mbox{$\displaystyle\int^0_{-H}$} \nabla \overline{p}~{\rm d}z + \mbox{$\displaystyle\int^0_{-H}$} \overline{w}^\mathbf{bt} \overline{p}_z\right)~{\rm d}z ~{\rm d}^2x. $$

(24)

Equation 24 has three important implications:

• Equation 24 can be derived by using the spatial integral $\int {\rm d}x^2$ not only in the global domain Ω but also in a band δΨ of barotropic streamlines.

• Equation 24 shows that the JEBAR term of Eq. 2 represents the conversion between mean KE and PE.

• Each of the two terms of Eq. 24 and the first term of Eq. 2 vanishes when the bottom is level (i.e., $\nabla H = 0$), when the density distribution is horizontally homogeneous (i.e., $\nabla \rho = 0$), or when the contours of $\mathcal{TPE}$ and H are parallel (i.e., $\nabla \mathcal{TPE} \times \nabla H = 0$).

The first implication is confirmed by the barotropic pressure flux on the left hand side of Eq. 21 having no component normal to barotropic streamlines: $\int^0_{-H} \overline{p}~{\rm d}z \overline{\mathbf{V}}^\mathbf{bt} \cdot \nabla \Psi = \int^0_{-H} \overline{p}~{\rm d}z \overline{\mathbf{V}}^\mathbf{bt} \cdot (H \overline{\mathbf{V}}^\mathbf{bt} \times \mathbf{z}) = 0$. The second implication is clarified by using Eqs. 22, 24, and $\overline{p}_z = - g \overline{\rho}$:

$$ \begin{array}{rll} \label{iijebar} && \int_{\delta \Psi, \Omega} \overline{\mathbf{V}}^\mathbf{bt} \cdot \mbox{$\displaystyle\int^0_{-H}$} \nabla \overline{p}~{\rm d}z ~{\rm d}^2x = \int_{\delta \Psi, \Omega} \mbox{$\displaystyle\int^0_{-H}$} g \overline{\rho}\, \overline{w}^\mathbf{bt} ~{\rm d}z ~{\rm d}^2x \nonumber\\ && =\int_{\delta \Psi, \Omega} \mathcal{TPE} \frac{\overline{\mathbf{V}}^\mathbf{bt}\cdot\nabla H}{H} ~{\rm d}^2x, \end{array}$$

(25)

where the last term is identical to the first term of Eq. 2. Given the vertical component of velocity $\overline{w}^\mathbf{bt}$ in the middle term of Eq. 25, it is natural to infer that the work of JEBAR is connected to PE as in Holland (1975) and Sakamoto and Umetsu (2006). This is in contrast to Treguier (1992), Ivchenko et al. (1997), and Best et al. (1999) who suggested that the work of JEBAR is directly connected to baroclinic KE.

Fig. 2

Energy diagram used in the present study. Energy budgets are evaluated after taking the volume integral in the global domain based on Eqs. 14, 15, 23, 24, and 29–31 as detailed in Section 2. Energy conversions represented by triple lines are investigated in the present study. The role of JEBAR is represented by $\int^0_{-H} g \overline{\rho}\, \overline{w}^\mathbf{bt}~{\rm d}z$ and the role of Ekman pumping/suction in the classical view is represented by $\int^0_{-H} g \overline{\rho}\, \overline{w}^\mathbf{bc}~{\rm d}z$ (Sections 2 and 3). The external source/sink terms for the eddy kinetic energy and total PE are not illustrated for simplicity

With Eq. 25 the third implication is obvious in the case of $\nabla H = 0$. In the case of $\nabla \rho = 0$, it can be shown that

$$ \begin{array}{rll}\label{mc} && \int_{\delta \Psi, \Omega} \overline{\mathbf{V}}^\mathbf{bt} \cdot \mbox{$\displaystyle\int^0_{-H}$} \nabla \overline{p}~{\rm d}z ~{\rm d}^2x \nonumber\\ [-1pt] && =\int_{\delta \Psi, \Omega} \overline{\mathbf{V}}^\mathbf{bt} \cdot \mbox{$\displaystyle\int^0_{-H}$} \nabla \overline{p}^s~{\rm d}z~{\rm d}^2x \nonumber\\ [-1pt] && =\int_{\delta \Psi, \Omega} H \overline{\mathbf{V}}^\mathbf{bt} \cdot \nabla \overline{p}^s~{\rm d}^2x \nonumber\\ [-1pt] && =\int_{\delta \Psi, \Omega} \nabla \cdot \left(H \overline{\mathbf{V}}^\mathbf{bt}\overline{p}^s\right)~{\rm d}^2x \nonumber\\ [-1pt] && = 0, \end{array}$$

(26)

where Eq. 18 has been used. In the case of $\nabla \mathcal{TPE} \times \nabla H = 0$, $\mathcal{TPE}$ can be written as a function of H. Here we introduce a new function Q(H) defined by

$$ \frac{{\rm d} Q}{{\rm d} H} \equiv \frac{\mathcal{TPE}}{H^2}. \label{qh} $$

(27)

Substitution of Eq. 27 into the last term of Eq. 25 yields

$$ \begin{array}{rll} && \int_{\delta \Psi, \Omega} \mathcal{TPE}\frac{\overline{\mathbf{V}}^ \mathbf{bt}\cdot \nabla H}{H}~{\rm d}^2x \nonumber\\ [-1pt] && = \int_{\delta \Psi, \Omega} \left(H \overline{\mathbf{V}}^\mathbf{bt}\cdot\nabla H\right) \frac{{\rm d}Q}{{\rm d}H}~{\rm d}^2 x \nonumber\\ [-1pt] && = \int_{\delta \Psi, \Omega} H \overline{\mathbf{V}}^\mathbf{bt}\cdot \nabla Q~{\rm d}^2 x \nonumber\\ [-1pt] && = \int_{\delta \Psi, \Omega} \nabla \cdot \left(H \overline{\mathbf{V}}^\mathbf{bt} Q\right)~{\rm d}^2 x \nonumber\\ [-1pt] && = 0, \label{tpe-h-align} \end{array}$$

(28)

where Eq. 18 has been used. Derivations of Eqs. 26 and 28 can be based on the spatial integral $\int {\rm d}x^2$ not only in the global domain Ω but also in a band δΨ of barotropic streamlines.

2.4 Baroclinic component of mean KE

The volume budgets of both mean baroclinic KE and pressure-flux divergence are given by subtracting Eqs. 23 and 24 from Eqs. 12 and 13, respectively,

$$ \begin{array}{rll} && \label{ibcmke} \frac{\rm d}{{\rm d}t} \int_{\Omega} \frac{\rho_0}{2} \mbox{$\displaystyle\int^0_{-H}$} |\overline{\mathbf{V}}^\mathbf{bc}|^2~{\rm d}z{\rm d}^2x =- \int_{\Omega}\overline{\mathbf{V}}^\mathbf{bt}\cdot \mathbf{N} ~{\rm d}^2x \\&&+ \int_{\Omega} \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc} \cdot (-\nabla \overline{p}+\mathbf{F}+\mathbf{D}+S_\mathbf{mid}\overline{\boldsymbol {\tau}}_z)~{\rm d}z ~{\rm d}^2x ,\end{array}$$

(29)

$$\label{ibcmpf} 0= \int_{\Omega} \left( \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc} \cdot \nabla \overline{p}~{\rm d}z + \mbox{$\displaystyle\int^0_{-H}$} \overline{w}^\mathbf{bc} \overline{p}_z~{\rm d}z \right)~{\rm d}^2x, $$

(30)

where S _m id(z) ≡ 1 − S _s rf − S _b tm is a step function which becomes unity at depths between the bottom of the surface Ekman layer and the top of the bottom Ekman layer and zero at other depths. The symbol $\overline{w}^\mathbf{bc} \equiv \overline{w}-\overline{w}^\mathbf{bt}$ represents the vertical component of mean baroclinic velocity. The baroclinic velocity $(\overline{\mathbf{V}}^\mathbf{bc},\overline{w}^\mathbf{bc})$ satisfies no-normal-flow boundary conditions at the top and bottom of the ocean as do $(\overline{\mathbf{V}},\overline{w})$ and $(\overline{\mathbf{V}}^\mathbf{bt},\overline{w}^\mathbf{bt})$. The baroclinic velocity $(\overline{\mathbf{V}}^\mathbf{bc},\overline{w}^\mathbf{bc})$ is three-dimensionally nondivergent as are $(\overline{\mathbf{V}},\overline{w})$ and $(\overline{\mathbf{V}}^\mathbf{bt},\overline{w}^\mathbf{bt})$.

2.5 Potential energy

Hydrostatic pressure is defined in terms of in situ density, as shown in Eq. 4. By using the equations for temperature, salinity, and in situ density that are used in OGCMs (not shown), one can derive an equation for the total (mean plus eddy) PE in the global domain Ω,

$$ \label{itpe} \frac{\rm d}{{\rm d} t} \int_{\Omega } \mathcal{TPE} ~{\rm d}^2x = \int_{\Omega } (g \overline{\rho}\ \overline{w}+ g \overline{\rho' w'} + Diabatic)~{\rm d}^3x, $$

(31)

where Diabatic represents the sum of the effects of buoyancy forcing, diabatic density mixing, and the nonlinearity of the state equation of seawater (cf. Gnanadesikan et al. 2005; Kuhlbrodt et al. 2007).

Now we have a complete set of equations for the barotropic and baroclinic parts of mean KE and their interactions with total PE, leading to an energy diagram shown in Fig. 2. The budget of each energy box is given by Eqs. 14, 23, 29, and 31 with the connections between them being given by Eqs. 15, 24, and 30. The external source/sink terms for the eddy KE and total PE are not illustrated in Fig. 2 for simplicity. The energy conversion routes represented by the triple lines in Fig. 2 are investigated in the rest of this paper.

Note that, with the assessment of the numerical simulation of the ACC in mind (Section 1), the present study investigates the work of JEBAR which is caused only by a time mean flow (hereafter stationary JEBAR). On the other hand previous studies, such as Treguier (1992), Ivchenko et al. (1997) and Best et al. (1999) investigated the combined effect of the stationary JEBAR and transient JEBAR (the latter of which is caused by both transient eddies and seasonal cycles) because they used the equation of total KE rather than mean KE. While the work of the stationary JEBAR maintains the interaction between mean KE and total PE (Fig. 2), the work of the transient JEBAR maintains the interaction between eddy KE and total PE (not shown). The roles of the stationary and transient JEBAR may mask each other in the previous analyses for the total KE.

3 Physical investigation

This section gives a physical interpretation of Fig. 2. We illustrate the relationship between the role of JEBAR and Ekman dynamics, which follows a debate raised by Warren et al. (1996) (see Appendix A for details). In particular the work of JEBAR, $\int^0_{-H} g \overline{\rho}\, \overline{w}^\mathbf{bt}$ ${\rm d}z (= - \int^0_{-H} \overline{p}_z \overline{w}^\mathbf{bt}~{\rm d}z)$, can be also interpreted as the work of the barotropic component of the Ekman velocity on the barotropic component of the horizontal pressure gradient (HPG), if a spatial integral is taken. On the other hand, the role of Ekman pumping/suction in classical views is represented by $\int^0_{-H} g \overline{\rho}\, \overline{w}^\mathbf{bc}~{\rm d}z (= - \int^0_{-H} \overline{p}_z \overline{w}^\mathbf{bc}~{\rm d}z)$.

3.1 Terminology

We first clarify names used for some components of the mean velocity $\overline{\mathbf{V}}$. Terminology and definitions provide a language that proves useful to our argument and discussion in the rest of this paper.

The geostrophic velocity $\overline{\mathbf{V}}_\mathbf{geo}$ is the velocity component in the Coriolis term that is balanced by the HPG term of Eq. 6: $\rho_0 \mathbf{f}\times \overline{\mathbf{V}}_\mathbf{geo}\equiv -\nabla \overline{p}$. The wind-induced Ekman velocity $\overline{\mathbf{V}}_\mathbf{wind}$—which is defined in the surface Ekman layer—is the velocity component in the Coriolis term that is balanced by the vertical mixing term of Eq. 6: $\rho_0 \mathbf{f}\times \overline{\mathbf{V}}_\mathbf{wind} = S_\mathbf{srf} \overline{\boldsymbol{\tau}}_z = \mathbf{F}$.

The bottom-friction Ekman velocity—which is defined in the bottom Ekman layer—is the velocity component in the Coriolis term that is balanced by the vertical mixing term of Eq. 6: $\rho_0 \mathbf{f}\times \overline{\mathbf{V}} = S_\mathbf{btm} \overline{\boldsymbol{\tau}}_z$. The terminology of “Ekman” is extended in Spall (2003, 2008) to refer to the velocity component in the Coriolis term that is balanced by the horizontal mixing term of Eq. 6 near the (subsurface) lateral boundaries of the ocean (i.e., the Stewartson layer): $\rho_0 \mathbf{f}\times \overline{\mathbf{V}} = \overline{\mathbf{B}}$. In an analogy to the above extended definition of Ekman velocity, if the role of the Reynolds stress divergence is similar to that of the horizontal mixing term (i.e., decelerating mean currents in coastal boundary regions), it is useful to consider the velocity component in the Coriolis term that is balanced by the Reynolds stress term of Eq. 6: $\rho_0 \mathbf{f}\times \overline{\mathbf{V}} = \mathbf{R}$. For convenience, the sum of the above three types of ageostrophic velocity is referred to in the present study as the total-drag ageostrophic velocity $\overline{\mathbf{V}}_\mathbf{td}$, and is defined by $\rho_0 \mathbf{f}\times \overline{\mathbf{V}}_\mathbf{td} \equiv S_\mathbf{btm} \overline{\boldsymbol{\tau}}_z + \overline{\mathbf{B}} + \mathbf{R} = \mathbf{D}$.²

The result is that the present study considers two kinds of ageostrophic velocity, namely the wind-induced Ekman velocity and the total-drag ageostrophic velocity. This simplification is aimed at offsetting the complexity arising from the barotropic-baroclinic decomposition.

3.2 Wind-induced and total-drag energy routes

The statistically steady state of mean KE is explained by a relationship between geostrophic velocity and Ekman (or ageostrophic) velocity, as shown below. We focus on two types of energy route (i.e., a partial energy cycle) for the mean KE, namely a wind-induced energy route and a total-drag energy route.

The energy route associated with the wind-induced Ekman velocity operates in regions away from bottom and side boundaries where the momentum balance is written by

$$\label{wek} \rho_0 \mathbf{f}\times \overline{\mathbf{V}} \simeq -\nabla \overline{p} + \mathbf{F}. $$

(32)

The product of Eq. 32 and $\overline{\mathbf{V}} \simeq \overline{\mathbf{V}}_\mathbf{geo} + \overline{\mathbf{V}}_\mathbf{wind}$ yields an equation for the balance of mean KE that corresponds to Eq. 10,

$$ 0 \simeq \label{wec} - \overline{\mathbf{V}}\cdot\nabla \overline{p} + \overline{\mathbf{V}}\cdot \mathbf{F} \simeq \underbrace{- \overline{\mathbf{V}}_\mathbf{wind} \cdot\nabla \overline{p}}_{\mbox{negative}} + \underbrace{\overline{\mathbf{V}}_\mathbf{geo}\cdot \mathbf{F}}_{\mbox{positive}}, $$

(33)

where the first term on the right-hand side is the rate of the work done by the wind-induced Ekman velocity on the HPG. Hereafter the second term $\overline{\mathbf{V}}\cdot\mathbf{F}$ or $\overline{\mathbf{V}}_\mathbf{geo}\cdot\mathbf{F}$ of Eq. 33 is called as “the work of wind forcing” (it is somewhat different from “the work of wind stress” used in previous studies, see Appendix B).

The right-hand side of Eq. 33 indicates that the HPG work term is typically negative since the wind work term is usually positive (but can be negative if ocean currents flow against the direction of wind forcing). An increase of mean KE by wind forcing is locally canceled by a decrease of mean KE by wind-induced Ekman velocity flowing toward a higher mean pressure (cf. Kuhlbrodt et al. 2007). This linkage of two work elements in Eq. 33—the work of wind forcing being locally canceled by the work of the HPG—is hereafter called the wind-induced energy route (WER: a clearer, but more cumbersome, term is the wind-to-HPG route) as it originates in the wind input of mean KE.

The energy route associated with the total-drag ageostrophic velocity operates near bottom and side boundaries where the momentum balance is written by

$$\label{e:pg2} \rho_0 \mathbf{f}\times \overline{\mathbf{V}} \simeq -\nabla \overline{p} + \mathbf{D}. $$

(34)

The product of Eq. 34 and $\overline{\mathbf{V}} \simeq \overline{\mathbf{V}}_\mathbf{geo} + \overline{\mathbf{V}}_\mathbf{td}$ yields an equation for the balance of mean KE that corresponds to Eq. 10,

$$ 0 \simeq \label{bec} - \overline{\mathbf{V}}\cdot\nabla \overline{p} + \overline{\mathbf{V}}\cdot \mathbf{D} \simeq \underbrace{- \overline{\mathbf{V}}_\mathbf{td} \cdot\nabla \overline{p}}_{\mbox{positive}} + \underbrace{\overline{\mathbf{V}}_\mathbf{geo}\cdot \mathbf{D}}_{\mbox{negative}}, $$

(35)

where the first term on the right-hand side is the rate of the work by the total-drag ageostrophic velocity on the HPG. The right-hand side of Eq. 35 indicates that the HPG work term is positive because the total-drag work term is usually negative (but can be positive if the Reynolds stress divergence causes an acceleration of the mean flow). A decrease of mean KE by dissipative processes is locally canceled by an increase of mean KE by the total-drag ageostrophic velocity flowing toward a lower mean pressure. This linkage of two work elements in Eq. 35—the work of dissipative processes being locally canceled by the work of the HPG—is hereafter called the total-drag energy route (abbreviated as DER: a clearer term is the HPG-to-total-drag route). The DER is associated with the buoyancy-induced circulation in that the source of this energy route is buoyancy (or more exactly, a nonzero $\nabla p$) which has already been present in each region of the ocean by processes such as (1) being carried from the other regions by both pressure fluxes and advection of PE, (2) local atmospheric buoyancy forcing, and (3) local diabatic density mixing.

Previous numerical investigations of the global energy budget have shown that the work of the HPG acts to feed PE, which can be interpreted as the work of the wind-induced Ekman velocity on the HPG prevailing over that of the total-drag ageostrophic velocity (cf. Kuhlbrodt et al. 2007; Aiki and Richards 2008). In this case, it can be said that the WER prevails over the DER in the global ocean. However the relative magnitude of the WER and DER may look different if the equation of mean KE is separated into the associated barotropic and baroclinic components of velocity.

3.3 Barotropic and baroclinic energy routes

We take the product of Eq. 35 and each of $\overline{\mathbf{V}}^\mathbf{bt}= \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{geo}+\overline{\mathbf{V}}^\mathbf{bt}_\mathbf{wind}$ and $\overline{\mathbf{V}}^\mathbf{bc}= \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{geo}+\overline{\mathbf{V}}^\mathbf{bc}_\mathbf{wind}$, and then take the depth integral of the two equations. Likewise, we take the product of Eq. 34 and each of $\overline{\mathbf{V}}^\mathbf{bt}= \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{geo}+\overline{\mathbf{V}}^\mathbf{bt}_\mathbf{td}$ and $\overline{\mathbf{V}}^\mathbf{bc}= \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{geo}+\overline{\mathbf{V}}^\mathbf{bc}_\mathbf{td}$, and then take the depth integral of the two equations. This yields the following four types of energy balance,

$$ \label{btwec} 0 \simeq - \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{wind} \cdot \mbox{$\displaystyle\int^0_{-H}$} \nabla \overline{p}~{\rm d}z + \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{geo} \cdot \mbox{$\displaystyle\int^0_{-H}$} \mathbf{F}~{\rm d}z, $$

(36)

$$ \label{bcwec} 0 \simeq - \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{wind}\cdot\nabla \overline{p}~{\rm d}z + \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{geo} \cdot \mathbf{F}~{\rm d}z, $$

(37)

$$ \label{btbec} 0 \simeq - \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{td} \cdot \mbox{$\displaystyle\int^0_{-H}$} \nabla \overline{p}~{\rm d}z + \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{geo} \cdot \mbox{$\displaystyle\int^0_{-H}$} \mathbf{D}~{\rm d}z, $$

(38)

$$ \label{bcbec} 0 \simeq - \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{td}\cdot\nabla \overline{p}~{\rm d}z + \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{geo} \cdot \mathbf{D}~{\rm d}z, $$

(39)

namely barotropic WER (Fig. 3a), baroclinic WER (Fig. 3b), barotropic DER (Fig. 3c), and baroclinic DER (Fig. 3d), respectively. No previous studies have investigated the relative magnitude of barotropic and baroclinic energy balances (Eqs. 36–39) in the global ocean.

Fig. 3

Comparisons of a barotropic wind-induced energy route, b baroclinic wind-induced energy route, c barotropic total-drag energy route, and d baroclinic total-drag energy route. These routes are defined by Eqs. 36–39, respectively

The first term in each of Eqs. 36 and 38 represents the work done by the barotropic component of the Ekman (or ageostrophic) velocity on the barotropic component of the HPG, which is connected to the work of JEBAR in Fig. 2 after a spatial integral is taken in a band of barotropic streamlines or the global domain (Section 2). It is worth noting that the work of JEBAR can act as either a sink or source of KE depending on the barotropic WER or DER, respectively, the latter of which has attracted less attention in previous studies.

If we consider an ocean with a flat bottom, the barotropic velocity $\overline{\mathbf{V}}^\mathbf{bt}$ is horizontally nondivergent (i.e., $\overline{w}^\mathbf{bt} = 0$), while the baroclinic velocity $\overline{\mathbf{V}}^\mathbf{bc}$ is horizontally divergent (i.e., $\overline{w}^\mathbf{bc} \neq 0$). It could be said that (the classical view of) an increase in available PE by wind- driven Ekman pumping and suction is related to the pressure term in the baroclinic balance (Eq. 37) but not in the barotropic balance (Eq. 36). Another interpretation is obtained if the pressure term in the baroclinic balance (Eq. 37) is written, using integration by parts, as

$$ \begin{array}{rll} &&{\kern-6.5pt} - \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{wind} \cdot\nabla \overline{p}~{\rm d}z \nonumber\\ [-4pt] &&{\kern-6.5pt} =\left[-\mbox{$\displaystyle\int^z_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{wind}{\rm d}z \!\cdot\! \nabla \overline{p}\right]^{z=0}_{z=-H} \!+\! \mbox{$\displaystyle\int^0_{-H}$} \mbox{$\displaystyle\int^z_{-H}$}\overline{\mathbf{V}}^\mathbf{bc}_\mathbf{wind}{\rm d}z\!\cdot\!\nabla\overline{p}_z~{\rm d}z \nonumber\\ [-4pt] &&{\kern-6.5pt} =- g \mbox{$\displaystyle\int^0_{-H}$} \mbox{$\displaystyle\int^z_{-H}$}\overline{\mathbf{V}}^\mathbf{bc}_\mathbf{wind}{\rm d}z\cdot\nabla\overline{\rho}~{\rm d}z, \end{array}$$

(40)

which is the depth integral of the product of the overturning vector, density gradient, and g. KE is decreased (i.e., converted to PE, see Fig. 4a) when the wind-induced Ekman velocity steepens the slope of density surfaces near the sea surface, which is the baroclinic WER.

Fig. 4

Side view of the baroclinic component of a the wind-induced Ekman velocity $\overline{\mathbf{V}}^\mathbf{bc}_\mathbf{wind}$ and b the bottom-frictional Ekman velocity $\overline{\mathbf{V}}^\mathbf{bt}_\mathbf{td}$, illustrated by black arrows. The dashed line is a density surface. The product of the overturning streamfunction and density gradient $\int^z_{-H} \overline{\mathbf{V}}^\mathbf{bc}{\rm d}z \cdot \nabla \overline{\rho}$ is positive in (a) and negative in (b) in each vertical column, suggesting an increase and decrease in available potential energy, respectively. The red, blue, and green symbols show the directions of wind stress, geostrophic current, and bottom frictional stress, respectively, in the northern hemisphere. The direction of each of wind stress (red symbol), geostrophic current (blue symbol), and bottom frictional stress (green symbol) reverses in the southern hemisphere, while there is no such change in the direction of the wind-induced and bottom-frictional Ekman velocities (black arrows)

Likewise, (the classical view of) a decrease in available PE by bottom-frictional Ekman flow is related to the pressure term in the baroclinic balance Eq. 39 which can be written, using integration by parts, as

$$ \begin{array}{rll} &&- \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{td} \cdot\nabla \overline{p}~{\rm d}z \nonumber\\ [-6pt] &&{\kern-6pt} =\left[-\mbox{$\displaystyle\int^z_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}_\mathbf{td}{\rm d}z \cdot \nabla \overline{p}\right]^{z=0}_{z=-H} + \mbox{$\displaystyle\int^0_{-H}$} \mbox{$\displaystyle\int^z_{-H}$}\overline{\mathbf{V}}^\mathbf{bc}_\mathbf{td}{\rm d}z\cdot\nabla\overline{p}_z~{\rm d}z \nonumber\\ [-6pt] &&{\kern-6pt} =- g \mbox{$\displaystyle\int^0_{-H}$} \mbox{$\displaystyle\int^z_{-H}$}\overline{\mathbf{V}}^\mathbf{bc}_\mathbf{td}{\rm d}z\cdot\nabla\overline{\rho}~{\rm d}z. \end{array}$$

(41)

This equation gives an interpretation that KE is increased (i.e., converted from PE, see Fig. 4b) when the total-drag ageostrophic velocity relaxes the slope of density surfaces near the ocean bottom, which is the baroclinic DER.

3.4 Application to the barotropic dynamics of the ACC

There are several theories for the depth-integrated balances of momentum and vorticity in the ACC, as reviewed by Nowlin and Klinck (1986), Warren et al. (1996, 1997), and Rintoul et al. (2001) and integrated by Hughes (2002) and Nadeau and Straub (2009). Depending on how the budget of barotropic KE is closed, the prototypes of these barotropic theories can be classified into nondissipative and dissipative KE models (Table 2). On the other hand, readers who are interested in the baroclinic dynamics of the ACC including the role of mesoscale eddies are referred to previous studies, such as Hallberg and Gnanadesikan (2001), Karsten and Marshall (2002), and Aiki and Richards (2008).

Table 2 Classification of theories for the barotropic dynamics of the ACC based on the budget of barotropic KE

The nondissipative KE model applies to the theories of MP51 and JB89 who suggested that the wind stress over the Southern Ocean must be canceled by the difference of pressure upstream and downstream of a bottom ridge (Section 1). This model assumes the presence of only $\nabla H \neq 0$ and $\nabla \rho \neq 0$ (Table 2). The balance of momentum is written by Eq. 1 which is the depth integral of Eq. 32. Thus the balance of mean KE becomes the barotropic WER (Eq. 36), with its spatial integral in a band δΨ of barotropic streamlines being written by

$$ \label{munk-palmen} 0\! \simeq\! - \!\int_{\delta\Psi} \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{wind} \cdot \mbox{$\displaystyle\int^0_{-H}$} \nabla \overline{p}~{\rm d}z~{\rm d}^2 x +\! \int_{\delta\Psi} \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{geo} \cdot \mbox{$\displaystyle\int^0_{-H}$} \mathbf{F}~{\rm d}z~{\rm d}^2x, $$

(42)

which is illustrated by Fig. 3a. Equation 42 is quantitatively identical to Eq. 2 because of Eq.  25. The HPG work in Eq. 42 and the JEBAR work in Eq. 2 are sequentially connected to the budget of total PE in Fig. 2. The nondissipative KE model, Eq. 42, can be viewed as a case where the work of wind stress on the barotropic component of geostrophic velocity is fully balanced by the creation of PE by the barotropic component of wind-induced Ekman velocity. This is the barotropic WER.

In Section 2 we have shown the mathematical constraint that the integrated pressure term in Eq. 42 vanishes in two cases: either when $\nabla H = 0$ or when $\nabla \rho = 0$. These conditions apply to the theories of Stommel (1957), Webb (1993), Ishida (1994a, b), Krupitsky and Cane (1994), Wang (1994) and Cessi (2007), and are classified in the present study as the dissipative KE model (Table 2). In order for the volume budget of the barotropic KE to be closed without conversion into PE, one needs to introduce dissipative processes for mean KE, such as boundary friction, horizontal mixing, and the Reynolds stress. The integrated balance of barotropic KE becomes,

$$ \label{webb-ishida} 0 \!\simeq\! \int_{\delta \Psi}\! \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{geo} \!\cdot\! \mbox{$\displaystyle\int^0_{-H}$} \mathbf{F}~{\rm d}z~{\rm d}^2x \!+\! \int_{\delta \Psi}\! \overline{\mathbf{V}}^\mathbf{bt}_\mathbf{geo} \!\cdot\! \mbox{$\displaystyle\int^0_{-H}$} \mathbf{D}~{\rm d}z~{\rm d}^2x, $$

(43)

which can be derived by taking the spatial integral in δΨ of the sum of Eqs. 36 and 38. In other words, the dissipative KE model can be regarded as a case where both WER and DER are present and of the same strength. The energy cycle of the dissipative KE model is illustrated by the composite of Fig. 3a, c.

To illustrate the local and integrated budgets of barotropic KE in the dissipative KE model, our explanation in the following is associated with the western boundary current theory of Munk (1950) that consists of a Sverdrup interior region and a frictional western boundary region. In regions where the path of the ACC is away from coastal boundaries or continental slopes—which correspond to the Sverdrup interior region in Munk (1950)—the positive work of wind stress is locally canceled by the negative work of the HPG (which is the WER). Because of the aforementioned mathematical constraint that the integrated HPG work should vanish, the local work of the HPG changes sign somewhere. Hence in regions where the path of the ACC touches coastal boundaries or continental slopes—with associated frictional western boundary layers—the positive work of the HPG is locally canceled by the negative work of boundary friction and the Reynolds stress (which is the DER).

With the above concepts in mind, the practical goals for the numerical analysis in Section 4 are to (1) determine the global distribution of the contributions of the wind-induced Ekman velocity and the total-drag ageostrophic velocity, which is intended to identify both wind- and buoyancy-induced circulations in the global ocean (Section 3.2), (2) quantify the relative magnitudes of Eqs. 36 and 37 in the global ocean, which is intended to compare the importance of JEBAR and Ekman pumping/suction, respectively, in feeding the PE (Section 3.3), and (3) examine the validities of the nondissipative and dissipative KE models for the barotropic dynamics of the ACC (Section 3.4).

4 Numerical investigation

We analyze the output of a high-resolution (0.1° × 0.1° in the horizontal direction with 54 depth levels) near-global OGCM simulation which was integrated for a 51-year period (Masumoto et al. 2004). This simulation, which is called the OFES (OGCM for the Earth Simulator) climatological run, was performed using the Geophysical Fluid Dynamics Laboratory Modular Ocean Model version 3 (MOM3, Pacanowski and Griffies 2000) and climatological atmospheric forcing (Kalnay et al. 1996). Our choice of analyzing the output of a climatological run (rather than the output of a hindcast run) is intended to minimize the effect of annual variability. The model domain extends from 75°S to 75°N. The artificial boundaries at 75°S and 75°N are solid (i.e., no meridional velocity is allowed), and have buffer zones on the equator side of each where the temperature and salinity field are relaxed to the monthly-mean climatological values at all depths.

The KPP mixing scheme (Large et al. 1994) was used for vertical subgrid-scale viscosity. However, this quantity was not available to our analysis: it had not been stored in the model output and we found it difficult to reproduce the parameters of the complex KPP scheme offline. A biharmonic operator was used in OFES for horizontal subgrid-scale mixing with a coefficient of − 27 × 10⁹  m⁴ s^− 1 at the equator (which decreases poleward in proportional to the cube of the zonal size of grid cells (Smith et al. 2000)). Since MOM3 (OFES) is discretized in z coordinates, boundary friction is caused at both bottom and (subsurface) sidewalls of grid cells. While the bottom friction in the model is parametrized by the standard quadratic bottom drag with a standard coefficient of 0.0025, the (subsurface) sidewall friction in the model is included as part of the biharmonic horizontal mixing operator mentioned above. These frictions maintain the Stommel (1948) and Munk (1950) layers of western boundary currents, respectively, but the relative importance in OGCMs has been less investigated in previous studies.

The volume transport of the ACC through the Drake Passage in the OFES climatological run is 152.5 Sv, where 1 Sv (a Sverdrup) is 10⁶ m³ s^− 1. This is reasonably realistic value if compared with the observed values of 134 ± 27 Sv (Cunningham et al. 2003). The OFES climatological run is also successful in simulating the overflows of North Atlantic Deep Water (hereafter NADW) from the Nordic Seas and Antarctic Bottom Water (AABW) from the Weddell Sea (Masumoto et al. 2004; Sasai et al. 2006), but not the overflows of Mediterranean Sea Water and Red Sea Water in the North Atlantic and Indian Oceans, respectively.

The bottom topography of OFES is represented by the so-called partial step scheme with its performance being partially assessed by Merryfield and Scott (2007). Further details and assessments of the OFES climatological run are given in Nakamura and Kagimoto (2006) and Aiki and Richards (2008).

The low-pass temporal filter (overbar) in Sections 1–3 was set to annual means in our model analysis. We analyzed the output from the 46th to 51th years of the OFES climatological run. The distributions and values of energies and energy conversions presented below refer to the composite of six sets of the annual results, unless noted otherwise. The hydrostatic pressure in the present analysis was calculated from in situ density, as in the primitive equations used in OGCMs including OFES. For simplicity, the sea surface in the present analysis was treated as a rigid rather than a free surface (the latter of which is included in OFES).

4.1 Barotropic and baroclinic KEs

The global distribution of the barotropic and baroclinic parts of mean KE in each vertical column is shown in Fig. 5. The volume integrals of the mean barotropic and baroclinic KEs in the global ocean amount to 500 and 681 PJ, respectively, where 1 PJ (a petajoule) is 10¹⁵J. We have confirmed that the annual variability for each of the barotropic and baroclinic KEs is sufficiently small (Appendix CC).

Fig. 5

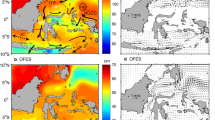
Vertical integrals $\int^0_{-H}~{\rm d}z$ of a mean barotropic KE and b mean baroclinic KE [J m^− 2]. All the distributions and values of energies and energy conversions shown in the present study are the composites of six sets of annual results from the 46th to 51th years of the OFES climatological run, unless noted otherwise. The net value over the global ocean, given to the top right of each figure, is calculated for each quantity (1 PJ = 10¹⁵ J)

The barotropic KE (Fig. 5a) depicts the positions of major currents at middle and high latitudes, such as the ACC, the Agulhas Current, and the western boundary currents in each basin. The barotropic KE has little signal at low latitudes, whereas the baroclinic KE (Fig. 5b) clearly captures the equatorial currents in each basin. The ratio of the barotropic component of mean KE to the total mean KE (Fig. 6) ranges 0–0.2 in equatorial regions where the thermocline is shallow. The ratio increases poleward, reaching a value 0.5 along a latitude of about 40°S in the Southern Ocean and 50°N in the North Atlantic Ocean, and is greater than 0.5 at higher latitudes. The ratio is more than 0.8 in the Weddell, Ross, and Labrador Seas where the surface mixed layer is deepened by atmospheric cooling.

Fig. 6

The ratio of barotropic KE to the sum of barotropic and baroclinic KEs in Fig. 5 (nondimensional)

4.2 Contribution of the wind-induced Ekman velocity

We first look at the work of wind forcing on the barotropic velocity (Fig. 7a) whose rate is given by $\overline{\mathbf{V}}^\mathbf{bt}\cdot \int^0_{-H} \mathbf{F}~{\rm d}z = \overline{\mathbf{V}}^\mathbf{bt}\cdot \overline{\boldsymbol{\tau}}^\mathbf{wind}$ in Eq. 23. Its global integral is 243 GW, where 1 GW is 10⁹ W, with main contributions coming from the Indian Ocean sector of the Southern Ocean. This is compared with the work of wind forcing on baroclinic velocity (Fig. 7b) whose rate is approximated by $\int^0_{-H} \overline{\mathbf{V}}^\mathbf{bc}\cdot \mathbf{F}~{\rm d}z \simeq \int^0_{-H} \overline{\mathbf{V}}^\mathbf{bc} \exp(z/\overline{l}_\mathbf{bld})~{\rm d}z\cdot\overline{\boldsymbol{\tau}}^\mathbf{wind}/\overline{l}_\mathbf{bld}$ from Eqs. 29 and 48, Its global value is 747 GW with main contributions coming from the entire Southern Ocean and the equatorial Pacific Ocean. Here, the ratio of the barotropic and baroclinic working rates of wind forcing (about 1:3) is determined for the first time in oceanic studies.

Fig. 7

The barotropic and baroclinic working rates of: a, b wind forcing; c, d pressure gradient; e, f overall dissipative processes for mean KE (W m^− 2) in Eqs. 23 and 29, respectively. The combined dissipative processes for mean KE consist of the work terms of horizontal viscosity, bottom friction, and the Reynolds stress divergence that are plotted in Fig. 8. The sign of each quantity is relative to the budget of the mean KE, with the net value over the global ocean being calculated (1 gigawatts (GW) = 10⁹ W). c, d The working rate of the HPG is plotted with horizontal Gaussian smoothing with a radius of 1.0°

The contribution of the barotropic component of the wind-induced Ekman velocity—the barotropic WER, Eq. 36, in Fig. 3a—can be identified by comparing the barotropic working rate of wind forcing (Fig. 7a) with the barotropic working rate of the HPG (Fig. 7c), the latter of which is given by $-\overline{\mathbf{V}}^\mathbf{bt}\cdot \int^0_{-H} \nabla \overline{p}~{\rm d}z$ in Eq. 23. In the entire Southern Ocean (excluding the Drake Passage region), the barotropic work of the HPG is largely negative which appears to cancel the positive work of wind forcing in the same region (boxed in Fig. 7a, c). This negative work of the barotropic HPG indicates a decrease in mean KE, which results from the Ekman velocity “pushing” water columns in the direction of higher pressure (i.e., northward). The northward HPG, $\int^0_{-H} \nabla p~{\rm d}z$, is associated with the eastward geostrophic velocity of the ACC, and is attributed mainly to the gradient in the sea surface pressure. The barotropic WER is also identified in the Labrador Sea (boxed in Fig. 7a, c) where the work of wind forcing and the HPG are anticorrelated. Elsewhere in the global ocean, there are some regions where the barotropic work of the HPG is locally positive: such regions are revisited in the next subsection. Because both positive and negative signals are scattered in the global ocean, the global barotropic working rate of the HPG—which can be interpreted as the global working rate of JEBAR (OFES has no fluxes through the model boundaries at 75°S and 75°N)—is nearly zero (− 2 GW) and cannot cancel the 243 GW from the barotropic working rate of wind forcing (Fig. 7a). As for the energy balance of the ACC, the positive work of the HPG in the Drake Passage region needs to be explained (Section 4.3) and the regional statistics for both the Southern Ocean and the streamlines of the ACC need to be calculated (Section 4.4) before determining the validities of the nondissipative and dissipative KE models.

The contribution of the baroclinic component of the wind-induced Ekman velocity—the baroclinic WER, Eq. 37, in Fig. 3b—can be identified by comparing the baroclinic working rate of wind forcing (Fig. 7b) with the baroclinic working rate of the HPG (Fig. 7d), the latter of which is given by $-\int^0_{-H}\overline{\mathbf{V}}^\mathbf{bc}\cdot\nabla\overline{p}~{\rm d}z$ in Eq. 29. Negative (positive) values indicate a decrease (increase) in the mean KE. Clearly there is a strong anticorrelation between the baroclinic wind work and the baroclinic HPG work in many regions of the global ocean (boxed in Fig. 7b, d), such as outside the Drake Passage region in the Southern Ocean, the equatorial Pacific Ocean, the North Pacific Ocean, the equatorial Indian Ocean, the North Atlantic Ocean, and the Caribbean Sea. This tendency for the two terms to cancel gives evidence of the wind-induced Ekman velocity steepening (relaxing) the slope of density surfaces near the sea surface in response to winds blowing in (against) the direction of surface currents (cf. Thomas and Lee 2005). Elsewhere in the global ocean, there are some regions—near the western boundaries of each basin—where the baroclinic work of the HPG is locally positive, and are explained in the next subsection. The global rate of − 577 GW for the baroclinic work of the HPG largely cancels the 747 GW from the wind forcing. The residual imbalance (− 577 + 747 GW = 170 GW) must be attributed to the effect of dissipative processes, as we see in the next subsection.

4.3 Contribution of the total-drag ageostrophic velocity

This section examines whether or not the aforementioned positive signals in the working rate of the HPG in near-coastal regions (Fig. 7c, d) are canceled by the effect of bottom friction, horizontal viscosity, and the Reynolds stress. The working rate of overall dissipative processes for mean KE on barotropic and baroclinic velocities in Eqs. 23 and 29 are estimated in the present study by using

$$\label{btds} \overline{\mathbf{V}}^\mathbf{bt} \cdot \mbox{$\displaystyle\int^0_{-H}$} \mathbf{D}~{\rm d}z \!=\! \overline{\mathbf{V}}^\mathbf{bt} \cdot \left[-\overline{\boldsymbol{\tau}}^\mathbf{btm}\!+\! \mbox{$\displaystyle\int^0_{-H}$} (\overline{\mathbf{B}} \!+\! \mathbf{R})~{\rm d}z \right], $$

(44)

and

$$ \begin{array}{rll}\label{bcds} \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}\cdot \mathbf{D}~{\rm d}z &\simeq& \overline{\mathbf{V}}^\mathbf{bc}|_{z=-H}\cdot (-\overline{\boldsymbol{\tau}}^\mathbf{btm}) \nonumber\\ [-7pt] && +\, \mbox{$\displaystyle\int^0_{-H}$} \overline{\mathbf{V}}^\mathbf{bc}\cdot(\overline{\mathbf{B}}+\mathbf{R})~{\rm d}z, \end{array}$$

(45)

espectively (Appendix D). The term $\int^0_{-H} S_\mathbf{mid} \overline{\mathbf{V}}^\mathbf{bc}\cdot\overline{\boldsymbol{\tau}}_z~{\rm d}z$ in Eq. 29, which is the working rate of vertical shear stress at mid depths of the ocean, was not analyzed in the present study, because the three-dimensional distribution of vertical viscosity was unavailable for the analysis. The Reynolds stress divergence R in Eqs. 44 and 45 is calculated from 3-day snapshots of three-dimensional velocity fields throughout the 46th year of the OFES climatological run; only for this year were 3-day snapshots stored as part of the model output. The 46th year has as many as 121 snapshots which is enough to remove the effect of inertial oscillations.

The contribution of the barotropic component of the total-drag ageostrophic velocity—the barotropic DER, Eq. 38, in Fig. 3c—can be identified by comparing the barotropic work of the HPG (Fig. 7c) and the barotropic work of overall dissipative processes (Fig. 7e). They are roughly anticorrelated in many regions of the global ocean (boxed in Fig. 7c, e), such as in the East Greenland Current, the Gulf Stream, the North Brazil Current, the eastern coast of the Weddell Sea, the region between 135°E–135°W in the Southern Ocean (the Tasman Fracture Zone, the Macquarie Ridge, the Campbel Plateau, and the Pacific–Antarctic Ridge), and in the Bering Strait. This tendency of anticorrelation gives evidence of the total-drag ageostrophic velocity pushing water columns in the direction of lower pressure to recover barotropic KE. Here we find that most of the positive signals in the work of the HPG (Fig. 7c) can be qualitatively explained by the DER. The lack of a clear local anticorrelation in some regions such as the region of the Drake Passage and the Malvinas Current (i.e., the Scotia Sea and the Falkland Plateau) suggests the advection of mean KE by the mean flow may be important. The global barotropic working rate of overall dissipative processes (− 216 GW) comprises − 133 GW for horizontal viscosity, − 67 GW for bottom friction, and − 16 GW for the Reynolds stress divergence (Fig. 8a, c, e), with the main contribution coming from horizontal viscosity particularly in the East Greenland Current and off the Antarctic Peninsula.³ These two regions are known for the overflows of NADW from both the Denmark Strait and the Faroe Bank Channel, and AABW from the Weddell Sea. Now most of the signals in the barotropic work of the HPG in the global ocean (boxed in Fig. 7c) are qualitatively explained by either the WER or DER, namely the role of the wind-induced Ekman or total-drag ageostrophic velocity.

Fig. 8

As in Fig. 7e, f, but separated into contributions from: a, b horizontal viscosity; c, d bottom friction; and e, f the Reynolds stress divergence in Eqs. 44 and 45, respectively. e, f The working rate of the Reynolds stress divergence is plotted with horizontal Gaussian smoothing with a radius of 1.0°

The contribution of the baroclinic component of the total-drag ageostrophic velocity—the baroclinic DER, Eq. 39, in Fig. 3d—can be identified by comparing the baroclinic work of the HPG (Fig. 7d) and the baroclinic work of overall dissipative processes (Fig. 7f). Much of the signal in the latter has an opposite signed signal to the former in many regions (boxed in Fig. 7d, f), such as in the region of the Denmark Strait and the Faroe Bank Channel, the extension of the Gulf Stream, the North Brazil Current, the extension of the Kuroshio, the Celebes Sea in the western equatorial Pacific Ocean, the eastern coast of Australia, the eastern coast of Africa and Madagascar, the Agulhas Current, and around 60°E, 40°S (i.e., east of the Crozet Plateau). This tendency for the baroclinic work of overall dissipative processes to be canceled by the baroclinic work of the HPG gives evidence of the total-drag ageostrophic velocity relaxing the slope of density surfaces to recover baroclinic KE. Again, we find that most of the signals in the baroclinic work of the HPG in the global ocean (boxed Fig. 7d) are qualitatively explained by either the WER or DER, namely the role of the wind-induced Ekman or total-drag ageostrophic velocity. As for the barotropic component, the lack of a clear local anticorrelation in some regions such as the region of the Drake Passage and the Malvinas Current suggests the possible importance of advection of mean KE by the mean flow.

The global baroclinic working rate of overall dissipative processes (−203 GW) comprises −121 GW for horizontal viscosity, 9 GW for bottom friction, and −91 GW for the Reynolds stress divergence (Fig. 8b, d, f). The energy decrease by horizontal viscosity is significant in the Denmark Strait and the Drake Passage (Fig. 8b). The energy decrease by the Reynolds stress (i.e., a deceleration of the mean flow) is significant in the western boundary currents of each ocean (Fig. 8f). There are some regions where the work of overall dissipative processes (Fig. 7f) is positive (i.e., increase of KE) which is an indication of mean flow acceleration caused by the Reynolds stress. Such regions are found in the extensions of the Gulf Stream and the Kuroshio, and some localized regions in the Southern Ocean where the path of the ACC is constrained by steep bottom topography (Fig. 8f). This result is partly consistent with Ivchenko et al. (1996) who identified an acceleration of the mean flow in the ACC.

4.4 Regional statistics

We examine the strengths of the WER and DER in each of the Southern, North Atlantic, North Pacific, Equatorial Pacific, Equatorial Atlantic, and Indian Oceans. Table 3 lists regional statistics for energy and working rate shown in Section 4.1–4.3. Note the definition of the WER and DER neglects the advection of mean KE by the mean flow. Since the residual of the sum of the calculated terms in each ocean is relatively small in most cases when compared the largest term (Table 3), we assume neglect of the advective flux does not compromise our physical interpretations. The exception is the sum of the barotropic terms in the Indian Ocean.

Table 3 The global and regional integrals of energies (PJ) and working rates (GW) in an annual mean, which is derived by composites from the 46th to 51th years of the OFES climatological run

The working rates in Table 3 are subject to about 10% error associated with inaccuracies of our assumptions and analysis code (Appendix C). These errors are within an acceptable range for our purpose of examining work balances to the leading order.

Assessing the validities of the nondissipative and dissipative KE models for the barotropic dynamics of the ACC is one of the purposes of the present study. As far as we know, the present study describes the first result of an analysis of the simulated ACC at 0.1°×0.1° resolution. Early reports of confirming the momentum balance between wind stress and the pressure difference across a bottom ridge (MP51; JB89) were derived by analyzing the outputs of eddy-permitting OGCM simulations at about 0.5° × 0.25° resolution where the transports of the model ACC was in an unrealistic range: 200 Sv in Gille (1997) and 18 Sv in Ivchenko et al. (1996). Recently the momentum balance between wind stress and the bottom pressure difference was again confirmed by Grezio et al. (2006) who analyzed the outputs of two OGCM simulations with the ACC transports being in a realistic range (152 and 134 Sv in the cases of a horizontal resolution of 0.25°×0.25° and 0.28°×0.14°, respectively). However their momentum analysis was performed over a relatively limited region (a latitude band between 55° and 63°S) which covers only half (the polar side) of the regions where the barotropic streamlines of the ACC are present. A related discussion appears in Olbers and Ivchenko (2001). We expect that the other half of the region (the equator side of 55°S) is more important for the budget of KE. This is because, in all OGCM simulations for the ACC, both wind stress and barotropic currents are more intense on the equator side (cf. Toggweiler and Russell 2008).

In the entire Southern Ocean (south of 20°S, Table 3), the barotropic working rate of wind forcing (191 GW) is balanced mainly by the working rate sum of the HPG (−99 GW) and horizontal viscosity (−87 GW). To exclude contributions from the Agulhas Current, the Malvinas Current, and the overflow of AABW (off the Antarctic Peninsula) from the above estimate, we performed another analysis for the regions between barotropic streamfunctions of 30 and 120 Sv of ACC (dotted lines in Figs. 9 and 10). The spatial integral in a band δΨ of barotropic streamlines allows us to interpret the barotropic work of the HPG as the work of JEBAR (Section 2). The result in Table 4 shows that again the barotropic working rate of wind forcing (81 GW) is balanced mainly by the working rate sum of the HPG (−42 GW) and horizontal viscosity (−25 GW) rate of working. The work of horizontal viscosity is significant (Fig. 10a) in only four localized regions in the band of streamlines of the ACC: the Kergulen Plateau (70°E), the Macquarie Ridge (160°E), the Pacific–Antarctic Ridge (140°W), and the Drake Passage. These steep topographies constrain the path of the ACC and apply (subsurface) sidewall friction. Moreover the ACC hits tiny islands in the Kergulen Plateau and the Macquarie Ridge. The magnitude of DER (38 GW = 25 + 5 + 8 GW in Table 4) in the ACC is about half of the magnitude of WER (81 GW). We see, therefore, that the KE budget of the ACC is explained by an equal blend of the nondissipative and dissipative KE models, given by Eqs. 42 and 43, respectively.

Fig. 9

As in Fig. 7 except for barotropic working rates in the Southern Ocean. Dotted contours in each figure are annual mean barotropic streamfunctions of 30 and 130 Sv. The net value over the regions banded by the contours (i.e., streamlines of ACC) is calculated for each quantity

Fig. 10

As in Fig. 9c, but separated into contributions from a horizontal viscosity, b bottom friction, and c the Reynolds stress divergence

Table 4 As in Table 3 except for barotropic working rates in the barotropic streamlines of the ACC between 30 and 130 Sv

Outside the Southern Ocean, the barotropic DER overwhelms the barotropic WER in every ocean. It is shown in Table 3 that the barotropic work of the HPG is positive in all of the North Atlantic, North Pacific, Equatorial Pacific, Equatorial Atlantic, and Indian Oceans, and is largely canceled by the work sum of horizontal viscosity and bottom friction in each ocean. In the North Atlantic and North Pacific Oceans, the working rates of the HPG (58 and 22 GW, respectively) are much larger than the working rates of wind forcing (17 and 4 GW, respectively), indicating that barotropic velocities in these oceans are maintained mainly by the dissipative processes rather than the wind. This positive work of the HPG is caused not only by the overflow of NADW in the North Atlantic Ocean (explained in Section 4.3) but also by the onshore intrusions of the Gulf Stream and the Kuroshio at latitudes between 20° and 30°N (Fig. 7c). In other words the mean currents are steered in the direction of lower pressure by barotropic ageostrophic velocities associated with bottom and (subsurface) sidewall friction. On the other hand in low latitudes (the Equatorial Pacific, Equatorial Atlantic, and Indian Oceans), the barotropic working rate of the HPG (4, 5, and 5 GW, respectively) is smaller than the barotropic working rate of wind forcing (12, 11, and 7 GW, respectively). This indicates that the WER is slightly strengthened in low latitudes.

Next we look at the budget of mean baroclinic KE in each ocean. The Southern and Equatorial Pacific Oceans are the main receivers of the baroclinic work of wind forcing (352 and 206 GW, respectively). In middle and high latitudes (i.e., the Southern, North Atlantic, and North Pacific Oceans), the work of wind forcing is largely canceled by the work of the HPG, which indicates the dominance of the WER. In the Equatorial Pacific Ocean, only half of the working rate of wind forcing (206 GW) is canceled by the working rate of the HPG (−120 GW). We expect the residual to be canceled by the work of vertical viscosity at mid depths of the ocean, because horizontal velocities in low latitudes have high vertical shears (Section 4.1, Fig. 6). Indeed Table 3 shows that the ratio of baroclinic/barotropic KEs is highest in the Equatorial Pacific Ocean (220 PJ/23 PJ). In the Equatorial Atlantic and Indian Oceans, the working rates of wind forcing (53 and 52 GW, respectively) is balanced mainly by the working rate sum of the HPG (−22 and −36 GW, respectively) and the Reynolds stress (−22 and −19 GW, respectively).

We have not explained the working rate of advective interaction listed in Table 3 and its global distribution shown in Fig. 11. These are calculated by $\overline{\mathbf{V}}^\mathbf{bt}\cdot N[\overline{\mathbf{V}}^\mathbf{bc}]$ in Eqs. 23 and 29. Although it is hard to characterize the noisy global distribution, the working rate of advective interaction in the North Atlantic Ocean is as significant as the other working rates (Table 3), which should be investigated in a future study.

Fig. 11

The energy conversion [W m^− 2] between mean barotropic and mean baroclinic KEs by the advective interaction term $\overline{\mathbf{V}}^\mathbf{bt}\cdot N[\overline{\mathbf{V}}^\mathbf{bc}]$ in Eqs. 23 and 29. The sign is relative to the budget of mean barotropic KE, with the net value over the global ocean being calculated

The working rate of the HPG in Table 4 is based on the volume integral in the band between two barotropic streamlines circling Antarctica, and thus can be interpreted as the working rate of JEBAR. On the other hand, the regional statistics for the working rate of the HPG in Table 3 are not necessarily equal to the working rate of JEBAR or Ekman pumping/suction in each region. This is because of pressure fluxes through the open boundaries of each region.

5 Summary

In order to develop an understanding of the maintenance mechanisms of the general circulation in the global ocean, this study investigates the budget of the annual mean KE in a climatological ocean simulation, and points out important regions concerning the dominant equilibria in the energy balance. The overall content of this study serves to promote model comparisons of energetics in future studies, assess parametrization of frictional processes in ocean models, and revisit hypotheses for the momentum and vorticity balances in general circulation theories.

5.1 Approach of the analysis

The dominant equilibria in the energy balance are explained using two separate energy routes. The WER represents the role of the wind-induced Ekman velocity. The DER represents the role of the total-drag ageostrophic velocity (which is defined in the present study to refer to the sum of the bottom-frictional Ekman velocity and its variants). The utility of looking at these energy routes has not been explored to any significant extent in previous numerical studies before Aiki and Richards (2008). This is because the interaction between KE and PE in a stratified fluid is traditionally examined through the term ρg w (rather than $- \mathbf{V}\cdot\nabla p$). This tradition comes from either a focus on the budget of PE or the use of the quasi-geostrophic potential vorticity equation (the latter of which yields a term proportional to wind stress curl in place of ρg w) in deriving the energy equations. While the horizontal distribution of ρg w displays both positive and negative signs (not shown), the horizontal distribution of $- \mathbf{V}\cdot\nabla p$ tends to be single signed (for each of the WER and DER), the latter of which greatly simplifies the interpretation of the KE budget.^{4 , 5} This has enabled us to determine the contributions of the wind-induced Ekman and total-drag ageostrophic velocities in the global ocean.

In order to investigate the energetics of JEBAR, the mean KE is separated into that associated with the barotropic and baroclinic components of velocity. We summarize the relationship between the role of JEBAR and the Ekman dynamics, as follows. The work of the barotropic component of the Ekman (or ageostrophic) velocity on the barotropic component of the HPG is connected to the work of JEBAR and then to the budget of PE. On the other hand the work of the baroclinic component of the Ekman (or ageostrophic) velocity on the baroclinic component of the HPG is connected to the work of Ekman pumping/suction and then to the budget of PE.

5.2 Result of the analysis

The budget of annual mean KE in a high-resolution semi-global simulation has been comprehensively analyzed in the present study. As expected, the budget of baroclinic KE is found to be maintained mainly by the WER rather than the DER: the wind-induced baroclinic circulation overwhelms the buoyancy-induced baroclinic circulation in the global ocean. Most of the wind-induced baroclinic energy is converted to PE by the sequentially connected work of the baroclinic HPG and the Ekman pumping/suction in the global ocean. In contrast to the baroclinic budget, the global work of the barotropic HPG—which is connected to the global work of JEBAR and then to the budget of PE—is found to be nearly zero, as it changes sign in the ACC (feeds PE) and in the overflows of NADW and AABW (releases PE). This indicates that the wind- and buoyancy-induced barotropic circulations in the global ocean are of the same strength with opposite sign, the reason for which should be investigated further in a future study. The relative importance of the barotropic and baroclinic dynamics in the global ocean can be quantified by the ratio between the working rates of the barotropic wind forcing (243 GW) and the baroclinic wind forcing (747 GW).

The above procedure of energy analysis has been applied to examine the validity of theories for the barotropic dynamics of the ACC. We have shown that depending on how the budget of barotropic KE is closed, these barotropic theories can be classified into nondissipative KE models (MP51 and JB89) and dissipative KE models, which has been little mentioned in previous studies. It is found that about half of the work of wind forcing on the barotropic component of the simulated ACC is canceled by the combined effect of the dissipative processes of mean KE, such as horizontal viscosity, bottom friction, and the Reynolds stress, with the other half being converted to PE by the sequentially connected work of the barotropic HPG and JEBAR. This indicates that the state of the simulated ACC is characterized by an equal blend of the dynamics of the nondissipative and dissipative models. The relative importance of the barotropic and baroclinic dynamics of the ACC can be quantified by the ratio between the working rates of the barotropic wind forcing (191 GW) and the baroclinic wind forcing (352 GW) in the Southern Ocean.

5.3 Future work

The result of the global analysis identifies some regions where the Reynolds stress divergence accelerates (rather than decelerates) mean currents and where the advection by mean flows is significant. These are less explained in the present study for priority reasons, and it would be worth focusing on such effects or regions in a future study (cf. Greatbatch et al. 2010).

Lastly the results of the present study have shown the importance of horizontal friction at (subsurface) sidewalls in the ACC, western boundary currents, and dense water overflows. Recently Sakamoto (2007) and Nakano et al. (2008), who investigated the separation of western boundary current in quasi-geostrophic and primitive equation ocean models, respectively, showed the dynamical importance of high potential vorticity water which is formed by friction at the western boundary. This result is in contrast to Hughes and Cuevas (2001) who suggested that the depth-integrated momentum and vorticity balances of western boundary currents are explained by the relationship between the wind stress and JEBAR, as in the case of MP51 and JB89 for the dynamics of the ACC. In other words the dynamics considered in Hughes and Cuevas (2001) and Nakano et al. (2008) are explained by the nondissipative and dissipative KE models, respectively. Our numerical analysis has shown that the barotropic work of the HPG is positive (which increases KE) outside the Southern Ocean. This indicates that in OFES the nondissipative KE model, Eq. 42, is not applicable in the Pacific, Atlantic, and Indian Oceans. The subsurface sidewall friction is an artifact of the way bottom topography is handled in many z coordinate ocean models. Its importance in the KE budget, as shown in this study, suggests the need for further investigation of dissipation at boundaries in OGCMs. It would be also interesting to replace the temporal filter in this study with a horizontal local filter, to see changes in the working rates of the Reynolds stress and horizontal viscosity terms.

Appendix

1.1 JEBAR and bottom form stress

The ocean has at least two kinds of form stress (the residual effect of the horizontal pressure gradient (HPG)), namely bottom form stress which is caused by bottom topography and layer-thickness form stress which is caused by the perturbation of layer interfaces. It is the bottom form stress which is similar to but slightly different from the joint effect of baroclinicity and bottom relief (JEBAR) (Sarkisyan and Ivanov 1971). Layer-thickness form stress concerns the role of mesoscale eddies in baroclinic instability. It has already been investigated by Aiki and Yamagata (2006) and Aiki and Richards (2008), and is out of the scope of the present study.

If the HPG term of Eq. 1 is rewritten as $-\int^0_{-H}$ $\nabla \overline{p}~{\rm d}z = -\nabla \int^0_{-H} \overline{p}~{\rm d}z + \overline{p}|_{z=-H}\nabla H$, the last term can be regarded as the bottom form stress vector. This vector has no vertical component because bottom form stress originates in the horizontal gradient of the sum of sea surface and hydrostatic pressure. One way to focus on the role of bottom form stress is to transform Eq. 1 into the vorticity equation. Two kinds of vorticity equations have been used in previous studies (cf Greatbatch et al. 1991; Mellor 1999; Zhang and Vallis 2007),

$$\label{btpv1} \rho_0 J(\Psi,f) \simeq J(\overline{p}|_{z=-H},H) + \nabla\times\mathbf{\overline{\boldsymbol{\tau}}^\mathbf{wind}}, $$

(46)

$$ \label{btpv2} \rho_0 J\left(\Psi, f/H\right) \simeq J\left(\mathcal{TPE}, 1/H \right) + \nabla\times \frac{\overline{\boldsymbol{\tau}}^\mathbf{wind}}{H}, $$

(47)

where ψ is a barotropic streamfunction defined by $\nabla \Psi \equiv \int^0_{-H} \overline{\mathbf{V}}~{\rm d}z \times \mathbf{z}$, and $J(A,B)\equiv\nabla A \times \nabla B$ and $\mathcal{TPE}\equiv \int^0_{-H} g \overline{\rho} z~{\rm d}z$. The first term on the right-hand side of Eq. 46 can be interpreted as the curl of bottom form stress, $J(\overline{p}|_{z=-H}, H) = \nabla \times (\overline{p}|_{z=-H} \nabla H)$, which is nonzero if the contours of bottom topography and bottom pressure are not parallel. The bottom pressure is the sum of the sea surface pressure and the hydrostatic pressure: $\overline{p}|_{z=-H}=\overline{p}^s+\int^0_{-H}g\rho~{\rm d}z$.

The first term on the right-hand side of Eq. 47 is traditionally called the JEBAR term because (1) it does not contain the sea surface pressure $\overline{p}^s$, which is in contrast to the bottom form stress term in Eq. 46, and (2) it is nonzero if the contours of $\mathcal{TPE}$ and H are not parallel: $J(\mathcal{TPE},H) \neq 0$.

If the spatial integral is taken in the band between two barotropic streamlines circling Antarctica, the left hand sides of Eqs. 1, 46 and 47 vanish (because of periodicity), resulting in the volume-integrated momentum and vorticity budgets of the ACC being maintained by the balance between wind-induced sources and pressure-induced sinks (MP51; JB89). Previous arguments for the budget of momentum or vorticity paid little attention to what the pressure-induced sinks are connected to. On the other hand, Warren et al. (1996) pointed out the dynamics of the ACC could be explained, not necessarily using the concept of bottom form stress and JEBAR, but using only the wind-induced Ekman velocity and geostrophic velocity. Their argument is straightforward in that the momentum equation (Eq. 1) represents the depth integral of the combined geostrophic and Ekman balance. The energetics of the flow are useful for clarifying such arguments, as is addressed throughout the present study.

The original JEBAR equation (Eq. 47) can be written $\nabla A \simeq (\rho_0 f/H) \nabla \psi + \mathcal{TPE} \nabla (1/H) + \overline{\boldsymbol{\tau}}^\mathbf{wind}/H$ using an arbitrary scalar quantity A. Taking the outer product of $\nabla \psi$, this equation yields $\nabla \psi \times \nabla A \simeq \mathcal{TPE} \nabla \psi \times \nabla (1/H) + \nabla \psi \times \overline{\boldsymbol{\tau}}^\mathbf{wind}/H$ whose left hand side vanishes after taking the surface integral $\int_{\delta\Psi, \Omega} {\rm d}x^2$ in the band between two barotropic streamlines or in a closed domain. This is Eq. 2.

1.2 B Work of wind forcing

The present study uses the term work of “wind forcing” to distinguish it from the work of “wind stress”. The work of “wind forcing” can be interpreted as the wind work on the geostrophic velocity (whose global rate is about 800–1,000 GW (Wunsch 1998)). The work of “wind stress” (whose global rate is about 2,000–3,000 GW (Wang and Huang 2004; Von Storch et al. 2007)) is the sum of the wind work on the geostrophic velocity and the wind work on the Ekman spiral velocity, the latter of which is canceled by dissipation within the surface Ekman layer.

By definition the Ekman spiral velocity $\overline{\mathbf{V}}_\mathbf{wind}$ is perpendicular to the wind forcing vector F (i.e., $\rho_0 \mathbf{f}\times\overline{\mathbf{V}}_\mathbf{wind} = \mathbf{F}$). Hence $\overline{\mathbf{V}}_\mathbf{wind}$ makes no contribution to the working rate of wind forcing $\overline{\mathbf{V}}\cdot\mathbf{F} \simeq (\overline{\mathbf{V}}_\mathbf{geo}+\overline{\mathbf{V}}_\mathbf{wind}) \cdot\mathbf{F} = \overline{\mathbf{V}}_\mathbf{geo}\cdot\mathbf{F}$ at each depth (i.e., the work of wind forcing is nearly equal to the wind work on the geostrophic velocity). On the other hand, Wang and Huang (2004) and Von Storch et al. (2007) use integration by parts, $\int^0_{-H} (\overline{\mathbf{V}}_\mathbf{geo} + \overline{\mathbf{V}}_\mathbf{wind}) \cdot \mathbf{F}~{\rm d}z \simeq (\overline{\mathbf{V}}_\mathbf{geo}+\overline{\mathbf{V}}_\mathbf{wind})|_{z=0}\cdot\overline{\boldsymbol{\tau}}^\mathbf{wind} - \int^0_{-H} S_\mathbf{srf} (\partial \overline{\mathbf{V}}_\mathbf{wind}/\partial z) \overline{\boldsymbol{\tau}}~{\rm d}z$. The first term on the right-hand side is the working rate of wind stress on both geostrophic and Ekman spiral velocities while the second term is the dissipation rate within the surface Ekman layer.

In other words, the wind work on the Ekman spiral velocity and the dissipation in the surface Ekman layer cancel out in the work of wind forcing $\overline{\mathbf{V}}\cdot\mathbf{F}$. This simplicity will serve to offset the complexity arising from the barotropic–baroclinic decomposition in the present study.

The above explanation interprets the work of wind forcing as the wind work on the geostrophic velocity for simplicity, with geostrophic balance in mid- and high-latitudes in mind. Nevertheless there is no need to single out the geostrophic velocity in estimating the $\overline{\mathbf{V}}\cdot\mathbf{F}$ term in our model analysis. Actually, the work of wind forcing includes not only the wind work on the geostrophic velocity but also the wind work on equatorial currents in low latitudes.

1.3 C Residuals in the budget calculation

Confidence in the result of the model analysis (Section 4) is increased if errors originating in inaccuracies of our assumptions and analysis code and are small. Below we show that the size of errors is generally about 10% and thus does not affect the budget of mean KE to the leading order.

In order to see if the mean KE is in a statistically steady state, we have computed the standard deviation for the year-to-year change of the annual mean KE during the 6 years of the analysis. The standard deviations for the barotropic and baroclinic KEs in the global ocean are 4.25 and 5.85 PJ, respectively, which can be interpreted as annual rates of 0.135 GW $(= 4.25~\mbox{PJ}/ 365~\mbox{day})$ and 0.186 GW $(= 5.85~\mbox{PJ}/ 365~\mbox{day})$. These rates are sufficiently small when compared with the working rate of wind forcing (Table 3).

The budget of barotropic KE should be closed in the (semi) global ocean because the OFES has no volume fluxes through the boundaries at 75°S and 75°N. The sum of the six working rates in Table 3 associated with the budget of barotropic KE is very small (−2 GW) when compared with the working rate of wind forcing (243 GW). It is also interesting to compute the residual of the barotropic KE budget over the barotropic streamlines of ACC which we have looked at in Section 4.4. The sum of the six barotropic working rates in Table 4 for the ACC is 6 GW (nonzero), suggesting the size of the error is about 7% (6 GW/81 GW) of the working rate of the barotropic wind forcing. It is concluded that the size of errors in the budget calculation of the barotropic KE does not unduly affect our conclusions.

On the other hand, it is difficult to close the budget of baroclinic KE because we (1) estimated the working rate of wind forcing by using the approximation (Eq. 48) and (2) did not estimate the working rate of vertical shear stress at mid depths of the ocean. As explained in Section 4.4, the work of mid-depth shear stress must be significant in the Equatorial Pacific Ocean where the ratio of barotropic / baroclinic KEs is lowest in the world’s oceans. If the budget of baroclinic KE in the Equatorial Pacific Ocean is nearly closed, the working rate of mid-depth shear stress would be about −53 GW which is the negative of the sum of the other six quantities for the Equatorial Pacific Ocean in Table 3. If this value is tentatively adopted as the global working rate of mid-depth shear stress, the sum of this and the other six quantities given in Table 3 for the global budget of the baroclinic KE becomes −59 GW, suggesting the size of the error is about 8% (59 GW/747 GW) of with the global working rate of the baroclinic wind forcing. Again, we conclude that the size of errors in the budget calculation of the baroclinic KE does not unduly affect our conclusions.

1.4 D Approximation of wind forcing and bottom friction

The equation for mean baroclinic KE, Eq. 29, includes the term representing the rate of the work done by the vertical viscosity, $\int^0_{-H}\overline{\mathbf{V}}^{\mathbf{bc}}\cdot\overline{\boldsymbol{\tau}}_z~{\rm d}z$, which consists of contributions from wind forcing $S_\mathbf{srf}\overline{\mathbf{V}}^{\mathbf{bc}}\cdot \overline{\boldsymbol{\tau}}_z$, shear stress at mid depths of the ocean $S_\mathbf{mid}\overline{\mathbf{V}}^{\mathbf{bc}}\cdot\overline{\boldsymbol{\tau}}_z$, and bottom friction $S_\mathbf{btm}\overline{\mathbf{V}}^{\mathbf{bc}}\cdot \overline{\boldsymbol{\tau}}_z$. Because the three-dimensional distribution of subgrid-scale vertical viscosity was not available for our analysis (see Section 4), we could not determine $S_\mathbf{mid}\overline{\mathbf{V}}^{\mathbf{bc}}\cdot\overline{\boldsymbol{\tau}}_z$ (this is indicated as mid-depth vertical viscosity in Fig. 2). Nevertheless, to analyze the working rate of wind forcing on the baroclinic velocity in Eq. 29, one needs the vertical profile of $\overline{\boldsymbol{\tau}}_z$ near the sea surface because horizontal velocities in model outputs contain the Ekman spiral velocity with (1) high vertical shear and (2) components in the direction of wind forcing.

In calculating $\int^0_{-H} S_\mathbf{srf}\overline{\mathbf{V}}^{\mathbf{bc}}\cdot\overline{\boldsymbol{\tau}}_z~{\rm d}z$, we approximated the vertical profile of $\overline{\boldsymbol{\tau}}$ near the sea surface by using the (surface) boundary layer depth l _b ld(x,y) > 0 which had been stored as part of our model output. The boundary layer depth is determined by the KPP scheme based on the Richardson number: see Fig. 7 of Von Storch et al. (2007) for the global distribution of l _b ld in the OFES output. The present study approximated the vertical profile of $\overline{\boldsymbol{\tau}}$ near the sea surface as,

$$\label{stress} \overline{\boldsymbol{\tau}}(x,y,z) \simeq \overline{\boldsymbol{\tau}}^\mathbf{wind} exp(z/\overline{l}_\mathbf{bld}). $$

(48)

This approximation originates in the classical linear solution of the Ekman spiral (Ekman 1905). According to analytical solutions, the vertical profile of shear stress inside the Ekman layer of depth l _w ind is given by $\boldsymbol{\tau}(z) = \boldsymbol{\tau}^\mathbf{wind} {\rm exp}[(z/l_\mathbf{wind})(1 + i)]$ and $\boldsymbol{\tau}^\mathbf{wind} {\rm exp}[(z/l_\mathbf{wind})(1 - i)]$ in the Northern and Southern Hemispheres, respectively. The complex (i.e., turning) part has a discontinuity at the equator and has been discarded in our approximation. The amplitude part of these solutions is adopted for our approximation (Eq. 48) assuming $\overline{l}_\mathbf{bld} \simeq l_\mathbf{wind}$. As shown in Section 4.2, the global working rate of wind forcing based on the approximation (Eq. 48) is consistent with values suggested by previous observational and numerical studies (cf. Wunsch 1998; Aiki and Richards 2008; Scott and Xu 2009). This suggests that the errors involved in using the approximation (Eq. 48) are not large enough to invalid the results.

On the other hand, the working rate of bottom friction $S_\mathbf{btm}\overline{\mathbf{V}}^{\mathbf{bc}}\cdot\overline{\boldsymbol{\tau}}_z$ was determined in the present study by assuming a linear decay of $\overline{\boldsymbol{\tau}}$ in each bottom cell. As such only the grid cell at the bottom of the ocean is subject to the sink of momentum and KE by bottom friction.