1 Introduction

Determining the underlying fluid motion generated by a wave propagating on an interface is an intriguing area of mathematical research which has important practical implications in the broad field of fluid mechanics. For surface water waves, it has been established in the past decade or so that fluid particle paths are uniformly nonclosed throughout the fluid domain, both in the (approximate) linearised setting [6, 11, 16, 20, 21, 26, 32], and for exact solutions of the fully nonlinear governing equations [2, 4, 7, 19, 22, 23, 31, 35]. These results relate to periodic travelling surface waves which, from a theoretical perspective, already present substantial theoretical challenges (cf. the discussions and references in [3, 5, 30]).

The scale of these theoretical challenges is greatly increased when one also considers an additional (unknown) free interface. Internal water waves, which arise where there is a jump in density between fluid layers, are particularly interesting from both the mathematical and physical viewpoints. Internal waves occur in an oceanographical context when variations in density occur due to variations in temperature, salinity, or other fluctuations in the equations of state. Given their intractability to mathematical analysis, it is not surprising that the literature detailing the underlying wave-field kinematics for coupled surface and internal wave motion is sparse, to the point of nonexistence. We note that there have been numerous significant developments in the mathematical analysis of other aspects of internal wave motion, particularly in relation to nonlinear waves, cf. [1, 8,9,10, 12,13,14], and the references therein. Furthermore, surveys and overviews outlining recent research relating to internal wave motion (ranging from applied to purely theoretical considerations) can be found in [9, 12, 17, 18, 29, 36].

Recently, in [25], the authors comprehensively detailed the fluid motion induced by linear internal water waves, coupled with surface waves, propagating on the interfaces of two immiscible fluid layers lying upon a flat bed. In this article, we extend these investigations to the deep-water setting whereby the lower (denser) fluid layer is taken to be infinitely deep. The setting in which one fluid layer is infinitely deep is known as the Benjamin–Ono regime and is the focus of much analysis in its own right (particularly with regard to deriving approximate model equations, cf. [12]). Although the linearised governing equations are studied, the resulting dynamical systems which prescribe the fluid motion are themselves nonlinear. In the deep-water regime, the wave-field kinematics in the lower-fluid layer are necessarily quite different to that of the finite depth case featured in [25]. However, a benefit of the deep-water setting is that we can particularise results from [25] concerning the dynamics of the upper-fluid layer. Phase-plane analysis is used to achieve a detailed qualitative description of the underlying wave-field kinematics in both fluid layers from an Eulerian viewpoint. A Lagrangian description of fluid particle trajectories in both fluid layers is also obtained.

2 Linear wave solutions

2.1 Governing equations for coupled wave motion

We consider the two-dimensional motion of a stratified fluid, denoting horizontal and vertical coordinates by x and y, respectively. The fluid is assumed inviscid and incompressible, with an external restoration force due to gravity.

Fig. 1
figure 1

Schematic of the coupled surface–internal water wave problem

Full size image

The physical regime consists of two vertically stratified fluid layers of differing (but constant) densities separated by a sharp internal interface denoted by \(y=\eta (x,t)\), which fluctuates about the mean water level \(y=0\); hence, \(\int _{\mathbb {R}} \eta (x,t)\mathrm{d}x=0\). The lower-fluid layer (denoted \(\Omega ^{l}\)) is of infinite extent, comprising the region \(-\infty< y < \eta (x,t)\), and the velocity field in the lower-fluid layer is expressed as (u, v). The upper-fluid layer (denoted by \(\Omega ^{u}\)) lies in the region \(\eta (x,t) \le y \le h_{1}+\eta _{1}(x,t)\), where the a priori unknown free-surface boundary \(\eta _{1}\) represents fluctuations around the undisturbed surface water level \( y=h_{1}\), that is \(\int _{\mathbb {R}} \eta _{1}(x,t)\mathrm{d}x=0\). The velocity field in the upper layer \(\Omega ^{u}\) is denoted \((u_{1},v_{1})\). Here, \(h_{1}>0\) is a physical constant, which determines the mean depth of the upper-fluid layer. We assume that the wave profiles \(\eta \) and \(\eta _{1}\) are such that and \(\max |\eta (x,t)|+\max |\eta _{1}(x,t)|<h_{1}\), which precludes any intersection of the surface and internal wave interfaces. We assume stable stratification, with the upper layer being less dense than the lower layer, in which case we denote the density of the upper layer by \(\rho \) and the lower layer by \((1+r)\rho \), where \(r>0\) is constant. In practice, \(r\ll 1\); for instance, in an oceanographical context, the value \(r=\mathcal {O} (10^{-3})\) may be taken as reasonable [9, 27].

The equations of motion for an inviscid and incompressible fluid are the Euler equation, which is expressed in the lower layer \(\Omega ^{l}\) by

$$\begin{aligned} u_{t}+u_{}u_{x}+v_{}u_{y}&=-\frac{P_{x}}{\rho (1+r)},\nonumber \\ v_{t}+u_{}v_{x}+v_{}v_{y}&=-\frac{P_{y}}{\rho (1+r)}-g, \end{aligned}$$
(1a)

together with the equation of continuity

$$\begin{aligned} u_{x}+v_{y}=0. \end{aligned}$$
(1b)

The scalar function P(x, y, t) represents the internal fluid pressure, and g denotes the gravitational acceleration constant. In the upper-fluid layer \(\Omega ^{u}\),

$$\begin{aligned} u_{1,t}+u_{1}u_{1,x}+v_{1}u_{1,y}&=-\frac{P_{1,x}}{\rho },\nonumber \\ v_{1,t}+u_{1}v_{1,x}+v_{1}v_{1,y}&=-\frac{P_{1,y}}{\rho }-g, \end{aligned}$$
(2a)
$$\begin{aligned} u_{1,x}+v_{1,y}&=0. \end{aligned}$$
(2b)

The kinematic boundary condition in the lower layer \(\Omega ^{l}\) expresses the fact that the fluid is motionless at large depths:

$$\begin{aligned} (u,v)\rightarrow 0 \quad \text{ as }\; y\rightarrow -\infty . \end{aligned}$$
(3a)

The dynamic and kinematic boundary conditions at the internal interface take the form

$$\begin{aligned} P&=P_{1} \quad \text{ at }\; y=\eta (x,t). \end{aligned}$$
(3b)
$$\begin{aligned} v_{1}&=\eta _{t}+u_{1}\eta _{x} \quad \text{ on }\; y=\eta (x,t), \end{aligned}$$
(3c)
$$\begin{aligned} v&=\eta _{t}+u\eta _{x} \quad \text{ on }\; y=\eta (x,t). \end{aligned}$$
(3d)

The dynamic boundary condition (3b) ensures that the pressure is always continuous throughout a fluid. The kinematic boundary conditions (3c) and (3d) ensure that the normal components of the respective velocity fields match, and are continuous, at the interface. For inviscid fluid motion, this need not be true for the tangential velocity components. Finally, at the free surface, the governing equations (2) in the upper layer \(\Omega ^{u}\) have the associated dynamic and kinematic boundary conditions

$$\begin{aligned} P_{1}&=P_{atm} \quad \text{ on }\; y=h_{1}+\eta _{1}(x,t), \end{aligned}$$
(3e)
$$\begin{aligned} v_{1}&=\eta _{1,t}+u_{1}\eta _{1,x} \quad \text{ on }\; y=h_{1}+\eta _{1}(x,t). \end{aligned}$$
(3f)

The fluid is assumed to be irrotational in each fluid layer separately which, in two dimensions, corresponds to

$$\begin{aligned} u_{y}=v_{x}, \qquad u_{1,y}=v_{1,x}. \end{aligned}$$
(4)

This implies the existence of velocity potentials \(\varphi (x,y,t)\) and \(\varphi _{1}(x,y,t)\) for which

$$\begin{aligned} \nabla \varphi =(u,v), \quad \nabla \varphi _{1}= (u_{1},v_{1}). \end{aligned}$$
(5)

The governing equations (1) and (2) and boundary conditions (3) can be reformulated in terms of the velocity potentials as follows. It follows from definition (5), coupled with the incompressibility equations (1b) and (2b), that the velocity potentials are harmonic functions:

$$\begin{aligned} \Delta \varphi =0 \ \text{ in }\; \Omega ^l, \quad \Delta \varphi _{1}= 0 \ \text{ in }\; \Omega ^u. \end{aligned}$$
(6a)

Furthermore, formulating the kinematic boundary conditions (3a), (3c), (3d) and (3f) in terms of the velocity potentials leads to

$$\begin{aligned} \nabla \varphi&\rightarrow 0 \quad \text{ as }\; y\rightarrow -\infty , \end{aligned}$$
(6b)
$$\begin{aligned} \eta _t&=\frac{\partial \varphi }{\partial \varvec{n}} \;\text{ and }\; \ \eta _t =\frac{\partial \varphi _1}{\partial \varvec{n}} \quad \text{ on }\; y=\eta (x,t), \end{aligned}$$
(6c)
$$\begin{aligned} \eta _{1,t}&=\frac{\partial \varphi _1}{\partial \varvec{n_1}} \quad \text{ on }\; y=h_{1}+\eta _{1}(x,t), \end{aligned}$$
(6d)

where \(\varvec{n}=(-\eta '(x),1))\) is the normal vector to the interface exterior to the lower domain, and \(\varvec{n_1}=(-\eta _1'(x),1))\) is the exterior normal vector to the free surface. The pressure-matching dynamic boundary condition (3b) formulated in terms of velocity potentials becomes

$$\begin{aligned} (1+r)\left( \varphi _t+{|\nabla \varphi |^2 \over 2} +gy \right) =\varphi _{1,t}+{|\nabla \varphi _1 |^2 \over 2} +gy \quad \text{ on }\; y=\eta (x,t), \end{aligned}$$
(6e)

while the dynamic surface condition (3e) becomes the Bernoulli condition

$$\begin{aligned} \varphi _{1,t}+{|\nabla \varphi _1 |^2 \over 2} +g\eta _1=0 \quad \text{ on }\; y=h_{1}+\eta _{1}(x,t). \end{aligned}$$
(6f)

2.2 Linearised equations

The governing equations and boundary conditions can be linearised by invoking nondimensionalisation and scaling procedures (cf. [25] for full details in the setting where the lower-fluid layer has finite depth). Let \(\lambda \) denote a characteristic wavelength for the water waves being considered, and let \(\mathfrak {h}\) be a characteristic depth scale (the choice \(\mathfrak h=h_{1}\) is natural in the present context). Let a be a characteristic amplitude of the internal wave, with \(a_{1}\) a characteristic amplitude for the surface wave. Then, the nondimensional parameters \(\epsilon =a/\mathfrak {h}\), \(\epsilon _{1}=a_{1}/\mathfrak {h}\) (which measure the magnitude of the wave amplitudes relative to the characteristic vertical depth scale) and \(\delta =\mathfrak {h}/\lambda \) (a ‘shallowness’ parameter which measures the magnitude of the characteristic vertical depth scale relative to the wavelength) are naturally introduced into the governing equations and boundary conditions. Furthermore, linearisation requires that the wave-steepness parameters \(\mathfrak {e}=a k=2\pi (a/\lambda )\) (for the internal wave) and \(\mathfrak {e}_{1}=a_1 k=2\pi (a_1/\lambda )\) (for the surface wave) are small. The linear wave approximation is valid under the assumption that these nondimensional parameters satisfy

$$\begin{aligned} \epsilon , \epsilon _{1}, \mathfrak {e}, \mathfrak {e}_{1} \ll 1. \end{aligned}$$
(7)

The linearisation process eliminates all product terms in the governing equations (1) and (2) and boundary conditions (3). Additionally, an important consequence of linearisation is that the boundary conditions (3) are now evaluated at the constant mean levels \(y=0,h_{1}\), as opposed to on the unknown interfaces \(y=\eta , h_1+\eta _1\), respectively. The linearisation of (6) results in the following Neumann boundary value problem for the velocity potential \(\varphi \) in \(\Omega ^{l}\),

$$\begin{aligned} \Delta \varphi&=0 \quad \text{ for }\; -h<y<0, \end{aligned}$$
(8a)
$$\begin{aligned} \varphi _{y}&= \eta _t \quad \text{ on }\; y=0, \end{aligned}$$
(8b)
$$\begin{aligned} \nabla \varphi&\rightarrow 0 \quad \text{ as }\; y\rightarrow -\infty , \end{aligned}$$
(8c)

while in the upper-fluid layer \(\Omega ^{u}\) the velocity potential \(\varphi _{1}\) must solve the Neumann boundary value problem

$$\begin{aligned} \Delta \varphi _{1}&=0 \quad \text{ for }\; 0<y<h_{1}, \end{aligned}$$
(8d)
$$\begin{aligned} \varphi _{1,y}&=\eta _{1,t} \quad \text{ on }\; y=h_{1}, \end{aligned}$$
(8e)
$$\begin{aligned} \varphi _{1,y}&=\eta _t \quad \text{ on }\; y=0. \end{aligned}$$
(8f)

The linearised dynamic boundary conditions (6f) and (6e) take the form

$$\begin{aligned} \varphi _{1,t} +g\eta _1=0 \quad \text{ on }\; y=h_{1} \end{aligned}$$
(8g)

and

$$\begin{aligned} (1+r)\left( \varphi _t+g\eta \right) =\varphi _{1,t}+g\eta \quad \text{ on }\; y=0. \end{aligned}$$
(8h)

2.3 Linear wave solutions

Seeking periodic travelling wave solutions of (8) which have a functional x, t dependence of the form \(kx-\omega t\), where \(\omega \) is the wave frequency, \(k=2\pi /\lambda \) is the wavenumber, and \(c=\omega /k\) is the wave phase speed, suggests the Ansatz:

$$\begin{aligned} \eta (x,t)=a\cos (kx-\omega t), \end{aligned}$$
(9a)
$$\begin{aligned} \eta _{1}(x,t)=a_{1} \cos (kx-\omega t). \end{aligned}$$
(9b)

Here, \(a_{1}\) and a are the amplitudes of the free surface and interface, respectively. Unless otherwise stated, in the following we assume that \(a,a_{1} \ne 0\), thereby implying a nontrivial coupling of wave motions at the free surface and the interface. The physical set-up illustrated in Fig. 1 represents waves where the crests (and the troughs) of the surface and internal interfaces coincide, which corresponds to the ratio \(a/a_{1}>0\) in (9). Ansatz (9) permits an alternative configuration, whereby the crests (respectively, the troughs) of the surface wave coincide with the troughs (respectively, the crests) of the internal wave. This scenario arises when \(a/a_{1}<0\) and is represented schematically in Fig. 2.

Fig. 2
figure 2

Coupled surface–internal water waves for \(a/a_1<0\)

Full size image

The coupled waves represented in Fig. 1, with \(a/a_{1}>0\), will be referred to as being ‘in-phase’, whereas the coupled waves represented in Fig. 2, with \(a/a_{1}<0\), will be referred to as being ‘out-of-phase’. We note that \(|a|+|a_{1}|<h_{1}\) must hold for out-of-phase waves. It will be established in relation (22) that there exists precisely one set of coupled wave solutions which are in-phase, and one set which are out-of-phase, for a given fixed wavelength (or, alternatively, fixed frequency). Implementing Ansatz (9b) in (8b), system (8a)–(8c) has the solution

$$\begin{aligned} \varphi (x,y,t)=ace^{ky}\sin (kx-\omega t) \quad \text{ in }\; -h<y<0. \end{aligned}$$
(10)

Invoking Ansatz (9b) in (8e) and (9a) in (8f), system (8d)–(8f) can be solved for

$$\begin{aligned} \varphi _{1}(x,y,t)=a_{1}c\sin (kx-\omega t)\left\{ \sinh k(y-h_{1})+A \cosh k(y-h_{1}) \right\} \nonumber \\ \text{ in }\; 0<y<h_{1}, \end{aligned}$$
(11)

where the nondimensional ‘wave amplitude ratio’ parameter A is given by

$$\begin{aligned} A=\left( {1-\frac{a}{a_{1}}{\text {sech\,}(kh_{1})} }\right) { \coth (kh_{1})}. \end{aligned}$$
(12)

It is convenient to re-express (12) in terms of the amplitude ratio

$$\begin{aligned} \frac{a}{a_{1}}=\cosh kh_{1}-A\sinh kh_{1}. \end{aligned}$$
(13)

The value of A is determined by two nondimensional parameters, namely the ratio of wave amplitudes \(a/a_{1}\) and the shallowness parameter \(kh_{1}=2\pi \cdot h_{1}/\lambda \).

Remark

Note that the limiting case \(a_{1}\rightarrow 0\) (no surface wave) in the upper-fluid layer corresponds to the classical ‘rigid-lid’ model of internal wave motion, with the associated velocity potential

$$\begin{aligned} \varphi _{1}(x,y,t)=-ac\frac{\cosh k(y-h_{1})}{\sinh (kh_{1})} \sin (kx- \omega t) \text{ in } 0<y<h_{1}. \end{aligned}$$
(14)

The boundary conditions (8b) and (8f) ensure that the velocity potentials \(\varphi \) and \(\varphi _1\) prescribe matching linearised normal velocities at the internal interface. Evaluating (8g) for the wave surface profile (9b) and velocity potential \(\varphi _1\) (11) leads to a dispersion relation at the free surface

$$\begin{aligned} c^{2}=\frac{g}{k}\frac{1}{A}=\frac{g}{k}\tanh (kh_{1})\left( 1- \frac{a}{a_{1}}\text {sech\,}(kh_{1})\right) ^{-1}. \end{aligned}$$
(15)

Note that this is not a dispersion relation for the surface wave alone: there is an intrinsic coupling between the surface and internal waves induced by the wave amplitude ratio \(a/a_{1}\). An immediate consequence of (15) is that the parameter A must be positive, which confers a bound on the internal wave amplitude for in-phase waves, namely:

$$\begin{aligned} a<a_{1}\cosh (kh_{1}), \qquad \text{ when } a/a_{1}>0. \end{aligned}$$

Evaluating (8h) for the velocity potentials (10) and (11) leads to the following dispersion relation at the interface:

$$\begin{aligned} akc^2(1+r) -gar=a_{1} k c^2\left[ A\cosh k h_{1}-\sinh kh_{1} \right] . \end{aligned}$$
(16)

As remarked above, this is not a dispersion relation for the interface alone: this relation prescribes coupling between surface and internal waves through terms involving the ratio of wave amplitudes.

2.4 Dispersion relations for the coupled waves

Dispersion relations are formulae which specify the linear wavespeed c in terms of various physical parameters. They are so-called since, if the wavespeed c varies with respect to some parameter, then the waves are dispersive: waves corresponding to different parameter values will travel at different speeds. Assuming we know (either by measurement, or prescription) the mean depth \(h_{1}\) of the upper-fluid layer, Eqs. (15) and (16) feature three unknown parameters, namely the wavenumber \(k=2\pi /\lambda \), the wavespeed \(c=\omega /k\) (or, alternatively, the frequency \(\omega \)) and the ratio of wave amplitudes \({a}/{a_{1}}\). Using (13), we can re-express (15) as

$$\begin{aligned} \frac{a{_{1}}}{a_{1}}=\cosh kh_{1}-\frac{g}{kc^{2}}\sinh kh_{1}, \end{aligned}$$
(17)

and (16) as another quadratic for c of the form:

$$\begin{aligned} \left[ \text {sech\,}kh_{1}-\frac{a}{a_{1}}\left\{ 1+(1+r)\tanh kh_{1}\right\} \right] \frac{k c^{2}}{g} +r \frac{a}{a_{1}}\tanh kh_{1}=0. \end{aligned}$$
(18)

The evident coupling between relations (17) and (18) illustrates that the wavespeed c depends on the ratio of wave amplitudes, \(a/a_{1}\), and vice versa. Together, Eqs. (17) and (18) constitute a system of dispersion relations prescribing the wavespeed c of coupled internal and surface waves, and the ratio \(a/a_{1}\) of associated wave amplitudes, in terms of the wavenumber k. To obtain a single dispersion relation involving the wavespeed c, we substitute (17) into (18) to obtain the classical dispersion relation [28, 36]:

$$\begin{aligned} \left\{ 1+\frac{1+r}{\tanh kh_{1}} \right\} \frac{k^{2}c^{4}}{g^{2}}-(1+r)\left\{ \frac{1}{\tanh kh_{1}}+ 1\right\} \frac{kc^{2}}{g}+r=0. \end{aligned}$$
(19)

The nondimensional wave amplitude ratio parameter A plays a key role in subsequent analysis of the underlying fluid motion induced by coupled waves. Hence, it is beneficial for our purposes to reformulate relation (19) as a dispersion relation in terms of A by substituting \(kc^{2}/g=1/A\):

$$\begin{aligned} r A^{2} -(1+r)\left\{ \frac{1}{\tanh kh_{1}}+1\right\} A+\left\{ 1+\frac{(1+r)}{\tanh kh_{1}}\right\} =0. \end{aligned}$$
(20)

This constitutes a dispersion relation for the ratio of wave amplitudes since, given solutions of (20), the ratio of the corresponding wave amplitudes \(a/a_{1}\) can be established directly from (13) (in terms of k). Denoting the polynomial (20) as \(\mathcal {P}(A)=0\), one root is \(A_1=1\) (since \(\mathcal P(1)=0\)) and the other is

$$\begin{aligned} A_2=\frac{1}{\tanh kh_1}+\frac{1}{r}\left[ \frac{1}{\tanh kh_1} +1 \right] . \end{aligned}$$
(21)

Typically \(r\ll 1\), with \(r=\mathcal {O}(10^{-3})\) constituting a reasonable value in the ocean [9, 27], in which case \(A_2\gg 1\) by (21). Relation (13) implies

$$\begin{aligned} \frac{a}{a_{1}}<0 \Longleftrightarrow A> \frac{1}{\tanh kh_{1}}, \end{aligned}$$

from which we conclude that

$$\begin{aligned} \frac{a}{a_{1}}>0 \text{ for } A=A_{1}=1, \qquad \frac{a}{a_{1}}<0 \text{ for } A=A_{2}. \end{aligned}$$
(22)

Coupled wave motions at the interface and free surface are in-phase for solutions corresponding to the root \(A=A_1=1\), and out-of-phase for \(A=A_{2}\).

Remark

Tangential fluid velocities at the internal interface are continuous for the coupled wave solutions corresponding to \(A=A_1=1\), and discontinuous for \(A=A_2\). This can be seen by comparing \(\varphi _{x}\) and \(\varphi _{1,x}\) (corresponding to linearised tangential velocities in the respective layers) at \(y=0\). By (10) and (11), these match only if \(a =a_{1}\left\{ -\sinh kh_{1}+A\cosh kh_{1} \right\} \) which, by (16), holds only if \(A=1\). For coupled wave solutions corresponding to \(A=A_2\), although the fluid is irrotational in each fluid layer separately, there must be a vortex sheet located at the internal interface. In practice, viscosity (neglected in this model) acts to blur the sheet into a vortex film.

The roots of (19), the dispersion relation for the wavespeeds, can be determined from \(c^{2}={g}/{kA}\) to get

$$\begin{aligned} c^{2}_{1}=\frac{g}{k}, \quad c^2_2=\frac{g}{k}\frac{r\tanh kh_1}{1+r+\tanh kh_1}. \end{aligned}$$
(23)

Each root \(c^{2}_{i}\) in (23) represents a given wavespeed, with the choice of sign \(+c_{i}\) (or \(-c_{i}\)) corresponding to right-moving (or left-moving) coupled waves, respectively. It follows from (23) that \(c_{1}>c_{2}>0\); indeed, \(c_2\ll c_1\) for \(r\ll 1\). Solutions corresponding to the wavespeeds \(c_{1}\) and \(c_{2}\) are referred to as barotropic and baroclinic, respectively, cf. [36]. In the ocean, it is observed that internal waves are typically much slower than surface waves, with significantly greater amplitudes. This is due to the restoring force at the internal interface being substantially less than at the free surface. Internal waves in the ocean can have periods ranging from tens of minutes to several hours, with wavelengths ranging from hundreds of metres to tens of kilometres, and their height can often exceed 50 m (cf. [17, 18, 29, 36]). In contrast, for ocean surface gravity waves the period ranges from 1 to 25 s, with ocean swell having a typical wavelength that is greater than 260 m (up to a maximum of approximately 900 m) with a period larger than 13 s (up to a maximum of 24 s) (cf. [37]). We expect these characteristic properties of surface and internal waves to be reflected in the solutions of the linear dispersion relations above. Since \(A_1=1\) for the larger wavespeed \(c_1\), from (13) we have

$$\begin{aligned} \frac{a}{a_{1}}=\cosh kh_{1}-\sinh kh_{1}=e^{-kh_1}<1, \end{aligned}$$
(24)

and so \(a_1>a\): the surface wave is more prominent than the internal wave for the coupled solution corresponding to the faster wavespeed \(c_1\). This distinction is more pronounced for shorter wavelengths (larger k) and greater upper-layer depths \(h_1\). Taking indicative values \(h_1=120\,\)m for the equatorial Pacific thermocline depth (cf. [9]), and \(k=2\pi /300 \,\)m\(^{-1}\), relation (24) gives \(a\approx 0.08 \, a_1\). For coupled waves propagating with the slower wavespeed \(c_2\),

$$\begin{aligned} \frac{a}{a_{1}}=\cosh kh_{1}\left[ 1 - A_2 \tanh kh_1\right] =-\frac{1}{r} \left[ \cosh kh_{1} + \sinh kh_1\right] =-\frac{1}{r}e^{kh_{1}}. \end{aligned}$$
(25)

Hence, the internal wave is (much) more prominent than the surface wave for the coupled wave solution corresponding to the slower wavespeed \(c_2\). Taking the indicative values \(h_1=120\,\)m, \(k=2\pi /5 \,\)km\(^{-1}\) and \(r=2\times 10^{-3}\), relation (25) gives \(|a|\approx 508 \, |a_1|\). Of course, relations (24) and (25) come with the caveat that they relate only to linear coupled waves satisfying conditions (7).

Remark

Letting \(r\rightarrow 0\) simplifies the physical model, which now consists of one homogeneous fluid layer of infinite depth. Taking \(r\rightarrow 0\) gives \(c_{2}=0\) and \(c_{1}^{2}=g/k\): this is the classical dispersion relation for a surface wave over a fluid of infinite depth.

Remark

The ‘rigid-lid’ model describes wave motion at the interface separating two fluid layers which are bounded above a by rigid horizontal wall. If the mean thickness of the upper layer is \(h_{1}\), and the lower layer is infinitely deep, the dispersion relation for the rigid-lid model takes the form

$$\begin{aligned} c^{2}={\frac{g}{k} \frac{\rho ^{\mathrm{lower}} -\rho ^{\mathrm{upper}}}{\rho ^{\mathrm{lower}}+\rho ^{\mathrm{upper}}\,\coth (kh_{1})}}. \end{aligned}$$
(26)

Relation (26) can be formally derived from (18) by letting \(a_{1}\rightarrow 0\) (with \(a\ne 0\)). Alternatively, it arises from ensuring continuity at the internal interface of normal velocities prescribed by velocity potentials (10) and (14).

Remark

When the depth of the upper-fluid layers becomes very large (\(h_{1}\rightarrow \infty \)), the influence of the upper boundary diminishes, and the dispersion relation (26) for the interface becomes:

$$\begin{aligned} c^{2}=\frac{g}{k}{ \frac{\rho ^{\mathrm{lower}} -\rho ^{\mathrm{upper}}}{\rho ^{\mathrm{lower}} +\rho ^{\mathrm{upper}}}}. \end{aligned}$$

This matches the wavespeed \(c_{2}\) obtained in (23) in the limit \(kh_{1}\rightarrow \infty \).

3 Dynamical systems formulation

If (x(t), y(t)) is the path of a particle in the lower-fluid layer \(\Omega ^{l}\), then the motion of the particle is described by the nonlinear dynamical system

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\mathrm{d}x}{\mathrm{d}t}=u=a\omega \cos (kx-\omega t)e^{ky} \\ \frac{\mathrm{d}y}{\mathrm{d}t}=v=a\omega \sin (kx-\omega t)e^{ky}, \end{array}\right. \end{aligned}$$
(27)

for \(-h<y<0\), with initial data \((x_{0},y_{0})\). In the upper-fluid layer \(\Omega ^{u}\), particle trajectories (x(t), y(t)) are determined by the nonlinear dynamical system

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\mathrm{d}x}{\mathrm{d}t}=u_{1}=a_{1}\omega \cos (kx-\omega t)\left\{ \sinh k(y-h_{1})+A\cosh k(y-h_{1}) \right\} \\ \frac{\mathrm{d}y}{\mathrm{d}t}=v_{1}=a_{1}\omega \sin (kx-\omega t)\left\{ \cosh k(y-h_{1})+A\sinh k(y-h_{1}) \right\} , \end{array}\right. \end{aligned}$$
(28)

for \(0<y<h_{1}\), with initial data \((x_{0},y_{0})\). The mean level of the oscillating internal wave interface \(y=\eta \) is located at \(y=0\), whereas the free surface \(y=h_{1}+\eta _{1}\) oscillates about the mean level located at \(y=h_{1}\). The right-hand sides of the differential systems (27) and (28) are smooth; therefore, the existence of unique local smooth solutions for both (27) and (28) is ensured by the Picard–Lindelöf theorem [33]. Furthermore, since the right-hand sides of (27) and (28) are bounded in the respective fluid layers, these unique solutions are defined globally [33]. The right-hand sides of both (27) and (28) are nonlinear, and thus, such systems cannot be solved explicitly. The fluid layers are separated by an impermeable interface \(y=\eta (x,t)\); therefore, we perform a phase-plane analysis of system (27) in the lower-fluid layer \(\Omega ^{l}\) and system (28) in the upper-fluid layer \(\Omega ^{u}\), separately, and then piece together the information to obtain the motion of the entire two-layer body.

As we are dealing with travelling waves it is possible to transform to moving frames where the motion is steady by the changes of variables

$$\begin{aligned} \left( X(t),Y(t)\right)&=\left( kx(t)-\omega t,ky(t)\right) \quad \text{ for }\; \left( x(t),y(t)\right) \in \Omega ^l, \end{aligned}$$
(29)
$$\begin{aligned} \left( X(t),Y_1(t)\right)&=\left( kx(t)-\omega t,k\left[ h_{1}-y(t)\right] \right) \quad \text{ for }\; \left( x(t),y(t)\right) \in \Omega ^u. \end{aligned}$$
(30)

The mapping (29) transforms system (27) to the autonomous system

with initial data \((X(0),Y(0))=(kx_{0},ky_{0})\). We denote \(M:=a k \omega =\mathfrak {e} \omega \ll \omega \), where \(\mathfrak {e}=a k\ll 1\) is the wave-steepness parameter for the internal wave (cf. Sect. 2.2). Note that (31) can be expressed as a Hamiltonian system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{X} =H_{Y},\\ \dot{Y}=-H_{X}, \end{array}\right. \end{aligned}$$

for the Hamiltonian function

$$\begin{aligned} H(X,Y)\equiv Me^Y\cos X-\omega Y. \end{aligned}$$
(32)

If (X(t), Y(t)) is a solution of (31), then \(\frac{\mathrm{d}{t}}{\mathrm{d}t}H(X(t),Y(t))=H_{X}\dot{X}+H_{Y}\dot{Y}=0\), and so, H is constant along the phase curves. The mapping (30) transforms (28) to the autonomous system

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\mathrm{d}X}{\mathrm{d}t}=F(X,Y_{1}),\\ \frac{\mathrm{d}Y_{1}}{\mathrm{d}t}=G(X,Y_{1}), \end{array}\right. \end{aligned}$$
(33)

with initial data \((X(0),Y(0))=(kx_{0},k(h_1-y_{0}))\). The right-hand side is denoted by \(F(X,Y_{1}):=M_{1}A\cos X\cosh Y_{1}-M_{1}\cos X\sinh Y_{1}-\omega \), and \(G(X,Y_{1}):=M_{1}A\sin X\sinh Y_{1}-M_{1}\sin X\cosh Y_{1}\), where A is defined by (12) and the parameter \(M_{1}:=a_{1}k\omega =\mathfrak {e}_{1} \omega \ll \omega \) (since the wave-steepness parameter for the surface wave satisfies \(\mathfrak {e}_{1}\ll 1\): cf. Sect. 2.2). System (33) also has a Hamiltonian structure for the Hamiltonian function

$$\begin{aligned} H_{1}(X,Y_{1})=M_{1}A \cos X \sinh Y_{1}-\omega Y_{1}-M_{1}\cos X\cosh Y_{1}. \end{aligned}$$
(34)

Since (31) and (33) are periodic with respect to X, we focus on the strip \(\{X:-\pi \le X\le \pi \}\). The change of variables (29) transforms the lower-fluid layer to the region \(\{Y: -\infty \le Y\le \mathfrak {e} \cos X\}\), while (30) transforms the upper-fluid layer to the region \(\{Y_{1}: -\mathfrak {e}_{1} \cos X \le Y_{1} \le kh_{1}- \mathfrak {e} \cos X\}\). It is important to note that the change of variables (30) reflects vertical coordinates through the line \(y=h_{1}\) with the effect that, when constructing phase-plane diagrams in terms of the transformed \((X,Y_{1})\) variables, wave crests in the physical system (28) correspond to troughs in the transformed system (33), with a similar correspondence between troughs for (28) and crests for (33). Additionally, the streamline denoting the surface wave lies beneath that representing the internal wave in the resulting phase portraits.

In subsequent phase portrait analysis of the dynamical systems (27) and (28), the parameters k and \(\omega \) will be regarded as fixed constants, with the nondimensional wave amplitude ratio parameter A taking the values \(A_1=1\) and \(A_2>1\) for the upper-fluid layer system (28). While these parameters are fixed for a given coupled wave motion, in general they are not free-parameters; rather, they are determined by the dispersion relations (15) and (16).

3.1 Phase portrait analysis: lower-fluid layer

The velocity field for the lower-fluid layer is qualitatively identical to one which describes fluid motion in a single homogenous (uniform density) fluid layer whose upper interface separates the fluid from a source of constant pressure (such as the atmosphere), cf. [6]. Indeed, we note phase-plane approaches have previously proven successful in revealing the underlying flow-structure of a variety of surface water waves (cf. [6, 11, 15, 16, 20, 21]. The physical influence of the upper-fluid layer is conveyed implicitly by way of the dispersion relations (17) and (18). The autonomous system (31) meets standard regularity assumptions for the uniqueness of the Cauchy problem [33]; therefore, its trajectories do not intersect. We note that the right-hand side of (31a) is an even function in X, while the right-hand side of (31b) is an odd function in X; therefore, the trajectories of (31) have a mirror symmetry with respect to the \(X-\)axis. Without loss of generality, we choose \(a>0\) (hence \(M>0\)) throughout this subsection.

The 0-isocline is defined to be the set where \(\mathrm{d}Y/\mathrm{d}t=0\), and the \(\infty \)-isocline is the set where \(\mathrm{d}X/\mathrm{d}t=0\). Therefore, the 0-isocline is given by the lines \(X=0,\pm \pi \). The \(\infty \)-isocline is given in the region \(X\in \left( -\frac{\pi }{2},\frac{\pi }{2}\right) \) by the curve \((X,\alpha (X))\), where \(\alpha \) is defined by \(\alpha (X)=\ln \left( \omega /M\cos X\right) \): \(\alpha (X)\in \left[ Y^{*},\infty \right) \) for \(Y^{*}=\ln \left( {\omega }/{M}\right) =\ln \left( 1/{\mathfrak {e}}\right) \), where \({\mathfrak {e}}=ak\) is the wave-steepness parameter. The even function \(\alpha \) is smooth, it takes on its infimum \(Y^{*}\) at \(X=0\), and it satisfies the limiting condition \(\lim _{X\rightarrow \pm \pi /2 }\alpha (X)=\infty \). The only singular point of system (31) is \(Q=(0,Y^{*})\), which is consequently a critical point of the Hamiltonian H(X, Y) defined by (32). The Hessian of H at Q is

$$\begin{aligned} \left( \begin{array}{cc} -\omega &{} 0 \\ 0 &{} \omega \end{array} \right) . \end{aligned}$$

It follows that Q is a nondegenerate singular point. By Morse’s lemma [34] in a neighbourhood of Q, there exists a diffeomorphic change of coordinates which sends the level lines of H to hyperbolas. Thus, Q is a saddle point for H. Away from the critical point Q, the separatrix \(H^{-1}\{H(Q)\}=\{(X,Y): H(X,Y)=H(Q)\}\) is a smooth curve, by the implicit function theorem, and it intersects the vertical line \(X=\pi \) at the point \((\pi , \beta )\), where \(\beta \) is implicitly defined by the equation \(H(\pi ,\beta )=-\omega \left( {\mathfrak {e}} e^{\beta }+ \beta \right) =H(Q)=\omega \left( 1-\ln \left( 1/{\mathfrak {e}}\right) \right) \). Note a unique positive solution \(\beta >0\) exists since \({\mathfrak {e}}\ll 1\). This implies that the streamline that represents the internal wave lies beneath the separatrix, as required, since the wave trough is located at \(X=\pi \) and \(Y=-{\mathfrak {e}}<\beta \).

For \(X\in (\frac{\pi }{2},\pi )\), we have \(\mathrm{d}X/\mathrm{d}t<0,\ \mathrm{d}Y/\mathrm{d}t>0\). If \(X\in (0,\frac{\pi }{2})\), then \(\mathrm{d}X/\mathrm{d}t<0\) below the curve of \(\alpha (X)\) and is positive above it, while \(\mathrm{d}Y/\mathrm{d}t\) remains positive in this region. The corresponding signs for \( X\in (-\pi ,0)\) are obtained using symmetry with respect to the Y-axis. A phase portrait for the lower-fluid layer is given in Fig. 3.

Fig. 3
figure 3

Phase portrait for the lower-fluid layer. The dotted grey line represents the \(\infty \)-isocline, with the dotted-dashed lines representing the 0-isoclines. The internal wave profile (blue dashed lines) with mean water level \(Y=0\) (corresponding to \(y=0\)) is also illustrated (colour figure online)

Full size image

3.2 Phase portrait analysis: upper-fluid layer

Phase-plane analysis for the upper-fluid layer proceeds along the lines of that for coupled waves propagating on a finite fluid domain over a flat bed [25], with simplifications resulting in the present setting due to the explicit form of the wave solution parameters \(A=A_1,A_2\) (given by (21)). For completeness, we present the salient aspects of the phase-plane analysis which are germane to the present context, referring to [25] for full details.

The autonomous system (33) meets the standard regularity assumptions for the uniqueness of the Cauchy problem [33]; therefore, its trajectories do not intersect. Moreover, since \(F(X,Y_{1})\) is an even function and \(G(X,Y_{1})\) an odd function, with respect to X, any trajectory of system (33) is symmetric with respect to the \(Y_{1}\)-axis when viewed as a curve in the \((X,Y_{1})-\)phase plane. Re-express the right-hand sides of (33) as

$$\begin{aligned} F(X,Y_{1})=M_{1}\cos (X)f(Y_{1})-\omega , \quad G(X,Y_{1})=M_{1}\sin (X)g(Y_{1}), \end{aligned}$$
(35a)

for the functions

$$\begin{aligned} f(Y_{1}):=A\cosh (Y_{1})-\sinh (Y_{1}), \quad g(Y_{1}):=A\sinh (Y_{1})- \cosh (Y_{1}). \end{aligned}$$
(35b)

Without loss of generality, we fix \(M_{1}>0\) (\(a_{1}>0\)) throughout subsequent considerations, with the sign of a matching that of the ratio \(a/a_{1}\) as prescribed by A in (22), namely: \(a/a_{1}>0\) for \(A=1\) and \(a/a_{1}<0\) for \(A=A_2.\)

figure a

Note that \(f'(Y_{1})=g(Y_{1})\) and \(g'(Y_{1})=f(Y_{1})\), where \((\cdot )'\) denotes differentiation with respect to \(Y_{1}\). In order to investigate the phase portrait of system (33), we must begin by investigating the 0-isocline (defined as the set of points where the vector field is horizontal, \(\dot{Y}_{1}=0\), and so \(G(X,Y_{1})=0\) in (35a)) and the \(\infty \)-isocline (defined as the set of points where the vector field is vertical, \(\dot{X}=0\), and so \(F(X,Y_{1})=0\) in (35a)).

3.2.1 System (33) with \(A=A_1=1\)

For \(A=1\), relations (35b) reduce to \(f(Y_{1})=e^{-Y_{1}}=-g(Y_{1})\). Accordingly, the phase portrait for positive values of \(Y_{1}\) rapidly converges to a series of flat, horizontal lines as \(Y_{1}\) increases, since the velocity field converges exponentially fast to the uniform system \(\dot{X}\equiv -\omega \) and \(\dot{Y_{1}}\equiv 0\). We have \(G(X,Y_{1})<0\) for \(0<X<\pi \) and vanishes at \(X=0\) and \(X=\pi \); hence, these vertical lines comprise the 0-isocline for system (33) in \([0,\pi ]\). The \(\infty \)-isocline consists of points \(Y_{1}\) where \(\cos (X)e^{-{Y_{1}}}=1/\mathfrak {e}_{1}\), and for \(X\in \left[ \frac{\pi }{2},\pi \right] \), there is no such solution. For each \(X\in \left[ 0,\frac{\pi }{2}\right) \), there is a solution, and for \(X=0\), we have \(e^{-{Y^{*}_{1}}}=1/\mathfrak {e}_{1}\) for \(Y_{1}^{*}=-\ln \left( 1/\mathfrak {e}_{1}\right) \). The point \(Q_{1}=(0,Y_{1}^{*})\) is a singular point, and since the Hessian of the Hamiltonian (34) is

$$\begin{aligned} M_{1}\left( \begin{array}{cc} e^{Y_{1}^{*}} &{} 0\\ 0 &{} -e^{Y_{1}^{*}} \end{array} \right) , \end{aligned}$$

it follows immediately that \(Q_{1}\) is a saddle point which lies at the confluence of four separatrices. The maximum value of the \(\infty \)-isocline is located at \(Q_{1}\), and it decreases monotonically to \(-\infty \) as \(X\rightarrow \frac{\pi }{2}\). The phase portrait for system (33) when \(A=1\) is given in Fig. 4.

Fig. 4
figure 4

Phase portrait of the upper-fluid layer when \(A=1\). The dotted grey line represents the \(\infty \)-isocline, while the dotted-dashed lines represent the 0-isoclines. The surface wave profile (thin blue dashed lines) has mean water level \(Y_1=0\), corresponding to \(y=h_1\). The internal wave profile (thick blue dashed lines) has mean water level \(Y=kh_1\), corresponding to \(y=0\). Recall that the streamline representing the surface wave lies beneath that of the internal wave in this phase portrait (colour figure online)

Full size image

Note the magnitude of the amplitude of the surface wave is greater than that of the internal wave, in accordance with (24). The surface wave streamline must be located above the separatrix for physically relevant solutions of (33), and this is the case if \(-\mathfrak {e}_{1}>Y_{1}^{*}\), that is, \(\mathfrak {e}_{1} e^{\mathfrak {e}_{1}}<1\): this holds since \({\mathfrak {e}}_1\ll 1\).

3.2.2 System (33) with \(A=A_2>1\)

To ascertain the 0-isocline, we must determine when \(G(X,Y_{1})=0\) in (35a). Firstly, it is obvious from (35a) that this occurs when \(X=0\) and \(X=\pi \). From direct computation in (35b), we have \(g(0)=-1\), while \(g'(Y_{1})>0\) and \({\lim _{Y_{1}\rightarrow +\infty }g(Y_{1})=+\infty }\) whenever \(A>1\). Hence, there exists a unique \(\bar{Y_{1}}\) such that \(g(\bar{Y_{1}})=0\), and we can calculate it directly to get

$$\begin{aligned} \bar{Y_{1}}=\frac{1}{2}\ln \left( \frac{A+1}{A-1}\right) . \end{aligned}$$
(36)

Hence, the 0-isocline is composed of the vertical half-lines \(X=0\), \(X=\pi \) and the horizontal line-segment \(Y_{1}=\bar{Y_{1}}\). The value for \(\bar{Y_{1}}\) as determined by (36), which is well defined for \(A>1\), corresponds to \(A=\coth (\bar{Y_{1}})\): it follows from (21) that \(kh_1>\bar{Y_{1}}\) for \(A=A_2\).

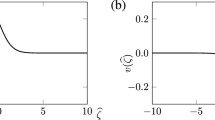
The study of the \(\infty \)-isocline, where \(F(X,Y_{1})=0\) in (35a), can be achieved through examining \(f(Y_{1})\) in (35b). The function f has a minimum at \(Y_{1}=\bar{Y_{1}}\), which can be calculated to get \(f(\bar{Y_{1}})=1/ \sinh (\bar{Y_{1}})<A\). If \(\hat{Y_{1}}>\bar{Y_{1}}\) is the unique value such that \(f(\hat{Y_{1}})=A\), then the function \(f(Y_{1})\) is invertible on the set \(Y_{1}\in (\hat{Y_{1}},\infty )\); a schematic for \(f(Y_{1})\) is given in Fig. 5.

Fig. 5
figure 5

Schematic of \(f(Y_1)\) for \(A>1\), where \(f(0)=A\), with \(A=\cosh (\bar{Y_1})/\sinh (\bar{Y_1})\), and the minimum value attained is \(f(\bar{Y_1})=1/\sinh (\bar{Y_1})\)

Full size image

For \(\frac{\pi }{2}\le X\le \pi \), \(F(X,Y_{1})\) is strictly positive since \(M_{1}>0\); hence, there are no \(\infty \)-isocline or singular points in this region. In the region \(0\le X <\frac{\pi }{2}\), the \(\infty \)-isocline is given by points \((X,Y_{1})\) where \(\cos (X) f(Y_{1})=\omega /M_{1}=1/\mathfrak {e}_{1}\); therefore, since the left-hand side is maximised at \(X=0\), an \(\infty \)-isocline exists in this region if \(f(Y^{*}_{1})=1/\mathfrak {e}_{1}\) for some value of \(Y^{*}_{1}\). It follows from the schematic in Fig. 5 that, if \(\mathfrak {e}_{1}<\max _{Y_{1}} 1/f(Y_{1})=\sinh (\bar{Y_{1}})\), there exists a pair of values, \(\tilde{Y^{*}_{1}}\), \(Y^{*}_{1}\) with \(\tilde{Y^{*}_{1}}\le Y^{*}_{1}\), say, such that \(f(Y^{*}_{1})=f(Y^{*}_{1})=1/\mathfrak {e}_{1}\). We denote these singular points of system (33) by \(\tilde{Q_{1}}=(\pi ,\tilde{Y_{1}^{*}})\), \(Q_{1}=(\pi ,Y_{1}^{*})\), and let us first examine the point \(Q_{1}\). By virtue of the properties of \(f(Y_{1})\), the \(\infty \)-isocline is given in the interval \(X\in \left[ 0,\frac{\pi }{2}\right) \) by the curve \((X,\alpha _{1}(X))\), where \(\alpha _{1}(X):\left[ 0,\frac{\pi }{2}\right) \rightarrow \left[ {Y_{1}}^{*},+ \infty \right) \) is the inverse of the function \(f(Y_{1})\) restricted to the interval \(\left[ {Y_{1}}^{*},+\infty \right) \). We note that \(\alpha _{1}(0)={Y_{1}}^{*},\lim _{X\rightarrow \frac{\pi }{2}^{+}} \alpha _{1}(X)=+\infty \) and, in the interval \(\left[ 0,\frac{\pi }{2}\right) \), \(\alpha _{1}\) is an increasing function. Given the Hamiltonian (34) for system (33), the Hessian at \(Q_{1}\) is

$$\begin{aligned} \left( \begin{array}{cc} M_{1}\cosh (Y_{1}^{*})-M_{1}A\sinh (Y_{1}^{*}) &{} 0 \\ 0 &{} -(M_{1}\cosh (Y_{1}^{*})-M_{1}A\sinh (Y_{1}^{*})) \end{array} \right) , \end{aligned}$$

and arguments similar to those above involving Morse theory imply that \(Q_{1}\) is a saddle point which lies at the intersection of four separatrices: two that reach \(Q_{1}\) in infinite time in the future and two that need infinite time backwards to reach the saddle point. Analogous reasoning shows that the singular point \(\tilde{Q_{1}}\) is also a saddle point, and the \(\infty \)-isocline emanating from \(\tilde{Q_{1}}\) is qualitatively similar to that described for \(Q_{1}\), except ‘flipped’ vertically. Having characterised the 0- and \(\infty \)-isoclines, we can easily determine the signs of the two components \(F(X,Y_{1})\) and \(G(X,Y_{1})\) of the vector field given by system (33), and employing symmetry properties of (33), we infer the phase portrait behaviour in the region \(-\pi \le X\le 0\). The complete phase portrait of system (33) is given in Fig. 6.

Fig. 6
figure 6

Phase portrait for the upper-fluid layer when \(A=A_2\). The dotted grey lines represent the \(\infty \)-isoclines, with the dotted-dashed lines representing the 0-isoclines. The surface wave profile (thin blue dashed lines) has mean water level \(Y_1=0\), corresponding to \(y=h_1\). The internal wave profile (thick blue dashed lines) has mean water level \(Y=kh_1> \bar{Y_1}\), corresponding to \(y=0\). Recall that the streamline representing the surface wave lies beneath those of the internal waves in this phase portrait (colour figure online)

Full size image

The surface wave profile has a mean water level \(Y_{1}=0\), which corresponds to \(y=h_{1}\), while the internal wave profile has a mean water level \(Y=kh_{1}\), which corresponds to \(y=0\). From the phase portrait in Fig. 6, we see that there are qualitatively different fluid motions possible in the upper-fluid layer. Streamlines located beneath \(Y_1= \bar{Y_{1}}\) in Fig. 6 are in-phase with the surface wave; the horizontal line \(Y_1=\bar{Y_{1}}\) is itself a (flat) streamline; streamlines located above \(\bar{Y_{1}}\) in Fig. 6 are out-of-phase with the surface wave: the internal wave with mean water level \(Y=kh_1\) lies in this region. Note that the magnitude of the internal wave amplitude is significantly greater than that of the surface wave, as prescribed by (25). In order for system (33) to describe physically relevant solutions, the singular points \(\tilde{Q_{1}}\) and \(Q_{1}\) must lie outside the upper-fluid layer; hence, we must have \(\tilde{Y_{1}^{*}}<-\mathfrak {e}_{1}\) and \(kh_{1} +\mathfrak {e}<Y_{1}^{*}\) or, equivalently (cf. Fig. 5), \(\max \left\{ f(-\mathfrak {e}_{1}), f(kh_{1} +\mathfrak {e}) \right\} <1/ \mathfrak {e}_{1}\). Since \(\mathfrak {e},\mathfrak {e}_{1}\ll 1\) in the linear regime, and \(f(-\mathfrak {e}_{1})\approx A+\mathfrak {e}_{1}\), for this condition to break-down requires A to be sufficiently large that \(\mathfrak {e}_{1}f(-\mathfrak {e}_{1})\approx \mathfrak {e}^{2}_{1}+ A \mathfrak {e}_{1}\approx A \mathfrak {e}_{1}>1\). Otherwise, the singular points lie outside the upper-fluid layer.

4 Particle trajectories

Phase portraits have been constructed for the nonlinear dynamical systems (31) and (33), which describe fluid motion in the lower- and upper-fluid layers, respectively. This analysis is performed in terms of the \((X,Y)-\) and \((X,Y_{1})\)-variables, in (moving) reference frames for which the flow is steady. For steady fluid motion, the dynamical systems (31) and (33) are autonomous and, hence, particle trajectories coincide with the streamlines. Accordingly, a complete qualitative picture of fluid motion may be ascertained in terms of the transformed coordinates. From the phase portraits in Figs. 3, 4, 6, it is also possible to ascertain which streamlines correspond to physically admissible fluid trajectories in each fluid layer. This global picture of the qualitative behaviour of the dynamical systems (31) and (33) provides an Eulerian description of the fluid motion.

In this section, we pursue a Lagrangian description of fluid motion by ascertaining qualitative features of the motion of specific fluid particles described in terms of the physical variables \(\left( x(t),y(t)\right) \). We prove that there does not exist any closed particle trajectory in either the lower, or upper, fluid layers, and prove that all particles experience a forward drift. Regarding particle drift, it bears remarking that the Stokes’ drift phenomenon (whereby fluid particles experience a mean net drift velocity in the direction of wave motion) is intrinsically nonlinear (cf. [24, 38]): the existence of a forward drift induced by linear internal waves for all fluid particles, first established in [25], is apparently new. Finally, we establish monotonicity properties for this forward drift.

4.1 Lower-fluid layer

The significant difference between systems (27) and (31) arises due to the latter being autonomous, while the former is nonautonomous and hence considerably more difficult to analyse. Nevertheless, it is possible to use qualitative properties of the fluid motion induced by (31), established in the phase portrait analysis of Sect. 3.1, to construct a qualitative description of fluid motion in terms of physical variables as prescribed by (27). System (27) is qualitatively similar to one which describes the motion of a surface wave propagating on a single homogeneous fluid layer of finite depth, cf. [6]. Physical variables are obtained by reversing the coordinate transformations (29) by defining

$$\begin{aligned} x(t)=\frac{X(t)}{k}+ct, \quad y(t)=\frac{Y(t)}{k}-h, \end{aligned}$$
(37)

in the lower-fluid layer. Suppose (X(t), Y(t)) describes a streamline in the lower-fluid layer (in the moving reference frame) such that \((X(0),Y(0))=(\pi ,Y^{0})\): in the lower-fluid layer focus is restricted to streamlines for which \(Y^{0}\in \left( -\infty ,k(h-a)\right] \). Let \(t_{Y^{0}}(-\pi )\) denote the time it takes for the particle to intersect the line \(X=-\pi \). The next lemma is stated for motion in the lower-fluid layer, but applies similarly to fluid motion in the upper layer.

Lemma 4.1

If the particle trajectory prescribed by (x(t), y(t)) is a closed path with period \(\tau \), then, necessarily, we have \(\tau =\frac{2\pi }{\omega }\). Conversely, suppose \(t_{Y^{0}}(-\pi )=\frac{2\pi }{\omega }\), then the particle path prescribed by (x(t), y(t)) is closed.

Proof

The proof follows from the periodicity of system (31) with respect to X, together with the definition (37). \(\square \)

The main result concerning motion in the lower-fluid layer is stated in the following.

Theorem 4.2

System (27) has no solutions (x(t), y(t)) which are periodic. Accordingly, there are no closed particle paths in the lower-fluid layer; instead, all fluid particles experience a positive horizontal drift.

Proof

The proof follows, bearing in mind Lemma 4.1, by proving that \(t_{Y^{0}}(-\pi )>\frac{2\pi }{\omega }\) for all \(Y^{0}\in \left( -\infty ,kh- \mathfrak {e}\right] \). For such \(Y^{0}\), along the streamlines we have \(\mathrm{d}Y/\mathrm{d}t>0\) for \(X\in (0,\pi )\), and \(\mathrm{d}Y/\mathrm{d}t<0\) when \(X\in (-\pi ,0)\). If this streamline intersects the line \(X=\frac{\pi }{2}\) at the value \(Y=\mathcal {Y}\), then (X(t), Y(t)) lies below the line \(Y=\mathcal {Y}\) for \(X(t)\in [-\pi , -\frac{\pi }{2})\cup (\frac{\pi }{2},\pi ]\) and lies above the line for \(X(t)\in (-\frac{\pi }{2},\frac{\pi }{2})\). Thus,

$$\begin{aligned} \dot{X}=Me^Y\cos (X)-\omega \ge Me^{\mathcal {Y}}\cos (X)- \omega , \quad t\ge 0. \end{aligned}$$
(38)

Introducing the differential equation

$$\begin{aligned} \dot{\mathfrak {X}}=Me^{\mathcal {Y}}\cos (\mathfrak {X})-\omega , \end{aligned}$$

with \(\mathfrak {X} (0)=\pi \), it follows immediately from (38) and the fact that \(X(0)=\mathfrak {X}(0)=\pi \) that \(X(t)\ge \mathfrak {X}(t)\) for \(t\ge 0\). Therefore, \(t_{Y^{0}}(-\pi )> t^{*}\), where \(t_{Y^{0}}^{*}\) is the time it takes for \(\mathfrak {X} (t^{*})=-\pi \), namely

$$\begin{aligned} t_{Y^{0}}^{*}= \int ^{\pi }_{-\pi }\frac{\mathrm{d}s}{\omega -Me^{\mathcal {Y}}\cos s}. \end{aligned}$$

For \(\mathfrak {M}<\omega \), the integral

$$\begin{aligned} \int ^{z}_{0}\frac{\mathrm{d}s}{\omega -\mathfrak {M}\cos s}={2}\sqrt{ \frac{1}{\omega ^{2}-\mathfrak {M}^{2}}}\arctan \left[ \sqrt{ \frac{\omega +\mathfrak {M}}{\omega -\mathfrak {M}}}\tan \left( \frac{z}{2}\right) \right] , \quad z>0, \end{aligned}$$

gives

$$\begin{aligned} \int ^{\pi }_{-\pi }\frac{\mathrm{d}s}{\omega -\mathfrak {M}\cos s}={2\pi } \sqrt{\frac{1}{\omega ^{2}-\mathfrak {M}^{2}}}>\frac{2\pi }{\omega }. \end{aligned}$$
(39)

Hence, \(t_{Y^{0}}^{*}>2\pi /\omega \) follows from (39) with \(\mathfrak M=Me^{\mathcal Y}\), with \(t_{Y^{0}}(-\pi )>\frac{2\pi }{\omega }\). \(\square \)

Proposition 1

The horizontal drift experienced by a fluid particle in the lower fluid layer over one wave period decreases strictly with depth, and furthermore, the drift goes to zero at great depths.

Proof

The horizontal drift experienced by a fluid particle over one wave period is given by \(D(Y^{0})=x(t_{Y^{0}}(-\pi ))-x(\pi )=(\omega t_{Y^{0}}(-\pi )-2\pi )/k>0\), which can be expressed from (31a) as

$$\begin{aligned} D(Y^{0})=2\int _{0}^{\pi } \frac{Me^Y \cos X \mathrm{d}X}{\omega -Me^Y \cos X}. \end{aligned}$$
(40)

If \(Y^{1}<Y^{0}\), with \(\tilde{Y}=\tilde{Y}(X)\) denoting the streamline with \(\tilde{Y}(\pi )=Y^{1}\), then

$$\begin{aligned} D(Y^{0})-D(Y^{1})=2\int _{0}^{\pi } \frac{\omega M\left( e^Y-e^{\tilde{Y}}\right) \cos X}{\left( \omega -Me^Y\cos X\right) \left( \omega -Me^{\tilde{Y}}\cos X\right) }\mathrm{d}X, \end{aligned}$$

which, in the limit \(Y^{1}\rightarrow Y^{0}\), has the same sign as

$$\begin{aligned} &\lim _{\tilde{Y}\rightarrow Y} 2\int _{0}^{\pi } \frac{\omega M\left( e^Y-e^{\tilde{Y}}\right) \cos X}{\left( \omega -Me^Y\cos X\right) \left( \omega -Me^{\tilde{Y}}\cos X\right) (Y-\tilde{Y})}\mathrm{d}X\\& \quad =2\int _{0}^{\pi } \frac{\omega Me^Y\cos X}{\left( \omega -Me^Y\cos X\right) ^{2}}\mathrm{d}X>2\int _{0}^{\pi }\frac{\omega Me^Y\cos X}{\omega ^{2}}\mathrm{d}X\\& \quad >2\int _{0}^{\pi }\frac{M}{\omega }e^{\mathcal {Y}}\cos X\mathrm{d}X=0. \end{aligned}$$

Thus, \(D(Y^{0})>D(Y^{1})\), and the particle drift is decreasing with depth. It is clear from (40) that particle drift goes to zero at great depths (as \(Y^0\rightarrow -\infty \)). \(\square \)

Combining these results with the phase-plane analysis of system (31) undertaken in Sect. 3.1, facilitates a qualitative description of physical particle motion in the lower-fluid layer as prescribed by (27). Assume a given fluid particle is initially at its lowest depth \(y(0)=y_{0}\): we label this position A. This corresponds to \(X(0)=\pi \), and since \(\dot{X}<0\) along streamlines it follows that, in the moving frame, the variable X(t) decreases continuously from \(\pi \) to \(-\pi \), and we have: \(\dot{x} <0\), \(\dot{y} >0\) for \(X(t)\in (\pi /2,\pi )\); \(\dot{x}>0\), \(\dot{y} >0\) for \(X(t)\in (0,\pi /2)\); \(\dot{x} >0\), \(\dot{y}<0\) for \(X(t)\in (-\pi /2,0)\); \(\dot{x} <0\), \(\dot{y}<0\) for \(X(t)\in (-\pi ,-\pi /2)\). The particle returns to its lowest position in the fluid layer (with depth \(y=y_{0}\)) at time \(t=t_{Y^{0}}(-\pi )>{2\pi }/{\omega }\), having experienced a positive horizontal drift: we label this position B. A representation of this qualitative particle motion is illustrated in Fig. 7.

Fig. 7
figure 7

Schematic of a typical particle trajectory in the lower-fluid layer, representing its location at time: \(t=0\) (A); \(t=t_{Y_0}(-\pi )\) (B); \(t=2t_{Y_0}(-\pi )\) (C); \(t=3t_{Y_0}(-\pi )\) (D)

Full size image

Remark

The primary qualitative difference between fluid particle motion in a lower-fluid layer which has infinite depth, rather than finite depth over a flat impermeable bottom, is that particle trajectories are (almost) circular in the present setting, as opposed to being (almost) elliptical in the finite depth case, when fluid motion is small. To see this, observe that making the approximation \((x,y)\approx (x_0,y_0)\) on the right-hand side of (27) enables system (27) to be integrated, leading to the solution

$$\begin{aligned}&\left( x(t)-x_0,y(t)-y_0\right) \\&\quad \approx ae^{ky_0}\left( -\sin (kx_0-\omega t)+\sin kx_0, \cos (kx_0-\omega t)- \cos kx_0\right) , \end{aligned}$$

which implies that

$$\begin{aligned} \left( x(t)-x^*_0\right) ^2+\left( y(t)-y^*_0\right) ^2= a^2e^{2ky_0}. \end{aligned}$$
(41)

Hence, assuming fluid motion is small, the fluid particles follow approximately circular trajectories, with centres located at \(x_0^*=x_0+ae^{ky_0}\sin kx_0\) and \(y_0^*=y_0-ae^{ky_0}\cos kx_0\), and radii \(ae^{ky_0}\) that decrease with increasing depth.

4.2 Upper-fluid layer

Physical variables in the upper-fluid layer are obtained by reversing the coordinate transformations (30) by defining

$$\begin{aligned} x(t)=\frac{X(t)}{k}+ct, \quad y(t)=h_{1}-\frac{Y_{1}(t)}{k}. \end{aligned}$$
(42)

Note the reflection involved in the vertical coordinate transformation in (42) reverses the vertical orientation of fluid motion when expressed in terms of the physical coordinate y, as opposed to the \(Y_{1}\) coordinate. If \((X(t),Y_{1}(t))\) is a solution to (33) in the upper-fluid layer with \((X(0),Y_{1}(0))=(\pi ,Y_{1}^{0})\), then \(Y_{1}^{0}\in [\mathfrak {e}_{1},kh_{1}+\mathfrak {e}]\) if \(A=A_1=1\) (for which \(a/a_{1}>0\)), whereas \(Y_{1}^{0}\in [\mathfrak {e}_{1},kh_{1}-\mathfrak {e}]\) for \(A=A_2\) (for which \(a/a_{1}<0\)). The analysis of particle motion in the upper-fluid layer follows along the lines of [25], although with more specificity due to the nature of the solutions \(A=A_1=1\) and \(A=A_2\) given by (21). For the sake of completeness, we present the main results and pertinent qualitative features, referring the reader to [25] for full details.

4.2.1 Upper-fluid layer with \(A=A_2\ (> 1)\)

Theorem 4.3

Let \(A=A_2\). There are no closed particle paths in the upper-fluid layer whose motion is governed by system (28). That is, system (28) has no solutions (x(t), y(t)), which are periodic.

Proof

With reference to Fig. 6, streamlines of the upper-fluid layer are restricted to the phase portrait region for which \(Y^{0}_{1}\in [\mathfrak {e}_{1},kh_{1}+\mathfrak {e}]\). Although there is a change in the qualitative behaviour of streamlines depending on whether \(Y^{0}_{1}<\bar{Y_{1}}\) or \(Y^{0}_{1}>\bar{Y_{1}}\), where \(\bar{Y_{1}}\) is prescribed by (36), it can be shown (cf.[25]) that in either case the inequality holds:

$$\begin{aligned} \dot{X}=M_{1}f(Y_{1})\cos X-\omega \ge M_{1}f(\mathcal {Y}_{1})\cos X- \omega , \quad t\ge 0. \end{aligned}$$
(43)

Noting similarities between inequalities (38) and (43), the arguments used in the proof of Theorem 4.2 apply here to the differential equation \( \dot{\mathfrak {X}}=M_{1} f(\mathcal {Y}_{1})\cos (\mathfrak {X})-\omega \), and it can be deduced that \(t_{Y^{0}_{1}}(-\pi )> t^{*}\), with

$$\begin{aligned} t^{*}={2\pi }\sqrt{ \frac{1}{\omega ^{2}-M_{1}^{2}f^{2}(\mathcal {Y}_{1})}}> \frac{2\pi }{\omega }. \end{aligned}$$

For the case \(Y_{1}= \bar{Y_{1}}\), in which the streamline is the flat 0-isocline, we note that \( f(Y_{1})\equiv f(\mathcal {Y}_{1})\equiv f(\bar{Y_{1}})\) and relation (43) becomes an equality, giving

$$\begin{aligned} t_{\bar{Y_{1}}}(-\pi )=t^{*}={2\pi }\sqrt{ \frac{1}{\omega ^{2}-M_{1}^{2}f^{2}\left( \bar{Y_{1}}\right) }}> \frac{2\pi }{\omega }. \end{aligned}$$

\(\square \)

Combining these results with the phase-plane analysis for system (33) presented in Sect. 3.2 facilitates a qualitative description of physical particle motion in the upper-fluid layer for \(A=A_2\). Note that, along streamlines in the moving frame, \(\dot{X}(t)<0\) for solutions of system (33): X(t) decreases continuously from \(X=\pi \) to reach \(X=-\pi \) in time \(t_{Y_{1}^{0}}(-\pi )\). For streamlines with \(Y^{0}_{1}\in [\mathfrak {e}_{1},\bar{Y_{1}})\) in this region (which corresponds physically to the top section of the upper-fluid layer) we have: \(\dot{x} <0\), \( \dot{y} >0\) for \(X(t)\in (\pi /2,\pi )\); \(\dot{x}>0\), \(\dot{y} >0\) for \(X(t)\in (0,\pi /2)\); \(\dot{x} >0\), \(\dot{y}<0\) for \(X(t)\in (-\pi /2,0)\); \(\dot{x} <0\), \(\dot{y}<0\) for \(X(t)\in (-\pi ,-\pi /2)\). Fluid particles in this region return to their lowest position in the fluid layer, with depth \(y=y_{0}\), say, after the time \(t_{Y_{1}^{0}}(-\pi )\), having experienced a forward horizontal drift \(x(t_{Y_{1}^{0}}(-\pi ))-x(0)=\left( {t_{Y_{1}^{0}}(-\pi )\omega -2 \pi }\right) /{k}>0\). This particle motion is captured in schematic (a) of Fig. 8.

At the 0-isocline \(Y=\bar{Y_{1}}\), the motion is given by \(\dot{x} <0\) for \(X(t)\in (\pi /2,\pi )\); \(\dot{x}>0\) for \(X(t)\in (0,\pi /2)\); \(\dot{x} >0\) for \(X(t)\in (-\pi /2,0)\); \(\dot{x} <0\) for \(X(t)\in (-\pi ,-\pi /2)\). Fluid particles located on the 0-isocline experience a forward horizontal drift \(x(t_{\bar{Y_{1}}}(-\pi ))-x(0)=\left( {t_{\bar{Y_{1}}}(-\pi )\omega -2 \pi }\right) /{k}>0\). This motion is represented by schematic (b) of Fig. 8.

For streamlines with \(Y_{1}^{0}\in (\bar{Y_{1}}, kh_{1}+\mathfrak {e}]\) (which corresponds physically to the bottom region of the upper-fluid layer), we get: \(\dot{x} <0\), \( \dot{y}<0\) for \(X(t)\in (\pi /2,\pi )\); \(\dot{x}>0\), \(\dot{y} <0\) for \(X(t)\in (0,\pi /2)\); \(\dot{x} >0\), \(\dot{y}>0\) for \(X(t)\in (-\pi /2,0)\); \(\dot{x} <0\), \(\dot{y}>0\) for \(X(t)\in (-\pi ,-\pi /2)\). Fluid particles in this region return to their highest position in the fluid layer, with depth \(y=y_{0}\), say, after the time \(t_{Y_{1}^{0}}(-\pi )\), having experienced a forward horizontal drift \(x(t_{Y_{1}^{0}}(-\pi ))-x(0)=\left( t_{Y_{1}^{0}}(-\pi )\omega -2 \pi \right) /{k}>0\). This particle motion is depicted in schematic (c) of Fig. 8.

Fig. 8
figure 8

Schematics of typical trajectories for particles a–c in the upper-fluid layer, for \(A=A_2\ (>1)\). Their locations at times \(t=0,t_{Y_1^0}(-\pi ),2t_{Y_1^0}(-\pi ),3t_{Y_1^0}(-\pi )\) are denoted by A, B, C, D, respectively

Full size image

In the upper-fluid layer, the horizontal drift experienced by a fluid particle over one wave period is given by \(D(Y_{1}^{0})=x(t_{Y_{1}^{0}}(-\pi ))-x(\pi )=(\omega t_{Y_{1}^{0}}(- \pi )-2\pi )/k>0\), which can be expressed from (33) as

$$\begin{aligned} D(Y_{1}^{0})=2\int _{0}^{\pi } \frac{M_{1}f(Y_{1})\cos X \mathrm{d}X}{\omega -M_{1}f(Y_{1})\cos X}. \end{aligned}$$

If \(Y_{1}^{1}<Y_{1}^{0}\), where \(\tilde{Y}_{1}=\tilde{Y}_{1}(X)\) denotes the streamline with \(\tilde{Y}_{1}(\pi )=Y_{1}^{1}\), then

$$\begin{aligned} D(Y_{1}^{0})-D(Y_{1}^{1})=2\int _{0}^{\pi } \frac{\omega M_{1}\left( f(Y_{1})-f(\tilde{Y})\right) \cos X}{\left( \omega -M_{1}f(Y_{1})\cos X\right) \left( \omega -M_{1}f(\tilde{Y})\cos X\right) }\mathrm{d}X. \end{aligned}$$

In the limit \(Y_{1}^{1}\rightarrow Y_{1}^{0}\), the drift \(D(Y_{1}^{0})-D(Y_{1}^{1})\) has the same sign as

$$\begin{aligned} & \lim _{\tilde{Y}_{1}\rightarrow Y_{1}}2\int _{0}^{\pi } \frac{\omega M_{1}\left( f(Y_{1})-f(\tilde{Y}_{1})\right) \cos X}{\left( \omega -M_{1}f(Y_{1})\cos X\right) \left( \omega -M_{1} f(\tilde{Y}_{1})\cos X\right) (Y_{1}-\tilde{Y}_{1})}\mathrm{d}X\nonumber \\& \quad =2\int _{0}^{\pi } \frac{\omega M_{1}f'(Y_{1})\cos X}{\left( \omega -M_{1}f(Y_{1})\cos X\right) ^{2}}\mathrm{d}X =2\int _{0}^{\pi } \frac{\omega M_{1}g(Y_{1})\cos X}{\left( \omega -M_{1}f(Y_{1})\cos X\right) ^{2}}\mathrm{d}X. \end{aligned}$$
(44)

The following result applies for particle drift in the upper-fluid layer (cf. [25]).

Proposition 2

Suppose \(A=A_2 \ (>1)\). The horizontal drift experienced by a fluid particle in the upper-fluid layer over one wave period decreases with depth for fluid motion of the type illustrated in schematic (a) of Fig. 8, while it increases with depth for fluid motion of the type illustrated in schematic (c) of Fig. 8. Accordingly, the minimum horizontal drift experienced by fluid particles occurs at \(Y=\bar{Y_{1}}\), as illustrated in schematic (b) of Fig. 8.

Remark

Fluid particle trajectories in the upper-fluid layer are (approximately) elliptical when fluid motion is small since making the approximation \((x,y)\approx (x_0,y_0)\) on the right-hand side of (28) enables this system to be integrated. This leads to the solution

$$\begin{aligned}&\left( x(t)-x_0,y(t)-y_0\right) \\&\quad \approx a_{1}\left( -\mathcal F(y_0)\sin (kx_0-\omega t)+\mathcal F(y_0)\sin kx_0, \mathcal G(y_0)\cos (kx_0-\omega t)-\mathcal G(y_0)\cos kx_0 \right) , \end{aligned}$$

for

$$\begin{aligned} \left\{ \begin{array}{l} \mathcal F(y_0)=\sinh k(y_0-h_{1})+A\cosh k(y_0-h_{1}),\\ \mathcal G(y_0)=\cosh k(y_0-h_{1})+A\sinh k(y_0-h_{1}). \end{array}\right. \end{aligned}$$
(45)

Hence, for small fluid motion in the upper-fluid layer, particle trajectories approximately follow the elliptical orbits prescribed by

$$\begin{aligned} \frac{\left( x(t)-x^*_0\right) ^2}{a_1^2\mathcal F^2(y_0)}+\frac{\left( y(t)-y^*_0\right) ^2}{a_1^2\mathcal G^2(y_0)}= 1, \end{aligned}$$
(46)

where \(x_0^*=x_0+a_1\mathcal F(y_0)\sin kx_0\) and \(y_0^*=y_0-a_1\mathcal G(y_0)\cos kx_0\). The depth-dependent parameters \(\mathcal F(y_0)\) and \(\mathcal G(y_0)\) determine the size of the major and minor axes, respectively. Note that \(\mathcal F(y_0)\) does not vanish in the upper-fluid layer for \(A=A_2\), while \(\mathcal G(y_0)\) vanishes for \(\bar{y}_0=h_1-\bar{Y}_1/k\): this value corresponds to particle trajectories prescribed by the flat line in schematic (b) of Fig. 8. The change in the sign of \(\mathcal G(y_0)\) that occurs at \(\bar{y}_0\) corresponds to the change in the orientation of particles trajectories, which move clockwise in schematic (a) and anticlockwise in schematic (c) of Fig. 8.

4.2.2 Upper-fluid layer with \(A=A_1\ (=1)\)

Due to the straightforward form that the functions \(f(Y_{1}),g(Y_{1})\) assume in the setting \(A=A_1=1\), a comprehensive qualitative description of fluid motion can be achieved.

Theorem 4.4

Let \(A=1\). There are no closed particle paths in the upper-fluid layer whose motion is governed by system (28).

Proof

For \(A=1\), we have \(f(Y_{1})=e^{-Y_{1}}=-g(Y_{1})\), and it can easily be shown that the analogue of inequality (43) holds for streamlines in the region \(Y_{1}^{0}\in [\mathfrak {e}_{1}, kh_{1}+\mathfrak {e}]\). Consequently,

$$\begin{aligned} t_{Y_{1}^{0}}(-\pi )>{2\pi }\sqrt{ \frac{1}{\omega ^{2}-M_{1}^{2}f^{2}(\mathcal {Y}_{1})}}> \frac{2\pi }{\omega }. \end{aligned}$$

\(\square \)

It follows immediately that: \(\dot{x} <0\), \( \dot{y} >0\) for \(X(t)\in (\pi /2,\pi )\); \(\dot{x}>0\), \(\dot{y} >0\) for \(X(t)\in (0,\pi /2)\); \(\dot{x} >0\), \(\dot{y}<0\) for \(X(t)\in (-\pi /2,0)\); \(\dot{x} <0\), \(\dot{y}<0\) for \(X(t)\in (-\pi ,-\pi /2)\). Furthermore, the following can be proven.

Proposition 3

([25]) If \(A=A_1\), the horizontal drift experienced by fluid particles in the upper-fluid layer over one wave period decreases with depth.

Fluid particle motion matches that illustrated in schematic (a) of Fig. 8, with all fluid particles experiencing a forward drift, except now fluid trajectories are approximately circular for \(A=1\) (rather than elliptical) since \(\mathcal F(y_0)=\mathcal G(y_0)=2e^{k(y_0-h_{1})}\) in (45). Hence, for \(A=1\) equation (46) prescribes approximately circular particle trajectories for small fluid motion in the upper-fluid layer.

5 Conclusions

In this article, the fluid motion underlying coupled linear internal and surface waves is studied, from both the Eulerian and Lagrangian viewpoints, for a deep-water two-fluid-layer model (with the lower layer being of infinite depth). Although the linearised governing equations are studied, the resulting dynamical systems which prescribe the fluid motion are themselves nonlinear. In contrast to the setting of two fluid layers of finite depth (recently studied in [25]), when the lower layer is of infinite extent the dispersion relations simplify, and the nondimensional wave amplitude ratio parameter A for the upper-fluid layer system (28) is restricted to either of the values \(A_1=1\) and \(A_2>1\).

A detailed Eulerian description of the wave-field kinematics for coupled linear travelling waves is achieved using phase-plane analysis, a by-product of which is an elegant graphical verification that coupled surface and internal waves are in-phase for the parameter value \(A=A_1=1\), while they are out-of-phase when \(A=A_2>1\). Furthermore, a complete qualitative Lagrangian description of the fluid particle trajectories in both fluid layers is obtained. In the deep-water regime, the wave-field kinematics in the lower-fluid layer are necessarily quite different to that of the finite depth case featured in [25]. Particle trajectories in the lower-fluid layer all exhibit a forward drift which decreases with increasing depth, and they are approximately circular. In the case of a lower-fluid layer of finite depth (as analysed in [25]), the particle motion is approximately elliptical (with similar forward drift properties).

A significant benefit of the deep-water setting under consideration here is that we can particularise results from [25] concerning the dynamics of the upper-fluid layer, giving a complete qualitative picture of fluid particle motion in the upper-fluid layer. All particles exhibit a forward drift: for \(A=A_1=1\) the particle motion is approximately circular, moving clockwise with a drift which decreases with increasing depth. For the parameter value \(A=A_2>1\), the particle motions are approximately elliptical, with upper particles moving clockwise and lower particles moving anticlockwise. A reverse in the orientation of particle trajectory motion occurs at the flat streamline located at \(Y_1=\bar{Y}_1\), which is also the location of minimum forward particle drift: particle drift decreases with depth for fluid particles located between the surface and this streamline, while it increases for fluid particles located between this streamline and the internal wave.