Abstract
We study the computational complexity of (deterministic or randomized) algorithms based on point samples for approximating or integrating functions that can be well approximated by neural networks. Such algorithms (most prominently stochastic gradient descent and its variants) are used extensively in the field of deep learning. One of the most important problems in this field concerns the question of whether it is possible to realize theoretically provable neural network approximation rates by such algorithms. We answer this question in the negative by proving hardness results for the problems of approximation and integration on a novel class of neural network approximation spaces. In particular, our results confirm a conjectured and empirically observed theory-to-practice gap in deep learning. We complement our hardness results by showing that error bounds of a comparable order of convergence are (at least theoretically) achievable.
Similar content being viewed by others
1 Introduction
The use of data-driven classification and regression algorithms based on deep neural networks—coined deep learning—has made a big impact in the areas of artificial intelligence, machine learning, and data analysis and has led to a number of breakthroughs in diverse areas of artificial intelligence, including image classification [24, 29, 32, 47], natural language processing [53], game playing [34, 45, 46, 51], and symbolic mathematics [31, 42].
More recently, these methods have been applied to problems from the natural sciences where data driven approaches are combined with physical models. Example applications in this field—called scientific machine learning—include the development of drugs [33], molecular dynamics [18], high-energy physics [5], protein folding [43], or numerically solving inverse problems and partial differential equations (PDEs) [4, 17, 26, 37, 40].
For this wide variety of different application areas, one can summarize the underlying computational problem as approximating an unknown function f (or a quantity of interest depending on f) based on possibly noisy and random samples \((f(x_i))_{i=1}^m\). In deep learning this is being done by fitting a neural network to these samples using stochastic optimization algorithms. While there is still no convincingly comprehensive explanation for the empirically observed success (or failure) of this methodology, its success critically hinges on the properties
-
A.
that f can be well approximated by neural networks, and
-
B.
that f (or a quantity of interest depending on f) can be efficiently and accurately reconstructed from a relatively small number of samples \((f(x_i))_{i=1}^m\).
In other words, the validity of both A and B constitutes a necessary condition for a deep learning approach to be efficient. This is especially true in applications related to scientific machine learning where often a guaranteed high accuracy is required and where obtaining samples is computationally expensive.
To date most theoretical contributions focused on Property A, namely studying which functions can be well approximated by neural networks. It is now well understood that neural networks are superior approximators compared to virtually all classical approximation methods, including polynomials, finite elements, wavelets, or low rank representations; see [15, 22] for two recent surveys. Beyond that it was recently shown that neural networks can approximate solutions of high dimensional PDEs without suffering from the curse of dimensionality [21, 27, 30]. In light of these results it becomes clear that neural networks are a highly expressive and versatile function class whose theoretical approximation capabilities vastly outperform classical numerical function representations.
On the other hand, the question of whether property B holds, namely to which extent these superior approximation properties can be harnessed by an efficient algorithm based on point samples, remains one of the most relevant open questions in the field of deep learning. At present, almost no theoretical results exist in this direction. On the empirical side, Adcock and Dexter [1] recently performed a careful study finding that the theoretical approximation rates are in general not attained by common algorithms, meaning that the convergence rate of these algorithms does not match the theoretically postulated approximation rates. In [1] this empirically observed phenomenon is coined the theory-to-practice gap of deep learning. In this paper we prove the existence of this gap.
1.1 Description of Results
To provide an appropriate mathematical framework for understanding Properties A and B we introduce neural network spaces which classify functions \(f:[0,1]^d \rightarrow \mathbb {R}\) according to how rapidly the error of approximation by neural networks with n weights decays as \(n\rightarrow \infty \). Specifically we consider neural networks using the rectified linear unit (ReLU) activation function, i.e., functions of the form
where
are affine mappings and \(\varrho \bigl ( (x_1,\dots ,x_n)\bigr ) = \bigl (\max \{x_1,0\},\dots ,\max \{x_n,0\}\bigr )\). Referring to L as the depth of the neural network (1.1) and to total number of nonzero coefficients of the matrix-vector pairs \((A_\ell ,b_\ell )_{\ell =1}^L\) in (1.2) as number of weights of the neural network, we can formalize the property of being well approximable by neural networks as follows.
For \(\alpha > 0\) let
In words, the sets \(U^\alpha \) consist of all functions that are approximable by neural networks with depth L and at most n uniformly bounded coefficients to within uniform accuracy \(\lesssim n^{-\alpha }\). For the remainder of the introduction we will say that f can be approximated at rate \(\alpha \) by depth L neural networks if \(f\in U^\alpha \).
We emphasize that all our results apply to much more general approximation spaces than the sets \(U^\alpha \) (which is in fact the unit ball of some approximation space), incorporating more complex constraints on the approximating neural network while considering approximation with respect to arbitrary \(L^p\) norms; see Sect. 2.2 for more details. In any case, for the current discussion it is sufficient to note that membership of f in such a space for large \(\alpha \) simply means that Property A is satisfied.
For the mathematical formalization of Property B we employ the formalism of Information Based Complexity (more precisely we will study sampling numbers of neural network approximation spaces), as for example presented in [25]. This theory provides a general framework for studying the complexity of approximating a given solution mapping \(S : U \rightarrow Y\), with \(U \subset C([0,1]^d)\) bounded, and Y a Banach space, under the constraint that the approximating algorithm is only allowed to access point samples of the functions \(f \in U\). Formally, a (deterministic) algorithm using m point samples is determined by a set of sample points \(\varvec{x}= (x_1,\dots ,x_m) \in ([0,1]^d)^m\) and a map \(Q : \mathbb {R}^m \rightarrow Y\) such that
The set of all such algorithms is denoted \({\text {Alg}}_m (U,Y)\) and we define the optimal order for (deterministically) approximating \(S : U \rightarrow Y\) using point samples as the best possible convergence rate with respect to the number of samples:
In a similar way one can define randomized algorithms and consider the optimal order \(\beta _*^{\textrm{ran}} (U, S)\) for approximating S using randomized algorithms based on point samples; see Sect. 2.4.2 below. We emphasize that all currently used deep learning algorithms, such as stochastic gradient descent (SGD) [44] and its variants (such as ADAM [28]) are of this form.
In this paper we derive bounds for the optimal orders \(\beta _*^{\textrm{det}} (U, S)\) and \(\beta _*^{\textrm{ran}} (U, S)\) for the unit ball \(U=U^\alpha \) and the following solution mappings:
-
1.
The embedding into \(C([0,1]^d)\), i.e., \(S = \iota _{\infty }\) for \(\iota _\infty : U \rightarrow C([0,1]^d), f \mapsto f\),
-
2.
The embedding into \(L^2([0,1]^d)\), i.e., \(S = \iota _2\) for \(\iota _2 : U \rightarrow L^2([0,1]^d), f \mapsto f\), and
-
3.
The definite integral, i.e., \(S = T_{\int }\) for \(T_{\int } : U \rightarrow \mathbb {R}, f \mapsto \int _{[0,1]^d} f(x) \, d x\).
1.1.1 Approximation with Respect to the Uniform Norm
We first consider the solution mapping \(S = \iota _{\infty }\) operating on \(U=U^\alpha \), i.e., the problem of approximation with respect to the uniform norm. Then the property \(\beta _*^{\textrm{ran}} (U, \iota _\infty )=\alpha \) would imply that the theoretical approximation rate \(\alpha \) with respect to the uniform norm can in principle be realized by a (randomized) algorithm such as SGD and its variants. On the other hand, if \(\beta _*^{\textrm{ran}} (U, \iota _\infty )<\alpha \), then there cannot exist any (randomized) algorithm based on point samples that realizes the theoretical approximation rate \(\alpha \) with respect to the uniform norm—that is, there exists a theory-to-practice gap. We now present (a slightly simplified version of) our first main result establishing such a gap for \(\iota _\infty \).
Theorem 1.1
(special case of Theorems 4.2 and 5.1) We have
Theorem 1.1 states that for every \(\beta < \frac{1}{d} \cdot \frac{\alpha }{\lfloor L /2\rfloor + \alpha }\) and for every \(m\in \mathbb {N}\) there exists an algorithm using m point samples such that every function \(f\in U^\alpha \) (i.e., f can be approximated at rate \(\alpha \) by depth L neural networks) can be reconstructed to within \(L^\infty \) error \(\lesssim m^{-\beta }\). Conversely, this rate is the maximally achievable rate. Note the big discrepancy between the approximation rate \(\alpha \) and the maximally achievable reconstruction rate \(\frac{1}{d} \cdot \frac{\alpha }{\lfloor L /2\rfloor + \alpha }\), especially for large input dimensions d. Probably the term “gap” is a vast understatement for the difference between the theoretical approximation rate \(\alpha \) and the rate \(\beta _*\le \min \{ \frac{1}{d},\frac{\alpha }{d}\}\) that can actually be realized by a numerical algorithm. A particular consequence of Theorem 1.1 is that if all one knows is that a function f is well approximated by neural networks— no matter how rapidly the approximation error decays—any conceivable numerical algorithm based on function samples (such as SGD and its variants) requires at least \(\Theta (\varepsilon ^{-d})\) many samples to guarantee an error \(\varepsilon >0\) with respect to the uniform norm. Since evaluating f takes a certain minimum amount of time, any conceivable numerical algorithm based on function samples (such as SGD and its variants) must have a worst-case runtime scaling at least as \(\Theta (\varepsilon ^{-d})\) to guarantee an error \(\varepsilon >0\) with respect to the uniform norm—irrespective of how well f can be theoretically approximated by neural networks. In particular:
-
Any conceivable numerical algorithm based on function samples (such as SGD and its variants) suffers from the curse of dimensionality—even if neural network approximations exist that do not.
-
On the class of all functions well approximable by neural networks it is impossible to realize these high convergence rates for uniform approximation with any conceivable numerical algorithm based on function samples (such as SGD and its variants).
-
If the number of layers is unbounded it is impossible to realize any positive convergence rate on the class of all functions well approximable by neural networks for the problem of uniform approximation with any conceivable numerical algorithm based on function samples (such as SGD and its variants).
Our findings disqualify deep learning-based methods for problems where high uniform accuracy is desired, at least if the only available information is that the function of interest is well approximated by neural networks.
1.1.2 Approximation with Respect to the \(L^2\) Norm
Next we consider the solution mapping \(S = \iota _{2}\) operating on \(U=U^\alpha \), i.e., the problem of approximation with respect to the \(L^2\) norm. Also in this case we establish a considerable theory-to-practice gap, albeit not as severe as in the case of \(S = \iota _{\infty }\). A slightly simplified version of our main result is as follows.
Theorem 1.2
(special case of Theorems 6.3 and 7.1) We have
We see again that it is impossible to realize a high convergence rate with any conceivable algorithm based on point samples, no matter how high the theoretically possible approximation rate \(\alpha \) may be. Indeed, the theorem easily implies \( \beta _*^{\textrm{ran}} \bigl ( U^\alpha , \iota _2 \bigr ), \beta _*^{\textrm{det}} \bigl ( U^\alpha , \iota _2 \bigr ) \le \frac{3}{2}, \) irrespective of \(\alpha \). This means that any conceivable (possibly randomized) numerical algorithm based on function samples (such as SGD and its variants) must have a worst-case runtime scaling at least as \(\Theta (\varepsilon ^{-2/3})\) to guarantee an \(L^2\) error \(\varepsilon >0\)—irrespective of how well the function of interest can be theoretically approximated by neural networks. On the positive side, there is a uniform lower bound of \(\frac{1}{2+\frac{2}{\alpha }}\) for the optimal rate, which means that there exist algorithms (in the sense defined above) that almost realize an error bound of \(\mathcal {O}(m^{-1/2})\), given m point samples, for \(\alpha \) sufficiently large. Note however that the existence of such an algorithm by no means implies the existence of an efficient algorithm, say, with runtime scaling linearly or even polynomially in m.
Our findings disqualify deep learning-based methods for problems where a high convergence rate of the \(L^2\) error is desired, at least if the only available information is that the function of interest is well approximated by neural networks. On the other hand, deep learning based methods may be a viable option for problems where a low—but dimension independent—convergence rate of the \(L^2\) error is sufficient.
1.1.3 Integration
Finally we consider the solution mapping \(S = T_{\int }\) operating on \(U=U^\alpha \). The question of estimating \(\beta _*^{\textrm{ran}}\bigl (U^\alpha ,T_{\int }\bigr )\) and \(\beta _*^{\textrm{det}} \bigl (U^\alpha , T_{\int }\bigr )\) can be equivalently stated as the question of determining the optimal order of (Monte Carlo or deterministic) quadrature on neural network approximation spaces. Again we exhibit a significant theory-to-practice gap that we summarize in the following simplified version of our main result.
Theorem 1.3
(special case of Theorems 9.1, 9.4, 8.1 and 8.4) We have
We see in particular that there are no (deterministic or Monte Carlo) quadrature schemes achieving a convergence order greater than 2. Further, if the number of layers is unbounded, there are no (deterministic or Monte Carlo) quadrature schemes achieving a convergence order greater than 1. On the other hand there exist Monte Carlo algorithms that almost realize a rate 1 for \(\alpha \) sufficiently large. This again does not imply the existence of an efficient algorithm with this convergence rate; but it is well-known that the error bound \(\mathcal {O}(m^{-1/2})\) can be efficiently realized by standard Monte Carlo integration, Theorem 1.3 implies that there is not much room for improvement.
1.1.4 General Comments
We close the overview of our results with the following general comments.
-
Our results for the first time shed light on the question of which problem classes can be efficiently tackled by deep learning methods and which problem classes might be better handled using classical methods such as finite elements. These findings enable informed choices regarding the use of these methods. Concretely, we find that it is not advisable to use deep learning methods for problems where a high convergence rate and/or uniform accuracy is needed. In particular, no high order (approximation or quadrature) algorithms exist, provided that the only available information is that the function of interest is well approximated by neural networks.
-
As another contribution, we exhibit the exact impact of the choice of the architecture, such as the number of layers, and magnitude of the coefficients. Particularly, we show that allowing the number of layers to be unbounded adversely affects the optimal rate \(\beta _*\).
-
Our hardness results hold universally across virtually all choices of network architectures. Concretely, all hardness results of Theorems 1.1, 1.2 and 1.3 hold true whenever at least 3 layers are used. This means that limiting the number of layers will not help. In this context we also note that it is known that at least \(\lfloor \alpha /2d \rfloor \) layers are needed for ReLU neural networks to achieve the (essentially) optimal approximation rate \(\frac{\alpha }{d}\) for all \(f\in C^{\alpha }([0,1]^d)\); see [36, Theorem C.6].
-
Our hardness results hold universally across all size constraints on the magnitudes of the approximating network weights. Furthermore, a careful analysis of our proofs reveals that our hardness results qualitatively remain true if analogous constraints are put on the \(\ell ^2\) norms of the weights of the approximating networks. Such constraints constitute a common regularization strategy, termed weight decay [23]. This means that applying standard regularization strategies—such as weight decay—will not help.
-
In many machine learning problems one assumes that one only has access to inexact (noisy) samples of a given function. Since this noise can be incorporated into the stochasticity of a randomized algorithm, our hardness results also hold for the case of noisy samples.
1.2 Related Work
To put our results in perspective we discuss related work.
1.2.1 Information-Based Complexity and Classical Function Spaces
The study of optimal rates \(\beta _*\) for approximating a given solution map based on point samples or general linear samples has a long tradition in approximation theory, function space theory, spectral theory and information based complexity. It is closely related to so-called Gelfand numbers of linear operators—a classical and well-studied concept in function space theory and spectral theory [38, 39]. It is instructive to compare our findings to these classical results, for example for U the unit ball in a Sobolev spaces \(W_\infty ^\alpha ([0,1]^d)\) and \(S=\iota _\infty \). These Sobolev spaces can be (not quite but almost, see for example [49, Theorem 5.3.2] and [16, Theorem 12.1.1]) characterized by the property that its elements can be approximated by polynomials of degree \(\le n\) to within \(L^\infty \) accuracy \(\mathcal {O}(n^{-\alpha })\). Since the set of polynomials of degree \(\le n\) in dimension d possesses \(\asymp n^d\) degrees of freedom, this approximation rate can be fully harnessed by a deterministic, resp. randomized algorithm based on point samples if \(\beta _*^{\textrm{det}} \bigl (U, S\bigr ) = \alpha /d\), resp. \(\beta _*^{\textrm{ran}} \bigl (U, S\bigr ) = \alpha /d\). It is a classical result that this is indeed the case, see [25, Theorem 6.1]. This fact implies that there is no theory-to-practice gap in polynomial approximation and can be considered the basis of any high order (approximation or quadrature) algorithm in numerical analysis.
In the case of classical function spaces it is the generic behavior that the optimal rate \(\beta _*\) increases (linearly) with the underlying smoothness \(\alpha \), at least for fixed dimension d. On the other hand, our results show that neural network approximation spaces have the peculiar property that the optimal rate \(\beta _*\) is always uniformly bounded, regardless of the underlying “smoothness” \(\alpha \).
To put our results in a somewhat more abstract context we can compare the optimal rate \(\beta _*\) to other complexity measures of a function space. A well studied example is the metric entropy related to the covering numbers \(\textrm{Cov}(V,\varepsilon )\) of sets \(V \subset C[0,1]^d\). The associated entropy exponent is
which, roughly speaking, determines the theoretically optimal rate \(\mathcal {O}(m^{-s_*})\) at which an arbitrary element of U can be approximated from a representation using at most m bits. On the other hand, \(\beta _*\) determines the optimal rate \(\mathcal {O}(m^{-\beta _*})\) that can actually be realized by an algorithm using m point samples of the input function \(f\in U\). For a solution mapping S to be efficiently computable from point samples, one would therefore expect that \(\beta _*= s_*\) or at least that \(\beta _*\) grows linearly with \(s_*\). For example, for U the unit ball in a Sobolev spaces \(W_\infty ^\alpha ([0,1]^d)\) and \(S=\iota _\infty \) we have \({ s_{*}(U) = \beta _*^{\textrm{det}} ( U, \iota _\infty ) = \beta _*^{\textrm{ran}} ( U, \iota _\infty ) =\frac{\alpha }{d} . }\) In contrast,  satisfies
satisfies  according to Lemma 6.2, while Theorem 1.1 shows
according to Lemma 6.2, while Theorem 1.1 shows  independent of \(\alpha \), and even
independent of \(\alpha \), and even  if the number of layers is unbounded. This is yet another manifestation of the wide theory-to-practice gap in neural network approximation.
if the number of layers is unbounded. This is yet another manifestation of the wide theory-to-practice gap in neural network approximation.
1.2.2 Other Hardness Results for Deep Learning
While we are not aware of any work addressing the optimal sampling complexity on neural network spaces, there exist a number of different approaches to establishing various “hardness” results for deep learning. We comment on some of them.
A prominent and classical research direction considers the computational complexity of fitting a neural network of a fixed architecture to given (training) samples. It is known that this can be an NP complete problem for certain specific architectures and samples; see [9] for the first result in this direction that has inspired a large body of follow-up work. This line of work does however not consider the full scope of the problem, namely the relation between theoretically possible approximation rates and algorithmically realizable rates. In our results we do not take into account the computational efficiency of algorithms at all. Our results are stronger in the sense that they show that even if there was an efficient algorithm for fitting a neural network to samples, one would need to access too many samples to achieve efficient runtimes.
Another research direction considers the existence of convergent algorithms that only have access to inexact information about the samples, as is commonly the case when computing in floating point arithmetic. Specifically, [3] identifies various problems in sparse approximation that cannot be algorithmically solved based on inputs with finite precision using neural networks. The deeper underlying reason is that these problems cannot be solved by any algorithm based on inexact measurements. Thus, the results of [3] are not really specific to neural networks. In contrast, our hardness results are highly specific to the structure of neural networks and do not occur for most other computational approaches.
A different kind of hardness results appears in the neural network approximation theory literature. There, typically lower bounds are provided for the number of network weights and/or number of layers that a neural network needs to have in order to reach a desired accuracy in the approximation of functions from various classical smoothness spaces [10, 36, 48, 52]. Yet, these bounds exclusively concern theoretical approximation rates for classical smoothness spaces while our results provide bounds for the realizability of these rates based on point samples
1.2.3 Other Work on Neural Network Approximation Spaces
Our definition of neural network approximation spaces is inspired by [20] where such spaces were first introduced and some structural properties, such as embedding theorems into classical function spaces, are investigated. The neural network spaces  introduced in the present work differ from those spaces in the sense that we also allow to take the size of the network weights into account. This is important, as such bounds on the weights are often enforced in applications through regularization procedures. Another construction of neural network approximation spaces can be found in [7] for the purpose of providing a calculus on functions that can be approximated by neural networks without curse of dimensionality. While all these works focus on aspects related to theoretical approximability of functions, our main focus concerns the algorithmic realization of such approximations.
introduced in the present work differ from those spaces in the sense that we also allow to take the size of the network weights into account. This is important, as such bounds on the weights are often enforced in applications through regularization procedures. Another construction of neural network approximation spaces can be found in [7] for the purpose of providing a calculus on functions that can be approximated by neural networks without curse of dimensionality. While all these works focus on aspects related to theoretical approximability of functions, our main focus concerns the algorithmic realization of such approximations.
1.3 Notation
For \(n \in \mathbb {N}\), we write \(\underline{n} := \{ 1,2,\dots ,n \}\). For any finite set \(I \ne \varnothing \) and any sequence \((a_i)_{i \in I} \subset \mathbb {R}\), we define  . The expectation of a random variable X will be denoted by \(\mathbb {E}[X]\).
. The expectation of a random variable X will be denoted by \(\mathbb {E}[X]\).
For a subset \(M \subset X\) of a metric space X, we write \(\overline{M}\) for the closure of M and \(M^\circ \) for the interior of M. In particular, this notation applies to subsets of \(\mathbb {R}^d\). We write \(\varvec{\lambda }(M)\) for the Lebesgue measure of a (measurable) set \(M \subset \mathbb {R}^d\).
1.4 Structure of the paper
Section 2 formally introduces the neural network approximation spaces  and furthermore provides a review of the most important notions and definitions from information based complexity. The basis for all our hardness results is developed in Sect. 3, where we show that the unit ball
and furthermore provides a review of the most important notions and definitions from information based complexity. The basis for all our hardness results is developed in Sect. 3, where we show that the unit ball  in the approximation space
in the approximation space  contains a large family of “hat functions”, depending on the precise properties of the functions \(\varvec{\ell },\varvec{c}\) and on \(\alpha > 0\).
contains a large family of “hat functions”, depending on the precise properties of the functions \(\varvec{\ell },\varvec{c}\) and on \(\alpha > 0\).
The remaining sections develop error bounds and hardness results for the problems of uniform approximation (Sects. 4 and 5), approximation in \(L^2\) (Sects. 6 and 7), and numerical integration (Sects. 8 and 9). Several technical proofs and results are deferred to Sect. A.
2 The Notion of Sampling Complexity on Neural Network Approximation Spaces
In this section, we first formally introduce the neural network approximation spaces  and then review the framework of information based complexity, including the notion of randomized algorithms and the concept of the optimal order of convergence based on point samples.
and then review the framework of information based complexity, including the notion of randomized algorithms and the concept of the optimal order of convergence based on point samples.
2.1 The Mathematical Formalization of Neural Networks
In our analysis, it will be helpful to distinguish between a neural network \(\Phi \) as a set of weights and the associated function \(R_\varrho \Phi \) computed by the network. Thus, we say that a neural network is a tuple \({\Phi = \big ( (A_1,b_1), \dots , (A_L,b_L) \big )}\), with \(A_\ell \in \mathbb {R}^{N_\ell \times N_{\ell -1}}\) and \(b_\ell \in \mathbb {R}^{N_\ell }\). We then say that \({\varvec{a}(\Phi ) := (N_0,\dots ,N_L) \in \mathbb {N}^{L+1}}\) is the architecture of \(\Phi \), \(L(\Phi ) := L\) is the number of layersFootnote 1 of \(\Phi \), and \({W(\Phi ) := \sum _{j=1}^L (\Vert A_j \Vert _{\ell ^0} + \Vert b_j \Vert _{\ell ^0})}\) denotes the number of (nonzero) weights of \(\Phi \). The notation \(\Vert A \Vert _{\ell ^0}\) used here denotes the number of nonzero entries of a matrix (or vector) A. Finally, we write \(d_{\textrm{in}}(\Phi ) := N_0\) and \(d_{\textrm{out}}(\Phi ) := N_L\) for the input and output dimension of \(\Phi \), and we set \(\Vert \Phi \Vert _{\mathcal{N}\mathcal{N}} := \max _{j = 1,\dots ,L} \max \{ \Vert A_j \Vert _{\infty }, \Vert b_j \Vert _{\infty } \}\), where \({\Vert A \Vert _{\infty } := \max _{i,j} |A_{i,j}|}\).
To define the function \(R_\varrho \Phi \) computed by \(\Phi \), we need to specify an activation function. In this paper, we will only consider the so-called rectified linear unit (ReLU) \({\varrho : \mathbb {R}\rightarrow \mathbb {R}, x \mapsto \max \{ 0, x \}}\), which we understand to act componentwise on \(\mathbb {R}^n\), i.e., \(\varrho \bigl ( (x_1,\dots ,x_n)\bigr ) = \bigl (\varrho (x_1),\dots ,\varrho (x_n)\bigr )\). The function \(R_\varrho \Phi : \mathbb {R}^{N_0} \rightarrow \mathbb {R}^{N_L}\) computed by the network \(\Phi \) (its realization) is then given by
2.2 Neural Network Approximation Spaces
Approximation spaces [14] classify functions according to how well they can be approximated by a family \(\varvec{\Sigma } = (\Sigma _n)_{n \in \mathbb {N}}\) of certain “simple functions” of increasing complexity n, as \(n \rightarrow \infty \). Common examples consider the case where \(\Sigma _n\) is the set of polynomials of degree n, or the set of all linear combinations of n wavelets. The notion of neural network approximation spaces was originally introduced in [20], where \(\Sigma _n\) was taken to be a family of neural networks of increasing complexity. However, [20] does not impose any restrictions on the size of the individual network weights, which plays an important role in practice and—as we shall see—also influences the possible performance of algorithms based on point samples.
For this reason, we introduce a modified notion of neural network approximation spaces that also takes the size of the individual network weights into account. Precisely, given an input dimension \(d \in \mathbb {N}\) (which we will keep fixed throughout this paper) and non-decreasing functions \({\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}}\) and \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) (called the depth-growth function and the coefficient growth function, respectively), we define

Then, given a measurable subset \(\Omega \subset \mathbb {R}^d\), \(p \in [1,\infty ]\), and \(\alpha \in (0,\infty )\), for each measurable \(f : \Omega \rightarrow \mathbb {R}\), we define

where \(d_{p}(f, \Sigma ) := \inf _{g \in \Sigma } \Vert f - g \Vert _{L^p(\Omega )}\).
The remaining issue is that since the set  is in general neither closed under addition nor under multiplication with scalars,
is in general neither closed under addition nor under multiplication with scalars,  is not a (quasi)-norm. To resolve this issue, taking inspiration from the theory of Orlicz spaces (see e.g. [41, Theorem 3 in Section 3.2]), we define the neural network approximation space quasi-norm
is not a (quasi)-norm. To resolve this issue, taking inspiration from the theory of Orlicz spaces (see e.g. [41, Theorem 3 in Section 3.2]), we define the neural network approximation space quasi-norm  as
as

giving rise to the approximation space

The following lemma summarizes the main elementary properties of these spaces.
Lemma 2.1
Let \(\varnothing \ne \Omega \subset \mathbb {R}^d\) be measurable, let \(p \in [1,\infty ]\) and \(\alpha \in (0,\infty )\). Then,  satisfies the following properties:
satisfies the following properties:
-
1.
 is a quasi-normed space. Precisely, given arbitrary measurable functions \(f,g : \Omega \rightarrow \mathbb {R}\), it holds that
is a quasi-normed space. Precisely, given arbitrary measurable functions \(f,g : \Omega \rightarrow \mathbb {R}\), it holds that  for \(C := 17^\alpha \).
for \(C := 17^\alpha \). -
2.
We have
 for \(c \in [-1,1]\).
for \(c \in [-1,1]\). -
3.
 if and only if
if and only if  .
. -
4.
 if and only if
if and only if  .
. -
5.
 . Furthermore, if \(\Omega \subset \overline{\Omega ^\circ }\), then
. Furthermore, if \(\Omega \subset \overline{\Omega ^\circ }\), then  , where \(C_b (\Omega )\) denotes the Banach space of continuous functions that are bounded and extend continuously to the closure \(\overline{\Omega }\) of \(\Omega \).
, where \(C_b (\Omega )\) denotes the Banach space of continuous functions that are bounded and extend continuously to the closure \(\overline{\Omega }\) of \(\Omega \).
Proof
See Sect. A.1. \(\square \)
2.3 Quantities Characterizing the Complexity of the Network Architecture
To conveniently summarize those aspects of the growth behavior of the functions \(\varvec{\ell }\) and \(\varvec{c}\) most relevant to us, we introduce three quantities that will turn out to be crucial for characterizing the sample complexity of the neural network approximation spaces. First, we set
Furthermore, we define
Remark 2.2
Clearly, \(\gamma ^{\flat }(\varvec{\ell },\varvec{c}) \le \gamma ^{\sharp }(\varvec{\ell },\varvec{c})\). Furthermore, since we will only consider settings in which \(\varvec{\ell }^*\ge 2\), we always have \(\gamma ^{\sharp }(\varvec{\ell },\varvec{c}) \ge \gamma ^{\flat }(\varvec{\ell },\varvec{c}) \ge 1\). Next, note that if \(\varvec{\ell }^*= \infty \) (i.e., if \(\varvec{\ell }\) is unbounded), then \(\gamma ^{\flat }(\varvec{\ell },\varvec{c}) = \gamma ^{\sharp }(\varvec{\ell },\varvec{c}) = \infty \). Finally, we remark that if \(\varvec{\ell }^*< \infty \) and if \(\varvec{c}\) satisfies the natural growth condition \(\varvec{c}(n) \asymp n^\theta \cdot (\ln (2 n))^{\kappa }\) for certain \(\theta \ge 0\) and \(\kappa \in \mathbb {R}\), then \( \gamma ^{\flat }(\varvec{\ell },\varvec{c}) = \gamma ^{\sharp }(\varvec{\ell },\varvec{c}) = \theta \cdot \varvec{\ell }^*+ \lfloor \varvec{\ell }^*/ 2 \rfloor . \) Thus, in most natural cases—but not always—\(\gamma ^{\flat }\) and \(\gamma ^{\sharp }\) agree.
An explicit example where \(\gamma ^{\flat }\) is not identical to \(\gamma ^{\sharp }\) is as follows: Define \(c_1 := c_2 := c_3 := 1\) and for \(n,m \in \mathbb {N}\) with \(2^{2^m} \le n < 2^{2^{m+1}}\), define \(c_n := 2^{2^m}\). Then, assume that \(\gamma _1,\gamma _2 \in [0,\infty )\) and \(\kappa _1,\kappa _2 > 0\) satisfy \(\kappa _1 \, n^{\gamma _1} \le c_n \le \kappa _2 \, n^{\gamma _2}\) for all \(n \in \mathbb {N}\). Applying the upper estimate for arbitrary \(m \in \mathbb {N}\) and \(n = n_m = 2^{2^m}\), we see \(n = c_n \le \kappa _2 \, n^{\gamma _2}\); since \(n_m = 2^{2^m} \rightarrow \infty \) as \(m \rightarrow \infty \), this is only possible if \(\gamma _2 \ge 1\). On the other hand, if we apply the lower estimate for arbitrary \(m \in \mathbb {N}\) and \(n = n_m = 2^{2^{m+1}} - 1\), we see because of \(c_n = 2^{2^m} = 2^{2^{m+1} / 2} = \sqrt{2^{2^{m+1}}} = \sqrt{n+1}\) that \( \kappa _1 \, n^{\gamma _1} \le c_n = \sqrt{n+1} . \) Again, since \(n_m = 2^{2^{m+1}} - 1 \rightarrow \infty \) as \(m \rightarrow \infty \), this is only possible if \(\gamma _1 \le \frac{1}{2}\).
Given these considerations, it is easy to see for \(\varvec{\ell } \equiv L \in \mathbb {N}_{\ge 2}\) that \(\gamma ^{\flat }(\varvec{\ell },\varvec{c}) \le \frac{L}{2} + \lfloor \frac{L}{2} \rfloor \), while \(\gamma ^{\sharp }(\varvec{\ell },\varvec{c}) \ge L + \lfloor \frac{L}{2} \rfloor \). In particular, \(\gamma ^{\flat }(\varvec{\ell },\varvec{c}) < \gamma ^{\sharp }(\varvec{\ell },\varvec{c})\). \(\triangle \)
2.4 The Framework of Sampling Complexity
Let \(d \in \mathbb {N}\), let \(\varnothing \ne U \subset C([0,1]^d)\) be bounded, and let Y be a Banach space. We are interested in numerically approximating a given solution mapping \(S : U \rightarrow Y\), where the numerical procedure is only allowed to access point samples of the functions \(f \in U\). The procedure can be either deterministic or probabilistic (Monte Carlo). In this short section, we discuss the mathematical formalization of this problem, based on the setup of numerical complexity theory, as for instance outlined in [25, Section 2].
The reader should keep in mind that we are mostly interested in the setting where U is the unit ball in the neural network approximation space  , i.e.,
, i.e.,

and where the solution mapping is one of the following:
-
1.
The embedding into \(C([0,1]^d)\), i.e., \(S = \iota _{\infty }\) for \(\iota _\infty : U \rightarrow C([0,1]^d), f \mapsto f\),
-
2.
The embedding into \(L^2([0,1]^d)\), i.e., \(S = \iota _2\) for \(\iota _2 : U \rightarrow L^2([0,1]^d), f \mapsto f\), or
-
3.
The definite integral, i.e., \(S = T_{\int }\) for \(T_{\int } : U \rightarrow \mathbb {R}, f \mapsto \int _{[0,1]^d} f(x) \, d x\).
2.4.1 The Deterministic Setting
A (potentially nonlinear) map \(A : U \rightarrow Y\) is called a deterministic method using m \(\in \) \(\mathbb {N}\) point measurements (written \(A \in {\text {Alg}}_m (U,Y)\)) if there exists \(\varvec{x}= (x_1,\dots ,x_m) \in ([0,1]^d)^m\) and a map \(Q : \mathbb {R}^m \rightarrow Y\) such that
Given a (solution) mapping \(S : U \rightarrow Y\), we define the error of A in approximating S as
The optimal error for (deterministically) approximating \(S : U \rightarrow Y\) using m point samples is then
Finally, the optimal order for (deterministically) approximating \(S : U \rightarrow Y\) using point samples is
2.4.2 The Randomized Setting
A randomized method using \(m \in \mathbb {N}\) point measurements (in expectation) is a tuple \((\varvec{A},\varvec{m})\) consisting of a family \(\varvec{A}= (A_\omega )_{\omega \in \Omega }\) of (potentially nonlinear) maps \(A_\omega : U \rightarrow Y\) indexed by a probability space \((\Omega ,\mathcal {F},\mathbb {P})\) and a measurable function \(\varvec{m}: \Omega \rightarrow \mathbb {N}\) with the following properties:
-
1.
for each \(f \in U\), the map \(\Omega \rightarrow Y, \omega \mapsto A_\omega (f)\) is measurable (with respect to the Borel \(\sigma \)-algebra on Y),
-
2.
for each \(\omega \in \Omega \), we have \(A_\omega \in {\text {Alg}}_{\varvec{m}(\omega )}(U,Y)\),
-
3.
\(\mathbb {E}_{\omega } [\varvec{m}(\omega )] \le m\).
We write \((\varvec{A}, \varvec{m}) \in {\text {Alg}}^{\textrm{ran}}_m (U,Y)\) if these conditions are satisfied. We say that \((\varvec{A},\varvec{m})\) is strongly measurable if the map \(\Omega \times U \rightarrow Y, (\omega ,f) \mapsto A_\omega (f)\) is measurable, where \(U \subset C([0,1]^d)\) is equipped with the Borel \(\sigma \)-algebra induced by \(C([0,1]^d)\).
Remark
In most of the literature (see e.g. [25, Section 2]), randomized algorithms are always assumed to be strongly measurable. All randomized algorithms that we construct will have this property. On the other hand, all our hardness results apply to arbitrary randomized algorithms satisfying Properties 1–3 from above. Thus, using the terminology just introduced we obtain stronger results than we would get using the usual definition.
The expected error of a randomized algorithm \((\varvec{A},\varvec{m})\) for approximating a (solution) mapping \(S : U \rightarrow Y\) is defined as
The optimal randomized error for approximating \(S : U \rightarrow Y\) using m point samples (in expectation) is
Finally, the optimal randomized order for approximating \(S : U \rightarrow Y\) using point samples is
The remainder of this paper is concerned with deriving upper and lower bounds for the exponents \(\beta _*^{\textrm{det}}(U,S)\) and \(\beta _*^{\textrm{ran}}(U,S)\), where  is the unit ball in
is the unit ball in  , and S is either the embedding of
, and S is either the embedding of  into \(C([0,1]^d)\), the embedding into \(L^2([0,1]^d)\), or the definite integral \(S f = \int _{[0,1]^d} f(t) \, d t\).
into \(C([0,1]^d)\), the embedding into \(L^2([0,1]^d)\), or the definite integral \(S f = \int _{[0,1]^d} f(t) \, d t\).
For deriving upper bounds (i.e., hardness bounds) for randomized algorithms, we will frequently use the following lemma, which is a slight adaptation of [25, Proposition 4.1]. In a nutshell, the lemma shows that if one can establish a hardness result that holds for deterministic algorithms in the average case, then this implies a hardness result for randomized algorithms.
Lemma 2.3
Let \(\varnothing \ne U \subset C([0,1]^d)\) be bounded, let Y be a Banach space, and let \(S : U \rightarrow Y\). Assume that there exist \(\lambda \in [0,\infty )\), \(\kappa > 0\), and \(m_0 \in \mathbb {N}\) such that for every \(m \in \mathbb {N}_{\ge m_0}\) there exists a finite set \(\Gamma _m \ne \varnothing \) and a family of functions \((f_{\gamma })_{\gamma \in \Gamma _m} \subset U\) satisfying

Then \(\beta _*^{\textrm{det}}(U,S),\beta _*^{\textrm{ran}}(U,S) \le \lambda \).
Proof
Step 1 (proving \(\beta _*^{\textrm{det}}(U,S) \le \lambda \)): For every \(A \in {\text {Alg}}_m(U,Y)\), Eq. (2.5) implies because of \(f_{\gamma } \in U\) that

Since this holds for every \(m \in \mathbb {N}_{\ge m_0}\) and every \(A \in {\text {Alg}}_m(U,Y)\), with \(\kappa \) independent of A, m, this easily implies \(e_{m}^{\textrm{det}}(U,S) \ge \kappa \, m^{-\lambda }\) for all \(m \in \mathbb {N}_{\ge m_0}\), and then \(\beta _{*}^{\textrm{det}}(U,S) \le \lambda \).
Step 2 (proving \(\beta _*^{\textrm{ran}}(U,S) \le \lambda \)): Let \(m \in \mathbb {N}_{\ge m_0}\) and let \((\varvec{A},\varvec{m}) \in {\text {Alg}}_{m}^{\textrm{ran}}(U,Y)\) be arbitrary, with \(\varvec{A}= (A_\omega )_{\omega \in \Omega }\) for a probability space \((\Omega ,\mathcal {F},\mathbb {P})\). Define \(\Omega _0 := \{ \omega \in \Omega :\varvec{m}(\omega ) \le 2 m \}\) and note \(m \ge \mathbb {E}_\omega [\varvec{m}(\omega )] \ge 2 m \cdot \mathbb {P}(\Omega _0^c)\), which shows \(\mathbb {P}(\Omega _0^c) \le \frac{1}{2}\) and hence \(\mathbb {P}(\Omega _0) \ge \frac{1}{2}\).
Note that \(A_\omega \in {\text {Alg}}_{2m} (U, Y)\) for each \(\omega \in \Omega _0\), so that Eq. (2.5) (with 2m instead of m) shows  for a constant \(\widetilde{\kappa } = \widetilde{\kappa }(\kappa ,\lambda ) > 0\). Therefore,
for a constant \(\widetilde{\kappa } = \widetilde{\kappa }(\kappa ,\lambda ) > 0\). Therefore,

and hence \( e_m^{\textrm{ran}} \big ( U, S \big ) \ge \frac{\widetilde{\kappa }}{2} \cdot m^{-\lambda } , \) since Eq. (2.6) holds for any randomized algorithm \((\varvec{A},\varvec{m}) \in {\text {Alg}}_m^{\textrm{ran}} (U, Y)\). Finally, since \(m \in \mathbb {N}_{\ge m_0}\) can be chosen arbitrarily, we see as claimed that \( \beta _*^{\textrm{ran}}(U, S) \le \lambda . \) \(\square \)
3 Richness of the Unit Ball in the Spaces 
In this section, we show that ReLU networks with a limited number of neurons and bounded weights can well approximate several different functions of “hat-function type,” as shown in Fig. 1. The fact that this is possible implies that the unit ball  is quite rich; this will be the basis of all of our hardness results.
is quite rich; this will be the basis of all of our hardness results.
A plot of the “hat-function” \(\Lambda _{M,y}\) formally defined in Eq. (3.1)
We begin by considering the most basic “hat function” \({\Lambda _{M,y} : \mathbb {R}\rightarrow [0,1]}\), defined for \(M > 0\) and \(y \in \mathbb {R}\) by
For later use, we note that \(\int _{\mathbb {R}} \Lambda _{M,y}(x) \, d x = M^{-1}\). Furthermore, we “lift” \(\Lambda _{M,y}\) to a function on \(\mathbb {R}^d\) by setting \(\Lambda _{M,y}^*: \mathbb {R}^d \rightarrow \mathbb {R}, x = (x_1,\dots ,x_d) \mapsto \Lambda _{M,y}(x_1)\). The following lemma gives a bound on how economically sums of the functions \(\Lambda _{M,y}\) can be implemented by ReLU networks.
Lemma 3.1
Let \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) and \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) be non-decreasing. Let \(M \ge 1\), \(n \in \mathbb {N}\), and \(0 < C \le \varvec{c}(n)\), as well as \(L \in \mathbb {N}_{\ge 2}\) with \(L \le \varvec{\ell }(n)\).
Then

Proof
Let \(\varepsilon _1,\dots ,\varepsilon _n \in [-1,1]\) and \(y_1,\dots ,y_n \in [0,1]\). Let \(e_1 := (1,0,\dots ,0) \in \mathbb {R}^{1 \times d}\) and define

as well as

Finally, set \(E := (C \mid -C) \in \mathbb {R}^{1 \times 2}\) and


Note that \( \Vert A \Vert _{\infty }, \Vert B \Vert _{\infty }, \Vert D \Vert _{\infty }, \Vert E \Vert _{\infty }, \Vert A_1 \Vert _{\infty }, \Vert A_2 \Vert _{\infty }, \Vert A_2^{(0)} \Vert _{\infty } \le C . \) Furthermore, since \(y_j \in [0,1]\) and \(M \ge 1\), we also see \(\Vert b_1 \Vert _{\infty } \le C\). Next, note that \(\Vert A_1 \Vert _{\ell ^0}, \Vert A_2^{(0)} \Vert _{\ell ^0}, \Vert b_1 \Vert _{\ell ^0} \le 3n\), \(\Vert A_2 \Vert _{\ell ^0} \le 6 n\), \(\Vert A \Vert _{\ell ^0}, \Vert B \Vert _{\ell ^0}, \Vert D \Vert _{\ell ^0} \le 2n\), and \(\Vert E \Vert _{\ell ^0} \le 2 \le 2 n\).
For brevity, set \(\gamma := \frac{C^L \, n^{\lfloor L/2 \rfloor }}{4 n M}\) and \(\Xi := \sum _{i=1}^n \varepsilon _i \Lambda _{M,y_i}^*\), so that \(\Xi : \mathbb {R}^d \rightarrow \mathbb {R}\). Before we describe how to construct a network \(\Phi \) implementing \(\gamma \cdot \Xi \), we collect a few auxiliary observations. First, a direct computation shows that
Based on this, it is easy to see
By definition of \(A_2\), this shows \(F(x) = \frac{C^2}{4 M} \bigl (\varrho (\Xi (x)) , \varrho (-\Xi (x))\bigr )^T\) for all \(x \in \mathbb {R}^d\), for the function \(F := \varrho \circ A_2 \circ \varrho \circ (A_1 \bullet + b_1) : \mathbb {R}^d \rightarrow \mathbb {R}^2\).
A further direct computation shows for \(x,y \in \mathbb {R}\) that
Thus, setting \( G := B \circ \varrho \circ A: \mathbb {R}^2 \rightarrow \mathbb {R}^2\), we see \(G(x,y) = C^2 n \bigl (\varrho (x), \varrho (y)\bigr )^T\). Therefore, denoting by \(G^j := G \circ \cdots \circ G\) the j-fold composition of G with itself, we see \(G^j (x,y) = (C^2 n)^j \cdot \bigl (\varrho (x), \varrho (y)\bigr )^T\) for \(j \in \mathbb {N}\), and hence
where the case \(j = 0\) (in which it is understood that \(G^j = \textrm{id}_{\mathbb {R}^2}\)) is easy to verify separately.
In a similar way, we see for \(H := D \circ \varrho \circ A : \mathbb {R}^2 \rightarrow \mathbb {R}\) that
Now, we prove the claim of the lemma, distinguishing three cases regarding \(L \in \mathbb {N}_{\ge 2}\).
Case 1 (\(L = 2\)): Define \(\Phi := \big ( (A_1, b_1), (A_2^{(0)}, 0) \big )\). Then Eq. (3.2) shows \(R_\varrho \Phi = \frac{C^2}{4 M} \Xi \). Because of \(\frac{C^L \, n^{\lfloor L/2 \rfloor }}{4 n M} = \frac{C^2}{4 M}\) for \(L = 2\), this implies the claim, once we note that
as well as \(W(\Phi ) \le 9 n \le (2 L + 8) n\), since \(L = 2\).
Case 2 (\(L \ge 4\) is even): In this case, define
and note for \(j := \frac{L - 4}{2}\) that \(j+1 = \frac{L-2}{2} = \lfloor L/2 \rfloor - 1\), so that a combination of Eqs. (3.5) and (3.4) shows
since \(\varrho (\varrho (z)) = \varrho (z)\) and \(\varrho (z) - \varrho (-z) = z\) for all \(z \in \mathbb {R}\). Finally, we note as in the previous case that \(L(\Phi ) = L \le \varvec{\ell }( (2 L + 8) n)\) and \(\Vert \Phi \Vert _{\mathcal{N}\mathcal{N}} \le C \le \varvec{c}( (2L + 8) n)\), and furthermore that
Overall, we see also in this case that  , as claimed.
, as claimed.
Case 3 (\(L \ge 3\) is odd): In this case, define
Then, setting \(j := \frac{L-3}{2}\) and noting \(j = \lfloor L/2 \rfloor - 1\), we see thanks to Eq. (3.4) and because of \(E = (C \mid -C)\) that
It remains to note as before that \(L(\Phi ) = L \le \varvec{\ell }( (2L + 8) n)\) and \(\Vert \Phi \Vert _{\mathcal{N}\mathcal{N}} \le C \le \varvec{c}( (2L + 8) n)\), and finally that \( W(\Phi ) \le 3 n + 3 n + 6 n + \frac{L-3}{2} (2 n + 2 n) + 2 = 2 + 6n + 2 L n \le (8 + 2 L) n, \) so that indeed  also in this case. \(\square \)
also in this case. \(\square \)
As an application of Lemma 3.1, we now describe a large class of functions contained in the unit ball of the approximation space  .
.
Lemma 3.2
Let \(\alpha > 0\) and let \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) and \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) be non-decreasing. Let \(\sigma \ge 2\), \(0< \gamma < \gamma ^{\flat }(\varvec{\ell },\varvec{c})\), \(\theta \in (0,\infty )\) and \(\lambda \in [0,1]\) with \(\theta \lambda \le 1\) be arbitrary and define
Then there exists a constant \(\kappa = \kappa (\alpha ,\theta ,\lambda ,\gamma ,\sigma ,\varvec{\ell },\varvec{c}) > 0\) such that for every \(m \in \mathbb {N}\), the following holds:
Setting \(M := 4 m\) and \(z_j := \frac{1}{4 m} + \frac{j-1}{2 m}\) for \(j \in \underline{2m}\), the functions \(\bigl (\Lambda _{M,z_j}^*\bigr )_{j \in \underline{2m}}\) are supported in \([0,1]^d\) and have disjoint supports, up to a null-set. Furthermore, for any \(\varvec{\nu }= (\nu _j)_{j \in \underline{2m}} \in [-1,1]^{2m}\) and \(J \subset \underline{2 m}\) satisfying \(|J| \le \sigma \cdot m^{\theta \lambda }\), we have

Proof
Since \(\gamma < \gamma ^{\flat }(\varvec{\ell },\varvec{c})\), we see by definition of \(\gamma ^{\flat }\) that there exist \(L = L(\gamma ,\varvec{\ell },\varvec{c}) \in \mathbb {N}_{\le \varvec{\ell }^*}\) and \(C_1 = C_1(\gamma ,\varvec{\ell },\varvec{c}) > 0\) such that \(n^\gamma \le C_1 \cdot (\varvec{c}(n))^L \cdot n^{\lfloor L/2 \rfloor }\) for all \(n \in \mathbb {N}\). Because of \(\varvec{\ell }\ge 2\), we can assume without loss of generality that \(L \ge 2\). Furthermore, since \(L \le \varvec{\ell }^*\), we can choose \(n_0 = n_0(\gamma ,\varvec{\ell },\varvec{c}) \in \mathbb {N}\) satisfying \(L \le \varvec{\ell }(n_0)\).
Let \(m \in \mathbb {N}\) and let \(\varvec{\nu }\) and J be as in the statement of the lemma. For brevity, define \({f_{\varvec{\nu },J}^{(0)} := \sum _{j \in J} \nu _j \Lambda _{M,z_j}^*}\). We note that \(\Lambda _{M,z_j}^*\) is continuous with \(0 \le \Lambda _{M,z_j}^*\le 1\) and
This shows that the supports of the functions \(\Lambda _{M,z_j}^*\) are contained in \([0,1]^d\) and are pairwise disjoint (up to null-sets), which then implies \(\big \Vert f_{\varvec{\nu },J}^{(0)} \big \Vert _{L^\infty } \le 1\).
Next, since \(\theta \lambda \le 1\), we have \(\lceil m^{\theta \lambda } \rceil \le \lceil m \rceil = m \le 2 m\). Thus, by possibly enlarging the set \(J \subset \underline{2m}\) and setting \(\nu _j := 0\) for the added elements, we can without loss of generality assume that \(|J| \ge \lceil m^{\theta \lambda } \rceil \ge 1\). Note that the extended set still satisfies \(|J| \le \sigma \cdot m^{\theta \lambda }\) since \(\lceil m^{\theta \lambda } \rceil \le 2 m^{\theta \lambda }\) and \(\sigma \ge 2\).
Now, define \(N := n_0 \cdot \big \lceil m^{(1-\lambda ) \theta } \big \rceil \) and \(n := N \cdot |J|\), noting that \(n \ge n_0\). Furthermore, writing \({J = \{ i_1,\dots ,i_{|J|} \}}\), define

By choice of \(C_1\), we have \(n^\gamma \le C_1 \cdot (\varvec{c}(n))^L \cdot n^{\lfloor L/2 \rfloor }\), so that we can choose \(0 < C \le \varvec{c}(n)\) satisfying \(n^\gamma \le C_1 \cdot C^L \cdot n^{\lfloor L/2 \rfloor }\). Since we also have \(L \ge 2\) and \(L \le \varvec{\ell }(n_0) \le \varvec{\ell }(n)\), Lemma 3.1 shows that

here the final equality comes from our choice of \(\varepsilon _1,\dots ,\varepsilon _n\) and \(y_1,\dots ,y_n\).
To complete the proof, we first collect a few auxiliary estimates. First, we see because of \({|J| \ge m^{\theta \lambda }}\) that \(n \ge n_0 \, m^{(1-\lambda ) \theta } \, m^{\theta \lambda } \ge m^\theta \).
Thus, setting \(C_2 := 16 \sigma C_1\) and recalling that \({\omega \le \theta \cdot (\gamma - \lambda ) - 1}\) by choice of \(\omega \), we see for any \(0 < \kappa \le C_2^{-1}\) that
Here, we used in the last step that \(|J| \le \sigma \, m^{\theta \lambda }\), which implies \( \frac{N}{n} = |J|^{-1} \ge \sigma ^{-1} m^{-\theta \lambda } . \) Thus, noting that \(c \Sigma _{t}^{\varvec{\ell },\varvec{c}} \subset \Sigma _{t}^{\varvec{\ell },\varvec{c}}\) for \(c \in [-1,1]\), we see  as long as \(0 < \kappa \le C_2^{-1}\).
as long as \(0 < \kappa \le C_2^{-1}\).
Finally, set \(C_3 := \max \bigl \{ 1, \,\, C_2, \,\, (2 L + 8)^\alpha \, (2 n_0 \sigma )^\alpha \bigr \}\). We claim that  for \(\kappa := C_3^{-1}\). Once this is shown, Lemma 2.1 will show that
for \(\kappa := C_3^{-1}\). Once this is shown, Lemma 2.1 will show that  as well. To see
as well. To see  , first note that \(\big \Vert \kappa \, m^\omega \, f_{\varvec{\nu },J}^{(0)} \big \Vert _{L^\infty } \le \Vert f_{\varvec{\nu },J}^{(0)} \Vert _{L^\infty } \le 1\) since \(\omega < 0\) and \(\kappa = C_3^{-1} \le 1\). Furthermore, for \(t \in \mathbb {N}\) there are two cases: For \(t \ge (2 L + 8) n\) we have shown above that
, first note that \(\big \Vert \kappa \, m^\omega \, f_{\varvec{\nu },J}^{(0)} \big \Vert _{L^\infty } \le \Vert f_{\varvec{\nu },J}^{(0)} \Vert _{L^\infty } \le 1\) since \(\omega < 0\) and \(\kappa = C_3^{-1} \le 1\). Furthermore, for \(t \in \mathbb {N}\) there are two cases: For \(t \ge (2 L + 8) n\) we have shown above that  and hence \(t^\alpha \, d_\infty (\kappa \, m^\omega \, f_{\mathbf {\nu },J}^{(0)}; \Sigma _{t}^{\varvec{\ell },\varvec{c}}) = 0 \le 1\). On the other hand, if \(t \le (2 L + 8) n\) then we see because of \( \big \lceil m^{(1-\lambda ) \theta } \big \rceil \le 1 + m^{(1-\lambda ) \theta } \le 2 \cdot m^{(1-\lambda ) \theta } \) and \(|J| \le \sigma \, m^{\theta \lambda }\) that \(n \le 2 n_0 \sigma \, m^\theta \). Since we also have \(\omega \le - \theta \alpha \), this implies
and hence \(t^\alpha \, d_\infty (\kappa \, m^\omega \, f_{\mathbf {\nu },J}^{(0)}; \Sigma _{t}^{\varvec{\ell },\varvec{c}}) = 0 \le 1\). On the other hand, if \(t \le (2 L + 8) n\) then we see because of \( \big \lceil m^{(1-\lambda ) \theta } \big \rceil \le 1 + m^{(1-\lambda ) \theta } \le 2 \cdot m^{(1-\lambda ) \theta } \) and \(|J| \le \sigma \, m^{\theta \lambda }\) that \(n \le 2 n_0 \sigma \, m^\theta \). Since we also have \(\omega \le - \theta \alpha \), this implies
All in all, this shows  . As seen above, this completes the proof. \(\square \)
. As seen above, this completes the proof. \(\square \)
For later use, we also collect the following technical result which shows how to select a large number of “hat functions” as in Lemma 3.2 that are annihilated by a given set of sampling points.
Lemma 3.3
Let \(m \in \mathbb {N}\) and let \(M = 4 m\) and \(z_j = \frac{1}{4 m} + \frac{j-1}{2 m}\) as in Lemma 3.2. Given arbitrary points \(\varvec{x}= (x_1,\dots ,x_m) \in ([0,1]^d)^m\), define
Then \(|I_{\varvec{x}}| \ge m\).
Proof
Let \(I_{\varvec{x}}^c := \underline{2m} \setminus I_{\varvec{x}}\). For each \(i \in I_{\varvec{x}}^c\), there exists \(n_i \in \underline{m}\) satisfying \(\Lambda _{M,z_i}^*(x_{n_i}) \ne 0\). The map \(I_{\varvec{x}}^c \rightarrow \underline{m}, i \mapsto n_i\) is injective, since \(\Lambda _{M,z_i}^*\Lambda _{M,z_\ell }^*\equiv 0\) for \(i \ne \ell \) (see Lemma 3.2). Therefore, \(|I_{\varvec{x}}^c| \le m\) and hence \(|I_{\varvec{x}}| = 2m - |I_{\varvec{x}}^c| \ge m\).
The function \(\Lambda _{M,y}^*: \mathbb {R}^d \rightarrow \mathbb {R}\) has a controlled support with respect to the first coordinate of x, but unbounded support with respect to the remaining variables. For proving more refined hardness bounds, we shall therefore use the following modified construction of a function of “hat-type” with controlled support. As we will see in Lemma 3.5 below, this function can also be well implemented by ReLU networks, provided one can use networks with at least two hidden layers.\(\square \)
Lemma 3.4
Given \(d \in \mathbb {N}\), \(M > 0\) and \(y \in \mathbb {R}^d\), define

Then the function \(\vartheta _{M,y}\) has the following properties:
-
a)
\(\vartheta _{M,y}(x) = 0\) for all \(x \in \mathbb {R}^d \setminus \bigl (y + M^{-1} (-1,1)^d\bigr )\);
-
b)
\(\Vert \vartheta _{M,y} \Vert _{L^p (\mathbb {R}^d)} \le (2 / M)^{d/p}\) for arbitrary \(p \in (0,\infty ]\);
-
c)
For any \(p \in (0,\infty ]\) there is a constant \(C = C(d,p) > 0\) satisfying
$$\begin{aligned} \Vert \vartheta _{M,y} \Vert _{L^p([0,1]^d)} \ge C \cdot M^{-d/p}, \qquad \forall \, y \in [0,1]^d \text { and } M \ge \tfrac{1}{2d} . \end{aligned}$$
Proof of Lemma 3.4
Ad a) For \(x \in \mathbb {R}^d \setminus \big ( y + M^{-1} (-1,1)^d \big )\), there exists \(\ell \in \underline{d}\) with \(|x_\ell - y_\ell | \ge M^{-1}\) and hence \(\Lambda _{M,y_\ell }(x_\ell ) = 0\); see Fig. 1. Because of \(0 \le \Lambda _{M,y_j} \le 1\), this implies
By elementary properties of the function \(\theta \) (see Fig. 2), this shows \(\vartheta _{M,y}(x) = \theta (\Delta _{M,y}(x)) = 0\).
Ad b) Since \(0 \le \theta \le 1\), we also have \(0 \le \vartheta _{M,y} \le 1\). Combined with Part a), this implies \( \Vert \vartheta _{M,y} \Vert _{L^p} \le \bigl [\varvec{\lambda }(y + M^{-1}(-1,1)^d)\bigr ]^{1/p} = (2/M)^{d/p} , \) as claimed.
Ad c) Set \(T := \frac{1}{2 d M} \in (0,1]\) and \(P := y + [-T,T]^d\). For \(x \in P\) and arbitrary \(j \in \underline{d}\), we have \(|x_j - y_j| \le \frac{1}{2 d M}\). Since \(\Lambda _{M,y_j}\) is Lipschitz with \({\text {Lip}}(\Lambda _{M,y_j}) \le M\) (see Fig. 1) and \(\Lambda _{M,y_j}(y_j) = 1\), this implies
Since this holds for all \(j \in \underline{d}\), we see \(\Delta _{M,y}(x) = \sum _{j=1}^d \Lambda _{M,y_j}(x_j) - (d \!-\! 1) \ge d \!\cdot \! (1 \!-\! \frac{1}{2 d}) - (d \!-\! 1) = \frac{1}{2} , \) and hence \(\vartheta _{M,y}(x) = \theta (\Delta _{M,y}(x)) \ge \theta (\frac{1}{2}) = \frac{1}{2}\), since \(\theta \) is non-decreasing.
Finally, Lemma A.2 shows for \(Q = [0,1]^d\) that \(\varvec{\lambda }(Q \cap P) \ge 2^{-d} T^d \ge C_1 \cdot M^{-d}\) with \(C_1 = C_1(d) > 0\). Hence, \( \Vert \vartheta _{M,y} \Vert _{L^p([0,1]^d)} \ge \frac{1}{2} [\varvec{\lambda }(Q \cap P)]^{1/p} \ge C_1^{1/p} M^{-d/p} , \) which easily yields the claim.
A plot of the function \(\theta \) appearing in Lemma 3.4. Note that \(\theta \) is non-decreasing and satisfies \(\theta (x) = 0\) for \(x \le 0\) as well as \(\theta (x) = 1\) for \(x \ge 1\)
The next lemma shows how well the function \(\vartheta _{M,y}\) can be implemented by ReLU networks. We emphasize that the lemma requires using networks with \(L \ge 3\), i.e., with at least two hidden layers. \(\square \)
Lemma 3.5
Let \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) and \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) be non-decreasing. Let \(M \ge 1\), \(n \in \mathbb {N}\) and \(0 < C \le \varvec{c}(n)\), as well as \(L \in \mathbb {N}_{\ge 3}\) with \(L \le \varvec{\ell }(n)\). Then

Proof
Let \(y \in [0,1]^d\) be fixed. For \(j \in \underline{d}\), denote by \(e_j \in \mathbb {R}^{d \times 1}\) the j-th standard basis vector. Define \(A_1 \in \mathbb {R}^{4 n d \times d}\) and \(b_1 \in \mathbb {R}^{4 n d}\) by
Furthermore, set \(b_2 := 0 \in \mathbb {R}^2\) and \(b_3 := 0 \in \mathbb {R}^n\), let \(\zeta := -\frac{1}{M}\frac{d-1}{d}\) and \(\xi := -\frac{1}{M}\), and define \(A_2 \in \mathbb {R}^{2 \times 4 n d}\) and \(A_3 \in \mathbb {R}^{n \times 2}\) by

Finally, set \(A := C \cdot (1,\dots ,1) \in \mathbb {R}^{1 \times n}\), \(B := C \cdot (1,\dots ,1)^T \in \mathbb {R}^{n \times 1}\), and \(D := C \cdot (1 , -1) \in \mathbb {R}^{1 \times 2}\), as well as \(E := (C) \in \mathbb {R}^{1 \times 1}\). Note that \( \Vert A_1 \Vert _{\infty }, \Vert A_2 \Vert _{\infty }, \Vert A_3 \Vert _{\infty }, \Vert A \Vert _{\infty }, \Vert B \Vert _{\infty }, \Vert D \Vert _{\infty }, \Vert E \Vert _{\infty } \le C \) and \(\Vert b_1 \Vert _{\infty }, \Vert b_2 \Vert _{\infty } \le C\), since \(M \ge 1\) and \(y \in [0,1]^d\). Furthermore, note \(\Vert A_1 \Vert _{\ell ^0} \le 3 d n\), \(\Vert A_2 \Vert _{\ell ^0} \le 8 d n\), \(\Vert A_3 \Vert _{\ell ^0} \le 2 n\), \(\Vert A \Vert _{\ell ^0}, \Vert B \Vert _{\ell ^0} \le n\), \(\Vert D \Vert _{\ell ^0} \le 2\), and finally \(\Vert b_1 \Vert _{\ell ^0} \le 4 d n\) and \(\Vert b_2 \Vert _{\ell ^0} = 0\). Furthermore, note \(C \le \varvec{c}(n) \le \varvec{c}(15 (d + L) n)\) and likewise \(L \le \varvec{\ell }(n) \le \varvec{\ell }(15 (d+L) n)\) thanks to the monotonicity of \(\varvec{c},\varvec{\ell }\).
A direct computation shows that
Combined with the positive homogeneity of the ReLU (i.e., \(\varrho (t x) = t \varrho (x)\) for \(t \ge 0\)), this shows
In the same way, it follows that \(\bigl (A_2 \, \varrho (A_1 x + b_1) + b_2\bigr )_2 = \frac{C^2 n}{4 M} \cdot (\Delta _{M,y}(x) - 1)\). We now distinguish three cases:
Case 1: \(L=3\). In this case, set \(\Phi := \big ( (A_1,b_1), (A_2,b_2), (D,0) \big )\). Then the calculation from above, combined with the positive homogeneity of the ReLU shows
Furthermore, it is straightforward to see \(W(\Phi ) \le 3 d n + 4 d n + 8 d n + 2 \le 2 + 15 d n \le 15 (L + d) n\). Combined with our observations from above, and noting \(\lfloor \frac{L}{2} \rfloor = 1\), we thus see as claimed that  .
.
Case 2: \(L \ge 4\) is even. In this case, define
Similar arguments as in Case 1 show that \( \bigl ( A_3 \, \varrho \bigl ( A_2 \, \varrho (A_1 x + b_1) + b_2 \bigr ) + b_3 \bigr )_j = \frac{C^3 n}{4 M} \, \vartheta _{M,y}(x) \) for all \(j \in \underline{n}\), and hence \(A \circ \varrho \circ A_3 \circ \varrho \circ A_2 \circ \varrho \circ (A_1 \bullet + b_1)\) Furthermore, using similar arguments as in Eq. (3.3), we see for \(z \in [0,\infty )\) that \(A (\varrho (B z)) = C^2 n z\). Combining all these observations, we see
Since also \(W(\Phi ) \le 3 d n + 4 d n + 8 d n + 2 n + n + \frac{L-4}{2} \cdot 2 n \le 15 (d + L) n\), we see overall as claimed that  .
.
Case 3: \(L \ge 5\) is odd. In this case, define
A variant of the arguments in Case 2 shows that \( R_\varrho \Phi = C \cdot (C^2 \, n)^{(L-5)/2} \cdot \frac{C^4 n^2}{4 M} \vartheta _{M,y} = \frac{C^L \cdot n^{\lfloor L/2 \rfloor }}{4 M} \vartheta _{M,y} \) and \(W(\Phi ) \le 15 d n + 2 n + \frac{L-5}{2} \cdot 2 n + 1 \le 15 (d + L) n\), and hence  also in this last case. \(\square \)
also in this last case. \(\square \)
Lemma 3.6
Let \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) and \(\varvec{\ell } : \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) be non-decreasing with \(\varvec{\ell }^*\ge 3\). Let \(d \in \mathbb {N}\), \(\alpha \in (0,\infty )\), and \(0< \gamma < \gamma ^{\flat }(\varvec{\ell },\varvec{c})\). Then there exists a constant \(\kappa = \kappa (\gamma ,\alpha ,d,\varvec{\ell },\varvec{c}) > 0\) such that for any \(M \in [1,\infty )\) and \(y \in [0,1]^d\), we have

Proof
Since \(\gamma < \gamma ^{\flat }(\varvec{\ell },\varvec{c})\), there exist \(L = L(\gamma ,\varvec{\ell },\varvec{c}) \in \mathbb {N}_{\ge \ell ^*}\) and \(C_1 = C_1 (\gamma ,\varvec{\ell },\varvec{c}) > 0\) satisfying \(n^\gamma \le C_1 \cdot (\varvec{c}(n))^L \cdot n^{\lfloor L/2 \rfloor }\) for all \(n \in \mathbb {N}\). Since \(\varvec{\ell }^*\ge 3\), we can assume without loss of generality that \(L \ge 3\). Furthermore, since \(L \le \ell ^*\), there exists \(n_0 = n_0(\gamma ,\varvec{\ell },\varvec{c}) \in \mathbb {N}\) satisfying \(L \le \varvec{\ell }(n_0)\).
Given \(M \in [1,\infty )\) and \(y \in [0,1]^d\), set \(n := n_0 \cdot \big \lceil M^{1/(\alpha +\gamma )} \big \rceil \), noting that \(n \ge n_0\). Since \(n^\gamma \le C_1 \cdot (\varvec{c}(n))^L \cdot n^{\lfloor L/2 \rfloor }\), there exists \(0 < C \le \varvec{c}(n)\) satisfying \(n^\gamma \le C_1 \cdot C^L n^{\lfloor L/2 \rfloor }\).
Set \(\kappa := \min \{ (15 (d+L))^{-\alpha } (2 n_0)^{-\alpha }, \, (4 \, C_1)^{-1} \} > 0\) and note \(\kappa = \kappa (d,\alpha ,\gamma ,\varvec{\ell },\varvec{c})\). Furthermore, note that \(n \ge M^{1/(\alpha + \gamma )}\) and hence \( \kappa \, M^{-\frac{\alpha }{\alpha +\gamma }} = \frac{\kappa }{M} \, M^{\frac{\gamma }{\alpha +\gamma }} \le \kappa \, \frac{n^\gamma }{M} \le 4 C_1 \, \kappa \, \frac{C^L \, n^{\lfloor L/2 \rfloor }}{4 M} \le \frac{C^L \, n^{\lfloor L/2 \rfloor }}{4 M} . \) Combining this with the inclusion  for \(c \in [-1,1]\), we see from Lemma 3.5 and because of \(3 \le L \le \varvec{\ell }(n_0) \le \varvec{\ell }(n)\) that
for \(c \in [-1,1]\), we see from Lemma 3.5 and because of \(3 \le L \le \varvec{\ell }(n_0) \le \varvec{\ell }(n)\) that  .
.
We claim that  . To see this, first note \(\Vert g_{M,y} \Vert _{L^\infty } \le \Vert \vartheta _{M,y} \Vert _{L^\infty } \le 1\). Furthermore, for \(t \in \mathbb {N}\), there are two cases: For \(t \ge 15 (d+L) n\), we have
. To see this, first note \(\Vert g_{M,y} \Vert _{L^\infty } \le \Vert \vartheta _{M,y} \Vert _{L^\infty } \le 1\). Furthermore, for \(t \in \mathbb {N}\), there are two cases: For \(t \ge 15 (d+L) n\), we have  , and hence
, and hence  . On the other hand, if \(t \le 15 (d+L) n\), then we see because of \(n \le 1 n_0 + n_0 \, M^{1/(\alpha +\gamma )} \le 2 n_0 \, M^{1/(\alpha +\gamma )}\) that
. On the other hand, if \(t \le 15 (d+L) n\), then we see because of \(n \le 1 n_0 + n_0 \, M^{1/(\alpha +\gamma )} \le 2 n_0 \, M^{1/(\alpha +\gamma )}\) that

Overall, this shows  , so that Lemma 2.1 shows as claimed that
, so that Lemma 2.1 shows as claimed that  . \(\square \)
. \(\square \)
4 Error Bounds for Uniform Approximation
In this section, we derive an upper bound on how many point samples of a function  are needed in order to uniformly approximate f up to error \(\varepsilon \in (0,1)\). The crucial ingredient will be the following estimate of the Lipschitz constant of functions
are needed in order to uniformly approximate f up to error \(\varepsilon \in (0,1)\). The crucial ingredient will be the following estimate of the Lipschitz constant of functions  . The bound in the lemma is one of the reasons for our choice of the quantities \(\gamma ^{\flat }\) and \(\gamma ^{\sharp }\) introduced in Eq. (2.2).
. The bound in the lemma is one of the reasons for our choice of the quantities \(\gamma ^{\flat }\) and \(\gamma ^{\sharp }\) introduced in Eq. (2.2).
Lemma 4.1
Let \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) and \(\varvec{c}: \mathbb {N}\rightarrow [1,\infty ]\) be non-decreasing. Let \(n \in \mathbb {N}\) and assume that \(L := \varvec{\ell }(n)\) and \(C := \varvec{c}(n)\) are finite. Then each  satisfies
satisfies
Proof
Step 1: For any matrix \(A \in \mathbb {R}^{k \times m}\), define \(\Vert A \Vert _{\infty } := \max _{i,j} |A_{i,j}|\) and denote by \(\Vert A \Vert _{\ell ^0}\) the number of nonzero entries of A. In this step, we show that
To prove the first part, note for arbitrary \(x \in \mathbb {R}^m\) and any \(i \in \underline{k}\) that
showing that \(\Vert A x \Vert _{\ell ^\infty } \le \Vert A \Vert _{\infty } \, \Vert x \Vert _{\ell ^1}\). To prove the second part, note for arbitrary \(x \in \mathbb {R}^m\) that
Step 2 (Completing the proof): Let  be arbitrary, so that \(F = R_\varrho \Phi \) for a network \(\Phi = \big ( (A_1,b_1),\dots ,(A_{\widetilde{L}},b_{\widetilde{L}}) \big )\) satisfying \(\widetilde{L} \le \varvec{\ell }(n) = L\) and \(\Vert A_j \Vert _{\infty } \le \Vert \Phi \Vert _{\mathcal{N}\mathcal{N}} \le \varvec{c}(n) = C\), as well as \(\Vert A_j \Vert _{\ell ^0} \le W(\Phi ) \le n\) for all \(j \in \underline{\widetilde{L}}\).
be arbitrary, so that \(F = R_\varrho \Phi \) for a network \(\Phi = \big ( (A_1,b_1),\dots ,(A_{\widetilde{L}},b_{\widetilde{L}}) \big )\) satisfying \(\widetilde{L} \le \varvec{\ell }(n) = L\) and \(\Vert A_j \Vert _{\infty } \le \Vert \Phi \Vert _{\mathcal{N}\mathcal{N}} \le \varvec{c}(n) = C\), as well as \(\Vert A_j \Vert _{\ell ^0} \le W(\Phi ) \le n\) for all \(j \in \underline{\widetilde{L}}\).
Set \(p_j := 1\) if j is even and \(p_j := \infty \) otherwise. Choose \(N_j\) such that \(A_j \in \mathbb {R}^{N_j \times N_{j-1}}\), and define \(T_j \, x := A_j \, x + b_j\). By Step 1, we then see that \( T_j : \bigl ( \mathbb {R}^{N_{j-1}}, \Vert \cdot \Vert _{\ell ^{p_j - 1}} \bigr ) \rightarrow \bigl ( \mathbb {R}^{N_j}, \Vert \cdot \Vert _{\ell ^{p_j}} \bigr ) \) is Lipschitz with
Next, a straightforward computation shows that the “vector-valued ReLU” is 1-Lipschitz as a map \(\varrho : (\mathbb {R}^k, \Vert \cdot \Vert _{\ell ^p}) \rightarrow (\mathbb {R}^k, \Vert \cdot \Vert _{\ell ^p})\), for arbitrary \(p \in [1,\infty ]\) and any \(k \in \mathbb {N}\). As a consequence, we see that
is Lipschitz continuous as a composition of Lipschitz maps, with overall Lipschitz constant
where we used the notation \(n_j := n\) if j is even and \(n_j := 1\) otherwise. Furthermore, we used in the last step that \(C \ge 1\). The final claim of the lemma follows from the elementary estimate \(\Vert x \Vert _{\ell ^1} \le d \cdot \Vert x \Vert _{\ell ^\infty }\) for \(x \in \mathbb {R}^d\). \(\square \)
Based on the preceding lemma, we can now prove an error bound for the computational problem of uniform approximation on the neural network approximation space  .
.
Theorem 4.2
Let \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) and \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) be non-decreasing and suppose that \(\gamma ^{\sharp }(\varvec{\ell },\varvec{c}) < \infty \). Let \(d \in \mathbb {N}\) and \(\alpha \in (0,\infty )\) be arbitrary, and let  as in Eq. (2.3). Furthermore, let
as in Eq. (2.3). Furthermore, let  . Then, we have
. Then, we have

Remark
a) The proof shows that choosing the uniform grid \(\{ 0, \frac{1}{N}, \dots , \frac{N-1}{N} \}^d\) as the set of sampling points (with \(N \sim m^{1/d}\)) yields an essentially optimal sampling scheme.
b) It is well-known (see [25, Proposition 3.3]) that the error of an optimal randomized algorithm is at most two times the error of an optimal deterministic algorithm. Therefore, the theorem also implies that

Proof
Since \(\gamma ^{\sharp }(\varvec{\ell },\varvec{c}) < \infty \), Remark 2.2 shows that \(L := \varvec{\ell }^*< \infty \). Let \(\gamma > \gamma ^{\sharp }(\varvec{\ell },\varvec{c}) \ge 1\) be arbitrary. By definition of \(\gamma ^{\sharp }(\varvec{\ell },\varvec{c})\), it follows that there exists some \(\gamma ' \in \bigl (\gamma ^{\sharp }(\varvec{\ell },\varvec{c}), \gamma \bigr )\) and a constant \(C_0 = C_0(\gamma ', \varvec{\ell },\varvec{c}) = C_0(\gamma ,\varvec{\ell },\varvec{c}) > 0\) satisfying \({ (\varvec{c}(n))^L \cdot n^{\lfloor L/2 \rfloor } \le C_0 \cdot n^{\gamma '} \le C_0 \cdot n^{\gamma } }\) for all \(n \in \mathbb {N}\). Let \(m \in \mathbb {N}\) be arbitrary and choose
Furthermore, let \(I := \bigl \{ 0, \frac{1}{N}, \dots , \frac{N-1}{N} \bigr \}^d \subset [0,1]^d\) and set \(C := \varvec{c}(n)\) and \(\mu := d \cdot C^L \cdot n^{\lfloor L/2 \rfloor }\), noting that \(\mu \le d \, C_0 \, n^{\gamma } =: C_1 \, n^{\gamma }\) and \(|I| = N^d \le m\).
Next, set  and define \(S := \Omega (B)\) for
and define \(S := \Omega (B)\) for
For each \(y = (y_i)_{i \in I} \in S\), choose some \(f_y \in B\) satisfying \(y = \Omega (f_y)\). Note by Lemma 2.1 that  ; by definition of
; by definition of  , we can thus choose
, we can thus choose  satisfying \(\Vert f_y - F_y \Vert _{L^\infty } \le 2 \cdot n^{-\alpha }\). Given this choice, define
satisfying \(\Vert f_y - F_y \Vert _{L^\infty } \le 2 \cdot n^{-\alpha }\). Given this choice, define
We claim that \(\Vert f - Q (\Omega (f)) \Vert _{L^\infty } \le C_2 \cdot m^{-\alpha / (d \cdot (\gamma + \alpha ))}\) for all \(f \in B\), for a suitable constant \(C_2 = C_2(d,\gamma ,\varvec{\ell },\varvec{c})\). Once this is shown, it follows that \( \beta _*^{\textrm{det}} (U, \iota _\infty ) \ge \frac{1}{d} \frac{\alpha }{\gamma + \alpha } , \) which then implies the claim of the theorem, since \(\gamma > \gamma ^{\sharp }(\varvec{\ell },\varvec{c})\) was arbitrary.
Thus, let \(f \in B\) be arbitrary and set \(y := \Omega (f) \in S\). By the same arguments as above, there exists  satisfying \(\Vert f - F \Vert _{L^\infty } \le 2 \cdot n^{-\alpha }\). Now, we see for each \(i \in I\) because of \(f(i) = (\Omega (f))_i = y_i = (\Omega (f_y))_i = f_y(i)\) that
satisfying \(\Vert f - F \Vert _{L^\infty } \le 2 \cdot n^{-\alpha }\). Now, we see for each \(i \in I\) because of \(f(i) = (\Omega (f))_i = y_i = (\Omega (f_y))_i = f_y(i)\) that
Furthermore, Lemma 4.1 shows that \(F - F_y : (\mathbb {R}^d, \Vert \cdot \Vert _{\ell ^\infty }) \rightarrow (\mathbb {R}, |\cdot |)\) is Lipschitz continuous with Lipschitz constant at most \(2 \mu \). Now, given any \(x \in [0,1]^d\), we can choose \(i = i(x) \in I\) satisfying \(\Vert x - i \Vert _{\ell ^\infty } \le N^{-1}\). Therefore, \( |(F - F_y)(x)| \le \frac{2 \mu }{N} + |(F - F_y)(i)| \le \frac{2 \mu }{N} + 4 \, n^{-\alpha } . \) Overall, we have thus shown \(\Vert F - F_y \Vert _{L^\infty } \le \frac{2 \mu }{N} + 4 \, n^{-\alpha }\), which finally implies because of \(Q(\Omega (f)) = Q(y) = F_y\) that
It remains to note that our choice of N and n implies \(m^{1/d} \le 1 + N \le 2 N\) and hence \(\frac{1}{N} \le 2 m^{-1/d}\) and furthermore \(n \le 1 + m^{1/(d \cdot (\gamma + \alpha ))} \le 2 \, m^{1/(d \cdot (\gamma + \alpha ))}\). Hence, recalling that \(\mu \le C_1 \, n^{\gamma }\), we see
Furthermore, since \(n \ge m^{1/(d \cdot (\gamma +\alpha ))}\), we also have \(n^{-\alpha } \le m^{-\frac{\alpha }{d \cdot (\gamma + \alpha )}}\). Combining all these observations, it is easy to see that \({\Vert f - Q(\Omega (f)) \Vert _{L^\infty } \le C_2 \cdot m^{-\frac{\alpha }{d \cdot (\gamma +\alpha )}}}\), for a suitable constant \(C_2 = C_2(d,\gamma ,\varvec{\ell },\varvec{c}) > 0\). Since \(f \in B\) was arbitrary, this completes the proof. \(\square \)
5 Hardness of Uniform Approximation
In this section, we show that the error bound for uniform approximation provided by Theorem 4.2 is optimal, at least in the common case where \(\gamma ^{\flat }(\varvec{\ell },\varvec{c}) = \gamma ^\sharp (\varvec{\ell },\varvec{c})\) and \(\varvec{\ell }^*\ge 3\). This latter condition means that the approximation for defining the approximation space  is performed using networks with at least two hidden layers. We leave it as an interesting question for future work whether a similar result even holds for approximation spaces associated to shallow networks.
is performed using networks with at least two hidden layers. We leave it as an interesting question for future work whether a similar result even holds for approximation spaces associated to shallow networks.
Theorem 5.1
Let \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) and \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) be non-decreasing with \(\varvec{\ell }^*\ge 3\). Given \(d \in \mathbb {N}\) and \(\alpha \in (0,\infty )\), let  as in Eq. (2.3) and consider the embedding
as in Eq. (2.3) and consider the embedding  . Then
. Then

Proof
Set \(K := [0,1]^d\) and  .
.
Step 1: Let \(0< \gamma < \gamma ^{\flat }(\varvec{\ell },\varvec{c})\). Let \(m \in \mathbb {N}\) be arbitrary and \(\Gamma _m := \underline{2k}^d \times \{ \pm 1 \}\), where \(k := \big \lceil m^{1/d} \big \rceil \). In this step, we show that there is a constant \(\kappa = \kappa (d,\alpha ,\gamma ,\varvec{\ell },\varvec{c}) > 0\) (independent of m) and a family of functions \((f_{\ell ,\nu })_{(\ell ,\nu ) \in \Gamma _m} \subset U\) which satisfies

To see this, set \(M := 4 k\), and for \(\ell \in \underline{2k}^d\) define \(y^{(\ell )} := \frac{(1,\dots ,1)}{4 k} + \frac{\ell - (1,\dots ,1)}{2 k} \in \mathbb {R}^d\). Then, we have
which shows that the functions \(\vartheta _{M,y^{(\ell )}}\), \(\ell \in \underline{2k}^d\), (with \(\vartheta _{M,y}\) as defined in Lemma 3.4), have disjoint supports contained in \([0,1]^d\). Furthermore, Lemma 3.6 yields a constant \(\kappa _1 = \kappa _1(\gamma ,\alpha ,d,\varvec{\ell },\varvec{c}) > 0\) such that \( f_{\ell ,\nu } := \kappa _1 \cdot M^{-\alpha /(\alpha +\gamma )} \cdot \nu \cdot \vartheta _{M,y^{(\ell )}} \in U \) for arbitrary \((\ell ,\nu ) \in \Gamma _m\).
To prove Eq. (5.1), let \(A \in {\text {Alg}}_m (U, C([0,1]^d))\) be arbitrary. By definition, there exist \(\varvec{x}= (x_1,\dots ,x_m) \in K^m\) and a function \(Q : \mathbb {R}^m \rightarrow \mathbb {R}\) satisfying \(A(f) = Q(f(x_1),\dots ,f(x_m))\) for all \(f \in U\). Choose \( I := I_{\varvec{x}} := \big \{ \ell \in \underline{2k}^d :\forall \, n \in \underline{m} : \vartheta _{M,y^{(\ell )}} (x_n) = 0 \big \} . \) Then for each \(\ell \in I^c = \underline{2k}^d \setminus I\), there exists \(n_\ell \in \underline{m}\) such that \(\vartheta _{M,y^{(\ell )}}(x_{n_\ell }) \ne 0\). Then the map \(I^c \rightarrow \underline{m}, \ell \mapsto n_\ell \) is injective, since \(\vartheta _{M,y^{(\ell )}} \, \vartheta _{M,y^{(t)}} = 0\) for \(t,\ell \in \underline{2k}^d\) with \(t \ne \ell \). Therefore, \(|I^c| \le m\) and hence \(|I| \ge (2k)^d - m \ge m\), because of \(k \ge m^{1/d}\).
Define \(h := Q(0,\dots ,0)\). Then for each \(\ell \in I_{\varvec{x}}\) and \(\nu \in \{ \pm 1 \}\), we have \(f_{\ell ,\nu }(x_n) = 0\) for all \(n \in \underline{m}\) and hence \(A(f_{\ell ,\nu }) = Q(0,\dots ,0) = h\). Therefore,
Furthermore, since \(k \le 1 + m^{1/d} \le 2 m^{1/d}\), we see \(k^d \le 2^d m\) and \(M = 4 k \le 8 \, m^{1/d}\) and hence \( M^{\frac{\alpha }{\alpha +\gamma }} \le 8^{\frac{\alpha }{\alpha +\gamma }} m^{\frac{1}{d} \frac{\alpha }{\alpha +\gamma }} . \) Combining these estimates with Eq. (5.2) and recalling that \(|I| \ge m\), we finally see

which establishes Eq. (5.1) for \(\kappa := \frac{\kappa _1/8}{4^d}\).
Step 2 (Completing the proof): Given Eq. (5.1), a direct application of Lemma 2.3 shows that \( \beta _*^{\textrm{det}}(U,\iota _\infty ), \beta _*^{\textrm{ran}}(U,\iota _\infty ) \le \frac{1}{d} \frac{\alpha }{\alpha + \gamma } . \) Since this holds for arbitrary \(0< \gamma < \gamma ^{\flat }(\varvec{\ell },\varvec{c})\), we easily obtain the claim of the theorem. \(\square \)
6 Error Bounds for Approximation in \(L^2\)
This section provides error bounds for the approximation of functions in  based on point samples, with error measured in \(L^2\). In a nutshell, the argument is based on combining bounds from statistical learning theory (specifically from [13]) with bounds for the covering numbers of the neural network sets
based on point samples, with error measured in \(L^2\). In a nutshell, the argument is based on combining bounds from statistical learning theory (specifically from [13]) with bounds for the covering numbers of the neural network sets  .
.
For completeness, we mention that the \(\varepsilon \)-covering number \(\textrm{Cov}(\Sigma , \varepsilon )\) (with \(\varepsilon > 0\)) of a (non-empty) subset \(\Sigma \) of a metric space (X, d) is the minimal number \(N \in \mathbb {N}\) for which there exist \(f_1,\dots ,f_N \in \Sigma \) satisfying \(\Sigma \subset \bigcup _{j=1}^N \overline{B}_\varepsilon (f_j)\). Here, \(\overline{B}_\varepsilon (f) := \{ g \in X :d(f,g) \le \varepsilon \}\). If no such \(N \in \mathbb {N}\) exists, then \(\textrm{Cov}(\Sigma ,\varepsilon ) = \infty \). If we want to emphasize the metric space X, we also write \(\textrm{Cov}_X (\Sigma ,\varepsilon )\).
For the case where one considers networks of a given architecture, bounds for the covering numbers of network sets have been obtained for instance in [8, Proposition 2.8]. Here, however, we are interested in sparsely connected networks with unspecified architecture. For this case, the following lemma provides covering bounds.
Lemma 6.1
Let \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2}\) and \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\) be non-decreasing. The covering numbers of the neural network set  (considered as a subset of the metric space \(C([0,1]^d)\)) can be estimated by
(considered as a subset of the metric space \(C([0,1]^d)\)) can be estimated by

for arbitrary \(\varepsilon \in (0,1]\) and \(n \in \mathbb {N}\).
Proof
Define \(L := \varvec{\ell }(n)\) and \(R := \varvec{c}(n)\). We will use some results and notation from [8]. Precisely, given a network architecture \(\varvec{a}= (a_0,\dots ,a_K) \in \mathbb {N}^{K+1}\), we denote by
the set of all network weights with architecture \(\varvec{a}\) and all weights bounded (in magnitude) by R. Let us also define the index set \( I(\varvec{a}) := \biguplus _{j=1}^{K} \big ( \{ j \} \times \{ 1,...,a_j \} \times \{ 1,...,1+a_{j-1} \} \big ) , \) noting that \(\mathcal{N}\mathcal{N}(\varvec{a}) \cong [-R,R]^{I(\varvec{a})}\). In the following, we will equip \(\mathcal{N}\mathcal{N}(\varvec{a})\) with the \(\ell ^\infty \)-norm. Then, [8, Theorem 2.6] shows that the realization map \(R_\varrho : \mathcal{N}\mathcal{N}(\varvec{a}) \rightarrow C([0,1]^d), \Phi \mapsto R_\varrho \Phi \) is Lipschitz continuous on \(\mathcal{N}\mathcal{N}(\varvec{a})\), with Lipschitz constant bounded by \(2 K^2 \, R^{K-1} \, \Vert \varvec{a}\Vert _\infty ^{K}\), a fact that we will use below.
For \(\ell \in \{ 1,\dots ,L \}\), define \(\varvec{a}^{(\ell )} := (d,n,\dots ,n,1) \in \mathbb {N}^{\ell +1}\) and \(I_\ell := I(\varvec{a}^{(\ell )})\), as well as
By dropping “dead neurons,” it is easy to see that each \(f \in \Sigma _\ell \) is of the form \({f = R_\varrho \Phi }\) for some \({\Phi \in \mathcal{N}\mathcal{N}(\varvec{a}^{(\ell )})}\) satisfying \(W(\Phi ) \le n\). Thus, keeping the identification \({\mathcal{N}\mathcal{N}(\varvec{a}) \cong [-R,R]^{I(\varvec{a})}}\), given a subset \(S \subset I_\ell \), let us write \(\mathcal{N}\mathcal{N}_{S,\ell } := \big \{ \Phi \in \mathcal{N}\mathcal{N}(\varvec{a}^{(\ell )}) :{\text {supp}}\Phi \subset S \big \}\); then we have \({\Sigma _\ell = \bigcup _{S \subset I_\ell , |S| = \min \{ n, |I_\ell | \} } R_\varrho (\mathcal{N}\mathcal{N}_{S,\ell })}\). Moreover, it is easy to see that \(|I_\ell | \le 2d\) if \(\ell = 1\) while if \(\ell \ge 2\) then \(|I_\ell | = 1 + n (d+2) + (\ell -2) (n^2 + n)\). This implies in all cases that \(|I_\ell | \le 2 n (L n + d)\).
Now we collect several observations which in combination will imply the claimed bound. First, directly from the definition of covering numbers, we see that if \(\Theta \) is Lipschitz continuous, then \(\textrm{Cov}(\Theta (\Omega ), \varepsilon ) \le \textrm{Cov}(\Omega , \frac{\varepsilon }{\textrm{Lip}(\Theta )})\), and furthermore \({\textrm{Cov}(\bigcup _{j=1}^K \Omega _j, \varepsilon ) \le \sum _{j=1}^K \textrm{Cov}(\Omega _j, \varepsilon )}\). Moreover, since \(\mathcal{N}\mathcal{N}_{S,\ell } \cong [-R,R]^{|S|}\), we see by [8, Lemma 2.7] that \(\textrm{Cov}_{\ell ^\infty }(\mathcal{N}\mathcal{N}_{S,\ell }, \varepsilon ) \le \lceil R/\varepsilon \rceil ^n \le (2R/\varepsilon )^n\). Finally, [50, Exercise 0.0.5] provides the bound \(\left( {\begin{array}{c}N\\ n\end{array}}\right) \le (e N / n)^n\) for \(n \le N\).
Recall that the realization map \(R_\varrho : \mathcal{N}\mathcal{N}(\varvec{a}^{(\ell )}) \rightarrow C([0,1]^d)\) is Lipschitz continuous with \({\textrm{Lip}(R_{\varrho }) \le C := 2 L^2 R^{L-1} \max \{ d,n \}^L}\). Combining this with the observations from the preceding paragraph and recalling that \({|I_\ell | \le 2 n (L n + d)}\), we see
Finally, noting that  and setting \({\eta := \max \{ d,n \}}\), we see via elementary estimates that
and setting \({\eta := \max \{ d,n \}}\), we see via elementary estimates that

which implies the claim of the lemma. \(\square \)
Using the preceding bounds for the covering numbers of the network sets  , we now derive covering number bounds for the (closure of the) unit ball
, we now derive covering number bounds for the (closure of the) unit ball  of the approximation space
of the approximation space  .
.
Lemma 6.2
Let \(d \in \mathbb {N}\), \(C_1,C_2,\alpha \in (0,\infty )\), and \(\theta ,\nu \in [0,\infty )\). Assume that \(\varvec{c}(n) \le C_1 \cdot n^\theta \) and \(\varvec{\ell }(n) \le C_2 \cdot \ln ^\nu (2 n)\) for all \(n \in \mathbb {N}\).
Then there exists \(C = C(d,\alpha ,\theta ,\nu ,C_1,C_2) > 0\) such that for any \(\varepsilon \in (0,1]\), the unit ball

satisfies

Here, we denote by  the closure of
the closure of  in \(C([0,1]^d)\).
in \(C([0,1]^d)\).
Proof
Let \(n := \big \lceil (8/\varepsilon )^{1/\alpha } \big \rceil \in \mathbb {N}_{\ge 2}\), noting \(n^{-\alpha } \le \varepsilon / 8\). Set \(C := \varvec{c}(n)\) and \(L := \varvec{\ell }(n)\). Lemma 6.1 provides an absolute constant \(C_3 > 0\) and \(N \in \mathbb {N}\) such that \(N \le \bigl (\frac{C_3}{\varepsilon } \, L^4 \cdot (C \, \max \{ d,n \})^{1+L} \bigr )^n\) and functions  satisfying
satisfying  ; here, \(\overline{B}_\varepsilon (h)\) is the closed ball in \(C([0,1]^d)\) of radius \(\varepsilon \) around h. For each \(j \in \underline{N}\) choose
; here, \(\overline{B}_\varepsilon (h)\) is the closed ball in \(C([0,1]^d)\) of radius \(\varepsilon \) around h. For each \(j \in \underline{N}\) choose  , provided that the intersection is non-empty; otherwise choose
, provided that the intersection is non-empty; otherwise choose  .
.
We claim that  . To see this, let
. To see this, let  be arbitrary; then Lemma 2.1 shows that
be arbitrary; then Lemma 2.1 shows that  . Directly from the definition of
. Directly from the definition of  we see that we can choose
we see that we can choose  satisfying \(n^\alpha \, \Vert f - h \Vert _{L^\infty } \le 2\) and hence \(\Vert f - h \Vert _{L^\infty } \le \frac{\varepsilon }{4}\). By choice of \(h_1,\dots ,h_N\), there exists \(j \in \underline{N}\) satisfying \(\Vert h - h_j \Vert _{L^\infty } \le \frac{\varepsilon }{4}\). This implies \(\Vert f - h_j \Vert _{L^\infty } \le \frac{\varepsilon }{2}\) and therefore
satisfying \(n^\alpha \, \Vert f - h \Vert _{L^\infty } \le 2\) and hence \(\Vert f - h \Vert _{L^\infty } \le \frac{\varepsilon }{4}\). By choice of \(h_1,\dots ,h_N\), there exists \(j \in \underline{N}\) satisfying \(\Vert h - h_j \Vert _{L^\infty } \le \frac{\varepsilon }{4}\). This implies \(\Vert f - h_j \Vert _{L^\infty } \le \frac{\varepsilon }{2}\) and therefore  . By our choice of \(g_j\), we thus have
. By our choice of \(g_j\), we thus have  and hence \(\Vert f - g_j \Vert _{L^\infty } \le \varepsilon \). All in all, we have thus shown
and hence \(\Vert f - g_j \Vert _{L^\infty } \le \varepsilon \). All in all, we have thus shown  and hence also
and hence also  . This implies
. This implies  , so that it remains to estimate N sufficiently well.
, so that it remains to estimate N sufficiently well.
To estimate N, first note that
for a suitable constant \(C_4 = C_4(\alpha ) > 0\). This implies
with a constant \(C_5 = C_5(C_2,\nu ,\alpha ) \ge 1\).
Now, using Eq. (6.1) and noting \(\max \{ d,n \} \le d \, n\), we obtain \(C_6 = C_6 (d,\alpha ,C_1) > 0\) and \(C_7 = C_7 (d,\alpha ,\theta ,\nu ,C_1,C_2) > 0\) satisfying
Furthermore, using the elementary estimate \(\ln x \le x\) for \(x > 0\), we see
for suitable constants \(C_8,C_9,C_10\) all only depending on \(\nu ,\alpha ,C_2\).
Overall, recalling the estimate for N from the beginning of the proof and using Eqs. (6.1), (6.2) and (6.3), we finally see
which easily implies the claim of the lemma. \(\square \)
Combining the preceding covering number bounds with bounds from statistical learning theory, we now prove the following error bound for approximating functions  from point samples, with error measured in \(L^2\).
from point samples, with error measured in \(L^2\).
Theorem 6.3
Let \(d \in \mathbb {N}\), \(C_1,C_2,\alpha \in (0,\infty )\), and \(\theta ,\nu \in [0,\infty )\). Let \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\) and \(\varvec{\ell } : \mathbb {N}\rightarrow \mathbb {N}_{\ge 2}\) be non-decreasing and such that \(\varvec{c}(n) \le C_1 \cdot n^\theta \) and \(\varvec{\ell }(n) \le C_2 \cdot \ln ^\nu (2 n)\) for all \(n \in \mathbb {N}\). Let  as in Eq. (2.3), and denote by
as in Eq. (2.3), and denote by  the closure of
the closure of  in \(C([0,1]^d)\).
in \(C([0,1]^d)\).
Then there exists a constant \(C = C(\alpha ,\theta ,\nu ,d,C_1,C_2) > 0\) such that for each \(m \in \mathbb {N}\), there are points \(x_1,\dots ,x_m \in [0,1]^d\) with the following property:

In particular, this implies for the embedding  that
that

Remark
The proof shows that the points \(x_1,\dots ,x_m\) can be obtained with positive probability by uniformly and independently sampling \(x_1,\dots ,x_m\) from \([0,1]^d\). In fact, an inspection of the proof shows for each \(m \in \mathbb {N}\) that this sampling procedure will result in “good” points with probability at least
Proof
Step 1: An essential ingredient for our proof is [13, Proposition 7]. In this step, we briefly recall the general setup from [13] and describe how it applies to our setting.
Let us fix a function  for the moment. In [13], one starts with a probability measure \(\rho \) on \(Z = X \times Y\), where X is a compact domain and \(Y = \mathbb {R}\). In our case we take \(X = [0,1]^d\) and we define \(\rho (M) := \rho _{f_0}(M) := \varvec{\lambda }(\{ x \in [0,1]^d :(x,f_0(x)) \in M \})\) for any Borel set \(M \subset X \times Y\). In other words, \(\rho \) is the distribution of the random variable \(\xi = (\eta , f_0(\eta ))\), where \(\eta \) is uniformly distributed in \(X = [0,1]^d\). Then, in the notation of [13], the measure \(\rho _X\) on X is simply the Lebesgue measure on \([0,1]^d\) and the conditional probability measure \(\rho (\bullet \mid x)\) on Y is \(\rho (\bullet \mid x) = \delta _{f_0(x)}\). Furthermore, the regression function \(f_\rho \) considered in [13] is simply \(f_\rho = f_0\), and the (least squares) error \(\mathcal {E}(f)\) of \(f : X \rightarrow Y\) is \(\mathcal {E}(f) = \int _{[0,1]^d} |f(x) - f_0(x)|^2 \, d\varvec{\lambda }(x) = \Vert f - f_0 \Vert _{L^2}^2\); to emphasize the role of \(f_0\), we shall write \(\mathcal {E}(f; f_0) = \Vert f - f_0 \Vert _{L^2}^2\) instead. The empirical error of \(f : X \rightarrow Y\) with respect to a sample \(\varvec{z}\in Z^m\) is
for the moment. In [13], one starts with a probability measure \(\rho \) on \(Z = X \times Y\), where X is a compact domain and \(Y = \mathbb {R}\). In our case we take \(X = [0,1]^d\) and we define \(\rho (M) := \rho _{f_0}(M) := \varvec{\lambda }(\{ x \in [0,1]^d :(x,f_0(x)) \in M \})\) for any Borel set \(M \subset X \times Y\). In other words, \(\rho \) is the distribution of the random variable \(\xi = (\eta , f_0(\eta ))\), where \(\eta \) is uniformly distributed in \(X = [0,1]^d\). Then, in the notation of [13], the measure \(\rho _X\) on X is simply the Lebesgue measure on \([0,1]^d\) and the conditional probability measure \(\rho (\bullet \mid x)\) on Y is \(\rho (\bullet \mid x) = \delta _{f_0(x)}\). Furthermore, the regression function \(f_\rho \) considered in [13] is simply \(f_\rho = f_0\), and the (least squares) error \(\mathcal {E}(f)\) of \(f : X \rightarrow Y\) is \(\mathcal {E}(f) = \int _{[0,1]^d} |f(x) - f_0(x)|^2 \, d\varvec{\lambda }(x) = \Vert f - f_0 \Vert _{L^2}^2\); to emphasize the role of \(f_0\), we shall write \(\mathcal {E}(f; f_0) = \Vert f - f_0 \Vert _{L^2}^2\) instead. The empirical error of \(f : X \rightarrow Y\) with respect to a sample \(\varvec{z}\in Z^m\) is
We shall also use the notation
Furthermore, as the hypothesis space \(\mathcal {H}\) we choose  . As required in [13], this is a compact subset of C(X); indeed
. As required in [13], this is a compact subset of C(X); indeed  is closed and has finite covering numbers
is closed and has finite covering numbers  for arbitrarily small \(\varepsilon > 0\) (see Lemma 6.2). Thus,
for arbitrarily small \(\varepsilon > 0\) (see Lemma 6.2). Thus,  is compact; see for instance [2, Theorem 3.28].
is compact; see for instance [2, Theorem 3.28].
Moreover, since every \((x,y) \in Z\) satisfies \(y = f_0(x)\) almost surely (with respect to \(\rho = \rho _{f_0}\)), and since all  satisfy \(\Vert f \Vert _{C([0,1]^d)} \le 1\), we see that \(\rho _{f_0}\)-almost surely, the estimate \(|f(x) - y| = |f(x) - f_0(x)| \le 2 =: M\) holds for all \(f \in \mathcal {H}\). Furthermore, in [13], the function \(f_{\mathcal {H}} \in \mathcal {H}\) is a minimizer of \(\mathcal {E}\) over \(\mathcal {H}\); in our case, since \(f_0 \in \mathcal {H}\), we easily see that \(f_{\mathcal {H}} = f_0\) and \(\mathcal {E}(f_{\mathcal {H}}) = 0\). Therefore, the error in \(\mathcal {H}\) of \(f \in \mathcal {H}\) as considered in [13] is simply \(\mathcal {E}_{\mathcal {H}}(f) = \mathcal {E}(f) - \mathcal {E}(f_{\mathcal {H}}) = \mathcal {E}(f)\). Finally, the empirical error in \(\mathcal {H}\) of \(f \in \mathcal {H}\) is given by \(\mathcal {E}_{\mathcal {H},\varvec{z}}(f) = \mathcal {E}_{\varvec{z}}(f) - \mathcal {E}_{\varvec{z}}(f_{\mathcal {H}})\). Hence, if \(\varvec{z}= \bigl ( (x_1,y_1),\dots ,(x_m,y_m)\bigr )\) satisfies \(y_i = f_0(x_i)\) for all \(i \in \underline{m}\), then \(\mathcal {E}_{\mathcal {H},\varvec{z}}(f) = \mathcal {E}_{\varvec{z}}(f) = \mathcal {E}_{\varvec{x}}(f; f_0)\), because of \(f_{\mathcal {H}} = f_0\).
satisfy \(\Vert f \Vert _{C([0,1]^d)} \le 1\), we see that \(\rho _{f_0}\)-almost surely, the estimate \(|f(x) - y| = |f(x) - f_0(x)| \le 2 =: M\) holds for all \(f \in \mathcal {H}\). Furthermore, in [13], the function \(f_{\mathcal {H}} \in \mathcal {H}\) is a minimizer of \(\mathcal {E}\) over \(\mathcal {H}\); in our case, since \(f_0 \in \mathcal {H}\), we easily see that \(f_{\mathcal {H}} = f_0\) and \(\mathcal {E}(f_{\mathcal {H}}) = 0\). Therefore, the error in \(\mathcal {H}\) of \(f \in \mathcal {H}\) as considered in [13] is simply \(\mathcal {E}_{\mathcal {H}}(f) = \mathcal {E}(f) - \mathcal {E}(f_{\mathcal {H}}) = \mathcal {E}(f)\). Finally, the empirical error in \(\mathcal {H}\) of \(f \in \mathcal {H}\) is given by \(\mathcal {E}_{\mathcal {H},\varvec{z}}(f) = \mathcal {E}_{\varvec{z}}(f) - \mathcal {E}_{\varvec{z}}(f_{\mathcal {H}})\). Hence, if \(\varvec{z}= \bigl ( (x_1,y_1),\dots ,(x_m,y_m)\bigr )\) satisfies \(y_i = f_0(x_i)\) for all \(i \in \underline{m}\), then \(\mathcal {E}_{\mathcal {H},\varvec{z}}(f) = \mathcal {E}_{\varvec{z}}(f) = \mathcal {E}_{\varvec{x}}(f; f_0)\), because of \(f_{\mathcal {H}} = f_0\).
Now, let \(\varvec{x}= (x_1,\dots ,x_m)\) be i.i.d. uniformly distributed in \([0,1]^d\) and set \(y_i = f_0(x_i)\) for \(i \in \underline{m}\) and \(\varvec{z}= (z_1,\dots ,z_m) = \bigl ( (x_1,y_1),\dots ,(x_m,y_m)\bigr )\). Then \(z_1,\dots ,z_m \overset{iid}{\sim }\ \rho _{f_0}\). Therefore, [13, Proposition 7] (applied with \(\alpha = \frac{1}{6}\)) shows for arbitrary \(\varepsilon > 0\) and \(m \in \mathbb {N}\) that there is a measurable set

Here, we remark that [13, Proposition 7] requires the hypothesis space \(\mathcal {H}\) to be convex, which is not in general satisfied in our case. However, as shown in [13, Remark 13], the assumption of convexity can be dropped provided that \(f_\rho \in \mathcal {H}\), which is satisfied in our case.
Step 2: In this step, we prove the first claim of the theorem. To this end, we first apply Lemma 6.2 to obtain a constant \(C_3 = C_3(\alpha ,\nu ,\theta ,d,C_1,C_2) > 0\) satisfying

Next, define \(C_4 := 1 + \frac{\alpha }{1 + \alpha }\) and \(C_5 := C_4^{1+\nu }\), and choose \(C_6 = C_6(\alpha ,\nu ,\theta ,d,C_1,C_2) \ge 1\) such that \(2 C_3 C_5 - \frac{C_6}{288} \le -1 < 0\).
Let \(m \in \mathbb {N}\) be arbitrary with \(m \ge m_0 = m_0(\alpha ,\nu ,\theta ,d,C_1,C_2) \ge 2\), where \(m_0\) is chosen such that \(\varepsilon := C_6 \cdot \big ( \ln ^{1+\nu }(2 m) \big / m \big )^{\alpha / (1+\alpha )}\) satisfies \(\varepsilon \in (0,1]\); the case \(m \le m_0\) will be considered below. Let \(N := N_\varepsilon \) as in Eq. (6.6). Since  , we can choose
, we can choose  such that
such that  , where \(\overline{B}_\varepsilon (f) := \bigl \{ g \in C([0,1]^d) :\Vert f - g \Vert _{L^\infty } \le \varepsilon \bigr \}\). Now, for each \(j \in \underline{N}\), choose \(E_j := E(m,\varepsilon ,f_j) \subset ([0,1]^d)^m\) as in Eq. (6.5), and define \(E^*:= \bigcup _{j=1}^N E_j\).
, where \(\overline{B}_\varepsilon (f) := \bigl \{ g \in C([0,1]^d) :\Vert f - g \Vert _{L^\infty } \le \varepsilon \bigr \}\). Now, for each \(j \in \underline{N}\), choose \(E_j := E(m,\varepsilon ,f_j) \subset ([0,1]^d)^m\) as in Eq. (6.5), and define \(E^*:= \bigcup _{j=1}^N E_j\).
Note because of \(C_6 \ge 1\) and \(\ln (2m) \ge \ln (4) \ge 1\) that \(\varepsilon \ge \big ( \ln ^{1+\nu }(2 m) \big / m \big )^{\alpha /(1+\alpha )} \ge m^{-\alpha /(1+\alpha )}\) and hence
Using the estimate for \(N = N_\varepsilon \) from Eq. (6.6) and the bound for the measure of \(E_j\) from Eq. (6.5), we thus see

Thus, we can choose \(\varvec{x}= (x_1,\dots ,x_m) \in ([0,1]^d)^m \setminus E^*\). We claim that every such choice satisfies the property stated in the first part of the theorem.
To see this, let  be arbitrary with \(f(x_i) = g(x_i)\) for all \(i \in \underline{m}\). By choice of \(f_1,\dots ,f_N\), there exists some \(j \in \underline{N}\) satisfying \(\Vert f - f_j \Vert _{L^\infty } \le \varepsilon \). Since \(\varvec{x}\notin E^*\), we have \(\varvec{x}\notin E_j = E(m,\varepsilon ,f_j)\). In view of Eq. (6.5), this implies \(\mathcal {E}(g;f_j) - \mathcal {E}_{\varvec{x}}(g;f_j) \le \frac{1}{2} (\mathcal {E}(g;f_j) + \varepsilon )\), and after rearranging, this yields \(\mathcal {E}(g;f_j) \le 2 \, \mathcal {E}_{\varvec{x}}(g;f_j) + \varepsilon \). Because of \(\Vert g - f_j \Vert _{L^2} \le \Vert g \Vert _{L^\infty } + \Vert f_j \Vert _{L^\infty } \le 2\) and thanks to the elementary estimate \((a + \varepsilon )^2 = a^2 + 2 a \varepsilon + \varepsilon ^2 \le a^2 + 5 \varepsilon \) for \(0 \le a \le 2\), we thus see
be arbitrary with \(f(x_i) = g(x_i)\) for all \(i \in \underline{m}\). By choice of \(f_1,\dots ,f_N\), there exists some \(j \in \underline{N}\) satisfying \(\Vert f - f_j \Vert _{L^\infty } \le \varepsilon \). Since \(\varvec{x}\notin E^*\), we have \(\varvec{x}\notin E_j = E(m,\varepsilon ,f_j)\). In view of Eq. (6.5), this implies \(\mathcal {E}(g;f_j) - \mathcal {E}_{\varvec{x}}(g;f_j) \le \frac{1}{2} (\mathcal {E}(g;f_j) + \varepsilon )\), and after rearranging, this yields \(\mathcal {E}(g;f_j) \le 2 \, \mathcal {E}_{\varvec{x}}(g;f_j) + \varepsilon \). Because of \(\Vert g - f_j \Vert _{L^2} \le \Vert g \Vert _{L^\infty } + \Vert f_j \Vert _{L^\infty } \le 2\) and thanks to the elementary estimate \((a + \varepsilon )^2 = a^2 + 2 a \varepsilon + \varepsilon ^2 \le a^2 + 5 \varepsilon \) for \(0 \le a \le 2\), we thus see
But directly from the definition and because of \(g(x_i) = f(x_i)\) and \(\Vert f - f_j \Vert _{L^\infty } \le \varepsilon \), we see \({ \mathcal {E}_{\varvec{x}}(g;f_j) = \frac{1}{m} \sum _{i=1}^m \bigl ( g(x_i) - f_j(x_i) \bigr )^2 \le \varepsilon ^2 \le \varepsilon . }\) Overall, we thus see that

We have thus proved the claim for \(m \ge m_0\). Since \(\Vert g - f \Vert _{L^2} \le \Vert f \Vert _{L^\infty } + \Vert g \Vert _{L^\infty } \le 2\) for arbitrary  , it is easy to see that this proves the claim for all \(m \in \mathbb {N}\), possibly after enlarging C.
, it is easy to see that this proves the claim for all \(m \in \mathbb {N}\), possibly after enlarging C.
Step 3: To complete the proof of the theorem, for each \(\varvec{y}= (y_1,\dots ,y_m) \in \mathbb {R}^m\), choose a fixed  satisfying
satisfying

existence of \(f_{\varvec{y}}\) is an easy consequence of the compactness of  . Define
. Define

Then given any  , the function
, the function  satisfies \(f(x_i) = g(x_i)\) for all \(i \in \underline{m}\), and hence \(\Vert f - A f \Vert _{L^2} \le C \cdot \bigl (\ln ^{1+\nu }(2 m) \big / m\bigr )^{\frac{\alpha /2}{1 + \alpha }}\), as shown in the previous step. By definition of \(\beta _*^{\textrm{det}}(\overline{U}_{\vec {\ell }, \vec {c}}^{\alpha ,\infty },\iota _2)\), this easily entails \(\beta _*^{\textrm{det}}(\overline{U}_{\vec {\ell }, \vec {c}}^{\alpha ,\infty },\iota _2) \ge \frac{\alpha /2}{1 + \alpha }\). \(\square \)
satisfies \(f(x_i) = g(x_i)\) for all \(i \in \underline{m}\), and hence \(\Vert f - A f \Vert _{L^2} \le C \cdot \bigl (\ln ^{1+\nu }(2 m) \big / m\bigr )^{\frac{\alpha /2}{1 + \alpha }}\), as shown in the previous step. By definition of \(\beta _*^{\textrm{det}}(\overline{U}_{\vec {\ell }, \vec {c}}^{\alpha ,\infty },\iota _2)\), this easily entails \(\beta _*^{\textrm{det}}(\overline{U}_{\vec {\ell }, \vec {c}}^{\alpha ,\infty },\iota _2) \ge \frac{\alpha /2}{1 + \alpha }\). \(\square \)
7 Hardness of Approximation in \(L^2\)
This section presents hardness results for approximating the embedding  using point samples.
using point samples.
Theorem 7.1
Let \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) and \(\varvec{\ell } : \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) be non-decreasing with \(\varvec{\ell }^*\ge 2\). Let \(d \in \mathbb {N}\) and \(\alpha \in (0,\infty )\). Set \(\gamma ^\flat := \gamma ^{\flat }(\varvec{\ell },\varvec{c})\) as in Eq. (2.2) and let  as in Eq. (2.3). For the embedding
as in Eq. (2.3). For the embedding  , we then have
, we then have

Remark
The bound from above might seem intimidating at first sight, so we point out two important consequences: First, we always have  which shows that no matter how large the approximation rate \(\alpha \) is, one can never get a better convergence rate than \(m^{-3/2}\). Furthermore, in the important case where \(\gamma ^{\flat } = \infty \) (for instance if the depth-growth function \(\varvec{\ell }\) is unbounded), then
which shows that no matter how large the approximation rate \(\alpha \) is, one can never get a better convergence rate than \(m^{-3/2}\). Furthermore, in the important case where \(\gamma ^{\flat } = \infty \) (for instance if the depth-growth function \(\varvec{\ell }\) is unbounded), then  These two bounds are the interesting bounds for the regime of large \(\alpha \).
These two bounds are the interesting bounds for the regime of large \(\alpha \).
For small \(\alpha > 0\), the theorem shows

since \(\gamma ^{\flat } \ge 1\). This shows that one cannot get a good rate of convergence for small exponents \(\alpha > 0\).
Proof
Step 1 (preparation): Let \(0< \gamma < \gamma ^{\flat }\) be arbitrary and let \(\theta \in (0,\infty )\) and \(\lambda \in [0,1]\) with \(\theta \lambda \le 1\) and set \(\omega := \min \{ -\theta \alpha , \,\, \theta \cdot (\gamma - \lambda ) - 1 \} \in (-\infty ,0)\).
Let \(m \in \mathbb {N}\) be arbitrary and set \(M := 4 m\) and \(z_j := \frac{1}{4 m} + \frac{j-1}{2 m}\) for \(j \in \underline{2 m}\). Then, Lemma 3.2 yields a constant \(\kappa = \kappa (\gamma ,\alpha ,\lambda ,\theta ,\varvec{\ell },\varvec{c}) > 0\) (independent of m) such that

Furthermore, Lemma 3.2 shows that the functions \((\Lambda _{M,z_i}^*)_{i \in \underline{2 m}}\) have supports contained in \([0,1]^d\) which are pairwise disjoint (up to null-sets). By continuity, this implies \(\Lambda _{M,z_i}^*\Lambda _{M,z_\ell }^*\equiv 0\) for \(i \ne \ell \).
Let \(k := \lceil m^{\theta \lambda } \rceil \), noting because of \(\theta \lambda \le 1\) that \(k \le \lceil m \rceil = m\) and \(k \le 1 + m^{\theta \lambda } \le 2 \cdot m^{\theta \lambda }\). Set \(\mathcal {P}_k (\underline{2m}):= \bigl \{ J \subset \underline{2m} :|J| = k \bigr \}\) and \(\Gamma _m := \{ \pm 1 \}^{2 m} \times \mathcal {P}_k (\underline{2m})\). The idea of the proof is to show that Lemma 2.3 is applicable to the family \((f_{\varvec{\nu },J})_{(\varvec{\nu },J) \in \Gamma _m}\).
Step 2: In this step, we prove

To see this, let \(\varvec{x}= (x_1,\dots ,x_m) \in ([0,1]^d)^{m}\) and \(Q : \mathbb {R}^m \rightarrow L^2([0,1]^d)\) be arbitrary. Define \({ I := I_{\varvec{x}} := \big \{ i \in \underline{2 m} \,\,:\,\, \forall \, n \in \underline{m} : \Lambda _{M,z_i}^*(x_n) = 0 \big \} }\) as in Lemma 3.3 and recall the estimate \(|I| \ge m\) from that lemma.
Now, given \(\varvec{\nu }^{(1)} \in \{ \pm 1 \}^{I}\) and \(\varvec{\nu }^{(2)} \in \{ \pm 1 \}^{I^c}\) as well as \(J \in \mathcal {P}_k (\underline{2m})\), define
and finally \( h_{\varvec{\nu }^{(2)}, J} := g_{\varvec{\nu }^{(2)}, J} - Q \bigl ( g_{\varvec{\nu }^{(2)}, J} (x_1), \dots , g_{\varvec{\nu }^{(2)}, J} (x_m) \bigr ) .\) Note by choice of \(I = I_{\varvec{x}}\) that \(f_{\varvec{\nu },J} (x_n) = g_{\varvec{\nu }^{(2)},J}(x_n)\) for all \(n \in \underline{m}\), if we identify \(\varvec{\nu }\) with \((\varvec{\nu }^{(1)}, \varvec{\nu }^{(2)})\), as we will continue to do for the remainder of the proof. Thus, we see for fixed but arbitrary \(\varvec{\nu }^{(2)} \in \{ \pm 1 \}^{I^c}\) and \(J \in \mathcal {P}_k (\underline{2m})\) that
Here, the step marked with \((*)\) used the identity \(F_{-\varvec{\nu }^{(1)}, J} = - F_{\varvec{\nu }^{(1)}, J}\) and the elementary estimate \( \Vert f + g \Vert _{L^2} + \Vert - f + g \Vert _{L^2} = \Vert f + g \Vert _{L^2} + \Vert f - g \Vert _{L^2} \ge \Vert f + g + f - g \Vert _{L^2} = 2 \, \Vert f \Vert _{L^2} . \) Finally, the step marked with \((*)\) used that the functions \(\bigl (\Lambda _{M,z_i}^*\bigr )_{i \in \underline{2m}}\) have disjoint supports (up to null-sets) contained in \([0,1]^d\) and that \(\Lambda _{M,z_j}^*(x) \ge \frac{1}{2}\) for all \(x \in [0,1]^d\) satisfying \(|x_1 - z_j| \le \frac{1}{2 M}\); since \(M = 4 m\), this easily implies \( \Vert \Lambda _{M,z_i}^{*} \Vert _{L^2([0,1]^d)} \ge \frac{1}{2} \big ( \frac{1}{2 M} \big )^{1/2} \ge \frac{m^{-1/2}}{8} \) and hence
Combining Eq. (7.3) with Lemma A.4 and recalling that \(k \ge m^{\theta \lambda }\), we finally see

Recall that this holds for any \(m \in \mathbb {N}\), arbitrary \(\varvec{x}= (x_1,\dots ,x_m) \in ([0,1]^d)^m\) and any map \(Q : \mathbb {R}^m \rightarrow L^2([0,1]^d)\). Thus, we have established Eq. (7.2).
Step 3: In view of Eq. (7.2), an application of Lemma 2.3 shows that
for arbitrary \(0< \gamma < \gamma ^\flat \), \(\theta \in (0,\infty )\) and \(\lambda \in [0,1]\) with \(\theta \lambda \le 1\); here, we note that \(\frac{1}{2} - \frac{\theta \lambda }{2} \ge 0\) and \(-\omega \ge 0\).
From Eq. (7.4), it is easy (but slightly tedious) to deduce the first line of Eq. (7.1); the details are given in Lemma A.5. Finally, the second line of Eq. (7.1) follows by a straightforward case distinction. \(\square \)
8 Error Bounds for Numerical Integration
In this section, we derive error bounds for the numerical integration of functions  based on point samples. We first consider (in Theorem 8.1) deterministic algorithms, which surprisingly provide a strictly positive rate of convergence, even for neural network approximation spaces without restrictions on the size of the network weights. Then, in Theorem 8.4, we consider the case of randomized (Monte Carlo) algorithms. As usual for such algorithms, they improve on the deterministic rate of convergence (essentially) by a factor of \(m^{-1/2}\), at the cost of having a non-deterministic algorithm and (in our case) of requiring a non-trivial (albeit mild) condition on the growth function \(\varvec{c}\) used to define the space
based on point samples. We first consider (in Theorem 8.1) deterministic algorithms, which surprisingly provide a strictly positive rate of convergence, even for neural network approximation spaces without restrictions on the size of the network weights. Then, in Theorem 8.4, we consider the case of randomized (Monte Carlo) algorithms. As usual for such algorithms, they improve on the deterministic rate of convergence (essentially) by a factor of \(m^{-1/2}\), at the cost of having a non-deterministic algorithm and (in our case) of requiring a non-trivial (albeit mild) condition on the growth function \(\varvec{c}\) used to define the space  .
.
Theorem 8.1
Let \(d \in N and C, \sigma , \alpha \in (0,\infty )\). Let \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) and \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) be non-decreasing and assume that \(\varvec{\ell }(n) \le C \cdot (\ln (en))^{\sigma }\) for all \(n \in \mathbb {N}\). Then, with  as in Eq. (2.3) and with
as in Eq. (2.3) and with  , we have
, we have

The proof relies on VC-dimension-based bounds for empirical processes. For the convenience of the reader, we briefly review the notion of VC dimension. Let \(\Omega \ne \varnothing \) be a set, and let \({\varnothing \ne \mathcal {H}\subset \{ 0,1 \}^{\Omega }}\) be arbitrary. In the terminology of machine learning, \(\mathcal {H}\) is called a hypothesis class. The growth function of \(\mathcal {H}\) is defined as
see [35, Definition 3.6]. That is, \(\tau _{\mathcal {H}}(m)\) describes the maximal number of different ways in which the hypothesis class \(\mathcal {H}\) can partition points \(x_1,\dots ,x_m \in \Omega \). Clearly, \(\tau _{\mathcal {H}}(m) \le 2^m\) for each \(m \in \mathbb {N}\). This motivates the definition of the VC-dimension \({\text {VC}}(\mathcal {H}) \in \mathbb {N}_0 \cup \{ \infty \}\) of \(\mathcal {H}\) as
For applying existing learning bounds based on the VC dimension in our setting, the following lemma will be essential.
Lemma 8.2
Let \(C_1 \ge 1\) and \(C_2, \sigma _1, \sigma _2 > 0\). Then there exist constants \(n_0 = n_0(C_1,C_2,\sigma _1,\sigma _2) \in \mathbb {N}\) and \({C = C(C_1) > 0}\) such that for every \(n \in \mathbb {N}_{\ge n_0}\) and every \(L \in \mathbb {N}\) with \(L \le C_2 \cdot (\ln (e n))^{\sigma _2}\), the following holds:
For any set \(\Omega \ne \varnothing \) and any hypothesis classes \({\varnothing \ne \mathcal {H}_1,\dots ,\mathcal {H}_N \subset \{ 0, 1 \}^{\Omega }}\) satisfying
we have
Proof
Choose \(C_0 = 10 \, C_1\) so that \(\ln 2 - \frac{C_1}{C_0} \ge \frac{1}{2}\); here we used that \(\ln 2 \approx 0.693 \ge \frac{6}{10}\). Set \(C_3 := 1 + 2 \ln (C_2) + 2 \sigma _2\) and choose \(n_0 = n_0(C_1,C_2,\sigma _1,\sigma _2) \in \mathbb {N}\) so large that for every \(n \ge n_0\), we have \(C_3 \cdot (\ln (e n))^{-\sigma _1} \le \frac{1}{6}\) and \(C_1 \, \ln (20 e) \cdot (\ln (e n))^{-1} \le \frac{1}{6}\).
For any subset \(\varnothing \ne \mathcal {H}\subset \{ 0, 1 \}^{\Omega }\), Sauer’s lemma shows that if \(d_\mathcal {H}:= {\text {VC}}(\mathcal {H}) \in \mathbb {N}\), then \(\tau _{\mathcal {H}}(m) \le (e m / d_{\mathcal {H}})^{d_{\mathcal {H}}}\) for all \(m \ge d_{\mathcal {H}}\); see [35, Corollary 3.18]. An elementary calculation shows that the function \((0,\infty ) \rightarrow \mathbb {R}, x \mapsto (e m / x)^x\) is non-decreasing on (0, m]; thus, we see
this trivially remains true if \(d_{\mathcal {H}} = 0\).
Let \(n \in \mathbb {N}_{\ge n_0}\), L, and \(\mathcal {H}_1,\dots ,\mathcal {H}_N\) as in the statement of the lemma. Set \({\mathcal {H}:= \mathcal {H}_1 \cup \cdots \cup \mathcal {H}_N}\) and \(m := \big \lceil C_0 \cdot n \cdot (\ln (e n))^{\sigma _1 + 1} \big \rceil \); we want to show that \({\text {VC}}(\mathcal {H}) \le m\). By definition of the VC dimension, it is sufficient to show that \(\tau _\mathcal {H}(m) < 2^m\). To this end, first note by a standard estimate for binomial coefficients (see [50, Exercise 0.0.5]) that
thanks to the elementary estimate \(\ln x \le x\), since \(\ln (e n) \ge 1\) and \(L \le C_2 \cdot (\ln (e n))^{\sigma _2}\), and by our choice of \(C_3\) at the beginning of the proof.
Next, recall that \(C_0 = 10 \, C_1\) and note \({d_{\mathcal {H}_j} \le d := C_1 \cdot n \cdot (\ln (e n))^{\sigma _1} \in [1,m]}\), so that Eq. (8.1) shows because of \({m\le 2 C_0 \cdot n \cdot (\ln (e n))^{\sigma _1 + 1}}\) that
Combining all these observations and using the subadditivity property \(\tau _{\mathcal {H}_1 \cup \mathcal {H}_2} \le \tau _{\mathcal {H}_1} + \tau _{\mathcal {H}_2}\) and the bounds \({m \ge C_0 \, n \, (\ln (e n))^{\sigma _1 + 1}}\) and \(\ln (2) - \frac{C_1}{C_0} \ge \frac{1}{2}\) as well as \(C_0 \ge 1\), we see with \({\theta := C_0 \, n \, (\ln (e n))^{\sigma _1 + 1}}\) that
since \(n \ge n_0\) and thanks to our choice of \(n_0\) from the beginning of the proof.
Overall, we have thus shown \(\tau _{\mathcal {H}}(m) < 2^m\) and hence \( {\text {VC}}(\mathcal {H}) \le m \le 2 C_0 \cdot n \cdot \, (\ln (en))^{\sigma _1 + 1} , \) which completes the proof, for \(C := 2 C_0 = 20 \, C_1\). \(\square \)
As a consequence, we get the following VC-dimension bounds for the network classes  .
.
Lemma 8.3
Let \(d \in \mathbb {N}\) and \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2}\) such that \(\varvec{\ell }(n) \le C \cdot (\ln (e n))^{\sigma }\) for all \(n \in \mathbb {N}\) and certain \(C,\sigma > 0\). Then there exist \({n_0 = n_0(C,\sigma ,d) \in \mathbb {N}}\) and \(C' = C'(C) > 0\) such that for all \(\lambda \in \mathbb {R}\) and \(n \ge n_0\), we have

Proof
Given a network architecture \(\varvec{a}= (a_0,\dots ,a_K) \in \mathbb {N}^{K+1}\), we denote the set of all networks with architecture \(\varvec{a}\) by
and by \( I(\varvec{a}) := \biguplus _{j=1}^{K} \big ( \{ j \} \times \{ 1,...,a_j \} \times \{ 1,...,1+a_{j-1} \} \big ) \) the corresponding index set, so that \(\mathcal{N}\mathcal{N}(\varvec{a}) \cong \mathbb {R}^{I(\varvec{a})}\).
Define \(L := \varvec{\ell }(n)\). For \(\ell \in \{ 1,\dots ,L \}\), define \(I_\ell := I(\varvec{a}^{(\ell )})\) and \(\varvec{a}^{(\ell )} := (d,n,\dots ,n,1) \in \mathbb {N}^{\ell +1}\), as well as
By dropping “dead neurons,” it is easy to see that each \(f \in \Sigma _\ell \) is of the form \({f = R_\varrho \Phi }\) for some \({\Phi \in \mathcal{N}\mathcal{N}(\varvec{a}^{(\ell )})}\) satisfying \(W(\Phi ) \le n\). In other words, keeping the identification \({\mathcal{N}\mathcal{N}(\varvec{a}) \cong \mathbb {R}^{I(\varvec{a})}}\), given a subset \(S \subset I_\ell \), let us write
then \({\Sigma _\ell = \bigcup _{S \subset I_\ell , |S| = \min \{ n, |I_\ell | \} } \mathcal {N}\mathcal {N}_{S,\ell }}\). Moreover, \(|I_\ell | \le 2d\) if \(\ell = 1\) while \(|I_\ell | = 1 + n (d+2) + (\ell -2) (n^2 + n)\) for \(\ell \ge 2\), and this implies in all cases that \(|I_\ell | \le 2 n (L n + d) \le L' \cdot n^2\) for \(L' := 4 d \, L\).
Overall, given a class \(\mathcal {F}\subset \{ f : \mathbb {R}^d \rightarrow \mathbb {R}\}\) and \(\lambda \in \mathbb {R}\), let us write \(\mathcal {F}(\lambda ) := \{ \mathbb {1}_{f > \lambda } :f \in \mathcal {F}\}\). Then the considerations from the preceding paragraph show that

Now, the set \(\mathcal{N}\mathcal{N}_{S,\ell }\) can be seen as all functions obtained by a fixed ReLU network (architecture) with at most n nonzero weights and \(\ell \) layers, in which the weights are allowed to vary. Therefore, [6, Eq. (2)] shows for a suitable absolute constant \({C^{(0)} > 0}\) that
Finally, noting that the number of sets over which the union is taken in Eq. (8.2) is bounded by \( \sum _{\ell =1}^L \left( {\begin{array}{c}|I_\ell |\\ n \min \{ n, |I_\ell | \} \end{array}}\right) \le \sum _{\ell =1}^L \left( {\begin{array}{c}L' \, n^2\\ n\end{array}}\right) \le L \cdot \left( {\begin{array}{c}L' \, n^2\\ n\end{array}}\right) \le L' \cdot \left( {\begin{array}{c}L' \, n^2\\ n\end{array}}\right) , \) we can apply Lemma 8.2 (with \(\sigma _1 = \sigma + 1\), \(\sigma _2 = \sigma \), \(C_1 = \max \{ 1, C^{(0)} C \}\), and \(C_2 = 4 d C\)) to obtain \(n_0 = n_0(d,C,\sigma ) \in \mathbb {N}\) and \(C' = C'(C) > 0\) satisfying  for all \(n \ge n_0\). \(\square \)
for all \(n \ge n_0\). \(\square \)
Proof of Theorem 8.1
Define \(\theta := \frac{1}{1 + 2 \alpha }\) and \({\gamma := - \frac{\sigma + 2}{1 + 2 \alpha }}\). Let \(m \ge m_0\) with \(m_0\) chosen such that \({n := \lfloor m^\theta \cdot (\ln (e m))^\gamma \rfloor }\) satisfies \(n \ge n_0\) for \(n_0 =n_0(\sigma ,C,d) \in \mathbb {N}\) provided by Lemma 8.3. Let  and note that Lemma 8.3 shows for every \(\lambda \in \mathbb {R}\) that \({{\text {VC}}(\{ \mathbb {1}_{g > \lambda } :g \in \mathcal {G}\}) \le C' \cdot n \cdot (\ln (en))^{\sigma + 2}}\) for a suitable constant \(C' = C'(C) > 0\). Therefore, [11, Proposition A.1] yields a universal constant \(\kappa > 0\) such that if \(X_1,\dots ,X_m \overset{\textrm{iid}}{\sim } U([0,1]^d)\), then
and note that Lemma 8.3 shows for every \(\lambda \in \mathbb {R}\) that \({{\text {VC}}(\{ \mathbb {1}_{g > \lambda } :g \in \mathcal {G}\}) \le C' \cdot n \cdot (\ln (en))^{\sigma + 2}}\) for a suitable constant \(C' = C'(C) > 0\). Therefore, [11, Proposition A.1] yields a universal constant \(\kappa > 0\) such that if \(X_1,\dots ,X_m \overset{\textrm{iid}}{\sim } U([0,1]^d)\), then
In particular, there exists \({\varvec{x}= (X_1,\dots ,X_m) \in ([0,1]^d)^m}\) such that
Next, note because of \(\gamma < 0\) that \(n \le m^\theta \, (\ln (e m))^{\gamma } \le m^\theta \) and hence \(\ln (e n) \lesssim \ln (em)\). Therefore,
where the implied constant only depends on \(\alpha \). Similarly, we have \(n^{-\alpha } \lesssim m^{-\alpha \theta } (\ln (em))^{-\alpha \gamma } = \varepsilon _2\), because of \(m^\theta \cdot (\ln (em))^{\gamma } \le n+1 \le 2 n\).
Finally, set \(Q : \mathbb {R}^m \rightarrow \mathbb {R}, (y_1,\dots ,y_m) \mapsto \frac{1}{m} \sum _{j=1}^m y_j\) and let  with
with  be arbitrary. By Lemma 2.1, we have
be arbitrary. By Lemma 2.1, we have  , which implies that \(\Vert f \Vert _{L^\infty } \le 1\), and furthermore that there is some
, which implies that \(\Vert f \Vert _{L^\infty } \le 1\), and furthermore that there is some  satisfying \(\Vert f - g \Vert _{L^\infty } \le 2 n^{-\alpha } \le 2\), which in particular implies that \(g \in \mathcal {G}\). Therefore,
satisfying \(\Vert f - g \Vert _{L^\infty } \le 2 n^{-\alpha } \le 2\), which in particular implies that \(g \in \mathcal {G}\). Therefore,
Since this holds for all  , with an implied constant independent of f and m, and since \(\varepsilon _2 = m^{-\frac{\alpha }{1 + 2 \alpha }} \cdot (\ln (em))^{-\alpha \gamma }\), this easily implies
, with an implied constant independent of f and m, and since \(\varepsilon _2 = m^{-\frac{\alpha }{1 + 2 \alpha }} \cdot (\ln (em))^{-\alpha \gamma }\), this easily implies  . \(\square \)
. \(\square \)
Our next result shows that randomized (Monte Carlo) algorithms can improve the rate of convergence of the deterministic algorithm from Theorem 8.1 by (essentially) a factor \(m^{-1/2}\). The proof is based on our error bounds for \(L^2\) approximation from Theorem 6.3.
Theorem 8.4
Let \(d \in \mathbb {N}\), \(C_1,C_2,\alpha \in (0,\infty )\), and \(\theta ,\nu \in [0,\infty )\). Let \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2}\) and \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\) be non-decreasing and such that \(\varvec{c}(n) \le C_1 \cdot n^\theta \) and \(\varvec{\ell }(n) \le C_2 \cdot \ln ^\nu (2 n)\) for all \(n \in \mathbb {N}\). Let  .
.
There exists \(C = C(\alpha ,\theta ,\nu ,d,C_1,C_2) > 0\) such that for every \(m \in \mathbb {N}\), there exists a strongly measurable randomized (Monte Carlo) algorithm \((\varvec{A},\varvec{m})\) with \(\varvec{m}\equiv m\) and \(\varvec{A}= (A_\omega )_{\omega \in \Omega }\) that satisfies
for all \(f \in U\). In particular, this implies

Proof
Set \(Q := [0,1]^d\). Let \(m \in \mathbb {N}_{\ge 2}\) and \(m' := \lfloor \frac{m}{2} \rfloor \in \mathbb {N}\) and note that \(\frac{m}{2} \le m' + 1 \le 2 m'\) and hence \(\frac{m}{4} \le m' \le \frac{m}{2}\). Let \(C = C(\alpha ,\theta ,\nu ,d,C_1,C_2) > 0\) and  as provided by Theorem 6.3 (applied with \(m'\) instead of m). Note that
as provided by Theorem 6.3 (applied with \(m'\) instead of m). Note that  is closed and nonempty, with finite covering numbers \(\textrm{Cov}_{C(Q)}(\mathcal {H},\varepsilon )\), for arbitrary \(\varepsilon > 0\); see Lemma 6.2. Hence, \(\mathcal {H}\subset C(Q)\) is compact, see for instance [2, Theorem 3.28]. Let us equip \(\mathcal {H}\) with the Borel \(\sigma \)-algebra induced by C(Q). Then, it is easy to see from Lemma A.3 that the map \({ M : \mathcal {H}\rightarrow \mathbb {R}^{m'}, f \mapsto \bigl (f(x_1),\dots ,f(x_{m'})\bigr ) }\) is measurable and that there is a measurable map \(B : \mathbb {R}^{m'} \rightarrow \mathcal {H}\) satisfying \(B(\varvec{y}) \in \mathop {\textrm{argmin}}\limits _{g \in \mathcal {H}} \sum _{i=1}^{m'} \bigl (g(x_i) - y_i\bigr )^2\) for all \(\varvec{y}\in \mathbb {R}^{m'}\).
is closed and nonempty, with finite covering numbers \(\textrm{Cov}_{C(Q)}(\mathcal {H},\varepsilon )\), for arbitrary \(\varepsilon > 0\); see Lemma 6.2. Hence, \(\mathcal {H}\subset C(Q)\) is compact, see for instance [2, Theorem 3.28]. Let us equip \(\mathcal {H}\) with the Borel \(\sigma \)-algebra induced by C(Q). Then, it is easy to see from Lemma A.3 that the map \({ M : \mathcal {H}\rightarrow \mathbb {R}^{m'}, f \mapsto \bigl (f(x_1),\dots ,f(x_{m'})\bigr ) }\) is measurable and that there is a measurable map \(B : \mathbb {R}^{m'} \rightarrow \mathcal {H}\) satisfying \(B(\varvec{y}) \in \mathop {\textrm{argmin}}\limits _{g \in \mathcal {H}} \sum _{i=1}^{m'} \bigl (g(x_i) - y_i\bigr )^2\) for all \(\varvec{y}\in \mathbb {R}^{m'}\).
Given \(f \in \mathcal {H}\), note that \(g := B(M(f)) \in \mathcal {H}\) satisfies \(g(x_i) = f(x_i)\) for all \(i \in \underline{m'}\), so that Theorem 6.3 shows
for a suitable constant \(C' = C'(\alpha ,\theta ,\nu ,d,C_1,C_2) > 0\).
Now, consider the probability space \(\Omega = Q^{m'} \cong [0,1]^{m' d}\), equipped with the Lebesgue measure \(\varvec{\lambda }\). For \(\varvec{z}\in \Omega \), write \(\Omega \ni \varvec{z}= (z_1,\dots ,z_{m'})\) and define
It is easy to see that \(\Psi \) is continuous and hence measurable; see Eq. (A.2) for more details.
Note that for \(\varvec{z}= (z_1,\dots ,z_{m'}) \in \Omega \), the random vectors \(z_1,\dots ,z_{m'} \in Q\) are stochastically independent. Furthermore, for arbitrary \(g \in C(Q)\), we have \(\mathbb {E}_{\varvec{z}} [g(z_j)] = \int _{[0,1]^d} g(t) \, dt = T_{\int }(g)\). Using the additivity of the variance for independent random variables, this entails
Finally, for each \(\varvec{z}\in \Omega \) define
Since the map \(T_{\int } : C([0,1]^d) \rightarrow \mathbb {R}\) is continuous and hence measurable, it is easy to verify that  is measurable. Furthermore, explicitly writing out the definition of \(A_{\varvec{z}}\) shows that
is measurable. Furthermore, explicitly writing out the definition of \(A_{\varvec{z}}\) shows that
only depends on \(m' + m' \le m\) point samples of f. Thus, if we set \(\varvec{m}\equiv m\), then \((\varvec{A},\varvec{m})\) is a strongly measurable randomized (Monte Carlo) algorithm  .
.
To complete the proof, note that a combination of Eqs. (8.5) and (8.6) shows
for all \(f \in U\). Combined with Jensen’s inequality, this proves Eq. (8.3) for the case \(m \in \mathbb {N}_{\ge 2}\). The case \(m = 1\) can be handled by taking \(A_{\omega } \equiv 0\) and possibly enlarging the constant C in Eq. (8.3). Directly from the definition of  , we see that Eq. (8.3) implies Eq. (8.4). \(\square \)
, we see that Eq. (8.3) implies Eq. (8.4). \(\square \)
9 Hardness of Numerical Integration
Our goal in this section is to prove upper bounds for the optimal order  of quadrature on the neural network approximation spaces, both for deterministic and randomized algorithms. Our bounds for the deterministic setting in particular show that regardless of the “approximation exponent”
of quadrature on the neural network approximation spaces, both for deterministic and randomized algorithms. Our bounds for the deterministic setting in particular show that regardless of the “approximation exponent”  , the quadrature error given m point samples can never decay faster than \(\mathcal {O}\bigl (m^{- \min \{2, 2 \alpha \}}\bigr )\). In fact, if the depth growth function \(\varvec{\ell }\) is unbounded, or if the weight growth function
, the quadrature error given m point samples can never decay faster than \(\mathcal {O}\bigl (m^{- \min \{2, 2 \alpha \}}\bigr )\). In fact, if the depth growth function \(\varvec{\ell }\) is unbounded, or if the weight growth function  grows sufficiently fast (so that \({\gamma ^{\flat }(\varvec{\ell },\varvec{c}) = \infty }\)), then no better rate than \(\mathcal {O}\bigl (m^{- \min \{1,\alpha \}}\bigr )\) is possible.
grows sufficiently fast (so that \({\gamma ^{\flat }(\varvec{\ell },\varvec{c}) = \infty }\)), then no better rate than \(\mathcal {O}\bigl (m^{- \min \{1,\alpha \}}\bigr )\) is possible.
For the case of randomized (Monte Carlo) algorithms, the bound that we derive shows that the expected quadrature error given at most m point samples (in expectation) can never decay faster than \(\mathcal {O}\big ( m^{- \min \{ 2, \frac{1}{2} + 2 \alpha \}} \big )\). In fact, if \(\gamma ^\flat = \infty \) then the error cannot decay faster than \(\mathcal {O}\big ( m^{- \min \{ 1, \frac{1}{2} + \alpha \}} \big )\).
Our precise bound for the deterministic setting reads as follows:
Theorem 9.1
Let \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) and \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) be non-decreasing, and let \(d \in \mathbb {N}\) and \(\alpha > 0\). Let \(\gamma ^\flat := \gamma ^\flat (\varvec{\ell },\varvec{c})\) as in Eq. (2.2) and  as in Eq. (2.3). For the operator
as in Eq. (2.3). For the operator  , we then have
, we then have


Remark
Since the bound above might seem intimidating at first sight, we discuss a few specific consequences. First, the theorem implies  and hence
and hence  as \(\alpha \downarrow 0\). Furthermore, the theorem shows that
as \(\alpha \downarrow 0\). Furthermore, the theorem shows that  , and if \(\gamma ^\flat = \infty \), then in fact
, and if \(\gamma ^\flat = \infty \), then in fact  .
.
Proof
For brevity, set  .
.
Step 1: Let \(0< \gamma < \gamma ^\flat \), \(\theta \in (0,\infty )\), and \(\lambda \in [0,1]\) with \(\theta \lambda \le 1\) be arbitrary and define \({\omega := \min \{ -\theta \alpha , \theta \cdot (\gamma - \lambda ) - 1 \}}\). In this step, we show that
for a suitable constant \({\kappa _2 = \kappa _2 (\alpha ,\gamma ,\theta ,\lambda ,\varvec{\ell },\varvec{c}) > 0}\).
To see this, let \(m \in \mathbb {N}\) and \(A \in {\text {Alg}}_m(U,\mathbb {R})\) be arbitrary. By definition, this means that there exist \(Q : \mathbb {R}^m \rightarrow \mathbb {R}\) and \(\varvec{x}= (x_1,\dots ,x_m) \in ([0,1]^d)^m\) satisfying \(A(f) = Q\bigl (f(x_1),\dots ,f(x_m)\bigr )\) for all \(f \in U\). Set \(M := 4 m\) and let \(z_j := \frac{1}{4m} + \frac{j-1}{2m}\) for \(j \in \underline{2m}\) as in Lemma 3.2. Furthermore, choose \( I := I_{\varvec{x}} := \big \{ i \in \underline{2 m} \,\,\, :\,\,\, \forall \, n \in \underline{m}: \Lambda _{M,z_i}^*(x_n) = 0 \big \} \) and recall from Lemma 3.3 that \(|I| \ge m\). Define \(k := \lceil m^{\theta \lambda } \rceil \) and note \(k \le 1 + m^{\theta \lambda } \le 2 \, m^{\theta \lambda }\). Since \(\theta \lambda \le 1\), we also have \(k \le \lceil m \rceil = m \le |I|\). Hence, there is a subset \(J \subset I\) satisfying \(|J| = k\).
Now, an application of Lemma 3.2 yields a constant \(\kappa _1 = \kappa _1(\alpha ,\gamma ,\theta ,\lambda ,\varvec{\ell },\varvec{c}) > 0\) (independent of m and A) such that \(f := \kappa _1 \, m^\omega \, \sum _{j \in J} \Lambda _{M,z_j}^*\) satisfies \(\pm f \in U\). Since \(J \subset I\), we see by definition of \(I = I_{\varvec{x}}\) that \(f(x_n) = 0\) for all \(n \in \underline{m}\) and hence \(A(\pm f) = Q(0,\dots ,0) =: \mu \). Using the elementary estimate \( \max \{ |x-\mu |, |-x-\mu | \} \ge \frac{1}{2} \big ( |x-\mu | + |x+\mu | \big ) \ge \frac{1}{2} |x-\mu +x+\mu | = |x| , \) we thus see
as claimed in Eq. (9.3). Here, the step marked with \((*)\) used that \(|J| = k \ge m^{\theta \lambda }\) and that \(M = 4 m\).
Step 2 (Completing the proof): Eq. (9.3) shows that \(e_m^{\textrm{det}}(U,T_{\int }) \ge \kappa _2 \cdot m^{-(1-\omega -\theta \lambda )}\) for all \(m \in \mathbb {N}\), with \(\kappa _2 > 0\) independent of m. Directly from the definition of \(\beta _*^{\textrm{det}}(U,T_{\int })\) and \(\omega \), this shows
and this holds for arbitrary \(0< \gamma < \gamma ^\flat \), \(\theta \in (0,\infty )\), and \(\lambda \in [0,1]\) satisfying \(\theta \lambda \le 1\). It is easy (but somewhat tedious) to shows that this implies Eq. (9.1); see Lemma A.6 for the details. Finally, Eq. (9.2) follows from Eq. (9.1) via an easy case distinction. \(\square \)
As our next results, we derive a hardness results for randomized (Monte Carlo) algorithms for integration on the neural network approximation space  . The proof hinges on Khintchine’s inequality, which states the following:
. The proof hinges on Khintchine’s inequality, which states the following:
Proposition 9.2
([12, Theorem 1 in Section 10.3]) Let \(n \in \mathbb {N}\) and let \((X_i)_{i=1,\dots ,n}\) be independent random variables (on some probability space \((\Omega ,\mathcal {F},\mathbb {P})\)) that are Rademacher distributed (i.e., \(\mathbb {P}(X_i = 1) = \frac{1}{2} = \mathbb {P}(X_i = -1)\) for each \(i \in \underline{n}\)). Then for each \(p \in (0,\infty )\) there exist constants \(A_p,B_p \in (0,\infty )\) (only depending on p) such that for arbitrary \(c = (c_i)_{i=1,\dots ,n} \subset \mathbb {R}\), the following holds:
Remark 9.3
Applying Khintchine’s inequality for \(p = 1\) and \(c_i = 1\), we see

which is what we will actually use below.
Our precise hardness result for integration using randomized (Monte Carlo) algorithms reads as follows.
Theorem 9.4
Let \(\varvec{\ell }: \mathbb {N}\rightarrow \mathbb {N}_{\ge 2} \cup \{ \infty \}\) and \(\varvec{c}: \mathbb {N}\rightarrow \mathbb {N}\cup \{ \infty \}\) be non-decreasing. Let \(d \in \mathbb {N}\) and \(\alpha \in (0,\infty )\). Let \(\gamma ^\flat := \gamma ^\flat (\varvec{\ell },\varvec{c})\) as in Eq. (2.2) and  as in Eq. (2.3). For the operator
as in Eq. (2.3). For the operator  , we then have
, we then have

Remark
We discuss a few special cases. First, we always have  which shows that no matter how large the approximation rate \(\alpha \) is, one can never get an (asymptotically) better error bound than \(m^{-2}\). Furthermore, if \(\gamma ^\flat = \infty \) (for instance if \(\varvec{\ell }\) is unbounded), then
which shows that no matter how large the approximation rate \(\alpha \) is, one can never get an (asymptotically) better error bound than \(m^{-2}\). Furthermore, if \(\gamma ^\flat = \infty \) (for instance if \(\varvec{\ell }\) is unbounded), then 
The previous bounds are informative for (somewhat) large \(\alpha \). For small \(\alpha > 0\), it is more useful to note that the theorem shows 
Proof
For brevity, set  and \(\gamma ^\flat := \gamma ^\flat (\varvec{\ell },\varvec{c})\).
and \(\gamma ^\flat := \gamma ^\flat (\varvec{\ell },\varvec{c})\).
The main idea of the proof is to apply Lemma 2.3 for a suitable choice of the family of functions \((f_{\varvec{\nu },J})_{(\varvec{\nu },J) \in \Gamma _m} \subset U\).
Step 1 (Preparation): Let \(0< \gamma < \gamma ^\flat \), \(\theta \in (0,\infty )\), and \(\lambda \in [0,1]\) with \(\theta \lambda \le 1\) be arbitrary and define \(\omega := \min \{ -\theta \alpha , \theta \cdot (\gamma - \lambda ) - 1 \}\). Given a fixed but arbitrary \(m \in \mathbb {N}\), set \(M := 4 m\) and \(z_j := \frac{1}{4 m} + \frac{j - 1}{2 m}\) as in Lemma 3.2. Furthermore, let \(k := \big \lceil m^{\theta \lambda } \big \rceil \) and note because of \(\theta \lambda \le 1\) that \(k \le \lceil m \rceil = m\) and \(k \le 1 + m^{\theta \lambda } \le 2 \, m^{\theta \lambda }\).
Define \(\mathcal {P}_k (\underline{2 m}) := \{ J \subset \underline{2m} :|J| = k \}\) and \(\Gamma _m := \{ \pm 1 \}^{2 m} \times \mathcal {P}_k (\underline{2 m})\). Then, Lemma 3.2 yields a constant \(\kappa _1 = \kappa _1(\gamma ,\theta ,\lambda ,\alpha ,\varvec{\ell },\varvec{c}) > 0\) such that for any \((\varvec{\nu },J) \in \Gamma _m\), the function
Step 2: We show for \(\gamma ,\theta ,\lambda ,\omega \) as in Step 2 that there exists \(\kappa _3 = \kappa _3(\gamma ,\theta ,\lambda ,\alpha ,\varvec{\ell },\varvec{c}) \!>\! 0\) (independent of \(m \in \mathbb {N}\)) such that

To see this, let \(A \in {\text {Alg}}_m (U, \mathbb {R})\) be arbitrary. By definition, we have \(A(f) = Q\bigl (f(x_1),\dots ,f(x_m)\bigr )\) for all \(f \in U\), for suitable \(\varvec{x}= (x_1,\dots ,x_m) \in ([0,1]^d)^m\) and \(Q : \mathbb {R}^m \rightarrow \mathbb {R}\). Now, define \({ I := I_{\varvec{x}} := \{ j \in \underline{2 m} \,\,:\,\, \forall \, n \in \underline{m} : \Lambda _{M,z_j}^*(x_n) = 0 \} }\) and recall from Lemma 3.3 that \(|I| \ge m\).
Set \(I^c := \underline{2m} \setminus I\). For \(\varvec{\nu }^{(1)} = (\nu _j)_{j \in I} \in \{ \pm 1 \}^I\) and \(\varvec{\nu }^{(2)} := (\nu _j)_{j \in I^c} \in \{ \pm 1 \}^{I^c}\) and \(J \in \mathcal {P}_k(\underline{2m})\), define
Furthermore, define \( \mu _{\varvec{\nu }^{(2)}, J} := T_{\int }(h_{\varvec{\nu }^{(2)},J}) - Q\big ( h_{\varvec{\nu }^{(2)},J}(x_1), \dots , h_{\varvec{\nu }^{(2)},J}(x_m) \big ) . \) By choice of I, we have \(g_{\varvec{\nu }^{(1)},J}(x_n) = 0\) for all \(n \in \underline{m}\), and hence \(f_{\varvec{\nu },J}(x_n) = h_{\varvec{\nu }^{(2)},J}(x_n)\), if we identify \(\varvec{\nu }\) with \((\varvec{\nu }^{(1)},\varvec{\nu }^{(2)})\), as we will do for the remainder of this step.
Finally, recall from Lemma 3.2 that \({\text {supp}}\Lambda _{M,z_j}^*\subset [0,1]^d\) and hence \(T_{\int }(\Lambda _{M,z_j}^*) = M^{-1} = \frac{1}{4 m}\). Overall, we thus see for arbitrary \(J \in \mathcal {P}_k(\underline{2m})\) and \(\varvec{\nu }^{(2)} \in \{ \pm 1 \}^{I^c}\) that

for a suitable constant \(\kappa _2 = \kappa _2(\gamma ,\theta ,\lambda ,\alpha ,\varvec{\ell },\varvec{c}) > 0\). Here, the very last step used Eq. (9.4) and the identity \(M = 4m\). Furthermore, the step marked with \((*)\) used that

while the elementary estimate \(|x + y| + |-x + y| = |x+y| + |x-y| \ge |x+y+x-y| = 2 |x|\) was used at the step marked with \((\blacklozenge )\).
Combining Eq. (9.7) and Lemma A.4, we finally obtain \(\kappa _3 = \kappa _3(\gamma ,\theta ,\lambda ,\alpha ,\varvec{\ell },\varvec{c}) > 0\) satisfying

as claimed in Eq. (9.6). Since \(m \in \mathbb {N}\) and \(A \in {\text {Alg}}_m(U;\mathbb {R})\) were arbitrary and \(\kappa _3\) is independent of A and m, Step 2 is complete.
Step 3: In view of Eq. (9.6), a direct application of Lemma 2.3 shows that
for arbitrary \(0< \gamma < \gamma ^\flat \), \(\theta \in (0,\infty )\), and \(\lambda \in [0,1]\) with \(\theta \lambda \le 1\). From this, the first part of Eq. (9.5) follows by a straightforward but technical computation; see Lemma A.5 for the details. The second part of Eq. (9.5) follows from the first one by a straightforward case distinction. \(\square \)
Notes
Note that the number of hidden layers is given by \(H = L-1\).
A set-valued map \(f : X \twoheadrightarrow Y\) is a map \(f : X \rightarrow 2^Y\), into the power set \(2^Y\) of Y.
References
B. Adcock and N. Dexter. The gap between theory and practice in function approximation with deep neural networks. SIAM Journal on Mathematics of Data Science, 3(2):624–655, 2021.
C. D. Aliprantis and K. C. Border. Infinite dimensional analysis. Springer, Berlin, third edition, 2006.
V. Antun, M. J. Colbrook, and A. C. Hansen. The difficulty of computing stable and accurate neural networks: On the barriers of deep learning and Smale’s 18th problem. Applied Mathematics, 119(12):e21071511, 2022.
S. Arridge, P. Maass, O. Öktem, and C.-B. Schönlieb. Solving inverse problems using data-driven models. Acta Numerica, 28:1–174, 2019.
P. Baldi, P. Sadowski, and D. Whiteson. Searching for exotic particles in high-energy physics with deep learning. Nature communications, 5(1):1–9, 2014.
P. L. Bartlett, N. Harvey, C. Liaw, and A. Mehrabian. Nearly-tight VC-dimension and Pseudodimension Bounds for Piecewise Linear Neural Networks. Journal of Machine Learning Research, 20(63):1–17, 2019.
P. Beneventano, P. Cheridito, A. Jentzen, and P. von Wurstemberger. High-dimensional approximation spaces of artificial neural networks and applications to partial differential equations. arXiv preprint arXiv:2012.04326, 2020.
J. Berner, P. Grohs, and A. Jentzen. Analysis of the Generalization Error: Empirical Risk Minimization over Deep Artificial Neural Networks Overcomes the Curse of Dimensionality in the Numerical Approximation of Black–Scholes Partial Differential Equations. SIAM Journal on Mathematics of Data Science, 2(3):631–657, 2020.
A. Blum and R. L. Rivest. Training a 3-node neural network is NP-complete. In Advances in neural information processing systems, pages 494–501, 1989.
H. Bölcskei, P. Grohs, G. Kutyniok, and P. C. Petersen. Optimal approximation with sparsely connected deep neural networks. SIAM J. Math. Data Sci., 1:8–45, 2019.
A. Caragea, P. Petersen, and F. Voigtlaender. Neural network approximation and estimation of classifiers with classification boundary in a Barron class. arXiv preprint arXiv:2011.09363, 2020.
Y. S. Chow and H. Teicher. Probability theory. Springer Texts in Statistics. Springer-Verlag, New York, third edition, 1997.
F. Cucker and S. Smale. On the mathematical foundations of learning. Bull. Amer. Math. Soc. (N.S.), 39(1):1–49, 2002.
R. A. DeVore and G. G. Lorentz. Constructive approximation, volume 303 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, Berlin, 1993.
R. DeVore, B. Hanin, and G. Petrova. Neural network approximation. Acta Numerica, 30:327–444, 2021.
Z. Ditzian and V. Totik. Moduli of smoothness, volume 9. Springer Science & Business Media, 2012.
W. E and B. Yu. The deep ritz method: a deep learning-based numerical algorithm for solving variational problems. Communications in Mathematics and Statistics, 6(1):1–12, 2018.
F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley, and O. A. Von Lilienfeld. Prediction errors of molecular machine learning models lower than hybrid DFT error. Journal of chemical theory and computation, 13(11):5255–5264, 2017.
G. B. Folland. Real analysis. Pure and Applied Mathematics (New York). John Wiley & Sons, Inc., New York, second edition, 1999.
R. Gribonval, G. Kutyniok, M. Nielsen, and F. Voigtlaender. Approximation spaces of deep neural networks. Constructive Approximation, 55:259–367, 2022.
P. Grohs, F. Hornung, A. Jentzen, and P. Von Wurstemberger. A proof that artificial neural networks overcome the curse of dimensionality in the numerical approximation of Black-Scholes partial differential equations. Memoirs of the American Mathematical Society, 2020.
P. Grohs, D. Perekrestenko, D. Elbrächter, and H. Bölcskei. Deep neural network approximation theory. IEEE Transactions on Information Theory, 67(5):2581–2623, 2021.
A. Gupta and S. M. Lam. Weight decay backpropagation for noisy data. Neural Networks, 11(6):1127–1138, 1998.
K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
S. Heinrich. Random approximation in numerical analysis. In Functional analysis (Essen, 1991), volume 150 of Lecture Notes in Pure and Appl. Math., pages 123–171. Dekker, New York, 1994.
J. Hermann, Z. Schätzle, and F. Noé. Deep-neural-network solution of the electronic Schrödinger equation. Nature Chemistry, 12(10):891–897, 2020.
M. Hutzenthaler, A. Jentzen, T. Kruse, and T. A. Nguyen. A proof that rectified deep neural networks overcome the curse of dimensionality in the numerical approximation of semilinear heat equations. SN Partial Differential Equations and Applications, 1(2):1–34, 2020.
D. P. Kingma and J. Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In F. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger, editors, Advances in Neural Information Processing Systems, volume 25, pages 1097–1105. Curran Associates, Inc., 2012.
G. Kutyniok, P. Petersen, M. Raslan, and R. Schneider. A theoretical analysis of deep neural networks and parametric PDEs. arXiv preprint arXiv:1904.00377, 2019.
G. Lample and F. Charton. Deep learning for symbolic mathematics. In International Conference on Learning Representations, 2019.
Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
J. Ma, R. P. Sheridan, A. Liaw, G. E. Dahl, and V. Svetnik. Deep neural nets as a method for quantitative structure–activity relationships. Journal of chemical information and modeling, 55(2):263–274, 2015.
V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, and M. Riedmiller. Playing Atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602, 2013.
M. Mohri, A. Rostamizadeh, and A. Talwalkar. Foundations of machine learning. MIT Press, Cambridge, MA, 2018.
P. Petersen and F. Voigtlaender. Optimal approximation of piecewise smooth functions using deep ReLU neural networks. Neural Networks, 108:296–330, 2018.
D. Pfau, J. S. Spencer, A. G. Matthews, and W. M. C. Foulkes. Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Physical Review Research, 2(3):033429, 2020.
A. Pietsch. Eigenvalues and s-numbers. Cambridge University Press, 1986.
A. Pinkus. N-widths in Approximation Theory, volume 7. Springer Science & Business Media, 2012.
M. Raissi, P. Perdikaris, and G. E. Karniadakis. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378:686–707, 2019.
M. M. Rao and Z. D. Ren. Theory of Orlicz spaces, volume 146 of Monographs and Textbooks in Pure and Applied Mathematics. Marcel Dekker, Inc., New York, 1991.
D. Saxton, E. Grefenstette, F. Hill, and P. Kohli. Analysing mathematical reasoning abilities of neural models. In International Conference on Learning Representations, 2018.
A. W. Senior, R. Evans, J. Jumper, J. Kirkpatrick, L. Sifre, T. Green, C. Qin, A. Žídek, A. W. Nelson, and A. Bridgland. Improved protein structure prediction using potentials from deep learning. Nature, 577(7792):706–710, 2020.
S. Shalev-Shwartz and S. Ben-David. Understanding Machine Learning: From Theory to Algorithms. Cambridge University Press, 2014.
D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. Van Den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, and M. Lanctot. Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587):484–489, 2016.
D. Silver, J. Schrittwieser, K. Simonyan, I. Antonoglou, A. Huang, A. Guez, T. Hubert, L. Baker, M. Lai, and A. Bolton. Mastering the game of Go without human knowledge. Nature, 550(7676):354–359, 2017.
C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1–9, 2015.
M. Telgarsky. Benefits of depth in neural networks. In Conference on learning theory, pages 1517–1539. PMLR, 2016.
A. F. Timan. Theory of approximation of functions of a real variable. Elsevier, 2014.
R. Vershynin. High-dimensional probability, volume 47 of Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge, 2018.
O. Vinyals, I. Babuschkin, W. M. Czarnecki, M. Mathieu, A. Dudzik, J. Chung, D. H. Choi, R. Powell, T. Ewalds, and P. Georgiev. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature, 575(7782):350–354, 2019.
D. Yarotsky. Optimal approximation of continuous functions by very deep ReLU networks. In Conference on Learning Theory, pages 639–649. PMLR, 2018.
T. Young, D. Hazarika, S. Poria, and E. Cambria. Recent trends in deep learning based natural language processing. IEEE Computational intelligence magazine, 13(3):55–75, 2018.
Funding
Open access funding provided by University of Vienna.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Teresa Krick and Hans Munthe-Kaas.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Invited paper associated to the FoCM 2021 Online Seminar lecture Deep Learning in Numerical Analysis presented by Philipp Grohs in May 2021.
F. Voigtlaender acknowledges support by the German Research Foundation (DFG) in the context of the Emmy Noether junior research group VO 2594/1–1.
Postponed Technical Results and Proofs
Postponed Technical Results and Proofs
1.1 Proof of Lemma 2.1
This section provides the proof of Lemma 2.1, which is based on the following lemma concerning closure properties of the sets  .
.
Lemma A.1
With \(\widetilde{\varvec{\ell }}(n) := \min \{ \varvec{\ell }(n), n \}\), we have  . Furthermore, for every \(n \in \mathbb {N}\), we have
. Furthermore, for every \(n \in \mathbb {N}\), we have  .
.
Proof
We first prove  . To this end, we prove for fixed \(n \in \mathbb {N}\) by induction on \(\ell \in \mathbb {N}_{\ge n}\) that
. To this end, we prove for fixed \(n \in \mathbb {N}\) by induction on \(\ell \in \mathbb {N}_{\ge n}\) that  . For \(\ell = n\), this is trivial. Thus, suppose that
. For \(\ell = n\), this is trivial. Thus, suppose that  for some \(\ell \in \mathbb {N}_{\ge n}\) and let
for some \(\ell \in \mathbb {N}_{\ge n}\) and let  , say \(f = R_\varrho \Phi \) with \(\Vert \Phi \Vert _{\mathcal{N}\mathcal{N}} \le \varvec{c}(n)\) and \(W(\Phi ) \le n\), as well as \(L(\Phi ) \le \ell + 1\). If \(L(\Phi ) \le \ell \), then
, say \(f = R_\varrho \Phi \) with \(\Vert \Phi \Vert _{\mathcal{N}\mathcal{N}} \le \varvec{c}(n)\) and \(W(\Phi ) \le n\), as well as \(L(\Phi ) \le \ell + 1\). If \(L(\Phi ) \le \ell \), then  by induction. Hence, we can assume that \(L(\Phi ) = \ell +1\).
by induction. Hence, we can assume that \(L(\Phi ) = \ell +1\).
Writing \(\Phi = \big ( (A_1,b_1), ..., (A_{\ell +1}, b_{\ell +1}) \big )\) with \(b_m \in \mathbb {R}^{N_m}\) and \(A_m \in \mathbb {R}^{N_m \times N_{m-1}}\), we have \({A_j = b_j = 0}\) for some \(j \in \underline{\ell +1}\), since otherwise \( n\!+\!1 \le \ell \!+\!1 \le \sum _{j=1}^{\ell +1} \bigl (\Vert A_j \Vert _{\ell ^0} \!+\! \Vert b_j \Vert _{\ell ^0}\bigr ) \!=\! W(\Phi ) \le n . \) If \(j = \ell +1\), we trivially have  ; thus, let us assume \(j \le \ell \) and define
; thus, let us assume \(j \le \ell \) and define
Since \(A_j = b_j = 0\) and \(\varrho (0) = 0\), it is straightforward to verify \(R_\varrho \widetilde{\Phi } = R_\varrho \Phi = f\). Since furthermore \(\Vert \widetilde{\Phi } \Vert _{\mathcal{N}\mathcal{N}} \le \Vert \Phi \Vert _{\mathcal{N}\mathcal{N}} \le \varvec{c}(n)\) and \(W(\widetilde{\Phi }) \le W(\Phi ) \le n\), as well as \(L(\widetilde{\Phi }) \le \ell - j + 1 \le \ell \), this implies  , where the last inclusion holds by induction. This completes the induction.
, where the last inclusion holds by induction. This completes the induction.
To prove  , let
, let  , so that \(f = R_\varrho \Phi \) and \(g = R_\varrho \Psi \) for networks \(\Phi ,\Psi \) satisfying \({W(\Phi ), W(\Psi ) \le n}\) and \(\Vert \Phi \Vert _{\mathcal{N}\mathcal{N}}, \Vert \Psi \Vert _{\mathcal{N}\mathcal{N}} \le \varvec{c}(n)\), as well as \(L(\Phi ), L(\Psi ) \le \min \{ n, \varvec{\ell }(n) \}\); here we used the first part of the lemma. By possibly swapping \(\Phi ,\Psi \) and f, g, we can assume that \(k := L(\Phi ) \le L(\Psi ) =: \ell \). If \(k = \ell \), define \(\widetilde{\Phi } := \Phi \). If otherwise \(k < \ell \), write \(\Phi = \big ( (A_1,b_1),\dots ,(A_k,b_k) \big )\) where \(A_k \in \mathbb {R}^{1 \times N_{k-1}}\) and \(b_k \in \mathbb {R}^1\), and define \( \Gamma := \big ( \left( {\begin{matrix} 1 \\ 1 \end{matrix}} \right) , \left( {\begin{matrix} 0 \\ 0 \end{matrix}} \right) \big ) \) and \( \Lambda := \big ( (1, -1), 0 \big ) \) and finally
, so that \(f = R_\varrho \Phi \) and \(g = R_\varrho \Psi \) for networks \(\Phi ,\Psi \) satisfying \({W(\Phi ), W(\Psi ) \le n}\) and \(\Vert \Phi \Vert _{\mathcal{N}\mathcal{N}}, \Vert \Psi \Vert _{\mathcal{N}\mathcal{N}} \le \varvec{c}(n)\), as well as \(L(\Phi ), L(\Psi ) \le \min \{ n, \varvec{\ell }(n) \}\); here we used the first part of the lemma. By possibly swapping \(\Phi ,\Psi \) and f, g, we can assume that \(k := L(\Phi ) \le L(\Psi ) =: \ell \). If \(k = \ell \), define \(\widetilde{\Phi } := \Phi \). If otherwise \(k < \ell \), write \(\Phi = \big ( (A_1,b_1),\dots ,(A_k,b_k) \big )\) where \(A_k \in \mathbb {R}^{1 \times N_{k-1}}\) and \(b_k \in \mathbb {R}^1\), and define \( \Gamma := \big ( \left( {\begin{matrix} 1 \\ 1 \end{matrix}} \right) , \left( {\begin{matrix} 0 \\ 0 \end{matrix}} \right) \big ) \) and \( \Lambda := \big ( (1, -1), 0 \big ) \) and finally

where \(\Gamma \) appears \(\ell - k - 1\) times, so that \(L(\widetilde{\Phi }) = \ell \). Using the identities \(x = \varrho (x) - \varrho (-x)\) and \(\varrho (\varrho (x)) = \varrho (x)\), it is easy to see \(R_\varrho \widetilde{\Phi } = R_\varrho \Phi = f\). Moreover, \(\Vert \widetilde{\Phi } \Vert _{\mathcal{N}\mathcal{N}} \le \max \{ 1, \varvec{c}(n) \} = \varvec{c}(n)\) and \(W(\widetilde{\Phi }) \le 2 W(\Phi ) + 2 (\ell - k) \le 4 n\).
Finally, explicitly writing \(\widetilde{\Phi } = \big ( (B_1, c_1), \dots , (B_\ell , c_\ell ) \big )\) and \(\Psi = \big ( (C_1, e_1), \dots , (C_\ell , e_\ell ) \big )\) with \(c_\ell , e_\ell \in \mathbb {R}^{1}\) and \(B_\ell ,C_\ell \in \mathbb {R}^{1 \times N_{\ell -1}}\), define
and set
Using the identities \(\varrho (\varrho (x)) = \varrho (x)\) and \(x = \varrho (x) - \varrho (-x)\), it is then straightforward to verify \(R_\varrho \Xi = R_\varrho \widetilde{\Phi } + R_\varrho \Psi = f + g\). Moreover, \(\Vert \Xi \Vert _{\mathcal{N}\mathcal{N}} \le \varvec{c}(n) \le \varvec{c}(9n)\), \(L(\Xi ) = \ell \le \varvec{\ell }(n) \le \varvec{\ell }(9n)\), and \(W(\Xi ) \le W(\widetilde{\Phi }) + W(\Psi ) + 4 \, \ell \le 9 n\). Here, we used that \(\varvec{\ell }\) and \(\varvec{c}\) are non-decreasing and that \(\ell \le n\). Overall, we have shown  , as claimed. \(\square \)
, as claimed. \(\square \)
With Lemma A.1 at our disposal, we can now prove Lemma 2.1.
Proof of Lemma 2.1
Step 1 (Showing  ): To see this, let \(n \in \mathbb {N}_{\ge 9}\) and write \(n = 9 m + k\) with \(m \in \mathbb {N}\) and \(k \in \{ 0, \dots , 8 \}\), noting that \(n \le 17 m\). By Lemma A.1, we have
): To see this, let \(n \in \mathbb {N}_{\ge 9}\) and write \(n = 9 m + k\) with \(m \in \mathbb {N}\) and \(k \in \{ 0, \dots , 8 \}\), noting that \(n \le 17 m\). By Lemma A.1, we have  and hence
and hence

Moreover, if \(n \le 8\), then we see because of  that
that

Overall, we thus see for every \(n \in \mathbb {N}\) that  . Since also
. Since also  we see that
we see that  , as claimed in this step.
, as claimed in this step.
Step 2 (Showing  for \(|c| \le 1\)): Since \(|c| \le 1\), it is straightforward to see
for \(|c| \le 1\)): Since \(|c| \le 1\), it is straightforward to see  and hence
and hence  This implies
This implies 
Step 3 (Showing  ):
):
“\(\Rightarrow \):” For  , Step 2 shows
, Step 2 shows  , and hence
, and hence  .
.
“\(\Leftarrow \):” Let  . Hence, there exists \(\theta > 0\) satisfying
. Hence, there exists \(\theta > 0\) satisfying  . Step 1 shows
. Step 1 shows  . Inductively, this implies
. Inductively, this implies  for every \(m \in \mathbb {N}\). Now, choosing \(m \in \mathbb {N}\) such that \(\theta \le 2^m\), Step 2 shows
for every \(m \in \mathbb {N}\). Now, choosing \(m \in \mathbb {N}\) such that \(\theta \le 2^m\), Step 2 shows

Step 4 (Homogeneity of  ): It is easy to see
): It is easy to see  . Moreover, given \(c \in \mathbb {R}\setminus \{ 0 \}\), Step 2 shows that
. Moreover, given \(c \in \mathbb {R}\setminus \{ 0 \}\), Step 2 shows that  . Therefore,
. Therefore,

Step 5 (Definiteness of  ): If
): If  , then for each \(n \in \mathbb {N}\) there exists \(\theta _n \in (0, \frac{1}{n})\) satisfying
, then for each \(n \in \mathbb {N}\) there exists \(\theta _n \in (0, \frac{1}{n})\) satisfying  . By Step 2, this implies
. By Step 2, this implies

and hence \(f = 0\).
Step 6 (If  , then
, then  ): By definition of
): By definition of  , there exists a sequence \((\theta _n)_{n \in \mathbb {N}} \subset (0,\infty )\) satisfying
, there exists a sequence \((\theta _n)_{n \in \mathbb {N}} \subset (0,\infty )\) satisfying  and
and  for all \(n \in \mathbb {N}\). Since \(\frac{f}{\theta _n} \rightarrow \frac{f}{\theta }\) and since
for all \(n \in \mathbb {N}\). Since \(\frac{f}{\theta _n} \rightarrow \frac{f}{\theta }\) and since  is continuous with respect to \(\Vert \cdot \Vert _{L^p}\), this implies for each \(m \in \mathbb {N}\) that
is continuous with respect to \(\Vert \cdot \Vert _{L^p}\), this implies for each \(m \in \mathbb {N}\) that

and hence  .
.
Step 7 (Showing  ): The claim is trivial if
): The claim is trivial if  or
or  . Hence, we can assume that
. Hence, we can assume that  and
and  . By Steps 1, 2, and 6, this implies
. By Steps 1, 2, and 6, this implies

and hence  as claimed.
as claimed.
Step 8 (Showing  ): “\(\Rightarrow \)” follows by definition of
): “\(\Rightarrow \)” follows by definition of  .
.
“\(\Leftarrow \)” is trivial if \(f = 0\). Otherwise, Steps 6 and 2 show for  that
that 
Step 9: In this step, we prove the last part of Lemma 2.1. First, note that if  , then
, then  thanks to Step 8. This proves
thanks to Step 8. This proves  .
.
Next, if \(\Omega \subset \overline{\Omega ^\circ }\), then it is easy to see for \(f \in C_b(\Omega )\) that \(\Vert f \Vert _{\sup ,\Omega } := \sup _{x \in \Omega } |f(x)| = \Vert f \Vert _{L^\infty (\Omega )}\), and this implies that \(C_b(\Omega ) \subset L^\infty (\Omega )\) is closed. Therefore, it suffices to show  . To see this, let
. To see this, let  ; by Step 3, this implies
; by Step 3, this implies  . Furthermore, \(\Vert f \Vert _{L^\infty } < \infty \). By definition of
. Furthermore, \(\Vert f \Vert _{L^\infty } < \infty \). By definition of  , for each \(n \in \mathbb {N}\) there exists
, for each \(n \in \mathbb {N}\) there exists  satisfying \(\Vert F_n - f \Vert _{L^\infty } \le 2 C n^{-\alpha } \rightarrow 0\) as \(n \rightarrow \infty \); in particular, \(\Vert F_n \Vert _{\sup ,\Omega } = \Vert F_n \Vert _{L^\infty } < \infty \). Finally, since \(F_n\) can be extended to a continuous function on all of \(\mathbb {R}^d\), we see \(F_n \in C_b(\Omega )\) and hence \(f \in \overline{C_b(\Omega )} = C_b(\Omega )\). \(\square \)
satisfying \(\Vert F_n - f \Vert _{L^\infty } \le 2 C n^{-\alpha } \rightarrow 0\) as \(n \rightarrow \infty \); in particular, \(\Vert F_n \Vert _{\sup ,\Omega } = \Vert F_n \Vert _{L^\infty } < \infty \). Finally, since \(F_n\) can be extended to a continuous function on all of \(\mathbb {R}^d\), we see \(F_n \in C_b(\Omega )\) and hence \(f \in \overline{C_b(\Omega )} = C_b(\Omega )\). \(\square \)
1.2 A Technical Result used in Sect. 3
Lemma A.2
For each \(d \in \mathbb {N}\), \(T \in (0,1]\), and \(x \in [0,1]^d\), we have
Proof
For brevity, set \(Q := [0,1]^d\). Below, we show
which clearly implies the claim for these T. Furthermore, for \(T \in [\frac{1}{2},1]\), the above estimate shows \( \varvec{\lambda }\big ( Q \cap (x + [-T,T]^d) \big ) \ge \varvec{\lambda }\big ( Q \cap (x + [-\frac{1}{2}, \frac{1}{2}]^d ) \big ) \ge 2^{-d} \ge 2^{-d} T^d , \) which proves the claim for general \(T \in (0,1]\).
Thus, let \(x \in Q\) and \(T \in (0,\frac{1}{2}]\). For each \(j \in \underline{d}\), define \(\varepsilon _j := -1\) if \(x_j \ge \frac{1}{2}\) and \(\varepsilon _j := 1\) otherwise. Let \(P := \prod _{j=1}^d \big ( \varepsilon _j \, [0,T] \big ) \subset [-T,T]^d\). We claim that \(x + P \subset Q\). Once this is shown, it follows that \( \varvec{\lambda }\bigl ( Q \cap (x + [-T,T]^d) \bigr ) \ge \varvec{\lambda }(x + P) = T^d , \) proving Eq. (A.1).
To see that indeed \(x + P \subset Q\), let \(y \in P\) be arbitrary. For each \(j \in \underline{d}\), there are then two cases:
-
1.
If \(x_j \ge \frac{1}{2}\), then \(\varepsilon _j = -1\) and \(-\frac{1}{2} \le -T \le y_j \le 0\). Thus, \(0 \le x_j - \frac{1}{2} \le x_j + y_j \le x_j \le 1\), meaning \((x + y)_j \in [0,1]\).
-
2.
If \(x_j < \frac{1}{2}\), then \(\varepsilon _j = 1\) and \(0 \le y_j \le T \le \frac{1}{2}\). Thus, \(0 \le x_j \le x_j + y_j \le \frac{1}{2} + \frac{1}{2} = 1\), so that we see again \((x + y)_j \in [0,1]\).
Overall, this shows in both cases that \(x + y \in [0,1]^d = Q\). \(\square \)
1.3 A Technical Result Regarding Measurability
Lemma A.3
Let \(\varnothing \ne \Omega \subset \mathbb {R}^d\) be compact and let \(\varnothing \ne \mathcal {H}\subset C(\Omega )\) be compact. Then, equipping \(\mathcal {H}\) with the Borel \(\sigma \)-algebra induced from \(C(\Omega )\), the following hold:
-
1.
The map
$$\begin{aligned}{} & {} M:\Omega ^m \times \mathcal {H}\rightarrow \Omega ^m \times \mathbb {R}^m,\\ {}{} & {} \quad (\varvec{x}, f) = \bigl ( (x_1,\dots ,x_m), f\bigr ) \mapsto \Big (\varvec{x}, \bigl ( f(x_1),\dots ,f(x_m) \bigr ) \Big ) \end{aligned}$$is continuous and hence measurable;
-
2.
there is a measurable map \(B : \Omega ^m \times \mathbb {R}^m \rightarrow \mathcal {H}\) satisfying
$$\begin{aligned}{} & {} B(\varvec{x}, \varvec{y}) \in \mathop {\textrm{argmin}}\limits _{g \in \mathcal {H}} \sum _{i=1}^m \big ( g(x_i) - y_i \big )^2\\ {}{} & {} \quad \forall \, \varvec{x}= (x_1,\dots ,x_m) \in \Omega ^m \text { and } \varvec{y}= (y_1,\dots ,y_m) \in \mathbb {R}^m. \end{aligned}$$
Proof
Part 1: It is enough to prove continuity of each of the components of M. For the component \((\varvec{x},f) \mapsto \varvec{x}\) this is trivial. For the component \((\varvec{x},f) \mapsto f(x_j)\) note that if \(\Omega ^m \ni \varvec{x}^{(n)} \rightarrow \varvec{x}\in \Omega ^m\) and \(\mathcal {H}\ni f_n \rightarrow f \in \mathcal {H}\) (with convergence in \(C(\Omega )\)), then
since f is continuous. Thus, M is continuous. To see that this implies that M is measurable, note that both \(\Omega ^m\) and \(\mathcal {H}\) are separable metric spaces (and hence second countable), so that the product \(\sigma \)-algebra on \(\Omega ^m \times \mathcal {H}\) coincides with the Borel \(\sigma \)-algebra on \(\Omega ^m \times \mathcal {H}\); see for instance [19, Theorem 7.20].
Part 2: For this part, we use the “Measurable Maximum Theorem,” [2, Theorem 18.19]. Thanks to this theorem, setting \(S := \Omega ^m \times \mathbb {R}^m\), it is enough to show that
-
1.
the set-valued mapFootnote 2\(\varphi : S \twoheadrightarrow C(\Omega ), (\varvec{x},\varvec{y}) \mapsto \mathcal {H}\) is weakly measurable with nonempty, compact values;
-
2.
the map \( F : S \times C(\Omega ) \rightarrow \mathbb {R}, \bigl ( (\varvec{x},\varvec{y}), g \bigr ) \mapsto -\sum _{i=1}^m \bigl (g(x_i) - y_i\bigr )^2 \) is a Carathéodory function (see [2, Definition 4.50]).
By our assumptions on \(\mathcal {H}\), it is clear that \(\varphi \) has nonempty, compact values. The weak measurability of \(\varphi \) follows directly from the definition, see [2, Definition 18.1]. For the second property, it is enough to show that F is continuous. This follows as in Eq. (A.2). \(\square \)
1.4 A Technical Result Regarding Random Subsets of \(\{ 1,\dots ,m \}\)
Lemma A.4
Let \(m \in \mathbb {N}\) and \(1 \le k \le 2 m\). Write \(\mathcal {P}_k (\underline{2m}) := \{ J \subset \underline{2m} :|J| = k \}\). Then, for each subset \(I \subset \underline{2m}\) with \(|I| \ge m\), we have

Proof
Let \(I^c := \underline{2m} \setminus I\). We note for any \(T \subset \underline{2m}\) that the quantity  only depends on the cardinality |T| and that \(\psi (T) \le \psi (S)\) if \(|T| \le |S|\). Since \(|I| \ge m \ge |I^c|\), this implies \(\psi (I) \ge \psi (I^c)\). Combined with the estimate
only depends on the cardinality |T| and that \(\psi (T) \le \psi (S)\) if \(|T| \le |S|\). Since \(|I| \ge m \ge |I^c|\), this implies \(\psi (I) \ge \psi (I^c)\). Combined with the estimate
which holds for all \(J \in \mathcal {P}_k (\underline{2m})\), we finally see

\(\square \)
1.5 Two Technical Optimization Results
Lemma A.5
Let \(\gamma ^\flat \in [1,\infty ]\) and \(\alpha > 0\). Let
Then
Remark
In fact, one has equality. But since we do not need this, we omit the proof (and the explicit statement) of this fact.
Proof
Step 1 (Preparations): Define \(f_1(\gamma ,\theta ,\lambda ) := \theta \cdot (\alpha - \frac{\lambda }{2})\) and \(f_2 (\gamma ,\theta ,\lambda ) := 1 + \theta \cdot (\frac{\lambda }{2} - \gamma )\) as well as \(f := \max \{ f_1, f_2 \}\) and \(\beta _*:= \inf _{(\gamma ,\theta ,\lambda ) \in \Psi } f(\gamma ,\theta ,\lambda )\). For arbitrary \(0< \gamma < \gamma ^\flat \), we have \((\gamma ,\frac{1}{\alpha +\gamma },0) \in \Psi \) and hence \( \beta _*\le f(\gamma ,\frac{1}{\alpha +\gamma },0) = \max \big \{ \frac{\alpha }{\alpha +\gamma }, 1 - \frac{\gamma }{\alpha + \gamma } \big \} = \frac{\alpha }{\alpha + \gamma } . \) Letting \(\gamma \uparrow \gamma ^\flat \), this implies
Step 2 (The case \(\gamma ^\flat = \infty \)): Let us first consider the case \(\gamma ^\flat = \infty \). In this case, Eq. (A.4) shows \(\beta _*\le 0\). Furthermore, given \(0< \gamma < \gamma ^\flat = \infty \), we have \((\gamma ,1,1) \in \Psi \), which shows that \(\beta _*\le f(\gamma ,1,1) = \max \bigl \{ \alpha - \frac{1}{2}, \frac{3}{2} - \gamma \bigr \}\). Letting \(\gamma \rightarrow \infty \), we thus see \(\beta _*\le \alpha - \frac{1}{2}\) and hence \(\beta _*\le \min \{ 0, \alpha - \frac{1}{2} \}\). It is easy to see that this implies the claim for \(\gamma ^\flat = \infty \).
Hence, we can assume from now on that \(\gamma ^\flat \) is finite. Then, we easily see for \(g_1(\theta ,\lambda ) := \theta \cdot (\alpha - \frac{\lambda }{2})\) and \(g_2(\theta ,\lambda ) := 1 + \theta \cdot (\frac{\lambda }{2} - \gamma ^\flat )\) as well as \(g := \max \{ g_1, g_2 \}\) and \(\Omega := \{ (\theta , \lambda ) \in (0,\infty ) \times [0,1] :\theta \lambda \le 1 \}\) that \(\beta _*\le \inf _{(\theta ,\lambda ) \in \Omega } g(\theta ,\lambda )\).
Step 3 (The case \(\alpha + \gamma ^\flat < 2\)): In this case, we have \(\frac{2}{\alpha + \gamma ^\flat } \in (1,\infty )\) and hence \((\frac{2}{\alpha +\gamma ^\flat }, \frac{\alpha + \gamma ^\flat }{2}) \in \Omega \). Furthermore, \( g_1(\frac{2}{\alpha +\gamma ^\flat }, \frac{\alpha + \gamma ^\flat }{2}) = g_2(\frac{2}{\alpha +\gamma ^\flat }, \frac{\alpha + \gamma ^\flat }{2}) = \frac{2 \alpha }{\alpha + \gamma ^\flat } - \frac{1}{2} \) and hence \(\beta _*\le \frac{2 \alpha }{\alpha + \gamma ^\flat } - \frac{1}{2}\). Together with Eq. (A.4), this proves the claim for \(\alpha + \gamma ^\flat < 2\).
Step 4 (The case \(\alpha + \gamma ^\flat \ge 2\)): Note \(g_1(1,1) = \alpha - \frac{1}{2}\) and \(g_2(1,1) = \frac{3}{2} - \gamma ^\flat \le \frac{3}{2} - (2 - \alpha ) = \alpha - \frac{1}{2}\). Since \((1,1) \in \Omega \), this implies \(\beta _*\le g(1,1) = \alpha - \frac{1}{2}\). Furthermore, \(\theta _0 := \frac{1}{\alpha + \gamma ^\flat - 1} \in (0,1]\) and hence \((\theta _0,1) \in \Omega \). It is easy to see \(g_1(\theta _0,1) = g_2(\theta _0,1) = \frac{\alpha - \frac{1}{2}}{\alpha + \gamma ^\flat - 1}\) and hence \(\beta _*\le g(\theta _0,1) = \frac{\alpha - \frac{1}{2}}{\alpha + \gamma ^\flat - 1}\). Combining these two estimates with Eq. (A.4) completes the proof for the case \(\alpha + \gamma ^\flat \ge 2\). \(\square \)
Lemma A.6
Let \(\gamma ^\flat \in [1,\infty ]\) and \(\alpha > 0\). Let \(\Psi \) be as in Eq. (A.3). Then
Proof
For brevity, denote the left-hand side of Eq. (A.5) by \(\beta _*\).
We first consider the special case \(\gamma ^{\flat } = \infty \). Define \(g := \max \{ g_1, g_2 \}\), where \(g_1(\gamma ,\theta ,\lambda ) := \theta \cdot (\alpha - \lambda )\) and \(g_2(\gamma ,\theta ,\lambda ) := 1 - \theta \gamma \). For any \(\gamma > 0\), we have \(g_1(\gamma ,1,1) = \alpha - 1\) and \(g_2(\gamma ,1,1) = 1 - \gamma \) and furthermore \((\gamma ,1,1) \in \Psi \). Therefore, \( \beta _*\le g(\gamma ,1,1) = \max \{ \alpha - 1, \,\, 1 - \gamma \} \xrightarrow [\gamma \rightarrow \infty ]{} \alpha - 1. \) Furthermore, for arbitrary \(\gamma > 0\) we have \((\gamma ,\frac{1}{\gamma },0) \in \Psi \) and \(g_1(\gamma ,\frac{1}{\gamma },0) = \frac{\alpha }{\gamma }\) and \(g_2(\gamma ,\frac{1}{\gamma },0) = 0\), so that \(\beta _*\le \min \{ 0, \frac{\alpha }{\gamma } \} \xrightarrow [\gamma \rightarrow \infty ]{} 0\). Overall, we have thus shown \(\beta _*\le \min \{ \alpha - 1, 0 \}\), which easily implies that Eq. (A.5) holds in case of \(\gamma ^\flat = \infty \).
Hence, we can assume that \(\gamma ^\flat < \infty \). Then, setting \(\Omega := \{ (\theta ,\lambda ) \in (0,\infty ) \times [0,1] :\theta \lambda \le 1 \}\) and furthermore \(f := \max \{ f_1, f_2 \}\) for \(f_1(\theta ,\lambda ) := \theta (\alpha - \lambda )\) and \(f_2(\theta ,\lambda ) := 1 - \theta \gamma ^\flat \), it is easy to see by continuity that \(\beta _*\le \inf _{(\theta ,\lambda ) \in \Omega } f(\theta ,\lambda )\). We now distinguish two cases:
Case 1 (\(\alpha + \gamma ^\flat \le 2\)): In this case, \(\theta _0 := \frac{2}{\alpha + \gamma ^\flat } \in [1,\infty )\) and \(\lambda _0 := \frac{1}{\theta _0} \in (0,1]\) satisfy \((\theta _0,\lambda _0) \in \Omega \). Furthermore, it is easy to see \(f_1(\theta _0,\lambda _0) = \frac{2 \alpha }{\alpha + \gamma ^\flat } - 1 = f_2(\theta _0,\lambda _0)\). Thus, \(\beta _*\le f(\theta _0,\lambda _0) = \frac{2 \alpha }{\alpha + \gamma ^\flat } - 1\), which proves Eq. (A.5) in this case.
Case 2 (\(\alpha + \gamma ^\flat > 2\)): First note because of \(\alpha + \gamma ^\flat > 2\) that \(f_1(1,1) = \alpha - 1 > 1 - \gamma ^\flat = f_2(1,1)\) and hence \(\beta _*\le f(1,1) = \alpha - 1\). Furthermore, we have \(\theta ^*:= \frac{1}{\alpha + \gamma ^\flat - 1} \in (0,1)\) and hence \((\theta ^*, 1) \in \Omega \). Furthermore, it is easy to see \(f_1(\theta ^*,1) = \frac{\alpha - 1}{\alpha + \gamma ^\flat - 1} = f_2(\theta ^*,1)\) which implies \(\beta _*\le f(\theta ^*,1) = \frac{\alpha - 1}{\alpha + \gamma ^\flat - 1}\). Overall, we see \(\beta _*\le \min \big \{ \alpha - 1, \frac{\alpha - 1}{\alpha + \gamma ^\flat - 1} \big \}\), which shows that Eq. (A.5) holds for \(\alpha + \gamma ^\flat > 2\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grohs, P., Voigtlaender, F. Proof of the Theory-to-Practice Gap in Deep Learning via Sampling Complexity bounds for Neural Network Approximation Spaces. Found Comput Math (2023). https://doi.org/10.1007/s10208-023-09607-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10208-023-09607-w
Keywords
- Deep neural networks
- Approximation spaces
- Information based complexity
- Gelfand numbers
- Theory-to-computational gaps
- Randomized approximation



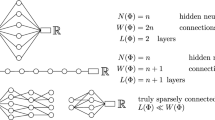
 is a quasi-normed space. Precisely, given arbitrary measurable functions
is a quasi-normed space. Precisely, given arbitrary measurable functions  for
for  for
for  if and only if
if and only if  .
. if and only if
if and only if  .
. . Furthermore, if
. Furthermore, if  , where
, where 

