The Topological Correctness of PL Approximations of Isomanifolds

Abstract

Isomanifolds are the generalization of isosurfaces to arbitrary dimension and codimension, i.e. manifolds defined as the zero set of some multivariate multivalued smooth function $f: {\mathbb {R}}^d\rightarrow {\mathbb {R}}^{d-n}$. A natural (and efficient) way to approximate an isomanifold is to consider its piecewise-linear (PL) approximation based on a triangulation $\mathcal {T}$ of the ambient space ${\mathbb {R}}^d$. In this paper, we give conditions under which the PL approximation of an isomanifold is topologically equivalent to the isomanifold. The conditions are easy to satisfy in the sense that they can always be met by taking a sufficiently fine and thick triangulation $\mathcal {T}$. This contrasts with previous results on the triangulation of manifolds where, in arbitrary dimensions, delicate perturbations are needed to guarantee topological correctness, which leads to strong limitations in practice. We further give a bound on the Fréchet distance between the original isomanifold and its PL approximation. Finally, we show analogous results for the PL approximation of an isomanifold with boundary.

1 Introduction

1.1 Isosurfacing

Given a surface represented in ${\mathbb {R}}^3$ as the zero set of a function $f: {\mathbb {R}}^3 \rightarrow {\mathbb {R}}$, the goal of isosurfacing is to find a piecewise-linear (PL) approximation of the surface. This question naturally extends to higher dimensions and codimensions, in which case the generalized surface is called an isomanifold. Isosurfaces play a crucial role in medical imaging, computer graphics and geometry processing [1]. Higher-dimensional isomanifolds are also of fundamental importance in many fields such as statistics [2], dynamical systems [3], econometrics or mechanics [1].

1.1.1 Marching Algorithms

The standard algorithmic solution to the isosurfacing problem is to use some marching algorithm. This approach was initiated by Lorensen and Cline, with their marching cube algorithm [4]. Many variants of the algorithm have been introduced, see, for example, [5,6,7,8], and the overview [1]. The approach, however, is always the same: one first subdivides the ambient space into cubes (in which case the algorithm is called a marching cube algorithm), or simplices [5, 6, 9] (in which case the algorithm is called a marching tetrahedra algorithm). One starts with a cube or a simplex (cell) in which a part of the zero set of the function is contained, and finds a piecewise-linear approximation of the zero set in that cell. One then propagates or marches to adjacent cells that also contain the zero set and approximates the zero set in that cell. This process can be continued until all cells that intersect the zero set have been visited.

For the marching cube algorithm [4], one also has to decide how to approximate the zero set inside a cube. As observed by Dürst, there is in general no canonical way how to do this due to ambiguous configurations, see [10] for an extensive discussion in the three-dimensional setting. For the marching tetrahedra algorithm, there is a canonical way to construct a piecewise-linear approximation of the zero set, as we will discuss below. However, the result of the algorithm is still not necessarily topologically correct.

1.1.2 Guarantees for Isosurfacing

For the marching simplex algorithm [5] in arbitrary dimensions, bounds have been given on the one-sided Hausdorff distance between the zero set of f and its PL approximation, and also on the difference between the gradient of f and the gradient of the PL approximation. It can be proven that the result of the algorithm is a manifold under appropriate assumptions [11, 12].

An important requirement in the work of Allgower and Georg [12] is that the zero set avoids simplices that have dimension less than the codimension, see [12, Definition 12.2.2] and the text above [12, Theorem 15.4.1]. The idea to avoid these low-dimensional simplices originates with Whitney [13], with whom Allgower and George [11, 12] were apparently unfamiliar. Very heavy perturbation schemes for the vertices of the ambient triangulation $\mathcal {T}$ are needed to ensure that the manifold stays sufficiently far from simplices in the ambient triangulation that have dimension less than the codimension of the manifold [13, 14]. Various techniques have been developed to compute such perturbations with guarantees. They typically consist in perturbing the position of the sample points or in assigning weights to the points. Complexity bounds are then obtained using volume arguments. See, for example, [15,16,17,18]. However, these techniques suffer from several drawbacks. The constants in the complexity depend exponentially on the ambient dimension. Moreover, the analysis assumes that the probability of the simplices of dimension less than the codimension to intersect the manifold is zero, which is not true when dealing with finite precision. As a result, the actual implementations we are aware of fail to work well in practice except in very simple cases.

More complete correctness results have been achieved in three dimensions in the computational geometry community:

Boissonnat, Cohen-Steiner and Vegter [19] base their proof on a combination of Morse theory and simplicial collapses. Vegter and Plantinga’s proof [20] is in its philosophy closely related to normal surface theory, see, for example, [21], but relies rather heavily on case analysis. The results of [19, 20] seem not extendable to higher dimensions.

1.1.3 Triangulating General Manifolds (Without Boundary)

The approximation of a manifold that is the zero set of a function is an example of the more general question of how to triangulate a manifold. It is known that $C^1$ manifolds are triangulable, see, for example, [13], and algorithms have been proposed recently to triangulate smooth manifolds [14, 17, 22, 23]. However, all known methods use intricate perturbation schemes to guarantee the correctness of the triangulation algorithms when the intrinsic dimension of the manifold exceeds 2. As for the case of isomanifolds, perturbation schemes work fine in theory but the constants are miserable and the methods do not work in practice in high dimensions.

1.1.4 Manifolds with Boundary

In this paper, we also consider the piecewise-linear approximation of manifolds with boundary (that are given as a zero set) and briefly mention the extension to stratifolds. Apart from some Delaunay-based work on triangulations of stratifolds in three dimensions [24,25,26,27,28], we are not aware of similar results on manifolds with boundary. Significant effort also went in the detection of strata, in this case in arbitrary dimension, see, for example, [29,30,31].

1.1.5 Contribution

This paper contains three main results, the first two (Theorem 25 and Corollary 27) concern manifolds without boundary and the third (Theorem 48) manifolds with boundary.

We state here simplified versions of the statements to be fully described later on.

Isomanifolds (without boundary)

Let $f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}^{d-n}$ be a smooth function and suppose that 0 is a regular value of f, meaning that at every point x such that $f(x)=0$, the Jacobian of f is non-degenerate. Assume that $\mathcal {T}$ is a triangulation of ${\mathbb {R}}^d$. Define the function $f_{PL}$ as the linear interpolation of the values of f at the vertices if restricted to a single simplex $\sigma \in \mathcal {T}$. Then,

Theorem 25 (Ambient isotopy) The zero set of $f_{PL}$ is a manifold that is ambient isotopic to the zero set of f, provided that the triangulation $\mathcal {T}$ is sufficiently fine and thick.

We recall that the thickness of a simplex is the ratio of the height (smallest altitude) over the longest edge length, and it is a measure for the quality or how well shaped a simplex is.

Corollary 27 (Bound on the Fréchet distance) The Fréchet distance between $f_{PL}$ and f is of the order of $D^2$, where D is the longest edge length of $\mathcal {T}$.

We also give a variant of a result due to Allgower and George [11]:

Proposition 10The difference between the gradient of f and the gradient of its piecewise-linear approximation is of order dD inside each simplex of $\mathcal {T}$.

Isomanifolds with boundary Suppose that apart from f we are also given another function $f_\partial : {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ and $f_{\partial , PL}$ is defined similar to $f_{PL}$. Write $f^{i}$ for the ith component of f. Let us further assume that the zero set is regular in the following sense: The gradients of $f^i$ span a $(d-n)$-dimensional space at each point of $f^{-1}(0)$ and the gradients of $f^i$ and $f_\partial$ span a $(d-n+1)$-dimensional space at each point of $\partial M= f^{-1}(0) \cap f_\partial ^{-1}(0)$. Then,

Theorem 48 (Manifolds with boundary) The set $f^{-1}(0) \cap f_\partial ^{-1}( [ 0, \infty ))$ is ambient isotopic to $f_{PL}^{-1}(0) \cap f_{\partial ,PL}^{-1}( [ 0, \infty ))$, provided that the triangulation $\mathcal {T}$ is sufficiently fine and thick.

An important aspect of these results is that they hold under mild conditions: they simply ask for a sufficiently fine and thick triangulation $\mathcal {T}$. In contrast to previous results on the triangulation of manifolds, no perturbations are needed to guarantee topological correctness.

Our method provides guarantees on the piecewise-linear (PL) approximation of isomanifolds, regarding the topology, the Fréchet distance and the approximation of the gradients (the latter was already known to Allgower and Georg [11]).

However, we stress that it does not give lower bounds on the quality of the linear pieces in the PL approximation. This is a clear difference with previous methods [13, 14, 16, 23] whose output is a thick triangulation. Although this is an appealing property, it complicates the analysis further and requires unpractical perturbation schemes. Such perturbation techniques could be added to our method to improve the simplex quality (to some limited extent). However, they are not required to make the algorithm work and to obtain the guarantees mentioned above.

The techniques used in this paper are also different from many of the standard tools and do not rely on

Delaunay triangulations [32, 33], the closed ball property [15, 34, 35], Whitney’s lemma [36] or collapses [37]. The current paper mainly relies on the non-smooth implicit function theorem [38] with some Morse theory.

1.1.6 Outline

The rest of this paper is subdivided as follows. In Sect. 2, we treat closed isomanifolds, i.e. compact manifolds without boundary. In Sect. 3, we treat isomanifolds with boundary. Extension to general isostratifolds is briefly discussed in Sect. 4. In the final section, we quantify the robustness of the method by studying how much the zero set of f changes if f is perturbed slightly in the $C^1$-sense [39].

This paper is closely related to another paper where the data structure needed to efficiently propagate along the manifold is presented [40]. Altogether, these two papers show that one can construct PL approximations of isomanifolds in space and time polynomial in the resolution 1/D of the ambient triangulation and in the dimension d of the ambient space.

2 Isomanifolds (Without Boundary)

Let $f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}^{d-n}$ be a smooth ($C^2$ suffices) function and suppose that 0 is a regular value of f, meaning that at every point x such that $f(x)=0$, the Jacobian of f is non-degenerate. Then, the zero set of f is an n-dimensional manifold as a direct consequence of the implicit function theorem, see, for example, [41, Section 3.5]. We further assume that $f^{-1}(0)$ is compact. As in [11] we consider a triangulation $\mathcal {T}$ of ${\mathbb {R}}^d$. The function $f_{PL}$ is the linear interpolation of the values of f at the vertices if restricted to a single simplex $\sigma \in \mathcal {T}$, i.e.

$$\begin{aligned} \forall x\in \sigma : \;\; f_{PL}(x) = \sum _{v\in \sigma } \lambda _v(x) f(v), \end{aligned}$$

where the $\lambda _v$ are the barycentric coordinates of x with respect to the vertices of $\sigma$. For any function $g:{\mathbb {R}}^d \rightarrow {\mathbb {R}}^{d-n}$, we write $g^i$, with $i=1 ,\ldots ,d-n$, for the components of g.

We prove that under certain conditions there is an ambient isotopy from the zero set of f to the zero set of $f_{PL}$. The proof will be using the piecewise-smooth map

$$\begin{aligned} F_{PL}(x,\tau ) = (1-\tau ) f(x) + \tau f_{PL}(x), \end{aligned}$$

(1)

which interpolates between f and $f_{PL}$ and is based on the generalized implicit function theorem.

We are, by definition, only interested in $f^{-1}(0)$ and so can ignore points that are sufficiently far from this zero set. More precisely, we observe the following: if $f^i(x)$ is positive for all x in a geometric simplex $\sigma$, then so is $f^i_{PL} (x)$ because $f^i_{PL} (x)$ is a convex combination of the (positive) values at the vertices. This in turn implies that $F^i_{PL} (x,\tau )$ is positive on $\sigma \times [0,1]$ as, for each $\tau$, it is a convex combination of positive numbers. The same argument holds for negative values. So we see that

Remark 1

Write $\mathcal {T}_0$ for the set of all $\sigma \in \mathcal {T}$, such that $(f^i)^{-1}(0) \cap \sigma \ne \emptyset$ for all i. Then, for all $\tau$, $\{x \mid F_{PL}(x,\tau ) =0\}\subset \mathcal {T}_0$.

The results will be expressed using constants defined in terms of f and the ambient triangulation $\mathcal {T}$.

Definition 2

We define

$$\begin{aligned} \gamma _{\max }&= \max _{x \in \mathcal {T}_0} \; (\max _i|\nabla f^i(x)| ) \end{aligned}$$

(2)

$$\begin{aligned} \lambda _{\min }&= \min _{x\in \mathcal {T}_0} \lambda _{\min } (x), \end{aligned}$$

(3)

$$\begin{aligned} \alpha _{\max } \;&= \max _{x \in \mathcal {T}_0} \max _i \Vert \text {Hes} (f^i) (x) \Vert _2 \end{aligned}$$

(4)

$$\begin{aligned} D \;&: \text{ the } \text{ longest } \text{ edge } \text{ length } \text{ of } \text{ a } \text{ simplex } \text{ in } \mathcal {T}_0 \end{aligned}$$

(5)

$$\begin{aligned} T\;&: \text{ the } \text{ smallest } \text{ thickness } \text{ of } \text{ a } \text{ simplex } \text{ in } \mathcal {T}_0, \end{aligned}$$

(6)

where

• $\nabla f^i = (\partial _j f_i)_j$ denotes the gradient of component $f^i$, for $i\in [1,d-n]$,

• $\mathrm {Gram}(\nabla f)$ denotes the Gram matrix whose elements are $\nabla f^i \cdot \nabla f^j$ where $\cdot$ stands for the dot product,

• $\lambda _{\min }(x)$ denotes the smallest absolute value of the eigenvalues of $\mathrm {Gram}(\nabla f (x))$,¹

• $\text {Hes} (f)= (\partial _k \partial _l f_i)_{k,l}$ denotes the Hessian matrix of second order derivatives,

• $|\cdot |$ denotes the Euclidean norm of a vector and $\Vert \cdot \Vert _2$ the operator 2-norm of a matrix.²

• The thickness is the ratio of the height (smallest altitude) over the longest edge length.

We will assume that $\gamma _{\max }, \lambda _{\min }, \alpha _{\max } , D , T \in (0, \infty )$. The constant $\lambda _{\min }$ quantifies how close 0 is to not being a regular value of f. D is a measure of the size of the simplices of $\mathcal {T}$. We will call $\delta =1/D$ the resolution of $\mathcal {T}$. The thickness is a quality measure of a simplex. A good choice for $\mathcal {T}$ is the Coxeter triangulation of type $A_d$, see [42, 43], or the related Freudenthal triangulations, see [3, 44,45,46], which can be defined for different values of D while keeping T constant (for a given dimension d).

Our results hold for any dimensions d and n. We are especially interested in the case where the ambient dimension d is large. We thus consider d and D as the two main parameters. For our bounds, we will give both exact and asymptotic expressions. The asymptotic expressions are given to emphasize the dependency on the two most important parameters d and D, and hold for any d, D and T such that $dD<T$ and for any fixed positive $\gamma _{\max }, \lambda _{\min }, \alpha _{\max }$. For Coxeter triangulations of type $\tilde{A}_d$ (the only type of Coxeter triangulations mentioned in this paper), we have $T > \frac{2}{\sqrt{d+2}}$, see [43]. Therefore, the condition $dD<T$ is satisfied for these triangulations when $D< (2d\sqrt{d+2})^{-1}$. For convenience, exact expressions are gathered in Appendix A.

2.1 The Result

We are going to construct an ambient isotopy based on (1), see Fig. 1 for a pictorial overview. In fact, the map $\tau \mapsto \{x \mid F_{PL}(x, \tau )=0\}$ gives an ambient isotopy between the zero set of $F_{PL}(x,0)$, which is identical to the smooth isosurface $f^{-1}(0)$, and the zero set of $F_{PL}(x,1)$, which is the PL approximation $f_{PL}^{-1}(0)$. The latter can be turned into a triangulation of the isosurface $f^{-1}(0)$ by triangulating the non-simplicial cells using barycentric subdivision. We will also bound the Fréchet distance between $f^{-1}(0)$ and $f^{-1}_{PL}(0)$ .

Fig. 1

A pictorial overview of the proof. The $\tau$-direction goes upwards. Similar to Morse theory, we find that $f^{-1}_{PL}(0)$ (top) and $f^{-1}(0)$ (bottom) are ambient isotopic if the function $\tau$ restricted to $F_{PL}^{-1}(0)$ does not encounter a Morse critical point

Proving the ambient isotopy consists of three technical steps. The first two consume most of the space in the proof namely:

• Local step. Let $\sigma \in \mathcal {T}$. We first show that $\{(x,\tau ) \mid F_{PL}(x, \tau )=0\} \cap (\sigma \times [0,1])$ is a smooth manifold, under certain conditions (Corollary 13).

• Global step. We prove that $F_{PL}^{-1}(0)$ is a manifold, under certain conditions, using techniques from non-smooth analysis (Corollary 24).

A crucial ingredient will be the implicit function theorem and its non-smooth extension. Along the way, we shall also see that $F_{PL}^{-1}(0)$ is never tangent to the $\tau = c$ planes, where c is a constant. The gradient of $(x, \tau ) ,\mapsto \tau$ in

${\mathbb {R}}^d \times {\mathbb {R}}$ is (0, 1). Projecting this vector onto the tangent space of $F_{PL}^{-1}(0)$ gives the gradient of $(x, \tau ) ,\mapsto \tau$ restricted to $F_{PL}^{-1}(0)$. Because of the non-tangency, this projection is nonzero. So the gradient field of the function $(x, \tau ) ,\mapsto \tau$ restricted to $F_{PL}^{-1}(0)$, is piecewise-smooth (because $F_{PL}^{-1}(0)$ is piecewise-smooth) and never vanishes.

The third step is similar to a standard observation in Morse theory [47, 48], with the exception that we now consider piecewise-smooth instead of smooth vector fields. We refer to Milnor [47] for an excellent introduction and to Lemma 2.4 and Theorem 3.1 in particular.

Lemma 3

(Gradient flow induced isotopies) The flow of a non-vanishing piecewise-smooth gradient vector field of a function $\tau$ on a compact manifold generates a isotopy from $\tau =c_1$ to $\tau =c_2$, where $c_1$ and $c_2$ are constants.

Proof

This is a straightforward consequence of the existence and uniqueness of the solution to a differential equation. $\square$

Bounds on the gradient of $\tau$ on the manifold give a bound on the Fréchet distance, which is defined in the following.

Definition 4

(Fréchet distance for embedded manifolds) Let $\mathcal {M}$ and $\mathcal {M}'$ be two homeomorphic, compact submanifolds of ${\mathbb {R}}^d$. Write $\mathcal {H}$ for the set of all homeomorphisms from $\mathcal {M}$ to $\mathcal {M}'$. The Fréchet distance between $\mathcal {M}$ and $\mathcal {M}'$ is

$$\begin{aligned} d_F (\mathcal {M}, \mathcal {M}') = \inf _{h \in \mathcal {H} } \sup _{x \in \mathcal {M}} d(x, h(x) ). \end{aligned}$$

2.2 Preliminaries

The following elementary lemma will be useful.

Lemma 5

$$\begin{aligned} | f^i (x_1) - f^i (x_2)|&\le \gamma _{\max } |x_1-x_2|. \end{aligned}$$

(7)

$$\begin{aligned} | \nabla f^i (x_1) - \nabla f^i (x_2)|&\le d \alpha _{\max } \; |x_1-x_2|. \end{aligned}$$

(8)

Proof

The first statement follows from the fact that the supremum of the absolute value of a derivative of a function bounds the Lipschitz constant of the function. The second statement follows from standard bounds on matrix norm (see, for example, [49, Equation (2.3.11)]) together with (4). These bounds imply that $\sqrt{d} \alpha _{\max } \ge | \partial _k \partial _l f^i|$, for all k, l and i. Arguing as before, we deduce a bound on the Lipschitz constant of $\partial _l f^i$:

$$\begin{aligned} | \partial _l f^i (x_1) -\partial _l f^i (x_2) | \le \sqrt{d} \alpha _{\max } |x_1-x_2| . \end{aligned}$$

Bound (8) now follows. $\square$

2.2.1 The Implicit Function Theorem

The main technical tool to prove the existence of the ambient isotopy from $f^{-1}(0)$ to $f_{PL}^{-1}(0)$ is the implicit function theorem which we recall now.

Theorem 6

(Smooth implicit function theorem) Let $F: {\mathbb {R}}^{d+1} \rightarrow {\mathbb {R}}^{d-n}$ be a continuously differentiable function. Write ${\mathbb {R}}^{d+1} = {\mathbb {R}}^{n+1} \times {\mathbb {R}}^{d-n}$ and denote the coordinates of ${\mathbb {R}}^{d+1}$ by (x, y) accordingly. Fix a point (a, b), with $F(a,b)=0 \in {\mathbb {R}}^{d-n}$. If the Jacobian $J_{F,y}(a,b) = (\frac{\partial F^i}{ \partial y^j } (a,b) )_{i,j}$ is of maximal rank (or equivalently is invertible), then there exists an open set $U \subset {\mathbb {R}}^{n+1}$ containing a such that there exists a unique continuously differentiable function $g: U \rightarrow {\mathbb {R}}^{d-n}$ such that $g(a)=b$ and $F( x, g(x))=0$ for all $x \in U$.

To prove the existence of the isotopy from $f^{-1}(0)$ to $f_{PL}^{-1}(0)$, we will apply the implicit function theorem (Theorem 6) to several functions g that are close to f and we will therefore need to prove that their Jacobians are of maximal rank. A matrix has maximal rank if and only if the Gram matrix of its columns has a nonzero determinant or, equivalently, nonzero eigenvalues. In our context, we will need lower bounds on the absolute values of the eigenvalues of the Gram matrices $\mathrm {Gram}(\nabla g)$, given the lower bound $\lambda _{\min }$ on the absolute values of the eigenvalues of $\mathrm {Gram}(\nabla f)$.

2.2.2 Eigenvalues and Perturbations

We will follow the convention that the eigenvalues of the matrices we consider are sorted by increasing order of their absolute values, i.e. $|\lambda _i|\le |\lambda _j|$ if $i\le j$. We first recall Weyl’s perturbation theorem that bounds the difference between the ith eigenvalues of two symmetric matrices:

Lemma 7

(Weyl’s bound, Corollary III.2.6 of [50]) Let A and $\tilde{A}=A+E$ be two symmetric (or Hermitian) matrices and write $\lambda _i$ and ${\tilde{\lambda }}_i$ for the eigenvalues of A and $\tilde{A}$, respectively. Then,

$$\begin{aligned} \max _{i} |\lambda _i - {\tilde{\lambda }}_i| \le \Vert E\Vert _2, \end{aligned}$$

where $\Vert \cdot \Vert _p$ denotes the p-norm.

We further note that $\Vert E\Vert _2 \le \Vert E\Vert _{F}$ where $\Vert \cdot \Vert _F$ denotes the Frobenius norm, see [49, (2.3.7)]. By definition of the Frobenius norm, we have that $|E_{ij}| \le e_{\max }$, for all $i,j\in [1, d-n]$, implies that $\Vert E\Vert _F \le (d-n) e_{\max }$ if $d-n$ is the dimension of E. Hence, we have

Corollary 8

Under the conditions of Lemma 7, and assuming $\dim (E)=d-n$, and $|E_{ij}| \le e_{\max }$, we have

$$\begin{aligned} \max _{i} |\lambda _i - {\tilde{\lambda }}_i| \le (d-n) e_{\max }. \end{aligned}$$

2.3 Estimates for a Single Simplex

In this section, we concentrate on a single simplex $\sigma$ and write $f_L$ for the linear function whose values on the vertices of $\sigma$ coincide with f. In other words, $f_L$ is the linear extension of the interpolation of f. Note that $f_L$ coincides with $f_{PL}$ within the geometric simplex $\sigma$ (but not necessarily outside).

2.3.1 Estimates on the Linear Approximation $f_L$ and Its Gradient

We need a simple estimate similar to Proposition 2.1 of Allgower and George [11].

Lemma 9

Let $\sigma \subset \mathcal {T}_0$ and let $f_L$ be as described above. Then, for all $x \in \sigma$,

$$\begin{aligned} |f^i_L (x)- f^i (x)| \le 2 D^2 \alpha _{\max } . \end{aligned}$$

We included a proof for completeness.

Proof

Let $v_k$ be a vertex of $\sigma$. Taylor’s theorem, see, for example, [41, Theorem 2.8.4], yields that

$$\begin{aligned} f^i (v_k)= f^i(x) + \sum _j \partial _j f^i (x) (v_k-x)^{j} + R(v_k), \end{aligned}$$

(9)

with

$$\begin{aligned} R(v_k)&= 2 \sum _{j \ne l} (v_k-x)^{j} (v_k-x)^{l} \int _0^1 (1-t)^2 \partial _j \partial _l f^i (v_k - t (v_k-x)) \mathrm {d}t \\&\quad +2 \sum _{j} \frac{((v_k-x)^{j})^2}{2} \int _0^1 (1-t)^2 \partial _j^2 f^i (v_k - t (v_k-x)) \mathrm {d}t \\&\le 2 |v_k-x|^2 \alpha _{\max } \qquad \qquad \qquad \text {by } (4) \text { and Cauchy--Schwarz} \\&\le 2 D^2 \alpha _{\max } \qquad \qquad \qquad \qquad \qquad \qquad \text {because }x \in \sigma . \end{aligned}$$

The function $f_L$ at the point $x=\sum _k \lambda _k v_k$, where $\sum _k \lambda _k=1$, is by construction

$$\begin{aligned} f_L^i (x)&= \sum _k \lambda _k f^i(v_k) \\&= \sum _k \lambda _k \left( f^i(x) + \sum _j \partial _j f^i (x) (v_k-x)^{j} + R(v_k) \right) \qquad \qquad (\text {by }(9)) \\&= \sum _k \lambda _k f^i(x) + \sum _j \partial _j f^i (x) \left( \sum _k \lambda _k v_k-x\right) ^{j} + \sum _k \lambda _k R(v_k) \\&= f^i(x) + 0 + \sum _k \lambda _k R(v_k). \end{aligned}$$

Thanks to the bounds on $R(v_k)$ and Cauchy–Schwarz, one has

$$\begin{aligned} |f^i_L (x)- f^i (x)| \le 2 D^2 \alpha _{\max }. \end{aligned}$$

$\square$

We will also be using an estimate similar to Proposition 2.2 of Allgower and George [11].

Proposition 10

Let $\sigma \subset \mathcal {T}_0$ and let $f_L$ be as described above. Then

$$\begin{aligned} | \nabla f_L^i(x) - \nabla f^i (x)| = \sqrt{ \sum _j (\partial _j f^i_L (x)- \partial _j f^i (x))^2 } \le \frac{4 d D \alpha _{\max } }{T}, \end{aligned}$$

for all x in the simplex $\sigma$.

We provide a proof for completeness. In this proof, we use the following variant of a common refinement of two sets:

Claim 11

Suppose we are given two finite sets $A=\{a_i \mid i = 0 , \ldots , i_{\max } \}, B=\{b_j \mid j = 0 , \ldots , j_{\max } \}$ of positive numbers such that $\sum a_i = \sum b_j$. Then, there exists a set $C=\{c_k \mid k = 0 , \ldots , k_{\max } \}$ of positive integers $0=k_0 \le k_1 \le \dots \le k_{ i_{\max } }$, $0=k_0' \le k_1' \le \dots \le k_{ j_{\max } }'$ such that

$$\begin{aligned} \sum _{k= k_i}^{k_{i+1}-1} c_k&= a_i&\sum _{k= k_j'}^{k_{j+1}'-1} c_k&= b_j. \end{aligned}$$

Proof

The proof goes via intersection as indicated in Fig. 2. In the figure, the sets A, B, C are represented as a union of intervals of lengths $a_i$, $b_j$, $c_k$, respectively. We observe the following:

• In the figure, the set C is obtained by the common refinement of the intervals. We thus have $k_{\max } \le i_{\max }+j_{\max }$ with equality if there are no $\iota$, $\iota '$ such that $\sum _{i=1}^{\iota } a_i= \sum _{j=1}^{\iota } b_j$.

• The total length of C is the same as the length of A and B, i.e. $\sum _k c_k = \sum _i a_i =\sum _j b_j$.

• Any interval of A or B is the union of consecutive intervals of C, and the result follows.

$\square$

Fig. 2

The construction of the $c_k$s from Claim 11

Proof of Proposition 10

We use the same notation as before and again use that

$$\begin{aligned} f^i (v_k)= f^i(x) + \sum _j \partial _j f^i (x) (v_k-x)^{j} + R(v_k), \qquad \qquad ({9}) \end{aligned}$$

with

$$\begin{aligned} |R(v_k)|&\le 2 D^2 \alpha _{\max }. \end{aligned}$$

(10)

Subtracting $f^i(v_l)$ from $f^i(v_k)$ now yields

$$\begin{aligned} f^i(v_k)-f^i(v_l)= \sum _j \partial _j f^i (x) (v_k- v_l )^j + R(v_k) -R(v_l). \end{aligned}$$

Because $f_L$ is the linear interpolation of f, we have

$$\begin{aligned} f^i(v_k)-f^i(v_l) = \sum _j \partial _j f^i_L (x) (v_k -v_l)^{j}, \end{aligned}$$

and thus

$$\begin{aligned} \left| \sum _j (\partial _j f^i_L (x)- \partial _j f^i (x)) (v_k- v_l )^j \right| \le | R(v_k) -R(v_l)| \le 4 D^2 \alpha _{\max } . \end{aligned}$$

(11)

Let now u and v be two points of $\sigma$. Writing u and v in terms of their barycentric coordinates with respect to the vertices $v_k$ of $\sigma$, we have $u= \sum \mu _k v_k$ and ${v}= \sum \nu _k v_k$, with $\sum \mu _k = \sum \nu _k=1$ and $\mu _k, \nu _k \ge 0$. We write K for the set of indices k, in particular $u-v=\sum _{k\in K} (\mu _k-\nu _k)$, $K^+$ for the set of $k\in K$ such that $\mu _k-\nu _k\ge 0$, and $K^-=K\setminus K^+$.

We can now apply Claim 11 to the two sets $\{ ( \mu _k-\nu _k), k\in K^+ \}$ and $\{ - (\mu _k-\nu _k), k\in K^-\}$ since $\sum _{k\in K^+} (\mu _k-\nu _k) = \sum _{k\in K^-} - (\mu _k-\nu _k)$. The refined set is denoted by $\{\pi _l | l=0,...,L\}$, where $L\le |K|$. The refinement associates with each l a $k^{+} \in K^{+}$ and a $k^{-} \in K^{-}$. We will write $l^+ = k^{+}(l)$ and $l^{-}= k^{-} (l)$ to emphasize this dependence. With this notation, we can write

$$\begin{aligned} u-v = \sum _{l\in L} \pi _l (v_{l^{+}}- v_{l^{-}}). \end{aligned}$$

(12)

By Claim 11, we have

$$\begin{aligned} \sum _{l\in L} \pi _l= \sum _{k\in K^+} (\mu _k-\nu _k) \le \sum _{k\in K} \mu _k=1. \end{aligned}$$

(13)

We now see that

$$\begin{aligned}&\left| \sum _j (\partial _j f^i_L (x)- \partial _j f^i (x)) (u- {v} )^j \right| \nonumber \\&= \left| \sum _{j} \sum _{l \in L} \pi _l (\partial _j f^i_L (x)- \partial _j f^i (x)) (v_{l^{+}}^j- v_{l^{-}}^j ) \right| \qquad \qquad \qquad (\text {by }(12)) \nonumber \\&\le \left| \left( \sum _{l\in L} \pi _l \right) \left| R(v_{l^{+}} ) -R(v_{l^{-}}) \right| \right| \qquad \qquad \qquad (\text {by the triangle inequality}) \nonumber \\&\le 4D^2 \alpha \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \qquad (\text {by }(11) \text { and }(13)). \end{aligned}$$

(14)

Because the simplex $\sigma$ contains a ball of radius the smallest altitude over d centred at its barycentre, that is, TD/d with T the thickness, the vector $u-w$ can be chosen to be any vector of length less than TD/d. In particular, we can choose

$$\begin{aligned} (u- w )^j = \frac{T D}{d} \frac{(\partial _j f^i_L (x)- \partial _j f^i (x))}{ \sqrt{ \sum _j (\partial _j f^i_L (x)- \partial _j f^i (x))^2 } }. \end{aligned}$$

Plugging this choice into (14) gives

$$\begin{aligned} \frac{T D}{d} \sqrt{ \sum _j (\partial _j f^i_L (x)- \partial _j f^i (x))^2 } \le 4 D^2 \alpha _{\max } \end{aligned}$$

so that

$$\begin{aligned} \sqrt{ \sum _j (\partial _j f^i_L (x)- \partial _j f^i (x))^2 } \le \frac{4 d D \alpha _{\max } }{T}. \end{aligned}$$

$\square$

We stress that the bound in Proposition 10 depends on the quality of the simplices in the ambient triangulation $\mathcal {T}$ but not on the shape of the cells of the PL approximation. This is fortunate since we know ambient triangulations of very good quality (e.g. Coxeter triangulations [43]), while we do not have control on the shapes of the cells of the PL approximation which depend on the way the isomanifold intersects $\mathcal {T}$.

2.3.2 Applying the Implicit Function Theorem

Let $\sigma$ be a simplex of ${\mathcal {T}}$ and let $f_L$ be the linear approximation defined above. We now define a homotopy $F_L: {\mathbb {R}}^d\times [0,1] \rightarrow {\mathbb {R}}^{d-n}$ :

$$\begin{aligned} F_L(x,\tau ) = (1-\tau ) f(x) + \tau f_L(x) . \end{aligned}$$

(15)

We intend to show that $F_L^{-1} (0)$ is a manifold in a neighbourhood of $\sigma \times [0,1]$. This follows from the Implicit function theorem (Theorem 6) provided that, for any point such that $F_L(x,\tau )=0$ in this neighbourhood, the Jacobian is of maximal rank or, equivalently as recalled above, if and only if the Gram matrix of its columns has nonzero eigenvalues. The following lemma will provide lower bounds on the eigenvalues of this Gram matrix.

We denote by $\nabla _x F_L$ or simply $\nabla F_L$ the gradient of the restriction of $F_L$ to the x variable and $\nabla _{x, \tau } F_L$ the gradient of $F_L$. Note that

$$\begin{aligned} \nabla _{x,\tau } F_{L}^i(x,\tau )&= \left( \begin{array}{c} \nabla ( f^i (x) + \tau (f_{L}^i(x)-f^i (x)) ) \\ f_{L}^i(x)-f^i (x) \end{array} \right) . \end{aligned}$$

(16)

For convenience, we will write $\nabla _{x,\tau }f(x)=\left( \begin{array}{c} \nabla f^i(x) \\ 0\end{array} \right)$.

Lemma 12

Let ${\mathrm{G}} =\mathrm {Gram}(\nabla f)$ and ${\widehat{\mathrm{G}} }= \mathrm {Gram}(\nabla _{x, \tau } F_L)$,³ and write $\lambda _{\min }$ and ${\widehat{\lambda }}_{\min }$ for the smallest absolute values of the eigenvalues of ${\mathrm{G}}$ and ${\widehat{\mathrm{G}} }$, respectively.

$$\begin{aligned} |{\widehat{\lambda }}_{\min }-\lambda _{\min }|&\le e_L \end{aligned}$$

(17)

where, assuming $dD<T$, $e_L= O (d^2D/T)$. If $\mathcal {T}$ is a Coxeter triangulation of type $\tilde{A}_d$,

$e_L = O(d^{5/2}D)$. The precise expression of $e_L$ is given in (19) and (18).

Proof

Let, in addition to the notations of the lemma, ${\widehat{\mathrm{G}} }'= \mathrm {Gram}(\nabla _x F_L)$, $\lambda _{\min }'$ be the smallest absolute value of the eigenvalues of ${\widehat{\mathrm{G}} }'$, and write ${\mathrm{G}} _{i,j}$, ${\widehat{\mathrm{G}} }'_{i,j}$ and ${\widehat{\mathrm{G}} }_{i,j}$ for the entries of ${\mathrm{G}}$, ${\widehat{\mathrm{G}} }'$ and ${\widehat{\mathrm{G}} }$, respectively. Proposition 10 yields that

$$\begin{aligned} |{\widehat{\mathrm{G}} }'_{i,j}(x)&- {\mathrm{G}} _{i,j}(x)| \nonumber \\ =&|\nabla ( f^i (x) + \tau (f_L(x)^i-f^i (x)) ) \cdot \nabla ( f^j (x) + \tau (f_L(x)^j-f^j (x)) ) \nonumber \\&- \nabla ( f^i (x) ) \cdot \nabla ( f^j (x) )| \nonumber \\ =&|\nabla ( \tau (f_L(x)^i-f^i (x)) ) \cdot \nabla ( f^j (x) ) \nonumber \\&+\nabla ( \tau (f_L(x)^j-f^j (x)) ) \cdot \nabla ( f^i (x) ) \nonumber \\&+ \nabla (\tau (f_L(x)^i-f^i (x)) ) \cdot \nabla ( \tau (f_L(x)^j-f^j (x)) ) | \nonumber \\ \le&2 \gamma _{\max } \frac{4d D \alpha _{\max }}{T} +\left( \frac{4d D \alpha _{\max }}{T}\right) ^2 {\mathop {=}\limits ^{{\mathrm{def}}}} e_L'. \end{aligned}$$

(18)

The addition of the $\tau$ component gives a small extra contribution.

$$\begin{aligned} |{\widehat{\mathrm{G}} }_{i,j} (x)- {\mathrm{G}} _{i,j} (x)|&= |\nabla _{x,\tau } F_L^i(x) \cdot \nabla _{x,\tau } F_L^j (x) - \nabla ( f^i (x) ) \cdot \nabla ( f^j (x) ) | \\&\!=\! |\nabla ( f^i (x) \!+\! \tau (f_L^i (x)\!-\!f^i (x)) ) \cdot \nabla ( f^j (x) \!+\! \tau (f_L^j(x)\!-\!f^j (x)) ) \\&\quad + (f_L^i(x)-f^i (x)) (f_L^j(x) -f^j (x)) - \nabla ( f^i (x) ) \cdot \nabla ( f^j (x) )| \\&\le e_L' + (2 D^2 \alpha _{\max })^2. \qquad \qquad \qquad \qquad \qquad \text {by Lemma}~9 \end{aligned}$$

Applying Corollary 8, we obtain

$$\begin{aligned} |{\widehat{\lambda }}_{\min }-\lambda _{\min }| \ge (d-n) (e_L'+(2 D^2 \alpha _{\max })^2) {\mathop {=}\limits ^{{\mathrm{def}}}} e_L. \end{aligned}$$

(19)

From (18) and assuming $dD<T$, we see that $e_L'= O (dD/T)$. Hence, $e_L= O (d^2D/T)$. For Coxeter triangulations of type $\tilde{A}_d$, we have $T > \sqrt{\frac{2}{d+2}}$, see [43]. $\square$

The following corollary follows directly from the previous lemma and the discussion before the lemma.

Corollary 13

($F_L^{-1} (0)$ is a manifold in a neighbourhood of $\sigma \times [0,1]$) Under the regularity condition

$$\begin{aligned} \lambda _{\min }> e_L, \end{aligned}$$

(20)

the implicit function theorem applies to $F_L(x,\tau )$ inside $\sigma \times [0,1]$. (In fact, it applies to an open neighbourhood of this set.) It follows that $\{(x,\tau ) \mid F_{L}(x, \tau )=0\} \cap (\sigma \times [0,1])$ is a smooth manifold.

2.3.3 Transversality with Regard to the $\tau$-Direction

We now prove that inside each $\sigma \times [0,1]$ the gradient of $\tau$ on $F_L=0$ is smooth and does not vanish.

We need the following straightforward lemma. We include a proof for completeness.

Lemma 14

Now suppose that $A= (v_i)^t(v_i)$ is a Gram matrix, where $(v_i)$ denotes the matrix whose column are the vectors $v_i$, that is, $A_{ij}= v_i \cdot v_j$. Similar to before, denote by $\lambda _{\min }(A)$ the smallest absolute value of an eigenvalue of the Gram matrix A. We have that $\sqrt{\lambda _{\min }(A)} \le |v_k|$, for all k.

Proof

We see that

$$\begin{aligned} \lambda _{\min }&= \min _{|u|=1} |u^t A u| \\&= \min _{|u|=1} |u^t (v_i)^t (v_i) u| \\&= \min _{|u|=1} | ((v_i) u )^t ((v_i ) u)| \\&= \min _{|u|=1} | ((v_i ) u)|^2 \\&\le \min _{u=e_j} | ((v_i ) u)|^2 \\&=\min _{j} | v_j|^2 \\&\le |v_k|^2. \end{aligned}$$

$\square$

We also need to bound the angle of the vectors $\nabla _{x,\tau }(F_L^i)$ and the x plane, that is ${\mathbb {R}}^d \subset {\mathbb {R}}^{d+1}$. We recall the definition. If $v\in {\mathbb {R}}^{d+1}$ is a vector and $\varXi = {\mathbb {R}}^d \subset {\mathbb {R}}^{d+1}$ is the space spanned by the d basis vectors corresponding to the x-directions, the angle between v and $\varXi$ is

$$\begin{aligned} \angle (v , \varXi )= \inf _{w \in \varXi } \angle (v,w) . \end{aligned}$$

Lemma 15

Let $\varXi$ be as above. We have

$$\begin{aligned} \tan \angle ( \nabla _{x,\tau }F_L^i , \varXi ) \le \theta {\mathop {=}\limits ^\mathrm{def}} \frac{2 D^2 \alpha _{\max }}{\sqrt{ \lambda _{\min }} - \frac{4dD \alpha _{\max }}{T} }. \end{aligned}$$

(21)

In particular, the manifold $F_L^{-1}(0)$ inside $\sigma \times [0,1]$ is never tangent to the $\tau = c$ planes, where c is a constant, provided that the following transversality condition holds

$$\begin{aligned} \lambda _{\min } > \left( \frac{4dD \alpha _{\max }}{T}\right) ^2 . \end{aligned}$$

(22)

Proof

By (16),

the absolute value of the $\tau$-component of $\nabla _{x,\tau }F_L^i$ is $|f_L(x)^i-f^i (x)|$, which is upper bounded by $2 D ^2 \alpha _{\max }$ (Lemma 9). On the other hand, the norm of the x-component of $\nabla _{x,\tau }F_L^i$ is lower bounded by

$$\begin{aligned} \sqrt{\lambda _{\min } } - \frac{4 d D \alpha _{\max }}{T}, \end{aligned}$$

as a consequence of Proposition 10 and Lemma 14. The result now follows since $\tan \angle ( \nabla _{x,\tau }F_L^i , \varXi )$ is the ratio between the absolute value of the $\tau$-component and the norm of the x-component of $\nabla _{x,\tau }F_L^i$. $\square$

From Corollary 13 and Lemma 15, we immediately deduce

Corollary 16

Under the regularity and transversality conditions (20) and (22), which both holds for $D/T= O(1/d^2)$, the gradient of $\tau$ on $F_L^{-1}(0)$ is smooth and does not vanish inside $\sigma \times [0,1]$ for any $\sigma \in \mathcal {T}_0$. If $\mathcal {T}$ is a Coxeter triangulation of type $\tilde{A}_d$, the condition reduces to $D=O(d^{-3/2})$.

2.4 Global Result

2.4.1 The Non-smooth Implicit Function Theorem

For the global result, we need to recall some definitions and results from non-smooth analysis. We refer to [38] for an extensive introduction.

Definition 17

(Generalized Jacobian, Definition 2.6.1 of [38]) Let $F: {\mathbb {R}}^{d+1} \rightarrow {\mathbb {R}}^{d-n}$, where F is assumed to be just Lipschitz. The generalized Jacobian of F at $x_0$, denoted by $J_F(x_0)$, is the convex hull of all $(d-n) \times (d+1)$-matrices B obtained as the limit of a sequence of the form $J_F(x_i)$, where $x_i \rightarrow x_0$ and F is differentiable at $x_i$.

Following [38, page 253], we also define:

Definition 18

The generalized Jacobian $J_F(x_0)$ is said to be of maximal rank, provided every matrix in $J_F(x_0)$ is of maximal rank.

Write ${\mathbb {R}}^{d+1} = {\mathbb {R}}^{n+1} \times {\mathbb {R}}^{d-n}$ and denote the coordinates of ${\mathbb {R}}^{d+1}$ by (x, y) accordingly. Fix a point (a, b), with $F(a,b)=0 \in {\mathbb {R}}^{d-n}$. We now write:

Notation 19

( [38, page 256]) $J_F ( x_0, y_0)| _y$ is the set of all $(n+1) \times (n+1)$-matrices M such that, for some $(n+1) \times (d-n)$-matrix N, the $(n+1) \times (d+1)$-matrix [N, M] belongs to $J_F ( x_0, y_0)$.

With these definitions and notations, we now have:

Theorem 20

(Generalized implicit function theorem [38, page 256]) Suppose that $J_F (a, b)| _y$ is of maximal rank. Then, there exists an open set $U \subset {\mathbb {R}}^{n+1}$ containing a such that there exists a Lipschitz function $g: U \rightarrow {\mathbb {R}}^{d-n}$, such that $g(a)=b$ and $F( x, g(x))=0$ for all $x \in U$.

2.4.2 Applying the Non-smooth Implicit Function Theorem

We recall the definition of $F_{PL}$:

$$\begin{aligned} F_{PL}(x,\tau ) = (1-\tau ) f(x) + \tau f_{PL}(x) .\qquad \qquad \qquad ({1}) \end{aligned}$$

Further recall that the closed star of a vertex v in a simplicial complex is the closure of all simplices in the complex that contain v. We will also be using the following remark often.

Remark 21

Let v be a vertex in $\mathcal {T}$, $x_1, x_2 \in \text {star}(v)$, then

$$\begin{aligned} |x_1- x_2 | \le 2 D. \end{aligned}$$

(23)

We now have

Lemma 22

Let v be a vertex in $\mathcal {T}$, $x_1, x_2 \in \text {star}(v)$, and $\tau _1,\tau _2 \in [0,1]$, such that $\nabla _{x,\tau } F_{PL}^i(x_1,\tau _1)$ and $\nabla _{x,\tau } F_{PL}^i(x_2,\tau _2)$ are well defined, then

$$\begin{aligned} |\nabla _{x,\tau } F_{PL}^i(x_1,\tau _1) -\nabla _{x,\tau } F_{PL}^i(x_2,\tau _2)| \le g_{PL} {\mathop {=}\limits ^\mathrm{def}} 2d D \alpha _{\max } + \frac{8 d D \alpha _{\max } }{T} + 4 D^2 \alpha _{\max } . \end{aligned}$$

(24)

Proof

Because

$$\begin{aligned} \nabla _{x,\tau } F_{PL}^i(x_1,\tau _1)&= \left( \begin{array}{c} \nabla ( f^i (x_1) + \tau _1 (f_{PL}^i(x_1)-f^i (x_1)) ) \\ f_{PL}^i(x_1)-f^i (x_1) \end{array} \right) , \end{aligned}$$

we get

$$\begin{aligned} |\nabla _{x,\tau }&F_{PL}^i(x_1,\tau _1) -\nabla _{x,\tau } F_{PL}^i(x_2,\tau _2)| \\ \le&\; |\nabla f^i(x_1)- \nabla f^i(x_2)| \\&+ |\nabla f_{PL}^i(x_1)- \nabla f^i (x_1) | + | \nabla f_{PL}^i(x_2)- \nabla f^i (x_2) | \qquad \qquad {\tau _i \in [0,1]} \\&+ |f_{PL}^i(x_1)-f^i (x_1) |+|f_{PL}^i(x_2)-f^i (x_2) | \\ \le&\; 2d D \alpha _{\max } + \frac{8 d D \alpha _{\max } }{T} + 4 D^2 \alpha _{\max }\\&\qquad \qquad \qquad \qquad \qquad \qquad (\text {by }(8) \text { and } (23), \text { Proposition }10 \text { and Lemma}~9). \end{aligned}$$

$\square$

We generalize Lemma 12 as follows.

Lemma 23

Let v be a vertex in $\mathcal {T}$, $x_1, \ldots , x_m \in \text {star}(v)$, and $\tau _1, \dots ,\tau _m \in [0,1]$. We assume that $\nabla _{x,\tau } F_{PL}^i(x_k,\tau _k)$ is well defined for $k = 1, \ldots ,m$. Define ${\widehat{{\mathbf{G}}} }=\mathrm {Gram}(\sum _{k=1}^m \mu _k \nabla _{x,\tau } F_{PL}(x_k,\tau _k))$, where $\mu _1,\dots , \mu _m$ are positive weights such that $\mu _1+ \cdots + \mu _m=1$, and let $\widehat{{\varvec{\varLambda }}}_{\min }$ be the smallest modulus of the eigenvalues of ${\widehat{{\mathbf{G}}} }$. Then,

$$\begin{aligned} |\widehat{{\varvec{\varLambda }}}_{\min } - {\widehat{\lambda }}_{\min } | \le e_{PL}, \end{aligned}$$

where $e_{PL} = O(d^2D/T)$ (assuming $dD<T$) and is precisely defined in (26). When $\mathcal {T}$ is a Coxeter triangulation of type $\tilde{A}_d$, $e_{PL} = O(d^{5/2}D)$.

Proof

Let ${\widehat{{\mathbf{G}}} }=\mathrm {Gram}(\nabla _{x,\tau } F_L(x_0,y_0))$ and let ${\widehat{\lambda }}_{\min }$ be the smallest modulus of the eigenvalues of ${\widehat{\mathrm{G}} }$. We claim that the elements of the two matrices ${\widehat{{\mathbf{G}}} }$ and ${\widehat{\mathrm{G}} }$ are pairwise close. Specifically, using the identity $A\cdot B-C\cdot D = A\cdot (B-D)+(A-C)\cdot D$:

$$\begin{aligned} | {\widehat{{\mathbf{G}}} }_{i,j}&-{\widehat{\mathrm{G}} }_{i,j}| \\ \le&\bigg | \sum _k \mu _k \nabla _{x,\tau } F_{PL}^i(x_k,\tau _k) \cdot \sum _k \mu _k \nabla _{x,\tau } F_{PL}^j(x_k,\tau _k) \\&- \sum _k \mu _k \nabla _{x,\tau } F_{PL}^i(x_0,\tau _0) \cdot \sum _k \mu _k \nabla _{x,\tau } F_{PL}^j(x_0,\tau _0)\bigg | \\ =&\bigg | \left( \sum _k \mu _k \nabla _{x,\tau } (F_{PL}^i(x_k,\tau _k)\right) \cdot \left( \sum _k \mu _k \left( \nabla _{x,\tau } F_{PL}^j(x_k,\tau _k) - \nabla _{x,\tau } F_{PL}^j(x_0,\tau _0)\right) \right) \\&\!+\! \left( \sum _k \mu _k \left( \nabla _{x,\tau } F_{PL}^i(x_k,\tau _k) \!-\! \nabla _{x,\tau } F_{PL}^i(x_0,\tau _0)\right) \right) \cdot \left( \sum _k \mu _k \nabla _{x,\tau } (F_{PL}^j(x_0,\tau _0)\right) \bigg | \\ \le&g_{PL} \cdot \sum _k \mu _k \left( \bigg | \nabla _{x,\tau } F_{PL}^i(x_k,\tau _k) \bigg | + \bigg | \nabla _{x,\tau } F_{PL}^j(x_0,\tau _0) \bigg | \right) \bigg | , \\&\qquad \qquad \qquad \qquad \qquad \text {{by Cauchy--Schwarz and the triangle inequality}} \end{aligned}$$

where $g_{PL}$ is given in Lemma 22. It remains to bound $|\nabla _{x,\tau } F_{PL}^i(x_k,\tau _k) |$:

$$\begin{aligned} |\nabla _{x,\tau } F_{PL}^i(x_k,\tau _k) |&\le |\nabla _{x} \left( f^i (x_k) + \tau (f^i_{PL}(x_k)-f^i (x_k))\right) | + | f^i_{PL}(x_k)-f^i (x_k)) ) | \nonumber \\&\le \gamma _{\max }+ \frac{4d D \alpha _{\max }}{T} + 2D^2\alpha _{\max }, \end{aligned}$$

(25)

where we used Lemma 9 and Proposition 10. We conclude that

$$\begin{aligned} | {\widehat{{\mathbf{G}}} }_{i,j}-{\widehat{\mathrm{G}} }_{i,j}| \le g_{PL} (\gamma _{\max }+ \frac{4d D \alpha _{\max }}{T} + 2D^2\alpha _{\max }). \end{aligned}$$

Applying Corollary 8, we get

$$\begin{aligned} |\widehat{{\varvec{\varLambda }}}_{\min } - {\widehat{\lambda }}_{\min } | \le (d-n) g_{PL} (\gamma _{\max }+ \frac{4d D \alpha _{\max }}{T} + 2D^2\alpha _{\max }) {\mathop {=}\limits ^{{\mathrm{def}}}} e_{PL} \end{aligned}$$

(26)

which completes the proof of the lemma. $\square$

From the previous lemmas, we immediately have that,

Corollary 24

($\{(x,\tau ) \mid F_{PL}(x, \tau )=0\}$ is a manifold) Under the regularity condition

$$\begin{aligned} \lambda _{\min }> e_{PL}, \end{aligned}$$

(27)

where $e_{PL}$ is defined in Lemma 23, the generalized implicit function theorem, Theorem 20, applies to $F_{PL}(x,\tau )=0$. In particular, $\{(x,\tau ) \mid F_{PL}(x, \tau )=0\}$ is a manifold.

The second technical step of the proof is now completed.

The third step follows from an application of Lemma 3. The fact that $F_L(x,\tau )=0$ is a piecewise-smooth manifold and transversality, as proven in Lemma 15, gives that the gradient of $\tau$ is a piecewise-smooth vector field whose flow we can integrate to give an ambient isotopy from the zero set of f to that of $f_{PL}$.

We summarize in a theorem:

Theorem 25

If the regularity condition (27) and the transversality condition (22) hold, the zero set of $f_{PL}$ is a manifold isotopic to the zero set of f. Note that both conditions hold when $D/T= O(d^{-2})$. For Coxeter triangulation of type $\tilde{A}_d$, the condition reduces to $D=O(d^{-5/2})$.

2.4.3 Fréchet Distance

To bound the Fréchet distance, denoted by $d_F$, between the zero sets of f(x) and $f_{PL}$, it suffices to bound the angle that the gradient of $\tau$ (as restricted to $F_L(x,\tau )=0$) makes with the $\tau$-direction (in ${\mathbb {R}}^{d+1}$). We write $e_\tau$ for the unit vector in the $\tau$ direction (again in ${\mathbb {R}}^{d+1}$).

For this, we will use the angle bound of Lemma 15, together with some estimates that are similar in spirit to those in [51, Lemma C.13].

Lemma 26

For any $w \in \mathrm {span}(\nabla _{x,\tau } F^i_L)$, we have

$$\begin{aligned} \cos \angle (w,e_\tau )&\le \frac{\sin (\theta ) ( \gamma _{\max }+ {\frac{4dD\alpha _{\max }}{T}})}{\sqrt{\lambda _{\min } -e_{PL} } } = O(D^2) \end{aligned}$$

where $e_{PL}= O(d^2D/T)$ is defined in (26) and $\theta = O(D^2)$ is defined in (21).

Proof

Write $v_i= \nabla _{x,\tau } F_L^i$ for $i\in [1,d-n]$, and $w=\mu _1 v^1 + \cdots + \mu _{d-n} v^{d-n}$ with $\mu _1 ,\ldots , \mu _{d-n} \in {\mathbb {R}}$. We have $|w|^{2}= \sum _{i,j} \mu _i \mu _j v^i \cdot v^j$, and, by definition,

$$\begin{aligned} \cos \angle (w,e_\tau ) = \frac{ \sum _i \mu _i v^i \cdot e_\tau }{|w| } \;\;\;\;\; \mathrm{and}\;\;\; \;\; |w|^2 =\sum _{i,j} \mu _i \mu _j v^i \cdot v^j \ge \widehat{{\varvec{\varLambda }}}_{\min } |\mu |^2, \end{aligned}$$

(28)

where $\widehat{{\varvec{\varLambda }}}_{\min }$ is defined in Lemma 23. Proposition 10 and $|\nabla (f^i)| \le \gamma _{\max }$ give

$$\begin{aligned} |v^i| \le \gamma _{\max } +\frac{4 d D \alpha _{\max } }{T}. \end{aligned}$$

(29)

Lemma 15 states that

$$\begin{aligned} \angle ( \nabla _{x,\tau }F_L^i , \varXi ) \le \theta = \arctan \frac{2 D^2 \alpha _{\max }}{\sqrt{ \lambda _{\min }} - \frac{4dD \alpha _{\max }}{T} } . \end{aligned}$$

By definition, $\varXi$ is the space orthogonal to $e_\tau$ (with $e_{\tau }$ aligned with the $\tau$ direction), so that

$$\begin{aligned} \cos (\angle \nabla _{x,\tau }F_L^i,e_\tau ) = \sin \angle (\nabla _{x,\tau } F_L^i , \varXi ). \end{aligned}$$

(30)

Hence, by definition of the cosine and (29), we see

$$\begin{aligned} | v^i \cdot e_\tau | \le \sin (\theta ) \left( \gamma _{\max } + \frac{4dD \alpha _{\max }}{T} \right) . \end{aligned}$$

Using (28) and Cauchy–Schwarz, we then obtain

$$\begin{aligned} \cos \angle (w,e_\tau ) \le \frac{|\mu | \sin (\theta ) ({\gamma }_{\max }+\frac{4 d D \alpha _{\max } }{T} ) }{\sqrt{{\widehat{{\varvec{\varLambda }}}}_{\min } |\mu | ^2 } } = \frac{ \sin (\theta ) ({\gamma }_{\max }+\frac{4 d D \alpha _{\max } }{T}) }{\sqrt{\widehat{{\varvec{\varLambda }}}_{\min } } }. \end{aligned}$$

The result now follows thanks to Lemma 23. $\square$

Let $F_{PL_0}$ be the restriction of $F_{PL}$ to $F_{PL}^{-1}(0, \tau )$.

Moreover, let $\nabla _{\tau } F_{PL_0}$ be the gradient of $\tau$ restricted to $F_{PL}^{-1}(0)$, whenever it exists. We want to bound the angle of $\nabla _{\tau } F_{PL_0}$ and the $\tau$-direction. Because the isotopy is given by the gradient flow and we have a bound on the norm of the gradient, the Fréchet distance is bounded. Specifically, the bound is equal to the norm of the gradient since the time we follow the flow is 1.

There is one subtlety. Because the manifold is only piecewise-smooth, we need to take into account the points where $\nabla _{\tau } F_{PL_0}$ is not uniquely defined. Because, for each simplex $\sigma$, $F_L$ extends to a neighbourhood of $\sigma \times [0,1]$, there exists a limit of $\nabla _{\tau } F_{PL_0}(x_i,\tau _i )$ for any sequence $(x_i,\tau _i)$ that lies in $\text {int} (\sigma ) \times [0,1]$, where $\text {int}$ denotes the interior. This means that, if we bound $\nabla _{\tau } F_{PL_0}$ for each simplex, we also bound its limits, where the limits are as just described.

Corollary 27

(Bound on the Fréchet distance) Suppose that the conditions of Theorem 25 are satisfied. Then,

$$\begin{aligned} d_F&( f^{-1} (0) , f_{PL}^{-1}(0) ) \le d_{PL} \end{aligned}$$

where $d_{PL}= O(D^2)$ is defined in (31).

Proof

Let, as before, $\varXi = {\mathbb {R}}^d \subset {\mathbb {R}}^{d+1}$ be the space spanned by the d basis vectors corresponding to the x-directions.

Lemma 26 gives, for $w \in \mathrm {span}_i ( \nabla _{x,\tau }(F^i) )$,

$$\begin{aligned} \cos \angle (w,e_\tau )&\le \frac{\sin (\theta ) ( \gamma _{\max }+\frac{4 d D \alpha _{\max } }{T})}{\sqrt{\lambda _{\min } -e_{PL} } }. \end{aligned}$$

Since the tangent space to $F_L=0$ is normal to $\mathrm {span}_i ( \nabla _{x,\tau }(F_L^i) )$, the same bound holds for $\sin \angle (\nabla _\tau F_{PL_0} ,e_\tau )$. This means that, as $\tau \in [0,1]$, the distance between the begin and the end points of the gradient flow, and thus the Fréchet distance, is bounded by $\tan \angle (\nabla _\tau F_{PL_0} ,e_\tau )$, that is,

$$\begin{aligned} d_F&( f^{-1} (0) , f_{PL}^{-1}(0) ) \le \tan \arcsin \frac{\sin (\theta ) ( \gamma _{\max }+\frac{4dD \alpha _{\max }}{T} )}{\sqrt{\lambda _{\min } -e_{PL} } }{\mathop {=}\limits ^{{\mathrm{def}}}} d_{PL}. \end{aligned}$$

(31)

The asymptotic dependence follows because $\sin (\arctan (x)) = \frac{x}{\sqrt{1+x^2}}$, and $\tan (\arcsin (x))= \frac{x}{\sqrt{1-x^2}}$. $\square$

3 Isomanifolds with Boundary

We will now consider isomanifolds with boundary. By this, we mean that on top of the function $f: {\mathbb {R}}^d \rightarrow {\mathbb {R}}^{d-n}$, we will have another function $f_\partial : {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ and the set we consider is $M= f^{-1}(0) \cap f_\partial ^{-1}( [ 0, \infty ))$. This is a manifold with boundary if the gradients of $f^i$ span a $(d-n)$-dimensional space at each point of $f^{-1}(0)$ and the gradients of $f^i$ and $f_\partial$ span a $(d-n+1)$-dimensional space at each point of $\partial M= f^{-1}(0) \cap f_\partial ^{-1}(0)$, as a consequence of the submersion theorem.

We will again write $f_{PL}$ for the PL interpolation of f. Similarly, we write $f_{\partial , PL}$ for the PL interpolation of $f_{\partial }$.

We prove that, under certain conditions, there is an isotopy from $f^{-1}(0) \cap f_\partial ^{-1}( [ 0, \infty ))$ to $f_{PL}^{-1}(0) \cap f_{\partial ,PL}^{-1}( [ 0, \infty ))$. The conditions are very similar to the conditions we have before but, of course, we need to include bounds on the gradient of $f_{\partial ,PL}$.

3.1 Overview of the Proof

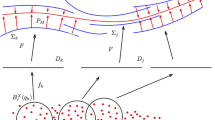
We will again construct an isotopy, but in this case it will consist of two steps, see Fig. 3 for a pictorial overview.

• In the first step, we isotope the part of $f^{-1}(0)$ that is far from $f_\partial ^{-1}(0)$ to its piecewise-linear approximation, while leaving the part of $f^{-1}(0)$ that is close to $f_\partial ^{-1}(0)$ smooth. We will denote the result by $M_1=(F_{PL,1} (\cdot , 1 ))^{-1}(0)$.

• In the second step, we consider a (small) tubular neighbourhood around $f_\partial ^{-1}(0)$ as restricted to $M_1$ by looking at all $f_\partial ^{-1}(\epsilon )$ for $|\epsilon |$ sufficiently small.⁴ We then isotope $M_1 \cap f_\partial ^{-1}(\epsilon )$ to its piecewise-linear approximation. Again, the isotopy is chosen in such a way that, for $\epsilon$ relatively large, it leaves

  $M_1 \cap f_\partial ^{-1}(\epsilon )$ invariant (for the points such that $M_1$ is already piecewise-linear). This gives an isotopy of a tubular neighbourhood of $M_1\cap f_\partial ^{-1}(0)$ to its piecewise-linear approximation.

Fig. 3

Top: we see the original isosurface with $f_\partial ^{-1} (-1/10)$, $f_\partial ^{-1} (0)$, $f_\partial ^{-1} (1/10)$, and $f_\partial ^{-1} (2/10)$ indicated in blue. Bottom left: we see that at the end of Step 1 the neighbourhood of the boundary is intact, while the rest has been isotoped to a piecewise-linear approximation. Bottom right: we have also isotoped the neighbourhood of the boundary to a piecewise-linear approximation by isotoping $f_\partial ^{-1} (\epsilon )$, to its piecewise-linear approximation for all sufficiently small $\epsilon$ (Color figure online)

We will first partition the manifold in two parts using a smooth bump function $\phi : {\mathbb {R}} \rightarrow [0,1]$, defined so that $\phi (y)=0$ in a neighbourhood of zero and $\phi (y)= 1$ if $|y|>y_0$, for some $y_0>0$. Such bump functions can be easily constructed, see, for example, [39, Section 2.2]. We will be using the function $\phi \left( \sum _i (f^i)^2+ f_{\partial }^2 \right)$ often. In fact, because it is used so often, it will be convenient to introduce the following shorthand

$$\begin{aligned} |f_B|^2=\sum _i (f^i)^2+ f_{\partial }^2. \end{aligned}$$

(32)

The first step will be using the zero set of the following function:

$$\begin{aligned} F_{PL,1}(x,\tau ) = \left( 1-\tau \phi \left( |f_B|^2\right) \right) f(x) + \tau \phi \left( |f_B|^2 \right) f_{PL}(x) , \end{aligned}$$

(33)

on which we will apply the same gradient flow argument as before.

The resulting set $M_1$ is the same zero set of $f_{PL}$ as before if we stay sufficiently far away from $\partial M$ and the isotopy leaves the manifold invariant close to $\partial M$. In particular, $\partial M_1=\partial M$ (Fig. 3).

In the second step, we define an isotopy that will act only on a small neighbourhood of $\partial M$. Consider the sets $B_1 (\epsilon ) = M_1\cap f^{-1}_{\partial } (\epsilon )$ and, for each of them, define the function

$$\begin{aligned} F_{PL,2,\epsilon } :&B_1(\epsilon ) \times [0,1] \rightarrow {\mathbb {R}}^{d-n+1} : \nonumber \\ F_{PL,2,\epsilon }(x,\tau ) =&\left( 1-\tau \psi \left( |f_B|^2 \right) \right) (F_{PL,1}(x,1), f_\partial (x)-\epsilon ) \nonumber \\&+ \tau \psi \left( |f_B|^2 \right) (f_{PL}(x), f_{\partial , PL} (x)-\epsilon ) , \end{aligned}$$

(34)

where $\psi : {\mathbb {R}} \rightarrow [0,1]$ is now a smooth bump function that is 1 in a sufficiently large neighbourhood of zero (somewhat larger than $y_0$) and zero outside some compact set. Using the result for isomanifolds (with some modifications), we can prove that each individual set $B_1 (\epsilon )$ is isotopic to $f^{-1}_{PL}(0) \cap f_{\partial , PL}^{-1} (\epsilon )$ for small $\epsilon$ while, for sufficiently large $\epsilon$, it leaves the set invariant.

3.2 Step 1

The proof closely follows the proof for the case without boundary in Sect. 2. The main technical difficulty will be to provide bounds that serve as the counterparts to Lemma 22 for both steps in the proof. To be able to do so, we first need to discuss bounds on the bump functions $\phi$ and $\psi$.

3.2.1 Bump Functions

Following [39, Section 2.2], we write,

$$\begin{aligned} \zeta _1 (x) = {\left\{ \begin{array}{ll} 0 &{} \text{ if } x\le 0 \\ e^{-1/x} &{} \text{ if } x> 0. \end{array}\right. } \end{aligned}$$

For $0<y_1<y_2$, we write $\zeta _2(x)= \zeta _1 ( x-y_1 ) \zeta _1 (y_2-x)$. Then, we define $\phi _{l}: {\mathbb {R}} \rightarrow [0,1]$ by $\phi _l (x) =\left. \int _{x}^{y_2} \zeta _2 (x') \mathrm {d}x' \bigg / \int _{y_1}^{y_2} \zeta _2(x') \mathrm {d}x' \right.$. Finally, define $\phi _b: {\mathbb {R}} \rightarrow [0,1]$ by $\phi _b(x) = \phi _l (|x|)$, and let $\phi (x)=1-\phi _b(x)$.

Lemma 28

We have $\phi _b(x) \in [0,1]$ and, writing $2 y_1= y_2=y_0$,

$$\begin{aligned} \partial _x( \phi _l (x))&\le 2 \frac{ e^{\frac{4}{ 3(y_2-y_1)} } }{ y_2-y_1 } = 4 \frac{ e^{\frac{2}{ 3y_0} } }{ y_0 } = \gamma _{\phi }. \end{aligned}$$

(35)

Proof

As mentioned, by construction $\phi _b(x) \in [0,1]$. Because $\partial _x \beta \left( \frac{y_1+y_2}{2} \right) = 0$ and this is the only zero of the derivative in the open interval $(y_1,y_2)$, we see that

$$\begin{aligned} \beta (x) \le \beta \left( \frac{y_1+y_2}{2} \right) = e^{\frac{4}{y_1-y_2}} . \end{aligned}$$

Hence, because $\beta (x)\ge 0$,

$$\begin{aligned} \int _{y_1}^{y_2} \beta (x) \le (y_2-y_1) e^{\frac{4}{y_1-y_2}}. \end{aligned}$$

Because $\beta (x)$ is monotone on $[y_1, \frac{y_1+y_2}{2} ]$, we also have

$$\begin{aligned} \int _{y_1}^{y_2} \beta (x) \ge \frac{y_2-y_1}{2} \beta \left( \frac{3}{4} y_1 + \frac{1}{4} y_2 \right) = \frac{y_2-y_1}{2} e^{\frac{16}{ 3(y_1-y_2)}}. \end{aligned}$$

We now have

$$\begin{aligned} \partial _x( \phi _l (x))&= \partial _x \left( \int _{x}^{y_2} \beta (x') \mathrm {d}x' \bigg / \int _{y_1}^{y_2} \beta (x') \mathrm {d}x' \right) \\&= \beta (x) / \int _{y_1}^{y_2} \beta (x') \mathrm {d}x' \\&\le \frac{e^{\frac{4}{y_1-y_2}} }{ \frac{y_2-y_1}{2} e^{\frac{16}{ 3(y_1-y_2)}} } \\&=2 \frac{ e^{\frac{4}{y_1-y_2}-\frac{16}{ 3(y_1-y_2)} } }{ y_2-y_1 } \\&=2 \frac{ e^{\frac{4}{ 3(y_2-y_1)} } }{ y_2-y_1 }. \end{aligned}$$

$\square$

3.2.2 Inside a Single Simplex

Similar to Corollary 13, we need a condition that ensures that the zero set of $F_{PL,1}^i (x,\tau )$ restricted to $\sigma \times [0,1]$is a smooth manifold. In fact, similar to (15), we define

$$\begin{aligned} F_{L,1}^i (x,\tau )&= \left( 1-\tau \phi \left( |f_B|^2\right) \right) f^i(x) + \tau \phi \left( |f_B|^2 \right) f^i_{L}(x) \\&= f^i(x) + \tau \phi \left( |f_B|^2\right) ( f^i_{L}(x) - f^i(x)) , \end{aligned}$$

where $\phi$ is as defined above. Observe that $F_{L,1}^i (x,\tau )$ can be extended to a neighbourhood of $\sigma \times [0,1]$.

Remark 29

For the constants, it is better if $y_0$ can be chosen as large as possible, but we need $y_1$ to be quite a bit larger than $y_0$. In turn, we cannot choose $y_1$ arbitrarily large because this would mean that the gradient field $\nabla f_\partial |_{f^{-1} (0)}$ (seen as restricted on $f^{-1} (0)$) would never vanish. The latter is in general impossible thanks to the hairy ball theorem [52].

We introduce the following definition that complements Definition 2:

Definition 30

$$\begin{aligned} \varGamma _{\max }^B&= \max _{x \in \mathcal {T}_0} \left| \nabla \left( |f_B|^2\right) \right| = 2 \max _{x \in \mathcal {T}_0} \left| \sum _l f^l \nabla f^l+ f_{\partial } \, \nabla f_{\partial } \right| \end{aligned}$$

(36)

$$\begin{aligned} {\hat{\lambda }}_{\min }^{B_1}&= \min _{x\in \mathcal {T}_0} \lambda _{\min }({{\widehat{{\mathrm{G}} }}^{B_1}})(x), \end{aligned}$$

(37)

where ${{\widehat{{\mathrm{G}} }}^{B_1}}= \mathrm {Gram}(\nabla _{x,\tau } F_{L,1})$ and $\lambda _{\min }(A)$ denotes, as before, the smallest absolute value of the eigenvalues of matrix A.

We have then the analogue of Lemma 12:

Lemma 31

We have,

$$\begin{aligned} | {\hat{\lambda }}_{\min }^{B_1} - \lambda _{\min } | \le e_L^{B_1} \end{aligned}$$

where $e_L^{B_1} = O(d^2D/T)$ is precisely defined in (41) and (38). For Coxeter triangulations of type $\tilde{A}_d$, $e_L^{B_1} = O(d^{5/2}D)$.

Proof

We start with an estimate on the individual $\nabla _{x,\tau } F_{L,1}^i (x,\tau )$. As noted before, we write for convenience $\nabla _{x,\tau }f(x)=\left( \begin{array}{c} \nabla f^i(x) \\ 0\end{array} \right)$.

$$\begin{aligned}&\left| \nabla _{x,\tau }f(x) - \nabla _{x,\tau } F_{L,1}^i (x,\tau )\right| \nonumber \\&= \left| \nabla _{x,\tau }f(x) - \nabla _{x,\tau } \left( f(x) + \tau \phi \left( |f_B|^2\right) ( f^i_{L}(x) - f^i(x)) \right) \right| \nonumber \\&= \left| - \nabla _{x,\tau } \left( \tau \phi \left( |f_B|^2 \right) ( f^i_{L}(x) - f^i(x)) \right) \right| \nonumber \\&= \left| \left( \begin{array}{c} -\tau \nabla \left( \phi \left( |f_B|^2\right) \right) ( f_{L}^i(x) - f^i(x)) \\ \phi \left( |f_B|^2 \right) ( f^i_{L}(x) - f^i(x)) \end{array} \right) \right. + \left. \left( \begin{array}{c}-\tau \phi \left( |f_B|^2 \right) \nabla ( f^i_{L}(x) - f^i(x)) \\ 0 \end{array} \right) \right| \nonumber \\&\le \left| \tau \nabla \left( \phi \left( |f_B|^2\right) \right) ( f^i_{L}(x) - f^i(x)) \right| + \left| \tau \phi \left( |f_B|^2 \right) \nabla ( f_{L}^i(x) - f^i(x)) \right| \nonumber \\&\quad + \left| \phi \left( |f_B|^2 \right) ( f_{L}^i(x) - f^i(x)) \right| \qquad \qquad \quad (\text {by the triangle inequality }) \nonumber \\&\le \varGamma _{\max }^B \gamma _{\phi } |f_{L}^i(x) \!-\! f^i(x)| \!+\! \left| \phi \left( |f_B|^2\right) \nabla ( f_{L}^i(x) \!-\! f^i(x)) \right| \!+\! |f_{L}^i(x) \!-\! f^i(x)| \qquad (\text {because }\tau \le 1, (36), (35), \phi \in [0,1]) \nonumber \\&\le \varGamma _{\max }^B \gamma _{\phi } | f_{L}^i(x) - f^i(x)| + \left| \nabla ( f_{L}^i(x) - f^i(x)) \right| \qquad \quad (\text {because }\phi \in [0,1] + |f_{L}^i(x) - f^i(x)|) \nonumber \\&\le 2 D^2 \alpha _{\max } + 2\varGamma _{\max }^B \gamma _{\phi } D^2 \alpha _{\max } + \frac{4 d D \alpha _{\max } }{T} \,\, {\mathop {=}\limits ^{{\mathrm{def}}}} \,\, 2D^2 \alpha _{\max } + e_t^{B_1} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (\text {by Lemma}~9 \text {and Proposition}~ 10). \end{aligned}$$

(38)

We now write ${\mathrm{G}} _{i,j}$ and ${{\widehat{{\mathrm{G}} }}^{B_1}}_{i,j}$ for the elements (i, j) of ${\mathrm{G}}$ and ${{\widehat{{\mathrm{G}} }}^{B_1}}$, respectively. Expanding yields

$$\begin{aligned} {{\widehat{{\mathrm{G}} }}^{B_1}}_{i,j}=&\left( \nabla _{x,\tau } F_{L,1}^i (x,\tau ) - \nabla _{x,\tau } f^i(x) + \nabla _{x,\tau } f^i(x) \right) \nonumber \\&\cdot \left( \nabla _{x,\tau } F_{L,1}^j (x,\tau ) - \nabla _{x,\tau } f^j(x) \right) \nonumber \\ =&\; {\mathrm{G}} _{i,j} + \left( \nabla _{x,\tau } F_{L,1}^i (x,\tau ) -\nabla _{x,\tau }f^j(x) \right) \cdot \nabla _{x,\tau } f^i(x) \nonumber \\&+ \nabla _{x,\tau }f^j(x) \cdot \left( \nabla _{x,\tau } F_{L,1}^j (x,\tau ) -\nabla _{x, \tau } f^j(x) \right) \nonumber \\&+ \left( \nabla _{x,\tau } F_{L,1}^i (x,\tau ) -\nabla _{x,\tau }f^j(x) \right) \cdot \left( \nabla _{x,\tau } F_{L,1}^j (x,\tau ) - \nabla _{x,\tau } f^j(x) \right) . \end{aligned}$$

(39)

We now see by Cauchy–Schwarz, the triangle inequality and Eq. (38) that

$$\begin{aligned}&|{{\widehat{{\mathrm{G}} }}^{B_1}}_{i,j}- {\mathrm{G}} _{i,j} | \le 2\gamma _{\max } \left( 2D^2 \alpha _{\max } + e_t^{B_1}\right) + \left( 2D^2 \alpha _{\max } + e_t^{B_1}\right) ^2. \end{aligned}$$

(40)

Corollary 8 now yields ${\hat{\lambda }}_{\min }^{B_1} > \lambda _{\min } - e_L^{B_1}$ where

$$\begin{aligned} e_L^{B_1} {\mathop {=}\limits ^\mathrm{def}} (d-n) \left( 2 \gamma _{\max } \left( 2D^2 \alpha _{\max } + e_t^{B_1}\right) + \left( 2D^2 \alpha _{\max } + e_t^{B_1}\right) ^2 \right) \end{aligned}$$

(41)

$\square$

and $e_t^{B_1}$ is defined in (38). The following corollary is then the analogue of Corollary 13:

Corollary 32

($F_{L,1}^{-1} (0)$ is a manifold) If the regularity condition

$$\begin{aligned} \lambda _{\min } > e_L^{B_1}, \end{aligned}$$

(42)

holds, then $F_{L,1}^{-1} (0)$ is a smooth manifold inside an $\epsilon$ neighbourhood of $\sigma \times [0,1]$.

3.2.3 Transversality with Regard to the $\tau$-Direction

We note that, similar to Lemma 15, we have

Lemma 33

Using the notation of Lemma 15, we have

$$\begin{aligned} \tan \angle ( \nabla _{x,\tau }(F_{L,1}) , \varXi ) \le \frac{2 D ^2 \alpha _{\max } }{ \sqrt{\lambda _{\min }} -e_t^{B_1}}. \end{aligned}$$

Proof

The proof is identical to the proof of Lemma 15 with the replacement of $\frac{4 d D \alpha _{\max }}{T}$ in the denominator by $e_t^{B_1}$

The latter constant is a consequence of (38). $\square$

Now, similar to Corollary 16, we find that

Corollary 34

(Transversality with respect to $\tau$ for Step 1) Assume that both the regularity condition (42) and the transversality condition

$$\begin{aligned} \lambda _{\min } > e_t^{B_1} \end{aligned}$$

(43)

hold.

Then, inside each $\sigma \times [0,1]$, the gradient of $\tau$ on $F_{L,1}^{-1} (0)$ is smooth and does not vanish. Both conditions are satisfied if $D/T = O(d^{-2})$. When $\mathcal {T}$ is a Coxeter triangulation of type $\tilde{A}_d$, the condition reduces to $D=O(d^{-5/2})$.

3.2.4 Global Result

We now have to prove that $F_{PL,1}^{-1}(0)$ is a manifold. For this, we again employ the generalized implicit function theorem. But first of all, we need the following bound, which is similar to Lemma 22.

Note that $\nabla _{x,\tau } F^i(x_0,\tau _0)$ is well defined as soon as $x_0$ lies in the interior of a d-simplex in $\mathcal {T}$.

Lemma 35

Assuming that the gradients are well defined, we have

$$\begin{aligned} |\nabla _{x,\tau } F^i_{PL,1}(x_1,\tau _1) -\nabla _{x,\tau } F^i_{PL,1} (x_2,\tau _2)| \le {g_{PL}^{B_1}} , \end{aligned}$$

where $g_{PL}^{B_1} = \mathcal {O}(dD/T)$ is precisely defined in (44). When $\mathcal {T}$ is a Coxeter triangulation of type $\tilde{A}_d$, $g_{PL}^{B_1} = \mathcal {O}(d^{3/2}D)$.

Proof

By expansion, we see that

$$\begin{aligned} |\nabla _{x,\tau }&F^i_{PL,1}(x_1,\tau _1) -\nabla _{x,\tau } F^i_{PL,1} (x_2,\tau _2)| \nonumber \\ =&\left| \nabla _{x,\tau } F^i_{PL,1}(x_1,\tau _1) -\nabla _{x,\tau } f^i(x_1) +\nabla _{x,\tau } f^i(x_1) \right. \nonumber \\&- \left. \nabla _{x,\tau f}^i(x_2) + \nabla _{x,\tau } f^i(x_2) -\nabla _{x,\tau } F^i_{PL,1} (x_2,\tau _2) \right| \nonumber \\ \le&\left| \nabla _{x,\tau } F^i_{PL,1}(x_1,\tau _1) -\nabla _{x, \tau } f^i(x_1) \right| \nonumber \\&+\left| \nabla _{x,\tau } f^i(x_1) - \nabla _{x,\tau } f^i(x_2) \right| \nonumber \\&+\left| \nabla _{x,\tau } f^i(x_2) -\nabla _{x,\tau } F^i_{PL,1} (x_2,\tau _2) \right| \qquad \qquad \quad (\text {by the triangle inequality}) \nonumber \\ \le&\; {2 d \alpha _{\max } D + 4D^2 \alpha _{\max } + 2e_t^{B_1}} \qquad \qquad \qquad \quad (\text {by }(23), (8), \text { and } (38) \text { twice}) \nonumber \\ {\mathop {=}\limits ^\mathrm{def}}&g_{PL}^{B_1}. \end{aligned}$$

(44)

This completes the proof. $\square$

Suppose $x_0, x_1, \ldots , x_m \in \text {star} (v)$, $\tau _0, \dots ,\tau _m \in [0,1]$ and that $\nabla _{x,\tau } F^i_{PL,1} (x_i,\tau _i)$ is well defined for all i. Further, assume that $\mu _1,\dots , \mu _m$ are positive weights such that $\mu _1+ \cdots + \mu _m=1$. We write

$$\begin{aligned} \widehat{\mathbf{G}}^{B_1}=\mathrm {Gram}\left( \sum _{k=1}^m \mu _k \nabla _{x,\tau } F_{PL,1}(x_k,\tau _k)\right) , \end{aligned}$$

and $\widehat{{\varvec{\varLambda }}}_{\min }^{B_1}$ for the smallest modulus of the eigenvalues of $\widehat{\mathbf{G}}^{B_1}$.

Lemma 36

We have

$$\begin{aligned} |\widehat{{\varvec{\varLambda }}}_{\min }^{B_1}- \lambda _{\min }| \le e_{PL}^{B_1} \end{aligned}$$

with $e_{PL}^{B_1}=O(d^2D/T)$ being precisely defined in (47). For Coxeter triangulations of type $\tilde{A}_d$, $e_{PL}^{B_1}=O(d^{5/2}D)$.

Proof

The proof is more or less the same as the proof of Lemma 23, but with more complicated bounds. We assume that $x_0 \in \text {star} (v)$ and $\tau _0 \in [0,1]$ are such that $\nabla _{x,\tau } F^i(x_0,\tau _0)$ is well defined (i.e. $x_0$ lies in the interior of a d-simplex of $\mathcal {T}$). Lemma 31 gives that

$$\begin{aligned} \widehat{{\varvec{\varLambda }}}_{\min }^{B_1} > \lambda _{\min } - e_L^{B_1}. \end{aligned}$$

Using $\nabla ( f^i) \le \gamma _{\max }$ and (38), we note that

$$\begin{aligned} \left| \nabla _{x,\tau } F^i_{PL,1}(x_0,\tau _0) \right|&\le \gamma _{\max }+ 2 D^2 \alpha _{\max } + e_t^{B_1}. \end{aligned}$$

(45)

We want to use Weyl’s bound to determine a bound on the smallest absolute value of the eigenvalues of $\widehat{\mathbf{G}}^{B_1}$. Writing ${{\widehat{{\mathrm{G}} }}^{B_1}}_{i,j}$ and $\widehat{\mathbf{G}}^{B_1}_{i,j}$ for element (i, j) of matrices ${{\widehat{{\mathrm{G}} }}^{B_1}}(x_0,\tau _0)$ and $\widehat{\mathbf{G}}^{B_1}$, respectively, we show that $\widehat{\mathbf{G}}^{B_1}_{i,j}$ and ${{\widehat{{\mathrm{G}} }}^{B_1}}_{i,j}(x_0,\tau _0)$ are pairwise close (compare to (40)).

$$\begin{aligned} |\widehat{\mathbf{G}}^{B_1}_{i,j}&- {{\widehat{{\mathrm{G}} }}^{B_1}}_{i,j}(x_0,\tau _0)| \nonumber \\ =&\left| \left( \sum _{k =1}^{m} \mu _k \, \nabla _{x,\tau } F^i_{PL,1}(x_k,\tau _k) \right) \cdot \left( \sum _{k =1}^{m} \mu _k \, \nabla _{x,\tau } F^j_{PL,1}(x_k,\tau _k) \right) \right. \nonumber \\&\left. -\nabla _{x,\tau } F^i_{PL,1}(x_0,\tau _0) \cdot \nabla _{x,\tau } F^i_{PL,1}(x_0,\tau _0) \right| \nonumber \\ \le&\left| \nabla _{x,\tau } F^i_{PL,1}(x_0,\tau _0) -\sum _{k =1}^{m} \mu _k \nabla _{x,\tau } F^i_{PL,1}(x_k,\tau _k) \right| \nonumber \\&\cdot \left| \nabla _{x,\tau } F^j_{PL,1}(x_0,\tau _0) \right| \nonumber \\&+ \left| \nabla _{x,\tau } F^j_{PL,1}(x_0,\tau _0) -\sum _{k =1}^{m} \mu _k \nabla _{x,\tau } F^j_{PL,1}(x_k,\tau _k) \right| \nonumber \\&\cdot \left| \nabla _{x,\tau } F^i_{PL,1}(x_0,\tau _0) \right| \nonumber \\&+ \left| \nabla _{x,\tau } F^i_{PL,1}(x_0,\tau _0) -\sum _{k =1}^{m} \mu _k \nabla _{x,\tau } F^i_{PL,1}(x_k,\tau _k) \right| \nonumber \\&\cdot \left| \nabla _{x,\tau } F^j_{PL,1}(x_0,\tau _0) -\sum _{k =1}^{m} \mu _k \nabla _{x,\tau } F^j_{PL,1}(x_k,\tau _k) \right| \nonumber \\ \le&\; 2 g_{PL}^{B_1} \cdot \left( \gamma _{\max }+ 2 D^2 \alpha _{\max } + e_t^{B_1} + \left( g_{PL}^{B_1} \right) ^2 \right) \nonumber \\ \text {by Lemma}~35 \text { and } (45). \end{aligned}$$

(46)

Using the result of Lemma 31 and invoking Corollary 8 once more gives

$$\begin{aligned} |\widehat{{\varvec{\varLambda }}}_{\min }^{B_1}- \lambda _{\min }| \le e_{PL}^{B_1} \end{aligned}$$

with

$$\begin{aligned} e_{PL}^{B_1} {\mathop {=}\limits ^\mathrm{def}} e_L^{B_1} -(d-n) \left( 2 g_{PL}^{B_1} \cdot \left( \gamma _{\max }+ 2 D^2 \alpha _{\max } + e_t^{B_1}\right) + \left( g_{PL}^{B_1} \right) ^2 \right) . \end{aligned}$$

(47)

$\square$

Lemma 36 immediately yields that

Corollary 37

($F_{PL,1}^{-1}(0)$ is a manifold)

If the regularity condition

$$\begin{aligned} \lambda _{\min } >e_{PL}^{B_1} \end{aligned}$$

(48)

holds, then the generalized implicit function theorem, Theorem 20, applies to $F_{PL,1}(x,\tau )=0$. In particular, $F_{PL,1}^{-1}(0)$ is a manifold.

We stress again that, inside the set $\{ x | \phi \left( \sum _i (f^i)^2(x)+ f_{\partial }^2 (x) \right) =1\}$, the zero set of $F_{PL,1} (x,1)$ coincides with the zero set of $f_{PL}(x)$.

3.3 Step 2

Before we can proceed, we have to specify the bump function $\psi$. We suppose that (the constants have not been optimized)

$$\begin{aligned} \psi (x) = {\left\{ \begin{array}{ll} 1 &{} \text {if } | x| \le \frac{101}{100} y_0 \\ 0 &{} \text {if } | x| \ge 2 y_0 . \end{array}\right. } \end{aligned}$$

In particular,

Definition 38

We pick $\psi (x)= \phi _b(x)$, with the choice $y_1= \frac{101}{100} y_0$ and $y_2= 2 y_0$.

Remark 39

We stress that the choice of $y_1$ and $y_2$ for the function $\psi$ is different from the choice we made for $\phi$, in the first step of the proof.

First, we stress that the zero set of $F_{PL,2,\epsilon }(x,1)$ coincides with the zero set of $(f_{PL}(x), f_{\partial ,PL}(x)-\epsilon )$, provided that $\psi ( \sum _i f_i(x)^2 + f_\partial (x)^2) =1$.

Secondly, we now claim the following:

Lemma 40

The zero set of $F_{PL,2,\epsilon }(x,1)$ is a subset of the zero set of $f_{PL}(x)$, for each $\epsilon$.

Proof

We focus on the first ${ d-n}$ coordinates of (34). We see that

$$\begin{aligned}&\left( 1- \psi \left( |f_B|^2 \right) \right) F_{PL,1}(x,1) + \psi \left( |f_B|^2\right) f_{PL}(x) \nonumber \\ =&\left( 1- \psi \left( |f_B|^2\right) \right) \left( \left( 1- \phi \left( |f_B|^2\right) \right) f(x) + \phi \left( |f_B|^2 \right) f_{PL}(x) \right) + \psi \left( |f_B|^2\right) f_{PL}(x) \nonumber \\ =&\left( 1- \psi \left( |f_B|^2 \right) \right) \left( 1- \phi \left( |f_B|^2\right) \right) f(x) +\left( \left( 1- \psi \left( |f_B|^2 \right) \right) \phi \left( |f_B|^2 \right) + \psi \left( |f_B|^2 \right) \right) f_{PL}(x) \nonumber \\ =&\left( \left( 1- \psi \left( |f_B|^2\right) \right) \phi \left( |f_B|^2 \right) + \psi \left( |f_B|^2\right) \right) f_{PL}(x), \end{aligned}$$

(49)

where we used that

$$\begin{aligned} 1- \psi \left( |f_B|^2 \right)= & {} 0, \;\;\; \mathrm{if}\;\;\; |f_B|^2 \le \frac{101}{100} y_0, \\ \left( 1- \phi \left( |f_B|^2\right) \right)= & {} 0 , \;\;\; \mathrm{if}\;\;\; |f_B|^2 \ge y_0. \end{aligned}$$

We can further rewrite (49),

$$\begin{aligned}&\left( \left( 1- \psi \left( |f_B|^2 \right) \right) \cdot \left( \phi \left( |f_B|^2 \right) -1+1\right) + \psi \left( |f_B|^2 \right) \right) f_{PL}(x) \\&= \left( \left( 1- \psi \left( |f_B|^2 \right) \right) \left( \phi \left( |f_B|^2 \right) -1\right) + 1 \right) f_{PL}(x) \\&= f_{PL}(x), \end{aligned}$$

where we used the same argument as before. $\square$

The technical result that remains to be proven is the counterpart of Theorem 25 for $F_{PL,2,\epsilon }(x,\tau )$ and for each sufficiently small $\epsilon$. To be precise, it suffices for $\epsilon \le 2 y_0$. We remark that it is likely that this bound on $\epsilon$ can be improved.

We again follow the same path to prove this result. That is, we first concentrate on a single simplex and prove that inside that simplex the zero set of $F_{PL,2,\epsilon }$ is a smooth manifold on which the gradient of $\tau$ as restricted to the manifold does not vanish. We then prove that the zero set of $F_{PL,2,\epsilon }$ is globally a manifold.

3.3.1 Assumptions and Notations

Because we are now faced with both f(x) and $f_\partial (x)$, we need to introduce a bound on how far the gradients of all the entrees of these functions are from being collinear. We write

$$\begin{aligned} f_B (x)= (f(x), f_\partial (x)) . \end{aligned}$$

(50)

Before we were only interested in the set $\mathcal {T}_0$. Similarly here, we sometimes concentrate on a neighbourhood of the zero set of both $f_\partial$ and f. Therefore, we write $\mathcal {T}_ B$ for all $\sigma \in \mathcal {T}$ such that $(\sum _l (f^l)^2+ (f_\partial )^2)^{-1} ( [-2 y_0 , 2y_0]) \cap \sigma \ne \emptyset$.

We also write ${{\mathrm{G}} ^{B}}= \mathrm {Gram}(\nabla f_B)$ and $\lambda _{\min }^{B}$ for the minimal absolute value of the eigenvalues of ${{\mathrm{G}} ^{B}}$, where the minimization is over all simplices in the set ${\mathcal {T}_ B \cap \mathcal {T}_0}$. The restriction to the set ${\mathcal {T}_ B \cap \mathcal {T}_0}$ is important, because if the minimization would be just over $\mathcal {T}_0$, ${{\mathrm{G}} ^{B}}$ would generically be 0 as a consequence of the hairy ball theorem.

We note that by taking gradients the $\epsilon$ constant drops from the expression, so that the properties we now define are independent of $\epsilon$. For the lengths of the gradients of $f_B$, we define,

$$\begin{aligned} \gamma _{\max }^B = \max _{x \in \mathcal {T}_0} \max _i |\nabla (f_B^i)| , \end{aligned}$$

(51)

for all $1\le i\le d-n+1$. Similar to $\alpha _{\max }$, we define $\alpha _{\max }^B$ as the bound on the operator 2-norm of all Hessians of $f_B$, that is,

$$\begin{aligned} \alpha _{\max }^B= \max _{x \in \mathcal {T}_0} \max _i \Vert \text {Hes} (f^i_B) \Vert _2= \max _{x \in \mathcal {T}_0 } \max _i \Vert (\partial _k \partial _l f^i_B)_{k,l} \Vert _2. \end{aligned}$$

(52)

We stress that that $\alpha _{\max } \le \alpha _{\max }^B$.

We use the same notation for the ambient triangulation $\mathcal {T}$, the lower bound on the thickness of the simplices $T$ and upper bound on the longest edge length D. We also need to introduce a bound on the differential of the bump function $\psi$. Similar to (35), we define

$$\begin{aligned} \gamma _{\psi }= 2 \frac{ e^{\frac{4}{ 3(y_2-y_1)} } }{ y_2-y_1 }= 2 \frac{ e^{\frac{4}{ 3(2 y_0-\frac{101}{100} y_0)} } }{ 2 y_0-\frac{101}{100} y_0 }= \frac{200}{99} \frac{ e^{\frac{400}{ 297 y_0} } }{ y_0 }, \end{aligned}$$

(53)

because we picked $y_1= \frac{101}{100} y_0$ and $y_2= 2 y_0$, for $\psi$, see Definition 38 and Remark 39.

3.3.2 Inside a Single Simplex

Similar to Lemma 31, we now give a condition that ensures that the zero set of $F_{PL,2,\epsilon } (x,\tau )$ is smooth inside $\sigma \times [0,1]$. In fact, similar to (15), we define

$$\begin{aligned} F_{L,2,\epsilon }(x,\tau ) =&\left( 1-\tau \psi \left( |f_B|^2 \right) \right) (F_{L,1}(x,1), f_\partial (x)-\epsilon ) \\&+ \tau \psi \left( |f_B|^2 \right) (f_{L}(x), f_{\partial , L} (x)-\epsilon ) , \end{aligned}$$

which can be extended to a neighbourhood of $\sigma \times [0,1]$.

We also write $\widehat{\mathbf{G}}^{B_2}= \mathrm {Gram}( \nabla _{x,\tau }F_{PL,2,\epsilon }$ and ${\hat{\lambda }}_{\min }^{B_2}$ for the smallest absolute value of the eigenvalues of $\widehat{\mathbf{G}}^{B_2}$.

Lemma 41

For all $\epsilon$

$$\begin{aligned} |{\hat{\lambda }}_{\min }^{B_2} - \lambda _{\min } ^B| \le e_{L}^{B2}, \end{aligned}$$

where $e_{L}^{B2}=O(d^2D/T)$ is precisely defined in (63). For Coxeter triangulations of type $\tilde{A}_d$, $e_{L}^{B_2}=O(d^{5/2}D)$.

Proof

We start with an estimate on the individual $\nabla _{x,\tau } F_{L,2,\epsilon }^i (x,\tau )$. We will write $(v,w)^i$ for the ith coordinate of the composed vector (v, w). We now see that

(54)

We now write ${{\mathrm{G}} ^{B}}= \mathrm {Gram}(\nabla f_B)$, ${\widehat{{\mathrm{G}} }}^{B_2}= \mathrm {Gram}(\nabla F_{L,2,\epsilon })$, and ${{\mathrm{G}} ^{B}}_{i,j}$ and ${\widehat{{\mathrm{G}} }}^{B_2}_{i,j}$ for their (i, j)th elements, respectively. Similar to (39) (we simply need to replace $F_{L,1}$ by $F_{L,2,\epsilon }$ and f by $f_B$), we obtain

$$\begin{aligned} |{\widehat{{\mathrm{G}} }}^{B_2}_{i,j}- {{\mathrm{G}} ^{B}}_{i,j} | \le&2 \gamma _{\max }^B {e_t^{B_2} + (e_t^{B_2})^2}. \end{aligned}$$

(55)

By Corollary 8, we finally obtain

$$\begin{aligned} |{\hat{\lambda }}_{\min }^{B_2} - {\lambda _{\min } ^B | \ge (d-n) \left( 2 \gamma _{\max }^B e_t^{B_2} +(e_t^{B_2})^2 \right) \; {\mathop {=}\limits ^\mathrm{def}} e_{L}^{B_2}} \end{aligned}$$

(56)

$\square$

We again have the following corollary.

Corollary 42

($F_{L,2,\epsilon }^{-1} (0)$ is a manifold) We have that $F_{L,2,\epsilon }^{-1} (0)$ is a smooth manifold inside an small neighbourhood of $\sigma \times [0,1]$ provided that the following regularity condition holds

$$\begin{aligned} \lambda _{\min } ^B > e_{L}^{B_2}, \end{aligned}$$

(57)

where $e_{L}^{B_2}$ is defined in Lemma 41.

3.3.3 Transversality with Regard to the $\tau$-Direction

Once more, similar to Lemma 15 we have

Lemma 43

Let $\varXi$ be as in Lemma 15. We have

$$\begin{aligned} \tan&\angle ( \nabla _{x,\tau }(F_{L,2,\epsilon }) , \varXi ) \le \frac{2 D ^2 \alpha _{\max }^B}{\sqrt{\lambda _{\min }^B} - {e_t^{B_2}}} \end{aligned}$$

where $e_t^{B_2} = O(dD/T)$ ($e_t^{B_2} = O(d^{3/2}D)$ if $\mathcal {T}$ is a Coxeter triangulation of type $\tilde{A}_d$) is precisely defined in (54). In particular, if the following transversality condition holds:

$$\begin{aligned} \sqrt{\lambda _{\min }^B}> e_t^{B_2} \end{aligned}$$

(58)

the manifold $F_{L,2,\epsilon }^{-1} (0)$ inside $\sigma \times [0,1]$, if well defined, is never tangent to the $\tau = c$ planes, where c is a constant.

Proof

The proof is identical to the proof of Lemma 15 with the replacement of $\alpha _{\max }$ by $\alpha _{\max }^B$ and of $\frac{4 d D \alpha _{\max }}{T}$ in the denominator by $e_t^{B_2}$. The latter constant is a consequence of (54). $\square$

Now, similar to Corollary 34, we have

Corollary 44

(Transversality with respect to $\tau$ for Step 2) If both the regularity condition (57) and the transversality condition (58) hold, then, inside each $\sigma \times [0,1]$, the gradient of $\tau$ on $F_{L,2,\epsilon }^{-1} (0)$ is smooth and does not vanish. Both conditions hold if $D=O(1/d^2)$.

3.3.4 Global Result

We now have to prove that $F_{PL,2,\epsilon }^{-1}(0)$ is a manifold, for all sufficiently small $\epsilon$. For this we first need the following bound, which is similar to the one in Lemma 35.

Lemma 45

Let v be a vertex in $\mathcal {T}$, $x_1, x_2 \in \text {star}(v)$, and $\tau _1,\tau _2 \in [0,1]$, such that $\nabla _{x,\tau } F^i_{PL,2,\epsilon }(x_1,\tau _1)$ and $\nabla _{x,\tau } F^i_{PL,2,\epsilon }(x_2,\tau _2)$ are well defined, then

$$\begin{aligned} |\nabla _{x,\tau }&F^i_{PL,2,\epsilon }(x_1,\tau _1) -\nabla _{x,\tau } F^i_{PL,2,\epsilon } (x_2,\tau _2)| \le g_{PL}^{B_2}, \end{aligned}$$

where $g_{PL}^{B_2} = \mathcal {O}(dD/T)$ is precisely defined in (59). If $\mathcal {T}$ is a Coxeter triangulation of type $\tilde{A}_d$, $g_{PL}^{B_2} = \mathcal {O}(d^{3/2}D)$.

Proof

The proof follows the same steps as the proof of Lemma 35. By expansion, we see that

$$\begin{aligned} |\nabla _{x,\tau }&F^i_{PL,2,\epsilon }(x_1,\tau _1) -\nabla _{x,\tau } F^i_{PL,2,\epsilon } (x_2,\tau _2)| \nonumber \\ =&\left| \nabla _{x,\tau } F^i_{PL,2,\epsilon }(x_1,\tau _1) -\nabla _{x,\tau } f^i_B(x_1)\right. \nonumber \\&+\nabla _{x,\tau } f^i_B(x_1) - \nabla _{x,\tau } f^i_B(x_2) \nonumber \\&+\left. \nabla _{x,\tau } f^i_B(x_2) -\nabla _{x,\tau } F^i_{PL,2,\epsilon } (x_2,\tau _2) \right| \nonumber \\ \le&\left| \nabla _{x,\tau } F^i_{PL,2,\epsilon }(x_1,\tau _1) - \nabla _{x,\tau } f^i_B(x_1) \right| \nonumber \\&+\left| \nabla _{x,\tau } f^i_B(x_1) -\nabla _{x,\tau } f^i_B(x_2) \right| \nonumber \\&+\left| \nabla _{x,\tau } f^i_B(x_2) -\nabla _{x,\tau } F^i_{PL,2,\epsilon } (x_2,\tau _2) \right| \qquad \qquad (\text {by the triangle inequality}) \nonumber \\ \le&2 d \alpha _{\max }^B D +2 e_t^{B_2} \qquad \qquad (\text {by } (8), |x_1- x_2 | \le 2 D, \text { and } (54) \text { twice}) \nonumber \\ {\mathop {=}\limits ^\mathrm{def}}&g_{PL}^{B_2}. \end{aligned}$$

(59)

$\square$

Suppose $x_0, x_1, \ldots , x_m \in \text {star} (v)$, $\tau _0, \dots ,\tau _m \in [0,1]$, and that, for all i, $\nabla _{x,\tau } F^i_{PL,2} (x_i,\tau _i)$ is well defined. Further assume that $\mu _1,\dots , \mu _m$ are positive weights such that $\mu _1+ \cdots + \mu _m=1$. We write

$$\begin{aligned} \widehat{\mathbf{G}}^{B_2}=\mathrm {Gram}\left( \sum _{k=1}^m \mu _k \nabla _{x,\tau } F_{PL,2}(x_k,\tau _k)\right) , \end{aligned}$$

(60)

and $\widehat{{\varvec{\varLambda }}}_{\min }^{B_2}$ for the smallest modulus of the eigenvalues of $\widehat{\mathbf{G}}^{B_2}$.

Lemma 46

$$\begin{aligned} |\widehat{{\varvec{\varLambda }}}_{\min }^{B_2} - \lambda _{\min }^B | \le e_{PL}^{B_2} \end{aligned}$$

(61)

where $e_{PL}^{B_2}=O(d^2D/T)$ is precisely defined in (63). If $\mathcal {T}$ is a Coxeter triangulation of type $\tilde{A}_d$, $e_{PL}^{B_2}=O(d^{5/2}D)$.

Proof

The proof is more or less the same as the proof of Lemma 36. Let $x_0 \in \text {star} (v)$ and $\tau _0 \in [0,1]$, be such that $\nabla _{x,\tau } F^i_{PL,2,\epsilon }(x_0,\tau _0)$ is well defined. Note that it is sufficient for $x_0$ to lie in the interior of a d-simplex in $\mathcal {T}$. Lemma 41 gives that

$$\begin{aligned} |\widehat{{\varvec{\varLambda }}}_{\min }^{B_2} - \lambda _{\min } ^B| \le e_L^{B_2}. \end{aligned}$$

Using $\nabla ( f_B^i) \le \gamma _{\max }^B$ and (54), we get

$$\begin{aligned} \left| \nabla _{x,\tau } F^i_{PL,2,\epsilon }(x_0,\tau _0) \right|&\le \gamma _{\max }^B+ {e_t^{B_2} }. \end{aligned}$$

(62)

We want to bound the smallest absolute value of the eigenvalues of ${\widehat{{\mathrm{G}} }}^{B_2}= \mathrm {Gram}(\nabla _{x,\tau } F_{L,2,\epsilon }))$. We proceed similarly to (46) (with $F_{PL,1}$ replaced by $F^i_{PL,2,\epsilon }$). Let $\widehat{\mathbf{G}}^{B_2}$ be as in (60), and denote by ${\widehat{{\mathrm{G}} }}^{B_2}_{i,j}$ and $\widehat{\mathbf{G}}^{B_2}_{i,j}$ the (i, j) elements of ${\widehat{{\mathrm{G}} }}^{B_2}$ and $\widehat{\mathbf{G}}^{B_2}$, respectively, and by $\widehat{{\varvec{\varLambda }}}_{\min }^{B_2}$ the smallest absolute value of the eigenvalues of $\widehat{\mathbf{G}}^{B_2}$.

$$\begin{aligned} |\widehat{\mathbf{G}}^{B_2}_{i,j}&- {\widehat{{\mathrm{G}} }}^{B_2}_{i,j}| \le \; 2 \left( g_{PL}^{B_2} \right) \cdot (\gamma _{\max }^B + {e_t^{B_2} } + (g_{PL}^{B_2})^2) \qquad \qquad \quad (\text {by } (62)). \end{aligned}$$

Thanks to Corollary 8 and Lemma 41, we have that

$$\begin{aligned} |\widehat{{\varvec{\varLambda }}}_{\min }^{B_2} -\lambda _{\min }^{B} |&\le e_L^{B_2} + (d-n) (2 g_{PL}^{B_2}) \cdot \left( \gamma _{\max }^B+e_t^{B_2} + (g_{PL}^{B_2})^2 \right) \;\; \nonumber \\&{\mathop {=}\limits ^\mathrm{def}} e_{PL}^{B_2}. \end{aligned}$$

(63)

$\square$

Lemma 46 immediately yields that

Corollary 47

(The generalized implicit function theorem in Step 2) If the regularity condition

$$\begin{aligned} \lambda _{\min }^B > e_{PL}^{B_2}, \end{aligned}$$

(64)

the generalized implicit function theorem, Theorem 20, applies to $F_{PL,1}(x,\tau )=0$. In particular, $F_{PL,1}^{-1}(0)$ is a manifold.

Theorem 48

If the regularity conditions (42) and (64) and the transversality conditions (43) and (58) hold, then $f^{-1}(0) \cap f_\partial ^{-1}( [ 0, \infty ))$ is isotopic to $f_{PL}^{-1}(0) \cap f_{\partial ,PL}^{-1}( [ 0, \infty ))$. All conditions hold when choosing $D=O(1/d^2)$.

Proof

The proof follows from Corollaries 32, 34, 37, 42, 44 and 47 . $\square$

3.4 Fréchet Distance

The bounds on the Fréchet distance can be achieved in the same way as before.

Theorem 49

Suppose that the conditions of Theorem 48 are satisfied. Then,

$$\begin{aligned} d_F&( f^{-1} (0) , f_{PL}^{-1}(0) ) \le d_{PL}^B \end{aligned}$$

where $d_{PL}^B= O(D^2)$ is defined in (65).

Proof

We apply the same argument as in Lemma 26 and Corollary 27, for both steps of the proof. This yields the sum of two terms that are of the same form as (31). For the first step, we need the following substitutions:

• $\theta$ is replaced by $\theta _1{\mathop {=}\limits ^\mathrm{def}} \arctan \frac{2 D ^2 \alpha _{\max } }{ \sqrt{\lambda _{\min }} -e_t^{B_1}}$, as a consequence of Lemma 33.

• ${\lambda _{\min } -e_{PL} }$ is replaced by ${\lambda _{\min } -e_{PL}^{B_1} }$, as a consequence of Lemma 36.

• $\gamma _{\max } +\frac{4 d D \alpha _{\max } }{T}$ is replaced by $\gamma _{\max } + 2D^2 \alpha _{\max } + e_t^{B_1}$, as a consequence of (38).

For the second step, we need the following substitutions:

• $\theta$ is replaced by $\theta _2{\mathop {=}\limits ^\mathrm{def}} \arctan \frac{2 D ^2 \alpha _{\max }^B}{\sqrt{\lambda _{\min }^B} - e_t^{B_2}}$, as a consequence of Lemma 43.

• $\sqrt{\lambda _{\min } -e_{PL} }$ is replaced by $\sqrt{\lambda _{\min } -e_{PL}^{B_2} }$, as a consequence of Lemma 46.

• $\gamma _{\max } +\frac{4 d D \alpha _{\max } }{T}$ is replaced by $\gamma _{\max }^B + e_t^{B_2}$ as a consequence of (54).

This yields

$$\begin{aligned} d_F&( f^{-1}(0) \cap f_\partial ^{-1}( [ 0, \infty )) , f_{PL}^{-1}(0) \cap f_{\partial ,PL}^{-1}( [ 0, \infty )) ) \nonumber \\&\le \tan \arcsin \frac{\sin (\theta _1) ( \gamma _{\max } + 2D^2 \alpha _{\max } + e_t^{B_1})}{\sqrt{\lambda _{\min } -e_{PL}^{B_1} } } \nonumber \\&\quad +\tan \arcsin \frac{\sin (\theta _2) ( \gamma _{\max }^B + e_t^{B_2})}{\sqrt{\lambda _{\min } -e_{PL}^{B_2} } } \nonumber \\ \;\;&{\mathop {=}\limits ^{\mathrm{def}}} \;\; d_{PL}^B. \end{aligned}$$

(65)

$\square$

4 Isostratifolds

Fig. 4

An example of an isostratifold

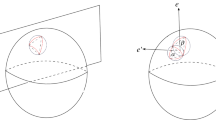
There is no obstruction that prevents us from extending the approach above to isostratifolds. By isostratifolds, we mean stratifolds that are given by the zero sets of functions and inequalities. For example, suppose that we want to find a PL approximation of the unit sphere centred at 0 in ${\mathbb {R}}^3$ including the PL approximations of the intersections of the sphere with slightly deformed $x=0$, $y=0$, and $z=0$-planes, as depicted in Fig. 4. This would also give PL approximations of the respective ‘octants’ of the sphere.

We could follow the same procedure as for a manifold with boundary to give precise bounds on the longest edge length D of the ambient triangulation that ensure that the PL approximation is correct. However, this would mean that we have to introduce an extra bump function for each stratum as well as an extra isotopy. Even though this should be relatively straightforward, finding the precise constants involved would become prohibitively lengthy.

5 Robustness

Suppose that f and $f_\delta$ are smooth functions and moreover $f_\delta$ is small in terms of the $C^1$-topology. Thanks to the implicit function theorem, we know that if 0 is a regular value of f, the zero set of f and the zero set of the slightly perturbed function $f+f_\delta$ are isotopic. We now give quantitative conditions that guarantee that $f^{-1}(0)$ and $(f+f_\delta )^{-1}(0)$ are ambient isotopic. Let $f, f_\delta : {\mathbb {R}}^d \rightarrow {\mathbb {R}}^{d-n}$, and write

$$\begin{aligned} {\tilde{\alpha }}_{\max }&= \max _{x } \left( \max \{ \max _i | \nabla (f_\delta ^i) (x) | , \max _i | f_\delta ^i (x) | \right) \} \end{aligned}$$

(66)

$$\begin{aligned} {\tilde{\lambda }}_{\min }&= \min _{x \in f^{-1} ( [ - {\tilde{\alpha }}_{\max }, {\tilde{\alpha }}_{\max }]^{d-n} ) } \lambda _{\min } (\mathrm {Gram}(\nabla f)) \end{aligned}$$

(67)

$$\begin{aligned} {\tilde{\gamma }}_{\max }&= \max _{x \in {\mathbb {R}}^d} \max _i|\nabla (f^i)| . \end{aligned}$$

(68)

Theorem 50

If

$$\begin{aligned} {\tilde{\lambda }}_{\min }>(d-n) ( 4 {\tilde{\gamma }}_{\max } {\tilde{\alpha }}_{\max } + {\tilde{\alpha }}_{\max }^2) . \end{aligned}$$

and $\sqrt{ {\tilde{\lambda }}_{\min }} >{\tilde{\alpha }}_{\max }$, then $f^{-1}(0)$ and $(f+f_\delta )^{-1}(0)$ are ambient isotopic.

Proof

We first note that if $|f^i(x)|> {\tilde{\alpha }}_{\max }$ then $f(x)+ \tau f_\delta (x) \ne 0$ for all $\tau \in [0,1]$, so we can restrict our attention to $f^{-1} ( [ - {\tilde{\alpha }}_{\max }, {\tilde{\alpha }}_{\max }]^{d-n} )$, conform (67). The proof is similar to the proof presented in the previous sections, but much simpler because here all functions are smooth. We start with the function $F(x,\tau )= f(x)+ \tau f_\delta (x)$, where $\tau \in [0,1]$. We, again, first establish that the zero set of this function is a $(n+1)$-dimensional manifold. Secondly, we will see that the gradient of $\tau$ restricted to this $(n+1)$-dimensional manifold never vanishes. As we have seen in the previous sections, this suffices to establish the isotopy $F^{-1}(0)$ from $f^{-1}(0)$ to $(f+f_\delta )^{-1}(0)$, by Lemma 3.

As before, it suffices to prove that $\lambda _{\min }(\nabla _{x,\tau }F)>0$ to establish that $F^{-1}(0)$ is a manifold. We write

$$\begin{aligned} {\widehat{\mathrm{G}} }=\mathrm {Gram}(\nabla _{x,\tau }F) \;\;\; \mathrm{and}\;\;\; {\mathrm{G}} = \mathrm {Gram}(\nabla f). \end{aligned}$$

We find that

$$\begin{aligned} | {\widehat{\mathrm{G}} }_{i,j} -{\mathrm{G}} _{i,j} |&= | (\nabla f^i+ \tau \nabla f^i_\delta , f^i_\delta ) \cdot (\nabla f^j+ \tau \nabla f^j_\delta , f^j_\delta ) - \nabla (f^i) \cdot \nabla (f^j)| \\ =&|\tau (\nabla f^i \cdot \nabla f^j_\delta + \nabla f^i_\delta \cdot \nabla f^j ) +f^i_\delta f^j_\delta | \\ \le&|\tau | |\nabla f^i | |\nabla f^j_\delta | + |\tau | |\nabla f^i_\delta | | \nabla f^j ) |+|f^i_\delta | |f^j_\delta | \\&\qquad \qquad \qquad \qquad \qquad (\text {by the triangle inequality and Cauchy--Schwarz}) \\ \le&2 |\tau | {\tilde{\gamma }}_{\max } {\tilde{\alpha }}_{\max } + {\tilde{\alpha }}_{\max }^2 \qquad \qquad (\text {by }(66), (67) \text { and } (68)) \\ \le&4 {\tilde{\gamma }}_{\max } {\tilde{\alpha }}_{\max } + {\tilde{\alpha }}_{\max }^2 \qquad \qquad (\text {because }|\tau |\le 1). \end{aligned}$$

Corollary 8 implies that $F^{-1}(0)$ is a manifold if

$$\begin{aligned} {\tilde{\lambda }}_{\min }>(d-n) ( 4 {\tilde{\gamma }}_{\max } {\tilde{\alpha }}_{\max } + {\tilde{\alpha }}_{\max }^2) . \end{aligned}$$

Lemma 14 further yields that $|\nabla f^i| \ge \sqrt{ {\tilde{\lambda }}_{\min }}$ in $f^{-1} ([ - {\tilde{\alpha }}_{\max }, {\tilde{\alpha }}_{\max }]^{d-n})$. This means that the x component of $\nabla _{x,\tau }(F)$ does not vanish (again in the domain $f^{-1} ([ - {\tilde{\alpha }}_{\max }, {\tilde{\alpha }}_{\max }]^{d-n})$) as long as

$$\begin{aligned} \sqrt{ {\tilde{\lambda }}_{\min }} >{\tilde{\alpha }}_{\max } . \end{aligned}$$

$\square$

A Notations and Overview of Constants

For notations, we followed the following rules:

• 1. Greek letters, except $\tau$ and $\epsilon$, are for constants related to functions.

• 2. We use $\widehat{.}$ for quantities related to PL functions.

• 3. Capital letters such as D, T are quantities related to the triangulation $\mathcal {T}$.

• 4. Bounds on gradients are denoted by $g_x^y$.

• 5. Bounds on eigenvalues are denoted by $e_x^y$.

• 6. For convenience, we write $\nabla _{x,\tau }f(x)=\left( \begin{array}{c} \nabla f^i(x) \\ 0\end{array} \right)$.

1.1 Overview of Constants

We give an overview. We write $\mathcal {T}_0$ for the set of all $\sigma \in \mathcal {T}$, such that $(f^i)^{-1}(0) \cap \sigma \ne$ for all i. We write $\mathcal {T}_ B$ for all $\sigma \in \mathcal {T}$ such that $(\sum _l (f^l)^2+ (f_\partial )^2)^{-1} ( [-2 y_0 , 2y_0]) \cap \sigma \ne \emptyset$. We write

1.1.1 Parameters of the Triangulation

$$\begin{aligned} D \;&:\; \text {the longest edge length of a simplex in } \mathcal {T}_0\\ T\;&: \; \text{ the } \text{ smallest } \text{ thickness } \text{ of } \text{ a } \text{ simplex } \text{ in } \mathcal {T}_0 \\ T\;&> \frac{2}{\sqrt{d+2}} \; \text{ for } \text{ Coxeter } \text{ triangulations }. \end{aligned}$$

1.1.2 Bump Functions

$\varXi = {\mathbb {R}}^d \subset {\mathbb {R}}^{d+1}$ is the space spanned by the d basis vectors corresponding to the x-directions.

1.1.3 Bounds on Gradients

1.1.4 Bounds on Eigenvalues

1.1.5 Bounds on Angles