Coxeter Triangulations Have Good Quality

Abstract

Coxeter triangulations are triangulations of Euclidean space based on a single simplex. By this we mean that given an individual simplex we can recover the entire triangulation of Euclidean space by inductively reflecting in the faces of the simplex. In this paper we establish that the quality of the simplices in all Coxeter triangulations is $O(1/\sqrt{d})$ of the quality of regular simplex. We further investigate the Delaunay property for these triangulations. Moreover, we consider an extension of the Delaunay property, namely protection, which is a measure of non-degeneracy of a Delaunay triangulation. In particular, one family of Coxeter triangulations achieves the protection $O(1/d^2)$. We conjecture that both bounds are optimal for triangulations in Euclidean space.

1 Introduction

1.1 Objectives and Motivation

Well-shaped simplices are of importance for various fields of application such as finite element methods and manifold meshing [2, 9, 10, 18, 21, 29]. Poorly-shaped simplices may induce various problems in finite element methods, such as large discretization errors or ill-conditioned stiffness matrices. Determining whether a simplex is well-shaped or not can be done with the help of various quality measures. Some examples of quality measures are: the ratio between minimal height and maximal edge length ratio called thickness [24, 33], the ratio between volume and a power of the maximal edge length called fatness [34], and the inradius–circumradius ratio [8]. Bounds on dihedral angles can also be included in the list of quality measures. We stress that there are many other quality measures in use and authors often find useful to introduce measures that are specific to whatever problem they study (see for example [27] for an overview on quality measures). Finding triangulations, even in Euclidean space, of which all simplices have good quality is a non-trivial exercise in arbitrary dimension.

In this paper we shall discuss Coxeter triangulations.

Definition 1

Coxeter triangulations are hyperplane arrangements of ${\mathbb {R}}^d$ whose cells are d-dimensional simplices with a special property that two adjacent d-dimensional simplices in a Coxeter triangulation are orthogonal reflections of one another.

To our knowledge, Coxeter triangulations are the triangulations with the best quality in arbitrary dimension. In particular, all dihedral angles of simplices in Coxeter triangulations are $45^\circ$, $60^\circ$ or $90^\circ$, with the exception of the ${\tilde{G}}_{2}$ triangulation of the plane where we also can find an angle of $30^\circ$. This is a clear sign of the exceptional quality of the simplices involved. Our goal is to exhibit the extraordinary properties of Coxeter triangulations.

The self-similarity and symmetry are another of the attractive points of Coxeter triangulations. Upon the first introduction, an unprepared reader might expect that the vertex sets of such triangulations form lattices, however it is not necessarily true, as we show in Sect. 5.

We are also interested in the stronger requirement of protection [4], which is specific to Delaunay triangulations. For a point set to have a unique well-defined Delaunay triangulation in the Euclidean space ${\mathbb {R}}^d$, one demands that there are no $d+2$ cospherical points, such that the interior of the sphere is empty, in a vertex set. Protection requires not only that there is no other vertex on the (empty) circumsphere of $d+1$ vertices, but that any other vertex is at distance $\delta$ away from the circumsphere. It has been proven that protection guarantees good quality [4]. Some algorithms were introduced for the construction of a protected set, such as the perturbation-based algorithms in [5] and [6]. Both of these algorithms take a general $\varepsilon$-net in ${\mathbb {R}}^d$ as input and output a $\delta$-protected net with $\delta$ of the order just $\varOmega (2^{-d^2}\varepsilon )$. On the other hand, take the $d$-dimensional Coxeter triangulation ${\tilde{A}}_{d}$. As we will see in the following, this highly-structured triangulation is Delaunay with protection $O(\frac{1}{d^2}\varepsilon )$. This protection value is the greatest in a general $d$-dimensional Delaunay triangulation we know.

1.2 Related Work

The notion of Coxeter triangulations was introduced to the computational geometry community by Dobkin, Wilks, Levy and Thurston in [14], where they tackled the problem of contour-tracing in ${\mathbb {R}}^d$. The choice of Coxeter triangulations was motivated by the following requirements:

• It should be easy to find the simplex that shares a facet with a given simplex.

• It should be possible to label the vertices of all the simplices at the same time with indices $0,\ldots ,d$, in such a way that each of the $d+1$ vertices of a $d$-simplex has a different label.

• The triangulations should be monohedral, meaning that all simplices are congruent. Here, by congruent, we mean that the simplices are identical up to reflections and rotations.

• All simplices should be isotropic, meaning that they should be roughly the same in all directions.

Thanks to the definition, this is exactly what Coxeter triangulations do. After comparing the inradius–circumradius ratio of the simplices in the triangulations they chose the ${\tilde{A}}_{d}$ Coxeter triangulation as the underlying triangulation for their contour-tracing algorithm.

Adams, Baek and Davis [1] chose the vertex set of ${\tilde{A}}_{d}$ Coxeter triangulation, also known as the permutahedral lattice, to accelerate the high-dimensional Gaussian filtering algorithm. This choice was again motivated by the fact that the triangulation has congruent and isotropic simplices.

The ${\tilde{A}}_{d}$ Coxeter triangulation was also used to approximate the Rips filtration of n points in ${\mathbb {R}}^d$ in a recent work by Choudhary et al. [11]. The authors arrived at an approximation scheme that achieved a significant reduction in size of the complex. The improvement came primarily from the fact that the permutahedral lattice is very well protected.

Coxeter triangulations also played an important role in [3, 17].

The Coxeter triangulations we study are intricately linked with root systems and root lattices. Delaunay triangulations of the root lattices have been studied by Conway and Sloane [12] and Moody and Patera [23]. These triangulations are different from the ones we study: the vertex sets we use are not necessarily lattices.

The three-dimensional Coxeter triangulation ${\tilde{A}}_{3}$ has attracted attention in the 3D mesh generation community for the high-quality of its simplices. The vertex set of this triangulation is also known as the body-centred cubic lattice, or bcc lattice, and its tetrahedron is sometimes referred as Sommerville’s type II tetrahedron (after [28]) or simply bcc-tetrahedron. This tetrahedron has been shown in [25] to be the best-conditioned space-filling tetrahedron out of all space-filling tetrahedra used in the 3D mesh community by a number of conditioning measures. This work led to the use of the bcc lattice in the isosurface stuffing algorithm [22].

Other examples of the use of the bcc lattice include the optimal sampling in image processing [30] and improving on the marching tetrahedra algorithm for isosurface extraction [32]. In both papers the main reason behind the choice of the bcc lattice was its sparse covering. This makes the sampling algorithm achieve the same accuracy as the usual cubic lattice with about 29.3% fewer samples.

Lastly, an observation that a bcc tetrahedron can be divided into eight half-sized bcc tetrahedra was used to make a variation of the octree algorithm [15].

1.3 Contribution

In this paper we give explicit expressions of a number of quality measures of Coxeter triangulations for all dimensions, presented in Sect. 5. This is an extension of the work by Dobkin et al. [14] who presented a table of the values of the inradius–circumradius ratio for the Coxeter triangulations up to dimension 8. We also provide explicit measures of the corresponding simplices in Sect. 6, allowing the reader to compute quality measures other than the ones listed.

In Sect. 2, we give a presentation of the theory of root systems. This presentation mostly follows the lecture notes of Jaap Top (in Dutch) [31] and a classical book by Humphreys [16] for the part on affine Weyl groups. In Sect. 3, we recall the definitions of the quality measures we are interested in, as well as the definition of protection. We further state the theorem of optimality of the regular $d$-simplex for each of the chosen quality measures. This theorem justifies the definition of the normalized versions of these quality measures. In Sect. 4, we established a criterion to identify if any given monohedral triangulation is Delaunay.

1.4 Future Work

The simplex qualities, defined in Definition 18, of the four families of Coxeter triangulations behave as $O(1/\sqrt{d})$ in terms of dimension. We conjecture that this quality is optimal for a general space-filling triangulation in ${\mathbb {R}}^{d}$. In addition, the $d$-dimensional Coxeter triangulation ${\tilde{A}}_{d}$ has the relative Delaunay protection $O(1/d^2)$. We further conjecture that it is optimal for a general space-filling triangulation in ${\mathbb {R}}^{d}$. These conjectures are motivated by the extraordinary lower and upper bounds on the dihedral angles of simplices in Coxeter triangulations; they are precisely $45^\circ$, $60^\circ$ or $90^\circ$ for the four families. Moreover the circumcentre of the simplices of ${\tilde{A}}_{d}$ lie very far inside the simplex.

2 Roots, Groups and Lattices: General Background

The Coxeter triangulations we use originate in group theoretical studies of reflections. This section provides a group-theoretical background for and gives a brief introduction to Coxeter triangulations. We follow the lecture notes by Top [31].

We first explain root systems as sets of vectors generated by undirected graphs. To an undirected graph without loops we associate a symmetric matrix. If the matrix is positive definite, it defines a (non-Euclidean) inner product and (non-Euclidean) orthogonal reflections. These orthogonal reflections generate a group and a set of vectors, called a root system. A classification of undirected graphs that generate finite root systems is presented.

We then proceed to study the geometrical properties of root systems in Euclidean space. Ultimately, we state the classification of root systems, which expands on the classification of the undirected graphs presented earlier.

After this, we proceed to define root lattices. Finally, we will give essential definitions and results from Chapter 4 of Humphreys [16] on affine reflection groups and conclude by defining Coxeter triangulations and classifying them.

2.1 Graphs and Cartan Matrices

We consider undirected connected graphs without loops with $d$ nodes $\{ v_1, \ldots , v_{d} \}$. One can associate an incidence matrix $A= (a_{ij})$ to any such graph. This is the symmetric $d\times d$-matrix with $a_{ij}=1$ if there is an edge between $v_i$ and $v_j$ and $a_{ij} = 0$ otherwise.

Definition 2

(Cartan matrix) The Cartan matrix of a graph $\varSigma$ with incidence matrix A is defined by $C = 2I - A$, where I is the identity matrix.

Note that Cartan matrices are symmetric. To each $d\times d$ Cartan matrix C we can associate a symmetric bilinear form $\left\langle \cdot ,\cdot \right\rangle _{C}$ on ${\mathbb {R}}^{d}$ defined by $\left\langle u,v \right\rangle _{C}= u^t Cv$, with $u,v \in {\mathbb {R}}^d$ and where $u^t$ denotes the transposition of u.

We are now interested in identifying the graphs for which the symmetric bilinear form is positive definite and therefore defines an inner product. Each such $d\times d$ Cartan matrix gives us $d$ linear maps $\sigma _i$, one for each vector $e_i$ of the canonical basis, defined by:

$$\begin{aligned}&\sigma _i : {\mathbb {R}}^{d} \rightarrow {\mathbb {R}}^{d}\\&\quad x \mapsto x - \left\langle x,e_i \right\rangle _{C} e_i = x - (x^t C e_i ) e_i . \end{aligned}$$

If the bilinear form $\left\langle \cdot ,\cdot \right\rangle _{C}$ is positive definite, the linear map $\sigma _i$ is the orthogonal reflection through the hyperplane, which is orthogonal to $e_i$ with respect to the inner product determined by C.

Definition 3

(Weyl group) The Weyl group $W_\varSigma$ of a graph $\varSigma$ is the group of invertible linear maps generated by all $\sigma _i$. The roots of $\varSigma$ are the vectors in the set $R_\varSigma = \{ \sigma (e_i)\mid 1 \le i \le d, \sigma \in W_\varSigma \}$.

We now have the following:

Theorem 1

[16, Section 1.3] For a graph $\varSigma$ with Cartan matrix C, Weyl group $W_\varSigma$ and root set $R_\varSigma$, the following three statements are equivalent:

• $\left\langle \cdot ,\cdot \right\rangle _{C}$ is positive definite, that is it defines an inner product.

• The root set $R_\varSigma$ is finite.

• The Weyl group $W_\varSigma$ is finite.

Section 1.8 of [16] also gives us the following proposition:

Proposition 1

For any graph $\varSigma$ with a positive definite inner product, the action of elements of Weyl group $W_\varSigma$ is simply transitive on the root set $R_\varSigma$.

The connected graphs $\varSigma$ that give a positive definite form $\left\langle \cdot ,\cdot \right\rangle _{C}$ have been classified to be the following (see Section 2.4 of [16]):

These graphs are called the Coxeter diagrams of type $A_{d}$, $D_{d}$, $E_6$, $E_7$ and $E_8$. The definition of Coxeter diagrams will be given in Definition 8.

2.2 Root Systems in Euclidean Space

We now want to make the Weyl groups as concrete as possible. To do this, we need to find vectors $r_1, \ldots r_{d} \in {\mathbb {R}}^m$, for $m \ge d$, and ${\mathbb {R}}^m$ endowed with the standard inner product $\left\langle \cdot ,\cdot \right\rangle$, such that $\left\langle r_i,r_j \right\rangle = c_{ij}$. These vectors are linearly independent because the Cartan matrix C is invertible. In general, such a matrix with scalar products as coefficients is called a Gram matrix.

Proposition 2

Let $C = (c_{ij})$ be a positive definite Cartan matrix. There exist vectors $r_1,\ldots ,r_d \in {\mathbb {R}}^{d}$, such that $\left\langle r_i,r_j \right\rangle = c_{ij}$.

Remark 1

This choice is not unique. However, in the context of root systems, nicer roots can be chosen, if we allow the roots to lie in ${\mathbb {R}}^{m}$ for $m > d$, see Humphreys [16, Section 2.10] for details.

As we have seen in the previous section, a root set R of each of the diagrams $A_{d}$, $D_{d}$, $E_6$, $E_7$ and $E_8$ is stable under the reflections of its roots. These reflections therefore generate a finite Weyl group. We will now construct more of finite Weyl groups based on root systems in Euclidean space in a broader sense than what was discussed before.

Definition and properties We work in ${\mathbb {R}}^{d}$ endowed with the standard inner product $\left\langle \cdot ,\cdot \right\rangle$. For $r \in {\mathbb {R}}^{d}$, with $r\ne 0$, the reflection $\sigma _r$ in the hyperplane $\{v \in {\mathbb {R}}^{d} | \left\langle v,r \right\rangle = 0\}$ is given by $\sigma _r (x) = x -2\frac{ \left\langle x,r \right\rangle }{ \left\langle r,r \right\rangle }r .$

We can now redefine root systems from a completely geometric point of view.

Definition 4

(Root system) A root system in ${\mathbb {R}}^{d}$ is a finite set $R \subset {\mathbb {R}}^{d}$ that satisfies:

• $0 \notin R$ and R contains a basis of ${\mathbb {R}}^{d}$,

• for all $r\in R$, $\sigma _r(R) \subset R$.

A root system is called crystallographic if for all $r,s \in R$, $\sigma _r(s)-s$ is an integer multiple of r. A root system is called reduced if $r \in R$ and $\lambda r\in R$ imply $\lambda = \pm 1$. A root system is called irreducible if there is no decomposition $R = R_1 \cup R_2$ with $R_1 \ne \emptyset \ne R_2$ and $\left\langle r_1,r_2 \right\rangle =0$ for all $r_1 \in R_1$ and $r_2\in R_2$ (that is $R_1$ and $R_2$ are orthogonal to one another).

The crystallographic property of the root systems will be important for the definition of root lattices and affine Weyl groups, so we will focus on root systems that are crystallographic. From this point onward we will assume that every root system under consideration is crystallographic, reduced and irreducible, unless stated otherwise.

Simple roots We will now define simple roots that form a basis of a root system.

Definition 5

Assume that for a root system R we are given an arbitrary $t\in {\mathbb {R}}^{d}$ such that $\left\langle t,r \right\rangle \ne 0$ for all $r \in R$. The root system now decomposes as $R= R_t^{+} \cup R_t^{-}$ into positive roots$R_t^{+} = \{ r \in R \mid \left\langle r,t \right\rangle >0\}$ and negative roots$R_t^{-} = \{ r \in R \mid \left\langle r,t \right\rangle <0\}$. A root $r\in R_t^+$ is called decomposable if $r = r_1 + r_2$, with $r_1, r_2\in R_t^+$, and a root $r\in R_t^+$ is called simple if it is not decomposable. The set of simple roots with respect to t is denoted by $S_t$.

Lemma 1

The action of the Weyl group that corresponds to a root system R on the collection of all sets of simple roots of R is simply transitive.

The proof of the lemma can be found in Section 1.8 of Humphreys [16]. Because all $S_t$ are similar one to another, we will omit the index t.

Lemma 2

Let R be a root system, and S be a set of simple roots in R.

• For any two distinct simple roots $r, s \in S$, we have $\left\langle r,s \right\rangle \le 0$.

• The set S forms a basis of ${\mathbb {R}}^{d}$.

• The Weyl group is generated by the reflections associated to the simple roots in S.

We refer to Sections 1.3 and 1.5 of Humphreys [16] for the proof of the lemma.

Definition 6

(Partial order on positive roots) Because simple roots $S$ form a basis of the root system $R$, any root can be decomposed as a sum of simple roots with integer coefficients. Using the decomposition, the positive roots (see Definition 5) can be characterized as the roots that have non-negative coefficients when expressed in terms of simple roots. For any two positive roots r and $r'$, we can write $r = \sum _{i=1}^{d} c_i s_i$ and $r' = \sum _{i=1}^{d} c'_i s_i$, where $S= \{s_1,\ldots ,s_{d} \}$ and the coefficients $c_i$ and $c'_i$ are integers. This gives a partial order $\preccurlyeq$ on the set of roots $R$, which compares the coefficients of two roots meaning that $r \preccurlyeq r'$ if and only if $c_i \le c'_i$ for all $1 \le i \le d$.

Angle between roots The angle $\phi$, with $0 \le \phi \le \pi$, between two roots r and s is given by $\cos \phi = \frac{ \left\langle r,s \right\rangle }{\Vert r\Vert \Vert s\Vert }$. Note that, due to the crystallographic condition, we have $\sigma _r(s) - s= 2 \frac{ \left\langle r,s \right\rangle }{ \left\langle r,r \right\rangle } r \in {\mathbb {Z}} \cdot r.$

Definition 7

For any two roots $r,s \in R$, we define $n(s,r) := 2 \frac{ \left\langle r,s \right\rangle }{ \left\langle r,r \right\rangle } \in {\mathbb {Z}}$. This integer is called Cartan integer.

It follows that $4 \cos ^2 \phi = n(s,r) n(r,s) \in {\mathbb {Z}}$. In the case $\left\langle r,s \right\rangle \ne 0$, observe that the ratio of the squared norms of these two roots is given by $\frac{\left\langle s,s \right\rangle }{\left\langle r,r \right\rangle } = \frac{2\left\langle r,s \right\rangle }{\left\langle r,r \right\rangle } \frac{\left\langle s,s \right\rangle }{2\left\langle r,s \right\rangle } = \frac{n(s,r)}{n(r,s)}$. This gives us, up to symmetry, the following table:

$4 \cos ^2 \phi$	n(s, r)	n(r, s)	$\varphi$	length relation
4	2	2	0	$\Vert s\Vert = \Vert r\Vert$
4	$-\,2$	$-\,2$	$\pi$	$\Vert s\Vert = \Vert r\Vert$
3	3	1	$\pi /6$	$\Vert s\Vert = \sqrt{3} \Vert r\Vert$
3	$-\,3$	$-\,1$	$5 \pi /6$	$\Vert s\Vert = \sqrt{3} \Vert r\Vert$
2	2	1	$\pi /4$	$\Vert s\Vert = \sqrt{2} \Vert r\Vert$
2	$-\,2$	$-\,1$	$3 \pi /4$	$\Vert s\Vert = \sqrt{2} \Vert r\Vert$
1	1	1	$\pi /3$	$\Vert s\Vert = \Vert r\Vert$
1	$-\,1$	$-\,1$	$2\pi /3$	$\Vert s\Vert = \Vert r\Vert$
0	0	0	$\pi /2$	(undetermined)

By inspection of the table, we observe that the length ratio of any two roots¹ can only be 1, $\sqrt{2}$ or $\sqrt{3}$. It implies that there are at most two different norms of roots. In this case, we speak about short and long roots.

Because $n(r,s) \in \{ -3,-2,-1,0 \}$ and $n(s,r) n(r,s) = 4 \cos ^2 \phi$, the angle $\phi$ between r and s equals one of $\frac{\pi }{2}$, $\frac{2\pi }{3}$, $\frac{3\pi }{4}$ or $\frac{5 \pi }{6}$.

From Lemma 1, we know that all simple root sets are similar one to another, therefore have the same angles. The information about the angles of simple roots can be represented in a graph.

Definition 8

(Coxeter diagram) Let R be a root system and S be a set of simple roots. The Coxeter diagram of R consists of a graph with the following data: for each $r\in S$, we insert one vertex. For every pair $r\ne s$ in S with $\left\langle r,s \right\rangle \ne 0$ we define a number $m(r,s) \in \{2,3,4,6\}$, such that $\frac{\pi }{m(r,s)} = \arccos |\cos \phi |$, where $\phi$ is the angle between r and s. We then insert an edge between r and s and write the number m(r, s) next to it.

We further follow the convention not to draw an edge labelled 2 and not to denote label 3 next to an edge.

Classification of root systems We will now state the complete classification of Coxeter diagrams of crystallographic, reduced and irreducible root systems.

Theorem 2

The complete list of Coxeter diagrams of crystallographic, reduced and irreducible root systems consists of $A_{d}$, $D_{d}$, $E_6$, $E_7$ and $E_8$ and the following diagrams:

In this list, the root system $C_{d}$ is defined as dual to $B_{d}$ (see Definition 10). As dual root systems, they share the same Coxeter diagram and Weyl group (see Sect. 2.3).

See for example Sections 2.4 and 2.7 of Humphreys [16] for a proof and more information on the classification of Coxeter diagrams.

The following theorem gives explicit sets of simple roots in Euclidean space:

Theorem 3

[7] Let $\{e_1,\ldots ,e_{d}\}$ be the canonical basis in ${\mathbb {R}}^{d}$. The complete list of simple root sets (up to scale, rotation and permutation) is the following:

• $\mathbf {A_{d}}$ (in ${\mathbb {R}}^{d+1}$): $s_1 = e_1 - e_2$, $s_2 = e_2 - e_3$, ..., $s_{d} = e_{d} - e_{d+1}$.

• $\mathbf {B_{d}}$: $s_1 = e_1 - e_2$, $s_2 = e_2 - e_3$, ..., $s_{d-1} = e_{d-1} - e_{d}$, $s_{d} = e_{d}$.

• $\mathbf {C_{d}}$: $s_1 = e_1 - e_2$, $s_2 = e_2 - e_3$, ..., $s_{d-1} = e_{d-1} - e_{d}$, $s_{d} = 2e_{d}$.

• $\mathbf {D_{d}}$: $s_1 = e_1 - e_2$, $s_2 = e_2 - e_3$, ..., $s_{d-1} = e_{d-1} - e_{d}$, $s_{d} = e_{d-1} + e_{d}$.

• $\mathbf {E_6}$ (in ${\mathbb {R}}^8$): $s_1 = \frac{1}{2}(e_1 + e_8) - \frac{1}{2}(e_2 + e_3 + e_4 + e_5 + e_6 + e_7)$, $s_2 = e_1 + e_2$, $s_3 = e_2 - e_1$, $s_4 = e_3 - e_2$, $s_5 = e_4 - e_3$, $s_6 = e_5 - e_4$.

• $\mathbf {E_7}$ (in ${\mathbb {R}}^8$): $s_1 = \frac{1}{2}(e_1 + e_8) - \frac{1}{2}(e_2 + e_3 + e_4 + e_5 + e_6 + e_7)$, $s_2 = e_1 + e_2$, $s_3 = e_2 - e_1$, $s_4 = e_3 - e_2$, $s_5 = e_4 - e_3$, $s_6 = e_5 - e_4$, $s_7 = e_6 - e_5$.

• $\mathbf {E_8}$: $s_1 = \frac{1}{2}(e_1 + e_8) - \frac{1}{2}(e_2 + e_3 + e_4 + e_5 + e_6 + e_7)$, $s_2 = e_1 + e_2$, $s_3 = e_2 - e_1$, $s_4 = e_3 - e_2$, $s_5 = e_4 - e_3$, $s_6 = e_5 - e_4$, $s_7 = e_6 - e_5$, $s_8 = e_7 - e_6$.

• $\mathbf {F_4}$: $s_1 = e_2 - e_3$, $s_2 = e_3 - e_4$, $s_3 = e_4$, $s_4 = \frac{1}{2}(e_1 - e_2 - e_3 - e_4)$.

• $\mathbf {G_2}$ (in ${\mathbb {R}}^3$): $s_1 = e_1 - e_2$, $s_2 = -2e_1 + e_2 + e_3$.

This list is essential for the calculations in Sect. 6.

2.3 Root Lattices

We can now define lattices based on the roots we discussed above. These lattices will be essential later in Sect. 2.4.

Definition 9

(Root lattice) The root lattice $\varLambda _{R}$ of a root system $R$ is defined as: $\varLambda _{R} = \left\{ \sum _{r\in R} n_r r \mid n_r \in {\mathbb {Z}} \right\}$.

It is indeed a lattice in the sense that it is a group under addition of vectors, contains a basis of a ${\mathbb {R}}^d$ and any bounded region contains only a finite number of elements.

Definition 10

(Dual root system) For each root $r \in R$, define its coroot (or dual root) to be $r^{\vee } = \frac{2r}{\left\langle r,r \right\rangle }$. The set of coroots forms a root system [16, Section 2.9] called dual root system and is denoted by $R^{\vee }$.

Fig. 1

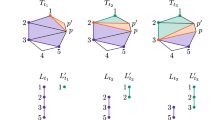
Above: Three root systems and corresponding affine hyperplanes in ${\mathbb {R}}^2$. Simple roots are marked in red, the highest root in blue and the fundamental domain in green. Each triangle in the background is an alcove. Below: The dual root systems put on the same grid of affine hyperplanes (Color figure online)

The duals of the three root systems in ${\mathbb {R}}^2$ are illustrated in Fig. 1.

Remark 2

Using the definition of the coroot, the Cartan integer n(r, s) from Definition 7 can be interpreted as $n(r,s) = 2\frac{\left\langle r,s \right\rangle }{\Vert r\Vert ^2} = \left\langle r^{\vee },s \right\rangle$.

Definition 11

(Coroot lattice) Similarly to root lattices, we define the coroot lattice: $\varLambda _{R^{\vee }} = \left\{ \sum _{r\in R} n_{r} r^{\vee } \mid n_{r} \in {\mathbb {Z}} \right\} .$

Another important family of lattices is so-called weight lattices:

Definition 12

(Weight and coweight lattices) The set of points which has an integer inner product with all coroots is called the weight lattice: $\varLambda ^{w}_{R} = \left\{ x \in {\mathbb {R}}^{d} \ |\ \left\langle x,r^{\vee } \right\rangle \in {\mathbb {Z}},\ \forall r \in R\right\}$. Similarly, the coweight lattice is defined as: $\varLambda ^{w}_{R^{\vee }} = \left\{ x \in {\mathbb {R}}^{d} \ |\ \left\langle x,r \right\rangle \in {\mathbb {Z}}, \forall r \in R\right\} .$

For a given root system, the coweight lattice in Definition 12 has a strong connection with the set of vertices of the Coxeter triangulation that will be defined in the Sect. 2.4 (see also Lemma 14).

2.4 Affine Reflection Groups

The goal for us now is to define a triangulation of the Euclidean space associated to every root system.

First, we need the following definitions:

Definition 13

We call a family of parallel hyperplanes relative to a normal vector $u \in {\mathbb {R}}^{d}$ and indexed by ${\mathbb {Z}}$ a set of hyperplanes ${\mathcal {H}}_{u} = \{H_{u,k},\ k\in {\mathbb {Z}}\}$ with $H_{u,k} = \{ x\in {\mathbb {R}}^{d}\ |\ \left\langle x,u \right\rangle = k\}$.

Definition 14

(Affine Weyl group) Let $R\subset {\mathbb {R}}^{d}$ be a finite root system. The set of affine hyperplanes $H_{r,k}$ for all $r \in R$ and $k \in {\mathbb {Z}}$ will be denoted as ${\mathcal {H}}$. To each $H_{r,k}$ we can associate an affine reflection $\sigma _{r,k}: x \mapsto x - (\left\langle x,r \right\rangle - k) r^{\vee }$. These reflections generate a subgroup of the group of affine transformations of ${\mathbb {R}}^{d}$, which is called the affine Weyl group and is denoted by $W_a$.

Roughly speaking, the affine Weyl group is a combination of the Weyl group and translations along a lattice. This can be made more precise using the coroot lattice $\varLambda _{R^{\vee }}$ defined in Definition 11:

Proposition 3

Let $R$ be a root system, W be a corresponding Weyl group and T be the translation group corresponding to the coroot lattice $\varLambda _{R^{\vee }}$. The group T is a normal subgroup of the affine Weyl group $W_a$ and $W_a$ is a semidirect product $T \rtimes W$.

We refer to Section 4.2 of [16] for more information.

The positions of hyperplanes $H_{r,k}$ with respect to primal and dual root systems in ${\mathbb {R}}^2$ are illustrated in Fig. 1. We notice that the open regions in between the hyperplanes $H_{r,k}$ are similar triangles. These regions are called alcoves and are the subject of our study in the following. We now formalize:

Definition 15

(Alcove) Define ${\mathcal {A}}$ to be the set of connected components of ${\mathbb {R}}^{d} {\setminus } \bigcup _{H \in {\mathcal {H}}} H$. Each element in ${\mathcal {A}}$ is called an alcove.

Let ${R_+}$ be a set of positive roots and $S$ the corresponding simple system. An alcove is characterized by a set of inequalities of the form: $\forall r \in {R_+}, k_r< \left\langle x,r \right\rangle < k_r + 1$, with $k_r$ integers. We will denote by $A^o$ the particular alcove for which all $k_r$ are equal to 0, that is $A^o= \{ x \in {\mathbb {R}}^{d}\ |\ \forall r \in {R_+}, 0< \left\langle x,r \right\rangle < 1 \} .$

Most of the inequalities that define $A^o$ are redundant. If we want to eliminate the redundant inequalities, we first need to define the so called highest root (illustrated in Fig. 1).

Proposition 4

(Existence and uniqueness of the highest root) For a root system $R$ and a simple root set $S\subset R$, there is maximum ${\tilde{s}} \in R^+$ for the partial order $\preccurlyeq$ (see Definition 6), which is called the highest root.

For the proof of Proposition 4 and more details on the highest root, we refer to Section 2.9 of Humphreys [16].

The following proposition states that there are exactly $d+1$ hyperplanes that define the facets of $A^o$: $d$ hyperplanes corresponding to simple roots and one corresponding to the highest root (see also Fig. 1):

Proposition 5

[16, Section 4.3] Let $R$ be a root system and $S\subset R$ a set of simple roots. The alcove $A^o$ is an open simplex delimited by $d+1$ hyperplanes. Of them, $d$ hyperplanes are of the form $H_{s,0} = \{ x \in {\mathbb {R}}^{d}\ |\ \left\langle x,s \right\rangle = 0 \}$, one for each simple root $s \in S$ and the final hyperplane is $H_{{\tilde{s}},1} = \{ x \in {\mathbb {R}}^{d}\ |\ \left\langle x,{\tilde{s}} \right\rangle = 1 \}$ where ${\tilde{s}}$ is the highest root.

Now, we are interested in the closure of the alcove $A^o$, which is a full-dimensional simplex. This simplex will be the starting point of the triangulations we will now construct.

Definition 16

Let $R$ be a root system and $S\subset R$ a set of simple roots. Let $A^o$ be the alcove as above. The closure F of $A^o$ is called the fundamental domain (or the fundamental simplex) of $R$ with respect to $S$.

The reason behind the name fundamental domain is the following proposition.

Proposition 6

[16, Section 4.3] The affine Weyl group $W_a$ acts simply transitively on ${\mathcal {A}}$.

By the simple transitivity of the action of $W_a$, all alcoves are similar to the fundamental alcove. This means that the closures of elements of ${\mathcal {A}}$ are all full-dimensional simplices in a monohedral triangulation of ${\mathbb {R}}^{d}$.

Corollary 1

The arrangement of ${\mathcal {H}}$ is a triangulation of ${\mathbb {R}}^{d}$.

We call such triangulations Coxeter triangulations.

Definition 17

The Coxeter diagrams for affine Weyl groups are defined in the same way as in Definition 8, except that we use not only the simple roots, but also the opposite of the highest root. This means that the nodes correspond to simple roots and the opposite of the highest root, and the edges correspond to angles between them.

The affine Weyl groups have also been classified:

Theorem 4

The complete list of affine Weyl groups and the corresponding Coxeter diagrams is as follows:

Fig. 2

On the top: Coxeter triangulations in ${\mathbb {R}}^2$. On the bottom: simplices of Coxeter triangulations in ${\mathbb {R}}^3$ represented as a portion of a cube

For a proof, we refer to Sections 2.5 and 2.7 of [16].

Fig. 3

Example of a monohedral triangulation of ${\mathbb {R}}^2$ generated by orthogonal reflections that is not a Coxeter triangulation

All three two-dimensional Coxeter triangulations are presented on the top of Fig. 2. On the bottom of Fig. 2, we illustrate the simplices of the three-dimensional Coxeter triangulations with vertices placed in vertices, centres of edges, centres of faces and at the centre of a cube.

We now have a classification of Coxeter triangulations, whose properties and applications are the topic of this paper.

Remark 3

From the classification it follows that the only possible dihedral angles in full-dimensional simplices in Coxeter triangulations are $\frac{\pi }{2}$, $\frac{\pi }{3}$, $\frac{\pi }{4}$ and $\frac{\pi }{6}$.

Table 1 Vertices of a simplex per Coxeter diagram type

Remark 4

If we would drop the condition that Coxeter triangulations are hyperplane arrangements, we would fine more triangulations, see Fig. 3.

The vertices of simplices in Coxeter triangulations up to similarity transformations are given in Table 1.

3 Quality Definitions

The quality measures we are interested in are aspect ratio, fatness, thickness and radius ratio. Their formal definitions are as follows:

Definition 18

Let $h(\sigma )$ denote the minimal height, $r(\sigma )$ the inradius, $R(\sigma )$ the circumradius, $vol(\sigma )$ the volume and $L(\sigma )$ the maximal edge length of a given $d$-simplex $\sigma$.

• The aspect ratio of $\sigma$ is the ratio of its minimal height to the diameter of its circumscribed ball: $\alpha (\sigma ) = \frac{h(\sigma )}{2R(\sigma )}$.

• The fatness of $\sigma$ is the ratio of its volume to its maximal edge length taken to the power $d$: $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^{d}}$.

• The thickness of $\sigma$ is the ratio of its minimal height to its maximal edge length: $\theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )}$.

• The radius ratio of $\sigma$ is the ratio of its inradius to its circumradius: $\rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )}$.

To be able to compare the presented quality measures between themselves, we will normalize them by their respective maximum value. As we show in Theorem 5, all of these quality measures are maximized by regular simplices.

Theorem 5

Out of all $d$-dimensional simplices, the regular $d$-simplex has the highest aspect ratio, fatness, thickness and radius ratio.

We prove Theorem 5 in Appendix A. For a quality measure $\kappa$ we will define the normalized quality measure ${\hat{\kappa }}$, such that for each $d$-simplex $\sigma$, ${\hat{\kappa }}(\sigma ) = \frac{\kappa (\sigma )}{\kappa (\varDelta )}$, where $\varDelta$ is the regular $d$-simplex. Theorem 5 ensure that the quality measures ${\hat{\rho }}$, ${\hat{\alpha }}$, ${\hat{\theta }}$ and ${\hat{\varTheta }}$ take their values in [0, 1] surjectively. Theorem 5 also justifies the emphasis on ${\tilde{A}}_d$ in the literature.

Because some of the triangulations that interest us here are Delaunay, we will also look at their protection values.

Definition 19

Let $\mathrm {vert}(\sigma )$ denote the set of vertices of a simplex $\sigma$. The protection of a $d$-simplex $\sigma$ in a Delaunay triangulation on a point set P is the minimal distance of points in $P {\setminus } \mathrm {vert}(\sigma )$ to the circumscribed ball of $\sigma$:

$$\begin{aligned} \delta (\sigma ) = \inf _{p \in P{\setminus }\mathrm {vert}(\sigma )} d(p, B(\sigma )) \text {, where }B(\sigma )\text { is the circumscribed ball of } \sigma . \end{aligned}$$

The protection$\delta$ of a Delaunay triangulation ${\mathcal {T}}$ is the infimum over the $d$-simplices of the triangulation: $\delta = \inf _{\sigma \in {\mathcal {T}}} \delta (\sigma )$. A triangulation with a positive protection is called protected. We define the relative protection${\hat{\delta }}(\sigma )$ of a given $d$-simplex $\sigma$ to be the ratio of the protection to its circumscribed radius: ${\hat{\delta }}(\sigma ) = \frac{\delta (\sigma )}{R(\sigma )}$. The relative protection${\hat{\delta }}$ of a Delaunay triangulation ${\mathcal {T}}$ is the infimum over the $d$-simplices of the triangulation: ${\hat{\delta }} = \inf _{\sigma \in {\mathcal {T}}} {\hat{\delta }}(\sigma )$.

4 Delaunay Criterion for Coxeter Triangulations

The goal of this section is to establish a criterion that tells if a given monohedral triangulation of ${\mathbb {R}}^d$ is Delaunay. Here, by monohedral triangulation, we mean that all its $d$-simplices are congruent. We would like to stress that the triangulations in this section are infinite and don’t have boundary. Most of the results in this section are not applicable to triangulations with a finite number of vertices.

This section deals with general monohedral triangulations of ${\mathbb {R}}^d$; the criterion for the particular case of Coxeter triangulations is presented in Theorem 7 at the end of the section.

Definition 20

A simplex is called self-centred if it contains its circumcentre inside or on the boundary.

From Rajan [26] we know that:

Lemma 3

[26, Theorem 5] If a triangulation of ${\mathbb {R}}^{d}$ consists of only self-centred simplices, then it is a Delaunay triangulation.

For any monohedral triangulation of ${\mathbb {R}}^d$, it is sufficient to check if one simplex in the triangulation is self-centred to conclude that the triangulation is Delaunay.

Corollary 2

If a simplex in a monohedral triangulation of ${\mathbb {R}}^d$ is self-centred, then this triangulation is Delaunay.

We now want to consider the converse:

Lemma 4

Let R be the maximum circumradius in a Delaunay triangulation ${\mathcal {D}}$ of ${\mathbb {R}}^{d}$. Then any simplex in ${\mathcal {D}}$ with circumradius R is self-centred.

The proof of Lemma 4 can be found in Appendix B. We would like to emphasize that Lemma 4 does not generalize to the standard definition of Delaunay triangulation on a finite set of points.

In monohedral triangulations, all simplices have the same circumradius. So trivially, all simplices have the maximum circumradius in the triangulation. This observation along with Lemma 4 leads us to conclude that if a simplex in a monohedral triangulation of ${\mathbb {R}}^d$ is not self-centred, then the triangulation is not Delaunay. Combining this with Corollary 2 yields:

Theorem 6

A monohedral triangulation of ${\mathbb {R}}^d$ is Delaunay if and only if its simplices are self-centred.

In the spirit of Theorem 6, we can easily spot if a Delaunay triangulation of ${\mathbb {R}}^d$ is not protected with the help of the following lemma:

Lemma 5

A Delaunay triangulation of ${\mathbb {R}}^d$ where a simplex with the maximal circumradius contains its circumcentre on the boundary is not protected.

We prove this lemma in Appendix B.

We can state the converse of Lemma 5 for monohedral triangulations of ${\mathbb {R}}^d$. For this, we slightly modify Lemma 8 and Theorem 5 in [26] by replacing all non-strict inequalities to strict inequalities to get a criterion for a non-zero protection:

Lemma 6

If a simplex of a monohedral triangulation of ${\mathbb {R}}^d$ contains the circumcentre strictly inside, then the triangulation is Delaunay with a non-zero protection.

By using the fact that Coxeter triangulations are monohedral, we derive from Theorem 6, Lemma 5 and Lemma 6 the following theorem:

Theorem 7

Let ${\mathcal {T}}$ be a Coxeter triangulation.

• If a simplex in ${\mathcal {T}}$ is not self-centred, then ${\mathcal {T}}$ is not Delaunay.

• If a simplex in ${\mathcal {T}}$ contains its circumcentre on the boundary, then ${\mathcal {T}}$ is Delaunay with zero protection.

• If a simplex in ${\mathcal {T}}$ contains its circumcentre strictly inside, then ${\mathcal {T}}$ is Delaunay with non-zero protection.

5 Main Result

In this section we present a table that summarizes explicit expressions of quality measures of Coxeter triangulations. Many of the provably good mesh generation algorithms are based on Delaunay triangulations [10]. This motivated us to investigate if Coxeter triangulations have the Delaunay property. We thus identify which Coxeter triangulations are Delaunay and give their protection values. Finally, we identify which Coxeter triangulations have vertex sets with lattice structure.

Table 2 Summary of quality measures of Coxeter triangulations

Theorem 8

The normalized fatness, aspect ratio, thickness and radius ratio of simplices in Coxeter triangulations, as well as Delaunay property are presented in Table 2. Out of them, only ${\tilde{A}}_{}$ and ${\tilde{C}}_{}$ family triangulations and ${\tilde{F}}_{4}$ and ${\tilde{G}}_{2}$ triangulations are Delaunay. Only ${\tilde{A}}_{}$ family triangulations have a non-zero relative protection value equal to:

$$\begin{aligned} {\hat{\delta }} = \frac{\sqrt{d^2+2d+24}-\sqrt{d^2+2d}}{\sqrt{d^2+2d}} \sim \frac{12}{d^2} \end{aligned}$$

Only ${\tilde{A}}_{}$ family, ${\tilde{C}}_{}$ family and ${\tilde{D}}_{4}$ triangulations have vertex sets with lattice structure.

The proof of this theorem and the table without normalization can be found in Sect. 6, except for the relative protection value for the ${\tilde{A}}_{}$ family triangulations, which is found in “Appendix C”.

The corresponding quality measures for the regular $d$-simplex $\varDelta$ (which does not correspond to a monohedral triangulation of ${\mathbb {R}}^d$ in general) are:

	Fatness $\varTheta$	Aspect Ratio $\alpha$	Thickness $\theta$	Radius Ratio $\rho$
$\varDelta$	$\frac{1}{d!}\sqrt{\frac{d+1}{2^d}}$	$\frac{d+1}{2d}$	$\sqrt{\frac{d+1}{2d}}$	$\frac{1}{d}$

All simplex quality measures in the table above are normalized with respect to the regular simplex. Note that the fatness values in the table are given powered $1/d$. This is due to the fact that fatness is a volume-based simplex quality.

Also note that all normalized simplex qualities for the families ${\tilde{A}}_{d}$, ${\tilde{B}}_{d}$, ${\tilde{C}}_{d}$ and ${\tilde{D}}_{d}$ behave as $O\big (\frac{1}{\sqrt{d}}\big )$.

The numerical values of these quality measures are given in Tables 3, 4, 5 and 6. A quick glance suffices to see that Coxeter triangulations of type ${\tilde{A}}_{d}$ achieve the greatest aspect ratio, fatness, thickness and radius ratio among the Coxeter triangulations in each dimension $d$.

Table 3 The normalized aspect ratio ${\hat{\alpha }}$ value for Coxeter triangulations

Table 4 The normalized radius ratio ${\hat{\rho }}$ value for Coxeter triangulations

Table 5 The normalized fatness ${\hat{\varTheta }}^{1/d}$ value for Coxeter triangulations

Table 6 The normalized thickness ${\hat{\theta }}$ value for Coxeter triangulations

6 Geometrical Analysis of Each Family of Coxeter Triangulations

In this section, we present the proof of Theorem 8. The proof consists of a case study for each individual family of Coxeter triangulations. All cases are independent one from another. We provide explicit measures, so that any reader interested in a quality measure that is not covered by the current study can compute its value for Coxeter triangulations. This can be useful for a comparison of Coxeter triangulations with any other triangulation based on any custom quality measure.

The study for each case starts by presenting two Coxeter diagrams. Each vertex in the Coxeter diagram on the left has a label. These labels are numbers proportional to the inverse heights of the fundamental simplex in the Coxeter triangulation (recall from Proposition 5 that the fundamental simplex is defined by hyperplanes that are orthogonal to simple roots and the highest root). This information is taken from [14]. The Coxeter diagram on the right indicates the notations of the corresponding facets in the proofs.

Each case follows the same plan:

• 1. Let $\sigma$ be the fundamental simplex in the Coxeter triangulation generated by the root system with simple roots from Theorem 3. We give equations of the hyperplanes that contain the facets $\tau _i$ of the simplex $\sigma$. The equations of the hyperplanes can be found in [7] or [12], or alternatively can be deduced from Theorem 3.

• 2. We give the coordinates of the vertices $u_i$ of the simplex $\sigma$. The vertices for each of the families of Coxeter triangulations are summarized in Table 1.

• 3. By using the augmented Coxeter diagram we find which height is the shortest (denoted by $h(\sigma )$). We then compute it as the distance from the corresponding vertex to the corresponding hyperplane.

• 4. We find the circumradius $R(\sigma )$ and the inradius $r(\sigma )$ of the simplex.

• 5. We find the length of the longest edge $L(\sigma )$, using the coordinates of the vertices found previously.

• 6. We compute the (non-normalized) thickness $\theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )}$, the aspect ratio $\alpha (\sigma ) = \frac{h(\sigma )}{2R(\sigma )}$ and the radius ratio $\rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )}$.

• 7. We compute the volume $vol(\sigma )$ and the (non-normalized) fatness $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^{d}}$.

• 8. We determine if the triangulation is Delaunay with the help of Theorem 7. If it is, we also determine if its protection is non-zero. The computation of the protection value of Coxeter triangulations of ${\tilde{A}}_{}$ family is done separately in Appendix C.

• 9. We determine if the vertex set of the triangulation form a lattice.

We will adopt the following writing convention: the powers in point coordinates correspond to duplications of the same coordinate. For example: $(0,1^{\{3\}},0)$ is the same as (0, 1, 1, 1, 0). The proofs of the lemmas and propositions in this section can be found in “Appendix D”.

${\tilde{\mathbf {A}}}_{\mathbf {d}}, \mathbf {d\geqslant 2}$

• 1. The hyperplanes that contain the facets of the fundamental simplex $\sigma$ in ${\mathbb {R}}^{d+1}$ can be defined as the intersection of the hyperplane $\sum _{i=0}^{d} x_i = 0$ and the following hyperplanes: for $\tau _0$: $\ -x_0 + x_{d} = 1$, and for $\tau _k$: $x_k - x_{k-1} = 0$ with $k \in \left\{ 1,\ldots ,d \right\}$.

• 2. From the equations of hyperplanes it is easy to check that the following points in ${\mathbb {R}}^{d+1}$: $u_0 = \left( 0^{\{d+1\}}\right)$ and $u_k = \left( (-\frac{d+1-k}{d+1})^{\{k\}}, (\frac{k}{d+1})^{\{d+1-k\}}\right)$, $\forall k \in \left\{ 1,\ldots ,d \right\}$ are the vertices of $\sigma$.

• 3. According to Fig. 4 left, all heights are equal. By computing, for example, the distance from $u_0$ to the hyperplane $-x_0 + x_{d} = 1$ we find that $h(\sigma ) = \frac{1}{\sqrt{2}}$.

• 4. The barycentre $c = \left( -\frac{d}{2(d+1)}, -\frac{d-2}{2(d+1)}, -\frac{d-4}{2(d+1)}, \ldots , \frac{d}{2(d+1)}\right)$ is the circumcentre and the incentre, which is easily verifiable. The circumradius is $R(\sigma ) =\sqrt{\frac{d(d+2)}{12(d+1)}}$ and the inradius is $r(\sigma ) =\frac{1}{\sqrt{2}(d+1)}$.

• 5. The edges of $\sigma$ are described by differences $u_k - u_j$, for certain $j,k \in \left\{ 0,\ldots ,d \right\}$ with $j<k$. The squared norm of such a difference is equal to $\Vert \mathbf {u}_k - \mathbf {u}_j \Vert ^2 = \frac{(k-j)(d+1-k+j)}{d+1}$. An easy analysis (substitute $k-j$ as a new variable) yields that this function on k and j is maximal when $k-j = (d+1)/2$. So the maximal edge in $\sigma$ has length $L(\sigma ) = \left\{ \begin{array}{ll} \frac{\sqrt{d+1}}{2} &{} \text { if }d\text { is odd,} \\ \frac{1}{2}\sqrt{\frac{d(d+2)}{(d+1)}} &{} \text { if }d\text { is even.} \end{array} \right.$

• 6. The aspect ratio, the thickness and the radius ratio are:

  $$\begin{aligned} \alpha (\sigma )&= \frac{h(\sigma )}{R(\sigma )} = \sqrt{\frac{3(d+1)}{2d(d+2)}} \\ \theta (\sigma )&= \frac{h(\sigma )}{L(\sigma )} = \left\{ \begin{array}{ll} \sqrt{\frac{2}{d}} &{}{} \quad \text{ if }\quad d \text{ is } \text{ odd, } \\ \sqrt{\frac{2(d+1)}{d(d+2)}} &{}{} \quad \text{ if }\quad d \text{ is } \text{ even. } \end{array}\right. \\ \rho (\sigma )&= \frac{r(\sigma )}{R(\sigma )}=\sqrt{\frac{6}{d(d+1)(d+2)}}. \end{aligned}$$

• 7. Lemma 7

  Simplices in the${\tilde{A}}_{d}$triangulation have fatness:

  $$\begin{aligned} \varTheta (\sigma ) = \left\{ \begin{array}{ll} \frac{2^{d}}{\left( \sqrt{d+1}\right) ^{d+1}d!} &{} \quad \text {if}\quad d\text { is odd,} \\ \frac{2^{d}(\sqrt{d+1})^{d-1}}{\left( \sqrt{d(d+2)}\right) ^{d}d!} &{}\quad \text {if}\quad d\text { is even.} \end{array}\right. \end{aligned}$$

  The lemma above relies on the that the fundamental simplex $\sigma$ has volume $vol(\sigma ) = \frac{1}{\sqrt{d+1}\ d!}.$

• 8. Because the circumcentre coincides with the incentre, it lies strictly inside the simplex. So by Theorem 7 the triangulation is Delaunay with non-zero protection. The exact value of protection is shown in Appendix C.

• 9. Proposition 7

  The vertex set of a${\tilde{A}}_{d}$triangulation is a lattice for all$d\ge 2$.

${\tilde{\mathbf {B}}}_{\mathbf {d}}, \mathbf {d\geqslant 3}$

• 1. The hyperplanes that contain facets of the fundamental simplex $\sigma$ can be defined as follows. For $\tau _0$: $x_1 + x_2 = 1$, for $\tau _k$: $x_k - x_{k+1} = 0, \forall k \in \left\{ 1,\ldots ,d-1 \right\}$, and for $\tau _{d}$: $x_{d} = 0$.

• 2. From the equations of hyperplanes it is easy to check that the following points:

  $$\begin{aligned} u_0 = \left( 0^{\{d\}}\right) u_1 = \left( 1, 0^{\{d-1\}} \right) \qquad u_k = \left( \frac{1}{2}^{\{k\}}, 0^{\{d-k\}} \right) , \forall k \in \left\{ 2,\ldots ,d \right\} . \end{aligned}$$

  are the vertices of $\sigma$.

• 3. According to Fig. 5, the minimal height falls on any $\tau _k$ for k in $\left\{ 2,\ldots ,d-1 \right\}$. By computing, for example, the distance from $u_1$ to the hyperplane $x_1 - x_2 = 0$ we get $h(\sigma ) = \frac{1}{2\sqrt{2}}.$

• 4. The circumcentre of the simplex is $(\frac{1}{2}, 0, \frac{1}{4}^{\{d-2\}})$ and the circumradius is $R(\sigma ) =\frac{\sqrt{d+2}}{4}$, which is easily verifiable. The incentre is:

  $$\begin{aligned} \left( \frac{1+(d-1)\sqrt{2}}{2(1+(d-1)\sqrt{2})}, \frac{1+(d-2)\sqrt{2}}{2(1+(d-1)\sqrt{2})}, \ldots , \frac{1}{2(1+(d-1)\sqrt{2})} \right) \end{aligned}$$

  and the inradius is $r(\sigma ) =\frac{1}{2(1+(d-1)\sqrt{2})}$, which is easily verifiable.

• 5. The longest edge is given by $\mathbf {u}_{d} - \mathbf {u}_0$ and is equal to $L(\sigma ) = \frac{\sqrt{d}}{2}$.

• 6. The aspect ratio is: $\alpha (\sigma ) = \frac{h(\sigma )}{R(\sigma )} = \frac{1}{\sqrt{2(d+2)}}.$ The thickness is: $\theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} = \frac{1}{\sqrt{2d}}.$ The radius ratio is: $\rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )} = \frac{2}{\sqrt{d+2}(1+(d-1)\sqrt{2})}.$

• 7. The volume of the simplex is given by the formula:

  $$\begin{aligned} vol(\sigma ) = \frac{1}{d!} \det \left( \begin{array}{cccc} 1 &{}\quad 1/2 &{}\quad \dots &{}\quad 1/2 \\ 0 &{}\quad 1/2 &{}\quad &{}\quad 1/2 \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad 1/2 \\ \end{array} \right) = \frac{1}{2^{d-1}d!}. \end{aligned}$$

  The fatness of the simplex is $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^{d}} = \frac{2}{d^{d/2}d!}.$

• 8. Observe that the inner products of the normal vector $s_2$ to the hyperplane that contains $\tau _2$ with the circumcentre and $u_2$ have different signs, namely $\left\langle s_2,c \right\rangle = -\frac{1}{4}$, and $\left\langle s_2,u_2 \right\rangle = \frac{1}{2}.$ Therefore the hyperplane that contains $\tau _2$ separates the circumcentre c from $u_2$, so by Theorem 7 the triangulation is not Delaunay.

• 9. Proposition 8

  No vertex set of a ${\tilde{B}}_{d}$ triangulation for $d\ge 3$ is a lattice.

${\tilde{\mathbf {C}}}_{\mathbf {{d}}}, \mathbf {d\geqslant 2}$

• 1. The hyperplanes that contain facets of the fundamental simplex $\sigma$ can be defined as follows:

  $$\begin{aligned}&\text {for}\quad \tau _0:\ 2x_1 = 1\quad \text {for}\quad \tau _k:\ x_k - x_{k+1} = 0,\qquad \forall k \in \left\{ 1,\ldots ,d-1 \right\} \\&\text {for}\quad \tau _{d}:\ x_{d} = 0. \end{aligned}$$

• 2. From the equations of hyperplanes it is easy to check that the following points:

  $$\begin{aligned} u_k = \left( \frac{1}{2}^{\{k\}}, 0^{\{d-k\}} \right) , \quad \forall k \in \left\{ 0,\ldots ,d \right\} .\quad \hbox {are the vertices of}~\sigma . \end{aligned}$$

• 3. According to Fig. 6, the minimal height falls on any $\tau _k$ for k in $\left\{ 1,\ldots ,d-1 \right\}$. By computing, for example, the distance from $u_1$ to the hyperplane $x_1 - x_2 = 0$ we get $h(\sigma ) = \frac{1}{2\sqrt{2}}.$

• 4. The circumcentre of the simplex is $(\frac{1}{4}^{\{d\}})$ and the circumradius is $R(\sigma ) =\frac{\sqrt{d}}{4}$, which is easily verifiable. The incentre is:

  $$\begin{aligned} \left( \frac{1+(d-1)\sqrt{2}}{2(2+(d-1)\sqrt{2})}, \frac{1+(d-2)\sqrt{2}}{2(2+(d-1)\sqrt{2})}, \ldots , \frac{1}{2(2+(d-1)\sqrt{2})} \right) \end{aligned}$$

  and the inradius is $r(\sigma ) =\frac{1}{2(2+(d-1)\sqrt{2})}$, which is easily verifiable.

• 5. The longest edge is given by $\mathbf {u}_{d} - \mathbf {u}_0$ and is equal to $L(\sigma ) = \frac{\sqrt{d}}{2}$.

• 6. The aspect ratio is $\alpha (\sigma ) = \frac{h(\sigma )}{R(\sigma )} = \frac{1}{\sqrt{2d}}.$ The thickness is $\theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} = \frac{1}{\sqrt{2d}}.$ The radius ratio is $\rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )} = \frac{2}{\sqrt{d}(2+(d-1)\sqrt{2})}.$

• 7. The volume of the simplex is given by the formula:

  $$\begin{aligned} vol(\sigma ) = \frac{1}{d!} \det \left( \begin{array}{cccc} 1/2 &{}\quad 1/2 &{}\quad \dots &{}\quad 1/2 \\ 0 &{}\quad 1/2 &{}\quad &{}\quad 1/2 \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad 1/2 \\ \end{array} \right) = \frac{1}{2^{d}d!}. \end{aligned}$$

  The fatness of the simplex is $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^{d}} = \frac{1}{d^{d/2}d!}.$

• 8. Observe that all inner products of the normals $s_i$ to hyperplanes that contain $\tau _i$ and the corresponding opposite vertices $u_i$ are positive. Observe as well that the inner products with the circumcentre $\left\langle s_i,c \right\rangle$ are either positive or zero. It implies that the circumcentre lies on the boundary of the simplex, therefore by Theorem 7 the triangulation is non-protected Delaunay.

• 9. Proposition 9

  The vertex set of a${\tilde{C}}_{d}$triangulation is a lattice for$d\ge 2$.

${\tilde{\mathbf {D}}}_{\mathbf {{d}}}, \mathbf { d\geqslant 4}$

• 1. The hyperplanes that contain facets of the fundamental simplex $\sigma$ can be defined as follows:

  $$\begin{aligned}&\text {for}\quad \tau _0:\ x_1 + x_2 = 1 \quad \text {for}\quad \tau _k:\ x_k - x_{k+1} = 0,\quad \forall k \in \left\{ 1,\ldots ,d-1 \right\} \\&\text {for }\tau _{d}:\ x_{d-1} + x_{d} = 0. \end{aligned}$$

• 2. From the equations of hyperplanes it is easy to check that the following points: $u_0 = \left( 0^{\{d\}} \right) ,\,\, u_{1} = \left( 1, 0^{\{d-1\}} \right) ,\,\, u_k = \left( \frac{1}{2}^{\{k\}}, 0^{\{d-k\}} \right) , \forall k \in \left\{ 2,\ldots ,d-2 \right\} , \,\,u_{d-1} = \left( \frac{1}{2}^{\{d-1\}}, -\frac{1}{2} \right) , \,\,u_{d} = \left( \frac{1}{2}^{\{d\}} \right)$ are the vertices of $\sigma$.

• 3. According to Fig. 7, the minimal height falls on any $\tau _k$ for k in $\left\{ 2,\ldots ,d-2 \right\}$. By computing, for example, the distance from $u_2$ to the hyperplane $x_2 - x_3 = 0$ we find $h(\sigma ) = \frac{1}{2\sqrt{2}}$.

• 4. The circumcentre of the simplex is $\left( \frac{1}{2}, 0, \frac{1}{4}^{\{d-4\}}, \frac{1}{2}, 0\right)$ and the circumradius is $R(\sigma ) =\frac{\sqrt{d+4}}{4}$, which is easily verifiable. The incentre is:

  $$\begin{aligned} \left( \frac{1}{2}, \frac{d-2}{2(d-1)}, \frac{d-3}{2(d-1)}, \ldots , \frac{1}{2(d-1)}, 0 \right) \end{aligned}$$

  and the inradius is $r(\sigma ) =\frac{1}{2\sqrt{2}(d-1)}$, which is easily verifiable.

• 5. The longest edge is given by $\mathbf {u}_{d} - \mathbf {u}_0$ and is equal to $L(\sigma ) = \frac{\sqrt{d}}{2}$.

• 6. The aspect ratio is $\alpha (\sigma ) = \frac{h(\sigma )}{R(\sigma )} = \frac{1}{\sqrt{2(d+4)}}.$ The thickness is $\theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} = \frac{1}{\sqrt{2d}}.$ The radius ratio is $\rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )} = \frac{\sqrt{2}}{\sqrt{d+4}(d-1)}.$

• 7. The volume of the simplex is:

  $$\begin{aligned} vol(\sigma )&= \frac{1}{d!} \det \left( \begin{array}{cccccc} 1 &{}\quad 1/2 &{}\quad \dots &{}\quad 1/2 &{}\quad 1/2 &{}\quad 1/2 \\ 0 &{}\quad 1/2 &{}\quad &{}\quad 1/2 &{}\quad 1/2 &{}\quad 1/2 \\ 0 &{}\quad 0 &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad 1/2 &{}\quad 1/2 &{}\quad 1/2 \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 1/2 &{}\quad 1/2 \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad -1/2 &{}\quad 1/2 \\ \end{array} \right) \\&=\frac{1}{2d!} \det \left( \begin{array}{ccccc} 1 &{}\quad 1/2 &{}\quad \dots &{}\quad 1/2 &{}\quad 1/2 \\ 0 &{}\quad 1/2 &{}\quad \dots &{}\quad 1/2 &{}\quad 1/2 \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad 1/2 &{}\quad 1/2 \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 &{}\quad 1/2 \\ \end{array} \right) + \frac{1}{2d!}\det \left( \begin{array}{ccccc} 1 &{}\quad 1/2 &{}\quad \dots &{}\quad 1/2 &{}\quad 1/2 \\ 0 &{}\quad 1/2 &{}\quad \dots &{}\quad 1/2 &{}\quad 1/2 \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad 1/2 &{}\quad 1/2 \\ 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 &{}\quad 1/2 \\ \end{array} \right) = \frac{1}{2^{d-2}d!}. \end{aligned}$$

  The fatness of the simplex is $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^{d}} = \frac{4}{d^{d/2}d!}.$

• 8. Observe that the inner products of the normal vector $s_{d-2}$ to the hyperplane that contains $\tau _{d-2}$ with the circumcentre and $u_{d-2}$ have different signs, that is $\left\langle s_{d-2},c \right\rangle = -\frac{1}{4}$, and $\left\langle s_{d-2},u_{d-2} \right\rangle = \frac{1}{2}.$ Therefore the hyperplane that contains $\tau _{d-2}$ separates the circumcentre from $u_{d-2}$, so by Theorem 7 the triangulation is not Delaunay.

• 9. Proposition 10

  (a) The vertex set of a${\tilde{D}}_{4}$triangulation is a lattice.

  (b) No other vertex set of a${\tilde{D}}_{d}$triangulation for$d\ge 5$is a lattice.

${\tilde{\mathbf {E}}}_{\mathbf {{6}}}$

• 1. The hyperplanes that contain facets of the fundamental simplex $\sigma$ can be defined as follows:

  $$\begin{aligned}&\text {for }\tau _0 : \frac{1}{2}((x_1 + x_2 + x_3 + x_4 + x_5 + x_8) - (x_6 + x_7)) = 1 \\&\text {for }\tau _1 : (x_1 + x_8) - (x_2 + x_3 + x_4 + x_5 + x_6 + x_7) = 0 \\&\text {for }\tau _2 : x_1 + x_2 = 0 \quad \text {for }\tau _3 : x_1 - x_2 = 0 \quad \text {for }\tau _4 : x_2 - x_3 = 0 \\&\text {for }\tau _5 : x_3 - x_4 = 0 \quad \text {for }\tau _6 : x_4 - x_5 = 0 \end{aligned}$$

• 2. The vertices of $\sigma$ are (in ${\mathbb {R}}^8$) [12, Chapter 21]:

  $u_0 = \left( 0^{\{8\}}\right) \quad u_1 = \left( 0^{\{5\}},-\frac{2}{3}^{\{2\}}, \frac{2}{3} \right) \quad u_2 = \left( \frac{1}{4}^{\{5\}},-\frac{1}{4}^{\{2\}}, \frac{1}{4}\right)$

  $$\begin{aligned}&u_3 = \left( -\frac{1}{4}, \frac{1}{4}^{\{4\}},-\frac{5}{12}^{\{2\}}, \frac{5}{12} \right) \quad u_4 = \left( 0^{\{2\}}, \frac{1}{3}^{\{3\}},-\frac{1}{3}^{\{2\}}, \frac{1}{3} \right) \\&u_5 = \left( 0^{\{3\}}, \frac{1}{2}^{\{2\}},-\frac{1}{3}^{\{2\}}, \frac{1}{3} \right) \quad u_6 = \left( 0^{\{4\}}, 1,-\frac{1}{3}^{\{2\}}, \frac{1}{3} \right) \\ \end{aligned}$$

• 3. According to Fig. 8 left, the smallest height falls on $\tau _4$. By computing, the distance from $u_4$ to the hyperplane $x_2 - x_3 = 0$ we find $h(\sigma ) = \frac{\sqrt{2}}{6}.$

• 4. The circumcentre is $(0^{\{2\}}, -\frac{1}{6}^{\{2\}}, \frac{1}{3}, -\frac{1}{3}^{\{2\}}, \frac{1}{3})$ and the circumradius is $R(\sigma ) =\frac{1}{\sqrt{2}}$, which is easily verifiable. The incentre is $(0,\frac{1}{12}, \frac{1}{6}, \frac{1}{4}, \frac{1}{3}, -\frac{1}{3}, -\frac{1}{3}, \frac{1}{3})$ and the inradius is $r(\sigma ) =\frac{1}{12\sqrt{2}}$, which is easily verifiable.

• 5. The longest edge is $L(\sigma ) = \frac{2}{\sqrt{3}}$.

• 6. The aspect ratio, the thickness and the radius ratio are $\alpha (\sigma ) = \frac{h(\sigma )}{R(\sigma )} = \frac{1}{6}$, $\theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} = \frac{1}{2\sqrt{6}}$, and $\rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )} = \frac{1}{12}$.

• 7. The volume of the simplex $\sigma$ is: $vol(\sigma ) = \frac{\sqrt{3}}{51840}$.

  Therefore, the fatness is: $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^6} = \frac{\sqrt{3}}{174960} \sim 9.900 \cdot 10^{-6}$

• 8. Observe that the inner products of the normal vector $n=(0^{\{3\}},1,0^{\{4\}})$ to the hyperplane $x_4 = 0$ with the circumcentre and the vertices have different signs: the inner product $\left\langle n,c \right\rangle = -\frac{1}{6}$ is strictly negative, whereas the inner products $\left\langle n,u_i \right\rangle$ are all non-negative. Therefore the hyperplane $x_4 = 0$ separates the circumcentre from the rest of the simplex, so by Theorem 7 the triangulation is not Delaunay.

• 8. Proposition 11

  The vertex set of a${\tilde{E}}_{6}$triangulation does not form a lattice (Fig. 9).

${\tilde{\mathbf {E}}}_\mathbf {{7}}$

• 1. The hyperplanes that contain facets of the fundamental simplex $\sigma$ can be defined as follows:

  $$\begin{aligned}&\text {for }\tau _0 : x_7 - x_8 = 1 \quad \text {for }\tau _1 : (x_1 + x_8) - (x_2 + x_3 + x_4 + x_5 + x_6 + x_7) = 0 \\&\text {for }\tau _2 : x_1 + x_2 = 0 \quad \text {for }\tau _3 : x_1 - x_2 = 0 \quad \text {for }\tau _4 : x_2 - x_3 = 0 \\&\text {for }\tau _5 : x_3 - x_4 = 0 \quad \text {for }\tau _6 : x_4 - x_5 = 0 \quad \text {for }\tau _7 : x_5 - x_6 = 0 \end{aligned}$$

• 2. The vertices of $\sigma$ are (in ${\mathbb {R}}^8$) [12, Chapter 21]:

  $$\begin{aligned} \begin{array}{ll} u_0 = \left( 0^{\{8\}}\right) &{}\quad u_1 = \left( 0^{\{6\}},\frac{1}{2}, -\frac{1}{2}\right) \\ u_2 = \left( -\frac{1}{4}^{\{6\}}, \frac{1}{2}, -\frac{1}{2} \right) &{}\quad u_3 = \left( \frac{1}{6}, -\frac{1}{6}^{\{5\}}, \frac{1}{2}, -\frac{1}{2} \right) \\ u_4 = \left( 0^{\{2\}}, -\frac{1}{4}^{\{4\}}, \frac{1}{2}, -\frac{1}{2} \right) &{}\quad u_5 = \left( 0^{\{3\}}, -\frac{1}{3}^{\{3\}}, \frac{1}{2}, -\frac{1}{2} \right) \\ u_6 = \left( 0^{\{4\}}, -\frac{1}{2}^{\{2\}}, \frac{1}{2}, -\frac{1}{2} \right) &{}\quad u_7 = \left( 0^{\{5\}}, -1, \frac{1}{2}, -\frac{1}{2} \right) \\ \end{array} \end{aligned}$$

• 3. According to Fig. 4 left, the smallest height falls on $\tau _4$. By computing, the distance from $u_4$ to the hyperplane $x_2 - x_3 = 0$ we get $h(\sigma ) = \frac{\sqrt{2}}{8}.$

• 4. The circumcentre is $(-\frac{1}{8}^{\{2\}}, 0^{\{3\}}, -\frac{1}{2}, \frac{1}{4}, -\frac{1}{4})$, which is easily verifiable. The incentre is $\left( 0,-\frac{1}{18}, -\frac{1}{9}, -\frac{1}{6}, -\frac{2}{9}, -\frac{5}{18}, \frac{17}{36}, -\frac{17}{36}\right)$, which is easily verifiable. The circumradius is $R(\sigma ) =\frac{1}{4}\sqrt{\frac{13}{2}}$ and the inradius is $r(\sigma ) =\frac{1}{18\sqrt{2}}$.

• 5. The longest edge is $L(\sigma ) = \sqrt{\frac{3}{2}}$.

• 6. The aspect ratio, the thickness and the radius ratio are: $\alpha (\sigma ) = \frac{h(\sigma )}{R(\sigma )} = \frac{1}{2\sqrt{13}}$, $\ \theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} = \frac{1}{4\sqrt{3}}$, and $\rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )} = \frac{2}{9\sqrt{13}}$

• 7. The volume of $\sigma$ is: $vol(\sigma ) = \frac{\sqrt{2}}{2903040}$.

  Therefore, the fatness is: $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^7} = \frac{\sqrt{3}}{14696640} \sim 1.179 \cdot 10^{-7}$

• 8. Observe that the inner products of the normal vector $s_4$ to the hyperplane that contains $\tau _4$ with the circumcentre and the vertices have different signs: the inner product $\left\langle s_4,c \right\rangle = -\frac{1}{8}$ is strictly negative, whereas the inner products $\left\langle n,u_i \right\rangle$ are all non-negative. Therefore the hyperplane that contains $\tau _4$ separates the circumcentre from the rest of the simplex, so by Theorem 7 the triangulation is not Delaunay.

• 9. Proposition 12

  The vertex set of a${\tilde{E}}_{7}$triangulation does not form a lattice (Fig. 10).

${\tilde{\mathbf {E}}}_\mathbf {{8}}$

• 1. The hyperplanes that contain facets of the fundamental simplex $\sigma$ can be defined as follows:

  $$\begin{aligned} \begin{array}{ll} &{}\text {for }\tau _0 : x_7 + x_8 = 1 \quad \text {for }\tau _1 : (x_1 + x_8) - (x_2 + x_3 + x_4 + x_5 + x_6 + x_7) = 0\\ &{}\text {for }\tau _2 : x_1 + x_2 = 0 \quad \text {for }\tau _3 : x_1 - x_2 = 0 \quad \text {for }\tau _4 : x_2 - x_3 = 0 \\ &{}\text {for }\tau _5 : x_3 - x_4 = 0 \quad \text {for }\tau _6 : x_4 - x_5 = 0 \quad \text {for }\tau _7 : x_5 - x_6 = 0 \\ &{}\text {for }\tau _8 : x_6 - x_7 = 0 \end{array} \end{aligned}$$

• 2. The vertices of $\sigma$ are [12, Chapter 21]:

  $$\begin{aligned} \begin{array}{lll} u_0 = \left( 0^{\{8\}}\right) &{}\quad u_1 = \left( 0^{\{7\}}, 1 \right) &{}\quad u_2 = \left( \frac{1}{6}^{\{7\}}, \frac{5}{6} \right) \\ u_3 = \left( -\frac{1}{8},\frac{1}{8}^{\{6\}}, \frac{7}{8} \right) &{}\quad u_4 = \left( 0^{\{2\}}, \frac{1}{6}^{\{5\}}, \frac{5}{6} \right) &{}\quad u_5 = \left( 0^{\{3\}}, \frac{1}{5}^{\{4\}}, \frac{4}{5} \right) \\ u_6 = \left( 0^{\{4\}}, \frac{1}{4}^{\{3\}}, \frac{3}{4} \right) &{}\quad u_7 = \left( 0^{\{5\}}, \frac{1}{3}^{\{2\}}, \frac{2}{3} \right) &{}\quad u_8 = \left( 0^{\{6\}},\frac{1}{2}^{\{2\}}\right) \\ \end{array} \end{aligned}$$

• 3. The circumcentre is $(-\frac{1}{12}^2, 0^5, \frac{1}{2})$ and the circumradius is $R(\sigma ) =\frac{\sqrt{38}}{12}$, which is easily verifiable. The incentre is $(0,\frac{1}{30}, \frac{1}{15}, \frac{1}{10}, \frac{2}{15}, \frac{1}{6}, \frac{1}{5}, \frac{23}{30})$ and the inradius is $r(\sigma ) =\frac{1}{30\sqrt{2}}$, which is easily verifiable.

• 4. According to Fig. 4 left, the smallest height falls on $\tau _4$. By computing, the distance from $u_4$ to the hyperplane $x_2 - x_3 = 0$ we find $h(\sigma ) = \frac{\sqrt{2}}{12}.$

• 5. The longest edge is $L(\sigma ) = 1$.

• 6. The aspect ratio, the thickness and the radius ratio are: $\alpha (\sigma ) = \frac{h(\sigma )}{R(\sigma )} = \frac{1}{2\sqrt{19}}$, $\theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} = \frac{1}{6\sqrt{2}}$, and $\rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )} = \frac{1}{5\sqrt{19}}$.

• 7. The volume of $\sigma$ is $vol(\sigma ) = \frac{1}{696729600} \sim 1.435\cdot 10^{-9}$. Therefore the fatness is $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^8} = \frac{1}{696729600} \sim 1.435\cdot 10^{-9}$

• 8. Observe that the inner products of the normal vector $n=(0,1,0^{\{6\}})$ to the hyperplane $x_2 = 0$ with the circumcentre and the vertices have different signs: the inner product $\left\langle n,c \right\rangle = -\frac{1}{12}$ is strictly negative, whereas the inner products $\left\langle n,u_i \right\rangle$ are all non-negative. Therefore the hyperplane $x_2 = 0$ separates the circumcentre from the rest of the simplex, so by Theorem 7 the triangulation is not Delaunay.

• 9. Proposition 13

  The vertex set of a ${\tilde{E}}_{8}$ triangulation does not form a lattice.

${\tilde{\mathbf {F}}}_\mathbf {4}$

• 1. The hyperplanes that contain facets of the fundamental simplex $\sigma$ can be defined as follows:

  $$\begin{aligned} \begin{array}{ll} {\text {for }}\tau _0 : x_1 + x_2 = 1 &{} \text {for }\tau _1 : x_2 - x_3 = 0,\quad \text {for }\tau _2 : x_3 - x_4 = 0, \\ {\text {for }}\tau _3 : x_4 = 0 &{} \text {for }\tau _4 : x_1 - x_2 - x_3 - x_4 = 0 \\ \end{array} \end{aligned}$$

• 2. From the equations of hyperplanes it is easy to check that the following points:

  $$\begin{aligned}&u_0 = \left( 0, 0, 0, 0 \right) \quad u_1 = \left( \frac{1}{2}, \frac{1}{2}, 0, 0 \right) \quad u_2 = \left( \frac{2}{3}, \frac{1}{3}, \frac{1}{3}, 0 \right) \quad u_3 = \left( \frac{3}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4} \right) \\&u_4 = \left( 1, 0, 0, 0 \right) \end{aligned}$$

  are the vertices of $\sigma$.

• 3. The inverse height proportions in Fig. 11 left suggest that the smallest height corresponds to $\tau _2$. By computing, the distance from $u_2$ to the hyperplane $x_3 - x_4 = 0$ we find $h(\sigma ) = \frac{\sqrt{2}}{6}.$

• 4. The circumcentre of the simplex is $(\frac{1}{2}, 0, 0, 0)$ and the circumradius is $R(\sigma ) = \frac{1}{2}$, which is easily verifiable. The incentre is $\left( \frac{6+5\sqrt{2}}{6(2+\sqrt{2})}, \frac{4+\sqrt{2}}{6(2+\sqrt{2})}, \frac{1}{6}, \frac{\sqrt{2}}{6(2+\sqrt{2})} \right)$ and the inradius is $r(\sigma ) =\frac{\sqrt{2}}{6(2+\sqrt{2})}$, which is easily verifiable.

• 5. The longest edge is given by $\mathbf {u}_4 - \mathbf {u}_0$ and is equal to $L(\sigma ) = 1$.

• 6. The aspect ratio, the thickness and the radius ratio are:

  $$\begin{aligned} \alpha (\sigma ) = \frac{h(\sigma )}{R(\sigma )} = \frac{\sqrt{2}}{6} \ \text { and }\ \theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} = \frac{\sqrt{2}}{6}\ \text { and }\ \rho (\sigma ) = \frac{r(\sigma )}{R(\sigma )} = \frac{\sqrt{2}}{3(2+\sqrt{2})} \end{aligned}$$

• 7. The volume of $\sigma$ is: $vol(\sigma ) = \frac{1}{576} = 0.00174$. Therefore the fatness is: $\varTheta (\sigma ) = \frac{vol(\sigma )}{L(\sigma )^4} = \frac{1}{576} \sim 0.00174$

• 8. Observe that all inner products of the normals $s_i$ to hyperplanes that contain $\tau _i$ and the corresponding opposite vertices $u_i$ are positive. Observe as well that the inner products with the circumcentre $\left\langle s_i,c \right\rangle$ are either positive or zero. It implies that the circumcentre lies on the boundary of the simplex, therefore by Theorem 7 the triangulation is non-protected Delaunay.

• 9. Proposition 14

  The vertex set of a ${\tilde{F}}_{4}$ triangulation does not form a lattice.

Simplex of ${\tilde{G}}_{2}$ triangulation (also called Kisrhombille tiling) is the right triangle with $\pi /6$ angle. By straightforward computation, the aspect ratio, thickness and radius ratio are $\alpha (\sigma ) = \theta (\sigma ) = \frac{\sqrt{3}}{4}$, and $\rho (\sigma ) = \frac{1}{1+\sqrt{3}}$. The fatness is $\varTheta (\sigma ) = \frac{\sqrt{3}}{8}$.

The circumcentre of any triangle lies on its hypotenuse, therefore by Theorem 7 the triangulation is non-protected Delaunay.

It is obvious from Fig. 1 that the vertex set of the triangulation does not form a lattice.

Appendices

Appendix A: Proofs of the Optimal Quality of Regular Simplices in Each Dimension

In this section we will prove Theorem 5. The proof will be subdivided into lemmas that prove that each individual quality measure we consider is maximized by the regular simplex.

Radius ratio The first result is by Klamkin for radius ratio [20]:

Lemma 8

[20] Out of all $d$-simplices, the regular $d$-simplex $\varDelta$ has the maximum radius ratio equal to $\rho (\varDelta ) = \frac{1}{d}$.

Aspect ratio We can adapt the proof by Klamkin to show the result for aspect ratio:

Lemma 9

(Maximum aspect ratio) Out of all $d$-simplices, the regular $d$-simplex $\varDelta$ has the maximum aspect ratio equal to $\alpha (\varDelta ) = \frac{d+1}{2d}$.

Proof

Let $\sigma$ be a $d$-simplex. We will now prove that $\alpha (\sigma ) = \frac{h(\sigma )}{2R(\sigma )} \le \frac{d+1}{2d}$.

Let $F_i$ be the $(d-1)$-dimensional volume of the ith facet (see Fig. 12 left). Denote $v_i$ the opposite vertex.

If p is an arbitrary point, we have by Cauchy–Schwarz inequality:

$$\begin{aligned} \sum _{i=0}^{d} F_i \cdot \sum _{i=0}^{d} F_i \overrightarrow{pv_i}^2 \ge \left( \sum _{i=0}^{d} F_i \overrightarrow{pv_i} \right) ^2. \end{aligned}$$

(1)

Note that the equality takes place if and only if p is the circumcentre (making all $\overrightarrow{pv_i}^2$ equal).

Let $F = \sum _{i=0}^{d} F_i$. Let $o \in {\mathbb {R}}^d$ be the circumcentre of $\sigma$ and $q \in {\mathbb {R}}^d$ be such that $\overrightarrow{oq} = \sum _{i=0}^{d} F_i \overrightarrow{ov_i} / F$. Then:

$$\begin{aligned} \sum _{i=0}^{d} F_i \overrightarrow{pv_i}^2= & {} \sum _{i=0}^{d} F_i \left( \overrightarrow{op} - \overrightarrow{ov_i} \right) \left( \overrightarrow{op} - \overrightarrow{ov_i} \right) = F \left( R(\sigma )^2 + \overrightarrow{op}^2 - 2 \overrightarrow{op} \cdot \overrightarrow{oq} \right) . \end{aligned}$$

Since $2 \overrightarrow{op} \cdot \overrightarrow{oq} = \overrightarrow{op}^2 + \overrightarrow{oq}^2 - \left( \overrightarrow{oq} - \overrightarrow{op} \right) ^2 = \overrightarrow{op}^2 + \overrightarrow{oq}^2 - \overrightarrow{pq}^2$, we have:

$$\begin{aligned} \sum _{i=0}^{d} F_i \cdot \sum _{i=0}^{d} F_i \overrightarrow{pv_i} = F^2 \left( R(\sigma )^2 + \overrightarrow{pq}^2 - \overrightarrow{oq}^2 \right) . \end{aligned}$$

(2)

Denote by $h_i$ and $r_i$ the distances from $v_i$ and p respectively to the affine hull of the ith facet. Then $d(p,v_i)$ is greater than $h_i - r_i$ as the hypotenuse is greater than a leg in a right triangle (see Fig. 12). So:

$$\begin{aligned} \sum _{i=0}^{d} F_i\ d(p,v_i) \ge \sum _{i=0}^{d} F_i h_i - \sum _{i=0}^{d} F_i r_i. \end{aligned}$$

Note that if V denotes the volume of the simplex, then for a fixed i we have $F_i h_i = dV$.

On the other hand, for all i, the $d$-simplex formed by p and $F_i$ has a height $r_i$ with respect to $F_i$ (see Fig. 12). It yields that $\sum _{i=0}^{d} F_i r_i = dV$. Therefore:

$$\begin{aligned} \sum _{i=0}^{d} F_i\ d(p,v_i) \ge (d+1)dV - dV = d^2V. \end{aligned}$$

(3)

As before, let $h(\sigma ) = \min _{i} h_i$. Now observe that:

$$\begin{aligned} (d+1)dV = \sum _{i=0}^{d} F_i h_i \ge \sum _{i=0}^{d} F_i h(\sigma ) = F h(\sigma ). \end{aligned}$$

(4)

Hence, if we combine the Eqs. (3) and (4):

$$\begin{aligned} \sum _{i=0}^{d} F_i\ d(p,v_i) \ge \frac{dFh(\sigma )}{d+1}. \end{aligned}$$

(5)

Thus combining (1), (2) and (5), we get:

$$\begin{aligned} F^2 \left( R(\sigma )^2 + \overrightarrow{pq}^2 - \overrightarrow{oq}^2 \right) = \sum _{i=0}^{d} F_i \sum _{i=0}^{d} F_i \overrightarrow{pv_i} \ge \left( \sum _{i=0}^{d} F_i \overrightarrow{pv_i} \right) ^2 \ge \left( \frac{dFh(\sigma )}{d+1} \right) ^2. \end{aligned}$$

Setting p equal to q removes the $\overrightarrow{pq}$ term:

$$\begin{aligned} R(\sigma )^2 \ge \left( \frac{d}{d+1} h(\sigma ) \right) ^2 + \overrightarrow{oq}^2 \ge \left( \frac{d}{d+1} h(\sigma ) \right) ^2, \end{aligned}$$

which gives the inequality that we sought to prove.

By a simple computation, we can further establish that the aspect ratio of the regular simplex is $\frac{d}{d+1}$, and thus we conclude the proof. $\square$

Thickness To prove the result for thickness, we will use Jung’s theorem [19].

Definition 21

The minimal enclosing ball of a bounded subset S of ${\mathbb {R}}^d$ is the Euclidean ball of the smallest radius that contains S.

Theorem 9

(Jung’s theorem) Let $S \subseteq {\mathbb {R}}^d$ be a compact set. Let L(S) be its diameter and $R_{enc}(S)$ be the radius of the minimum enclosing ball. Then, $R_{enc}(S) \le L(S) \sqrt{\frac{d}{2(d+1)}}.$

We can combine Lemma 9 with Jung’s theorem [19] to prove the result for thickness:

Lemma 10

(Maximum thickness) Out of all $d$-simplices, the regular $d$-simplex $\varDelta$ has the maximum thickness equal to $\theta (\varDelta ) = \sqrt{\frac{d+1}{2d}}$.

Proof

Assume that $\sigma$ is a $d$-simplex. We will distinguish two cases: namely $\sigma$ is self-centred or not (as in Definition 20).

Let $\sigma$ be not self-centred. Let $\tau$ be a facet of $\sigma$ that separates $\sigma$ from its circumcentre c. Let p be the vertex of $\sigma$ opposite to $\tau$. Denote by h the height from p to $\tau$ and L be the length of the longest edge e adjacent to p (see Fig. 12 right). By construction, $h \le L/\sqrt{2}$, because the angle of the edge e with $\tau$ is less or equal to $\pi /4$. Therefore,

$\theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} \le \frac{h}{L} \le \frac{1}{\sqrt{2}} \le \sqrt{\frac{d+1}{2d}}.$

From now on we assume that $\sigma$ is self-centred. This implies in particular that the circumradius of $\sigma$ is equal to the radius of the minimal enclosing ball of $\sigma$. So, by combining Lemma 9 and Jung’s theorem we get:

$$\begin{aligned} \theta (\sigma ) = \frac{h(\sigma )}{L(\sigma )} = \frac{h(\sigma )}{2R(\sigma )}\frac{2R(\sigma )}{L(\sigma )} =\frac{h(\sigma )}{2R(\sigma )}\frac{2R_{enc}(\sigma )}{L(\sigma )} \le \frac{d+1}{2d} \cdot 2\sqrt{\frac{d}{2(d+1)}} = \sqrt{\frac{d+1}{2d}}. \end{aligned}$$

Jung’s theorem becomes equality in the case of the regular $d$-simplex [13], so its thickness is $\theta (\varDelta ) = \sqrt{\frac{d+1}{2d}}$.

$\square$

Fatness Finally, we prove the result for fatness.

Lemma 11

(Maximum fatness) Out of all $d$-simplices, the regular $d$-simplex $\varDelta$ has the maximum fatness equal to $\varTheta (\varDelta ) = \frac{1}{d!}\sqrt{\frac{d+1}{2^d}}$.

Proof

Let $\sigma _d$ be a $d$-simplex. We define a sequence of faces $\sigma _1 \subset \cdots \subset \sigma _d$ of $\sigma _d$, such that for each $i \in \{1,\ldots ,d-1\}$, $\sigma _i$ has dimension i and the height falling on $\sigma _i$ is the minimum height in $\sigma _{i+1}$.

We can now express the volume of $\sigma$ in the following manner:

$$\begin{aligned} V(\sigma _d) = \frac{1}{d!}\prod _{i=1}^dh(\sigma _i). \end{aligned}$$

Observe that for each i, the set of edges of $\sigma _d$ is a subset of the set of edges of $\sigma$, therefore we have $L(\sigma _i) \le L(\sigma _d)$. By combining this fact with the volume expression we get:

$$\begin{aligned} \varTheta (\sigma _d) = \frac{V(\sigma _d)}{L(\sigma _d)^d} = \frac{1}{d!} \prod _{i=1}^d\frac{h(\sigma _i)}{L(\sigma _d)} \le \frac{1}{d!} \prod _{i=1}^d\frac{h(\sigma _i)}{L(\sigma _i)} = \frac{1}{d!} \prod _{i=1}^d\theta (\sigma _i). \end{aligned}$$

From Lemma 10, we have for each i, $\theta (\sigma _i) \le \sqrt{\frac{i+1}{2i}}$. Therefore:

$$\begin{aligned} \varTheta (\sigma _d) \le \frac{1}{d!} \prod _{i=1}^d\sqrt{\frac{i+1}{2i}} = \frac{1}{d!} \sqrt{\frac{d+1}{2^d}}. \end{aligned}$$

By a simple computation we can further establish that the fatness of the regular simplex is $\frac{1}{d!} \sqrt{\frac{d+1}{2^d}}$, and thus we conclude the proof. $\square$

Appendix B: Proof of Lemmas 4 and 5

Proof of Lemma 4

Let $\sigma$ be a simplex in ${\mathcal {D}}$ with circumsphere S, whose circumcentre is c and circumradius is R. We assume that the circumcentre c lies outside of $\sigma$ and derive a contradiction. Because the circumcentre lies outside $\sigma$, there exists a facet $\tau$ of $\sigma$ whose supporting hyperplane $H_\tau$ separates c from $\sigma$. We denote by $\sigma '$ the simplex in ${\mathcal {D}}$ that shares the facet $\tau$ with $\sigma$. We write $S'$ for the circumsphere of $\sigma '$ and denote its circumcentre by $c'$ and circumradius by $R'$. The $(d-2)$-dimensional sphere T that forms the intersection of S and $S'$, divides S into a part that lies inside $S'$ and a cap that lies outside $S'$.

We shall call $\ell$ the line on which c and $c'$ lie. If we restrict to any two-dimensional plane P that contains $\ell$, we see that $S \cap P$ and $S' \cap P$ are circles. We shall think of $\ell$ as vertical in P (see Fig. 13). The circumcentres can’t coincide, because otherwise they would lie on $H_\tau$. So the circles $S \cap P$ and $S' \cap P$ intersect transversely in two points. This means that $S \cap P$ is subdivided into two parts: a part inside $S' \cap P$ and a cap outside $S' \cap P$.

We shall assume that the cap lies below the part inside $S' \cap P$, see Fig. 13. This implies that c lies below $c'$ on $\ell$. This can be seen as follows: assume that both S and $H_\tau$ are fixed. This means that points of intersection of $S \cap P$ and $S' \cap P$ are fixed, but the circumcentre $c'$ can be varied. We now let $c'$ descend along $\ell$ from $+\infty$ to $-\infty$. As long as c and $c'$ do not coincide, the cap of $S\cap P$ outside $S'\cap P$ remains stable. At the point of coincidence of c and $c'$ the inside and outside switch. It follows by considering the limit cases that the cap $S \cap P$ outside $S' \cap P$ lies below the cap inside as long as c lies below $c'$ on $\ell$, as in Fig. 13.

We now make two important observations. Firstly, because the triangulation ${\mathcal {D}}$ is Delaunay, the sphere $S'$ does not contain the vertex p of $\sigma$ not on $\tau$. Hence p lies on the cap of S which is outside $S'$. Secondly, as we assume that the circumcentre c lies outside of $\sigma$, c lies above $H_\tau \cap P$.

Now let o be the centre of $T= S \cap S'$ and let q be a vertex of $\tau$. Because $d(c,o) < d(c',o)$, the distance $d(c,q)$ is strictly smaller than $d(c',q)$ (see Fig. 13). By remarking that $d(c,q) = R$ and $d(c',q) = R'$, we get $R < R'$, which is a contradiction with the hypothesis that R is the largest circumradius in ${\mathcal {D}}$. $\square$

Proof of Lemma 5

We use the same construction and the same notations as in the proof of Lemma 4 (see Fig. 13). Observe that by hypothesis o coincides with c. If c was different from $c'$, then the radius $R'$ would be greater than R, which would lead to a contradiction. Therefore c coincides with $c'$, so $\sigma$ and $\sigma '$ share the same circumball. We conclude the proof by observing that the vertex of $\sigma '$ not in $\tau$ lies on the circumball of $\sigma$, therefore the protection of $\sigma$ is zero. $\square$

Appendix C: Protection value of an ${\tilde{A}}_{d}$ triangulation

In this appendix we will prove the bound on the protection stated in Theorem 8.

Lemma 12

A Coxeter triangulation of type ${\tilde{A}}_{d}$ has a relative protection equal to

$$\begin{aligned} {\hat{\delta }} = \frac{\sqrt{d^2+2d+24}-\sqrt{d^2+2d}}{\sqrt{d^2+2d}} \sim \frac{12}{d^2}. \end{aligned}$$

Proof

Let V be the vertex set of the triangulation containing the simplex in the ${\tilde{A}}_{d}$ row of Table 1. By Proposition 7 in Sect. 6, V coincides with the coweight lattice, which corresponds to a root system R of type $A_d$.

Take the following basis vectors of the coweight lattice V:

$$\begin{aligned} \mathbf {u}_k=\frac{1}{d+1}\left( (k-(d+1))^{\{k\}}, k^{\{d+1-k\}}\right) ,\quad \text {for}\quad 0\le k\le d. \end{aligned}$$

This means that any point of V can be expressed as $\sum _{k=1}^{d} \alpha _k\mathbf {u}_k$, with $\alpha _k\in {\mathbb {Z}}$ for all $k \in \left\{ 1,\ldots ,d \right\}$. Each coordinate of $(d+1) \mathbf {u}_k$ is an integer congruent to k modulo $(d+1)$. Following the definition of [1], we call a point a remainder-k point if its coordinates are congruent to k modulo $(d+1)$. Since any lattice point z in V can be written as $z=\sum \alpha _k\mathbf {u}_k$, it follows that z is a ${\tilde{k}}$-remainder point, where ${\tilde{k}}$ is congruent to $(\sum \alpha _k\cdot k)$ modulo $(d+1)$.

We will now look at the circumcentre $c = \frac{1}{d+1}\left( -\frac{d}{2}, -\frac{d-2}{2}, -\frac{d-4}{2}, \ldots , \frac{d}{2}\right)$ of $\sigma$ and find its nearest neighbours in the lattice. Take

$$\begin{aligned} z=\frac{1}{d+1}\big (n_1(d+1)+{\tilde{k}},\ldots ,n_{d+1}(d+1)+{\tilde{k}}\big ), \end{aligned}$$

a remainder-${\tilde{k}}$ lattice point, for some ${\tilde{k}} \in \left\{ 0,\ldots ,d \right\}$. Note that because the lattice V resides in the hyperplane $\sum _{i=1}^{d+1} x_i = 0$, we have $\left\langle z,(1^{\{d+1\}}) \right\rangle =0$, and therefore $\sum n_i=-{\tilde{k}}$. We need to find the value of $n=(n_1,\ldots ,n_{d+1}) \in N = \left. \left\{ x \in {\mathbb {Z}}^{d+1} \right| \sum x_i = -{\tilde{k}} \right\}$ which minimizes $d(z,c)$ for a given ${\tilde{k}}$. We now state the following claim, which will be proved below.

Claim

For each $k \in {\mathbb {Z}}/(d+1){\mathbb {Z}}$, the closest remainder-k point in V to c is $u_k$. A remainder-k point that is the second closest corresponds to the vector n equal to

$$\begin{aligned} \left\{ \begin{array}{ll} (-1^{\{k-1\}},0,-1,0^{\{d-k\}}),&{}\quad \text {for}\quad k\in \{1,\ldots ,d\}\\ (-1,0^{\{d-1\}},1),&{}\quad \text {if}\quad k=0 \end{array} \right. \end{aligned}$$

and has the coordinates

$$\begin{aligned} \left\{ \begin{array}{ll} \left( (k-(d+1))^{\{k-1\}},k,k-(d+1),k^{\{d-k\}}\right) ,&{}\quad \text {for}\quad k\in \{1,\ldots ,d\}\\ (-(d+1),0^{\{d-1\}},d+1),&{}\quad \text {if}\quad k=0 \end{array} \right. . \end{aligned}$$

Each of these points are at a distance $R'=\sqrt{\frac{d(d+2)}{12(d+1)}+\frac{2}{d+1}}$ from c.

This claim implies that the protection radius of $\sigma$ is $R'-R=\sqrt{\frac{d(d+2)}{12(d+1)}+\frac{2}{d+1}}-\sqrt{\frac{d(d+2)}{12(d+1)}}.$ Thus, the relative protection is

$$\begin{aligned} {\hat{\delta }} = \frac{\sqrt{d^2+2d+24}-\sqrt{d^2+2d}}{\sqrt{d^2+2d}} = \sqrt{1 + \frac{24}{d^2+2d}}-1 \sim \left( 1 + \frac{12}{d^2+2d} \right) - 1 \sim \frac{12}{d^2}. \end{aligned}$$

This completes the proof of Lemma 12 apart from the claim, which we will focus on now. $\square$

The main ingredient for the proof of the Claim is the following lemma.

Lemma 13

The difference between the two squared distances $d(z,c)^2$ and $d(z',c)^2$ for two points z and $z'$ of the lattice V is of the form $\frac{2q}{d+1}$ where q is an integer.

Proof

It is enough to compare the distances for z and $z'$ of the same congruence class. Indeed, each congruence class k already contains the point $u_k$, which is of squared distance $R^2$ from c. The difference between any two squared distances $d(z,c)^2$ and $d(z',c)^2$, for z and $z'$ a remainder-k and a remainder-$k'$ point respectively, can be expressed as

$$\begin{aligned} d(z,c)^2 - d(z',c)^2 = (d(z,c)^2 - d(z,u_k)^2) - (d(z',c)^2 - d(z',u_{k'})'^2). \end{aligned}$$

If both differences are in $\frac{2}{d+1}{\mathbb {Z}}$, the overall difference is in $\frac{2}{d+1}{\mathbb {Z}}$ as well.

So let:

$$\begin{aligned} z= & {} \frac{1}{d+1}\big (n_0(d+1)+k,\ldots ,n_{d}(d+1)+k\big )\quad \text {and}\\ z'= & {} \frac{1}{d+1}\big (n'_0(d+1)+k,\ldots ,n'_{d}(d+1)+k\big ) \end{aligned}$$

be two remainder-k points of V, with $n_i$ and $n'_i$ integers for all $i \in \left\{ 1,\ldots ,d+1 \right\}$. The difference between $d(z,c)^2$ and $d(z',c)^2$ can be expressed as:

$$\begin{aligned} d(z,c)^2 - d(z',c)^2= & {} (\Vert z\Vert ^2 - 2\left\langle z,c \right\rangle + \Vert c\Vert ^2) - (\Vert z'\Vert ^2 - 2\left\langle z',c \right\rangle + \Vert c\Vert ^2) \\= & {} \Vert z\Vert ^2 - \Vert z'\Vert ^2 - 2\left\langle z-z',c \right\rangle \\= & {} \sum ^{d}_{i=0} \left( n_i + \frac{k}{d+1}\right) ^2 - \sum ^{d}_{i=0}\left( n'_i + \frac{k}{d+1}\right) ^2\\&- 2\sum ^{d}_{i=0} \left( n_i + \frac{k}{d+1} - n'_i - \frac{k}{d+1}\right) \left( - \frac{d}{2(d+1)} +\frac{i}{d+1} \right) \\= & {} \sum ^{d}_{i=0} (n_i - n'_i)\left( n_i+n'_i + \frac{2k}{d+1}\right) + 2\sum ^{d}_{i=0} (n_i - n'_i)\left( \frac{d/2-i}{d+1}\right) \\= & {} \sum ^{d}_{i=0} (n_i - n'_i)\left( n_i+n'_i + \frac{2k+d-2i}{d+1}\right) \end{aligned}$$

Because $\sum ^{d}_{i=0} n_i = -k$, we can express $n_0 = -k - \sum ^{d}_{i=1} n_i$. Therefore:

$$\begin{aligned} d(z,c)^2 - d(z',c)^2= & {} \sum ^{d}_{i=1} (n_i - n'_i)\left( n_i+n'_i + \frac{2k+d-2i}{d+1}\right) +(n_0 - n'_0)\left( n_0+n'_0 + \frac{2k+d}{d+1}\right) \\= & {} \sum ^{d}_{i=1} (n_i - n'_i)\left( n_i+n'_i + \frac{2k+d-2i}{d+1}\right) - \left( \sum ^{d}_{i=1}(n_i - n'_i) \right) \left( -2k - \sum ^{d}_{i=1}(n_i + n'_i)+ \frac{2k+d}{d+1}\right) \\ \end{aligned}$$

The last expression is further simplified to

$$\begin{aligned} \sum ^{d}_{i=1} (n_i - n'_i)\left( n_i+n'_i+2k+\sum ^{d}_{j=1}(n_j + n'_j)-\frac{2i}{d+1}\right) . \end{aligned}$$

We will split this expression into two parts:

$$\begin{aligned} \sum ^{d}_{i=1} (n_i - n'_i)\left( n_i+n'_i+\sum ^{d}_{j=1}(n_j + n'_j)\right) + \frac{2}{d+1}\sum ^{d}_{i=1} (n_i - n'_i)((d+1)k -i). \end{aligned}$$

(6)

The second part of the expression (6) is already of the form $\frac{2q'}{d+1}$ with $q'$ an integer, so we will be interested in the first part.

Let $a_i \in {\mathbb {Z}}/2{\mathbb {Z}}$ be the congruence class of $(n_i - n'_i)$ modulo 2. At the same time, $a_i$ is the congruence class of $(n_i + n'_i)$ modulo 2. So the first part of the expression has the congruence class modulo 2 as follows:

$$\begin{aligned} \sum ^{d}_{i=1} a_i \left( a_i+\sum ^{d}_{j=1}a_j\right) = \sum ^{d}_{i=1} a^2_i + \left( \sum ^{d}_{i=1}a_i\right) ^2 = 2 \sum ^{d}_{i=1} \sum ^{d}_{\begin{array}{c} j=0\\ j \ne i \end{array}} a_i a_j = 0. \end{aligned}$$

It implies that the first part of (6) is an even integer and it can be represented as $\frac{2q''}{d+1}$ for some integer $q''$. Thus, the difference $d(z,c)^2 - d(z',c)^2$ can be expressed as $\frac{2q}{d+1}$ for some integer q. $\square$

Proof of Claim

A consequence of Lemma 13 is that the minimal positive difference between two squared distances is $\frac{2}{d+1}$. By Theorem 7 we know that the triangulation has a non-zero protection, so out of all points in V only the vertices of $\sigma$ are distant from c by the circumradius R, and they are unique to be so in their respective congruence class. The squared distance $R'^2$ between the points in the statement of the Claim and the circumcentre c is exactly different from $R^2$ by $\frac{2}{d+1}$, so these points are indeed second closest points to c after the vertices of $\sigma$, which concludes the proofs of the Claim and Lemma 12. $\square$

Remark 5

One can verify that the points in the statement of the Claim are the only second closest points to c in V, but it goes beyond the scope of this paper.

Appendix D: Proofs from Section 6

Proof of Lemma 7

Fix the dimension $d\ge 2$. Let $a_k$ denote $-\frac{d+1-k}{d+1}$ and $b_k$ denote $\frac{k}{d+1}$.

Denote by $\sigma$ the $d$-simplex of a ${\tilde{A}}_{d}$ triangulation described above. We build a $(d+1)$-simplex $\sigma '$, which consists of the $d$-face $\sigma$ and a vertex $u_{d+1} = (1^{\{d+1\}})$. Note that the edge $u_0u_{d+1}$ is orthogonal to the face $\sigma$.

The $(d+1)$-dimensional volume of $\sigma '$ can be expressed as a determinant:

$$\begin{aligned} vol(\sigma ') = \left| \frac{1}{(d+1)!} \det \left( \begin{array}{ccccc} a_1 &{}\quad a_2 &{}\quad \dots &{}\quad a_{d} &{}\quad 1 \\ b_1 &{}\quad a_2 &{}\quad \dots &{}\quad a_{d} &{}\quad 1 \\ b_1 &{}\quad b_2 &{}\quad \dots &{}\quad a_{d} &{}\quad 1 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ b_1 &{}\quad b_2 &{}\quad \dots &{}\quad b_{d} &{}\quad 1 \end{array} \right) \right| . \end{aligned}$$

First, we subtract the last row from all other rows. It gives us:

$$\begin{aligned} vol(\sigma ')= & {} \left| \frac{1}{(d+1)!} \det \left( \begin{array}{ccccc} a_1-b_1 &{}\quad a_2-b_2 &{}\quad \dots &{}\quad a_{d}-b_{d} &{}\quad 0 \\ 0 &{}\quad a_2-b_2 &{}\quad \dots &{}\quad a_{d}-b_{d} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad a_{d}-b_{d} &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ b_1 &{}\quad b_2 &{}\quad \dots &{}\quad b_{d} &{}\quad 1 \end{array} \right) \right| \\= & {} \left| \frac{1}{(d+1)!} \det \left( \begin{array}{cccc} a_1-b_1 &{}\quad a_2-b_2 &{}\quad \dots &{}\quad a_{d}-b_{d} \\ 0 &{}\quad a_2-b_2 &{}\quad \dots &{}\quad a_{d}-b_{d} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad a_{d}-b_{d} \end{array} \right) \right| \\= & {} \left| \frac{1}{(d+1)!} \prod _{k=1}^{d}(a_k - b_k) \right| = \left| \frac{1}{(d+1)!} \prod _{k=1}^{d}\left( -\frac{d+1-k}{d+1} - \frac{k}{d+1}\right) \right| \\= & {} \frac{1}{(d+1)!}. \end{aligned}$$

The volume of $\sigma$ can be found to be: $vol(\sigma ) = \frac{(d+1)vol(\sigma ')}{\Vert (1^{\{d+1\}}) \Vert } = \frac{(d+1)}{\sqrt{d+1} (d+1)!} = \frac{1}{\sqrt{d+1}\ d!}$. $\square$

Proof of Proposition 7

As we will show, this lattice is in fact the coweight lattice introduced in Sect. 2.3. The fact that the vertex set is a lattice is not entirely obvious. This lattice happens to be equal to the permutahedral lattice studied in for example [12]. $\square$

Before proving the proposition, we will need the following lemmas:

Lemma 14

Let $R$ be a crystallographic root system. Let V be the vertex set of the Coxeter triangulation corresponding to $R$. The coweight lattice $\varLambda ^{w}_{R^{\vee }}$ is a subset of V.

Proof

Let $S= \{s_1,\ldots ,s_{d}\}$ be a set of simple roots in $R$. For any point p in $\varLambda ^{w}_{R^{\vee }}$ there exist integers $n_1,\ldots ,n_{d}$ such that for every i, $\left\langle p,s_i \right\rangle = n_i$. The point p lies in the intersection of the hyperplanes $H_{s_i,k_i}$. Therefore, being in the intersection of $d$ linearly independent hyperplanes in ${\mathcal {H}}$, it is a vertex in the Coxeter triangulation. $\square$

Lemma 15

Let $R$ be a crystallographic root system. The coweight lattice $\varLambda ^{w}_{R^{\vee }}$ is stable by the action of elements of the affine group $W_a$ that corresponds to $R$.

Proof

Take $x \in \varLambda ^{w}_{R^{\vee }}$. Let $r \in R$ and $k \in {\mathbb {Z}}$. The image of x by the affine reflection $\sigma _{r,k}$ is:

$$\begin{aligned} \sigma _{r,k}(x) = x - (\left\langle x,r \right\rangle -k)r^{\vee }. \end{aligned}$$

Let $r'$ be another root in $R$. The scalar product of $\sigma _{r,k}(x)$ with $r'$ is:

$$\begin{aligned} \left\langle \sigma _{r,k}(x),r' \right\rangle = \left\langle x,r' \right\rangle - (\left\langle x,r \right\rangle -k)\left\langle r^{\vee },r' \right\rangle . \end{aligned}$$

(7)

The first term in Eq. 7 is an integer by assumption that x lies in the coweight lattice. By Remark 2, the second term in Eq. 7 can be expressed as $(\left\langle x,r \right\rangle -k) n(r,r')$ (see the definition of $n(r,r')$ in Sect. 2.2). The scalar product $\left\langle x,r \right\rangle$ is an integer by assumption that x lies in the coweight lattice. From Sect. 2.2, we know that $n(r,r')$ is an integer, and k is an integer by definition.

We conclude that $\left\langle \sigma _{r,k}(x),r' \right\rangle$ is an integer for all $r' \in R$. This implies that $\sigma _{r,k}(x)$ lies in the coweight lattice for all $r \in R$ and $k \in {\mathbb {Z}}$.

By definition, the affine Weyl group $W_a$ is generated by the affine reflections $\sigma _{r,k}$ for all $r \in R$ and $k \in {\mathbb {Z}}$. So we conclude that the coweight lattice $\varLambda ^{w}_{R^{\vee }}$ is stable by the action of elements of the affine group $W_a$. $\square$

Now, we are ready to prove Proposition 7.

Proof of Proposition 7

Fix a Coxeter triangulation of type ${\tilde{A}}_{d}$ that corresponds to a root system $R$ and let V be its vertex set. We will prove the proposition by double inclusion.

The inclusion $\varLambda ^{w}_{R^{\vee }} \subseteq V$ follows from Lemma 14. We will now prove that $V \subseteq \varLambda ^{w}_{R^{\vee }}$.

Let v be a vertex in V. Let $\sigma$ be the fundamental simplex from the beginning of the section, and $\sigma '$ be an simplex in the triangulation, such that v is its vertex. Let $\omega$ be an affine group transformation that maps $\sigma$ to $\sigma '$. In particular, $\omega$ maps a vertex in $\sigma$ to v.

Observe that all vertices in $\sigma$ have integer scalar products with all roots, so they lie in the coweight lattice. With this observation, Lemma 15 yields that v lies in the coweight lattice too.

Thus, we conclude that $V \subseteq \varLambda ^{w}_{R^{\vee }}$, so the double inclusion is complete. $\square$

1.1 Proofs of further results

Proof of Proposition 8

A point $v \in {\mathbb {R}}^d$ is a vertex of the triangulation if and only if it lies in the intersection of at least $d$ hyperplanes in ${\mathcal {H}}$ (as defined in Sect. 2.4) that are linearly independent. Equivalently, the inner products of at least $d$ linearly independent positive roots should be integers.

Let $E=\{e_1,\ldots ,e_d\}$ be the canonical basis of ${\mathbb {R}}^{d}$. Bourbaki [7, Planche II] gives the explicit expressions of positive roots:

$$\begin{aligned} R^+&= \{e_i\ |\ i \in \left\{ 1,\ldots ,d \right\} \} \cup \{e_i - e_j\ |\ i,j \in \left\{ 1,\ldots ,d \right\} \ \text{ and }\ i< j\} \\ {}&\cup \{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,d \right\} \ \text{ and }\ i < j\}. \end{aligned}$$

We will now prove that $v = u_{d} - u_{d-1} = \frac{1}{2}e_{d}$ is not in the vertex set, which implies that V does not form a lattice.

The positive roots that have integer inner product with v are exactly:

$$\begin{aligned}&\{e_i\ |\ i \in \left\{ 1,\ldots ,d-1 \right\} \} \cup \{e_i - e_j\ |\ i,j \in \left\{ 1,\ldots ,d-1 \right\} \ \text {and}\ i< j\} \\&\quad \cup \{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,d-1 \right\} \ \text {and}\ i < j\}, \end{aligned}$$

which is easily verifiable.

These roots span the vector space $\mathrm {Vect}(E {\setminus } \{e_{d}\})$, which is $(d-1)$-dimensional. Thus, there do not exist $(r_1,\ldots ,r_d)\subseteq R^+$ that are linearly independent and have integer inner products with v. Therefore v does not belong to V. $\square$

Proof of Proposition 9

A point $v \in {\mathbb {R}}^d$ is a vertex of the triangulation if and only if it lies in the intersection of at least $d$ hyperplanes in ${\mathcal {H}}$ (as defined in Sect. 2.4) that are linearly independent. Equivalently, the inner products of at least $d$ linearly independent positive roots should be integers.

Let $E=\{e_1,\ldots ,e_d\}$ be the canonical basis of ${\mathbb {R}}^{d}$. Bourbaki [7, Planche III] gives the explicit expressions of positive roots:

$$\begin{aligned} R^+&= \{2e_i\ |\ i \in \left\{ 1,\ldots ,d \right\} \} \cup \{e_i - e_j\ |\ i,j \in \left\{ 1,\ldots ,d \right\} \ \text {and}\ i< j\} \\&\cup \{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,d \right\} \ \text {and}\ i < j\}. \end{aligned}$$

We will denote by V the vertex set of the ${\tilde{C}}_{d}$ triangulation that contains the simplex $\sigma$. The goal is to prove that V is equal to $(\frac{1}{2}{\mathbb {Z}})^{d}$, which is a lattice.

We will first prove that $V \subseteq (\frac{1}{2}{\mathbb {Z}})^{d}$. This follows from the fact that $(\frac{1}{2}{\mathbb {Z}})^{d}$ is stable by the action of elements of the affine Weyl group $W_a$. Indeed, for any $x \in (\frac{1}{2}{\mathbb {Z}})^{d}$, its image by an affine reflection $\sigma _{r,k}$ for $r \in R$ and $k \in {\mathbb {Z}}$, as defined in Sect. 2.4, is $\sigma _{r,k}(x) = x - (\left\langle x,r \right\rangle - k) r^{\vee }$. For any $r \in R$ and $x \in (\frac{1}{2}{\mathbb {Z}})^{d}$, the inner product $\left\langle x,r \right\rangle$ is in $\frac{1}{2}{\mathbb {Z}}$, hence $(\left\langle x,r \right\rangle - k)$ is in $\frac{1}{2}{\mathbb {Z}}$ as well. The dual root $r^{\vee }$ has integer coefficients, so $\sigma _{r,k}(x) = x - (\left\langle x,r \right\rangle - k) r^{\vee }$ is in $(\frac{1}{2}{\mathbb {Z}})^{d}$. Now recall that one can obtain any simplex from another one by an element of $W_a$, which is generated by affine reflections $\sigma _{r,k}$. All vertices of $\sigma$ are in $(\frac{1}{2}{\mathbb {Z}})^{d}$, so with the above observation we conclude that any vertex in V is in $(\frac{1}{2}{\mathbb {Z}})^{d}$ as well.

To prove the other inclusion, observe that $\{2e_i\ |\ i \in \left\{ 1,\ldots ,d \right\} \}$ is a set of $d$ linearly independent positive roots that have integer inner products with any element in $(\frac{1}{2}{\mathbb {Z}})^{d}$.

With both inclusions proven, we conclude that $V = (\frac{1}{2}{\mathbb {Z}})^{d}$, which is a lattice. $\square$

Proof of Proposition 10

• 1. A point $v \in {\mathbb {R}}^d$ is a vertex of the triangulation if and only if it lies in the intersection of at least $d$ hyperplanes in ${\mathcal {H}}$ (as defined in Sect. 2.4) that are linearly independent. Equivalently, the inner products of at least $d$ linearly independent positive roots should be integers.

  Let $E=\{e_1,\ldots ,e_d\}$ be the canonical basis of ${\mathbb {R}}^{d}$. Bourbaki [7, Planche IV] gives the explicit expressions of positive roots:

  $$\begin{aligned} R^+ =&\{e_i - e_j\ |\ i,j \in \left\{ 1,\ldots ,d \right\} \ \text {and}\ i< j\} \cup \{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,d \right\} \ \text {and}\ i <j\}. \end{aligned}$$

  Denote by V the vertex set of the triangulation. Let $\varLambda = \{ x \in (\frac{1}{2}{\mathbb {Z}})^4 \ |\ x_1+x_2+x_3+x_4 \in {\mathbb {Z}}\}$. We will now prove that $V = \varLambda$.

  We will first prove that $V \subseteq \varLambda$. This follows from the fact that $\varLambda$ is stable by the action of elements of the affine Weyl group $W_a$. Indeed, for any $x \in \varLambda$, its image by an affine reflection $\sigma _{r,k}$ for $r \in R$ and $k \in {\mathbb {Z}}$, as defined in Sect. 2.4, is $\sigma _{r,k}(x) = x - (\left\langle x,r \right\rangle - k) r^{\vee }$. For any $r \in R$ and $x \in (\frac{1}{2}{\mathbb {Z}})^4$, the inner product $\left\langle x,r \right\rangle$ is in $\frac{1}{2}{\mathbb {Z}}$, hence $(\left\langle x,r \right\rangle - k)$ is in $\frac{1}{2}{\mathbb {Z}}$ as well. The coefficients of the dual root $r^{\vee }$ are integers, so $(\left\langle x,r \right\rangle - k) r^{\vee } \in (\frac{1}{2}{\mathbb {Z}})^4$, hence $\sigma _{r,k}(x) \in (\frac{1}{2}{\mathbb {Z}})^4$. By assumption, the sum of coefficients of x is an integer. For any $r \in R^+$ defined above, the sum of coefficients of $\frac{1}{2}r$ is an integer as well. Therefore $\sigma _{r,k}(x) \in \varLambda$. Now recall that one can obtain any simplex from another simplex by an element of $W_a$, which is generated by affine reflections $\sigma _{r,k}$. All vertices of $\sigma$ are in $\varLambda$, so with the above observation we conclude that any vertex in V is in $\varLambda$ as well.

  To prove the other inclusion, observe that $\{e_1+e_2, e_1-e_2, e_3+e_4, e_3-e_4\}$ is a set of four linearly independent positive roots that have integer inner products with any element in $\varLambda$.

  With both inclusions proven, we conclude that $V = \varLambda$, which is a lattice.

• 2. Let V be the the vertex set of the triangulation. We will now prove that $v = u_{3} - u_{2} = \frac{1}{2}e_{3}$ is not in the vertex set, which implies that V does not form a lattice.

  One can easily check that the positive roots that have integer inner product with v are exactly:

  $$\begin{aligned} \{e_i - e_j\ |\ i,j \in \left\{ 1,\ldots ,d \right\} {\setminus }\{3\} \ \text {and}\ i< j\} \cup \{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,d \right\} {\setminus }\{3\}\ \text {and}\ i < j\} \end{aligned}$$

  and these roots span the vector space $\mathrm {Vect}(E {\setminus } \{e_{3}\})$, which is $(d-1)$-dimensional. Thus, there does not exist $(r_1,\ldots ,r_d) \subseteq R^+$ that are linearly independent and have integer inner products with v. We therefore conclude that v does not belong to V. $\square$

Proof of Proposition 11

A point $v \in {\mathbb {R}}^8$ is a vertex of the triangulation if and only if it lies in the intersection of at least 6 hyperplanes in ${\mathcal {H}}$ (as defined in Sect. 2.4) that are linearly independent. Equivalently, the inner products of at least 6 linearly independent positive roots should be integers.

Let $E=\{e_1,\ldots ,e_8\}$ be the canonical basis of ${\mathbb {R}}^{8}$. Bourbaki [7, Planche V] gives the explicit expressions of positive roots:

$$\begin{aligned} R^+= & {} \{e_j - e_i\ |\ i,j \in \left\{ 1,\ldots ,5 \right\} \ \text {and}\ i< j\} \cup \\&\{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,5 \right\} \ \text {and}\ i < j\} \cup \\&\left\{ \frac{1}{2}\left( e_8-e_7-e_6+\sum _{i=1}^{5}(-1)^{\nu (i)}e_i\right) \ \left| \ \sum _{i=1}^{5}\nu (i) \text { is even}\right. \right\} . \end{aligned}$$

Let V be the vertex set of the corresponding triangulation. We will now prove that $v = -2u_1+3u_2+3u_3-2u_4 = \frac{3}{2}e_2$ is not in the vertex set, which implies that V does not form a lattice.

One can easily check that the positive roots that have integer inner product with v are exactly:

$$\begin{aligned} \{e_j - e_i\ |\ i,j \in \{1,3,4,5\}\ \text {and}\ i< j\} \cup \{e_i + e_j\ |\ i,j \in \{1,3,4,5\}\ \text {and}\ i < j\}. \end{aligned}$$

These roots span the vector space $\mathrm {Vect}(\{e_1,e_3,e_4,e_5\})$, and this vector space is 4-dimensional. Thus, there do not exist $(r_1,\ldots ,r_6)$ that are linearly independent and have integer inner products with v. We therefore conclude that v does not belong to V. $\square$

Proof of Proposition 12

A point $v \in {\mathbb {R}}^8$ is a vertex of the triangulation if and only if it lies in the intersection of at least 7 hyperplanes in ${\mathcal {H}}$ (as defined in Sect. 2.4) that are linearly independent. Equivalently, the inner products of at least 7 linearly independent positive roots should be integers.

Let $E=\{e_1,\ldots ,e_8\}$ be the canonical basis of ${\mathbb {R}}^{8}$. Bourbaki [7, Planche VI] gives the explicit expressions of positive roots:

$$\begin{aligned} R^+= & {} \{e_j - e_i\ |\ i,j \in \left\{ 1,\ldots ,6 \right\} \ \text {and}\ i< j\} \cup \\&\{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,6 \right\} \ \text {and}\ i < j\} \cup \\&\left\{ \frac{1}{2}\left( e_8-e_7+\sum _{i=1}^{6}(-1)^{\nu (i)}e_i\right) \ \left| \ \sum _{i=1}^{6}\nu (i) \text { is odd}\right. \right\} . \end{aligned}$$

Let V be the vertex set of the corresponding triangulation. We will now prove that $v = -6u_1+2u_2+3u_3-4u_4 = e_2$ is not in the vertex set, which implies that V does not form a lattice.

One can easily check that the positive roots that have integer inner product with v are exactly

$$\begin{aligned} \{e_j - e_i\ |\ i,j \in \left\{ 1,\ldots ,6 \right\} \ \text {and}\ i< j\} \cup&\{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,6 \right\} \ \text {and}\ i < j\}, \end{aligned}$$

and these roots span the vector space $\mathrm {Vect}(\{e_1,\ldots ,e_6\})$, which is 6-dimensional. Thus, there does not exist $(r_1,\ldots ,r_7) \subseteq R^+$ that are linearly independent and have integer inner products with v. We therefore conclude that v does not belong to V. $\square$

Proof of Proposition 13

A point $v \in {\mathbb {R}}^8$ is a vertex of the triangulation if and only if it lies in the intersection of at least 8 hyperplanes in ${\mathcal {H}}$ (as defined in Sect. 2.4) that are linearly independent. Equivalently, the inner products of at least 8 linearly independent positive roots should be integers.

Let $E=\{e_1,\ldots ,e_8\}$ be the canonical basis of ${\mathbb {R}}^{8}$. Bourbaki [7, Planche VII] gives the explicit expressions of positive roots:

$$\begin{aligned} R^+ =&\{e_j - e_i\ |\ i,j \in \left\{ 1,\ldots ,7 \right\} \ \text {and}\ i< j\} \cup \{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,7 \right\} \ \text {and}\ i < j\} \\&\cup \left\{ \frac{1}{2}\left( e_8+\sum _{i=1}^{7}(-1)^{\nu (i)}e_i\right) \ \left| \ \sum _{i=1}^{7}\nu (i) \text { is even}\right. \right\} . \end{aligned}$$

Let V be the vertex set of the corresponding triangulation. We will now prove that $v = -u_1+3u_2+4u_3-6u_4 = e_2$ is not in the vertex set, which implies that V does not form a lattice.

One can easily check that the positive roots that have integer inner product with v are exactly

$$\begin{aligned} \{e_j - e_i\ |\ i,j \in \left\{ 1,\ldots ,7 \right\} \ \text {and}\ i< j\} \cup \{e_i + e_j\ |\ i,j \in \left\{ 1,\ldots ,7 \right\} \ \text {and}\ i < j\}, \end{aligned}$$

and these roots span the vector space $\mathrm {Vect}(\{e_1,\ldots ,e_7\})$, which is 7-dimensional. Thus, there does not exist $(r_1,\ldots ,r_8) \subseteq R^+$ that are linearly independent and have integer inner products with v. We therefore conclude that v does not belong to V. $\square$

Proof of Proposition 14

A point $v \in {\mathbb {R}}^4$ is a vertex of the triangulation if and only if it lies in the intersection of at least 4 hyperplanes in ${\mathcal {H}}$ (as defined in Sect. 2.4) that are linearly independent. Equivalently, the inner products of at least 4 linearly independent positive roots should be integers.

Let $E=\{e_1,\ldots ,e_4\}$ be the canonical basis of ${\mathbb {R}}^{4}$. Bourbaki [7, Planche VIII] gives the explicit expressions of positive roots:

$$\begin{aligned} R^+ = E \cup \{e_i \pm e_j\ |\ i,j \in \left\{ 1,\ldots ,4 \right\} \ \text {and}\ i < j\} \cup \left\{ \frac{1}{2}\left( e_1 \pm e_2 \pm e_3 \pm e_4\right) \right\} . \end{aligned}$$

Let V be the vertex set of the corresponding triangulation. We will now prove that $v = u_1+u_2 = \left( \frac{7}{6}, \frac{5}{6}, \frac{1}{3}, 0\right)$ is not in the vertex set, which implies that V does not form a lattice.

One can easily check that the positive roots that have integer inner product with v are exactly $\left\{ e_4, e_1+e_2, \frac{1}{2}(e_1-e_2-e_3 \pm e_4) \right\} .$ Note that $\frac{1}{2}(e_1-e_2-e_3+e_4) = \frac{1}{2}(e_1-e_2-e_3-e_4) + e_4$, so these roots are not linearly independent. Thus, there does not exist $(r_1,\ldots ,r_4) \subseteq R^+$ that are linearly independent and have integer inner products with v. We therefore conclude that v does not belong to V. $\square$