Abstract
We study the geometric Whitney problem on how a Riemannian manifold (M, g) can be constructed to approximate a metric space \((X,d_X)\). This problem is closely related to manifold interpolation (or manifold reconstruction) where a smooth n-dimensional submanifold \(S\subset {{\mathbb {R}}}^m\), \(m>n\) needs to be constructed to approximate a point cloud in \({{\mathbb {R}}}^m\). These questions are encountered in differential geometry, machine learning, and in many inverse problems encountered in applications. The determination of a Riemannian manifold includes the construction of its topology, differentiable structure, and metric. We give constructive solutions to the above problems. Moreover, we characterize the metric spaces that can be approximated, by Riemannian manifolds with bounded geometry: We give sufficient conditions to ensure that a metric space can be approximated, in the Gromov–Hausdorff or quasi-isometric sense, by a Riemannian manifold of a fixed dimension and with bounded diameter, sectional curvature, and injectivity radius. Also, we show that similar conditions, with modified values of parameters, are necessary. As an application of the main results, we give a new characterization of Alexandrov spaces with two-sided curvature bounds. Moreover, we characterize the subsets of Euclidean spaces that can be approximated in the Hausdorff metric by submanifolds of a fixed dimension and with bounded principal curvatures and normal injectivity radius. We develop algorithmic procedures that solve the geometric Whitney problem for a metric space and the manifold reconstruction problem in Euclidean space, and estimate the computational complexity of these procedures. The above interpolation problems are also studied for unbounded metric sets and manifolds. The results for Riemannian manifolds are based on a generalization of the Whitney embedding construction where approximative coordinate charts are embedded in \({{\mathbb {R}}}^m\) and interpolated to a smooth submanifold.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and the Main Results
1.1 Geometrization of Whitney’s Extension Problem
In this paper, we develop a geometric version of Whitney’s extension problem. Let \(f : K \rightarrow {\mathbb {R}}\) be a function defined on a given (arbitrary) set \(K \subset {\mathbb {R}}^n\), and let \(m \ge 1\) be a given integer. The classical Whitney problem is the question whether f extends to a function \(F \in C^m({\mathbb {R}}^n)\) and if such an F exists, what is the optimal \(C^m\) norm of the extension. Furthermore, one is interested in the questions if the derivatives of F, up to order m, at a given point can be estimated, or if one can construct extension F so that it depends linearly on f.
These questions go back to the work of Whitney [95,96,97] in 1934. In the decades since Whitney’s seminal work, fundamental progress was made by Glaeser [50], Brudnyi and Shvartsman [19,20,21,22,23,24] and [86,87,88], and Bierstone et al. [10]. (See also Zobin [101, 102] for the solution of a closely related problem.)
The above questions have been answered in the last few years, thanks to work of Bierstone et al. (see [10, 18, 19, 21, 22, 24, 37,38,39,40,41,42]). Along the way, the analogous problems with \(C^m({\mathbb {R}}^n)\) replaced by \(C^{m,\omega }({\mathbb {R}}^n)\), the space of functions whose mth derivatives have a given modulus of continuity \(\omega \), (see [41, 42]), were also solved.
The solution of Whitney’s problems has led to a new algorithm for interpolation of data, due to Fefferman and Klartag [45, 46], where the authors show how to compute efficiently an interpolant F(x), whose \(C^m\) norm lies within a factor C of least possible, where C is a constant depending only on m and n.
In recent years, the focus of attention in this problem has moved to the direction when the measurements \({\widetilde{f}}:K\rightarrow {\mathbb {R}}\) on the function f are given with errors bounded by \(\varepsilon >0\). Then, the task is to find a function \(F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) such that \(\sup _{x\in K} |F(x)-{\widetilde{f}}(x)| \le \varepsilon \). Since the solution is not unique, one wants to find the extensions that have the optimal norm in \(C^m({\mathbb {R}}^n)\), see, e.g., [45, 46]. Finding F can be considered as the task of finding a graph \(\varGamma (F)=\{(x,F(x)):\ x\in {\mathbb {R}}^n\}\subset {\mathbb {R}}^{n+1}\) of a function in \(C^m({\mathbb {R}}^n)\) that passes near the points \(\{(x,{\widetilde{f}}(x)):\ x\in K\}\). To formulate the above problems in geometric (i.e., coordinates invariant) terms, instead of a graph set \(\varGamma (F)\), we aim to construct a general submanifold or a Riemannian manifold that approximates the given data. Also, instead of the \(C^m({\mathbb {R}}^n)\)-norms, we will measure the optimality of the solution in terms of invariant bounds for the curvature and the injectivity radius.
In this paper, we consider the following two geometric Whitney problems:
-
A.
Let E be a separable Hilbert space, e.g., \({\mathbb {R}}^N\), and assume that we are given a set \(X\subset E\). When can one construct a smooth n-dimensional submanifold \(M\subset E\) that approximates X with given bounds for the geometry of M and the Hausdorff distance between M and X? How can the submanifold M be efficiently constructed when X is given?
-
B.
Let \((X,d_X)\) be a metric space. When there exists a Riemannian manifold (M, g) that has given bounds for geometry and approximates well X? How can the manifold (M, g) be constructed when X is given? What is an algorithm that constructs (M, g) when X is finite?
In Question B, by ‘approximation’ we mean Gromov–Hausdorff or quasi-isometric approximation, see definitions in Definition 3 and Sect. 2.1.
We answer the Question A in Theorem 2, by showing that if \(X\subset E\) is locally (i.e., at a certain small scale) close to affine n-dimensional planes, see Definition 4, there is a submanifold \(M\subset E\) such that the Hausdorff distance of X and M is small and the second fundamental form and the normal injectivity radius of M are bounded.
The answer to the Question B is given in Theorem 1. Roughly speaking, it asserts that the following natural conditions on X are necessary and sufficient: Locally, X should be close to \({\mathbb {R}}^n\), and globally, the metric of X should be almost intrinsic.
The conditions in Theorem 1 are optimal, up to multiplying the obtained bounds by a constant factor depending on n. Theorem 1 gives sufficient conditions for metric spaces that approximate smooth manifolds. In Corollary 1, we show that similar conditions, with modified values of parameters, are necessary.
The result of Theorem 2 is optimal, up to multiplication the obtained bounds by a constant factor depending on n.
The proofs of Theorems 1 and 2 are constructive and give raise to manifold reconstruction algorithms when X is a finite set. Moreover, we give algorithms that verify if a finite data set X satisfies the characterizations given in Theorems 1 and 2. We analyze in Sect. 7.2 the computational complexity of these algorithms, but emphasize that to keep the algorithms simple, the algorithms have not been optimized in this paper to have the minimal complexity.
Finally, we note that this paper is related to two rather different theorems of Whitney: One is the Whitney embedding theorem of smooth manifolds into an Euclidean space and the other is the Whitney extension theorem for functions in \({\mathbb {R}}^n\).
Next we formulate the definitions needed to state the results rigorously.
Notations For a metric space X and sets \(A,B\subset X\), we denote by \(d_H^X(A,B)\), or just by \(d_H(A,B)\), the Hausdorff distance between A and B in X.
By \(d_{\mathrm{GH}}(X,Y)\), we denote the Gromov–Hausdorff (GH) distance between metric spaces X and Y. For the reader’s convenience, we collect definitions and elementary facts about the GH distance in Sect. 2.1. For more detailed account of the topic, see, e.g., [26, 79, 85]. In most cases, we work with pointed GH distance between pointed metric spaces \((X,x_0)\) and \((Y,y_0)\), where \(x_0\in X\) and \(y_0\in Y\) are distinguished points. For the definition of pointed GH distance, see [79, §1.2 in Ch. 10]) or Sect. 2.1.
For a metric space X, \(x\in X\) and \(r>0\), we denote by \(B^X_r(x)\) or \(B_r(x)\) the ball of radius r centered at x. For \(X={\mathbb {R}}^n\), we use notation \(B_r^n(x)=B_r^{{\mathbb {R}}^n}(x)\) and \(B_r^n=B_r^n(0)\). For a set \(A\subset X\) and \(r>0\), we denote by \({{\mathcal {U}}}_r^X(A)\) or \({{\mathcal {U}}}_r(A)\) the metric neighborhood of A of radius r that is the set points within distance r from A.
When speaking about GH distance between metric balls \(B_r^X(x)\) and \(B_r^Y(y)\), we always mean the pointed GH distance where the centers x and y are distinguished points of the balls. We abuse notation and write \(d_{\mathrm{GH}}(B_r^X(x),B_r^Y(y))\) to denote this pointed GH distance.
For a Riemannian manifold M, we denote by \({\text {Sec}}_M\) its sectional curvature and by \({{\,\mathrm{inj}\,}}_M\) its injectivity radius.
Small metric balls in a Riemannian manifold are GH close to Euclidean balls. More precisely, let M be a Riemannian n-manifold with \(|{\text {Sec}}_M|<K\) where K is a positive constant, and \(0<r\le \frac{1}{2}\min \{\frac{\pi }{\sqrt{K}},{{\,\mathrm{inj}\,}}_M\}\). Then, for every \(x\in M\), the metric balls \(B^M_r(x)\) in M and \(B_r^n\) in \({\mathbb {R}}^n\) satisfy
For a proof of this estimate, see Sect. 4.
If M is a submanifold of \({\mathbb {R}}^N\), one can write a similar estimate for the Hausdorff distance in \({\mathbb {R}}^N\). Namely, if the principal curvatures of M are bounded by \(\kappa >0\), then M deviates from its tangent space by at most \(\tfrac{1}{2} \kappa r^2\) within a ball of radius r. Thus, the Hausdorff distance between r-ball \(B^M_r(x)\) in M and the ball \(B_r^{T_xM}(x)=B_r^N(x)\cap T_xM\) of the affine tangent space of M at x satisfies
Note the different order of the above estimates for the intrinsic distances (1) and the extrinsic distances (2).
With (1) in mind, we give the following definition.
Definition 1
Let X be a metric space, \(r>\delta >0, \, n \in {\mathbb {N}}\). We say that X is \(\delta \)-close to \({\mathbb {R}}^n\)at scale r if, for any \(x \in X\),
Condition (3) can be effectively verified, up to a constant factor, see Algorithm GHDist. The condition can be also formulated for finite subsets: If sequences \((y_j)_{j=1}^N\subset B_r^n\) and \((x_j)_{j=1}^N\subset B_r^X(x)\) are \(\frac{\delta }{4}\)-nets such that \(|d_{{\mathbb {R}}^n}(y_j,y_k)-d_X(x_j,x_k)|<\frac{\delta }{4}\) for all \(j,k=1,2,\dots ,N\), then (3) is valid by [26, Prop. 7.3.16 and Corollary 7.3.28]. On the other hand, if X is \(\frac{\delta }{16}\)-close to \({\mathbb {R}}^n\) at scale r, then such \(\frac{\delta }{4}\)-nets exist.
In a Riemannian manifold, large-scale distances are determined by small-scale ones through the lengths of paths. However, Definition 1 does not impose any restrictions on distances larger that 2r in X. To rectify this, we need to make the metric ‘almost intrinsic’ as explained below.
Definition 2
Let \(X=(X,d)\) be a metric space and \(\delta >0\). A \(\delta \)-chain in X is a finite sequence \(x_1,x_2,\dots ,x_N\in X\) such that \(d(x_i,x_{i+1})<\delta \) for all \(1\le i\le N-1\). A sequence \(x_1,x_2,\dots ,x_N\in X\) is said to be \(\delta \)-straight if
for all \(1\le i<j<k\le N\). We say that X is \(\delta \)-intrinsic if for every pair of points \(x,y\in X\) there is a \(\delta \)-straight \(\delta \)-chain \(x_1,\dots ,x_N\) with \(x_1=x\) and \(x_N=y\).
Clearly, every Riemannian manifold (more generally, every length space) is \(\delta \)-intrinsic for any \(\delta >0\). Moreover, if X lies within GH distance \(\delta \) from a length space, then X is \(C\delta \)-intrinsic. In fact, this property characterizes \(\delta \)-intrinsic metrics, see Lemma 2.
In order to conveniently compare metric spaces at both small scale and large scale, we need the notion of quasi-isometry.
Definition 3
Let X, Y be metric spaces, \(\varepsilon >0\) and \(\lambda \ge 1\). A (not necessarily continuous) map \(f:X\rightarrow Y\) is said to be a \((\lambda ,\varepsilon )\)-quasi-isometry if the image f(X) is an \(\varepsilon \)-net in Y and
for all \(x,y\in X\), where \(d_X\) and \(d_Y\) denote the distances in X and Y, resp.
Unlike the use of quasi-isometries in, e.g., geometric group theory, in this paper we consider quasi-isometries with parameters \(\varepsilon \approx 0\) and \(\lambda \approx 1\). The quasi-isometry relation is almost symmetric: If there is a \((\lambda ,\varepsilon )\)-quasi-isometry from X to Y, then there exists a \((\lambda ,{3}\lambda \varepsilon )\)-quasi-isometry from Y to X. We say that metric spaces X and Y are \((\lambda ,\varepsilon )\)-quasi-isometric if there are \((\lambda ,\varepsilon )\)-quasi-isometries in both directions.
The existence of a \((\lambda ,\varepsilon )\)-quasi-isometry \(f:X\rightarrow Y\) implies that
See Sect. 2.1 for the proof.
Now we formulate our main result.
Theorem 1
For every \(n\in {\mathbb {N}}\), there exist \(\sigma _1=\sigma _1(n)>0\) and \(C_1=C_1(n),C_2=C_2(n)>0\) such that the following holds. Let \(r>0\), X be a metric space with \({{\,\mathrm{diam}\,}}(X)>r\), and
Suppose that X is \(\delta \)-intrinsic and \(\delta \)-close to \({\mathbb {R}}^n\) at scale r, see Definitions 1 and 2. Then, there exists a complete n-dimensional Riemannian manifold M such that
-
1.
X and M are \((1+C_1\delta r^{-1},C_1\delta )\)-quasi-isometric. Moreover, when the diameter of X is finite, we have
$$\begin{aligned} d_{\mathrm{GH}}(X,M) \le {2C_1}\delta r^{-1}{{\,\mathrm{diam}\,}}(X). \end{aligned}$$(8) -
2.
The sectional curvature \({\text {Sec}}_M\) of M satisfies \(|{\text {Sec}}_M|\le C_2\delta r^{-3}\).
-
3.
The injectivity radius of M is bounded below by r / 2.
By following the steps of the proof, one can obtain explicit formulas for the values of \(\sigma _1(n)\), \(C_1(n)\), and \(C_2(n).\)
The estimate (8) follows from the existence of a \((1+C_1\delta r^{-1},C_1\delta )\)-quasi-isometry from X to M due to (6) and the fact that \({{\,\mathrm{diam}\,}}(X)>r\). The proof of Theorem 1 is given in Sect. 5.
The quasi-isometry parameters and sectional curvature bound in Theorem 1 are optimal up to constant factors depending only on n, see Remark 9.
Remark 1
The assumption that X is \(\delta \)-intrinsic in Theorem 1 is not crucial. Without this assumption, the following more technical variant of the theorem holds:
If a metric space X is \(\delta \)-close to \({\mathbb {R}}^n\) at scale r, where \(\delta /r\) is bounded above by a constant depending on n, then there exists a complete (possibly not connected) Riemannian n-manifold M which satisfies properties (2) and (3) from Theorem 1 and approximates X in the following sense: There is a map \(f:X\rightarrow M\) such that
for all \(x,y\in X\) such that \(d_X(x,y)<r\) or \(d_M(f(x),f(y))<r\).
This variant follows from Theorem 1 and the fact that one can modify ‘large’ distances in X so that the resulting metric is \(C\delta \)-intrinsic and coincides with d within balls of radius r. The new distances are measured along ‘discrete shortest paths’ in X, see (32) and Lemma 3 in Sect. 2.2.
This procedure may split X into several ‘components’ with modified distances between them being infinite. In the original metric space, these components are subsets separated by distances greater that r. They correspond to connected components of the approximating manifold M.
For \(\delta \)-intrinsic metrics, an approximation f as above is \((1+C\delta r^{-1},C\delta )\)-quasi-isometry and vice versa. This follows from Lemmas 1 and 4, see Sect. 2.
Furthermore, Theorem 1 gives a characterization result for metric spaces that GH approximate smooth manifolds with certain geometric bounds. The precise formulation is the following.
Let \({\mathcal {M}}(n,K,i_0,D)\) denote the class of n-dimensional compact Riemannian manifolds M satisfying \(|{\text {Sec}}_M|\le K\), \({{\,\mathrm{inj}\,}}_M\ge i_0\), and \({{\,\mathrm{diam}\,}}(M)\le D\). Denote by \(\mathcal M_\varepsilon (n,K,i_0,D)\) the class of metric spaces X such that \(d_{\mathrm{GH}}(X,M)<\varepsilon \) for some \(M\in {\mathcal {M}}(n,K,i_0,D)\). Also, let \({\mathcal {X}}(n,\delta ,r,D)\) denote the class of metric spaces X that are \(\delta \)-intrinsic and \(\delta \)-close to \({\mathbb {R}}^n\) at scale r, and satisfy \({{\,\mathrm{diam}\,}}(X)\le D\). Theorem 1 has the following corollary that concerns neighborhoods of smooth manifolds and the class of metric spaces that satisfy a weak \(\delta \)-flatness condition in the scale of injectivity radius and a strong \(\delta \)-flatness condition in a small-scale r.
Corollary 1
For every \(n\in {\mathbb {N}}\), there exist \({\sigma _1}={\sigma _1}(n)>0\) and \(C_3=C_3(n),C_4=C_4(n)>0\) such that the following holds. Let \(K,i_0,D>0\) and assume that \(i_0<\sqrt{{\sigma _1}/K}\). Let \(\delta _0=Ki_0^3\), \(0<\delta <\delta _0\), and \(r=(\delta /K)^{\frac{1}{3}}\). Let \({\mathcal {X}}\) be the class of metric spaces defined by
Then,
where \(\varepsilon _1=\delta /6\) and \(\varepsilon _2=C_4DK^{1/3}\delta ^{2/3}\).
For a metric space X, the first inclusion in (9) means that the condition \(X\in {\mathcal {X}}\) is necessary for X to approximate a manifold from \(\mathcal M(n,K/2,2i_0,D-\delta )\) with accuracy \(\varepsilon _1\). Likewise, the second inclusion in (9) says that \(X\in {\mathcal {X}}\) is a sufficient condition for X to approximate a manifold from \({\mathcal {M}}(n,C_3K,i_0/{2},D)\) with accuracy \(\varepsilon _2\).
The optimal values of \(\varepsilon _1\) and \(\varepsilon _2\) in Corollary 1 remain an open question. The proof of Corollary 1 is given in Sect. 6. It is based on Theorem 1 and Proposition 2.
Another application of Theorem 1 is the following characterization of Alexandrov spaces with two-sided curvature bounds.
Corollary 2
For a complete geodesic metric space X and \(n\in {\mathbb {N}}\), the following two conditions are equivalent:
-
1.
There exists \(K>0\) such that for all \(x\in X\) and \(r>0\),
$$\begin{aligned} d_{\mathrm{GH}}(B^X_r(x),B^n_r) \le Kr^3 . \end{aligned}$$(10) -
2.
X is an n-dimensional manifold, its metric has two-sided bounded curvature in the sense of Alexandrov, and its injectivity radius is bounded away from 0.
Furthermore, if (1) holds, then X has Alexandrov curvature bounds between \(-C_5K\) and \(C_5K\) and injectivity radius at least \(1/(C_6\sqrt{K})\), where \(C_5\) and \(C_6\) are positive constants depending only on n.
The proof of Corollary 2 is given in Sect. 6. We refer to [17, 26, 27] or [8] for the definition and basic properties of Alexandrov curvature bounds. Here we only mention the fact that finite-dimensional boundaryless Alexandrov spaces with two-sided curvature bounds are Riemannian manifolds with \(C^{1,\alpha }\) metrics ([71], see also [8, Theorem 14.1]).
1.1.1 On the Proof of Theorem 1
In the proof of Theorem 1, M is constructed as a submanifold of a separable Hilbert space E, which is either \({\mathbb {R}}^N\) with a large N (in case when X is bounded) or \(\ell ^2\) endowed with the standard \(\Vert \,\cdot \,\Vert _{\ell ^2}\) norm. However, the Riemannian metric on M is different from the one inherited from E.
We note that an algorithm based on Theorem 1, which also summarizes some of the main objects used in the proof, is given in Sect. 7, see also Fig. 1 in Sect. 5.
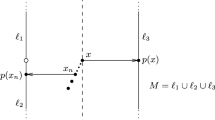
A schematic visualization of the interpolation algorithm ‘ManifoldConstruction’ based on Theorem 1, see Sect. 7. Assume that a finite metric space \((X,d_X)\) is given. First we construct a maximal (r / 100)-separated subset \(X_0=\{q_i,\ i=1,2,\dots ,N\}\subset X\) and r-neighborhoods \(B^X_r(x_i)\subset X\) of points \(q_i\in X_0\). Then, we construct balls \(D_i\subset {\mathbb {R}}^n\) approximating the r-balls \(B^X_r(q_i)\) and local embeddings \(f_i:B^X_r(q_i)\rightarrow D_i\). The balls \(D_i\) are considered as local coordinate charts. We embed these local charts to an Euclidean space \(E={\mathbb {R}}^m\) using Whitney-type embeddings \({F^{(i)}=F|_{D_i^{r/10}}:D_i^{r/10}\rightarrow \varSigma _i}\). Submanifolds \(\varSigma _i\subset E\) are denoted by blue curves. Using the algorithm SubmanifoldInterpolation, the union \(\bigcup _i\varSigma \) is interpolated to a red submanifold \(M\subset E\). When \(P_M\) is the normal projector onto M, denoted by the red arrows, we can determine a metric tensor \(g_i\) on \(P_M(\varSigma _i)\) by pushing forward the Euclidean metric from \(D_i\) to \(P_M(\varSigma _i)\) by the map \(P_M\circ F|_{D_i}\). The metric tensor g on M is obtained by computing a smooth weighted average of tensors \(g_i\) (Color figure online)
Here is the idea of the proof of Theorem 1. Since the r-balls in X are GH close to the Euclidean ball \(B_r^n\), they admit nice maps (\(2\delta \)-isometries) to \(B_r^n\). These maps can be used as a kind of coordinate charts for X, allowing us to argue about X as if it were a manifold. In particular, we can mimic the proof of Whitney embedding theorem (on the classical Whitney embedding, see [98, 99]). If X were a manifold, this would give us a diffeomorphic submanifold of a higher-dimensional Euclidean space E. In our case, we get a set \(\varSigma \subset E\) which is a Hausdorff approximation of a submanifold \(M\subset E\). In order to prove this, we use Theorem 2 (see Sect. 1.3) which characterizes sets approximable by (nice) submanifolds. We emphasize that the resulting submanifold \(M\subset E\) is the image of a Whitney embedding but not of a Nash isometric embedding [68, 69]. As the last step of the construction (see Sect. 5.4), we construct a Riemannian metric g on M so that a natural map from X to (M, g) is almost isometric at scale r. The construction is explicit and can be performed in an algorithmic manner, see Sect. 7. Then, with the assumption that X is \(\delta \)-intrinsic, it is not hard to show that X and (M, g) are quasi-isometric with small quasi-isometry constants (Table 1).
Convention Here and later, we fix the notation n for the dimension of a (sub)manifold in question. Throughout the paper, we denote by \(c,\,C\), \(C_1,C_2,\) etc., various constants depending only on n and, when dealing with derivative estimates, on the order of the derivative involved. The same letter C can be used to denote different constants, even within one formula. The constants with a number are used for two reasons: First, to make it possible to compute the values of these constants when needed, and second, to make the presentation easier, so that the reader can see what earlier estimates are involved in each formula. However, to keep the presentation simpler, some constants that are not needed in later estimates or are not main in focus of the interest of this paper are not numbered. To indicate dependence on other parameters, when we introduce a new constant, we use notation like C(M, k) or \(C_j{(M,k)}\) for numbers depending on manifold M and number k. The locations where the constants appear first time are listed in Table 2. Constants that do not depend on any parameters, including the dimension n of the manifold, are called universal constants. Most of the constants \(C_j\) depend on the intrinsic dimension n, and we do not usually indicate it (except in the introduction where main results are stated), that is, we have \(C_j=C_j(n)\), \(C(M,k)= C(M,k,n)\), etc. We note that several constants \(C_j\) have an exponential dependency in n. One of the reasons for this is that in a manifold having a negative sectional curvature, e.g., in the hyperbolic space, a ball of radius r contains \(e^{cr/\delta }\) points that are \(\delta \)-separated. We emphasize that n is the intrinsic dimension of the manifold that is relatively small in several applications, and the constants do not depend on the dimension of an ambient space where a considered manifold may be embedded in.
1.2 Manifold Reconstruction and Inverse Problems
Theorem 1 and Corollary 1 give quantitative estimates on how one can use discrete metric spaces as models of Riemannian manifolds, for example for the purposes of numerical analysis. With this approach, a data set representing a Riemannian manifold is just a matrix of distances between points of some \(\delta \)-net. Naturally, the distances can be measured with some error. In fact, only ‘small-scale’ distances need to be known, see Corollary 3.
The statement of Theorem 1 provides a verifiable criterion to tell whether a given data set approximates any Riemannian manifold (with certain bounds for curvature and injectivity radius). See Sect. 2.4 for an explicit algorithm.
The proof of Theorem 1 is constructive. It provides an algorithm, although a rather complicated one, to construct a Riemannian manifold approximated by a given discrete metric space X. See Sect. 7 for an outline of the algorithm.
Next we formulate results that describe properties of the manifold M constructed from data X that approximates some smooth manifold \({\widetilde{M}}\) and discuss how this result is used in inverse problems.
1.2.1 Reconstructions with Data that Approximate a Smooth Manifold
When dealing with inverse problems, it is assumed that the data set X comes from some unknown Riemannian manifold \({\widetilde{M}}\), and moreover, some a priori bounds on the geometry of this manifold are given. Applying Theorem 1 to this data set yields another manifold M which is \((1+C\delta r^{-1},C\delta )\)-quasi-isometric to \({\widetilde{M}}\). One naturally asks what information about the original manifold \({\widetilde{M}}\) can be recovered, in particular, if the topological and differentiable type of the manifold \({\widetilde{M}}\) can be determined using the set X. An answer is given by the following proposition.
Proposition 1
(cf. Theorem 8.19 in [51]) There exist \({\kappa _0}>0\) and \(C_7>0\) such that the following holds. Let M and \({\widetilde{M}}\) be complete Riemannian n-manifolds with \(|{\text {Sec}}_M|\le K\) and \(|{\text {Sec}}_{\widetilde{M}}|\le K\), where \(K>0\).
Let \(0<{\kappa }<{\kappa _0}\) and assume that M and \({\widetilde{M}}\) are \((1+{\kappa },{\kappa } r)\)-quasi-isometric, where \( r < \min \{({\kappa }/K)^{1/2}, {{\,\mathrm{inj}\,}}_M, {{\,\mathrm{inj}\,}}_{{\widetilde{M}}} \} . \)
Then, M and \({\widetilde{M}}\) are diffeomorphic. Moreover, there exists a bi-Lipschitz diffeomorphism \(\varPsi \) between M and \({\widetilde{M}}\) with bi-Lipschitz constant bounded by \(1+C_7{\kappa }\),
We do not prove Proposition 1 because it is essentially the same as Theorem 8.19 in [51], except that the approximation is quasi-isometric rather than GH. To prove Proposition 1, one can apply the same arguments as in [51, 8.19] using coordinate neighborhoods of size r. The estimates are not given explicitly in [51], but they follow from the argument. These results can be regarded as quantitative versions of Cheeger’s Finiteness Theorem [30], see [79, Ch. 10] and [78] for different proofs.
Remark 2
Using results of [2], one can show that for any \(\alpha <1\), M and \({\widetilde{M}}\) in Proposition 1 are close to each other in \(C^{1,\alpha }\) topology. However, we do not know explicit estimates in this case.
1.2.2 An Improved Estimate for the Injectivity Radius
The injectivity radius estimate provided by Theorem 1 is not good enough in the context of manifold reconstruction. Indeed, in order to obtain a good approximation one has to begin with a small r. (Recall that for Theorem 1 to work, \(\delta \) should be of order \(Kr^3\) where K is the curvature bound.) However, Theorem 1 guarantees only a lower bound of order r for \({{\,\mathrm{inj}\,}}_M\), so a priori one could end up with an approximating manifold M with a very small injectivity radius. In order to rectify this, we need the following result.
Proposition 2
There exists a universal constant \(C_8>0\) such that the following holds. Let \(K>0\) and let \(M, {\widetilde{M}}\) be complete n-dimensional Riemannian manifolds with \(|{\text {Sec}}_M|\le K\) and \(|{\text {Sec}}_{{\widetilde{M}}}|\le K\).
1. Let \(x\in M\), \({\widetilde{x}}\in {\widetilde{M}}\), and \( 0 < \rho \le \min \{{{\,\mathrm{inj}\,}}_{{\widetilde{M}}}({\widetilde{x}}) , \tfrac{\pi }{\sqrt{K}} \} . \) Then,
2. Suppose that M and \({\widetilde{M}}\) are \((1+\varepsilon ,\delta )\)-quasi-isometric where \(\varepsilon ,\delta \ge 0\). Then,
This result is important for the inverse problems of an approximate recovery of an unknown manifold \({\widetilde{M}}\). It is often the case that we a priori know bounds for the sectional curvature, injectivity radius, etc., of \({\widetilde{M}}\). On the other hand, any other manifold M described by Theorem 1 is \((1+C\delta r^{-1},C\delta )\)-quasi-isometric to \({\widetilde{M}}\). Thus, the second part of Proposition 2 gives a better estimate for \({{\,\mathrm{inj}\,}}_M\) than Theorem 1.
The proof of Proposition 2 is given in Sect. 4.
1.2.3 An Approximation Result with Only One Parameter
We summarize the manifold reconstruction features of Theorem 1 in the following corollary where all approximations, errors in data, as well as the errors in the reconstruction are given in terms of a single parameter \({\widehat{\delta }}\). Essentially, the corollary tells that a manifold N can be approximately reconstructed from a \({\widehat{\delta }}\)-net X of N and the information about local distances between points of X containing small errors. This type of results is useful, e.g., in inverse problems discussed below.
Corollary 3
Let \(K>0\), \(n\in {\mathbb {Z}}_+\) and (N, g) be a compact n-dimensional manifold with sectional curvature bounded by \(|{\text {Sec}}_N|\le K\). There exist \(\delta _0=\delta _0(n,K)\) and \(C_9=C_9(n),C_{10}=C_{10}(n)>0\) such that if \(0<\widehat{\delta }<\delta _0\), then the following holds:
Let \(r=({\widehat{\delta }}/K)^{1/3}\) and suppose that the injectivity radius \({{\,\mathrm{inj}\,}}_N\) of N satisfies \({{\,\mathrm{inj}\,}}_N>2r\). Also, let \(X=\{x_j:\ j=1,2,\dots ,J\}\subset N\) be a \({\widehat{\delta }}\)-net of N and \(\widetilde{d} :X\times X\rightarrow {\mathbb {R}}_+\cup \{0\}\) be an approximate local distance function that satisfies for all \(x,y\in X\)
and
Given the set X and the function \({\widetilde{d}}\), one can effectively construct a compact, smooth n-dimensional Riemannian manifold \((M,g_M)\), with distance function \(d_M\). This manifold approximates the manifold (N, g) in the following way:
-
1.
There is a diffeomorphism \(F:M\rightarrow N\) satisfying
$$\begin{aligned} \frac{1}{L}\le \frac{d_N(F(x),F(y))}{d_M(x,y)}\le L,\quad \hbox {for all }x,y\in M, \end{aligned}$$(15)where \(L=1+C_{10}K^{1/3}{\widehat{\delta }}\,{}^{2/3}\).
-
2.
The sectional curvature \({\text {Sec}}_M\) of M satisfies \(|{\text {Sec}}_M|\le C_9K\).
-
3.
The injectivity radius \({{\,\mathrm{inj}\,}}_M\) of M satisfies
$$\begin{aligned} {{\,\mathrm{inj}\,}}_M\ge \min \{(C_9K)^{-1/2}, (1-C_{10}K^{1/3}\widehat{\delta }\,{}^{2/3}){{\,\mathrm{inj}\,}}_N\} . \end{aligned}$$
The proof of Corollary 3 is given in the end of Sect. 6.
We call the function \({\widetilde{d}}:X\times X\rightarrow {\mathbb {R}}_+\cup \{0\}\), defined on the \({\widehat{\delta }}\)-net X and satisfying the assumptions of Corollary 3, an approximate local distance function with accuracy \({\widehat{\delta }}\). Many inverse problems can be reduced to a setting where one can determine the distance function \(d_N(x_j,x_k)\), with measurement errors \(\epsilon _{j,k}\), in a discrete set \(\{x_j\}_{j\in J}\subset N\). Thus, if the set \(\{x_j\}_{j\in J}\) is \({\widehat{\delta }}\)-net in N, the errors \(\epsilon _{j,k}\) satisfy conditions (14), and \({\widehat{\delta }}\) is small enough, then the diffeomorphism type of the manifold can be uniquely determined by Corollary 3. Moreover, the bi-Lipschitz condition (15) means that also the distance function can be determined with small errors. We emphasize that in (14) one needs to approximately know only the distances smaller than \(r=({\widehat{\delta }}/K)^{1/3}\). The larger distances can be computed as in (32).
1.2.4 Manifold Reconstructions in Imaging and Inverse Problems
Recently, geometric models have became an area of focus of research in inverse problems. As an example of such problems, one may consider an object with a variable speed of wave propagation. The travel time of a wave between two points defines a natural non-Euclidean distance between the points. This is called the travel time metric, and it corresponds to the distance function of a Riemannian metric. In many topical inverse problems, the task is to determine the Riemannian metric inside an object from external measurements, see, e.g., [61, 62, 75, 76, 89,90,91, 93]. These problems are the idealizations of practical imaging tasks encountered in medical imaging or in Earth sciences. Also, the relation of discrete and continuous models for these problems is an active topic of research, see, e.g., [9, 13, 14, 57]. In these results, discrete models have been reconstructed from various types of measurement data. However, a rigorously analyzed technique to construct a smooth manifold from these discrete models to complete the construction has been missing until now.
In practice, the measurement data always contain measurement errors and the amount of these data is limited. This is why the problem of the approximate reconstruction of a Riemannian manifold and the metric on it from discrete or noisy data is essential for several geometric inverse problems. Earlier, various regularization techniques have been developed to solve noisy inverse problems in the PDE setting, see, e.g., [36, 65], but most of such methods depend on the used coordinates and, therefore, are not invariant. One of the purposes of this paper is to provide invariant tools for solving practical imaging problems.
An example of problems with limited data is an inverse problem for the heat kernel, where the information about the unknown manifold (M, g) is given in the form of discrete samples \((h_M(x_j, y_k, t_i))_{j,k\in J,i\in I}\) of the heat kernel \(h_M(x, y, t)\), satisfying
where the Laplace operator \(\varDelta _g\) operates in the x variable, see, e.g., [56]. Here \(y_j=x_j\), where \(\{x_j:\ j\in J\}\) is a finite \(\varepsilon \)-net in an open set \(\varOmega \subset M\), while \(\{t_i:\ i\in I\}\) is in \(\varepsilon \)-net of the time interval \((t_0, t_1)\). It is also natural to assume that one is given measurements \(h_M^{(m)}(x_j, y_k, t_i)\) of the heat kernel with errors satisfying \(|h_M^{(m)}(x_j, y_k, t_i)-h_M(x_j, y_k, t_i)|<\varepsilon \). Several inverse problems for the wave equation lead to a similar problem for the wave kernel \(G_M(x,y,t)\) satisfying
see, e.g., [53, 56, 72]. In the case of complete data (corresponding to the case when \(\varepsilon \) vanishes), the inverse problem for heat kernel and wave kernel is equivalent to the inverse interior spectral problem, see [55]. In this problem, one considers the eigenvalues \(\lambda _k\) of \(-\varDelta _g\), counted by their multiplicity, and the corresponding \(L^2(M)\)-orthonormal eigenfunctions, \(\varphi _k(x)\), that satisfy
In the inverse interior spectral problem, one assumes that we are given approximations \({\widetilde{\lambda }}_k,\)\(k=0,1, 2,\dots , N-1\), to the first N smallest eigenvalues of \(-\varDelta _g\), and values \(\varphi _k^{\prime }(x_j)\), at points \(x_j\), of approximations to the eigenfunctions \(\varphi _k\). Here \(x_j\) form an \(\varepsilon \)-net \(\{x_j:\ j\in J\}\subset \varOmega \), where \(\varOmega \subset M\) is open, and \(|{\widetilde{\lambda }}_k -\lambda _k| \le \varepsilon \) and \(|\varphi _k^{\prime }(x_j)-\varphi _k(x_j)|<\varepsilon \).
It is shown in [15] that these data determine a metric space \((X, d_X)\) which is a \(\delta -\)approximation (in the Gromov–Hausdorff distance) to the unknown manifold M, where \(\delta = \delta (\varepsilon ,N; \varOmega )\) tends to 0 as \(\varepsilon \rightarrow 0\) and \(N\rightarrow \infty \). It may be noted that the earlier works [3, 57] dealt with similar approximations (under other geometric conditions) for the case of manifolds with boundary and the Laplace operators with some classical boundary conditions.
Returning to the case when M has no boundary, Theorem 1 completes the solution of the above inverse problems by constructing a smooth manifold that approximates M.
1.3 Interpolation of Manifolds in Hilbert Spaces
As already mentioned, in the proof of Theorem 1 we need to approximate a set in a Hilbert space by an n-dimensional submanifold (with bounded geometry). At small scale, the set in question should be close to affine subspaces in the following sense.
Definition 4
Let E be a Hilbert space, \(X\subset E\), \(n\in {\mathbb {N}}\) and \(r,\delta >0\). We say that X is \(\delta \)-close to n-flats at scale r if for any \(x\in X\), there exists an n-dimensional affine space \(A_x\subset E\) through x such that
To formulate our result for the sets in Hilbert spaces, we recall some definitions. By a closed submanifold of a Hilbert space E, we mean a finite-dimensional smooth submanifold which is a closed subset of E.
Let \(M\subset E\) be a closed submanifold. The reach of M, denoted by \({{\,\mathrm{Reach}\,}}(M)\), is the supremum of all \(r>0\) such that for every \(x\in {{\mathcal {U}}}_r(M)\) there exists a unique nearest point in M. We denote this nearest point by \(P_M(x)\) and refer to the map \(P_M:{{\mathcal {U}}}_r(M)\rightarrow M\) as the normal projection.
For \(x\in M\), we denote by \(T_xM\) the tangent space of M at x. The tangent space is regarded as an affine subspace of E containing x. We denote by \(\mathbf {T}_xM\) the linear subspace of E parallel to \(T_xM\).
Theorem 2
For every \(n,k\in {\mathbb {N}}\), there exist positive constants \({\sigma _2}\), \(C_{11}\), \(C_{12}\) depending only on n and a positive constant \(C_{13}({n,k})>0\) such that the following holds. Let E be a separable Hilbert space, \(X\subset E\), \(r>0\) and
Suppose that X is \(\delta \)-close to n-flats at scale r (see Definition 4). Then, there exists a closed n-dimensional smooth submanifold \(M\subset E\) such that:
-
1.
\(d_H(X,M)\le 5\delta \).
-
2.
The second fundamental form of M at every point is bounded by \(C_{11}\delta r^{-2}\).
-
3.
\({{\,\mathrm{Reach}\,}}(M)\ge r/3\).
-
4.
The normal projection \(P_M:{{\mathcal {U}}}_{r/3}(M)\rightarrow M\) is smooth and satisfies for all \(x\in {{\mathcal {U}}}_{r/3}(M)\)
$$\begin{aligned} \Vert d^k_x P_M\Vert < C_{13}(n,k) \delta r^{-k}, \qquad k\ge 2 , \end{aligned}$$(18)and
$$\begin{aligned} \Vert d_x P_M - P_{\mathbf {T}_yM}\Vert < C_{13}(n,1) \delta r^{-1} \end{aligned}$$(19)where \(y=P_M(x)\) and \(P_{\mathbf {T}_yM}\) is the orthogonal projector to \(\mathbf {T}_yM\).
-
5.
The tangent spaces of M approximate subspaces \(A_x\) from Definition 4 in the following sense. If \(x\in X\) and \(y=P_M(x)\), then the angle between \(A_x\) and the tangent space \(T_yM\) satisfies
$$\begin{aligned} \angle (A_x,T_yM) < C_{12}\delta r^{-1} . \end{aligned}$$(20)
Notations In (19), (18) and throughout the paper, \(d_x\) and \(d^k_x\) denote the first and kth differentials of a smooth map at a point x. The norm of the kth differential is derived from the inner product norm on E in the standard way. As usual, we define the \(C^k\)-norm of a map f defined on an open set \(U\subset E\), by
where \(d_x^0f=f(x)\).
The angle \(\angle (A_1,A_2)\) between n-dimensional linear subspaces \(A_1,A_2\subset E\) is defined by
where \(\angle (u_1,u_2) = \arccos \frac{\langle u_1,u_2\rangle }{|u_1||u_2|}\) and \(\langle \,\cdot ,\cdot \,\rangle \) is the inner product in E. The angle between affine subspaces is defined as the angle between their parallel translates containing the origin. Note that if \(A_1\) and \(A_2\) are linear subspaces and \(P_{A_1}\) and \(P_{A_2}\) are orthogonal projectors onto \(A_1\) and \(A_2\), respectively, then
The proof of Theorem 2 is given in Sect. 3. An algorithm based on Theorem 2, which also summarizes the main objects used in its proof, is given in Sect. 7, see also Fig. 2.
The above question of submanifold interpolation has attracted recently much interest in geometry and machine learning. For example, an interpolation problem similar to Theorem 2 has been considered in the recent paper of Kleiner and Lott concerning Perelman’s proof of the geometrization conjecture, see [60, Lemma B.2]. Compared to these results, our method provides explicit geometric bounds for M in claims (2)–(4) of Theorem 2, whereas the bounds in [60, Lemma B.2] arise from a contradiction argument and have the form of an unknown \(\varepsilon =\varepsilon (\delta ,\dots )\) which just goes to 0 along with \(\delta \). In particular, Theorem 2 provides explicit curvature bounds that are linear in \(\delta \). This is essential in the proof of Theorem 1 as well as in applications.
In Remark 7, we show that the bounds in claims (2) and (3) in Theorem 2 are optimal, up to constant factors depending on n. Thus, Theorem 2 gives necessary and sufficient conditions (up to multiplication of the bounds by a constant factor) for a set \(X\subset E\) to approximate a smooth submanifold with given geometric bounds.
A schematic visualization of the interpolation algorithm ‘SubmanifoldInterpolation’ based on Theorem 2. In the figure, on the top, the black data points \(X\subset E={\mathbb {R}}^m\) have a \(\delta \)-neighborhood \(U={\mathcal U}_\delta (X)\). The boundary of U is marked by blue. In the figures below, we determine, near points \(x_i\in X\), \(i=1,2,3\) the approximating n-dimensional planes \(A_i\), marked by red lines. Then, we map the set U by applying to it iteratively functions \(\varphi _i:E\rightarrow E\), defined in (71). The maps \(\varphi _i\) are convex combinations of the projector \(P_{A_i}\), onto \(A_i\), and the identity map. The three figures on the bottom show the sets \(\varphi _1(U)\), \(\varphi _2(\varphi _1(U))\), and \(\varphi _3(\varphi _2(\varphi _1(U)))\), respectively. The limit of these sets converges to the n-dimensional submanifold \(M\subset E\) (Color figure online)
In order to approximate a submanifold M as in Theorem 2, the set X must contain as many points as a \(C\delta \)-net in M. This is an unreasonably large number of points when \(\delta \) is small. The following corollary allows one to reconstruct M from a smaller approximating set. It involves two parameters \(\varepsilon \) and \(\delta \) where \(\varepsilon \) is a ‘density’ of a net and \(\delta \) is a ‘measurement error.’ Note that \(\delta \) may be much smaller than \(\varepsilon \). A similar generalization is possible for Theorem 1, but we omit these details.
Corollary 4
For every \(n\in {\mathbb {N}}\), there exist \({\sigma _2}={\sigma _2}(n)>0\) and \(C_{14}=C_{14}(n)>0\) such that the following holds. Let E be a Hilbert space, \(X\subset E\), \(0<\varepsilon <r/10\) and \(0<\delta <{\sigma _2}r\). Suppose that for every \(x\in X\) there exists an n-dimensional affine subspace \(A_x\subset E\) such that the set \(X\cap B_r(x)\) is within Hausdorff distance \(\delta \) from an \(\varepsilon \)-net of the affine n-ball \(A_x\cap B_r(x)\).
Then, there exists a closed n-dimensional submanifold \(M\subset E\) satisfying properties 2–4 of Theorem 2 and an \(\varepsilon \)-net Y of M such that
Proof sketch
Consider the set \( X' = \bigcup _{x\in X} (A_x \cap B_r(x)) \subset E . \) A suitably modified version of Lemma 9 implies that \(\angle (A_x,A_y)<C\delta r^{-1}\) for all \(x,y\in X\) such that \(|x-y|<r\). It then follows that \(X'\) is \(C\delta \)-close to n-flats at scale \(r-C\delta \). Now the corollary follows from Theorem 2 applied to \(X'\). \(\square \)
1.4 Submanifold Interpolation and Machine Learning
The construction of a manifold that approximates, in some suitable sense, the given data points is a classical problem of machine learning. We emphasize that we consider reconstruction of manifolds which are either considered as (differentiable) Riemannian manifolds or embedded submanifolds of an Euclidean space but not immersed submanifolds of an Euclidean space (i.e., a submanifold that intersects itself) that are outside the context of this paper.
Next we give a short review on existing methods and discuss how Theorem 2 is applied for problems of manifold learning.
1.4.1 Literature on Submanifold Interpolation
The question of fitting a manifold to data has been of interest to data analysts and statisticians of late. There are several results dealing exclusively with sample complexity such as [1, 48, 64, 66, 67]. We will restrict our attention to results that provide an algorithm for describing a manifold to fit the data together with upper bounds on the sample complexity.
A work in this direction, [49], building over [74] provides an upper bound on the Hausdorff distance between the output manifold and the true manifold equal to \(O((\frac{\log N}{N})^{\frac{2}{D+8}}) + \widetilde{O}(\sigma ^2\log (\sigma ^{-1}))\). In order to obtain a Hausdorff distance of \(c\varepsilon \), one needs more than \(\varepsilon ^{-D/2}\) samples, where D is the ambient dimension. The results of [43] guarantee (for sufficiently small \(\sigma \)) a Hausdorff distance of
with less than
samples, where d is the dimension of the submanifold, V is in upper bound in the \(d-\)dimensional volume, and \(\sigma \) is the standard deviation of the noise projected in one dimension. The question of fitting a manifold \({{\mathcal {M}}}_o\) to data with control both on the reach \(\tau _o\) and mean squared distance of the data to the manifold was considered in [44]. The paper [44] did not assume a generative model for the data and had to use an exhaustive search over the space of candidate manifolds whose time complexity was doubly exponential in the intrinsic dimension d of \({{\mathcal {M}}}_o\). In [43], the construction of \({{\mathcal {M}}}_o\) has a sample complexity that is singly exponential in d, made possible by the generative model, while [44] did not specify the bound on \(\tau _o\), beyond stating that the multiplicative degradation \(\frac{\tau }{\tau _o}\) in the reach depends on the intrinsic dimension alone. In [43], this degradation is pinned down to within \((0, C d^7]\), where C is an absolute constant and d is the dimension of \({{\mathcal {M}}}\).
There are also methods which map high-dimensional data points to low-dimensional piecewise linear manifolds. Cheng, Dey and Ramos present an algorithm [32] to reconstruct a smooth k-dimensional manifold \({\mathcal {M}}\) embedded in a Euclidean space from a sufficiently dense point sample on the manifold. The algorithm outputs a simplicial manifold that is homeomorphic to \({\mathcal {M}}\) and close to \({\mathcal {M}}\) in Hausdorff distance (see also the related work using witness complexes in [12]). In recent work, Aamari and Levrard [1] derive optimal rates for the estimation of tangent spaces the second fundamental form, and the submanifold \({\mathcal {M}}\) given a sample drawn from a submanifold \({\mathcal {M}}\) of Euclidean space. Unlike this paper or [43, 44, 49], they do not, however, provide a method to produce a single consistent manifold from finitely many samples. In other recent work [11], Boissonnat et al. presented an algorithm for producing Delaunay triangulations of manifolds. Given a set of sample points and an atlas on a compact manifold, a manifold Delaunay complex is produced for a perturbed point set provided the transition functions are bi-Lipschitz with a constant close to 1, and the original sample points meet a local density requirement. The output complex is endowed with a piecewise-flat metric which is a close approximation of the original Riemannian metric. This is similar to our present work, except that our metric is \(C^\infty \), and not just piecewise linear.
1.4.2 Literature on Manifold Learning
The following methods aim to transform data lying near a d-dimensional manifold in an N-dimensional space into a set of points in a low-dimensional space close to a d-dimensional manifold. During transformation, all of them try to preserve some geometric properties, such as appropriately measured distances between points of the original data set. Usually the Euclidean distance to the ‘nearest’ neighbors of a point is preserved. In addition, some of the methods preserve, for points farther away, some notion of geodesic distance capturing the curvature of the manifold.
Perhaps the most basic of such methods is ‘principal component analysis’ (PCA), [52, 77] where one projects the data points onto the span of the d eigenvectors corresponding to the top d eigenvalues of the (\(N\times N\)) covariance matrix of the data points.
An important variation is the ‘Kernel PCA’ [84] where one defines a feature map \(\varphi (\cdot )\) mapping the data points into a Hilbert space called the feature space. A ‘kernel matrix’ K is built whose (i, j)th entry is the dot product \(\langle \varphi (x_i), \varphi (x_j)\rangle \) between the data points \(x_i,x_j.\) From the top d eigenvectors of this matrix, the corresponding eigenvectors of the covariance matrix of the image of the data points in the feature space can be computed. The data points are projected onto the span of these eigenvectors of this covariance matrix in the feature space.
In the case of ‘multi-dimensional scaling’ (MDS) [34], only pairwise distances between points are attempted to be preserved. One minimizes a certain ‘stress function’ which captures the total error in pairwise distances between the data points and between their lower-dimensional counterparts. For instance, a raw stress function could be \(\varSigma (\Vert x_i-x_j\Vert -\Vert y_i-y_j\Vert )^2,\) where \(x_i\) are the original data points, \(y_i,\) the transformed ones, and \(\Vert x_i-x_j\Vert ,\) the distance between \(x_i, x_j.\)
‘Isomap’ [92] attempts to improve on MDS by trying to capture geodesic distances between points while projecting. For each data point, a ‘neighborhood graph’ is constructed using its k neighbors (k could be varied based on various criteria), the edges carrying the length between points. Now the shortest distance between points is computed in the resulting global graph containing all the neighborhood graphs using a standard graph theoretic algorithm such as Dijkstra’s. Let \(D = [d_{ij}]\) be the \(n\times n\) matrix of graph distances. Let \(S = [d_{ij}^2]\) be the \(n \times n\) matrix of squared graph distances. Form the matrix, \(A =\frac{1}{2}HSH,\) where \(H = I - n^{-1}{\mathbf {1}}{\mathbf {1}}^T\). The matrix A is of rank \(t < n\), where t is the dimension of the manifold. Let \(A^Y =\frac{1}{2}HS^YH\), where \([S^Y]_{ij} = \Vert y_i - y_j\Vert ^2.\) Here the \(y_i\) are arbitrary t-dimensional vectors. The embedding vectors \({\widehat{y}}_i\) are chosen to minimize \(\Vert A - A^Y\Vert \). The optimal solution is given by the eigenvectors \(v_1, \dots , v_t\) corresponding to the t largest eigenvalues of A. The vertices of the graph G are embedded by the \(t \times n\) matrix
‘Maximum variance unfolding’ (MVU) [94] also constructs the neighborhood graph as in the case of Isomap but tries to maximize distance between projected points keeping distance between the nearest points unchanged after projection. It uses semidefinite programming for this purpose.
In ‘Diffusion Maps’ [33], a complete graph on the data points is built and each edge is assigned a weight based on a gaussian: \(w_{ij}\equiv \exp ({\frac{\Vert x_i-x_j\Vert ^2}{\sigma ^2}}).\) Normalization is performed on this matrix so that the entries in each row add up to 1. This matrix is then used as the transition matrix P of a Markov chain. \(P^t\) is therefore the transition probability between data points in t steps. The d nontrivial eigenvalues \(\lambda _i\) and their eigenvectors \(v_i\) of \(P^t\) are computed, and the data are now represented by the matrix \([\lambda _1v_1, \cdots , \lambda _dv_d], \) with the row i corresponding to data point \(x_i.\)
The following are essentially local methods of manifold learning in the sense that they attempt to preserve local properties of the manifold around a data point.
‘Local linear embedding’ (LLE) [81] preserves solely local properties of the data. Let \(N_i\) be the neighborhood of \(x_i\), consisting of k points. Find optimal weights \({\widehat{w}}_{ij}\) by solving \( {\widehat{W}} := \arg \min _W \sum _{i=1}^n \Vert x_i - \sum _{j=1}^n w_{ij}x_j\Vert ^2,\) subject to the constraints (i) \(\forall i, \sum _j w_{ij} = 1\), (ii) \(\forall i,j, w_{ij} \ge 0,\) (iii) \(w_{ij} = 0 \) if \(j \not \in N_i.\) Once the weight matrix \({\widehat{W}}\) is found, a spectral embedding is constructed using it. More precisely, a matrix \({\widehat{Y}}\) is a \(t \times n\) matrix constructed satisfying \( {\widehat{Y}} = \arg \min _Y Tr( {YMY^T}),\) under the constraints \(Y{\mathbf {1}} = 0\) and \(YY^T = nI_t\), where \(M = (I_n - {\widehat{W}})^T(I_n - {\widehat{W}})\). \({\widehat{Y}}\) is used to get a t-dimensional embedding of the initial data.
In the case of the ‘Laplacian eigenmap’ [4, 54] again, a nearest neighbor graph is formed. The details are as follows. Let \(n_i\) denote the neighborhood of i. Let \(W = (w_{ij})\) be a symmetric \((n \times n)\) weighted adjacency matrix defined by (i) \(w_{ij} = 0\) if j does not belong to the neighborhood of i; (ii) \(w_{ij} = \exp (\Vert x_i - x_j\Vert ^2/{2\sigma ^2}),\) if \(x_j\) belongs to the neighborhood of \(x_i\). Here \(\sigma \) is a scale parameter. Let G be the corresponding weighted graph. Let \(D = (d_{ij})\) be a diagonal matrix whose ith entry is given by \((W {\mathbf {1}})_i\). The matrix \(L = D - W\) is called the Laplacian of G. We seek a solution in the set of \(t \times n\) matrices \( {\widehat{Y}} = \arg \min _{Y:YDY^T = I_t}\hbox {Tr}(YLY^T).\) The rows of \({\widehat{Y}}\) are given by solutions of the equation \(Lv = \lambda D v\).
Hessian LLE (HLLE) (also called Hessian eigenmaps) [35] and ‘local tangent space alignment’ (LTSA) [100] attempt to improve on LLE by also taking into consideration the curvature of the higher-dimensional manifold while preserving the local pairwise distances. We describe LTSA below.
LTSA attempts to compute coordinates of the low-dimensional data points and align the tangent spaces in the resulting embedding. It starts with computing bases for the approximate tangent spaces at the datapoints \(x_i\) by applying PCA on the neighboring data points. The coordinates of the low-dimensional data points are computed by carrying out a further minimization \(min_{Y_i,L_i}\varSigma _i \Vert Y_iJ_k -L_i\varTheta _i\Vert ^2\). Here \(Y_i\) has as its columns, the lower- dimensional vectors, \(J_k\) is a ‘centering’ matrix, \(\varTheta _i\) has as its columns the projections of the k neighbors onto the d eigenvectors obtained from the PCA, and \(L_i\) maps these coordinates to those of the lower-dimensional representation of the data points. The minimization is again carried out through suitable spectral methods.
The alignment of local coordinate mappings also underlies some other methods such as ‘local linear coordinates’ (LLC) [82] and ‘manifold charting’ [16].
Each of the algorithms is based on strong domain-based intuition and in general performs well in practice at least for the domain for which it was originally intended. PCA is still competitive as a general method.
Some of the algorithms are known to perform correctly under the hypothesis that data lie on a manifold of a specific kind. In Isomap and LLE, the manifold has to be an isometric embedding of a convex subset of Euclidean space. In the limit as the number of data points tends to infinity, when the data approximate a manifold, then one can recover the geometry of this manifold by computing an approximation of the Laplace–Beltrami operator. Laplacian eigenmaps and diffusion maps rest on this idea. LTSA works for parameterized manifolds, and detailed error analysis is available for it.
1.4.3 Theorems 1 and 2 and the Problems of Machine reconstruction
Theorem 1 addresses the fundamental question, when a given metric space \((X,d_X)\), corresponding to data points and their ‘abstract’ mutual distances, approximates a Riemannian manifold with a bounded sectional curvature and injectivity radius. In the context of Theorem 1, the distances are measured in intrinsic sense in M and X.
Theorem 2 deals with approximating a subset of a Hilbert space E satisfying certain local constraints by a manifold having bounded second fundamental form and reach. In the context of Theorem 2, the distances are measured in extrinsic sense in E. Such approximations have extensively been considered in machine learning or, more precisely, manifold learning and nonlinear dimensionality reduction, where the goal is to approximate the set of data lying in a high-dimensional space like E by a submanifold in E of a low enough dimension in order to visualize these data, see, e.g., references of Sect. 1.4.2.
The results of this paper provide for the observed data an abstract low-dimensional representation of the intrinsic manifold structure that the data may possess. In particular, the topology of the manifold structure is determined, assuming that the sampling density has been sufficient. As described in Sect. 3, the proof of Theorem 2 is of a constructive nature and provides an algorithm to perform such visualization. Note that this algorithm starts with tangent-type planes which makes it distantly similar to the LTSA method in machine learning, see, e.g., [63, 100]. In paper [44], the authors provide a method of visualization of a given data using a probabilistic setting. In comparison, Theorem 2 helps us visualize data in a deterministic setting.
The results of this paper are also related to dimensionality reduction considered extensively in machine learning, see, e.g., [4,5,6, 80]. Using the constructions of Sect. 5.2, we can associate with given data not only the metric structure but also point measures. Combining this with the constructions of [28], one could analyze the approximate determination of the eigenvalues and eigenfunctions of a manifold that approximates the data set.
2 Approximation of Metric Spaces
In this section, we collect preliminaries about GH and quasi-isometric approximation of metric spaces. In Sects. 2.4 and 2.5, we present algorithms that can be used to verify the assumptions of Theorems 1 and 2 .
2.1 Gromov–Hausdorff Approximations
Let X be a metric space. Recall that the Hausdorff distance between sets \(A,B\subset X\) is defined by
where \({{\mathcal {U}}}_r\) denotes the r-neighborhood of a set.
The Gromov–Hausdorff (GH) distance \(d_{\mathrm{GH}}(X,Y)\) between metric spaces X and Y is the infimum of all \(\varepsilon >0\) such that there exist a metric space Z and subsets \(X',Y'\subset Z\) isometric to X and Y, resp., such that \(d_H(X',Y')<\varepsilon \). One can always assume that Z is the disjoint union of X and Y with a metric extending those of X and Y. The pointed GH distance between pointed metric spaces \((X,x_0)\) and \((Y,y_0)\) is defined in the same way with an additional requirement that \(d_Z(x_0,y_0)<\varepsilon \). See, e.g., [79, §1.2 in Ch. 10] or [26] for details.
Example 1
(Distorted net) Recall that a subset S of a metric space X is called an \(\varepsilon \)-net if \({{\mathcal {U}}}_\varepsilon (S)=X\). Let S be an \(\varepsilon \)-net in X and imagine that we have measured the distances between points of S with an absolute error \(\varepsilon \), that is, we have a distance function \(d'\) on \(S\times S\) such that \(|d'(x,y)-d(x,y)|<\varepsilon \) for all \(x,y\in S\). Then, the GH distance between X and \((S,d')\) is bounded by \(2\varepsilon \). This follows from the fact that the inclusion \(S\hookrightarrow X\) is an \(\varepsilon \)-isometry from \((S,d')\) to (X, d), see below.
Strictly speaking, the ‘measurement errors’ in this example may break the triangle inequality so that \((S,d')\) is no longer a metric space. This can be fixed by adding \(3\varepsilon \) to all \(d'\)-distances.
Let X, Y be metric spaces, \(f:X\rightarrow Y\) a (not necessarily continuous) map, and \(\varepsilon >0\). The distortion of f, denoted by \({{\,\mathrm{dis}\,}}f\), is defined by
and f is called an \(\varepsilon \)-isometry if \({{\,\mathrm{dis}\,}}f<\varepsilon \) and f(X) is an \(\varepsilon \)-net in Y.
If \(d_{\mathrm{GH}}(X,Y)<\varepsilon \), then there exists a \(2\varepsilon \)-isometry from X to Y, and conversely, if there is an \(\varepsilon \)-isometry from X to Y, then \(d_{\mathrm{GH}}(X,Y)<2\varepsilon \). Moreover,
Also, if f(X) is \(\varepsilon -\)net in Y, then
See [26, §7.3.3] for proofs of these facts. They also hold for the pointed GH distance between pointed metric spaces \((X,x_0)\) and \((Y,y_0)\), provided that \(f(x_0)=y_0\). Throughout the paper, we use these properties without explicit reference.
If f is a \((\lambda ,\varepsilon )\)-quasi-isometry (see Definition 3), then \({{\,\mathrm{dis}\,}}f\le (\lambda -1){{\,\mathrm{diam}\,}}(X)+\varepsilon \). This together with (25)–(26) implies (6). The next lemma is a variant of (6) for metric balls.
Lemma 1
Let \(f:X\rightarrow {M}\) be a \((\lambda ,\varepsilon )\)-quasi-isometry and suppose that \(({M,d_M)}\) is a Riemannian manifold. Then, every r-ball in M is within GH distance \(2(\lambda -1) r + {5}\varepsilon \) from some r-ball in X. More precisely,
for all \(x\in X\) and \(y\in {M}\) such that \(d_{M}(f(x),y)<\varepsilon \).
Proof
Let x and y be as in the formulation. Then,
for all \(r_1,r_2>0\).
Fix \(r>0\) and denote \({X_1}=B^X_r(x)\) and \({{M}_1}={B^{M}_r(y)}\). Since \({{\,\mathrm{diam}\,}}({X_1})\le 2r\), the distortion of \(f|_{{X_1}}\) is bounded by \(2(\lambda -1)r+\varepsilon \). Hence, by (26),
where \(f({X_1})\) is regarded as a pointed metric space with distinguished point f(x). Now we estimate the Hausdorff distance \(d_H(f({X_1}),{{M}_1})\) in M. By (5) and (28),
To prove that \({{M}_1}\) is contained in a suitable neighborhood of \(f({X_1})\), let \(r_1=\lambda ^{-1}r-3\varepsilon \) and consider \(z\in {B^{M}_{r_1}(y)}\). Since f(X) is an \(\varepsilon \)-net in M, there is \(x'\in X\) such that \(d_{M}(z,f(x'))<\varepsilon \), and hence, \(d_{M}(f(x),f(x'))<r_1+2\varepsilon \). This and (5) imply that
hence, \(x'\in {X_1}\). Thus, \( {B^{M}_{r_1}(y)} \subset \mathcal U_{\varepsilon }(f({X_1})) \). This and (28) imply that
Thus, \(d_H(f({X_1}),{{M}_1}) \le \max (\varepsilon ,\varepsilon _1,\varepsilon _2) < (\lambda -1)r+4\varepsilon \). Since the Hausdorff distance is an upper bound for the GH distance, this and (29) imply (27). \(\square \)
2.2 Almost Intrinsic Metrics
Here we discuss properties of \(\delta \)-intrinsic metrics and related notions from Definition 2. First observe that, if \(x_1,x_2,\dots ,x_N\) is a \(\delta \)-straight sequence, then its ‘length’ satisfies
This follows by induction from (4) and the triangle inequality.
The next lemma characterizes almost intrinsic metrics as those that are GH close to Riemannian manifolds. However, manifolds provided by this lemma may have extremely large curvatures and tiny injectivity radii.
Lemma 2
Let X be a metric space and \(\delta >0\). 1. If there exists a length space Y such that \(d_{\mathrm{GH}}(X,Y)<\delta \), then X is \(6\delta \)-intrinsic. 2. Conversely, if X is compact and \(\delta \)-intrinsic, then there exists a two-dimensional Riemannian manifold M such that
where \(C_{15}\) is a universal constant.
Proof
1. By the definition of the GH distance, there exists a metric d on the disjoint union \(Z:=X\sqcup Y\) such that d extends \(d_X\) and \(d_Y\) and \(d_H(X,Y)<\delta \) in (Z, d). Let \(x,x'\in X\). Since \(d_H(X,Y)<\delta \), there exist \(y,y'\in Y\) such that \(d(x,y)<\delta \) and \(d(x',y')<\delta \). Connect y to \(y'\) by a minimizing geodesic and let \(y=y_1,y_2,\dots ,y_N=y'\) be a sequence of points along this geodesic such that \(d(y_i,y_{i+1})<\delta \) for all i. For each \(i=2,\dots ,N-1\), choose \(x_i\in X\) such that \(d(x_i,y_i)<\delta \). Then, \(x,x_2,\dots ,x_{N-1},x'\) is a \(6\delta \)-straight \(3\delta \)-chain connecting x and \(x'\). Since x and \(x'\) are arbitrary points of X, the claim follows.
2. Since we do not use this claim, we do not give a detailed proof of it. Here is a sketch of the construction. First, arguing as in [26, Proposition 7.5.5], one can approximate X by a metric graph. If X is \(\delta \)-intrinsic, the graph can be made GH \(C_{15}\delta \)-close to X. Consider a piecewise-smooth arcwise isometric embedding of the graph into \({\mathbb {R}}^3\), and let M be a smoothed boundary of a small neighborhood of the image. Then, M is a two-dimensional Riemannian manifold which can be made arbitrarily close to the graph and hence \(C_{15}\delta \)-close to X. \(\square \)
Now we describe a construction that makes a \(C\delta \)-intrinsic metric out of a metric which is \(\delta \)-close to \({\mathbb {R}}^n\) at scale r (see Definition 1). More generally, let \(X=(X,d)\) be a metric space in which every ball of radius r is \(\delta \)-intrinsic, where \(r>\delta >0\). For \(x,y\in X\), define the new distance \(d'(x,y)\) by
where the infimum is taken over all finite sequences \(x_1,\dots ,x_N\) connecting x to y and such that every pair of subsequent points \(x_i,x_{i+1}\) is contained in a ball of radius r in (X, d).
In order to avoid infinite \(d'\)-distances, we need to assume that any two points can be connected by such a sequence. If this is not the case, X divides into components separated from one another by distance at least r. For our purposes, such components are unrelated to one another just like disconnected components of a manifold.
Lemma 3
Under the above assumptions, the function \(d'\) given by (32) is a \(8\delta \)-intrinsic metric on X. Furthermore, d and \(d'\) coincide within any ball of radius r.
Proof
The triangle inequality for d implies that \(d'\) is a metric, \(d'\ge d\), and \(d'(x,y)=d(x,y)\) if x and y belong to an r-ball in (X, d). It remains to verify that \((X,d')\) is \({8}\delta \)-intrinsic. Let \(x,y\in X\) and let \(x=x_1,\dots ,x_N=y\) be a sequence realizing the infimum in (32) with an error less than \(\delta \). Then,
hence, the sequence \(\{x_i\}\) is \(\delta \)-straight with respect to \(d'\). Recall that every pair \(x_i,x_{i+1}\) belongs to an r-ball and this ball is \(\delta \)-intrinsic. Hence, there is a \(\delta \)-straight \(\delta \)-chain \(S_i=\{z_j^{(i)}\}_{j=1}^{N_i}\) connecting \(x_i\) to \(x_{i+1}\) and contained in an r-ball. Joining the sequences \(S_i\) together yields a \(\delta \)-chain \(\{y_k\}_{k=1}^{N'}\), \(N'=\sum N_i\), connecting x to y.
It suffices to prove that the sequence \(\{y_k\}\) is \(8\delta \)-straight with respect to \(d'\). Note that the chains \(S_i\) are \(\delta \)-straight with respect to both d and \(d'\) since the two metrics coincide in any r-ball. Let \(a_i=d'(x,x_i)\) for \(i=1,\dots ,N\). Then, for \(i\le j\) we have
by the triangle inequality and the \(\delta \)-straightness of \(\{x_i\}\). For \(k\in \{1,\dots ,N'\}\), define
where \(i=i(k)\) is the index such that \(y_k\) belongs to \(S_i\). Note that, for \(y_k\in S_i\),
due to the \(\delta \)-straightness of \(S_i\) and (33). We claim that
for all \(k,m\in \{1,\dots ,N'\}\) such that \(k\le m\). If both \(y_k\) and \(y_m\) are from one sub-chain \(S_i\), then (36) follows from the \(\delta \)-straightness of \(S_i\). Assume that \(y_k\in S_i\) and \(y_m\in S_j\) where \(i<j\). Then, the triangle inequality
and relations \(d'(y_k,x_{i+1})<a_{i+1} - b_k + 2\delta \) (cf. (35)), \(d'(x_{i+1},x_j)< a_j-a_{i+1} + \delta \) (cf. (33)), and \(d'(x_j,y_m)=b_m-a_j\) (cf. (34)) imply the upper bound in (36). Similarly, the lower bound in (36) follows from the triangle inequality
and relations \(d'(x_i,x_{j+1}) \ge a_{j+1}-a_i\) (cf. (33)), \(d'(x_i,y_k) = b_k-a_i\) (cf. (34)), and \(d'(y_m,x_{j+1}) < a_{j+1}-b_m+2\delta \) (cf. (35)). This finishes the proof of (36).
For \(k,m,n\in \{1,\dots ,N'\}\) such that \(k\le m\le n\), (36) implies that
Thus, \(\{y_k\}\) is a \(8\delta \)-straight sequence and the lemma follows. \(\square \)
The next lemma shows that if a map is almost isometric at small scale, then it is a quasi-isometry with small constants. It is used in the proof of Theorem 1.
Lemma 4
Let \(r>{15}\delta >0\). Let X and Y be \(\delta \)-intrinsic metric spaces and \(f:X\rightarrow Y\) a map such that f(X) is a \(\delta \)-net in Y and
for all \(x,y\in X\) such that
Then, f is a \((1+{10}r^{-1}\delta ,{3\delta })\)-quasi-isometry.
Proof
Let \(p,q\in X\) and \(D=d_X(p,q)\). We have to verify that
Since X is \(\delta \)-intrinsic, p and q can be connected by a \(\delta \)-straight \(\delta \)-chain, see Definition 2. This chain contains a subsequence \(p=x_1,x_2,\dots ,x_N=q\) such that \( r-\delta< d_X(x_i,x_{i+1}) < r \) for all \(i=1,\dots ,N-2\) and \(d_X(x_{N-1},q)<r\). Since the subsequence is also \(\delta \)-straight, by (30) we have
Since \(d_X(x_i,x_{i+1})>r-\delta \) for each \(i\le N-2\), the left-hand side of (39) is bounded below by \((N-2)(r-\delta )\). Hence,
By (37), we have \(d_Y(f(x_i),f(x_{i+1})) < d_X(x_i,x_{i+1})+\delta \) for all i. Therefore,
Thus,
Since \(r-2\delta >r/2\), the second inequality in (38) follows.
To prove the first inequality in (38), interchange the roles of X and Y and apply the same argument to an ‘almost inverse’ map \(g:Y\rightarrow X\) constructed as follows: For each \(y\in Y\), let g(y) be an arbitrary point from the set \(f^{-1}(B_\delta (y))\). This map satisfies the assumptions of the lemma with \(3\delta \) in place of \(\delta \) and \(r-2\delta \) in place of r. We may assume that \(g(f(p))=p\) and \(g(f(q))=q\); then, (41) for g takes the form
This implies the first inequality in (38) and the lemma follows. \(\square \)
2.3 GH Approximations of the Disk
Here we prove a technical Lemma 6 about \(\delta \)-isometries to subsets of \({\mathbb {R}}^n\). For a matrix \(A\in {\mathbb {R}}^{n\times n}\), the norm \(\Vert A\Vert \) is the operator norm of the map \(A:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\), unless stated otherwise. First we need the following estimate.
Lemma 5
Let \(\varepsilon >0\) and \(v_1,\dots ,v_n\in {\mathbb {R}}^n\) be such that \(\left| |v_i|^2-1\right| < \varepsilon \) and \(|\langle v_i,v_j \rangle | < \varepsilon \) if \(i\ne j\), for all \(i,j\in \{1,\dots ,n\}\). Define a linear map \(L:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) by \( L(v) = (\langle v,v_i\rangle )_{i=1}^n \). Then, there exists an orthogonal operator \(U:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) such that \( \Vert L-U\Vert < n\varepsilon \).
Proof
We regard L as an \(n\times n\) matrix whose ith row consists of coordinates of \(v_i\). The inner products \(\langle v_i,v_j\rangle \) are elements of the matrix \(LL^t\). By assumptions of the lemma, all elements of the matrix \(LL^t-I\) are bounded by \(\varepsilon \). Therefore, the operator norm \(\Vert LL^t-I\Vert \) is bounded by \(n\varepsilon \). Decompose L as \(L=U_1DU_2\) where \(U_1\) and \(U_2\) are orthogonal matrices and D is a diagonal matrix with nonnegative entries. Then, \(LL^t=U_1D^2U^{-1}_1\) and
Thus, the operator \(U=U_1U_2\) satisfies the desired inequality. \(\square \)
Lemma 6
There is a universal constant \(C_{16}>0\) such that the following holds. Let X be a metric space, \(x_0\in X\), and \(f,g:X\rightarrow {\mathbb {R}}^n\) maps with \(f(x_0)=g(x_0)=0\). Let \(R\ge r\ge \delta > 0\) and assume that f and g are \(\delta \)-isometries to sets \(Y_1\subset {\mathbb {R}}^n\) and \(Y_2\subset {\mathbb {R}}^n\), resp., such that \(B_r^n\subset Y_i\subset B_R^n\) for \(i=1,2\).
Then, there exists an orthogonal operator \(U:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) such that
for all \(x\in X\).
Proof
The statement of the lemma is scale invariant, i.e., one can multiply the parameters \(R,r,\delta \), the maps f, g, and the distances in X by the same scale factor. Thus, we may assume that \(r=1\). Since f and g are \(\delta \)-isometries, we have
for all \(x,y\in X\). In particular, \( \bigl ||f(x)| - |g(x)|\bigr | < 2\delta \) since \(f(x_0)=g(x_0)=0\). Hence,
and
for all \(x,y\in X\). These inequalities and the polarization identity
imply that
for all \(x,y\in X\).
Since \(B_1^n\subset Y_1\), there exist \(x_1,\dots ,x_n\in X\) such that \(|f(x_i)-e_i|<\delta \) for all i, where \((e_i)_{i=1}^n\) is the standard basis of \({\mathbb {R}}^n\). Let \(v_i=g(x_i)\), \(i=1,\dots ,n\). Then, by (44) applied to \(x=x_i\) and \(y=x_j\), for all \(i,j\in \{1,\dots ,n\}\) we have
since \(|f(x_i)|<1+\delta \) and \(|g(x_i)|<1+3\delta \). Therefore,
since \(|\langle f(x_i),f(x_j)-\langle e_i,e_j\rangle |<2\delta +\delta ^2\). Thus, the vectors \(v_i\) satisfy the assumptions of Lemma 5 with \(\varepsilon =\delta _1\). As in Lemma 5, define \(L(v)=(\langle v ,v_i\rangle )_{i=1}^n\) for all \(v\in {\mathbb {R}}^n\) and let U be an orthogonal operator such that \(\Vert L-U\Vert <n\delta _1\).
Since f(X) and g(Y) are contained in \(B_R^n\), the right-hand side of (44) is bounded by \(8R\delta \). Hence, by (44) applied to \(y=x_i\),
for all \(x\in X\) and \(i\in \{1,\dots ,n\}\). We also have
This and (45) imply that
The term \(\langle g(x),v_i)\rangle \) is the ith coordinate of the vector L(g(x)) (recall the definition of L above), and \(\langle f(x),e_i\rangle \) is the ith coordinate of f(x). Hence, (46) implies that
Since \(\Vert L-U\Vert <n\delta _1\), we also have
Therefore,
since \(\delta _1\le 27\delta \). Thus, (42) holds with \(C_{16}=36\). \(\square \)
2.4 Verifying GH Closeness to the Disk
Here we present an algorithm that can be used to verify the main assumption of Theorem 1. Namely, given a discrete metric space X, \(n\in {\mathbb {N}}\) and \(r>0\), one can approximately (i.e., up to a factor \(C=C(n)\)) find the smallest \(\delta \) such that X is \(\delta \)-close to \({\mathbb {R}}^n\) at scale r (see Definition 1). Due to rescaling, it suffices to handle the case \(r=1\).
Thus, the problem boils down to the following: Given a point \(x_0\in X\), find approximately the (pointed) GH distance between the metric ball \(B^X_1(x_0)\subset X\) of radius 1 centered at \(x_0\) and the Euclidean unit ball \(B_1^n\subset {\mathbb {R}}^n\). In the case, when X is finite, the following algorithm solves this problem.
Algorithm GHDist: Assume that we are given n, the point \(x_0\in X\), and the ball \({X_1}=B^X_1(x_0)\subset X\). We regard \({X_1}\) as a metric space with metric \(d=d_X|_{{X_1}\times {X_1}}\). We implement the following steps:
-
1.
Let \(x_1\in {X_1}\) be a point that minimizes \( |1 - d(x_0, x)|\) over all \(x\in {X_1}\).
-
2.
Given \(x_1, x_2,\dots x_m\) for \(m \le n\), we define the coordinate function
$$\begin{aligned} f_m(x)=\tfrac{1}{2} \bigl (d(x,x_0)^2-d(x,x_m)^2+d(x_0,x_m)^2\bigr ) \end{aligned}$$(47) -
3.
Given \(x_1, x_2,\dots x_m\) and coordinate functions \(f_1(x),f_2(x),\dots ,f_m(x)\) for \(m \le n-1\), choose \(x_{m+1}\) that is the solution of the minimization problem
$$\begin{aligned} \min _{x\in {X_1}} K_m(x),\quad K_m(x)=\max (|1-{d(x_0, x)^2}|, |f_1(x)|,\dots ,|f_{m}(x)| ). \end{aligned}$$ -
4.
When \(x_1, x_2,\dots ,x_n\) and coordinate functions \(f_1(x),f_2(x),\dots ,f_n(x)\) are determined, compute the map \({\mathbf{F}}:{X_1}\rightarrow B_1^n\) defined by
$$\begin{aligned} {\mathbf{F}}(x)=P(f_1(x),\dots ,f_n(x)) \end{aligned}$$(48)where P is the map from \({\mathbb {R}}^n\) to \(B_1^n\) defined as follows: \(P(v)=v\) if \(|v|\le 1\); otherwise, \(P(v)=v/|v|\).
-
5.
Let \(\ell _1=\# X_1\) be the number of elements in \(X_1\) and compute the values
$$\begin{aligned}&\delta _1=\sup _{x,x'\in {X_1}} \bigg |d(x',x)-|{\mathbf{F}}(x')-{\mathbf{F}}(x)|\bigg |,\nonumber \\&\delta _2=\sup _{y\in Y(\ell _1)} \inf _{x\in {X_1}} |{\mathbf{F}}(x)-y| + \ell _1^{-1/n},\nonumber \\&\qquad \delta _a=\max (\delta _1,\delta _2). \end{aligned}$$(49)where \(Y(\ell _1)=(h{\mathbb {Z}}^n)\cap B^n_1\) is the set of points in the unit ball whose coordinates are integer multiplies of \(h=\ell _1^{-1/n}/\sqrt{n}\). Finally, the algorithm outputs the value of \(\delta _a\) and the map \({\mathbf{F}}\).
Lemma 7
There is a universal constant \(C_{17}>0\) such that the following holds. Let \({X_1}\), \(x_0\) be as in the above algorithm, \(\delta >0\), and suppose that \(d_{\mathrm{GH}}({X_1},B_1^n)<\delta \) where \({X_1}\) and \(B_1^n\) are regarded as pointed metric spaces with distinguished points \(x_0\) and 0, resp. Then,
-
1.
The output value \(\delta _a\) of the algorithm satisfies \(\delta _a<C_{17}n\delta \).
-
2.
The output map \({\mathbf{F}}:{X_1}\rightarrow B_1^n\) is a \(\delta _a\)-isometry with \({\mathbf{F}}(x_0)=0\).
Proof
First we make some preliminary considerations. Let \(\delta _1\) be as in (49), and define
Here, \(\delta _a'\) is considered as a better approximation of the Gromov–Hausdorff distance \(d_{\mathrm{GH}}({X_1},B_1^n)\) than \(\delta _a\), but it is computationally more difficult to obtain.
Next we show that
To show this, denote \(\# X_1=\ell _1\). By (50), the unit ball \(B^n_1\) can be covered with closed \(\delta _2'\)-balls whose center points are in \(\mathbf{F}(X_1)\). Considering their volumes, we obtain an estimate \(\ell _1(\delta _2')^n \ge 1\), or, equivalently, \(\delta _2' \ge \ell _1^{-1/n}\). As \(Y(\ell _1)\) is a \((\ell _1^{-1/n})\)-net in the unit ball, we see that the supremums in the definitions of \(\delta _2\) and \(\delta _2'\) differ by no more than \(\ell _1^{-1/n}\). This yields the first inequality in (51). The second inequality in (51) follows from the fact that both the supremum in (49) and \(\ell _1^{-1/n}\) are no greater than \(\delta _2'\). Thus, (51) is valid and we have
Now we are ready to prove the claims of the lemma. By construction of \({\mathbf{F}}\), we have \({\mathbf{F}}(x_0)=0\) and the definition of \(\delta _a'\) implies that \({\mathbf{F}}\) is a \(\delta _a'\)-isometry from \({X_1}\) to \(B^n_1\). This proves the second claim of the lemma. It remains to prove the first one.
Consider the points \(x_1,\dots ,x_n\) constructed by the algorithm and the corresponding functions \(f_1(x),\dots ,f_n(x)\), see (47). Note that \(f_i(x_i)=d(x_i,x_0)^2\). Fix a \(2\delta \)-isometry \(h:{X_1}\rightarrow B_1^n\) with \(h(x_0)=0\) and define functions \(h_i:{X_1}\rightarrow {\mathbb {R}}\), \(i=1,\dots ,n\), by
Since h is a \(3\delta \)-isometry, \(h(x_0)=0\), \(d(x,x_0)\le 1\) and \(|h(x)|\le 1\) for all \(x\in {X_1}\), we have \( \left| d(x,x_0)^2-|h(x)|^2\right| <4\delta \) and \( \left| d(x,y)^2-|h(x)-h(y)|^2\right| <8\delta \) for all \(x,y\in {X_1}\). Therefore,
for all \(x\in {X_1}\), \(i=1,\dots ,n\).
Now we estimate \(K_m(x_{m+1})\) for \(m\in \{0,1,\dots ,n-1\}\), assuming that \(K_0\) is defined by \(K_0(x)=|1-d(x,x_0)^2|\). Since \(m<n\), there exists \(y_{m+1}\in \partial B_1^n\) orthogonal to all vectors \(h(x_1),\dots ,h(x_m)\). Since h is a \(2\delta \)-isometry, there exists \(x_{m+1}'\in {X_1}\) such that \(|h(x_{m+1}')-y_{m+1}|<2\delta \). This implies that \({d(x_0,x_{m+1}')}>|h(x_{m+1}')|-2\delta >1-4\delta \), and therefore,
Moreover, for all \( i=1,2, \dots , m\), we have
since \(y_{m+1}\) is orthogonal to \(h(x_i)\) and \(|h(x'_{m+1})-y_{m+1}\rangle |<2\delta \). Hence, by (53), \(|f_i(x'_{m+1})|<10\delta \). This and (54) imply that \(K_m(x_{m+1}')<10\delta \). Hence, the minimizer \(x_{m+1}\) of \({K_m}\) also satisfies \({K_m}(x_{m+1})<10\delta \). Equivalently, \(|f_i(x_{m+1})| < 10\delta \) for \(i=1,\dots ,m\) and \(f_{m+1}(x_{m+1})=d(x_0,x_{m+1})^2 > 1-10\delta \). Since \(m+1\) is an arbitrary element of \(\{1,\dots ,n\}\), we have shown that, for all \(i,j\in \{1,\dots ,n\}\), \(|f_i(x_j)| < 10\delta \) if \(i<j\) and \(|f_i(x_i)-1| < 10\delta \).
These inequalities and (53) imply that
and
Thus, the vectors \(v_i=h(x_i)\) satisfy the assumptions of Lemma 5 for \({\varepsilon =18\delta }\). Let \(L:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) be as in Lemma 5, namely \(L(v)=(L_i(v))_{i=1}^n\) where \(L_i(v)=\langle v,h(x_i)\rangle \). Then, Lemma 5 provides an orthogonal operator \(U:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) such that \(\Vert L-U\Vert \le 18n\delta \).
For every \(x\in {X_1}\) and \(i\in \{1,\dots ,n\}\), we have \(L_i(h(x))=\langle h(x),h(x_i)\rangle =h_i(x)\). This and (53) imply that \(|f_i(x)-L_i(h(x))| < 8\delta \). Thus, for \(f(x)=(f_i(x))_{i=1}^n\) we have \( |f(x) - L(h(x))| < 8n\delta . \) Since \(\Vert L-U\Vert \le 18n\delta \) and \(|h(x)|\le 1\), it follows that \( | f(x) - U(h(x)) | < 26n\delta \) for all \(x\in {X_1}\). Since \({\mathbf{F}}(x)=P(f(x))\) where \(P:{\mathbb {R}}^n\rightarrow B_1^n\) is a retraction that does not increase distances, \({\mathbf{F}}(x)\) satisfies the same inequality:
for all \(x\in {X_1}\). Since h is a \(2\delta \)-isometry to \(B_1^n\), so is \(U\circ h\). This and (55) imply that \({\mathbf{F}}\) is a \(54n\delta \)-isometry from \({X_1}\) to \(B_1^n\). Thus, the first claim of the lemma holds with \(C_{17}=54\). \(\square \)
The above lemma and (52) imply that the (pointed) Gromov–Hausdorff distance between \({X_1}\) and \(B_1^n\) satisfies
Thus, the algorithm GHDist gives the Gromov–Hausdorff distance of \({X_1}\) and \(B_1^n\) up to a constant factor \(2C_{17}\) depending only on dimension n.
2.5 Learning the Subspaces that Approximate the Data Locally
Let X be a finite set of points in \(E= {\mathbb {R}}^N\) and \(X \cap B_1(x) := \{x, \widetilde{x}_1, \dots , \widetilde{x}_s\}\) be a set of points within a Hausdorff distance \(\delta \) of some (unknown) unit n-dimensional disk \(D_1(x)\) centered at x. Here \(B_1(x)\) is the set of points in \({{\mathbb {R}}}^N\) whose distance from x is less or equal to 1. We give below a simple algorithm that finds a unit n-disk centered at x within a Hausdorff distance \(C{n}\delta \) of \({X_1}:= X \cap B_1(x)\), where C is a universal constant.
The basic idea is to choose a near orthonormal basis from \({X_1}\) where x is taken to be the origin and let the span of this basis intersected with \(B_1(x)\) be the desired disk.
Algorithm FindDisc:
-
1.
Let \(x_1\) be a point that minimizes \( |1 - |x- x'||\) over all \(x' \in {X_1}\).
-
2.
Given \(x_1, \dots x_m\) for \(m \le n-1\), choose \(x_{m+1}\) such that
$$\begin{aligned} \max (|1-|x- x'||, |\langle x_1/|x_1|, x'\rangle |, \dots , |\langle x_m/|x_m|, x'\rangle |) \end{aligned}$$is minimized among all \(x' \in {X_1}\) for \(x'= x_{m+1}\).
The output of the algorithm is the sequence \((x_1,x_2,\dots ,x_n)\). Let \(\widetilde{A}_x\) be the affine n-dimensional subspace containing \(x, x_1, \dots , x_n\) and the unit n-disk \(\widetilde{D}_1(x)\) be \(\widetilde{A}_x \cap B_1(x)\). Recall that for two subsets A, B of \({\mathbb {R}}^N\), \(d_H(A, B)\) represents the Hausdorff distance between the sets. The same letter C can be used to denote different constants, even within one formula.
Lemma 8
Suppose there exists an n-dimensional affine subspace \(A_x\) containing x such that \(D_1(x) = A_x \cap B_1(x)\) satisfies \(d_H({X_1}, D_1(x)) \le \delta \). Suppose \(0< \delta < \frac{1}{20n}\). Then, \(d_H({X_1}, \widetilde{D}_1(x)) \le C_{18}{n}\delta \).
Proof
Without loss of generality, let x be the origin. Let d(x, y) be used to denote \(|x-y|\). We will first show that for all \(m \le n-1\),
To this end, consider the function \(L_{m+1}:D_1(x)\rightarrow {\mathbb {R}}\), given by
and let \(z_{m+1}\in D_1(x)\) be the point where \(L_{m+1}\) obtains its minimum in \(D_1(x)\). The minimal value \(L_{m+1}(z_{m+1})\) is 0, because the dimension of \(D_1(x)\) is n and there are only \(m \le n-1\) linear equality constraints. Also, the radius of \(D_1(x)\) is 1, so \(|1 - d(x, z_{m+1})|\) has a value of 0 where a minimum of (57) occurs at \(y = z_{m+1}\). Since the Hausdorff distance between \(D_1(x)\) and \({X_1}\) is less than \( \delta \), there exists a point \(y_{m+1} \in {X_1}\) whose distance from \(z_{m+1}\) is less than \(\delta \). For this point \(y_{m+1}\), we have \(\delta \) greater than
Since
is no more than the corresponding quantity in (58), we see that for each \(m+1 \le n\),
Let \({\widetilde{V}}\) be an \(N \times n\) matrix whose ith column is the column \(x_i\). We recall that the operator norm of a matrix Z is denoted by \(\Vert Z\Vert \). For any distinct i, j we have \(|\langle x_i , x_j \rangle |<\delta \), and for any i, \(|\langle x_i, x_i\rangle - 1|<2\delta \), because \(0< 1-\delta< |x_i| < 1\). For a matrix X, let \(\Vert X\Vert _F\) denote its Frobenius norm. Therefore,
Therefore, the singular values of \({\widetilde{V}}\) lie in the interval
For each \(i \le n\), let \(x'_i\) be the nearest point on \(D_1(x)\) to the point \(x_i\). Since the Hausdorff distance of \({X_1}\) to \(D_1(x)\) is less than \(\delta \), this implies that \(|x'_i - x_i| < \delta \) for all \(i \le n\). Let \({\widehat{V}}\) be an \(N \times n\) matrix whose ith column is \( x'_i\). Since for any distinct i, j, \(|\langle x'_i, x'_j\rangle |<3\delta +\delta ^2 < 4\delta \), and for any i, \(|\langle x'_i , x'_i \rangle - 1|<4\delta \). This means that the singular values of \({\widehat{V}}\) lie in the interval \(I_C\).
We shall now proceed to obtain an upper bound of \(Cn\delta \) on the Hausdorff distance between \({X_1}\) and \(\widetilde{D}_1(x)\). Recall that the unit n-disk \(\widetilde{D}_1(x)\) is \(\widetilde{A}_x \cap B_1(x)\). By the triangle inequality, since the Hausdorff distance of \({X_1}\) to \(D_1(x)\) is less than \(\delta \), it suffices to show that the Hausdorff distance between \(D_1(x)\) and \(\widetilde{D}_1(x)\) is less than \( {6}n\delta .\)
Let \(x'\) denote a point on \(D_1(x)\). We will show that there exists a point \(z' \in \widetilde{D}_1(x)\) such that \(|x' - z'| < {4} n \delta .\)
Let \({\widehat{V}}\alpha = x'\). Assuming that \(\delta <1/(16{n}\delta )\) and using the bound on the singular values of \({\widehat{V}}\), we have \(|\alpha | \le 1+4 {n}\delta .\) Let \(y' = \widetilde{V}\alpha \). Then, by the bound on the singular values of \(\widetilde{V}\), we have \(|y'| \le ( 1+4 {n}\delta )^2\le 1+10 {n}\delta \). Let \(z' = \min (1-\delta ,|y'|)\, |y'|^{-1}y' \). By the preceding two lines, \( z'\) belongs to \(\widetilde{D}_1(x).\) We next obtain an upper bound on \(|x' - z'|\)
We examine the first term in the right side of (59)
We next bound the second term in the right side of (59). We have
Together, these calculations show that
A similar argument shows that if \( z''\) belongs to \(\widetilde{D}_1(x)\), then there is a point \(p' \in D_1(x)\) such that \(|p'-z''| < {6} {n}\delta \); the details follow. Again, assume that \(\delta <1/(16{n}\delta )\) and let \({\widehat{V}}\beta = z''\). From the bound on the singular values of \({\widehat{V}}\), \(|\beta |<( 1+4 {n}\delta ).\) Let \(q' := \widetilde{V}\beta \). Let \(p' := {z' = \min (1-\delta ,|q'|)\, |q'|^{-1}q'}\). Then,
This proves that the Hausdorff distance between \({X_1}\) and \(\widetilde{D}_1(x)\) is bounded above by \( C_{18}{n}\delta =6n\delta \). \(\square \)
Remark 3
Let us consider the computational complexity of the above algorithms GHDist and FindDisc in terms the number of elementary operations one has to perform. Here, we count the computation of an algebraic function of the distance \(d_X(x_i,x_j),\) of two elements of \(x_i,x_j\in X\) and a computations of a piecewise analytic function \(t\mapsto f(t)\) of a real variable, as one operation and the computation of the inner product of two m-dimensional vectors in \({\mathbb {R}}^m\) as m operations. We note that computing an inverse of an \(n\times n\) matrix requires a number of elementary operations that depend only on the intrinsic dimension n, and thus, it requires in our notation convention \(C=C(n)\) elementary operations.
Let us consider the algorithm GHDist. When the set \(X_1\) has \(\ell _1 =\# X_1\) elements, the steps 1–3 of the algorithm GHDist need \(C\ell _1\) steps, where C is a generic constant depending on the dimension n. The step 4 needs \(C\ell _1\) steps. In the step 5, the set \(Y(\ell _1)\) contains at most \(C\ell _1\) points, and hence, the step 5 needs at most \(C\ell _1^2\) steps. Thus, the computational complexity of GHDist is \(C\ell _1^2\).
We assume that \(E={\mathbb {R}}^m\) and X satisfies assumptions of Theorem 2, so that the set X is \(\delta \)-close to n-flats in scale r. When the set X has \(\ell =\# X\) elements, the algorithm FindDisc minimizes n times functions that are the maximum of at most n functions on involving inner products of m-dimensional vectors (i.e., points of X). Thus, the computational complexity of FindDisc is \(Cm\ell \).
3 Proof of Theorem 2
The statement of Theorem 2 is scale invariant: It does not change if one multiplies r and \(\delta \) by \(\lambda >0\) and applies a \(\lambda \)-homothety to all subsets of E. Hence, it suffices to prove the theorem only for \(r=1\). We recall that we use the notation \({\widehat{\delta }}_0=\sigma _2 r\). Thus, to prove Theorem 2 with \(r=1\), it is enough to prove the following proposition (where \({\sigma _2}\) is renamed to \({{\widehat{\delta }}_0}\)):
Proposition 3
There exist positive constants \(\delta _0<1\), \(C_{11}\), \(C_{12}\) depending only on n, and \(C_{13}(k)>0\) such that the following holds. Let E be a separable Hilbert space, \(X\subset E\) and \(0<\delta <{{\widehat{\delta }}_0} \). Suppose that for every \(x\in X\) there is an n-dimensional affine subspace \(A_x\subset E\) through x such that
Then, there is a closed n-dimensional smooth submanifold \(M\subset E\) such that
1. \(d_H(X,M)\le 5\delta \).
2. The second fundamental form of M at every point is bounded by \({C_{11}}\delta \).
3. \({{\,\mathrm{Reach}\,}}(M)\ge 1/3\).
4. The normal projection \(P_M:{{\mathcal {U}}}_{1/3}(M)\rightarrow M\) is smooth and for all \(x\in {{\mathcal {U}}}_{1/3}(M)\)
and
5. Let \(x\in X\) and \(y=P_M(x)\). Then,
The proof of Proposition 3 occupies the rest of this section. Let X and \(\{A_x\}_{x\in X}\) be as in the proposition. Let
be the orthogonal projection to \(A_x\). By \(\mathbf {A}_x\), we denote the linear subspace parallel to \(A_x\). For \(x\in X\) and \(\rho >0\), we define \(B_\rho ^X(x)=X\cap B_\rho (x)\) and \(D_\rho (x)=A_x\cap B_\rho (x)\). In this notation, (60) takes the form
In the sequel, we assume that \(\delta \) is sufficiently small so that the inequalities arising throughout the proof are valid, that is, we have
where \({\sigma _0}(n)>0\) depends only on n. The number \({\sigma _0}(n)\) can be explicitly estimated by numbers \(C_k\) appearing in the proof.
Lemma 9
Let \(p,q\in X\) be such that \(|p-q|<1\). Then, \({{\,\mathrm{dist}\,}}(q,A_p)<\delta \) and \(\angle (A_p,A_q)<5\delta \).
Proof
Since \(q\in B_1^X(p)\), we have
by (65). It remains to prove the second claim of the lemma.
Let \(z=P_{A_p}(\frac{p+q}{2})\). Then, \(|z-p|<\tfrac{1}{2}\) and \(|z-q|<\tfrac{1}{2}+\delta \) by the triangle inequality. Define \(B=A_p\cap B_{1/2-2\delta }(z)\). We claim that \({{\,\mathrm{dist}\,}}(y,A_q)<2\delta \) for every \(y\in B\). Indeed, let \(y\in B\). Then, \(|y-q|<1-\delta \) and \(|y-p|<1-2\delta \). The latter implies that \(y\in D_1(p)\); hence, by (65) there exists \(x\in X\) such that \(|x-y|<\delta \). By the triangle inequality we have \(x\in B_1^X(q)\); hence, (65) implies that \({{\,\mathrm{dist}\,}}(x,A_q)<\delta \). Therefore, \( {{\,\mathrm{dist}\,}}(y,A_q)\le |y-x|+{{\,\mathrm{dist}\,}}(x,A_q)<2\delta \) as claimed.
Define a function \(h:\mathbf {A}_p\rightarrow {\mathbb {R}}_+\) by \( h(v) = {{\,\mathrm{dist}\,}}(z+v,A_q)^2 . \) As shown above, \(h(v)\le 4\delta ^2\) for all \(v\in \mathbf {A}_p\) such that \(|v|\le \frac{1}{2}-2\delta \). The function h is polynomial of degree 2, i.e., \( h(v) = Q(v) + L(v) + h_0 \) where Q is a (nonnegative) quadratic form, L is a linear function, and \(h_0=h(0)\). Furthermore,
for all \(v\in \mathbf {A}_p\). Let \(\alpha =\angle (A_p,A_q)\), and let \(v_0\in \mathbf {A}_p\) be such that \(\angle (v_0,\mathbf {A}_q)=\alpha \) and \(|v_0|=\frac{1}{2}-2\delta \). Then,
since \(h(\pm v_0)\le 4\delta ^2\) and \(h(0)\ge 0\). Thus, \( \sin ^2(\alpha ) \cdot |v_0|^2 \le 4\delta ^2 , \) or, equivalently,
If \(\delta \) is sufficiently small, this implies the desired inequality \(\alpha <5\delta \). \(\square \)
Let \(X_0\) be a maximal (with respect to inclusion) \(\frac{1}{100}\)-separated subset of X, that is, a maximal subset \(X_0\subset X\) satisfying
Note that \(X_0\) is a \(\frac{1}{100}\)-net in X and \(X_0\) is at most countable. Let \(X_0=\{q_i\}_{i=1}^{|X_0|}\). For brevity, we introduce notation \(A_i=A_{q_i}\) and \(P_i=P_{A_{q_i}}\).
Throughout the argument below, we assume that \(|X_0|=\infty \), i.e., \(X_0\) is a countably infinite set. In the case when \(X_0\) is finite, the proof is the same, except that ranges of some indices should be restricted.
Assuming that \(\delta <\frac{1}{300}\), there is a number \(N=N(n)\) such that every set of the form \(X_0\cap B_1(q_i)\) contains at most N points. This follows from the fact that this set is \(\frac{1}{100}\)-separated and contained in the \(\delta \)-neighborhood of a unit n-dimensional ball \(D_1(q_i)\).
Let us fix a smooth function \(\mu :{\mathbb {R}}_+\rightarrow [0,1]\) such that \(\mu (t)=1\) for all \(t\in [0,\frac{1}{3}]\) and \(\mu (t)=0\) for all \(t\ge \frac{1}{2}\). Below, we will use the function \(\mu (t)=\alpha _{1/3,1/2}(t)\), where
For each \(i\ge 1\), define a function \(\mu _i:E\rightarrow [0,1]\) by
Clearly, \(\mu _i\) is smooth and
for every \(k\ge 1\). Here, \(C_{19}(k)\) can be chosen uniformly over n as by Lemma 41 in ‘Appendix A,’ the supremum of the kth order derivative \(d_x^k\mu _i\), considered as a multilinear form, is attained at a derivative corresponding to vectors that are all equal, which in turn implies that for all \(n\ge 2\), \(\Vert d_x^k\mu _i\Vert _{L^\infty ({\mathbb {R}}^n)}\) is independent of n. Let \(\varphi _i:E\rightarrow E\) be a map given by
Now define a map \(f_i:E\rightarrow E\) by
for all \(i\ge 1\), and let \(f_0=id_E\).
For \(x\in E\) and \(i\ge 1\), we have \(f_i(x)=f_{i-1}(x)\) if \(|f_{i-1}(x)-q_i|\ge \frac{1}{2}\). This follows from the relation \(f_i=\varphi _i\circ f_{i-1}\) and the fact that \(\varphi _i\) is the identity outside the ball \(B_{1/2}(q_i)\).
Let \(U={{\mathcal {U}}}_{1/4}(X_0)\subset E\). We are going to show that for every \(x\in U\) the sequence \(\{f_i(x)\}\) stabilizes, and hence, a map \(f=\lim _{i\rightarrow \infty } f_i\) is well defined on U.
Define \(B_m=B_{1/4}(q_m)\) for \(m=1,2,\dots \). Note that \(U=\bigcup _m B_m\).
Lemma 10
If \(x\in B_m\), then \(|f_i(x)-q_m| < \tfrac{1}{3}\) for all \(i\ge 1\).
Proof
Suppose the contrary and let
Let \(i\le i_0\) be such that \(|q_i-q_m|<1\). Such i does exist since otherwise \(|q_i-q_m|>1\) for all \(i\le i_0\) implying that \(f_i(x)=x \in B_m\). In particular, for \(i=i_0\), \(|f_{i_0}(x) -q_m| <1/3\) which is a contradiction. Next let \(z=f_{i-1}(x)\). Since \(i-1<i_0\), we have \(|z-q_m|<\frac{1}{3}\). Lemma 9 applied to \(p=q_i\) and \(q=q_m\) implies that \(|P_i(z)-P_m(z)| < 6\delta \). Since \(P_m\) is the orthogonal projection to a subspace containing \(q_m\), we have \(|P_m(z)-q_m| \le |z-q_m|\); therefore,
and hence, the point
satisfies
Thus,
for all \(i\le i_0\) such that \(|q_i-q_m|<1\). For indices \(i\le i_0\) such that \(|q_i-q_m|\ge 1\), we have
and hence, \(f_i(x)=f_{i-1}(x)\). Since there are at most \(N=N(n)\) indices \(i\le i_0\) such that \(|q_i-q_m|<1\), by (73), it follows that
provided that \(\delta < 1/(120N)\). This contradicts the choice of \(i_0\). \(\square \)
Lemma 10 implies that there exist only finitely many indices i such that \(f_i|_{B_m}\ne f_{i-1}|_{B_m}\). Indeed, if \(f_i(x)\ne f_{i-1}(x)\) for some \(x\in B_m\), then \(|q_i-q_m|<1\) because \(|f_{i-1}(x)-q_m|<\frac{1}{3}\) by Lemma 10 and \(|f_{i-1}(x)-q_i|<\frac{1}{2}\) (since \(\varphi _i\) is the identity outside \(B_{1/2}(q_i)\)). Thus, the sequence \(\{f_i|_{B_m}\}_{i=1}^\infty \) stabilized, and hence, the map
is well defined and smooth on \(B_m\). Since m is arbitrary, f is well defined and smooth on \(U=\bigcup _m B_m\).
Remark 4
We note that in the case when X and thus \(X_0\subset X\) are finite sets and when N is the number of the elements in \(X_0\), we define instead of (74)
3.1 Estimates for Interpolation Maps \(f_i\) and f
Next, we consider functions f and \(f_i\) defined in (71), (72), and (74).
Lemma 11
Let \(k\ge 0\). There is \(C_{21}(k)= {(C(k))^{N(n)}} >0\) such that
and therefore,
Below we denote \(C_{21}=C_{21}(0)\), \(C_{21}'=C_{21}(1)\), and \(C_{21}''=C_{21}(2)\).
Proof
Let \(I_m=\{i:|q_i-q_m|<1\}\) and let \(j_1<\dots <j_{N_m}\) be all elements of \(I_m\). Recall that \(N_m=|I_m|\le N=N(n)\). As shown above, Lemma 10 implies that \(\varphi _i\) is the identity on \(f_{i-1}(B_m)\) for \(i\notin I_m\). Therefore, for every i we have
where \(l(i)=\max \{k: j_k\le i \}\).
We compare \(\varphi _i\) and \(f_i\) with maps \({\widehat{\varphi _i}}\) and \({{\widehat{f}}}_i\) defined by
and
By induction, one easily sees that
for some \(\lambda _i(x)\in [0,1]\), \(\lambda _1(x)\le \lambda _2(x)\le \dots \). Therefore, \({{\widehat{f}}}_i(B_m)\subset B_m\) for all i. Similar to the case of \(f_i\), this implies that
Let
and
By Lemma 9 and (22), for every \(i\in I_m\) we have
for all \(x\in B_1(q_m)\), and therefore, as \(P_i\) and \(P_m\) are affine maps,
where the factor \(k^2\) appears due to the Leibniz rule for derivatives of the product and the fact that the second- and the higher-order derivatives of affine maps vanish. This estimate, (78), (82) and the fact that \(l(i)\le |I_m|\le N(n)\) imply that
As
we see by using Lemma 42(2) in ‘Appendix A’ with \(f=f_{i'}=\varPhi _{i}^{i'+1}\), \(h=h_{i'}= \varphi _{j_{i'}}\circ {\widehat{\varPhi }}_{i}^{i'}\) and \(g=g_{i'}= {\widehat{\varphi }}_{j_{i'}}\circ \widehat{\varPhi }_{i}^{i'}\), we see for \(k\ge 1\) that
Here, by Lemma 42(1) in ‘Appendix A’ and (83) we have
and
By substituting formulas (85) and (86) in to formula (84), and using that \({l(i)} \le N(n)\), we see that
for all i and \(k\ge 0\), where \(C_{21}(k)\) can be written as an explicit formula involving k, \(C_{19}(k)\), \( C_{19}(k+1)\), and N(n). Observe that \({\widehat{\varphi _m}}|_{B_m}=P_m|_{B_m}\) since \(\mu _m=1\) on \(B_m\). This fact together with \({{\widehat{f}}}_m= {\widehat{\phi }}_m \circ {{\widehat{f}}}_{m-1}\) and (81) implies that \({{\widehat{f}}}_m|_{B_m}=P_m|_{B_m}\). Thus, \({{\widehat{f}}}_i|_{B_m}=P_m|_{B_m}\) for all \(i\ge m\). Therefore, for \(i\ge m\) the estimate (84) turns into (76) and the claim of the lemma follows. \(\square \)
Lemma 12
\(f_m(B_m)\subset D_{1/3}(q_m)\).
Proof
Let \(x\in B_m\) and \(y=f_{m-1}(x)\), then \(f_m(x)=\varphi _m(y)\). By Lemma, 10, \(|y-q_m|<\frac{1}{3}\). Therefore, \(\mu _m(y)=1\), and hence, \(\varphi _m(y)=P_m(y)\). Thus, \(f_m(x)=P_m(y)\in D_{1/3}(q_m)\). \(\square \)
By definition, \(f=g\circ f_m\) for some smooth map \(g:E\rightarrow E\). Therefore, \(f(B_m)\) is contained in an image of the n-dimensional disk \(D_{1/3}(q_m)\) under a smooth map g.
Lemma 13
\(f(B_m)\subset {\mathcal U}_{4\delta }(D_{1/3}(q_m))\) for every m, and \(f(U)\subset {\mathcal U}_{5\delta }(X)\).
Proof
Let \(x\in B_m\). By Lemma 10, we have \(f_i(x)\in B_{1/3}(q_m)\) for all i. Let us show that \(f_i(x)\in {\mathcal U}_{4\delta }(A_m)\) for all \(i\ge m\). This is true for \(i=m\) since \(f_m(x)\in D_{1/3}(q_m)\subset A_m\) by Lemma 12. Arguing by induction, let \(i>m\) and assume that \(y=f_{i-1}(x)\in {{\mathcal {U}}}_{4\delta }(A_m)\). If \(|y-q_i|\ge \frac{1}{2}\), then \({f_i(x)}=y\in {{\mathcal {U}}}_{4\delta }(A_m)\), so we assume that \(|y-q_i|<\frac{1}{2}\). Note that
By definition, the point \(f_i(x)=\varphi _i(y)\) belongs to the line segment [yz] where \(z=P_i(y)\). Since \(z\in A_i\) and \(|q_i-z| \le |q_i-y|<\frac{1}{2}\), we have
where the second inequality follows from Lemma 9. Thus, \(z\in {{\mathcal {U}}}_{4\delta }(A_m)\). Since \(f_i(x)\in [yz]\), both y and z belong to \({{\mathcal {U}}}_{4\delta }(A_m)\) and \({\mathcal U}_{4\delta }(A_m)\) is a convex set, \(f_i(x)\in {\mathcal U}_{4\delta }(A_m)\) as claimed.
Thus, \(f_i(x)\in {{\mathcal {U}}}_{4\delta }(A_m)\cap B_{1/3}(q_m)\) for all \(x\in B_m\) and all \(i\ge m\). This implies the first claim of the lemma. To prove the second one, recall that \(D_1(q_m)\subset {{\mathcal {U}}}_\delta (X)\) by (65). Hence, \(f(B_m)\subset {{\mathcal {U}}}_{4\delta }(D_{1/3}(q_m))\subset {{\mathcal {U}}}_{5\delta }(X)\). Since m is arbitrary, the second assertion of the lemma follows. \(\square \)
3.2 Construction and Properties of the Submanifold M
Now define
We are going to show that M is a desired submanifold.
Lemma 14
For every \(y\in M\), there exists \(q_m\in X_0\) such that \(|y-q_m|<\frac{1}{100}+5\delta \) and
In particular, \(M=\bigcup _m f(D_{1/10}(q_m))\).
Proof
By Lemma 13, \(y\in {{\mathcal {U}}}_{5\delta }(X)\). Since \(X_0\) is a \(\frac{1}{100}\)-net in X, there is point \(q_m\in X_0\) such that \(|y-q_m|<\tfrac{1}{100}+5\delta \). Let us show that this point satisfies the requirements of the lemma. Let \(W=M\cap B_{1/100}(y)\) and \(D=D_{1/10}(q_m)\). We are to show that \(W\subset f(D)\). Fix a point \(z\in W\). Observe that
Since \(z\in M\), we have \(z=f(x)\) for some \(x\in {\mathcal U}_{1/5}(X_0)\). Let \(p\in X_0\) be such that \(|x-p|<\frac{1}{5}\). Then, \(|z-P_{A_p}(x)|<C_{21}\delta \) by Lemma 11. On the other hand,
Therefore, assuming that \(\delta \) is smaller than some constant depending only on n (see (66)), we have
thus, \(x\in B_m\).
By Lemma 11, it follows that \(|z-P_m(x)|=|f(x)-P_m(x)|<C_{21}\delta \) and \(|f_m(x)-P_m(x)|<C_{21}\delta \). Therefore, \(|f_m(x)-z| < 2C_{21}\delta \), and hence,
By Lemma 12, we have \(f_m(x)\in A_m\); hence, \(f_m(x)\in D_{1/50+{(2C_{21}+5)}\delta }(q_m)\).
Now consider the map \(f_m|_D\). By Lemma 12, its image \(f_m(D)\) is contained in \(A_m\). By Lemma 11, \(f_m|_D\) is \(C_{21}\delta \)-close to the projection \(P_m|_D\), which equals \(id_D\) since \(D\subset A_m\). Thus, \(f_m|_D\) is \(C_{21}\delta \)-close to the identity and maps D to a subset of the n-dimensional subspace \(A_m\). By topological reasons, see [73, Thm. 1.2.6], this implies that \(f_m(D)\) contains an n-ball \(D_{1/10-C_{21}\delta }(q_m)\), see (66). Since \(f_m(x)\in D_{1/50+(2C_{21}+5)\delta }(q_m)\subset D_{1/10-C_{21}\delta }(q_m)\), it follows that there exists a point \(x'\in D\) such that \(f_m(x')=f_m(x)\). Since f factors through \(f_m\), this implies that \(f(x')=f(x)=z\). Thus, \(z\in f(D)\). Since z is an arbitrary point of W, the lemma follows. \(\square \)
Now we prove that M is a submanifold.
Lemma 15
M is a closed n-dimensional smooth submanifold of E. Every \(y\in M\) has a neighborhood in M that admits a parametrization by a smooth map \(\varphi :V\rightarrow E\), \(V\subset {\mathbb {R}}^n\), which is \(C_{21}(k)\delta \)-close to an affine isometric embedding in the \(C^k\)-topology for any \(k\ge 0\), where \(C_{21}(k)\) is the constant provided by Lemma 11.
Proof
Pick \(y\in M\) and let \(q_m\in X_0\) be as in Lemma 14. As in the proof of Lemma 14, we use the notation \(D=D_{1/10}(q_m)\). By Lemma 11, \(f|_D\) is \(C_{21}(k)\delta \)-close to the inclusion \(D\hookrightarrow E\) in the \(C^k\)-topology. Assuming that \(\delta <C_{21}(1)^{-1}\), it follows that \(f|_D\) is a smooth embedding, and hence, f(D) is a smooth submanifold of E. By Lemma 14,
Thus, \(M\cap B_{1/100}(y)\) is a submanifold for every \(y\in M\), hence so is M.
To see that M is closed, recall that \(|y-q_m|<\frac{1}{100}+5\delta \). Since \(f|_D\) is \(C_{21}\delta \)-close to identity, this implies that the f-image of the boundary of D is separated away from y by distance at least \(\frac{1}{10}-\frac{1}{100}-{5\delta }-C_{21}\delta >\frac{1}{100}\). Therefore, \(M\cap B_{1/100}(y)\) is contained in a compact subset of the submanifold f(D). Since this holds within a uniform radius \(\frac{1}{100}\) from any \(y\in M\), it follows that M is a closed set in E.
To construct the desired local parametrization \(\varphi \), just compose \(f|_D\) with an affine isometry between D and an appropriate ball \(V\subset {\mathbb {R}}^n\). \(\square \)
The bounds on derivatives of \(\varphi \) from Lemma 15 imply that the second fundamental form of M is bounded by
provided that \(\delta <(4C_{21}')^{-1}\). See Lemma 11 for the notation \(C_{21}'\) and \(C_{21}''\). The inequality (88) proves the second assertion of Proposition 3 with \(C_{11}=2C_{21}''\).
The first assertion of Proposition 3 is the following lemma.
Lemma 16
\(d_H(M,X)\le 5\delta \).
Proof
By Lemma 13, we have \(M\subset {\mathcal U}_{5\delta }(X)\). It remains to prove the inclusion \(X\subset {\mathcal U}_{5\delta }(M)\). Fix \(x\in X\) and let \(q_m\in X_0\) be such that \(|q_m-x|\le \frac{1}{100}\). Consider the map \(P_m\circ f|_{D_{1/5}(q_m)}\) from \(D_{1/5}(q_m)\subset A_m\) to \(A_m\). By Lemma 11, this map is \(C_{21}\delta \)-close to the identity. Therefore, its image contains the n-disk \(D_{1/5-C_{21}\delta }(q_m)\). This disk contains the point \(P_m(x)\) because
Hence, \(P_m(x)\in P_m(f(D_{1/5}(q_m)))\). This means that there exists \(y\in D_{1/5}(q_m)\) such that \(P_m(f(y))=P_m(x)\). By Lemma 13, we have \({{\,\mathrm{dist}\,}}(f(y),A_m)<4\delta \), and therefore,
By Lemma 9, we have \({{\,\mathrm{dist}\,}}(x,A_m)\le \delta \), and therefore, \(|x-P_m(x)|\le \delta \). Hence,
Observe that \(f(y)\in M\) since \(y\in D_{1/5}(q_m)\subset {\mathcal U}_{1/5}(X_0)\). This and the above inequality imply that \(x\in {{\mathcal {U}}}_{5\delta }(M)\). Since x is an arbitrary point of X, we have shown that \(X\subset {{\mathcal {U}}}_{5\delta }(M)\). The lemma follows. \(\square \)
Remark 5
We observe that
(compare with (87)). Indeed, we have \( M \subset \bigcup _m f(D_{1/10}(q_m)) \) by Lemma 14 and \( D_{1/10}(q_m) \subset {{\mathcal {U}}}_\delta (X) \) by (65).
One can think of (89), (87) and the last claim of Lemma 14 as various reconstruction procedures for M.
Lemma 17
\(|f(y)-y|< C_{20}\delta \) for every \(y\in {{\mathcal {U}}}_\delta (X)\).
Proof
Since \(y\in {{\mathcal {U}}}_\delta (X)\), there is \(x\in X\) such that \(|x-y|<\delta \). Pick \(q_m\in X_0\) such that \(|x-q_m|<\tfrac{1}{100}\). Then, \(y\in B_m\), and hence, \(|f(y)-P_m(y)|<C_{21}\delta \) by Lemma 11. By Lemma 9, we have \({{\,\mathrm{dist}\,}}(x,A_m)<\delta \), and hence,
Therefore, \( |f(y)-y| \le |f(y)-P_m(y)| + |y-P_m(y)| <(C_{21}+2)\delta =C_{20}\delta \). \(\square \)
For \(x,y\in M\), we denote by \(d_M(x,y)\) the intrinsic arc-length distance between x and y in M. If x and y are from different connected components of M, then \(d_M(x,y)=\infty \). Since M is closed in E, each component of M is a complete Riemannian manifold.
Lemma 18
Let \(x,y\in M\) be such that \(|x-y|<\tfrac{4}{5}\). Then, \(d_M(x,y) < 1\).
Proof
Let \(x,y\in M\) be as above. Then, by (89) there are points \(x',y'\in {{\mathcal {U}}}_\delta (X)\) such that \(f(x')=x\) and \(f(y')=y\). By Lemma 17, we have \(|x-x'| < C_{20}\delta \) and \(|y-y'|< C_{20}\delta \), hence \(|x'-y'|<\frac{4}{5}+2 C_{20}\delta \) by the triangle inequality. Let \(x'',y''\in X\) be such that \(|x'-x''|<\delta \) and \(|y'-y''|<\delta \).
Then, when \(\delta \) is smaller than a bound depending on n, see (66),
Hence, \(y''\in B_1^X(x'')\). This and (65) imply that \(y''\in {{\mathcal {U}}}_\delta (D_1(x''))\). Therefore, both \(x'\) and \(y'\) and hence the line segment \([x',y']\) are contained in the \(2\delta \)-neighborhood of the affine n-disk \(D_1(x'')\). Since \(B_1^X(x'') \subset X\), it follows from (65) that \(D_1(x'')\subset {\mathcal {U}}_\delta (B_1^X(x''))\subset \mathcal U_\delta (X)\). Hence, the \(2\delta \)-neighborhood of \(D_1(x'')\) is contained in \({{\mathcal {U}}}_{3\delta }(X)\). Thus, \([x',y']\) is contained in \({{\mathcal {U}}}_{3\delta }(X)\) and hence in the domain of f.
Consider the f-image of the line segment \([x',y']\). It is a smooth path in M connecting x and y. Lemma 11 for \(k=1\) implies that f is locally Lipschitz with Lipschitz constant \(1+{C_{21}'}\delta \). Therefore,
see (66). Hence, \(d_M(x,y)<1\). \(\square \)
Now we are in position to prove the third assertion of Proposition 3.
Lemma 19
\({{\,\mathrm{Reach}\,}}(M)\ge \frac{1}{3}\). Furthermore, for every \(p\in \mathcal U_{1/3}(M)\) there exists a unique \(x\in M\) such that \(|p-x|<\frac{1}{3}\) and \(p-x\perp T_xM\).
Proof
Fix \(p\in {\mathcal {U}}_{1/3}(M)\). By Lemma 18, the set \(B_{1/3}(p)\cap M\) is contained in a unit ball of \((M,d_M)\), since the diameter of this set in E is bounded by \(\frac{2}{3}<\frac{4}{5}\). Since M is a complete Riemannian manifold, closed balls in \((M,d_M)\) are compact. Hence, there exists \(x\in M\) nearest to p. It remains to prove that x is a unique nearest point and that it is also a unique point of \(B_{1/3}(p)\cap M\) such that \(p-x\perp T_xM\).
Let y be another point from \(B_{1/3}(p)\cap M\). By Lemma 18, we have \(d_M(x,y)<1\). Connect x to y by a unit speed minimizing geodesic \(\gamma :[0,L]\rightarrow M\), and consider the function \(f(t)=\frac{1}{2}|p-\gamma (t)|^2\), \(t\in [0,L]\). Computing the second derivative of f(t) yields
where \(\langle \cdot ,\cdot \rangle \) is the inner product in E.
Let \(\kappa \) denote our bound on the second fundamental form of M, i.e., \(\kappa =C_{11}\delta \). Since \(\gamma \) is a geodesic, \(|\gamma ''(t)|\le \kappa \). This and (90) imply that \( |f''(t)-1| \le \kappa |p-\gamma (t)| \) for all t. Thus, \(0<f''(t)<2\) as long as \(|p-\gamma (t)|<\kappa ^{-1}\). Since \(p-x\perp T_x\varSigma \), we have \(f'(0)=0\). Therefore, \(0<f''(t)<2\), \(0<f'(t)<2t\), and \(f(0)<f(t)<f(0)+ t^2\) for all \(t\in (0,L]\) such that \(f(0)+ t^2<\frac{1}{2}\kappa ^{-2}\).
Assuming that \(\kappa =C_{11}\delta <\frac{1}{2}\) (see (66)) and using estimates \(|p-x|<1\) and \(L=d_M(x,y)<1\), we see that the above inequalities hold for all \(t\in [0,L]\). In particular \(f(L)>f(0)\) and \(f'(L)>0\); hence, \(|p-y|>|p-x|\) and \(p-y\) is not orthogonal to \(T_yM\). \(\square \)
Now we have the normal projection map \(P_M:\mathcal U_{1/3}(M)\rightarrow M\). Let us prove the fifth assertion of Proposition 3. Let \(x\in X\) and \(y=P_M(x)\). Then, \(|x-y|<5\delta \) by Lemma 16. By Lemma 14, there exists \(q_m\in X_0\) such that \(|y-q_m|<\frac{1}{100}+5\delta \) and \(y\in f(D)\) where \(D=D_{1/10}(q_m)\). By Lemma 11, \(f|_D\) is \(C_{21}'{\delta }\)-close to \(P_m|_D=\text {id}_D\) in the \(C^1\)-topology. Therefore,
provided that \(\delta <(2C_{21}')^{-1}\). By Lemma 9, we have \(\angle (A_x,A_{q_m})<5\delta \). Hence,
and (63) follows with \(C_{12}=2C_{21}'+5\).
It remains to prove the fourth assertion of Proposition 3. Consider the normal disk bundle
and the map \(J:\nu _{1/3}M\rightarrow E\) given by \(J(x,v)=x+v\). Lemma 19 implies that J is a bijection onto \(\mathcal U_{1/3}(M)\). The normal projection \(P_M:{\mathcal {U}}_{1/3}(M)\rightarrow M\) can be written as \(P_M=\pi \circ J^{-1}\) where \(\pi (x,v)=x\) for \((x,v)\in \nu _{1/3}M\). Thus, it suffices to show that \(J^{-1}\) is smooth and estimates its derivatives.
Let \((x_0,v_0)\in \nu _{1/3}M\). By means of a parallel translation, we may assume that \(x_0\) is the origin of E. By Lemma 15, a neighborhood of \(x_0\) in M admits a local parametrization \(\varphi :V\rightarrow M\) which is \(C_{21}(k)\delta \)-close in \(C^k\)-topology to an affine isometric embedding. We identify V with a neighborhood of the origin in the tangent space \(T_{x_0}M\subset E\) so that \(\varphi \) is \(C_{21}(k)\delta \)-close to the identity in \(C^k\)-topology. Let B be the ball of radius 1 / 3 in the orthogonal complement \((T_{x_0}M)^\perp \) of \(T_{x_0}M\) in E. Parametrize a neighborhood of \((x_0,v_0)\) in \(\nu _{1/3}M\) by \((\varphi (x), \, v- P_{\varphi (x)}(v))\), and introduce a map \(\varPhi :V\times B\rightarrow E \) given by
where \(P_{\varphi (x)}\) is the orthogonal projection from E to \(T_{\varphi (x)}M\). The projection \(P_{\varphi (x)}(v)\) can be written explicitly as an arithmetic formula involving the first derivatives of \(\varphi \) and their inner products with each other and v; hence, the kth derivatives of \({\varPhi }\) can be written explicitly in terms of the derivatives of \(\varphi \) up to the order \(k+1\) and the inner product in E. If \(\varphi \) is the identity, then so is \({\varPhi }\). Since \(\varphi \) is \(C_{21}(k+1)\delta \)-close to the identity in \(C^{k+1}\)-topology, this implies an estimate
where \(C_{22}(k)\) is a constant that can be written explicitly in terms of \(C_{21}(k+1)\). By the inverse function theorem, this implies that \({\varPhi }\) is a local diffeomorphism provided that \(\delta <C(k)^{-1}\). The normal projection \(P_M\) in a neighborhood of \((x_0,v_0)\) is given by \(P_M=\varphi \circ \pi _1\circ {\varPhi }^{-1}\) where \(\pi _1:V\times B\rightarrow V\) is the first coordinate projection. The kth differential of \({\varPhi }^{-1}\) can be written as an explicit dimension-independent formula in terms of differentials of \(\varphi \) up the kth order. If \(\varphi \) is the identity, then \(P_M\) is the orthogonal projection \(P_{T_{x_0}M}\). This implies an estimate
for all \(k\ge 0\), where \(C_{13}(k)\) can be written explicitly in terms of \(C_{21}(k+1)\). These bounds imply (61) and (62).
This finishes the proof of Proposition 3. As explained in the beginning of this section, Theorem 2 follows via a rescaling argument.
Remark 6
Assuming in Theorem 2 that \(\delta <r/100\) and by scaling metric by factor \(r^{-1}\) in Lemmas 11 and 16, the above arguments about \(P_M\) imply that
for all k. Thus, for computation purposes, the explicitly constructed map f is as good as the normal projection \(P_M\).
Remark 7
Let us show that the constants in Theorem 2 are optimal, up to constant factors. Let \(M\subset E\) be a closed n-dimensional submanifold whose the second fundamental form is bounded by \(\kappa _{\delta ,r}=\frac{1}{2}\delta r^{-2}\), with \(0<\delta<r<1\), and \({{\,\mathrm{Reach}\,}}(M)>2r\). Let \(x\in M\). Using formula (2), we see that
Here \(B^M_{2r}(x)\) is the intrinsic ball in M of radius 2r centered at x.
Our assumptions on M imply that the normal projection \(P_M\) is well defined and 2-Lipschitz in the ball \(B^E_r(x)\). Hence, for any \(z\in M \cap B^E_r(x)\) the projection \(P_M([x,z])\) of the line segment [x, z] is a curve of length at most 2r. Therefore, \(z=P_M(z)\in B^M_{2r}(x)\). Thus, \(M \cap B_r^E(x) \subset B^M_{2r}(x)\). Also note that \( B^M_{r}(x)\subset M \cap B_r^E(x) \). These relations, (95) and (2), imply that \(d_{H}(M\cap B^E_r(x),B_{r}^{T_xM}(x))\le \delta \). As x above is an arbitrary point of M, we have that M is \(\delta \)-close to n-flats at scale r. This shows that in Theorem 2 the bounds in claims (2) and (3) on the second fundamental form and reach are optimal, up to multiplying these bounds by constant factors depending on n.
4 Proof of Proposition 2 and Injectivity Radius Estimates
The main goal of this section is to prove Proposition 2. We begin with recalling some facts about Riemannian manifolds of bounded curvature and proving the estimate (1)
Let \(M=(M,g)\) be a complete Riemannian manifold with \(|{\text {Sec}}_M|\le K\) where \(K>0\). For \(p\in M\), consider the exponential map \(\exp _p:T_pM\rightarrow M\). We restrict this map to the ball of radius \(r<\frac{\pi }{\sqrt{K}}\) in \(T_pM\) centered at the origin. As a consequence of Rauch Comparison Theorem, \(\exp _p\) is non-degenerate in this ball and we have the following estimates on its local bi-Lipschitz constants: For \({v}\in T_pM\) such that \(|{v}|\le r<\frac{\pi }{\sqrt{K}}\) and every \(\xi \in T_pM\setminus \{0\}\),
(see, e.g., [79, Thm. 27 in Ch. 6] and [83, Thm. IV.2.5 and Remark IV.2.6]).
If \(r\le {\frac{1}{2}\min \{\frac{\pi }{\sqrt{K}},{{\,\mathrm{inj}\,}}_M(p) \}}\), then the geodesic r-ball \(B^M_r(p)\) is convex, i.e., minimizing geodesics with endpoints in this ball do not leave it (see, e.g., [79, Thm. 29 in Ch. 6]). This makes the local bi-Lipschitz estimate (96) global. Hence,
and therefore,
for all \({u,v}\in T_pM\) such that \(|{u}|,|{v}|\le r\). Here (98) follows from (97) and the estimates \(|{u}-{v}|\le 2r\) and
Thus, the distortion of \(\exp _p\) within the r-ball is bounded by \(\tfrac{1}{2} Kr^3\) provided that \(r\le \frac{1}{2} \min \{\frac{\pi }{\sqrt{K}},{{\,\mathrm{inj}\,}}_M(p) \}\). This proves (1).
The upper bound in (97) does depend on the assumption that \(r\le \frac{1}{2} {{\,\mathrm{inj}\,}}_M(p) \). Moreover, the distances within a ball of radius \(\frac{\pi }{2\sqrt{K}}\) have a better upper bound stated in Lemma 20. This lemma is a variant of Toponogov’s Comparison Theorem (see, e.g., [79, Thm. 79 in Ch. 11]) for geodesics that are not necessarily minimizing but whose lengths are bounded in terms of curvature.
Let \(M^2_{-K}\) denote the rescaled hyperbolic plane of curvature \(-K\). For real numbers \(a,b>0\) and \(\alpha \in [0,\pi ]\), denote by \(\curlyvee _{-K}(a,b,\alpha )\) the length of the side \(x_1x_2\) of a triangle \(\triangle x_0x_1x_2\) in \(M^2_{-K}\) whose sides \(x_0x_1\) and \(x_0x_2\) equal a and b, resp., and the angle at \(x_0\) equals \(\alpha \). Note that
where \(\curlyvee _0\) is defined similarly using the Euclidean plane as \(M^2_0\). This follows from (98) applied to \(M^2_{-K}\) in place of M.
Lemma 20
Let \(M=(M^n,g)\) be a complete Riemannian manifold, \(|{\text {Sec}}_M|\le K\) where \(K>0\), \(p\in M\), and \(0<r\le \frac{\pi }{2\sqrt{K}}\). Then,
for all \(u,v\in T_pM\) such that \(|u|,|v|\le r\).
Proof
This lemma is a standard application of Rauch comparison. We give a proof for the reader’s convenience.
Let \({\widetilde{M}}\) be the rescaled hyperbolic n-space of curvature \(-K\) and \({\widetilde{p}}\in {\widetilde{M}}\). Denote by B and \({\widetilde{B}}\) the closed r-balls centered at p and \({\widetilde{p}}\) in M and \(\widetilde{M}\), resp. Define a map \(f:{\widetilde{B}}\rightarrow B\) by \( f = \exp _p\circ I \circ \exp _{{\widetilde{p}}}^{-1}|_{{\widetilde{B}}} \) where \(\exp _p\) and \(\exp _{{\widetilde{p}}}\) are the Riemannian exponential maps of M and \({\widetilde{M}}\), resp., and I is a linear isometry from \(T_{\widetilde{p}}{\widetilde{M}}\) to \(T_pM\). Since \(r<\frac{\pi }{\sqrt{K}}\), \(\exp _p\) is non-degenerate within the r-ball. Therefore, by [83, Thm. IV.2.5], the map f does not increase lengths of smooth curves.
Let \(u,v\in T_pM\) be such that \(|u|,|v|\le r\), and let \({\widetilde{\gamma }}\) be a geodesic segment in \({\widetilde{M}}\) between the points \(\exp _{\widetilde{p}}(I^{-1}(u))\) and \(\exp _{{\widetilde{p}}}(I^{-1}(v))\). Then, \({\widetilde{\gamma }}\) is contained in \({\widetilde{B}}\) and
Since \(\gamma :=f\circ \gamma \) is a path connecting \(\exp _p(u)\) and \(\exp _p(v)\) in M, we have
where the second inequality follows from the above-mentioned fact that f does not increase lengths. This and (102) imply the first inequality in (101). The second inequality in (101) follows from (100). \(\square \)
The next lemma is a quantified version of the fact that, for Riemannian manifolds with two-sided curvature bounds, collapsing in the Gromov–Hausdorff sense is equivalent to injectivity radii going to zero (see [31, 47] or [51, Ch. 8]). The advantage of Lemma 21 over collapsing technique is that it provides bounds independent of the dimension.
Lemma 21
Let M be a complete Riemannian manifold with \(|{\text {Sec}}_M|\le K\) where \(K>0\). Let \(p\in M\) and \(r>0\) be such that \(Kr^2\le 10^{-3}\) and
where \(n=\dim M\). Then, \( {{\,\mathrm{inj}\,}}_M(p) \ge \tfrac{9}{10}r \).
Proof
Define \(\varepsilon =10^{-3}\). The statement of the lemma is scale invariant so it suffices to prove it for \(r=1\). More precisely, we rescale M by the factor \(r^{-1}\). The rescaled manifold, for which we reuse the notation M, satisfies
and
The desired inequality now takes the form \({{\,\mathrm{inj}\,}}_M(p) \ge \tfrac{9}{10}\). We rewrite it as
The rest of the proof works for any \(\varepsilon \le 10^{-3}\).
First we informally explain the idea of this long and technical proof. Since the curvature of M is small, the ball \(B_1^M(p)\) is GH close to the set of vectors in the unit ball of \(T_pM\) corresponding to minimizing geodesics starting at p. This is shown in Step 1. (In fact, the proof deals with spheres rather than balls, but we speak about balls in this informal explanation). If the injectivity radius \({{\,\mathrm{inj}\,}}_M(p)\) is small, there is a short geodesic loop from p to itself. Using triangle comparison, one can see that minimizing geodesics of length close to 1 cannot have too small angles with this loop. This part of the argument is contained in Step 5. One concludes that if \({{\,\mathrm{inj}\,}}_M(p)\) is small, then \(B_1^M(p)\), and hence \(B_1^n\), is GH close to a subset of the Euclidean unit ball where a significant part (namely a ball of certain smaller radius) is removed. Clearly, this is impossible in any fixed dimension, but it is not so obvious when \(n\rightarrow \infty \) while the radius of the removed ball stays fixed. This issue is handled in Steps 2–4 with Kirszbraun’s and Ulam–Borsuk theorems applied to suitable maps. Now we proceed with the formal proof.
By (104), there is a \(2\varepsilon \)-isometry \(f:B_1^n\rightarrow B_1^M(p)\) such that \(f(0)=p\). We denote by B the unit ball in \(T_pM\) and construct a map \(h:B_1^n\rightarrow B\) as follows: For every \(x\in B_1^n\), choose \(h(x)\in B\) such that \(\exp _p(h(x))=f(x)\) and \(|h(x)|=d_M(p,f(x))\). (Note that the choice of h(x) is not necessarily unique). We proceed in a number of steps.
Step 1 We show that h has a small distortion on the unit sphere \(S^{n-1}=\partial B_1^n\), see (106) and (111).
For every \(x,y\in B_1^n\), we have \( |f(x)-f(y)| \le |h(x)-h(y)| + \tfrac{1}{2}\varepsilon \) by (103) and Lemma 20 applied to \(u=h(x)\), \(v=h(y)\) and \(r=1\). Hence,
since f is a \(2\varepsilon \)-isometry. In particular, since \(h(0)=0\),
for all \(x\in B_1^n\).
Pick \(x,y\in S^{n-1}\). By (106) with \(-x\) in place of x, we have
since \(|x+y|\le 2\). By the parallelogram identity, we have
and \( |x+y|^2 + |x-y|^2 = 2(|x|^2+|y|^2) = 4 . \) These relations and (108) imply that
Therefore,
for all \(x,y\in S^{n-1}\). In particular, substituting \(y=x\) yields that
for all \(x\in S^{n-1}\). By the triangle inequality, (109) and (110) imply that
where \(\varepsilon _1=2\sqrt{10\varepsilon }\). Note that \(\varepsilon _1\le \frac{1}{5}\) since \(\varepsilon \le 10^{-3}\).
Step 2 Let Z be a maximal \(\varepsilon _1\)-separated subset of \(S^{n-1}\). The inequality (111) implies that the restriction \(h|_Z\) is 2-Lipschitz: \(|h(x)-h(x)|\le 2 |x-y|\) for any \(x,y\in Z\). Since \(T_pM\) is isometric to \({\mathbb {R}}^n\), Kirszbraun’s theorem [58] implies that \(h|_Z\) admits a 2-Lipschitz extension \({\widetilde{h}}:{\mathbb {R}}^n\rightarrow T_pM\). We need only the restriction of \({\widetilde{h}}\) to the unit sphere.
Pick \(x\in S^{n-1}\). By the maximality of Z, there exists \(z\in Z\) such that \(|x-z|\le \varepsilon _1\). The 2-Lipschitz continuity of \({\widetilde{h}}\) implies that \(|{\widetilde{h}}(x)-{\widetilde{h}}(z)| \le 2\varepsilon _1\), and (111) implies that \(|h(x)-h(z)|\le 2\varepsilon _1\). Since \({\widetilde{h}}(z)=h(z)\), it follows that
This and (107) imply that \( |{\widetilde{h}}(x)| \ge |h(x)|-\tfrac{4}{5} \ge \tfrac{1}{5} - \tfrac{5}{2}\varepsilon > 0 . \) Thus, we can define a continuous map \(\phi :S^{n-1}\rightarrow \partial B\) by
Step 3 We show that \(\phi \) maps \(S^{n-1}\) surjectively onto \(\partial B\). Arguing by contradiction, suppose that there exists \(w_0\in \partial B\setminus \phi (S^{n-1})\). Then, \(\phi \) is a map from \(S^{n-1}\) to the set \(\partial B\setminus \{w_0\}\), which is homeomorphic to \({\mathbb {R}}^{n-1}\). Hence, by the Borsuk–Ulam theorem, there exists \(x_0\in S^{n-1}\) such that \(\phi (x_0)=\phi (-x_0)\). This means that the vectors \({\widetilde{h}}(x_0)\) and \({\widetilde{h}}(-x_0)\) are positively proportional:
Let \(u=h(x_0)\) and \(v=h(-x_0)\). By (107), we have \(1-\frac{5}{2}\varepsilon \le |u|,|v|\le 1\). Therefore,
On the other hand, \(|u-v|\ge 2-\frac{5}{2}\varepsilon \) by (106). Hence,
Adding (115) to (114) and dividing by two yield that \( \langle u,u-v\rangle \ge 2 - \tfrac{15}{2}\varepsilon \). Since \(|{\widetilde{h}}(x_0)-u|\le 4\varepsilon _1\) by (112) and \(|u-v|\le 2\), it follows that
where the last inequality follows from the bounds \(\varepsilon _1\le \frac{1}{5}\) and \(\varepsilon \le 10^{-3}\). Similarly, switching the roles of \(x_0\) and \(-x_0\) we obtain that
Thus, the products \(\langle {\widetilde{h}}(x_0),u-v\rangle \) and \(\langle {\widetilde{h}}(-x_0),u-v\rangle \) have opposite signs. This contradicts (113); therefore, \(\phi \) is surjective.
Step 4 The surjectivity of \(\phi \) implies that for every \(v_0\in \partial B\) there exists \(z\in S^{n-1}\) such that
Indeed, let \(x\in S^{n-1}\) be such that \(\phi (x)=v_0\). By the construction of Z, there exists \(z\in Z\) such that \(|x-z|\le \varepsilon _1\). Then, \(|{\widetilde{h}}(x)-h(z)|\le 2\varepsilon _1\) since \(\widetilde{h}\) is a 2-Lipschitz extension of \(h|_Z\). The direction of \(v_0=\phi (x)\) is the same as that of \({\widetilde{h}}(x)\); hence,
where the first inequality follows from the Euclidean law of sines in the triangle with vertices 0, \({\widetilde{h}}(x)\), h(z). Also note that \(|{\widetilde{h}}(x)-h(z)|<2\varepsilon _1\le \frac{2}{5}<|h(z)|\) by (107). Hence, \(|{\widetilde{h}}(x)-h(z)|\) is not the largest side of this Euclidean triangle, and therefore, \(\angle (v_0,h(z))<\frac{\pi }{2}\). This and (117) imply (116).
Step 5 Now we prove (105). Let \(r_0={{\,\mathrm{inj}\,}}_M(p)\). We may assume that \(r_0<1\); otherwise, (105) holds trivially. Since \(|{\text {Sec}}_M|\le \varepsilon <1\) and \(r_0<1<\pi \), Klingenberg’s Lemma (see [79, Lemma 16 in Ch. 5]) implies that there exists a geodesic loop \(\gamma \) of length \(2r_0\) in M starting and ending at p. Equivalently, there exists \(v\in T_pM\) such that \(|v|=2r_0\) and \(\exp _p(v)=p\). Let \(v_0=v/2r_0\), then \(v_0\in \partial B\). By the result of Step 4, there exists \(z\in S^{n-1}\) satisfying (116). Define \(u=h(z)\), \(a=|u|=|h(z)|\), and \(\beta =\angle (v,u)=\angle (v_0,u)\); then, (116) takes the form
By the definition of h and (107), we have
We apply Lemma 20 with parameters \(K=\varepsilon \) and \(r=2r_0<2\) and obtain that
(recall that \(\exp _p(u)=\exp _p(h(z))=f(z)\) by the definition of h). On the other hand, \( d_M(p,f(z)) = |h(z)| = a \) by the definition of h. Thus,
We deduce (105) from (118), (119), and (120) via elementary hyperbolic geometry. Let \({\widetilde{M}}=M^2_{-\varepsilon }\) and construct points \({\widetilde{p}},{\widetilde{p}}_1,{\widetilde{z}}\in {\widetilde{M}}\) such that \(d_{\widetilde{M}}({\widetilde{p}},{\widetilde{p}}_1)=2r_0\), \(d_{{\widetilde{M}}}({\widetilde{p}},{\widetilde{z}})=a\) and \(\angle {\widetilde{z}}{\widetilde{p}}{\widetilde{p}}_1=\beta \). By construction, we have \(d_{{\widetilde{M}}}({\widetilde{z}},\widetilde{p}_1)=\curlyvee _{-\varepsilon }(2r_0,a,\beta )\); hence, by (120),
Let \(\ell \subset {\widetilde{M}}\) be the geodesic line through \({\widetilde{p}}\) and \({\widetilde{p}}_1\). Let \({\widetilde{q}}\in \ell \) be the orthogonal projection of \({\widetilde{z}}\) to \(\ell \), and define \(r_1=d_{{\widetilde{M}}}({\widetilde{p}},\widetilde{q})\). The inequality (121) implies that \( d_{\widetilde{M}}({\widetilde{p}},{\widetilde{q}}) \le d_{{\widetilde{M}}}({\widetilde{p}}_1,{\widetilde{q}}) \); hence, \(r_1\le \frac{1}{2}d_{{\widetilde{M}}}({\widetilde{p}},{\widetilde{p}}_1) = r_0\). Thus, it suffices to prove that \(r_1\ge 1-100\varepsilon \). Define \(b=d_{\widetilde{M}}({\widetilde{z}},{\widetilde{q}})\), and let \({\widetilde{z}}_1\in {\widetilde{M}}\) be the point symmetric to \({\widetilde{z}}\) with respect to \(\ell \). From the triangle \(\triangle {\widetilde{p}}{\widetilde{z}}{\widetilde{z}}_1\) with sides \(d_{\widetilde{M}}({\widetilde{p}},{\widetilde{z}})=d_{{\widetilde{M}}}({\widetilde{p}},{\widetilde{z}}_1)=a\) and angle \(\angle {\widetilde{z}}{\widetilde{p}}{\widetilde{z}}_1=2\beta \), one sees that
where the inequality in the middle follows from (100) since \(a\le 1\) by (119). Hence,
by (118). Now from the triangle \(\triangle \widetilde{q}{\widetilde{p}}{\widetilde{z}}\) with sides \(d_{{\widetilde{M}}}({\widetilde{q}},{\widetilde{p}})=r_1\) and \(d_{{\widetilde{M}}}({\widetilde{q}},{\widetilde{z}})=b\) and angle \(\angle \widetilde{z}{\widetilde{q}}{\widetilde{p}}=\frac{\pi }{2}\), one sees that
where the inequality again follows from (100). This, (119), and (122) imply that
where the last inequality holds since \(\varepsilon _1\le \frac{1}{5}\) and \(\varepsilon \le 10^{-3}\). Substituting \(\varepsilon _1=2\sqrt{10\varepsilon }\), we obtain that \(r_1^2 \ge 1-167\varepsilon \). Since \(\varepsilon \le 10^{-3}\), \(\sqrt{1-167\varepsilon } \ge 1-100\varepsilon \), \(r_1\ge 1-100\varepsilon \). Since \({{\,\mathrm{inj}\,}}_M(p)=r_0\ge r_1\); this proves (105) and Lemma 21 follows. \(\square \)
Now we prove Proposition 2. We restate the first part of Proposition 2 as the following lemma, which also provides an explicit value of the constant \(C_8\).
Lemma 22
Let \(K>0\) and let \(M, {\widetilde{M}}\) be complete n-dimensional Riemannian manifolds with \(|{\text {Sec}}_M|\le K\) and \(|{\text {Sec}}_{{\widetilde{M}}}|\le K\), and
Then,
Proof
Define
We may assume that \(\delta <10^{-6}r\); otherwise, (124) is trivial. We may also assume that \(\delta >0\), otherwise \({{\,\mathrm{inj}\,}}_M(x)\ge r\) since \(B_r^M(x)\) is isometric to \(B_r^{{\widetilde{M}}}({\widetilde{x}})\). Below we prove a stronger inequality \({{\,\mathrm{inj}\,}}_M(x) \ge r - 20\delta \), assuming that \(0<\delta <10^{-6}r\).
First we apply Lemma 21 to the smaller ball \(B_\rho ^M(x)\) where \(\rho =10^{-2}r\). To verify the assumptions of Lemma 21, observe that
since \( Kr^2 \le \pi ^2<10\) by (123). Then, by (1), (123), and (126),
Since \(\rho <r\), (125) and the definition of the pointed GH distance imply that
Hence, by the triangle inequality for \(d_{\mathrm{GH}}\),
since \(\delta \le 10^{-6} r=10^{-4}\rho \). By (126) and (127), the assumptions of Lemma 21 are satisfied for \(p=x\) and \(\rho \) in place of r. Now Lemma 21 implies that
We need this preliminary lower bound for the subsequent argument to work.
Let \(r_0={{\,\mathrm{inj}\,}}_M(x)\) and assume toward a contradiction that
Since \({\text {Sec}}_M\le K\) and \(r_0<r\le \frac{\pi }{\sqrt{K}}\), by Klingenberg’s Lemma (see [79, Lemma 16 in Ch. 5]), there is a geodesic loop \(\gamma \) of length \(2r_0\) in M starting and ending at x. Let y be the midpoint of this loop and \(\gamma _1\), \(\gamma _2\) the two halves of \(\gamma \) between x and y. Note that \(\gamma _1\) and \(\gamma _2\) are minimizing geodesics and \(d_M(x,y)=r_0\).
By (125), there is a correspondence \({\mathcal {R}}\) between the balls \(B_r^M(x)\) and \(B_r^{{\widetilde{M}}}({\widetilde{x}})\) with distortion at most \(2\delta \), see [26, Theorem 7.3.25]. Recall that a correspondence between metric spaces X and \(\widetilde{X}\) is a subset \({\mathcal {R}}\subset X\times {\widetilde{X}}\) with surjective coordinate projections to X and \({\widetilde{X}}\), and the distortion of \({\mathcal {R}}\) is defined by
We fix \({\mathcal {R}}\) with \( {\text {dis}}{\mathcal {R}}\le 2\delta \) for \(X=B_r^M(x)\) and \({\widetilde{X}}=B_r^{{\widetilde{M}}}({\widetilde{x}})\) and say that \(y\in B_r^M(x)\) and \({\widetilde{y}}\in B_r^{{\widetilde{M}}}({\widetilde{x}})\)correspond to each other if \((y,{\widetilde{y}})\in {\mathcal {R}}\). Since we are working with pointed GH distance, the centers x and \({\widetilde{x}}\) correspond to each other.
Pick \({\widetilde{y}}\in B_r^{{\widetilde{M}}}({\widetilde{x}})\) corresponding to the point y constructed above. Then,
by (129). Since \({{\,\mathrm{inj}\,}}_{{\widetilde{M}}}({\widetilde{x}})\ge r\), it follows that there is a point \({\widetilde{z}}\in B^{{\widetilde{M}}}_r({\widetilde{x}})\) such that \({\widetilde{y}}\) belongs to the minimizing geodesic from \(\widetilde{x}\) to \({\widetilde{z}}\) and \(d_{{\widetilde{M}}}({\widetilde{y}},{\widetilde{z}})=18\delta \). Pick \(z\in B_r^M(x)\) corresponding to \({{\widetilde{z}}}\), and let \(a=d_M(y,z)\). Since \({\text {dis}}{\mathcal {R}}\le 2\delta \) and the triangle inequality in \({\widetilde{M}}\) turns to equality for \({\widetilde{x}},\widetilde{y},{\widetilde{z}}\), we have
Thus,
Also note that \( |a-18\delta | = |d_M(y,z)-d_{{\widetilde{M}}}({\widetilde{y}},\widetilde{z})| \le {\text {dis}}{\mathcal {R}}\le 2\delta . \) Therefore,
where the last inequality follows from (128).
Let \(\gamma _3\) be a minimizing geodesic between y and z. Consider the angles \(\angle (\gamma _3,\gamma _1)\) and \(\angle (\gamma _3,\gamma _2)\) at y. Their sum equals \(\pi \); hence, at least one of them is no greater than \(\frac{\pi }{2}\). Assume w.l.o.g. that \(\angle (\gamma _3,\gamma _1)\le \frac{\pi }{2}\) and let \(u,v\in T_yM\) be the vectors tangent to \(\gamma _3\) and \(\gamma _1\), resp., and such that \(|u|=|v|=a\). Since \(\angle (u,v)=\angle (\gamma _3,\gamma _1)\le \frac{\pi }{2}\), we have \(|u-v|\le \sqrt{2} a\). Note that \(z=\exp _y(u)\). Let \(x'=\exp _y(v)\). Then, by (131), \(x'\) lies on \(\gamma _1\) at distance \(r_0-a\) from x. By Lemma 20 applied to \(p=y\) and a in place of r,
Hence,
By (131) and the assumption \(\delta <10^{-6}r\),
since \( Kr^2 \le \pi ^2<10\) by (123). This and (132) imply that
This and (130) imply that \(a<12\delta \). This contradicts (131); hence, the assumption (129) was false. Thus, \(r_0\ge r-20\delta \) and Lemma 22 follows. \(\square \)
Proof of Proposition 2
Lemma 22 implies the first claim of Proposition 2 for any \(C_8\ge 10^6\). To prove the second one, let \(f:M\rightarrow {\widetilde{M}}\) be a \((1+\varepsilon ,\delta )\)-quasi-isometry and \(\rho =\min \{{{\,\mathrm{inj}\,}}_{{\widetilde{M}}} , \tfrac{\pi }{\sqrt{K}} \}\). By Lemma 1,
for all \(x\in M\). Hence, by Lemma 22,
for all \(x\in M\). Thus, the second claim of Proposition 2 holds for any \(C_8\ge {5}\cdot 10^6\). \(\square \)
5 Proof of Theorem 1
Similar to the proof of Theorem 2, we first observe that the statement of Theorem 1 is scale invariant and it suffices to prove it for \(r=1\). When \(r=1\), Theorem 1 is equivalent to the following proposition with \(\delta _0(n)={\sigma _2}(n)>0\).
Proposition 4
For every positive integer n, there exists \(\delta _0=\delta _0(n)>0\) such that the following holds. Let \(0<\delta <\delta _0\) and let X be a metric space which is \(\delta \)-intrinsic and \(\delta \)-close to \({\mathbb {R}}^n\) at scale 1. Then, there exists a complete n-dimensional Riemannian manifold M such that
1. There is a \((1+C_1\delta ,C_1\delta )\)-quasi-isometry from X to M.
2. The sectional curvature \({\text {Sec}}_M\) of M satisfies \(|{\text {Sec}}_M|\le C_2\delta \).
3. The injectivity radius of M is bounded below by 1 / 2.
The proof of Proposition 4 occupies the rest of this section, which is split into several subsections.
Remark 8
In the proof of Proposition 4, the bounds \(C_j\), etc., are constructed via explicit arguments. Thus, by following the steps of the proof, one can obtain an explicit formula for the value \(\delta _0(n)\). However, the details of this go outside the framework of this paper.
We recycle the letter r for use in other notation. We fix n and assume that a metric space X satisfies the assumption of the proposition for a sufficiently small \(\delta >0\).
Fix a maximal \(\frac{1}{100}\)-separated set \(X_0\subset X\). We say that two points \(x,y\in X_0\) are adjacent if \(d_X(x,y)<1\) and say that they are neighbors if \(d_X(x,y)<\tfrac{1}{2}\).
The adjacency relation defines a graph which we refer to as the adjacency graph. The set of vertices of this graph is \(X_0\), and the edges are between all pairs of adjacent points. We need the following properties of this graph.
Lemma 23
1. The adjacency graph is connected.
2. Its vertex degrees are bounded by a number \(N_1(n)\) depending only on n.
Proof
1. Let \(x,y\in X_0\). Since X is \(\delta \)-intrinsic, there is a \(\delta \)-chain \(x_1,\dots ,x_N\in X\) with \(x_1=x\) and \(x_N=y\). For each \(x_i\), there is a point \(x_i'\in X_0\) with \(d_X(x_i,x_i')\le \frac{1}{100}\). By the triangle inequality, \(d_X(x_i',x_{i+1}')<2\delta +\frac{1}{50}<1\) for all i, and we may assume that \(x_1'=x\) and \(x_N'=y\). Then, the sequence \(x_1',\dots ,x_N'\) is a path connecting x to y in the adjacency graph.
2. Let \(q\in X_0\). Since we have \(d_H(B_1(q),B_1^n)<\delta \), there exists a \(2\delta \)-isometry \(f:B_1(q)\rightarrow B_1^n\). Let \(Y=X_0\cap B_1(q)\) be the set of points adjacent to q. Since Y is \(\frac{1}{100}\)-separated, its image f(Y) is a \((\frac{1}{100}-2\delta )\)-separated subset of \(B_1^n\). We may assume that \(\delta \) is so small that \(\frac{1}{100}-2\delta >\frac{1}{200}\). Then, the cardinality of Y is no greater than the maximum possible number of \(\frac{1}{200}\)-separated points in \(B_1^n\). \(\square \)
Lemma 23 implies that the set \(X_0\) is at most countable. In the sequel, we assume that \(X_0\) is countably infinite, \(X_0=\{q_i\}_{i=1}^\infty \). In the case when \(X_0\) is finite, the proof is the same except that the indices are restricted to a finite set.
5.1 Approximate Charts
Fix a collection of points \(\{p_i\}_{i=1}^\infty \) in \({\mathbb {R}}^n\) such that the Euclidean unit balls \(D_i:=B_1(p_i)\) are disjoint. For \(r>0\), we denote by \(D_i^r\) the Euclidean ball \(B_r(p_i)\subset {\mathbb {R}}^n\).
Recall that \(X_0=\{q_i\}_{i=1}^\infty \). For each \(i\in {\mathbb {N}}\), we have \(d_{\mathrm{GH}}(B_1(q_i),D_i)<\delta \) since \(D_i\) is isometric to \(B_1^n\). Recall that here we are dealing with pointed GH distance between balls where the centers are distinguished points. Hence, there exists a \(2\delta \)-isometry \(f_i:B_1(q_i)\rightarrow D_i\) such that \(f_i(q_i)=p_i\).
We fix \(2\delta \)-isometries \(f_i:B_1(q_i)\rightarrow D_i\), \(i\in {\mathbb {N}}\), for the rest of the proof. The balls \(D_i\) and the maps \(f_i\) play the role of coordinate charts in X. The next lemma provides a kind of transition map between charts.
Lemma 24
For each pair of adjacent points \(q_i,q_j\in X_0\), there exists an affine isometry \(A_{ij}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) such that
for every \(x\in B_1(q_i)\cap B_1(q_j)\).
Proof
Let \(Y=B_1(q_i)\cap B_1(q_j)\). Since \(d_{\mathrm{GH}}(B_1(q_i),B_1^n)<\delta \) and \(q_j\in B_1(q_i)\), there exists \(x_0\in Y\) such that
Define maps \(h_1,h_2:Y\rightarrow {\mathbb {R}}^n\) by \(h_1(x)=f_i(x)-f_i(x_0)\) and \(h_2(x)=f_j(x)-f_j(x_0)\). Since \(B_{1/2-3\delta }(x_0)\subset Y\subset B_{3/2+3\delta }(x_0)\) and \(f_i,f_j\) are \(2\delta \)-isometries, \(h_1\) and \(h_2\) satisfy the assumptions of Lemma 6 with parameters \(3/2+3 \delta , 3/2-3 \delta , 2\delta \) in place of \(R,r,\delta \), respectively. Hence, by Lemma 6 there exists an orthogonal map \(U:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) such that
for all \(x\in Y\). Now define \(A_{ij}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) by
This definition and (134) imply (133). \(\square \)
We fix maps \(A_{ij}\) constructed in Lemma 24 for the rest of the proof. We may assume that \(A_{ji}=A_{ij}^{-1}\) for all i, j and \(A_{ii}\) is the identity map.
Lemma 25
Let \(q_i,q_j,q_k\in X_0\) be three pairwise adjacent points. Then,
for all \(x\in D_i\).
Proof
Let \(a=f_i(q_j)\) and \(b=f_i(q_k)\). Consider the intersection of Euclidean balls
Let \(x\in Z\). Since \(f_i\) is a \(2\delta \)-isometry, there is \(q\in B_1(q_i)\) such that \(|f_i(q)-x|<2\delta \). Note that q belongs to the balls \(B_1(q_j)\) and \(B_1(q_k)\) as well. Then,
by (133) and the fact that \(A_{ik}\) is an isometry. Similarly,
and therefore,
where the first inequality follows from (133) and the second one from (138) and the fact that \(A_{jk}\) is an isometry. Now (137) and (139) imply that
for all \(x\in Z\).
Observe that Z contains a ball of radius \(\frac{1}{3}-3\delta \). Indeed, consider the point \(p=\frac{1}{3}(p_i+a+b)\). By the triangle inequality, \( |p-p_i| = \tfrac{1}{3} |(a-p_i) + (b-p_i) | \le \tfrac{2}{3} \) since \(a,b\in D_i=B_1(p_i)\). Hence, \(D_i\) contains the ball \(B_{1/3}(p)\). Similarly, since \(|b-a|<1+2\delta \), we have \(|p-a|<\frac{2}{3}+\delta \) and \(|p-b|<\frac{2}{3}+\delta \); hence, the ball \(B_{1/3-3\delta }(p)\) is contained in \(B_{1-2\delta }(a)\) and in \(B_{1-2\delta }(b)\).
Thus, (140) holds for all \(z\in B_{1/4}(p)\). The affine map \(A=A_{jk}\circ A_{ij}-A_{ik}\) can be written in the form \(A(x) = A(p) + L(x-p)\) where \(L:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) is a linear map. Then, (140) implies that \(|A(p)|<{2\delta _1}\) and \(|L(v)|<{2\delta _1}\) for all \(v\in B_{1/4}^n\). Hence, \(\Vert L\Vert \le {8\delta _1}\). Therefore, for all \(x\in B_2(p)\),
Since \(D_i\subset B_2(p)\), it follows that (136) holds for all \(x\in D_i\). \(\square \)
Lemma 26
Let \(q_i,q_j,q_k\in X_0\). Then,
1. If \(q_i\) and \(q_j\) are adjacent, then
2. If \(q_k\) is adjacent to both \(q_i\) and \(q_j\), then
Proof
The first assertion follows from the second one by setting \(k=j\) (recall that \(A_{jj}\) is the identity map). Let us prove the second assertion.
Since \(p_i=f_i(q_i)\), (133) implies that \(A_{ik}(p_i)\) is \(C_{23}\delta \)-close to \(f_k(q_i)\). Similarly, \(A_{jk}(p_j)\) is \(C_{23}\delta \)-close to \(f_k(q_j)\). Hence, the distance \(|A_{ik}(p_i)-A_{jk}(p_j)|\) differs from \(|f_k(q_i)-f_k(q_j)|\) by at most \(2C_{23}\delta \). In its turn, the distance \(|f_k(q_i)-f_k(q_j)|\) differs from \(d_X(q_i,q_j)\) by at most \(2\delta \) because \(f_j\) is a \(2\delta \)-isometry. Thus, \(|A_{ik}(p_i)-A_{jk}(p_j)|\) differs from \(d_X(q_i,q_j)\) by at most \((2C_{23}+2)\delta ={C_{25}}\delta \) and the lemma follows. \(\square \)
Lemma 27
For every \(i\in {\mathbb {N}}\) and every \(x\in D_i^{1/3}\), there exist \(j\in {\mathbb {N}}\) such that \(q_i\) and \(q_j\) are neighbors and \(A_{ij}(x)\in D_j^{1/50}\).
Proof
Since \(f_i\) is a \(2\delta \)-isometry from \(B_1(q_i)\) to \(D_i\), there exists \(y\in B_1(q_i)\subset X\) such that \(|f_i(y)-x|\le 2\delta \). Since \(X_0\) is a \(\frac{1}{100}\)-net in X, there is a point \(q_j\in X_0\) such that \(d_X(y,q_j)\le \frac{1}{100}\). For this point \(q_j\), we have
since \(f_i\) is a \(2\delta \)-isometry. This and the fact that \(x\in D_i^{1/3}\) imply that
Since \(p_i=f_i(q_i)\) and \(f_i\) is a \(2\delta \)-isometry, it follows that
Thus, \(q_i\) and \(q_j\) are neighbors; in particular, there is a well-defined map \(A_{ij}\). Since \(A_{ij}\) is an isometry, we have
By (133), we have \(|A_{ij}(f_i(q_j))-f_j(q_j)|< C_{23}\delta \); hence,
provided that \(\delta \) is sufficiently small. Thus, \(A_{ij}(x)\in D_j^{1/50}\) as claimed. \(\square \)
5.2 Approximate Whitney Embedding
At this point, we essentially forget about the original metric space X and use the collection of balls \(D_i\subset {\mathbb {R}}^n\) and maps \(A_{ij}\) from the previous section for the rest of the construction. Let \(\varOmega =\bigcup D_i\subset {\mathbb {R}}^n\) and \(\varOmega _0= \bigcup D_i^{1/10}\).
Let \(S={\mathbb {S}}^n\) be the unit sphere in \({\mathbb {R}}^{n+1}\) centered at \(e_{n+1}\), where \(e_1,\dots ,e_{n+1}\) is the standard basis of \({\mathbb {R}}^{n+1}\). Note that S contains the points 0 and \(2e_{n+1}\). For every \(r>0\), we denote by \(S_r\) the set of points in S lying at distance less than r from the ‘north pole’ \(2e_{n+1}\), that is, \(S_r=S\cap B_r(2e_{n+1})\).
Fix a smooth map
with the following properties:
-
1.
\({\phi }(x)=0\) for all \(x\in {\mathbb {R}}^n\setminus B_{1/5}(0)\).
-
2.
\({\phi }|_{B_{1/5}(0)}\) is a diffeomorphism onto \(S\setminus \{0\}\).
-
3.
\({\phi }|_{B_{1/10}(0)}\) is a diffeomorphism onto the spherical cap \(S_1\).
-
4.
\({\phi }|_{B_{1/50}(0)}\) is a diffeomorphism onto the spherical cap \(S_{1/10}\).
For algorithmic constructions discussed below, we can assume that \({\phi }\) is given as a function that is defined piecewisely by explicit, real analytic formulas. For each i, let \({\phi }_i(x)={\phi }(x-p_i)\) and define a map \(F_i:\varOmega \rightarrow S\subset {\mathbb {R}}^{n+1}\) as follows. If a point \(x\in \varOmega \) belongs to a ball \(D_j\), put
In particular, \(F_i(x)={\phi }_i(x)\) if \(x\in D_i\).
Lemma 28
If \(F_i(x)\ne 0\) for some \(x\in D_j^{1/5}\), then \(q_i\) and \(q_j\) are neighbors.
Proof
The assumption \(F_i(x)\ne 0\) implies that \(q_i\) and \(q_j\) are adjacent, and therefore, \(F_i(x) = {\phi }_i(A_{ji}(x))\). Thus, \({\phi }_i(A_{ji}(x))\ne 0\), and hence, \( |A_{ji}(x)-p_i| < \tfrac{1}{5} \). Since \(A_{ji}\) is an isometry and \(|p_j-x|<\frac{1}{5}\), we have
This and Lemma 26(2) imply that \(d_X(q_i,q_j)< \tfrac{2}{5}+{{C_{25}}}\delta < \tfrac{1}{2}\); hence, \(q_i\) and \(q_j\) are neighbors. \(\square \)
Let E be the space of square-summable sequences \((u_i)_{i=1}^\infty \) in \({\mathbb {R}}^{n+1}\) equipped with the norm defined by \(|u|^2=\sum |u_i|^2\) for \(u=(u_i)_{i=1}^\infty \). This is a Hilbert space naturally isomorphic to \(\ell ^2\). Define a map \(F:\varOmega \rightarrow E\) by
Lemma 23 implies that for every \(x\in U\) there are only finitely many indices i such that \(F_i(x)\ne 0\). Therefore, the sequence \(F(x)\in ({\mathbb {R}}^{n+1})^\infty \) is finite and hence indeed belongs to E.
Lemma 29
1. F is smooth, and there is \(C_{26}(k)>0\) depending only on n and k such that
for all \(k\ge 0\).
2. For every \(i\in {\mathbb {N}}\), the restriction \(F|_{D_i^{1/10}}\) is uniformly bi-Lipschitz, that is,
for all \(x,y\in D_i^{1/10}\).
Proof
1. Let \(x\in D_i\). By Lemma 23, there is at most \({N_1(n)}\) indices j such that \(F_j|_{D_i}\ne 0\). For every such j, we have \(\Vert d^k_xF_j\Vert \le \Vert {\phi }\Vert _{C^k({\mathbb {R}}^n)}\); therefore, \(\Vert d^k_xF\Vert \le {N_1(n)}\cdot \Vert {\phi }\Vert _{C^k({\mathbb {R}}^n)}=C_{26}(k)\).
2. The second inequality in (146) follows from (145) when \(C_{27}\ge C_{26}(1)\). To prove the first one, observe that \(C_{27}>0\) can be chosen so that \(|F(x)-F(y)|\ge |F_i(x)-F_i(y)|\ge C_{27}^{-1}{|x-y|}\) for \(x,y\in D_i^{1/10}\) since the ith coordinate projection from E to \({\mathbb {R}}^n\) does not increase distances and \(F_i|_{D_i^{1/10}}={\phi }_i|_{D_i^{1/10}}\) is bi-Lipschitz. \(\square \)
Equation (146) implies that the first derivative of F is uniformly bi-Lipschitz, i.e.,
for all \(x\in D_i^{1/10}\) and \(v\in {\mathbb {R}}^n\).
Lemma 29 implies that for each i the image \(\varSigma _i:=F(D_i^{1/10})\) is a smooth submanifold of E. We are going to apply Theorem 2 to the union \(\varSigma =\bigcup _i\varSigma _i\) in E. As the first step, we show that these submanifolds lie close to one another.
Lemma 30
There are \(C_{28}=C_{28}(0)>0\) and \( C_{28}(m)>0\) such that if \(q_i\) and \(q_j\) are neighbors and let \(x\in D_i^{1/5}\), then \(A_{ij}(x)\in D_j\) and
and
for all \(m\ge 1\).
Proof
By Lemma 26,
Since \(A_{ij}\) is an isometry, \( |A_{ij}(x)-A_{ij}(p_i)| = |x-p_i| < \tfrac{1}{5} \). Therefore,
hence, \(A_{ij}(x)\in D_j\). Since x is an arbitrary point of \(D_i^{1/5}\), we have shown that \(A_{ij}(D_i^{1/5})\subset D_j\).
Recall that the number of indices k such that \(F_k\) does not vanish on \(D_i\cup D_j\) is bounded by a constant depending only on n. Hence, in order to verify (149) it suffices to show that
for every fixed k. Consider four cases.
Case 1 \(q_k\) is adjacent to both \(q_i\) and \(q_j\). In this case,
and
Now (150) follows from the fact that the affine isometries \(A_{ik}\) and \(A_{jk}\circ A_{ij}\) are \(4C_{24}\delta \)-close on \(D_i\) by Lemma 25.
Case 2 \(q_k\) is not adjacent to \(q_i\) and \(q_j\). This case is trivial because \(F_k|_{D_i}\) and \(F_k\circ A_{ij}|_{D_i}\) both vanish by definition.
Case 3 \(q_k\) is adjacent to \(q_j\) but not to \(q_i\). In this case \(F_k|_{D_i}=0\) by definition. Let us show that \(F_k\circ A_{ij}|_{D_i^{1/5}}\) also vanishes. Since \(d_X(q_k,q_i)\ge 1\), Lemma 26 implies that \( |A_{kj}(p_k)-A_{ij}(p_i)| > 1 -{C_{25}}\delta \). Hence, for every \(y\in D_i^{1/5}\),
Since \(A_{kj}=A_{jk}^{-1}\) and \(A_{kj}\) is an isometry, this implies that \( |p_k-A_{jk}\circ A_{ij}(y)| > \tfrac{1}{5} \), and hence,
for every \(y\in D_i^{1/5}\).
Case 4 \(q_k\) is adjacent to \(q_i\) but not to \(q_j\). In this case \(F_k\circ A_{ij}|_{D_i^{1/5}}=0\), so it suffices to prove that \(F_k|_{D_i^{1/5}}=0\). Suppose the contrary, then Lemma 28 implies that \(q_k\) and \(q_i\) are neighbors. Since \(q_i\) and \(q_j\) are also neighbors, it follows that \(q_k\) and \(q_j\) are adjacent. This contradiction proves the claim. \(\square \)
We introduce the following notation for some important subsets of E. For every \(i\in {\mathbb {N}}\), define
Let \(\varSigma =\bigcup _i\varSigma _i\) and \(\varSigma ^0=\bigcup _i\varSigma _i^0\).
Recall that \(\varSigma _i\) is a smooth n-dimensional submanifold of E. For a point \(x\in \varSigma _i\), we denote by \(T_x\varSigma _i\) the tangent space of \(\varSigma _i\) at x realized as an affine subspace of E containing x, that is, \(T_x\varSigma _i\) is the n-dimensional affine subspace of E tangent to \(\varSigma _i\) at x.
Lemma 31
There is \(C_{29}>C_{28}(0)\) such that the following holds. For every \(x\in \varSigma _i\), there exist \(j\in {\mathbb {N}}\) and \(y\in \varSigma _j^0\) such that
and
Proof
Since \(x\in \varSigma _i\), we have \(x=F(z)\) for some \(z\in D_i^{1/10}\). By Lemma 27, there exists j such that \(q_i\) and \(q_j\) are neighbors and \(A_{ij}(z)\in D_ j^{1/50}\). Let \(y=F(A_{ij}(z))\), then \(y\in \varSigma _j^0\). Lemma 30 for \(m=0\) implies that
proving (152). To prove (153), observe that \(T_x\varSigma _i\) and \(T_y\varSigma _j\) are parallel to the images of the derivatives \(d_zF\) and \(d_{A_{ij}(z)}F\), resp. The image of \(d_{A_{ij}(z)}F\) coincides with the image of \(d_z(F\circ A_{ij})\). By Lemma 30 for \(m=1\), we have
This and (147) imply (153) with an appropriate \(C_{29}>C_{28}(0)\). \(\square \)
We use general metric space notation for subsets of E. In particular, for a set \(Z\subset E\) and \(r>0\) we denote by \({\mathcal U}_r(Z)\) the r-neighborhood of Z in E.
Lemma 32
\(\varSigma \cap {{\mathcal {U}}}_{1/2}(\varSigma _i^0)\subset {{\mathcal {U}}}_{C_{29}\delta }(\varSigma _i)\) for every \(i\in {\mathbb {N}}\).
Proof
Let \(q\in \varSigma \cap {{\mathcal {U}}}_{1/2}(\varSigma _i^0)\). Since \(q\in {{\mathcal {U}}}_{1/2}(\varSigma _i^0)\), there exists \(y\in D_i^{1/50}\) such that \(|q-F(y)|<\frac{1}{2}\). Since \(q\in \varSigma \), we have \(q=F(z)\) where \(z\in D_j^{1/10}\) for some j. Since the ith coordinate projection from E to \({\mathbb {R}}^{n+1}\) does not increase distances,
Recall that \(F_i(y)={\phi }_i(y)\) because \(y\in D_i\). Since \(y\in D_i^{1/50}\), the point \({\phi }_i(y)\) belongs to the spherical cap \(S_{1/10}\). Hence, \(|F_i(y)-2e_{n+1}|<\frac{1}{10}\). Therefore,
Thus, \(F_i(z)\) belongs to the spherical cap \(S_1\subset S\subset {\mathbb {R}}^{n+1}\), in particular \(F_i(z)\ne 0\). Hence, \(F_i(z)={\phi }_i(A_{ji}(z))\), and therefore, \(A_{ji}(z)\in {\phi }_i^{-1}(S_1)=D_i^{1/10}\).
Since \(F_i(z)\ne 0\), Lemma 28 implies that \(q_i\) and \(q_j\) are neighbors. Now, by Lemma 30 (for \(m=0\)) and the inequality \(C_{29}>C_{28}(0)\), we have
Since \(A_{ji}(z)\in D_i^{1/10}\), this inequality implies that
Since q is an arbitrary point from the set \(\varSigma \cap {\mathcal U}_{1/2}(\varSigma _i^0)\), the lemma follows. \(\square \)
Lemma 33
There is \(C_{30}{>C_{28}(0)}\) such that for every \(q\in \varSigma _i^0\) and \(r>0\),
Proof
By Lemma 29, \(\varSigma _i=F(D_i^{1/10})\) is a submanifold parametrized by a uniformly bi-Lipschitz smooth map \(F|_{D_i^{1/10}}\). We may assume that \(r<\frac{1}{50C_{27}}\) where \(C_{27}\) is the bi-Lipschitz constant in (146). Indeed, if \(r\ge \frac{1}{50C_{27}}\), then (154) holds for any \(C_{30}> 50C_{27}\) since the left-hand side of (154) is bounded by r.
Let \(q=F(x)\) where \(x\in D_i^{1/50}\). Then, every point \(q'\in \varSigma _i\cap B_r(q)\) is the image of some \(x'\in B_{C_{27}r}(x)\subset B_{1/50}(x)\subset D_i^{1/10}\). Hence,
where \( C_{30}= C_{26}(2)\) is the uniform bound of the second derivatives of \(F|_{D_i^{1/10}}\), see (145). This means that \(\varSigma _i\) deviates from its tangent space \(T_q\varSigma _i\) within the r-ball \(B_r(q)\) by distance at most \( C_{30}r^2\).
In addition, the point \(q\in \varSigma _i^0=F(D_i^{1/50})\) is separated by a distance at least \(\frac{1}{20C_{27}}>2r\) from the boundary of \(\varSigma _i\). Therefore, for each point from \(T_q\varSigma _i\cap B_r(q)\) there exists a point in \(\varSigma _i\) within distance \( C_{30}r^2\). \(\square \)
The next lemma essentially says that the \(\varSigma \subset E\) is \(C\delta \)-close to affine spaces in E at a scale of order \(\delta ^{1/2}\).
Lemma 34
There is \(C_{31}>0\) such that for every \(x\in \varSigma _i\) and \(r\ge \delta ^{1/2}\),
Proof
We may assume that \(r\le \frac{1}{4}\); otherwise, (155) holds for any \(C_{31}\ge 4\) since the left-hand side is bounded by r. By Lemma 31, there exist \(j\in {\mathbb {N}}\) and \(q\in \varSigma ^0_j\) such that \(|x-q|<C_{29}\delta \) and \(\angle (T_x\varSigma _i,T_q\varSigma _j)<C_{29}\delta \). Let \(A=T_q\varSigma _j\). Observe that the Hausdorff distance between the affine balls \(T_x\varSigma _i\cap B_r(x)\) and \(B_r^A(q)=A\cap B_r(q)\) is bounded by
since \(\delta \le r^2\) and \(\delta \le \delta ^{1/2}\le r\). Assuming that \(C_{31}>4C_{29}\), it suffices to verify that \( d_H(\varSigma \cap B_r(x),B_r^A(q)) < \frac{1}{2} C_{31}r^2 . \) By the definition of the Hausdorff distance, this is equivalent to the following pair of inclusions:
and
Since \(|x-q|<C_{29}\delta \), we have \(B_r(x) \subset B_{r+C_{29}\delta }(q)\), and therefore,
where the last inclusion follows from Lemma 32 provided that \(r+C_{29}\delta <\frac{1}{2}\). The latter follows from the inequality \(r\le \frac{1}{4}\) if \(\delta \) is so small that \(C_{29}\delta <\frac{1}{4}\). Hence,
where the last inclusion follows from Lemma 33. Since
this implies (156) when \(C_{31}\ge 2(C_{30}+2C_{29})\).
It remains to verify (157). We assume that \(\delta \) is so small that \(C_{29}\delta ^{1/2}<1\); then, \(C_{29}\delta < \delta ^{1/2} \le r\). Since \(|x-q|<C_{29}\delta \), this implies that \(|x-q|<r\). Let \(r_1=r-|x-q|\). By Lemma 33,
Since \(B^A_r(q)\subset {{\mathcal {U}}}_{r-r_1}(B^A_{r_1}(q))\), and inequality \({C_{30}} >C_{28}(0)\) and \(r-r_1=|x-q|< {{C_{30}} } \delta < {{C_{30}} } r^2\), this implies (157) when \(C_{31}\ge 4{C_{30}} . \) By choosing \(C_{31}\) so that the above inequalities are valid, the lemma follows. \(\square \)
5.3 The Manifold M
We choose a positive constant \(r_0<1\) such that
where \(C_{29}\) is the constant from Lemma 31 and \({\sigma _2}\) is the constant from Theorem 2. Some additional requirements on \(r_0\) arise in the course of the argument below, but the final value of \(r_0\) depends only on n.
We may assume that the constant \(\delta _0\) in Proposition 4 satisfies \(\delta _0< r_0^2\) (see Lemma 34). Then, for \(\delta <\delta _0\), Lemma 34 implies that
for every \(x\in \varSigma _i\). This and (159) imply that the assumptions of Theorem 2 are satisfied for \(\varSigma \) in place of X, \(r_0\) in place of r, \( C_{31}r_0^2\) in place of \(\delta \), and \(T_x\varSigma _i\) in place of \(A_x\) (for \(x\in \varSigma _i\)). Then, the conclusion of Theorem 2 with these settings, and with \( C_{33}(m)= C_{31}C_{13}(m)\) and \(C_{33}'={C_{31}C_{12}}\), is the following lemma.
Lemma 35
There are \(C_{32}>0\) and \(C_{33}(m)>0,\)\(C_{33}'>0\) such that the following holds. If \(r_0<C_{32}\) and \(\delta < r_0^2\), then there exists a closed n-dimensional smooth submanifold \(M\subset E\) such that
1. \(d_H(\varSigma ,M)< {5}C_{31}r_0^2<\frac{1}{10}r_0<\frac{1}{100}\).
2. The second fundamental form of M at every point is bounded by \(C_{31}C_{11}\).
3. \({{\,\mathrm{Reach}\,}}(M)\ge r_0/3\).
4. The normal projection \(P_M:{{\mathcal {U}}}_{r_0/3}(M)\rightarrow M\) satisfies for all \(x\in {\mathcal {U}}_{r_0/3}(M)\)
and
5. \(\angle (T_x\varSigma _i,T_{y}M)< C_{33}' r_0 {< \frac{1}{10}}\) for every \(x\in \varSigma _i\) and \(y=P_M(x)\). \(\square \)
These inequalities in Lemma 35 that are not present in Theorem 2 follow from the choice of \(C_{32}\) (and thus \(r_0\)) sufficiently small. The inequality \(d_H(\varSigma ,M)<\frac{1}{10}r_0\) ensures that \(\varSigma \) lies ‘deep inside’ the domain of \(P_M\). The second inequality in (162) implies that
and hence, \(P_M\) is locally 2-Lipschitz.
Let M be a submanifold from Lemma 35. Recall that \(\varSigma =\bigcup _i\varSigma _i=\bigcup _i F(D_i^{1/10})\) and \(\varSigma \) is contained in the domain of \(P_M\). For each i, define a map \(\psi _i:D_i^{1/10}\rightarrow M\) by
and let \(V_i\) be the image of \(\psi _i\), that is,
Observe that
and
for every \(x\in D_i^{1/10}\). This follows from Lemma 35(1) and the fact that \(\psi _i(x)\) is the nearest point in M to F(x).
The next lemma shows that the maps \(\psi _i\) provide a nice family of coordinate charts for M.
Lemma 36
If \(r_0<C_{35}\), where \(C_{35}\) is sufficiently small, and \(\delta <r_0^2\), then
1. \(\psi _i\) is uniformly bi-Lipschitz, that is,
for all \(x,y\in D_i^{1/10}\). In particular, \(V_i\) is an open subset of M and \(\psi _i\) is a diffeomorphism between \(D_i^{1/10}\) and \(V_i\).
2. \(\bigcup _i \psi _i(D_i^{1/{30}})=M\).
3. If \(i,j\in {\mathbb {N}}\) are such that \(V_i\cap V_j\ne \emptyset \), then \(q_i\) and \(q_j\) are neighbors.
Proof
1. The Lipschitz continuity of \(\psi _i\) follows from the bounds on the first derivatives of F and \(P_M\), see Lemma 29 and (163). More precisely, the second inequality in (168) holds for any \(C_{36}\ge 2C_{26}(1)\).
It remains to prove that with a suitable \(C_{36}>0\), we have
for all \(x,y\in D_i^{1/10}\). For every \(x\in D_i^{1/10}\) and \(v\in {\mathbb {R}}^n\), we have
The first inequality in (169) follows from the first inequality in (163), Lemma 35(5), and the fact that \(d_xF(v)\) belongs to \(T_{F(x)}\varSigma _i\). The second inequality in (169) follows from (147).
By Lemma 35(4) and (145), the first and second derivatives of \(P_M\) and F are bounded by constants independent of \(r_0\). These bounds imply that \( \Vert d^2_x\psi _i\Vert \le C_{37}\) for all \(x\in D_i^{1/10}\) and a suitable constant \(C_{37}>0\). Hence,
for all \(x,y\in D_i^{1/10}\). This and (170) imply that
for all \(x,y\in D_i^{1/10}\) such that
To handle the case when \(|x-y|>C_{38}\), observe that
by (167). Since \(F|_{D_i}\) in uniformly bi-Lipschitz (by Lemma 29), it follows that
for all \(x,y\in D_i^{1/10}\). If \(|x-y|>C_{38}\) and \(r_0\) is so small that \(2C_{31}r_0^2<\tfrac{1}{2} C_{27}^{-1}C_{38}\), then the right-hand side of (173) is bounded below by \(\frac{1}{2}C_{27}^{-1}|x-y|\). Thus, (169) holds with a suitable constant \( C_{36}>0\) for all \(x,y\in D_i^{1/10}\) and the first claim of the lemma follows.
2. Let \(x\in M\). By Lemma 35(1), there exists \(z\in \varSigma \) such that \(|x-z|< C_{31}r_0^2\). By Lemma 31, there exist \(i\in {\mathbb {N}}\) and \(y\in \varSigma _i^0\) such that \(|y-z|< {{C_{29}}}\delta \). Then,
where in the last inequality we assume that \(r_0<C_{35}\) and \(C_{35}<\frac{1}{3}(C_{31}+C_{29})^{-1}\). We are going to show that \(x\in F(D_i^{1/{30}})\).
Since \(x\in M\) and \(|x-y|<r_0/3\), the straight line segment [x, y] is contained in the domain of \(P_M\). Let \(\gamma \) be the image of this segment under \(P_M\). Then, \(\gamma \) is a smooth curve in M connecting x to the point \(P_M(y)\in P_M(\varSigma _i^0)=\psi _i(D_i^{1/50})\). Since \(P_M\) is locally 2-Lipschitz, we have \({{\,\mathrm{length}\,}}(\gamma ) \le 2 |x-y| < 2(C_{31}+C_{29})r_0^2\). We parametrize \(\gamma \) by [0, 1] in such a way that \(\gamma (0)=P_M(y)\) and \(\gamma (1)=x\). Suppose that \(x\notin \psi _i(D_i^{1/{30}})\) and let
This minimum exists since \(\psi _i(D_i^{1/{30}})\) is an open subset of M. Define \( {\widetilde{\gamma }}(t)=\psi _i^{-1}(\gamma (t)) \) for all \(t\in [0,t_0)\). Note that \(t_0>0\) and \({\widetilde{\gamma }}(0)\in D_i^{1/50}\) because \(P_M(y)\in \psi _i(D_i^{1/50})\). Since \(\psi _i\) is a diffeomorphism onto its image, \({\widetilde{\gamma }}\) is a smooth curve in \(D_i\). Moreover, since \(\psi _i\) is uniformly bi-Lipschitz, we have
Hence, the limit point \( p = \lim _{t\rightarrow t_0} {\widetilde{\gamma }}(t) \) exists and satisfies
We may assume that \(r_0\) is so small that the right-hand side of this inequality is smaller than \(\frac{1}{{30}}-\frac{1}{50}\). Since \({\widetilde{\gamma }}(0)\in D_i^{1/50}\), it follows that \(z\in D_i^{1/50}\). Hence, \(\gamma (t_0)=\psi _i(p)\in \psi _i(D_i^{1/{30}})\), contrary to the choice of \(t_0\). This contradiction shows that \(x\in \psi _i(D_i^{1/{30}})\). Since x is an arbitrary point of M, the second claim of the lemma follows.
3. Assume that \(V_i\cap V_j\ne \emptyset \). Then, there exist \(x\in D_i^{1/10}\) and \(y\in D_j^{1/10}\) such that \(\psi _i(x)=\psi _j(y)\). This equality and (167) imply that \(|F(x)-F(y)| < \tfrac{1}{5}\); hence,
(recall that \(F_i:\varOmega \rightarrow {\mathbb {R}}^{n+1}\) is the ith coordinate projection of F). Since \(x\in D_i^{1/10}\), the point \(F_i(x)\in {\mathbb {R}}^{n+1}\) belongs to the spherical cap \(S_1\), and therefore, \(|F_i(x)|>1\). This and (174) imply that \(F_i(y)\ne 0\), and hence, \(q_i\) and \(q_j\) are neighbors by Lemma 28. \(\square \)
Note that Lemma 36(3) and Lemma 23(2) imply that the sets \(V_i\) cover M with bounded multiplicity \(N_1(n)\), that is, for every \(x\in M\) the number of indices i such that \(x\in V_i\) is bounded by a \(N_1(n)\) depending only on n.
Now we can fix the value of \(r_0\) such that Lemma 35 and Lemma 36 work. Since \(r_0\) is yet another constant depending only on n, we omit the dependence on \(r_0\) in subsequent estimates and just use the generic notation C. In particular, the fourth assertion of Lemma 35 now implies that
where \(C_{39}(k)=C_{13}(k) r_0^{1-k}\) for all \(k\ge 1\) and \(C_{39}(0)=2\). By applying Lemma 42(1) in “Appendix A,” (145), and (175), we obtain
for all \(m\ge 0\).
Lemma 37
There is \(C_{41}>0\) such that the following is valid. If \(x\in D_i^{1/10}\), \(y\in D_j^{1/10}\) and \(\psi _i(x)=\psi _j(y)\), then
Proof
Applying Lemma 31 to the point \(F(x)\in \varSigma _i\) yields that there exist \(k\in {\mathbb {N}}\) and a point \(z\in D_k^{1/50}\) such that \(|F(x)-F(z)|< {{C_{29}}}\delta \). Since \(P_M\) is uniformly Lipschitz, see (175) with \(C_{39}(0)=2\), and \(C_{29}>C_{28}(0)\), it follows that
and (since \(\psi _i(x)=\psi _j(y)\))
This and (167) imply that \( |F(y)-F(z)|< \tfrac{1}{5}+{4} {{C_{29}}}\delta < \tfrac{1}{2} \); hence, \(F(y)\in {\mathcal U}_{1/2}(\varSigma _k^0)\). By Lemma 32, it follows that \(F(y)\in {{\mathcal {U}}}_{C_{29}\delta }(\varSigma _k)\). This means that there exists \(z'\in D_k^{1/10}\) such that
Then,
since \(P_M\) is uniformly Lipschitz. This and (179) imply that \(|\psi _k(z)-\psi _k(z')|<( {{2}} +{C_{13}(1)})C_{29}\delta \). Since \(\psi _k\) is uniformly bi-Lipschitz by the first claim of Lemma 36, it follows that
and hence, \(|F(z)-F(z')|<C_{27}C_{41}\delta \) by Lipschitz continuity of F, see Lemma 29. This and (180) imply that \(|F(y)-F(z)|<\tfrac{1}{2}C_{41},\) where \(C_{41}= (C_{27}C_{42}+C_{29})\delta \).
Thus, we have shown that (179) implies that \(|F(y)-F(z)|<\tfrac{1}{2}C_{41}\delta \). Similarly, (178) implies that \(|F(x)-F(z)|<\tfrac{1}{2}C_{41}\delta \) and (177) follows. \(\square \)
We are going to restrict our coordinate maps \(\psi _i\) to smaller balls \(D_i^{1/15}\). Let \(V_i'=\psi _i(D_i^{1/15})\) and \(U_{ij}=\psi _i^{-1}(V_i'\cap V_j')\). The set \(U_{ij}\subset D_i^{1/15}\) is the natural domain of the transition map \(\psi _j^{-1}\circ \psi _i\) between the restricted coordinate charts.
Lemma 38
There is \(C_{43}=C_{43}(m)>0\) such that the following is valid. Let \(i,j\in {\mathbb {N}}\) be such that \(V'_i\cap V'_j\ne \emptyset \). Then,
for all \(m\ge 0\).
Proof
Note that \(q_i\) and \(q_j\) are neighbors by Lemma 36(3). By Lemma 30, it follows that \(A_{ij}(D_i^{1/10})\subset D_j\). Consider the map \(G:D_i^{1/10}\rightarrow E\) defined by \(G=F\circ A_{ij}|_{D_i^{1/10}}\). By Lemma 30, we have
This and Lemma 35(1) imply that the image of G is contained in the domain of \(P_M\), so we can consider a map \({\widetilde{\psi }}_i:D_i^{1/10}\rightarrow M\) defined by \({\widetilde{\psi }}_i=P_M\circ G\).
Next we apply Lemma 42(2) in ‘Appendix A’ with \(f=P_M\), \(g=F\), and \(h=G\), where F and G are defined in arbitrary ball \(B^n(x',\rho )\subset {\mathbb {R}}^n\), centered at \(x'\in D_i^{1/10}\), and having radius \(\rho <r_0/(10C_{26}({m}))\). Then, by Lemma 29, \(F(B^n({p_i},\rho )) \subset B(F(x'),r_0/10)\subset E\). Assuming that \(\delta <1/(10{C_{29}})\), the inequality (183) implies that \(G(B^n(x_0,\rho )) \subset Y=B(F(x'),r_0/3)\subset E\). As \(F(x')\in M\), these imply that the image of both F and G is in \(Y\subset {{\mathcal {U}}}_{r_0/3}(M)\) where \(P_M\) is defined. Using Lemma 42(2) in ‘Appendix A’ in these small balls with (175) and (183) and combining these local estimates, we obtain
Assume that \(\delta < \min (1,C_{36}/(2C_{44}(1)))\). Then, (176) and (184) imply that \({\widetilde{\psi }}_i^{-1}\) has locally the Lipschitz constant \(2C_{36}^{-1}\). Then, (184) and Lemma 36(1) imply that \({\widetilde{\psi }}_i\) is a diffeomorphism onto its image, and the image of \({\widetilde{\psi }}_i\) contains \(V_i'\). Using (176) and (184), we see that
Moreover, by Lemma 42(1) in ‘Appendix A’, (184) and (185) imply that the composition \({\widetilde{\psi }}_i^{-1}\circ \psi _i\) is \(C\delta \)-close to the identity; more precisely,
where \( C_{43}(m)=m^m C_{45}(m) (1+ C_{44}(m))^m+{C_{44}(0)}. \)
Let us show that \(A_{ij}(U_{ij})\subset D_j^{1/10}\). Let \(x\in U_{ij}\) and \(z=A_{ij}(x)\). Then, \(|F(x)-F(z)|<{C_{29}}\delta \) by Lemma 30. Let \(y\in U_{ji}\) be such that \(\psi _j(y)=\psi _i(x)\). Then, \(|F(x)-F(y)|<C_{41}\delta \) by Lemma 37. Therefore, \(|F(y)-F(z)|<({C_{29}}+C_{41})\delta \). Since \(F|_{D_j}\) is uniformly bi-Lipschitz by Lemma 29(2), it follows that
if \(\delta \) is sufficiently small. Since \(y\in U_{ji}\subset D_j^{1/15}\), this implies that \(z\in D_j^{1/10}\).
Thus, we have shown that \(A_{ij}(U_{ij})\subset D_j^{1/10}\). This implies that
and therefore,
Then, (186) implies that
and (182) follows as \(A_{ij}\) is an affine isometry. \(\square \)
5.4 Riemannian Metric and Quasi-Isometry
Now we are going to equip M with a Riemannian metric g such that the resulting Riemannian manifold (M, g) satisfies the assertions of Proposition 4. (The metric induced from E is not suitable for this purpose. One of the reasons is that its curvature is bounded by C but not by \(C\delta \). Another reason is that the map \(\phi \) is arbitrary, so distances may be distorted.)
First we observe that there exists a smooth partition of unity \(\{u_i\}\) on M subordinate to the covering \(\{V_i'\}\) and \(C_{46}(m)>0\) such that
for all \(i,j\in {\mathbb {N}}\) and all \(m\ge 0\). To construct such a partition of unity, fix a smooth function \(h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}_+\) which equals 1 within the ball \(B_{1/{30}}(0)\) and 0 outside the ball \(B_{1/15}(0)\), given by \(h(t)=\alpha _{1/30,1/15}(t)\), see (68). Then, define \({\widetilde{u}}_i:M\rightarrow {\mathbb {R}}_+\) by
Finally, let \(u(x)=\sum _i{\widetilde{u}}_i(x)\) and \(u_i(x)=\widetilde{u}_i(x)/u(x)\). Lemma 38 implies that there is \(C_{46}(m)>0\) such that
for all \(i,j\in {\mathbb {N}}\) and all \(m\ge 0\). As in Lemma 36(3) and Lemma 23(2), we see that there is \(N_2(n)\) depending only on n such that for every \(x\in M\) the number of indices i such that \(x\in V_i'\) is bounded by a \(N_2(n)\). Hence, the sets \(V_i'\) cover M with bounded multiplicity \(N_2(n)\) and it follows from Lemma 36(2) that a similar estimate holds for \(u\circ \psi _i\) and (187) follows.
For every \(i\in {\mathbb {N}}\), define a Riemannian metric \(g_i\) on \(V_i\) by
where \(g_E\) is the standard Euclidean metric in \(D_i^{1/10}\subset {\mathbb {R}}^n\) and the star denotes the pullback of the metric by a map. In the other words, \(g_i\) is the unique Riemannian metric on \(V_i\) such that \(\psi _i\) is an isometry between \(D_i^{1/10}\) and \((V_i,g_i)\). Then, Lemma 38 implies that
for all \(m\ge 0\) and \(i,j\in {\mathbb {N}}\) such that \(V_i'\cap V_j'\ne \emptyset \). Define a metric g on M by
The pullback \(\psi _j^*g\) of this metric by a coordinate map \(\psi _j\) has the form
By (187) and (190), it follows that
Let \(C_{48}=C_{47}({n},0).\) So in the local coordinates defined by \(\psi _j\) on \(V_j'\), the metric tensor is \( C_{48}\delta \)-close to the Euclidean one and its derivatives up to the second order are bounded by \( C_{47}({n},2)\delta \). So are the sectional curvatures of the metric. Thus, (M, g) satisfies the second assertion of Proposition 4 with a suitable constant \(C_2\).
Let \(d_g:M\times M\rightarrow {\mathbb {R}}_+\) be the distance induced by g. The estimate (193) implies that the coordinate maps \(\psi _i\) are almost isometries between the Euclidean metric on \(D_i^{1/15}\) and the metric g on \(V_i'\). More precisely, \(\psi _i\) distorts the lengths of tangent vectors by a factor of at most \(1+C_{48}\delta \). Therefore,
for all \(x,y\in D_i^{1/30}\). (The ball \(D_i^{1/30}\) here is twice smaller than the domain where \(\psi _i\) is almost isometric. This adjustment is needed because the \(d_g\)-distance between points in \(V_i'\) can be realized by paths that leave \(V_i'\).)
Below we will assume that \(\delta <C_{48}^{-1}\) so that \(1+ C_{48}\delta <2\) in (194). This and bi-Lipschitz continuity of charts \(\psi _i\) (see Lemma 36(1)) imply that \(d_g\) is bi-Lipschitz equivalent to the intrinsic metric \(d_M\) induced on M from E. Namely,
for all \(x,y\in M\).
Now we construct a \((1+C\delta ,C\delta )\)-quasi-isometry \(\varPsi :X\rightarrow M\). Recall that \(X_0=\{q_i\}_{i=1}^\infty \) is a \(\frac{1}{100}\)-net in our original metric space X and for each \(i\in {\mathbb {N}}\) we have a \(2\delta \)-isometry \(f_i:B_1(q_i)\rightarrow D_i\) such that \(f_i(q_i)=p_i\). We construct \(\varPsi :X\rightarrow M\) as follows. For every \(x\in X\), pick a point \(q_j\in X_0\) such that \(d_X(x,q_j)\le \frac{1}{100}\) and define
The next lemma shows that the choice of \(q_j\) does not make much difference.
Lemma 39
There is \(C_{49}>0\) such that the following holds. Let \(x\in X\) and \(q_i\in X_0\) be such that \(d_X(x,q_i)<\frac{1}{20}\). Then, \(f_i(x)\in D_i^{1/15}\) and
Proof
Let \(q_j\) be the point of \(X_0\) chosen for x in the construction of \(\varPsi \). Then, \(d_X(x,q_j)\le \frac{1}{100}\) and \(\varPsi (x)=\psi _j(f_j(x))\). By the triangle inequality,
hence, \(q_i\) and \(q_j\) are neighbors. Observe that \( |f_i(x)-p_i|<\tfrac{1}{20}+{2}\delta \) since \(p_i=f_i(q_i)\) and \(f_i\) is a \(2\delta \)-isometry. Similarly, \( |f_j(x)-p_j|<\tfrac{1}{100}+{2}\delta \). Hence, \(f_i(x)\in D_i^{1/15}\) and \(f_j(x)\in D_j^{1/50}\). By (133), the point \(f_j(x)\) is \(C_{23}\delta \)-close to \(A_{ij}(f_i(x))\). Hence, by Lemma 29,
By Lemma 30, we have \(|F(f_i(x))-F(A_{ij}(f_i(x)))|<{C_{29}}\delta \). Therefore,
Denote \(a=F(f_j(x))\) and \(b=F(f_i(x))\); then, \(\varPsi (x)=P_M(a)\) and \(\psi _i(f_i(x))=P_M(b)\). Assuming that \(C_{50}\delta <r_0/10\), (198) implies that \(|a-b|<C_{50}\delta <r_0/10\). Since \(a\in \varSigma \subset {\mathcal {U}}_{r_0/10}(M)\) and \(P_M\) is defined in \({\mathcal {U}}_{r_0/3}(M)\), it follows that the line segment [a, b] is contained in the domain of \(P_M\). This and (163) giving the upper bound 2 for the local Lipschitz constant of \(P_M\) imply that
Hence, by (195),
Since \(P_M(a)=\varPsi (x)\) and \(P_M(b)=\psi _i(f_i(x))\), (197) follows. \(\square \)
Now let us show that \(\varPsi (X)\) is a \(C_{51}\delta \)-net in \((M,d_g)\), where \(C_{51}=C_{49}+4\). Pick \(z\in M\). By Lemma 36(2), \(z\in \psi _i(D_i^{1/30})\) for some i. Let \(y\in D_i^{1/30}\) be such that \(\psi _i(y)=z\). Since \(f_i\) is a \(2\delta \)-isometry, there is \(x\in B_1(q_i)\) such that \(|y-f_i(x)|<2\delta \). By the bi-Lipschitz estimate (194),
Since \(y\in D_i^{1/30}\), \(|y-f_i(x)|<2\delta \), and \(f_i\) is a \(2\delta \)-isometry with \(f_i(q_i)=p_i\), we have \( d(x,q_i)< \tfrac{1}{30} + 4\delta < \tfrac{1}{20} . \) Hence, \(d_g(\varPsi (x),\psi _i(f_i(x))) <C_{49}\delta \) by Lemma 39. This and (199) imply that
Since \(z\in M\) is arbitrary, it follows that \(\varPsi (X)\) is a \(C_{51}\delta \)-net in \((M,d_g)\).
Lemma 40
There is \(C_{52}\ge C_{51}\) such that the following holds. For all \(x,y\in X\) such that \(d_X(x,y)<\frac{1}{100}\) or \(d_g(\varPsi (x),\varPsi (y))<\frac{1}{100}\), one has
Proof
Let \(x\in X\) and \(q_i\) be the point of \(X_0\) chosen for x in the construction of \(\varPsi \), so that \(d_X(x,q_i)\le \frac{1}{100}\). Then, \(\varPsi (x)=\psi _i(f_i(x))\). Note that \(|f_i(x)-p_i|<\frac{1}{100}+{2}\delta <\frac{1}{30}\) since \(p_i=f_i(q_i)\) and \(f_i\) is a \(2\delta \)-isometry.
First, we consider the case when \(y\in X\) is such that \(d_X(y,q_i)<\frac{3}{100}\). Since \(f_i\) is a \(2\delta \)-isometry, \(|f_i(y)-p_i|<\frac{3}{100}+{2}\delta <\frac{1}{30}\) and the distance \(|f_i(x)-f_i(y)|\) differs from \(d_X(x,y)\) by at most \(2\delta \). The above and (194) imply that
This and Lemma 39 prove (201) when \(d_X(y,q_i)<\frac{3}{100}\).
In particular, this proves the claim of the lemma in the case when \(d_X(x,y)<\frac{1}{100}\), by the triangle inequality we have \(d_X(y,q_i)<\frac{1}{100}+\frac{1}{100}<\frac{3}{100}\) .
Second, we consider the case when \(y\in X\) is such that \(d_g(\varPsi (x),\varPsi (y))<\frac{1}{100}\). For every \(r>0\), denote by \(B_i(r)\) the ball of radius r in M with respect to \(d_g\) centered at \(\psi _i(p_i)\). Since \(\psi _i\) almost preserves the metric tensor in the sense of (193), by denoting \(C_{49}=C_{47}(0)\) we have
Since \(|f_i(x)-p_i|<\frac{1}{100}+{2}\delta \), it follows from (194) that the point \(\varPsi (x)=\psi _i(f_i(x))\) belongs to \(B_i((1+C_{48}\delta )(\frac{1}{100}+{2}\delta ))\subset B_i(\frac{1}{100}+3(1+C_{48})\delta )\), and hence,
Let \(q_j\) be the point of \(X_0\) chosen for y when defining \(\varPsi \) that satisfies \(d_X(y,q_j)\le \frac{1}{100}\). Since \(\varPsi (y)\in V_i'\), the point \(z:=\psi _i^{-1}(\varPsi (y))=\psi _i^{-1}\circ \psi _j(f_j(y))\) is well defined. Moreover, z lies within distance \(\frac{1}{50}+{2}\delta \) from \(p_i\) since \(\varPsi (y)\in B_i(\frac{1}{50}+{2}\delta )\). By Lemma 38, z is \( C_{43}(0)\delta \)-close to \(A_{ij}(f_j(y))\) and the latter is \(C_{23}\delta \)-close to \(f_i(y)\) by (133). Hence, \(|f_i(y)-p_i|<\frac{1}{50} +{( C_{43}(0)+C_{23}+2)}\delta \). Since \(f_i\) is a \(2\delta \)-isometry, it follows that \(d_X(y,q_i)<\frac{1}{50}+{( C_{43}(0)+C_{23}+4)}\delta <\frac{3}{100}\). Thus, (201) follows from the first part of the proof. \(\square \)
Lemma 40 and the fact that \(\varPsi (X)\) is a \(C_{51}\delta \)-net in \((M,d_g)\) imply that \(\varPsi \) satisfies the assumptions of Lemma 4 with \(r=\frac{1}{100}\) and \( C_{52}\delta \) in place of \(\delta \). Thus, \(\varPsi \) is a \((1+{10^3C_{52}}\delta ,{3C_{52}}\delta )\)-quasi-isometry from X to \((M,d_g)\) and the first claim of Proposition 4 follows. The second claim is already proved above. It remains to prove the third claim of Proposition 4.
Since \(\varPsi \) is a \((1+{10^3}{C_{52}}\delta ,{3}{C_{52}}\delta )\)-quasi-isometry, Lemma 1 implies that every unit ball in \((M,d_g)\) is GH (\( 2015C_{52}\delta \))-close to a unit ball in X and hence also \({(2015C_{52}+1)}\delta \)-close to a unit ball in \({\mathbb {R}}^n\). Thus, for every \(p\in M\),
see (66). Also, we have already shown that (M, g) satisfies the second assertion of Proposition 4 so that its sectional curvature is bounded by \(C_2{\delta }\). Therefore, one can apply Lemma 21 with \(r=1\) and \(K=C_2\delta <10^{-3}\) (see (66)) and conclude that \({{\,\mathrm{inj}\,}}_M\ge \frac{9}{10}>\frac{1}{2}\). This finishes the proof of Proposition 4 and the proof of Theorem 1.
Remark 9
The quasi-isometry parameters in Theorem 1 are optimal up to constant factors. To see this, assume that a metric space X is \((1+\delta r^{-1},\delta )\)-quasi-isometric to an n-dimensional manifold M with \(|{\text {Sec}}_M|\le \delta r^{-3}\) and \(|{{\,\mathrm{inj}\,}}_M|\ge 2r\). Then, by Lemma 1 the r-balls in X are GH \(C\delta \)-close to r-balls in M. Furthermore, by (1) the r-balls in M are GH \(C\delta \)-close to r-balls in \({\mathbb {R}}^n\). Hence, X is \(C\delta \)-close to \({\mathbb {R}}^n\) at scale r.
Thus, the assumption of Theorem 1 that X is \(\delta \)-close to \({\mathbb {R}}^n\) at scale r is necessary, up to multiplication of the parameters by a constant factor depending on n. The assumption that X is \(\delta \)-intrinsic could be weakened, but it is not really restrictive due to Lemma 3.
Remark 10
We note in the proof of Proposition 4 the construction of the manifold M uses only the r-balls \(B_r(q_i)\) centered in a maximal \(\frac{r}{100}\)-separated subset \(X_0=\{q_i\}_{i=1}^N\) in X and the fact that the Gromov–Hausdorff distance between any balls \(B_r(q_i)\) and \(B_r^n\) is less than \(\delta \). We will later use this observation in Algorithm ManifoldConstruction.
We also note that the assumptions of Theorem 1 can be relaxed: It is enough to assume that X is \(\delta \)-intrinsic and there is a (r / 100)-net \(X_0\subset X\) such that for any \(x\in X_0\) the ball \(B_r(x)\subset X\) is \(\delta \)-close to the Euclidean ball \(B_r^n\). Indeed, when this is valid, we see that the ball of radius \(\tfrac{99}{100}r\) centered at any point \(x\in X\) is \(3\delta \)-close to the Euclidean ball of the same radius. Then, the assumptions in the claim of Theorem 1 are valid with parameters r and \(\delta \) replaced by \(\tfrac{99}{100}r\) and \(3\delta \), respectively.
6 Proof of Corollaries 1, 2 and 3
Proof of Corollary 1
First we prove the first inclusion in (9). Let X be a metric space from the class \(\mathcal M_{\delta /6}(n,K/2,2i_0,D-\delta )\). Then, there exists a manifold \(M\in {\mathcal {M}}(n,K/2,2i_0,D-\delta )\) such that \(d_{\mathrm{GH}}(M,X)<\frac{\delta }{6}\). Hence, every r-ball in X is GH \(\frac{\delta }{2}\)-close to an r-ball in M. Since \(r=(\delta /K)^{1/3}\), by (1) we have \(d_{\mathrm{GH}}(B_r^M(x),B^n_r)<\frac{1}{2} Kr^3=\frac{\delta }{2}\) for every \(x\in M\). Hence, every r-ball in X is GH \(\delta \)-close to \(B^n_r\). Thus, X is \(\delta \)-close to \({\mathbb {R}}^n\) at scale r. Similarly, X is \(\delta _0\)-close to \({\mathbb {R}}^n\) at scale \({i_0}\). Since \(d_{\mathrm{GH}}(M,X)<\frac{\delta }{6}\), Lemma 2(1) implies that X is \(\delta \)-intrinsic. We also have \({{\,\mathrm{diam}\,}}(X)\le {{\,\mathrm{diam}\,}}(M)+2d_{\mathrm{GH}}(X,M)\le D\). Thus, \(X\in {\mathcal {X}}\), proving the first inclusion in (9).
Now we prove the second inclusion in (9). Let \(X\in {\mathcal {X}}\). Recall that \(\delta =Kr^3\), \(\delta _0=Ki_0^3\), \(\delta <\delta _0\), and \(Ki_0^2<{\sigma _1}\). Therefore, \(r<i_0\) and \(\delta r^{-1}<\delta _0 i_0^{-1}<{\sigma _1}\). If \({\sigma _1}\) is sufficiently small, then by Theorem 1 there exists a manifold M which is \((1+C_1\delta r^{-1},C_1\delta )\)-quasi-isometric to X and has \(|{\text {Sec}}_M|\le C_2\delta r^{-3}=C_2K\). Let us show that \({{\,\mathrm{inj}\,}}_M>{2}i_0/3\). Since \(X\in {\mathcal {X}}(n,\delta _0,i_0,D)\) and \(r<i_0\), the above quasi-isometry and Lemma 1 imply that
for all \(x\in M\). By Proposition 2(1) applied to \({\widetilde{M}}={\mathbb {R}}^n\) and \(\rho =i_0\), it follows that
provided that \({\sigma _1}\) is sufficiently small. (Recall that \(i_0<\sqrt{{\sigma _1}/K}\) and \(\delta _0<{\sigma _1}i_0\).)
By (8), we have \(d_{\mathrm{GH}}(X,M) \le {2C_1} \delta r^{-1} D\); hence, \({{\,\mathrm{diam}\,}}(M) \le D (1+{4C_1}\delta r^{-1})\). We may assume that \({\sigma _1}\) is so small that \({4C_1}\delta r^{-1}<\tfrac{1}{4}\), and let \(M_1\) be the result of rescaling M by the factor \((1+{4C_1}\delta r^{-1})^{-1}\). Then, \({{\,\mathrm{diam}\,}}(M_1)\le D\) and \(d_{\mathrm{GH}}(M,M_1)\le {2C_1}\delta r^{-1}D\). Hence,
Note that the above scale factor between M and \(M_1\) is greater than \(\frac{3}{4}\). Then, \({{\,\mathrm{inj}\,}}_{M_1}\ge \frac{3}{4}{{\,\mathrm{inj}\,}}_M \ge i_0/{2}\), and therefore, \(M_1\in {\mathcal {M}}(n,{\tfrac{4}{3}C_2} K,i_0/{2},D)\). This and (204) imply the second inclusion in (9) and Corollary 1 follows. \(\square \)
Proof of Corollary 2
In this proof, we assume that the reader is familiar with basics of Alexandrov space geometry, see, e.g., [17, 26, 27].
The implication (2)\(\Rightarrow \)(1) of Corollary 2 is standard. Let X be an n-manifold equipped with a metric of curvature bounded between \(-K_0\) and \(K_0\) in the sense of Alexandrov and injectivity radius bounded below by \(i_0>0\). Then (see, e.g., [8] for proofs), the tangent cone of X at every point is isometric to \({\mathbb {R}}^n\), all geodesics are uniquely extensible, and hence, X has a well-defined exponential map. The definition of Alexandrov curvature bounds implies that the exponential map features the same distance comparison properties as a Riemannian manifold with \(|{\text {Sec}}|\le K_0\), in particular (98), holds. Hence, just like in the Riemannian case (cf. (1) and Sect. 4), we have \(d_{\mathrm{GH}}(B^X_r(x), B_r^n) \le K_0r^3\) for all \(x\in X\) and \(0<r\le r_0:=\min \{K^{-1/2},i_0/2\}\). For \(r\ge r_0\), one can use the trivial estimate \( d_{\mathrm{GH}}(B^X_r(x), B_r^n) \le 2r \). Thus, (205) holds for \(K=\max \{K_0,2r_0^{-2}\}\) and all \(r>0\). This proves the implication (2)\(\Rightarrow \)(1) of Corollary 2.
Now we prove the implication (1)\(\Rightarrow \)(2). Let X be a complete geodesic space satisfying
for some \(K>0\) and all \(r>0\). Pick a decreasing sequence \(r_i\rightarrow 0\) such that \(r_1\le {\min (1,}\sqrt{\sigma _1/K})\) where \(\sigma _1\) is the constant from Theorem 1. Due to (205) and the bound on \(r_1\), we can apply Theorem 1 to X with \(r=r_i\) and \(\delta =Kr_i^3\). This yields a sequence of Riemannian n-manifolds \(M_i\) such that \(|{\text {Sec}}_{M_i}|\le C_2K\), \({{\,\mathrm{inj}\,}}_{M_i}\ge r_i/2\), and \(M_i\) is \((1+C_1Kr_i^2,C_1Kr_i^3)\)-quasi-isometric to X. By Lemma 1, it follows that (X, p) is a pointed GH limit of \((M_i,p_i)\) where \(p\in X\) is an arbitrary marked point and \(p_i\in M_i\) corresponds to p via the quasi-isometry.
Let us show that the injectivity radii of \(M_i\) are uniformly bounded away from 0. To do this, we apply Proposition 2 to \(M=M_i\) and \({\widetilde{M}}=M_1\). Due to their quasi-isometry to X, the manifolds \(M_i\) and \(M_1\) are \((1+2C_1Kr_1^2,2C_1Kr_1^3)\)-quasi-isometric to each other. Hence, by Proposition 2(2)
The right-hand side of (206) is bounded below by \(r_1/4\) if \(r_1\le C_{53}/\sqrt{K}\) for a suitable constant \(C_{53}>0\) (whose value is determined by the constants provided by Theorem 1 and Proposition 2). Thus, all \(M_i\) have a uniform lower bound for the injectivity radius and hence X is a non-collapsed limit of \(\{M_i\}\). As explained in, e.g., [51, §8.20], it follows that X is an n-manifold (with a low regularity Riemannian metric) with the same bounds for curvature and injectivity radius.
It remains to prove the last claim of Corollary 2 (that estimates curvature and injectivity radius of X in terms of K). The curvature bound \(C_2K\) obtained above already has the desired form. The injectivity radius bound \(r_1/4\) gets the desired form \(1/(C_{53}\sqrt{K})\) if we choose \(r_1=\min \{\sqrt{\sigma _1},C_{53}\}/\sqrt{K}\). \(\square \)
Finally, we prove Corollary 3.
Proof of Corollary 3
Let us consider \({\widehat{\delta }}<\delta _0\), where \(\delta _0=\delta _0(n,K)\) is chosen later in the proof, and \(r=({\widehat{\delta }}/K)^{1/3}\). Then, \(r<r_0\), where \(r_0=(\delta _0/K)^{1/3}\). By (1), the manifold N is \({\widehat{\delta }}\)-close to \({\mathbb {R}}^n\) at scale r / 2 provided that above \(r_0\le \min \{K^{-1/2},\frac{1}{2}{{\,\mathrm{inj}\,}}_N\}\). Hence, the set X with the approximate distance function \({\widetilde{d}}\) is \({2{\widehat{\delta }}}\)-close to \({\mathbb {R}}^n\) at scale r / 2. As in Lemma 3, we can replace \({\widetilde{d}}\) by a \({10}{\widehat{\delta }}\)-intrinsic metric \(d'\) on X. This can be done with standard algorithms for finding the shortest paths in graphs. By Lemma 4, \((X,d')\) is \((1+{40}{\widehat{\delta }} r^{-1},{20}{\widehat{\delta }})\)-quasi-isometric to N.
The metric space \((X,d')\) is \({40}{\widehat{\delta }}\)-close to \({\mathbb {R}}^n\) at scale r / 2. We may assume that \(\delta _0=\delta _0(n,K)\) satisfies \(\delta _0< K^{- 1/2} \sigma _1^{3/2}\), where \(\sigma _1=\sigma _1(n)\) is given in Theorem 1. Then, \(\delta _0< \sigma _1 r_0\).
As in Theorem 1 (see also the algorithm ManifoldConstruction below), using the given data one can construct a manifold \(M=(M,g)\) which is \((1+{40}C_1{\widehat{\delta }} r^{-1},{20}C_1{\widehat{\delta }})\)-quasi-isometric to \((X,d')\) and has \(|{\text {Sec}}_M|\le C_2\,{40}{\widehat{\delta }} \, (r/2)^{-3}= C_9K,\) where \( C_9={80}C_2\). Since both M and N are quasi-isometric to X with these parameters, they are \((1+{80}C_1{\widehat{\delta }} r^{-1},{40}C_1{\widehat{\delta }})\)-quasi-isometric to each other. By Proposition 1, it follows that there exists a bi-Lipschitz diffeomorphism between M and N with bi-Lipschitz constant \(1+C_7\,{80}C_1{\widehat{\delta }} r^{-1}= 1+{80}C_7C_1K^{1/3}{\widehat{\delta }}\,{}^{2/3}\). Thus, M satisfies the statements 1 and 2 of Corollary 3.
To verify the last statement of Corollary 3, assume that \(\delta _0=\delta _0(n,K)\) is chosen to be so small that \(r_0=(\delta _0/K)^{1/3}<(C_2K)^{-1/2}\). Then, Proposition 2(2) applies to M and \({\widetilde{M}}=N\) with \({40}C_1{\widehat{\delta }}\) in place of \(\delta \) and \(C_2K\) in place of K. It implies that
We may assume that \(\delta _0\) is so small that the term \(1- {80} C_8C_1{\widehat{\delta }} r^{-1} =1-{80}C_8C_1K^{1/3}\widehat{\delta }\,{}^{2/3}\) in this estimate is greater than \(\frac{1}{2}\). Then, the last statement of Corollary 3 follows. Choosing \(\delta _0=\delta _0(n,K)\) so that the above conditions for \(\delta _0\) and \(r_0\) are satisfied, we obtain Corollary 3. \(\square \)
7 Manifold Reconstructions Based on Theorems 1 and 2
Now we change the gear and explain how the above geometric proofs can be developed to manifold reconstruction procedures.
7.1 Outline of Reconstruction Procedures
The constructive proofs of Theorems 1 and 2 yield algorithms that can be used to produce submanifolds or manifolds from finite data sets. We give only the sketches of the algorithms that could be written of based on these theorems. Adding the necessary details to make these sketches numerically implementable algorithms needs more work, and it is outside the scope of this paper. However, for sake of brevity, we below refer these sketches as algorithms and procedures. These algorithms use the sub-algorithms FindDisc and GHDist given in Sects. 2.4 and 2.5. In the description of the algorithm, we assume that the data set X is finite.
First we outline the algorithm based on Theorem 2.
Algorithm SubmanifoldInterpolation: Assume that we are given the dimension n, the scale parameter r, and a finite set points \(X\subset E={\mathbb {R}}^m\). We suppose that X is \(\delta r\)-close to n-flats at scale r where \(\delta \) is sufficiently small. Our aim is to construct a submanifold \(M\subset {{\mathbb {R}}^m}\) that approximates X. We implement the following steps:
-
1.
We rescale X by the factor 1 / r. After this scaling, the problem is reduced to the case when \(r=1\).
-
2.
We choose a maximal \(\frac{1}{100}\)-separated set \(X_0\subset X\) and enumerate the points of \(X_0\) as \(\{q_i\}_{i=1}^{N}\). We apply the algorithm FindDisc to every point \(q_i\in X_0\) to find an affine subspace \(A_i\) through \(q_i\) such that the unit n-disk \(A_i\cap B_1(q_i)\) lies within Hausdorff distance \({C_{18}{n}}\delta \) from the set \(X \cap B_1(q_i)\). We construct the orthogonal projectors \(P_i:{{\mathbb {R}}^m}\rightarrow {{\mathbb {R}}^m}\) onto \(A_i\).
-
3.
We construct the functions \(\varphi _i:{{\mathbb {R}}^m}\rightarrow {{\mathbb {R}}^m}\), defined in (71), that are convex combinations of the projector \(P_i\) and the identity map. Then, we iterate these maps to construct \(f:{{\mathbb {R}}^m}\rightarrow {{\mathbb {R}}^m}\), \(f= \varphi _{N}\circ \varphi _{{N}-1}\circ \ldots \circ \varphi _1\), see (72).
-
4.
We construct the image \(M= f({{\mathcal {U}}}_\delta (X))\) of the \(\delta \)-neighborhood of the set X in the map f, see Remark 5.
The output of the algorithm SubmanifoldInterpolation is the n-dimensional submanifold \(M\subset {{\mathbb {R}}^m}\).
The algorithm based on Theorem 1 is the following.
Algorithm ManifoldConstruction: Assume that we are given the dimension n, the scale parameter r, and a finite metric space (X, d). Our aim is to construct a smooth n-dimensional Riemannian manifold (M, g) approximating (X, d). We implement the following steps:
-
1.
We multiply all distances by 1 / r. After this scaling, the problem is reduced to the case when \(r=1\).
-
2.
We select a maximal \(\frac{1}{100}\)-separated subset \(X_0\subset X\) and enumerate the points of \(X_0\) as \(\{q_i\}_{i=1}^N\). We choose a set \(\{p_i\}_{i=1}^N\) such that the unit balls \(D_i=B_1^n(p_i)\subset {\mathbb {R}}^n\) are disjoint.
-
3.
For each \(q_i\in X_0\), we apply the algorithm GHDist to the ball \(B_1(q_i)\subset X\) to find the value \(\delta _a(q_i)\). Define \(\delta _a=\max _{q\in X_0} \delta _a(q)\), see (49) and (56).
-
4.
For all \(q_i,q_j\in X_0\) such that \(d_X(q_i,q_j)<1\), we construct the affine transition maps \(A_{ij}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) using the maps \({\mathbf{F}_{(i)}}:B_1(q_i)\rightarrow D_i\) and \({\mathbf{F}_{(j)}}:B_1(q_j)\rightarrow D_j\) and the construction given in Lemma 6 and formula (135).
-
5.
Denote \(\varOmega _0= \bigcup _{i=1}^N D_i^{1/10}\), where \(D_i^{1/10}=B_{1/10}(p_i)\subset {\mathbb {R}}^n\), and \(E={\mathbb {R}}^m\), \(m={(n+1)N}\). We construct a Whitney embedding-type map
$$\begin{aligned} F:\varOmega _0\rightarrow {{\mathbb {R}}^m},\quad F(x)=(F_i(x))_{i=1}^N \end{aligned}$$where \(F_i:\varOmega _0\rightarrow {\mathbb {R}}^{n+1}\) are given by (143).
-
6.
We construct the local patches \(\varSigma _i=F(D_i^{1/10})\) and \({\kappa _0}\)-net \(Y_i=\{y_{i,k}\}_{k=1}^{K_i}\) in \(\varSigma _i\) that is \({(\kappa _0}/2)\)-separated, where \({\kappa _0}\) is the constant from Proposition 1.
-
7.
We apply algorithm SubmanifoldInterpolation for the points \(\{y_{i,k};\ 1\le i\le N,\ 1\le k\le K_j\}\) to obtain a submanifold \(M\subset {{\mathbb {R}}^m}\). We construct the normal projector \(P_M:{{\mathcal {U}}}_{2/5}(M)\rightarrow M\) for the submanifold M.
-
8.
We construct maps \( \psi _i = P_M\circ F|_{D_i^{1/10}}:D_i^{1/10}\rightarrow P_M(\varSigma _i)\subset M\).
-
9.
We construct metric tensors \(g_i\) on sets \(P_M(\varSigma _i)\subset M\) by pushing forward the Euclidean metric \(g^e\) on \(\varOmega _0\) to the sets \(P_M(\varSigma _i)\) using the maps \(\psi _i\). Then, metric g on M is constructed by using a partition of unity to compute a weighted average of the obtained metric tensors, see (192).
The output of the algorithm is the submanifold \(M\subset {{\mathbb {R}}^m}\) and the metric g on it.
We note that by Lemma 7 and formula (56), we have for all \(x\in X_0\) that the Gromov–Hausdorff distance between the ball \(B_1(x)\) and \(B_1^n\) is at most \(2\delta _a(x)\). A sufficient condition for the correctness of the algorithm ManifoldConstruction is that \(\delta _a\) computed in the step (3) is smaller than the constant \(\delta _0(n)/2\), where \(\delta _0(n)\) is given in Proposition 4, see Remark 8.
Also, we note that in the proof of Proposition 4 the construction of the submanifold M and in the above algorithm we use only the r-balls in X centered at the points of a maximal \(\frac{r}{100}\)-separated subset \(X_0\) of X, see Remark 10.
7.1.1 An Alternative Construction with the Map f Replacing the Projector \(P_M\)
The numerical computation of the projector \(P_M\), mapping a point to the nearest point on manifold M, may be difficult. To overcome this practical difficulty, we observe that the manifold M given by the algorithm ManifoldConstruction can be constructed using the functions \({\widetilde{\psi }}_i=f\circ F|_{D_i^{1/10}}\), instead of functions \(\psi _i = P_M\circ F|_{D_i^{1/10}}\), see Remarks 6 and 75. In other words, the steps (7), (8), and (9) can be replaced by
-
(7’)
We apply algorithm SubmanifoldInterpolation for the points \(\{y_{i,k};\ 1\le i\le N,\ 1\le k\le K_j\}\) to obtain a submanifold \(M\subset {{\mathbb {R}}^m}\). The map f constructed in the step 3 of the algorithm SubmanifoldInterpolation gives a map \(f:{{\mathcal {U}}}_{r/10}(M)\rightarrow M\) from the neighborhood of M onto M, see Remark 6.
-
(8’)
We construct maps \( {\widetilde{\psi }}_i=f\circ F|_{D_i^{1/10}}:D_i^{1/10}\rightarrow f(\varSigma _i)\subset M\).
-
(9’)
We construct metric tensors \(g_i\) on sets \(f(\varSigma _i)\subset M\) by pushing forward the Euclidean metric \(g^e\) on \(\varOmega _0\) to the sets \(f(\varSigma _i)\) using the maps \({\widetilde{\psi }}_i\). Then, the metric g on M is a weighted average of the these metric tensors using a suitable partition of unity, see (208) below.
When \({\widetilde{D}}_i=B^n_{1/{30}}(p_i)\subset {\mathbb {R}}^n\) and \(\widetilde{\varSigma }_i={\widetilde{\psi }}_i({\widetilde{D}}_i)\), \(i=1,2,\dots ,N\) the algorithm gives the maps \({\widetilde{\psi }}_i^{-1}:{\widetilde{\varSigma }}_i\rightarrow {\widetilde{D}}_i\) that by Lemma 36 can be considered as local coordinate charts of M that cover the whole manifold M and the transition functions \({\widetilde{\eta }}_{ji}= {\widetilde{\psi }}_j^{-1}\circ {\widetilde{\psi }}_i\) that map
Note that the transition functions \({\widetilde{\eta }}_{ji}\) need to be approximated numerically, e.g., using Newton’s algorithm.
To construct the metric tensor g on these charts, we can first take a family nonnegative functions \({v}_i\in C^\infty _0(\widetilde{D}_i)\) such that \({v}_i(x)=1\) for \(x\in B^n_{1/{50}}(p_i)\). Then, the sets \(\{x\in M:\ ({\widetilde{\psi }}_i^{-1})^*{v}_i(x)>0\}\) cover M and define a partition of unity on M by
Then, the metric tensor \(({\widetilde{\psi }}_j)^*g\) on the chart \(\widetilde{D}_j\) is given by
where \(g_e\) is the Euclidean metric on \({\widetilde{D}}_k\).
The collection of local coordinate charts \({\widetilde{D}}_j\), metric tensors \(g^{(j)}=({\widetilde{\psi }}_j)^*g:{\widetilde{D}}_j\rightarrow {\mathbb {R}}^{n\times n}\), and transition functions \({\widetilde{\eta }}_{ij} :{\widetilde{V}}_{ij}\rightarrow \widetilde{V}_{ji}\) is a representation of the Riemannian manifold M in local coordinate charts. Using this representation, we can determine the image of a geodesic \(\gamma _{x_0,\xi _0}(s)\), emanating from \((x_0,\xi _0)\in TM\), on several coordinate charts \(\widetilde{\psi }_i^{-1}:{\widetilde{\varSigma }}_i\rightarrow {\widetilde{D}}_i\) and determine the metric tensor in the Riemannian normal coordinates, [79]. Thus, for practical imaging purposes, for instance to visualize the n-dimensional manifold (M, g), the algorithm ManifoldConstruction can be continued with the following steps
-
(10)
For given \(x_0\in M\), determine the metric tensor g in the normal coordinates given by the map \(\exp _{x_0}:\{\xi \in T_{x_0}M:\ \Vert \xi \Vert _g<\rho \}\), where \(\rho <\hbox {inj}_M\).
-
(11)
For given \(x_0\in M\) and two linearly independent vectors \(\xi _1,\xi _2 \in T_{x_0}M\), visualize the properties of the metric g, e.g., the determinant of the metric, in the normal coordinates, by computing the map
$$\begin{aligned} s=(s_1,s_2)\mapsto \det (g(\exp _{x_0}(s_1\xi _1+s_2\xi _2))), \end{aligned}$$(209)in the set \(\{s\in {\mathbb {R}}^2: \Vert s_1\xi _1+s_2\xi _2\Vert _g<\rho \}\). This produces an image of the metric in a two-dimensional slice of the manifold. Moreover, consider a data point \(x\in X\) such that \(x\in B^X_r(q_j)\), with some index j, and that its image \(y=\widetilde{\psi }_j(f_j(x))\) on M satisfies \(y\in B_\rho ^M(x_0)\). Then, the vector \(\xi =\exp _{x_0}^{-1}(y)\in T_{x_0}M\) corresponds to the data point x in the tangent space of M at \(x_0\). In the visualization of the two-dimensional slice, the data point x can be visualized as the projection \({\bar{\xi }}\) of the vector \(\xi \) to the plane span\((\xi _1,\xi _2)\). In this way, both the metric and the original data points X can be visualized in two-dimensional slices of the manifold.
Practical imaging methods similar to step (11) above have been used in seismic imaging, for example in the imaging of the wave speed function in the time migration coordinates, see, e.g., [29].
7.1.2 Numerical Approximation of the Extended Transition Functions Using a Newton-Type Algorithm
The functions \({\widetilde{\psi }}_i=f\circ F|_{D^{1/10}_i}\), \(i=1,2,\dots , N\), discussed in Sect. 7.1.1 and used in the steps (8’)–(9’) of the algorithm, are piecewisely defined by explicit formulas. Next we discuss, how the inverse functions of these maps and the extensions of the transition functions \({\widetilde{\eta }}_{ji}\) can be approximated using a Newton-type algorithm.
To consider the inverse function of \({\widetilde{\psi }}_i\), we first reduce the problem to finding an inverse function to a map between n-dimensional spaces.
We construct the tangent spaces
of the n-dimensional submanifolds \(\widetilde{\psi }_i(D^{1/10}_i)\subset {\mathbb {R}}^m\) at \(y_i={\widetilde{\psi }}_i(p_{i})\), where \(i=1,2,\dots , N\), and \(\hbox {Ran}(A)\) denotes the range (i.e., the image) of the operator A. Recall that for \(x\in M\), the map \(dP_M(x)\) is the orthogonal projector in \(T_x{{\mathbb {R}}^m}={{\mathbb {R}}^m}\) onto \(T_xM\). Denote \(P_x=dP_M(x)\) and \(P_{i}=dP_M(y_{i})\). Then, \(P_{i}:{\mathbb {R}}^m\rightarrow T_{i}\) are the orthogonal projections. Below, \(B^m_R(y)\subset {\mathbb {R}}^m\) is the ball having the radius R and the center y.
Then, we compose \( {\widetilde{\psi }}_i\) with a projector \(P_j\) and an affine isometry \(A_j: T_i \rightarrow {\mathbb {R}}^n\) and obtain a map
In particular, we are interested in the maps \( G_{j}= G_{j,j}\). These maps are used below to determine the extended transition functions in formula (228).
First we recall some estimates proved above. We recall that the constants C and \(C_k\) depend only on dimension n. By Lemma 29,
where \({C_{30}}=C_{26}(2)\).
Next we use Lemma 35 or, equivalently, Theorem 2 with \(r_0\le 1 \) in place of r and \( C_{31}r_0^2\) in place of \(\delta \), and choose later the value of \(r_0\) so that it depends only on n. We also use the fact that by (145) and (166), \(M\subset E\) is in the ball of radius \(C_{26}(0)+\tfrac{1}{10}\) centered at zero, and hence,
When we denote \({C_{55}}={{{{C_{54}}}}}+C_{33}(2)+C_{33}(1)\), we have by Lemma 35 and the fact that \(r_0\le 1\),
By Remark 6,
where \({C_{56}}=C_{31}\max (C_{21}(2),C_{21}(1),C_{21}(0)) \). Then, using interpolation in Hölder spaces [7] to inequalities (214) with k being 1 and 2, we see that
Lemma 35(1) and the formulas (211), (215), and (214) yield that there is \({C_{57}}>0\) such that
By (168), there is a constant \({{C_{58}}=C_{36}^{-1}}>0\) such that the maps \(\psi _i = P_M\circ F:D^{1/10}_i\rightarrow {\mathbb {R}}^m\), defined in (164), satisfy
When \(r_0 <({C_{58}}/ (2{C_{56}}))^2,\) the formulas (215), (217), and the identity \(P_M\circ {\widetilde{\psi }}_i={\widetilde{\psi }}_i\) imply that for \(z=\widetilde{\psi }_i(x)\) we have
Assume next that
Then, we have, by (215) and (216), for \(z\in {\widetilde{\psi }}_i(D^{1/10}_i)\) that
So, when \(r_0 < ({C_{58}}/({2{C_{56}}} {C_{57}}))^2\), we have
Now we choose \(r_0=\min (({C_{58}}/ (2{C_{56}}))^2,( {C_{58}}/({4{C_{56}}} {C_{57}}))^2)\) in the above use of Lemma 35 so that the above conditions for \(r_0\) are valid.
As \({A_j} :T_j\rightarrow {\mathbb {R}}^n\) is an affine isometry, (220) implies
Denote \( {C_{60}}=\max (3{C_{57}}{C_{59}},1), \) and choose
Recall that \(D_i=B_{1/10}^n(p_i)\) and \({\widetilde{D}}_i=B_{1/30}^n(p_i)\) and let \(R_n={C_{57}}\rho _n\). As \(\rho _n\le 1/100,\) formula (216) yields for \(x\in B^n_{1/20}(p_i)\) that \(\widetilde{\psi }_i(B^n_{\rho _n}(x))\subset B^m_{R_n}({\widetilde{\psi }}_i(x)).\)
Our next aim is to cover the set \({\widetilde{D}}_i\) by small balls of radius \(\rho _n\) and to use Newton’s method to find the transition functions in these balls.
To consider how the transition functions can be constructed with a numerical algorithm, we first will extend these functions to be defined in larger domains. We call these functions the extended transition functions. To this end, let \(h_k\in B^n_{1/30}(0)\subset {\mathbb {R}}^n\), \(k=1,2,\dots ,K\) be a maximal set of \(\rho _n\)-separated points in \(B^n_{1/30}(0)\). Note that K is bounded by \(\hbox {vol}( B^n_{1/10}(0))/\hbox {vol}( B^n_{\rho _n/2}(0))\).
For \(a\in {\mathbb {Z}}_+\), denote
Assume next that \({\widetilde{\psi }}_i({\widetilde{D}}_i)\cap {\widetilde{\psi }}_j(\widetilde{D}_j)\not =\emptyset \). If \(x_i\in {\widetilde{D}}_i= B^n_{1/30}(p_i)\) is such that
there exists \(x_j\in {\widetilde{D}}_j\) so that \({\widetilde{\psi }}_j(x_j)={\widetilde{\psi }}_i(x_i)\). Then, there are \(k_i\) and \(k_j\) such that \(x_i\in B^n_{\rho _n}(p_i+h_{k_i})\) and \(x_j\in B^n_{\rho _n}(p_j+h_{k_j})\) and we see that
Let \({\mathcal {K}}(j,i)=\{k\in \{1,2,\dots ,K\}:\ \widetilde{\psi }_i(p_i+h_{k})\in {\mathcal {V}}_j(2)\}\) and
By (223), we have
and the function
is an extension of the transition function \({\widetilde{\eta }}_{ji}\), that is, it coincides with \( {\widetilde{\eta }}_{ji}\) in the set \({\widetilde{\psi }}_i^{-1}( {\widetilde{\psi }}_i({\widetilde{D}}_i)\cap {\widetilde{\psi }}_j({\widetilde{D}}_j))\). Moreover, for \(k\in {\mathcal {K}}(j,i)\)
that implies
where, as \(P_j\) is an orthogonal projector and \(A_j\) is an affine isometry,
and \(p_{j,k}=A_j(P_j({\widetilde{\psi }}_j(p_j+h_k)))\). To compute the extended transition function \({\widetilde{\eta }}_{ji}^e\), it is enough to compute the inverse function
and then, we can write
Next, to consider various push forwards of metric tensors (see (231) below), we analyze the computation of the restrictions of the inverse functions in balls \({B^n_{3R_n}(p_{j,k})}\), that is, \(G_{j,i}^{-1}|_{B^n_{3R_n}(p_{j,k})}:{B^n_{3R_n}(p_{j,k})}\rightarrow D_i\). These maps give us the inverse maps \(G_{j,i}^{-1}:{\mathcal {W}}_j(3)\rightarrow D_i\). In the case when i and j are equal, this gives us also the function \(G_j^{-1}:{\mathcal {W}}_j(3)\rightarrow D_j\).
To consider (227), assume that we are given \(z\in {\mathcal {W}}_j(3)\). Then, we can determine \(k_0\in \{1,2,\dots ,K\}\) such that \(z\in {B^n_{3R_n}(p_{j,k_0})}\). Then, we will start the iteration in Newton’s algorithm from \({x}_0=p_{i}+h_{k_0}\). The iterations of Newton’s method proceed as follows. For \(p\ge 0\),
As
and \( q:={C_{57}}{C_{59}}({C_{60}}\rho _n){\le ({C_{60}})^2\rho _n}<\frac{1}{2}\), it follows by the convergence theorem for Newton’s algorithm [59, Thm. 6.14] that the sequence \(({x}_p)_{p=1}^\infty \) stays in \({B^n_{r_1}(p_{i}+h_{k_0})} \subset D_{i}\) and it converges to the limit point \({x}={G_{j,i}^{-1}(z)}\), and moreover, this sequence satisfies
Note that the above also shows that \({\mathcal {W}}_j(3)\subset G_{j,i}( D_i)\).
Summarizing the above shows that the Newton’s algorithm can be used to compute the inverse functions of \({G_{j,i}}\) and of the extensions of the transition functions \({{\widetilde{\eta }}}^e_{ji}\).
7.2 Analysis of the Computational Complexity
7.2.1 Computational Complexity of the Algorithm SubmanifoldInterpolation
We analyze the computational complexity of the above algorithms in terms the number of elementary computational operations needed (see Remark 3). We note that as we have only presented the sketches of the above algorithms, in the considerations below we do not analyze the real computational requirements, in particular in the sense that we do not consider how much computational resources the needed elementary operations use. Below we consider two types of computational requirements: First the requirements for the one-time work that corresponds to the preparatory work and second the computational work required to answer to a query that produces a point of the constructed manifold. These are then combined to estimate the computational work required to obtain a grid of points on the manifold. We also recall that below C denotes a constant which depends only on n, that is, \(C=C(n)\), but the value of C may change even inside a formula line.
Let \(\ell =\# X\) be the number of elements in the set X. We assume that \(E={\mathbb {R}}^m\) and \(X\subset {{\mathbb {R}}^m}\) satisfies the assumptions of Theorem 2 with sufficiently small \(\delta \) and \(r\le 1\) so that the set X is \(\delta \)-close to n-flats in scale r. Also, we assume that \({{\,\mathrm{diam}\,}}(X)<D\). In the step 2 of SubmanifoldInterpolation, we construct a maximal r / 100 separated subset \(X_0\subset X\). Since \(\sec (M)\le K=C\delta r^{-3}\), the number \(N=\# X_0\) of elements in the set \(X_0\) satisfies \(N\le \min (\ell ,C\left( e^{CKD}/ r \right) ^n).\) In the step 2, the construction of the set \(X_0\) can be done by going through all points x in X one by one and include it in \(X_0\) if the distance from x to some of the points chosen earlier to be included in \(X_0\) at least 1 / 100. This requires at most \(N\ell \le \ell ^2\) operations. Also, in the steps 2–3 of the algorithm, one applies algorithm FindDisc N times to a set consisting of \(\ell \) points in an m-dimensional space and this requires \(CmN\ell \) operations. Thus, the steps 1–3, which construct a function f, require altogether \(CmN\ell \) operations. Observe that f is given as a composition of explicit functions containing parameters that depend on the data, that is, the coordinates of the points \(q_i\) in (69) and the matrixes and vectors that determine the affine projectors \(P_i=P_{A_{q_i}}\) in (64). Thus, the construction of f means the determination of the values of these parameters. These steps for finish the one-time work requited for the preparatory steps. The preparatory steps require altogether
elementary operations.
Recall that the submanifold \(M\subset {{\mathbb {R}}^m}\) is the image of a \(\delta \)-neighborhood of the set X in the constructed function f. Moreover, by Lemma 14, M is the union images of the n-dimensional disks \(A_i\cap B_1(q_i,r)\) of radii r, that is, \(M=\bigcup _{i=1}^N f(A_i\cap B_1(q_i,r))\). Obtaining one point of manifold M can be considered as a query where the input consists of an index i and a point \(z\in B_1(q_i,r)\) and the query gives the answer f(z). As we have already constructed the function f, or more precisely the parameters that determine this function taking values in \({\mathbb {R}}^m\), answering such a query requires Cm elementary operators (that is, finitely many operations for each m coordinates of f(x)).
Let us next consider computing a grid of points on M. To this end, let \(0<\eta <\delta \) be a small parameter. Then, choose an \(\eta \)-dense computational grids in the n-dimensional disks \(A_i\cap B_1(q_i,r)\), having radii r. Let us denote these computational grids by \((z_{i,j})_{j=1}^J\), \(J\le C(r/\eta )^n\). Then, we obtain a grid of points on the submanifold M by constructing a \((C\eta )\)-dense subset \(\{f(z_{i,j});\ i=1,2,\dots ,N,\ j=1,\dots ,J\}\) of M. This requires CNJm operations. Summarizing, computing the points \(\{f(z_{i,j});\ i=1,2,\dots ,N,\ j=1,\dots ,J\}\) on M using the algorithm SubmanifoldInterpolation requires altogether
operations.
7.2.2 Computational Complexity of the Algorithm ManifoldConstruction
We estimate the number of elementary operations needed in ManifoldConstruction to compute the transition functions between local charts and the metric on the charts with given numerical accuracy. By rescaling in the step 1, that is, by multiplying the distance function \(d_X:X\times X\rightarrow {\mathbb {R}}\) and the geometric parameters r and \(\delta \) by factor 1 / r, it suffices to handle the case \(r=1\). Because of this, we analyze the complexity of the algorithm in the case when \(r=1\) and \(\delta <\delta _0(n)\), where \(\delta _0(n)<1\) appearing in Proposition 3 depends only on n.
We will analyze the computational complexity of the alternative version of the algorithm described in Sects. 7.1.1 and 7.1.2.
Again, we start with the requirements of the one-time work needed for the preparatory work. We assume that a finite metric space X satisfies assumptions of Theorem 1 and that \({{\,\mathrm{diam}\,}}(X)<D\). Again, let \(\ell =\# X\) be the number of elements in the set X. Below, \(\theta >0\) will be the parameter corresponding to the required numerical accuracy.
We first observe that the step 2 of the algorithm requires \(C\ell ^2\) steps.
In the step 3, we apply algorithm GHDist to all balls \(X_1^{(i)}:=B_1(q_i)\subset X\) with \(i=1,2,\dots ,N\), that is, for balls centered in points of \(X_0\). Let \(\ell _i=\#X_1^{(i)}\). By Lemma 23, each point \(x\in X\) belongs at most \(C=C(n)\) balls \(X_1^{(i)}\), and thus, \(\sum _{i=1}^N \ell _i\le C\ell \). Applying algorithm GHDist to the ball \(X_1^{(i)}\) requires \(C\ell _i^2\) elementary operations, so step 3 requires altogether
elementary operations.
Since by Theorem 1, the set X is \((C\delta )\)-close to a smooth n-dimensional manifold M such that \(\sec (M)\le K=C\delta \), we have that the number \(N=\# X_0\) of elements in the maximal \(\frac{1}{100}\)-separated set \(X_0\) satisfies \(N\le \min (\ell ,C(e^{CKD})^n).\) Below, we give estimates in terms of N and \(\ell \). In the step 3, we construct the set \(X_0=\{q_i\}_{i=1}^N\subset X\) and at the same time make a record of those elements \(q_i,q_j\in X_0\) for which \(d_X(q_i,q_j)<1\). This requires \(CN\ell \) operations. Below, we use the fact that by Lemma 23, for any i the number of j such that \(d_X(q_i,q_j)<1\) is bounded by a number depending only on n.
In the step 4, finding maps \(A_{ij}\), \(i,j=1,2,\dots ,N\) as in Lemma 6 and formula (135) requires \(CN\ell \) operations. Indeed, for each \(i\in \{1,\dots ,N\}\) there is a bounded number of maps \(A_{ij}\) to construct, see Lemma 23. The construction of \(A_{ij}\) described in the proof of Lemma 6 requires a number of operations proportional to the number of points in the ball \(B_1(q_i)\). In the step 5, we introduce the space \(E={\mathbb {R}}^{m}\), where \(m=(n+1)N\). We emphasize that here the dimension m of the space \({{\mathbb {R}}^m}\) depends on N and therefore on the metric space X. In this step, the construction of the map F requires \(CN^2\) operations. The construction of the \({\kappa _0}\)-nets in \(Y_i\subset \varSigma _i\) in the step 6 requires \(CN\,\cdot m\) operations. Note that by Lemma 29, the maps \(F:D_i^{1/10}\rightarrow \varSigma _i\) are bi-Lipschitz with the Lipschitz constant \(C_{27}\), and therefore, we can first choose a \((2C_{27})^{-1}\kappa _0\)-net \(Z_i\subset D_i^{1/10}\) and then choose \(Y_i\subset F(D_i^{1/10})\) to be a maximal \((\kappa _0/2)\)-separated subset of \(F(Z_i)\).
In the step 7, we apply the steps 1–3 of algorithm SubmanifoldInterpolation for the set \(Y=\bigcup _i Y_i\), consisting of CN points that are in \(E={\mathbb {R}}^m\). This requires \(CmN^2\) operations and gives us functions f and \({\widetilde{\psi }}_i=f\circ F|_{D^{1/10}_i}\), \(i=1,2,\dots , N\). This implements also the step 8’ of the algorithm.
Next we construct for all \(j\in \{1,2,\dots ,N\}\) the sets \({\mathcal {I}}(j)\subset \{1,2,\dots ,N\}\) of those i for which \(d_X(q_i,q_j)<1\). By Lemma 23, the number of elements in the set \({\mathcal {I}}(j)\) is bounded by a number depending only on n. Thus, the construction of sets \({\mathcal {I}}(j)\) for all \(j\in \{1,2,\dots ,N\}\) requires \(CN^2\) elementary operations.
Next we consider pairs (i, j) such that \(i\in {\mathcal {I}}(j)\). The functions f and \({\widetilde{\psi }}_i\) are piecewisely defined by explicit formulas. As explained in Sect. 7.1.2, we can construct numerically the inverse maps
see (210). There, the construction of the orthogonal projections \(P_i\) onto the tangent spaces \(T_i\) requires CmN operations. This finishes one-time work needed for the preparatory work that has required
operations.
Next we consider several queries. The first query we consider takes as an input a point \(z\in {\mathcal {W}}_i(3)\) and gives as the output a numerical approximation for the inverse of the map \(G_{j,i}\) at the point z. To do that, we compute the inverse of the map \(G_{j,i}\) by using Newton’s method. By (230), to compute numerically the value \(G_{j,i}^{-1}(z)\) for a given \(z\in \mathcal W_i(3)\) and with the precision of \(\theta \in (0,\frac{1}{4})\), it suffices to take \(C \log _2 \log _2 (1/\theta )\) iterations. Below in this section, when we consider the computation of the transition functions and the metric tensor, all computations are done with the precision \(C\theta \).
Let \(i\in {\mathcal {I}}(j) \) and \(y^{(j)}\in {\widetilde{D}}_j\) and \(y^{(j,i)}\in W_{ji}\). Using the numerical computations described above, one can compute the values of the values of \(z^{(j,i)}=G_{j,i}(y^{(j,i)})\) and \(G_j^{-1}(z^{(j,i)})\). Observe that \(G_{j,i}\) is a composition of the linear operators \(A_j\) and \(P_j\) and \({\mathbb {R}}^m\)-valued functions \( {\widetilde{\psi }}_i\) having explicit formulas containing parameters that we have already computed using the data. Hence, this requires Cm elementary operations. The second query we consider takes as an input a point \(y^{(j,i)}\) and gives as an output the value the extended transition function \(\widetilde{\eta }_{ji}^e(y^{(j,i)})=G_j^{-1}(G_{j,i}(y^{(j,i)}))\) with the precision of \(C\theta \), see (228). As the computation of the derivative of the \({\mathbb {R}}^m\)-valued function \(G_j\) requires Cm operations, this query requires \(Cm \log _2 \log _2 (1/\theta )\) elementary operations.
Next we consider the query where the input is a pair (i, j), satisfying \(i\in {\mathcal {I}}(j)\), and a point \(y^{(j,i)}\) and the output is the metric tensor
evaluated at the point \(y^{(j,i)}\). Here, using the matrix notation, \({\widetilde{g}}_{(ji)}= ({{\widetilde{\eta }}}^e_{ji})_*g^e\) is given by
where \(g^e_{ab}=\delta _{ab}\) is the Euclidean metric. We note that since \(G_{j,i}\) is a composition of linear operators and functions having explicit formulas, the derivative \(DG_{j,i}\) can be computed at any given point using elementary operations whose number depends only on n. Using the Lipschitz estimates (216) and (221), we see that computing \(({\widetilde{\eta }}^e_{ji})_*g^e\) at the point \(y^{(j,i)}\) with the precision \(C\theta \) requires \(C \log _2 \log _2 (1/\theta )\) elementary operations.
Next we consider the computation of the metric tensor \((\widetilde{\psi }_j)^*g\) at \(y^{(j)}\in {\widetilde{D}}_j\) with the precision \(C\theta \). This is done by using a partition of unity (207) on M and computing a weighted sum of tensors \(({\widetilde{\eta }}^e_{ij})_*g^e\), as described in formula (208) where the sum needs to be taken over the indexes i and k that satisfy \(i,k\in {\mathcal {I}}(j)\). As the number of elements in \(\mathcal I(j)\) is bounded by \(C=C(n)\), this requires \(C \log _2 \log _2 (1/\theta )\) elementary operations. Finally, we consider the query, where the input is \(y^{(j)}\) and the output is \(f(y^{(j)})\). As discussed above in the context of the algorithm SubmanifoldInterpolation, this takes Cm elementary operations as we have already computed the parameters that determine the function f. Summarizing the above, after the one-time work described above, we can consider a query, where the input is an index j and a point \(y^{(j)}\in {\widetilde{D}}_j\) and the output is the collection
with the precision \(C\theta \), that is, the output is the point \( f(y^{(j)})\) on M that corresponds to \(y^{(j)}\) on the local coordinate chart \(D_j\), the metric tensor on \(D_j\) at the point \(y^{(j)}\), and the values of the transition functions from the chart \(D_j\) to the charts \(D_i\) at \(y^{(j)}\). After the one-time work, answering the query (232) requires
elementary operations.
To construct a grid of points on the manifold M, let \(\mathcal Q_{j}={\widetilde{D}}_j\cap ({\rho }{\mathbb {Z}}^n),\)\(j=1,2,\dots ,N,\) be computational grids in the sets \({\widetilde{D}}_j\), where \({\rho }>0\) is the grid size parameter. We write these grids as
We see that the numbers \(L_j\) of the points in \({\mathcal {Q}}_{j}\) are bounded by \(C{\rho }^{-n}\). Answering to the query (232) for all points \(y^{(i)}_l\) in the computational grid \(\bigcup _{j=1}^N {\mathcal {Q}}_{j}\) produces a \(C\rho \)-dense set of grid points on the manifold M and the values of the metric tensors on all local coordinate charts \(D_j\) at these grid points. Summarizing the above analysis, the computation work to do this requires altogether
elementary operations. We recall that here \(r=1\), C depends on the intrinsic dimension n of the manifold, \(\rho \) is the size parameter of the computational grid, \(m=(n+1)N\), \(C\theta \) is the required numerical accuracy, N is the number of points in the maximal \((r/100)-\)separated set in X, and \(\ell \) is the number of points in X.
References
E. Aamari, C. Levrard, Non-Asymptotic Rates for Manifold, Tangent Space, and Curvature Estimation, Annals of Statistics, To appear.
M. Anderson, Convergence and rigidity of manifolds under Ricci curvature bounds, Invent. Math. 102, 429–445, (1990).
M. Anderson, A. Katsuda, Y. Kurylev, M. Lassas, M. Taylor, Boundary regularity for the Ricci equation, geometric convergence, and Gel’fand’s inverse boundary problem, Invent. Math. 158, 261–321, (2004).
M. Belkin, P. Niyogi, Laplacian eigenmaps and spectral techniques for embedding and clustering, Adv. in Neural Inform. Process. Systems, 14, 586–691, (2001).
M. Belkin, P. Niyogi, Semi-Supervised Learning on Riemannian Manifolds, Machine Learning, 56, 209–239, (2004).
M. Belkin, P. Niyogi, Convergence of Laplacian eigenmaps, Adv. in Neural Inform. Process. Systems 19, 129–136, (2007).
J. Bergh, J. Löfström, Interpolation spaces. An introduction. Springer-Verlag, pp. x+207, (1976)
V. Berestovskij, I. Nikolaev, Multidimensional generalized Riemannian spaces, In: Geometry IV, Encyclopaedia Math. Sci. 70, Springer, pp. 165–243, (1993).
E. Beretta, M. de Hoop, L. Qiu, Lipschitz Stability of an Inverse Boundary Value Problem for a Schrödinger-Type Equation SIAM J. Math. Anal. 45, 679-699, (2012).
E. Bierstone, P. Milman, W. Paulucki, Differentiable functions defined on closed sets. A problem of Whitney, Invent. Math., 151, 329–352, (2003).
J. Boissonnat, R. Dyer, A. Ghosh. Delauney triangulations of manifolds Foundations of Computational Mathematics, Volume 18, Issue 2, pp 399–431, (2018).
J. Boissonnat, L. Guibas, S. Oudot, Manifold reconstruction in arbitrary dimensions using witness complexes, Discrete & Computational Geometry 42, 37–70, (2009).
L. Borcea, V. Druskin, F. Guevara Vasquez, Electrical impedance tomography with resistor networks Inverse Problems 24, 035013, (2008).
L. Borcea, V. Druskin, L. Knizhnerman, On the continuum limit of a discrete inverse spectral problem on optimal finite difference grids, Comm. Pure Appl. Math. 58, 1231-1279, (2005).
R. Bosi, Y. Kurylev, M. Lassas, Reconstruction and stability in Gel’fand’s inverse interior spectral problem.arXiv:1702.07937, (2017).
M. Brand, Charting a manifold,NIPS 15, 985–992, (2002).
M. Bridson, A. Haefliger, Metric spaces of non-positive curvature, Springer-Verlag, (1999).
S. Bromberg, An extension in the class C1, Bol. Soc. Mat. Mex. II, Ser. 27, 35–44, (1982).
Y. Brudnyi, On an extension theorem, Funk. Anal. i Prilzhen. 4 (1970), 97–98; English transl. in Func. Anal. Appl. 4, 252–253, (1970).
Y. Brudnyi, P. Shvartsman, The traces of differentiable functions to closed subsets of\({\mathbb{R}}^n\), in Function Spaces, Teubner-Texte Math. 120, 206–210, (1989).
Y. Brudnyi, P. Shvartsman, A linear extension operator for a space of smooth functions defined on closed subsets of\({\mathbb{R}}^n\), Dokl. Akad. Nauk SSSR 280 (1985), 268–270. English transl. in Soviet Math. Dokl. 31, No. 1, 48–51, (1985).
Y. Brudnyi, P. Shvartsman, Generalizations of Whitney’s extension theorem, Int. Math. Research Notices 3, 129–139 (1994).
Y. Brudnyi, P. Shvartsman, The traces of differentiable functions to closed subsets of\({\mathbb{R}}^n\), Dokl. Akad. Nauk SSSR 289, 268–270, (1985).
Y. Brudnyi, P. Shvartsman, The Whitney problem of existence of a linear extension operator, J. Geom. Anal. 7, 515–574, (1997).
Y. Brudnyi, P. Shvartsman, Whitney’s extension problem for multivariate\(C^{1,\omega }\)functions, Trans. Amer. Math. Soc. 353 No. 6, 2487–2512, (2001).
D. Burago, Yu. Burago, S. Ivanov, A course in metric geometry, Graduate Studies in Mathematics, 33, Amer. Math. Soc., (2001).
Yu. Burago, M. Gromov, G. Perelman, A. Aleksandrov spaces with curvatures bounded below, Russian Math. Surveys 47, 1–58, (1992).
D. Burago, S. Ivanov, Y. Kurylev, A graph discretisation of the Laplace-Beltrami operator, J. Spectr. Theory 4, 675–714, (2014).
M. Cameron, S. Fomel, J. Sethian, Seismic velocity estimation from time migration. Inverse Problems. 23, 1329, (2007).
J. Cheeger, Finiteness theorems for Riemannian manifolds. Am. J. Math. 92, 61–75, (1970).
J. Cheeger, K. Fukaya, M. Gromov, Nilpotent structures and invariant metrics on collapsed manifolds, J. Amer. Math. Soc. 5 No. 2, 327–372, (1992).
S. Cheng, T. Dey, E. Ramos, Manifold reconstruction from point samples,SODA (2005), 1018–1027.
R. Coifman, et al. Geometric diffusions as a tool for harmonic analysis and structure definition of data Part II: Multiscale methods. Proc. of Nat. Acad. Sci. 102, 7432–7438, (2005).
T. Cox, M. and Cox Multidimensional Scaling. Chapman & Hall, London, (1994).
D. Donoho, D. Grimes, Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data, Proceedings of the National Academy of Sciences, 100, 5591–5596 (2003).
H. Engl, M. Hanke, A. Neubauer, Regularization of inverse problems, Springer, (1996).
Ch. Fefferman, A sharp form of Whitney’s extension theorem, Ann. of Math. 161, 509–577, (2005).
Ch. Fefferman, Whitney’s extension problem for\(C^m\), Ann. of Math. 164, 313–359, (2006).
Ch. Fefferman, \(C^m\)-extension by linear operators, Ann. of Math. 166, 779–835, (2007).
Ch. Fefferman, Whitney’s extension problem in certain function spaces, (preprint).
Ch. Fefferman, A generalized sharp Whitney theorem for jets, Rev. Mat. Iberoam.21, No. 2 , 577–688, (2005).
Ch. Fefferman, Extension of \( C^{m,\omega }\)smooth functions by linear operators, Rev. Mat. Iberoam. 25, No. 1, 1–48, (2009).
Ch. Fefferman, S. Ivanov, Y. Kurylev, M. Lassas, H. Narayanan, Fitting a Putative Manifold to Noisy Data.Proceedings of the 31st Conference On Learning Theory, in PMLR. 75688–720, (2018).
Ch. Fefferman, S. Mitter, H. Narayanan, Testing the manifold hypothesis, J. Amer. Math. Soc. 29, 983–1049, (2016).
Ch. Fefferman, B. Klartag, Fitting\(C^m\)-smooth function to data I, Ann. of Math, 169, 315–346, (2009).
Ch. Fefferman, B. Klartag, Fitting\(C^m\)-smooth function to data II, Rev. Mat. Iberoam. 25, 49–273, (2009).
K. Fukaya, A boundary of the set of the Riemannian manifolds with bounded curvatures and diameters J. Differential Geom. 28, No. 1, 1–21, (1988).
C. Genovese, M. Perone-Pacifico, I. Verdinelli, L. Wasserman. Manifold estimation and singular deconvolution under Hausdorff loss. Ann. of Statistics, 40, 941–963, (2012).
C. Genovese, M. Perone-Pacifico, I- Verdinelli, L. Wasserman, Nonparametric ridge estimation. Ann. of Statist., 42, 1511–1545, (2014).
G. Glaeser, Etudes de quelques algebres Tayloriennes, J. d’Analyse 6, 1–124, (1958).
M. Gromov with appendices by M. Katz, P. Pansu, and S. Semmes, Metric Structures for Riemannian and Non-Riemanian Spaces. Birkhauser (1999).
H. Hotelling, Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology24, 417–441, 498–520, (1933).
E. Iversen, M. Tygel, B. Ursin, M. de Hoop, Kinematic time migration and demigration of reflections in pre-stack seismic data, Geophys. J. Int. 189 , 1635–1666, (2012).
P. Jones, M., Maggioni, R. Schul, Universal local parametrizations via heat kernels and eigenfunctions of the Laplacian, Ann. Acad. Scient. Fen. 35, 1–44, (2010).
A. Katchalov, Y. Kurylev, M. Lassas, N. Mandache, Equivalence of time-domain inverse problems and boundary spectral problem. Inverse problems 20, 419–436, (2004).
A. Katchalov, Y. Kurylev, M. Lassas, Inverse Boundary Spectral Problems, Monographs and Surveys in Pure and Applied Mathematics 123, CRC-press, xi+290 pp, (2001).
A. Katsuda, Y. Kurylev, M. Lassas, Stability and Reconstruction in Gel’fand Inverse Boundary Spectral Problem, in: New analytic and geometric methods in inverse problems. (Ed. K. Bingham, Y. Kurylev, and E. Somersalo), 309–320, Springer-Verlag, (2003).
M. Kirszbraun, Über die zusammenziehende und Lipschitzsche Transformationen, Fund. Math. 22, 77–108, (1934).
R. Kress, Numerical analysis. Springer-Verlag,. xii+326 pp, (1998).
B. Kleiner, J. Lott, Locally collapsed 3-manifolds, Asterisque 365, 7–99, (2014).
M. Lassas, G. Uhlmann, Determining Riemannian manifold from boundary measurements, Ann. Sci. École Norm. Sup. 34, 771–787, (2001).
J. Lee, G. Uhlmann, Determining anisotropic real-analytic conductivities by boundary measurements, Comm. Pure Appl. Math. 42, 1097–1112, (1989).
L. Ma, M. Crawford, J. W. Tian, Generalised supervised local tangent space alignment for hyperspectral image classification, Electronics Letters 46, 497, (2010).
K. Mohammed, H. Narayanan, Manifold learning using kernel density estimation and local principal components analysis. CoRR, abs/1709.03615., (2017).
J. Mueller, S. Siltanen, Linear and nonlinear inverse problems with practical applications. SIAM, Philadelphia, xiv+351 pp, (2012).
H. Narayanan, S. Mitter, On the sample complexity of testing the manifold hypothesis. NIPS, (2010).
H. Narayanan, P. Niyogi, On the sample complexity of learning smooth cuts on a manifold. Proc. of the 22nd Annual Conference on Learning Theory (COLT), (2009).
J. Nash, \(C^1\)-isometric imbeddings, Ann. of Math. 60, 383–396, (1954).
J. Nash, The imbedding problem for Riemannian manifolds, Ann. of Math. 63 , 20–63, (1956).
Y. Nesterov, A. Nemirovskii, Interior-Point Polynomial Algorithms in Convex Programming, SIAM Studies in Applied and Numerical Mathematics, 416 pp, (1995).
I. Nikolaev, Smoothness of the metric of spaces with curvature that is bilaterally bounded in the sense of A.D. Aleksandrov, Sib. Mat. Zh. 24, 114–132 (Russian). English translation: Sib. Math. J. 24, 247–263 (1983).
L. Oksanen, Solving an inverse problem for the wave equation by using a minimization algorithm and time-reversed measurements. Inv. Prob. and Imag. 5, 731–744, (2011).
D. O’Regan, Y. Cho, Y. Chen, Topological Degree Theory and Applications, CRC, (2006).
U. Ozertem and D. Erdogmus. Locally defined principal curves and surfaces. Journal of Machine Learning Research 12, 1249–1286, (2011).
G. Paternain, M. Salo, G. Uhlmann, Tensor Tomography on Simple Surfaces, Inventiones Math. 193, 229–247, (2013).
L. Pestov, G. Uhlmann, Two Dimensional Compact Simple Riemannian manifolds are Boundary Distance Rigid, Ann. of Math. 161, 1089–1106, (2005).
K. Pearson, On lines and planes of closest fit to systems of points in space, Philosophical Magazine 2, 559–572, (1901).
S. Peters, Cheeger’s finiteness theorem for diffeomorphism classes of Riemannian manifolds, J. Reine Angew. Math. 349, 77–82, (1984).
P. Petersen, Riemannian geometry. 2nd Ed. Springer, xvi+401 pp, (2006).
G. Rosman, M. M. Bronstein, A. M. Bronstein, R. Kimmel, Nonlinear Dimensionality Reduction by Topologically Constrained Isometric Embedding, International Journal of Computer Vision, 89, 56–68, (2010).
S. Roweis, L. Saul, Nonlinear dimensionality reduction by locally linear embedding, Science, 290, 2323–326, (2000).
S. Roweis, L. Saul, G. Hinton, Global coordination of local linear models, Advances in Neural Information Processing Systems 14, 889–896, (2001).
T. Sakai, Riemannian geometry. AMS, xiv+358 pp, (1996).
J. Shawe-Taylor, N. Christianini, Kernel Methods for Pattern Analysis, Cambridge University Press, (2004).
K. Shiohama, An introduction to the geometry of Alexandrov spaces. Lecture Notes Series, 8. Seoul National University, Seoul, ii+78 pp, (1993).
P. Shvartsman, Lipschitz selections of multivalued mappings and traces of the Zygmund class of functions to an arbitrary compact, Dokl. Acad. Nauk SSSR 276 (1984), 559–562; English transl. in Soviet Math. Dokl. 29, 565–568, (1984).
P. Shvartsman, On traces of functions of Zygmund classes, Sibirskyi Mathem. J. 28 (1987), 203–215; English transl. in Siberian Math. J. 28, 853–863, (1987).
P. Shvartsman, Lipschitz selections of set-valued functions and Helly’s theorem, J. Geom. Anal. 12, 289–324, (2002).
J. Sylvester, G. Uhlmann, A global uniqueness theorem for an inverse boundary value problem, Ann. of Math. 125, 153–169, (1987).
P. Stefanov, G. Uhlmann, A. Vasy, Local and global boundary rigidity and the geodesic X-ray transform in the normal gauge, preprint, arXiv:1702.03638, 2017.
P. Stefanov, G. Uhlmann, A. Vasy, Boundary rigidity with partial data. J. Amer. Math. Soc. (JAMS) 29, 299–332, (1987).
J. Tenenbaum, V. de Silva, J. Langford, A global geometric framework for nonlinear dimensionality reduction, Science, 290 5500, 2319–2323, (2000).
G. Uhlmann, A. Vasy, The inverse problem for the local geodesic ray transform. Invent. Math. 205, 83–120, (2016).
K. Weinberger, L. Saul, Unsupervised learning of image manifolds by semidefinite programming, Int. J. Comput. Vision 70, 1, 77–90, (2006).
H. Whitney, Analytic extensions of differentiable functions defined on closed sets, Trans. Amer. Math. Soc., 36, 63–89, (1934).
H. Whitney, Differentiable functions defined in closed sets I, Trans. Amer. Math. Soc. 36, 369–389, (1934).
H. Whitney, Functions differentiable on the boundaries of regions, Ann. of Math. 35, 482–485, (1934).
H. Whitney, Differentiable manifolds, Ann. of Math. 37, 645–680, (1936).
H. Whitney, J. Eells, D. Toledo, eds., The collected papers of Hassler Whitney. Volumes I-II., Contemporary Mathematicians, Birkhäuser, (1992).
Z. Zhang, H. Zha, Principal manifolds and nonlinear dimension reduction via local tangent space alignment, SIAM J. Sci. Computing, 26, 313–338, (2005).
N. Zobin, Whitney’s problem on extendability of functions and an intrinsic metric, Advances in Math. 133, 96–132, (1998).
N. Zobin, Extension of smooth functions from finitely connected planar domains, J. Geom. Anal. 9, 489–509, (1999).
Acknowledgements
Open access funding provided by University of Helsinki including Helsinki University Central Hospital. The authors express their gratitude to the Mittag-Leffler Institute, the Institut Henri Poincare, and the Fields Institute, where parts of this work have been done. Ch.F. was partly supported by AFOSR, Grant DMS-1265524, and NSF, Grant FA9550-12-1-0425. S.I. was partly supported by RFBR, Grants 14-01-00062 and 17-01-00128-A, Y.K. was partly supported by EPSRC and the AXA professorship, M.L. was supported by Academy of Finland, Grants 273979, 284715, 312110, and H.N. was partly supported by NSF Grant DMS-1620102 and a Ramanujan Fellowship.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Shmuel Weinberger.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Estimates for Higher Derivatives of a Composition of Functions
Appendix A: Estimates for Higher Derivatives of a Composition of Functions
For a function \(f :X\rightarrow {\mathbb {R}}^n\) defined in an open set \(X\subset {\mathbb {R}}^n\), let \(D_vf(x)=\partial _vf(x)\) be derivative of f to direction \(v\in {\mathbb {R}}^n\) at x. We denote \(D_vf(x)=\partial f(x)\,\cdot v\). The derivatives of order k are below considered as multilinear forms
where \(v_1, \dots v_k\in {\mathbb {R}}^n \) and \(x \in X\).
We consider higher-order derivatives as multilinear forms and use the following lemma for multilinear forms, proved in [70, Prop. 9.1.1].
Lemma 41
Let \(A[h_1,\dots , h_k]\) be a \(k-\)linear symmetric form on \({\mathbb {R}}^n\) and \(B[h_1, h_2]\) be a symmetric positive semidefinite \(2-\)linear form on \({\mathbb {R}}^n\). Assume that for some \(\alpha \), one has \(|A[h,\dots ,h]|\le \alpha (B[h,h])^{k/2}\), for \(h\in {\mathbb {R}}^n\). Then, for all \(h_1, \dots , h_k \in {\mathbb {R}}^n\),
We will refer to the above result as the Nesterov–Nemirovski lemma.
When \(h:X\subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\), we define
where the equalities in (233) and (234) follow from Lemma 41. We note that by Lemma 41, we have, for example, that
We denote \(C^k(X)=C^k(X;{\mathbb {R}}^n)\) and use the Euclidean norm \(a\mapsto \Vert a\Vert _{{\mathbb {R}}^n}\) in \({\mathbb {R}}^n\).
When \(L_s^m({\mathbb {R}}^n)\) is the set of symmetric m-multilinear maps \(A:({\mathbb {R}}^n)^m\rightarrow {\mathbb {R}}^n\), we define
and
for \(H:X\subset {\mathbb {R}}^n\rightarrow L^m({\mathbb {R}}^n)\), define
where we have again used the Nesterov–Nemirovskii lemma.
In the main text of the paper, we use the following lemma:
Lemma 42
(1) Let \(k\in {\mathbb {N}}\) and \(f_i : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\), \(i=1,2,\dots ,N\) be \(C^k-\)smooth functions. Then,
(2) Let \(k\in {\mathbb {Z}}_+\). When \(X\subset {\mathbb {R}}^n\) is open, \(Y\subset {\mathbb {R}}^n\) is open and convex, and \(f :Y\rightarrow {\mathbb {R}}^n\) is \(C^{k+1}-\)smooth and \(g,h:X\rightarrow {\mathbb {R}}^n\) are \(C^{k}-\)smooth functions such that \(g(X)\subset Y\) and \(h(X)\subset Y\), we have
Proof
(1) Consider first the case \(N=2\). The claim is clearly valid for \(k=0\). Let us next assume that (238) is valid for \(k-1\). Then,
This and (238) for \(k-1\) yield that (238) is valid for k. By induction, (238) is valid for \(N=2\).
Iterating (238) for composition of two functions N times yields (238) for general N. This proves the claim (1).
(2) We have
and \( \partial _w ((\partial ^i_v f) \circ g)= ( \partial (\partial ^i_v f)) \circ g) \partial _w g \), where \({w=\partial _v g}\), and
For an integer \(i\le k\), let \(a_{i, k-i} := \Vert ((\partial ^i f) \circ g)-((\partial ^i f) \circ h)\Vert _{C^{k-i}(X;L_s^i)}.\)
When \(g(X)\subset X\) and \(i\le k-1\) is an integer, the Nesterov–Nemirovskii lemma (see also (235)) implies
Thus,
Using this and the claim (1) of the lemma, we see that
satisfy
where
Since Y is convex, we have by the Nesterov–Nemirovskii lemma
Using this and induction for (240) in the index i, we see that
This yields the claim (2). \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fefferman, C., Ivanov, S., Kurylev, Y. et al. Reconstruction and Interpolation of Manifolds. I: The Geometric Whitney Problem. Found Comput Math 20, 1035–1133 (2020). https://doi.org/10.1007/s10208-019-09439-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-019-09439-7