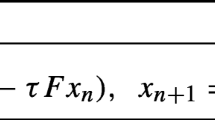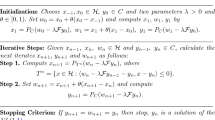Abstract
This paper deals with a class of inertial gradient projection methods for solving a variational inequality problem involving pseudomonotone and non-Lipschitz mappings in Hilbert spaces. The proposed algorithm incorporates inertial techniques and the projection and contraction method. The weak convergence is proved without the condition of the Lipschitz continuity of the mappings. Meanwhile, the linear convergence of the algorithm is established under strong pseudomonotonicity and Lipschitz continuity assumptions. The main results obtained in this paper extend and improve some related works in the literature.
Similar content being viewed by others
References
Alvarez, F., Attouch, H.: An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping, Set-Valued Anal., 9, 3–11 (2001)
Antipin, A. S.: On a method for convex programs using a symmetrical modification of the Lagrange function, Ekon. Mat. Metody, 12, 1164–1173 (1976)
Cai, G., Dong, Q. L., Peng, Y.: Strong convergence theorems for solving variational inequality problems with pseudo-monotone and non-Lipschitz operators, J. Optim. Theory Appl., 188, 447–472 (2021)
Cai, X., Gu, G., He, B.: On the O(1/t) convergence rate of the projection and contraction methods for variational inequalities with Lipschitz continuous monotone operators, Comput. Optim. Appl., 57, 339–363 (2014)
Cegielski, A.: Iterative Methods for Fixed Point Problems in Hilbert Spaces, Lecture Notes in Mathematics, vol. 2057, Springer, Berlin, 2012
Censor, Y., Gibali A, Reich, S.: The subgradient extragradient method for solving variational inequalities in Hilbert space, J. Optim. Theory Appl., 148, 318–335 (2011)
Censor, Y., Gibali, A., Reich, S.: Extensions of Korpelevich’s extragradient method for the variational inequality problem in Euclidean space, Optimization, 61, 1119–1132 (2011)
Cottle, R. W., Yao, J. C.: Pseudo-monotone complementarity problems in Hilbert space, J. Optim. Theory Appl., 75, 281–295 (1992)
Denisov, S. V., Semenov, V. V., Chabak, L. M.: Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators, Cybern. Syst. Anal., 51, 757–765 (2015)
Dong, L. Q., Cho, J. Y., Zhong, L. L., et al.: Inertial projection and contraction algorithms for variational inequalities, J. Glob. Optim., 70, 687–704 (2018)
Dong, Q. L., Gibali, A., Jiang, D.: A modified subgradient extragradient method for solving the variational inequality problem, Numer. Algorithms, 79, 927–940 (2018)
Facchinei, F., Pang, J. S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer Series in Operations Research, vols. I and II. Springer, New York, 2003
Fichera, G.: Sul problema elastostatico di Signorini con ambigue condizioni al contorno, Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat., 34, 138–142 (1963)
Gibali, A., Thong, D. V., Tuan, P. A.: Two simple projection-type methods for solving variational inequalities, Anal. Math. Phys., 9, 220–2225 (2019)
Goebel, K., Reich, S.: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, Marcel Dekker, New York, 1984
He, B. S.: A class of projection and contraction methods for monotone variational inequalities, Appl. Math. Optim., 35, 69–76 (1997)
Karamardian, S., Schaible, S.: Seven kinds of monotone maps, J. Optim. Theory Appl., 66, 37–46 (1990)
Kim, D. S., Vuong, P. T., Khanh P. D.: Qualitative properties of strongly pseudomonotone variational inequalities, Optim. Lett., 10, 1669–1679 (2016)
Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications, Academic Press, New York, 1980
Korpelevich, G.M.: The extragradient method for finding saddle points and other problems, Ekon. Mat. Metody, 12, 747–756 (1976)
Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings, Bull. Amer. Math. Soc., 73, 591–597 (1967)
Ortega, J. M., Rheinboldt, W. C.: Iterative Solution of Nonlinear Equations in Several Variables, Academic Press, New York, 1970
Polyak, B. T.: Some methods of speeding up the convergence of iteration methods, U.S.S.R. Comput. Math. Math. Phys., 4, 1–17 (1964)
Stampacchia, G.: Formes bilineaires coercitives sur les ensembles convexes, C. R. Acad. Sci., 258, 4413–4416 (1964)
Sun, D. F.: A class ofiterative methods for solving nonlinear projection equations, J. Optim. Theory Appl., 91, 123–140 (1996)
Thong, D. V., Hieu, D. V.: Modified subgradient extragradient method for variational inequality problems, Numer. Algorithms, 79, 597–610 (2018)
Thong, D. V., Hieu, D. V., Rassias, T. M.: Self adaptive inertial subgradient extragradient algorithms for solving pseudomonotone variational inequality problems, Optimization Lett., 14, 115–144 (2020)
Thong, D. V.: Extragradient method with a new adaptive step size for solving non-Lipschitzian pseudomonotone variational inequalities, Carpathian J. Math., 38, 503–516 (2022)
Vuong, P. T.: On the weak convergence of the extragradient method for solving pseudo-monotone variational inequalities, J. Optim. Theory Appl., 176, 399–409 (2018)
Vuong P. T., Shehu, Y.: Convergence of an extragradient-type method for variational inequality with applications to optimal control problems, Numer. Algorithms, 81, 269–291 (2019)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare no conflict of interest.
Rights and permissions
About this article
Cite this article
Thong, D.V. Modified Inertial Projection Method for Solving Pseudomonotone Variational Inequalities with Non-Lipschitz in Hilbert Spaces. Acta. Math. Sin.-English Ser. 39, 2374–2392 (2023). https://doi.org/10.1007/s10114-023-2080-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10114-023-2080-3
Keywords
- Inertial method
- projection and contraction method
- variational inequality problem
- pseudomonotone mapping
- convergence rate