Abstract
Optimization problems with uncertain black-box constraints, modeled by warped Gaussian processes, have recently been considered in the Bayesian optimization setting. This work considers optimization problems with aggregated black-box constraints. Each aggregated black-box constraint sums several draws from the same black-box function with different decision variables as arguments in each individual black-box term. Such constraints are important in applications where, e.g., safety-critical measures are aggregated over multiple time periods. Our approach, which uses robust optimization, reformulates these uncertain constraints into deterministic constraints guaranteed to be satisfied with a specified probability, i.e., deterministic approximations to a chance constraint. While robust optimization typically considers parametric uncertainty, our approach considers uncertain functions modeled by warped Gaussian processes. We analyze convexity conditions and propose a custom global optimization strategy for non-convex cases. A case study derived from production planning and an industrially relevant example from oil well drilling show that the approach effectively mitigates uncertainty in the learned curves. For the drill scheduling example, we develop a custom strategy for globally optimizing integer decisions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In mathematical programming, optimization under uncertainty often focuses on parametric uncertainty [10, 13, 16, 53, 58]. But many application areas rely on uncertain, expensive to evaluate black-box functions, e.g., automatic chemical design, production planning, scheduling with equipment degradation, adaptive vehicle routing, automatic control and robotics, and biological systems [15, 21, 23, 29, 37, 59, 63].
Bayesian optimization optimizes such functions by (i) fitting a Gaussian process to a small number of collected data points and (ii) subsequently choosing new sampling points using an acquisition function [42, 55, 57]. The Bayesian optimization literature also considers problems with black-box constraints, e.g., by multiplying the acquisition function with the probability of constraint satisfaction [25, 26, 49]. The global optimization community often handles black-box constraints by (i) generating a small data set from the black box function, (ii) fitting a surrogate model to this data, and (iii) replacing the black box constraint by the surrogate model [14, 18, 19, 30, 40, 43, 52]. This approach, however, rarely considers uncertainty in the black box function.
One way of including uncertain black-box function into the optimization problem is to consider the surrogate model’s parameters to be uncertain and use classical parametric uncertainty methods. Hüllen et al. [33] recently demonstrated this approach for polynomial surrogates using robust optimization. This paper proposes a more direct approach utilizing probabilistic surrogate models to model the uncertain curves. We study optimization problems with constraints which aggregate black-box functions:
where \(x_i\) is a decision variable and \(\tilde{a}_{i}\) depends on a vector of decision variables \({\varvec{z}_i}\in {\mathbb {R}}^k\) through a black-box function \(g(\cdot )\). Constraint (1) occurs in many highly relevant applications. In production planning, one may limit the total allowed equipment degradation \(\sum _{i} r(p_i)\varDelta t_i \le b\), where \(r(p_i)\) is the black-box degradation rate depending on production \(p_i\) in time period i and \({\varDelta t}_i\) is equipment operation time in period i [63]. A second example is vehicle routing, where the total travelling time \(\sum _{i}\varDelta t(t_i, s_i, d_i) \gamma _i\) is the sum of travelling times \(\varDelta t(t_i, s_i, d_i)\) for individual legs i, dependent on starting time \(t_i\), source \(s_i\), and destination \(d_i\), and \(\gamma _i\) is a binary variable indicating whether leg i is part of the route. A third example is project scheduling under uncertainty in which duration uncertainty may be aggregated over multiple activities [60]. Lastly, the drill scheduling case study described in detail later in this paper is an industrially relevant example.
When black-box constraints are risk or safety-critical, hedging solutions against uncertainty is essential. Evaluating black-box functions may require expensive computer simulations or physical experiments, so available data is generally limited and may be subject to model errors and measurement noise. We therefore consider the function \(g(\cdot )\) to be uncertain and aim to find solutions for which Constraint (1) holds with confidence \(1 - \alpha \):
To capture the uncertainty in \(g(\cdot )\), we model it by stochastic surrogate models. A common stochastic surrogate is the Gaussian process (GP) model. Depending on the underlying data generating distribution, however, a GP may be an inadequate model. Warped Gaussian processes, which map observations to a latent space using a warping function, are an alternative, more flexible model [56]. This paper considers both standard and warped GPs.
We note that other contributions have connected Bayesian optimization with robust optimization [7, 11, 12, 17]. These works have focused on implementation errors. An adversary can perturb the input \(\varvec{x}\) to a black-box function f by \(\varvec{\delta } \in \mathcal {U}\). Robust solutions optimize performance under the worst-case perturbation realization: \(\min \limits _{\varvec{x}\in {\mathbb {R}}^n} \max \limits _{\varvec{\delta } \in \mathcal {U}} f(\varvec{x}+\varvec{\delta })\). Our work does not consider implementation errors. We instead focus on the setting where the uncertainty is in the output of the black-box function. Most of these works also focus on uncertain black-box objective functions with some making extensions to uncertain black-box constraints [7, 11]. Our work focuses on aggregated black-box constraints which are relevant in safety-critical applications. To the best of our knowledge, no prior work has connected either warped GPs or aggregated black-box constraints with robust optimization.
1.1 Contributions
For the standard GP model, we show how chance constraint Eq. (2) can be exactly reformulated as a deterministic constraint using existing approaches. For the warped case, we develop a robust optimization approach which conservatively approximates the chance constraint. By constructing decision-dependent uncertainty sets from confidence ellipsoids based on the warped GP models, we obtain probabilistic constraint violation bounds. We utilize Wolfe duality to reformulate the resulting robust optimization problem and obtain explicit deterministic robust counterparts. This reformulation expresses uncertain constraints, modeled by GPs, as deterministic constraints with a guaranteed probability of constraint satisfaction, i.e., deterministic approximations to a chance constraint. We analyze convexity conditions of the warping function under which the Wolfe duality based reformulation is applicable. For non-convex cases, we develop a global optimization strategy which utilizes problem structure. To reduce solution conservatism, we furthermore propose an iterative a posteriori procedure of selecting the uncertainty set size which complements the obtained a priori guarantee.
We show how the proposed approach hedges against uncertainty in learned curves for two case studies: (i) a production planning-inspired case study with an uncertain price-supply curve and (ii) an industrially relevant drill-scheduling case study with uncertain motor degradation characteristics. For the drill-scheduling case study we develop a custom strategy for dealing with discrete decisions.
1.2 Notation
See “Appendix A” for a table of notation.
2 Method
Sections 2.1–2.3 review (warped) GPs, robust optimization, and chance constraint reformulations for Gaussian distributions. Sections 2.4 and 2.5 outline our proposed robust approximation approach.
2.1 Warped Gaussian processes
GPs are widely used for Bayesian optimization and non-parametric regression [51, 55, 64].
Definition 1
(Gaussian process) A continuous stochastic process \(G(\varvec{x})\) for which \( G_{\varvec{x}_1,\ldots ,\varvec{x}_l} = (G_{\varvec{x}_1}, \ldots , G_{\varvec{x}_l})\) is a multivariate Gaussian random variable for every finite set of points \(\varvec{x}_1, \ldots , \varvec{x}_l\).
A GP defines a probability distribution over functions and it is fully specified by its mean function \(m(\cdot )\) and kernel function \(k(\cdot , \cdot )\). Given a set of N data points \(X = [\varvec{x}_1, \ldots , \varvec{x}_N], \varvec{y} = [y_1, \ldots , y_N]^\intercal \) and using a zero mean function, we can predict the mean \(\varvec{\mu }\) and covariance matrix \(\varSigma \) of the multivariate Gaussian distribution defined by a set of new test points \(X_* = [\varvec{x}^*_1, \ldots , \varvec{x}^*_n]\):
where \(\sigma _n\) is the standard deviation of noise in the data, \(K(X_*, X) = K(X, X_*)^\intercal \) is the \(n \times N\) covariance matrix between test and training points, K(X, X) the \(N \times N\) covariance matrix between training points, \(K(X_*, X_*)\) the \(n \times n\) covariance matrix between test points, and I the identity matrix. We denote the ij-element of \(\varSigma \) as \(\sigma ^2_{ij} = \sigma ^2(\varvec{x}^*_i, \varvec{x}^*_j)\).
The standard GP approach assumes that the data follows a multivariate Gaussian. While this assumption allows prediction using simple matrix multiplication, it can be an unreasonable for non-Gaussian data [56]. A slightly more flexible model, which still retains many of the benefits of GPs, is the warped GP model. The key idea is to warp the observations \({\varvec{z}}\) to a latent space \(\varvec{\xi }\) using a monotonic warping function \(\varvec{\xi }= h({\varvec{z}}, \varvec{\varPsi })\) , where \(\varvec{\varPsi }\) is a vector of parameters. A standard GP then models the data in the latent space \(\varvec{\xi }\sim \mathcal {GP}(\varvec{x})\). The Jacobian \(\frac{\partial h({\varvec{z}})}{\partial y}\) is included in the likelihood and the GP and warping parameters are learned simultaneously. A common warping function is the neural net style function:
where \(a_j \ge 0, b_j \ge 0, \forall j\) to guarantee monotonicity [35, 39, 56] and \(n_w\) is the number of warping terms. Note that we use \(\varvec{h}(\cdot )\) to denote the vector version \(\varvec{h}: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n, \varvec{h}({\varvec{z}}) = [h(z_1), \ldots , h(z_n)]^\intercal \), which warps each component individually.
2.2 Robust optimization
Robust optimization immunizes optimization problems against (typically parametric) uncertainty by requiring constraints with uncertain parameters \(\tilde{a}_{i}\) to hold for all values inside some uncertainty set \(\mathcal {U}\) [27]. Application areas range from finance and engineering to scheduling and compressed least squares [6, 27]. The uncertainty set \(\mathcal {U}\) can take many different geometries, e.g., box [58], ellipsoidal [9], and polyhedral sets [13]. When \(\mathcal {U}\) is convex and the constraint is concave, the semi-infinite constraint can often be reformulated into a deterministic equivalent using duality [8]. The general case can be solved using bilevel optimization [3, 41], but this requires solving the inner maximization problem to global optimality, even to obtain feasible solutions.
2.3 Standard GPs: chance constrained optimization
When \(g(\cdot )\) is modeled well by a standard GP, chance constraint Eq. (2) can be exactly replaced by a deterministic equivalent [20]. Since \(\left\{ g({\varvec{z}_i}), i \in S\right\} \sim \mathcal {N}\left( \varvec{\mu }, \varSigma \right) \) is normal distributed, the linear combination:
is also normal distributed with distribution:
Note that we have suppressed the dependence of \(\varvec{\mu }\) and \(\varSigma \) on \({\varvec{z}}_i\) for notational simplicity. For a given confidence level \(\alpha \), we can therefore replace chance constraint Eq. (2) by:
where \(F(\cdot )\) is the cumulative distribution function of the standard normal distribution. If the GP models \(g(\cdot )\) well, Eq. (4) is an exact deterministic reformulation of chance constraint Eq. (2).
2.4 Warped GPs: robust approximation
If \(g(\cdot )\) is insufficiently modeled by a standard GP, a warped GP may be a more suitable model [56]. In this case, a direct reformulation of the chance constraint as outlined above for the standard GP case is not known. Such chance constraints are generally addressed by (i) sample approximation [38, 47, 48] or (ii) safe outer-approximation [1, 36, 45, 46, 50, 65]. Instead, we develop a robust approximation. First consider an optimization problem containing a nominal version of Constraint (1):
where \({\varvec{z}}\) is the vector containing all elements of \({\varvec{z}}_i, \forall i\) and the objective function \(f: \varvec{x}, {\varvec{z}}\rightarrow {\mathbb {R}}\) is assumed to be known explicitly, i.e., it is not a black-box function. Here, the inversely warped mean prediction of the GP \(h^{-1}(\mu (\cdot ))\) replaces the black-box function \(g(\cdot )\). Clearly, a solution to Problem (5) is not guaranteed to be feasible in practice if the prediction \(\mu ({\varvec{z}_i})\) is uncertain. Using the full multivariate distribution generated by the sampling points \(\{{\varvec{z}_i}\}\), we can construct an \(\alpha \)–confidence ellipsoid in the latent space:
Here, \(F_n^{1-\alpha }\) is the cumulative distribution function of the \(\chi ^2\) distribution with n degrees of freedom. Note that when the GP kernel is positive definite, the covariance matrix \(\varSigma \) is also positive definite and the inverse \(\varSigma ^{-1}\) exists. Assuming that the warped GP models the black-box function well, \(\mathcal {E}^\alpha ({\varvec{z}})\) contains the true value \(h(g({\varvec{z}_i}))\) with probability at least \(1 - \alpha \). We therefore construct the following robust optimization problem:
Any solution to Problem (7) is feasible with probability at least \(1-\alpha \) given that the warped GP models the underlying data generating distribution well. Alternatively, we can take the warping into the uncertainty set:
where \(\mathcal {U}\):
Note that Problem (8) can also be interpreted as approximating a robust problem with an uncertainty set over functions \(\tilde{g}\in \mathcal {U}^g\) (see Theorem 3, “Appendix B”). Figure 1 shows an example of the ellipsoidal and warped sets \(\mathcal {E}^\alpha \) and \(\mathcal {U}\) for \(n=2\). The warped set \(\mathcal {U}\) (Eq. 9) may or may not be convex, depending on the warping function \(h(\cdot )\).
2.4.1 Reformulation for convex warped sets \(\mathcal {U}\)
We first assume that the warped set \(\mathcal {U}\) retains convexity and utilize Wolfe duality to reformulate the semi-infinite Problem (8) into a deterministic problem with a finite number of constraints. Consider the min-max equivalent of Problem (8):
When \(\mathcal {U}\) is convex, the inner maximization, Eq. (10b), is convex:
Note that we suppress the dependence of \(\varvec{\mu }\) and \(\varSigma \) on \({\varvec{z}}\) for notational simplicity from here onward. Problem (11) generally doesn’t have a simple closed form solution. Instead, we can use Wolfe duality to transform Problem (11) into an equivalent minimization problem, leading to a deterministic reformulation of Problem (8):
where u is a dual variable,  , and Constraint (12c) is the Karush–Kuhn–Tucker (KKT) stationarity condition. Note that, unless \(\varvec{x}= \varvec{0}\), the stationarity condition means that \(u \ne 0\) and, due to complementary slackness, \(w({\varvec{y}}, {\varvec{z}}) = 0\), i.e.:
, and Constraint (12c) is the Karush–Kuhn–Tucker (KKT) stationarity condition. Note that, unless \(\varvec{x}= \varvec{0}\), the stationarity condition means that \(u \ne 0\) and, due to complementary slackness, \(w({\varvec{y}}, {\varvec{z}}) = 0\), i.e.:
Furthermore, we can reformulate Eq. (12c) to:
Substituting this in Eq. (13) yields:
This leads to a slightly different formulation which has the advantage that it does not depend on the inverse of the covariance matrix \(\varSigma ^{-1}\):
where the inverse \(\left( \nabla \varvec{h}({\varvec{y}})\right) ^{-1}\) exists when \(h'(y) \ne 0\) because \(\nabla \varvec{h}({\varvec{y}})\) is a diagonal matrix. Note that \(h(y_i) > 0, \; \forall y_i \in {\mathbb {R}}\) for the neural net style warping function in Eq. (3). Formulation (14) has the advantages that it does not depend on the inverse \(\varSigma ^{-1}({\varvec{z}})\), which generally cannot be formulated explicitly, and that it can be solved using off-the-shelf solver software. While Problem (14) is non-convex due to bilinearities between \({\varvec{y}}\) and \(\varvec{x}\), the potentially non-convex objective function f, and the dependence of \(\mu \) and \(\varSigma \) on \({\varvec{z}}\), even a non-optimal solution will be robustly feasible.
2.4.2 Convexity conditions
Section 2.4.1 relies on the convexity of the inner maximization problem. If \(\mathcal {U}\) is non-convex, Problem (14) is not necessarily equivalent to Problem (8) as there may be more than one KKT point. Since \(\mathcal {U}\) is the confidence set of a multivariate distribution, however, may often be convex, especially when the distribution is unimodal. The following section analyzes conditions where the Wolfe duality approach is justified.
First consider the inner maximization Problem (11) transformed into the latent space by substituting \({\varvec{y}}= \varvec{h}^{-1}(\varvec{\xi })\):
which depends on the generally not explicitly known inverse warping function \(h^{-1}\). We further state the well known result on the derivative of inverse functions [4]:
Lemma 1
If \(f: {\mathbb {R}}\rightarrow {\mathbb {R}}\) is continuous, bijective, and differentiable and \(f'(f^{-1}(x)) \ne 0\), then \([f^{-1}]'(x) = \frac{1}{f'(f^{-1}(x))}\).
Using this, we can show the following proposition.
Theorem 1
Let the warping function \(h(\cdot )\) be concave (convex) and let \(x_i \ge 0 \; (\le 0), \; \forall i\), then the inner maximization Problem (11) has a unique KKT point.
Proof
Note that Problem (15) is convex when \(\varvec{h}^{-1}\) is concave (convex) and \(x_i \ge 0\; (x_i \le 0 ), \forall i\). The KKT conditions for Problems (11) and (15) are:
and:
where:
By Lemma 1:
So Problem 17 is equivalent to:
Let \({\varvec{y}^*}\) be a KKT point for Problem (11), then \({\varvec{z}^*}= h({\varvec{y}^*})\) is clearly a solution to Problem (20), and therefore a KKT point for Problem (15). Since Problem (15) is convex, \({\varvec{y}^*}\) is unique.\(\square \)
2.4.3 Strategy for non-convex warped sets \(\mathcal {U}\)
When \(\mathcal {U}\) is non-convex, we need to globally optimize the inner maximization problem efficiently. To this end we develop a custom divide and conquer strategy which makes use of the problems special structure. We first note the following properties of the inner maximization problem.
Lemma 2
Let \({\varvec{y}^*}\) be the solution of Problem 11, then \({\varvec{y}^*}\) is on the boundary of \(\mathcal {U}\), i.e., \({\varvec{y}^*}\in \partial \mathcal {U}\).
Proof
See “Appendix C”. \(\square \)
Lemma 3
The bounding box of an ellipsoid \({\left( \varvec{x}-\varvec{\mu }\right) }^\intercal \varSigma ^{-1}{\left( \varvec{x}-\varvec{\mu }\right) } \le r^2\) is given by the extreme points \(x_i = {\mu _i} \pm r \sigma _{ii}\).
Proof
See “Appendix C”. \(\square \)
Lemma 4
Consider a version of Problem (15) in which the ellipsoidal feasible region is replaced by its bounding box:
If \(x_i \ge 0, \forall i\), the optimal solution \(\xi ^*\) to this problem is the corner of the bounding box with \(\xi ^*_i = \mu _i + r\sigma _{ii}, \forall i\).
Proof
Let \(\varvec{\xi }^*\) be the optimal solution to Problem (4). Note that \(\varvec{\xi }^*\) lies on the boundary of the feasible space (Lemma 2). Assume \(\exists i\), s.t., \(\xi ^*_i < \mu + r\sigma _{ii}\). Because \(h^{-1}\) is strictly monotonically increasing and \(x_i \ge 0\), \(x_i h^{-1}(\xi _i) > x_i h^{-1}(\mu + r\sigma _{ii})\). Therefore we can construct a new solution \(\hat{\varvec{\xi }}\):
for which \(\varvec{x}^\intercal \hat{\varvec{\xi }} \ge \varvec{x}^\intercal \varvec{\xi }^*\), which is a contradiction. \(\square \)
Theorem 2
Let  be \(\bar{\xi }_i = \mu _i + r \sigma _{ii}\) (
be \(\bar{\xi }_i = \mu _i + r \sigma _{ii}\) ( ) and \(\varvec{\xi }^*\) the optimal solution to Problem (15). Then (i)
) and \(\varvec{\xi }^*\) the optimal solution to Problem (15). Then (i)  and (ii) \(\frac{\varvec{x}^\intercal \varvec{h}^{-1}(\bar{\varvec{\xi }})}{\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\xi }^*)} \le \frac{\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\mu }+ r\varvec{\sigma })}{\varvec{x}^\intercal \varvec{h}^{-1}(\mu + r\varvec{\sigma }/\sqrt{\varvec{\sigma }^\intercal \varSigma ^{-1} \varvec{\sigma }})}\) where \(\varvec{\sigma } = \left[ \sigma _{11}, \ldots , \sigma _{nn}\right] ^\intercal \).
and (ii) \(\frac{\varvec{x}^\intercal \varvec{h}^{-1}(\bar{\varvec{\xi }})}{\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\xi }^*)} \le \frac{\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\mu }+ r\varvec{\sigma })}{\varvec{x}^\intercal \varvec{h}^{-1}(\mu + r\varvec{\sigma }/\sqrt{\varvec{\sigma }^\intercal \varSigma ^{-1} \varvec{\sigma }})}\) where \(\varvec{\sigma } = \left[ \sigma _{11}, \ldots , \sigma _{nn}\right] ^\intercal \).
Proof
Part (i) follows immediately from Lemma 4 because Problem (4) is a relaxation of Problem (15). To prove (ii), first consider a scaled version of the bounding box with corner \(\hat{\varvec{\xi }} = \varvec{\mu }+ \lambda r \varvec{\sigma } \). Assume that scaling factor \(\lambda \in [0, 1]\) is chosen so that the corner of the scaled box \(\hat{\varvec{\xi }}\) lies on the ellipsoid, i.e.:
Substituting \(\hat{\varvec{\xi }} = \varvec{\mu }+ \lambda r \varvec{\sigma }\) and rearranging leads to
Furthermore, since \(\hat{\varvec{\xi }}\) is contained in the ellipsoid, \(\frac{\varvec{x}^\intercal \varvec{h}^{-1}(\bar{\varvec{\xi }})}{\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\xi }^*)} \le \frac{\varvec{x}^\intercal \varvec{h}^{-1}(\bar{\varvec{\xi }})}{\varvec{x}^\intercal \varvec{h}^{-1}(\hat{\varvec{\xi }})}\). Substituting \(\bar{\varvec{\xi }} = \varvec{\mu }+ r \varvec{\sigma }\) and \(\hat{\varvec{\xi }} = \varvec{\mu }+ \frac{r\varvec{\sigma }}{\sqrt{\varvec{\sigma }\varSigma ^{-1}\varvec{\sigma }}}\) concludes the proof. \(\square \)
Using Lemma 2 and Theorem 2 we develop the spatial branching strategy shown in Algorithm 1. Algorithm 1 works similarly to other elimination-based algorithms [34, 44]. It starts by outer-approximating the ellipsoid by its bounding box and evaluating the objective \(\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\xi })\) at the two corner points  ,
obtaining an upper and lower bound (Theorem 2). The algorithm then branches on the dimension of largest width. Boxes can be pruned if they are fully inside or outside the ellipsoid (Lemma 2). Theorem 2 also provides an a-posteriori bound for the tightness of the outer approximation. In the special case when the ellipsoid is an n-D ball with zero mean, the bound can be simplified to an a-priori bound: \(\frac{\varvec{x}^\intercal \varvec{h}^{-1}(\bar{\varvec{\xi }})}{\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\xi }^*)} \le \frac{h^{-1}(r)}{h^{-1}(\frac{r}{\sqrt{n}})}\).
,
obtaining an upper and lower bound (Theorem 2). The algorithm then branches on the dimension of largest width. Boxes can be pruned if they are fully inside or outside the ellipsoid (Lemma 2). Theorem 2 also provides an a-posteriori bound for the tightness of the outer approximation. In the special case when the ellipsoid is an n-D ball with zero mean, the bound can be simplified to an a-priori bound: \(\frac{\varvec{x}^\intercal \varvec{h}^{-1}(\bar{\varvec{\xi }})}{\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\xi }^*)} \le \frac{h^{-1}(r)}{h^{-1}(\frac{r}{\sqrt{n}})}\).

2.5 Iterative a posteriori approximation
The a priori probabilistic bound implied by \(\mathcal {E}^\alpha \) may be overly conservative. Algorithm 2 is an alternative, less conservative strategy that iteratively determines the uncertainty set size.

Starting with the confidence level \(\alpha \) equal to the target feasibility \(\epsilon _0\), Algorithm 2 iteratively solves the robust optimization problem, estimates the feasibility of the solution, and consequently adjusts the confidence level \(\alpha \) using bisection search. To estimate the feasibility of a solution, we generate 10,000 random samples \(\varvec{\xi }_i\) from the warped GP distribution \(\mathcal {N}\left( \varvec{\mu }({\varvec{z}}), \varSigma ({\varvec{z}})\right) \), evaluate the constraint \(\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\xi }_i)\) for each sample i, and calculate the percentage of samples for which \(\varvec{x}^\intercal \varvec{h}^{-1}(\varvec{\xi }_i) \le b\). The search terminates when a solution has been found that is sufficiently close (tolerance \(\delta \)) to the target feasibility \(\epsilon _0\).
3 Case studies
3.1 Production planning
Our first case study is inspired by production planning. Assume that a company wants to decide how much product \(x_t\) to produce in a number of subsequent time periods \(\varvec{x}= [x_1, \ldots , x_t, \ldots , x_T]\). There is a known cost of production \(c_t\) which may vary from period to period. The company seeks to maximize its profit \(\psi \), which depends on the total production cost \(\sum \nolimits _t c_t x_t\) and revenue \(\sum \nolimits _t \tilde{p}_t x_t\). Here \(\tilde{p}_t\) is the price at which the product can be sold in period t. The company has to sell all its product in the same time period, e.g., because the product is perishable. The sale price depends on the amount the company produces in that period \(\tilde{p}_t = \tilde{p}(x_t)\), e.g., because the company has a very large market share.
The company uses GP regression to predict \(\tilde{p}(x_t)\) based on limited historical data. Additional features, e.g., season and general state of the economy, could be part of this regression but are irrelevant for our purpose as they are not decision variables. The prediction has to be considered uncertain and the company wants a production plan guaranteeing a certain profit with some confidence. This decision problem can be formulated as a chance constrained optimization problem:
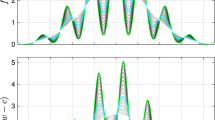
Choosing \(p(x_t) = \exp \left( -x_t\right) \) as ground truth for the price-supply curve, we generate noisy data \(\tilde{p}(x_t) = p(x_t) + \epsilon \) and fit a GP surrogate as shown in Fig. 2. We consider uniform Gaussian noise (\(\epsilon \sim \mathcal {N}(0, \sigma _{\text {noise}})\)) and non-uniform Gaussian noise (\(\epsilon \sim \mathcal {N}(0, 4\cdot \sigma _{\text {noise}}\cdot \exp (-x/2))\)), where \(\sigma _{\text {noise}}\) is a parameter determining the amount of noise. We use a squared exponential kernel for this case study, but the proposed method does not generally rely on a specific choice for \(k(\cdot , \cdot )\).
3.2 Drill scheduling
The objective in drilling oil wells is generally minimizing total well completion time. The aim of the drill scheduling problem, illustrated in Fig. 3, is to find a schedule of the two decision variables, rotational speed \(\dot{N} \in {\mathbb {R}}\) and weight on bit \(W \in {\mathbb {R}}\), as a function of depth \(x \in {\mathbb {R}}\). Current practice often consists of minimizing the total drilling time, which depends on \(\dot{N}\) and W through a non-linear bit-rock interaction model [22] and the motor’s power-curves (see “Appendix D”). Total well completion time, however, also depends on maintenance time. Current practice may increase maintenance time because drilling quickly can detrimentally effect motor degradation. Furthermore, the motors degradation characteristics are subject to uncertainty and are often obtained through a mixture of experiments and expensive numerical simulations [2]. Other works have considered uncertain equipment degradation in scheduling applications [5, 63], but not with predicted degradation rates.
To find the optimal trade off between drilling and maintenance time, we propose a drill scheduling model which explicitly considers uncertainty in the motor degradation characteristics. First consider a model which discretizes the drill trajectory into \({n_d}\) equidistant intervals:
The rate of penetration \(V_i\) in each segment depends on the drill parameters (\(\dot{N}_i\) and \(W_i\)) through the non-linear model in “Appendix D”. The rate of degradation \(r(\cdot )\) is a black-box function of the differential pressure across the motor \({\varDelta p}\). We model \(r(\cdot )\) with a warped GP based on 10 data points from a curve obtained by Ba et al. [2] through a combination of experiments and numerical simulation. The maintenance indicator \(R_i\) keeps track of the total cumulative degradation of the motor. We assume the motor fails when \(R_i\) reaches 1. Binary variable \(z_i\) indicates whether maintenance is scheduled in segment i. If maintenance is scheduled, the continuous variable \(y_i\) resets the total degradation indicator \(R_i\) to zero. Note that the bit-rock interaction model depends on rock parameters which can change from segment to segment.
A major disadvantage of Model (24) is that it requires a large number of segments in order to get a good resolution on the optimal maintenance depth. To avoid this we propose, in analogy with continuous time formulations [24, 54], an alternative continuous depth scheduling formulation:
Model (25) only considers geological segments (segments with constant rock parameters) and maintenance induced segments. The vector \(\varvec{x}\) is ordered and contains the fixed rock formation depths as well as the variable maintenance depths. M is a set containing the indices of the variable maintenance depths. Figure 3 shows an example instance where \(x_0, x_1, x_3\) are fixed depths and \(x_2\) is the variable depth of a maintenance event, i.e., \(\varvec{x}= [x_0, x_1, x_2, x_3]\) and \(M = \{2\}\). The indices \(i \in M\) of the variable maintenance depths are determined a priori, i.e., we decide both the number of maintenance events as well as the geological segment in which they occur a priori. \(m^-\) is either the index of the previous maintenance event or 1 if m is the first element in M.
While Problem (25) cannot decide the optimal number of maintenance events, it is easier to solve than Problem (24) because it does not contain integer variables and generally has a much smaller number of segments, i.e., fewer variables and constraints. The following discusses strategies for deciding the optimal number and segment assignment of maintenance events.
3.2.1 Integer strategy
In drill scheduling, the number of maintenance events m is generally small (\(m\le 4\)). The number of geological segments \({n_d}\) can be large in practice but will not be known a priori. We therefore consider groupings of segments into a small number (\({n_d} \le 10\)) of longer segments with average rock parameters which are known a priori. Given \({n_d}\) and m, the combinatorial complexity of enumerating the maintenance-segment assignment problem is \(N = {{n_d} + m - 1 \atopwithdelims ()m}\). However, the optimal number of maintenance events m is a decision variable. Therefore, finding the globally optimal maintenance-segment assignment also requires enumerating different values of m.

Algorithm 3 derives upper bounds for the number of maintenance events m as well as their location. It starts by solving Problem (25) without any maintenance events and ignoring the upper bound on the degradation indicator \(R_{{n_d}} \nleq 1\). The floor of the maintenance indicator at the target depth \({x_{n_d}}\), \(\lfloor R_{{n_d}}\rfloor \) is an upper bound for the necessary number of maintenance events m. Algorithm 3 then starts at the target depth \({x_{n_d}}\) and inserts \(\lfloor R_{n_d}\rfloor \) maintenance events at the earliest possible points that satisfy the maintenance constraint. The locations \(\hat{x}_m\) are upper bounds for the maintenance locations.
Lemma 5
Let \(\hat{\varvec{x}}^m\) be the maintenance depths determined by Algorithm 3. Let \(\varvec{x}^{*,m}\) contain the globally optimal maintenance depths. Let \(\varvec{x}^{m,*}\) further be padded with zeroes at the beginning such that \(\hat{\varvec{x}}^m\) and \(\varvec{x}^{*,m}\) have the same length. Then \(x^{*,m}_{i} \le \hat{x}^m_{i}\).
Proof
Assume \(x^{*,m}_{i} \le \hat{x}^m_{i}\) but \(x^{*,m}_{i+1} > \hat{x}^m_{i+1}\). Construct a new solution \((\varvec{x}'^{,m}, \varvec{V}')\) by moving \(x^{*,m}_{i+1}\) to \(\hat{x}^m_{i+1}\) and drilling at maximum speed \(\hat{V}_{i+1}\) between \(\hat{x}^m_{i+1}\) and \(x^{*,m}_{i+1}\):
\((\varvec{x}'^m, \varvec{V}')\) has drilling and maintenance cost lower than \((\varvec{x}^{*,m}, \varvec{V}^*)\), which is a contradiction. Therefore \(x^{*,m}_{i} \le \hat{x}^m_{i} \implies x^{*,m}_{i+1} \le \hat{x}^m_{i+1}\). Furthermore, note that \(x^{*,m}_{m} \le \hat{x}^m_{m}\) (last maintenance event) has to be true by the same logic as above. The proposition follows by induction.\(\square \)
Lemma 5 reduces the number of maintenance-segment assignments to enumerate:
Note 1 Let \(\hat{\varvec{x}}\) be the upper bounds on maintenance locations from Algorithm 3. Let \(n_i\) be the segment containing \(\hat{x}_i\). The complexity of enumerating the maintenance-segment assignment problem using the upper bounds from Algorithm 3 is:
3.2.2 Heuristics
Algorithm 3 is equivalent to minimizing the drilling cost without considering degradation—a strategy often used in practice. It provides feasible but likely suboptimal solutions to Problem (25), i.e., it can be used as a heuristic. We call this the no–degradation heuristic and propose a second, improved heuristic: the boundary heuristic, outlined in Algorithm 4. Algorithm 4 starts with the solution of the no–degradation heuristic (Algorithm 3). It improves the solution by iteratively solving Problem (25) and reassigning maintenance events occurring at geological boundaries to the adjacent segment. It terminates after finding a solution with all maintenance events occurring in the interior of their segment. Note that moving a maintenance event occurring at a geological boundary to the adjacent segment cannot lead to a worse solution, i.e. Algorithm 4 is an anytime algorithm.

While it does not guarantee global optimality of the maintenance-segment assignment, the boundary heuristic may be useful for very large instances when enumeration is prohibitive.
4 Results
The deterministic reformulations of both case studies were implemented in Pyomo (Version 5.6.8) [31, 32], an algebraic modeling language for expressing optimization problems. As part of this work, we developed a Python (Version 3.6.8) module which takes a GP model trained using the Python library GPy (Version 1.9.6) [28] and predicts \(\mu (\varvec{x})\) and \(\varSigma (\varvec{x})\) as Pyomo expressions. The module is available open source on GitHub [62]. This allows the easy incorporation of GP models into Pyomo optimization models. We use the interior-point convex optimization solver Ipopt [61] with a multistart strategy to solve the problem. Each instance was solved 30 times with a random starting point. The multistart procedure ends prematurely if it finds the same optimal solution (with a relative tolerance of \(10^{-4}\)) 5 times.
Figure 4 shows the warping functions for both case studies. Since the production planning warping function is concave and the production amounts \(x_t\) are strictly positive, Theorem 1 applies and the warped set \(\mathcal {U}\) is convex. Theorem 1 cannot be applied to the drill scheduling case, because its warping function is neither convex nor concave. However, because the warping function is only slightly non-convex, the warped set \(\mathcal {U}\) may still be convex for many instances. To avoid solving the bilevel problem directly we therefore use the following strategy: (i) solve the robust reformulation (Eq. 14), (ii) check feasibility of the obtained solution using Algorithm 1 (to a tolerance of \(10^-2\)), and (iii) only solve the bilevel problem (Eq. 8) directly if the obtained solution is infeasible. For the instances considered in this work, the obtained solution always turns out to be feasible.
4.1 Production planning
For the production planning case study, we consider 4 model instances with \(T = 1, 2, 3\) and 6 time periods.
Fraction of feasible solutions as a function of confidence \(1 - \alpha \) for the planning problem with three time periods. \(1 - \alpha = 0\) corresponds to the nominal case and \(1 - \alpha = 1\) to 0% chance of constraint violation. The noise in the data is uniform Gaussian with \(\sigma _{\text {noise}}= 0.01, 0.03, 0.05\) and 0.08 and a standard GP model was used. The smaller the noise, the closer the actual feasibility is to the expected confidence (dotted line)
Fraction of feasible solutions as a function of confidence \(1-\alpha \) for non-uniform Gaussian noise with \(\sigma _{\text {noise}}= 0.01, 0.03, 0.05\), and 0.08 for the production planning case study. Results are shown for four different numbers of time periods \(T = 1, 2, 3\) and 6. The dotted line shows the a priori bound. With increasing numbers of time periods, the robust approximation becomes increasingly conservative
Table 1 shows the cost of production \(\varvec{c}\). We solve each instance for 30 different confidence values \(1 - \alpha \). The GP was trained based on 20 randomly generated data points using both uniform and non-uniform Gaussian noise with \(\sigma _{\text {noise}}= 0.01, 0.03, 0.05\), and 0.08.
4.1.1 Standard GP
Figure 5 shows results for the chance constrained approach using a standard GP model. We plot the fraction of feasible scenarios out of 1 million random samples from the true underlying distribution. Figure 5 shows results for four different noise scenarios. By varying the confidence \(1-\alpha \), we adjust the robustness of the obtained solution. Clearly, the resulting feasibility does not exactly match the expected feasibility (shown as a dotted line) determined by the confidence level \(1-\alpha \). This is due to a mismatch between the true underlying distribution and the normal distribution estimated by the GP. As the amount of noise increases, the GP estimate deteriorates and the mismatch between feasibility and confidence increases.
4.1.2 Warped GP
Figure 6 shows solution feasibility as a function of confidence \(1- \alpha \) for non-uniform noise using a warped GP model and the proposed robust approach. We show results for four different numbers of time periods. In the nominal case (\(1 - \alpha = 0\)), the feasibility is always close to \(50\%\) because a solution which is valid for the mean price-supply curve will also be valid for many scenarios with higher prices. In the robust case, as expected, feasibility increases as the size of the uncertainty set, i.e. \(1 - \alpha \), increases. Notice that the robust approach is almost always a conservative approximation to the chance constraint, as the achieved feasibility is generally larger than the confidence \(1 - \alpha \). Small violations of the a priori bound (dotted line) can still occur due to a mismatch between the GP model and the true underlying data generating distribution. The solution conservatism also varies with the number of time periods considered. The a priori bound relaxes as T increases.
Profit, normalized with respect to nominal profit with \(\sigma _{\text {noise}}= 0.01\) (objective of Problem (5)), as a function of confidence \(1 - \alpha \) for four different noise scenarios and time periods \(T=1, 2, 3\) and 6. As expected, the objective value decreases with increasing confidence \(1-\alpha \), because more extreme worst case scenarios are considered
Figure 7 shows the worst case profit, normalized with respect to the nominal profit for \(\sigma _{\text {noise}}=0.01\), achieved as a function of the confidence level \(1-\alpha \). As expected, increasing the confidence \(1-\alpha \) leads to a lower worst case profit, because a larger confidence hedges against more uncertain price outcomes. Note that results are shown for values of \(1-\alpha \) between 0.001 and 0.999. At \(1 - \alpha = 1\), the profit is always zero, because the uncertainty set includes negative prices and the optimal solution is to not produce anything. For a fixed confidence level, noisier data will generally lead to a smaller objective value as there is more uncertainty to hedge against.
4.1.3 Iterative procedure
Figure 8 shows solution feasibility for the iterative a posteriori procedure (Algorithm 2). We use confidence values between 0.55 and 0.999, since smaller confidences can often not be achieved using the iterative approach (the smallest achievable confidence is the feasibility of the nominal solution, i.e., \(\sim \,50\%\)). The a posteriori approach is clearly less conservative than the a priori approach, however, this comes at the cost of additional computational expense and also potential bound violations when the warped GP does not model the underlying distribution perfectly. The a posteriori approach could therefore be a viable less conservative alternative in relatively low noise scenarios or when more training data is available.
Fraction of feasible solutions versus confidence \(1 - \alpha \) for the iterative a posteriori procedure (Algorithm 2). If the noise is small, feasibility generally tracks the expected confidence (dotted line) well. For larger noise, deviations can occur due to mismatch between the warped GP model and the true data generating distribution
4.1.4 Comparison
Figures 9 and 10 compare the performance of the chance constraint reformulation using the standard GP, the Wolfe duality based robust approximation of the warped GP, and the a-posteriori approach. In addition to the non-uniform Gaussian distribution, we also generate training data by sampling from a Gaussian distribution and warping the samples through a square root function. Figures 9 and 10 show results for \(T = 3\) only, but the results for other uncertainty set dimensions follow the same patterns.
Percentage of \(\alpha \)’s for which chance constraint is violated for non-uniform Gaussian data and Gaussian data warped through a square root function. Results are shown for the standard GP chance constraint approach (Standard), the warped GP robust approximation (Wolfe), and the a-posteriori approach (posteriori). For an ideal approximation of the chance-constraint Eq. 23b, the percentage of \(\alpha \)’s would always be 100%. All results are for the production planning case study with \(T = 3\)
Violation of the chance constraint (when it is violated), averaged of different values of \(\alpha \), for non-uniform Gaussian data and Gaussian data warped through a square root function. Results are shown for the standard GP chance constraint approach (Standard), the warped GP robust approximation (Wolfe), and the a-posteriori approach (Posteriori). All results are for the production planning case study with \(T = 3\). Some lines do not start at \(\sigma _{\text {noise}}= 0\) because for small noise values all instances are feasible and the average violation doesn’t exist
Figure 9 shows the percentage of 30 solutions with different values of \(\alpha \) for which the chance constraint is feasible. To determine if the chance constraint is feasible for a given solution we draw 10,000 samples from the true data-generating distribution, calculate the percentage of samples for which the constraint is satisfied, and compare it to the intended feasibility of the chance constraint \(1-\alpha \). I.e., Fig. 9 shows the percentage of instances for which the probability of constraint violation is actually smaller than \(\alpha \). Ideally, this percentage should always be 100%. The standard GP chance constraint reformulation comes fairly close to 100% for the non-uniform Gaussian data with small noise, but does considerably worse for the square root warped data and for larger noise in general. The robust approximation leads to the highest percentage of feasible solutions for both data generating distributions. Solutions also remain largely feasible even as the noise in the data becomes very large. In safety-critical applications with non-Gaussian noise, the proposed approach is therefore clearly beneficial. The proposed a-posteriori strategy achieves high rates of feasibility when the noise in the data is small, but deteriorates quickly as noise increases. It may therefore be beneficial in applications with relatively low noise and where the robust approximation leads to overly conservative solutions.
Figure 10 shows the average violation of the chance constraint in percentage points, i.e., the average absolute difference between the actual feasibility of the solution and the intended feasibility \(1-\alpha \) is shown. Only instances for which the chance constraint is indeed violated are included in the average, so Figs. 9 and 10 show complementary aspects of the competing approaches. Figure 10 shows that, even when the chance constraint is violated, the robust approximation leads to smaller violations than the standard GP chance constraints approach, again motivating the use of our proposed approach in safety-critical applications.
4.2 Drill scheduling
For the drill scheduling case study, we consider two different geologies with 2 and 6 geological segments. We consider a range of target depths and confidence values. Figure 11 shows the drilling, maintenance, and total cost for a target depth of 2200 m as a function of the confidence parameter \(1-\alpha \). In the deterministic case (\(1-\alpha = 0.5\)), the optimal strategy is to not do maintenance at all and drill as fast as possible. As we increase \(1-\alpha \) to obtain more robust solutions, we eventually reach a point where the average rate of penetration is slightly lower in order to reduce degradation and guarantee that the well can be completed without a motor failure. For the 2-segment geology the increased cost of drilling outweighs the zero maintenance cost at around \(1-\alpha = 0.92\). After this point the optimal strategy is to do maintenance once.
Results are shown for both the no-degradation and boundary heuristics as well as total enumeration. For this instance, the boundary heuristic leads to the same solution as the globally optimal enumeration strategy. The no-degradation heuristic, on the other hand, leads to suboptimal solutions when the optimal maintenance number is lower than the upper bound \(\lfloor R_n\rfloor \).
Cost of drilling to a depth of 2200 m through a geologies with 2 and 6 segments for different values of confidence parameter \(\alpha \). Results are shown for three different integer strategies. The boundary heuristic gives the same results as total enumeration, while the no-degradation heuristic gives suboptimal solutions
Figure 12 shows the same cost components as Fig. 11 as a function of the target depth \({x_{n_d}}\). Results are shown for three different values of \(1-\alpha \) (0.5, 0.75, and 0.99). A larger confidence always leads to a higher cost, as would be expected, but the difference between the deterministic solution and a \(99\%\)—confidence robust solution can be larger or small, depending on the target depth, e.g., for a target depth of \({x_{n_d}}=3000\text {m}\) hedging against uncertainty does not lead to significant cost increases.
Finally, Fig. 13 shows the total solution time for the three integer strategies for the instance with 6 geological segments as a function of confidence parameter \(1 - \alpha \). While the no-degradation heuristic often leads to suboptimal solutions, as seen above, it is computationally very cheap. The boundary heuristic comprises a good compromise: it frequently finds the global optimum while being much cheaper computationally. Especially for instances with many geological segments and maintenance events, where the combinatorial complexity of the enumeration strategy becomes prohibitive, it may therefore be a good alternative.
5 Conclusion
Our approach reformulates uncertain black-box constraints, modeled by warped Gaussian processes, into deterministic constraints guaranteed to hold with a given confidence. We achieve this deterministic reformulation of chance constraints by constructing confidence ellipsoids and utilizing Wolfe duality. We show that this approach allows the solution conservatism to be controlled by a sensible confidence probability choice. This could be especially useful in safety-critical settings where constraint violations should be avoided.
References
Ahmed, S.: Convex relaxations of chance constrained optimization problems. Optim. Lett. 8(1), 1–12 (2014)
Ba, S., Pushkarev, M., Kolyshkin, A., Song, L., Yin, L.L.: Positive displacement motor modeling: skyrocketing the way we design, select, and operate mud motors. In: Abu Dhabi International Petroleum Exhibition and Conference, Dd. Society of Petroleum Engineers (2016)
Bard, J.F.: Practical Bilevel Optimization, Nonconvex Optimization and Its Applications, vol. 30. Springer, Boston (1998)
Baxandall, P.R., Liebeck, H.: Vector Calculus, Dover Dover Publications, Mineola (2008)
Başçiftci, B., Ahmed, S., Gebraeel, N., Yildirim, M.: Integrated generator maintenance and operations scheduling under uncertain failure times. IEEE Trans. Power Syst. 33(6), 6755–6765 (2018)
Becker, S., Kawas, B., Petrik, M.: Robust partially-compressed least-squares. In: AAAI (2017)
Beland, J.J., Nair, P.B.: Bayesian optimization under uncertainty. In: NIPS (2017)
Ben-Tal, A., den Hertog, D., Vial, J.P.: Deriving robust counterparts of nonlinear uncertain inequalities. Math. Program. 149(1–2), 265–299 (2014)
Ben-Tal, A., Nemirovski, A.: Robust solutions of Linear Programming problems contaminated with uncertain data. Math. Program. 88(3), 411–424 (2000)
Bertsimas, D., Brown, D.B., Caramanis, C.: Theory and applications of robust optimization. SIAM Rev. 53(3), 464–501 (2011)
Bertsimas, D., Nohadani, O., Teo, K.M.: Nonconvex robust optimization for problems with constraints. INFORMS J. Comput. 22(1), 44–58 (2010)
Bertsimas, D., Nohadani, O., Teo, K.M.: Robust optimization for unconstrained simulation-based problems. Oper. Res. 58(1), 161–178 (2010)
Bertsimas, D., Sim, M.: The price of robustness. Oper. Res. 52(1), 35–53 (2004)
Beykal, B., Boukouvala, F., Floudas, C.A., Sorek, N., Zalavadia, H., Gildin, E.: Global optimization of grey-box computational systems using surrogate functions and application to highly constrained oil-field operations. Comput. Chem. Eng. 114, 99–110 (2018)
Bhosekar, A., Ierapetritou, M.: Advances in surrogate based modeling, feasibility analysis, and optimization: a review. Comput. Chem. Eng. 108, 250–267 (2018)
Birge, J.R., Louveaux, F.: Introduction to Stochastic Programming. Springer, Berlin (2011)
Bogunovic, I., Scarlett, J., Jegelka, S., Cevher, V.: Adversarially robust optimization with gaussian processes. In: NIPS (2018)
Boukouvala, F., Floudas, C.A.: ARGONAUT: algorithms for global optimization of constrained grey-box computational problems. Optim. Lett. 11(5), 895–913 (2017)
Boukouvala, F., Misener, R., Floudas, C.A.: Global optimization advances in mixed-integer nonlinear programming, MINLP, and constrained derivative-free optimization. CDFO. Eur. J. Oper. Res. 252(3), 701–727 (2016)
Charnes, A., Cooper, W.W.: Deterministic equivalents for optimizing and satisficing under chance constraints. Oper. Res. 11(1), 18–39 (1963)
Deisenroth, M.P., Fox, D., Rasmussen, C.E.: Gaussian processes for data-efficient learning in robotics and control. IEEE Trans. Pattern Anal. Mach. Intell. 37(2), 408–423 (2015)
Detournay, E., Richard, T., Shepherd, M.: Drilling response of drag bits: theory and experiment. Int. J. Rock Mech. Min. Sci. 45(8), 1347–1360 (2008)
Dolatnia, N., Fern, A., Fern, X.: Bayesian optimization with resource constraints and production. In: Twenty-Sixth International Conference on Automated Planning and Scheduling (ICAPS), pp. 115–123 (2016)
Floudas, C.A., Lin, X.: Continuous-time versus discrete-time approaches for scheduling of chemical processes: a review. Comput. Chem. Eng. 28(11), 2109–2129 (2004)
Gardner, J.R., Kusner, M.J., Xu, Z., Weinberger, K.Q., Cunningham, J.P.: Bayesian optimization with inequality constraints. In: ICML (2014)
Gelbart, M.A., Snoek, J., Adams, R.P.: Bayesian Optimization with Unknown Constraints. arXiv e-prints arXiv:1403.5607 (2014)
Gorissen, B.L., Yanikoǧlu, I., den Hertog, D.: A practical guide to robust optimization. Omega (UK) 53, 124–137 (2015)
GPy.: GPy: a Gaussian process framework in python. http://github.com/SheffieldML/GPy (2012)
Griffiths, R.R., Hernández-Lobato, J.M.: Constrained Bayesian optimization for automatic chemical design. In: NIPS (2018)
Grossmann, I.E.: Pyrolysis of heavy oil in the presence of supercritical water: the reaction kinetics in different phases. AIChE J. 61(3), 857–866 (2015)
Hart, W.E., Laird, C.D., Watson, J.P., Woodruff, D.L., Hackebeil, G.A., Nicholson, B.L., Siirola, J.D.: Pyomo–Optimization Modeling in Python, vol. 67, 2nd edn, Springer (2017)
Hart, W.E., Watson, J.P., Woodruff, D.L.: Pyomo: modeling and solving mathematical programs in Python. Math. Progam. Comput. 3(3), 219–260 (2011)
Hüllen, G., Zhai, J., Kim, S.H., Sinha, A., Realff, M.J., Boukouvala, F.: Managing uncertainty in data-driven simulation-based optimization. Comput. Chem. Eng. 136, 106519 (2019)
Jones, D.R., Perttunen, C.D., Stuckman, B.E., Dixon, L.C.W.: Lipschitzian optimization without the lipschitz constant. J. Optim. Theory Appl. 79, 157 (1993)
Kou, P., Gao, F., Guan, X.: Sparse online warped Gaussian process for wind power probabilistic forecasting. Appl. Energy 108, 410–428 (2013)
Li, Z., Li, Z.: Optimal robust optimization approximation for chance constrained optimization problem. Comput. Chem. Eng. 74, 89–99 (2015)
Liu, S., Yue, Y., Krishnan, R.: Adaptive collective routing using Gaussian process dynamic congestion models. In: Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD ’13, ACM Press, p. 704 (2013)
Luedtke, J., Ahmed, S.: A sample approximation approach for optimization with probabilistic constraints. SIAM J. Optim. 19(2), 674–699 (2008)
Mateo-Sanchis, A., Muñoz-Marí, J., Pérez-Suay, A., Camps-Valls, G.: Warped Gaussian processes in remote sensing parameter estimation and causal inference. IEEE Geosci. Remote Sens. Lett. 15(11), 1647–1651 (2018)
Mistry, M., Letsios, D., Krennrich, G., Lee, R.M., Misener, R.: Mixed-integer convex nonlinear optimization with gradient-boosted trees embedded (2018). arxiv:1803.00952
Mitsos, A., Lemonidis, P., Barton, P.I.: Global solution of bilevel programs with a nonconvex inner program. J. Global Optim. 42(4), 475–513 (2008)
Mockus, J.: On Bayesian methods for seeking the extremum. In: Proceedings of the IFIP Technical Conference, Springer, London, pp. 400–404 (1974)
Müller, J., Shoemaker, C.A., Piché, R.: SO-MI: a surrogate model algorithm for computationally expensive nonlinear mixed-integer black-box global optimization problems. Comput. Oper. Res. 40(5), 1383–1400 (2013)
Munos, R.: Optimistic Optimization of a Deterministic Function Without the Knowledge of Its Smoothness, pp. 783–791 (2011)
Nemirovski, A.: On safe tractable approximations of chance constraints. Eur. J. Oper. Res. 219(3), 707–718 (2012)
Nemirovski, A., Shapiro, A.: Convex approximations of chance constrained programs. SIAM J. Optim. 17(4), 959–996 (2006)
Nemirovski, A., Shapiro, A.: Scenario approximations of chance constraints. In: Calafiore, G., Dabbene, F. (eds.), Probabilistic and Randomized Methods for Design Under Uncertainty, vol. 2, Springer, pp. 3–47 (2006)
Pagnoncelli, B.K., Ahmed, S., Shapiro, A.: Sample average approximation method for chance constrained programming: theory and applications. J. Optim. Theory Appl. 142(2), 399–416 (2009)
Picheny, V., Gramacy, R.B., Wild, S., Le Digabel, S.: Bayesian optimization under mixed constraints with a slack-variable augmented Lagrangian. In: NIPS (2016)
Pintér, J.: Deterministic approximations of probability inequalities. ZOR Z. Oper. Res. Methods Models Oper. Res. 33(4), 219–239 (1989)
Rasmussen, C.E., Williams, C.K.I.: Gaussian Processes for Machine Learning. MIT Press, Cambridge (2006)
Regis, R.G., Shoemaker, C.A.: Constrained global optimization of expensive black box functions using radial basis functions. J. Global Optim. 31(1), 153–171 (2005)
Sahinidis, N.V.: Optimization under uncertainty: State-of-the-art and opportunities. Comput. Chem. Eng. 28(6–7), 971–983 (2004)
Schilling, G., Pantelides, C.C.: A simple continuous-time process scheduling formulation and a novel solution algorithm. Comput. Chem. Eng. 20(96), 1221–1226 (1996)
Shahriari, B., Swersky, K., Wang, Z., Adams, R.P., De Freitas, N.: Taking the human out of the loop: a review of Bayesian optimization. Proc. IEEE 104(1), 148–175 (2016)
Snelson, E., Rasmussen, C.E., Ghahramani, Z.: Warped Gaussian processes. In: NIPS (2003)
Snoek, J., Larochelle, H., Adams, R.P.: Practical Bayesian optimization of machine learning algorithms. In: NIPS, pp. 2951–2959 (2012)
Soyster, A.L.: Technical note—convex programming with set-inclusive constraints and applications to inexact linear programming. Oper. Res. 21(5), 1154–1157 (1973)
Ulmasov, D., Baroukh, C., Chachuat, B., Deisenroth, M.P., Misener, R.: Bayesian optimization with dimension scheduling: application to biological systems. In: Kravanja, Z., Bogataj, M. (eds.), 26th European Symposium on Computer Aided Process Engineering, vol. 38, Elsevier, pp. 1051–1056 (2016)
Varakantham, P., Fu, N., Lau, H.C.: A proactive sampling approach to project scheduling under uncertainty. In: AAAI (2016)
Wächter, A., Biegler, L.T.: On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 106(1), 25–57 (2006)
Wiebe, J.: ROGP: Robust GPs in Pyomo. https://github.com/johwiebe/rogp (2020)
Wiebe, J., Cecílio, I., Misener, R.: Data-driven optimization of processes with degrading equipment. Ind. Eng. Chem. Res. 57(50), 17177–17191 (2018)
Williams, C.K.I., Rasmussen, C.E.: Gaussian processes for regression and classification. In: NIPS, pp. 514–520 (2008)
Xie, W., Ahmed, S.: Distributionally robust chance constrained optimal power flow with renewables: a conic reformulation. IEEE Trans. Power Syst. 33(2), 1860–1867 (2018)
Acknowledgements
This work was funded by the Engineering & Physical Sciences Research Council (EPSRC) Center for Doctoral Training in High Performance Embedded and Distributed Systems (EP/L016796/1), an EPSRC/Schlumberger CASE studentship to J.W. (EP/R511961/1, voucher 17000145), and an EPSRC Research Fellowship to R.M. (EP/P016871/1).
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Table of notation
See Table 2.
B Connection to uncertain functions
Consider the following robust optimization problem:
Instead of uncertain parameters, Problem (26) considers an uncertainty set \(\mathcal {U}^g\) over uncertain functions \(\tilde{g}(\cdot )\). We are interested in defining \(\mathcal {U}^g\) in a way that it contains “likely” realizations of the GP.
Recall that for any finite set of points \({\varvec{z}}_1, \ldots , {\varvec{z}}_l\), \(l \in {\mathbb {N}}\), \(G_{{\varvec{z}}_1, \ldots , {\varvec{z}}_l} = [G({\varvec{z}}_1), \ldots , G({\varvec{z}}_l)]^\intercal \) is a multivariate Gaussian with mean \(\varvec{\mu }({\varvec{z}}_1, \ldots , {\varvec{z}}_l)\) and covariance matrix \(\varSigma ({\varvec{z}}_1, \ldots , {\varvec{z}}_l)\). For any such \(G_{{\varvec{z}}_1, \ldots , {\varvec{z}}_l}\), we can construct a confidence ellipsoid \(\mathcal {E}^\alpha ({\varvec{z}}_1, \ldots , {\varvec{z}}_l)\) containing the true values \([g({\varvec{z}}_1), \ldots , g({\varvec{z}}_l)]^\intercal \) with probability \(1 - \alpha \):
where \(F_l^{1-\alpha } = F_l(1-\alpha )\) is the cumulative distribution function of the \(\chi ^2\) distribution with l degrees of freedom. We then construct a set \(\mathcal {U}^g\) over functions \(\tilde{g}(\cdot )\) for which \([\tilde{g}({\varvec{z}}_1), \ldots , \tilde{g}({\varvec{z}}_l)]\) lies in the corresponding \(\alpha \)-confidence ellipsoid \(\mathcal {E}^\alpha ({\varvec{z}}_1, \ldots , {\varvec{z}}_l)_l\) for any \(l \in {\mathbb {N}}\) and \({\varvec{z}}_1, \ldots , {\varvec{z}}_l\) with \({\varvec{z}}_i \in {\mathbb {R}}^k\):
Replacing \(\mathcal {U}^g\) with \(\mathcal {U}^{\mathcal {E}}\) transforms Problem (26) into a robust optimization problem with an uncertainty set over functions defined by an infinite number of confidence ellipsoids which can have arbitrarily many dimensions. This set is not semialgebraic and it is not clear how it could practically be used in optimization. In practice, however, we are only interested in evaluating the GP at a finite number of points. Here, the number of evaluation points is the number of times |S| that the GP occurs in the optimization problem. Consider the following robust optimization problem:
Theorem 3
A vector \(\varvec{x}^*\) which is a feasible solution to Problem (27) is also a feasible solution to Problem (26).
Proof
Assume \(\varvec{x}^*\) is a solution to Problem (27) but not to Problem (26). Then \(\exists \hat{g}\in \mathcal {U}^g\) s.t. \(\sum \nolimits _{i\in S} \hat{g}({\varvec{z}}_i^*)x_i^* > 0\). The definition of \(\mathcal {U}^g\) implies that \([\hat{g}({\varvec{z}}^*_i) : i \in S]^\intercal \in \mathcal {E}^\alpha ({\varvec{z}}^*_i: i \in S)\). Choosing \(\hat{{\varvec{y}}} = [\hat{g}({\varvec{z}}^*_i): i \in S]^\intercal \), it follows that \(\sum \nolimits _{i \in S} \hat{y}_i x^*_i = \sum \nolimits _{i \in S} \hat{g}({\varvec{z}}^*_i)x^*_i > 0\), meaning that \(\{\varvec{x}^*, \hat{{\varvec{y}}}\}\) is not feasible in Problem (27). But \(\hat{{\varvec{y}}} \in \mathcal {E}^\alpha ({\varvec{z}}^*_i : i \in [n])\), which is a contradiction. \(\square \)
Figure (14) shows that the converse of Theorem (3) is not necessarily true. Because all confidence ellipsoids are symmetric and centered at the mean of the distribution, any lower dimensional ellipsoid \(\mathcal {E}^\alpha _l = \mathcal {E}^\alpha ({\varvec{z}}_1, \ldots , {\varvec{z}}_l), l < n\) is a strict subset of the projection of \(\mathcal {E}^\alpha _n = \mathcal {E}^\alpha ({\varvec{z}})\) onto the l-dimensional space (otherwise it would have to contain a larger probability mass). Problem (27) therefore conservatively approximates Problem (26). Furthermore, the \(\alpha \)-confidence ellipsoid \(\mathcal {E}^\alpha ({\varvec{z}})\) implies that a solution to Problem (27) is a feasible solution to the black-box constrained problem with a probability of at least \(1 - \alpha \) (see Theorem 1).
C Globally optimizing non-convex inner maximization problems
Lemma 2
Let \({\varvec{y}^*}\) be the solution of Problem 11, then \({\varvec{y}^*}\) is on the boundary of \(\mathcal {U}\), i.e., \({\varvec{y}^*}\in \partial \mathcal {U}\).
Proof
For the sake of contradiction assume \({\varvec{y}^*}\in int(\mathcal {U})\), then \(\exists \; \epsilon > 0\) s.t. \({\varvec{y}}_0 \in \mathcal {U}\; \forall {\varvec{y}}_0 \in \{{\varvec{y}}_0 \; | \; \Vert {\varvec{y}^*}- {\varvec{y}}_0\Vert < \epsilon \}\). Let:
then:
and therefore \(\varvec{\hat{z}}\in \mathcal {U}\), but:
which is a contradiction. \(\square \)
Lemma 3
The bounding box of an ellipsoid \({\left( \varvec{x}-\varvec{\mu }\right) }^\intercal \varSigma ^{-1}{\left( \varvec{x}-\varvec{\mu }\right) } \le r^2\) is given by the extreme points \(x_i = {\mu _i }\pm r \sigma _{ii}\).
Proof
Consider the optimization problem:
It’s stationarity condition is:
Pre-multiplying by \((\varvec{x}- \varvec{\mu })^\intercal \) and substituting primal feasibility leads to the expression:
Substituting this back into the stationarity condition and rearranging gives:
which, substituted into the primal constraint leads to the desired results:
\(\square \)
D Drill scheduling model
In order to connect the penetration rate V and degradation rate r to the drilling parameters, weight-on-but W and rotational speed \(\dot{N}\), we require two models:
-
A bit-rock interaction model [22] connecting W and \(\dot{N}\) with V and differential pressure across the mud motor \({\varDelta p}\)
-
A mud motor degradation model [2] connecting the degradation rate r with the differential pressure \(\varDelta p\).
1.1 D.1 Detournay’s bit-rock interaction model
To model the connection between W, \(\dot{N}\), V, and \({\varDelta p}\), we combine the bit-rock interaction model by Detournay et al. [22] with the PDM’s powercurve. There are three relevant rotational speeds in the drilling process: The drill-string speed \(\dot{N}_{top}\), the PDM speed (relative to the drill string) \(\dot{N}_{PDM}\), and the drill-bit speed \(\dot{N}_{bit}\):
Based on Detournay et al. [22], the following drilling response model can be formulated relating \(N_{bit}\) with the weight-on-bit W and the rate of penetration V:



where d is the depth of cut per revolution, w is a scaled weight-on-bit, and a, \(\rho \), \(S^*\), \(w^*\), \(\xi \epsilon \), \(N^{max}\), and \(W^{max}\) are rock and equipment parameters.
The relationship between torque T and weight-on-bit W is given by:

For the bit parameters \(a = 100.4\) and \(\rho = 0.0\) was used. Rock parameters are available for Lower Jurassic shale and Sandstone in the open literature [22]:
Parameter | Lower Jurassic shale | Sandstone |
|---|---|---|
\(S^*\) [MPa] | 278 | 315 |
\(w^*\) [N/mm] | 199 | 59 |
\(\xi \epsilon \) [MPa] | 125 | 50 |
\(\mu \gamma '\) [–] | 0.48 | 0.93 |
\((1-\beta )w_{f*}\) [N/mm] | 157 | 33 |
\(\xi \) [–] | 0.98 | 0.65 |
Using the PDM’s power curve (Fig. 15), the bit rotational speed \(\dot{N}_\text {bit}\) can be determined as a function of \(\dot{N}\), T, and \({\varDelta p}\). Figure 15 shows the relationship between T, \(\dot{N}_{PDM}\), the differential pressure over the PDM \(\varDelta p\), and the flow rate through the PDM \(\dot{Q}\). Since torque T is specified through W (Eq. 35), \(\varDelta p\) can be determined from the power curve (Fig. 15). If additionally the flow \(\dot{Q}(t)\) is given, \(\dot{N}_{PDM}\) is also fully specified.
Example of a PDM power curve [2]
Putting this together, we obtain the following model relating V to W and \(\dot{N}\):
Assuming that the flow rate \(\dot{Q}(t)\) is treated as a parameter, the only decision variables are W(t), and \(\dot{N}_{top}(t)\). For the purpose of this work we model the above power curves using quadratic equations. Notice that the variables w, t, d, and \(\dot{N}_\text {PDM}\) could easily be eliminated, resulting in a more compact albeit less intuitive/physically meaningful formulation.
1.2 D.2 Mud motor degradation model
For the mud motor degradation characteristics we use data obtained by Ba et al. [2], determined through a combination of simulation and experiments, shown in Fig. 16 [2].
Maximum lifetime of a PDM as a function of differential \(\varDelta p\) (for a given PDM geometry and elastomer, mud, flow, and temperature) [2]
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wiebe, J., Cecílio, I., Dunlop, J. et al. A robust approach to warped Gaussian process-constrained optimization. Math. Program. 196, 805–839 (2022). https://doi.org/10.1007/s10107-021-01762-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-021-01762-8