Introduction

As a result of the worldwide energy demand and its corresponding environmental problems, renewable energy sources (RESs) are attracting more and more attention (Kong et al. 2020). The development of alternative and renewable energy sources has become an important factor in satisfying the world’s rising energy demand (Abdalrahman et al. 2017). Many countries have already embraced renewable energy technologies to satisfy their electrical demands with clean and inexhaustible energy. In certain locations, renewable energy resources fulfill 100% of the typical annual demand (Chong et al. 2017). Wind energy capacity was expanding quickly since 1996 to be the fastest growing RES worldwide. By the end of 2015, around 433 GW of wind energy was generated (Chong et al. 2017) due to its availability, economic benefits, and lack of pollution (Kong et al. 2020). In addition, it is considered a zero-emissions energy source and is gaining worldwide importance in meeting the global need for clean energy while averting global warming (Liu et al. 2015). It can also offer electricity in remote regions when other sources of energy are unavailable. For example, India, where more than 33% of communities presently lack access to electricity (Chawla et al. 2014). Wind power prediction is critical for the effective integration of wind farms into the power grid (Neshat et al. 2021), where electric vehicles are now invading the utility grid in search of a smooth charging operation. In general, the output power of the wind turbine increases with increasing the turbine rotational speed until reaching a maximum power point for each wind speed; to obtain the maximum efficacy of the system, it is desired to charge the battery using this maximum power points.

There are two types of wind turbines: horizontal axis wind turbines (HAWT) and vertical axis wind turbines (VAWT). HAWTs generate the bulk of the electricity (Kumar et al. 2018) due to their higher efficiency compared to VAWTs. Upscaling, maintenance, and installation of VAWT are nevertheless less challenging than those of HAWT (Abdalrahman et al. 2017; Bouzaher et al. 2017; V. Kumar et al. 2018; Rezaeiha et al. 2017; Wang et al. 2016). Additionally, VAWT offers reduced maintenance expenses (Rezaeiha et al. 2017; Sun et al., 2020a, b; Wang et al. 2016), as well as lower installation costs (Liu et al. 2015). The production cost of VAWT is often low due to the simplicity of the blade design (Abdalrahman et al. 2017; Bouzaher et al. 2017; Rezaeiha et al., 2017). Furthermore, locating the generator, gearbox, and other heavy components on the ground level increases the VAWT structural stability (V. Kumar et al. 2018). Furthermore, VAWTs can withstand higher wind speeds (V. Kumar et al. 2018) and have a high level of environmental flexibility (YAMADA et al. 2012). They are unaffected by wind direction changes (Ahmadi-Baloutaki et al. 2015; J. Sun et al. 2020a, b; YAMADA et al. 2012). Since they are omnidirectional, there is no need for a yaw mechanism (Abdalrahman et al. 2017; Liu et al. 2015; Ma et al. 2019; Rezaeiha et al. 2017; Wang et al. 2016). When compared to HAWT, VAWT has less oscillation, a higher high start-up torque, and is easier to integrate with high-rise buildings (Liu et al. 2015). It is also more effectively incorporated into architectural designs (Ma et al. 2019). When compared to HAWT, VAWT emits less noise (Ahmadi-Baloutaki et al. 2015; Rezaeiha et al. 2017; Rezaeiha et al. 2019; J. Sun et al. 2020a, b; Wang et al. 2016; YAMADA et al. 2012) and is more favorable to birds and bats (Wang et al. 2016).

To improve the wind turbine’s aerodynamic adaptability capabilities and achieve optimal functioning in response to quick fluctuations in the incoming wind, Saenz-Aguirre applied the active Gurney flap (AGF) flow management approach. The aerodynamic data computed by computational fluid dynamics (CFD) are stored in an artificial neural network (ANN) to make managing the information utilized by the AGF approach easier. To investigate the aerodynamic behavior of the WTBs with the suggested AGF method and compute the related operation of the wind turbine, boundary element method (BEM)-based calculations have been implemented. For the steady BEM computations, real wind speed statistics from a meteorological station in Salt Lake City, Utah, were used (Saenz-Aguirre et al. 2019). Based on the full variable-speed wind turbine (VSWT) model, encompassing the dynamics of the tower and the gearbox in (Kong et al. 2020), a nonlinear Economic model-predictive control (EMPC) technique including power maximization and mechanical load reduction is suggested. Three sets of simulations have been utilized to validate the proposed nonlinear EMPC strategy’s efficacy, dependability, and practicability.

Several studies have used wind energy in alleviating the power stress on the utility grid, especially due to the rapid adoption of electric vehicles (EVs) in the global vehicle electrification market (Noman et al. 2020). The EVs are expanding exponentially in the automobile industry market to reduce greenhouse gas emissions, and air pollution, and replace conventional cars (Ahmad et al. 2018). Integration of RESs (and especially wind energy) into the utility grid could be a difficult task because of the intermittency and inconsistency with energy usage, in addition, the grid could suffer from an unpredictable supply of electricity (Jin et al. 2014; Mwasilu et al. 2014). In this paper, the feasibility of charging an EV is proposed based on a robust experimental model for small vertical axis wind turbine VAWT based on the ANN algorithm (unlike previous studies that implemented simulated energy system analysis) (Chellaswamy et al., 2018; Kou et al. 2015). The ANN algorithm has a very good performance under varying wind conditions and very good convergence speed with respect to the other conventional and advanced maximum power point tracking algorithms proposed in (D. Kumar & Chatterjee 2016). ANN has been used in a lot of wind energy systems such as fault detection and diagnosis (FDD), design optimization, optimal control, and power prediction model optimization of yaw angles which are used to minimize wake impact on wind turbines (Marugán et al. 2018; H. Sun et al. 2020a, b). In this manuscript, ANN has been used for the first time in the framework of EV charging. There are many charging protocols to fast charge the EVs such as the constant current constant voltage (CC-CV), multistage charging current (MSCC), pulsating charging current (PCS), and changing the material aspects protocols (Makeen et al. 2022a). The charging method that has been used in this paper is the CC-CV protocol since it is easy to implement, has simple requirements, and avoids overcharging due to the constant voltage mode (Chu et al. 2017; Makeen et al. 2022a). The CC-CV depends on charging the battery by a constant rated charging current until the voltage reaches the cut-off value and then the voltage is held constant while the current decays to the minimum value (Makeen et al. 2020; Makeen et al. 2022a). In (Makeen, Memon, Elkasrawy, Abdullatif, & Ghali, 2021), the EV station has been supported by a PV system to ensure CC-CV and MSCC fast charging protocols. The goal of (Messaoud et al. 2021)’s research is to come up with a practical way of getting the necessary energy from other sources and feeding it to the relevant pieces. The intelligent tool serving as the fuzzy logic controller is the foundation of the solution. Furthermore, (Kraiem et al. 2022) used fuzzy logic, neural network, relay and PI controllers for providing the appropriate portions with the necessary power from wind energy and PV system to charge a battery pack. The fuzzy logic and neural network have a good impact on the given duty cycle and reached the maximum value with respect to the PID controller and relay controller. In (Makeen et al. 2022b), an experimental small-scale EV controller has been implemented while implementing the PID, fuzzy logic (FL) and neural network predictive (NNPC) controllers. The NNPC ensured a high-speed response combined with a very low voltage and current ripples concerning the PID and FL.

Thus, the main contributions of this paper could be summarized as follows:

  • Real wind turbine measurements have been obtained experimentally based on a small vertical axis wind turbine VAWT, and an extensive data analysis is performed.

  • An ANN model has been implemented to estimate the maximum generated power from the wind turbine using the experiment’s measurements regardless of the stochastic wind speed.

  • A novel framework that includes the wind turbine aerodynamics performance, wind turbine transit behavior, battery, and battery charging controller has been presented. This framework is very helpful to predict the charging performance of an actual electric car when the wind turbine is in a certain location with a known wind speed pattern.

  • The generated power is utilized to feed the battery charger which uses the CC-CV charging protocol. The charger is supported by the utility grid due to the intermittency of wind energy and is also used as a backup scenario for any shortage in the required power.

Experimental setup

A test rig has been designed, built, and deployed at the British University in Egypt (BUE) in a modified outlet portion of a low-speed wind tunnel, as illustrated in Fig. 1. The test rig consists of a tower for wind turbine installation, a torque sensor, a brake system, and a pulley. All of these items are mounted within the tower, as illustrated in Fig. 1. To measure the turbine torque and rotational speed at a sample rate of 100 samples/sec, the Datum M425 rotary torque sensor with a complete range of 10 Nm torque has been used. A mechanical cycling disk brakes system was also used to vary the loading on the turbine in order to acquire the whole performance curve of the turbine at variable wind speed. A high inertia large diameter pulley has also been used to decrease turbine rotational variation and enhance the generator revolution per minute (RPM).

Fig. 1
figure 1

Wind turbine experimental setup

Full size image

The basic turbine is made up of six Artelon NACA 0018 airfoils that were CNC machined, with a chord length of 200 mm, and a height of 500 mm. The wind turbine performance has been measured at wind speeds ranging from 5 to 13 m/s, with the wind turbine free to rotate until the steady state RPM is reached. Then, the torque and the corresponding rpm are measured for each imposed load on the turbine shaft. For each measurement, the average value of torque and RPM have been calculated and used to calculate the output turbine power. The measurements for each wind speed were repeated three times.

Experiment results and artificial neural network modelling

The obtained measurement data have been used for building a wind turbine model for predicting the output power based on an artificial neural network (ANN) algorithm that handles the nonlinearity and chaotic behavior of wind speed on a given wind turbine. The ANN proved its accuracy and efficiency with respect to the conventional and advanced modelling algorithms in (Makeen et al. 2022b). The torque, power, and the RPM of the wind turbine have been measured using a Datum M425 rotary torque sensor (10 N.m) based on discrete samples at variable wind speeds. The measurement system specifications are summarized in Table 1.

Table 1 Measurement system specifications
Full size table

The power curves were obtained for different wind speeds and different RPMs as expressed in Fig. 2. These data have been used to build the ANN algorithm, which will model the wind turbine performance and will be used to simulate the wind turbine in Simulink. The power produced by a wind turbine is a function of its RPM and torque. As the wind turbine's RPM increases, the torque decreases due to blade dynamic stall. Therefore, as the RPM increases, the reduction in torque is overcome, resulting in an increase in output power up till the peak power. At that point, the reduction in torque is too great to be counted by the rotational speed increase, leading to a decrease in output power.

Fig. 2
figure 2

Experiment output power

Full size image

The proposed ANN algorithm has been constructed and simulated by the MATLAB R2021a and trained throughout the experimental obtained data as shown in Fig. 2. The schematic diagram of the proposed ANN is consisting of three layers, namely the input layer, the hidden layer, and the output layer with two inputs (Wind speed V and Rotational speed rpm.), and wind turbine output power P, as shown in Fig. 3.

Fig. 3
figure 3

Wind turbine ANN model structure

Full size image

ANN has been trained by the Bayesian Regularization algorithm which is minimizing the squared error to generalize the quality network. About 70% of the experimental data have been used in the training phase except 30% that has been used in the validation of the proposed algorithm as shown in Fig. 4. First, an ANN with 10, 100 and 1000 neurons have been investigated, and the results have been compared with the experimental data. Figure 5 presents the actual and trained data for different neurons number at wind speed of 7 m/s. Furthermore, uncertainty analysis was conducted to determine the convergence in chosen the neurons’ numbers. The purpose of this check is to ensure that the result of the chosen neuron number is within the asymptotic range of convergence. It was decided to adopt a constant neuro-increasing ratio (r = 10). If the findings of the three neurons are reported as N1, N2, and N3, the relative error (\(\upvarepsilon\)) between them is defined in (Aboelezz et al. 2022) as

$$\varepsilon_{12} = \frac{N1 - N2}{{N1}},\;\varepsilon_{23} = \frac{N2 - N3}{{N2}}$$
(1)
Fig. 4
figure 4

Artificial neural network schematic diagram, training and testing performance

Full size image
Fig. 5
figure 5

Neurons number affect the model output

Full size image

Equation (2) specifies the order of solution convergence (SC) based on the three neurons’ numbers.

$$SC = \frac{{\ln \frac{N3 - N2}{{N2 - N1}}}}{\ln r}$$
(2)

The Neurons number conversion index (NCI) for two comparing neuron numbers is thus expressed by Eq. (3).

$$NCI = \frac{f\varepsilon }{{r^{SC} - 1}}$$
(3)

where \(\mathrm{f}\) is a safety factor (often 1.25 for three solutions) (Kundu 2020). If the solutions generate asymptotic convergence results, two GCI values calculated across three neurons’ numbers will be joined as shown in Eq. (4), and RR should equal 1 to indicate convergence.

$$RR = \frac{NCI23}{{NCI12*r^{SC} }}$$
(4)

The results of the neurons convergence check are summarized in Table 2. As all RR values are around 1, the 100 Neurons hidden layer was chosen for the rest of the work in the paper.

Table 2 The results of the neurons number convergence check
Full size table

In addition, the training trial number was investigated, and the results are presented in Fig. 6. The ANN was trained four times until the solution did not change significantly. Overfitting is a modeling error that occurs when a function is too closely aligned to a small set of data points. As a result, the model is only useful in reference to its initial data set and not in reference to any other data sets. To avoid overfitting, the errors in results from ANN modeling was evaluated for all power curves for all RPM range. Figure 6 a shows how the training affects the solution. Figure 6 b and c presents the comparison between the first and the fourth training of the ANN for two wind speeds of 8 m/s, and 13 m/s, respectively. The uncertainty at the maximum power was calculated as shown in Table 3 based on these results.

Fig. 6
figure 6

Model train number effect on the model output a training time effect on results, b comparing the results of the first and fourth train for a wind speed of 8 m/s, c comparing the results of the first and fourth train for a wind speed of 13 m/s, d comparing the results of the first and fourth train for a wind speed of 15 m/s

Full size image
Table 3 Maximum power and power error calculations for wind speeds of 8 m/s and 13 m/s
Full size table

Figure 6(d) presents the prediction of the turbine output power at a wind speed of 15 m/s which was not obtained from the experiment. As shown in the results, the fourth time-trained ANN gave more logical results when compared with the well know power curve of the wind turbine. Therefore, the fourth time-trained ANN was considered for the rest of the research.

According to the performance and validation of the proposed ANN algorithm, a prediction of all the wind speeds from 5 m/s to 13 m/s with an incremental change of 1 m/s has been investigated and obtained as shown in Fig. 7. The prediction of the proposed wind turbine output power is essential at all wind speeds in defining the characteristics of wind turbines and maximum power point tracking will be used to charge the battery of the electrical vehicle. The maximum power and the corresponding rpm are presented in Fig. 8. The rpm versus wind speed curve was used to obtain the relation between the maximum power corresponding to rpm and the wind speed with cubic curve fitting. The results were used to obtain Eq. (5), which will be used in the simulation later.

$${\text{RPM }} = { }0.0407{\text{V}}^{3} { } - { }0.5811{\text{V}}^{{2{ }}} + { }6.3633{\text{V }} + { }7.0378$$
(5)
Fig. 7
figure 7

A prediction of the wind turbine power at wind speed from 5 to 13 m/s

Full size image
Fig. 8
figure 8

ANN model output: (a) the maximum power for each wind speed; and (b) the corresponding rpm for maximum power for each wind speed

Full size image

Wind turbine dynamic response and system identification

Changing the wind speed approaching the wind speed will result in changing the rotational speed of the wind turbine. This change will take some time due to the inertia of the wind turbine. Therefore, an additional experiment was conducted to determine this relationship. The wind turbine was prevented from rotation, and for wind speeds of 6 m/s and 8 m/s, it was released from rest and free to rotate till the steady state rpm. This input–output relation was used in the MATLAB system identification toolbox to obtain the transfer function of the turbine's response at different wind speeds. The results are shown in Fig. 9, where the red curve is the measured data, and the blue curve is obtained from the transfer function. The transfer function obtained from the system identification is presented by Eq. (6), where s is the output variable from the Laplace transform of the time form for the system time response. This transfer function will be used with the Simulink model to simulate the transition response of the wind turbine.

$${\text{G}}\left( {\text{s}} \right) = \frac{{11.72{\text{s}} + 46.16}}{{{\text{s}}^{2} + 168.6{\text{s}} + 46.29}}$$
(6)
Fig. 9
figure 9

System identification output validation for wind speed (a) 6 m/s and (b) 8 m/s

Full size image

Hence, a random variation in wind speed was introduced to the wind turbine using SIMULINK and the response is presented in Fig. 10.

Fig. 10
figure 10

A random variation in wind turbine speed

Full size image

Simulink Modelling and EV Battery Charging

The predicted output power in this paper has been used to charge a real EV according to the datasheet specifications. The vehicle used is a 2014 BMW i3 with rated pack energy of 18.8 kWh, and a capacity of 60 Ah (Laboratory and A. V. T. A. 2022). The battery model understudy used in the Simulink model is based on the real datasheet specification of the manufacturer. Hence, the scale of the wind turbine used is scaled up to be in 10 kW. In this study, the wind speed signature characteristics at the British University in Egypt (BUE) have been utilized in the simulation. The location has latitude and longitude coordinates of 30.117849388288, 31.605975392471. A full day of the 2019 year (January 16, 2019) is simulated with the wind speed characterization and presented in Fig. 11 (NASA 2021).

Fig. 11
figure 11

The proposed wind speed system is under study for one day on January 16, 2019

Full size image

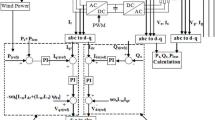
The MATLAB/Simulink model is presented in Fig. 12a and consists of three main stages: the performance prediction model of the wind turbine at various operating points, the CC-CV battery charger, and finally the electric vehicle battery understudy.

Fig. 12
figure 12figure 12

The proposed simulated model includes a the model by MATLAB/SIMULINK; b the CC-CV battery charger input and output parameters; c the battery charging parameters; d the input wind speed and output generated power from the ANN, and e the necessary power to charge the EV and the needed power from the utility grid

Full size image

Firstly, the wind speed signature on January 16, 2019, is fed to the artificial neural network (ANN) model. The ANN controller ensured a perfect speed response combined with very low ripples with respect to the conventional PID controller and Fuzzy logic controller in EV fast charging (Makeen et al. 2022b). Hence, the ANN is used to estimate and predict the maximum power point generated from the wind turbine at each wind speed based on deep learning. Then the values are fed to the CC-CV battery charger to charge the EV with a constant current of 60 A despite the intermittent nature of wind energy. The simulated stop time is set to be 100 s which represents the wind speed across the day as expressed in Fig. 10c.

The input and output current and voltage of the CC-CV battery charger, respectively, are presented in Fig. 12b. The output current is maintained at 60 A; however, the input variation is in power, current and voltage. The Simulink ensured very high accuracy in maintaining and obtaining a 60 A charging current. From the other perspective, the charging parameters of the battery are expressed in Fig. 12c where the charging current reached the desired value of 60 A in a settling time of 4.5 s and the state of charge (SOC) reached 22.75% in 100 s with an initial SOC of 20%.

The wind speed in (m/s) fed to the ANN and the output power generated from the model in (W) are presented in Fig. 12d. The utility grid is used to support the wind turbine generator due to the stochastic behavior of the wind energy where the required power from the battery charger and the required power from the grid are presented in Fig. 12e. It should be noted that the charging current is maintained at a constant value despite the change in the generated power from the wind turbine or the utility grid.

Conclusions

This paper proposes a novel approach for predicting the maximum power of a small vertical axis wind turbine (VAWT) based on the artificial neural network whatever the variation in the input wind speed. For a wind turbine with 1 m height and 1 diameter, the maximum power was about 15 watts for a wind speed of 13 m/s. The uncertainty analysis which has been developed and presented in this paper could successfully determine the sufficient number of neurons needed to predict the wind turbine performance. This method is recommended for similar research which will use ANN to predict wind turbine performance. The paper presented the transfer function of the turbine transient response from the experiment; as the wind turbine weight was 13 kg, scaling can be made to use the presented transfer function in similar research. The location of the British University in Egypt has been used to be the wind speed signature of our model. The generated power is considered as an input to the battery charger which is used to charge the EV using the CC-CV charging protocol. The utility grid is used as a backup scenario for the wind energy system to supply the EV because of the intermittency of wind energy. The CC-CV protocol has been used to charge the battery with a constant current of 60 A. The charging current reached the desired value of 60 A in a settling time of 4.5 s and the state of charge (SOC) reached 22.75% in 100 s with an initial SOC of 20%. The model ensured a sufficient estimation of the generated power from the wind turbine at any wind speed and maintained a constant charging current stage at the charging process. For future work, it will be necessary to add the battery and the controllers in an actual framework to obtain experimentally the accuracy of the Simulink modeling.