1 Introduction

Conventional energy utilization for the transportation sectors is not only costly but also causing adverse environmental impact (Zin et al. 2013; Abdullah et al. 2011). Though several article has been conducted (Bianchi et al. 2007; Gopal Sharma et al. 2013) to proposed a wind turbine system in which the AC power form the wind is directly supplied to the load via un-interruptible power supply (UPS) to be provided utility company or national grid, but no one has been studied the integration of wind energy directly into vehicle yet. Interestingly, the this article described the wind power technology can be implemented into the all vehicles directly to meet its total energy demand while it is in a motion which indeed shall mitigate the energy and climate change crisis. Thus, wind energy has the high potential to produce energy for transportation vehicles once it is utilized by a sophisticated technology. Modern wind turbines are small, simple and highly sophisticated devices compared with turbines from the mid-twentieth century, when turbines were extremely tall and large where the turbine engine capacity from roughly 5–10 kW; rotors now often exceed 0.25 meters in diameter and are positioned on towers exceeding 1 m in height. Thus, modern turbines are indeed much cheaper than previous ones which could be the best tool to implement into the vehicle to produce energy naturally. In this article, an innovative theory was analyzed to implement this wind energy into vehicles while the vehicles are in motion. The wind turbine modeling and drive train modeling (by one-mass model) was conducted using the MATLAB Simulink software package. The kinetic energy conversion process was divided into two main interacting subsystems, and the detailed process of conversion procedure was modeled; results of the energy conversion chain analysis were also analyzed using the MATLAB software. Subsequently, the control structure, design and generator model were also analyzed using a series of mathematical calculations to prepare a theoretical model for total process energy capture by wind turbine and utilization by running vehicles. Finally this model was hypothetically applied into a car as an experimental tool which revealed that wind energy-generated transportation vehicles could indeed be a cutting-edge technology to reduce to eliminate the cost of energy for all transportation vehicles.

2 Theoretical modeling of wind energy

2.1 Turbine modeling

A wind turbine generator for power electronic equipment (Abdullah et al. 2011) is governed by the operation of variable-speed wind turbines. The reasons for using variable-speed operating wind turbines include possibilities for reducing stress and control of active and reactive power. MATLAB Simulink model wind generation modules that are unique to one of the following with a series of mathematical equations were used for modeling the turbines (Fig. 1).

Fig. 1
figure 1

Conceptual MATLAB Simulink model of the wind generator energy module

Full size image

In this paper, the model that was developed was used to study and simulate the doubly fed induction generator (DFIG) for producing electricity for transportation vehicles. A vector control strategy involving the DFIG order, power storage box active stator is presented in the following matrix.

$$ \frac{\text{d}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}c} {\Delta \omega_{t} } \\ {\Delta \omega_{r} } \\ {T_{g} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{ - D_{t} - D_{tg} }}{{2H_{t} }}} & {\frac{{D_{tg} }}{{2H_{t} }}} & {\frac{ - 1}{{2H_{t} }}} \\ {\frac{{D_{tg} }}{{2H_{g} }}} & {\frac{{ - D_{g} - D_{tg} }}{{2H_{g} }}} & {\frac{1}{{2H_{g} }}} \\ {K_{tg} \omega_{e} } & { - K_{tg} \omega_{e} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \omega_{t} } \\ {\Delta \omega_{r} } \\ {T_{g} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{{T_{m} }}{{\begin{array}{*{20}c} {2H_{t} } \\ {\frac{{ - T_{e} }}{{2H_{g} }}} \\ \end{array} }}} \\ 0 \\ \end{array} } \right] $$

The fundamental equation governing the mechanical power of the wind turbine is

$$ p_{w} = \frac{1}{2}c_{p} \left( {\lambda ,\beta } \right)\rho AV^{3} $$

where ρ is the air density (kg/m3), C p is the power coefficient, A is the intercepting area of the rotor blades (m2), V is the average wind speed (m/s), and λ is the tip speed ratio. The theoretical maximum value of the power coefficient C p is 0.593; C p is also known as Betz’s coefficient (Abdullah et al. 2011; Junyent-Ferré et al. 2010). Mathematically,

$$ \lambda = \frac{R\omega }{V} $$

R is the radius of the turbine (m), ω is the angular speed (rad/s), and V is the average wind speed (m/s). The energy generated by wind can be obtained by

$$ Q_{w} = P \times \left( {\text{Time}} \right) \left[ {\text{kWh}} \right] $$

It is well known that wind velocity cannot be obtained by a direct measurement from any particular motion. In data taken from any reference, the motion needs to be determined for that particular motion; then, the velocity needs to be measured at a lower motion (Gaillard et al. 2009).

$$ v(z)\ln \left( {\frac{{z_{r} }}{{z_{0} }}} \right) = v(z_{r} )\ln \left( {\frac{z}{{z_{0} }}} \right) $$

where Z r is the reference height (m), Z is the height at which the wind speed is to be determined, Z 0 is the measure of surface roughness (0.1–0.25 for crop land), v(z) is wind speed at height z (m/s), and v(z r ) is wind speed at the reference height z (m/s). The power output in terms of the wind speed can be estimated using the following equation:

$$ P_{\text{w}} \left( v \right) = \left\{ {\begin{array}{*{20}l} {\frac{{v^{k} - v_{\text{C}}^{k} }}{{ v_{\text{R}}^{ k} - v_{\text{C}}^{k} }} \cdot P_{\text{R}} } \hfill & {v_{\text{C}} \le v \le v_{\text{R}} } \hfill \\ {P_{\text{R}} } \hfill & {v_{\text{R}} \le v \le v_{\text{F}} } \hfill \\ 0 \hfill & {v \le v_{\text{C}} \;{\text{and}}\;v \ge v_{\text{F }} } \hfill \\ \end{array} } \right. $$

where P R is rated power, v C is the cut-in wind speed, v R is the rated wind speed, v F is the rated cut-out speed, and k is the Weibull shape factor. The angular speed of the generator must be changed to extract the maximum power; this process is known as maximum power point tracking (MPPT). When the blade pitch angle is zero, the power coefficient is maximized for an optimal TSR (Gaillard et al. 2009; Ali 2013). The optimal rotor speed is given by

$$ \omega_{\text{opt}} = \frac{{\lambda_{\text{opt}} }}{R} V_{\text{wn}} $$

which gives

$$ V_{\text{wn}} = \frac{{R \omega_{\text{opt}} }}{{\lambda_{\text{opt}} }} $$

where ω opt is the optimal rotor angular speed in rad/s, λ opt is the optimal tip speed ratio, R is the radius of the turbine in meters, and V wn is the wind speed in m/s.

2.2 Drive train modeling

The basic concept is for a drive train to transfer high aerodynamic torque at the rotor to the low-speed shaft of the generator through a gearbox. Because the generator is coupled to the rotor to reduce complexity, a model of the generator is needed and is presented later in this section. Consequently, the drive train can be modeled using a one-mass model (Bhandari et al. 2014) based on the torsional multibody dynamic model per the following matrix:

$$ \left[ {\begin{array}{*{20}c} {\dot{\omega }_{t} } \\ {\dot{\omega }_{r} } \\ {\dot{T}_{ls} } \\ \end{array} } \right] \,= \,\left[ {\begin{array}{*{20}c} {\frac{{K_{i} }}{{J_{i} }}} & 0 & {\frac{1}{{J_{i} }}} \\ 0 & - { \frac{{K_{g} }}{{J_{g} }}} & {\frac{1}{{n_{g} J_{g} }}} \\ {\left( {B_{ls} - \frac{{K_{ls} K_{r} }}{{J_{r} }}} \right)} & {\frac{1}{{n_{g} }}\left( {\frac{{K_{ls} K_{r} }}{{J_{g} }} - B_{ls} } \right)} & -{K_{ls } \left( {\frac{{J_{r} + n_{g}^{2} J_{g} }}{{n_{g}^{2} J_{g} J_{r} }}} \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\omega_{t} } \\ {\omega_{r} } \\ {T_{ls} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{J_{r} }}} \\ 0 \\ {\frac{{K_{ls} }}{{J_{r} }}} \\ \end{array} } \right]T_{m} + \left[ {\begin{array}{*{20}c} 0 \\ -{\frac{1}{{J_{g} }}} \\ {\frac{{K_{ij} }}{{n_{g} J_{g} }}} \\ \end{array} } \right]T_{g} $$

2.3 One-mass model

The turbine inertia can be calculated from the combined weight of the blades and the hub. Therefore, the turbine can be viewed as a large disk with a small thickness. If proper data are not available, the simple equation below can be used to estimate the mass moment of inertia of a disk with a small thickness, and the turbine can be considered.

$$ J_{{{\text{t}} }} \dot{\omega }_{\text{t}} = T_{\text{a}} - K_{\text{t}} \omega_{\text{t}} - T_{\text{g}} $$

and

$$ J_{\text{t}} = J_{\text{r}} + n_{\text{g}}^{2} J_{\text{g}} $$
$$ K_{\text{t}} = K_{\text{r}} + n_{\text{g}}^{2} K_{\text{g}} $$
$$ T_{\text{g}} = n_{\text{g}} T_{\text{em}} $$

where J t is the moment of inertia in (kg m2); ω t is the low shaft angular speed in (rad s−2); K t is the turbine damping coefficient in (Nm rad−1 s−1) which represents the aerodynamic resistance; and K g is the generator damping coefficient in (Nm rad−1 s−1) (Fig. 2).

Fig. 2
figure 2

Schematic diagram of a one-mass model of a wind turbine system: a full-scale converter wind turbine with synchronous machine shows the detailed process of energy accumulation

Full size image

Therefore, the maximum power is calculated with the following equation with the one-mass model diagram and series of equations. This shows that the theoretical maximum power extracted from the wind is 0.5825 times its kinetic power.

$$ \begin{aligned} \frac{{{\text{d}}P_{k} }}{{{\text{d}}V_{2} }} &= \frac{1}{4}\rho AV_{1}^{3} \left( { - 3 \frac{{V_{2}^{2} }}{{V_{1}^{3} }} - 2 \frac{{V_{2} }}{{V_{1}^{2} }} + \frac{1}{{V_{1} }}} \right) = 0 \hfill \\ &\Rightarrow \frac{1}{4} \rho A \left( { - 3V_{2}^{2} - 2V_{2} V_{1} + V_{1}^{2} } \right) = 0 \hfill \\ &\Rightarrow \frac{1}{4} \rho A \left( { - 3V_{2}^{2} - 3V_{2} V_{1} + V_{2 } V_{1} + V_{1}^{2} } \right) = 0 \hfill \\ &\Rightarrow \frac{1}{4} \rho A \left[ { - 3V_{2}^{2} \left( {V_{2} + V_{1} } \right) + V_{1} \left( {V_{2} + {\text{V}}_{1} } \right)} \right] = 0 \hfill \\ &\Rightarrow \frac{1}{4} \rho A\left( { - 3 V_{2} + V_{1} } \right)\left( {V_{2} + V_{1} } \right) = 0 \hfill \\ \end{aligned} $$

Here \( \rho ,{\rm A}\;{\text{and}}\;\left( {V_{2} + V_{2} } \right) \) can not be zero, therefore,

$$ \left( { - 3 V_{2} + V_{1} } \right) = 0 \Rightarrow \frac{{V_{2} }}{{V_{1} }} = \frac{1}{3} $$

Now, putting this value of \( {\raise0.7ex\hbox{${V_{2} }$} \!\mathord{\left/ {\vphantom {{V_{2} } {V_{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${V_{1} }$}} \) in Eq. (3), we get,

$$ \begin{aligned} P_{k } &= \frac{1}{4}\rho {\rm A}V_{1}^{3} \left( {1 - \frac{1}{{ 3^{3} }} - \frac{1}{{ 3^{2} }} - \frac{1}{{ 3^{3} }}} \right) \hfill \\ & \Rightarrow P_{k} = 0.5925 \times \frac{1}{2} \rho {\rm A}V_{1}^{3} \ldots (4) \end{aligned} $$

3 Wind energy conversion

Given the above conditions, the airflow mass has a certain energy called kinetic energy (Bhandari et al. 2014; Beltran et al. 2011). The kinetic energy is shown in Fig. 3, which presents a wind energy conversion system (WECS) that uses a DFIG these are the aerodynamic subsystem (wind speed, wind turbine and gearbox) and the electrical subsystem (DFIG).

Fig. 3
figure 3

Typical wind energy conversion chain

Full size image

3.1 Aerodynamic subsystem

Signals in the simulations may be to use logs of real speed at the real location of the wind turbine generation system (WTGS).

The choice for the wind speed model is described and proposed in Robyns et al. (2012). The deterministic and stochastic parts are added together to obtain the total equivalent wind speed (V), and expression has the following form:

$$ V\left( t \right) = V_{0} + \mathop \sum \limits_{i = 1}^{n} {\rm A}_{i } \sin \left( {\omega_{i} t + \varphi_{i} } \right) $$
(1)

where V 0 is the mean component and A i , ω i and ψ i are the magnitude, pulsation and initial phase of each turbulent mode, respectively. In this article, the turbulence experienced by the rotating wind turbines blades is taken into account. The WTGS converts power from the kinetic energy of the wind and expressed as C p, which is called the power coefficient or Betz’s factor.

The aerodynamic power is given by (Robyns et al. 2012)

$$ P_{\text{aer}} = \frac{1}{2} C_{\text{p}} \left( {\lambda ,\beta } \right)\rho R\pi^{2} V^{3} $$
(2)

where ρ is the air density, R is the blade length, and V is the wind velocity. The percentage is represented by a coefficient C p(λ), which is function of the wind speed, turbine speed and pith angle of the specific wind turbine blades (Dürr et al. 2006; Mamdani and Assilina 1975).

Although this equation seems simple, C p depends on the ratio between the turbine shaft speed Ω t and the wind speed V. This ratio is called the tip speed ratio:

$$ \lambda = \frac{{\varOmega_{t} \cdot R}}{V} $$
(3)

Typical C p versus TSR curves for different values of pitch angle β are shown in Fig. 4. In a wind turbine, there is an optimal value for the TSR for which C p is maximal; thus, this TSR value maximizes the power for a given wind speed. The peak power for each wind speed occurs at the point at which C p is maximized. To maximize the generated power, it is therefore desirable for the generator to have a power characteristic that follows the maximum C pmax line.

Fig. 4
figure 4

Power coefficient variation with TSR and pitch angle

Full size image

The turbine torque is the ratio of the aerodynamic power to the turbine shaft speed (Kamal et al. 2010). The turbine is normally coupled to the generator shaft through a gearbox whose gear ratio G is chosen to set the generator shaft speed within a desired speed range. Neglecting the transmission losses, the torque and shaft speed of the wind turbine, referred to the generator side of the gearbox, are given by

$$ \left\{ {\begin{array}{*{20}l} {T_{\text{g }} = \frac{{T_{\text{aer}} }}{G}} \hfill \\ {\varOmega_{t} = \frac{{\varOmega_{\text{g}} }}{G}} \hfill \\ \end{array} } \right. $$
(4)

where T g is the driving torque of the generator and Ω g is the generator shaft speed.

3.2 Electrical subsystem

Variable-speed operation is obtained by injecting a controllable voltage into the rotor at the desired slip frequency (Kamal et al. 2012). The equations for the DFIG are identical to a squirrel-cage induction generator except that the rotor voltages are not zeros (Kamal et al. 2012, 2013) and can be expressed followings (Eltamaly et al. 2011):

$$ \left\{ {\begin{array}{*{20}l} {v_{ds} = \frac{{{\text{d}}\phi_{ds} }}{{{\text{d}}t}} + \frac{{R_{s} }}{{L_{s} }} \phi_{ds} - \omega_{s} \cdot \phi_{qs} - M\frac{{R_{s} }}{{L_{s} }}i_{dr} } \hfill \\ {v_{qs} = \frac{{{\text{d}}\phi_{qs} }}{{{\text{d}}t}} + \omega_{s} \cdot \phi_{ds} + \frac{{R_{s} }}{{L_{s} }} \phi_{qs} - M\frac{{R_{s} }}{{L_{s} }}i_{qr} } \hfill \\ {\left( {v_{dr} - \frac{M}{{L_{s} }} v_{ds} } \right) = \sigma L_{r} \frac{{{\text{d}}i_{dr} }}{{{\text{d}}t}} - M\frac{{R_{s} }}{{L_{s}^{2} }}\phi_{ds} + \omega \frac{M}{{L_{s} }} \phi_{qs} + \left( {R_{r} + \frac{{M^{2} }}{{L_{s}^{2} }} R_{s} } \right)i_{dr} - \sigma L_{r} \omega_{r} i_{qr} } \hfill \\ {\left( {v_{qr} - \frac{M}{{L_{s} }} v_{qs} } \right) = \sigma L_{r} \frac{{{\text{d}}i_{qr} }}{{{\text{d}}t}} - \frac{M}{{L_{s} }}\omega \phi_{qs} - M\frac{{R_{s} }}{{L_{s}^{2} }}\phi_{qs} + \sigma L_{r} \omega_{r} i_{dr} + \left( {R_{r} + \frac{{M^{2} }}{{L_{s}^{2} }} R_{s} } \right)i_{qr} } \hfill \\ \end{array} } \right. $$
(5)

where R s and R r are the stator and rotor resistances, respectively; L s , L t are the stator and rotor inductances, respectively; M, σ are the mutual inductance and leakage coefficient, respectively; Ω = pΩ g is the electrical speed, and p is the pair pole number.

The stator and rotor flux can be expressed as

$$ \left\{ {\begin{array}{*{20}l} {\phi_{ds} = L_{s} i_{ds} + Mi_{dr} } \hfill \\ { \phi_{sq} = L_{s} i_{qs} + Mi_{qr} } \hfill \\ {\begin{array}{*{20}c} { \phi_{rd} = L_{r} i_{dr} + Mi_{ds} } \\ { \phi_{rd} = L_{s} i_{qr} + Mi_{qs} } \\ \end{array} } \hfill \\ \end{array} } \right. $$
(6)

where i ds , i qs , i dr and i qr are the direct, quadrate stator and rotor currents, respectively. The active and reactive powers at the stator, in addition to those provided for the grid, are defined as

$$ \left\{ {\begin{array}{*{20}c} {P_{s} = v_{ds } \,.\,i_{ds } + v_{qs }\, .\,i_{qs } } \\ {Q_{s} = v_{qs }\, .\,i_{ds } - v_{ds }\, .\,i_{qs } } \\ \end{array} } \right. $$
(7)

The electromagnetic torque is expressed as

$$ T_{\text{em}} = p\left( {i_{qs } \phi_{ds} - i_{ds} \phi_{qs} } \right). $$
(8)

4 Control structure

The wind turbine electric system time responses are much faster than those of the mechanical parts in the WECS. This makes it possible to dissociate the wind turbine and the DFIG control designs and thus describe a cascade control structure based on two subsystem controls:

  1. 1.

    The wind turbine subsystem control concerns the aerodynamic subsystem, which provides the reference inputs for the DFIG subsystem control.

  2. 2.

    The DFIG subsystem control concerns the electric generator via the power converter.

Subsequently, these two control levels will be considered separately, as shown in Fig. 5.

Fig. 5
figure 5

Block diagram of the whole system

Full size image

It is worth mentioning that there is no need for a reference voltage, torque limiter or saturation block because of the inherent limits of the references generated at the transients. After obtaining the voltage, pulse width modulation (PWM) is used to generate the gating pulses with a fixed switching frequency for the load-side converter.

4.1 Wind turbine subsystem control

Figure 6 shows the four distinct regions in a typical WECS, where Vmax is the wind speed at which the maximum allowable rotor speed is reached and V cut-off is the furling wind speed at which the turbine needs to be shut down for protection.

Fig. 6
figure 6

Areas of operation and control WECS

Full size image

In practice, there are two possible regions of turbine operation: high- and low-speed regions (E.W.E Association 2012). High-speed operation (IV) is frequently bounded by the speed limit of the machine. Conversely, regulation in the low-speed region (II) is usually not restricted by speed constraints.

However, the system has nonlinear non-minimum phase dynamics in this region. Generally, wind turbine control objectives are functions of the wind speed. For low wind speed, the objective is to optimize the capture of wind power through tracking the optimal rotor speed signals (Faida and Saadi 2010; Bianchi et al. 2007; Ghennam et al. 2007). Once the wind speed increases above its nominal value, the control objective moves to the rated regulating power. Numerous methods for MPPT have been proposed in the literature (Gopal Sharma et al. 2013; Gupta et al. 2011).

The method proposed in this paper is simple and is based on the tip speed of the wind turbine. Therefore, an anemometer is required for measuring the wind speed on the wind turbine. Assuming that the optimal value of the TSR λ can be obtained from Fig. 4, the optimal speed of the turbine can be determined as follows using Eq. (3):

$$ \varOmega_{{t,{\text{opt}}}} = \frac{{\lambda_{\text{opt}} \cdot V}}{R} $$
(9)

For this MPPT method, the speed controller continuously adjusts the generator shaft speed to impose the reference electromagnetic torque of the DFIG with the aim of tracking, as shown in Fig. 7. The turbine shaft speed is then controlled to obtain a maximum power coefficient. The MPPT method significantly increases the efficiency of the wind turbine. For each wind speed, there is a certain rotational speed at which the power curve of a given wind turbine has a maximum (C p reaches its maximum value). Starting the description of the WECS with the aerodynamic subsystem, it should be mentioned that the present work focuses on region II. A block diagram of the MPPT control system for the wind turbine is shown in Fig. 7.

Fig. 7
figure 7

Block diagram of the MPPT with enslaved speed at regulating the power harvested from wind to apply it to the sequence of turbine, gear and DFIG shaft; in particular, the control objective consists to capture the maximum power available from wind

Full size image

This control block diagram of variable-speed fixed pitch WECS in region II generally aims at regulating the power harvested from wind by modifying the generator speed; in particular, the control objective captures the maximum power efficiency (MPE) of the power rotational speed curves for the 7.8-kW wind turbine that is considered in the present paper under different wind speeds. Connecting all of the MPPs from each power curve, the optimal power curve is obtained, and the control system should follow the tracking characteristic curve (TCC) of the wind turbine. Each wind turbine has a TCC similar to the one in the figure below. When operating in region IV, which occurs above the rated wind speed, the turbine must limit the captured wind power such that safe electrical and mechanical loads are not exceeded (Fig. 8).

Fig. 8
figure 8

Aerodynamic powers various speed characteristics for different wind speeds, with indication of the maximum power with tracking curve

Full size image

4.2 DFIG subsystem control

The principle of this method consists of orientating the stator flux in such a manner that the stator flux vector points in the d-axis direction (Heier 1998; Hossain 2016). This approach is realized by setting the quadratic component of the stator flux to the null value:

$$ \phi_{s} = \phi_{ds} \Rightarrow \phi_{qs} = 0 $$
(10)

In the Park reference frame, this approach is shown in Fig. 9. Using the above condition and supposing that the grid system is steady with a single voltage V s , which leads to a constant flux in the stator ϕ s , we can easily deduce the voltage as

Fig. 9
figure 9

Block diagram of the fuzzy controller

Full size image
$$ \left\{ {\begin{array}{*{20}l} {v_{ds} = 0 } \hfill \\ {v_{qs} = \omega_{s} \cdot \phi_{s} = V_{s} } \hfill \\ \end{array} } \right. $$
(11)

The per-phase stator resistance is neglected (the realistic approximation for medium power machines used in WECS).

The stator voltage vector is consequently a quadratic advance compared with the stator flux vector. By using Eqs. (5) and (11), we obtain the rotor voltages:

$$ \left\{ {\begin{array}{*{20}l} { v_{dr} = \sigma L_{r} \frac{{{\text{d}}i_{dr} }}{{{\text{d}}t}} + R_{r} i_{dr} - \sigma L_{r} \omega_{r} i_{qr} + \frac{M}{{L_{s} }}\frac{{{\text{d}}\phi_{ds} }}{{{\text{d}}t}}} \hfill \\ { v_{qr} = \sigma L_{r} \frac{{{\text{d}}i_{qr} }}{{{\text{d}}t}} + R_{r} i_{qr} + \sigma L_{r} \omega_{r} i_{dr} + g\frac{M}{{L_{s} }}V_{s} } \hfill \\ \end{array} } \right. $$
(12)

where V s is the stator voltage magnitude, which is assumed to be constant, and g is the slip range. We can rewrite the rotor voltages as follows:

$$ \left\{ {\begin{array}{*{20}l} { v_{dr} = \sigma L_{r} \frac{{di_{dr} }}{dt} + R_{r} i_{dr} + {\text{fem}}_{d} } \hfill \\ {v_{qr} = \sigma L_{r} \frac{{di_{qr} }}{dt} + R_{r} i_{qr} + {\text{fem}}_{q} } \hfill \\ \end{array} } \right. $$
(13)

With fem d and fem q , the crossed coupling terms between the d-axis and q-axis are as follows:

$$ \left\{ {\begin{array}{*{20}l} {{\text{fem}}_{d} = - \sigma L_{r} \omega_{r} i_{qr} } \hfill \\ {{\text{fem}}_{q} = \sigma L_{r} \omega_{r} i_{dr} + s\frac{M}{{L_{s} }}V_{s} } \hfill \\ \end{array} } \right. $$
(14)

Consequently, regarding (10), the fluxes of (6) are simplified as follows:

$$ \left\{ {\begin{array}{*{20}l} {\phi_{ds} = L_{s} i_{ds} + Mi_{dr} } \hfill \\ {0 = L_{s} i_{qs} + Mi_{qr} } \hfill \\ \end{array} } \right. $$
(15)

From (15), we can deduce the currents to be

$$ \left\{ {\begin{array}{*{20}l} {i_{ds} = \frac{{\phi_{ds} - Mi_{dr} }}{{L_{s} }}} \hfill \\ {i_{qs} = - \frac{M }{{L_{s} }}i_{qr} } \hfill \\ \end{array} } \right. $$
(16)

Using Eqs. (7), (11) and (16), the stator active and reactive powers can then be linked to these rotor currents as follows:

$$ \left\{ {\begin{array}{*{20}l} {P_{s} = - V_{s} \cdot \frac{M }{{L_{s} }}i_{qr} } \hfill \\ {Q_{s} = - V_{s} \frac{M }{{L_{s} }}\left( {i_{dr} - \frac{{\phi_{ds} }}{M}} \right)} \hfill \\ \end{array} } \right. $$
(17)

Because of the constant stator voltage, the stator active and reactive powers are controlled via i qr and i dr .

Therefore, field-oriented control of the DFIG can then be performed, with the rotor currents considered as the variables to be controlled.

Decoupled control is guaranteed without feed-forward compensation because the FLC inherently eliminates the cross-coupling terms between the two axes [Eq. (14)]. In steady state for a lossless generator, we can use the following energy balance: P s  + Pr = P m , where P s  = T em ω s and P m  = T q ω.

From the MPPT method, the electromagnetic torque is used to calculate the reference value for the stator’s active power, which follows a pre-defined turbine power–speed characteristic to track the maximum power point (Hossain 2016; Tsourakisa et al. 2009; Grätzel 2001).

The turbine shaft speed is then controlled to give the maximum power coefficient. It follows that P s  = T em ω s , where T em * is the reference electromagnetic torque that is deduced from the MPPT control strategy. The MPPT method significantly increases the efficiency of the wind turbine. Using (17), we can calculate the rotor current references, which allow setting the desired reference active and reactive powers, as follows:

$$ \left\{ {\begin{array}{*{20}l} {i_{qr}^{*} = - \frac{{L_{s} }}{{MV_{s} }}P_{s}^{*} } \hfill \\ { i_{dr}^{*} = - \frac{{L_{s} }}{{MV_{s} }}\left( {Q_{s}^{*} - \frac{{V_{s}^{2} }}{{\omega_{s} L_{s} }}} \right)} \hfill \\ \end{array} } \right. $$
(18)

5 Controller design

Because of the robustness of the fuzzy logic controller for many nonlinear procedures and characteristics, this paper suggests the design of a fuzzy logic controller (FLC) with a Mamdani fuzzy inference system (Slootweg 2005; Kerrouche et al. 2014). The fuzzy logic controller includes four parts: (1) a fuzzification block that determines the input membership values; (2) a fuzzy inference system (FIS) that evaluates which control rules are appropriate at each time by using the fuzzy knowledge-based block (Kazemi et al. 2012; Stieber 2008; Boutotbat et al. 2013); (3) a defuzzification block that calculates the output of the rules leading to the defuzzification technique (Pichan et al. 2013; Publishing and Agency 2010). Figure 9 shows the block diagram of the fuzzy controller.

For a successful design, proper selection of the gains in the FLC is crucial, and in many cases, this is performed through trial and error to achieve the best possible control performance.

In this section, FLC is used to control the wind turbine subsystem and the DFIG subsystem. For the proposed FLC of a wind turbine, we use the scheme shown in Fig. 7. There are two input signals to the FLC, the generator shaft speed error and the change of the error, are as follows:

$$ \left\{ {\begin{array}{*{20}l} {e_{{\varOmega_{g} }} \left( n \right) = \varOmega_{g}^{*} \left( n \right) - \varOmega_{g} \left( n \right) } \hfill \\ {\Delta e_{{\varOmega_{g} }} \left( n \right) = \varOmega_{g}^{*} \left( n \right) - \varOmega_{g} \left( {n - 1} \right)} \hfill \\ \end{array} } \right. $$
(19)

The input and output linguistic variables of the fuzzy controller are quantized based on the three fuzzy subsets. The fuzzy sets have been determined to be NG (negative great), EX (zero) and PG (positive great).

The input/output variables used in this paper are fuzzified and evaluated by triangular, trapezoidal and symmetrical membership functions (MFs). Thus, the input of the generator speed shaft fuzzy controller is T em *. For the proposed FLC of the DFIG, the diagram scheme shown in Fig. 11 was used; the inputs of the direct and quadrate axis rotor current fuzzy controllers are the d- and q-axis rotor current errors:

$$ \left\{ {\begin{array}{*{20}l} {e_{{i_{dr} }} \left( n \right) = i_{dr}^{*} \left( n \right) - i_{dr} \left( n \right)} \hfill \\ {e_{{i_{qr} }} \left( n \right) = i_{qr}^{*} \left( n \right) - i_{qr} \left( n \right)} \hfill \\ \end{array} } \right. $$
(20)

Their changes in error are

$$ \left\{ {\begin{array}{*{20}l} {\Delta e_{{i_{dr} }} \left( n \right) = i_{dr}^{*} \left( n \right) - i_{dr} \left( {n - 1} \right)} \hfill \\ {\Delta e_{{i_{qr} }} \left( n \right) = i_{qr}^{*} \left( n \right) - i_{qr} \left( {n - 1} \right)} \hfill \\ \end{array} } \right. $$
(21)

The input and output linguistic variables of the two fuzzy controllers have been quantized in the following five fuzzy subsets. The fuzzy sets have been defined as NL (negative large), NS (negative small), ZQ (zero), PS (positive small), Pm (positive medium) and PL (positive large).

Short-term fluctuations in the wind speed may result in a change in the output power and a shift in the operating point (Pichan et al. 2013). Thus, to avoid these undesirable effects, reducing the number of MFs is a solution to smooth the changes in the output power; increasing the number of MFs will produce a delay because of the increased number of computational steps required for some bands (Li et al. 2010; Tazil et al. 2010; Brekken and Mohan 2007).

To trade-off between accuracy and complexity, rigorous simulation studies found that five MFs are sufficient to produce the desired results in the required bands.

6 Generator modeling

Either induction and synchronous generators can be used for wind turbine systems (Takagi and Sugeno 1985; Vieira et al. 2007). Using a directly driven PMSG not only increases the reliability but also decreases the weight of the nacelle (Wang and Truong 2013). The PMSG model was designed based on a d–q synchronous reference frame. The PMSG voltage equation is

$$ V_{q} = - R_{s} i_{q} - L_{q} \frac{{{\text{d}}i_{a} }}{{{\text{d}}t}} - \omega L_{d} i_{d} + \omega \lambda_{m} $$
(22)
$$ V_{d} = - R_{s} i_{d} - L_{d} \frac{{{\text{d}}i_{a} }}{{{\text{d}}t}} + \omega L_{q} i_{q} $$
(23)

The electronic torque is

$$ T_{e} = 1.5\rho \left[ {\lambda i_{q} + \left( {L_{d} - L_{q} } \right)i_{d} i_{q} } \right] $$
(24)

where L q is the q-axis inductance, L d is the d-axis inductance, i q is the q-axis current, i d is the d-axis current, V q is the q-axis voltage, V d is the d-axis voltage, ω r is the angular velocity of the rotor, λ is the amplitude of the flux induced, and p is the number of pairs of poles. In the case of a squirrel-cage induction generator (SCIG), the following equation in a stationary d–q frame of reference can be used for dynamical modeling:

$$ \left[ {\begin{array}{*{20}c} {V_{qs} } \\ {V_{ds} } \\ {V_{qr} } \\ {V_{dr} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{s} + pL_{s} } & 0 & {pL_{m} } & 0 \\ 0 & {R_{s} + pL_{s} } & 0 & {pL_{m} } \\ {pL_{m} } & { - \omega_{r} L_{m} } & {R_{r} + pL_{r} } & { - \omega_{r} L_{r} } \\ {\omega_{r} L_{m} } & {pL_{m} } & {\omega_{r} L_{r} } & {R_{r} + pL_{r} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{qs} } \\ {i_{ds} } \\ {i_{qr} } \\ {i_{dr} } \\ \end{array} } \right] $$
(25)

From the stator side, the equations are as follows:

$$ \begin{aligned} & \lambda_{ds} = L_{s} i_{ds} + L_{m} i_{dr} \\ & \lambda_{qs} = L_{s} i_{qs} + L_{m} i_{dr} \\ & L_{s} = L_{is} + L_{m} \\ & L_{r} = L_{lr} + L_{m} \\ & V_{ds} = R_{s} i_{ds} + \frac{\text{d}}{{{\text{d}}t}}\lambda_{ds} \\ & V_{qs} = R_{s} i_{qs} + \frac{\text{d}}{{{\text{d}}t}}\lambda_{qs} \\ \end{aligned} $$
(26)

From the rotor side, the equations are as follows:

$$ \begin{aligned} & \lambda_{dr} = L_{r} i_{dr} + L_{m} i_{ds} \\ & \lambda_{qr} = L_{r} i_{qr} + L_{m} i_{qs} \\ & V_{dr} = R_{r} i_{dr} + \frac{\text{d}}{{{\text{d}}t}}\lambda_{dr} + \omega_{r} \lambda_{qr} \\ & V_{qr} = R_{r} i_{qr} + \frac{\text{d}}{{{\text{d}}t}}\lambda_{qr} - \omega_{r} \lambda_{dr} \\ \end{aligned} $$
(27)

For the air gap flux linkage, the equations are as follows:

$$ \begin{aligned} \lambda_{dm} & = L_{m} \left( {i_{ds} + i_{dr} } \right) \\ \lambda_{qr} & = L_{m} \left( {i_{qr} + i_{qs} } \right) \\ \end{aligned} $$
(28)

where R s , R r , L m , L ls , L lr , ω r , i d , i q , V d , V q , λ d and λq are the stator winding resistance, and fluxes of the d–q model, respectively (Brekken and Mohan 2007). The output power and torque of the turbine (T t) in terms of rotational speed can be obtained by substituting Eq. (17) into Eq. (16):

$$ P_{w} = \frac{1}{2}\rho AC_{p} \left( {\lambda ,\beta } \right)\left( {\frac{{R\omega_{\text{opt}} }}{{\lambda_{\text{opt}} }}} \right)^{3} $$
(29)
$$ T_{\text{t}} = \frac{1}{2}\rho AC_{p} \left( {\lambda ,\beta } \right)\left( {\frac{R}{{\lambda_{\text{opt}} }}} \right)^{3} \omega_{\text{opt}} $$
(30)

The power coefficient (C p) is a nonlinear function that is expressed by fitting Eq. (31) with the form

$$ C_{p} \left( {\lambda ,\beta } \right) = c_{1} \left( {c_{2} \frac{1}{{\lambda_{i} }} - c_{3} \beta - c_{4} } \right)e^{{ - c_{5} \frac{1}{{\lambda_{i} }}}} + c_{6} \lambda $$
(31)

with

$$ \frac{1}{{\lambda_{i} }} = \frac{1}{\lambda + 0.08\beta } - \frac{0.035}{{\beta^{3} + 1}} $$
(32)

The values of constants c1–c6 are discussed below.

The output of the wind energy generator module is processed by an energy conversion circuit diagram-implemented inverter from the standard Simulink/Sim Power Systems (Fig. 5). The resulting MATLAB Simulink circuit model for the wind generator is a particular case of the more general model of an electrical generator that is presented in Fig. 10.

Fig. 10
figure 10

Equivalent circuit diagram of a small wind generator considering all applications of rotor winding resistance and separate generator excitation winding; current through the winding generates a main field, induced voltage and terminal voltage

Full size image

7 Simulation and discussion

In this paper, a complete model was presented for a wind turbine generation system based on an induction generator. A cascade control algorithm was properly designed to ensure optimal operation of the whole system and was based on an FLC with stator flux orientation and the MPPT technique. Furthermore, the output power is smoothed despite wind fluctuations, which is commonly required in a grid connected to a wind farm. This technique has been successfully applied to generate a reference for tracking the active power by using the rotor-side converter control. Additionally, this strategy can reduce the stress in the pitch control system by adjusting the value of the power coefficient according to wind speed variations to extract the maximum wind power and limit it to its rated value. In simulations, a robustness test was performed by adding a wind speed signal and voltage dips. The simulation results demonstrate the inherent ability of the FLC to address this type of noise while operating under fault conditions at the rated wind speed.

Figure 4 shows that the maximum values of C p are achieved for the curve associated with β = 2°. From this curve, the maximum value of C p (C p,max = 0.5) is obtained for λ opt = 0.91. This value (λ opt) represents the optimal speed ratio. These conditions permit application of MPPT control. For the DFIG control, we use indirect power control with an FLC. The wind profile was considered to be a wind speed signal with a mean value of 8 m/s and a rated wind speed of 10 m/s; the whole system is tested under standard conditions with a stator voltage of approximately 50% for 0.5 s between 4 and 4.5 s, approximately 25% between 6 and 6.5 s and 50% between 8 and 8.5 s (Wang and Truong 2013; Wang et al. 2010). Thus, the machine is considered to be functioning in ideal conditions (no perturbations and no parameter variations). Moreover, to guarantee a unity power factor at the stator side, the reference for the reactive power is set to zero. The stator active and reactive powers are controlled according to the MPPT and FLC.

As a result of increasing wind speed, the generator shaft speed achieved maximum angular speed by tracking the maximum power point speed. Thus, the wind turbine always works optimally. Consequently, decoupling among the components of the rotor current was also performed to confirm that the control system worked effectively.

The bidirectional active and reactive power transfer between the rotor and power system is exchanged by the generator according to the super synchronous operation, achieving the nominal stator power, and the reactive power can be controlled by the load-side converter to obtain the unit’s power factor to generate energy for powering vehicles.

8 Theoretical experiment on a car

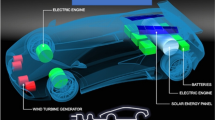
The theoretical assumption of this wind energy is thus modeled on a car as an experimental tool with the aim to ultimately use wind energy for all vehicles. The design of the wind turbines, materials used in all mechanical and electrical construction of the car, and all related issues have been considered, including all of the machine’s operational systems, wind strength, wind shears, and intensity and frequency of turbulence fluctuations (Fig. 11).

Fig. 11
figure 11

Conceptual model of a wind turbine for energy production to power a car while it is in motion

Full size image

The turbine speed and mechanical powers are depicted in the following graph with increasing and decreasing rates of wind speed while the car is in motion. When the wind is steady, the persistence forecasts yield good results. However, when the wind speed is increased rapidly, sudden “ramps” in power output are generated, which are of tremendous benefit for capturing the energy (Fig. 12).

Fig. 12
figure 12

Relationship between mechanical power generation and turbine speeds at different wind speeds for an implementation in a car

Full size image

Specifically, the following matrix presents the mathematical calculations for wind energy-capturing strategies when the car is running. Sr 1−b represents the direct wind energy capture, S r2−b represents the rotation of the generator, S r3−b represents the converting process of wind energy, and S r4−b is the total electricity production to run the car. The matrix calculation shows that 100% of the wind energy is utilized for conversion into electrical energy.

$$ \begin{aligned} & S_{r1 - b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ {\cos \left( { - \left( {90 - \varpi } \right)} \right)} & {\sin \left( { - \left( {90 - \varpi } \right)} \right)} & 0 \\ { - \sin \left( { - \left( {90 - \varpi } \right)} \right)} & {\cos \left( { - \left( {90 - \varpi } \right)} \right)} & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ {\sin \varpi } & { - \cos \varpi } & 0 \\ {\cos \varpi } & {\sin \varpi } & 0 \\ \end{array} } \right] \\ & S_{r2 - b} = \left[ {\begin{array}{*{20}c} {\cos 120^{{^\circ }} } & {\sin 120^{{^\circ }} } & 0 \\ { - \sin 120^{{^\circ }} } & {\cos 120^{{^\circ }} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ {\sin \varpi } & { - \cos \varpi } & 0 \\ {\cos \varpi } & {\sin \varpi } & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{1}{2}} & {\left( {\frac{\sqrt 3 }{2}} \right)\sin \varpi } & { - \left( {\frac{\sqrt 3 }{2}} \right)\cos \varpi } \\ { - \frac{\sqrt 3 }{2}} & {\left( { - \frac{1}{2}} \right)\sin \varpi } & {\left( {\frac{1}{2}} \right)\cos \varpi } \\ 0 & {\cos \varpi } & {\sin \varpi } \\ \end{array} } \right] \\ & S_{r3 - b} = \left[ {\begin{array}{*{20}c} {\cos \left( { - 120^{{^\circ }} } \right)} & {\sin \left( { - 120^{{^\circ }} } \right)} & 0 \\ { - \sin \left( { - 120^{{^\circ }} } \right)} & {\cos \left( { - 120^{{^\circ }} } \right)} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ {\sin \varpi } & { - \cos \varpi } & 0 \\ {\cos \varpi } & {\sin \varpi } & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{1}{2}} & {\left( {\frac{\sqrt 3 }{2}} \right)\sin \varpi } & {\left( {\frac{\sqrt 3 }{2}} \right)\cos \varpi } \\ {\frac{\sqrt 3 }{2}} & {\left( {\frac{1}{2}} \right)\sin \varpi } & {\left( {\frac{1}{2}} \right)\cos \varpi } \\ 0 & {\cos \varpi } & {\sin \varpi } \\ \end{array} } \right] \\ & S_{r4 - b} = S_{r1 - b} ,\;S_{r5 - b} = S_{r2 - b} ,\;S_{r6 - b} = S_{r3 - b} \\ \end{aligned} $$

In a WECS, the accuracy with which the peak power output of electricity is obtained from a point of the maximum power point tracking control system by the controller depends on the track. This experiment thus fed the induction generator stand (DFIG) that is used for extracting the maximum power from the use of a WECS. With the MPPT control method, the MPPT WECS are presented as controllers that are used for extracting the maximum possible energy from wind power generation, which, interestingly, is related to the speed of the car.

The analysis was then clarified with the following figure (Fig. 13) that depicts the relationship between the wind speed (resulting from the motion of the car) in miles per hour (MPH) and kWh power production. Interestingly, it is revealed that at a maximum mean of 8 kWh at an average speed of 10 MPH, energy is produced at a wind speed of 2 MPH immediately after the engine is started by the battery. For a standard car to become fully energized, 20 kWh is required.

Fig. 13
figure 13

Conversion of wind energy into the car is described in this figure and shows the relationship between the wind speed and energy production considering mean hours (10 MPH average), kWh from the induction generator, and kWh calculated from the revolutions per minute of speed range generator current and voltage

Full size image

9 Battery modeling

A battery is used as a backup power source to store the power when power production exceeds the demand. For a standard car to become fully energized, 20 kWh is required. Thus, if the car runs at 10 MPH for 2 h, it will fully charge and be able to run for an average of 200 miles; consequently, if the car runs at 60 MPH, it will only take 20 min to fully charge and be able to run for the same number of miles.

In this model, a battery is used as a storage buffer, and all the electricity is supplied through the battery according to Peukert’s law to predict battery discharge considering the nonlinear properties of the battery (Watanakul 2012); this law is stated as follows:

$$ t_{\text{discharge}} = H\left( {\frac{C}{IH}} \right)^{k} $$

where t is the battery discharge time, C is the battery capacity (Ampere hour value), I is the current that is drawn, H is the rated discharge time, and k is Peukert’s coefficient. Peukert’s coefficient is an empirical value that can be determined using the following formula:

$$ k = \frac{{\log T_{2} - \log T_{1} }}{{\log I_{2} - \log I_{1} }} $$

where I 1 and I 2 are the two discharge current rates and T 1 and T 2 are the corresponding discharge durations, respectively. The battery capacity decreases with time; i.e., the time for charging and discharging will change.

Thus, the value of k should be determined after a certain number of recharge cycles. The value of k for a lead acid battery is 1.3–1.4.

The charging time for a completely discharged battery is given by following equation and shown in Fig. 14.

$$ t_{\text{charging}} = \frac{{{\text{Ampere}}\;{\text{hour}}\;{\text{of}}\;{\text{battery}}}}{{{\text{Charging}}\;{\text{current}}}} $$
Fig. 14
figure 14

Model of a car with a battery as the backup power source to start the engine and for when the car is not in motion

Full size image

9.1 Conceptual estimate for design and construction of a renewable wind energy-powered car

List of components

Materials cost

Labor cost

Equipment cost

GC and OH cost

Total cost

Brand new car

$30,000

0

0

0

$30,000

Wind turbine

$3000

$900

$500

$880

$5280

Instrumentation

$500

$500

$400

$280

$1680

Electrical and mechanical control

$750

$600

$800

$430

$2580

Supply for 20 years cost is $0.00, but maintenance cost is $200/year

    

$4000

Total cost

$43,000

    
  1. This estimate was prepared using current (March 2016) material costs from top manufacturers and labor costs to install materials per international union labor wages. The equipment purchase was calculated according to current market costs in conjunction with production rates of standard construction practices

9.2 Savings in terms of energy costs

Twenty years of operation of a conventionally powered standard car (15,000 miles/year) requires 750 gallons of gasoline per year at an average rate of 20 miles/gallon (750 × 33.70 = 25,275 kWh/year), which is equivalent to 505,500 kWh of energy for 20 years. The cost of this conventional energy is (750 gallons × 20 years × $2.25, or $0.067/kWh for total of 505,500 kh) $33,750, and cost of a car of $25,000 will make a combined cost of $58,750. This comparison between conventional energy usage and wind turbine energy production for a car clearly shows cost savings of $15,210 when a wind energy system is used as the energy source for a car. In addition to that, the cost of $13,000 (furnish and install) for a turbine can also be eliminated once the turbine system is commercially installed in cars, and the maintenance costs will be covered by the manufacturer’s warranty. Therefore, this estimate suggests that most of the $28,210 cost for running a car for 20 years can be saved once it is powered by wind energy. Subsequently, all other transportation energy costs can also be saved once vehicles are powered by wind energy.

10 Conclusions

Sustainability nowadays is a crucial issue globally because of the climate change due to the fossil fuel consumption where neatly 30% climate change is responsible by transportation sector. Naturally it causes the sea level rising, ocean acidification, ozone layer depletion, and threatening public and animal health (Kazemi et al. 2012). Though the evolution of wind energy over the past decade has surpassed which abundantly available anywhere in world which can be utilized with zero emission for transportations and with low production cost has not been studied yet. Research and development efforts in wind power integration into vehicles are thus required to continue for establishing techniques to eliminate the energy cost and environmental problem since transportation sectors throughout the world are powered by fossil fuels. This sector draws on finite resources that are already dwindling, resulting in increased costs. Fossil fuel retrieval is becoming ever more environmentally damaging. It is now generally accepted that meeting the steadily increasing demand for energy in transportation sectors solely on the basis of conventional generation technologies puts an unacceptably high stress on the environment. In combination, these factors have led to a major impetus for renewable energy-based power generation during the preceding two to three decades, and the trend is set to continue. Thus, when considering efficiency, WECSs have been receiving the most attention among the various renewable energy systems. Extraction of the maximum possible power from available wind power is indeed an innovative source because the development of smaller wind turbines and advanced technology could enable wind energy to serve as a power source for transportation sectors.

Interestingly, this article revealed that natural wind speed is not required because the turbine will start to rotate once the vehicle is in motion. This emergent new technology, together with the favorable framework for renewable energy, can play a prime role in renewable energy utilization for massive use in transportation sectors. The transportation sector needs 5.6 × 1020 J/y (560 EJ/y); currently, this energy is obtained by burning fossil fuel, which accounts for nearly 30% of the total annual global energy demand (Zerikat et al. 2010).

Therefore, if vehicles could be powered by wind, it would be a new of era of science to utilize wind energy in transportation sectors. Wind energy-powered vehicles would not only eliminate the energy cost for the transportation sector but also play a vital role in drastically reducing global warming.