Introduction

During the last decades, numerical models have been extensively used to gain insights into aquifer system behavior. The interest of water managers in model-based decision support is still growing, and models are more than ever expected to guide the definition of sustainable management policies (Elshall et al. 2020). Groundwater models are necessarily a simplification of the geology, and hydraulic properties are most often heterogeneous and poorly constrained by direct measurements (Anderson et al. 2015). In this context, the precision and reliability of model-predicted values is a critical issue that justifies the need for practical and robust parameter estimation methods (Delottier et al. 2017).

A number of parameter estimation methods have been used in the last few decades (Doherty 2015; Zhou et al. 2014). Manual trial-and-error calibration that prevailed historically is gradually replaced by algorithmic methods such as the Gauss-Levenberg-Marquardt approach, which iteratively seeks the minimum error variance solution to the inverse problem from local finite-difference linearization of the model (Doherty 2015; Poeter et al. 2014). Such methods are widely used as they are easy to implement and effective for regularized inversion (Anderson et al. 2015); yet, they suffer from the computational burden associated with the estimation of the Jacobian matrix and the linear assumption is a limitation for uncertainty quantification. More recently, ensemble-based methods such as the Iterative-Ensemble-Smoother (IES) have been proposed as an alternative (White 2018). They also rely on strong assumptions but present the advantage of joining the parameter estimation and uncertainty quantification steps. The relevance of these algorithms largely depends on the context of the application, data availability, and the purpose of the modeling exercise; however, in a large majority of cases, it is neither relevant nor practical to consider the value of hydraulic properties at each model cell as an independent, adjustable parameter. Therefore, a common and crucial step is choosing an appropriate parameterization method, which consists of the definition of a mapping between model properties and adjustable parameters to be estimated by the algorithm (Cui et al. 2021).

Zonation and ‘pilot points’ methods are the most common approaches for the parameterization of spatially distributed parameters. The former divides the model domain into a finite number of zones where parameters are assumed to be constant (Neuman 1973; Carrera 1986). Although some algorithms allow identifying the number of zones and the positions of the discontinuities (Hayek et al. 2009), this approach is still conditioned by prior knowledge of geological information and stratigraphy (Klaas and Imteaz 2017). As stated by Zhou et al. (2014), such parameterization may cause a structural error by introducing unrealistic, arbitrary discontinuities between zones. As an alternative to zones, the pilot points method introduced by de Marsily (1978) estimates the parameter values at a predetermined number of fixed points distributed in the model domain. Values at model cells are obtained by a smooth interpolation technique such as kriging (de Marsily 1984). A brief overview and history of the method has been recently proposed by White and Lavenue (2023).

Pilot points have been widely used for groundwater model calibration, and several practical concerns for implementing this approach have been widely discussed (Certes and de Marsily 1991; Doherty 2003; Doherty et al. 2010; Fienen et al. 2009). Pilot points generally lead to smooth isotropic fields, but recent studies have focused on the representation of hydraulic connectivity (Schilling et al. 2022; Trabucchi et al. 2022). Despite these advances, some issues are not fully addressed, particularly regarding the distribution of pilot points in the model domain, which can lead to subjective choices and diminish the feasibility or efficiency of the method. Choosing a small number of pilot points can lead to satisfactory identification of pilot-point parameter values with limited computational resources, but it decreases the level of detail and the description of heterogeneities and therefore misses the opportunity to explore some structural errors that could be made when conceptualizing the model (LaVenue and Pickens 1992). In contrast, using numerous pilot points can improve the description of heterogeneities, although this increases the need for computational resources. Additionally, using too many pilot points can lead to overparameterization where the model becomes too complex and sensitive to noise in the data, which can result in numerical instability and difficulty in obtaining a unique solution to the inverse problem. Regularization can avoid the latter (Alcolea et al. 2006; Fienen et al. 2009); however, the numerical burden remains an issue. To date, a limited series of recommendations are available to define the appropriate number of pilot points and their suitable location. Gómez-Hernánez et al. (1997) recommend placing pilot points in a regular grid with a spacing of one-third of the variogram range. Wen et al. (2006) reported that placing pilot points with random methods yields better results. Doherty (2003) and Alcolea et al. (2006) suggested including as many pilot points as possible with the appropriate mathematical regularization and subspace methods (Christensen and Doherty 2008). It is not often mentioned that for real-world studies, measurements tend to be heterogeneously distributed in the model domain, so pilot points may be unevenly constrained if they are homogeneously distributed. Few authors discussed the relationship between pilot point placement and measurement availability, except Doherty et al. (2010), who recommended placing pilot points in areas with the highest data density (typically between wells in the groundwater flow direction). Klaas and Imteaz (2017) investigated the effects of pilot point density in a regular grid and discussed the interest in placing pilot points based on the experimental groundwater head contours. More recently, Baalousha et al. (2019) highlighted the effect of pilot point numbers and configurations on calibrated parameters, and Kapoor and Kashyap (2021) proposed a hybrid placement method based on both hydraulic head measurements and transmissivity estimates derived from pumping tests.

Despite the studies already mentioned, configuring pilot points remains challenging and mainly constrained by practical concerns and manual placement. This paper aims to define a reproducible strategy that would minimize the number of pilot points, save computational resources, and maximize the fit to measured data for the heterogeneities to be described at best, given measurements unevenly distributed in space.

This study investigates the efficiency of parameterization for both regular and adaptive grids of pilot points, where the density of pilot points is increased in the function of refinement criteria. The following questions arise: What is the optimum spacing for regular grids of pilot points? Can irregular, adaptive grids of pilot points improve the calibration process? If so, what are the optimum refinement criteria for these grids? And eventually, should iterative refinements of pilot points be considered? This paper addresses these issues by performing a series of tests on a synthetic model. The best approach is eventually implemented in a real-world case study: the multilayered groundwater model of the south-western geological basin of France.

Methods

Parameter estimation

The calibration has been conducted with the Gauss–Levenberg–Marquardt Algorithm (GLMA) as implemented in PEST_HP (Doherty 2020). The Jacobian matrix is computed at each iteration to form a linearized version of the model, containing parameter sensitivities to each measured observation. Sensitivities can be estimated with a classical 2-point finite difference approach or a more robust 3-point parabolic approximation (Doherty 2015). The former approach requires m + 1 model calls, while the second, more demanding method requires (2m + 1) model calls for each iteration, with m being the number of adjustable parameters. The computational burden associated with the computation of the Jacobian matrix increases with the number of adjustable parameters, which constrains the application of the GLMA to highly parameterized models.

At each iteration of the calibration process, the algorithm upgrades the parameter vector to reduce the misfit between model outputs and the measurements by minimizing the measurement objective function corresponding to the sum of weighted squared residuals, \({\phi}_{\mathrm{m}}=\sum_i{\left({w}_i{r}_i\right)}^2\), where the residual ri refers to the difference between the ith model output and its observed counterparts and the weights (wi) are assigned based on the inverse of the standard deviation of measurement error. With this weighting scheme and assuming a perfect model, the target value for ϕm is the number of measurements. For real-world cases, the occurrence of model structural error entails that ϕm converges to higher values (Doherty 2015). The closer the final objective function value is to the target objective function value, the better the calibration is in terms of fitting of measured data.

This study employed the truncated singular value decomposition (SVD) and Tikhonov regularizations to stabilize the inversion of the underdetermined problem and guarantee the convergence to a unique solution (Tonkin and Doherty 2005). Zero-order (preferred value) and first-order (preferred homogeneity) Tikhonov regularizations were both employed (Tikhonov and Arsenin 1977; Doherty 2015). The former attempts to draw estimated pilot point values toward their initial (prior) value. The latter promotes homogeneity between neighboring pilot point values by introducing the weighted difference between pilot point values in the regularization objective function. The termination criteria were chosen for the algorithm to stop when the reduction in the objective function is less than 1% for the last three iterations, or when the total number of iterations exceeds 30.

Pilot point parameterization

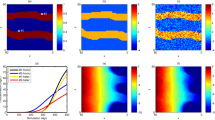
In this approach, pilot points are placed according to a grid, which is necessarily coarser than the model grid and should not be confused with it. Two different strategies for pilot point placement have been considered: (1) regular grids with uniform spacings and (2) adaptive grids with local refinements (Fig. 1). In addition, an iterative strategy was explored, involving the estimation of parameters between successive refinements of the pilot point grids. The refinement is conducted following a 2D quadtree style, which allows cells to be subdivided repeatedly into four child cells. It should be noted that the parent pilot points are kept throughout refinement steps to facilitate the implementation of the iterative approach. Four refinement criteria were evaluated for each pilot point: the composite scaled sensitivity, the component of the gradient of the objective function corresponding to the pilot point, the parameter identifiability, and the density of the measurement data, which corresponds to the number of measures in the cell of the pilot points grid (Fig. 1). The positioning of the pilot points was achieved using Python scripts.

Fig. 1
figure 1

a Base pilot-points distribution according to a regular grid and b adaptive parameterization where pilot points constrained by measurements are refined following the quadtree grid method. Cells with black bold outlines are for the grid of pilot points, and cells with thin grey outlines are for the model grid

Full size image

The composite scaled sensitivities (CSS) describe the intensity of the control provided by a measured dataset over a given parameter (Hill and Tiedeman 2006):

$${\mathrm{css}}_{\mathrm{i}}=\left.\left(\frac{{\textbf{J}}^{\mathrm{t}}\textbf{QJ}\Big){}_{\mathrm{i}\mathrm{i}}^{\frac{1}{2}}}{n}\right)\right)\times \mid {\textbf{b}}_{\mathrm{i}}\mid$$
(1)

where J is the Jacobian matrix, Q is the measurement weight matrix, b is the vector of (transformed) parameter values, and n is the number of nonzero-weighted observations (Doherty 2015). The component of the gradient of the objective function pertaining to the i-th parameter can be expressed as follows (Doherty 2015):

$$\frac{\partial \phi }{\partial {b}_{\mathrm{i}}}=2{\left[{\textbf{J}}^{\mathrm{t}}\textbf{Qr}\right]}_{\mathrm{i}}\kern0.5em$$
(2)

where r is the vector of the model to measurement residuals. \(\frac{\partial \phi }{\partial {b}_{\mathrm{i}}}\) is the partial derivative of the objective function ϕ with respect to a parameter bi.

The parameter identifiability, fi corresponds to the cosine of the angle between the vector pointing in the parameter’s direction and its projection onto the calibration solution space (Doherty and Hunt 2009). It ranges between 0 for complete nonidentifiability and 1 for complete identifiability. It can be used to describe the capability of a calibration dataset to constrain a parameter value as it accounts for both parameter sensitivity and correlation. The computation of fi is conducted after singular value decomposition (SVD) of the weighted Jacobian matrix and subdivision of the parameter space into a “solution” and a “null” space. The dimension of the solution space is considered optimal when the introduction of additional eigenvectors leads to an increase (rather than a decrease) in the associated error variance (Doherty 2015). This was performed with the PEST SUPCALC utility (Doherty 2019).

The adaptive approach is tested with refinements of the pilot points grid conducted prior to the calibration process, and in an iterative manner (Fig. 2). The iterative refinement procedure starts with the initial, regular grid of pilot points until the convergence of the objective function. The parameterization is then updated by refining the pilot points satisfying the refinement criteria. The calibration is then resumed with the new parameterization and the procedure continues until the objective function reaches the target value.

Fig. 2
figure 2

Summary of tested strategies for optimizing the pilot points configuration

Full size image

The calibration efficiency has been evaluated for both regular and adaptive parameterization approaches. The comparison is conducted by analyzing the evolution of the objective function with respect to the number of model calls. The best configuration presents the fastest decrease of the objective function to the target value at the minimum calculation costs.

The interpolation of hydraulic conductivity at model cells was undertaken by kriging from pilot point values as implemented in the PyEMU Python package (White et al. 2016). For all the configurations considered in this study, the kriging factors were computed with Python considering an exponential variogram with a range of twice the largest spacing between pilot points. This as a ratio avoids the “bulls-eyes” effect in the interpolated field. The exponential variogram model is recommended when describing the heterogeneity of hydraulic properties because it avoids the occurrence of parasitic values between closely spaced pilot points of very different values (Doherty et al. 2010).

Synthetic model

Model description

Investigations are conducted on a synthetic model derived from Moore and Doherty (2005), which considers steady-state flow in a confined aquifer described with a single 10-m-thick layer over a domain of 500 m × 800 m, discretized with a regular grid of 10 m square cells (Fig. 3). A fixed inflow of 1 m3 day-1 is imposed at the model upper boundary, and heads are fixed at 0 m along the lower boundary.

Fig. 3
figure 3

The synthetic model: a model domain and boundary conditions, b True hydraulic conductivity distribution, and c Simulated heads and locations of observation wells (red crosses)

Full size image

The reference hydraulic conductivity field was generated by Gaussian sequential simulation with Gstat (Pebesma 2004) using a log exponential variogram with a range of 100 m and a sill of 0.3. Flow within the domain was simulated using the finite-difference MARTHE model (Thiery 2015). Simulated heads were extracted at 26 observation wells unevenly distributed over the model domain to reflect real-world configurations. Indeed, observation networks typically present clusters with high measurement density and areas deprived of measurements. Gaussian noise was added to the simulated heads with a standard deviation of 0.01 m to introduce measurement error. Following the weighing strategy described in section ‘Parameter estimation’, an equal weight of 100 was assigned to each measure, corresponding to the inverse of the standard deviation of measurement error. In such conditions, the target measurement objective function corresponds to the number of measured data (here, 26).

Pilot points

The initial exploration involved regular grids of pilot points, covering spacings ranging from 24 to 3 model cells (Fig. 4). This resulted in varying numbers of pilot points, starting at 12 for the largest spacing (240 m) and reaching 456 for the shortest spacing (50 m).

Fig. 4
figure 4

Regular grids of pilot points with four different spacing (a REG 24, b REG 12, c REG 16, d REG 3 model cells). Measurements are depicted with red crosses and pilot points with black points. N is the total number of pilot points

Full size image

Adaptive grids of pilot points were obtained by local refinements of the coarse regular grid with a spacing of 24 model cells with 12 pilot points (referred as “REG 24”). Different refinement strategies were tested with 4 different criteria (refer to section ‘Parameter estimation’ for a description of these criteria). In all, 30% of the pilot points presenting the highest criteria values were subsequently refined to reach a resolution twice finer than the original grid. The number of pilot points after the refinement is 52, except for the refinement based on the measurement availability, where the total number is 40. There are fewer pilot points for this criterion due to successive refinements of the same points, which are discarded. The adaptive parameterization was tested from the beginning of the calibration (Fig. 5) and iteratively (Fig. 6). In the first approach, the grid of pilot points is refined according to the criteria inferred from the initial parameter values. In the second approach, the first calibration is conducted with a regular grid of pilot points, and the refinement criteria are then computed from the Jacobian matrix with updated parameter values. As for consequence, the set of pilot points to be refined may differ between the two approaches.

Fig. 5
figure 5

Initial adaptive grid with refinement of pilot points based on a measurements availability, b sensitivity, c identifiability, and d the gradient objective function. “Parent” pilot points (pp) are displayed as large grey points, “child” pilot points as small black points, and measurements as red crosses

Full size image
Fig. 6
figure 6

Iterative adaptive grids. “Parent” pilot points (pp) are displayed as large grey points, “child” pilot points as small black points, and measurements as red crosses. 30% of the initial pilot points are refined two successive times based on a measurements availability, b sensitivity, c identifiability, and d the highest value of the objective function’s gradient

Full size image

Results

The calibration efficiency for the configurations of pilot points is evaluated by comparing the evolution of the measurement objective function with the number of model runs. The discussion begins with the results achieved using regular grids of pilot points (Fig. 7a). Large spacings between pilot points with 24 and 12 model cells (REG 24 and REG 12) led to fast convergence of the objective function value but did not wholly assimilate the measurements dataset. The objective function target value was reached with small spacings but with increased calculation times (REG 6 and REG 3). The best convergence of the objective function at minimum calculation costs is obtained with a spacing of 6 (REG 6) model cells. Configurations with spacings of 3 (REG 3) model cells provide the same level of fit but require almost double model runs. This demonstrates the effect of pilot point numbers on fitting the measurements and the importance of choosing adequate spacing for the regular grid. Though it may be of interest for uncertainty analysis, including as many pilot points as possible for the calibration step increases the computational burden, which can be a limiting factor when dealing with highly parameterized models with long computation time.

Fig. 7
figure 7

Evolution of the measurement objective function with the number of model runs for different pilot point parameterizations: a regular grids, b initial adaptive grids, and c iterative adaptive grids. Results of regular grids are also presented to facilitate the comparison (b–c)

Full size image

The size of the solution space for the configurations with regular grids increases with the number of adjustable parameters (pilot points) but reaches a plateau beyond 126 pilot points (spacing of 6 grid cells; Fig. 8). Thus, when seeking to enhance the fit of measurements, it is unnecessary to increase the number of parameters beyond a certain threshold.

Fig. 8
figure 8

Evolution of the dimension of the solution space for the regular grids of pilot points with different spacing

Full size image

The performance of the initial adaptive configurations appears to be largely dependent on the choice of the refinement criterion (Fig. 7b). Refinements based on measurement availability and parameter identifiability lead to better performance than regular grids. In contrast, refinements based on CSS and the gradient of the objective function did not reach the target objective function and required more than 4,400 model runs for convergence.

For the adaptive approach (Fig. 7c), the refinements of the pilot points grid with the different criteria were conducted after calibration with the regular grid with a spacing of 24 model cells. From these results, the interest of the iterative approach is not salient compared to the initial adaptive approach. Except for the refinement based on the number of measurements, the performance of the iterative adaptive strategy is poor compared to the best configuration with the regular grid.

The results for the three different approaches for pilot point placement (regular grid, initial adaptive grid, iterative adaptive grid) are summarized in Fig. 9. The best configurations with low objective function and a small number of model runs (bottom left portion of the plot) correspond to the initial adaptive approach based on measurement availability (N = 40 pilot points). The regular grid with a spacing of 6 model cells also reaches the target objective function value, but at a much greater cost in terms of model runs. The hydraulic conductivity fields for these two “best” configurations are compared to the “reference” field in Fig. 10. As expected, only large-scale heterogeneities can be described with a better resolution where the measured dataset is dense. In areas poorly constrained by measurements, the pilot points of the regular grid present similar values, which leads to an outcome similar to the more parsimonious adaptive approach.

Fig. 9
figure 9

Values of measurement objective functions against the total number of model calls at convergence for the regular, initial adaptive, and iterative adaptive parameterizations. The best parameterization is obtained with the initial adaptive approach (bottom left), which presents the lower number of model runs to reach the target objective function. “nobs” stands for the number of observations, “ident” represents identifiability criteria, “css” denotes the composite scaled sensitivity, “grad” signifies the gradient of the objective function, and “reg” refers to the regular grid, followed by the corresponding spacing. For example, “reg12” indicates that the spacing for the regular grid is 12

Full size image
Fig. 10
figure 10

Comparison of the a “true” hydraulic conductivity field with b its estimated counterparts obtained with the best regular grid (pilot point spacing of six model cells), and c the adaptive grid refined according to the measurement density

Full size image

Application to a regional flow model

The findings obtained with the synthetic model have been applied to estimate the hydraulic properties of the regional groundwater "MOdel of North Aquitania" (MONA). The model was developed by the French Geological Survey (BRGM) to simulate flow and investigate the impact of pumping in the extensive unconfined aquifers supplying the city of Bordeaux. The model covers the northern part (46,032 km2) of the French south-west sedimentary basin (Fig. 11). It has 15 aquifers interbedded by aquitards discretized with a regular grid of 2 × 2 km from Plio-Quaternary down to Jurassic units (Thiéry et al. 2011). The model does not explicitly simulate flow in the aquitards but accounts for vertical flows adjusted by a conductance parameter (pseudo-3-D assumption). The domain is bounded by Cretaceous and Jurassic outcrops to the east and north, the Atlantic Ocean and the Gironde Estuary to the west. Hydraulic heads are imposed on the western boundary, accounting for seawater level along the Atlantic Coast. Heads are also prescribed along the Garonne River and its estuary, and no-flow boundaries are assumed at the southern limit, which corresponds with the separation from the southern part of the Aquitaine basin (Buscarlet et al. 2019). Recharge is estimated annually by an empirical formula using climatic data (precipitation and evapotranspiration) from a series of weather stations (Pédron and Platel 2005). The pumping database includes 6,235 wells distributed within the 15 geological formations (Saltel et al. 2016). The diffusivity equation is solved at the annual time step in a finite volume scheme with MARTHE (Thiery 2015).

Fig. 11
figure 11

Representation of the aquifers considered in the MONA. The insert shows the location of the Aquitaine region in France

Full size image

The purpose of this calibration exercise is to use historical head measurements to improve the predictive capacity of the model for simulating heads in different prospective management scenarios over the next decades. The model was calibrated in the transient state over the 1972–2011 period using 423 observation wells. To assess the measurement noise and assign weights, two types of uncertainties were considered: the measurement uncertainty, 𝜎m, and the uncertainty raised from the aggregation of incomplete daily data at the annual time step, 𝜎a. Assuming a standard deviation of ±3 m at the 68% confidence level for measurement uncertainty, arising from all potential errors in the measurements (groundwater depth and borehole leveling), the aggregation uncertainty was determined for each individual annual value by calculating the standard error of the mean (Hughes and Hase 2013).

The parameter estimation procedure focused on the distributed hydraulic properties: the horizontal hydraulic conductivity of aquifers, Kh, the vertical hydraulic conductivity of aquitards, Kv,, the unconfined specific yield ω, and the specific storage, Ss. Prior information on these parameters was first collected for each layer of the model from the French geological database (BSS) and several local studies (Moussié 1972; Hosteins 1982; Larroque 2004). These values were used as a starting point for the GLMA and were considered the preferred value for 0-order Tikhonov regularization.

Parameterization

Both pilot points (PP) and zones of piecewise constancy (ZPC) were used for the parameterization of this regional model, which is summarized in Table 1. The specific yield (ω) was parameterized with pilot points for the first layer (QUAT) with regular grids of pilot points with a spacing of 20 model cells (40 km). ZPC were used for layers 2–15 since most parts of these aquifers remain confined and the annual time step reduces the sensitivity of this parameter in unconfined areas. For the specific storage (Ss), pilot points were placed with a spacing of 40 model cells (80 km) in the permanently confined parts of the layers, and ZPC were used for the permanently unconfined parts, where Ss are insensitive. The vertical hydraulic conductivity of aquitards was parameterized with a regular grid of pilot points with a spacing of 40 model cells (80 km). Maps with the locations of pilot points are provided in all the items in the Appendix Figs. 14, 15, 16, 17, 18, 19 and Table 2.

Table 1 Summary of the parameterization of the regional model
Full size table

Several configurations were considered for the parameterization of horizontal hydraulic conductivity (Kh). A coarse regular grid with a 20-model-cell spacing (40 km) and a finer regular grid with a 5-model-cell spacing (10 km) were considered. An adaptive grid of pilot points was also taken into account, employing measurement density as the refinement criterion. Pilot points with a minimum of 1 measurement within their neighboring values were refined twice, resulting in a 5-model-cell spacing (10 km) between pilot points in areas with a high measurement density and 20-model-cell spacing (40 km) in areas with sparse measurements. Both the initial and iterative adaptive refinement strategies were tested. In areas with high measurement density, the adaptive grids present the same spacing as the fine regular grid. It should be noted that spacings between pilot points are large (10–80 km), even with the local refinements. With such parameterizations, only the most salient heterogeneities impacting the regional groundwater flow can be described. This can be appropriate for the simulation of the long-term regional flow dynamics; however, this approach would not be relevant to describe small-scale local heterogeneities in the hydraulic property fields, which would require a much denser measurement dataset.

Results

The calibration was conducted with three different strategies for the parameterization of hydraulic conductivities with pilot points: the coarse regular grid, the initial adaptive grid, and the adaptive grid with an iterative approach. Each model run took ~ 20 min of CPU time and calculations were parallelized over 114 CPU cores. The fine regular grid of pilot points resulted in an excessive number of parameters and prohibitive computation time, so it could not be tested.

The evolution of the objective function for the tested configurations is presented in Fig. 12. As expected, the configuration with the coarse grid of pilot points converged to a relatively high value of the objective function, illustrating the incapacity of this parameterization to represent sufficiently fine details in the hydraulic conductivity field to satisfy the measurement dataset. The iterative adaptive approach performed well but with results close to the initial adaptive approach, which is easier to implement. The initial adaptive approach, which took a week and 56,393 model runs to converge, can therefore be considered the best approach.

Fig. 12
figure 12

Summary of objective function vs. the number of model runs for regular and adaptive approaches

Full size image

The post-calibration hydraulic conductivity fields obtained with the “best” initial adaptive approach are provided in Fig. 13. The other estimated fields and performance statistics are provided in the Appendix Figs. 14, 15, 16, 17, 18, 19 and Table 2. Overall, simulated values reproduce their observed counterparts with a root mean squared error (RMSE) of 6 m and a mean bias of −0.16 m. The goodness of fit varies substantially between layers. Errors are the largest for the deep layers, for which the density of measurements is low. The misfit is more heterogeneous in those layers that include some outliers with high error values that affect the average. The outliers are mostly related to insufficient or inconsistent data to constrain the calibration; therefore, the algorithm is not focusing on their fits since the weight assigned is low.

Fig. 13
figure 13

Post-calibration horizontal hydraulic conductivities (Kh) obtained with the initial adaptive approach

Full size image

Discussion

The present study confirmed the importance of pilot point distribution on calibration efficiency and provides guidelines for optimizing the placement of pilot points when the computational burden matters, such as for highly parameterized regional models with long execution times. The purpose was to identify the configuration leading to the fastest convergence of the objective function to the target value, indicative of appropriate assimilation of the measured dataset.

Investigations were conducted on a synthetic model with both regular and adaptive grids of pilot points. The first analysis with regular grids revealed the importance of choosing an appropriate spacing between pilot points. Large spacings lead to fast convergence of the objective function but do not allow complete assimilation of the measured dataset. In contrast, including as many pilot points as possible for calibration, as suggested by Alcolea et al. (2006), leads to a good fit of observed data but increases the computational burden. The optimum spacing, leading to the fastest convergence of the objective function to the target value was obtained with a pilot point spacing of 60 m and a variogram range of 120 m, which is close to the variogram used for the generation of the synthetic hydraulic conductivity field (100 m). Such a result is in line with the expectations for a synthetic case, but further questions remain when dealing with unknown, real-world hydraulic conductivity fields, for which the structure of heterogeneities that matter for the modeling exercise is not precisely known. An option can be to use the calibration dataset to investigate the size of solution space and get insights on the optimum number of pilot points by truncated singular value decomposition. This requires the computation of a Jacobian matrix for each configuration which may be computationally intensive. Furthermore, the size of the solution space suggested by this approach is often too large because its computations fail to account for the contribution made to measurement uncertainty by structural noise of unknown covariance structure (Doherty et al. 2010).

Results of the synthetic case also revealed that an adaptive approach with refinement based on measurement density leads to better performances than the optimum regular grid of pilot points. Both configurations reached the target objective function and a similar description of the heterogeneity, but the adaptive approach required much fewer model calls. This stems from the fact that measurements were heterogeneously distributed, as is often the case in the real world. The refinement criteria based on the measurement density outperformed the criteria derived from parameter sensitivities (CSS, identifiability, gradient of the objective function). This is quite unexpected given previous studies on this topic (Ackerer et al. 2014; RamaRao et al. 1995) but can be interpreted as an effect of the local and approximate nature of model derivatives obtained by perturbation of prior (initial) parameter values in this study. Apart from its efficiency, a great advantage of the criteria based on measurement density is that it does not require any model runs to be evaluated. In contrast, the iterative adaptive approach, which involves parameter calibration before the refinement of the pilot points grid, yields disappointing results. This may be explained by the characteristics of the GLMA, which could remain “trapped” in a local optimum in the parameter space and prevent further descent of the objective function after refinement. Another tuning factor of the adaptive strategy is the proportion of pilot points to be refined. This threshold was set to 30% in this study, and those pilot points were refined two successive times, leading to the best results in this case but may be subject to further investigation and adjustments in other case studies.

The best strategy identified with the synthetic model (adaptive grid of pilot points refined according to measurement density) was tested on a real-world, regional groundwater model together with two other configurations for comparative purposes: a coarse grid and an iterative adaptive approach. As expected, the objective function converged to a high value with the coarse grid. The iterative adaptive approach gave satisfactory results but was outperformed by the adaptive approach, which is easier to implement. This approach can therefore be recommended for similar configurations, which is a step forward, but a series of improvements and perspectives can be outlined.

While it can significantly facilitate parameter estimation of highly parameterized models, the main limitation of the presented approach is its implication for uncertainty quantification. The proposed refinement strategy focuses on the heterogeneity that can be described by the assimilation of the measured dataset, not necessarily on the heterogeneity that matters for the predictions of interest. As for consequence, heterogeneities in areas with no data may be poorly described, and the uncertainty of related predictions can be underestimated. Measurements are usually conducted where they are supposed to be of greater interest, but this is not always the case. The proposed approach could be extended with refinement criteria not only based on the measurement dataset but also criteria derived from prediction sensitivities, which would allow better consideration of heterogeneities that matter for predictions of interest for decision-making.

The presented approach is optimum in the sense that it maximizes data assimilation while minimizing the number of parameters, and consequently, the computational burden of parameter estimation. This effort on pilot point parameterization may yet be insufficient for parameter estimation to become tractable. It should be accompanied by optimizing the numerical solver and model complexity level that may reduce computation times (Doherty and Moore 2020; Guthke 2017). Apart from reducing the number of parameters and model run times, more frugal parameter estimation algorithms may also be considered. Randomized Jacobian estimates (Doherty 2020) can reduce the need for model calls, and ensemble-based approaches such as IES (White 2018) can also be considered. Most likely, a smart combination of these options may be relevant to address impractical inverse problems.

Conclusion

The parameter estimation of highly parameterized models with long run times, such as regional multilayered groundwater models, is often associated with challenges that threaten its practicality. In such models, most parameters are representative of parameter values at pilot points. A series of configurations was explored to optimize their distribution and reduce their number. The strategy leading to the best data assimilation, while minimizing the computational burden, is an adaptive grid of pilot points with a refinement based on measurement density. In this approach, the grid of pilot points was refined in areas with the largest number of measurements. This strategy was successfully implemented on a regional flow model, illustrating its efficiency; however, the best parameterization approach to fit the available measurements may not be optimum for uncertainty quantification. To this purpose, the current approach could be extended with pilot point refinement criteria accounting for the sensitivity of predictions of interest. Evaluating these options is a topic for future work.