Introduction

A fundamental goal of hydrogeophysics is to quantify the in-situ hydraulic conductivity of aquifers from remotely sensed geophysical data. There are a variety of established methods for quantifying hydraulic conductivity (Butler 2005), but most are point-scale methods that provide low horizontal resolution and are generally impractical for parameterizing large-scale groundwater-flow models with complex transmissivity and hydraulic conductivity frameworks. The term “framework” is used herein to represent the spatial distribution of a hydrogeologic or geophysical property, such as hydraulic conductivity or electrical resistivity, within a gridded three-dimensional (3D) volume of Earth. This paper summarizes work done by the United States Geological Survey (USGS) whereby a geophysical approach featuring AEM data was applied to better understand selected aquifer properties (transmissivity and hydraulic conductivity) of the Mississippi River Valley alluvial aquifer.

The electrical resistivity framework is the product of an airborne electromagnetic (AEM) survey and provides a means of quantifying the transmissivity and hydraulic conductivity frameworks over thousands of square kilometers (km2) while still capturing relatively small-scale heterogeneity with horizontal and vertical resolutions of about 25 and 5 m, respectively (Bowling et al. 2006; Siemon et al. 2009; Dickinson et al. 2010; Høyer et al. 2011; Wojnar et al. 2013; Schamper et al. 2014; Marker et al. 2015; Christensen et al. 2016; Christensen et al. 2017; Knight et al. 2018; Minsley et al. 2021), provided that a petrophysical relation between electrical resistivity and either aquifer transmissivity or hydraulic conductivity is established, and the depth-of-investigation achieved by the AEM survey is greater than the depth of interest in the aquifer (Asch et al. 2015). The petrophysical relation—herein referred to as an “electric (e) – hydraulic (h) relation”—is typically difficult to establish because (1) no analytical e–h relation is known to exist (Slater 2007), (2) the resistivity ranges of different earth materials overlap and are not mutually exclusive (Palacky 1987), (3) the resistivity framework is a regularized solution of an ill-posed geophysical inverse problem and will change as the regularization is varied (Vignoli et al. 2015, 2017), and (4) the mathematical forms of empirical and semiempirical e–h relations are generally nonlinear, and the coefficients of log-linear relations (slope of the relation and y-axis intercept) can vary spatially within and between different hydrogeologic environments (Christensen et al. 2016).

Numerous empirical and semiempirical e–h relations have been proposed in the literature. Empirical e–h relations are frequently predicated upon the mutual dependence of electrical resistivity and hydraulic conductivity on porosity (Slater 2007; Kaleris and Ziogas 2015) as expressed by Archie’s law (Archie 1942; Glover 2010). Archie’s law, expressed in Eq. (1) in its basic form (excluding modifications to account for effective saturation and clay content of the geologic medium), relates the electrical resistivity (r; ohm-m) to the groundwater resistivity (rw; ohm-m), aquifer porosity (ϕ; m3 m-3), lithologic cementation exponent (m; unitless), and the electric formation factor (F = ϕ−m; unitless), but it is only applicable to fully saturated, clay-free quartz-sand formations where either the mineral grains are perfect insulators or the groundwater is electrically conductive relative to the mineral grains (Fagbenro and Woma 2013). Deviations from these conditions invalidate the resistivity–porosity relation expressed by Archie’s law (Worthington 1993).

$$r={r}_{\mathrm{w}}{\phi}^{-m}={r}_{\mathrm{w}}F$$
(1)

Common practice is to relate electrical resistivity to formation porosity by Eq. (1) and use the Kozeny-Carman model expressed by Eq. (2) (Kozeny 1927; Carman 1939; Domenico and Schwartz 1990; Revil and Cathles 1999; Slater 2007) to relate formation porosity to saturated aquifer hydraulic conductivity by the hydraulic radius, where Ks (m/s) is the saturated hydraulic conductivity, and the hydraulic radius is defined by the ratio of pore volume (Vp; m3) to pore-surface area (As; m2). Specific gravity (γ; N m–3) and dynamic viscosity (μ; N s m–2) in Eq. (2) are properties of the groundwater. The primary drawbacks of Eq. (2) are that it requires effective porosity rather than total porosity, which is challenging to quantify over large volumes of Earth, and as demonstrated by Revil and Cathles (1999) it can overestimate the hydraulic conductivity (via conversion from permeability) of a variety of porous geologic materials by more than two orders of magnitude.

$${K}_{\mathrm{s}}=\frac{\gamma }{\mu}\frac{\phi }{2}{\left(\frac{V_{\mathrm{p}}}{A_{\mathrm{s}}}\right)}^2$$
(2)

Semi-empirical e–h relations that are independent of the assumptions and constraints of Eqs. (1)–(2) have also been developed. Purvance and Andricevic (2000a, b) applied the bond-shrinkage process described by Wong et al. (1984) to the random pore-network models of Bernabe and Revil (1995) to develop generalized, semiempirical log-linear e–h relations (power-law relations in linear data space) of the form depicted in Eq. (3) between saturated hydraulic conductivity and electrical resistivity. The log10α (ft/day) and β (ft/day/ohm-m) coefficients in Eq. (3) represent the y-intercept and the slope, respectively, of the log-linear e–h relation and are spatially variable functions of the hydrogeologic environment that can be gridded to define complex hydraulic conductivity frameworks from electrical resistivity (Purvance and Andricevic 2000a, b; Christensen et al. 2017).

$${\log}_{10}{K}_{\mathrm{s}}={\log}_{10}\alpha \pm \beta {\log}_{10}r$$
(3)

The semiempirical e–h relation in Eq. (3) accounts for electrical conduction and consists of two components: (1) electrolytic conduction through the groundwater in the pore volume, characteristic of high groundwater salinity or clay-free lithologies where the mineral grains have a relatively low specific surface area (sands, gravels, and coarse silts), and (2) electrical conduction along the pore surfaces, characteristic of lithologies where mineral grains have a high specific surface area (fine silts and clays) or where groundwater resistivity is high compared to the resistivity of the mineral grains. The e–h relations described by Eq. (3) are expected to have negative slopes in lithologies dominated by electrolytic conduction through the pore volume because of the mutual increase of electrical conductivity and hydraulic conductivity with porosity. In contrast, e–h relations described by Eq. (3) are expected to have positive slopes in lithologies dominated by electrical conduction along the pore surfaces because pore-surface area increases as permeability decreases and electrical surface conduction increases as pore-surface area increases (Faye and Smith 1994; Slater 2007). Note that the signs of the slopes of the e–h relations are negated when Eq. (3) is expressed in terms of electrical conductivity, σ (S/m), because σ = r−1. The primary limitation associated with the e–h relations described by Eq. (3) is that quantification of the coefficients as functions of the variables in the hydrogeologic environment can be cumbersome.

The geoelectric parameters of transverse resistance, longitudinal conductance, and mean resistivity offer an alternative semiempirical approach to developing e–h relations to estimate aquifer hydraulic properties from electric properties (Maillet 1947; Orellana 1963; Zhody 1965, 1974, 1975; Zhody et al. 1974; Kelly 1977; Kelly and Reiter 1984; Kelly and Frohlich 1985; Mazáč et al. 1985). The geoelectric parameters are expressed as functions of layer resistivity and layer thickness in Eqs. (4)–(6), where R (ohm-m2; Eq. 4) is transverse resistance, S (Siemens; Eq. 5) is longitudinal conductance, re (ohm-m; Eq. 6) is the mean resistivity expressed as a geometric mean of the ratio of transverse resistance to longitudinal conductance, and h (m) is the layer thickness. Collectively, the geoelectric parameters describe the bulk electric properties of a layered hydrogeologic formation consisting of N layers, each characterized by finite resistivity and thickness.

$${R}_j=\sum \nolimits_{i=1}^j{h}_i{r}_i=\sum \nolimits_{i=1}^j\frac{h_i}{\sigma_i}\kern0.5em j=1,2,\dots, N$$
(4)
$${\displaystyle \begin{array}{cc}{S}_j=\sum_{i=1}^j\frac{h_i}{r_i}==\sum_{i=1}^j{h}_i{\sigma}_i& j=1,2,\dots, N\end{array}}$$
(5)
$${\displaystyle \begin{array}{cc}{r}_{{\mathrm{e}}_j}={\left[\sum_{i=1}^j{R}_i/\sum_{i=1}^j{S}_i\right]}^{{~}^{1}\!\left/ \!{~}_{2}\right.}& j=1,2,\dots, N\end{array}}$$
(6)

Researchers have shown that one or more geoelectric parameters are often correlated to aquifer transmissivity to some degree (Ikard and Kress 2016). The basis for correlation arises from the similarity of their physical representations of bulk hydraulic and electric flow, respectively. Transmissivity, being a bulk hydraulic property, represents groundwater flow parallel to the layering (typically assumed horizontal) in the hydrogeologic formation and depends on the saturated thickness of the aquifer and the hydraulic conductivity distribution within the saturated aquifer. Similarly, transverse resistance and longitudinal conductance, being bulk electrical properties, represent electrical current flow perpendicular and parallel to the geoelectric layering, respectively (Mazáč et al. 1985). Transverse resistance and longitudinal conductance are dependent upon the cumulative effects of the resistivity and thickness of the N individual layers in a composite geoelectric formation, which act as resistors in series and in parallel and control predominant current flow directions through the formation (Zhody et al. 1974). In general, the conceptual hydrogeologic and geoelectric formations are one and the same, although the hydrogeologic layering may not necessarily conform to the geoelectric layering because of micro- and macro-anisotropy in the layering. Despite anisotropy, in many cases, entire aquifer thicknesses can be represented as a single electrically equivalent layer with a finite thickness and finite mean resistivity (Kelly 1977; Kelly and Reiter 1984). The mean resistivity parameter represents the mean resistivity of the single electrically equivalent layer. Note that the mean resistivity at any given depth in the geoelectric formation is dependent on the electrical layering above and independent of the electrical layering below (Zhody et al. 1974).

This paper presents a method for developing semiempirical log-linear e–h relations between transmissivity and mean resistivity to quantify the transmissivity and hydraulic conductivity frameworks of the Mississippi River Valley alluvial aquifer (hereinafter referred to as the “alluvial aquifer”) from the electrical resistivity framework determined by frequency-domain AEM surveying (Burton et al. 2019, 2020; Pace et al. 2020; Minsley et al. 2021). Equations (4)–(6) are applied to 16,816 line-km of laterally-constrained inverted resistivity soundings covering 95,000 km2 of the Mississippi Alluvial Plain (MAP) (Burton et al. 2020) to calculate the geoelectric-parameter distributions beneath the land surface within the AEM survey area. The calculated geoelectric parameters were correlated to a compiled geospatial database of 160 historical alluvial-aquifer transmissivity data values (Pugh 2008, 2022a), quantified from aquifer tests performed within the AEM survey area of the MAP, to develop log-linear e–h relations between alluvial aquifer transmissivity and mean resistivity that have the form depicted in Eq. (7), where T (ft2/day) is transmissivity and log10α and β coefficients are as defined in Eq. (3) with empirical units of ft2/day and ft2/day/ohm-m, respectively when used in Eq. (7).

$${\log}_{10}T={\log}_{10}\alpha \pm \beta {\log}_{10}{r}_{\mathrm{e}}$$
(7)

The e–h relations described by Eq. (7) were applied to 2,364 line-km of laterally constrained inverted resistivity soundings of Burton et al. (2019) covering the 1,000-km2 30-layer, 301-row, 351-column grid for the Shellmound, Mississippi, study area (hereinafter referred to as the “Shellmound grid”) to calculate transmissivity and hydraulic conductivity frameworks within the Shellmound grid where aquifer-test data are currently (2023) sparse. The Shellmound grid is intended for use in future groundwater flow models of the Shellmound study area. The values of transmissivity and hydraulic conductivity calculated in cells of the Shellmound grid with each e–h relation were compared to transmissivity and hydraulic conductivity data quantified by recent (2019–2020) slug tests in alluvial-aquifer wells within the Shellmound grid to assess the accuracy of each e–h relation for defining the complex hydraulic frameworks from the electrical resistivity framework.

Description of the Study Area

Mississippi Alluvial Plain

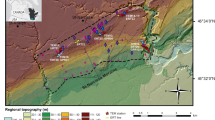
The Mississippi Alluvial Plain (MAP; Fig. 1) is a physiographic province within the larger Mississippi Embayment aquifer system (hereinafter referred to as the “embayment aquifer”; Fig. 1a and b, purple boundary). The sediments that contain the embayment aquifer were deposited in the Gulf Coast geosyncline and the Mississippi embayment during the Paleocene, Eocene, and early Oligocene epochs of the Tertiary period, and during the Pleistocene and Holocene epochs of the Quaternary period (Hosman and Weiss 1991). The Gulf Coast geosyncline is a plunging geosyncline whose axis roughly parallels the Mississippi River and trends southward from its northern terminus in Illinois toward the Gulf of Mexico (Hosman and Weiss 1991); its southwestern extent is the Sabine Uplift in Texas and its southeastern extent is western Florida (Hosman and Weiss 1991; Arthur 2001; Stanton and Clark 2003; Hart and Clark 2008; Hart et al. 2008; Clark and Hart 2009). From the land surface down, the sediments of the embayment aquifer are grouped into numerous hydrogeologic units, starting with Quaternary (Holocene alluvial and Pleistocene terrace) alluvial and terrace deposits that form the alluvial aquifer. The alluvial aquifer is underlain by Tertiary (Oligocene) deposits that form the Vicksburg-Jackson confining unit contained in the Vicksburg Formation of the Vicksburg Group (where present) and in the Jackson Formation of the Jackson Group (Hosman and Weiss 1991; Hart and Clark 2008; Hart et al. 2008; Clark and Hart 2009). The structural and stratigraphic relations and spatial correlations of these units across several states are illustrated and described in detail by Hart et al. (2008), Hart and Clark (2008), and Clark and Hart (2009), and interpreted by Minsley et al. (2021) from AEM resistivity data covering more than 140,000 km2 in the MAP physiographic province.

Fig. 1
figure 1

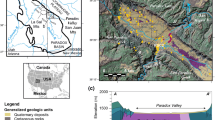
a Location map of the study area. b Map of the Mississippi Alluvial Plain (MAP) showing the locations of historical aquifer test data (blue circles; Pugh (2008), (2022a), recent (2019–2020) slug test data (red circles; Pugh 2022b), flight lines of airborne electromagnetic (AEM) surveys (gray lines; Burton et al. 2020), and contours of the 2018 potentiometric surface in the Mississippi River Valley alluvial aquifer (blue contours in units of feet; McGuire et al. 2020; 1 foot = 0.3048 m). Each sounding along the AEM flight lines represents a resistivity sounding with depth-of-investigation between 60 and 80 m beneath the land surface. The black square represents the 1,000-km2 grid for the Shellmound, Mississippi AEM survey area of Burton et al. (2019) (Shellmound grid). c Enlarged view of the Shellmound grid with 2018 potentiometric contours and locations of recent slug tests. Note that flight lines of the Burton et al. (2019) AEM survey are not depicted for clarity

Full size image

Mississippi River Valley Alluvial Aquifer

The alluvial aquifer, deposited by the Mississippi River and its tributaries, provides the most aerially extensive and abundant source of water in the embayment aquifer (Stanton and Clark 2003). It is present at the land surface in parts of southeast Missouri, northeast Louisiana, western Mississippi, western Tennessee and Kentucky near the Mississippi River, and throughout eastern Arkansas (Hart et al. 2008). The alluvial aquifer overlies subcrops of all tertiary aquifers and confining units within the MAP physiographic province. The potential for hydraulic connection between the alluvial aquifer and underlying tertiary aquifers is variable and exists where the alluvial aquifer overlies or is incised into tertiary aquifers (Hosman and Weiss 1991; Minsley et al. 2021).

Alluvial-aquifer sediments range in size from coarse gravel to clay but are primarily sand and gravel (Hart et al. 2008; Hart and Clark 2008). Coarse sands and gravels are located in the basal layers of the alluvial aquifer, and the alluvial sediments typically grade upwards into fine sands, silts, and clays at the top (Hart et al. 2008), although fine sediments occur to varying degrees throughout the entire thickness of the alluvial aquifer (Sumner and Wasson (1990); Hosman and Weiss 1991; Arthur 2001). The fine sands, silts, and clays at the top confine the aquifer over most of its surface area (Arthur 2001; Stanton and Clark 2003) and are referred to herein as the “confining layer,” (Minsley et al. 2021) whereas the coarse sands and gravels at the base form the productive zone and are capable of yielding more than 11,000 L/min to water wells (Hosman and Weiss 1991; Hart et al. 2008). The reported saturated thickness of the alluvial aquifer generally varies between 30.5 and 61 m, and the thickest sections of up to 88 m are in southeast Missouri and northwest Mississippi (Hart et al. 2008). The mean saturated thickness of the alluvial aquifer reported by Hart et al. (2008) was 40 m.

Resistivity of the Mississippi Alluvial Plain

The resistivity structure of the MAP physiographic province is illustrated in detail by Minsley et al. (2021) by the resistivity soundings along flight lines depicted in Fig. 1b, and interpreted by Minsley et al. (2021) in terms of regional and local-scale hydrogeology. According to Minsley et al. (2021), lithology appears to be a primary driver for resistivity structure in the MAP physiographic province, and specific conductance of the groundwater appears to exert slight overall influence on the resistivity variation across the study domain except in specific regions where specific conductance of the groundwater is high. In the regional-scale resistivity structure, Wisconsin-age valley train deposits (Saucier 1994), as well as point bars and meanders of modern river networks appear as resistive features in the uppermost 5 m, whereas fine-grained backswamp deposits are characterized by low resistivity in the upper 5 m (Minsley et al. 2021). Lateral resistivity transitions between about 5 and 30-m depths correspond to braid belts mapped by Rittenour et al. (2007). At 20–25 m depth, intermediate to high-resistivity values are consistent with coarse-grained sediments of the alluvial aquifer, and lower resistivity values are consistent with fine sediments and structural highs where Tertiary units are close to the surface (Minsley et al. 2021). Beneath the alluvial aquifer, about 30–50 m below the land surface in most of the region, Minsley et al. (2021) showed that resistivity values were strongly correlated with Tertiary subcropping units through a comparison of the hydrogeologic layers in the Mississippi Embayment Regional Aquifer Study (MERAS) groundwater-flow model published by Clark and Hart (2009), particularly the low resistivity values that correspond to the clay- and shale-rich Vicksburg-Jackson confining unit.

Materials and Methods

Data Compilation

The datasets used in this work (Figs. 1 and 2), and the computer codes used to operate on these datasets and produce electric and hydraulic frameworks described herein, are published online as a US Geological Survey data release by Ikard et al. (2022). The datasets used in this work were produced and reformatted from the parent datasets described and cited in this section and consisted of historical (1940–2006) and recent (2019–2020) aquifer test data distributed throughout the MAP (Fig. 1), AEM resistivity soundings surveyed over the 1,000-km2 Shellmound grid in 2018 and over a larger 95,000-km2 area of the MAP in 2018–2019 (Fig. 1), and gridded surfaces defining hydrogeologic layers in the Shellmound grid (Fig. 2). The historical aquifer-test data consisted of 160 published alluvial-aquifer transmissivity data quantified by pumping-tests performed throughout the MAP area in Louisiana, Mississippi, and Arkansas (Pugh 2008; Pugh 2022a), although none were available within the Shellmound grid. The historical aquifer-test data were produced by commercial, academic, and government sources and dispersed in various databases and scientific publications. These data were used to develop e–h relations between alluvial-aquifer transmissivity and mean resistivity over the MAP physiographic province. The recent aquifer-test data consisted of 16 alluvial-aquifer transmissivity and hydraulic conductivity data quantified by slug tests performed in wells within the Shellmound grid during 2019–2020 (Pugh 2022b). The recent slug-test data were used to assess the accuracy of the e–h relations developed from historical aquifer-test data by comparison with transmissivities and hydraulic conductivities simulated in the Shellmound grid from electrical resistivity (section ‘Geoelectric and hydrogeologic frameworks of Shellmound, Mississippi’).

Fig. 2
figure 2

Images of gridded surfaces used to quantify hydraulic properties of the Mississippi River Valley alluvial aquifer in the Shellmound, Mississippi study area from e–h relations between mean electrical resistivity and transmissivity of the alluvial aquifer. a Surface elevation in meters. b 2018 potentiometric-surface elevation, in meters (McGuire et al. 2020). Note that corresponding potentiometric surface contours in Fig. 1 are in feet. c Elevation of the base of the alluvial aquifer, in meters (Torak and Painter 2019a, b). d Alluvial aquifer saturated thickness, in meters. All surfaces are referenced to the North American Vertical Datum of 1988

Full size image

Laterally constrained inverted-resistivity-soundings produced by frequency-domain AEM surveys of Burton et al. (2019) and (2020) were used to calculate the mean resistivity of the alluvial aquifer within the MAP physiographic province and Shellmound grid areas. The AEM survey of Burton et al. (2019) was flown with 250–1,000-m spaced east-west flight lines over the Shellmound grid and produced 2,364 line-kilometers (km) of high-resolution inverted resistivity soundings covering an area of about 1,000 km2. The AEM survey of Burton et al. (2020) was flown over the larger MAP physiographic province (including the Shellmound grid), with 6–12-km spaced east–west flight lines. This regional AEM survey of the MAP produced 16,816 line-km of inverted resistivity soundings covering an area of about 95,000 km2 (Fig.1a) and also included about 2,000 line-km of data acquired directly along several rivers to characterize connectivity between surface water and groundwater (Minsley et al. 2021). Both AEM surveys of the MAP physiographic province and the Shellmound grid utilized the helicopter-based RESOLVE frequency-domain AEM system slung 30-m above the terrain and acquiring sounding data at a frequency of 10 soundings per second while traveling at a nominal flight speed of 130 km/h (Minsley et al. 2021). Together, the Burton et al. (2019, 2020) AEM resistivity datasets represent an initiative to acquire system-scale airborne geophysical data over the full aerial extent of the Mississippi River Valley alluvial aquifer (Minsley et al. 2021) with high vertical resolution in the upper 2–5 m below the land surface, data coverage to 125 m depth below the land surface, and a maximum depth-of-investigation of about 60–80 m (Minsley et al. 2021).

The gridded surfaces (Fig. 2) incorporated into the e–h relations developed in sections ‘Electric–hydraulic relations for the alluvial aquifer’ and ‘Geoelectric and hydrogeologic frameworks of Shellmound, Mississippi’ included a 100-m digital surface elevation model in the Shellmound grid (Fig. 2a), and gridded surfaces for the elevation of the 2018 potentiometric surface in the alluvial aquifer (Figs. 1a,b and 2b; McGuire et al. 2020), and the elevation of the base of the alluvial aquifer in the Shellmound grid (Fig. 2c; Torak and Painter 2019a, b), each referenced to North American Vertical Datum of 1988. The 2018 potentiometric surface in the MAP (Figs. 1 and 2) was reproduced from McGuire et al. (2020); the contours in Fig. 1 represent the elevation of the 2018 potentiometric surface in the alluvial aquifer throughout the MAP (Fig. 1b) and Shellmound grid (Fig. 1c). The blue contours within the black box depicted in Fig. 1c show the 2018 potentiometric surface in the Shellmound grid and correspond to the colored surface in Fig. 2b. Bottom elevations of the alluvial aquifer, depicted in Fig. 2c, were produced by Torak and Painter (2019a, b) from a database of 6,604 interpreted elevations of the base of the hydrogeologic unit that contains the alluvial aquifer made from geophysical logs obtained from wells and boreholes throughout the MAP. The thickness of the alluvial aquifer in the Shellmound grid was calculated by subtracting the base elevations of the alluvial aquifer from the surface elevation model, and the saturated thickness of the alluvial aquifer in the Shellmound grid (Fig 2d) was calculated by subtracting the base elevations of the alluvial aquifer from the 2018 potentiometric-surface elevations.

Electric–Hydraulic Relations for the Alluvial Aquifer

The e–h relations between alluvial-aquifer transmissivity and mean resistivity were first defined by calculating parametric curves of the geoelectric parameters with Eqs. (4)–(6) from the Burton et al. (2020) resistivity soundings covering the MAP, and then correlating the historical aquifer-test transmissivity data of Pugh (2008, 2022a) with the geoelectric parameter values at the base of the alluvial aquifer at the nearest AEM sounding. Figure 3 shows example parametric curves calculated from the AEM resistivity dataset of Burton et al. (2020) as functions of depth below the land surface at a single sounding location along the AEM flight lines in Fig. 1b. Electrical resistivity is represented by the black curve (Burton et al. 2020), transverse resistance by the bolded blue curve (Eq. 4), longitudinal conductance by the bolded red curve (Eq. 5), and mean resistivity by the green curve (Eq. 6). The thin blue and red curves represent the product and quotient terms, respectively, in Eqs. (4)–(5), respectively. The solid curves show the vertical interval used to calculate geoelectric frameworks (illustrated in section ‘Geoelectric and hydrogeologic frameworks of Shellmound, Mississippi’), and the dotted curves show the vertical interval used to develop the e–h relations described in the following.

Fig. 3
figure 3

Illustration of parametric curves for geoelectric parameters calculated from resistivity soundings (Burton et al. 2020), and general comparison of resistivity sounding data (black line) with the geoelectric parameters of transverse resistance (R; bold blue line), longitudinal conductance (S; bold red line), and mean resistivity (re; green line). The thin blue and red lines represent the Eq. (4) product term and Eq. (5) quotient term, respectively. The dots between the base of the confining layer and the base of the alluvial aquifer illustrate the interval over which parametric curves were calculated between the base of the confining layer and the base of the aquifer

Full size image

Parametric curves were calculated over two separate depth intervals in the resistivity curves from every AEM sounding. First, geoelectric parameters were calculated from electric resistivity over a depth interval that started at the base of the confining layer (defined from AEM resistivity models in Minsley et al. 2021) and ended at the base of the alluvial aquifer. This depth interval, depicted in Fig. 3 by the dots between the base of the confining layer and the base of the alluvial aquifer, represented the entire thickness of the alluvial-aquifer and is referred to herein as “simulation condition 1.” Second, geoelectric parameters were calculated over a depth interval between the 2018 potentiometric surface and the base of the aquifer. This interval represented the 2018 saturated thickness of the alluvial aquifer and is referred to herein as “simulation condition 2.” To calculate the parametric curves of geoelectric parameters corresponding to both simulation conditions, the resistivity curves were vertically interpolated at an increment of 1 m and the vertical interpolation increment was used for incremental thicknesses entering into product and quotient terms in Eqs. (4)–(5). The historical aquifer-test data were associated with values of mean resistivity at the base of the alluvial aquifer (Fig. 3) because of the dependence of mean resistivity at a given depth on the resistivity layering and layer thicknesses above (Zhody et al. 1974).

Correlation between the alluvial-aquifer transmissivity data and mean resistivity calculated over different depth intervals resulted in a point cloud of correlation data corresponding to each simulation condition. The point clouds are depicted by the black and gray points in Fig. 4, which represent simulation conditions 1 and 2, respectively. Neither point cloud in Fig. 4 displayed a well-defined e–h relation for the MAP, and the absence of a well-defined e–h relation was attributed to the aforementioned challenges in developing them: (1) no analytical e–h relation between electric and hydraulic properties of the alluvial aquifer likely exists, and (2) the slope and y-intercept coefficients of semiempirical e–h relations defined from field data can vary spatially as functions of other variables in the hydrogeologic environment. To overcome these challenges, the black and gray point clouds in Fig. 4 were considered composites of numerous log-linear e–h relations that represented the alluvial aquifer over the spatial extent of the MAP, and a procedure was implemented to manually calibrate Eq. (7) coefficients to yield an e–h relation that best replicated the recent slug-test data acquired in the Shellmound grid. Six e–h relations, depicted by the correlations in Fig. 5, were defined from the point clouds in Fig. 4 and tested for their ability to replicate the slug-test data acquired in the Shellmound grid from the geoelectric frameworks. The e–h relations 1–3 represented simulation condition 1, whereas e–h relations 4–5 represented simulation condition 2, and e–h relation 6 was defined from e–h relations 3 and 5. The Eq. (7) slope and y-intercept coefficients and corresponding coefficients of determination are summarized in Tables 1 and 2 for each e–h relation depicted in Fig. 5. The coefficients of generalized log-linear relations of the form log10y = log10α + βlog10x between alluvial aquifer transmissivity (y) and the transverse resistance and longitudinal conductance geoelectric parameters (x), depicted in Fig. 5, are summarized in Table 2 with the corresponding coefficients of determination.

Fig. 4
figure 4

Point clouds of correlation data between alluvial aquifer transmissivity and mean resistivity calculated from AEM resistivity soundings for the MAP physiographic province. Black circles represent the point cloud corresponding to simulation condition 1, where geoelectric parameters were computed over the entire thickness of the alluvial aquifer. Gray circles represent the point cloud corresponding to simulation condition 2, where the geoelectric parameters were computed over the saturated thickness of the alluvial aquifer

Full size image
Fig. 5
figure 5

Electric–hydraulic (e–h) relations between transmissivity data from historical aquifer-tests of the Mississippi River Valley alluvial aquifer and the geoelectric parameters of transverse resistance (blue), longitudinal conductance (red), and mean resistivity (green) calculated from the electrical resistivity framework determined by airborne frequency-domain electromagnetic induction sounding. The slope and y-intercept coefficients of generalized log-linear equations describing the relations between alluvial aquifer transmissivity and each geoelectric parameter, corresponding to each e–h relation, are summarized in Tables 1–2: a e–h relation 1; b e–h relation 2; c e–h relation 3; d e–h relation 4; e e–h relation 5; f e–h relation 6

Full size image
Table 1 Summary of Eq. (7) coefficients for tested e–h relations depicted in Fig. 5 between alluvial aquifer transmissivity and mean resistivity calculated from the resistivity curves inverted from AEM soundings
Full size table
Table 2 Summary of slope and y-intercept coefficients, and coefficients of determination of generalized log-linear e–h relations of the form log10y = log10α + βlog10x between alluvial aquifer transmissivity (y) and transverse resistance and longitudinal conductance geoelectric parameters (x) for correlation data underlying the e–h relations depicted in Fig. 5
Full size table

e–h relation 1 (Fig. 5a) was defined from the black point cloud in Fig. 4 based on offset distances between aquifer-test wells and the nearest AEM soundings. If the distance between an aquifer-test well and the nearest AEM sounding exceeded 1 km, the corresponding point was removed from the point cloud in Fig. 4 based on the assumption that that transmissivity was more likely to correlate with mean resistivity at nearby AEM soundings than with mean resistivity at distant AEM soundings. By removing points characterized by offset distances greater than 1 km, e–h relation 1 became apparent by visual inspection of the remaining points and was therefore used as a starting point for manually calibrating Eq. (7) coefficients that best replicated the recent slug-test data. The correlation data from the black point cloud in Fig. 4 that defined e–h relation 1 are shown in Fig. 5a with the corresponding correlations between alluvial aquifer transmissivity and mean resistivity (Fig. 5a, green), transverse resistance (Fig. 5a, blue), and longitudinal conductance (Fig. 5a, red). e–h relation 1 was tested by calculating geoelectric and transmissivity frameworks with Eqs. (4)–(7), converting the transmissivity framework into the hydraulic conductivity framework by dividing by the saturated thickness of the alluvial aquifer in the Shellmound grid (Fig. 2d), and then comparing the simulated transmissivity and hydraulic conductivity data with the recent slug-test data (section ‘Geoelectric and hydrogeologic frameworks of Shellmound, Mississippi’). Despite the well-defined apparent e–h relation shown in Fig. 5a, e–h relation 1 overestimated the Shellmound slug-test data and was therefore shifted vertically downwards on the y-axis of Fig. 4 to reduce the ranges of simulated values to one that more closely approximated the range of the slug-test data. Points were sequentially removed from the Fig. 4 point cloud until three criteria were upheld by the points remaining around the shifted e–h relation: (1) the points spanned the full domain of the point cloud data and yielded a relation that maintained approximately the same slope as e–h relation 1, (2) the coefficient of determination (R2; Helsel et al. 2020) corresponding to the points around the shifted e–h relation exceeded 0.5, and (3) the retained points produced discernable e–h relations between transmissivity and all three geoelectric parameters, as is depicted in Fig. 5b. The first criteria reflected a consideration that the slope coefficient of e–h relation 1 could be reasonably accurate but the y-intercept coefficient could be inaccurate, whereas the second and third criteria were implemented to provide a basis for producing notable, yet imperfect correlations guided by the underlying physics pertinent to the geoelectric parameters (Ikard and Kress 2016).

e–h relation 2, defined from the black point cloud in Fig. 4, is represented by the correlation data points shown in Fig. 5b, which represent correlations between alluvial-aquifer transmissivity and each geoelectric parameter. e–h relation 2 was tested in the same manner as the first, and testing resulted in the rejection of the relation and the application of a second shift and data-elimination process to reduce the range of simulated data and define e–h relation 3, depicted by the correlation data points shown in Fig. 5c. After testing, e–h relation 3 was considered a viable e–h relation for the alluvial aquifer in the Shellmound grid based on comparison of the simulated transmissivity and hydraulic conductivity framework data with the recent slug test data. e–h relation 3 is described by Eq. (7) with log10α and β coefficients of 3.2434 ft2/day (0.3013 m2/day) and 0.502 ft2/day/ohm-m (0.0466 m2/day/ohm-m), respectively (Table 1), and characterized by a coefficient of determination R2 = 0.7805 with respect to the points that defined e–h relation 3 (Table 3). The associated correlations between transmissivity and transverse resistance and longitudinal conductance (Fig. 5c) are characterized by coefficients of determination of R2 = 0.3488 and R2 = 0.2649 (Table 2), respectively.

Table 3 Historical aquifer-test data underlying e–h relations 3 and 6 between alluvial-aquifer transmissivity (Pugh 2008, 2022a) and the geoelectric parameters of transverse resistance, longitudinal conductance, and mean resistivity calculated from the Burton et al. (2020) AEM data
Full size table

The same process of definition and subsequent testing of e–h relations was completed for simulation condition 2. Correlation data characterized by offset distances greater than 1 km were omitted from the gray point cloud in Fig. 4, and e–h relations 4 and 5 became apparent by visual inspection of the remaining points. e–h relations 4 and 5 are represented by the Fig. 4 correlation data points shown in Fig. 5d,e, respectively. e–h relations 4 and 5 were tested in the same manner as the first three, and e–h relation 4 was ultimately rejected because of the poor comparison between simulated framework data and recent slug-test data. e–h relation 5 underestimated the recent slug-test data, albeit with less residual error than e–h relation 4, and was therefore ultimately rejected but used in combination with e–h relation 3 to define e–h relation 6.

e–h relation 6 (Fig. 5f) was identified from e–h relations attributed to both simulation conditions 1 and 2 by combining the black and gray point clouds in Fig. 4 and removing all points from the combined point clouds that were below the e–h relation 3 data points and above the e–h relation 5 data points to yield the correlations shown in Fig. 5f. e–h relation 6 was tested like the others and ultimately considered a viable e–h relation for the alluvial aquifer in the Shellmound grid based on comparison of simulated transmissivity and hydraulic conductivity framework data with recent slug-test data. e–h relation 6 is described by Eq. (7) with corresponding log10α and β coefficients of 2.8346 ft2/day (0.2633 m2/day) and 0.6951 ft2/day/ohm-m (0.0646 m2/day/ohm-m), respectively (Table 1), and characterized by an R2 = 0.9345 for the data points that defined the e–h relation (Table 3). The corresponding correlations between alluvial-aquifer transmissivity and transverse resistance and longitudinal conductance data shown in Fig. 5f are characterized by coefficients of determination of R2 = 0.6764 and R2 = 0.2756 (Table 2), respectively.

Geoelectric and Hydrogeologic Frameworks of Shellmound, Mississippi

To test the e–h relations shown in Fig. 5, the Burton et al. (2019) AEM resistivity soundings were horizontally interpolated over a 100-m interval in the x and y directions to create a three-dimensional (3D) grid of 301 rows, 351 columns, and 30 layers (Fig. 6a) that spatially aligned with the discretization of the Shellmound grid (depicted in Figs. 1b and 2). The initial 30-layer vertical discretization was defined by vertical discretization of the AEM resistivity soundings, which increased successively with depth and varied between a minimum of 1-m thickness in the top layer of the resistivity framework and a maximum of 11.3-m thickness in the bottom layer. Each tested e–h relation in Table 1 was used to calculate the transmissivity framework from the mean-resistivity framework, and the transmissivity framework was vertically interpolated at a 1-m interval between the land surface and a depth of 125 m. The hydraulic-conductivity framework was computed by dividing the interpolated transmissivity framework by the saturated thickness of the alluvial aquifer at each horizontal grid cell in every layer of the framework, and subsequently removing all grid cells below the base of the aquifer to produce the simulated hydraulic conductivity in the alluvial aquifer within the Shellmound grid. The 3D geoelectric frameworks in the Shellmound grid, calculated from Eqs. (4)–(6), are depicted in Fig. 6, in addition to the transmissivity framework calculated from the mean-resistivity framework using Eq. (7) with coefficients corresponding to e–h relation 6 (Table 1).

Fig. 6
figure 6

Gridded 30-layer, 301-row, 351-column, resistivity, geoelectric parameter, and transmissivity frameworks of the Shellmound grid. The left column depicts parameter distributions along selected horizontal and vertical planes internally within the grid, and the right column depicts parameter distributions at the land surface and below land surface around the perimeter of the grid by horizontal planes for each grid layer. a Resistivity framework (Burton et al. 2019). b Transverse resistance framework. c Longitudinal conductance framework. d Mean-resistivity framework. e Transmissivity framework calculated from the mean-resistivity framework using the e–h relation 6 coefficients (Table 1)

Full size image

Simulated transmissivity and hydraulic-conductivity framework data were extracted from the vertically interpolated frameworks at the horizontal coordinates of the slug-test wells and averaged vertically over the depths of the screened intervals of the slug-test wells (Table 4 and Fig. 1c). Averaged simulated values were compared with the slug-test data by calculating the root mean square errors (RMSE; Helsel et al. 2020) between averaged simulated data and slug-test data with Eq. (8), where dsim represents simulated data and dslug represents slug-test data. Figure 7a depicts the comparison of the averaged simulated hydraulic conductivity in the Shellmound grid to the slug-test hydraulic conductivity data collected at locations depicted in Fig. 1c, for each e–h relation defined in Fig. 5. Figure 7b shows the comparison of the averaged simulated transmissivity in the Shellmound grid with the transmissivity determined by slug tests, for each e–h relation depicted in Fig. 5. The plotted data in Fig. 7 are color-coded to correspond with the e–h relations depicted in Fig. 5, and transmissivity and hydraulic conductivity quantified using e–h relation 3 (red) and 6 (light-blue) are summarized in Table 5 with the corresponding residuals. The RMSE between simulated data and slug test data were calculated from Eq. (8) and were 57 ft/day (17.4 m/day) and 53 ft/day (16.2 m/day), respectively (Table 1), for hydraulic conductivity produced by e–h relations 3, 6 and 7, 264 ft2/day (674.8 m2/day) and 8,101 ft2/day (752.6 m2/day), respectively, for transmissivity produced by e–h relations 3 and 6.

$$\mathrm{Root}\ \mathrm{Mean}\ \mathrm{Square}\ \mathrm{Error}\ \left(\mathrm{RMSE}\right)={\left[\frac{1}{N}\sum \nolimits_{i=1}^N{\left({d}_{\mathrm{sim}}-{d}_{\mathrm{slug}}\right)}^2\right]}^{{~}^{1}\!\left/ \!{~}_{2}\right.}$$
(8)
Table 4 Distribution of hydraulic conductivity (ft/day) and transmissivity (ft2/day) of the Mississippi River Valley alluvial aquifer determined from slug tests in wells within the Shellmound grid (Pugh 2022b)
Full size table
Fig. 7
figure 7

Comparison of slug-test hydraulic conductivity and transmissivity data with the vertically averaged simulated hydraulic-conductivity and transmissivity framework data in the Shellmound grid, with spatial distributions of one-layer vertically averaged values of hydraulic conductivity and transmissivity in the Shellmound grid. a Comparison of simulated hydraulic conductivity of the alluvial aquifer with slug-test data at the locations of slug-test wells depicted in Fig. 1c. Colors represent the corresponding e–h relations depicted in Fig. 5, from which the hydraulic conductivity and transmissivity values were simulated. b Comparison of simulated transmissivity of the alluvial aquifer with slug-test data at the locations of slug-test wells depicted in Fig. 1c. c Horizontal distribution of 1-layer vertically averaged hydraulic conductivity values in the Shellmound grid quantified from the transmissivity framework calculated with e–h relation 6. Black circles show the locations of slug-test data in Fig. 1c and have a diameter proportional to the corresponding residuals between simulated hydraulic conductivity and slug-test data summarized in Tables 4 and 5. d Horizontal distribution of 1-layer vertically averaged transmissivity values in the Shellmound grid simulated with e–h relation 6. White circles show the locations of slug-test data in Fig. 1c and have a diameter proportional to the corresponding residuals between simulated transmissivity and slug-test data summarized in Tables 4 and 5

Full size image
Table 5 Simulated hydraulic conductivity and transmissivity corresponding to e–h relations 3 and 6 with corresponding residuals relative to the slug-test values
Full size table

Horizontal distributions of the simulated alluvial-aquifer hydraulic conductivity and transmissivity are represented in Fig. 7c,d, which shows 1-layer representations of the hydraulic properties of the alluvial aquifer in the Shellmound grid. The horizontal distributions shown in Fig. 7c,d were calculated by vertically averaging the simulated values in the grid cells that represent the alluvial aquifer. Figure 7c shows the horizontal distribution of vertically averaged hydraulic conductivity, calculated from the transmissivity framework in Fig. 6e, which was produced from the AEM resistivity framework in Fig. 6a using Eqs. (4)–(7) and substituting e–h relation 6 coefficients into Eq. (7). The corresponding e–h relation 6 residuals summarized in Table 5 are plotted spatially by the black circles centered at the locations of slug-test data with diameters proportional to the magnitude of the corresponding residuals. The vertically averaged transmissivity grid is shown in Fig. 7d with residuals plotted spatially by the white circles with diameters proportional to the magnitude of the corresponding residuals in Table 5.

Results and Discussion

Electric–Hydraulic Relations for the Alluvial Aquifer

Prior research has shown that e–h relations, at the aquifer scale, depend on the geologic material-level relations between electric and hydraulic properties of an aquifer and its substratum, and the way those properties influence the directions of current and groundwater flows within the aquifer (Cassiani and Medina Jr. 1997). Most sedimentary aquifers are anisotropic and characterized by a longitudinal resistivity in the direction parallel to the layering and a transverse resistivity in a direction perpendicular to the layering (Mazáč et al. 1985). The geoelectric parameters (Eqs. 4–6), therefore, provide a means of developing e–h relations at the aquifer scale to quantify hydraulic properties of an aquifer from the electrical resistivity distribution because of their representations of transverse and longitudinal electric current flow within the aquifer, which often results in notable correlations between one or more geoelectric parameter and aquifer transmissivity. Correlations are common between transmissivity and transverse resistance, longitudinal conductance, and mean resistivity of the formation (Fig. 5; see also Ikard and Kress 2016), or between the hydraulic conductivity parallel to the bedding and the mean resistivity (Kelly 1977; Kelly and Reiter 1984; Kelly and Frolich 1985), and generally reflect a monotonic increase of transmissivity and hydraulic conductivity with increasing mean resistivity in sand-clay layered aquifers (Mazáč et al. 1985). In many cases, an entire hydrogeologic formation composed of multiple layers of rock with different resistivity can be represented as a single electrically equivalent layer with finite thickness and finite mean-resistivity, despite anisotropy resulting from the hydrogeologic and geoelectric layering (Kelly 1977; Kelly and Reiter 1984; Kelly and Frolich 1985).

The point clouds of correlation data in Fig. 4, produced by correlating spatially distributed aquifer test transmissivity data with mean resistivity computed from AEM resistivity soundings, are considered composites of numerous apparent e–h relations for the alluvial aquifer within the Mississippi Alluvial Plain. Despite several of the tested e–h relations being founded upon data showing notable correlations between alluvial aquifer transmissivity and all three geoelectric parameters (Fig. 5), most did not accurately replicate any of the slug-test data from the Shellmound grid (Fig.7). e–h relations 3 and 6 (Table 1) produced the smallest RMSE of the six e–h relations that were tested, with respect to simulating transmissivity and hydraulic conductivity in the Shellmound grid frameworks. The corresponding RMSE achieved between simulated and observed slug-test data with e–h relations 3 and 6 were 7,264 ft2/day (674.8 m2/day) and 8,101 ft2/day (752.6 m2/day) and 57 ft/day (17.4 m/day) and 53 ft/day (16.2 m/day), respectively, for transmissivity and hydraulic conductivity, respectively (Table 1). These e–h relations were developed from alluvial-aquifer transmissivity data in the range of about 4,000–39,000 ft2/day (371.6–3,623.2 m2/day) (Table 3), and simulated transmissivity values in the range of about 4,000–16,000 ft2/day (371.6–1,486.4 m2/day) (Table 5) for corresponding mean resistivity between 26 and 165 ohm-m. e–h relations 3 and 6 have positive slopes, which indicates that (1) transmissivity and hydraulic conductivity increase as mean resistivity increases, such that more resistive regions of the aquifer in the Shellmound grid generally correspond to more transmissive and hydraulically conductive regions of the aquifer, and (2) electrical conduction within the alluvial aquifer sediments likely occurs predominantly by surface conduction along the pore surfaces according to the model of Purvance and Andricevic (2000a, b).

Geoelectric Frameworks

The geoelectric frameworks in the Shellmound grid (Fig. 6) show the general relations between the alluvial-aquifer resistivity (Burton et al. 2019), transverse resistance, longitudinal conductance, mean resistivity, and transmissivity. The general electrical resistivity structure of the Shellmound grid (Fig. 6a) consists of a resistor, present roughly in layers 1–15 and characterized by yellow and red shades with resistivity in the range of 30–100 ohm-m, overlying a conductor in layers 15–30 of the resistivity framework characterized by blue and green shades and having resistivity less than about 30 ohm-m. The mean-resistivity framework (Fig. 6d), calculated from the transverse-resistance (Fig. 6b) and longitudinal-conductance (Fig. 6c) frameworks, shows a different general electrical structure than the resistivity framework because of its dependence upon the thickness and resistivity of the conductive and resistive regions in the resistivity framework and the nonlinear relation between resistivity and mean resistivity described by Eqs. (4)–(6). Because mean resistivity is calculated as a nonlinear function of the resistivity layering and thicknesses of the layers, regions of high or low mean resistivity do not necessarily correspond to regions of high or low resistivity. The mean-resistivity framework, rather than the resistivity framework, is related to the transmissivity framework by the log-linear e–h relations described by Eq. (7). The spatial heterogeneity of the hydraulic conductivity framework (Fig. 7c), being a function of transmissivity and saturated thickness, is therefore controlled by the resistivity framework but not necessarily related to the resistivity framework in a log-linear manner. Nevertheless, the effect of the resistivity distribution on the spatial heterogeneity of the simulated hydraulic properties is evident in the one-layer vertically averaged hydraulic conductivity and transmissivity values of the Shellmound grid framework, shown in Fig. 7c,d, which appear to show some geologic structure imparted by the resistivity distribution in the Shellmound grid and some influence of the surface-elevation grid shown in Fig. 2b.

Hydraulic Frameworks

The simulated transmissivity and hydraulic-conductivity framework data calculated with e–h relations 3 and 6 compare reasonably well with the recent slug-test data (generally within an order of magnitude or less) for a fairly narrow range of transmissivity between about 8,000 ft2/day (743.2 m2/day) and 30,000 ft2/day (2,787.1 m2/day; Tables 4 and 5) and hydraulic conductivity between about 60 ft/day (18.3 m/day) and 200 ft/day (61 m/day). e–h relation 3 shows some clustering of simulated data around the line y = x in both the simulated transmissivity and hydraulic conductivity data (Fig. 7), and the smallest value of the mean transmissivity residual of –1,630 ft2/day (–151.4 m2/day). Minimum and maximum transmissivity residuals associated with e–h relation 3 were –12,646 ft2/day (–1,174.9 m2/day) and 15,668 ft2/day (1,455.6 m2/day), respectively. The mean hydraulic conductivity residual achieved with e–h relation 3 was 21.7 ft/day (6.6 m/day) and minimum and maximum hydraulic conductivity residuals were –54.4 ft/day (–16.6 m/day) and 144 ft/day (43.9 m/day), respectively. Transmissivity framework data simulated by e–h relation 6 tend to fall below the line y = x and are underestimated. Minimum and maximum transmissivity residuals associated with e–h relation 6 were –14,168 ft2/day (–1,316.3 m2/day) and 14,539 ft2/day (1,350.7 m2/day), respectively. Hydraulic conductivity values simulated with e–h relation 6, generally cluster around the line y = x for values between approximately 60 ft/day (18.3 m/day) and approximately 100–200 ft/day (30.5–61 m/day), and e–h relation 6 shows the smallest value of mean hydraulic conductivity residual of 0.8 ft/day (0.2438 m/day), with maximum and minimum residuals of 82.9 ft/day (25.3 m/day) and –130.4 ft/day (–39.7 m/day).

Simulated transmissivity and hydraulic-conductivity framework data that are characterized by large residuals around the line y = x in Fig. 7, may be better approximated by different Eq. (7) coefficients. This implies that the procedure described herein to manually calibrate the Eq. (7) coefficients to recent slug-test data has a more practical use for defining spatial heterogeneity of the simulated hydraulic properties. Slug-test data acquired from focus regions of the MAP can be used to define spatial heterogeneity of the Eq. (7) coefficients that minimize residuals between simulated data and slug-test data at various locations within the focus regions. The Eq. (7) coefficients that minimize the residual at each slug-test location can be plotted and spatially and gridded to define heterogeneous frameworks of the coefficients within the focus regions, which can be used to better explore the spatial heterogeneity of the hydraulic properties. Furthermore, although the resistivity framework is imperfect, the historical aquifer-test dataset provides an evolving constraint for defining the values of the Eq. (7) coefficients throughout the MAP. For example, if it is considered that every two-point combination of points from the Fig. 4 point cloud defines a potentially valid e–h relation for some arbitrary region of the alluvial aquifer, the historical aquifer-test dataset then provides a means to constrain the values and spatial distributions of the coefficients within focus regions by testing every e–h relation defined by two-point combinations of data. As recent slug-test calibration data are appended to the historical aquifer-test dataset, the expanded point cloud expands the ranges of the Eq. (7) coefficients that can be defined from the historical aquifer-test and AEM resistivity datasets.

With respect to the Shellmound grid frameworks, the full range of simulated hydraulic conductivity values falls well within the ranges of published values quantified by scientific studies completed throughout the MAP physiographic province (Table 6). Table 6 summarizes alluvial-aquifer horizontal hydraulic conductivity values published between 1987 and 2009 that were quantified by methods including aquifer tests (pumping tests and slug tests) and automated groundwater-flow model calibration. Published hydraulic-conductivity values vary between a minimum of 1.1 ft/day (0.3353 m/day) and a maximum of 700 ft/day (213.4 m/day); the averages of published values are between 262 ft/day (79.9 m/day) and 448 ft/day (136.6 m/day), respectively.

Table 6 Summary of reported values of horizontal hydraulic conductivity of the Mississippi River Valley alluvial aquifer in scientific studies published between 1987 and 2009. Min. minimum, Max. maximum, Avg. average
Full size table

Uncertainty

While the MAP and Shellmound geoelectric and hydraulic frameworks adhere to a generally anticipated relation that electrically resistive sediments are typically more hydraulically conductive, and transmissivities and hydraulic conductivities simulated with e–h relations 3 and 6 compare reasonably well with recent slug-test data (to the same order of magnitude or less) and hydraulic-conductivity values reported in the scientific literature, there is uncertainty associated with the e–h relations presented herein and the magnitudes and spatial heterogeneity of the hydraulic-property values that they simulate. The largest uncertainty is attributed to the accuracy of the resistivity framework, which is critical to the validity of the e–h relations developed from correlations between alluvial aquifer transmissivity and the geoelectric parameters. The accuracy of the resistivity framework is affected by the regularization enforced during the inversion of the AEM data and the depth-of-investigation (DOI) of the RESOLVE frequency-domain EM instrument given the electrical structure of the survey area and the background electromagnetic noise level. As noted in the Introduction, the resistivity framework is a regularized solution of an ill-posed geophysical inverse problem, and a unique framework model can be obtained for different regularizations. Uncertainty is therefore inherent within the resistivity framework because the solution of the AEM inversion is nonunique. Vignoli et al. (2017) demonstrated on three synthetic AEM datasets that sharp and smooth spatially constrained inversions applied to the same dataset produced different resistivity models at depths well above the DOI estimated by the approach described by Christiansen and Auken (2012). Christensen et al. (2017) found that a resistivity model inverted using sharp structural-inversion constraints to produce well-defined resistivity boundaries produced a more-accurate groundwater-flow model parameterization than a smooth resistivity model, although Vignoli et al. (2015) demonstrated on synthetic geologic models that smooth spatially constrained inversion was generally successful at recovering the main features of the true synthetic models reasonably well. With these considerations in mind, it is worth noting that the Burton et al. (2019) and (2020) resistivity frameworks were both produced by laterally constrained smooth deterministic inversion, and therefore the hydraulic frameworks produced from the e–h relations described herein are an end result of calculations beginning with a smooth resistivity model that does not reproduce sharp resistivity boundaries. With respect to the DOI, Christiansen and Auken (2012) provide estimates of a range of DOI between about 20 and 53 m for the RESOLVE frequency-domain electromagnetic system slung 30 m above homogenous and layered half-space models and acquiring synthetic sounding data at five frequencies between 390 and 132.7 kHz (see Christiansen and Auken 2012, their Figs. 2 and 3). The DOI for the Burton et al. (2019) and (2020) AEM resistivity datasets, as calculated in the inversion software by the method described by Christiansen and Auken (2012), is between 60 and 80 m given the electrical structure of the survey area and the cumulative sensitivities of the Jacobian matrix of the inversion scheme (Asch et al. 2015; Vignoli et al. 2015, 2017). For comparison, the depths-to-aquifer in the wells used to define e–h relations 3 and 6 vary between about 1 and 99 m (Table 3), and the well-screen depths corresponding to recent slug-test data vary between a minimum of 5.8 m and a maximum of 27.6 m (Table 4). The estimated DOIs of the AEM surveys are therefore greater than the depth range of interest corresponding to the historical aquifer-test data and recent slug-test data.

A second uncertainty and potential source of error in the simulated values of transmissivity and hydraulic lies in the accepted values of the coefficients of the e–h relations and their assumed spatial homogeneity within the Shellmound grid. Despite several studies demonstrating spatial heterogeneity of the coefficients being dependent upon varying hydrogeologic conditions (Christensen et al. 2016), in the model presented herein the spatial heterogeneity of the coefficients is exclusively controlled by the resistivity distribution. Additional uncertainty in the coefficients of the log-linear e–h relations is attributed to subjective elimination of points from the point cloud of e–h correlation data (Fig. 4) from which the six tested e–h relations were defined, and to the small number of e–h correlation data from which the coefficients of the e–h relations were quantified by ordinary least-squares regression (Fig. 5). Both are factors that control the values of the coefficients of the log-linear e–h relations. The true coefficients of the e–h relations likely vary as functions of the hydrogeologic environment and are expected to vary spatially as lithology and groundwater chemistry and salinity vary. In general, Mazáč et al. (1985) noted that the error in hydraulic conductivity quantified from resistivity increased as the slope of the e–h relation increased between 0 and 90° (positive slope), whereas error was reduced as the slope of the e–h relation increased between 90 and 180° (negative slopes).

The accuracy of the historical and recent aquifer-test data used in the development of the e–h relation is a third uncertainty and potential source of error between simulated hydraulic-framework data and slug-test data. Large-scale equivalent volumetric averages of transmissivity and hydraulic conductivity are represented by the historical aquifer-test data that the e–h relations are founded upon, whereas the recent slug-test data represent geologic material near the slug-tested wells, which may be affected by the drilling and well-completion process (Butler 2005; Slater 2007). Scale differences between the electric and hydraulic datasets are also considerable. The resistivity data of Burton et al. (2019) represent higher-resolution hydrogeologic structure of the 100 × 100-m Shellmound grid, whereas the resistivity data of Burton et al. (2020) represents a lower-resolution regional-scale structure on a 1 × 1-km grid. The simulated transmissivity and hydraulic-conductivity data in the Shellmound grid frameworks were therefore compared to slug-test data whose resolution exceeds that of historical aquifer test data underlying the e–h relations developed from the regional-scale resistivity framework of the MAP physiographic province. Furthermore, the quality of the historical aquifer-test data may vary substantially among individual aquifer-test data and data sources. Historical transmissivity data may not reflect common test dates or consistent hydraulic conditions between different aquifer tests and may not accurately reflect current hydraulic conditions in the alluvial aquifer throughout the MAP physiographic province including the Shellmound grid. The Pugh (2022b) slug-test data in Table 4 indicate that most of the slug-tested wells in the Shellmound grid do not fully penetrate the alluvial aquifer, such that hydraulic properties of the alluvial aquifer that are quantified by the slug tests do not represent the full thickness of the aquifer. Screened intervals were unavailable for wells corresponding to historical aquifer test data in Table 3, and therefore the wells were assumed screened over the full thickness of the alluvial aquifer; however, it is unknown if the historical aquifer tests do indeed represent the full thickness of the alluvial aquifer. Additionally, slug-test hydraulic conductivity data were quantified by the Bouwer and Rice (1976) method (Pugh 2022b), which tends to underestimate hydraulic conductivity (Butler 2005).

Additional uncertainties and potential sources of error in simulated transmissivity and hydraulic-conductivity data are attributed to the accuracy of the surfaces used in the calculations to determine the thickness and saturated thickness of the alluvial aquifer, including the surface-elevation model, 2018 potentiometric-surface elevation, and the base elevations of the alluvial aquifer. Each of these aforementioned uncertainties is a potential source of discrepancy between the simulated hydraulic conductivity and transmissivity-framework data and the slug-test data from the Shellmound grid, and may be influential where the comparisons between simulated and observed slug-test data are rather poor. Despite these uncertainties, some of the recent slug test data were simulated to a reasonable degree of accuracy within one order of magnitude or less. This is notable considering the large spatial scale of the alluvial aquifer that is represented by the AEM resistivity soundings and historical aquifer-test transmissivity data underlying the e–h relations and the localized point-scale represented by slug test data that are compared to the simulated transmissivity and hydraulic conductivity framework data in the Shellmound grid.

Conclusions

e–h relations were defined for the Mississippi River Valley alluvial-aquifer from mean-resistivity and transmissivity data encompassing an area of the Mississippi Alluvial Plain physiographic province from Mississippi to northern Arkansas and into Tennessee. Each e–h relation was tested for its ability to simulate transmissivity and hydraulic conductivity of the alluvial aquifer at 16 locations in the Shellmound grid where recent (2019–2020) slug-test data were available for comparison but where aquifer-test data are currently (2023) sparse. Two of the six log-linear e–h relations simulated transmissivity and hydraulic conductivity values at points in the Shellmound grid that compared reasonably well with slug-test data. A reasonable comparison was achieved for transmissivity and hydraulic conductivity values that fell within fairly narrow ranges between about 8,000 ft2/day (743.2 m2/day) and 30,000 ft2/day (2,787.1 m2/day) and about 60 ft/day (18.3 m/day) and 200 ft/day (61 m/day), respectively, representing approximately the range of transmissivity entering into the underlying e–h relations. Simulated hydraulic conductivity values were also well within the range of independently quantified hydraulic conductivity values published in the scientific literature.

The workflow described herein illustrates a semiempirical model of alluvial-aquifer transmissivity and hydraulic conductivity based on the electrical resistivity of the Mississippi River Valley alluvial aquifer. Calculation of the geoelectric parameters of transverse resistance, longitudinal conductance, and mean resistivity from AEM-derived electrical resistivity soundings, and subsequent correlation of mean resistivity to historical aquifer-test transmissivity data, circumvents the necessary assumptions that are required to quantify the slope and y-intercept coefficients of other empirical and semiempirical models that yield log-linear e–h relations with coefficients quantified as functions of the variables in the hydrogeologic environment. This approach may be useful for parameterizing groundwater-flow models from AEM resistivity data and constraining the allowable ranges in which transmissivities and hydraulic conductivities are allowed to vary during calibration of the groundwater-flow model, particularly when stochastic or otherwise automated approaches are considered for extracting and testing apparent e–h relations in the hydraulic and geophysical datasets.