Introduction

Groundwater is among the most important reserves of freshwater on the planet, critical for drinking water resources as well as for healthy ecosystem functioning. Groundwater reserves are replenished through aquifer recharge, which is highly responsive to climate change and land development (Gurdak et al. 2007). Unconfined shallow aquifers in particular are inherently vulnerable to short-term dynamics such as precipitation excess or deficit, or to quality degradation from surface influences (Thomas et al. 2017; Vogt and Somma 2000). This vulnerability translates into increased risk of contamination in areas impacted by human land use (Burri et al. 2019; Hale et al. 2014; Jurado et al. 2014; K’oreje et al. 2016; Meyer et al. 2005; Scanlon et al. 2007; Schirmer et al. 2011; Sharp et al. 2003; Vázquez-Suñé et al. 2005). As more than 50% of the world’s population is now living in cities, an increasing number of studies have been dedicated to investigating the numerous and complex changes in the water cycle in general, and groundwater recharge in particular, in urbanizing environments (Barron et al. 2013; Ficklin et al. 2010; Lerner 1990; Minnig et al. 2018; Schirmer et al. 2013; Wakode et al. 2018). Groundwater recharge is influenced by many factors; therefore, its accurate characterization requires properly accounting for the individual environmental variables (e.g. soil texture, land cover) and water balance components (e.g. climatic forcing functions) that contribute to its dynamics.

Surface runoff in particular is one of several important components in a groundwater recharge balance, acting as a direct link between surface flow conditions and groundwater bodies via groundwater-surface water interactions (Foster and Chilton 2004; Musolff et al. 2010). Surface runoff is defined here as the excess precipitation that flows at the land surface immediately following a storm event (Harbor 1994). Like recharge, surface runoff dynamics have been shown to be heavily altered by human activity, often in very complex ways (Eshtawi et al. 2016; Gremillion et al. 2000; Harbor 1994). Increases in the amount surface runoff are often observed in developed areas as a result of increased impervious surfaces, soil compaction, and drainage infrastructure (Eshtawi et al. 2016; Rose and Peters 2001).

As neither groundwater recharge nor surface runoff can be directly measured on large scales, both must be inferred indirectly (Foster et al. 1999; Rammal et al. 2018). This typically leads to great uncertainties in estimates, difficulties in characterizing runoff–recharge relationships in changing environments, and subsequent difficulties in effectively protecting and managing groundwater resources. Great efforts have been made to improve understanding of these dynamics, and many different approaches of varying complexity have been implemented to study rainfall routing and groundwater recharge (Scanlon et al. 2002). Examples include empirical and conceptual water balances (e.g. Bergström and Lindström 2015; Minnig et al. 2018; Wittenberg and Sivapalan 1999); thermal, chemical, or isotopic tracers (e.g. Meriano et al. 2011; Solomon et al. 1993); timeseries analyses (e.g. Bakker and Schaars 2019; Crosbie et al. 2005); statistical and numerical modeling (e.g. Bakker et al. 2016; Döll and Fiedler 2008; Moeck et al. 2017); remote sensing and Geographic Information Systems (e.g. Sheffield et al. 2018; Tweed et al. 2007), as well as combined method approaches (e.g. Brunner et al. 2004; Hornero et al. 2016; von Freyberg et al. 2015). In general, it is considered good practice to carry out estimations using multiple approaches because of the differing spatio-temporal applicability between different methods, as well as the uncertainties involved in all approaches (Crosbie et al. 2010; Healy and Cook 2002).

Surface runoff can be quantified in a number of ways, most commonly with pluviometric methods based on precipitation data, or with hydrograph methods based on river discharge data (Hernández-Guzmán and Ruiz-Luna 2013; Kirchner 2019; Rammal et al. 2018; Woldemeskel and Sharma 2016). Pluviometric methods based wholly or partially on the Natural Resources Conservation Service Curve Number equations (USDA Natural Resources Conservation Service 1986) are popular due to their suitability for small-scale applications, applicability in ungauged catchments, low data requirements, and thorough documentation and case studies in literature (Ajmal et al. 2016; Arnold et al. 2012; Hernández-Guzmán and Ruiz-Luna 2013; Minnig et al. 2018; Mishra and Singh 2003; Soulis and Valiantzas 2012; Thomas and Tellam 2006; Verma et al. 2017; Wakode et al. 2018; Wang et al. 2012; Zope et al. 2017). Modern adaptations of the method attempt to improve soil-moisture accounting (e.g. Bartlett et al. 2016; Michel et al. 2005; Mishra et al. 2003; Sahu et al. 2010; Singh et al. 2015; Wałȩga and Rutkowska 2015), or to explore the proportionality concept that is of unclear origins (Hooshyar and Wang 2016).

For hydrograph methods, river discharge gives a great deal of insight into storm runoff response and changing water dynamics within a catchment. River discharge, also referred to as streamflow, is composed largely of slow-moving baseflow and the rapid-response of quickflow. A discharge hydrograph can be separated into individual components using simple recursive digital filters (Chapman 1991; Li et al. 2014; Nathan and McMahon 1990; Willems 2009), or with more sophisticated methods using high-frequency chemical or isotope composition in addition to streamflow timeseries (Jasechko et al. 2016; Lyon et al. 2012; Penna et al. 2015; Von Freyberg et al. 2017).

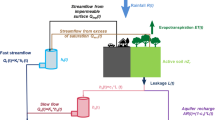
Groundwater recharge for shallow aquifers is often determined via “top-down” water balancing, which uses data on surface conditions in order to estimate the partitioning of precipitation between evapotranspiration, runoff, and recharge (e.g. Arnold and Allen 1999; Minnig et al. 2018; Seibert and Vis 2012). Major control factors for precipitation partitioning include climate, geology, geomorphology, precipitation intensity, and land cover, among others (Gannon et al. 2014; Moeck et al. 2020a; Stanton et al. 2013). In urban environments, water balances can be expanded to account for additional inputs such as sewer leakage, effluent, or irrigation. However, recharge estimates from these water balances are only as good as the estimates of their individual variables, and are thus contingent on identifying and accurately quantifying the significant input and output variables.

While increases in computational power have enabled the development of fully distributed, physically based numerical models, the use of empirical and conceptual models remains popular. This can be attributed to the large data requirements and consequent uncertainty in parameters that are necessary for numerical modeling, while simple methods are more widely accessible due to minimal data requirements, relatively straightforward parameterization, and simplicity in application (Bakker and Schaars 2019). Because of this fact, it is important to continually explore the performance of simplified approaches in different environments to validate their applicability. The basic data necessary for simpler methods are readily accessible on large spatial scales, due in great part to the organization of free databases provided by local governments up to global organizations such as the Center for Global Environmental Research (CGER) or the United Nations Food and Agriculture Organization (UN FAO). In addition, many small-scale published datasets from around the world (e.g. Crosbie et al. 2010; Moeck et al. 2020a) are also freely available.

With these ideas in mind, the objective of this study is to apply empirical and conceptual methods to quantify and explore runoff dynamics, and to assess their suitability to estimate groundwater recharge in an urbanizing environment. This is carried out in a small catchment located on the Swiss Plateau that is undergoing active transition from an agricultural landscape into an urban landscape. This catchment is of interest as the groundwater is the principal source of drinking water for the local population and is representative of the active increase in urbanization that many towns are currently undergoing. This offers a prime opportunity to observe these changes as they occur. The relative strengths and shortcomings of each of the investigated methods are discussed. With these comparisons, it is possible to gauge the ability of these straightforward methods to offer satisfactory characterization of the water cycle in a human-impacted catchment.

Two approaches were used to estimate catchment surface runoff: (1) a modified version of the NRCS-CN method, called the Sahu-Mishra-Eldho (SME) model after its authors (Sahu et al. 2010, 2012); compared to (2) an automated hydrograph separation using the popular recursive digital filter as outlined by Nathan and McMahon (1990). In this application of the SME model, additional modifications were made for soil-moisture calculations, making use of an antecedent precipitation index. For hydrograph separation, a wide range of filter parameters suited to urban environments were explored. Two approaches were then used to estimate groundwater recharge: (1) an empirical water balance using the surface runoff estimates as input, followed by (2) application of the conceptual HBV Light model (Seibert and Vis 2012). As a final step, these results were compared with recharge estimates found in the literature for similar Swiss catchments.

Case study

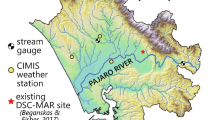
The upper Kempttal catchment on the Swiss Plateau is located approximately 10 km east of the city of Zürich, Switzerland (Fig. 1). The catchment is defined topographically from publicly available data (Swiss Federal Office of Topography), and covers an area of approximately 35 km2 with an increasing elevation from NW–SE: 520 masl at the lower outlet area (NW), and up to approximately 900 masl in the upper headwater area (SE). The catchment contains a small tributary network feeding into the Kempt River, which is modified via canalization and deepening of the river bed within the central urban municipality, Fehraltorf. Flow in the Kempt River is supplemented by wastewater effluent released near its outflow, and is conceptualized here as an integral contribution to river baseflow. Shallow geology is composed of unconsolidated fluvio-glacial sediments that are host to an unconfined aquifer (Fig. 1a). The deepest zones of the aquifer body are in the central valley and have been reported at 10–20 m, with thinner portions between 1 and 8 m on the valley edges (Krejci et al. 1994), though these estimates are uncertain. The residence time of groundwater is assumed to be relatively short, on the order of months to 2 years (Krejci et al. 1994). The aquifer provides approximately 80% of freshwater resources for local communities (Reinhardt et al. 2019).

Fig. 1
figure 1

a Shallow geology of the upper Kempttal catchment. The aquifer is principally located within the glacial, loamy, and alluvial sediments of the catchment. b Sealed surfaces and drained areas in the catchment correspond to impervious surfaces in the urban area and drainage networks in agricultural areas. Public sources: Swiss Federal Office of Meteorology and Climatology (MeteoSwiss); Canton Zürich Office for Waste, Water, Energy, and Air (AWEL); Swiss Federal Office for the Environment (FOEN), Swiss Federal Office of Topography (Swisstopo)

Full size image

Currently, land cover consists of 53% agriculture, 25% forest, and 22% urban area. Sealed surfaces and drained areas are present within both urban and agricultural areas, covering approximately 10% of the entire catchment (Fig. 1b; Federal Statistical Office of Switzerland GEOSTAT). Sealed surfaces correspond principally to roads and buildings, whereas drained areas correspond to tile drains and open ditches. Surface and underground drainage systems exist in several areas. Most storm drains are separated from the sewer network and direct runoff into the river network within the catchment via sewer inflow. However, some central areas are still served with storm-water systems combined to the sewer network, diverting runoff towards the wastewater treatment plant via sewer inflow. These combined systems can lead to combined sewer overflow (CSO) during heavy storms when network flow capacity is exceeded; additional details on the study site may be referenced in Ramgraber et al. (2021).

Observation data

Table 1 gives a summary of the principal datasets considered, all on a daily timescale. Surface-water discharge (Q) was collected from a single gauging station near the outflow of the catchment, approximately 500 m downstream of the wastewater treatment plant for the municipality of Fehraltorf. Table 2 lists annual values of the water balance variables over the study period. For these calculations, Q as well as pumping rates were converted into units of depth by dividing their values by the catchment area. As the Kempttal catchment is in fact a subcatchment of the greater Tösstal catchment, regional flow is expected from the surrounding hillslopes, such that this catchment is not a closed system (Ramgraber et al. 2021).

Table 1 Summary of main databases considered in the current study
Full size table
Table 2 Annual sums of major water balance variables during the period of study
Full size table

Materials and methods

Surface runoff

SME method

The SME method was first proposed by Sahu et al. (2010) as an improvement of the NRCS-CN method (USDA Natural Resources Conservation Service 1986). A brief introduction of the NRCS-CN method and its governing equations can be found in the electronic supplementary material (ESM), with more thorough information found in Mishra and Singh (2003). The SME method is based on the same water balance as that of the original CN (Eq. S1 of the ESM) plus adaptations to the two fundamental hypotheses that underlie the method (Eqs. S2 and S3 of the ESM). The authors adapted the estimation of soil moisture, while maintaining a relatively straightforward implementation and a restricted number of required parameters. A computer program was developed in Python to implement the SME model in this study.

The SME method decouples soil moisture from catchment potential retention, which are lumped in the original NRCS-CN method. Several simplifying assumptions are then applied in order to derive an expression for soil moisture on daily time steps, using a 5-day antecedent rainfall condition P5 (Eq. S8 of the ESM). The principal assumption in formulating this soil-moisture equation is that the catchment is completely dry prior to the 5-day antecedent precipitation window P5. This assumption is, however, generally invalid for temperate regions, regions with regular winter snowfall, and for urban landscapes where, despite potential decreases in infiltration, impervious surfaces and compacted soils may lead to prolonged soil-moisture retention due to reduced ET (Bhaskar et al. 2016). Antecedent rainfall may be taken over longer time periods (Px for x > 5) for calculations, but this does not resolve the issue of subjectivity in choosing an antecedent moisture window, and subsequent disregard of conditions prior to that window.

Given the significant dependence of runoff generation on antecedent moisture conditions in many catchments (e.g. Bennett et al. 2018; Hrachowitz et al. 2013; Penna et al. 2011), an attempt to further improve upon soil-moisture characterization is merited. An alternative is the antecedent precipitation index (Fedora and Beschta 1989; Kohler and Linsley 1951), which is proposed here to replace P5. The antecedent precipitation index (API) applies an exponential decay factor over a rainfall timeseries, in order to estimate the amount of prior rainfall that may be contributing to current soil-moisture conditions. APIs are regularly used as soil-moisture proxies in rainfall–runoff modeling (e.g. Bennett et al. 2018; Descroix et al. 2002; Ma et al. 2014; Woldemeskel and Sharma 2016). Various, closely related formulations are given in the literature, and a generalized form of the API is used in this study:

$$ \mathrm{API}={\sum}_{t=1}^T{P}_{-t}\times {k}^t $$
(1)

In Eq. (1), T is the total number of time steps in the series, t = 1, 2, …, T are the individual time steps, and k is a dimensionless decay factor, with 0 < k < 1 (often in the range of 0.6–0.99 for temperate areas). P–t is the amount of precipitation at a prior time step –t. As t increases, the term kt vanishes. The factor k is conceptualized as representing how quickly moisture is lost from a catchment through any process: higher values of k represent a slow draining landscape (including soil-moisture drainage), and lower values represent a quickly draining landscape (Ali et al. 2010; Lee and Huang 2013; Woldemeskel and Sharma 2016). In reality, the decay factor is proportional to evapotranspiration and likely related to water table depth, and thus should vary seasonally (Pui et al. 2011). In practice, it is often taken as a constant through time, assumed to represent average annual conditions. The API rids the need for the user to determine an arbitrary, fixed-window sum of antecedent precipitation, at the expense of having to estimate the parameter k.

For this study, values of k between 0.8 and 0.95 for daily time steps were considered. The calculated API was in fact relatively insensitive within this range, with an average difference of 2.5 mm between the API using k = 0.8 and k = 0.95. Without further information to constrain this value, a value of k = 0.9 was selected for the API. The length of T for the API covered the entire timeseries (2007–2018) on daily time steps.

The original SME equation for soil moisture, M, (Eq. S8 in the ESM) is thus modified and applied here as:

$$ M=\beta \left[\frac{\left( API-\lambda {S}_0\right){S}_0}{API+\left(1-\lambda \right){S}_0}\right]\mathrm{for}\ \mathrm{API}>\lambda {S}_0 $$
(2)

where β (dimensionless) represents the fraction of antecedent precipitation that is contributing to soil moisture, S0 (units of depth) represents maximum potential retention of a catchment, and λ (dimensionless) is the so-called initial abstraction (Ia) coefficient, where Ia = λS0.

From the decoupling of soil moisture and maximum potential retention, S0 is determined as a function of physical catchment characteristics including soil type, unsaturated zone depth, land cover, and vegetation types. Initial S0 values can be approximated with values of S in dry conditions from the NRCS-CN method (Mishra and Singh 2003; USDA Natural Resources Conservation Service 1986), and adjusted through calibration. The parameter λ is generally deduced from geological maps, drainage tests, soil cores, climatic factors, or other aspects of the current conceptual model for the site under study. Values of λ are referenced in literature between the ranges of 0.05 and 0.3, and are closer to 0.05 in urbanized areas (e.g. Minnig et al. 2018; Mishra and Singh 2003). Values of β may range between 0 and 1, though more precise information on this parameter in literature is sparse. Further, the fraction β is most certainly affected by the use of the API in place of P5, and is expected to be closer to 1 in this formulation of M due to the decay factor inherent to the API.

Further, it was deemed important to expand the representation of runoff beyond soil-controlled, saturation-excess overland flow. This was done by explicitly accounting for paved and drained surfaces with a preprocessing of rainfall partitioning. Runoff over paved and drained surfaces was decoupled from soil-controlled runoff dynamics with the simplified assumption that all precipitation falling onto these surfaces immediately becomes runoff. As 10% of the entire catchment is covered and connected to storm drainage, 10% of all precipitation was routed directly to runoff, and the remaining 90% of precipitation then used as input for both API and SME runoff calculations. This treatment is equivalent to routing 10% of precipitation directly into surface water via storm sewers and drainage systems. With these added considerations, the following equation for runoff Roff is applied:

$$ {R}_{\mathrm{off}}=\frac{\left(0.9P-{I}_{\mathrm{a}}\right)\left(0.9P-{I}_{\mathrm{a}}+M\right)}{0.9P-{I}_{\mathrm{a}}+{S}_0}+0.1P,\kern0.75em \mathrm{for}\kern0.5em 0.9P>{I}_{\mathrm{a}} $$
(3)

where Ia corresponds to rainfall interception, which is the fraction of precipitation that is lost from a catchment during a storm event through processes such as infiltration, canopy interception, or ponding at the surface (Lee and Huang 2013; Van Dijk et al. 2015). In Eq. (3), the factors of 0.9 and 0.1 will change from catchment-to-catchment depending on the ratio of area that is covered by impervious surfaces. Calculations were carried out on a daily basis and upscaled to weekly, monthly, and annual scale in order to explore storm-by-storm, seasonal, and annual runoff.

Hydrograph separation

Hydrograph separation (HS) involves dividing a hydrograph into its assumed subflow components, which consist principally of quickflow and baseflow. Baseflow corresponds to sustained streamflow during dry weather periods and is largely sourced from groundwater, where quickflow is largely sourced from surface runoff from storm events. Land development often leads to significant changes in baseflow and quickflow dynamics (Gremillion et al. 2000; Liu et al. 2013; Meriano et al. 2011).

The basic approach for hydrograph separation uses recursive digital filters (RDFs) to separate quickflow and baseflow (Chapman 1991; Nathan and McMahon 1990; Willems 2009). The RDF first proposed by Lyne and Hollick (1979), as outlined by Nathan and McMahon (1990) was applied with the EcoHydrology package available in R (Fuka et al. 2018) for this study. The filter is expressed as such:

$$ {\mathrm{qf}}_t=\alpha \times {\mathrm{qf}}_{t-1}+\frac{1+\alpha }{2}\times \left({Q}_t-{Q}_{t-1}\right) $$
(4)

where qf is quickflow (units of depth), Q is measured streamflow (units of depth), and α is the filter parameter (dimensionless). It can be seen from Eq. 4 that larger values of α lead to lower estimates of baseflow and higher estimates of quickflow, and vice versa. For the purpose of this study, qf is assumed to correspond to surface runoff.

In most applications, α is set at or near the value of 0.925 proposed by Nathan and McMahon (1990), which is applied as standard practice (e.g. Bennett et al. 2018; Burns et al. 2012; Partington et al. 2012). However, the original work by Lyne and Hollick (1979) suggested varying the filter parameter between 0.75 < α < 0.9, and more recent work by Li et al. (2014) has demonstrated that α can and does widely vary between 0 < α < 1, depending on baseflow dynamics and the underlying conceptual model. Knowledge of land cover, soil types, water-table depth, and visual inspection of a streamflow hydrograph can be used as a preliminary assessment of potential value ranges of α. It is generally assumed that the lower end of the hydrograph recession curve should coincide with baseflow. Visual inspection of the upper Kempttal hydrograph show that values of α lower than the commonly used 0.925 better portray the expected behavior of a flashier runoff response to storm events that is characteristic of urbanizing areas. For the current work, a range of values between 0.3 and 0.95 were explored with an uncertainty analysis (see section ‘Uncertainty analysis’ for details).

As the river gauging station at this study site is located directly downstream of the wastewater treatment plant (WWTP), wastewater effluent is integrated into the streamflow signal, supplementing groundwater-sourced baseflow due to its relatively lagged response relative to quickflow. Because of this, a higher quantity of baseflow (and thus a lower value for α) is deemed more appropriate to account for this effluent; an example hydrograph from this exercise is available in the supplementary information (Fig. S2 of the ESM). As with the SME method, HS calculations were calculated on a daily basis and upscaled to weekly, monthly, and annual scale in order to explore storm-by-storm, seasonal, and annual runoff.

Streamflow, runoff, and quickflow coefficients

The streamflow coefficient CQ = \( \raisebox{1ex}{$Q$}\!\left/ \!\raisebox{-1ex}{$P$}\right. \) is an often-used index to characterize the relative response of river discharge to storm events, and has been applied in numerous studies to this end (e.g. Barron et al. 2013; Penna et al. 2015; von Freyberg et al. 2018). Similarly, runoff coefficients using Roff and qf from SME and HS calculations, respectively, can be used to specifically characterize the relative surface runoff response to storm events. These are expressed as CRoff = \( \raisebox{1ex}{${R}_{\mathrm{off}}$}\!\left/ \!\raisebox{-1ex}{$P$}\right. \) and Cqf = \( \raisebox{1ex}{$\mathrm{qf}$}\!\left/ \!\raisebox{-1ex}{$P$}\right. \), respectively. It is important to note that CQ only represents how much water is mobilized by a storm event, and does not track the source of water in the streamflow response (von Freyberg et al. 2018). It is only Roff, which is calculated from the SME method, that is physically derived from precipitation. All three of these coefficients were calculated over the entire timeseries in an attempt to gain insight on the proportional streamflow or runoff response from a given storm event, the potential presence of runoff inputs additional to rainfall (i.e. pre-event water, CSO), and the catchment contributing area to runoff generation. These coefficients were explored as a function of both precipitation magnitude as well as antecedent precipitation conditions.

Uncertainty analysis

Uncertainty in the parameters for both runoff methods were explored. First, the SME method is a relatively new approach as compared to the original CN method, and plausible ranges of parameter values are less documented. To address the uncertainty for this method, a Monte Carlo sampling approach was used to generate an ensemble of 10,000 random parameter combinations from independent prior probability distributions for S0, λ, and β (Table 3; Fig. S1 of the ESM), resulting in 10,000 runoff estimates. The lower and upper limits of S0 and λ were constructed to be larger than the ranges of these parameters found in literature for the original CN method (Minnig et al. 2018; Mishra and Singh 2003; Sahu et al. 2012). It should be noted that during construction of parameter ranges, S0 values greater than 300 mm led to very minimal surface runoff estimates, and values greater than 450 mm led to a complete absence of surface runoff. Finally, each parameter was allowed to vary independently during the sampling process.

Table 3 Ranges of prior parameter values considered for SME and HS calculations
Full size table

With regard to hydrograph separation, the filter parameter α was similarly tested. In this case, a manual sampling of 23 random values between 0.3 and 0.95 was carried out (Table 3).

Groundwater recharge

Water balance

In this text, the water balance calculates groundwater recharge (GWR) as the residual of relevant terms including precipitation (P), evapotranspiration (ET), and surface runoff (Runoff). The basic form was calculated in the current study:

$$ \mathrm{GWR}=P-\mathrm{ET}-\mathrm{Runoff} $$
(5)

Using Eq. (5), GWR was estimated on a daily basis over the entire catchment, and then upscaled to annual sums for the purpose of identifying long-term trends (i.e. dry years or wet years). The estimates of surface runoff and quickflow outlined in sections ‘SME method’ and ‘Hydrograph separation’ were used in turn as the runoff input. As reference ET inputs were available from public data, their uncertainties were not explored, and the same ET dataset was used for water balance calculations.

Human systems in general, and urban systems in particular, may contain additional artificial inputs into a groundwater recharge balance such as sewer leakage, water mains leakage, or irrigation return flow (Bhaskar et al. 2016). However, such sources are highly uncertain and are difficult to identify, particularly when their impact is small or is balanced out with artificial losses such as groundwater pumping. The net impact of these artificial sources on the overall mass balance is expected to be minimal at our study site and without further data, are therefore not considered.

HBV Light model

HBV Light is a rainfall-runoff model developed by Seibert and Vis (2012) as an adaptation to the original HBV model developed by Bergström (1976). HBV Light is regularly applied by hydrologists to partition measured streamflow into its assumed subcomponents, and has been used in numerous studies for various objectives (e.g. Etter et al. 2017; Gebrehiwot et al. 2013; Griessinger et al. 2016; Orth et al. 2015). Thorough overviews are available in literature (Bergström and Lindström 2015; Seibert 1999; Seibert and Vis 2012). The model is built around the following water balance equation:

$$ P-\mathrm{AET}-Q=\frac{d}{dt}\left(\mathrm{SP}+\mathrm{SM}+\mathrm{SUZ}+\mathrm{SLZ}+\mathrm{lakes}\right) $$
(6)

where P is precipitation, AET is evapotranspiration, Q is river discharge, SP is snow pack, SM is soil moisture, and SUZ and SLZ are storage in upper and lower subsurface zones, respectively. The model output variable labeled as recharge is conceptualized as all water infiltrating from the surface into both upper and (SUZ) and lower (SLZ) subsurface zones. All variables are in units of depth over a specified time step. In its simplest form, timeseries for precipitation, air temperature, river discharge, and potential ET (PET) are needed, where river discharge is fitted to calibrate model parameters. AET is then calculated from PET and air temperature within the model. The model may be solved in either a lumped-catchment manner or in a semidistributed manner by defining elevation and vegetation zones. Model structures are available that account for multiple groundwater bodies, snow packs, or a heterogeneous unsaturated zone.

For this study, the standard HBV Light model structure was applied in order to represent both unsaturated and saturated zones. Five different elevation zones and one vegetation zone were defined in order to create a semidistributed framework. There are in fact three streamflow components in the model structure that correspond to the groundwater recharge output from SUZ and SLZ. These components are labeled Q0, Q1, and Q2, and account for unsaturated zone and shallow percolation contribution into streamflow (Q0, Q1), followed by baseflow that is connected to deep percolation (Q2). Q0 is calculated as 0 except during strong storm events and when soil moisture is above a predefined threshold, and Q1 is activated during most storm events as well as when soil moisture is above a second predefined threshold. Therefore, for the purpose of this study, Q0 and Q1 were subtracted from the given recharge variable in order to calculate GWR that is consistent with the empirical water balance applied for this study.

Built-in calibration methods are available to explore model uncertainty. Automatic sampling of parameter values between user-defined bounds can be carried out with either Monte Carlo (MC) random sampling or a Genetic Algorithm and Powell optimization (GAP). Parameter sets are then evaluated by applying one or more objective functions between simulated and observed streamflow, and best-fit combinations are determined by optimizing the chosen objective function(s). The model was calibrated between the years 2008–2012 and validated from 2013 to 2016, using both MC and GAP to find the best parameter sets. From these, the six best performing parameter sets were selected each from the MC and GAP simulations, for a total of six optimized estimates. Three objective functions were used to assess model performance: efficiency Reff, log of efficiency Log Reff, and the coefficient of determination R2. Optimal values for each of these objective functions is 1. Results only from the validation period 2013–2016 are presented in this study.

Results

Runoff response to rainfall

Streamflow dynamics

The streamflow coefficient CQ is plotted in Fig. 2 against precipitation (Fig. 2a), and then as the API, over daily timesteps (Fig. 2b). The relationship is shown for days where P > 10 mm; amounts below 10 mm in 1 day were generally observed to generate little to no streamflow response, which has been observed in studies of similar climate (e.g. Thomas and Tellam 2006). Figure 2a shows that the streamflow coefficient for precipitation amounts >30 mm/day does not exceed 0.5. In contrast, when CQ is compared to the API (Fig. 2b), a positive and exponential relationship is exposed. These relations suggest that higher antecedent catchment moisture is a strong indicator for greater streamflow response, whereas higher absolute rainfall does not seem to lead to a relatively higher streamflow response. Conditions when CQ > 1 are observed for several instances when the API surpasses 30 mm, and may be an indication of greater pre-event soil-water input or CSO, although this should be interpreted with care because CQ > 1 can be influenced by the frequency of measurements, as streamflow recession can occur over periods longer than 1 day.

Fig. 2
figure 2

Streamflow coefficient CQ with measured discharge Q as a function of a daily precipitation and b the antecedent precipitation index (API)

Full size image

Figure 3 exposes the temporal relationship between streamflow, precipitation, and the API for the example year 2010 (time series for all years available in Fig. S4 of the ESM). It can be seen that the two largest storms and river discharge peaks occur immediately following a mostly dry period with a low API. It is interesting to note that during prolonged periods of increased soil moisture and consistent small storms, major peaks in streamflow are not always observed. A notable example in Fig. 3 is the month of July, where the API is elevated from small storms, but streamflow exhibits few major peaks. Despite increases in sealed surfaces and presence of drainage systems, it is suggested that much of the precipitation during small storms ends up infiltrating soils and recharging the aquifer rather than being lost to surface runoff.

Fig. 3
figure 3

Daily time series of precipitation, river discharge, and calculated API. Time series for all years included in this study are available in Fig. S4 of the ESM

Full size image

Comparing estimates of surface runoff

The surface runoff coefficient CRoff was calculated using the mean values of all SME surface runoff simulations as a function of precipitation. When CRoff is plotted against precipitation and against the API (Fig. 4), a similar pattern to those of Fig. 2 emerges: smaller amounts of precipitation correspond more strongly to proportionally higher runoff responses, whereas higher API values correspond to proportionally higher runoff responses. Regardless that SME calculations explicitly account for direct runoff from paved surfaces, increases in precipitation do not seem to have a significant, positive impact on CRoff.

Fig. 4
figure 4

SME runoff coefficient (CRoff) as a function of a daily precipitation and b the API. The mean SME runoff was used to calculate CRoff

Full size image

Likewise, the quickflow coefficient Cqf was calculated using the mean values of all qf estimations, and is plotted against precipitation and then the API in Fig. 5. A major difference between CRoff and Cqf is in their maximum values. Whereas the maximum value of CRoff is below 0.5, the maximum value of Cqf surpasses 1. While SME runoff estimates are ‘blind’ to additional contributions to storm runoff, any additional inputs to quickflow (i.e. pre-event water, CSO) are integrated into the hydrograph such that Cqf is not subject to the constraint of precipitation as an upper threshold. Further, contrary to the discharge coefficient CQ, lags in streamflow recession are assumed to have less of an impact as much of the recession limb is filtered out when calculating qf.

Fig. 5
figure 5

HS quickflow runoff coefficient (Cqf) as a function of a daily precipitation and b the API. The mean quickflow estimates were used to calculate Cqf

Full size image

Simulations of the resulting surface runoff time series for the example year 2010 are plotted on a weekly and monthly basis in Fig. 6, where the solid and dashed lines represent the average of all simulations, and the shaded areas represent their respective standard deviations (time series for all years are available in Fig. S3 of the ESM). The weekly time scale is used to compare results on an approximately storm-by-storm basis, whereas monthly time scales are used to compare seasonal dynamics. On a weekly basis, Fig. 6 reveals that the temporal trends in runoff estimates tend to agree well for greater runoff magnitude. Greater mismatches with regard to magnitude as well as response trends are present in consistent, low levels of precipitation, where soil moisture is high—for example, storms in early August 2010. This same tendency is observed for all years (see Figs. S3.a and S3.b in the ESM). Runoff estimates on a monthly basis show good agreement in general. During the month of August, discrepancies can at least partially be attributed once again to the higher values of the API that are used for SME runoff estimates.

Fig. 6
figure 6

Time series comparison of surface runoff estimated from the SME method versus HS on a weekly and b monthly time steps. Additional time series over the entire course of study can be found in Fig. S3 of the ESM

Full size image

A summary of the runoff simulations for both SME runoff and HS quickflow are visualized in Fig. 7 (numeric values may be referenced in Table S1 in the ESM). The average runoff estimates from the SME method are generally lower than quickflow estimates from HS during moderate and wet years, yet higher during dry years. These relatively higher SME runoff estimates during dry years can partially be attributed to the uncertainties surrounding consistent low levels of precipitation that are predominant in drier years, as opposed to large storm events. Relatively higher SME estimates may also be due to the direct routing of precipitation over impervious areas into runoff, such that even moderate storms will lead to a small runoff response estimated using the SME method. For its part, overall higher values of surface runoff estimated from HS may be due to additional inputs to streamflow (such as sewer effluent) that are not fully filtered out with α.

Fig. 7
figure 7

Sum of annual surface runoff estimated including all simulations for both methods for each year of the study period

Full size image

Annual groundwater recharge

Groundwater balance of the upper Kempttal catchment

As groundwater recharge generally portrays a slower response time than surface runoff, annual estimations were explored. Figure 8 compares annual groundwater recharge calculated with the two runoff estimates, where the P and ET inputs were kept constant. The magnitude of the two resulting GWR estimates are generally in good agreement, and the inter-annual recharge trend is coherent between the two water balances as well. The largest difference between these estimates is on the order of 50 mm/year; a small and satisfactory difference. However, despite accounting for runoff uncertainty, there is a pattern of the HS quickflow input leading to lower recharge estimates between the years 2012 to 2018, consistent with higher runoff values in those years. This is likely a carryover effect to the fact that SME runoff estimates only account for losses from precipitation, where HS quickflow integrates potential signals from pre-event soil-moisture losses.

Fig. 8
figure 8

Annual time series comparing recharge estimates via water balance. Solid lines represent the mean value from all simulations, and shaded areas represent the standard deviation

Full size image

Results from the water balance were then compared to estimates of groundwater recharge from the HBV Light model for the years 2013–2016, which is the period where all three methods are covered. Figure 9 shows the spread of these estimates, where the boxplots represent all simulations for each method (numerical values may be referenced in Table S2 in the ESM). In general, the average estimates between the water balance and the HBV Light model are also in good agreement. For the years 2013 and 2014, when annual precipitation was close to its 10-year average, the average difference between the lowest and highest recharge estimates is below 100 mm/year. However, differences increase for both the extremely dry year of 2015 and the wet year of 2016, reaching approximately 200 mm/year of difference in 2016. Indeed, such reduced performance under extreme conditions is a known issue for lumped models (Crosbie et al. 2011; Moeck et al. 2018). Regardless of these differences, estimates of groundwater recharge generally equate to 40–45% of annual precipitation recharging the aquifer from all methods. The exception to this is seen during the particularly dry years of 2015 and of 2018, where recharge estimates dropped as low as 20% of annual precipitation.

Fig. 9
figure 9

Comparison of annual recharge estimates with HBV Light model results for overlapping years 2013–2016

Full size image

Performance metrics of the HBV Light model runs are available in Table S3 of the ESM. It can be seen in Fig. 9 that, despite a formal calibration in the HBV Light model against streamflow, the inter-quartile range of HBV Light groundwater recharge estimates is larger than is found with the water balance. This spread is certainly affected by uncertainties in ET in addition to runoff uncertainties. While the same reference ET data was used for the water balance calculations, the HBV Light model calculates AET internally from PET, using temperature and soil moisture as a limiting factor.

Groundwater recharge across Switzerland

To further assess the relative performance of GWR calculations, results were compared with additional estimates of GWR found at a number of study sites across Switzerland. The studies listed in Table 4 were all carried out in unconfined catchments similar to the Kempttal (based on geographical proximity, elevation, climatic forcing functions, geology, and land cover). These GWR estimates are plotted together as a function of annual precipitation in Fig. 10.

Table 4 Compilation of groundwater recharge studies across Switzerland in comparison to this study (data in italic). Note: values for this study are averaged over the entire 12-year period and appear in italic font
Full size table
Fig. 10
figure 10

Annual average groundwater recharge as a function of precipitation for study sites across Switzerland

Full size image

Different objectives, approaches and assumptions were used in each of the studies listed in Table 4. Baillieux et al. (2015) investigated the use of transfer functions and the importance of recharge estimates on contaminant transport dynamics. Epting et al. (2021) investigated the impact of climate change, and of groundwater temperature increase in particular, on recharge rates for aquifers in high-production valleys all across the Swiss plateau. Minnig et al. (2018) carried out a groundwater balance over four time periods of increasing urbanization, explicitly accounting for reduced ET under paved surfaces plus input from sewer leakage and water mains losses. Mdaghri-Alaoui and Eugster (2001) estimated groundwater recharge for an aquifer with historical nitrate contamination, with particular focus on quantifying evapotranspiration. Moeck et al. (2016) explored the effects of different hydrological model structures, calibration on groundwater recharge estimates within the context of climate change, using a lysimeter to construct a reference model. Moeck et al. (2020b) evaluated the impact of uncertainties in hydraulic conductivities and boundary conditions on flow pathways for a managed aquifer recharge system. Finally, Stoll et al. (2011) made use of groundwater and climate models to assess the impact of climate change on water fluxes, and the uncertainties tied to downscaling large-scale to local-scale models.

Regardless of these different approaches, estimates of annual groundwater recharge as well as the ratio of recharge to precipitation are in satisfactory agreement between all of these studies. This serves as an indirect validation of the methods applied in this study, and shows that the magnitude of groundwater recharge found here for the Kempttal catchment is in a similar range as what is found by other independent studies.

Discussion

The results presented in this study have indicated that reasonable estimates of surface runoff and groundwater recharge for an urbanizing catchment can be obtained with minimal data using empirical methods. Comparing annual groundwater recharge estimates with Swiss case studies found in literature further served as a useful tool to confirm that the results found here are within a credible range. In spite of satisfactory performance, uncertainties persist in the estimation of surface runoff on shorter timescales. This highlights the difficulty in capturing specific processes that influence the runoff response (and resulting groundwater recharge) without more robust databases. However, the necessity to characterize such responses in ungauged, data-poor catchments has been widely recognized (Hrachowitz et al. 2013). Better constraining physical catchment properties such as topography, vegetation type, or land use, may be of equal, or even greater, value for improving understanding of flow processes in the absence of robust, high temporal resolution databases (e.g. Carlier et al. 2018; Moeck et al. 2020a; Tweed et al. 2007). Indeed, an important step in all CN-based methods is the determination of soil types (USDA Natural Resources Conservation Service 1986). In the case of the SME method, constraining maximum catchment potential retention and soil moisture using physical catchment characteristics could improve estimates of surface runoff without increasing the demand for on-the-ground measurement data.

Assessment of conventions in estimation methods

An important step in this study was to critically assess appropriate values of the parameters used in both runoff estimation methods. For the well-known hydrograph separation using a recursive digital filter, the commonly used value for the filter parameter α = 0.925 was interrogated by exploring a wider range of parameter values, as suggested in several recent studies (e.g. Li et al. 2014). It has long been recognized that at least in some catchments, pre-event baseflow plays a significant role in the storm runoff response (Klaus and McDonnell 2013), which would be better represented by lower values of α. It is believed that variations in the filter parameter should regularly be included in uncertainty analysis when applying the RDF to a hydrograph.

With respect to the SME method, by implementing the exponential decay factor through the API in place of P5, the method is one step closer to representing a more continuous accounting of soil moisture, removing the assumptions tied to catchment dryness prior to a user-defined window as identified by the authors of the method. Use of the API could be further strengthened by adjusting k as a function of time in order to account for seasonal differences in catchment moisture retention. Some authors have additionally determined the value of this decay factor as a function of physical processes within a given catchment (Descroix et al. 2002).

The second modification to the SME method, of rerouting a fixed percentage of rainfall directly into runoff, was an attempt to capture some of the runoff dynamics that are inherent in urban areas with impervious surfaces, albeit in a simplified manner. In future work, it would be of great value to include a measure of the level of connectivity of impervious surfaces if using this approach. The assumption that impervious surfaces are 100% impermeable could also be explored; as noted by previous authors, roads sometimes portray ‘leaky’ behavior, such that some level of infiltration occurs in these areas as well (Fidal and Kjeldsen 2020).

With regard to groundwater recharge methods, the definition of recharge in the HBV Light model was critically assessed. When applying this model as a tool to estimate recharge specifically to the aquifer, the underlying conceptual model was adjusted in a way that input from the unsaturated zone was subtracted from the recharge term. In the first iteration of the model, using the recharge estimate without considering the soil-moisture variables Q0 and Q1, estimates of more than 70% of rainfall becoming recharge were consistently found, which is considerably higher than what is found with the water balance and with other values found in the literature noted in Table 4. With the adjustment made in the current study, HBV Light results are in close agreement with empirical water balance estimates, with the exception of extreme years.

Differences in estimations as a function of data input

When comparing simplified pluviometric versus hydrographic methods to estimate runoff, many differences are drawn directly from the data input. Indeed, differences in even the most accurate of estimates are to be expected, as each data type only contains part of the story. For this reason, determining one method as being ‘better’ is evasive. The pluviometric calculations made here inherently assume an immediate response to rainfall, and that the amount of precipitation serves as the upper limit of potential surface runoff. For its part, streamflow is an integrated signal of any present runoff inputs and their relative time lags. While most of the information that is being sought is present in the signal, the difficulty lies in accurately identifying and separating these different signals (Klaus and McDonnell 2013). In addition, using a hydrograph to estimate direct storm runoff has an inherent assumption that all storm runoff is directly routed into a stream, which is not always the case (Brandes et al. 2005). In the Kempttal catchment, the dynamics of sewer effluent and combined sewer overflow, for example, are a notable source of uncertainty when using hydrograph separation. Such inputs, if not properly quantified, could lead to over-estimations of surface runoff from precipitation. However, the strength of comparing different approaches comes from the same source as their difficulties; there is a potential to use such discrepancies in estimates to identify system unknowns. When possible, it is always suggested to apply multiple methods when estimating the water balance using empirical methods and minimal data.

Importance of the runoff–recharge relationship

There are many important sources, processes, and interactions that impact groundwater recharge. The current study was motivated by the fact that runoff carries particular importance with regard to water quality. This increased risk of quality degradation is notably relevant in human-impacted areas due to the cocktail of chemicals that are present in such environments (e.g. Barlow et al. 2012; Hollender et al. 2018). Pollutants carried with runoff from the surface can make their way into the groundwater in several ways—through the use of infiltration basins, through combined sewer overflow during storms, and through groundwater interactions with quality-impacted surface water, to name a few.

As a final consideration, when studying changes in the water cycle in a changing environment, it is important to keep in mind that relative changes of each input are occurring on top of the absolute changes of each. While the latter was the focus of the current study, it is nonetheless worth mentioning that increases in runoff do not necessarily signal a decrease in overall groundwater recharge. Particularly in urban areas, the observed increases in surface runoff that result from impervious surfaces can be accompanied by decreases in actual evapotranspiration due to these same impervious surfaces, which can in fact lead to an increase in recharge rather than a decrease in these areas (Barron et al. 2013; Brandes et al. 2005; Minnig et al. 2018). While these relative changes were beyond the scope of this study, the interested reader may refer to literature (Appleyard 1995; Bhaskar et al. 2015; Feng et al. 2012; Sharp 2010; Wittenberg and Sivapalan 1999) for a more in-depth discussion on the feedback between ET, runoff, and recharge.

Summary and conclusions

This study has compared multiple methods to estimate surface runoff and its impact on groundwater recharge in the small urbanizing Kempttal catchment on the Swiss Plateau. Straightforward methods with low data requirements were chosen in order to test their appropriateness in changing environments. Two approaches to estimate surface runoff—one pluviometric and one hydrographic—were applied, with modifications that attempt to better capture soil-moisture accounting and to explicitly account for runoff from impervious surfaces. The results were used in a water balance to calculate groundwater recharge for the shallow, unconfined aquifer within the study catchment. To evaluate the accuracy of these water balance estimates, a comparison was made to additional estimates of groundwater recharge using the conceptual HBV Light model. Finally, these recharge estimates were assessed against several literature studies from similar catchments in Switzerland. From these results, an approximate range of groundwater recharge was obtained on a spatial scale, offering insight into the sources of uncertainty in both runoff and groundwater recharge estimates.