Does migration depress regional human capital accumulation in the EU’s new member states? Theoretical and empirical evidence

Abstract

During the first decade of the present century the countries which accessed the EU were characterised by high GDP growth rates while most of their regions displayed negative net-migration rates. At the same time, the new member states’ human capital endowments were high relative to their GDP levels, creating incentives to emigrate. The present paper takes a detailed look at the interplay of regional human capital endowments and migration. First, by theoretically examining migration’s determinants and second, by testing the corresponding findings via panel econometric regressions for the EU’s new member states’ regions. The results display positive impacts of net-migration on regional human capital growth rates, improving the economic potential of thriving regions but possibly increasing disparities within countries.

Zusammenfassung

Jene Staaten, die der EU während der 2000er-Jahre beigetreten sind, zeigten hohe Wirtschaftswachstumsraten, gleichzeitig waren die meisten ihrer Regionen durch negative Nettomigrationsquoten gekennzeichnet. Aufgrund des im Verhältnis zur Wirtschaftsleistung hohen Humankapitalbestands bestanden Anreize zur Emigration. Der vorliegende Artikel beleuchtet das Wechselspiel zwischen regionalen Humankapitalbeständen und Migration. Zunächst werden die Determinanten der Migration theoretisch diskutiert, daran anschließend werden die theoretischen Ergebnisse mittel panel-ökonometrischer Methoden für die Regionen der neuen EU-Mitgliedstaaten getestet. Die Ergebnisse zeigen, dass die Nettomigrationsquote einen positiven Effekt auf die Wachstumsrate des regionalen Humankapitalbestands hat, wodurch sich das ökonomischen Potenzial wachsender Regionen weiter verbessert, während sich die Disparitäten innerhalb der Länder möglicherweise weiter vergrößern.

Introduction

In July 2016, the International Monetary Fund (IMF) released a discussion note entitled “Emigration and Its Economic Impact on Eastern Europe” (Atoyan et al. 2016). The article acknowledges that “emigration from Central, Eastern, and Southeastern Europe has been unusually large, persistent, and dominated by educated and young people” and discusses its impact on the future development of the concerned countries. In brief, the discussion note (ibid.) understands that a continuing outflow of human capital severely decreases prospects of growth and income convergence for those economies within the EU which currently lag behind in terms of productivity and income.

From an economic geography perspective, this development hardly comes as a surprise. In the same year the Treaty of Rome was signed, Myrdal (1957) released his theory on core-periphery relationships according to which a system of regional economies at different stages of development is characterised by outflows of young and well-educated workers from the periphery to the core. The issue was later taken up by Krugman (1991a, 1991b), who formally shows that a reduction of trade costs results in a concentration of production and skilled workers, i.e. skilled workers migrate to where advanced technologies are located. As it happens, Krugman released his influential model at the advent of the introduction of the European Single Market, which allows for free movement of persons. The issue of intra-EU migration following the eastern enlargements of the 2000s has indeed drawn considerable political concern, as income differences in connection with the free movement of people within the European Single Market have the potential to create high incentives for workers from the new member states that accessed since 2004 (“NMS” henceforth) to emigrate to the wealthier western member states (“EU15” henceforth).

What does come as a surprise, however, is that the economic literature tends to concentrate on the benefits of migration, typically focussing on the receiving economies. For instance, Fertig (2001) and Kahanec and Zimmermann (2010) estimate EU15 migration inflows and discuss their expected effects on the receiving economies. In contrast, the number of studies analysing the consequences of migration on origin regions is extremely limited (Faggian et al. 2017) and little is known about the impact of the EU enlargement on the NMS’ human capital accumulation and economic development. This lack of evidence may partly be due to a lack of interest, as most scientists who publish in peer-reviewed journals reside in receiving regions, either originating in such regions or having moved there. Another reason, however, relates to limited data availability. The European Union keeps no tracks of interregional migration within its territory, while labour force surveys’ samples are far too small to gain information regarding the geographical origins of foreign workers, even at the national level, let alone regions at the sub-national level.

For these reasons, researchers have to draw conclusions from other sources. In one of the few studies which focus on NMS economies, Gödri et al. (2014) point out that due to lack of accurate data it can only be assumed rather than measured whether emigrants are more skilled than the Hungarian average. In addition, the scale of migration is difficult to predict. For instance, Hárs and Neumann (2008) investigate the migration potential and intention in Hungary as measured by interviews in 2003 and compare this to the realised emigration of the same sample in 2007. They find that only 25 per cent of those announcing a willingness to migrate had actually worked abroad at any point in time between 2003 and 2007. It follows that data based on surveys are not reliable in quantifying intra-EU migration.

Public policy advisors typically recommend improving the educational system to increase human capital (e.g. Atoyan et al. 2016; European Bank for Reconstruction and Development 2013). Investments in human capital are necessary for economic development, this issue remains largely undisputed in the literature. As noted by Faggian and McCann (2009), however, the presence of human capital can result in a major spatial reallocation of factors, where labour mobility may cause human capital to have different impacts on national as compared to regional growth. In particular, the dynamics become more complex on regional levels, as interregional migration is usually not restricted, and those supplying human capital are usually more mobile as the profitability of migrating is positively related to education (Borjas 2010). Against this background, human capital investments (i.e. educational spending) can be viewed as a “necessary but not sufficient condition” to ensure regional development due to the impact of interregional migration (Faggian and Franklin 2014, pp. 377). The resulting dynamics are of special concern with respect to the European Union, where disparities regarding income and development are vast, while people are free to move. The fact that the NMS are geographically close to, or adjoining EU15 regions, adds to the issue.

The present paper’s point of departure relates to the interplay of human capital production and migration as the main determinants of actual human capital accumulation. Furthermore, the paper considers region-specific characteristics, as opportunities within one region are expected to affect individual human capital incentives. The crucial question is: Did EU-membership benefit or harm the NMS’ regional human capital endowments? To this end, the present article focuses on the first decade of the present century, i.e. a period which was characterised by high GDP growth rates of the NMS and—as a consequence of EU accession—increased opportunities to migrate for the EU’s in general and NMS’ labour forces in particular.

The present study addresses the research gap as discussed above by investigating the development dynamics of regional human capital accumulation in the NMS shortly before and after their EU accessions. The paper proposes a theoretical framework which takes into account that the NMS are by no means homogenous within their territories—some regions may win, some may lose. The contribution of the present paper lies in identifying the mechanisms and forces that potentially increase or decrease regional human capital accumulation in the NMS regions. The paper is structured as follows: The next Section discusses the empirical circumstances of the NMS and why it is attractive to emigrate. After that, the Myrdal and the Roy models of migration are merged to explain theoretically what motivates people to migrate. In Sect. 4 the empirical framework is presented, with the corresponding results being discussed in the following Section. Conclusions can be found in the sixth Section.

The NMS’ human capital accumulation record

The roots of the NMS’ peculiar circumstances

As one would expect, wage inequality in centrally planned economies was lower than in Western European market economies. Simpson (1990) estimates the Gini coefficients of selected nations between 1965 and 1975 to equal 20.4 in the German Democratic Republic (GDR) and 24.8 in Hungary, compared to 36.7 in the Federal Republic of Germany (FRG) and 37.1 in Austria. By further considering that member states of the Council for Mutual Economic Assistance (Comecon) usually subsidised daily needs by taxes on luxury goods, inequality in real terms was probably even lower.

Two observations are related to these basic findings. First, low wage-inequality means that mark-ups for scarce skills (i.e. human capital) are low. Therefore, income incentives for skilled workers to emigrate from Comecon member states were not just caused by wage differentials within Comecon states but also due to higher mark-ups in Western Europe. The legal barriers to such intentions are historically symbolised by the Berlin Wall, whose military monitoring followed the main objective to prevent emigration.¹ Second, despite relatively low mark-ups, incentives to invest in human capital were still present in the centrally planned economies (Flemming and Micklewright 1999). As a consequence, human capital levels were comparable to EU and EFTA levels.²

It is natural to assume that once such barriers were lifted, incentives to emigrate from the NMS were high and, indeed, despite legal barriers to immigration in EU and EFTA countries, in 1990 alone about 1.3 million Eastern Europeans moved to Western Europe (Burda and Wyplosz 1992). In the following years, incentives for emigrating were further amplified by the deep recession which resulted from the former Comecon’s economic transformation. Furthermore, wage and household income inequality has considerably increased in former centrally planned economies (Krueger and Pischke 1995; Flemming and Micklewright 1999), while relative income compared to the EU and EFTA has rapidly decreased.³

The NME’s accession to the EU Single Market

From this background it follows that during the 1990s high human capital endowments in former Comecon member states relative to GDP, on the one hand, improved the prospects of thriving economically, while on the other hand, they created incentives for emigration. At the eve of the NMS’ accession to the EU as well as years after the former were still characterised by high human capital endowments relative to GDP, as illustrated by Fig. 1a, b for the years 2003 and 2012, respectively: The Figures plot population with tertiary education against GDP per inhabitant levels relative to the EU average, where diamonds mark NMS and dots mark EU15 states. As a general impression, it can be seen that a positive relationship between tertiary education and productivity exists. However, a closer look at Fig. 1a reveals that in 2003 this relationship can only be observed for the EU15 states. Furthermore and most strikingly, all EU15 states are located above the NMS. Given that a positive relationship between human capital and productivity exists, Fig. 1a indicates that before EU accession, either (i) the NMS’ GDP relative to human capital levels were too low and hence expected to increase, or (ii) their human capital endowments relative to GDP were too high and hence expected to decrease, or (iii) both.⁴

Fig. 1

a and b Tertiary education shares (x-axis) and GDP per capita levels (y-axis) of NMS (diamonds) and EU15 (dots) states, as of 2003 (left) and 2012 (right), relative to EU average, with respective OLS lines. Notes: GDP per capita is given as the percentage level relative to the EU at current market prices, tertiary education shares refer to the percentage share of the population 15–64 years old with a tertiary degree (ISCED97 5 or 6); the graph includes the EU member states as of 2007 except for countries with less than one million inhabitants; tertiary education in (a) for Austria as of 2004; the OLS lines’ R² values equal 0.438 for EU15 in 2003, 0.001 for NMS in 2003, 0.270 for EU15 in 2012 and 0.061 for NMS in 2012; data source: Eurostat

Fig. 1b plots the same relationship nine years later. By comparing Fig. 1b to Fig. 1a, three developments can be observed. First, the NMS have converged in terms of GDP per capita, as each of them has moved up. Second, the relationship between GDP per capita and tertiary education has become slightly more pronounced for the NMS. Thirdly, each of the NMS has moved towards the right, which means that within these countries, the shares of tertiary educated people have increased. However, since the EU15 states have also generally increased these shares, the question is whether the NMS were also able to increase their shares relative to the EU15.

The development within the NMS

During the years of high economic growth following transition-induced recessions the NMS’ capital city regions’ growth rates were typically much higher than those of non-metropolitan regions, leading to increasing disparities in terms of productivity within the respective countries (Sardadvar 2011). Hence, there exist two sides of the same coin: The emergence of growth poles around the metropolitan areas supported the NMS’ catching-up at the national level while simultaneously increasing interregional disparities within the respective countries. This process coincides with positive net-migration rates of the NMS’ capital city regions, while most other regions experienced negative net-migration rates (see Sardadvar and Rocha-Akis 2016; Fig. 1). The question arises whether the divergence of GDP levels within the NMS also coincided with a divergence regarding human capital endowments.

Measuring human capital

Although tertiary education serves as an indicator of human capital and is frequently applied in the literature, it ignores most of the available human capital as it, by definition, captures all types of skills. A more comprehensive measure should hence capture the skills of the whole workforce. One option is to rely on schooling of all persons considered. Following Barro and Lee (2010), in the present paper human capital endowments of region $i$ at point in time $t$ is henceforth estimated as

$$S_{i,t}=\sum _{k=1}^{3}H_{i,k,t}D_{k}$$

(1)

where $S$ symbolises total schooling years accumulated by the population aged 24–64. $H_{i,k,t}$ equals $i$’s population aged 24–64 which has attained educational level $k$ at $t$. Three levels of $k$ are considered, namely lower secondary, higher secondary and tertiary education. Duration $D_{k}$ corresponds to the number of years spent in schooling necessary to achieve a particular educational level: Based on the International Standard Classification of Education (ISCED, see UNESCO 2011), lower secondary education corresponds to nine, higher secondary education to 13, and tertiary education to 17 years. The data source for $H$ and $D$ is Eurostat.⁵ In order to receive average schooling years of the labour force, total schooling years are divided by the respective population number:

$$s_{i,t}=\sum _{k=1}^{3}\frac{H_{i,k,t}D_{k}}{P_{i,t}}$$

(2)

where $P_{i,t}$ symbolises $i$’s population aged 24–64 at $t$, the source of which is also Eurostat.

Based on these measures, Fig. 2 illustrates the evolution of human capital endowments for the seven countries that this paper focuses on, relative to the EU as a whole for 2004–2011.⁶ In the Figure, each country’s evolution of its share of the EU’s total human capital stock is displayed as $\sum _{i=1}^{n^{*}}S_{i,t}/S_{EU,t}/\sum _{i=1}^{n^{*}}S_{i,2004}/S_{EU,2004}$, where $n^{*}$ refers to the total number of regional economies in a particular member state, and $EU$ refers to the EU as a whole. It can be seen that—except for Slovakia—none of the NMS managed to increase its human capital endowment relative to the EU by much more than one per cent. Taking Figs. 1a,b and 2 together, a first conclusion emerges: The NMS’ remarkable catch-up process in terms of GDP per capita did not coincide with a relative increase in human capital.

Fig. 2

Total human capital stock relative to the EU, 2004 = 100. Notes: Total human capital stock as measured by Eq. 1, EU refers to its territory as of 2011; data source: Eurostat

Developments within the NMS

For the following calculations, a region’s human capital share within its nation state is measured as $S_{i,t}/\sum _{i=1}^{n*}S_{i,t}$. Fig. 3a–h display four indicators of human capital distribution within Bulgaria, the Czech Republic, Hungary, Poland, Romania, Slovakia, Slovenia, as well as the entire subsample over 2000–2011 on the NUTS2 level, where the reader should be aware that different scales are used to make the diagrams easier to interpret.⁷ The first indicator, “capital”, represents the respective capital city’s share in its country’s total human capital stock. The second, “Herfindahl”, equals the Herfindahl index of $s_{i,t}$. Third, “St. dev.” equals the non-weighted standard deviation of the logarithmised values of $s_{i,t}$. Finally, “Gini” equals the Gini coefficient of $s_{i,t}$, where regional population numbers are taken as frequency measures. As indicated in the respective legends, some measures are multiplied by ten for scaling purposes.

Fig. 3

a–h Intra country and area distributions of human capital 2000–2011. a Bulgaria, b Czech Republic, c Hungary, d Poland, e Romania, f Slovakia, g Slovenia, h Observation area

The overall picture indicates an increase in human capital concentration within each country. Though exceptions can be found, in each case where measures show a trend, they point upwards. Accordingly, on an aggregate level, all four measures point upward in Fig. 3h, i.e. indicating increasing interregional inequality with respect to human capital endowments.⁸ From Fig. 3a–h, a second conclusion emerges: Within the NMS, interregional concentration of human capital has generally increased.

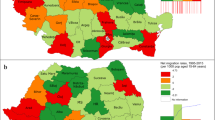
Finally, Fig. 4 displays the average regional net-migration rates during the observation period. There seems to exist a tendency according to which countries with increasing interregional disparities in Fig. 3a–h are those in which most of the regions have negative net-migration rates. Furthermore, the map shows that regions with positive rates are either capital city regions, or geographically close to Austria and Germany. Taking the empirics together, by induction, the following hypothesis may be formulated: In total, the NMS lose human capital to the EU15, while within the NMS some growth poles gather human capital which originates in other NMS regions. In the next Section, this hypothesis is embedded into theory and extended to a model.

Fig. 4

Average regional net-migration rates in the observation area, 2000–2009

Theoretical framework

The Myrdal model

Myrdal’s (1957) model is designed to explain interregional as well as international relations. In both cases the core and the periphery of an economic system depend on each other, with the core dominating the periphery, both economically and politically. At most times in net-terms the core absorbs factors from the periphery, including human capital: Well-educated and young people tend to emigrate from the periphery, leaving the old and less educated behind, thereby increasing the attractiveness of the core for investments and further immigration.

Myrdal’s model refers to regions in a broader sense: A region is not necessarily a spatial unit below the national level but may as well refer to a group of regions or countries. Thus, the model acknowledges that core regions may exist within a periphery—typically, but not necessarily, capital city regions. In what follows such cores within a periphery (e.g., a capital city region within an NMS) are referred to as semi-periphery. In this sense, the semi-periphery is able to absorb resources from within the periphery. A likely scenario is one in which the semi-periphery gains human capital, among other resources, from the periphery while simultaneously losing them to the core.

The Roy model

Labour and migration theories stress the importance of employment and income opportunities for potential migrants (Greenwood 1997). The question of the migrants’ self-selection in connection with their individual human capital endowments is taken up by Borjas (1987, 1991) by referring to Roy (1951).⁹ This model considers labour migration to depend not only on average wage, but additionally accounts for returns to skills. Each worker is assumed a potential migrant if people are free to move. Seen from the source economy’s perspective, workers choose their destinations with respect to the relative skills-payoff they expect, which in turn determines the skill-compositions of the immigrant flows (Borjas 2010). These relative payoffs can be considered as a function of average wage and skill mark-ups.

In general, the greater the return on human capital in a potential destination economy the more likely it is that the immigrants are relatively skilled (Borjas 1999a). Borjas (1999b, 2010) distinguishes two types of self-selection, as seen from the destination economy: “Positive selection” occurs if immigrants have above-average earnings in both the source and host countries, while “negative selection” occurs if immigrants have below-average earnings in both countries. It follows that, ceteris paribus, higher returns to skills leads to a positive selection, or, in other words, economies with higher wage inequality receive higher-skilled immigrants.¹⁰

The Myrdal and Roy models combined

For the purpose of the present paper, the Roy model is extended by replacing the mark-up for skills by demand for particular skills: While it is assumed that skill-related mark-ups are identical across all regions, what differs are the chances for a skilled worker to find a job paying an adequate mark-up for his or her skills. As a ceteris paribus condition, it follows that regions which demand a wider range of skills attract a higher number of skilled migrants.

A hierarchy of regions emerges in the sense that the semi-periphery demands a wider range of skills than the periphery, while the core demands the widest range. Fig. 5 combines these assumptions to a model of interregional human capital migration: Circles represent the three types of regions, with the unidirectional black arrows indicating the net-migration of human capital carriers. While migration of skilled workers principally flows in any direction, at any time the core demands more human capital than the semi-periphery, and at any time the semi-periphery demands more human capital than the periphery; on the net, the directions are unidirectional.

Fig. 5

Interregional human capital migration

What decides whether a worker will actually emigrate is displayed by the three wide arrows pointing at each type of region. Note that impacts which increase the likelihood that a particular worker stays have the same effect on potential immigrants, i.e. any effect which makes a region more attractive simultaneously attracts skilled immigrants and makes skilled inhabitants stay. For this reason, in what follows, both effects may be used synonymously and are considered to increase regional human capital endowments.

Empirical implementation

The theoretical considerations above make no prediction of how many people will actually migrate. Rather, it is hypothesised that a hierarchy of job opportunities exists: The core is expected to attract more people than the semi-periphery, with the latter offering more such opportunities than the periphery. From this, it follows that a mirroring hierarchy regarding net-migration flows exists.

The empirical implementation is complicated by the fact that the status of a region is not determined a priori. Furthermore, due to language and other barriers, or during periods of exceptional economic growth, the semi-periphery may actually attract more migrants than some core regions. It should also be mentioned that in the sense of Myrdal’s model, what is considered as the core in the broad sense (i.e., the EU15) contains semi-peripheral and peripheral regions, too.

These issues, however, simplify if the observation area consists only of the NMS’ sub-national regions. The considered regions are hence representing semi-peripheral and peripheral regions, with the EU15 (and other high-income countries) corresponding to the core. From the hypothesis that the semi-periphery offers more job opportunities than the periphery, and the assumption that these opportunities attract people with higher qualifications, it follows that within the NMS schooling and net-migration should be positively correlated. Table 5 in the Appendix shows that this is indeed the case.

In addition to migration there exist many factors affecting regional schooling. In order to test whether this positive relationship holds in what follows various variables that may have an impact on schooling are controlled for. These variables which are likely to determine the individual decisions are subsumed under the dimensions income, jobs and future:

• “Income” refers to a region’s productivity and, in this sense, to its average wage level. It includes both current wealth and income prospects, i.e. economic growth. If economic growth is above average, more labour is demanded, increasing not only the likelihood of finding a job, but also the incentives for the local population to acquire human capital, therefore increasing local skill levels. In addition, higher income usually also results in higher tax revenues and therefore allows regions to provide better framework conditions and amenities, which in turn attracts people. On the other hand, the relationship between GRP levels and schooling may be negative when considering decreasing returns to schooling. Given the heterogeneous characteristics of the observation area (the regions with the lowest GDP per capita within the EU are found here) the particular effect is ambiguous. Income differences matter both on the interregional level (periphery versus semi-periphery) as well as the international level (periphery and semi-periphery versus core).

• The second arrow, “jobs”, reflects how opportunities available in potential destinations relative to the current residence regions determine the net-gains of moving and hence the likelihood that a worker does so (Borjas 2010). Wider job opportunities increase the chance of job matching for any type of workers, but in particular for highly skilled workers. Furthermore, unemployment is widely regarded as a major push factor, reducing a region’s attractiveness. On the other hand, high unemployment rates may also be associated with economies receiving a high number of migrants if the latter remain unemployed, hence the actual effect is ambiguous, or people being less mobile, as mentioned above. High unemployment may also coincide with low geographic mobility over time, as discussed, among others, in Autor et al. (2013).

• Finally, “future” represents the prospects of regional development in the medium run. In particular, investments in the physical capital stock (either by the private or state sector) imply favourable prospects for future production and growth. This may increase the local population’s incentives to acquire skills but also increase or induce immigration. The current age structure is also relevant, as younger people in general have higher formal qualifications, which, in turn, makes a region more attractive for other migrants as well as physical capital investments.

In addition, actual migration decisions are also influenced by interregional relationships, such as the distance between regions, or whether they are found in the same country. Such interregional relationships may be considered a fourth dimension.

Variables and econometric specifications

In what follows, indicators and the corresponding data sources are assigned to the model’s four dimensions. In each of the econometric specifications the dependent variable is $s_{i,t}$, either measured by its level or yearly growth rate of total schooling years accumulated by the population aged 24–64. The observation area consists of the 51 NUTS2 regions as introduced in Sect. 2. The full list of regions and the respective capital-city centres can be found in Appendix B.

The five dimensions, indicators, and variables

In Table 1, each variable as applied in the following estimations is assigned to the indicators and dimensions discussed in the previous section. In addition, Table 1 provides information on variable definitions and data sources. The respective variables are as follows:

Table 1 Explanatory variables applied in the econometric specifications

The “income” dimension refers to current wealth and income prospects, which are captured by current GRP per inhabitant (measured in euros) and its real growth rate (measured in percentage numbers), respectively. Although purchasing power parities (PPP) may be preferred to account for actual living standards in the EU such data are available for countries only, resulting in identical relative GRP levels across regions within a country making them inadequate for the study’s purposes. A third variable, “share7”, captures the total observation area’s share of the EU’s absolute GDP to account for income differences on country levels and hence incentives to migrate to the core regions. Hence, while GRP per inhabitant levels and growth control for differences within the observation area and therefore distinguishes the periphery from the semi-periphery, share7 controls for differences of the periphery and semi-periphery to the core.

Second, the “jobs” dimension takes the presumed higher mobility of young people into account, by considering the youth unemployment rate in addition to the general unemployment rate in each region. The expected effect is ambiguous due to the various impacts it may have, as discussed above.

The third dimension, “future”, is represented by gross fixed capital formations and the age structure.¹¹ The share of the population that has most likely completed its education and is in working age, i.e. 25–64, is included to account for the hypothesis that they are most likely to benefit from migration (Sjastaad 1962). Its impact may be either positive, by making a region more attractive, perhaps via network effects, but it may also increase migration as people in this age group are more likely to migrate.

Fourth, “interregional relationships” are accounted for by two variables. The first, modified from Comin et al. (2013), captures a region’s economic distance to its respective country’s capital city region divided by the geographic distance between them:

$$\delta _{i,t}=\frac{\ln q_{i,t}-\ln q_{c\left(i\right),t}}{\ln d_{i,c\left(i\right)}}$$

(3)

where $q$ refers to GRP per inhabitant, $c(i)$ refers to the capital city region of $i$’s country and $d$ symbolises road distance. The variable $\delta$ is intended to control for the interplay of the attractiveness of moving from the periphery to the semi-periphery and the cost to do so. A greater distance increases the cost of migration and should therefore have a negative impact on $\delta$, as it is found in the denominator. A lower GRP in the periphery relative to the capital city region should have a negative impact, too, as it decreases the numerator. Therefore, a larger $\delta _{i}$ should have a positive impact on $i$’s human capital, especially if it increases over time.

The second variable capturing interregional relationships, $E$, equals one for years the respective region was a member of the EU, zero otherwise. The impact of $E$ may intuitively expected to be negative, as migration was eased with EU accession. However, due to the special role of the semi-periphery, the actual effect is ambiguous and may change over time.

Finally, regional net-migration rates capture the impact of the fifth dimension, “migration”. Note that this variable serves as the key variable in the following estimations, as the impact on human capital is ambiguous: Since net-migration may take on positive or negative values, with most of the sample’s regions displaying negative values for most periods (see Fig. 4), the interpretation differs whether human capital stocks or growth rates are considered. If the dependent variable is the current stock of human capital, a positive coefficient simply means that human capital is positively correlated with net-migration, and vice versa. If the dependent variable is human capital growth the interpretation becomes more complex:

• A negative impact means that regions with negative net-migration rates actually benefit from migration: A decrease in net-migration (i.e. an increase of the absolute value) has a positive impact on human capital, and vice versa for regions with positive net-migration rates.

• Consequently, a positive impact means that regions with negative rates would lose from an increase, while regions with positive rates would benefit.

To account for international migrants’ contribution to skills an additional variable is added, equalling the share of working-age foreign-born inhabitants with “advanced skills” (= tertiary education) as defined by the International Labour Organization by the total number of working-age foreign-born people. The expected impact of this variable is ambiguous. On the one hand, skilled immigrants may crowd out skilled internal migrants and hence reduce their otherwise positive impact on human capital. On the other hand, a higher share of tertiary educated immigrants may induce or reflect agglomeration effects leading to ever-increasing (or, if absent, decreasing) skill levels (McCann 2013). Due to data limitations this variable is available on the national level only, which means that each region within a country displays the same value for each year.

Level estimations

In the first set of estimations the correlations with levels of schooling years are estimated, the observation period covers the years 2000–2009:

$$\begin{aligned} \ln s_{i,t} =&\,\alpha _{i}+\beta _{1}\ln x_{1,i,t-1}+\beta _{2}\ln x_{2,i,t-1}+\beta _{3}x_{3,i,t-1}+\beta _{4}\ln x_{4,i,t-1}\\ &+\beta _{5}\ln x_{5,i,t-1}+\beta _{6}\ln x_{6,i,t-1}+\beta _{7}\ln x_{7,i,t-1}+\beta _{8}\delta _{i,t-1}\\ &+\beta _{9}E _{i,t-1}+\beta _{10}\ln m_{i,t-1}+\beta _{11}\ln \varsigma _{i,t-1}+\varepsilon _{i,t} \end{aligned}$$

(4)

where $\alpha$ and the $\beta$s symbolise the regression coefficients, the dependent variable is defined as in Eq. 2, the explanatory variables are as defined in Table 1 and $\varepsilon _{i,t}$ captures the regression residuals. The explanatory variables are lagged by one period to reduce endogeneity. Real GRP growth and net-migration rates may take on negative values, which is why the lowest value plus some small additive is subtracted in each case to guarantee defined logarithms.¹² A variant of Eq. 4 includes an interaction term to test whether EU-membership has an impact on migration:

$$\begin{aligned} \ln s_{i,t} =&\,\alpha _{i}+\beta _{1}\ln x_{1,i,t-1}+\beta _{2}\ln x_{2,i,t-1}+\beta _{3}x_{3,i,t-1}+\beta _{4}\ln x_{4,i,t-1}\\ &+\beta _{5}\ln x_{5,i,t-1}+\beta _{6}\ln x_{6,i,t-1}+\beta _{7}\ln x_{7,i,t-1}+\beta _{8}\delta _{i,t-1}\\ &+\beta _{9}E _{i,t-1}+\beta _{10}\ln m_{i,t-1}+\beta _{11}\left(E _{i,t-1}m_{i,t-1}\right)+\beta _{12}\ln \varsigma _{i,t-1}+\varepsilon_{i,t} \end{aligned}$$

(5)

Note that the inclusion of an interaction variable as in Eq. 5 implies that

$$\frac{\partial \ln s_{i,t}}{\partial \ln m_{i,t-1}}=\beta _{10}+\beta _{11}E _{i,t-1}$$

(6)

which means that the total effect of net-migration is the sum of net-migration’s coefficient plus the value of the EU dummy, i.e. the interaction variable’s coefficient must be added for the years in which a region was part of the EU. A further variant replaces $E _{i,t-1}$ by year dummies.

Growth rates estimations

The second set of estimations focuses on the growth rates of schooling years, i.e. except for the dependent variable, the specification is identical to above:

$$\begin{aligned} \ln s_{i,t}-\ln s_{i,t-1} =&\,\alpha _{i}+\beta _{1}\ln x_{1,i,t-1}+\beta _{2}\ln x_{2,i,t-1}+\beta _{3}x_{3,i,t-1}+\beta _{4}\ln x_{4,i,t-1}\\ &+\beta _{5}\ln x_{5,i,t-1}+\beta _{6}\ln x_{6,i,t-1}+\beta _{7}\ln x_{7,i,t-1}+\beta _{8}\delta _{i,t-1}\\ &+\beta _{9}E _{i,t-1}+\beta _{10}\ln m_{i,t-1}+\beta _{11}\ln \varsigma _{i,t-1}+\varepsilon _{i,t,t-1} \end{aligned}$$

(7)

and may, in analogy to Eqs. 5 and 6, include interaction terms.

Results and interpretation

Table 2 displays the results corresponding to Eqs. 4 and 5, including $E$ (column 1) or year dummies (column 3), and interactions of $E$ and year dummies with $m$ (columns 2 and 4, respectively). Note that estimations including year dummies exclude $E$ as well as the share7 variable as the latter is identical for each region in a given year. The results are presented for fixed effects only as these are preferred by the Hausman test.

Table 2 Regressions results for levels of schooling years

Autocorrelation is tested for as by Wooldridge (2002), who implements a test for serial correlation in the idiosyncratic errors of a linear panel-data model. Drukker (2003) presents simulation evidence that this test has good size and power properties in reasonable sample sizes. To correct for heteroskedasticity, spatial and autocorrelation spatial robust standard errors are used, following Hoechle (2007) who develops Driscoll and Kraay (1998) standard errors. According to Hoechle (2007, pp. 286), “The error structure is assumed to be heteroscedastic, autocorrelated up to some lag, and possibly correlated between the groups (panels). These standard errors are robust to very general forms of cross-sectional (‘spatial’) and temporal dependence when the time dimension becomes large.” Because no restrictions on the limiting behaviour of the number of panels is taken, the size of the cross-sectional dimension in finite samples does not constitute a constraint on feasibility. In the present paper maximum lag orders of autocorrelation by default are used, yielding second order autocorrelation correction. Therefore, the coefficients of the models and the model’s characteristics (R² and AIC) are the same, but the standard errors and hence significance levels change. This way, heteroskedasticity, spatial correlation, and autocorrelation are accounted for.¹³

The results in Table 2 hinge on which control variables for development are included. The EU dummy $E$ is positive but may simply reflect a general trend of increasing education (column 2). This interpretation is supported by increasing year dummy coefficients and the positive impact of the share of working age population. Furthermore, the trend seems to have stronger effects than GRP per inhabitant which is even negative when year dummies are included (columns 3 and 4). The $\delta$ variable is, as expected, positive, reflecting increasing disparities within countries. Indeed, nearly all regions in each country display a decreasing value of $\delta$ over time except for the Czech Republic and Slovenia (which consists of only one non-capital city region) where a turnaround towards the end of the observation period can be observed.

Migrants’ skills are negative but not significant if year dummies are included. Net-migration is significant when interacting with year dummies, the total effect of net-migration is positive for the years 2002, 2004, 2005, 2006, and 2010, negative for the remaining years.

Table 3 shows the results corresponding to Eq. 7, i.e., the impact on human capital growth. The Hausman test prefers random effects if year dummies are included, the corresponding results are given in the additional fifth and sixth columns. The following discussion hence ignores the fixed effects regressions with year dummies but they are provided in Table 3.

Table 3 Regressions results for growth rates of schooling years

Perhaps surprisingly, most control variables are not statistically significant, except for the share of working age population and $\delta$, which, however, are statistically significant and positive only with fixed or random effects, respectively. Net-migration is positive and highly significant in each case except when interacting with year dummies (columns 4 and 6). When interacting, the total effect is also positive in each case though statistically non-significant for some years. Overall, the results show a positive impact of net-migration which is robust over varying specifications. Thus, the interpretation is straightforward: If a region with positive net-migration experiences an increase in net-migration rates, its human capital increases. These regions are mainly those in the west of the observation area as well as its capital city regions (see Fig. 4). It may be concluded that if a region already has a positive net-migration rate it benefits from a further increase in immigration as immigrants bring human capital with them. If a region currently displays a negative net-migration rate, then it would benefit from a reduction of emigration, as emigrants take human capital with them.

Conclusions

The present paper has taken up an issue that tends to be neglected, namely whether free movement of people within the EU benefits or harms the regional economies of the EU’s new member states. The issue is theoretically interesting as the formerly centrally planned economies, which accessed the EU in 2004 and 2007, were characterised by high human capital endowments relative to their productivity levels. This means that income relative to education was low at the eve of the countries’ accession, creating incentives to emigrate.

The theoretical discussion combines Myrdal’s (1957) model on interregional development with Roy’s (1951) and Borjas’ (1987, 1991) models on migrant selection. It is argued that the area of the EU’s new member states represents peripheral and semi-peripheral regions within the EU. Migrants may choose between these or core regions within the EU15. It is assumed that the core and the semi-periphery represent prosperous regions, offering wider ranges of job opportunities and making them more attractive for migrants with relatively high human capital levels. As a consequence, these regions advance economically and become more attractive for future migrants, increasing the gap between the semi-periphery and the periphery.

The empirical analyses show two relevant results: First, the net-migration level is positively correlated with human capital stocks, but shows no clear effects in regressions where these stocks are the dependent variable. It may be tentatively concluded that when controlling for relative wealth, migration’s effects are weaker than would be suggested by descriptive statistics.

Second, the net-migration rate has a positive impact on a region’s human capital growth rate, whereas the effect of international migrants’ skill levels is weak. This means that within the observation area, international and, probably more crucial, internal emigrants take human capital with them while immigrants bring human capital. Hence Table 3’s results, especially those in column 5, indicate that negative net-migration depresses human capital accumulation.

How do these results fit in the euphoria which accompanied the NMS’ high GDP growth rates during the observation period? First, they underline that national growth is unevenly distributed and may coincide with rising interregional disparities, where, in particular, capital city regions may contribute disproportionally to national growth. Second, it supports the view that the new member states’ GDP growth was largely supported by a technology transfer which eventually must come to an end. After technology transfers cease to benefit the new member states, their future growth depends on available knowledge and skills. With a lack of human capital it will become difficult to further converge to the EU’s core regions.

Appendix

Appendix A

Estimation method of missing data

For some countries, regional educational attainment data is available only for some years of the observation period, while national educational and population numbers as well as regional population numbers are typically available for each year. The missing values of regional schooling attainment are estimated as follows. The first step is to calculate $P_{i,k,t}/\sum _{i,k,t}^{n*}P_{i,k,t}$, where $P_{i,k,t}$ represents the number of inhabitants who acquired a particular educational level educational level $k$ at $t$. Then, $\left(P_{i,k,T}/\sum _{i=1}^{n*}P_{i,k,T}-P_{i,k,0}/\sum _{i=1}^{n*}P_{i,k,0}\right)/T$ is added for each missing value, with $0$ and $T$ representing the first and last year of the observation period, respectively. This way it is guaranteed that $\sum _{i=1}^{n*}\left(P_{i,k,t}/\sum _{i=1}^{n*}P_{i,k,t}\right)=1$ for each $k$ at each $t$. Finally, multiplying $P_{i,k,t}/\sum _{i=1}^{n*}P_{i,k,t}$, either given or estimated, by $P_{i,t}/\sum _{i=1}^{n*}P_{i,t}$ gives $H_{i,k,t}$.

If data of one or more years at the beginning of the observation period are missing then the estimated share of population with educational level $k$, $p_{i,k,t}^{e}$, is calculated as $p_{i,k,t}^{e}=P_{i,t+1}\times \sum _{i=1}^{n*}P_{i,k,t}/\sum _{i}^{n*}P_{i,k,t+1}$, i.e. the regional number of inhabitants with educational level $k$ is assumed to be proportional to the national change in persons with educational level $k$. After that, $p_{i,k,t}^{e}\times \sum _{k=1}^{3}P_{i,k,t}/\sum _{i=1}^{n*}\sum _{k=1}^{3}P_{i,k,t}$ yields the estimated number of inhabitants with educational level $k$, where the sum of inhabitants in the relevant age group, $\sum _{k=1}^{3}P_{i,k,t}$, is known from population statistics.

In similar but simpler vein cases of missing unemployment values and real GRP growth rates are estimated from changes in national rates and regional population changes, where in this case the total population is taken.

The availability of calculating the share of foreign-born inhabitants with tertiary education is different for each country. For years where no data is available the average growth of the three succeeding years is taken to estimate missing numbers.

Appendix B

Table 4 NUTS regions and designated capitals

Appendix C

Table 5 Correlation coefficients