Neighborhood influences on the diffusion of residential photovoltaic systems in Kyoto City, Japan

Abstract

This study investigates the factors influencing the diffusion of residential photovoltaic systems. Factors examined are related to social attributes, such as population structure and living environment within neighborhoods and those close by, together with a neighbor effect revealed as a positive spatial dependency of the diffusion. To examine these factors simultaneously, the study applies a spatial econometric analysis, taking advantage of the availability of cumulative data on installed residential photovoltaic systems and census-based social attributes in about 4000 census blocks in Kyoto City, which include 1.47 million people. Results include: (1) an observed neighbor effect, especially between census blocks within a radius of 1000 m; (2) evidence that diffusion is positively influenced in a census block by lower population density and higher number of household members, as well as by lower ratios of detached houses and lower population densities in nearby census blocks; and (3) indication that diffusion is positively influenced by a higher proportion of young people through various mechanisms. To further facilitate the diffusion, implementing non-economic measures designed in light of the observed neighborhood influences is recommended, in addition to conventional economic support measures.

Introduction

Background and literature review

Various solar photovoltaic (PV) power generation systems are currently available, ranging from residential to utility-scaled. Small-scale residential systems that can be installed on rooftops of detached houses are expected to play a leading role in accelerating the deployment of PV systems (IEA 2010). Empirical studies on the diffusion trends for residential PV systems have been carried out in response to the recent accumulation of data on such systems. Studies of this sort are important, as they contribute to the discussion of effective policy measures to further facilitate the deployment of PV systems by elucidating the factors affecting their installation and diffusion.

Most published studies have explained the diffusion ratio of PV systems in municipal areas statistically, based on areal attributes such as: natural attributes such as amount of solar radiation; social attributes, such as the density and age of the population; and economic attributes, such as income level and subsidies for system installation (Li et al. 2012). Recent examples of such studies include Yoshida (2012) and Kwan (2012), who focus on solar radiation conditions as an explanatory factor; Drury et al. (2012) and Davidson et al. (2014), who focus on population age structure; and Zhang et al. (2011) and Nakata and Matsumoto (2014), who focus on system pricing, subsidies, and residents’ income level.

In addition to these areal attributes, a recent set of studies attempted to perform spatial analyses focusing on the influence of system installations in neighborhoods and word-of-mouth communications between neighbors, i.e., the so-called neighbor effect.¹ The present study seeks to contribute to the knowledge regarding influences on the diffusion of PV systems, including the neighbor effect, by investigating residential PV installations in a Japanese city. This focus is based on a theory by Rogers (2003), who considers information exchange to be the essence of innovation propagation.

Bollinger and Gillingham (2012) were the pioneers of studies analyzing the diffusion of residential PV systems spatially. Based on diffusion data for every zip code in California, United States (US), they showed that the installation of a system in a district increased the probability of additional installations in the same district. Subsequent spatial statistical analyses have been conducted for other countries, including Seki et al. (2013, 2014), who considered diffusion data for every prefecture and municipality in Japan, and Richter (2013) and Snape (2016), who investigated every postal code in the United Kingdom (UK).

However, analytical capability is limited when diffusion data are available only at a low spatial resolution. The studies referenced above used diffusion data aggregated by municipality or zip/postal code, and, thus, the distances between the center points of such areas might range from a few kilometers (km) to many dozens. It is difficult for studies using lower spatial resolution data to assess the spread of information regarding PV systems through visual awareness of installations in the neighborhood or word-of-mouth communications with neighbors.

Data analysis with spatial resolution high enough to address these issues is rare due to poor data availability. To the best of our knowledge, there have been only a few exceptions: a study by Müller and Rode (2013), who investigated Wiesbaden City, and later extended their target area to all of Germany (Rode and Weber 2016); and, studies focused on Connecticut in the US (Graziano and Gillingham 2015), and Shanghai, China (Zhao et al. 2017). These studies successfully conducted analyses at the smaller district level by referring to the position coordinates of individual system installations. The Rode and Weber (2016) analysis targeting all of Germany indicated that the neighbor effect on system installations within a radius of 1 km was statistically significant.

A subsequent analysis by these researchers using extended time series data (Rode and Müller 2016) found a clear neighbor effect within a radius of 200 m, which weakened with the passage of time according to a detailed spatiotemporal analysis. Results of the study also indicated that system adopters tended to have higher income and to reside in large dwellings. Meanwhile, the Graziano and Gillingham (2015) Connecticut analysis demonstrated a statistically significant neighbor effect within a radius of four miles (≅  6.4 km), with especially high effects within one mile (≅ 1.6 km). It also showed that building density influenced the diffusion ratio in districts. A later study by these researchers (Graziano et al. 2019) found that the neighbor effect, living environment, and socioeconomic attributes affected the system diffusion ratio differently in different municipalities.

Analyses taking other approaches to assessing the neighbor effect have also been conducted. These adopted spatial econometric models (LeSage and Pace 2009), which introduce spatial lag into the diffusion ratio, with regional attributes as independent variables to explain the ratio. This approach has advantages in that it can simultaneously examine the influence of the spatial distribution of various social attributes and of the neighbor effect through information exchange that cannot be explained by other attributes. Schaffer and Brun (2015) and Dharshing (2017) used attribute and PV diffusion values for each of some 400 counties in Germany. Schaffer and Brun (2015) adopted a spatial lag or spatial autoregression (SAR) model for cross-sectional data, while Dharshing (2017) adopted SAR and spatial error models (SEM) for panel data. Applying a more developed model enabled Balta-Ozkan et al. (2015) to investigate the spillover effects of social attributes on diffusion in nearby regions. They applied a spatial Durbin model (SDM) to data from 134 diffusion regions in the UK and showed that the diffusion ratio in a region was positively correlated with the ratio of detached houses and negatively correlated with the average number of household members, not only a single region but also in neighboring regions.

While past studies have verified the existence of the neighbor effect in residential PV diffusion, only a few regions have been analyzed. Meanwhile, diffusion mechanisms may differ due to characteristics such as living environment. Thus, further study of a variety of regions is needed to obtain improved insights.

Objective and significance

While Japan is a top-ranking country in PV deployment, there are few studies exploring neighborhood influences on PV diffusion, mainly due to limited data. To date, residential PV diffusion data in Japan have been publicly available only as municipal-level aggregated numbers at the highest spatial resolution.

Under a cooperative research agreement with the Kyoto City government, we were granted exclusive use (for research purposes) of census-block level data with higher resolution aggregated numbers of residential PV systems installed with subsidies from the city government. Each census block corresponds to a minimum unit of the data aggregation area adopted in the Japanese Population Census (Statistics Bureau of Ministry of Internal Affairs and Communications 2012). This enabled us to conduct an analysis with cumulative diffusion data aggregated for each of the 5215 census blocks, instead of the 11 wards currently publicly available.

Kyoto City was once the capital of Japan. It currently has a population of 1.47 million and the city features many historical streets and buildings developed before World War II. The average area per census block is 158,400 square meters (m²), while the median is as small as 23,426 m², corresponding to an approximately 150-m square, according to the census-block level geographic information data provided by the Statistics Bureau of Ministry of Internal Affairs and Communications (2013). This skewed distribution of census-block areas reflects a large number of small-area census blocks located in the central part of the city. The population density is 1780 people per km² in the city overall, while more than half of census blocks contain dense populations of more than 10,000 per km², according to the 2010 Population Census (Statistics Bureau of Ministry of Internal Affairs and Communications 2012). Compared to other major cities in Japan, Kyoto City strictly constrains the height of buildings.

In this study, we consider that the factors affecting residential PV diffusion in a census block include economic factors and neighborhood influences consisting of the following factors: (1) the influence of social attributes relevant to demographic structure and living environment in the census block; (2) the influence of those attributes in nearby census blocks; and (3) the influence of the spatial interdependency of the diffusion among nearby census blocks that cannot be explained by other attributes. In this study, we define the neighbor effect as the third factor.

This study analyzes the breakdown of neighborhood influences described above. Specifically, we analyze the relationship between diffusion ratios and social attributes in census blocks, while simultaneously considering their spatial impact. The analysis quantitatively verifies the impact of the spatial distribution of attributes, and the possible existence of the neighbor effect.

In that sense, this study has similarities to Schaffer and Brun (2015), Balta-Ozkan et al. (2015), and Dharshing (2017), all of whom applied spatial econometric models. While this study will also apply such model-based analysis, it is expected to obtain clearer insights into the neighborhood influences within a radius of several hundred meters by taking advantage of the census-block level, high spatial resolution data for both the diffusion ratio and social attributes.

The remainder of this paper is organized as follows. In Sect. 2, we describe the data used for this study and then present a preliminary panel data analysis to verify the extent of influence of economic factors such as resident income level, which is assumed to be a primary factor for residential PV adoption, on PV diffusion using the 11-ward level data in Kyoto City. In Sect. 3, we present our spatial econometric analysis, based on the census-block level cross-sectional data, to investigate neighborhood influences including the neighbor effect on the PV diffusion. In Sect. 4, we discuss the causes of the neighborhood influences determined in the analysis with reference to relevant studies and insights from an analysis based on questionnaire surveys conducted in Kyoto City. Policy implications are also presented based on those analyses. Finally, Sect. 5 concludes the study, summarizing the outcomes of the analyses as well as their limitations, and future research directions.

Residential installations of PV systems and a preliminary economic analysis

Residential PV adoption in Kyoto City

Kyoto City launched a subsidy program for the residential installation of PV systems in fiscal year (FY) 2003. This study uses actual subsidy data for the period FYs 2003–2014 provided by Kyoto City under a cooperative research agreement. Figure 1 shows the evolution of city-subsidized PV installations in detached houses (separate counts for existing and newly built structures²) and apartments in that period. The figure also indicates the average price per output to install the systems in Japan at 2010 prices (RTS Corporation 2013; Japan Photovoltaic Energy Association 2015; for deflators, Cabinet Office 2018). A total of 6573 units with a capacity for 21.21 MW were installed in existing detached homes by the end of FY 2014. Meanwhile, 1850 units with a capacity for 5.62 MW were installed in newly built detached houses, and 120 units with 0.85-MW capacity were installed in apartment houses. In this study, the analysis focuses on installations in detached houses. Considering the small proportion of apartment houses among the total, we considered it is unlikely that excluding those from the analysis would have a noticeable effect.

Fig. 1

The number of residential PV system adoptions in Kyoto City and the average system price per output between FYs 2003 and 2014

It is considered that the evolution of residential PV adoption shown in Fig. 1 was driven not only by the declining price of systems, but also by public economic support measures. In addition to the ongoing municipal subsidy available to Kyoto City residents who installed PV systems in their houses or purchased homes already equipped with PV systems, the Japanese national government implemented a subsidy scheme for residential PV system adoption for the periods FYs 1994–2005 and January 2009 to the end of FY 2013. Furthermore, any surplus electricity after in-house consumption was voluntarily purchased at a price equivalent to retail residential electricity rates by general electric utilities from FY 1992 (Federation of Electric Power Companies of Japan 2000). The purchase of surplus electricity was guaranteed at a higher fixed price for 10 years according to the excess electricity purchasing scheme for PV power generation officially introduced in FY 2009 (Kansai Electric Power Company 2014). The scheme was succeeded in FY 2012 by the feed-in tariff scheme for renewable energy (Agency for Natural Resources and Energy 2018).

Preliminary economic analysis of panel data for the eleven wards of Kyoto City

In general, economic factors are considered to influence household adoption of various facilities. These factors can be divided into the economic efficiency of facilities and the purchasing power of households; however, we face limited availability of local statistical data for the latter. In Kyoto City, while the Housing and Land Survey (Statistics Bureau of Ministry of Internal Affairs and Communications 2015) provides the estimates of the number of households by income groups for the city’s 11 wards, no higher resolution data are available. Given this situation, prior to our main analysis of neighborhood influences with census-block level data, this section presents a preliminary panel data analysis to assess the degree of the influence of economic factors not dealt with directly in the main analysis.

In this panel analysis, the dependent variable is the annual adoption ratio of residential PV systems, while the independent variables are the economic efficiency of the systems and the income level of residents. The details of these variables are as follows.

1. The annual adoption ratio of residential PV systems is defined as the number of system installations per year divided by the estimated number of detached housing stock for each ward and year (FYs 2003–2014). The installation numbers were provided by the Kyoto City government, while the detached housing stock number for each ward and year was estimated by linear interpolation based on the number of households living in detached houses per ward and at five-year intervals (i.e., 2000, 2005, 2010, and 2015) from the Population Census.

2. The economic efficiency of residential PV systems is defined as the undiscounted payback period for each year of adoption. Based on Endo (2012), we estimate the years necessary to meet the net initial system cost after deducting the municipal and national subsidies to be paid back by the undiscounted revenues from PV electricity generation using the following equations:

$$T = \left\{ {\begin{array}{*{20}l} {10 + \left( {I_{\text{N}} - 10B_{\text{F}} } \right)/B_{\text{L}} } & {\quad \left( {{\text{for}} \quad I_{\text{N}} /B_{\text{F}} \ge 10} \right)} \\ {I_{\text{N}} /B_{\text{F}} } & {\quad \left( {{\text{for}}\quad I_{\text{N}} /B_{\text{F}} < 10} \right)} \\ \end{array} ,} \right.$$

$$I_{\text{N}} = I_{\text{P}} - I_{\text{B}} ,$$

$$B_{\text{F}} = r(1 - s)E + sP \cdot E,$$

$$B_{\text{L}} = rE,$$

where T is the undiscounted payback period (years), I_P is the average adoption price of a residential PV systems per output (JPY/kW) (RTS Corporation 2013; Japan Photovoltaic Energy Association 2015), I_B is the sum of municipal and national governments’ subsidies for PV adoption per output (JPY/kW) (New Energy Foundation 2005; Japan Photovoltaic Energy Association 2015), I_N is the net initial adoption cost after deducting the subsidies per output (JPY/kW), B_F is the annual revenue during the first 10 years after PV adoption (JPY/year), B_L is the annual revenue after 10 years, r is the retail residential electricity rate estimated as the electric utility operating revenue from the residential sector divided by the electric energy sold from the electric utility to the residential sector (Kansai Electric Power Company 2015), s is the ratio of surplus electricity in the total PV power generation (assumed to be 0.58; New Energy Foundation 2008), P is the purchase price of the surplus electricity (assumed to be the same as r for FY 2008 and before; Kansai Electric Power Company 2014; Agency for Natural Resources and Energy 2018), and E is the annual PV power generation (assumed to be 1027 kWh per kW of PV system; New Energy Foundation 2008). We assume that the value of T is determined irrespective of ward.

3. Residents’ income level is defined as the proportion of households with an annual income of < 3 million, ≥ 5 million, or ≥ 7 million JPY, for each of 11 wards relative to those for Kyoto City overall. Using the results of the Housing and Land Survey conducted in FYs 2003, 2008, and 2013 (Statistics Bureau of Ministry of Internal Affairs and Communications 2015), we estimated the proportion of households by income groups for every ward and year via linear interpolation (except for FY 2014, which were set as to be the same as those for FY 2013). However, because of the deflation trend during the evaluation period,³ a comparison based on the absolute proportion of households by income groups was valid only for the same year, not among different years. For this reason, this analysis instead applies a relative proportion of households by income groups defined by the following equation:

$$r_{ij} = \frac{{h_{ij} /\sum\nolimits_{i} {h_{ij} } }}{{\sum\nolimits_{j} {h_{ij} } /\sum\nolimits_{i,j} {h_{ij} } }},$$

where r_ij is the relative proportion of households belonging to income group i in ward j, and h_ij is the number of households belonging to income group i in ward j. The value of r_ij is greater than one if the absolute proportion of households belonging to income group i in ward j exceeds the absolute proportion of households belonging to that income group in Kyoto City overall, and otherwise is less than one.

The present panel analysis takes into account the three model structures adopting the independent variable regarding residents’ income level corresponding to one of three income groups: < 3 million, ≥ 5 million, and ≥ 7 million JPY. For the computation, we used statistical analysis software R (Bivand and Piras 2015) and its package for panel analysis plm (Croissant et al. 2017). We choose the random effects approach rather than pooled ordinary-least-squares or the fixed effects approaches for all the model structures, confirming statistical significance by an F test and non-significance by Hausman test at 1% level for both. Table 1 shows the coefficients for the models, together with their statistical significance.

Table 1 Results of panel data analysis on the annual adoption ratio of residential PV systems by 11 wards in Kyoto City

The table indicates that variation in economic efficiency after support measures and residents’ income level can explain 58% of the variation in the annual adoption ratio. It also suggests that economic efficiency has a statistically significant effect on adoption (p < 0.001). Regarding income level, the proportion of households with annual incomes of < 3 million and ≥ 5 million JPY negatively and positively influenced adoption, respectively (p < 0.05), while there was no significant influence for the proportion of households with annual income ≥ 7 million JPY.

Analysis of neighborhood influences based on spatial econometric models

Analytic approach

This section analyzes the breakdown of neighborhood influences on PV diffusion, including the spatial distribution of social attributes and the neighbor effect that cannot be explained by the attributes alone, using a spatial econometric framework, mainly SDM, based on census-block level cross-sectional data. While ordinary econometric, multiple regression models can explain the diffusion ratio using various areal attributes as independent variables, the spatial econometric framework is capable of dealing with the spatial interdependency of both independent and dependent variables. The analysis considers multiple definitions of the contiguity among census blocks based on the distance between the blocks and assesses the dependence of the neighborhood influences on these definitions.

The dependent variable is the cumulative diffusion ratio of residential PV systems by census blocks in Kyoto City as of the end of FY 2014. While the total number of installed systems and capacity data are available for all the census blocks in the city, only the data for existing detached houses (i.e., excluding those for newly built houses), were used for the analysis in this section. This was because we consider the mutual influences among nearby census blocks on diffusion to be associated with installations in existing houses rather than newly built houses, around half of which are built for sale by contractors (Data System Promotion Office of Kyoto City 2015).

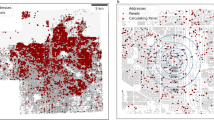
Figure 2 presents the distribution of the diffusion ratio for each census block.⁴ The diffusion ratio for the city overall was 2.2%. In some census blocks, the number of detached houses in the denominator was so small that the diffusion ratio was significantly influenced by chance factors. Hence, to exclude outliers, the census blocks used in this analysis were limited to those with 10 or more detached houses according to the Population Census. Figure 2 shows the distribution of the diffusion ratios for the 3929 census blocks ultimately included in the analysis. Many census blocks with a diffusion ratio of zero and/or ratios over 10 were removed because of the limitation.

Fig. 2

Frequency diagram of the diffusion ratio of PV systems in census blocks in Kyoto City

The analysis uses the data reported by the 2010 Population Census for the census-block level attributes adopted as the independent variables that could potentially influence the diffusion of PV systems. The variety of attributes reported in the Population Census is limited at the census-block level, compared to the prefecture and municipality levels.

Among the attributes reported for census-block level values in the Population Census, this analysis focuses on those related to living environment and demographic conditions. The attributes related to living environment include the ratio of households residing in detached houses among all households (hereafter, simply referred to as the ratio of detached houses), and the population density; the demographic attributes consist of the proportion of the total population that is young (under age 15), the proportion that is elderly (age 65 or over), the average number of household members, the proportion of the population that has lived at the same address for 5 years or less, and the proportion of the population that has lived at the same address for 20 years or more, including those who have lived at the same address since birth (hereafter, the proportion of residents of 5 years or less, and 20 years or more, respectively). Other factors, such as the PV system price, public subsidy, and amount of solar radiation,⁵ which could influence diffusion, were supposed to be unvarying among the census blocks as cross-section data, since the analysis target region was limited to Kyoto City. While attributes related to income level are also a critical factor influencing diffusion, as already mentioned, this analysis does not directly consider such attributes due to the lack of statistical data at the census-block level. We note this as a limitation of this study.

The analysis here also examines the potential variation in neighborhood influences depending on the definition of census-block contiguity. For this purpose, we consider seven definitions of contiguity: the distance between the centroids of census blocks ≤ 200, ≤ 300, ≤ 500, ≤ 700, ≤ 1000, ≤ 1500, and ≤ 2000 m.

We apply analytical methods based on spatial econometric models developed for the purposes described above. Details on the methods can be found in textbooks on spatial econometric modeling such as LeSage and Pace (2009). As mentioned, this analysis mainly applies the SDM model, which is expressed as follows: let y denote the dependent variable (i.e., the diffusion ratio) and X the set of independent variables (i.e., the selected social attributes),

$$y = \rho Wy + X\beta + WX\theta + u,$$

where W is the spatial weight matrix representing contiguity relationships between the census blocks, ρ is the spatial autoregression coefficient for y, β is the regression coefficients for X, θ is the regression coefficients for WX, and u is the error term. The spatial weight matrix W is derived from the contiguity matrix that contains the elements 1 or 0, according to the presence or absence of contiguity within a given defined distance between the centroids of census blocks. The derivation is based on a row standardization; i.e., the contiguity matrix is normalized such that the sum of each row is unity in this analysis. The first and third terms of the right-hand side of the above equation indicate that the model deals with the influences on the diffusion ratio in a census block using both the diffusion ratios and explanatory social attributes in nearby census blocks.

The analysis adopts the census-block level geographic information data provided by the Statistics Bureau of Ministry of Internal Affairs and Communications (2013). We use the statistical analysis software R (Bivand and Piras 2015) and its spatial analysis packages spdep (Bivand and Piras 2015; Bivand et al. 2013) and maptools (Bivand and Lewin-Koh 2015) for the data analysis.

Results of SDM analysis

Table 2 shows the maximum-likelihood estimates of the regression coefficients for the SDM. We observe the impacts of the three factors constituting the neighborhood influences assumed in Sect. 1.2 on the diffusion ratio in a census block as follows.

Table 2 Results of an SDM-based spatial regression analysis to explain the diffusion ratio of PV systems

1. Influence of social attributes in the same census block

The upper rows in Roman of Table 2 shows this type of influence. It indicates that a higher proportion of young people, the average number of household members, and the proportion of residents of 5 years or less in a census block positively influence diffusion in that block (p < 0.01), while greater population density and proportion of residents of 20 years or more influence it negatively (p < 0.01). However, the analysis shows no significant influence of the ratio of detached houses or the proportion of elderly people on the diffusion. This implies a clearer influence of the younger population compared to the elderly on the diffusion ratio. These observations are independent of the contiguity definitions.

2. Influence of the attributes in nearby census blocks

The italicised rows in Table 2 explain this type of influence. It shows that PV diffusion in a census block tends to be negatively influenced by the ratio of detached houses and population density in the nearby census blocks irrespective of the contiguity distances (significance levels vary depending on the distance; in the case of ≤ 500 m, 1% for the former and 5% for the latter). The negative influence of population density is consistent with that in the same census block observed earlier; noteworthy is the negative influence of the ratio of detached houses in nearby census blocks, which was not observed for the same census block. We discuss our interpretation of this result later in Sect. 4. The influences of the other attributes in the nearby census blocks are unstable, depending on the definition of census-block contiguity, and accordingly show no confidence tendencies.

3. Influence of spatial dependency of the diffusion among nearby census blocks that cannot be explained by the attributes, i.e., the neighbor effect

The bold row in Table 2, indicating the estimated spatial autoregression coefficient ρ, explains the effects. When a narrower (≤ 200 m and ≤ 300 m) or wider (≤ 1500 m and ≤ 2000 m) distance is used for the definition of census-block contiguity, the value of ρ is not statistically significant even at the 10% level based on LR test, which suggests that incorporating the spatial interdependency of the diffusion ratio somewhat weakens the model fit. This is due to the methodological difficulty of observing the neighbor effect in such cases. For narrower definitions, the number of nearby census blocks per census block is smaller, even zero for some; in contrast, for wider definitions, the diffusion ratio and attribute values lose their significance with a greater number of nearby census blocks.

For definitions in between, that is, contiguity distances ≤ 500, ≤ 700, and ≤ 1000 m, the diffusion ratio shows a spatial dependence at the 5% significance level, implying the neighbor effect. It also shows that PV diffusion in a census block is negatively influenced by the ratio of detached houses and population density in nearby census blocks.

The robustness of the above results was verified by sensitivity analyses regarding the structure of the regression model, as shown in Appendix 1.

Discussion

Interpretation of the analysis results

The analyses conducted in this study found that, in addition to economic factors, a lower population density, high proportion of young people, larger number of household members, and fewer years living at the same address were demographic and living environmental factors that enhanced the diffusion ratio of PV systems. These findings are generally consistent with those of previous studies targeting other regions. Nevertheless, while the positive influence of a larger proportion of young residents on diffusion is in line with the results by Drury et al. (2012), it contradicts those of Dharshing (2017), where young people were defined as less than 20 years old. A deep observation of the age structure groups in census blocks with broad diffusion of PV systems indicates a higher population proportion in their 30s and early 40s that are parents rearing children. Thus, we can interpret the results to be consistent with the explanation by Kwan (2012), referring to Pickett-Baker and Ozaki (2008), that in areas where the population is composed largely of those aged 35–45, there is a relatively high installation rate, as this age group has greater motivation to purchase green products.

While the panel analysis in Sect. 2 considered an independent variable expressing residents’ income level, the spatial econometric analysis in Sect. 3 did not address this factor due to the unavailability of data at the census-block level. However, some demographic attributes considered as independent variables in the latter analysis could be associated with income level to a certain extent. Actually, a correlation analysis indicated that a ward with relatively high-income level tends to have a higher proportion of young people, a lower proportion of elderly people, and a lower proportion of residents of 20 years or more (see the Appendix 2). Therefore, we may interpret that the positive and negative impacts of a higher proportion of young people and a longer duration of residence, respectively, arise partly from high- and low-income levels, respectively.

The spatial econometric analysis also indicated a potentially positive spatial spillover influence on diffusion in a census block through lower ratios of detached houses and lower population densities in nearby census blocks. Census blocks with lower ratios of detached houses, and accordingly higher ratios of multiple dwellings, yet with lower population densities, suggest that such census blocks contain a station or arterial street together with a surrounding commercial district. That is, conveniences of daily life such as transportation and shopping provided by the surrounding environment seem to affect diffusion. Relatively wealthier people are assumed to gather and live in residential areas located near a station and commercial facilities, considering the potentially high land price of such areas (Ministry of Land, Infrastructure, Transport and Tourism 2018). We cannot state this with certainty, however, since this spatial econometric analysis did not deal with economic factors directly.

The analysis detected a statistically significant neighbor effect only for census block contiguity distances of ≤ 500 m, and ≤ 1000 m, and distances in between. These distances fall within the range implied by the three prior studies that targeted all of Germany (Rode and Weber 2016; Rode and Müller 2016) and Connecticut in the US (Graziano and Gillingham 2015), which analyzed the distance significantly influenced by the neighbor effect. It is still worth noting that the present study yielded similar distances by applying the SDM while simultaneously considering the spatial spillover of social attributes in Kyoto City, where half of census blocks are densely populated, with more than 10,000 people per km². Rai and Robinson (2013), who investigated the neighbor effect in detail through surveys of residents, broke down the effect into a passive effect through witnessing PV panels being installed by neighbors, and an active effect through word-of-mouth communications with neighbor PV system adopters. The distances detected in this study seem to be consistent with their finding.

In other studies attempting to examine the neighbor effect in Japan, the municipality-level data analysis by Seki et al. (2013) verified that, in explaining the diffusion ratio in a municipality, adopting the mean diffusion ratio within the range of 30 km from the municipality as an independent variable improved the explanatory power; meanwhile, the prefecture-level data analysis by Seki et al. (2014) observed no significant neighbor effect of PV diffusion. Considering the more than tenfold difference in the range of the distance to define neighbors between that study and ours, the neighbor effect they verified might have been the result of other mechanisms than those confirmed in this study. Targeting only Kyoto City and covering an area of 828 km², we were unable to detect such a long-range neighbor effect.

Implications from questionnaire surveys in Kyoto City

Here, we attempt to provide more background and greater context for our analysis by analyzing the results of two questionnaire surveys regarding citizens’ installation of PV systems in Kyoto City.

(1) Survey targeted at PV installers

Kyoto City government conducted questionnaire surveys targeted at the installers of PV systems subsidized by the city. The Global Environment Policy Office, where one of this study’s authors (TT) is employed, was charged with implementing the surveys. The survey conducted in FY 2013 obtained 891 responses out of 1580 questionnaires distributed⁶ (Global Environment Policy Office of Kyoto City 2013).

We extracted and sorted the respondents’ answers to a multiple-choice questionnaire regarding their incentive to install PV systems.⁷ As shown in Table 3, a high proportion of responses indicated that a house manufacturer was their incentive, as the responses included individuals who live in newly built houses where PV systems were preinstalled. In principle, the choices presented should not be considered independent of each other; in all likelihood, a person would not pursue PV installation only based on a single incentive, but rather on a hierarchical series of decision-making steps driven by multiple incentives. Although this study did not investigate further the decision-making mechanisms, Table 3 does indicate that communication with a peer (i.e., information from a peer or PV installation by a peer) constituted an influential incentive to a certain degree. This fact could be an explanation for the neighbor effect detected in Sect. 3.

Table 3 Responses to the questionnaire on the incentive to install PV systems

(2) Attitude survey from citizens

A basic questionnaire survey on environmental behavior conducted by a study group on global warming countermeasures in Kyoto City in 2015 (Global Environment Policy Office of Kyoto City 2015a, b) is another useful source of information. The survey sought to assess overall trends in environmental awareness and the activities of citizens and was not limited to PV installers. One of the current study’s authors (TK) was involved in designing the questionnaire and another (TT) was engaged in processing the data. The survey was administered to a random sample of citizens; 3000 questionnaires were distributed, and there were 1058 responses⁸ (Global Environment Policy Office of Kyoto City 2015b).

Using the survey response data, we performed a correlation analysis between the set of answers regarding respondents’ intentions to install PV systems in their homes⁹ and answers to five sets of questions regarding: (1) installations by respondents’ relatives, neighbors, and business peers; (2) the frequency of conversations about global warming and energy-saving behavior among respondents’ family members who lived together; (3) the frequency of similar conversations with respondents’ child(ren); (4) the frequency of such conversations with respondents’ neighbors and/or business peers; and (5) the frequency of such conversations with respondents’ friends.¹⁰ Answers were selected on a five-point Likert scale, but we computed a Pearson product-moment correlation coefficient treating the Likert scale as an interval scale.

Table 4 shows the correlation coefficient obtained. The results confirmed a positive, statistically significant correlation between respondents’ intentions to install and every one of the factors listed above. This suggests that the installation of PV systems near a respondent’s home and conversations with family members influenced the respondents’ intentions to install. We should note that, however, the intention does not necessarily lead to PV installation, owing to a so-called intention–behavior gap.

Table 4 Correlation coefficients between respondents’ intentions to install PV systems in their homes and (1) installations by people around them, and (2) the frequency of conversations about global warming and energy-saving behavior

It is worth mentioning a finding from a prior analysis by the Global Environment Policy Office of Kyoto City (2015b) that used the same survey data and indicated that the frequency of conversations on global warming and energy-saving behavior was especially high in households with a child(ren) in the fourth and fifth grades. This potential influence of children is likely at least partly attributable to environmental education activities in elementary schools. In fact, as of FY 2005, Kyoto municipal elementary schools established a program to prompt children to contribute to global warming countermeasures through lessons followed by assignments to put countermeasures into practice at home, including but not limited to keeping a household environmental account book (Global Environment Policy Office of Kyoto City 2014). We concluded that parents’ conversations with offspring could positively influence their intention to install a PV system. This can serve as another explanation regarding the cause of the positive relationship between the proportion of young people and the diffusion ratio yielded by the analysis in Sect. 3.

Policy implications

This analysis revealed a tendency for steady PV system deployment to occur in areas convenient for daily life, characterized by ample living environments with low population density, and a large proportion of multiple households raising one or more children. Nevertheless, even in such areas, the diffusion ratio is still below 10%, except in a few census blocks. To further accelerate diffusion, it would be effective to provide information to promote system diffusion selectively to the residents in areas expected to have a greater diffusion potential, especially districts located in the centers of these areas. Given the questionnaire results that promotion by PV dealers increases the opportunities for residents to consider system installation, we recommend providing residents with information from the government on the subsidy and other advantages of PV installation through dealers. Considering a potential indirect influence of promoting communications among residents with children in local communities within an area of a few hundred meters squared, other effective measures could include the activities of organizations such as the Solar Community Organization described by Noll et al. (2014) to facilitate PV installation (Palm 2016), and strengthening communications to children in school through energy education.

We also suggest that policy makers identify the many areas with no PV diffusion and without effective neighborhood influences and investigate their barriers to diffusion. Taking a longer view, we would recommend considering policy measures to extend the areas with demographic and living environmental conditions suitable for the diffusion identified by our analysis. Such policy measures might include supporting schemes for families with young children to acquire detached houses or to live in detached houses owned by their parents (grandparents for the young children) with necessary home renovations, thereby extending residential areas with detached houses occupied by families with young children and more household members. Such policy measures would need to be carefully examined beyond the specific issues of PV deployment.

The spatial statistical analysis also implied that certain social conditions tended to limit PV diffusion, especially in densely built areas with small detached houses. Such areas include zones highly vulnerable to disasters such as earthquakes and fire. We expect future opportunities for living environment improvements, as disaster prevention measures would also facilitate diffusion.

Conclusions

This study conducted a regression analysis based on a spatial econometric model using the census-block level number of residential installations of PV systems and social attributes, following a preliminary panel data analysis of the extent of economic influences on system adoptions using the ward-level data in Kyoto City.

The preliminary economic analysis indicated that the economic factors, including the net economic efficiency after financial support measures and residents’ purchasing power (a smaller proportion of low-income households in particular), could explain 58% of the adoptions. In addition, the spatial econometric analysis found that lower population density, a larger number of household members, and fewer years living in a census block were factors that enhanced PV diffusion in the same census block. The neighbor effect also appeared as a spatial dependency among the diffusion ratios in nearby census blocks. These findings have similarities to those of previous studies targeting other regions.

This study also yielded the following insights distinct from previous studies. (1) The analysis based on the SDM incorporating the attributes of nearby census blocks as independent variables detected a statistically significant neighbor effect for the defined census-block contiguity distances of ≤ 500 m, and ≤ 1000 m, and distances in between. (2) The SDM-based analysis also indicated a positive influence on PV diffusion of residential areas convenient to everyday life in census blocks containing a station or arterial street with surrounding commercial buildings (such conditions were inferred from a lower proportion of detached houses and lower population densities). (3) Furthermore, the analysis indicated the potential influence of young people under 15 years old on the spatial spread of PV diffusion through various mechanisms. While economic support measures are very effective in the diffusion of residential PV systems, we also recommend implementing non-economic measures designed in the light of the neighborhood influences as confirmed here.

Finally, we address the limitations of this study and future research directions. This study attempted a census-block level spatial econometric analysis. While such high-geographic-resolution analysis has the advantage of directly investigating neighborhood influences on the diffusion of PV systems, there are less statistical data available at the census-block level than at the prefecture or municipal level. Thus, analyses have been limited in their ability to account for economic attributes such as residents’ income level, which could have considerable influence on diffusion, as implied by the preliminary ward-level analysis. Therefore, the present census-block level spatial analysis should be regarded as complementary to prefectural-, municipal-, and ward-level analyses.

This analysis did not consider social and geologic factors such as the shape and slope of residential land and the orientation of a house and its roof, which cannot be expressed in statistical data. Detecting individual situations by focusing on census blocks with especially high diffusion ratios would be an interesting direction for future research. Moreover, neighborhood influences on the temporal diffusion process remain unaddressed in this study. Examining how much time is needed for spatial diffusion to occur and which factors control the rate over time would contribute to a deeper understanding of the determining factors behind diffusion.

Appendices

Appendix 1

To examine the robustness of the insights obtained in Sect. 3.2 of the main text on the factors influencing PV diffusion as a result of the analysis based on the SDM, the following apply other variations of the model. To avoid complexity, we focus on the case when census-block contiguity is defined as the distance between the centroids of census blocks ≤ 500 m.

We apply three variations of the model including a linear regression model (LM) without considering spatial autoregression, a spatial error model (SEM) that considers spatial autoregression only for the error term,¹¹ and a spatial lag or spatial autoregression (SAR) model that considers spatial autoregression only for the dependent variable (i.e., the diffusion ratio); seven attributes were selected as independent variables and adopted as in the analysis in the main text. Table 5 shows the results of the analysis based on those models; we found no conflict with that based on the SDM.

Table 5 Results of regression analysis based on LM, SEM, and SAR models for census-block contiguity distance ≤ 500

Table 6 shows the results of SDM-based analysis as in the main text, but considering seven variations that combine six of the seven independent variables used in the analysis. While the estimated regression coefficients varied somewhat, depending on the selection of independent variables, the coefficient signs were consistent with the results in the main text for the coefficients significant at 10% or more. Also, the Akaike Information Criterion (AIC) values suggest that the SDM considering all seven independent variables in the main text is an equal or better fit than those with a reduced number of variables.

Table 6 Sensitivity of variable selection in the SDM analysis for the census-block contiguity distance ≤ 500

Appendix 2

Table 7 indicates Pearson’s correlation coefficients between variables expressing residents’ income level used in the panel analysis in Sect. 2.2 and each of the demographic and living environment-relevant variables adopted in the spatial econometric model analysis in Sect. 3.2, based on the 11-ward level data in FY 2010 (Statistics Bureau of Ministry of Internal Affairs and Communications 2017).

Table 7 Correlation coefficients between residents’ income levels and social attributes for the 11 wards in Kyoto City

The table shows that, in wards with relatively high-income levels, the proportion of young people tends to be high, while the proportion of elderly people and of residents living at the current address for 20 years or more are low.