1 Motivation

Wind energy is the most important renewable energy source in Germany [1, 2]. In the course of the expansion of onshore wind energy, wind turbine operators are confronted with the current legal limitations on sound emission which prescribes a minimum distance between wind turbines and inhabited buildings [3]. With a market share of around 50% in Germany, direct drive wind turbines currently play a crucial role in the onshore wind power generation [4]. Apart from aeroacoustic phenomena the electromagnetically excited vibration of the generator is the dominant noise source of a direct drive wind turbine. Unlike aeroacoustic sound emissions, which are well understood and tend to be distributed over a broad frequency spectrum, the sound from an electric generator has tonal characteristics. Since the human perception is particularly sensitive to tonal sounds, those sound emissions receive a particularly strict limitation [5]. To optimize the acoustic behavior of a direct drive wind turbine generator NVH models (noise vibration harshness) can be applied to evaluate noise sources and remedial measures against noise generation, transmission and emission [6]. Such models are often highly sensitive to parameterization and modelling depths [7]. Thus, this paper presents an approach to parametrize and validate the system model of a direct drive wind turbine generator.

2 Introduction to the modelling approach

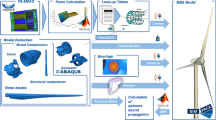
In recent research works a novel multi-physical system model for the NVH-behavior of a direct drive wind turbine drive train has been developed to predict the sound pressure level at arbitrary measurement points in the vicinity of the turbine. The novelty of this model lies in the representation of electromagnetic excitation, structure-borne sound transfer, sound radiation and the calculation of airborne sound in one system model. [8]. The model consists of a multi-body-simulation (MBS) model of the mechanical drive train and an electromagnetic model of the direct drive generator based on a finite element analysis of the magnetic flux inside the airgap of the generator. The magnetic air gap field imposes an oscillating magnetic pulling force on the rotor and stator of the generator causing the structure to vibrate. This effect is simulated by the application of oscillating forces to the airgap surfaces of the flexible MBS-model of the generator [8, 9]. The excited oscillation propagates through the machine in the form of structure-borne sound. Comparable approaches are presented in [10, 11].

The coupling between the two physical domains is achieved through a novel force-routine software in the MBS-model that derives the airgap forces from look-up tables containing the results of the electromagnetic finite element simulation of the generator [7]. These tables are parametrized by means of electromagnetic finite-element analysis of the airgap field in a pre-processing step of the MBS [12]. During model run time, the force-routine introduces radial and tangential forces to the flexible bodies as a function of the local airgap width δ, the rotational angle of the rotor φ and the rotational speed ω [8, 13]. This approach is illustrated in Fig. 1. For the application of the air gap forces, individual FE nodes are specified as load points along the airgap surfaces of the structural models of rotor and stator. On the stator side, a load point is placed in the center of each stator tooth. Between the teeth, the stator slots are located, in which the stator windings of the generator are placed. The rotor is built up by pairs of salient poles, which conduct the magnetic excitation field. Analogously to the stator teeth a load point is provided in the center of each pole for the magnetic attraction forces.

Fig. 1
figure 1

Sketch of the forces on the rotor poles and stator teeth in the MBS model [8] (a) and Correlation between the local air gap width at a specific rotor pole and the air gap forces (b)

Full size image

According to [7] the airgap forces can be derived from the flux density inside the airgap. The flux density distribution inside the generator airgap B(x,t) along the circumferential coordinate x can be approximated by

$$B_{\delta }\left(x{,}t\right)=\frac{\mu _{0}}{2\cdot \delta \left(x{,}t\right)}\cdot \theta \left(x{,}t\right)$$
(1)

where δ(x,t) is the airgap width distribution over the circumference of the generator, μ0 is the vacuum permeability and θ(x,t) is the magnetomotive force. This inversely proportional relationship between the flux density and the local airgap width is an important influence on the noise of an electrical machine since maximum flux density causes high airgap force amplitudes and vice versa. Therefore, the local air gap width at the force application points of the model is measured at each time step [13]. The resulting forces are calculated accordingly and applied to the load points as depicted in Fig. 1. Consequently, the local airgap width distribution has a major influence on the local force amplitude. Fig. 1 also shows, that the applied force signal is composed of several frequencies. These superimposed frequency components are harmonic to the rotational speed frequency of the synchronous generator and arise from the alternating permeance, the magnetic conductivity, of rotor and stator due to poles and slots [7]. This leads to frequencies in the force signal which can be calculated by

$$f_{p}=\frac{\omega }{2\pi }\cdot 2p\cdot k\mathrm{and}$$
(2)
$$f_{S}=\frac{\omega }{2\pi }\cdot Z\cdot k$$

with 2p being the number of rotor poles (or Z being the number of stator slots) and k being the harmonic order. Fig. 2 shows the resulting frequency spectrum of the simulated airgap forces applied to the stator. The spectrum shows that the amplitude of the harmonic components decreases with increasing frequency order. A significant force amplitude in the spectrum can be observed up to the frequency excited by the first slot harmonic at the order Z.

Fig. 2
figure 2

Frequency spectra of the airgap forces on the stator at rated speed based on [8]

Full size image

3 Validation approach and model parameterization

The validation of the simulation model is achieved through the comparison of measurement data of the real drive train system, which the model is based on, with the model behavior itself. For this purpose, a measurement campaign was carried out on a system test bench for wind turbines and the machine characteristics which are crucial for model validation (turbine vibration in the form of structure-borne sound and the air gap width of the generator) were recorded. The measurements from the test bench are used to parameterize a structural damping model for the generator structure in the MBS-domain to ensure a realistic model behavior.

3.1 Test setup for the validation

For the validation of the previously presented model, measurement data from a full-scale test run on a 4 MW test rig is examined. The test rig allows the realistic simulation of wind loads for the device under test (DUT). In this work the DUT is the nacelle of a direct drive wind turbine with an electrically excited synchronous generator and a rated power output of 3 MW [14]. Fig. 3 shows the DUT on the test rig.

Fig. 3
figure 3

System test rig setup at the Center for Wind Power Drives (a) and Sensor position for the measurement of the surface acceleration according to [15] (b)

Full size image

The relevant measurement data recorded during this measurement campaign are the structure-borne sound and the air gap width distribution of the generator. One suitable metric for the evaluation of structure borne sound is the surface acceleration. This is measured at the support arm of the stator in radial and tangential direction as depicted in Fig. 3. This sensor position was selected according to current industry standards for vibration assessment on direct drive wind turbines [15]. In Fig. 2 it has been shown that the harmonic frequency components of the force signals in the simulation model extend up to the first slot harmonic of the stator. This also defines the relevant frequency range for the validation. Therefore, the acceleration signals recorded at the DUT during the test run are sampled at a frequency which is approximately twice the first stator slot harmonic frequency fS at rated speed.

The air gap width distribution is measured using capacitive proximity sensors mounted on the inner airgap surface of the generator rotor. Hereby the air gap width distribution over the entire circumference can be scanned with just one sensor while the generator is rotating.

3.2 Development of a structural damping model

The MBS-model of the generator consists of two flexibly modelled bodies: rotor and stator. Both structures are modelled using the approach of modal reduction by Craig-Bampton based on the finite element method [16]. The approach of modal reduction describes the deformation of a flexible body by the superposition of its considered eigenmodes. The Craig-Bampton method considers the undamped case due to numerical advantages. This would lead to an unrealistic behavior of the model if no damping is introduced afterwards. Since this work focusses on validating an NVH-model a suitable solution for the damping of the structure is needed. This requires a parameterization of the damping parameters of the model.

In the MBS-model damping is introduced by the so-called damping ratio ζ which can be parameterized individually for every single eigenmode of the structure. For most applications, it is sufficient to use the same damping ratio for all modes. For NVH analyses this assumption of uniform damping does not apply anymore, since the sound transfer behavior in the frequency domain is highly influenced by the damping of every eigenmode and broader frequency ranges have to be considered [17]. Consequently, a more detailed damping model must be derived that describes damping as a function of the eigenfrequencies.

At first a sensitivity analysis of the RMS surface acceleration \(\hat{a}\) at the measurement point on the support arm of the stator over the uniform damping is performed

$$\hat{a}=\sqrt{\frac{1}{T}{\int }_{t_{0}}^{t_{0}=T}a\left(\tau \right)^{2}d\tau }$$
(3)

where a is the acceleration signal and T is the observed time period. The RMS value is a commonly used metric for the energy content of a vibration signal. Fig. 4 shows that the amplitude of the surface acceleration decreases exponentially with an increasing uniform damping ratio. For \(\zeta =6.5{\%}\) the root mean square (RMS) value of the surface acceleration in the MBS-model agrees with the measured value from the test rig.

Fig. 4
figure 4

Sensitivity of the RMS acceleration over the uniform modal damping [9]

Full size image

The damping ratio of 6.5% is then used as the starting value for the iterative determination of a suitable frequency-selective damping model. A common approach for such a damping model is the so-called Rayleigh Damping. This model is a special case of the stiffness proportional viscous damping approach [18]. Rayleigh Damping describes the damping matrix C as a linear combination of the mass matrix M and the stiffness matrix K of the structural model.

$$\boldsymbol{C}=\alpha \cdot \boldsymbol{M}+\beta \cdot \boldsymbol{K}$$
(4)

with α and β being the so-called Rayleigh parameters.

$$\zeta _{i}=\frac{\alpha \cdot m_{i}+\beta \cdot k_{i}}{2\sqrt{k_{i}\cdot m_{i}}}=\frac{\alpha }{2\omega _{n{,}i}}+\frac{\beta \omega _{n{,}i}}{2}$$
(5)

According to Eq. 5 the damping ratio ζ  of an eigenmode i can be described as a function of the frequency ωn. The individual damping ratio for each vibrational mode of the system depends on the eigenvalue accordingly. The Rayleigh parameters characterize the system’s behavior and can be obtained when two specific damping values are known.

$$\left[\begin{array}{c} \alpha \\ \beta \end{array}\right]=\frac{2\cdot \omega _{n{,}1}\cdot \omega _{n{,}2}}{{\omega }_{n{,}2}^{2}-{\omega }_{n{,}1}^{2}}\cdot \left[\begin{array}{cc} \omega _{n{,}2} & -\omega _{n{,}1}\\ -\frac{1}{\omega _{n{,}2}} & \frac{1}{\omega _{n{,}1}} \end{array}\right]\cdot \left[\begin{array}{c} \zeta _{1}\\ \zeta _{2} \end{array}\right]$$
(6)

The fundamental pole frequency 2p and the fundamental slot frequency Z are chosen as ωn,1 and ωn,2. Based on the previously determined start value for the damping ratio, the two values ζ1 and ζ2 are determined by iteratively adjusting the damping at these frequencies until the vibration of the model matches the measurement. Fig. 5 shows the resulting Rayleigh model for the generator structure derived from the two damping values ζ1 and ζ2 according to Eq. 6. Fig. 5 depicts that by applying the developed damping model the structure-borne sound spectrum of the model can be adapted to the measurement.

Fig. 5
figure 5

Rayleigh damping model for the generator structure (a) and Structure-borne sound spectrum of the generator at rated speed using the final damping model (b)

Full size image

4 Results and discussion

In this section the validation results will be presented and discussed. First, the measurements of the air gap width distribution are compared with the simulation results. Secondly, the measured acceleration signals are considered in the time domain. The frequency analysis of the oscillations is used to perform a modal analysis of the generator.

4.1 Air gap width distribution

As it is depicted in Fig. 1, the local airgap width influences the local distribution of the magnetic flux and therefore affects the airgap forces as well. Consequently, a good agreement between the model airgap in the simulation and the measured airgap in the real machine is crucial to create a realistic model behavior. There exist several influences on the airgap width distribution. Contrary to the dynamic eccentricity and bending of the rotor, which dominate the NVH-behavior of high-speed electrical machines [11], the predominant influence on the airgap width distribution within a direct-drive wind turbine generator is is the structural deformation of the generator due to gravity causing a so-called static eccentricity. As depicted in Fig. 6, the static eccentricity is a non-rotating offset of the rotor axis from the stator. This axis offset causes the airgap width δ measured at a rotating pole to alternate sinusoidally. This is described by

$$\delta \left(\varphi \right)=\delta _{0}+\delta _{\epsilon }\cos \left(\varphi \right)$$
(7)

where δϵ is the static eccentricity, φ is the rotational angle and δ0 is the mean value of the airgap width.

Fig. 6
figure 6

Illustration of the eccentric rotor position inside the generator (a) and comparison of the airgap width distribution evaluated at a specific rotor pole during the simulation and measurement (b)

Full size image

Fig. 6 provides a comparison of the local airgap width in the simulation and measurement from one rotor pole shoe’s point of view over the duration of the two and a half revolutions at rated speed. With regard to the mean value of the air gap width δ0and the periodicity a good agreement between the two signals can be observed. The major dynamic influence on the air gap width distribution is static eccentricity. The DUT shows an eccentricity that is around 70% smaller than in the simulation. In relation to the airgap width the static eccentricity measured at the DUT is around 9% of the nominal mean value of the airgap width. This deviation can be explained by a possible deviation in the parameterization of the bearing clearances in the model and the mounting of the DUT on the test rig. During the test run the rotor hub of the DUT is supported by the drive flanges, whereas in the simulation a standalone model of the generator is considered without the connection to a test rig drive.

Unlike the smooth sinusoidal airgap width from the simulation, the measured airgap signal also shows harmonics of higher order. A frequency analysis of the signal shows that the sixth order is dominant. This can be explained by an uneven deformation of the stator ring for example due to thermal loads. The sixth order results from the six support arms of the stator (see also Fig. 3). In [9] it has been shown, that thermal expansion effects have an influence on the sound emission of the generator. Since these thermal effects and their influence on the model behavior are neglected in this work, the smooth model airgap seen in Fig. 6 can be considered a simplification. For a representation of thermal expansion effects in the model, the local airgap width distribution has to be adjusted accordingly, which is not part of this work.

The deviation between the model and the real machine in terms of the static eccentricity in this work is not further adjusted in the MBS model. A further analysis of the sensitivity of the surface acceleration at the measurement point for both the mean airgap width and the static eccentricity provided by Fig. 7 shows that the mean value airgap width influences the structure-borne sound amplitude to a higher extend than the static eccentricity. Consequently, the adjustment of the mean air gap width can be considered the essential parameterization step.

Fig. 7
figure 7

Sensitivity analysis of the radial surface acceleration at the measurement point for the mean air-gap width (a) and Sensitivity of the radial surface acceleration at the measurement point for the static eccentricity (b)

Full size image

4.2 Structure-borne sound analysis in the time domain

In the following section, it will be investigated to what extent deviations between the model behavior and the real system occur at different operating points regarding the structure-borne sound transfer between the air gap and the measuring point at the support arm of the stator. At first the root mean square (RMS) value \(\hat{a}\) of the surface acceleration measured at the stator arm was evaluated at equidistant operating points.

Fig. 8 provides the comparison of the normalized RMS value of the surface acceleration measured at the support arm of the stator for both the DUT and the simulation model. In general, a good agreement can be observed between the two signals. At lower rotational speeds under 11 rpm the model shows a slightly higher vibration in radial and tangential direction than the DUT. This can be attributed, for example, to the parameterization of the previously presented damping model, which is a simplification of the real damping behavior.

Fig. 8
figure 8

Comparison of the normalized RMS acceleration at different operating points between the test rig measurement (a) and the simulation (b)

Full size image

In both cases the amplitude of vibration increases noticeably at around 12.5 rpm with the tangential vibration amplitude exceeding the radial vibration by almost one order of magnitude, although Fig. 2 shows, that the radial excitation amplitude is higher than the tangential. This allows for the assumption of a torsional vibration mode of the generator being excited at this operating point. To verify this assumption further analyses are carried out.

4.3 Structure-borne sound analysis in the frequency domain

Fig. 9 shows the time signal of the rotational speed of the DUT during the considered test run. In this test run laminar wind inflow has been simulated on the test rig at 8 different wind speeds. The DUT reaches 8 different operating points accordingly, with the rated operating condition occurring at around 13 rpm (approx. 650 sec. into the test run). The same load input is applied to the model to create an identical representation of the test run in the simulation.

Fig. 9
figure 9

Rotational speed during the validation measurement on the test bench

Full size image

The acceleration signals measured at the support arm of the stator during the given test run and in the simulation are then analyzed in the frequency domain. Fig. 10 shows the spectrograms of both signals. Both plots are referenced to the same maximum value for the radial surface acceleration arad,max. The frequency lines of the individual harmonic force excitations are clearly visible both on the real machine and in the model. Small deviations in the amplitude of the excitations occur at lower speeds like it has been shown before. The spectrogram of the experimental measurement shows additional resonances which are not found in the simulation. One potential cause for these deviations are the dynamic excitations of the test rig drive, which are not considered in the MBS-model of the generator.

Fig. 10
figure 10

Spectrograms of the radial surface acceleration at the stator measured on the test rig (a) and from simulation (b) [9]

Full size image

A good agreement in the vibration amplitude can be found for the rated operation mode. In the spectrogram of the acceleration signal measured on the DUT, additional frequency lines can be seen which are missing in the spectrogram from the simulation. These occur due to the excitations generated by the motor of the test rig. Those frequencies are labelled with the index m.

4.4 Operational modal analysis

The modal vibration behavior of the generator decisively influences its sound radiation characteristics [19]. The mode shapes of the stator of the generator are particularly decisive for the noise emission of the whole wind turbine, since the stator is directly bolted to the housing of the nacelle which is one of the sound radiating surfaces. Also, the ring vibration of the stator has an influence on the deformation of the generator’s airgap width distribution which strongly influences the excitation behavior as shown before. Therefore, a modal analysis of the generator stator is carried out in addition to the structure-borne sound analysis. For this purpose, 12 accelerometers are positioned at equidistant locations on the outer ring surface of the stator measuring the ring vibration in radial and tangential direction as it is shown in Fig. 11. The same analysis is performed on the MBS-model and the frequency response to the electromagnetic excitations as well as mode shapes are compared.

Fig. 11
figure 11

Sensor configuration for the operational modal analysis of the stator

Full size image

One common approach for the operational modal analysis is the correlation between two signals at different sensor locations. This can be done by using the so-called cross-spectral density function

$$\Gamma _{S1x{,}S4x}\left(f\right)=\mathcal{F}\left\{\gamma _{S1x{,}S4x}\right\}(f)={\sum }_{i=-\infty }^{\infty }\gamma _{S1x{,}S4x}\left(\tau \right)e^{-j2\uppi \mathrm{f}\uptau }$$
(8)

for two Signals (e.g. S1 and S4). Unlike a standard transfer function, which relates an input signal to an output, the cross-spectral density function indicates the correlation between two Signals in the frequency domain, where γS1x,S4x(τ) is the correlation function of the two sensor signals in the time domain [20]. This is particularly useful for operational modal analyses where only the vibration output can be measured. Resonant frequencies in a pair of signals are indicated by sharp peaks in the spectrum as it is shown in Fig. 12. The following analysis is carried out for the rated speed operating conditions since here the excitations are maximal. In total all possible combinations of signals have been examined by cross-spectral analysis and show similar behavior. The given example shows the cross-spectral density function between Sensor 1 and 4 calculated using Eq. 8.

Fig. 12
figure 12

Cross spectral density functions between the Sensors 1 and 4 of the DUT (upper plot) and the MBS-model (lower plot) under the electromagnetic excitations at rated speed

Full size image

The analysis of the measurement shows that the DUT strongly resonates under the electromagnetic excitations with the frequency orders 2p, Z and Zm. The other excitations in the regarded frequency range lead to less vibrations. The simulation shows a similar spectrum. The MBS-model also resonates comparably at the 2p and Z excitation lacking the resonance at Zm since it results from the test rig which is not part of the model. In the following the mode shapes of the stator ring of the DUT are reconstructed at the mentioned resonance points using the signals from the 12 accelerometers as shown in Fig. 11.

The reconstructed vibration shape in Fig. 13 shows that all 12 signals of the tangential acceleration oscillate in phase which suggests a torsional mode of the stator ring. The MBS-model shows the same behavior at this frequency. The previous assumption of a torsional ring mode resonating under the 2p excitation at rated speed is therefore confirmed. The analysis of the radial acceleration at the frequency order Z shows a deviation between the real mode shape and the model. The measurement shows a ring mode of spatial order 3. The MBS-model has 5th order mode at the same frequency. This can be explained by the numerous simplifications that occur during the modelling process of a flexible structure for the MBS (e.g. finite element size, damping, etc.) (Fig. 14).

Fig. 13
figure 13

Modal analysis results of the stator for the 2p excitation: mode shape reconstructed from tangential vibration measurement on the DUT (a) and mode shape of the model (b)

Full size image
Fig. 14
figure 14

Modal analysis results of the stator for the Z excitation: mode shape reconstructed from radial vibration measurement on the DUT (a) and mode shape of the model (b)

Full size image

5 Conclusion

In this paper the validation of a multi-physical modelling approach for a direct drive wind turbine generator is presented. The presented model has the purpose of analyzing impacts on electromagnetic excitations resulting in sound emission of the wind turbine and evaluating possible remedial measures against sound emission. The model validation is necessary for this purpose to ensure a realistic behavior of the model. The validation metric for this model is structure borne sound which is quantified by accelerations measured on the generator surface in a full-scale test rig environment for wind turbines.

First, the structural model is parameterized regarding the modal damping to adapt the model behavior to the measurement. Secondly, structure-borne measurements from the test run on a full-size system test bench are compared with the model behavior both in the time and frequency domain.

It is seen that the model behavior and the measurement show good agreement regarding vibration amplitude and excitation frequencies. The operational modal analysis of the generator shows that both the real generator and its model have a torsional mode at a low frequency which is excited by the first pole harmonic of the generator at rated speed resulting in a high vibrational amplitude at the stator ring.

This work demonstrates that the MBS-based modelling of a direct-drive wind turbine generator coupled with an electromagnetic finite-element model of the harmonic force excitation delivers a valid representation of the NVH-behavior of the real asset. The optimization of structural design and NVH-behavior of wind turbine drive trains can be achieved through experimental test campaigns and model-based approaches. Due to lower costs and more agile adaptability compared with full-size testing the model-based approach has a considerable advantage. It is shown that a suitable parameterization and validation is crucial to guarantee the necessary accuracy.

In future research the validated model of the generator will be integrated in a system model of the whole turbine to model air-borne sound radiation. This enables the analysis of critical tonalities and transfer paths. Such a system-model can be used for the derivation of suitable measures for the reduction of wind turbine sound emission.