Introduction

The high interest in irreversible adsorption results from its numerous practical applications in many fields such as medicine and material sciences as well as in the pharmaceutical and cosmetic industries. Adsorption is crucial in blood coagulation [1], inflammatory response [2], plaque formation [3], fouling of contact lenses [4] as well as for ultrafiltration and the operation of membrane filtration units [5]. Controlled adsorption is a prerequisite for efficient chromatographic separation and purification, and gel electrophoresis.

The simplest algorithm used for numerical modelling of irreversible adsorption processes is the random sequential adsorption (RSA) algorithm introduced by Feder [6]. It was first used to model the adsorption of spherical molecules, but soon came to be used also for modelling more complex particles like ellipsoids, spherocilinders, and so on (e.g., [7–13]). However, it has been shown only recently that, for the purposes of adsorption modelling, complex molecules can be approximated successfully using coarse-grain models [14–17]. For example, a coarse-grain model of fibrinogen can successfully explain the density of an adsorbed monolayer for a wide range of experimental conditions [18–20].

This study focuses on the RSA of trimers and hexamers built of identical spheres on a flat and homogeneous two-dimensional surface. There are at least two reasons to justify making a study of this subject. Firstly, trimers and hexamers are the only basic structures that have not yet been analyzed using coarse-grain models and RSA, despite the interest in simpler models like dimers [21], tetramers [22] or polymers [23]. This work simply completes the library of RSA properties for common basic structures. Secondly, it has been shown that RSA kinetics for tetramers are similar to those observed for anisotropic molecules and different from those of spheres [22]. As a sphere is a better approximation of a hexamer than a tetramer it would be interesting to explore its RSA kinetics. The primary aim of this paper was to find the saturated random coverage ratio of monolayers built as a result of irreversible trimer and hexamer adsorption. Additionally, we want to determine available surface function, which is crucial for estimating the kinetics of the adsorption process.

Model

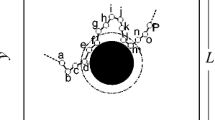
The model of a trimer and a hexamer consists of three or seven identical spheres, respectively, as shown in Fig. 1. The radius of a single sphere is r 0, and it functions as a length unit.

Fig. 1
figure 1

Models of a trimer (left) and a hexamer (right). All spheres (monomers) have radius r 0

Full size image

The molecules are placed on a square flat collector surface according to the RSA algorithm [6], which is described in detail elsewhere [22]. The algorithm iteratively attempts to place a randomly oriented and positioned particle on the collector. If this particle does not overlap with previously adsorbed particles it is irreversibly adsorbed and holds its place until the end of the simulation. If there is an overlap, the particle is removed and abandoned. The number of algorithm iterations N is commonly expressed using dimensionless time:

$$ t=N\frac{S_{\mathrm{M}}}{S_{\mathrm{C}}}, $$
(1)

where S M is an area covered by a single trimer (3πr 20 ) or hexamer (7πr 20 ) and S C is collector size. In the case of these simulations, square collectors of side 103 r 0 were used, so S C = 106 r 20 . Simulations were run until t = 105, which corresponds to \( N={10}^5{\scriptscriptstyle \frac{10^6{r}_0^2}{S_{\mathrm{M}}}} \) algorithm steps.

During simulation, the current coverage ratio θ(t) was monitored:

$$ \theta (t)=n(t)\frac{S_{\mathrm{M}}}{S_{\mathrm{C}}}, $$
(2)

where n(t) is the number of adsorbed particles after the number of steps corresponding to dimensionless time t. To decrease statistical error, 100 independent RSA simulations were performed for each model.

Results and discussion

Obtained example coverages are presented in Fig. 2.

Fig. 2
figure 2

Example coverages built of trimers (left) and hexamers (right)

Full size image

In general, saturated coverage ratio—one of the most important characteristic of an adsorption layer—is reached after an infinite number of RSA iterations: θ max ≡ θ(t → ∞). Therefore, to determine it from a finite time simulation, the RSA kinetics model has to be used.

Kinetics of RSA

For spheres, the kinetics of the RSA obeys the Feder law [24, 25]:

$$ {\theta}_{\max }-\theta (t)\sim {t}^{-1/d}, $$
(3)

where d is a collector dimension and t is a dimensionless time (1). Relation (3) has been tested numerically and appears to be valid for one to six dimensional collectors [26] as well as for fractal collectors having 0 < d < 3 [27, 28]. For different adsorbates: ellipsoids, dimers and polymers, it is also valid; however, parameter d depends also on particle anisotropy and their number of degrees of freedom [23, 29]. For example for dimers, tetramers and adsorption of stiff elongated particles on a two-dimensional surface, d ≈ 3.

For a large enough time, t, the exponent in Eq. 3 can be measured directly from dθ/dt dependence on t using the least squares approximation method (see Fig. 3).

Fig. 3
figure 3

Dependence of time derivative of the mean number of adsorbed particles on dimensionless time. Triangles and circles are simulation data for trimer and hexamer, respectively, whereas solid lines correspond to power fits obtained for t > 1,000: dn/dt = 9865.7t − 1.325 for the trimer model and dn/dt = 2375.6t − 1.301 for the hexamer model. Determined values of exponent d in Eq. (3) are as follows: d = 3.08 and d = 3.32 for trimer and hexamer model, respectively

Full size image

For both trimer and hexamer, the obtained values of parameter d are significantly larger than 2—the value expected for spherical particles. This is particularly surprising in the case of hexamer adsorption, for which the shape anisotropy is very small, and d is bigger than for a trimer.

Saturated random coverage ratio

Having determined the RSA kinetics, Eq. (3) can be rewritten as θ(y) = θ max − Ay, where A is a constant coefficient and y = t − 1/d. Saturated random coverage ratio θ max is obtained by a linear approximation of this relation for y = 0. Here, θ max = 0.5234 and θ max = 0.4920 for trimers and hexamers, respectively. The relative error for both the values is approximately 0.5 %. This originates mainly from the statistics: the standard deviation of deposited particles at the end of a simulation, as well as from error of adsorption kinetics fit. The ratio obtained is smaller than θ max ≈ 0.54 obtained for spheres [26], dimers [21] or very short polymers [23]. The θ max for trimers is, however, very similar to the value obtained for the rhomboid model of a tetramer [22].

Adsorption kinetics

The kinetics of the adsorption process depends on two factors. The first is a transport process, which shifts particles close to the surface or interface, where they are then adsorbed. As it depends on the specific experimental conditions, it is rarely the subject of general theoretical analysis. The second factor is probability of adsorption, which changes with diminishing area of uncovered surface. The dependence between adsorption probability and temporary coverage ratio is defined as the available surface function (ASF) and can be determined easily from the RSA simulation. Figure 4 shows the ASF dependence on normalized coverage \( \overline{\theta}=\theta /{\theta}_{\max } \).

Fig. 4
figure 4

Dependence of available surface function (ASF) on a normalized coverage ratio. Triangles and circles are simulation data for the trimer and hexamer model, respectively. Solid lines correspond to the fits (4) obtained for \( \overline{\theta}<0.2 \): ASF(θ) = 1 − 4.755 θ + 5.107 θ 2 for the trimer adsorption and ASF(θ) = 1 − 4.664 θ + 4.797 θ 2 for the hexamer adsorption. Inset Same data on a logarithmic scale, and fits there correspond to: \( \mathrm{ASF}\left(\overline{\theta}\right)=\left(1-1.315\kern0.33em \overline{\theta}+4.007\kern0.33em {\displaystyle {\overline{\theta}}^2}-5.977\kern0.33em {\displaystyle {\overline{\theta}}^3}\right)\left(1-{\displaystyle {\overline{\theta}}^4}\right) \) for trimer and \( \mathrm{ASF}\left(\overline{\theta}\right)=\left(1-0.121\kern0.33em \overline{\theta}+10.884\kern0.33em {\displaystyle {\overline{\theta}}^2}-8.684\kern0.33em {\displaystyle {\overline{\theta}}^3}\right)\left(1-{\displaystyle {\overline{\theta}}^4}\right) \) for hexamer model

Full size image

For almost empty collector (small θ), the probability decreases linearly because each successful adsorption act blocks a specified amount of the collector surface. As θ grows, these blocked areas start to overlap, which slows down the rate of probability decrease. Therefore, for low values of θ, the ASF(θ) is typically approximated by a quadratic fit [9, 11, 30]:

$$ \mathrm{ASF}\left(\theta \right)=1-{C}_1\theta +{C}_2{\theta}^2+o\left({\theta}^2\right), $$
(4)

where the expansion coefficient C 1 corresponds to the surface area blocked by a single particle, whereas C 2 denotes a cross-section of the area blocked by two independent molecules. Both are directly related to the second B 2 = 1/2C 1 and third B 3 = 1/3C 21  − 2/3C 2 viral coefficients of the equilibrium trimer or hexamer monolayer [9, 30]. For example, the 2D pressure P and the chemical potential of particle μ can be expressed via the series expansion at a low coverage limit [30]

$$ \begin{array}{c}\hfill P=\frac{k_{\mathrm{B}}T}{S_{\mathrm{F}}}\left(\theta +{B}_2{\theta}^2+{B}_3{\theta}^3+o\left({\theta}^3\right)\right),\hfill \\ {}\hfill \mu ={\mu}_0+{k}_{\mathrm{B}}T\left( ln\theta +2{B}_2\theta +\frac{3}{2}{B}_3{\theta}^3+o\left({\theta}^3\right)\right),\hfill \end{array} $$
(5)

where k B is the Boltzmann constant, T is the absolute temperature, and μ 0 is the reference potential.

Results presented in Fig. 4 show that C 1 for both particle types is approximately 15 % bigger than for a spherical particle, for which C 1 = 4. Parameter C 2 is almost 50 % larger than for spheres (C 2 ≈ 3.308), which is probably the result of more irregular shape as this parameter is significantly bigger for the trimer model than for the hexamer model.

The saturation limit of the ASF, is more important for adsorption kinetics calculations [18, 31], and is, for particles characterized by exponent d ≈ 3, typically approximated by [11]:

$$ \mathrm{ASF}\left(\overline{\theta}\right)=\left(1+{a}_1\overline{\theta}+{a}_2{\displaystyle {\overline{\theta}}^2}+{a}_3{\displaystyle {\overline{\theta}}^3}\right){\left(1-\overline{\theta}\right)}^4. $$
(6)

The last factor in the above equation is related directly to Eq. 3 as the adsorption probability is proportional to the growth rate of θ. Exponent 4 here results from d ≈ 3. As shown in the inset in Fig. 4, the above relation is also valid for trimer and hexamer adsorption.

Coverage structure

Although the saturated random coverage ratio is the main characteristic of RSA monolayer structure, it carries only information about the mean density of adsorbed particles. To gain a deeper insight into the structure of RSA monolayers, we measured density fluctuations as well as density autocorrelations for obtained coverages.

Density fluctuations

The typical experimental procedure used for estimation of density fluctuations of adsorbed particles, described by Adamczyk et al. [32], can be used also for monolayers generated by the RSA. Here, for a given coverage ratio θ, the collector was divided into square boxes containing at average ten particles. The normalized variance of the number of particles in the box n B for the given coverage θ: \( {\displaystyle {\overline{\sigma}}^2}\left(\theta \right)={\sigma}^2\left({n}_B\left(\theta \right)\right)<{n}_B\left(\theta \right)> \) is used as a density fluctuation measure. Its dependence on the coverage ratio θ is shown in Fig. 5.

Fig. 5
figure 5

Dependence of normalized density variance on coverage ratio. Triangles and circles are measured values for the trimer and the hexamer model, respectively; whereas solid lines correspond to the ASF fit in a low coverage limit (4)

Full size image

It is worth noting that, in a limit of small coverages \( \mathrm{ASF}\left(\theta \right)={\displaystyle {\overline{\sigma}}^2}\left(\theta \right) \) [33] . Plots in Fig. 5 confirm this agreement for \( \overline{\theta}<0.2 \).

Density autocorrelation

The density autocorrelation function is defined as:

$$ G(r)=\frac{P(r)}{2\pi r\rho}, $$
(7)

where P(r)dr is the probability of finding two particles at a distance between r and r + dr. Here, the distance r is measured between the geometric centers of the molecules. As ρ is the mean density of particles inside a covering layer, then G(r → ∞) = 1. In the case of spherical particles, G(r) has a logarithmic singularity in the touching limit [24] and superexponential decay at large distances [34]. Density autocorrelation functions for trimer and hexamer monolayers are shown in Fig. 6.

Fig. 6
figure 6

Density autocorrelation function G(r) for trimer and hexamer models. Inset Logarithmic singularity at r → r t +, where r t is a maximum of G(r). Parameter r t = 4.28 and r t = 5.98 for the trimer and hexamer model, respectively

Full size image

Due to different sized particles, the density autocorrelation function for hexamers is shifted right compared to that for trimers. For trimers the first maximum is wide due to particle shape anisotropy. Therefore, for dense packing, the distance between closest particles varies because it depends on trimers’ relative orientations. For hexamers of significantly smaller shape anisotropy, the density autocorrelation function looks similar to that for spherical particles, and the analytically predicted logarithmic singularity in the touching limit [24] can be seen clearly. For trimers, it can also be observed when restricting to the region to the right of the flat maximum. For large r, autocorrelations approach the mean density value very fast, as is also the case for spheres and other particles like dimers or tetramers.

Summary

The saturated random coverage ratio of a trimer monolayer is θ max = 0.5234. It is smaller than the one for spheres and dimers and similar to that obtained for rhomboid tetramers [22]. The saturated coverage ratio for hexamers is θ max = 0.4920, which is similar to the value obtained for the square model of a tetramer [22]. At the jamming limit, the kinetics of RSA of trimers and hexamers shows behavior typical of anisotropic molecules, which is highly unexpected, especially for hexamers, considering their small shape anisotropy. Properties of the density autocorrelation function in dense monolayers are, in general, similar to those observed for spheres monolayers.

This work completes the analysis of RSA monolayers built of basic particles composed of identical spheres. Therefore, for convenience, Table 1 presents together the most important parameters of such monolayers, based on the results presented here and the work of others [21–23, 26].

Table 1 Saturated random coverage ratio θ max, random sequential adsorption (RSA) kinetics exponent d and available surface function (ASF) low coverage limit coefficient for the most common models of particles
Full size table