Introduction

IR and Raman vibrational spectroscopies are used widely for characterization of both novel chemical compounds and natural products. Calculated harmonic frequencies are usually overestimated due to neglect of anharmonicity effects [1]. For example, the high frequency wavelengths calculated by Hartree-Fock method are typically overestimated by about 10%. Although scaling of harmonic frequencies computed at the Hartree-Fock and other levels of theory gives reasonable results, the development of hardware and software allow the a priori prediction of anharmonic wavenumbers. There are three fundamental studies [2–4] on scaling factors used in frequency and ZPV calculations. Evaluation of scaling factors is very laborious work and, therefore, despite the presence of myriad methods and basis sets, only a few scaling factors are available in the literature. In particular, scaling of results obtained with the recently introduced Jensen’s basis sets [5–10] and very large Dunning’s [11–14] basis sets are lacking. Moreover, in more accurate theoretical vibrational studies, the effect of solvent, present in most experimental works should be also included.

Among the high number of basis sets available, the so-called Pople basis sets (see ref. [1]), though fairly old, are robust and relatively small. Sometimes, they reproduce very well the experimental parameters of medium-sized molecules. However, no regular change of atomic and molecular energy is calculated with the Pople basis sets toward the complete basis set limit (CBS). Dunning and coworkers [11–14] utilized the idea of smooth and regular converging energy toward the CBS for constructing correlation-consistent basis set hierarchies. Thus, in theoretical thermochemical calculations, the energy, and some other structural and spectral parameters, have been estimated accurately using simple 2- and 3-parameter formulae [12, 15–17]. Later, Jensen [5–10] designed another family of converging basis sets, the so-called polarized-consistent basis sets pc-n, where n = 0, 1, 2, 3 and 4. These basis set series, developed explicitly for DFT, seem to converge faster than those of Dunning while reproducing the parameters calculated with the latter in the corresponding SCF, DFT, MP2 and CCSD(T) basis set limits [18]. Despite the fact that the use of the CBS approach in DFT methods can be controversial, several studies have shown regular convergence of molecular energy and other parameters toward the corresponding Kohn-Sham (KS) limit [19, 20].

Formamide is the simplest model of a peptide bond and is often used for model experimental and theoretical studies related to protein chemistry. Cappelli [22] reported anharmonic frequencies of selected formamide modes in the gas phase and in water solution calculated by B3LYP/6-311 + + G** method. There have been several detailed and high-level studies on anharmonicity of formamide modes [23–25]. However, to the best of our knowledge, there have been no studies on formamide harmonic and anharmonic frequencies convergence toward the KS limit using a hierarchy of systematically changed basis sets and the influence of solvent on the obtained results. Do harmonic and anharmonic vibrations of formamide calculated with pc-n basis set hierarchy monotonically converge toward the KS limit? This question would be of interest for future detailed studies of vibrational problems. Boese and coworkers [21] used Dunning’s and pc-1, 2 and 3 basis sets, and reported on convergence of anharmonic vibrations in case of 17 small molecules but formamide was not considered. Besides, no CBS estimates were reported in their paper.

In this work, we report on the convergence of harmonic and anharmonic fundamental frequencies of formamide modes in the gas phase and solution, calculated with second-order vibrational perturbation theory (VPT2) [26, 27] and pc-n polarization-consistent basis sets toward the B3LYP CBS. The results of individual calculations using a hierarchy of pc-n basis sets were fitted using a simple two-parameter mathematical formula. For comparison, calculations using several Pople basis sets were performed. The results obtained with individual basis sets and the estimated CBS values were critically compared with available experimental data in the gas phase [28] and solution [29].

Computational details

All calculations were performed using the Gaussian 09 program [30].

Basis sets and density functionals

Pople’s 3-21G, 6-31G, 6-31G*, 6-31+G**, 6-311++G** and 6-311++G(3df,2pd) (see details in ref. [30] and references therein), and Jensen’s pc-n polarized-consistent basis sets [5–10] were used. Efficient B3LYP density functional was selected. The pc-n basis sets were downloaded from EMSL [31].

Geometry

Fully optimized geometries of formamide in the gas phase, and solution (with PCM model [32]) were obtained using default and tight convergence criteria for each method and basis set selected. All positive harmonic vibration frequencies were obtained ensuring ground state structures.

Harmonic and anharmonic vibration calculations

The calculations were carried out in the gas phase and for eight selected solvents (n-hexane, chloroform, carbon tetrachloride, acetone, acetonitrile, DMSO, water and formamide) using the VPT2 method as implemented by Barone [26, 27] in the Gaussian program package [30]. In all cases, the finest DFT integration grid was selected by using SCF = tight and Int(Grid = 150590) in the command line instead of Int(Grid = ULTRAFINE) keyword. The use of such a fine grid is critical in the case of anharmonic frequency calculations with large basis sets [33]. Fermi resonances were handled in all calculations by default settings in the G09 anharmonic calculations.

CBS calculations

The harmonic and anharmonic frequencies, Y(X), were calculated using polarization-consistent pc-n basis sets, where n = 0, 1, 2, 3 and 4, and subsequently extrapolated to the B3LYP CBS limit, Y(∞), by fitting the individual results to the two-parameter function [15]:

$$ Y \left( {\rm X} \right){ } = Y { }\left( \infty \right) + {\rm A}/{{\rm X}^3} $$
(1)

The extrapolated value Y(∞) corresponds to the best estimate of the predicted frequency for infinite zeta (or cardinal number “X”), and A and Y(∞) are fitted parameters. In case of Jensen’s pc-n basis sets, X = n + 2, was assumed for graphical fitting purposes only [18, 34]. All the fittings were performed with two-parameter formula (Eq. 1). Since smaller values of “X” and “n” yield results (frequencies in this study) more corrupted by errors due to basis set imperfections, the CBS values are often estimated using higher cardinal numbers. For example, the abbreviation CBS(4,5,6) indicates estimation using X = Q, 5 and 6, or n = 2, 3 and 4, respectively.

Scaling factors

Single scaling factors were used for low and high frequencies. Thus, in several cases we arbitrary took the values from partly similar basis sets [2–4]. For the reader’s convenience, all the scaling factors used in our work are collected in one table (Table S4 in the supporting material).

Results and discussion

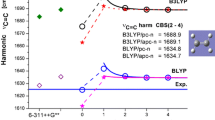
Figure 1 shows B3LYP calculated harmonic and anharmonic frequencies of six selected (amidic) formamide modes in the gas phase as a function of selected Pople and Jensen basis set size. Experimental values [28] are added as solid straight lines and the results obtained with pc-2, pc-3 and pc-4 basis sets are nonlinearly fitted toward the CBS using Eq. 1. The corresponding CBS values for harmonic and anharmonic frequencies are shown as straight dashed lines. Most results obtained with Jensen’s basis set (starting from pc-2) converge smoothly toward the B3LYP KS limit. On the other hand, both harmonic and anharmonic frequencies obtained with selected Pople type basis set show some irregular dependence on basis set quality but the values obtained with the largest [6-311 + + G(3df,2pd)] are close to those estimated in the CBS limit. CBS values of harmonic and anharmonic frequencies of asymmetric and symmetric NH2 stretching modes behave typically, e.g., the anharmonic ones are lower by about 200 and 170 cm−1, respectively, and are closer to experimental values [28]. The excellent agreement with experiment is visible for anharmonic CBS values of carbonyl stretching and NH2 scissoring modes. However, in the VPT2 method it is more challenging to take into account the anharmonicity of low frequency modes. Thus, for example, the harmonic frequencies of CN stretch predicted with both Pople and Jensen’s basis sets are close to experimental values and show very little dependence on basis set quality. On the contrary, the corresponding anharmonic frequencies for pc-n basis sets regularly (and significantly) decrease toward the CBS. This leads to the highest absolute deviation in the CBS (−117 cm−1), significantly larger than that produced with smaller basis sets. The reason for such a large dependence on basis set size is probably the Fermi resonance between this mode and the first overtone of NCO bending. Surprisingly, in the case of in plane NH2 bending, the anharmonic frequencies calculated with the 6-31G* and 6-31+G** basis sets are higher than the corresponding harmonic ones. It difficult to explain this result since this mode does not participate in Fermi resonance with any other vibrational mode.

Fig. 1
figure 1

Sensitivity of B3LYP-calculated selected harmonic and anharmonic frequencies of formamide in the gas phase to selected Pople and polarization consistent basis sets quality. The results for pc-n basis sets were fitted with Eq. 1 and the complete basis set limit (CBS) (2,3,4) estimated

Full size image

Table 1 gathers the deviations from experimental values of all harmonic and anharmonic frequencies of formamide in the gas phase calculated using the B3LYP hybrid density functional and selected Pople and Jensen basis sets. Results obtained with several additional basis sets are collected in Table S1 in the electronic supplementary material. The accuracy of frequency prediction depends strongly on the mode type. In most cases, the deviations from experimental values of anharmonic frequencies are smaller as compared to those of harmonic frequencies [28]. Moreover, the anharmonic frequency of the C = O stretch is predicted accurately, while the NH2 wagging is very erratic for all basis sets used. In particular, for the 6-31G* basis set an abnormal change of frequency deviation for this mode from −207 (∆harm) to 2245 cm−1 (∆anharm) is observed. This results in a very large root mean square (RMS) for this particular basis set (650 cm−1). When the deviations for this mode are excluded, the corresponding RMS values are significantly smaller (see Table 1). The inability of the VPT2 method to properly treat formamide NH2 wagging (and other modes that exhibit large anharmonicity and strong resonances) in comparison to other methods, like VSCF or VCI, was already reported by Bounouar [23]. Earlier, Bour [24] observed poor agreement with experimental values in the case of six lower frequency anharmonic modes calculated by the VPT2 method. Among Pople’s basis set, the smallest RMS for anharmonic vibrations was observed for the 6-31 + G** and 6-311++ G** basis sets, and the largest used basis set produced a significantly poorer result (RMS of 30, 34 and 46 cm−1). Similarly, RMS deviation of anharmonic frequencies calculated for the pc-2 basis set is smaller than estimated for the CBS limit (42 vs 59 cm−1). On the other hand, the use of a single scaling factor (the scaling factors used are gathered in Table S4 of the supplementary material) results in deviations significantly smaller than those observed for anharmonic frequencies [28].

Table 1 Deviations from experimental values of formamide harmonic (∆harm), anharmonic (∆anharm) and scaled harmonic ∆scal) frequencies (cm−1) calculated with B3LYP and selected Pople and Jensen’s basis sets. RMS Root mean square
Full size table

The performance of the VPT2 method depends also on the method of calculation. For example, the MP2/aug-cc-pVTZ calculated anharmonic NH2 stretch modes [23] reproduced the experimental data ideally (by about 2 cm−1) while our B3LYP results with both Pople and Jensen’s basis sets show large discrepancies (about 30–50 cm−1). However, both methods predict very well the CNO bending mode, probably due to the very low degree of anharmonicity.

Next, the performance of VPT2 in predicting anharmonic formamide frequencies in solution was studied using the PCM approach. Both low and high polarity solvents were tested. First, the impact of low polarity solvent (CCl4) on anharmonic vibrations for the studied Pople and Jensen basis sets was checked; a picture very similar to that presented in Fig. 1 was obtained (see Fig. S1 in the supplementary material). Similarly to formamide in the gas phase, the CBS values of anharmonic frequencies of two NH2 and C = O stretch modes reproduced very well the available experimental wavenumbers (the corresponding deviations are −30, −19 and −6 cm−1[29]). However, the anharmonic frequency of C-N stretching is very sensitive to the basis set quality and its CBS value underestimates the experimental value in CCl4 solution significantly (by −102 cm−1) [29]. On the contrary, the calculated harmonic CN stretching mode is almost independent of the basis set size and quality, and overestimates the corresponding experimental values by only 23 cm−1.

Table 2 presents all formamide harmonic and anharmonic frequencies in CCl4 solution calculated using selected Pople and Jensen basis sets; the complete set of results is shown in the electronic supplementary material (Table S2). First, a very nice reproduction of experimental C = O frequency [29] by the VPT2 method is visible for better quality basis sets [6-31 + G**, 6-311 + + G**, 6-311 + + G(3df,2pd) and pc-n, for n = 2–4] is apparent. On the contrary, the NH2 wagging frequency (observed at 323 cm−1) is correctly predicted by a simple harmonic model but significantly overestimated by VPT2 method (1,186 cm−1 for 6-31 G* basis set and about 500 cm−1 for 6-311 + + G(3df,2pd) and pc-n, for n = 2–4). The best overall result for the VPT2 method is observed for the 6-31G* basis set (RMS of 105 and 61 cm−1 for harmonic and anharmonic frequencies), and there is no accuracy gain when using pc-n basis sets (RMS of 98 and 86 cm−1 for harmonic and anharmonic frequencies calculated using pc-2 basis set, and 93 vs 89 cm−1 in the CBS limit). The apparently best result for the 6-31G* basis set is, however, due to incidental error cancellation since the corresponding results for 6-311 ++ G(3df,2pd) basis set are similar to those obtained in the complete basis set limit (see Table 2). Surprisingly, the largest deviation in CCl4 (about −200 cm−1) is observed for anharmonic NH2 in plane bending. On the contrary, this mode is very well predicted in the gas phase (deviation of about 5 cm−1). However, comparing the experimental wavenumbers, assigned in the gas phase and solution (1046 vs 1216 cm−1), one could question the latter assignment. The overall RMS values for both harmonic and anharmonic frequencies in CCl4 solution are significantly larger than the corresponding numbers in the gas phase. Thus, the results from Table 2 show no advantage of using the VPT2 approach to calculate accurate frequencies of formamide in CCl4 solution (C = O mode is a striking exception to this rule).

Table 2 Deviationsa of formamide harmonic (∆harm) and anharmonic (∆anharm) frequencies (cm−1) in CCl4 solution calculated by B3LYP with selected Pople and Jensen’s basis sets. CBS Complete basis set limit
Full size table

There are no reported experimental data on all the different formamide vibrational modes in various solvents and only some sparse data exist [29]. This is partly due to problems caused by formamide association. Therefore, Table 3 compares harmonic and anharmonic frequencies calculated at B3LYP/pc-2 level of theory for selected vibrational modes of formamide in vacuum and in eight solvents. It is apparent from Table 3 that, both for the isolated molecule and in solution, the anharmonic frequency of the C = O mode is lower than the harmonic frequency. Moreover, upon using more polar solvent, the harmonic and anharmonic frequency of this vibration decreases in a roughly linearly manner. However, the changes in frequency introduced by solvent are more complex for other vibrational modes. In the case of the three amide modes (NH2 scissoring, NH2 in plane bend and NCO bending modes) an unphysical positive anharmonicity is observed for more polar solvents. A particularly high positive anharmonicity (~ 200 cm−1) in all solvents is calculated for NH2 wagging mode. In fact, four cases of Fermi resonances were calculated in the gas phase and solvents of low polarity, and seven Fermi resonances in more polar solvents. For example, NH2 scissoring mode (ν5) is in Fermi resonance with modes ν9 + ν8. Quite a similar pictures was obtained from the corresponding B3LYP/6-31 + G** calculations (for brevity these results are presented in Table S4 in the electronic supplementary material). Thus, Fermi resonance could be responsible for the observed unphysical behavior of several anharmonic modes calculated in polar solvents.

Table 3 Harmonic (harm) and deviation of anharmonic (Δ aanharm ) frequencies (cm−1) of formamide in different solvents calculated using B3LYP/pc-2 method
Full size table

Figure 2 presents selected formamide harmonic and anharmonic frequencies, calculated at the B3LYP/pc-2 level of theory as a function of medium polarity, expressed as (ε − 1)/(2ε + 1). The regular changes in harmonic frequencies are roughly linear and agree with our chemical intuition. However, the corresponding anharmonic frequencies show some abrupt and unexpected behavior (there is a kind of more or less pronounced minimum for CCl4). Moreover, anharmonic frequencies of NH2 scissoring and NH2 in plane bending in more polar solvents are higher than the corresponding harmonic frequencies. A very similar result is produced by B3LYP/6-31 + G** calculations (see Fig. S2 in the supplementary material). This is clearly some kind of artifact of handling anharmonicity in solution, possibly introduced by the VPT2 method. To the best of our knowledge, this artificial behavior of anharmonic frequencies upon solvent polarity change has not been reported before.

Fig. 2
figure 2

Solvent dependence of selected formamide harmonic and anharmonic frequencies calculated at the B3LYP/pc-2 level

Full size image

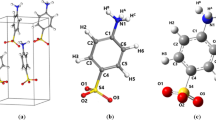
Looking for a possible explanation for the poor behavior of anharmonic frequencies of formamide in solution, we considered two reasons: limitations of the PCM model or VPT2 method, and/or its implementation for studies in solution. Intuitively, the correct behavior of the PCM model in solvents of increased polarity should results in linear changes of structural parameters optimized for both equilibrium and rovibrationally averaged geometry. We thus analyzed the corresponding changes introduced by solvent to selected geometrical parameters of formamide. First, the percentage changes of C = O and C – N bonds at equilibrium in the gas phase, and rovibrationally averaged by the VPT2 method were plotted as a function of medium polarity in Fig. 3. These results show that both bond lengths change linearly in response to medium polarity. Thus, in comparison to vacuum, the C = O bond is longer by about + 1%, and the C–N bond is shorter by about −1% in formamide solution. It is also apparent that the equilibrium C = O bond length and rovibrationally averaged length are essentially similar (the corresponding lines are parallel and separated by only 0.2% of the initial equilibrium structure in vacuum). On the other hand, the corresponding C–N bond lengths are fairly different (well separated lines are observed in Fig. 3). Obviously, the elongation of the C = O and shortening of the C–N bond in response to solvent polarity reflects the increased contribution of the more polar structure B due to amide resonance (Fig. 4). We also noted that the equilibrium and rovibrationally averaged structural parameters obtained for the isolated formamide molecule reproduces experimental gas phase data fairly well [35, 36]. Similarly, the agreement between our rovibrational averaged formamide structural parameters calculated in formamide solution is close to recent ab initio molecular-dynamic data for liquid formamide reported by Tsuchida [37].

Fig. 3
figure 3

Solvent dependence of equilibrium and anharmonically averaged formamide C = O and C–N bond lengths relative to equilibrium gas phase values calculated at B3LYP/pc-2 level (in %)

Full size image
Fig. 4
figure 4

Amidic resonance of formamide

Full size image

We conclude that the VPT2 method in combination with the PCM model is able to correctly predict changes of rovibrationally averaged structural parameters in response to solvent polarity. On the other hand, calculated frequencies are second derivatives of total energy of the system and changes of atomic positions. Thus, all minute errors in geometry or energy calculations are seen as if through a “magnifying glass” in the calculated anharmonic frequencies. Therefore, in the case of formamide, some anharmonic frequencies behave erratically upon increasing solvent polarity. A similar sensitivity of calculated magnetic parameters, for example, the accuracy of nuclear isotropic shieldings, is observed upon application of correlation-consistent or polarization-consistent basis set [18, 34]. Another reason for the unphysical changes in anharmonic CN stretch vibration with solvent polarity could be Fermi resonance with a 2ν11 overtone.

Conclusions

In this paper, for the first time, we showed the convergence of formamide harmonic and anharmonic (calculated using the VPT2 method) frequencies toward their corresponding B3LYP/pc-n CBS limits in the gas phase and in solution. A systematic study of the basis set convergence was carried out. From our results, the following conclusions can be drawn:

  1. 1.

    In the case of polarization consistent basis sets, starting from pc-2, a regular and systematic convergence (leading mainly to a decrease in wavenumber) of both harmonic and anharmonic frequencies in the gas phase and solution is observed. In fact, harmonic and anharmonic wavenumbers practically converge for pc-2, and sometimes for pc-3, basis sets, making calculations with larger basis sets unnecessary. Only in the case of anharmonic C–N stretching mode (and contrary to the corresponding harmonic counterpart), is a very strong dependence on Jensen’s basis set size observed, and the corresponding CBS limit underestimates the experimental value. Thus, this mode is difficult to predict correctly by VPT2 combined with B3LYP.

  2. 2.

    Increasing the size and quality (flexibility) of Pople basis set leads to irregular and non-monotonic changes in formamide harmonic and anharmonic frequencies. However, the frequencies calculated with fairly large 6-311++G** and 6–311++G(3df,2pd) basis sets approach the CBS limit observed for pc-n basis sets.

  3. 3.

    The most important and diagnostic amide mode (C = O stretching), relevant to studies on amides and peptides, is fairly well predicted by VPT2 method, both in the gas phase and in solvents of low, medium and high polarity.

  4. 4.

    The quality of anharmonic frequencies is inferior to simple harmonic frequency scaling procedures (RMS in case of B3LYP/6-31G* calculations is 53 vs 19 cm−1, and for B3LYP/CBS results is 59 vs 23 cm−1). This fact is important for studies on peptide systems.

  5. 5.

    Solvent dependence of some low frequency anharmonic amide modes of formamide (e.g., CN stretch, NH2 scissoring, and NH2 in plane bend) is incorrect. The VPT2 method reproduces some formamide frequencies in solution in an irregular way, probably due to the presence of severe anharmonicity and Fermi resonance.