Optimal trade execution under small market impact and portfolio liquidation with semimartingale strategies

Abstract

We consider an optimal liquidation problem with instantaneous price impact and stochastic resilience for small instantaneous impact factors. Within our modelling framework, the optimal portfolio process converges to the solution of an optimal liquidation problem with general semimartingale controls when the instantaneous impact factor converges to zero. Our results provide a unified framework within which to embed the two most commonly used modelling frameworks in the liquidation literature and provide a foundation for the use of semimartingale liquidation strategies and the use of portfolio processes of unbounded variation. Our convergence results are based on novel convergence results for BSDEs with singular terminal conditions and novel representation results of BSDEs in terms of uniformly continuous functions of forward processes.

1 Introduction

The impact of limited liquidity on optimal trade execution has been extensively analysed in the mathematical finance and stochastic control literature in recent years. The majority of the optimal portfolio liquidation literature allows one of two possible price impacts. The first approach, pioneered by Bertsimas and Lo [6] and Almgren and Chriss [3], divides the price impact into a purely temporary effect, which depends only on the present trading rate and does not influence future prices, and a permanent effect, which influences the price depending only on the total volume that has been traded in the past. The temporary impact is typically assumed to be linear in the trading rate, leading to a quadratic term in the cost functional. The original modelling framework has been extended in various directions, including general stochastic settings with and without model uncertainty and multi-player and mean-field-type models by many authors, including Ankirchner et al. [4], Cartea et al. [9], Fu et al. [14], Gatheral and Schied [17], Graewe et al. [19], Horst et al. [23], Kruse and Popier [24] and Neuman and Voß [29].

A second approach, initiated by Obizhaeva and Wang [30], assumes that price impact is not permanent but transient, with the impact of past trades on current prices decaying over time. When impact is transient, one often allows both absolutely continuous and singular trading strategies. When singular controls are admissible, optimal liquidation strategies usually comprise large block trades at the initial and terminal time. The work of Obizhaeva and Wang has been extended by Alfonsi et al. [2], Chen et al. [11], Fruth et al. [13], Gatheral [16], Guéant [20], Horst and Naujokat [21], Lokka and Xu [27] and Predoiu et al. [31], among many others.

Single- and multi-asset liquidation problems with instantaneous and transient market impact and stochastic resilience where trading is confined to absolutely continuous strategies have been analysed in Graewe and Horst [18] and Horst and Xia [22], respectively. This is consistent with the empirical work of Large [25] and Lo and Hall [26], which suggests that this resilience does indeed vary stochastically. Although only absolutely continuous trading strategies were admissible in [18, 22], numerical simulations reported in [18] suggest that if all model parameters are deterministic constants, then the optimal portfolio process converges to the solution in [30] with two block trades and a constant trading rate as the instantaneous impact parameter converges to zero. Cartea and Jaimungal [10] provide empirical evidence that the instantaneous price impact is indeed (much) smaller than permanent (or transient) price impact. The numerical simulations in [18] suggest that the model in [18] provides a common framework within which to embed the two most commonly used liquidation models [3, 30] as limiting cases.

This paper provides a rigorous convergence analysis within a Markovian factor model. It turns out that the stochastic setting is quite different from the deterministic one. Most importantly, we show that in the stochastic setting, the optimal portfolio processes obtained in [18] converge in the Skorohod $\mathcal {M}_{2}$-topology to a process of infinite variation with jumps as the instantaneous market impact parameter converges to zero. Our second main result is to prove that the limiting portfolio process is optimal in a liquidation model with semimartingale execution strategies and to explicitly compute the optimal trading cost in the semimartingale execution framework.

Showing that the limiting model solves a liquidation model with semimartingale execution strategies is more than a mere byproduct. Control problems with semimartingale strategies are usually difficult to solve because there are no canonical candidates for the value function and/or optimal strategies. We show that the solution in the limiting model is fully determined by the unique bounded solution to a one-dimensional quadratic BSDE. Our limit result provides a novel approach to solving control problems with semimartingale strategies that complements the approaches in Ackermann et al. [1] and Lorenz and Schied [15]. They solved related models by passing to a continuous-time limit from a sequence of discrete-time models.

Within a portfolio liquidation framework, inventory processes with infinite variation were first considered by Lorenz and Schied [28] to the best of our knowledge. Later, Becherer et al. [5] considered a trading framework with generalised price impact and proved that the cost functional depends continuously on the trading strategy, considered in several topologies. Bouchard et al. [7] considered infinite-variation inventory processes in the context of hedging.

The paper closest to ours is the recent work by Ackermann et al. [1]. They considered a liquidation model with general RCLL semimartingale trading strategies. Their framework is more general than ours as they allow more general filtrations and stochastic order book depth. At the same time, their analysis is confined to risk-neutral traders. In our setting, when the model parameters are deterministic and the instantaneous price impact goes to zero, the case of risk-neutral traders – which is then a special case of the model studied in [1] – is explicitly solvable. Allowing for risk aversion renders the impact model significantly more complicated as it adds a quadratic dependence of the integrated trading rate into the HJB equation; cf. [18] for details.

Our work also complements the work of Gârleanu and Pedersen [15]. They consider an array of market impact models, including a model with purely transient costs. They write [15, beginning of Sect. 1.3] that “with purely persistent price-impact costs, the optimal portfolio policy can have jumps and infinite quadratic variation.” As in [1], they justify portfolio holdings with infinite quadratic variation by taking a limit of a sequence of discrete-time models with increasing trading frequency. They also prove that the optimal portfolio processes in the discrete-time models converge to the optimal portfolio process in the corresponding continuous-time model if either the instantaneous price impact converges to a positive constant or the instantaneous price impact factor multiplied by the (increasing) trading frequency converges to zero. However, they do not consider the general case of an instantaneous price impact factor converging to zero. Most importantly, they consider a portfolio choice problem on an infinite time horizon, which avoids the liquidation constraint at the terminal time.

Last but not least, our work complements the work of Carmona and Webster [8], who provide strong evidence that inventories of large traders often do have indeed a nontrivial quadratic-variation component. For instance, for the Blackberry stock, they analyse the inventories of “the three most active Blackberry traders” on a particular day, namely CIBC World Markets Inc., Royal Bank of Canada Capital Markets and TD Securities Inc. From their data, they “suspect that RBC (resp. TD Securities) were trading to acquire a long (resp. short) position in Blackberry” and found that the corresponding inventory processes were of infinite variation. More generally, they find that systematic tests “on different days and other actively traded stocks give systematic rejections of this null hypothesis [quadratic variation of inventory being zero], with a $p$-value never greater than $10^{-5}$”. Our results suggest that inventories with nontrivial quadratic variation arise naturally when market depth is high and resilience and/or market risk fluctuates stochastically. This is very intuitive; in deep markets, it is comparably cheap to frequently adjust portfolios to stochastically varying market environments.

The main technical challenge in establishing our convergence results is that the solution to the limiting model cannot be obtained by taking the limit of the three-dimensional quadratic BSDE system that characterises the solution in the model with positive instantaneous impact. Instead, we prove that the limit is fully characterised by the solution to a one-dimensional quadratic BSDE. Remarkably, this BSDE is independent of the liquidation requirement. As a result, full liquidation takes place if the instantaneous impact parameter converges to zero even if full liquidation is not strictly required. The reason is a loss in book value of the remaining shares that outweighs the liquidation cost for small instantaneous impact. Our convergence result is based on a novel representation result for solutions to BSDEs driven by Itô processes in terms of uniformly continuous functions of the forward process and on a series of novel convergence results for sequences of singular stochastic integral equations and random ODEs, which we choose to report in an abstract setting in Appendix A and B, respectively.

The limiting portfolio process is optimal in a liquidation model with general semimartingale execution strategies. Within our modelling framework where the cost coefficients are driven by continuous factor processes, block trades optimally occur only at the beginning and the end of the trading period. This is very intuitive as one would expect large block trades to require some form of trigger such as an external shock leading to a discontinuous change of cost coefficients. The proof of optimality proceeds in three steps. We first prove that the jump part of the limiting portfolio process can be approximated by absolutely continuous processes. This allows us to approximate the trading costs in the semimartingale model by trading costs in the pre-limit models from which we finally deduce the optimality of the limiting process in the semimartingale model by using the optimality of the approximating inventory processes in the pre-limit models. As a byproduct of our approximation, we also obtain that the optimal costs are given in terms of the aforementioned one-dimensional quadratic BSDE.

The rest of the paper is organised as follows. In Sect. 2, we recall the modelling setup from [18, 22] and summarise our main results. The proofs are given in Sects. 3 and 4. A series of fairly abstract convergence results for various stochastic equations with singularities upon which our convergence results are based is postponed to two appendices.

Notation. Throughout, randomness is described by an $\mathbb{R}^{m}$-valued Brownian motion $(W_{t})_{t\in [0,T]}$ defined on $(\Omega ,\mathcal {F}, (\mathcal {F}_{t})_{t \in [0,T]}, \mathbb{P})$, a complete probability space, where $(\mathcal {F}_{t})_{t \in [0,T]}$ denotes the filtration generated by $W$, augmented by the ℙ-nullsets. Unless otherwise specified, all equations and inequalities hold in the ℙ-a.s. sense. For a subset $A \subseteq \mathbb{R}^{d}$, we denote by $\mathcal {L}_{\mathrm{Prog}}^{2}(\Omega \times [0,T];A)$ the set of all progressively measurable $A$-valued stochastic processes $(X_{t})_{t\in [0,T]}$ such that $\mathbb{E}[ \int ^{T}_{0} \vert X_{t}\vert ^{2} \, \mathrm {d} t] < \infty$, while $\mathcal {L}_{\mathrm{Prog}}^{\infty}(\Omega \times [0,T];A)$ denotes the subset of essentially bounded processes. By $\mathcal {L}_{\mathcal {P}}^{2}(\Omega \times [0,T];A)$ and $\mathcal {L}_{\mathcal {P}}^{\infty}(\Omega \times [0,T];A)$, we denote the respective subsets of predictable processes. Whenever $T-$ appears, we mean that there exists an $\varepsilon > 0$ such that a statement holds for all $T' \in (T-\varepsilon ,T)$.

2 Problem formulation and main results

In this section, we introduce two portfolio liquidation models with stochastic market impact. In the first model, analysed in Sect. 2.1, the investor is confined to absolutely continuous trading strategies. For small instantaneous market impact, we prove that the optimal liquidation strategy converges to a semimartingale with jumps. In Sect. 2.2, we therefore analyse a liquidation model with semimartingale trading strategies. We prove that the limiting process obtained in Sect. 2.1 is optimal in a model where semimartingale strategies that satisfy a suitable regularity condition are admissible.

2.1 Portfolio liquidation with absolutely continuous strategies

We take the liquidation model analysed in Graewe and Horst [18] and Horst and Xia [22] as our starting point and consider an investor that needs to close, within a given time interval $[0,T]$, a (single-asset) portfolio of $x_{0}>0$ shares using a trading strategy $\xi = (\xi _{t})_{t \in [0,T]}$. If $\xi _{t} < 0$, the investor is selling the asset at a rate $\xi _{t}$ at time $t \in [0,T]$; otherwise she is buying it. For a given strategy $\xi$, the corresponding portfolio process $X^{\xi }= (X^{\xi}_{t})_{t \in [0,T]}$ satisfies the ODE

$$\begin{aligned} \mathrm {d}X^{\xi}_{t} = \xi _{t} \, \mathrm {d} t, \qquad X^{\xi}_{0} = x_{0}. \end{aligned}$$

The set of admissible strategies is given by

$$ \mathcal {A} := \mathcal {L}_{\mathrm{Prog}}^{2}(\Omega \times [0,T]; \mathbb{R}). $$

For a general inventory process $X \in \mathcal {L}_{\mathcal {P}}^{2} (\Omega \times [0,T];\mathbb{R})$, the corresponding transient price impact is described by the unique stochastic process $Y^{X} = (Y^{X}_{t})_{t \in [0,T]}$ that satisfies the ODE

$$\begin{aligned} \mathrm {d}Y^{X}_{t} = \gamma \, \mathrm {d}X_{t} - \rho _{t} Y^{X}_{t} \, \mathrm {d} t, \qquad Y^{X}_{0} = 0, \end{aligned}$$

(2.1)

for some constant $\gamma > 0$ and some essentially bounded, progressively measurable, $(0,\infty )$-valued process $\rho =(\rho _{t})_{t \in [0,T]}$. The process $Y^{X}$ may be viewed as describing an additional shift in the unaffected benchmark price process generated by the large investor’s trading activity. For $\xi \in \mathcal {A}$, we write $Y^{\xi }:= Y^{X^{\xi}}$.

For any instantaneous impact factor $\eta > 0$ and any penalisation factor

$$ N \in \mathcal {N} = \mathcal {N}(\eta ) := [\underline{N}(\eta ),\infty ], $$

where

$$ \underline{N}(\eta ) := \gamma + 1 + \sqrt{ 2 \eta \max ( \Vert \lambda \Vert _{L^{\infty}}, \gamma \Vert \rho \Vert _{L^{\infty}} ) }, $$

the cost functional is given by

$$\begin{aligned} J^{\eta ,N}(\xi ) &= \mathbb{E}\bigg[ \frac {\eta }{2} \int ^{T}_{0} ( \xi _{t})^{2} \, \mathrm {d} t+ \int ^{T}_{0} Y^{\xi}_{t} \, \mathrm {d}X^{ \xi}_{t} + \frac {1}{2} \int ^{T}_{0} \lambda _{t} (X^{\xi}_{t} )^{2} \, \mathrm {d} t \\ & \hphantom{=:\mathbb{E}\bigg[} + \frac {N}{2} (X^{\xi}_{T} )^{2} - X^{\xi}_{T} Y^{\xi}_{T} \bigg]. \end{aligned}$$

The first term in $J^{\eta ,N}(\xi )$ captures the instantaneous trading costs, the second the costs from a transient price impact, and the third captures market risk, where the adapted and nonnegative process $\lambda = (\lambda _{t})_{t\in [0,T]}$ specifies the degree of risk. If $N=\infty$, the fourth term should formally be read as $+\mathrm{\infty }{\mathbb{1}}_{\{X_T^{\xi }\ne 0\}}$ with the convention $0 \cdot \infty = 0$. This captures the case where full liquidation is required; this case is analysed in [18]. The case $\gamma + 1 \leq N < \infty$ is analysed in [22]. The fifth term captures an additional loss in the book value of the remaining shares. It drops out of the cost function if $N = \infty$; see [18, 22] for further details on the impact costs and cost coefficients.

It has been shown in [18, 22] that the optimisation problem

$$\begin{aligned} \min _{\xi \in \mathcal {A}} J^{\eta ,N}(\xi ) \end{aligned}$$

(2.2)

has a solution $\hat{\xi}^{\eta ,N}$ for any $N \in {\mathcal{N}}$ and any $\eta > 0$. The solution is given in terms of a backward SDE system with possibly singular terminal condition. We index the optimal trading strategies and state processes by $\eta$ and $N$ as we are interested in their behaviour for small instantaneous impact factors for both finite and infinite $N$.

The next theorem follows directly from [18, Theorems 2.5 and 2.6] and [22, Theorem 2.1].

Theorem 2.1

With the above assumptions, for all $\eta \in (0,\infty )$ and $N\in \mathcal {N}$, the following hold:

i) The BSDE system

$$\begin{aligned} -dA^{\eta ,N}_{t} &= \bigg(\lambda _{t} - \frac {1}{\eta }( A^{\eta ,N}_{t} - \gamma B^{\eta ,N}_{t} )^{2} \bigg) \, \mathrm {d} t- Z^{\eta ,N,A}_{t} \, \mathrm {d}W_{t}, \\ - dB^{\eta ,N}_{t} &= \bigg( - \rho _{t} B^{\eta ,N}_{t} + \frac {1}{\eta }(\gamma C^{\eta ,N}_{t} - B^{\eta ,N}_{t} + 1 ) ( A^{ \eta ,N}_{t} - \gamma B^{\eta ,N}_{t} ) \bigg) \, \mathrm {d} t \\ & \hphantom{=:} - Z^{\eta ,N,B}_{t} \, \mathrm {d}W_{t}, \\ - dC^{\eta ,N}_{t} &= \bigg( - 2\rho _{t} C^{\eta ,N}_{t} - \frac {1}{\eta }(\gamma C^{\eta ,N}_{t} - B^{\eta ,N}_{t} + 1 )^{2} \bigg) \, \mathrm {d} t- Z^{\eta ,N,C}_{t} \, \mathrm {d}W_{t} \end{aligned}$$

with terminal condition

$$\begin{aligned} B^{\eta ,N}_{T} = 1, \qquad C^{\eta ,N}_{T} = 0, \end{aligned}$$

together with $A^{\eta ,N}_{T} = N$ for $N < \infty$ and $\lim _{t\nearrow T} A^{\eta ,\infty}_{t} = \infty$ in $L^{\infty}$ if $N=\infty$, has a solution

$$ \big( ( A^{\eta ,N},B^{\eta ,N},C^{\eta ,N} ) , (Z^{\eta ,N,A}, Z^{ \eta ,N,B}, Z^{\eta ,N,C} ) \big) $$

that belongs to the space $\mathcal {L}^{\infty}_{\mathcal {P}}(\Omega \times [0,T];\mathbb{R}^{3}) \times \mathcal {L}^{2}_{\mathrm{Prog}}(\Omega \times [0,T];\mathbb{R}^{3 \times m})$ if $N<\infty$ and to the space $\mathcal {L}^{\infty}_{\mathcal {P}}(\Omega \times [0,T-];\mathbb{R}^{3}) \times \mathcal {L}^{2}_{\mathrm{Prog}}(\Omega \times [0,T-];\mathbb{R}^{3 \times m})$ if $N=\infty$.

ii) The liquidation problem (2.2) has a solution $\hat{\xi}^{\eta ,N}$. The corresponding state process

$$ (\hat{X}^{\eta ,N},\hat{Y}^{\eta ,N} ) := (X^{\hat{\xi}^{\eta ,N}},Y^{ \hat{\xi}^{\eta ,N}} ) $$

is given by the (unique) solution to the ODE system

$$\begin{aligned} \partial _{t} \hat{X}^{\eta ,N}_{t} &= - \frac {1}{\sqrt{\eta}} D^{ \eta ,N}_{t} \hat{X}^{\eta ,N}_{t} - \frac {1}{\sqrt{\eta}} E^{\eta ,N}_{t} \hat{Y}^{\eta ,N}_{t}, \\ \partial _{t} \hat{Y}^{\eta ,N}_{t} &= - \frac {\gamma }{\sqrt{\eta}} D^{ \eta ,N}_{t} \hat{X}^{\eta ,N}_{t} - \frac {\gamma }{\sqrt{\eta}} E^{ \eta ,N}_{t} \hat{Y}^{\eta ,N}_{t} - \rho _{t} \hat{Y}^{\eta ,N}_{t} \end{aligned}$$

(2.3)

with initial conditions $\hat{X}^{\eta ,N}_{0} = x_{0}$ and $\hat{Y}^{\eta ,N}_{0} = 0$, where

$$\begin{aligned} D^{\eta ,N} := \frac {1}{\sqrt{\eta}} (A^{\eta ,N}-\gamma B^{\eta ,N} ), \qquad E^{\eta ,N} := \frac {1}{\sqrt{\eta}} (\gamma C^{\eta ,N} - B^{\eta ,N} + 1 ). \end{aligned}$$

Let us now define the process

$$ \hat{Z}^{\eta ,N} := \gamma \hat{X}^{\eta ,N} - \hat{Y}^{\eta ,N}. $$

The benefit of defining this process is that in the ODE (2.3), the terms that are multiplied by $\sqrt{\eta ^{-1}}$ drop out so that we expect that the process $\hat{Z}^{\eta ,N}$ remains stable for small values of $\eta$. Next, we state a result on the optimal state process and the previously introduced process $\hat{Z}^{\eta ,N}$ that will be important for our subsequent analysis. In particular, we show that the optimal portfolio process $\hat{X}^{\eta ,N}$ never changes its sign. The proof is given in Sect. 3.1.1.

Theorem 2.2

For all $\eta \in (0,\infty )$, $N\in \mathcal {N}$, the process $\hat{Z}^{\eta ,N}$ is nonincreasing on $[0,T]$. Moreover,

$$\begin{aligned} \mathbb{P}[ \hat{X}^{\eta ,N}_{t} \in (0,x_{0}), \hat{Y}^{\eta ,N}_{t} \in (-\gamma x_{0},0), \hat{Z}^{\eta ,N}_{t} \in (0,\gamma x_{0}) \textit{ for all } t \in (0,T) ] = 1. \end{aligned}$$

We are interested in the dynamics of the optimal portfolio processes for small instantaneous price impact. We address this problem within a factor model where the cost coefficients $\lambda$ and $\rho$ are driven by an Itô diffusion, which is given by the unique strong solution to the SDE

$$\begin{aligned} d\chi _{t} = \mu (t,\chi _{t}) \, \mathrm {d} t+ \sigma (t,\chi _{t}) \, \mathrm {d}W_{t}, \qquad \chi _{0} = \overline{\chi}_{0} \end{aligned}$$

on $[0,T]$ with $\overline{\chi}_{0} \in \mathbb{R}^{n}$. We assume throughout that the function

$$\begin{aligned} (\mu , \sigma ) \colon [0,T] \times \mathbb{R}^{n} \to \mathbb{R}^{n} \times \mathbb{R}^{n\times m} \end{aligned}$$

is bounded, measurable and uniformly Lipschitz-continuous in the space variable, i.e.,

$$ \vert (\mu , \sigma )(t,x_{1}) - (\mu , \sigma )(t,x_{2}) \vert \le c \vert x_{1} - x_{2}\vert . $$

Assumption 2.3

The processes $\rho$ and $\lambda$ are of the form

$$ (\rho _{t},\lambda _{t}) = f(t,\chi _{t}) $$

for some bounded $C^{1,2}$ function $f = (f^{\rho},f^{\lambda}) \colon [0,T] \times \mathbb{R}^{n} \to [0, \infty )^{2}$ with bounded derivatives. Moreover, the function $f^{\rho}$ is bounded away from zero.

For convenience, we define the stochastic process $\varphi = (\varphi _{t})_{t \in [0,T]}$ by

$$ \varphi _{t} := \sqrt{\lambda _{t} + 2 \gamma \rho _{t}} $$

and choose constants $\underline{\rho}, \overline{\rho}, \underline{\varphi}, \overline{\varphi}, \overline{\lambda}\in (0,\infty )$ such that

$$\begin{aligned} \underline{\rho}\le \rho \le \overline{\rho}, \qquad 0 \le \lambda \le \overline{\lambda}, \qquad \underline{\varphi}\le \varphi \le \overline{\varphi}. \end{aligned}$$

In what follows, we heuristically argue that the processes $\hat{X}^{\eta ,N}$ converge to a limit process $\hat{X}^{0}$ (independent of $N$) as $\eta \to 0$ and identify the limit $\hat{X}^{0}$. Since the ODE system (2.3) is not defined for $\eta =0$, we cannot define the limiting process as the solution to this system. Instead, we first identify the limits of the coefficients of the ODE system and then derive candidate limits for the state processes in terms of the limiting coefficients.

2.1.1 Convergence of the coefficient processes

In this section, we state the convergence results for the coefficient processes $D^{\eta ,N}$ and $E^{\eta ,N}$ of the ODE system (2.3) as $\eta \to 0$. In particular, we prove that their limits $D^{0}$ and $E^{0}$ exist and are driven by a common factor, which is given by the solution of a quadratic BSDE.

Before proceeding to the limit result, we provide some heuristics for the convergence. Assuming for simplicity that all coefficients are deterministic, the dynamics of the coefficient processes satisfy

$$\begin{aligned} \sqrt {\eta}\dot{D}^{\eta ,N}_{t} &= ( D^{\eta ,N}_{t} )^{2} - \lambda _{t} - \gamma \dot{B}^{\eta ,N}_{t}, \\ \sqrt {\eta}\dot{E}^{\eta ,N}_{t} &= 2 \sqrt {\eta}\rho _{t} E^{\eta ,N}_{t} + \gamma ( E^{\eta ,N}_{t} )^{2} - 2 \rho _{t} ( 1 - B^{\eta ,N}_{t} ) - \dot{B}^{\eta ,N}_{t}. \end{aligned}$$

Letting $\eta \to 0$, we expect that

$$\begin{aligned} 0 &= ( D^{0}_{t} )^{2} - \lambda _{t} - \gamma \dot{B}^{0}_{t}, \\ 0 &= \gamma ( E^{0}_{t} )^{2} - 2 \rho _{t} (1 - B^{0}_{t} ) - \dot{B}^{0}_{t}, \end{aligned}$$

that is, we expect that

$$\begin{aligned} D^{0}_{t} = \sqrt{ \gamma \dot{B}^{0}_{t} + \lambda _{t} } , \qquad E^{0}_{t} = \sqrt{ \gamma ^{-1} \big( \dot{B}^{0}_{t} + 2 \rho _{t} ( 1 - B^{0}_{t} ) \big) }. \end{aligned}$$

(2.4)

Moreover, by the choice of the coefficients $D^{\eta ,N}$ and $E^{\eta ,N}$ and by the BSDE in Theorem 2.1 i), we expect that in the limit,

$$\begin{aligned} - \dot{B}^{0}_{t} &= - \rho _{t} B^{0}_{t} + D^{0}_{t} E^{0}_{t}. \end{aligned}$$

(2.5)

The three equalities combined yield

$$\begin{aligned} ( D^{0}_{t} + \gamma E^{0}_{t} )^{2} &= \gamma \dot{B}^{0}_{t} + \lambda _{t} + 2 \gamma D^{0}_{t} E^{0}_{t} + \gamma \big( \dot{B}^{0}_{t} + 2 \rho _{t} ( 1 - B^{0}_{t} ) \big) \\ &= (\varphi _{t})^{2} + 2 \gamma ( \dot{B}^{0}_{t} + D^{0}_{t} E^{0}_{t} - \rho _{t} B^{0}_{t} ) \\ &= (\varphi _{t})^{2}. \end{aligned}$$

(2.6)

Plugging (2.5) and (2.6) back into (2.4) yields

$$\begin{aligned} D^{0}_{t} = (\varphi _{t})^{-1} ( \lambda _{t} + \gamma \rho _{t} B^{0}_{t} ), \qquad E^{0}_{t} = (\varphi _{t})^{-1} \rho _{t} ( 2 - B^{0}_{t} ). \end{aligned}$$

Hence we expect $D^{0}$ and $E^{0}$ to be driven by $B^{0}$ and $B^{0}$ to satisfy the ODE

$$\begin{aligned} - \dot{B}^{0}_{t} &= - \rho _{t} B^{0}_{t} + D^{0}_{t} E^{0}_{t} \\ &= - \frac {1}{\varphi _{t}^{2}} \big(\gamma (\rho _{t} B^{0}_{t} )^{2} - 2 \lambda _{t} \rho _{t} (1 - B^{0}_{t} )\big) \end{aligned}$$

with terminal condition $B^{0}_{T}=1$ (because $B^{\eta ,N}_{T} = 1$). Our heuristic also suggests that the limit processes are independent of the liquidation requirement.

Example 2.4

If $\lambda = C \rho$ for some constant $C \geq 0$, then the process $B^{0}$ can be computed explicitly. If $C = 0$, then $B^{0}_{t} = 2/({2 + \int _{t}^{T} \rho _{s} \, \mathrm {d} s})$. If $C > 0$, then

$$\begin{aligned} B^{0}_{t} = - \frac {C}{\gamma }+ \frac {1}{\gamma }\sqrt{C(C+2 \gamma )} \coth \bigg(& \!\mathrm{arcoth}\Big( \frac{C+\gamma}{\sqrt{C(C+2\gamma )}} \Big) + \sqrt{ \frac {C}{C+2\gamma}} \int _{t}^{T} \!\!\!\rho _{s} \, \mathrm {d} s \bigg). \end{aligned}$$

The preceding heuristic suggests that the limiting coefficient processes are driven by a solution to the BSDE corresponding to the above ODE for $B^{0}$. The following lemma is proved in Sect. 3.1.2.

Lemma 2.5

There exists a unique solution $(B^{0},Z^{0,B})$ in the space

$$ \mathcal {L}^{\infty}_{\mathcal {P}} \big( \Omega \times [0,T];(0,\infty ) \big) \times \mathcal {L}^{2}_{\mathcal {P}} ( \Omega \times [0,T]; \mathbb{R}^{m} ) $$

to the BSDE

$$\begin{aligned} - \mathrm {d}B^{0}_{t} = - \frac {1}{\varphi _{t}^{2}} \big(\gamma ( \rho _{t} B^{0}_{t} )^{2} - 2 \lambda _{t} \rho _{t} (1 - B^{0}_{t} ) \big) \, \mathrm {d} t- Z^{0,B}_{t} \, \mathrm {d}W_{t}, \qquad B^{0}_{T} = 1. \end{aligned}$$

(2.7)

The process $B^{0}$ is bounded from above by 1 and from below by

$$\begin{aligned} \underline{B}^{0}_{t} := \exp \big( - \underline{\varphi}^{-2} \gamma \overline{\rho}^{2} (T-t)\big). \end{aligned}$$

(2.8)

Moreover, there exists a uniformly continuous function (a so-called “decoupling field”) $h\colon [0,T]\times \mathbb{R}^{n} \to \mathbb{R}$ such that $B^{0}$ and $(h(t,\chi _{t}))_{t \in [0,T]}$ are indistinguishable.

We prove below that the process $B^{\eta ,N}$ converges to $B^{0}$ as $\eta \to 0$ and that $D^{\eta ,N}$ and $E^{\eta ,N}$ converge to the processes

$$ \begin{aligned} D^{0}_{t} := (\varphi _{t})^{-1} ( \lambda _{t} + \gamma \rho _{t} B^{0}_{t} ), \qquad E^{0}_{t} := (\varphi _{t})^{-1} \rho _{t} ( 2 - B^{0}_{t} ), \end{aligned} $$

(2.9)

respectively. In view of Lemma 2.5, these processes are well defined, and so the dynamics (2.7) of the process $B^{0}$ can be rewritten as

$$\begin{aligned} - \mathrm {d}B^{0}_{t} = - ( \rho _{t} B^{0}_{t} - D^{0}_{t} E^{0}_{t} ) \, \mathrm {d} t- Z^{0,B}_{t} \, \mathrm {d}W_{t}, \qquad B^{0}_{T} = 1. \end{aligned}$$

Likewise, the BSDE for the process $B^{\eta ,N}$ in Theorem 2.1 can be rewritten as

$$\begin{aligned} - \mathrm {d}B^{\eta ,N}_{t} &= - ( \rho _{t} B^{\eta ,N}_{t} - D^{ \eta ,N}_{t} E^{\eta ,N}_{t} ) \, \mathrm {d} t- Z^{\eta ,N,B}_{t} \, \mathrm {d}W_{t}, \qquad B^{\eta ,N}_{T} = 1. \end{aligned}$$

(2.10)

This suggests that the process $B^{\eta ,N}$ converges to $B^{0}$ on the entire interval $[0,T]$, and this is proved below; note that all the processes $B$ have the same terminal condition at time $T$. By contrast, convergence of the processes $D^{\eta ,N}$ and $E^{\eta ,N}$ can only be expected to hold on compact subintervals $[0,T -\varepsilon ]$ of $[0,T)$ because the terminal conditions of the limiting and approximating processes are different. It turns out that we can prove a slightly stronger result for the supremum of the processes $D$ and $E$, and this explains the different choices of intervals for the supremum and the infimum in the following lemma. Specifically, we have the following result. Its proof is given in Sect. 3.2.1.

Proposition 2.6

Let

$$\begin{aligned} b^{\eta ,N} := B^{\eta ,N} - B^{0}, \qquad d^{\eta ,N} := D^{\eta ,N} - D^{0}, \qquad e^{\eta ,N} := E^{\eta ,N} - E^{0}. \end{aligned}$$

Then for all $\varepsilon > 0$, there exists an $\eta _{0}>0$ such that for all $\eta \in (0,\eta _{0}]$ and for all $N \in \mathcal {N}$,

$$\begin{aligned} \mathbb{P}\Big[ &\sup _{t \in [0,T)} \max ( |b^{\eta ,N}_{t} | , -d^{ \eta ,N}_{t} , e^{\eta ,N}_{t}, - d^{\eta ,N}_{t} - \gamma e^{\eta ,N}_{t} ) \le \varepsilon , \\ & \inf _{t \in [0,T-\varepsilon ]} \min (-d^{\eta ,N}_{t}, e^{\eta ,N}_{t}, - d^{\eta ,N}_{t} - \gamma e^{\eta ,N}_{t} ) \ge -\varepsilon \Big] = 1. \end{aligned}$$

2.1.2 Convergence of the state process

Having derived the limits of the coefficient processes, we can now heuristically derive the limits of the processes $\hat{X}^{\eta ,N}$, $\hat{Y}^{\eta ,N}$ and $\hat{Z}^{\eta ,N}$, which we denote by $\hat{X}^{0}$, $\hat{Y}^{0}$ and $\hat{Z}^{0}$, respectively.

Since $\hat{X}^{\eta ,\infty}_{T} = 0$ for all $\eta > 0$, we expect that $\hat{X}^{0}_{T} = 0$. We prove in Lemma 3.11 that this convergence also holds if $N$ is finite. The proof heavily relies on the optimality of $\hat{X}^{0}$ in the semimartingale portfolio liquidation model.

Assuming that the optimal trading strategy remains stable if $\eta \to 0$, the ODE (2.3) suggests that the term $D^{\eta ,N} \hat{X}^{\eta ,N} + E^{\eta ,N} \hat{Y}^{\eta ,N}$ is small for small $\eta$ and hence that

$$ D^{0}_{t} \hat{X}^{0}_{t} = - E^{0}_{t} \hat{Y}^{0}_{t} \qquad \text{on } [0,T). $$

We do not conjecture the above relation at the terminal time because the convergence of $D^{\eta ,N}$ and $E^{\eta ,N}$ only holds on $[0,T)$. Assuming that

$$\begin{aligned} \hat{Z}^{0} = \gamma \hat{X}^{0} - \hat{Y}^{0} \qquad \text{on } [0,T), \end{aligned}$$

equation (2.6) implies

$$ \hat{Z}^{0} = - \frac{\varphi}{D^{0}} \hat{Y}^{0} \qquad \text{and hence} \qquad \hat{Y}^{0} = - \frac{D^{0}}{\varphi} \hat{Z}^{0}. $$

On the other hand, by definition, $\partial _{t} \hat{Z}^{\eta ,N} = \rho \hat{Y}^{\eta ,N}$. As $\eta \to 0$, this suggests that $\partial _{t} \hat{Z}^{0} = \rho \hat{Y}^{0}$ and hence that

$$\begin{aligned} \partial _{t} \hat{Z}^{0}_{t} = - \frac {\rho _{t} D^{0}_{t}}{\varphi _{t}} \hat{Z}^{0}, \qquad \hat{Z}^{0}_{0} = \gamma x_{0}. \end{aligned}$$

This motivates us to define the process

$$\begin{aligned} \hat{Z}^{0}_{t} := \gamma x_{0} \exp \bigg( -\int ^{t}_{0} \frac{\rho _{s}}{\varphi _{s}} D^{0}_{s} \, \mathrm {d} s\bigg), \qquad t \in [0,T]. \end{aligned}$$

Since we expect that $\hat{X}^{0}_{T} = 0$ and that $\hat{Z}^{0} = \gamma \hat{X}^{0} - \hat{Y}^{0}$, we now introduce the candidate limiting state processes

$$\begin{array}{rl}{\hat{X}}_t^0& :={\mathbb{1}}_{[0,T)}(t)\frac{E_t^0}{{\phi }_t}{\hat{Z}}_t^0,\\ {\hat{Y}}_t^0& :=-{\mathbb{1}}_{[0,T)}(t)\frac{D_t^0}{{\phi }_t}{\hat{Z}}_t^0-{\mathbb{1}}_{\{T\}}(t){\hat{Z}}_T^0,t\in [0,T].\end{array}$$

(2.11)

Since $(\hat{X}^{0}_{0-},\hat{Y}^{0}_{0-}) = (x_{0},0)$, we expect that the limiting state process jumps at the initial and the terminal time. In particular, we cannot expect uniform convergence on $[0,T]$.

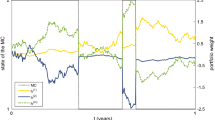
We also expect the limiting state processes to be of unbounded variation, as suggested by Fig. 1. The figure also suggests that the portfolio process is more or less monotone for large $\eta$, while this property is lost for small $\eta$. When $\eta \to 0$, adjustments to small changes in market environments are cheap. This is very different from round-trip strategies where an investor uses the price impact caused by him/herself to drive market prices into a favourable direction.

Fig. 1

Optimal trading strategies $\hat{X}^{\eta ,\infty}$ for the liquidation model for different instantaneous impact factors, and their limit $\hat{X}^{0}$ for $m=n=T=x_{0}=1$, $\gamma =3$, $\rho _{t} = 1 + 0{.}9 \sin (2{.}5 W_{t})$, $\lambda \equiv 1$

Figure 1 also suggests that the limiting portfolio process jumps only at the times 0 and $T$. This is consistent with the definition of the candidate processes (2.11) as well as the observation in Horst and Naujokat [21], according to which jumps in the optimal strategy can only be triggered by exogenous shocks like jumps in the cost coefficients, which are absent in the present model.

It remains to clarify in which sense the state processes converge. In contrast to the convergence result in Proposition 2.6, we can only expect convergence in probability because the state process follows a forward ODE while the coefficient processes follow backward SDEs; see also Appendix B.2. The following result establishes uniform convergence in probability on compact subintervals of $(0,T)$ along with some “upper/lower convergence” at the initial and terminal time. The proof is given in Sect. 3.2.2.

Theorem 2.7

For all $\varepsilon >0$ and $\delta > 0$, there exists an $\eta _{0}>0$ such that for all $\eta \in (0,\eta _{0}]$ and all $N \in \mathcal {N}$,

$$\begin{aligned} \mathbb{P}\Big[ & \sup _{t\in [\varepsilon ,T)} \max ( \hat{X}^{\eta ,N}_{t} - \hat{X}^{0}_{t} , \hat{Y}^{\eta ,N}_{t} - \hat{Y}^{0}_{t} ) \le \varepsilon , \\ & \inf _{t\in [0,T-\varepsilon ]} \min ( \hat{X}^{\eta ,N}_{t} - \hat{X}^{0}_{t} , \hat{Y}^{\eta ,N}_{t} - \hat{Y}^{0}_{t} ) \ge - \varepsilon \Big] \ge 1 - \delta . \end{aligned}$$

The preceding theorem does not provide a convergence result on the whole time interval, due to the jumps of the limit processes at the initial and terminal time. However, along with our results from Sect. 2.2, it allows us to prove the convergence of the graphs of the state processes on the entire time interval. The completed graph of an RCLL function $X \colon \{0-\}\cup [0,T] \to \mathbb{R}$ with finitely many jumps is defined by

$$\begin{aligned} G_{X} := \{ (t,x) \in [0,T]\times \mathbb{R}: \, & x = X_{t} = X_{t-} \text{ or } X_{t-} < X_{t}, x \in [X_{t-}, X_{t}] \\ & \text{or } X_{t-} > X_{t}, x \in [X_{t}, X_{t-}] \}. \end{aligned}$$

The Skorohod $\mathcal {M}_{2}$-distance between $X$ and $Y$ is defined as the Hausdorff distance between their completed graphs, i.e.,

$$\begin{aligned} d_{\mathcal {M}_{2}}(X,Y) := \max \Big( \sup _{p \in G_{X}} \min _{q \in G_{Y}} \vert p-q\vert _{\infty}, \sup _{q \in G_{Y}} \min _{p \in G_{X}} \vert p-q\vert _{\infty }\Big) \in [0,\infty ], \end{aligned}$$

where

$$\begin{aligned} \vert (s,y) \vert _{\infty }:= \max ( |s|,|y| ). \end{aligned}$$

If strict liquidation is required, then Theorem 2.7 is sufficient to prove convergence of the state processes in the Skorohod $\mathcal {M}_{2}$ sense. Even if liquidation is not required, it turns out that the terminal position converges to zero as $\eta \to 0$. Heuristically, this can be seen as follows.

Let $t_{0} \in (0,T)$. Disregarding market risk costs, which we expect to be of order $\mathcal {O}(T-t_{0})$ and hence negligible if $t_{0} \to T$, and disregarding instantaneous impact costs for the moment, the cost functional for any given admissible strategy $\xi$ is given by

$$\begin{aligned} & \int ^{T}_{t_{0}} Y^{\xi}_{s} \xi _{s} \, \mathrm {d} s- X^{\xi}_{T} Y^{ \xi}_{T} + \frac {N}{2} ( X^{\xi}_{T} )^{2} \\ &= Y^{\xi}_{T} X^{\xi}_{T} - Y^{\xi}_{t_{0}} X^{\xi}_{t_{0}} - \int ^{T}_{t_{0}} \dot{Y}^{\xi}_{s} X^{\xi}_{s} \, \mathrm {d} s- X^{\xi}_{T} Y^{\xi}_{T} + \frac {N}{2} ( X^{\xi}_{T} )^{2} \\ &= - Y^{\xi}_{t_{0}} X^{\xi}_{t_{0}} - \int ^{T}_{t_{0}} \gamma \xi _{s} X^{\xi}_{s} \, \mathrm {d} s+ \int ^{T}_{t_{0}} \rho Y^{\xi}_{s} X^{\xi}_{s} \, \mathrm {d} s+ \frac {N}{2} ( X^{\xi}_{T} )^{2} \\ &= - Y^{\xi}_{t_{0}} X^{\xi}_{t_{0}} - \frac {\gamma }{2} \big( ( X^{ \xi}_{T} )^{2} - ( X^{\xi}_{t_{0}} )^{2} \big) + \int ^{T}_{t_{0}} \rho Y^{\xi}_{s} X^{\xi}_{s} \, \mathrm {d} s+ \frac {N}{2} ( X^{\xi}_{T} )^{2} \\ &= - Y^{\xi}_{t_{0}} X^{\xi}_{t_{0}} + \frac {\gamma }{2} ( X^{\xi}_{t_{0}} )^{2} + \frac {N - \gamma}{2} ( X^{\xi}_{T} )^{2} + \int ^{T}_{t_{0}} \rho Y^{\xi}_{s} X^{\xi}_{s} \, \mathrm {d} s. \end{aligned}$$

Hence we expect the controllable costs to satisfy

$$ \mathbb{E} \bigg[ \frac {N - \gamma}{2} ( X^{\xi}_{T} )^{2} + \int ^{T}_{t_{0}} \rho Y^{\xi}_{s} X^{\xi}_{s} \, \mathrm {d} s\bigg] = \mathbb{E} \bigg[ \frac {N - \gamma}{2} ( X^{\xi}_{T} )^{2} \bigg] + \mathcal{O}(T-t_{0}) $$

plus instantaneous impact costs. Since $N > \gamma$, this suggests to make $X^{\xi}_{T}$ small, which is cheap if $\eta$ is small. More precisely, we have the following result; its proof is given in Sect. 3.2.3.

Proposition 2.8

For all $\varepsilon >0$ and $\delta >0$, there exists an $\eta _{0}>0$ such that for all $\eta \in (0,\eta _{0}]$ and all $N \in \mathcal {N}$,

$$\begin{aligned} \mathbb{P}[d_{\mathcal {M}_{2}} (\hat{X}^{\eta ,N},\hat{X}^{0} ) \le \varepsilon ] \ge 1 - \delta . \end{aligned}$$

2.2 Optimal liquidation with semimartingale strategies

In this section, we prove that the limit process $\hat{X}^{0}$ is the optimal portfolio process in a trade execution model with semimartingale trading strategies.

In our semimartingale model, a trading strategy is given by a triple

$$ \theta =(j^{+},j^{-},V), $$

where $j^{+}$ and $j^{-}$ are real-valued, nondecreasing pure jump processes and $V$ is with respect to the Brownian filtration a real-valued continuous semimartingale starting in zero. The jump processes $j^{+}$ and $j^{-}$ describe the cumulative effects of buying, respectively selling, large blocks of shares, while the continuous semimartingale $V$ describes the effect of continuously trading small amounts of the stock. The portfolio process $X^{\theta }= (X^{\theta}_{t})_{t\in [0,T]}$ associated with a strategy $\theta$ is then given by

$$\begin{aligned} X^{\theta}_{t} = x_{0} + j^{+}_{t} - j^{-}_{t} + V_{t}. \end{aligned}$$

The associated price impact process, again given by (2.1), is denoted by $Y^{\theta}$. We note that $X^{\theta}$ and $Y^{\theta}$ are semimartingales.

We assume that strict liquidation is required and that the cost associated with a trading strategy $\theta$ is given by

$$\begin{aligned} J^{0}(\theta ) := \mathbb{E}\bigg[ \int _{(0,T]} Y^{\theta}_{s-} \, \mathrm {d}X^{\theta}_{s} + \int ^{T}_{0} \frac {1}{2} \lambda _{s} ( X^{ \theta}_{s} )^{2} \, \mathrm {d} s+ \frac {\gamma }{2} [ X^{\theta }]_{T} \bigg]. \end{aligned}$$

The first term captures the transient price impact cost; the second captures market risk. The third term emerges as an additional cost term when passing from discrete to continuous time, as shown in Ackermann et al. [1]. Moreover, in the absence of this term, arbitrarily low costs can be achieved; see [1] for details.

The cost function can be conveniently rewritten as

$$\begin{aligned} J^{0}(\theta ) &= \mathbb{E}\bigg[ \frac {\gamma }{2} (j^{+}_{0} - j^{-}_{0})^{2} + \int _{(0,T]} \frac {1}{2} ( Y^{\theta}_{s-} + Y^{\theta}_{s} ) \, \mathrm {d}X^{\theta}_{s} \\ & \hphantom{=:\mathbb{E}\bigg[} + \int ^{T}_{0} \frac {1}{2} \lambda _{s} ( X^{\theta}_{s} )^{2} \, \mathrm {d} s+ \frac {\gamma }{2} [V]_{T} \bigg]. \end{aligned}$$

This representation supports our intuition that the price impact before and the price impact after the jump equally influence the total cost. The first term in this expression captures the cost of the initial block trade at time $t=0$.

The cost functional is well defined under the following admissibility condition.

Definition 2.9

A trading strategy $\theta = (j^{+},j^{-},V)$ is called admissible if the liquidation constraint $X^{\theta}_{T} = 0$ holds, if $j^{\pm}$ are RCLL, predictable, real-valued, nondecreasing and square-integrable pure jump processes, and if $V$ is a continuous semimartingale starting in zero with

$$\begin{aligned} \mathbb{E}\Big[ \max _{t \in [0,T]} \vert V_{t}\vert ^{2} \Big] < \infty . \end{aligned}$$

(2.12)

The set of all admissible trading strategies is denoted by $\mathcal {A}^{0}$.

Our goal is now to solve the optimisation problem

$$\begin{aligned} \min _{\theta \in \mathcal {A}^{0}} J^{0}(\theta ). \end{aligned}$$

To this end, we verify directly that the limit process $\hat{X}^{0}$ obtained in Sect. 2.1 is optimal. The results there show that the process has the representation

$$ \hat{X}^{0}_{t} = x_{0} - \hat{j}^{-}_{t} + \hat{V}_{t}, $$

where the jump process $\hat{j}^{-}$ and the continuous part are given by, respectively,

$$\begin{array}{rl}{\hat{j}}_t^{-}& :=x_0-{\hat{X}}_0^0+{\mathbb{1}}_{\{T\}}(t){\hat{X}}_{t-}^0,\\ {\hat{V}}_t& :={({\phi }_t)}^{-2}{\rho }_t(2-B_t^0){\hat{Z}}_t^0-{({\phi }_0)}^{-2}{\rho }_0(2-B_0^0){\hat{Z}}_0^0.\end{array}$$

In view of Assumption 2.3 and because $B^{0}$ is a continuous semimartingale and $\hat{Z}^{0}$ is differentiable, the process $\hat{V}$ is a continuous semimartingale starting in zero. Hence the following holds.

Lemma 2.10

The strategy $\hat{\theta}= (0,\hat{j}^{-}, \hat{V})$ is admissible.

In order to prove that $\hat{\theta}$ is optimal, we approximate the cost and the portfolio process associated with any strategy $\theta \in \mathcal {A}^{0}$ by the cost and portfolio processes corresponding to absolutely continuous trading strategies. To this end, we first approximate the continuous semimartingale part $V$ by differentiable processes. The proof of the following result is given in Sect. 4.1.

Lemma 2.11

For all $\theta = (j^{+},j^{-},V) \in \mathcal {A}^{0}$ and all $\beta ,\delta > 0$, there exist a constant $\nu > 0$ and an adapted and continuous $\dot{V}^{\beta ,\nu} \colon \Omega \times [0,T] \to [- \frac {\beta }{\nu},\frac {\beta }{\nu}]$ such that

$$\begin{aligned} \max _{t \in [0,T]} \bigg\vert \int ^{t}_{0} \dot{V}^{\beta ,\nu}_{s} \, \mathrm {d} s\bigg\vert \le \max _{t \in [0,T]} \vert V_{t}\vert \end{aligned}$$

(2.13)

and

$$\begin{aligned} \mathbb{P}\bigg[ \sup _{t \in [0,T]} \bigg\vert \int ^{t}_{0} \dot{V}^{ \beta ,\nu}_{s} \, \mathrm {d} s- V_{t} \bigg\vert \le 3\beta \bigg] \ge 1 - \delta . \end{aligned}$$

(2.14)

Next, we approximate the portfolio process $X^{\theta}$ by a portfolio process associated with an absolutely continuous strategy. To this end, for all $\theta \in \mathcal {A}^{0}$ and $\beta ,\nu ,\varepsilon > 0$, we define the integrable process

$$\begin{aligned} \xi ^{\theta ,\beta ,\nu ,\varepsilon }_{t} := \textstyle\begin{cases} \frac {1}{\varepsilon }( j^{+}_{t} - j^{+}_{t-\varepsilon } ) - \frac {1}{\varepsilon }( j^{-}_{t} - j^{-}_{t-\varepsilon } ) + \dot{V}^{\beta ,\nu}_{t}, &\quad t \le T - \varepsilon , \\ - \frac {1}{\varepsilon }( x_{0} + \int ^{T-\varepsilon }_{0} \xi ^{ \theta ,\beta ,\nu ,\varepsilon }_{u} \, \mathrm {d} u), &\quad t > T- \varepsilon . \end{cases}\displaystyle \end{aligned}$$

In view of the square-integrability of $j^{\pm}$, we see that $\xi ^{\theta ,\beta ,\nu ,\varepsilon }$ belongs to $\mathcal {A}$. The corresponding portfolio process is denoted by $X^{\theta ,\beta ,\nu ,\varepsilon }$. The proof of the following result is given in Sect. 4.2.

Lemma 2.12

For all $\theta = (j^{+},j^{-},V) \in \mathcal {A}^{0}$ and for all $\delta >0$, there exist $\beta >0$, $\nu >0$ and $\varepsilon >0$ such that

$$\begin{aligned} \mathbb{E}\bigg[ \int ^{T}_{0} ( X^{\theta ,\beta ,\nu ,\varepsilon }_{t} - X^{\theta}_{t} )^{2} \, \mathrm {d} t\bigg] \le \delta . \end{aligned}$$

For all $\xi \in \mathcal {A}$ with $\int ^{T}_{0} \xi _{s} \, \mathrm {d} s= -x_{0}$, we can define $V^{\xi}_{t} := \int ^{t}_{0} \xi _{s} \, \mathrm {d} s$ to obtain that $(0,0,V^{\xi}) \in \mathcal {A}^{0}$ and for all $\eta >0$, we have

$$\begin{aligned} J^{\eta ,\infty}(\xi ) = J^{0} ( 0, 0, V^{\xi }) + \frac {\eta }{2} \mathbb{E}\bigg[ \int ^{T}_{0} (\xi _{t})^{2} \, \mathrm {d} t\bigg]. \end{aligned}$$

(2.15)

The preceding lemma allows us to establish a cost estimate. The proof is given in Sect. 4.3.

Lemma 2.13

For all $C > 0$, there exists a constant $D(C) > 0$ such that for all $\theta = (j^{+},j^{-},V) \in \mathcal {A}^{0}$ with $\mathbb{E}[ \int ^{T}_{0} (X^{\theta}_{t})^{2} \, \mathrm {d} t] \le C$ and all $\xi \in \mathcal {A}$ with $\int ^{T}_{0} \xi _{s} \, \mathrm {d} s= -x_{0}$, we have

$$\begin{aligned} & \vert J^{0}(\theta ) - J^{0} (0,0,V^{\xi }) \vert \\ &\le D(C) \bigg( \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} (X^{\theta}_{t} - X^{\xi}_{t} )^{2} \, \mathrm {d} t\bigg] } + \mathbb{E}\bigg[ \int ^{T}_{0} (X^{\theta}_{t} - X^{\xi}_{t} )^{2} \, \mathrm {d} t\bigg] \bigg). \end{aligned}$$

As a consequence of the previous results, the optimal instantaneous price impact term converges to zero as $\eta \to 0$. The proof is given in Sect. 4.4.

Lemma 2.14

We have

$$\begin{aligned} & \lim _{\eta \to 0} \frac {\eta }{2} \mathbb{E}\bigg[ \int ^{T}_{0} ( \hat{\xi}^{\eta ,\infty}_{t} )^{2} \, \mathrm {d} t\bigg] = 0. \end{aligned}$$

The cost estimate in Lemma 2.13 allows us to establish the optimality of the trading strategy $\hat{\theta}$ by using the optimality of $\hat{\xi}^{\eta ,\infty}$ in the strict liquidation model with absolutely continuous strategies. It turns out that the minimal trading costs are fully determined by the initial value $B^{0}_{0}$ of the process $B^{0}$ along with the impact factor $\gamma$ and the initial portfolio.

Theorem 2.15

It holds that

$$\begin{aligned} \min _{\theta \in \mathcal {A}^{0}} J^{0}(\theta ) = J^{0} ( \hat{\theta}) = \frac {1}{2} \gamma (x_{0})^{2} B^{0}_{0}. \end{aligned}$$

Proof

Let us assume to the contrary that $\hat{\theta}$ does not minimise the cost functional $J^{0}$ over the set $\mathcal {A}^{0}$. Then there exist a strategy $\theta = (j^{+},j^{-},V) \in \mathcal {A}^{0}$ and a constant $\delta \in (0,\infty )$ such that $J^{0}(\theta ) + \delta \le J^{0}(\hat{\theta})$. Moreover, due to (2.15) and Lemma 2.13, for all $\eta ,\beta ,\nu ,\varepsilon \in (0,\infty )$, we have (for convenience, let $p(x) := x + \sqrt {x}$)

$$\begin{aligned} & J^{\eta ,\infty} ( \xi ^{\theta ,\beta ,\nu ,\varepsilon } ) - J^{ \eta ,\infty} ( \hat{\xi}^{\eta ,\infty} ) \\ &\le J^{\eta ,\infty} ( \xi ^{\theta ,\beta ,\nu ,\varepsilon } ) - J^{0}( \theta ) + J^{0}( \hat{\theta}) - \delta - J^{0} ( 0, 0, V^{\hat{\xi}^{ \eta ,\infty}} ) \\ &\le - \delta + \frac {\eta }{2} \mathbb{E}\bigg[ \int ^{T}_{0} ( \xi ^{ \theta ,\beta ,\nu ,\varepsilon }_{t} )^{2} \, \mathrm {d} t\bigg] + | J^{0}( \theta ) - J^{0} ( 0, 0, V^{\xi ^{\theta ,\beta ,\nu ,\varepsilon }} ) | \\ & \hphantom{=:} + | J^{0} ( \hat{\theta}) - J^{0} ( 0, 0, V^{\hat{\xi}^{\eta ,\infty}} ) | \\ & \le - \delta + \frac {\eta }{2} \mathbb{E}\bigg[ \int ^{T}_{0} ( \xi ^{\theta ,\beta ,\nu ,\varepsilon }_{t} )^{2} \, \mathrm {d} t \bigg] \\ & \hphantom{=:} + D \bigg(\mathbb{E}\bigg[ \int ^{T}_{0} ( X^{\theta}_{t} )^{2} \, \mathrm {d} t\bigg] \bigg) p\bigg( \mathbb{E}\bigg[ \int ^{T}_{0} ( X^{ \theta}_{t} - X^{\theta ,\beta ,\nu ,\varepsilon }_{t} )^{2} \, \mathrm {d} t\bigg] \bigg) \\ & \hphantom{=:} + D \bigg(\mathbb{E}\bigg[ \int ^{T}_{0} ( X^{\hat{\theta}}_{t} )^{2} \, \mathrm {d} t\bigg) \bigg] p\bigg( \mathbb{E}\bigg[ \int ^{T}_{0} ( \hat{X}^{0}_{t} - \hat{X}^{\eta ,\infty}_{t} )^{2} \, \mathrm {d} t\bigg] \bigg). \end{aligned}$$

(2.16)

According to Lemma 2.12, we can first choose $\beta ,\nu ,\varepsilon \in (0,\infty )$ and then, due to $|\hat{X}^{\eta ,\infty}_{t}| \le x_{0}$ (cf. Theorem 2.2), choose $\eta \in (0,\infty )$ small enough according to Theorem 2.7 such that the right-hand side of (2.16) is negative. This contradicts the optimality of $\hat{\xi}^{\eta ,\infty}$ for $J^{\eta ,\infty}$ and proves the optimality of $\hat{\theta}$.

It remains to compute $J^{0} ( \hat{\theta})$. In view of (2.15), for all $\eta \in (0,\infty )$, we have

$$\begin{aligned} J^{0} ( \hat{\theta}) = J^{0} ( \hat{\theta}) - J^{0} ( 0, 0, V^{ \hat{\xi}^{\eta ,\infty}} ) - \frac {\eta }{2} \mathbb{E}\bigg[ \int ^{T}_{0} ( \xi ^{\eta ,\infty}_{t} )^{2} \, \mathrm {d} t\bigg] + J^{\eta , \infty} ( \hat{\xi}^{\eta ,\infty} ). \end{aligned}$$

The difference of the first two terms converges to zero as $\eta \to 0$, which is verified by using Lemma 2.13 and Theorem 2.7 as in the above calculation. The third term converges to zero by Lemma 2.14. Hence, using the representation of the value function given in [18],

$$\begin{aligned} J^{0} ( \hat{\theta}) &= \lim _{\eta \to 0} J^{\eta ,\infty} ( \hat{\xi}^{\eta ,\infty} ) = \lim _{\eta \to 0} \frac {1}{2} A^{\eta , \infty}_{0} (x_{0})^{2} \\ &= \frac {(x_{0})^{2}}{2} \lim _{\eta \to 0} ( \sqrt{\eta} D^{\eta , \infty}_{0} + \gamma B^{\eta ,\infty}_{0} ) = \frac {1}{2} \gamma (x_{0})^{2} B^{0}_{0}. \end{aligned}$$

 □

Remark 2.16

If $\lambda \equiv 0$, our model is a special case of the model analysed in Ackermann et al. [1], which also contains cases when there is no optimal trading strategy. However, since $\gamma$ is constant in our model, the processes “$\mu$” and “$\sigma$” introduced in [1] are equal to zero. This implies that the equation “$\tilde{\beta}= Y$” holds in their notation. As shown in [1, Sect. 5], the process “$M^{ \perp}$” introduced therein is also equal to zero, which implies that “$Y$” and hence “$\tilde{\beta}$” is a semimartingale. Thus [1, Theorem 2.3 (ii)] confirms that under this property, an optimal trading strategy does indeed exist.

3 Proofs for Sect. 2.1

This section proves the results stated in Sect. 2.1. We start with a priori estimates and regularity properties for the coefficient processes that specify the optimal state processes.

3.1 A priori estimates and regularity properties

3.1.1 The case $\eta > 0$

The following estimates have been established in Graewe and Horst [18] and Horst and Xia [22], except for the upper bound on $E^{\eta ,N}$ for finite $N$ which is stronger than the corresponding one in [22]. It can be established using the same arguments as in [18, proof of Proposition 3.2] by noting that $D^{\eta ,N}_{T} < \infty$ if $N$ is finite.

Lemma 3.1

Let

$$ \overline{\kappa}:= \sqrt{2 \max (\overline{\lambda},\gamma \overline{\rho})}. $$

For all $\eta \in (0,\infty )$, $N\in \mathcal {N}$ and $s,t \in [0,T)$ with $s \le t$, we have that

$$\begin{aligned} e^{ -\overline{\rho}(T-s) } &\le B^{\eta ,N}_{s} \le 1, \\ 0 &\le E^{\eta ,N}_{s} \le \gamma ^{-1} \overline{\kappa}\tanh \big( \sqrt{\eta ^{-1}}\, \overline{\kappa}(T-s) \big) \le \gamma ^{-1} \overline{\kappa}, \quad \\ 0 &< D^{\eta ,N}_{s} \le \overline{\kappa}\coth \big(\sqrt{\eta ^{-1}} \,\overline{\kappa}(T-s)\big) \le \overline{\kappa}\coth \big(\sqrt{ \eta ^{-1}}\, \overline{\kappa}(T-t)\big). \end{aligned}$$

The preceding estimates allow us to prove that neither the optimal portfolio process nor the corresponding spread process change sign.

Proof

of Theorem 2.2 Put $V(t) := \hat{X}^{\eta ,N}_{t} \hat{Y}^{\eta ,N}_{t}$. Then $V(0) = 0$ and $V$ satisfies the ODE

$$\begin{aligned} \dot{V}(t) &= -\big( \sqrt{\eta ^{-1}} ( D^{\eta ,N}_{t} + \gamma E^{ \eta ,N}_{t} ) + \rho _{t} \big) V(t) \\ & \hphantom{=:} - \sqrt{\eta ^{-1}} \big( E^{\eta ,N}_{t} (\hat{Y}^{\eta ,N}_{t} )^{2} + \gamma D^{\eta ,N}_{t} (\hat{X}^{\eta ,N}_{t} )^{2} \big). \end{aligned}$$

As a result,

$$\begin{aligned} V(t) &= - \exp \bigg( - \int ^{t}_{0} \big( \sqrt{\eta ^{-1}} ( D^{ \eta ,N}_{u} + \gamma E^{\eta ,N}_{u} ) + \rho _{u} \big) \, \mathrm {d} u\bigg) \\ & \hphantom{=:-} \times \int ^{t}_{0} \sqrt{\eta ^{-1}} \big( E^{\eta ,N}_{s} (\hat{Y}^{ \eta ,N}_{s} )^{2} + \gamma D^{\eta ,N}_{s} (\hat{X}^{\eta ,N}_{s} )^{2} \big) \\ & \hphantom{=:-} \times \exp \bigg( \int _{0}^{s} \big( \sqrt{\eta ^{-1}} ( D^{\eta ,N}_{u} + \gamma E^{\eta ,N}_{u} ) + \rho _{u} \big) \, \mathrm {d} u\bigg) \, \mathrm {d} s. \end{aligned}$$

In view of Lemma 3.1, this shows that $V(t) < 0$ on $(0,T)$. Hence strict positivity of $\hat{X}^{\eta ,N}_{0}$ yields

$$\begin{aligned} \mathbb{P}[ \hat{X}^{\eta ,N}_{t} > 0, \hat{Y}^{\eta ,N}_{t} < 0 \text{ for all } t \in (0,T) ] = 1. \end{aligned}$$

Thus the definition of $\hat{Z}^{\eta ,N}$ along with (2.3) yields $\partial _{t} \hat{Z}^{\eta ,N}_{t} = \rho _{t} \hat{Y}^{\eta ,N}_{t} < 0$ on $(0,T)$. Moreover,

$$\begin{aligned} & \hat{X}^{\eta ,N}_{t} < \gamma ^{-1} \hat{Z}^{\eta ,N}_{t} \le \gamma ^{-1} \hat{Z}^{\eta ,N}_{0} = x_{0} \qquad \text{and} \qquad \hat{Y}^{\eta ,N}_{t} > - \hat{Z}^{\eta ,N}_{t} \ge - \gamma x_{0}. \end{aligned}$$

 □

Next, we prove that the process $B^{\eta ,N}$ satisfies an $L^{1}$ uniform continuity property. We refer to Appendix A for a discussion of general regularity properties of stochastic processes.

Lemma 3.2

The process $B^{\eta ,N}$ satisfies Condition A.1stated in Appendix Aon $[0,T]$ uniformly in $N \in \mathcal {N}$ and $\eta \in (0,H]$, for all $H \in (0,\infty )$.

Proof

Let $\varepsilon , \varepsilon _{1} > 0$, $s > T-\varepsilon _{1}$ and let $V$ and $\tau$ be arbitrary according to the definition of Condition A.1. By Lemma 3.1, if $\varepsilon _{1}$ is small enough,

$$\begin{aligned} | \mathbb{E}[ V ( B^{\eta ,N}_{\tau }- B^{\eta ,N}_{s} ) ] | \le \big( 1 - \exp ( -\overline{\rho}\varepsilon _{1} ) \big) \mathbb{E}[ |V| ] \le \varepsilon \mathbb{E}[ |V| ]. \end{aligned}$$

If $s \leq T - \varepsilon _{1}$, the assertion follows from the integral representation (2.10) along with the estimates established in Lemma 3.1 by using that the stochastic integral in (2.10) is a martingale on $[0,T-\varepsilon _{1}]$. We emphasise that $Z^{\eta ,N,B}$ is possibly defined only on $[0,T-]$, and so the stochastic integral may be a martingale only away from the terminal time. □

3.1.2 The case $\eta =0$

We are now going to establish a priori estimates on the candidate limiting coefficient processes. First, we show that Assumption 2.3 directly implies the following regularity result for the parameter processes.

Lemma 3.3

The processes $\chi$, $\rho$, $\lambda$, $\varphi$ and $\varphi ^{-1}$ satisfy Condition A.2introduced in Appendix A.

Proof

The process $\chi$ satisfies Condition A.2 due to Lemmas A.11, A.4 and A.7. The rest immediately follows by Lemma A.10. □

We are now ready to prove that the process $B^{0}$ is well defined.

Proof

of Lemma 2.5 The existence result follows from a standard argument. In fact, it is well known that for any $\overline{b} \in [1,\infty )$, the BSDE

$$\begin{aligned} - \mathrm {d}B^{\overline{b}}_{t} = \psi ^{\overline{b}} ( t, \chi _{t} , B^{ \overline{b}}_{t} ) \, \mathrm {d} t- Z^{\overline{b}}_{t} \, \mathrm {d}W_{t}, \qquad B^{\overline{b}}_{T} = 1 \end{aligned}$$

(3.1)

with Lipschitz-continuous driver (we recall $f^{\lambda}$, $f^{\rho}$ defined in Assumption 2.3)

$$\begin{aligned} \psi ^{\overline{b}}(t,\chi ,b) &:= - \frac{1}{f^{\lambda}(t,\chi ) + 2 \gamma f^{\rho}(t,\chi )} \\ & \hphantom{=::-} \times \bigg( \gamma f^{\rho}(t,\chi )^{2} (\overline{b}^{2} \wedge b^{2} ) - 2 f^{\lambda}(t,\chi ) f^{\rho}(t,\chi ) \big( 1 - (b\wedge \overline{b})^{+} \big) \bigg) \end{aligned}$$

has a unique solution $(B^{\overline{b}},Z^{\overline{b}}) \in \mathcal {L}_{\mathcal {P}}^{2}( \Omega \times [0,T];\mathbb{R}\times \mathbb{R}^{m})$ (cf. Theorem A.13). Let us then define the functions $\underline{\phi}, \overline{\phi}\colon \Omega \times [0,T] \times \mathbb{R}\times \mathbb{R}^{m} \to \mathbb{R}$ by

$$ \underline{\phi}(t,b,z) := - \underline{\varphi}^{-2} \gamma \overline{\rho}^{2} b ,\qquad \overline{\phi}(t,b,z) := 0. $$

By definition, $(\underline{B}^{0},0)$ is the unique solution to the BSDE with driver $\underline{\phi}$ and terminal condition 1, where the lower bound $\underline{B}^{0}$ on the process $B^{0}$ was defined in (2.8). Likewise, $(1,0)$ is the unique solution of the BSDE with driver $\overline{\phi}$ and the same terminal condition. Since

$$ \psi ^{\overline{b}} (t,\chi _{t},\underline{B}^{0}_{t} ) > \underline{\phi}(t,\underline{B}^{0}_{t},0 ) \qquad \text{and} \qquad \psi ^{\overline{b}}(t,\chi _{t},1) < \overline{\phi}(t,1,0), $$

the standard comparison principle for BSDEs with Lipschitz-continuous drivers yields

$$ \underline{B}^{0} \leq B^{\overline{b}} \leq 1. $$

This proves that $(B^{1},Z^{1})$ is the desired unique bounded solution to the BSDE (2.7). The second assertion follows Theorem A.13 applied to the BSDE (3.1) for $\overline{b} = 1$. □

Having established the existence of the process $B^{0}$, the processes $D^{0}$ and $E^{0}$ are well defined. The following lemma establishes estimates and regularity properties for $D^{0}$ and $E^{0}$.

Lemma 3.4

We have the a priori estimates

$$\begin{aligned} \frac{\gamma \underline{\rho}}{\overline{\varphi}} \exp \bigg( - \frac{\gamma \overline{\rho}^{2}}{\underline{\varphi}^{2}} T \bigg) & \le D^{0}_{t} \le \underline{\varphi}^{-1} ( \overline{\lambda}+ \gamma \overline{\rho}), \\ \overline{\varphi}^{-1} \underline{\rho}&\le E^{0}_{t} \le 2 \underline{\varphi}^{-1} \overline{\rho}. \end{aligned}$$

Moreover, the processes $D^{0}$ and $E^{0}$ satisfy Condition A.2.

Proof

The a priori estimates can be obtained by plugging the bounds on $B^{0}$ from Lemma 2.5 into the definitions of $D^{0}$ and $E^{0}$ given in (2.9). Moreover, if we denote by $h$ the function derived from Lemma 2.5, then for all $t \in [0,T]$,

$$\begin{aligned} &D^{0}_{t} = \bigg( \frac{ f^{\lambda }+ \gamma f^{\rho }h }{ \sqrt{ f^{\lambda }+ 2 \gamma f^{\rho }} } \bigg) (t,\chi _{t}), \qquad E^{0}_{t} = \bigg( \frac{ (2 - h) f^{\rho }}{ \sqrt{ f^{\lambda }+ 2 \gamma f^{\rho }} } \bigg) (t,\chi _{t}). \end{aligned}$$

In view of Assumption 2.3, the processes $D^{0}$ and $E^{0}$ can be represented as uniformly continuous functions of the factor process $\chi$, and hence the assertion follows from Lemmas 3.3 and A.10. □

The next lemma can be viewed as the analogue to Theorem 2.2 in the case $\eta = 0$.

Lemma 3.5

It holds

$$\begin{aligned} \mathbb{P}[ \hat{X}^{0}_{t} \in (0,x_{0}), \hat{Y}^{0}_{t} \in (-\gamma x_{0},0) \textit{ for all } t \in (0,T) ] = 1. \end{aligned}$$

Proof

Due to Lemma 3.4, $D^{0}$ is positive and hence, for $t \in (0,T)$,

$$\begin{aligned} 0 < \hat{Z}^{0}_{t} < x_{0} \gamma . \end{aligned}$$

Since $D^{0} + \gamma E^{0} = \varphi$ on $[0,T)$, it thus follows from Lemma 3.4 that for all $t\in (0,T)$,

$$\begin{aligned} 0 < \hat{X}^{0}_{t} & = \frac{\varphi _{t} - D^{0}_{t}}{\gamma \varphi _{t}} \hat{Z}^{0}_{t} < \gamma ^{-1} \hat{Z}^{0}_{t} < x_{0}, \\ 0 > \hat{Y}^{0}_{t} & = - \frac{\varphi _{t} - \gamma E^{0}_{t}}{\varphi _{t}} \hat{Z}^{0}_{t} > - \hat{Z}^{0}_{t} > -\gamma x_{0}. \end{aligned}$$

 □

3.2 Proof of the convergence results

In this section, we prove our main convergence results. We start with the convergence of the coefficients of the ODE system (2.3). Subsequently, we prove that the convergence of the coefficients yields convergence of the state process.

3.2.1 Proof of Proposition 2.6

The proof of Proposition 2.6 is split into a series of lemmas. In the first step, we establish the convergence, as $\eta \to 0$, of the auxiliary processes

$$\begin{aligned} F^{\eta ,N}_{t} := D^{\eta ,N}_{t} + \gamma E^{\eta ,N}_{t} \longrightarrow F^{0} := \varphi \end{aligned}$$

and

$$\begin{aligned} G^{\eta ,N} := \rho B^{\eta ,N} + \varphi E^{\eta ,N} \longrightarrow G^{0} := \rho B^{0} + \varphi E^{0} = 2 \rho . \end{aligned}$$

On $[0,T)$, the processes $F^{\eta ,N}$ and $G^{\eta ,N}$ satisfy the dynamics

$$\begin{aligned} \mathrm {d}F^{\eta ,N}_{t} &= \sqrt{\eta ^{-1}} \big( ( F^{\eta ,N}_{t} )^{2} - (\varphi _{t})^{2} \big) \, \mathrm {d} t+ 2 \gamma \rho _{t} E^{ \eta ,N}_{t} \, \mathrm {d} t \\ & \hphantom{=:} + \sqrt{\eta ^{-1}} ( Z^{\eta ,N,A}_{t} - 2 \gamma Z^{\eta ,N,B}_{t} + \gamma ^{2} Z^{\eta ,N,C}_{t} ) \, \mathrm {d}W_{t}, \end{aligned}$$

(3.2)

$$\begin{aligned} - \mathrm {d} ( \varphi ^{-1} G^{\eta ,N} )_{t} &= \sqrt{\eta ^{-1}} \big( - G^{\eta ,N}_{t} + 2 \rho _{t} - E^{\eta ,N}_{t} ( F^{\eta ,N}_{t} - \varphi _{t} ) \big) \, \mathrm {d} t- 2 \rho _{t} E^{\eta ,N}_{t} \, \mathrm {d} t \\ & \hphantom{=:} - \mathrm {d} ( \varphi ^{-1} \rho B^{\eta ,N} )_{t} + \sqrt{\eta ^{-1}} ( Z^{\eta ,N,B}_{t} - \gamma Z^{\eta ,N,C}_{t} ) \, \mathrm {d}W_{t}. \end{aligned}$$

(3.3)

A general convergence result for integral equations of the above form is established in Appendix B.1.2. It allows us to prove the following two results.

Lemma 3.6

Let $f^{\eta ,N} := F^{\eta ,N} - \varphi$. For all $\varepsilon >0$, there exists an $\eta _{0}>0$ such that for all $\eta \in (0,\eta _{0}]$ and all $N \in \mathcal {N}$,

$$\begin{aligned} \mathbb{P}\Big[ \sup _{s \in [0,T-\varepsilon ]} f^{\eta ,N}_{s} \le \varepsilon , \inf _{s \in [0,T)} f^{\eta ,N}_{s} \ge -\varepsilon \Big] = 1. \end{aligned}$$

Proof

For every $N \in \mathcal {N}$, we apply Lemma B.4 to $P^{\eta }:= F^{\eta ,N}$ with

$$\begin{aligned} \psi &:= 1, \qquad a(x,y) := (x^{+})^{2} - y^{2}, \quad P^{0} := \varphi , \\ q^{\eta} &:= 0, \qquad L^{\eta}_{t} := 2\gamma \int ^{t}_{0} \rho _{s} E^{\eta ,N}_{s} \, \mathrm {d} s, \end{aligned}$$

noticing that $\varepsilon \mapsto \eta _{0} = \eta _{0}(\varepsilon )$ is independent of $N$. Assumption B.3 i) is satisfied with $\overline{P} := \overline{\varphi}+ 3 \overline{\kappa}$ due to Lemma 3.1. If $N = \infty$, then Assumption B.3 ii) a) is satisfied due to Theorem 2.1 and the a priori estimates derived in Lemmas 3.1 and 3.4. If $N<\infty$ and $\eta \le \overline{\varphi}^{-2}$, then $E^{\eta ,N}_{T} = 0$ and

$$\begin{aligned} f^{\eta ,N}_{T} = D^{\eta ,N}_{T} + \gamma E^{\eta ,N}_{T} - D^{0}_{T} - \gamma E^{0}_{T} = \sqrt{\eta ^{-1}} (N - \gamma ) - \varphi _{T} \ge \sqrt{\eta ^{-1}} - \overline{\varphi}\ge 0, \end{aligned}$$

which shows Assumption B.3 ii) b). Assumption B.3 iii) is trivially satisfied because $q^{\eta} = 0$. Assumption B.3 iv) follows by direct computation using $\overline{\varepsilon }:= \underline{\varphi}/2$ and $\beta := \underline{\varphi}/2$. Assumption B.3 v) follows from Lemmas 3.3 and 3.1. □

It is not difficult to show that similar arguments as those used to prove the convergence of $f^{\eta ,N}$ can be applied to $-g^{\eta ,N} := -G^{\eta ,N} + 2 \rho$. As a result, the intervals $[0,T)$ and $[0,T-\varepsilon ]$ in the statement of the convergence result for $g^{\eta ,N}$ need to be swapped. We omit the proof of the corresponding next result.

Lemma 3.7

For all $\varepsilon >0$, there exists an $\eta _{0}>0$ such that for all $\eta \in (0,\eta _{0}]$ and all $N \in \mathcal {N}$,

$$\begin{aligned} \mathbb{P}\Big[ \sup _{s \in [0,T)} g^{\eta ,N}_{s} \le \varepsilon , \inf _{s \in [0,T-\varepsilon ]} g^{\eta ,N}_{s} \ge -\varepsilon \Big] = 1. \end{aligned}$$

We are now going to prove the almost sure convergence to zero of the process $b^{\eta ,N} := B^{\eta ,N} - B^{0}$. To this end, we first observe that

$$\begin{aligned} D^{\eta ,N} = F^{\eta ,N} - \gamma E^{\eta ,N}, \qquad \varphi E^{ \eta ,N} = G^{\eta ,N} - \rho B^{\eta ,N} \end{aligned}$$

yields

$$\begin{aligned} & - D^{\eta ,N} E^{\eta ,N} = - f^{\eta ,N} E^{\eta ,N} - G^{\eta ,N} + \rho B^{\eta ,N} + \gamma \varphi ^{-2} ( G^{\eta ,N} - \rho B^{\eta ,N} )^{2}. \end{aligned}$$

Plugging this into (2.10) shows that

$$\begin{aligned} \mathrm {d}B^{\eta ,N}_{t} &= \big( - G^{\eta ,N}_{t} - f^{\eta ,N}_{t} E^{ \eta ,N}_{t} + 2 \rho _{t} B^{\eta ,N}_{t} + \gamma (\varphi _{t})^{-2} ( G^{\eta ,N}_{t} - \rho _{t} B^{\eta ,N}_{t} )^{2} \big) \, \mathrm {d} t \\ & \hphantom{=:} + Z^{\eta ,N,B}_{t} \, \mathrm {d}W_{t} \end{aligned}$$

on $[0,T)$. Performing an analogous computation for $B^{0}$ and subtracting the two equations yields

$$\begin{aligned} \mathrm {d}b^{\eta ,N}_{t} &= \Big( ( b^{\eta ,N}_{t} )^{2} \gamma ( \varphi _{t})^{-2} (\rho _{t})^{2} + b^{\eta ,N}_{t} \big( 2 \rho _{t} - 2 \gamma (\varphi _{t})^{-2} \rho _{t} ( G^{0}_{t} - \rho _{t} B^{0}_{t} ) \big) \\ & \hphantom{=:\Big(} - f^{\eta ,N}_{t} E^{\eta ,N}_{t} - g^{\eta ,N}_{t} \\ & \hphantom{=:\Big(} + \gamma (\varphi _{t})^{-2} g^{\eta ,N}_{t} \big( g^{\eta ,N}_{t} + 2 G^{0}_{t} - \rho _{t} ( 2 b^{\eta ,N}_{t} + 2 B^{0}_{t} ) \big) \Big) \, \mathrm {d} t \\ & \hphantom{=:} + ( Z^{\eta ,N,B}_{t} - Z^{0,B}_{t} ) \, \mathrm {d}W_{t} \end{aligned}$$

on $[0,T)$. Using that

$$\begin{aligned} 2 \rho _{t} - 2 \gamma (\varphi _{t})^{-2} \rho _{t} ( G^{0}_{t} - \rho _{t} B^{0}_{t} ) & = 2 \rho _{t} (\varphi _{t})^{-1} D^{0}_{t}, \\ g^{\eta ,N}_{t} + 2 G^{0}_{t} - \rho _{t} ( 2 b^{\eta ,N}_{t} + 2 B^{0}_{t} ) & = - g^{\eta ,N}_{t} + 2 \varphi _{t} E^{\eta ,N}_{t} \end{aligned}$$

shows that

$$\begin{aligned} \mathrm {d}b^{\eta ,N}_{t} &= \Big( ( b^{\eta ,N}_{t} )^{2} \gamma ( \varphi _{t})^{-2} (\rho _{t})^{2} + b^{\eta ,N}_{t} 2 (\varphi _{t})^{-1} \rho _{t} D^{0}_{t} - f^{\eta ,N}_{t} E^{\eta ,N}_{t} \\ & \hphantom{=:\big(} + g^{\eta ,N}_{t} \big( - 1 - \gamma (\varphi _{t})^{-2} g^{\eta ,N}_{t} + 2 \gamma (\varphi _{t})^{-1} E^{\eta ,N}_{t} \big) \Big) \, \mathrm {d} t \\ & \hphantom{=:} + ( Z^{\eta ,N,B}_{t} - Z^{0,B}_{t} ) \, \mathrm {d}W_{t} \end{aligned}$$

on $[0,T)$. This BSDE is different from (3.2) and (3.3). We apply Lemma B.2 to prove the following result.

Lemma 3.8

For all $\varepsilon >0$, there exists an $\eta _{0}>0$ such that for all $\eta \in (0,\eta _{0}]$ and all $N \in \mathcal {N}$,

$$\begin{aligned} \mathbb{P}\Big[ \sup _{s \in [0,T]} | b^{\eta ,N}_{s} | \le \varepsilon \Big] = 1. \end{aligned}$$

Proof

For every $N \in \mathcal {N}$, we apply Lemma B.2 with

$$\begin{aligned} a(t,b) &:= b^{2} \gamma (\varphi _{t})^{-2} (\rho _{t})^{2} + b 2 ( \varphi _{t})^{-1} \rho _{t} D^{0}_{t}, \\ q^{\eta}_{t} &:= - f^{\eta ,N}_{t} E^{\eta ,N}_{t} + g^{\eta ,N}_{t} \big( 2 \gamma (\varphi _{t})^{-1} E^{\eta ,N}_{t} - 1 - \gamma ( \varphi _{t})^{-2} g^{\eta ,N}_{t} \big). \end{aligned}$$

Assumption B.1 i) follows from the a priori estimates on $B^{\eta ,N}$ (Lemma 3.1), $B^{0}$ (Lemma 2.5) and $D^{0}$ (Lemma 3.4). Assumption B.1 ii) follows from the a priori estimates on $B^{\eta ,N}$ and $B^{0}$, where the mapping $\varepsilon \mapsto \delta$ is independent of $N$. Assumption B.1 iii) follows from the same estimates and Lemmas 3.6 and 3.7, where the choice of $\eta _{1}$ is independent of $N$. Assumption B.1 iv) is satisfied because we can choose $\varepsilon _{1} > 0$ small enough such that

$$ -\varepsilon _{1} \gamma (\varphi )^{-1} \rho + 2 D^{0} \ge 0. $$

 □

3.2.2 Proof of Theorem 2.7

First we need to prove an auxiliary result:

Lemma 3.9

Let $I \subseteq \mathbb{R}$ be a compact interval and $Y = (Y_{t})_{t\in I}$ a continuous, adapted, $\mathbb{R}^{d}$-valued stochastic process. Then the modulus of continuity

$$ \sup _{s,t\in I, |s-t| \le \nu} \vert Y_{t} - Y_{s} \vert $$

converges to 0 in probability as $\nu \to 0$.

Proof

For all $\omega \in \Omega$, $Y(\omega )$ is uniformly continuous; hence the modulus of continuity converges to 0 as $\nu \to 0$ ℙ-a.s. This implies convergence in probability. □

Proof

of Theorem 2.7 Convergence on compact subintervals of $[0,T)$ follows from Theorem B.8 applied to the ODEs

$$\begin{aligned} \partial _{t} \hat{X}^{\eta ,N}_{t} &= - \sqrt{\eta ^{-1}} F^{\eta ,N}_{t} \bigg( \hat{X}^{\eta ,N}_{t} - \frac{E^{\eta ,N}_{t}}{F^{\eta ,N}_{t}} \hat{Z}^{\eta ,N}_{t} \bigg), \\ \partial _{t} \hat{Z}^{\eta ,N}_{t} &= \gamma \rho _{t} \hat{X}^{\eta ,N}_{t} - \rho _{t} \hat{Z}^{\eta ,N}_{t} \end{aligned}$$

(3.4)

and

$$\begin{aligned} \begin{aligned} \hat{X}^{0}_{t} = \frac{E^{0}_{t}}{\varphi _{t}} \hat{Z}^{0}_{t}, \qquad \hat{Z}^{0}_{t} = \hat{Z}^{0}_{0} \exp \bigg( \int ^{t}_{0} \Big( \gamma \rho _{s} \frac {E^{0}_{s}}{\varphi _{s}} - \rho _{s} \Big) \, \mathrm {d} s\bigg) \end{aligned} \end{aligned}$$

on $[0,T)$. In fact, Condition (B.10) follows from Proposition 2.6 and Condition (B.11) from Theorem 2.2. Finally, $D^{0} > 0$ (see Lemma 3.4), from which we deduce that $x_{0} > \frac{E^{0}_{0}}{\varphi _{0}} \hat{Z}^{0}_{0}$. Thus by Theorem B.8, applied once for every $N \in \mathcal {N}$ and every $\nu > 0$, there exists for all $\nu ,\delta \in (0,\infty )$ some $\eta _{1} = \eta _{1}(\nu ,\delta ) \in (0,\infty )$ such that for all $\eta \in (0,\eta _{1}]$ and all $N \in \mathcal {N}$, the set

$$\begin{aligned} M_{0}^{\nu ,\eta ,N} &:= \Big\{ \sup _{t\in [0,T-\nu ]} \max ( | \hat{Z}^{0}_{t} - \hat{Z}^{\eta ,N}_{t} |, \hat{X}^{0}_{t} - \hat{X}^{ \eta ,N}_{t} ) \le \nu , \\ & \hphantom{=::\bigg\{ } \inf _{t\in [\nu ,T-\nu ]} ( \hat{X}^{0}_{t} - \hat{X}^{\eta ,N}_{t} ) \ge -\nu \Big\} \end{aligned}$$

satisfies

$$\begin{aligned} \mathbb{P}[ M_{0}^{\nu ,\eta ,N} ] > 1-\delta /2. \end{aligned}$$

(3.5)

Near the terminal time, we cannot use this theorem since the convergence $\frac{E^{\eta ,N}}{F^{\eta ,N}} \to \frac{E^{0}}{\varphi}$ holds only on $[0,T-]$. Instead, we apply increment bounds on intervals of the form $[T-\nu ,T]$ to prove that for all $\eta > 0$, $N \in \mathcal {N}$ and for all sufficiently small

$$\begin{aligned} \nu \in (0,\varepsilon /2] \quad \text{and} \quad \beta \in (0, \varepsilon /3], \end{aligned}$$

(3.6)

the set

$$\begin{aligned} M_{1}^{\nu ,\varepsilon ,\eta ,N} &:= \Big\{ \inf _{t \in [T-\nu ,T)} ( \hat{X}^{0}_{t} - \hat{X}^{\eta ,N}_{t} ) \ge -\varepsilon \Big\} \end{aligned}$$

contains the set $M_{0}^{\nu ,\eta ,N} \cap M_{2}^{\beta ,\nu} \cap M_{3}^{\nu ,\eta ,N}$, where

$$\begin{aligned} M_{2}^{\beta ,\nu} &:= \Big\{ \sup _{s,t\in [T-\nu ,T)} (| \varphi _{s} - \varphi _{t} | \vee | E^{0}_{s} - E^{0}_{t} | \vee | \hat{X}^{0}_{s} - \hat{X}^{0}_{t} |) \le \beta \Big\} , \\ M_{3}^{\nu ,\eta ,N} &:= \Big\{ \sup _{t \in [T-\nu ,T)} \big( e^{ \eta ,N}_{t} \vee (-f^{\eta ,N}_{t} ) \big)\le \nu \Big\} . \end{aligned}$$

The probability of the last two events can be made large by Lemma 3.9 and Proposition 2.6: for all $\beta ,\delta ,\nu \in (0,\infty )$, there exist $\nu _{0}(\beta ,\delta ), \eta _{2}(\nu ) \in (0,\infty )$ such that

$$\begin{aligned} \inf _{\nu \le \nu _{0}(\beta ,\delta )} \mathbb{P}[M_{2}^{\beta ,\nu} ] > 1 - \delta /2, \qquad \inf _{\eta \le \eta _{2}(\nu )} \inf _{N \in \mathcal {N}} \mathbb{P}[M_{3}^{\nu ,\eta ,N} ] = 1. \end{aligned}$$

In order to see that $M_{1}^{\nu ,\varepsilon ,\eta ,N} \supseteq M_{0}^{\nu ,\eta ,N} \cap M_{2}^{\beta ,\nu} \cap M_{3}^{\nu ,\eta ,N}$, we assume to the contrary that there exists

$$ \omega \in ( M_{0}^{\nu ,\eta ,N} \cap M_{2}^{\beta ,\nu} \cap M_{3}^{ \nu ,\eta ,N} ) \backslash M_{1}^{\nu ,\varepsilon ,\eta ,N}. $$

To obtain the desired contradiction, we show that for any such $\omega$, there exists a time $s(\omega ) \in [T-\nu ,T)$ for which we can deduce both nonnegativity and strict negativity of $\partial _{t} \hat{X}^{\eta ,N}_{s(\omega )}(\omega )$ simultaneously.

We start with the choice of $s(\omega )$. Because we have $\omega \notin M_{1}^{\nu ,\varepsilon ,\eta ,N}$, there exists some $t \in [T-\nu ,T)$ with $\hat{X}^{\eta ,N}_{t}(\omega ) - \hat{X}^{0}_{t}(\omega ) > \varepsilon$. Since $\omega \in M_{2}^{\beta ,\nu}$ and due to (3.6), this yields that

$$\begin{aligned} \hat{X}^{\eta ,N}_{t}(\omega ) > \hat{X}^{0}_{T-\nu}(\omega ) + \frac {2\varepsilon }{3}. \end{aligned}$$

Since $\omega$ belongs to $M_{0}^{\nu ,\eta ,N}$ and due to (3.6), this implies that

$$\begin{aligned} \hat{X}^{\eta ,N}_{T-\nu}(\omega ) < \hat{X}^{0}_{T-\nu}(\omega ) + \frac{2\varepsilon }{3} < \hat{X}^{\eta ,N}_{t}(\omega ). \end{aligned}$$

Now we can choose $s(\omega ) \in (T-\nu ,t)$ minimal with the property that

$$\begin{aligned} \hat{X}^{\eta ,N}_{s(\omega )}(\omega ) = \hat{X}^{0}_{T-\nu}(\omega ) + \frac{2\varepsilon }{3}. \end{aligned}$$

(3.7)

Due to the minimality of $s(\omega )$, we have $\partial _{t} \hat{X}^{\eta ,N}_{s(\omega )}(\omega ) \ge 0$.

We now show that this derivative must also be strictly negative. In fact, due to (3.4),

$$\begin{aligned} \sqrt {\eta}\partial _{t} \hat{X}^{\eta ,N}_{s(\omega )}(\omega ) &= - F^{ \eta ,N}_{s(\omega )}(\omega ) \hat{X}^{\eta ,N}_{s(\omega )}(\omega ) + E^{\eta ,N}_{s(\omega )}(\omega ) \hat{Z}^{\eta ,N}_{s(\omega )}( \omega ). \end{aligned}$$

Since $\hat{Z}^{\eta ,N}$ is nonincreasing (Theorem 2.2), using (3.7) again, the right-hand side of the above equation can be bounded from above by

$$\begin{aligned} & - \varphi _{T-\nu}(\omega ) \hat{X}^{0}_{T-\nu}(\omega ) + \big( \varphi _{T-\nu}(\omega ) - \varphi _{s(\omega )}(\omega ) \big) \hat{X}^{0}_{T-\nu}(\omega ) - f^{\eta ,N}_{s(\omega )}(\omega ) \hat{X}^{0}_{T-\nu}(\omega ) \\ & - F^{\eta ,N}_{s(\omega )}(\omega ) \frac{2\varepsilon }{3} + E^{0}_{T- \nu}(\omega ) \hat{Z}^{0}_{T-\nu}(\omega ) + E^{0}_{T-\nu}(\omega ) \big( \hat{Z}^{\eta ,N}_{T-\nu}(\omega ) - \hat{Z}^{0}_{T-\nu}(\omega ) \big) \\ & + \big( E^{0}_{s(\omega )}(\omega ) - E^{0}_{T-\nu}(\omega ) \big) \hat{Z}^{\eta ,N}_{T-\nu}(\omega ) + e^{\eta ,N}_{s(\omega )}(\omega ) \hat{Z}^{\eta ,N}_{T-\nu}(\omega ). \end{aligned}$$

Since $\omega \in M_{3}^{\nu ,\eta ,N}$, we have $F^{\eta ,N}_{s(\omega )}(\omega ) = \varphi _{s(\omega )}(\omega ) + f^{\eta ,N}_{s(\omega )}(\omega ) \ge \underline{\varphi}- \nu$, which is strictly positive if $\nu < \underline{\varphi}$. Moreover, we have $- \varphi \hat{X}^{0} + E^{0} \hat{Z}^{0} = 0$ on $[0,T)$. Because also $\omega \in M_{0}^{\nu ,\eta ,N} \cap M_{2}^{\beta ,\nu} \cap M_{3}^{ \nu ,\eta ,N}$ and $\hat{X}^{0}$, $E^{0}$ and $\hat{Z}^{\eta ,N}$ are bounded, this shows that $\partial _{t} \hat{X}^{\eta ,N}_{s(\omega )}(\omega ) < 0$ if $\nu$ and $\beta$ are chosen small enough. The convergence of $\hat{Y}^{\eta ,N} - \hat{Y}^{0}$ on $[0,T-]$ follows from

$$\begin{aligned} \hat{Y}^{\eta ,N} - \hat{Y}^{0} = \gamma ( \hat{X}^{\eta ,N} - \hat{X}^{0} ) - ( \hat{Z}^{\eta ,N} - \hat{Z}^{0} ) \end{aligned}$$

and (3.5). The convergence on $[T-,T]$ follows from the fact that

$$\begin{aligned} \sup _{s\in [T-\nu ,T]} | ( \hat{Z}^{\eta ,N}_{s} - \hat{Z}^{0}_{s} ) - ( \hat{Z}^{\eta ,N}_{T-\nu} - \hat{Z}^{0}_{T-\nu} ) | \end{aligned}$$

can be made arbitrarily small by choosing $\nu$ small since $\partial _{t} \hat{Z}^{\eta ,N} = \rho \hat{Y}^{\eta ,N}$, $\partial _{t} \hat{Z}^{0} = \rho \hat{Y}^{0}$ and both $\hat{Y}^{\eta ,N}$ and $\hat{Y}^{0}$ are bounded. □

3.2.3 Proof of Proposition 2.8

The proof of the convergence of the optimal portfolio processes in the Skorohod $\mathcal {M}_{2}$-sense follows from Theorem 2.7 if strict liquidation is required. If strict liquidation is not required, the results of Sect. 2.2 are required to establish the assertion. This is not a circular argument since the proofs of Sect. 2.2 only use the results of Sect. 2.1 concerning the liquidating case $N=\infty$.

Since $\hat{\theta}=(0,\hat{j}^{-}, \hat{V})$ is optimal in the model introduced in Sect. 2.2 (cf. Theorem 2.15), it is easy to show that the strategy $\hat{\theta}^{q}:=(\hat{j}^{+,q},\hat{j}^{-,q},\hat{V}^{q})$ is admissible for every $q \in \mathbb{R}$, where

$$\begin{array}{rl}{\hat{V}}_t^q& ={\hat{V}}_t+qt,\\ {\hat{j}}_t^{+,q}-{\hat{j}}_t^{-,q}& =-{\hat{j}}_t^{-}-{\mathbb{1}}_{\{T\}}(t)qT.\end{array}$$

The following lemma shows that we can express the cost term corresponding to the transient price impact without Itô integrals. The proof is an immediate consequence of Itô’s formula for semimartingales (see Protter [32, Theorem II.32]) and the fact that $\gamma ^{2} [V]$ is equal to the continuous part of $[Y^{\theta}]$. We omit it.

Lemma 3.10

For all $\theta = (j^{+},j^{-},V) \in \mathcal {A}^{0}$ and all $t \in [0,T]$, it holds that

$$ \int _{(0,t]} \frac {1}{2} ( Y^{\theta}_{s-} + Y^{\theta}_{s} ) \, \mathrm {d}X^{\theta}_{s} = \frac {1}{2\gamma} (Y^{\theta}_{t} )^{2} - \frac {\gamma }{2} (j^{+}_{0} - j^{-}_{0})^{2} - \frac {\gamma }{2} [V]_{t} + \frac {1}{\gamma }\int ^{t}_{0} \rho _{s} (Y^{\theta}_{s} )^{2} \, \mathrm {d} s. $$

Using Lemma 3.10, it is not difficult to check that the mapping $q \mapsto J^{0}(\hat{\theta}^{q})$ is differentiable and that

$$\begin{aligned} 0 & = \frac {\partial J^{0}(\hat{\theta}^{q})}{\partial q} \bigg|_{q=0} \\ &= \mathbb{E}\bigg[ - \hat{Y}^{0}_{T} e^{-\int ^{T}_{0} \rho _{u} \, \mathrm {d} u} \int ^{T}_{0} t \rho _{t} e^{\int _{0}^{t} \rho _{u} \, \mathrm {d} u} \, \mathrm {d} t+ \int ^{T}_{0} 2 t \rho _{t} \hat{Y}^{0}_{t} \, \mathrm {d} t \\ & \hphantom{=:\mathbb{E}\bigg[} - \int ^{T}_{0} 2 \rho _{t} \hat{Y}^{0}_{t} e^{-\int ^{t}_{0} \rho _{u} \, \mathrm {d} u} \int ^{t}_{0} s \rho _{s} e^{\int _{0}^{s} \rho _{u} \, \mathrm {d} u} \, \mathrm {d} s\, \mathrm {d} t+ \int ^{T}_{0} t \lambda _{t} \hat{X}^{0}_{t} \, \mathrm {d} t\bigg]. \end{aligned}$$

(3.8)

This allows us to prove that full liquidation is optimal if $\eta \to 0$ even if it is not formally required.

Lemma 3.11

We have that $\lim _{\eta \to 0} \sup _{N\in \mathcal {N}} \mathbb{E}[\hat{X}^{\eta ,N}_{T}] = 0$.

Proof

We assume to the contrary that $\limsup _{\eta \to 0} \sup _{N\in \mathcal {N}} \mathbb{E}[\hat{X}^{ \eta ,N}_{T}] > 0$ and prove that this contradicts the optimality of $J^{\eta ,N}(\hat{\xi}^{\eta ,N})$. To this end, we consider the admissible trading strategies

$$\begin{aligned} \hat{\xi}^{\eta ,N,q}_{t} := \hat{\xi}^{\eta ,N}_{t} + q, \end{aligned}$$

compute the derivative of the function $q \mapsto J^{\eta ,N}(\hat{\xi}^{\eta ,N,q})$ and show that the derivative at $q=0$ does not vanish for small $\eta$ if

$$\begin{aligned} \limsup _{\eta \to 0} \sup _{N\in \mathcal {N}} \mathbb{E}[ \hat{X}^{ \eta ,N}_{T} ] > 0. \end{aligned}$$

Obviously, $\hat{\xi}^{\eta ,N,q} \in \mathcal {A}$ and

$$\begin{aligned} \hat{X}^{\eta ,N,q}_{t} := X^{\hat{\xi}^{\eta ,N,q}}_{t} = \hat{X}^{ \eta ,N}_{t} + q t. \end{aligned}$$

Straightforward computations lead to

$$\begin{aligned} 0 &= \frac {\partial J^{\eta ,N}(\hat{\xi}^{\eta ,N,q})}{\partial q} \bigg|_{q=0} \\ &= \mathbb{E}\bigg[ \eta ( \hat{X}^{\eta ,N}_{T} - x_{0} ) - \hat{Y}^{ \eta ,N}_{T} e^{ -\int ^{T}_{0} \rho _{u} \, \mathrm {d} u} \int ^{T}_{0} t \rho _{t} e^{ \int _{0}^{t} \rho _{u} \, \mathrm {d} u} \, \mathrm {d} t+ \int ^{T}_{0} 2 t \rho _{t} \hat{Y}^{\eta ,N}_{t} \, \mathrm {d} t \\ & \hphantom{=:\mathbb{E}\bigg[} - \int ^{T}_{0} 2 \rho _{t} \hat{Y}^{\eta ,N}_{t} e^{ -\int ^{t}_{0} \rho _{u} \, \mathrm {d} u} \int ^{t}_{0} s \rho _{s} e^{\int _{0}^{s} \rho _{u} \, \mathrm {d} u} \, \mathrm {d} s\, \mathrm {d} t+ \int ^{T}_{0} t \lambda _{t} \hat{X}^{\eta ,N}_{t} \, \mathrm {d} t \\ & \hphantom{=:\mathbb{E}\bigg[} + (N - \gamma ) T \hat{X}^{\eta ,N}_{T} + \gamma \hat{X}^{\eta ,N}_{T} e^{ -\int ^{T}_{0} \rho _{u} \, \mathrm {d} u} \int ^{T}_{0} t \rho _{t} e^{ \int _{0}^{t} \rho _{u} \, \mathrm {d} u} \, \mathrm {d} t\bigg]. \end{aligned}$$

Subtracting (3.8) yields

$$\begin{aligned} 0 &= \mathbb{E}\bigg[ - \eta x_{0} + \hat{X}^{\eta ,N}_{T} \big( \eta + (N - \gamma ) T \big) + \int ^{T}_{0} 2 t \rho _{t} ( \hat{Y}^{\eta ,N}_{t} - \hat{Y}^{0}_{t} ) \, \mathrm {d} t \\ & \hphantom{=:\mathbb{E}\bigg[} + ( \hat{Z}^{\eta ,N}_{T} - \hat{Z}^{0}_{T} ) e^{ -\int ^{T}_{0} \rho _{u} \, \mathrm {d} u} \int ^{T}_{0} t \rho _{t} e^{ \int _{0}^{t} \rho _{u} \, \mathrm {d} u} \, \mathrm {d} t+ \int ^{T}_{0} t \lambda _{t} ( \hat{X}^{ \eta ,N}_{t} - \hat{X}^{0}_{t} ) \, \mathrm {d} t \\ & \hphantom{=:\mathbb{E}\bigg[} - \int ^{T}_{0} 2 \rho _{t} ( \hat{Y}^{\eta ,N}_{t} - \hat{Y}^{0}_{t} ) e^{ -\int ^{t}_{0} \rho _{u} \, \mathrm {d} u} \int ^{t}_{0} s \rho _{s} e^{ \int _{0}^{s} \rho _{u} \, \mathrm {d} u} \, \mathrm {d} s\, \mathrm {d} t \bigg] \\ &\ge - \eta x_{0} + \big( \eta + (N - \gamma ) T \big) \mathbb{E}[ \hat{X}^{\eta ,N}_{T} ] - T \overline{\lambda}\mathbb{E}\bigg[ \int ^{T}_{0} | \hat{X}^{\eta ,N}_{t} - \hat{X}^{0}_{t} | \, \mathrm {d} t\bigg] \\ & \hphantom{=:} - 2 ( T \overline{\rho}+ \overline{\rho}^{2} T^{2} e^{ T \overline{\rho}} ) \mathbb{E}\bigg[ \int ^{T}_{0} | \hat{Y}^{\eta ,N}_{t} - \hat{Y}^{0}_{t} | \, \mathrm {d} t\bigg] - T^{2} \overline{\rho}e^{ T \overline{\rho}} \mathbb{E}[ | \hat{Z}^{\eta ,N}_{T} - \hat{Z}^{0}_{T} | ]. \end{aligned}$$

In view of Theorems 2.2 and 2.7, Lemma 3.5 and using

$$\begin{aligned} \partial _{t} ( \hat{Z}^{\eta ,N} - \hat{Z}^{0} ) = \rho ( \hat{Y}^{\eta ,N} - \hat{Y}^{0} ), \end{aligned}$$

the sum of the three last expected values is small uniformly in $N$ if $\eta$ is small. Hence, if $\limsup _{\eta \to 0} \sup _{N \in \mathcal {N}} \mathbb{E}[\hat{X}^{ \eta ,N}_{T}] > 0$, then the sum on the right-hand side of the above inequality is strictly positive when first choosing $\eta _{0}>0$ small enough and then choosing $(\tilde{\eta},\tilde{N})$ with $\tilde{\eta}\le \eta _{0}$ such that

$$ \mathbb{E}[ \hat{X}^{\tilde{\eta},\tilde{N}}_{T} ] \ge \frac {1}{2} \limsup _{\eta \to 0} \sup _{N \in \mathcal {N}} \mathbb{E}[ \hat{X}^{ \eta ,N}_{T} ]. $$

 □

We are now ready to prove the convergence of $\hat{X}^{\eta ,N}$ to $\hat{X}^{0}$ in the Skorohod $\mathcal {M}_{2}$-sense. To this end, we have to bound the distance of each point of any of the graphs to the other graph. In the inner interval $[\varepsilon ,T-\varepsilon ]$, it is enough to consider $\hat{X}^{\eta ,N}-\hat{X}^{0}$, which we have bounded by Theorem 2.7.

Proof

of Proposition 2.8 To prove that the probability of

$$\begin{aligned} d_{\mathcal {M}_{2}} (\hat{X}^{\eta ,N},\hat{X}^{0} ) \le \varepsilon \end{aligned}$$

is large for small $\eta > 0$, we need to prove that the distance of any point $(t,x)$ from either $G_{\hat{X}^{\eta ,N}(\omega )}$ or $G_{\hat{X}^{0}(\omega )}$ to the respective other graph is small on a set of large probability. To this end, we fix a small enough $\nu \in (0,\varepsilon )$. If $t\in [\nu ,T-\nu ]$, the claim follows directly from Theorem 2.7. For $t \in [0,\nu ) \cup (T-\nu ,T]$, we use Theorem 2.7 along with the facts that (i) the completed graph of a discontinuous function contains the line segments joining the values of the function at the points of discontinuity, (ii) the increments of $\hat{X}^{0}$ are small in the sense of Lemma 3.9, and (iii) $\lim _{\eta \to 0} \sup _{N\in \mathcal {N}} \mathbb{E}[\hat{X}^{\eta ,N}_{T}] = 0$ by Lemma 3.11. For instance, consider an $\omega \in \Omega$ with

$$\begin{aligned} \sup _{u \in [0,T-\nu ]} \big( \hat{X}^{0}_{u}(\omega ) - \hat{X}^{ \eta ,N}_{u}(\omega ) \big) \le \nu \end{aligned}$$

and assume that $(t,x) \in G_{\hat{X}^{\eta ,N}(\omega )}$ with $t < \nu$ and $x < \hat{X}^{0}_{0}(\omega ) - \nu$. Since $x = \hat{X}^{\eta ,N}_{t}(\omega )$, the mean value theorem yields an $s \in [0,t]$ such that $\hat{X}^{0}_{s}(\omega ) = x + \nu$, which proves that $(s,x+\nu ) \in G_{\hat{X}^{0}(\omega )}$ and

$$\begin{aligned} d_{\infty }\big( (t,x),(s,x+\nu ) \big) = (t-s) + \nu \le 2 \nu . \end{aligned}$$

 □

4 Proofs for Sect. 2.2

4.1 Proof of Lemma 2.11

In order to prove Lemma 2.11, we first define, for all $\beta ,\nu \in (0,\infty )$ and $x \in \mathbb{R}$,

$$\begin{aligned} f^{\beta ,\nu}(x) := \textstyle\begin{cases} -\beta /\nu , &\quad x \le -\beta , \\ x/\nu , &\quad -\beta \le x \le \beta , \\ \beta /\nu , &\quad x \ge \beta . \end{cases}\displaystyle \end{aligned}$$

For any admissible strategy $(j^{+},j^{-},V) \in \mathcal {A}^{0}$, there exists a unique pathwise differentiable, adapted stochastic process $(\tilde{V}^{\beta ,\nu}_{t})_{t \in [0,T]}$ such that $\tilde{V}^{\beta ,\nu}_{0} = 0$ and its time derivative satisfies

$$\begin{aligned} \dot{V}^{\beta ,\nu}_{t}(\omega ) = f^{\beta ,\nu} \big( V_{t}(\omega ) - \tilde{V}^{\beta ,\nu}_{t}(\omega ) \big). \end{aligned}$$

Now (2.13) can easily be verified by the comparison principle: For all $\varepsilon > 0$ and all $t \in [0,T]$, we have

$$\begin{aligned} f^{\beta ,\nu} \bigg( V_{t} - \Big( \max _{s \in [0,T]} \vert V_{s} \vert + \varepsilon \Big) \bigg) < 0 \end{aligned}$$

and hence, for all $\varepsilon > 0$ and $t \in [0,T]$,

$$\begin{aligned} \tilde{V}^{\beta ,\nu}_{t} \le \max _{s \in [0,T]} \vert V_{s}\vert + \varepsilon . \end{aligned}$$

Analogously, we can prove that $\tilde{V}^{\beta ,\nu}_{t} \ge - \max _{s \in [0,T]} \vert V_{s} \vert - \varepsilon$.

Now we are going to prove (2.14). For $\beta ,\nu \in (0,\infty )$, let

$$\begin{aligned} M := \Big\{ \sup _{s,t\in [0,T], |s-t| \le \nu} | V_{s} - V_{t} | \le \beta \Big\} . \end{aligned}$$

In view of Lemma 3.9, it is enough to prove that

$$\begin{aligned} | V_{t}(\omega ) - \tilde{V}^{\beta ,\nu}_{t}(\omega ) | < 3 \beta \end{aligned}$$

for all $\omega \in M$ and $t\in [0,T]$. In order to see this, let us assume to the contrary that the statement is wrong. Then by continuity, since $V_{0} - \tilde{V}^{\beta ,\nu}_{0} = 0$, there exist some $\omega \in M$ and $t_{1} \in [0,T]$ such that

$$\begin{aligned} | V_{t_{1}}(\omega ) - \tilde{V}^{\beta ,\nu}_{t_{1}}(\omega ) | = 3 \beta . \end{aligned}$$

We choose the smallest such $t_{1} \in [0,T]$. Then for each $t \in [(t_{1}-\nu )^{+},t_{1}]$,

$$\begin{aligned} | V_{t}(\omega ) - \tilde{V}^{\beta ,\nu}_{t}(\omega ) | &\geq | V_{t_{1}}( \omega ) - \tilde{V}^{\beta ,\nu}_{t_{1}}(\omega ) | - | V_{t_{1}}( \omega ) - V_{t}(\omega ) | \\ & \hphantom{=:} - | \tilde{V}^{\beta ,\nu}_{t_{1}}(\omega ) - \tilde{V}^{\beta ,\nu}_{t}( \omega ) | \\ &\ge 3 \beta - \beta - (t_{1} - t) \frac {\beta }{\nu }\ge \beta . \end{aligned}$$

Since $V_{0} - \tilde{V}^{\beta ,\nu}_{0} = 0$, we have $t_{1} > \nu$. Since $V_{\cdot}(\omega ) - \tilde{V}^{\beta ,\nu}_{\cdot}(\omega )$ is continuous and has no roots in $[t_{1}-\nu ,t_{1}]$, it does not change sign on this interval. We may hence without loss of generality assume that $V_{t_{1}}(\omega ) - \tilde{V}^{\beta ,\nu}_{t_{1}}(\omega ) = 3 \beta$. This implies that

$$\begin{aligned} V_{t}(\omega ) - \tilde{V}^{\beta ,\nu}_{t}(\omega ) \ge \beta \end{aligned}$$

for all $t \in [t_{1}-\nu ,t_{1}]$. By definition, for all those $t$, we have $\dot{V}^{\beta ,\nu}_{t}(\omega ) = \beta /\nu$. This, however, contradicts the minimality of $t_{1}$ as $\dot{V}^{\beta ,\nu}_{s} =\beta /\nu$ and

$$\begin{aligned} V_{t_{1}-\nu}(\omega ) - \tilde{V}^{\beta ,\nu}_{t_{1}-\nu}(\omega ) &= V_{t_{1}-\nu}(\omega ) - V_{t_{1}}(\omega ) + V_{t_{1}}(\omega ) - \tilde{V}^{\beta ,\nu}_{t_{1}}(\omega ) \\ & \hphantom{=:} + \tilde{V}^{\beta ,\nu}_{t_{1}}(\omega ) - \tilde{V}^{\beta ,\nu}_{t_{1}- \nu}(\omega ) \\ &\ge - \beta + 3 \beta + \int _{t_{1}-\nu}^{t_{1}} \dot{V}^{\beta ,\nu}_{s} \, \mathrm {d} s= 3 \beta . \end{aligned}$$

This finishes the proof of Lemma 2.11. $\Box$

4.2 Proof of Lemma 2.12

The proof of Lemma 2.12 requires the following result on the jump processes.

Lemma 4.1

Let $(j_{t})_{t\in [0,T]}$ be a $[0,\infty )$-valued, nondecreasing and progressively measurable stochastic process with $\mathbb{E}[(j_{T})^{2}] < \infty$. Then (putting $j_{t} = 0$ for $t < 0$)

$$\begin{aligned} \lim _{\varepsilon \to 0} \mathbb{E}\bigg[ \int ^{T}_{0} (j_{t} - j_{t- \varepsilon })^{2} \, \mathrm {d} t\bigg] = 0. \end{aligned}$$

Proof

First we want to bound $\int ^{T}_{0} (j_{t} - j_{t-\varepsilon })^{2} \, \mathrm {d} t$ through a term that depends on $\int ^{T}_{0} (j_{t} - j_{t-2\varepsilon })^{2} \, \mathrm {d} t$ and apply this bound inductively. For every $\varepsilon > 0$, we have

$$\begin{aligned} \int ^{T}_{0} (j_{t} - j_{t-2\varepsilon })^{2} \, \mathrm {d} t& = \int ^{T}_{0} (j_{t} - j_{t-\varepsilon } + j_{t-\varepsilon } - j_{t-2 \varepsilon })^{2} \, \mathrm {d} t \\ &\ge \int ^{T}_{0} (j_{t} - j_{t-\varepsilon })^{2} \, \mathrm {d} t+ \int _{0}^{T-\varepsilon } ( j_{t} - j_{t-\varepsilon } )^{2} \, \mathrm {d} t \\ & = 2\int ^{T}_{0} (j_{t} - j_{t-\varepsilon })^{2} \, \mathrm {d} t- \int _{T-\varepsilon }^{T} ( j_{t} - j_{t-\varepsilon } )^{2} \, \mathrm {d} t. \end{aligned}$$

Moreover, $j_{t} \leq j_{T}$ and $j_{t-\varepsilon } \geq j_{T-\varepsilon -\varepsilon }$ for $t \in [T-\varepsilon , T]$ give

$$\begin{aligned} \int _{T-\varepsilon }^{T} ( j_{t} - j_{t-\varepsilon } )^{2} \, \mathrm {d} t\le \int _{T-\varepsilon }^{T} ( j_{T} - j_{T-2 \varepsilon } )^{2} \, \mathrm {d} t\le \varepsilon ( j_{T} - j_{T-2 \varepsilon } )^{2}. \end{aligned}$$

As a result,

$$\begin{aligned} \frac {1}{\varepsilon }\int ^{T}_{0} (j_{t} - j_{t-\varepsilon })^{2} \, \mathrm {d} t\le \frac {1}{2\varepsilon } \int ^{T}_{0} (j_{t} - j_{t-2 \varepsilon })^{2} \, \mathrm {d} t+ \frac {1}{2} ( j_{T} - j_{T-2 \varepsilon } )^{2}. \end{aligned}$$

Hence, inductively, for all $\varepsilon \in (0,T)$ and $k \in \{1,2,\ldots \}$, we have

$$\begin{aligned} \frac {1}{\varepsilon } \int ^{T}_{0} (j_{t} - j_{t-\varepsilon })^{2} \, \mathrm {d} t& \le \frac {1}{2 \varepsilon } \int ^{T}_{0} (j_{t} - j_{t-2 \varepsilon })^{2} \, \mathrm {d} t+ \frac {1}{2} ( j_{T} - j_{T-2 \varepsilon } )^{2} \\ & \le \frac {1}{4\varepsilon } \int ^{T}_{0} (j_{t} - j_{t-4 \varepsilon })^{2} \, \mathrm {d} t+ \frac {1}{4} ( j_{T} - j_{T-4 \varepsilon } )^{2} \\ & \hphantom{=:} + \frac {1}{2} ( j_{T} - j_{T-2\varepsilon } )^{2} \\ & \le \cdots \\ & \le \frac {1}{2^{k}\varepsilon } \int ^{T}_{0} (j_{t} - j_{t-2^{k} \varepsilon })^{2} \, \mathrm {d} t+ \sum _{\ell =1}^{k} \frac {1}{2^{\ell}} ( j_{T} )^{2} \\ & \le \frac {1}{2^{k}\varepsilon } \int ^{T}_{0} (j_{t} - j_{t-2^{k} \varepsilon })^{2} \, \mathrm {d} t+ ( j_{T} )^{2}. \end{aligned}$$

Hence for all $k \in \mathbb{N}$,

$$\begin{aligned} \mathbb{E}\bigg[ \int ^{T}_{0} (j_{t} - j_{t-\varepsilon })^{2} \, \mathrm {d} t\bigg] \le \bigg( \frac {T}{2^{k}} + \varepsilon \bigg) \mathbb{E}[ ( j_{T} )^{2} ]. \end{aligned}$$

This shows the desired result. □

We are now ready to prove the approximation of arbitrary portfolio processes by absolutely continuous ones.

Proof

of Lemma 2.12 By the triangle inequality, for all $\beta ,\nu ,\varepsilon > 0$,

$$\begin{aligned} & \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} ( X^{\theta ,\beta ,\nu , \varepsilon }_{t} - X^{\theta}_{t} )^{2} \, \mathrm {d} t\bigg] } \\ & \le \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \int ^{t}_{(T- \varepsilon )\wedge t} \dot{V}^{\beta ,\nu}_{s} \, \mathrm {d} s\bigg)^{2} \, \mathrm {d} t\bigg] } \\ & \hphantom{=:} + \sum _{* \in \{+,-\}} \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \int _{0}^{(T-\varepsilon )\wedge t} \frac {1}{\varepsilon }(j^{*}_{s} - j^{*}_{s-\varepsilon } ) \, \mathrm {d} s- j^{*}_{t} \bigg)^{2} \, \mathrm {d} t\bigg] } \\ & \hphantom{=:} + \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \frac {1}{\varepsilon }\big(t - (T-\varepsilon ) \big)^{+} X^{ \theta ,\beta ,\nu ,\varepsilon }_{T-\varepsilon } \bigg)^{2} \, \mathrm {d} t\bigg] } \\ & \hphantom{=:} + \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \int ^{t}_{0} \dot{V}^{ \beta ,\nu}_{s} \, \mathrm {d} s- V_{t} \bigg)^{2} \, \mathrm {d} t\bigg] }. \end{aligned}$$

(4.1)

We analyse the four terms separately. The first can be bounded by

$$\begin{aligned} \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \int ^{t}_{(T- \varepsilon )\wedge t} \dot{V}^{\beta ,\nu}_{s} \, \mathrm {d} s\bigg)^{2} \, \mathrm {d} t\bigg] } & \le \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{T- \varepsilon } \bigg( \int ^{t}_{T-\varepsilon } \dot{V}^{\beta ,\nu}_{s} \, \mathrm {d} s\bigg)^{2} \, \mathrm {d} t\bigg] } \\ & \le \frac {\varepsilon ^{\frac {3}{2}} \beta}{\nu } \longrightarrow 0 \qquad \text{for } \varepsilon \to 0. \end{aligned}$$

Regarding the second term, for all $\varepsilon < T/2$,

$$\begin{aligned} \int _{0}^{(T-\varepsilon )\wedge t} \frac {1}{\varepsilon }(j^{*}_{s} - j^{*}_{s-\varepsilon } ) \, \mathrm {d} s- j^{*}_{t} = - \int _{((T- \varepsilon )\wedge t) - \varepsilon }^{(T-\varepsilon )\wedge t} \frac {1}{\varepsilon }(j^{*}_{t} - j^{*}_{s}) \, \mathrm {d} s. \end{aligned}$$

Using the monotonicity of the jump processes, it follows from Lemma 4.1 that

$$\begin{aligned} & \sqrt{\mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \int _{0}^{(T- \varepsilon )\wedge t} \frac {1}{\varepsilon }(j^{*}_{s} - j^{*}_{s- \varepsilon } ) \, \mathrm {d} s- j^{*}_{t} \bigg)^{2} \, \mathrm {d} t \bigg] } \\ &= \sqrt{\mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \int _{((T-\varepsilon ) \wedge t) - \varepsilon }^{(T-\varepsilon )\wedge t} \frac {1}{\varepsilon }(j^{*}_{t} - j^{*}_{s} ) \, \mathrm {d} s\bigg)^{2} \, \mathrm {d} t\bigg] } \\ & \le \frac {1}{\varepsilon }\sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \int _{((T-\varepsilon )\wedge t) - \varepsilon }^{(T- \varepsilon )\wedge t} ( j^{*}_{t} - j^{*}_{s} ) \, \mathrm {d} s\bigg)^{2} \, \mathrm {d} t\bigg] } \\ &= \sqrt{ \mathbb{E}\bigg[ \int _{0}^{T-\varepsilon } ( j^{*}_{t} - j^{*}_{t - \varepsilon } )^{2} \, \mathrm {d} t\bigg] + \mathbb{E}\bigg[ \int _{T- \varepsilon }^{T} ( j^{*}_{t} - j^{*}_{T-2\varepsilon } )^{2} \, \mathrm {d} t\bigg] } \\ & \le \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} ( j^{*}_{t} - j^{*}_{t - \varepsilon } )^{2} \, \mathrm {d} t\bigg] + \varepsilon \mathbb{E}[ ( j^{*}_{T} )^{2} ] } \longrightarrow 0 \qquad \text{ for } \varepsilon \to 0. \end{aligned}$$

(4.2)

For the third term, we conclude from the Itô isometry and the definition of $\xi ^{\theta ,\beta ,\nu ,\varepsilon }$ that

$$\begin{aligned} & \sqrt{\mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \frac {1}{\varepsilon } \big(t - (T-\varepsilon ) \big)^{+} X^{\theta ,\beta ,\nu , \varepsilon }_{T-\varepsilon } \bigg)^{2} \, \mathrm {d} t\bigg]} \\ &= \sqrt{\frac {\varepsilon }{3} \mathbb{E}\bigg[ \bigg( x_{0} + \int _{0}^{T- \varepsilon } \xi ^{\theta ,\beta ,\nu ,\varepsilon }_{s} \, \mathrm {d} s\bigg)^{2} \bigg]} \\ & \le x_{0} \sqrt{\frac {\varepsilon }{3} } + \sum _{* \in \{+,-\}} \sqrt{\frac {\varepsilon }{3} \mathbb{E}\bigg[ \bigg( \int _{0}^{T- \varepsilon } \frac {1}{\varepsilon }( j^{*}_{s} - j^{*}_{s- \varepsilon } ) \, \mathrm {d} s\bigg)^{2} \bigg]} \\ & \hphantom{=:} + \sqrt{\frac {\varepsilon }{3} \mathbb{E}\bigg[ \bigg( \int _{0}^{T- \varepsilon } \dot{V}^{\beta ,\nu}_{s} \, \mathrm {d} s\bigg)^{2} \bigg]}. \end{aligned}$$

Now we can bound

$$\begin{aligned} \sqrt{\frac {\varepsilon }{3} \mathbb{E}\bigg[ \bigg( \int _{0}^{T- \varepsilon } \dot{V}^{\beta ,\nu}_{s} \, \mathrm {d} s\bigg)^{2} \bigg]} \le T \frac {\beta }{\nu }\sqrt{\frac {\varepsilon }{3}} \longrightarrow 0 \qquad \text{for } \varepsilon \to 0. \end{aligned}$$

Moreover, in view of (4.2),

$$\begin{aligned} & \sqrt{\frac {\varepsilon }{3} \mathbb{E}\bigg[ \bigg( \int _{0}^{T- \varepsilon } \frac {1}{\varepsilon }( j^{*}_{s} - j^{*}_{s- \varepsilon } ) \, \mathrm {d} s\bigg)^{2} \bigg]} \\ & = \sqrt{\frac {1}{3} \mathbb{E}\bigg[ \int _{T-\varepsilon }^{T} \bigg( \int _{0}^{(T-\varepsilon )\wedge t} \frac {1}{\varepsilon }( j^{*}_{s} - j^{*}_{s-\varepsilon } ) \, \mathrm {d} s\bigg)^{2} \, \mathrm {d} t \bigg]} \\ & \le \sqrt{\frac {1}{3} \mathbb{E}\bigg[ \int ^{T}_{0} \bigg( \int _{0}^{(T- \varepsilon )\wedge t} \frac {1}{\varepsilon }( j^{*}_{s} - j^{*}_{s- \varepsilon } ) \, \mathrm {d} s- j^{*}_{t} \bigg)^{2} \, \mathrm {d} t \bigg]} + \sqrt{\frac {1}{3} \mathbb{E}\bigg[ \int _{T-\varepsilon }^{T} ( j^{*}_{t} )^{2} \, \mathrm {d} t\bigg]} \\ & \le \frac {1}{\sqrt {3}} \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} ( j^{*}_{t} - j^{*}_{t - \varepsilon } )^{2} \, \mathrm {d} t\bigg] + \varepsilon \mathbb{E}[ ( j^{*}_{T} )^{2} ] } + \sqrt{\frac {\varepsilon }{3} \mathbb{E}[ ( j^{*}_{T} )^{2} ]} \longrightarrow 0 \qquad \text{for $\varepsilon \to 0$}. \end{aligned}$$

It remains to consider the fourth term in (4.1). To this end, let

$$ M^{\beta ,\nu} := \bigg\{ \sup _{t \in [0,T]} \bigg\vert \int ^{t}_{0} \dot{V}^{\beta ,\nu}_{s} \, \mathrm {d} s- V_{t} \bigg\vert \le 3\beta \bigg\} . $$

Then using (2.13) in the last step,

$$\begin{array}{rl}& \sqrt{\mathbb{E}\left[{\int }_0^T{({\int }_0^t{\dot{V}}_s^{\beta ,\nu }\mathrm{d}s-V_t)}^2\mathrm{d}t\right]}\\ & \le \sqrt{\mathbb{E}\left[{\int }_0^T{\mathbb{1}}_{M^{\beta ,\nu }}{({\int }_0^t{\dot{V}}_s^{\beta ,\nu }\mathrm{d}s-V_t)}^2\mathrm{d}t\right]}+\sqrt{\mathbb{E}\left[{\mathbb{1}}_{\mathrm{\Omega }\mathrm{\setminus }{M}^{\beta ,\nu }}{\int }_0^T{(V_t)}^2\mathrm{d}t\right]}\\ & \phantom{=:}+\sqrt{\mathbb{E}\left[{\mathbb{1}}_{\mathrm{\Omega }\mathrm{\setminus }{M}^{\beta ,\nu }}{\int }_0^T{\left({\int }_0^t{\dot{V}}_s^{\beta ,\nu }\mathrm{d}s\right)}^2\mathrm{d}t\right]}\\ & \le 3\beta \sqrt{T}+\sqrt{T\mathbb{E}[{\mathbb{1}}_{\mathrm{\Omega }\mathrm{\setminus }{M}^{\beta ,\nu }}\underset{t\in [0,T]}{max}|V_t{|}^2]}\\ & \phantom{=:}+\sqrt{T\mathbb{E}\left[{\mathbb{1}}_{\mathrm{\Omega }\mathrm{\setminus }{M}^{\beta ,\nu }}\underset{t\in [0,T]}{max}{\left({\int }_0^t{\dot{V}}_s^{\beta ,\nu }\mathrm{d}s\right)}^2\right]}\\ & \le 3\beta \sqrt{T}+2\sqrt{T\mathbb{E}[{\mathbb{1}}_{\mathrm{\Omega }\mathrm{\setminus }{M}^{\beta ,\nu }}\underset{t\in [0,T]}{max}|V_t{|}^2]}.\end{array}$$

By (2.12), the single random variable $\max _{t \in [0,T]} \vert V_{t} \vert ^{2}$ is in $L^{1}$ and hence uniformly integrable. So we can first choose $\beta >0$ small enough, then, according to Lemma 2.11, choose $\nu >0$ small enough such that $\mathbb{P}[\Omega \backslash M^{\beta ,\nu}]$ is sufficiently small, and finally choose $\varepsilon >0$ small enough in order to obtain the desired result. □

4.3 Proof of Lemma 2.13

We start with a technical lemma.

Lemma 4.2

Let $(M,\mathcal {A},\mu )$ be a measure space and $u,v \in \mathcal {L}^{2}(M)$. Then

$$\begin{aligned} \int _{M} | u^{2} - v^{2} | \, \mathrm {d}\mu \le \int _{M} (u-v)^{2} \, \mathrm {d}\mu + 2 \sqrt{ \int _{M} (u-v)^{2} \, \mathrm {d}\mu \int _{M} v^{2} \, \mathrm {d}\mu }. \end{aligned}$$

Proof

Due to the Hölder and triangle inequalities,

$$\begin{aligned} \int _{M} | u^{2} - v^{2} | \, \mathrm {d}\mu &= \sqrt{ \int _{M} (u-v)^{2} \, \mathrm {d}\mu } \sqrt{ \int _{M} (u+v)^{2} \, \mathrm {d}\mu } \\ & \le \sqrt{ \int _{M} (u-v)^{2} \, \mathrm {d}\mu } \bigg( \sqrt{ \int _{M} (u-v)^{2} \, \mathrm {d}\mu } + \sqrt{ \int _{M} (2v)^{2} \, \mathrm {d}\mu } \bigg). \end{aligned}$$

 □

The following technical lemma provides useful estimates for the impact process.

Lemma 4.3

Let $X \in \mathcal {L}_{\mathcal {P}}^{2}(\Omega \times [0,T];\mathbb{R})$. Then the transient price impact process $Y^{X}$ given by (2.1) satisfies $Y^{X} \in \mathcal {L}_{\mathcal {P}}^{2}(\Omega \times [0,T];\mathbb{R})$ and

$$\begin{aligned} &\sqrt{\mathbb{E}[ (Y^{X}_{T} )^{2} ]} \le \gamma \bigg( X_{0} + \sqrt{ \mathbb{E}[ (X_{T})^{2} ]} + \overline{\rho}\exp (T \overline{\rho}) \sqrt{T \mathbb{E}\bigg[ \int ^{T}_{0} (X_{s})^{2} \, \mathrm {d} s \bigg]} \bigg), \end{aligned}$$

(4.3)

$$\begin{aligned} & \sqrt{\mathbb{E}\bigg[ \int ^{T}_{0} ( Y^{X}_{t} )^{2} \, \mathrm {d} t \bigg]} \le \gamma X_{0} \sqrt {T} + \gamma \big( 1 + T \overline{\rho}\exp ( T \overline{\rho}) \big) \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} (X_{t})^{2} \, \mathrm {d} t\bigg] }. \end{aligned}$$

(4.4)

If $X_{0} = 0$, then we additionally have for all $s,t \in [0,T]$ with $s < t$ that

$$\begin{aligned} \sqrt{ \mathbb{E}\bigg[ \int _{s}^{t} ( Y^{X}_{u} )^{2} \, \mathrm {d} u \bigg] } &\le \gamma \overline{\rho}\exp ( T \overline{\rho}) \sqrt{ (t-s) T \mathbb{E}\bigg[ \int _{0}^{s} ( X_{u} )^{2} \, \mathrm {d} u\bigg] } \\ & \hphantom{=:} + \gamma \big( 1 + \overline{\rho}\exp ( T \overline{\rho}) \sqrt{ (t-s) T } \big) \sqrt{ \mathbb{E}\bigg[ \int _{s}^{t} ( X_{u} )^{2} \, \mathrm {d} u\bigg] }. \end{aligned}$$

(4.5)

Proof

Inequality (4.3) follows from the explicit formula

$$ Y^{X}_{t} = \gamma X_{t} - \gamma \exp \bigg( -\int ^{t}_{0} \rho _{u} \, \mathrm {d} u\bigg) \bigg( X_{0} + \int ^{t}_{0} \rho _{s} X_{s} \exp \Big( \int _{0}^{s} \rho _{u} \, \mathrm {d} u\Big) \, \mathrm {d} s \bigg) $$

(4.6)

and the triangle inequality. Moreover,

$$\begin{aligned} & \sqrt{\mathbb{E}\bigg[ \int ^{T}_{0} ( Y^{X}_{t} )^{2} \, \mathrm {d} t \bigg]} \\ &\le \gamma \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} (X_{t})^{2} \, \mathrm {d} t\bigg] } \\ & \hphantom{=:} + \gamma \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} \exp \bigg( -2 \int ^{t}_{0} \rho _{u} \, \mathrm {d} u\bigg) \bigg( X_{0} + \int ^{t}_{0} \rho _{s} X_{s} \exp \Big( \int _{0}^{s} \rho _{u} \, \mathrm {d} u\Big) \, \mathrm {d} s \bigg)^{2} \, \mathrm {d} t\bigg] }. \end{aligned}$$

(4.7)

Substituting the inequality

$$\begin{aligned} &\sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} \exp \bigg( -2 \int ^{t}_{0} \rho _{u} \, \mathrm {d} u\bigg) \bigg( X_{0} + \int ^{t}_{0} \rho _{s} X_{s} \exp \Big( \int _{0}^{s} \rho _{u} \, \mathrm {d} u\Big) \, \mathrm {d} s \bigg)^{2} \, \mathrm {d} t\bigg] } \\ & \le \sqrt{ \mathbb{E}[T (X_{0})^{2} ] } + \overline{\rho}\exp ( T \overline{\rho}) \sqrt{ T \mathbb{E}\bigg[ \bigg( \int ^{T}_{0} |X_{s}| \, \mathrm {d} s\bigg)^{2} \bigg] } \\ & \le X_{0} \sqrt {T} + T \overline{\rho}\exp ( T \overline{\rho}) \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} (X_{s})^{2} \, \mathrm {d} s\bigg] } \end{aligned}$$

into (4.7) yields (4.4). To prove (4.5), let $X_{0} = 0$. Then due to (4.6),

$$\begin{aligned} | Y^{X}_{u} - \gamma X_{u} | \le \gamma \overline{\rho}\exp ( T \overline{\rho}) \int _{0}^{u} | X_{r} | \, \mathrm {d} r \end{aligned}$$

for all $u \in [0,T]$ and so

$$\begin{aligned} \mathbb{E}\bigg[ \int _{s}^{t} (Y^{X}_{u} - \gamma X_{u} )^{2} \, \mathrm {d} u\bigg] \le (t-s) T \gamma ^{2} \overline{\rho}^{2} \exp ( 2 T \overline{\rho}) \mathbb{E}\bigg[ \int ^{t}_{0} (X_{u})^{2} \, \mathrm {d} u\bigg]. \end{aligned}$$

Using the subadditivity of the square root, we now obtain (4.5) from

$$\begin{aligned} & \sqrt{ \mathbb{E}\bigg[ \int _{s}^{t} ( Y^{X}_{u} )^{2} \, \mathrm {d} u \bigg] } \\ &\le \sqrt{ \mathbb{E}\bigg[ \int _{s}^{t} ( Y^{X}_{u} - \gamma X_{u} )^{2} \, \mathrm {d} u\bigg] } + \sqrt{ \mathbb{E}\bigg[ \int _{s}^{t} ( \gamma X_{u})^{2} \, \mathrm {d} u\bigg] } \\ & \le \gamma \overline{\rho}\exp ( T \overline{\rho}) \sqrt{ (t-s) T \mathbb{E}\bigg[ \int _{0}^{s} (X_{u})^{2} \, \mathrm {d} u\bigg] } \\ & \hphantom{=:} + \gamma \overline{\rho}\exp ( T \overline{\rho}) \sqrt{ (t-s) T \mathbb{E}\bigg[ \int _{s}^{t} (X_{u})^{2} \, \mathrm {d} u\bigg] } + \gamma \sqrt{ \mathbb{E}\bigg[ \int _{s}^{t} (X_{u})^{2} \, \mathrm {d} u \bigg] }. \end{aligned}$$

 □

We are now ready to prove our approximation result for the cost functional.

Proof

of Lemma 2.13 For $\theta = (j^{+},j^{-},V) \in \mathcal {A}^{0}$ and $\xi \in \mathcal {A}$,

$$\begin{aligned} & \vert J^{0}(\theta ) - J^{0} (0,0,V^{\xi }) \vert \\ & \le \bigg| \mathbb{E}\bigg[ \frac {\gamma }{2} ( j^{+}_{0} - j^{-}_{0} )^{2} + \int _{(0,T]} \frac {1}{2} ( Y^{\theta}_{t-} + Y^{\theta}_{t} ) \, \mathrm {d}X^{\theta}_{t} - \int ^{T}_{0} Y^{\xi}_{t} \, \mathrm {d}X^{ \xi}_{t} + \frac {\gamma }{2} [V]_{T} \bigg] \bigg| \\ & \hphantom{=:} + \frac {\overline{\lambda}}{2} \mathbb{E}\bigg[ \int ^{T}_{0} | (X^{ \theta}_{t} )^{2} - (X^{\xi}_{t} )^{2} | \, \mathrm {d} t\bigg]. \end{aligned}$$

Due to Lemma 4.2, the last term can be estimated as

$$\begin{aligned} & \mathbb{E}\bigg[ \int ^{T}_{0} | (X^{\theta}_{t} )^{2} - (X^{\xi}_{t} )^{2} | \, \mathrm {d} t\bigg] \\ & \le \mathbb{E}\bigg[ \int ^{T}_{0} ( X^{\theta}_{t} - X^{\xi}_{t} )^{2} \, \mathrm {d} t\bigg] + 2 \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} ( X^{ \theta}_{t} - X^{\xi}_{t} )^{2} \, \mathrm {d} t\bigg] \mathbb{E}\bigg[ \int ^{T}_{0} ( X^{\theta}_{t} )^{2} \, \mathrm {d} t\bigg] }. \end{aligned}$$

Moreover, using first Lemma 3.10 and then Lemmas 4.3 and 4.2, we obtain

$$\begin{aligned} & \bigg| \mathbb{E}\bigg[ \frac {\gamma }{2} ( j^{+}_{0} - j^{-}_{0} )^{2} + \int _{(0,T]} \frac {1}{2} ( Y^{\theta}_{t-} + Y^{\theta}_{t} ) \, \mathrm {d}X^{\theta}_{t} - \int ^{T}_{0} Y^{\xi}_{t} \, \mathrm {d}X^{ \xi}_{t} + \frac {\gamma }{2} [V]_{T} \bigg] \bigg| \\ & = \bigg| \mathbb{E}\bigg[ \frac {\gamma }{2} ( j^{+}_{0} - j^{-}_{0} )^{2} + \frac {1}{2\gamma} (Y^{\theta}_{T} )^{2} - \frac {\gamma }{2} (j^{+}_{0} - j^{-}_{0} )^{2} - \frac {\gamma }{2} [V]_{T} + \frac {1}{\gamma } \int ^{T}_{0} \rho _{t} (Y^{\theta}_{t} )^{2} \, \mathrm {d} t \\ & \hphantom{=:\bigg|\mathbb{E}\bigg[} - \frac {1}{2\gamma} (Y^{\xi}_{T} )^{2} - \frac {1}{\gamma }\int ^{T}_{0} \rho _{t} (Y^{\xi}_{t} )^{2} \, \mathrm {d} t+ \frac {\gamma }{2} [V]_{T} \bigg] \bigg| \\ & \le \frac {1}{2\gamma} \mathbb{E}[ | (Y^{\theta}_{T} )^{2} - (Y^{ \xi}_{T} )^{2} | ] + \frac {\overline{\rho}}{\gamma }\mathbb{E}\bigg[ \int ^{T}_{0} | (Y^{\theta}_{t} )^{2} - (Y^{\xi}_{t} )^{2} | \, \mathrm {d} t\bigg] \\ & \le \bigg( \frac {1}{2} T \gamma \overline{\rho}^{2} e^{2 T \overline{\rho}} + \overline{\rho}\gamma (1 + T \overline{\rho}e^{T \overline{\rho}} )^{2} \bigg) \mathbb{E}\bigg[ \int ^{T}_{0} (X^{\theta}_{t} - X^{\xi}_{t} )^{2} \, \mathrm {d} t\bigg] \\ & \hphantom{=:} + \sqrt {T} \gamma \overline{\rho}e^{T \overline{\rho}} \sqrt{ \mathbb{E} \bigg[ \int ^{T}_{0} (X^{\theta}_{t} - X^{\xi}_{t} )^{2} \, \mathrm {d} t \bigg] } \bigg( x_{0} + \overline{\rho}e^{T \overline{\rho}} \sqrt{T \mathbb{E}\bigg[ \int ^{T}_{0} (X^{\theta}_{t})^{2} \, \mathrm {d} t \bigg]} \bigg) \\ & \hphantom{=:} + 2 \overline{\rho}\big(1 + T \overline{\rho}e^{T \overline{\rho}} \big) \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} (X^{\theta}_{t} - X^{\xi}_{t} )^{2} \, \mathrm {d} t\bigg] } \\ & \hphantom{=:+} \times \bigg( \gamma x_{0} \sqrt {T} + \gamma (1 + T \overline{\rho}e^{T \overline{\rho}} ) \sqrt{ \mathbb{E}\bigg[ \int ^{T}_{0} (X^{\theta}_{t})^{2} \, \mathrm {d} t\bigg] } \bigg). \end{aligned}$$

 □

4.4 Proof of Lemma 2.14

We assume the contrary, i.e., that there exists a constant $c > 0$ such that for all $H > 0$, there exists some $\eta \in (0,H)$ with

$$\begin{aligned} \frac {\eta }{2} \mathbb{E}\bigg[ \int _{0}^{T} ( \hat{\xi}^{\eta , \infty}_{t} )^{2} \, \mathrm {d} t\bigg] > c. \end{aligned}$$

(4.8)

The optimality of $\hat{\xi}^{\eta ,\infty}$ and (2.15) imply that for all $\eta ,\nu ,\beta ,\varepsilon > 0$,

$$\begin{aligned} 0 &\ge J^{\eta ,\infty} (\hat{\xi}^{\eta ,\infty} ) - J^{\eta ,\infty} ( \xi ^{\hat{\theta},\beta ,\nu ,\varepsilon } ) \\ &= \frac {\eta }{2} \mathbb{E}\bigg[ \int _{0}^{T} ( \hat{\xi}^{\eta , \infty}_{t} )^{2} \, \mathrm {d} t\bigg] - \frac {\eta }{2} \mathbb{E} \bigg[ \int _{0}^{T} ( \xi ^{\hat{\theta},\beta ,\nu ,\varepsilon }_{t} )^{2} \, \mathrm {d} t\bigg] \\ & \hphantom{=:} + J^{0} ( 0,0,V^{\hat{\xi}^{\eta ,\infty}} ) - J^{0} ( \hat{\theta}) + J^{0} ( \hat{\theta}) - J^{0} ( 0, 0, V^{\xi ^{\hat{\theta},\beta ,\nu , \varepsilon }} ). \end{aligned}$$

(4.9)

We now prove that (4.8) contradicts (4.9). By Theorem 2.13 and since $|\hat{X}^{0}_{t}| \le x_{0}$, we obtain (for convenience, let $p(x) := x + \sqrt {x}$)

$$\begin{aligned} | J^{0} ( 0,0,V^{\hat{\xi}^{\eta ,\infty}} ) - J^{0} ( \hat{\theta}) | \le D \big( T (x_{0})^{2} \big) p \bigg( \mathbb{E}\bigg[ \int ^{T}_{0} ( \hat{X}^{\eta ,\infty}_{t} - \hat{X}^{0}_{t} )^{2} \, \mathrm {d} t \bigg] \bigg) \end{aligned}$$

and

$$\begin{aligned} | J^{0} ( \hat{\theta}) - J^{0} ( 0, 0, V^{\xi ^{\hat{\theta},\beta , \nu ,\varepsilon }} ) | \le D \big( T (x_{0})^{2} \big) p \bigg( \mathbb{E}\bigg[ \int ^{T}_{0} ( X^{\hat{\theta}}_{t} - X^{\hat{\theta}, \beta ,\nu ,\varepsilon }_{t} )^{2} \, \mathrm {d} t\bigg] \bigg). \end{aligned}$$

Plugging the results into (4.9) yields that for all $\eta > 0$ that satisfy (4.8), we have

$$\begin{aligned} 0 &> c - \frac {\eta }{2} \mathbb{E}\bigg[ \int _{0}^{T} ( \xi ^{ \hat{\theta},\beta ,\nu ,\varepsilon }_{t} )^{2} \, \mathrm {d} t\bigg] \\ & \hphantom{=:} - D \big( T (x_{0})^{2} \big) \bigg( p \Big( \mathbb{E}\Big[ \int ^{T}_{0} ( \hat{X}^{\eta ,\infty}_{t} - \hat{X}^{0}_{t} )^{2} \, \mathrm {d} t \Big] \Big) \\ & \hphantom{=:- D \big( T (x_{0})^{2} \big) \bigg(} + p \Big( \mathbb{E}\Big[ \int ^{T}_{0} ( X^{\hat{\theta}}_{t} - X^{ \hat{\theta},\beta ,\nu ,\varepsilon }_{t} )^{2} \, \mathrm {d} t\Big] \Big) \bigg). \end{aligned}$$

(4.10)

Due to Lemma 2.12, we can first choose $\beta , \nu , \varepsilon > 0$ sufficiently small to get

$$\begin{aligned} D \big( T (x_{0})^{2} \big) p \bigg( \mathbb{E}\bigg[ \int ^{T}_{0} ( X^{ \hat{\theta}}_{t} - X^{\hat{\theta},\beta ,\nu ,\varepsilon }_{t} )^{2} \, \mathrm {d} t\bigg] \bigg) < \frac {c}{2}. \end{aligned}$$

Since $|\hat{X}^{\eta ,\infty}_{t}| \le x_{0}$ (cf. Theorem 2.2) and in view of Theorem 2.7, we can then choose $\eta > 0$ sufficiently small and satisfying (4.8) such that the right-hand side of (4.10) is larger than zero, which is a contradiction. This finishes the proof of Lemma 2.14.

Appendices

Appendix A: Regularity properties of Itô processes and BSDEs

In this appendix, we introduce some regularity properties of stochastic processes, which we use to prove various convergence results for stochastic processes.

We consider a continuous, adapted, $\mathbb{R}^{d}$-valued stochastic process $Y = (Y_{t})_{t\in I}$ on some interval $I$ (i.e., a convex subset of ℝ) and introduce the following continuity conditions.

Condition A.1

For all $\varepsilon \in (0,\infty )$, there exists $\delta \in (0,\infty )$ such that for all $s \in I$, $\mathcal {F}_{s}$-measurable and integrable $V \colon \Omega \to \mathbb{R}$ and stopping times $\tau \colon \Omega \to [s,s+\delta ]\,\cap \, I$,

$$ \vert \mathbb{E}[ V ( Y_{\tau }- Y_{s} ) ] \vert \le \varepsilon \mathbb{E}[ |V| ]. $$

Condition A.2

For all $\varepsilon \in (0,\infty )$, there exists $\delta \in (0,\infty )$ such that for all $s \in I$,

$$ \mathbb{E}\Big[ \sup _{t\in [s,s + \delta ]\cap I} \vert Y_{t} - Y_{s} \vert \Big| \mathcal {F}_{s} \Big] \le \varepsilon . $$

Definition A.3

A family of stochastic processes is said to uniformly satisfy Condition A.1 or A.2 on $I$ if all processes satisfy the respective property and $\delta$ can be chosen uniformly for all processes.

In what follows, we list some auxiliary results.

Lemma A.4

An $\mathbb{R}^{d}$-valued stochastic process $Y = ((Y^{1}_{t},\ldots ,Y^{d}_{t}))_{t\in I}$ satisfies Condition A.1 (resp. Condition A.2) if and only if all components $Y^{i}$ satisfy Condition A.1 (resp. Condition A.2).

Lemma A.5

Condition A.2implies Condition A.1.

Proof

Due to Lemma A.4, it is enough to consider a real-valued $Y$. To show the assertion, we then calculate

$$ | \mathbb{E}[ V ( Y_{\tau }- Y_{s} ) ] | = \big| \mathbb{E}\big[ V \mathbb{E}[ Y_{\tau }- Y_{s} | \mathcal {F}_{s} ] \big] \big| \le \mathbb{E}\Big[ |V| \mathbb{E}\big[ | Y_{\tau }- Y_{s} | \big| \mathcal {F}_{s} \big] \Big] \le \mathbb{E}[ |V| ] \varepsilon . $$

 □

Remark A.6

If we want to bound a term of the form $|\mathbb{E}[{\mathbb{1}}_N(Y_{\tau }-Y_s)]|$ for some $N \subseteq M \in \mathcal {F}_{s}$ with $N \notin \mathcal {F}_{s}$, then Condition A.1 is not enough; in this case, we need the stronger Condition A.2.

Lemma A.7

Let $X = (X_{t})_{t\in I}$ and $Y = (Y_{t})_{t\in I}$ be continuous, adapted, real-valued processes which satisfy Condition A.1 (resp. Condition A.2). Then $X + Y$ satisfies Condition A.1 (resp. Condition A.2).

Theorem A.8

Let $X = (X_{t})_{t\in I}$ and $Y = (Y_{t})_{t\in I}$ be continuous, adapted, essentially bounded, real-valued processes. Then:

– If $X$ satisfies Condition A.2and $Y$ satisfies Condition A.1, then $X Y$ satisfies Condition A.1.

– If $X$ and $Y$ both satisfy Condition A.2, then $X Y$ also satisfies Condition A.2.

Proof

The second part of the statement can be proved directly via

$$ |X_{t} Y_{t} - X_{s} Y_{s}| \le |X_{t}| |Y_{t} - Y_{s}| + |Y_{s}| |X_{t} - X_{s}|. $$

The first part of the statement follows from

$$\begin{aligned} & | \mathbb{E}[ V ( X_{\tau }Y_{\tau }- X_{s} Y_{s} ) ] | \le | \mathbb{E}[ V Y_{\tau }(X_{\tau }- X_{s}) ] | + | \mathbb{E}[ V X_{s} (Y_{ \tau }- Y_{s}) ] |. \end{aligned}$$

 □

Next, we prove some properties of the concave envelope of the modulus of continuity of a uniformly continuous function. We use these results to show that a uniformly continuous function of an Itô process with bounded coefficients satisfies Condition A.2.

Lemma A.9

Let $(X,\Vert \cdot \Vert _{X})$ be a normed space with a nonempty and convex subset $D$, let $(Y,d_{Y})$ be a metric space, let $f\colon D \to Y$ and for every $t \in [0,\infty )$, let

$$\begin{aligned} \tilde{\omega}_{f}(t) &:= \sup _{x_{1},x_{2} \in D, \Vert x_{1}-x_{2} \Vert _{X} \le t} d_{Y}\big( f(x_{1}),f(x_{2}) \big), \\ \omega _{f}(t) &:= \inf \{ \psi (t) : \psi \colon [0,\infty ) \to [0, \infty ) \, \textit{is concave and} \, \psi \ge \tilde{\omega}_{f} \}. \end{aligned}$$

Then $\tilde{\omega}_{f} \colon [0,\infty ) \to [0,\infty ]$ is nondecreasing and satisfies $\tilde{\omega}_{f}(0) = 0$, and for all $s,t \in [0, \infty )$ with $s > 0$, we have

$$\begin{aligned} \tilde{\omega}_{f}(t) \le \frac{t+s}{s} \tilde{\omega}_{f}(s). \end{aligned}$$

(A.1)

If $\tilde{\omega}_{f}$ is finite-valued, then $\omega _{f}$ takes values in $[0,\infty )$, is concave, nondecreasing and for all $x_{1},x_{2} \in D$,

$$ d_{Y}\big( f(x_{1}),f(x_{2}) \big) \le \omega _{f} ( \Vert x_{1} - x_{2} \Vert _{X} ). $$

(A.2)

If $f$ is uniformly continuous, then $\tilde{\omega}_{f}$ is finite-valued, $\tilde{\omega}_{f}$ and $\omega _{f}$ are continuous in 0 and $\omega _{f}(0) = 0$.

Proof

By definition, $\tilde{\omega}_{f}$ is nondecreasing and satisfies $\tilde{\omega}_{f}(0)=0$. To prove (A.1), let $s,t\in [0, \infty )$ with $s > 0$ and $x_{1},x_{2} \in D$ with $\Vert x_{1}-x_{2}\Vert _{X} \le t$. Let $N := \lceil t/s \rceil$ and

$$\begin{aligned} x^{k} := \frac {k}{N} x_{1} + \frac {N-k}{N} x_{2} \qquad \text{for $k=0,\ldots ,N$}. \end{aligned}$$

Then $x^{k} \in D$ because $D$ is convex and $\Vert x^{k} - x^{k+1} \Vert _{X} = \frac {1}{N} \Vert x_{1} - x_{2} \Vert _{X} \le s$. Hence

$$\begin{aligned} d_{Y}\big( f(x_{1}),f(x_{2}) \big) &\le \sum _{k=0}^{N-1} d_{Y}\big( f(x^{k}), f(x^{k+1}) \big) \\ &\le N \max _{k} \tilde{\omega}_{f} (\Vert x^{k} - x^{k+1} \Vert _{X} ) \le (t + s) \frac {\tilde{\omega}_{f}(s)}{s}. \end{aligned}$$

Having established (A.1), we know that if $\tilde{\omega}_{f}$ is finite-valued, then it is bounded above by an affine (hence concave) function. In particular, the concave envelope is well defined and satisfies (A.2). Concavity and monotonicity of $\omega _{f}$ are clear. Finally, uniform continuity of $f$ implies that $\tilde{\omega}_{f}$ is finite-valued and continuous in 0. In order to see $\omega _{f}(0) = 0$ and continuity of $\omega _{f}$ in 0, let $\varepsilon > 0$ be arbitrary and let $\delta > 0$ be such that $\tilde{\omega}_{f}(\delta ) \le \varepsilon /2$. Due to (A.1), $\tilde{\omega}_{f}$ and hence $\omega _{f}$ is bounded above by the affine and hence concave function $t \mapsto ((t+\delta )/\delta ) (\varepsilon /2)$. In particular, for all $t \le \delta$, we obtain $\omega _{f}(t) \le \varepsilon$. □

Lemma A.10

Let $X = (X_{t})_{t\in I}$ be a continuous, adapted, $\mathbb{R}^{d}$-valued process which satisfies Condition A.2and let $f \colon [0,T] \times \mathbb{R}^{d} \to \mathbb{R}$ be uniformly continuous. Then $(f(t,X_{t}))_{t\in [0,T]}$ also satisfies Condition A.2.

Proof

There exists a function $\omega _{f}$ with the properties listed by Lemma A.9 (with the max-norm $\vert \cdot \vert _{\infty}$ on $[0,T]\times \mathbb{R}^{d}$). Now let $\delta > 0$ be arbitrary. Using (A.2) and the concavity and monotonicity of $\omega _{f}$, we obtain that

$$\begin{aligned} & \mathbb{E}\Big[ \max _{s \le t\le T\wedge (s + \delta )} | f(t,X_{t}) - f(s,X_{s}) | \Big| \mathcal {F}_{s} \Big] \\ & \le \mathbb{E}\Big[ \max _{s \le t\le T\wedge (s + \delta )} \omega _{f} ( |t-s| \vee \vert X_{t} - X_{s} \vert _{\infty }) \Big| \mathcal {F}_{s} \Big] \\ & \le \mathbb{E}\Big[ \omega _{f}\Big( \delta \vee \max _{s \le t\le T \wedge (s + \delta )} \vert X_{t} - X_{s} \vert _{\infty }\Big) \Big| \mathcal {F}_{s} \Big] \\ & \le \omega _{f}\Big( \delta + \mathbb{E}\Big[ \max _{s \le t\le T \wedge (s + \delta )} \vert X_{t} - X_{s} \vert _{\infty }\Big| \mathcal {F}_{s} \Big] \Big). \end{aligned}$$

Since $\omega _{f}$ is continuous in 0 and $X$ satisfies Condition A.2, we can choose $\delta >0$ small enough such that this term is not greater than $\varepsilon$. □

Lemma A.11

Let $(\tilde{\sigma}_{t})_{t\in [0,T]} \in \mathcal {L}^{\infty}_{\mathcal {P}}( \Omega \times [0,T];\mathbb{R}^{m})$. Then $(\int ^{t}_{0} \tilde{\sigma}_{u} \, \mathrm {d}W_{u})_{t\in [0,T]}$ satisfies Condition A.2.

Proof

Let $\overline{\sigma}> 0$ be a componentwise bound on $\tilde{\sigma}$. By Jensen’s inequality,

$$\begin{aligned} \mathbb{E}\bigg[ \max _{s \le t\le T\wedge (s + \delta )} \Big| \int ^{t}_{s} \tilde{\sigma}_{u} \, \mathrm {d}W_{u} \Big| \bigg| \mathcal {F}_{s} \bigg] \le \sqrt{ \mathbb{E}\bigg[ \max _{s \le t\le T\wedge (s + \delta )} \Big| \int ^{t}_{s} \tilde{\sigma}_{u} \, \mathrm {d}W_{u} \Big|^{2} \bigg| \mathcal {F}_{s} \bigg] }. \end{aligned}$$

In order to prove that the conditional expectation on the right-hand side is bounded, we apply the classical Doob maximal inequality for the conditional measures with respect to all sets $A \in \mathcal {F}_{s}$ with positive probability and obtain

$$\begin{aligned} \sqrt{ \mathbb{E}\bigg[ \max _{s \le t\le T\wedge (s + \delta )} \Big| \int ^{t}_{s} \tilde{\sigma}_{u} \, \mathrm {d}W_{u} \Big|^{2} \bigg| \mathcal {F}_{s} \bigg] } \le 2 \sqrt{ \mathbb{E}\bigg[ \Big| \int _{s}^{T \wedge (s + \delta )} \tilde{\sigma}_{u} \, \mathrm {d}W_{u} \Big|^{2} \bigg| \mathcal {F}_{s} \bigg] }. \end{aligned}$$

Then by combining these inequalities and using the Itô isometry for conditional expectations, we finally obtain

$$\begin{aligned} \mathbb{E}\bigg[ \max _{s \le t\le T\wedge (s + \delta )} \Big| \int ^{t}_{s} \tilde{\sigma}_{u} \, \mathrm {d}W_{u} \Big| \bigg| \mathcal {F}_{s} \bigg] \le 2 \sqrt{ m \mathbb{E}\bigg[ \int _{s}^{T\wedge (s + \delta )} m \overline{\sigma}^{2} \, \mathrm {d} u\bigg| \mathcal {F}_{s} \bigg] } \le 2 m \overline{\sigma}\sqrt{ \delta }. \end{aligned}$$

 □

Remark A.12

Obviously, we have the same result for the drift part of an Itô process, i.e., if $\tilde{\mu}\in \mathcal {L}^{\infty}_{\mathrm{Prog}}(\Omega \times [0,T]; \mathbb{R}^{m})$, then $(\int ^{t}_{0} \tilde{\mu}_{u} \, \mathrm {d}u)_{t\in [0,T]}$ satisfies Condition A.2. However, we cannot expect the weaker Condition A.1 under weaker integrability assumptions, as the following example shows. Take $T = 2$, ${\tilde{\mu }}_u:={\mathbb{1}}_{[1,2]}(u)|W_1|$, $\varepsilon := 1$, $\delta \in (0,1)$ arbitrary and $s := 1$, $\tau := 1 + \delta$, $V:={\mathbb{1}}_{\{\delta |W_1|>1\}}$. Then

$$\frac{|\mathbb{E}[V{\int }_1^{1+\delta }{\tilde{\mu }}_u\mathrm{d}u]|}{\mathbb{E}[|V|]}=\frac{\mathbb{E}[{\mathbb{1}}_{\{\delta |W_1|>1\}}\delta |W_1|]|}{\mathbb{E}[{\mathbb{1}}_{\{\delta |W_1|>1\}}]}>1.$$

Finally, we prove that the strong Condition A.2 holds for a certain class of BSDEs driven by forward SDEs. Specifically, we prove that the solution to the BSDE can be expressed as a uniformly continuous function of the forward process and then we apply Lemma A.10. The representation of the solution in terms of a continuous function has already been proved by El Karoui [12].

For all $(t,x) \in [0,T]\times \mathbb{R}^{n}$, we consider on $[t,T]$ the SDE

$$\begin{aligned} \mathrm {d}X^{t,x}_{s} = \tilde{\mu}( s, X^{t,x}_{s} ) \, \mathrm {d} s+ \tilde{\sigma}( s, X^{t,x}_{s} ) \, \mathrm {d}W_{s}, \qquad X^{t,x}_{t} = x, \end{aligned}$$

where $\tilde{\mu}, \tilde{\sigma}\colon [0,T] \times \mathbb{R}^{n} \to \mathbb{R}^{n} \times \mathbb{R}^{n\times m}$ are measurable and bounded and satisfy the Lipschitz condition

$$ \vert (\tilde{\mu}, \tilde{\sigma})(t,x_{1}) - (\tilde{\mu}, \tilde{\sigma})(t,x_{2}) \vert \le L \vert x_{1} - x_{2}\vert . $$

By the previous results, we obtain that $X^{t,x}$ satisfies Condition A.2. Standard computations show that there exists a constant $C \in (0,\infty )$ such that for all $t \in [0,T]$ and $x_{1},x_{2} \in \mathbb{R}^{n}$,

$$\begin{aligned} \mathbb{E}\Big[ \sup _{s\in [t,T]} \vert X^{t,x_{1}}_{s} - X^{t,x_{2}}_{s} \vert ^{2} \Big] \le C \vert x_{1} - x_{2}\vert ^{2}. \end{aligned}$$

(A.3)

Theorem A.13

Let $\Psi \colon \mathbb{R}^{n} \to \mathbb{R}$ be bounded, $\psi \colon [0,T]\times \mathbb{R}^{n}\times \mathbb{R}\to \mathbb{R}$ continuous and bounded and let both functions satisfy the Lipschitz condition

$$ | \Psi (x_{1}) - \Psi (x_{2}) | + | \psi (t,x_{1},y_{1}) - \psi (t,x_{2},y_{2}) | \le L ( \vert x_{1} - x_{2}\vert + \vert y_{1} - y_{2}\vert ). $$

For $(t,x) \in [0,T]\times \mathbb{R}^{n}$, let $(Y^{t,x},Z^{t,x}) \in \mathcal {L}_{\mathcal {P}}^{2}(\Omega \times [0,T]; \mathbb{R}\times \mathbb{R}^{m})$ be the unique solution to the BSDE on $[t,T]$ given by

$$\begin{aligned} - \mathrm {d}Y^{t,x}_{s} = \psi (s, X^{t,x}_{s}, Y^{t,x}_{s} ) \, \mathrm {d} s- Z^{t,x}_{s} \, \mathrm {d}W_{s}, \qquad Y^{t,x}_{T} = \Psi ( X^{t,x}_{T} ) \end{aligned}$$

driven by the forward process $X^{t,x}$ ($Y^{t,x}$ exists due to [12, Theorem 2.1]). Then there exists a uniformly continuous function $h\colon [0,T]\times \mathbb{R}^{n} \to \mathbb{R}$, which does not depend on $(t,x)$, such that

$$\begin{aligned} \mathbb{P}\big[ h (s,X^{t,x}_{s} ) = Y^{t,x}_{s} \textit{ for all } s \in [t,T] \big] = 1. \end{aligned}$$

(A.4)

In particular, the process $Y^{t,x}$ satisfies Condition A.2on $[t,T]$.

Proof

By [12, Theorem 3.4] and the remark following it, there exists a decoupling field $h\colon [0,T]\times \mathbb{R}^{n} \to \mathbb{R}$ that is $1/2$-Hölder continuous in $t$ and locally Lipschitz-continuous in $x$ such that (A.4) holds. It therefore remains to prove the uniform continuity of $h$. Since

$$\begin{aligned} h(t,x) = \mathbb{E}\bigg[ \Psi ( X^{t,x}_{T} ) + \int _{t}^{T} \psi \big(u, X^{t,x}_{u}, h ( u,X^{t,x}_{u} ) \big) \, \mathrm {d} u\bigg], \end{aligned}$$

we see that $h$ is bounded, say $|h| \le \overline{h}$. Then

$$\begin{aligned} \tilde{\omega}_{h}(s,\delta ) := \sup _{\vert x_{1}-x_{2} \vert \le \delta} | h(s,x_{1}) - h(s,x_{2}) | \end{aligned}$$

is finite-valued, and Lemma A.9 therefore allows us to define its concave envelope $\omega _{h}(s,\,\cdot \,)\colon [0,\infty ) \to [0,\infty )$.

Using the Lipschitz-continuity of $\psi$, we obtain for all $x_{1},x_{2} \in \mathbb{R}^{n}$ and $t \in [0,T]$ that

$$\begin{aligned} & | h(t,x_{1}) - h(t,x_{2}) | \\ &\le L \mathbb{E}[ | X^{t,x_{1}}_{T} - X^{t,x_{2}}_{T} | ] \\ & \hphantom{=:} + L \int _{t}^{T} \big( \mathbb{E}[ | X^{t,x_{1}}_{u} - X^{t,x_{2}}_{u} | ] + \mathbb{E}[ \tilde{\omega}_{h} ( u, | X^{t,x_{1}}_{u} - X^{t,x_{2}}_{u} | ) ] \big) \, \mathrm {d} u. \end{aligned}$$

Using (A.3) along with Lemma A.9, if $| x_{1}-x_{2} | \le \delta$, then

$$\begin{aligned} \mathbb{E}[ | X^{t,x_{1}}_{T} - X^{t,x_{2}}_{T} | ] & \le C \delta \end{aligned}$$

and

$$\begin{aligned} \mathbb{E}[ \tilde{\omega}_{h} ( u, \vert X^{t,x_{1}}_{u} - X^{t,x_{2}}_{u} \vert ) ] & \le \omega _{h} ( u, \mathbb{E}[ \vert X^{t,x_{1}}_{u} - X^{t,x_{2}}_{u} \vert ] ) \le \omega _{h}( u, C \delta ) \end{aligned}$$

for some constant $C \in (0,\infty )$ that depends only on $\tilde{\mu}$, $\tilde{\sigma}$ and $L$. In view of (A.1),

$$\begin{aligned} \omega _{h}(u,C\delta ) \le (C+1) \tilde{\omega}_{h}(u,\delta ). \end{aligned}$$

This shows that

$$\begin{aligned} \tilde{\omega}_{h}(t,\delta ) &\le L C \delta + L \int _{t}^{T} \big( C \delta + (C+1) \tilde{\omega}_{h}(u,\delta ) \big) \, \mathrm {d} u \\ &= L C \delta (1 + T-t) + L (C+1) \int _{t}^{T} \tilde{\omega}_{h}(u, \delta ) \, \mathrm {d} u. \end{aligned}$$

Hence Gronwall’s inequality implies that $h$ is uniformly Lipschitz-continuous in the second variable. Since $h$ is uniformly $1/2$-Hölder-continuous in the first variable, this proves the assertion. □

Appendix B: Convergence results for SDEs and random ODEs

In this appendix, we establish three convergence results for stochastic integral equations that are useful to establish the convergence of our coefficient and state processes. In Sect. B.1, we consider sequences of SDEs parametrised by $\eta \to 0$ with “positive feedback”, i.e., sequences of equations that are driven away from their limits. In Sect. B.2, we consider sequences of random ODE systems parametrised by $\eta \to 0$ with “negative feedback”, which are driven towards their limit.

For equations with positive feedback, we require a priori information about the terminal value and the increments of the coefficient processes to be bounded independently of their past (see Conditions A.1 and A.2). These bounds prevent the stochastic process from reaching its terminal value if a large difference between the limit and the pre-limit occurs at some time $s \in (0,T)$. This will imply a.s. uniform convergence. An almost sure statement under negative feedback cannot be expected. Instead, we follow a pathwise approach and establish uniform convergence in probability.

2.1 B.1 SDEs with positive feedback

2.1.1 B.1.1 An equation without scaling

We first consider a family of real-valued, adapted, continuous stochastic processes $b^{\eta}=(b^{\eta}_{t})_{t \in (0,T)}$ that satisfy the integral equation

$$\begin{aligned} \mathrm {d} b^{\eta}_{t} = \big( a ( t, b^{\eta}_{t} ) + q^{\eta}_{t} \big) \, \mathrm {d} t+ \overline{Z}^{\eta}_{t} \, \mathrm {d}W_{t} \qquad \text{on } (0,T), \end{aligned}$$

(B.1)

where $a\colon \Omega \times (0,T) \times \mathbb{R}\to \mathbb{R}$ is adapted and continuous and $(q^{\eta}_{t})_{t\in (0,T)}$ is an adapted, real-valued, continuous stochastic process and

$$ (\overline{Z}^{\eta}_{t})_{t\in (0,T)} \in \mathcal {L}_{\mathrm{Prog}}^{2} \big(\Omega \times (0,T-];\mathbb{R}^{m}\big). $$

Our goal is to prove that the processes $(b^{\eta}_{t})_{t \in (0,T)}$ with terminal conditions $b^{\eta}_{T} = 0$ converge to 0 as $\eta \to 0$ uniformly on $(0,T)$ if the process $q^{\eta}$ does and if the mapping $a$ is such that $b^{\eta}$ is driven away from 0. Intuitively, the last condition makes it impossible for $b^{\eta}$ to return to 0 at the terminal time once it has left a neighbourhood of 0. Specifically, we assume that the following assumption is satisfied.

Assumption B.1

• i) There exists a real constant $\overline{a} > 0$ such that

  $$ \sup _{t \in (0,T)} \sup _{\eta > 0} | a ( t, b^{\eta}_{t} ) | \le \overline{a}. $$

• ii) For all $\varepsilon > 0$, there exists a $\delta > 0$ such that for all $\eta >0$,

  $$ \mathbb{P}\Big[ \sup _{t \in [T-\delta ,T)} | b^{\eta}_{t} | \le \varepsilon \Big] = 1. $$

• iii) There exists a function $\eta _{1} \colon (0,\infty ) \to (0,\infty )$ such that for all $\varepsilon >0$ and $\eta \le \eta _{1}(\varepsilon )$,

  $$\begin{aligned} \mathbb{P}\Big[ \sup _{t \in (0,T-\varepsilon ]} | q^{\eta}_{t} | \le \varepsilon \Big] = 1. \end{aligned}$$

• iv) There exists an $\varepsilon _{1} > 0$ such that

  $$ \inf _{t \in (0,T)} \inf _{b \in [-\varepsilon _{1},\varepsilon _{1}]} b a(t,b) \ge 0. $$

Lemma B.2

Under Assumption B.1, there exists a function $\eta _{0}\colon (0,\infty ) \to (0,\infty )$, which depends only on $\eta _{1}$ and the mapping $\varepsilon \mapsto \delta$ introduced in Assumption B.1 ii), such that for all $\varepsilon >0$ and all $\eta \in (0,\eta _{0}(\varepsilon )]$,

$$\begin{aligned} \mathbb{P}\Big[ \sup _{s \in (0,T)} \big| b^{\eta}_{s} \big| \le \varepsilon \Big] = 1. \end{aligned}$$

Proof

Let $\varepsilon \in (0,\varepsilon _{1}]$. In the first step, we show that there exists an $\eta _{0}(\varepsilon ) > 0$ such that

$$\begin{aligned} \sigma ^{\varepsilon ,\eta} := \inf \{ t \in (0,T) : \mathbb{P}[b^{ \eta}_{s} < -\varepsilon ] = 0 \text{ for all } s \in [t,T) \} \end{aligned}$$

satisfies $\sigma ^{\varepsilon ,\eta} = 0$ for all $\eta \in (0,\eta _{0}(\varepsilon )]$. Since $b^{\eta}$ is continuous, this will imply that for all $\eta \in (0,\eta _{0}(\varepsilon )]$,

$$ \mathbb{P}\Big[ \inf _{s \in (0,T)} b^{\eta}_{s} \ge -\varepsilon \Big] = 1. $$

The other part of the statement can be proved analogously.

We now assume to the contrary that $0 < \sigma ^{\varepsilon ,\eta}$ and prove that this leads to a contradiction if $\eta$ is small enough. For all $s\in (0,T)$ and $\eta \in (0,\infty )$, we can define the stopping time

$$\begin{aligned} \tau ^{s} := \tau ^{s,\varepsilon ,\eta} := \inf \{ u \in [s,T) : b^{ \eta}_{u} = -\varepsilon /2 \}. \end{aligned}$$

By Assumption B.1 ii), there exists a small enough $\delta > 0$ such that for all $s\in (0,T)$ and $\eta \in (0,\infty )$,

$$\begin{aligned} \mathbb{P}[ b^{\eta}_{s} < -\varepsilon , \tau ^{s} > T - \delta ] = 0. \end{aligned}$$

(B.2)

Since $\tau ^{s}$ is a stopping time, the square-integrability of $\overline{Z}^{\eta}$, the optional sampling theorem and Assumption B.1 i), iv), (B.1) and (B.2) yield that for all $s\in (0,\sigma ^{\varepsilon ,\eta})$ and $\eta \in (0,\infty )$,

$$\begin{array}{rl}\frac{\epsilon }{2}\mathbb{P}[b_s^{\eta }<-\epsilon ]& \le \mathbb{E}[{\mathbb{1}}_{\{b_s^{\eta }<-\epsilon \}}(b_{{\tau }^s}^{\eta }-b_s^{\eta })]\\ & =\mathbb{E}\left[{\mathbb{1}}_{\{b_s^{\eta }<-\epsilon \}}\right({\int }_s^{{\tau }^s\wedge {\sigma }^{\epsilon ,\eta }}a(t,b_t^{\eta })\mathrm{d}t\\ & \phantom{=:\mathbb{E}\left[{\mathbb{1}}_{\{b_s^{\eta }<-\epsilon \}}\right(}+{\int }_{{\tau }^s\wedge {\sigma }^{\epsilon ,\eta }}^{{\tau }^s}a(t,b_t^{\eta })\mathrm{d}t+{\int }_s^{{\tau }^s}{q}_t^{\eta }\mathrm{d}t\left)\right].\end{array}$$

Inside the second integral, if $\sigma ^{\varepsilon ,\eta} < \tau ^{s}$, we have $b^{\eta}_{t} \in [-\varepsilon ,-\varepsilon /2]$. Hence

$$\begin{aligned} \begin{aligned} \frac {\varepsilon }{2} \mathbb{P}[b^{\eta}_{s} < -\varepsilon ] \le \mathbb{P}[ b^{\eta}_{s} < -\varepsilon ] \Big( ( \sigma ^{ \varepsilon ,\eta} - s ) \overline{a} + T \sup _{t\in [0,T-\delta ]} | q^{ \eta}_{t} | \Big). \end{aligned} \end{aligned}$$

(B.3)

The assumption $0 < \sigma ^{\varepsilon ,\eta}$ implies that for any $\alpha > 0$, we can find

$$ \sigma ^{\varepsilon ,\eta} - \alpha \le s \le \sigma ^{\varepsilon , \eta} $$

with $\mathbb{P}[ b^{\eta}_{s} < -\varepsilon ] > 0$. However, due to Assumption B.1 ii) and iii), we can choose $\alpha \le \varepsilon /(5\overline{a})$, $\delta \le \varepsilon /(5T)$ and $\eta _{0}(\varepsilon ) < \eta _{1}(\delta )$ such that (B.3) leads to a contradiction because $\mathbb{P}[ b^{\eta}_{s} < -\varepsilon ] > 0$. This implies $0 = \sigma ^{\varepsilon ,\eta}$. □

2.1.2 B.1.2 An equation with scaling

In this section, we establish an abstract convergence result for stochastic processes $(P^{\eta}_{t})_{t \in (0,T)}$ indexed by some parameter $\eta > 0$ that satisfy the integral equation

$$\begin{aligned} \mathrm {d} ( \psi P^{\eta })_{t} = \sqrt{\eta ^{-1}} \big( a (P^{\eta}_{t}, P^{0}_{t} ) + q^{\eta}_{t} \big) \, \mathrm {d} t+ \mathrm {d}L^{\eta}_{t} + \overline{Z}^{\eta}_{t} \, \mathrm {d}W_{t} \qquad \text{on } (0,T), \end{aligned}$$

(B.4)

where $a:\mathbb{R}^{2} \to \mathbb{R}$ is a measurable mapping, $(\psi _{t})_{t\in (0,T)}$, $(P^{\eta}_{t})_{t\in (0,T)}$, $(P^{0}_{t})_{t\in (0,T)}$, $(q^{\eta}_{t})_{t\in (0,T)}$ and $(L^{\eta}_{t})_{t\in (0,T)}$ are adapted, real-valued, continuous stochastic processes and

$$ (\overline{Z}^{\eta}_{t})_{t\in (0,T)} \in \mathcal {L}_{\mathrm{Prog}}^{2} \big(\Omega \times (0,T-];\mathbb{R}^{m}\big). $$

Our goal is to prove that the processes $P^{\eta}$ converge to $P^{0}$ as $\eta \to 0$ uniformly on compact subintervals of $(0,T)$ if the mapping $a$ is such that $P^{\eta}$ is driven away from $P^{0}$ and if the boundary condition $\lim _{t\to T} ( P^{\eta}_{t} - P^{0}_{t} ) \ge 0$ holds. If the integral equation (B.4) holds on the whole interval $(0,T]$, then it is enough to assume that $P^{\eta}_{T} \ge P^{0}_{T}$. When applying the abstract convergence result to the BSDEs (3.2) and (3.3), the former condition holds if $N = \infty$, while the latter holds if $N$ is finite.

Assumption B.3

i) There exist positive constants $\underline{\psi}$, $\overline{\psi}$, $\overline{P}$ such that $\underline{\psi}\le \psi \le \overline{\psi}$, $|P^{0}| \le \overline{P}$ and $P^{\eta }\ge - \overline{P}$. Moreover, there exists a function $\eta _{1} \colon (0,\infty ) \to (0,\infty )$ such that

$$ P^{\eta}|_{\Omega \times (0,T-\varepsilon ]} \le \overline{P} \qquad \text{for all } \varepsilon > 0 \text{ and } \eta \le \eta _{1}( \varepsilon ). $$

ii) One of the following two “boundary conditions” holds:

a) For all $\eta > 0$, there exists a $T_{\eta }< T$ such that

$$ \mathbb{P}\Big[ \inf _{T_{\eta }\le t < T} ( P^{\eta}_{t} - P^{0}_{t} ) \ge 0 \Big] = 1. $$

b) The integral equation (B.4) holds on the whole interval $(0,T]$ and $P^{\eta}_{T} \ge P^{0}_{T}$. Thus in particular, the processes $\psi$, $P^{\eta}$, $P^{0}$, $q^{\eta}$ and $L^{\eta}$ are continuous on $(0,T]$ and $\overline{Z}^{\eta } \in \mathcal {L}_{\mathrm{Prog}}^{2}(\Omega \times (0,T];\mathbb{R}^{m})$.

iii) There exists a function $\eta _{2} \colon (0,\infty ) \to (0,\infty )$ such that for all $\varepsilon >0$ and all $\eta \in (0,\eta _{2}(\varepsilon )]$,

$$\begin{aligned} \mathbb{P}\Big[ \inf _{t \in (0,T-\varepsilon ]} q^{\eta}_{t} \ge - \varepsilon , \sup _{t \in (0,T)} q^{\eta}_{t} \le \varepsilon \Big] = 1. \end{aligned}$$

iv) The function $a \colon \mathbb{R}^{2} \to \mathbb{R}$ is nondecreasing and differentiable in the first variable and $a(P^{0}_{t}(\omega ),P^{0}_{t}(\omega )) \equiv 0$. Moreover, there exist $\overline{\varepsilon }, \beta > 0$ such that

$$ \frac{\partial }{\partial x}a\big(x,P^{0}_{t}(\omega )\big) \ge \beta \qquad \text{for all} \, | x-P^{0}_{t}(\omega ) | \le \overline{\varepsilon }. $$

v) The processes $\psi$ and $P^{0}$ satisfy Condition A.2, and the processes $L^{\eta}$ $(\eta > 0)$ satisfy Condition A.1 uniformly in $\eta >0$.

Lemma B.4

Under Assumption B.3, there exists a mapping $\eta _{0}\colon (0,\infty ) \to (0,\infty )$ that depends only on $\psi$, $\overline{P}$, $\eta _{1}$, $\eta _{2}$, $P^{0}$, $\overline{\varepsilon }$, $\beta$ and the mapping $\varepsilon \mapsto \delta$ corresponding to the uniform satisfaction of Condition A.1by $(L^{\eta})_{\eta >0}$ such that for all $\varepsilon >0$ and $\eta \in (0,\eta _{0}(\varepsilon )]$,

$$\begin{aligned} \mathbb{P}\Big[ \sup _{s \in (0,T-\varepsilon ]} ( P^{\eta}_{s} - P^{0}_{s} ) \le \varepsilon , \inf _{s \in (0,T)} ( P^{\eta}_{s} - P^{0}_{s} ) \ge -\varepsilon \Big] = 1. \end{aligned}$$

Proof

Let $p^{\eta }:= P^{\eta }- P^{0}$ and fix $\varepsilon \in (0,\overline{\varepsilon }]$. We first show that there exists $\eta _{0}(\varepsilon ) > 0$ such that

$$\begin{aligned} \sup _{\eta \le \eta _{0}(\varepsilon )} \sup _{s \in (0,T- \varepsilon ]} \mathbb{P}[ p^{\eta}_{s} > \varepsilon ] = 0. \end{aligned}$$

(B.5)

Since $p^{\eta}$ is continuous, this proves that, for all $\eta \le \eta _{0}(\varepsilon )$,

$$ \mathbb{P}\Big[ \sup _{s \in (0,T-\varepsilon ]} p^{\eta}_{s} \le \varepsilon \Big]=1. $$

To show (B.5), we fix $\delta \leq \varepsilon /2$ and $s \in (0,T-\varepsilon ]$. For all $\eta > 0$, we define the stopping time

$$\begin{aligned} \tau ^{\eta }:= (s+\delta ) \wedge \inf \{ u \in [s,T) : | p^{\eta}_{u} | = \varepsilon /2 \} \le T - \frac {\varepsilon }{2}. \end{aligned}$$

The $L^{2}$-integrability of $\overline{Z}^{\eta}$ on $[s,T-\varepsilon /2]$ and the optional sampling theorem give

$$\begin{array}{rl}0& =\mathbb{E}\left[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \}}\right(\sqrt{{\eta }^{-1}}{\int }_s^{{\tau }^{\eta }}(a(P_u^{\eta },P_u^0)+q_u^{\eta })\mathrm{d}u+L_{{\tau }^{\eta }}^{\eta }-L_s^{\eta }\\ & \phantom{=:\mathbb{E}\left[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \}}\right(}+{\psi }_s{P}_s^0-{\psi }_{{\tau }^{\eta }}{P}_{{\tau }^{\eta }}^0+{\psi }_s{p}_s^{\eta }-{\psi }_{{\tau }^{\eta }}{p}_{{\tau }^{\eta }}^{\eta }\left)\right].\end{array}$$

(B.6)

We now analyse the various terms in (B.6) separately to deduce that $\mathbb{P}[p^{\eta}_{s} > \varepsilon ] = 0$ if

$$ \eta \le \eta _{0}(\varepsilon ) := \min \Big( \eta _{1}(\varepsilon / 2), \eta _{2} \big( \min ( \delta , \beta \varepsilon /4 ) \big) \Big). $$

We first consider the term

$$\mathbb{E}\left[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \}}\sqrt{{\eta }^{-1}}{\int }_s^{{\tau }^{\eta }}\right(a(P_u^{\eta },P_u^0)+q_u^{\eta }\left)\mathrm{d}u\right].$$

On $\{p^{\eta}_{s} > \varepsilon \}$, we have $p^{\eta}_{u} \ge \varepsilon /2$ for all $u \in [s,\tau ^{\eta}]$ and hence

$$\begin{aligned} a (P^{\eta}_{u}, P^{0}_{u} ) = a ( P^{0}_{u} + p^{\eta}_{u}, P^{0}_{u} ) \ge a ( P^{0}_{u} + \varepsilon /2, P^{0}_{u} ) \ge \frac {\beta \varepsilon }{2}. \end{aligned}$$

(B.7)

Together with our assumption on the process $q^{\eta}$ and our choice of $\eta$, this implies by using (B.7) and $q^{\eta}_{u} {\ge -\beta \varepsilon /4}$ that

$$\begin{array}{rl}& \mathbb{E}\left[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \}}\sqrt{{\eta }^{-1}}{\int }_s^{{\tau }^{\eta }}\right(a(P_u^{\eta },P_u^0)+q_u^{\eta }\left)\mathrm{d}u\right]\\ & \ge \mathbb{E}[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \}}\sqrt{{\eta }^{-1}}({\tau }^{\eta }-s)\frac{\beta \epsilon }{4}]\\ & \ge \delta \sqrt{{\eta }^{-1}}\frac{\beta \epsilon }{4}\mathbb{P}[p_s^{\eta }>\epsilon \text{and}{\tau }^{\eta }=s+\delta ].\end{array}$$

By Assumption B.3 v), Lemma A.5 and Theorem A.8, we can choose for any $\varepsilon _{0} > 0$ some $\delta > 0$, which does not depend on $\eta$, such that

$$|\mathbb{E}[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \}}(Y_{{\tau }^{\eta }}-Y_s)]|\le {\epsilon }_0\mathbb{P}[p_s^{\eta }>\epsilon ]\text{for}Y=\psi P^0,L^{\eta }$$

(B.8)

and

$$\begin{aligned} \mathbb{E}\big[ | \psi _{\tau ^{\eta}} - \psi _{s} | \big| \mathcal {F}_{s} \big] \le \varepsilon _{0}. \end{aligned}$$

Using (B.8), the fact that $P^{\eta}|_{\Omega \times (0,T-\varepsilon ]} \le \overline{P}$ by Assumption B.3 i) and $p^{\eta}_{\tau ^{\eta}} \le 2 \overline{P}$ yields

$$\begin{array}{rl}\mathbb{E}[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \}}({\psi }_s{p}_s^{\eta }-{\psi }_{{\tau }^{\eta }}{p}_{{\tau }^{\eta }}^{\eta })]& \ge \mathbb{E}\left[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \text{and}{\tau }^{\eta }<s+\delta \}}\right({\psi }_s\epsilon /2+({\psi }_s-{\psi }_{{\tau }^{\eta }})\epsilon /2\left)\right]\\ & \phantom{=:}+\mathbb{E}[{\mathbb{1}}_{\{p_s^{\eta }>\epsilon \text{and}{\tau }^{\eta }=s+\delta \}}({\psi }_s\epsilon -{\psi }_{{\tau }^{\eta }}{p}_{{\tau }^{\eta }}^{\eta })]\\ & \ge \frac{\epsilon }{2}\underset{\_}{\psi }\mathbb{P}[p_s^{\eta }>\epsilon \text{and}{\tau }^{\eta }<s+\delta ]-\frac{\epsilon {\epsilon }_0}{2}\mathbb{P}[p_s^{\eta }>\epsilon ]\\ & \phantom{=:}+(\epsilon \underset{\_}{\psi }-2\bar{\psi }\bar{P})\mathbb{P}[p_s^{\eta }>\epsilon \text{and}{\tau }^{\eta }=s+\delta ].\end{array}$$

Altogether this yields

$$\begin{aligned} 0 &\ge \mathbb{P}[ p^{\eta}_{s} > \varepsilon \, \text{and} \, {\tau ^{ \eta}} = s + \delta ] \bigg( \delta \sqrt{\eta _{0}(\varepsilon )^{-1}} \frac {\beta \varepsilon }{4} - 2 \varepsilon _{0} - \frac {\varepsilon \varepsilon _{0}}{2} + \varepsilon \underline{\psi}- 2 \overline{\psi}\, \overline{P} \bigg) \\ & \hphantom{=:} + \mathbb{P}[ p^{\eta}_{s} > \varepsilon \, \text{and} \, {\tau ^{\eta}} < s + \delta ] \bigg( - 2 \varepsilon _{0} + \frac {\varepsilon }{2} \underline{\psi}- \frac {\varepsilon \varepsilon _{0}}{2} \bigg). \end{aligned}$$

(B.9)

Now if we choose first $\varepsilon _{0}$ and then $\eta _{0}(\varepsilon )$ small enough, the coefficients that multiply the probabilities in (B.9) become positive. Hence both probabilities must be equal to zero, and so we have $\mathbb{P}[ p^{\eta}_{s} > \varepsilon ] = 0$ if $\eta \le \eta _{0}(\varepsilon )$. Analogously, we can prove that $\mathbb{P}[ p^{\eta}_{s} < -\varepsilon ] = 0$ for all $s \in (0,T)$. The main difference is that ${\tau ^{\eta}} < T-\delta$ does not hold on the set $\{p^{\eta}_{s} < -\varepsilon \}$. Instead, we only obtain $\tau ^{\eta }< T$ (if Assumption B.3 ii) b) holds) or $\tau ^{\eta }< T_{\eta}$ (if Assumption B.3 ii) a) holds). □

2.2 B.2 ODE systems with negative feedback

In this section, we establish a convergence result for ODEs with random coefficients and a “nearly singular” driver. Specifically, we consider pairs of continuously differentiable stochastic processes $(X^{\eta},Z^{\eta})$ which satisfy the ODE system

$$\begin{aligned} \dot{X}^{\eta}_{t} &= - A^{\eta}_{t} ( X^{\eta}_{t} + B^{\eta}_{t} Z^{ \eta}_{t} ), \qquad X^{\eta}_{0} = x_{0}, \\ \dot{Z}^{\eta}_{t} &= C_{t} X^{\eta}_{t} + D_{t} Z^{\eta}_{t}, \qquad Z^{ \eta}_{0} = z_{0} \end{aligned}$$

on some time interval $[0,S]$ for all $\eta > 0$, where $A^{\eta}$, $B^{\eta}$, $C$ and $D$ are continuous, adapted, real-valued stochastic processes. We assume that the process $A^{\eta}$ converges in probability to infinity as $\eta \to 0$, that the process $B^{\eta}$ converges to a process $B^{0}$ in probability and that the processes $(X^{\eta},Z^{\eta})$ are uniformly bounded in probability.

Assumption B.5

There exists a continuous adapted process $B^{0}$ such that for all $\varepsilon ,\delta \in (0,\infty )$, there exists some $\eta _{0} = \eta _{0}(\varepsilon , \delta ) > 0$ such that for all $\eta \in (0,\eta _{0}]$,

$$\begin{aligned} \mathbb{P}\bigg[ \inf _{t\in [0,S]} A^{\eta}_{t} \ge \frac {1}{\varepsilon }, \sup _{t\in [0,S]} | B^{\eta}_{t} - B^{0}_{t} | \le \varepsilon \bigg] \ge 1 - \delta . \end{aligned}$$

(B.10)

Moreover, for all $\delta \in (0,1)$, there exists an $L > 0$ such that for all $\eta >0$,

$$ \mathbb{P}\Big[ \sup _{t\in [0,S]} ( | X^{\eta}_{t} | + | Z^{\eta}_{t} | ) \le L \Big] \ge 1 - \delta . $$

(B.11)

In terms of the process $B^{0}$, we define

$$\begin{aligned} X^{0}_{t} & := - B^{0}_{t} Z^{0}_{t}, \\ Z^{0}_{t} & := z_{0} \exp \bigg( \int ^{t}_{0} ( - C_{s} B^{0}_{s} + D_{s} ) \, \mathrm {d} s\bigg). \end{aligned}$$

Our goal is to prove that $(X^{\eta},Z^{\eta}) \to (X^{0},Z^{0})$ in a suitable sense as $\eta \to 0$. Since the initial condition of the processes $X^{\eta}$ does not vary with $\eta$ and since $A^{\eta}_{0} \uparrow \infty$, we cannot expect convergence in $t=0$. Instead, we first prove that $\frac{\dot{X}^{\eta}}{A^{\eta}}$ converges to 0 on any compact subinterval of $(0,S]$, with lower, respectively upper convergence near the origin. More precisely, we have the following result.

Lemma B.6

If Assumption B.5holds and if $x_{0} + B^{0}_{0} z_{0} > 0$, then for all $\varepsilon ,\delta \in (0,\infty )$, there exists $\eta _{1}=\eta _{1}(\varepsilon ,\delta ) > 0$ such that for all $\eta \in (0,\eta _{1}]$,

$$\begin{aligned} \mathbb{P}\bigg[ \sup _{t\in [0,S]} \frac {\dot{X}^{\eta}_{t}}{A^{\eta}_{t}} \le \varepsilon , \inf _{t \in [\varepsilon ,S]} \frac {\dot{X}^{\eta}_{t}}{A^{\eta}_{t}} \ge - \varepsilon \bigg] \ge 1 - \delta . \end{aligned}$$

If $x_{0} + B^{0}_{0} z_{0} < 0$, then the intervals $[0,S]$ and $[\varepsilon ,S]$ in the above statement are to be swapped. The mapping $\eta _{1}$ depends only on $B^{0}$, $C$, $D$, $x_{0}$, $z_{0}$ and the mappings $(\varepsilon ,\delta ) \mapsto \eta _{0}(\varepsilon , \delta )$ and $\delta \mapsto L$ introduced in Assumption B.5.

Proof

Let $y_{0} := x_{0} + B^{0}_{0} z_{0}$. We assume without loss of generality that $y_{0} > 0$. Then there exists $\alpha _{0} > 0$ such that

$$\begin{aligned} y_{0} - \alpha | z_{0} | > 0 \qquad \text{for all} \, \alpha \leq \alpha _{0}. \end{aligned}$$

Let us now put

$$\begin{aligned} M^{L,\eta} &:= \Big\{ \sup _{t \in [0,S]} ( | B^{0}_{t} | + |C_{t}| + |D_{t}| + | X^{\eta}_{t} | + | Z^{\eta}_{t} | ) \le L \Big\} , \\ M^{\alpha ,\eta} &:= \bigg\{ \inf _{t\in [0,S]} A^{\eta }\ge \frac {1}{\alpha}, \sup _{t\in [0,S]} | B^{\eta}_{t} - B^{0}_{t} | \le \alpha \bigg\} , \\ M^{\beta ,\nu} &:= \Big\{ \sup _{s,t\in [0,S],|s-t|\le \nu} | B^{0}_{s} - B^{0}_{t} | \le \beta \Big\} . \end{aligned}$$

Due to Assumption B.5 and Lemma 3.9, for all $\delta >0$, $\beta >0$ and $\alpha \leq \alpha _{0}$, there exist constants $L_{0}(\delta )$, $\eta _{0}(\alpha ,\delta )$ and $\nu _{0}(\beta ,\delta )$ such that

$$ \inf _{L \ge L_{0}} \inf _{\eta }\mathbb{P}[M^{L,\eta}] \geq 1- \frac{\delta}{6}, \qquad \inf _{\eta \leq \eta _{0}}\mathbb{P}[M^{ \alpha ,\eta}] \geq 1-\frac{\delta}{6}, \qquad \inf _{\nu \le \nu _{0}} \mathbb{P}[M^{\beta ,\nu}] \geq 1-\frac{\delta}{6}. $$

Moreover, for all $\alpha \le \alpha _{0}$ and ℙ-a.a. $\omega \in M^{\alpha ,\eta}$,

$$ \dot{X}^{\eta}_{0}(\omega ) \le - A^{\eta}_{0}(\omega ) \big( y_{0} - | B^{\eta}_{0}(\omega ) - B^{0}_{0}(\omega ) | | z_{0} | \big) \leq - \frac {1}{\alpha }( y_{0} - \alpha |z_{0}| ) < 0. $$

(B.12)

We are now ready to prove that for all $\varepsilon ,\delta >0$, there exists $\eta _{1}>0$ such that for all $\eta \le \eta _{1}$,

$$ \mathbb{P}\bigg[ \sup _{t\in [0,S]} \frac {\dot{X}^{\eta}_{t}}{A^{\eta}_{t}} \le \varepsilon \bigg] \geq 1- \frac{\delta}{2}. $$

(B.13)

To this end, we take an $\omega \in M^{L,\eta} \cap M^{\alpha ,\eta} \cap M^{\beta ,\nu}$ where (B.12) holds and assume that there exists some $t \in [0,S]$ such that $\frac{\dot{X}^{\eta}_{t}(\omega )}{A^{\eta}_{t}(\omega )} \ge \varepsilon$. It is enough to show that such a $t$ cannot exist for $L$ large and $\alpha$, $\beta$, $\nu$, $\eta$ small enough. Since $\frac{\dot{X}^{\eta}(\omega )}{A^{\eta}(\omega )}$ is continuous and $\frac{\dot{X}^{\eta}_{0}(\omega )}{A^{\eta}_{0}(\omega )} < 0$ if $\alpha \le \alpha _{0}$, we can choose a minimal $t \in [0,S]$ with the property that $\frac{\dot{X}^{\eta}_{t}(\omega )}{A^{\eta}_{t}(\omega )} = \varepsilon$. Let

$$\begin{aligned} s := \sup \bigg\{ u \in (0,t) : \frac{\dot{X}^{\eta}_{u}(\omega )}{A^{\eta}_{u}(\omega )} = \varepsilon /2 \bigg\} . \end{aligned}$$

Then $\frac{\dot{X}^{\eta}_{s}(\omega )}{A^{\eta}_{s}(\omega )} = \frac{\varepsilon }{2}$ and $\frac{\dot{X}^{\eta}_{u}(\omega )}{A^{\eta}_{u}(\omega )} > \frac{\varepsilon }{2}$ for all $u \in (s,t]$. We now distinguish two cases. If $t - s \ge \nu$, then the fact that $\omega \in M^{L,\eta} \cap M^{\alpha ,\eta}$ yields

$$\begin{aligned} 2 L \ge X^{\eta}_{t}(\omega ) - X^{\eta}_{s}(\omega ) = \int ^{t}_{s} \frac {\dot{X}^{\eta}_{u}(\omega )}{A^{\eta}_{u}(\omega )} A^{\eta}_{u}( \omega ) \, \mathrm {d} u\ge \frac {\nu \varepsilon }{2\alpha} . \end{aligned}$$

(B.14)

If $t - s < \nu$, we have

$$\begin{aligned} \frac {\varepsilon }{2} &= \frac {\dot{X}^{\eta}_{t}(\omega )}{A^{\eta}_{t}(\omega )} - \frac {\dot{X}^{\eta}_{s}(\omega )}{A^{\eta}_{s}(\omega )} \\ &= - X^{\eta}_{t}(\omega ) - B^{\eta}_{t}(\omega ) Z^{\eta}_{t}( \omega ) + X^{\eta}_{s}(\omega ) + B^{\eta}_{s}(\omega ) Z^{\eta}_{s}( \omega ). \end{aligned}$$

Using that $\omega \in M^{\alpha ,\eta}$ yields $-X_{t}^{\eta}(\omega )+X^{\eta}_{s}(\omega ) = - \int ^{t}_{s} \frac {\dot{X}^{\eta}_{u}(\omega )}{A^{\eta}_{u}(\omega )} A^{\eta}_{u}( \omega ) \, \mathrm {d} u< 0$. Using that $\omega \in M^{L,\eta} \cap M^{\beta ,\nu}$ yields

$$\begin{aligned} \frac{\varepsilon }{2} & \le - B^{\eta}_{t}(\omega ) \int ^{t}_{s} \dot{Z}^{\eta}_{u}(\omega ) \, \mathrm {d} u- Z^{\eta}_{s}(\omega ) \big( B^{\eta}_{t}(\omega ) - B^{\eta}_{s}(\omega ) \big) \\ & \le 2L^{2} \nu \big( | B^{0}_{t}(\omega ) | + | B^{\eta}_{t}( \omega ) - B^{0}_{t}(\omega ) | \big) \\ & \hphantom{=:} + L \big( | B^{\eta}_{t}(\omega ) - B^{0}_{t}(\omega ) | + | B^{0}_{t}( \omega ) - B^{0}_{s}(\omega ) | + | B^{0}_{s}(\omega ) - B^{\eta}_{s}( \omega ) | \big) \\ & \le 2 L^{2} \nu ( L + \alpha ) + L ( 2\alpha + \beta ). \end{aligned}$$

(B.15)

Now we first choose $L \geq L_{0}(\delta )$, then $\beta > 0$ such that $3L\beta < \frac{\varepsilon }{4}$, then $\nu \leq \nu _{0}(\beta ,\delta )$ such that $2 L^{2} \nu ( L + \alpha _{0} ) < \frac{\varepsilon }{4}$, then $\alpha \leq \alpha _{0}$ such that $\frac{\nu \varepsilon }{2 \alpha} > 2 L$ and $\alpha \leq \beta$, and finally $\eta _{1}(\varepsilon ,\delta ) \leq \eta _{0}(\alpha ,\delta )$. Then both (B.14) and (B.15) are violated. As a result,

$$\begin{aligned} M^{L,\eta} \cap M^{\alpha ,\eta} \cap M^{\beta ,\nu} \subseteq \bigg\{ \sup _{t\in [0,S]} \frac {\dot{X}^{\eta}_{t}}{A^{\eta}_{t}} \le \varepsilon \bigg\} , \end{aligned}$$

and hence (B.13) holds.

It remains to prove that for suitably chosen parameters,

$$\begin{aligned} M^{L,\eta} \cap M^{\alpha ,\eta} \cap M^{\beta ,\nu} \subseteq \bigg\{ \inf _{t\in [\varepsilon ,S]} \frac {\dot{X}^{\eta}_{t}}{A^{\eta}_{t}} \ge -\varepsilon \bigg\} . \end{aligned}$$

To this end, we fix $\omega \in M^{L,\eta} \cap M^{\alpha ,\eta} \cap M^{\beta ,\nu}$ and assume that there exists a minimal $t \in [\varepsilon ,S]$ such that $\frac{\dot{X}^{\eta}_{t}(\omega )}{A^{\eta}_{t}(\omega )} \le - \varepsilon$. Using that $\omega \in M^{L,\eta} \cap M^{\alpha ,\eta}$, it is straightforward to show that for all sufficiently small $\alpha$, there exists an $r \in [0,\varepsilon ]$ such that $\frac{\dot{X}^{\eta}_{r}(\omega )}{A^{\eta}_{r}(\omega )} \ge - \varepsilon /2$. Hence we can define

$$\begin{aligned} s := \sup \bigg\{ u \in [0,t) : \frac{\dot{X}^{\eta}_{u}(\omega )}{A^{\eta}_{u}(\omega )} = - \varepsilon /2 \bigg\} . \end{aligned}$$

Then $0 \leq s < t$ and $\frac{\dot{X}^{\eta}_{u}(\omega )}{A^{\eta}_{u}(\omega )} \in [- \varepsilon ,-\varepsilon /2]$ for all $u \in [s,t]$. We can now use the same arguments as in the first step to conclude that

$$\begin{aligned} \mathbb{P}\bigg[ \inf _{t\in [\varepsilon ,S]} \frac {\dot{X}^{\eta}_{t}}{A^{\eta}_{t}} \ge -\varepsilon \bigg] \ge 1 - \frac {\delta }{2}. \end{aligned}$$

(B.16)

Combining (B.13) and (B.16) yields the desired result. □

Lemma B.7

Let Assumption B.5be satisfied and let $x_{0} + B^{0}_{0} z_{0} \ne 0$. Then for all $\varepsilon ,\delta \in (0,\infty )$, there exists $\eta _{2}=\eta _{2}(\varepsilon ,\delta ) > 0$ such that for all $\eta \in (0,\eta _{2}]$,

$$\begin{aligned} \mathbb{P}\Big[ \sup _{t\in [0,S]} | Z^{\eta}_{t} - Z^{0}_{t} | \le \varepsilon \Big] \ge 1 - \delta . \end{aligned}$$

The mapping $\eta _{2}$ depends only on $B^{0}$, $C$, $D$, $x_{0}$, $z_{0}$ and the mappings $(\varepsilon ,\delta ) \mapsto \eta _{0}( \varepsilon ,\delta )$ and $\delta \mapsto L$ introduced in Assumption B.5.

Proof

Since

$$\begin{aligned} Z^{\eta}_{t} - Z^{0}_{t} &= \exp \bigg( \int ^{t}_{0} ( D_{u} - B^{ \eta}_{u} C_{u} ) \, \mathrm {d} u\bigg) \\ & \hphantom{=::} \times \int ^{t}_{0} \exp \bigg( - \int _{0}^{s} ( D_{u} - B^{\eta}_{u} C_{u} ) \, \mathrm {d} u\bigg) \bigg( ( B^{0}_{s} - B^{\eta}_{s} ) C_{s} Z^{0}_{s} - C_{s} \frac{\dot{X}^{\eta}_{s}}{A^{\eta}_{s}} \bigg) \, \mathrm {d} s, \end{aligned}$$

the assertion follows from Assumption B.5 and Lemma B.6. □

The next theorem follows by Assumption B.5 and Lemmas B.6 and B.7.

Theorem B.8

If Assumption B.5holds and $x_{0} + B^{0}_{0} z_{0} > 0$, then for all $\varepsilon ,\delta \in (0,\infty )$, there exists $\eta _{3} = \eta _{3}(\varepsilon ,\delta ) > 0$ such that for all $\eta \in (0,\eta _{3}]$,

$$\begin{aligned} \mathbb{P}\Big[ \sup _{t\in [0,S]} \max ( | Z^{0}_{t} - Z^{\eta}_{t} |, X^{0}_{t} - X^{\eta}_{t} ) \le \varepsilon , \inf _{t\in [ \varepsilon ,S]} ( X^{0}_{t} - X^{\eta}_{t} ) \ge -\varepsilon \Big] \ge 1 - \delta . \end{aligned}$$

If $x_{0} + B^{0}_{0} z_{0} < 0$, then the intervals $[0,S]$ and $[\varepsilon ,S]$ in the statement are to be swapped. The mapping $\eta _{3}$ depends only on $B^{0}$, $C$, $D$, $x_{0}$, $z_{0}$ and the mappings $(\varepsilon ,\delta ) \mapsto \eta _{0}(\varepsilon , \delta )$ and $\delta \mapsto L$ introduced in Assumption B.5.