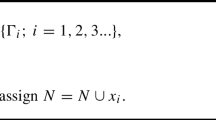Simulation of the drawdown and its duration in Lévy models via stick-breaking Gaussian approximation

Abstract

We develop a computational method for expected functionals of the drawdown and its duration in exponential Lévy models. It is based on a novel simulation algorithm for the joint law of the state, supremum and time the supremum is attained of the Gaussian approximation for a general Lévy process. We bound the bias for various locally Lipschitz and discontinuous payoffs arising in applications and analyse the computational complexities of the corresponding Monte Carlo and multilevel Monte Carlo estimators. Monte Carlo methods for Lévy processes (using Gaussian approximation) have been analysed for Lipschitz payoffs, in which case the computational complexity of our algorithm is up to two orders of magnitude smaller when the jump activity is high. At the core of our approach are bounds on certain Wasserstein distances, obtained via the novel stick-breaking Gaussian (SBG) coupling between a Lévy process and its Gaussian approximation. Numerical performance, based on the implementation in Cázares and Mijatović (SBG approximation. GitHub repository. Available online at https://github.com/jorgeignaciogc/SBG.jl (2020)), exhibits a good agreement with our theoretical bounds. Numerical evidence suggests that our algorithm remains stable and accurate when estimating Greeks for barrier options and outperforms the “obvious” algorithm for finite-jump-activity Lévy processes.

1 Introduction

1.1 Setting and motivation

Lévy processes are increasingly popular for the modelling of market prices of risky assets. They naturally address the shortcoming of diffusion models by allowing large (often heavy-tailed) sudden movements of the asset price as observed in the markets; see Schoutens [63, Chap. 4], Kou [43, Sect. 1], Cont and Tankov [20, Chap. 1]. While Lévy models with finite jump activity (i.e., jump-diffusions) can model large instantaneous movements (jumps) and small-time fluctuations (Gaussian component), infinite activity Lévy models often provide better parsimonious statistical and/or risk-neutral descriptions of asset returns (e.g. Carr et al. [13]) and exhibit a more flexible implied volatility behaviour over short time horizons (e.g. Mijatović and Tankov [54]). For risk management, it is thus crucial to quantify the probabilities of rare and/or extreme events under all Lévy models. Of particular interest in this context are the distributions of the drawdown (the current decline from a historical peak) and its duration (the elapsed time since the historical peak); see e.g. Sornette [65, Chap. 1], Večeř [67], Carr et al. [15], Baurdoux et al. [5], Landriault et al. [48]. Together with the hedges for barrier options (Avram et al. [3], Schoutens [64], Kudryavtsev and Levendorskiĭ [45], Giles and Xia [30]) and ruin probabilities in insurance (Mordecki [55], Klüppelberg et al. [41], Li et al. [49]), the expected drawdown and its duration constitute risk measures dependent on the following random vector, which is a statistic of the path of a Lévy process $X$: a historic maximum $\overline{X}_{T}$ at a time $T$, the time $\overline{\tau }_{T}(X) \leq T$ at which this maximum was attained, and the value $X_{T}$ of the process at $T$. Since neither the distribution of the drawdown $1-\exp (X_{T}-\overline{X}_{T})$ nor of its duration $T-\overline{\tau }_{T}(X)$ is analytically tractable for a general $X$, simulation provides a natural alternative. The main objective of the present paper is to develop and analyse a novel practical simulation algorithm for the joint law of $(X_{T},\overline{X}_{T},\overline{\tau }_{T}(X))$ which is applicable to a general Lévy process $X$.

Exact simulation of the drawdown of a Lévy process is currently out of reach except for the stable (González Cázares et al. [33]) and jump-diffusion cases. However, even in the stable case, it is not known how to jointly simulate any two components of $(X_{T},\overline{X}_{T},\overline{\tau }_{T}(X))$. Among the approximate simulation algorithms, the recently developed stick-breaking approximation in González Cázares et al. [35] is the fastest in terms of its computational complexity, as it samples from the law of $(X_{T},\overline{X}_{T},\overline{\tau }_{T}(X))$ with a geometrically decaying bias. However, like most approximate simulation algorithms for a statistic of the entire trajectory, it is only valid for a Lévy process whose increments can be sampled. Such a requirement does not hold for large classes of widely used Lévy processes, including the general CGMY (aka KoBoL) model in Carr et al. [14]. Moreover, nonparametric estimation of Lévy processes typically yields Lévy measures whose transitions cannot be sampled (Neumann and Reiß[56], Chen et al. [17], Comte and Genon-Catalot [19], Cai et al. [11], Qin and Todorov [59]), which again makes a direct application of the algorithm in [35] infeasible.

If the increments of $X$ cannot be sampled, a general approach is to use the Gaussian approximation introduced by Asmussen and Rosiński [2], which substitutes the small-jump component of the Lévy process by a Brownian motion. Thus the Gaussian approximation process is a jump-diffusion, and the exact sample of the random vector (consisting of the state of the process, the supremum and the time the supremum is attained) can be obtained by applying Devroye’s sampler, see Devroye [23, Alg. MAXLOCATION], between the consecutive jumps. However, little is known about how close these quantities are to the vector $(X_{T},\overline{X}_{T},\overline{\tau }_{T}(X))$ that is being approximated, in either Wasserstein or Kolmogorov distances. Indeed, bounds on the distances between the marginals of the Gaussian approximation and $X_{T}$ have been considered by Dia [24] and recently improved by Mariucci and Reiß[50] and Carpentier et al. [12]. A Wasserstein bound on the supremum is given by Dia [24], but so far, no improvement analogous to the marginal case has been established. Moreover, to the best of our knowledge, there are no corresponding results for either the joint law of $(X_{T},\overline{X}_{T})$ or the time $\overline{\tau }_{T}(X)$. Furthermore, as explained in Remark 4.1 below, the exact simulation algorithm for the supremum and the time of the supremum of a Gaussian approximation based on Devroye [23, Alg. MAXLOCATION] is unsuitable for the multilevel Monte Carlo estimation.

The main motivation for the present work is to provide an operational framework for Lévy processes which allows us to settle the issues raised in the previous paragraph, develop a general simulation algorithm for $(X_{T},\overline{X}_{T},\overline{\tau }_{T}(X))$ and analyse the computational complexity of its Monte Carlo (MC) and multilevel Monte Carlo (MLMC) estimators.

1.2 Contributions in the present paper

Our main contributions are as follows.

(Ia) We establish bounds on the Wasserstein and Kolmogorov distances between the vector $\overline{\chi }_{T}=(X_{T},\overline{X}_{T},\overline{\tau }_{T}(X))$ and its Gaussian approximation, denoted by $\overline{\chi }_{T}^{( \kappa )} = (X_{T}^{(\kappa )},\overline{X}_{T}^{(\kappa )}, \overline{\tau }_{T}(X^{(\kappa )}))$, where $X^{(\kappa )}$ is a jump-diffusion equal to the Lévy process $X$ with the jumps smaller than $\kappa \in (0,1]$ substituted by a Brownian motion (see (2.5) below) and $\overline{X}^{(\kappa )}_{T}$ (resp. $\overline{\tau }_{T}(X^{(\kappa )})$) is the supremum of $X^{(\kappa )}$ (resp. the time $X^{(\kappa )}$ attains the supremum) over the time interval $[0,T]$.

(Ib) These results enable us to control the bias $|\mathbb{E}[f({\bar{\chi }}_T)]-\mathbb{E}[f({\bar{\chi }}_T^{(\kappa )})]|$ for a discontinuous and/or locally Lipschitz payoff $f$, a fundamental advance in the area of Gaussian approximation of Lévy processes.

(II) We introduce a simple and fast algorithm, SBG-Alg, which samples exactly the vector of interest for the Gaussian approximation of any Lévy process $X$, develop an MLMC estimator based on SBG-Alg (see González Cázares and Mijatović [31] for an implementation in Julia), and analyse its complexity for discontinuous and locally Lipschitz payoffs arising in applications.

Before discussing contributions (Ia)+ (Ib) and (II) in more detail, note that the role in the present paper of the main algorithm from González Cázares et al. [35] is analogous to the role the simulation of Brownian increments plays in the sampling of Euler scheme chains approximating the law of the solutions of stochastic differential equations. Differently put, the present paper analyses the convergence of a family of algorithms, indexed by the cutoff parameter $\kappa >0$ and essentially given by the algorithm in [35] for each approximation $\overline{\chi }_{T}^{(\kappa )}$, analogous to the analysis of the convergence of Euler schemes indexed by the step size $h>0$ that controls the volatility in the simulation algorithm for Brownian increments. The underlying ideas in the present paper and in [35] are based on the theory of convex minorants of general Lévy processes (see e.g. González Cázares and Mijatović [32]). While [35] has a theoretical obstruction as it is applicable only if the increments of $X$ can be sampled, the results and algorithms in the present paper are applicable to essentially all Lévy processes. This requires fundamental advances in both bias and level variance control, which we now discuss briefly.

(Ia) In Theorem 3.4 (see also Corollary 3.5), we establish novel bounds on the Wasserstein distance between $\overline{\chi }_{T}$ and $\overline{\chi }_{T}^{(\kappa )}$ (as $\kappa$ tends to 0) under weak assumptions, typically satisfied by the models used in applications. The proof of Theorem 3.4 has two main ingredients. First, in Sect. 7.2 below, we construct a novel stick-breaking Gaussian (SBG) coupling between $\overline{\chi }_{T}$ and $\overline{\chi }_{T}^{(\kappa )}$, based on the stick-breaking (SB) representation of $\overline{\chi }_{T}$ in (2.1) and the minimal transport coupling between the increments of $X$ and its approximation $X^{(\kappa )}$. The second ingredient consists of new bounds on the Wasserstein and Kolmogorov distances between the laws of $X_{t}$ and $X^{(\kappa )}_{t}$ for any $t>0$, given in Theorems 3.1 and 3.3, respectively. The improvement of our bounds on the existing literature on the Gaussian approximation for the marginals of a Lévy process is reflected both in the bounds of Theorem 3.4 (for which there is no comparison in the literature) as well as in the performance of SBG-Alg. Moreover, even though the bounds in Theorem 3.4 are of Wasserstein type, the estimates in Theorem 3.3 of the Kolmogorov distance of the marginals of a Gaussian approximation are crucial in the proof of Theorem 3.4 because of the presence of the indicator functions in SB representations (2.1).

(Ib) In Sect. 3.2, we give novel bounds on the bias of locally Lipschitz and barrier payoffs of $\overline{\chi }_{T}$; see Propositions 3.7, 3.9 and 3.12. Their proofs are based on Theorem 3.4 and Lemma 7.5, which essentially converts the Wasserstein distance into the Kolmogorov distance for sufficiently regular distributions. In particular, note that Theorem 3.4 is used to control the distance between a non-Lipschitz functional $\overline{\tau }_{T}(X)$ of the path of $X$ and $\overline{\tau }_{T}(X^{(\kappa )})$. Thus Proposition 3.12 bounds the bias of a discontinuous payoff of a non-Lipschitz functional of $X$. Applications related to the duration of the drawdown and the risk-management of barrier options require bounding the bias of certain discontinuous functions of $\overline{\chi }_{T}$. We thus develop explicit general sufficient conditions on the characteristic triplet of the Lévy process $X$ (see Proposition 3.15 below) which guarantee the applicability of the results of Sect. 3.2 to models typically used in practice. Finally, Propositions 3.9 and 3.12 yield new bounds on the Kolmogorov distance between the components of $(\overline{X}_{T},\overline{\tau }_{T}(X))$ and $(\overline{X}^{(\kappa )}_{T},\overline{\tau }_{T}(X^{(\kappa )}))$ (see Corollary 3.14 below) which we hope are of independent interest, complementing the Wasserstein bounds of Corollary 3.5.

(II) Our main simulation algorithm, SBG-Alg, samples jointly coupled Gaussian approximations of $\overline{\chi }_{T}$ at distinct approximation levels (i.e., two different values of the cutoff $\kappa$). The coupling in SBG-Alg exploits the following simple observations:

– Any Gaussian approximation $\overline{\chi }^{(\kappa )}_{T}$ has an SB representation in (2.2), where the law of $Y$ in (2.2) must equal that of $X^{(\kappa )}$.

– For any two Gaussian approximations, the stick-breaking process in (2.2) can be shared.

– The increments in (2.2) over the shared sticks can be coupled using the definition (2.5) of the Gaussian approximation $X^{(\kappa )}$.

We analyse the computational complexity of the MLMC estimator based on SBG-Alg for a variety of payoff functions arising in applications. Figure 1 shows the leading power of the resulting MC and MLMC complexities, summarised in Tables 1 and 2 below (see Theorem 7.17 for full details), for locally Lipschitz and discontinuous payoffs used in practice. To the best of our knowledge, neither locally Lipschitz nor discontinuous payoffs have been previously considered in the context of MLMC estimation under Gaussian approximation.

Fig. 1

Dashed (resp. solid) line plots the power of $\epsilon ^{-1}$ in the computational complexity of an MC (resp. MLMC) estimator, as a function of the BG index $\beta$ defined in (2.6), for discontinuous functions in $\mathrm{BT}_{1}$ (3.12) and $\mathrm{BT}_{2}$ (3.14), locally Lipschitz payoffs as well as Lipschitz functions of $\overline{\tau }_{T}(X)$. The cases are split according to whether $X$ is with ($\sigma \ne 0$) or without ($\sigma =0$) a Gaussian component. The pictures are based on Tables 1 and 2 under assumptions typically satisfied in applications; see Sect. 4.2 below for details

Table 1 Asymptotic behaviour of the level $\kappa$ and the complexity $\mathcal{C}_{\mathrm{MC}}(\epsilon )$ as $\epsilon \to 0$ for the MC estimator in (4.2)

Table 2 The table presents the power of $\epsilon ^{-1}$ in $\epsilon ^{2} \mathcal{C}_{\mathrm{ML}}(\epsilon )$ as $\epsilon \to 0$, neglecting only the logarithmic factors (see Theorem 7.17 below for the complete result). The parameter $a$ in the table determines the decreasing sequence of cutoff levels ${({\kappa }_j)}_{j\in \mathbb{N}}$ as follows: $\kappa _{j}=(1+|a|/q)^{-2(j-1)/|a|}$ if $a\neq 0$, and $\kappa _{j}= \exp (-(2/q)(j-1))$ otherwise. The corresponding increasing number $n_{j}$ of sticks in the definition of the law $\underline{\Pi }_{n_{j},T}^{\kappa _{j},\kappa _{j+1}}$ can be taken to grow asymptotically as $\log ^{2}(1+\overline{\nu }(\kappa _{j})T)$ for large $j$; see Theorem 7.17 below

A key component of the analysis of the complexity of an MLMC estimator is the rate of decay of level variances (see Appendix A.2 for the definition). In the case of SBG-Alg, the rate of decay is given in Theorem 7.10 below for locally Lipschitz and discontinuous payoffs of interest. The analysis in the proof of Theorem 7.10 of the coupling simulated in SBG-Alg (between two Gaussian approximations at distinct cutoff levels) relies on the SBG coupling (between a Gaussian approximation and its limit) to control the rate of decay of level variances. Moreover, the proof of Theorem 7.10 shows that the decay of the level variances for Lipschitz payoffs under SBG-Alg is asymptotically equal to that of Algorithm 1, which samples jointly the increments at two distinct levels only. The principal reason for this equality between the “marginal” Algorithm 1 and the “path-dependent” SBG-Alg lies in the fact that it is the increments that dominate in the SB representation in (2.2). Furthermore, an improved coupling in Algorithm 1 for the increments of the Gaussian approximations (cf. the final of the three observations listed in the previous paragraph) would further reduce the computational complexity of the MLMC estimator for all payoffs considered in this paper (including the discontinuous ones). However, such a coupling is currently out of reach; cf. the discussion following Algorithm 1 in Sect. 4.1.1 below. To the best of our knowledge, SBG-Alg is the first exact simulation algorithm for coupled Gaussian approximations of $\overline{\chi }_{T}$ with vanishing level variances for a general Lévy process $X$; see Remark 4.1 below for further details.

In Sect. 6, using the code in the repository González Cázares and Mijatović [31], we test our theoretical findings against numerical results. In Sect. 6.1, we run SBG-Alg for models in the tempered stable and Watanabe classes. The former is a widely used class of processes whose increments cannot be sampled for all parameter values, and the latter is a well-known class of processes with infinite activity but singular continuous increments. In both cases, we find a good agreement between the theoretical prediction and the estimated decays of the bias and level variance; see Figs. 4 and 5 below.

In the context of MC estimation, a direct simulation algorithm based on Devroye’s sampler [23, Alg. MAXLOCATION] (Algorithm 2 below) can be used instead of SBG-Alg. In Sect. 6.2, we compare numerically its cost with that of SBG-Alg. In the examples we considered, the speedup of SBG-Alg over Algorithm 2 is about 50, see Fig. 6, remaining significant even for processes with finite jump activity; see Fig. 7. In fact, these examples demonstrate that SBG-Alg (with $\kappa =0$) is preferable for jump-diffusions as it significantly outperforms Algorithm 2.

In Sect. 6.3, we provide numerical evidence demonstrating that SBG-Alg (combined with central finite differences) remains very stable and fast for computing Delta and Gamma of barrier options under exponential Lévy models. Interestingly, the error of the Delta remains bounded all the way to the barrier (see Fig. 10 below), a property crucial in practice and very rare for Monte Carlo algorithms.

1.3 Organisation

The remainder of the paper is organised as follows. Section 2 recalls the SB representation (2.1), (2.2) and the Gaussian approximation (2.5) developed in González Cázares et al. [35] and Asmussen and Rosiński [2], respectively. Section 3 presents bounds on the Wasserstein and Kolmogorov distances between $\overline{\chi }_{T}$ and its Gaussian approximation $\overline{\chi }^{(\kappa )}_{T}$ and the biases of certain payoffs arising in applications. Section 3 also provides simple sufficient conditions, in terms of the Lévy triplet, under which these bounds hold. Section 4 constructs our main algorithm, SBG-Alg, and presents the computational complexity of the corresponding MC and MLMC estimators for all payoffs considered in this paper. Having stated our main results, we present a thorough comparison with the literature in Sect. 5. In Sect. 6, we illustrate numerically our results for a widely used class of Lévy models. The proofs and technical results are found in Sect. 7. Appendix A.1 gives a brief account of the complexity analysis of MC and MLMC (introduced in Heinrich [37] and Giles [28]) estimators.

2 The stick-breaking representation and the Gaussian approximation

Let $f:[0,\mathrm{\infty })\to \mathbb{R}$ be a right-continuous function with left limits. For $t\in (0,\infty )$, define $\underline{f}_{t}:=\inf _{s\in [0,t]}f(s)$, $\overline{f}_{t}:=\sup _{s\in [0,t]}f(s)$ and let $\underline{\tau }_{t}(f)$ (resp. $\overline{\tau }_{t}(f)$) be the last time before $t$ that the infimum $\underline{f}_{t}$ (resp. supremum $\overline{f}_{t}$) is attained. Throughout, $X=(X_{t})_{t\geq 0}$ denotes a Lévy process, i.e., a stochastic process started at the origin with independent, stationary increments and right-continuous paths with left limits; see Bertoin [7, Chap. 1], Kyprianou [47, Chaps. 1 and 2] and Sato [62, Chaps. 1 and 2] for background on Lévy processes. In mathematical finance, the risky asset price $S=(S_{t})_{t\geq 0}$ under an exponential Lévy model is given by $S_{t}:=S_{0}e^{X_{t}}$. The price $S_{t}$, its drawdown $1-S_{t}/\overline{S}_{t}$ (resp. drawup $S_{t}/\underline{S}_{t}-1$) and duration $t-\underline{\tau }_{t}(S)$ (resp. $t-\overline{\tau }_{t}(S)$) at time $t$ can be recovered from the vector $\overline{\chi }_{t}:=(X_{t},\overline{X}_{t}, \overline{\tau }_{t}(X))$ (resp. $\underline{\chi }_{t} :=(X_{t},\underline{X}_{t},\underline{\tau }_{t}(X))$). Because $Z:=-X$ is a Lévy process and we have $\overline{\chi }_{t}=(-Z_{t},-\underline{Z}_{t},\underline{\tau }_{t}(Z))$, it is sufficient to analyse the vector $\underline{\chi }_{t}$.

2.1 The stick-breaking (SB) representation

Given a Lévy process $X$ and a time horizon $t>0$, there exist a coupling $(X,Y)$, where $Y\overset {d}{=}X$ (throughout the paper, $\overset {d}{=}$ denotes equality in law), and a stick-breaking process $\ell ={({\ell }_n)}_{n\in \mathbb{N}}$ on $[0,t]$ based on the uniform law $\mathrm{U}(0,1)$ (i.e., $L_{0}:=t$, $L_{n}:=L_{n-1}U_{n}$, $\ell _{n}:=L_{n-1}-L_{n}$ for $n\in \mathbb{N}$, where ${(U_n)}_{n\in \mathbb{N}}$ is an i.i.d. sequence following $U_{n}\sim \mathrm{U}(0,1)$), which is independent of $Y$, such that a.s.,

(2.1)

The coupling $(X,Y)$ and $\ell$ can be constructed easily using the equality in law in González Cázares and Mijatović [32, Theorem 11]. For a construction of this coupling, see González Cázares et al. [35, Sect. 4.1]. Since given $L_{n}$, $(\ell _{k})_{k>n}$ is a stick-breaking process on $[0,L_{n}]$, for any $n\in \mathbb{N}$, (2.1) implies that

(2.2)

Observe that the vector $(Y_{L_{n}},\underline{Y}_{L_{n}},\underline{\tau }_{L_{n}}(Y))$ and the sum on the right-hand side of the identity in (2.2) are conditionally independent given $L_{n}$: the former (resp. latter) is a function of $(Y_{s})_{s\in [0,L_{n}]}$ (resp. $(Y_{s}-Y_{L_{n}})_{s\in [L_{n},t]}$), cf. Fig. 2. The vector $\underline{\chi }_{t}$ of interest is thus represented by the corresponding vector $(Y_{L_{n}},\underline{Y}_{L_{n}},\underline{\tau }_{L_{n}}(Y))$ over an exponentially small interval (since $\mathbb{E}[L_n]=2^{-n}t$) and $n$ independent increments of the Lévy process over random intervals independent of $Y$. In (2.2) and throughout, is the indicator function of the set $A$.

Fig. 2

The figure illustrates the first $n=4$ sticks of a stick-breaking process. The increments of $Y$ in (2.2) are taken over the intervals $[L_{k},L_{k-1}]$ of length $\ell _{k}$. Crucially, the time $L_{n}$ featuring in the vector $(Y_{L_{n}},\underline{Y}_{L_{n}},\underline{\tau }_{L_{n}}(Y))$ in (2.2) is exponentially small in $n$

We stress that (2.1) and (2.2) reduce the analysis of the path-functional $\underline{\chi }_{t}$ to that of the increments of $X$, since the “error term” $(Y_{L_{n}},\underline{Y}_{L_{n}},\underline{\tau }_{L_{n}}(Y))$ in (2.2) is typically exponentially small in $n$. For an arbitrary Lévy process $X'$, the vector $(X'_{t},\underline{X}_{t}',\underline{\tau}_{t}(X'))$ has a representation as in (2.1) for a Lévy process $Y'\overset {d}{=}X'$ independent of the stick-breaking process $\ell$. Thus more generally, the laws of the vectors $\underline{\chi}_{t}$ and $(X'_{t},\underline{X}_{t}',\underline{\tau}_{t}(X'))$ will be close if the laws of the increments of $Y$ and $Y'$ over the intervals $[L_{k}, L_{k-1}]$ are close. Indeed, by the identity in law (2.1), in order to quantify the distance between the vectors $\underline{\chi}_{t}$ and $(X'_{t},\underline{X}_{t}',\underline{\tau}_{t}(X'))$, it suffices to couple the increments of $Y$ and $Y'$ over the intervals $[L_{k}, L_{k-1}]$, $k\in \mathbb{N}$, with a common stick-breaking process $\ell$ independent of $(Y,Y')$ and compare the corresponding sums appearing on the right-hand side of (2.1). This observation constitutes a key step in the construction of the coupling used in the proof of Theorem 3.4 below, which in turn plays a crucial role in controlling the bias (see the subsequent results of Sect. 3) of our main simulation algorithm SBG-Alg described in Sect. 4 below. SBG-Alg is based on (2.2) with $X'$ being the Gaussian approximation of a general Lévy process $X$ introduced in Asmussen and Rosiński [2] and recalled briefly in the next subsection.

2.2 The Gaussian approximation

The law of a Lévy process $X=(X_{t})_{t\ge 0}$ is uniquely determined by the law of its marginal $X_{t}$ (for any $t>0$), which is in turn given by the Lévy–Khintchine formula [62, Theorem 8.1]: for $u\in \mathbb{R}$,

(2.3)

The Lévy measure $\nu$ is required to satisfy ${\int }_{\mathbb{R}\setminus \{0\}}min\{x^2,1\}\nu (dx)<\mathrm{\infty }$, while $\sigma \geq 0$ specifies the volatility of the Brownian component of $X$. Note that the drift $b\in \mathbb{R}$ depends on the cutoff function . Thus the Lévy triplet $(\sigma ^{2},\nu ,b)$, with respect to the cutoff function , determines the law of $X$. All Lévy triplets in the present paper use this cutoff function.

The Lévy–Itô decomposition at level $\kappa \in (0,1]$ (see [62, Theorems 19.2 and 19.3]) is given by

$$ X_{t}=b_{\kappa }t+\sigma B_{t}+J^{1,\kappa}_{t}+J^{2,\kappa}_{t}, \qquad t\geq 0, $$

(2.4)

where $b_{\kappa }:=b-\int _{(-1,1)\setminus (-\kappa ,\kappa )} x \nu (dx)$, $B=(B_{t})_{t\geq 0}$ is a standard Brownian motion and the processes $J^{1,\kappa}=(J^{1,\kappa}_{t})_{t\geq 0}$ and $J^{2,\kappa}=(J^{2,\kappa}_{t})_{t\geq 0}$ are Lévy with triplets $(0,\nu |_{(-\kappa ,\kappa )},0)$ and $(0,\nu {|}_{\mathbb{R}\setminus (-\kappa ,\kappa )},b-b_{\kappa })$, respectively. The processes $B$, $J^{1,\kappa}$, $J^{2,\kappa}$ in (2.4) are independent, $J^{1,\kappa}$ is an $L^{2}$-bounded martingale with jumps of magnitude less than $\kappa$ and $J^{2,\kappa}$ is a driftless (i.e., piecewise constant) compound Poisson process with intensity $\bar{\nu }(\kappa ):=\nu (\mathbb{R}\setminus (-\kappa ,\kappa ))$ and jump distribution $\nu {|}_{\mathbb{R}\setminus (-\kappa ,\kappa )}/\bar{\nu }(\kappa )$.

In applications, the main problem lies in the user’s inability to simulate the increments of $J^{1,\kappa}$ in (2.4), i.e., the small jumps of the Lévy process $X$. Instead of ignoring this component for a small value of $\kappa$, the Gaussian approximation in Asmussen and Rosiński [2],

$$ X^{(\kappa )}_{t} :=b_{\kappa }t + {\textstyle \sqrt {\overline {\sigma}_{\kappa}^{2}+\sigma ^{2}}} \, W_{t} + J^{2, \kappa}_{t}, \qquad \text{where } \overline{\sigma }^{2}_{\kappa} :=\int _{(-\kappa ,\kappa )\setminus \{0\}}x^{2}\nu (dx), $$

(2.5)

substitutes the martingale $\sigma B + J^{1,\kappa}$ in (2.4) with a Brownian motion with variance $\overline{\sigma }^{2}_{\kappa} + \sigma ^{2}$. In (2.5), the standard Brownian motion $W=(W_{t})_{t\geq 0}$ is independent of $J^{2,\kappa}$. Let $\overline{\sigma }_{\kappa}$ denote the nonnegative square root of $\overline{\sigma }^{2}_{\kappa}$. The Gaussian approximation of $X$ at level $\kappa$, given by the Lévy process $X^{(\kappa )}=(X^{(\kappa )}_{t})_{t\ge 0}$, is natural in the following sense: the weak convergence $\overline{\sigma }_{\kappa}^{-1}J^{1,\kappa}\overset{d}{\to }W$ (in the Skorokhod space $\mathcal{D}[0,\infty )$) as $\kappa \to 0$ holds if and only if $\overline{\sigma }_{\min \{K\overline{\sigma }_{\kappa},\kappa \}}/ \overline{\sigma }_{\kappa}\to 1$ for every $K>0$ (see [2]). This condition holds if $\overline{\sigma }_{\kappa}/\kappa \to \infty$, and the two conditions are equivalent if $\nu$ has no atoms in a neighbourhood of zero; see [2, Proposition 2.2].

Since $J^{2,\kappa}$ has an average of $\overline{\nu }(\kappa )t$ jumps on $[0,t]$, the expected cost of simulating the increment $X_{t}^{(\kappa )}$ is a constant multiple of $1+\overline{\nu }(\kappa )t$ (see Algorithm 1 below). Moreover, the user need only be able to sample from the normalised tails of $\nu$, which can typically be achieved in multiple ways (see e.g. Rosiński [61]). The behaviour of $\overline{\nu }(\kappa )$ and $\overline{\sigma }_{\kappa}$ as $\kappa \downarrow 0$, key in the analysis of the MC/MLMC complexity, can be described in terms of the Blumenthal–Getoor (BG) index $\beta$ from Blumenthal and Getoor [9], defined by

$$\begin{aligned} \beta :=\inf \{p>0:I_{0}^{p}< \infty \},\qquad \text{where $I_{0}^{p}:=\int _{(-1,1)\setminus \{0\}}|x|^{p}\nu (dx)$ for $p\geq 0$}. \end{aligned}$$

(2.6)

Note that $\beta \in [0,2]$, since $I_{0}^{2}<\infty$ for any Lévy measure $\nu$. Furthermore, $I_{0}^{1}<\infty$ if and only if the paths of $J^{1,\kappa}$ have finite variation. Moreover, $I_{0}^{p}<\infty$ for any $p>\beta$, but $I_{0}^{\beta}$ can be either finite or infinite. If $q\in [0,2]$ satisfies $I_{0}^{q}<\infty$, we have for all $\kappa \in (0,1]$ the inequalities (see e.g. [35, Lemma 9])

$$ \overline{\sigma }^{2}_{\kappa}\leq I_{0}^{q} \kappa ^{2-q}\qquad \text{and}\qquad \overline{\nu }(\kappa )\leq \overline{\nu }(1)+I_{0}^{q} \kappa ^{-q}. $$

(2.7)

Algorithm 1

Simulation of the law $\Pi _{t}^{\kappa _{1},\kappa _{2}}$

Finally, we stress that the dependence between $W$ in (2.5) and $\sigma B + J^{1,\kappa}$ in (2.4) has not been specified. This coupling can vary greatly, depending on the circumstance (e.g. the analysis of the Wasserstein distance between functionals of $X$ and $X^{(\kappa )}$ (Sect. 3) or the minimisation of level variances in MLMC (Sect. 4)). Thus unless otherwise stated, no explicit form for the dependence between $\sigma B + J^{1,\kappa}$ and $W$ is assumed.

3 Distance between the laws of $\underline{\chi }_{t}$ and its Gaussian approximation $\underline{\chi }_{t}^{(\kappa )}$

In this section, we present bounds on the distance between the laws of $\underline{\chi }_{t}$, defined in Sect. 2 above, and its Gaussian approximation $\underline{\chi }_{t}^{(\kappa )} :=(X_{t}^{(\kappa )}, \underline{X}_{t}^{(\kappa )},\underline{\tau }_{t}(X^{(\kappa )}))$, based on the Lévy process $X^{(\kappa )}$ in (2.5). The results in this section are crucial for the analysis of the computational complexity of the MC and MLMC estimators based on SBG-Alg discussed in Sect. 4 below.

Our bounds on the Wasserstein distance (see Theorem 3.4 and Corollary 3.5) are based on the SBG coupling constructed in Sect. 7.2 below, which in turn draws on the coupling in (2.1). Theorems 3.1 and 3.3 provide fundamental improvements (discussed in Sect. 3.1.1 below) for the bounds on the Wasserstein and Kolmogorov distances of the marginals $X_{t}$ and $X_{t}^{(\kappa )}$, which play a key role in the proof of Theorem 3.4. In Sect. 3.2 below, Theorem 3.4 is applied to control the bias of some discontinuous and non-Lipschitz payoffs of $\underline{\chi }_{t}$ arising in applications as well as the Kolmogorov distances between the components of $(\underline{X}_{t},\underline{\tau }_{t}(X))$ and $(\underline{X}_{t}^{(\kappa )},\underline{\tau }_{t}(X^{(\kappa )}))$.

3.1 The Wasserstein distance between the vectors $\underline{\chi }_{t}$ and $\underline{\chi }_{t}^{(\kappa )}$

In order to study the Wasserstein distance between $\underline{\chi }_{t}$ and $\underline{\chi }_{t}^{(\kappa )}$ via (2.1), (2.2), we have to quantify the Wasserstein and Kolmogorov distances between the increments $X_{s}$ and $X^{(\kappa )}_{s}$ for any time $s>0$. With this in mind, we start with Theorems 3.1 and 3.3, which play a key role in the proofs of the main results of the subsection, Theorem 3.4 and Corollary 3.5 below, and are of independent interest.

Theorem 3.1

There exist universal constants $K_{1}:=1/2$ and $K_{p}>0$, $p\in (1,2]$, independent of $(\sigma ^{2},\nu ,b)$, such that for any $t>0$ and $\kappa \in (0,1]$, there exists a coupling $(X_{t},X_{t}^{(\kappa )})$ satisfying for all $p\in [1,2]$ that

$$\mathbb{E}{[{|X_t-X_t^{(\kappa )}|}^p]}^{1/p}\le min\{\sqrt{2t}{\bar{\sigma }}_{\kappa },K_p\kappa {\phi }_{\kappa }^{2/p}\},\mathit{\text{where}}{\phi }_{\kappa }:=\frac{{\bar{\sigma }}_{\kappa }}{\sqrt{{\bar{\sigma }}_{\kappa }^2+{\sigma }^2}}.$$

(3.1)

Bounds on the Kolmogorov distance may require the following generalisation of Orey’s condition, which makes the distribution of $X_{t}$ sufficiently regular (see Sato [62, Proposition 28.3]).

Assumption 3.2

We have $\inf _{u\in (0,1]}u^{\delta -2}(\overline{\sigma }^{2}_{u}+\sigma ^{2})>0$ for some $\delta \in (0,2]$.

Note that if $\sigma \ne 0$, Assumption 3.2 holds with $\delta =2$. If $\sigma = 0$ and $\delta$ satisfies the inequality in Assumption 3.2, we must have $\beta \ge \delta$, where $\beta$ is the Blumenthal–Getoor index defined in (2.6) above. In fact, models typically used in applications either have $\sigma \neq 0$ or Assumption 3.2 holds with $\delta =\beta$. However, for Orey’s process (defined in [62, Example. 41.23]), Assumption 3.2 holds for some $\delta < \beta$, but not for $\delta = \beta$ (see details in Bang et al. [4, Example. 2.7]).

Theorem 3.3

(a) There exists a constant $C_{\mathrm{BE}}\in (0,\frac{1}{2})$ such that for any $t>0$, $\kappa \in (0,1]$, we have

$$\underset{x\in \mathbb{R}}{sup}|\mathbb{P}[X_t\le x]-\mathbb{P}[X_t^{(\kappa )}\le x]|\le \frac{C_{\mathrm{BE}}\kappa {\phi }_{\kappa }^3}{{\bar{\sigma }}_{\kappa }\sqrt{t}}.$$

(3.2)

(b) Let Assumption 3.2hold. Then for every $T>0$, there exists a constant $C>0$, depending only on $(T,\delta ,\sigma ,\nu )$, such that for any $\kappa \in (0,1]$ and $t\in (0,T]$, we have

$$\underset{x\in \mathbb{R}}{sup}|\mathbb{P}[X_t\le x]-\mathbb{P}[X_t^{(\kappa )}\le x]|\le {(C{t}^{-1/\delta }min\{\sqrt{t}{\bar{\sigma }}_{\kappa },\kappa {\phi }_{\kappa }\})}^{2/3}.$$

(3.3)

Denote $x^{+}:=\max \{x,0\}$ for $x\in \mathbb{R}$. The next result quantifies the Wasserstein distance between the laws of the vectors $\underline{\chi }_{t}$ and $\underline{\chi }_{t}^{(\kappa )}$.

Theorem 3.4

For any $\kappa \in (0,1]$ and $t>0$, there exists a coupling between $X$ and $X^{(\kappa )}$ on the interval $[0,t]$ such that we have for $p\in \{1,2\}$ the inequalities

$$\mathbb{E}{[max{\{|X_t-X_t^{(\kappa )}|,|{\underset{\_}{X}}_t-{\underset{\_}{X}}_t^{(\kappa )}|\}}^p]}^{1/p}\le {\mu }_p(\kappa ,t),$$

(3.4)

where

$$\begin{aligned} \mu _{1}(\kappa ,t) &: = \min \{2\sqrt{2t}\overline{\sigma }_{\kappa}, \kappa \varphi _{\kappa}^{2} \} \Big(1+\log ^{+}\big(2\sqrt{2t}( \overline{\sigma }_{\kappa}/\kappa ) \varphi _{\kappa}^{-2}\big)\Big), \\ \mu _{2}(\kappa ,t)&:= \sqrt{2} \mu _{1}(\kappa ,t) \\ & \phantom{=:} + \min \{\sqrt{2t}\overline{\sigma }_{\kappa}, K_{2}\kappa \varphi _{ \kappa }\} \sqrt{1+2\log ^{+}\big(K_{2}^{-1}\sqrt{2t}( \overline{\sigma }_{\kappa}/ \kappa )\varphi _{\kappa}^{-1}\big)}, \end{aligned}$$

(3.5)

with $\varphi _{\kappa}=\overline{\sigma }_{\kappa}/ \sqrt{ \overline{\sigma }_{\kappa}^{2}+\sigma ^{2}}$ and the universal constant $K_{2}$ from Theorem 3.1, and

$$\mathbb{E}[|{\underset{\_}{\tau }}_t(X)-{\underset{\_}{\tau }}_t(X^{(\kappa )})|]\le {\mu }_0^{\tau }(\kappa ,t):=\sqrt{t}(\kappa /{\bar{\sigma }}_{\kappa }){\phi }_{\kappa }^3.$$

(3.6)

Moreover, under Assumption 3.2for some $\delta \in (0,2]$, there exists for every $T>0$ a constant $C>0$, dependent only on $(T,\delta ,\sigma ,\nu )$, such that for all $t\in [0,T]$ and $\kappa \in (0,1]$, we have

$$\mathbb{E}[|{\underset{\_}{\tau }}_t(X)-{\underset{\_}{\tau }}_t(X^{(\kappa )})|]\le {\mu }_{\delta }^{\tau }(\kappa ,t),$$

(3.7)

where $\psi _{\kappa} :=C\kappa \varphi _{\kappa}$ and

$$\begin{aligned} & \mu ^{\tau}_{\delta}(\kappa ,t) \!:=\textstyle\begin{cases} \min \{t,\psi _{\kappa}^{\delta}\} +t^{1-\frac{2}{3\delta}}\psi _{\kappa}^{\frac{2}{3}} (1-\min \{1,t^{- \frac{1}{\delta}} \psi _{\kappa }\}^{\delta -\frac{2}{3}} ), &\quad \delta \ne \frac{2}{3}, \\ \min \{t,\psi _{\kappa}^{\frac{2}{3}}\} (1+\log ^{+}(t\psi _{\kappa}^{- \frac{2}{3}}) ), &\quad \delta =\frac{2}{3}. \end{cases}\displaystyle \end{aligned}$$

(3.8)

The proof of Theorem 3.4, given in Sect. 7.2 below, constructs the SBG coupling $(X,X^{(\kappa )})$, satisfying the above inequalities, in terms of the distribution functions of the marginals $X_{s}$ and $X^{(\kappa )}_{s}$ (for $s>0$) and the coupling used in (2.1); see González Cázares et al. [35] for the latter. The key idea is to couple $\underline{\chi }_{t}$ and $\underline{\chi }_{t}^{(\kappa )}$ so that they share the stick-breaking process in their respective SB representations (2.1), while the increments of the associated Lévy processes over each interval $[L_{n},L_{n-1}]$ are coupled so that they minimise appropriate Wasserstein distances. This coupling produces a bound on the distance between $\underline{\chi }_{t}$ and $\underline{\chi }_{t}^{(\kappa )}$ that depends only on the distances between the marginals of $X_{s}$ and $X_{s}^{(\kappa )}$, $s>0$, so that Theorems 3.1 and 3.3 can be applied. We stress that the bound in (3.4) cannot be obtained from Doob’s $L^{2}$-maximal inequality and Theorem 3.1: if the processes $X$ and $X^{(\kappa )}$ are coupled in such a way that $X_{t}-X_{t}^{(\kappa )}$ satisfies the inequality in (3.1), the difference process $(X_{s}-X_{s}^{(\kappa )})_{s\in [0,t]}$ need not be a martingale.

Inequality (3.4) holds without assumptions on $X$ and is at most a logarithmic factor worse than the marginal inequality (3.1) for $p\in \{1,2\}$, with the upper bound satisfying $\mu _{p}(\kappa ,t)\leq 2\kappa \log (1/\kappa )$ for all sufficiently small $\kappa$. Moreover, by Jensen’s inequality, the SBG coupling satisfies for all $1< p<2$ the inequality

$$\mathbb{E}{[max{\{|X_t-X_t^{(\kappa )}|,|{\underset{\_}{X}}_t-{\underset{\_}{X}}_t^{(\kappa )}|\}}^p]}^{1/p}\le {\mu }_2(\kappa ,t).$$

In the absence of a Brownian component (i.e., $\sigma =0$), we have $\varphi _{\kappa}=1$, making the upper bound $\mu _{2}(\kappa ,t)$ proportional to $\mu _{1}(\kappa ,t)$ as $\kappa \to 0$. If $\sigma >0$, then $\mu _{1}(\kappa ,t)\leq 2\kappa \overline{\sigma }_{\kappa}^{2}\log (1/( \kappa \overline{\sigma }_{\kappa}))/\sigma ^{2}$ for all small $\kappa$ and typically, $\mu _{2}(\kappa ,t)$ is proportional to $\kappa \overline{\sigma }_{\kappa } {\textstyle \sqrt {\log (1/(\kappa \overline {\sigma}_{\kappa}))}}$ as $\kappa \to 0$, which dominates $\mu _{1}(\kappa ,t)$.

The bound in (3.6) holds without assumptions on the Lévy process $X$, while (3.7) requires Assumption 3.2 and is the sharper the larger the value of $\delta \in (0,2]$ satisfying Assumption 3.2. If $\sigma >0$, the inequality in (3.6) is sharper than (3.7), i.e. $\mu _{0}^{\tau}(t,\kappa )\le \mu _{2}^{\tau}(t,\kappa )$ for all small $\kappa >0$. However, if $\sigma =0$ and $\delta \in (0,2)$ satisfies Assumption 3.2, then typically $\mu _{0}^{\tau}(\kappa ,t)$ is proportional to $\kappa ^{\delta /2}$, while $\mu _{\delta}^{\tau}(\kappa ,t)$ behaves as as $\kappa \to 0$, implying that (3.7) is sharper than (3.6) for $\delta <4/3$. The smallest of the upper bounds in (3.6) and (3.7) is

$$\mu ^{\tau}_{*}(\kappa ,t) :=\min \big\{ \mu _{0}^{\tau}( \kappa ,t), \inf \{\mu _{\delta}^{\tau}(\kappa ,t) :\delta \in (0,2] \enskip \text{satisfies Assumption\ 3.2} \}\big\} . $$

Under Assumption 3.2, for some constant $c_{t}>0$ and all $\kappa \in (0,1]$, we have

(3.9)

For any $a\in {\mathbb{R}}^d$, let $|a|:=\sum _{i=1}^{d}|a_{i}|$ denote its $\ell ^{1}$-norm. Recall that for $p\ge 1$, the $L^{p}$-Wasserstein distance (Villani [68, Definition 6.1]) between the laws of random vectors $\xi$ and $\zeta$ in ${\mathbb{R}}^d$ can be defined as

$${\mathcal{W}}_p(\xi ,\zeta ):=inf\{\mathbb{E}{[{|{\xi }^{\prime }-{\zeta }^{\prime }|}^p]}^{1/p}:{\xi }^{\prime }\stackrel{d}{=}\xi ,{\zeta }^{\prime }\stackrel{d}{=}\zeta \}.$$

(3.10)

Theorem 3.4 implies a bound on the $L^{p}$-Wasserstein distance between the vectors $\underline{\chi }_{t}$ and $\underline{\chi }_{t}^{(\kappa )}$, extending the bound on the distance between the laws of the marginals $X_{t}$ and $X_{t}^{(\kappa )}$ in Mariucci and Reiß[50, Theorem 9].

Corollary 3.5

Fix $\kappa \in (0,1]$ and $t>0$. Then

Moreover, $\mathcal{W}_{p}(\underline{\chi }_{t},\underline{\chi }_{t}^{( \kappa )})$ is bounded by twice the sum of both bounds for $p\in [1,2]$.

Given the bounds in Corollary 3.5 and Theorem 3.3, it is natural to inquire about the convergence in the Kolmogorov distance of the components of the vector $(\underline{X}_{t}^{(\kappa )}, \underline{\tau }_{t}(X^{(\kappa )}))$ to those of $(\underline{X}_{t},\underline{\tau }_{t}(X))$ as $\kappa \to 0$. This question is addressed by Corollary 3.14 below.

Dereich [21, Theorem 6.1] used the famous Komlós–Major–Tusnády (KMT) coupling to bound the $L^{2}$-Wasserstein distance between the paths of $X$ and $X^{(\kappa )}$ on $[0,t]$ in the supremum norm, implying a bound on $\mathcal{W}_{2}((X_{t},\underline{X}_{t}),(X_{t}^{(\kappa )}, \underline{X}_{t}^{(\kappa )}))$ proportional to $\kappa \log (1/\kappa )$ as $\kappa \to 0$; cf. [21, Corollary 6.2]. If $\sigma >0$, $\mu _{2}(\kappa ,t)$ in (3.4) is bounded by a multiple of $\kappa \overline{\sigma }_{\kappa }\log (1/(\kappa \overline{\sigma }_{\kappa}))$ for small $\kappa$ and is thus smaller than a multiple of $\kappa ^{2-q/2}$ for any $q\in (\beta ,2)$ (where $\beta$ is the BG index defined in (2.6)). As mentioned above, $\mu _{2}(\kappa ,t)$ is bounded by a multiple of $\kappa \log (1/\kappa )$ for small $\kappa$. Unlike the SBG coupling which underpins Theorem 3.4, the KMT coupling does not imply a bound on the distance between the times of the infima $\underline{\tau }_{t}(X)$ and $\underline{\tau }_{t}(X^{(\kappa )})$ as these are not Lipschitz functionals of the trajectories with respect to the supremum norm.

Remark 3.6

The bounds on $\mathbb{E}[|{\underset{\_}{\tau }}_t(X)-{\underset{\_}{\tau }}_t(X^{(\kappa )})|]$ in Theorem 3.4 and Corollary 3.5, based on the SB representation in (2.1), require a control on the expected difference between the signs of the components of $(X_{s}, X_{s}^{(\kappa )})$ as either $s$ or $\kappa$ tend to zero. This is achieved via the minimal transport coupling (see (7.1) and Lemma 7.2 below) and a general bound in Theorem 3.3 on the Kolmogorov distance. However, further improvements seem possible in the finite variation case if the natural drift (i.e., the drift of $X$ when small jumps are not compensated) is nonzero. Intuitively, the sign of the natural drift determines the sign of both components of $(X_{s}, X_{s}^{(\kappa )})$ with overwhelming likelihood as $s\to 0$. This suggestion is left for future research.

3.1.1 Why are Theorems 3.1 and 3.3 an improvement on the existing bounds on the distance between the laws of $X_{t}$ and its Gaussian approximation $X_{t}^{(\kappa )}$?

Theorem 3.1 bounds the Wasserstein distance between $X_{t}$ and $X_{t}^{(\kappa )}$. The inequality in (3.1) sharpens the bound $\mathbb{E}{[{|X_t-X_t^{(\kappa )}|}^p]}^{1/p}\le min\{\sqrt{2t}{\bar{\sigma }}_{\kappa },K_p\kappa \}$, established by Mariucci and Reiß [50, Theorem 9], as follows. The factor $\varphi _{\kappa}^{2/p}\in [0,1]$ tends to zero (as $\kappa \to 0$) as a constant multiple of $\overline{\sigma }_{\kappa}^{2/p}$ if the Brownian component is present (i.e., $\sigma >0$) and is equal to 1 when $\sigma =0$. The bound in (3.1) cannot be improved in general in the sense that there exists a Lévy process for which, up to constants, the reverse inequality holds (see Mariucci and Reiß[50, Remark 3] and Fournier [27, Sect. 4]).

The proof of Theorem 3.1, given in Sect. 7.1 below, decomposes the increment $M_{t}^{(\kappa )}$ of the Lévy martingale $M^{(\kappa )}:=\sigma B + J^{1,\kappa}$ into a sum of $m$ i.i.d. copies of $M_{t/m}^{(\kappa )}$ and applies a Berry–Esseen-type bound established by Rio [60] for the Wasserstein distance in the context of a central limit theorem (CLT) as $m\to \infty$. The small-time moment asymptotics of $M_{t/m}^{(\kappa )}$ in Figueroa-López [26] imply that $M^{(\kappa )}_{t}$ is much closer to the Gaussian limit in the CLT if the Brownian component is present than if $\sigma =0$. This explains a vastly superior rate in (3.1) in the case $\sigma ^{2}>0$.

The proof of Theorem 3.3 is in Sect. 7.1 below. Part (a) follows a similar strategy as in the proof of Theorem 3.1, applying the Berry–Esseen theorem (instead of [60, Theorem 4.1]) to bound the Kolmogorov distance. By the same reasoning applied in the previous paragraph to the bound in (3.1), the rate in (3.2) is far better if $\sigma ^{2}>0$. The proof of Theorem 3.3 (b) bounds the density of $X_{t}$ using results due to Picard [58] and applies (3.1).

Note that no assumption is made on the Lévy process $X$ in Theorem 3.3 (a). In particular, Assumption 3.2 is not required in part (a); however, if Assumption 3.2 is not satisfied, implying in particular that $\sigma =0$, it is possible for the bound in (3.2) not to vanish as $\kappa \to 0$ even if the Lévy process has infinite activity, i.e., $\nu (\mathbb{R}\setminus \{0\})=\mathrm{\infty }$. In fact, if $\sigma =0$, the bound in (3.2) vanishes (as $\kappa \to 0$) if and only if $\overline{\sigma }_{\kappa}/\kappa \to \infty$, which is also a necessary and sufficient condition for the weak limit $\overline{\sigma }_{\kappa}^{-1}J^{1,\kappa}\overset{d}{\to }W$ to hold whenever $\nu$ has no atoms in a neighbourhood of 0 (see Asmussen and Rosiński [2, Proposition 2.2]).

If $X$ has a Brownian component (i.e., $\sigma \ne 0$), the bound on the total variation distance between the laws of $X_{t}$ and $X^{(\kappa )}_{t}$ established in Mariucci and Reiß[50, Proposition 8] implies the bound

$$\underset{x\in \mathbb{R}}{sup}|\mathbb{P}[X_t\le x]-\mathbb{P}[X_t^{(\kappa )}\le x]|\le \frac{min\{\sqrt{8t}{\bar{\sigma }}_{\kappa },\kappa \}}{\sqrt{2\pi {\sigma }^{2}t}}$$

on the Kolmogorov distance. This inequality is both generalised and sharpened (as $\kappa \to 0$) by the bound in (3.2). Further improvements to the bound on the total variation were made in Carpentier et al. [12], but the implied rates for the Kolmogorov distance are worse than the ones in Theorem 3.3 and require model restrictions when $\sigma =0$ (beyond those of Theorem 3.3 (b)) that can be hard to verify (see [12, Sect. 2.1.1]).

We stress that the dependence on $t$ in the bounds of Theorem 3.3 is explicit. This is crucial in the proof of Theorem 3.4 as we need to apply (3.2), (3.3) over intervals of small random lengths. A related result proved by Dia [24, Proposition 10] contains similar bounds which are non-explicit in $t$ and suboptimal in $\kappa$.

If Assumption 3.2 is satisfied, the parameter $\delta$ in part (b) of Theorem 3.3 should be taken as large as possible to get the sharpest inequality in (3.3). If $\sigma \ne 0$ (equivalently $\delta =2$), the bound in part (a) has a faster decay in $\kappa$ than the bound in part (b). If $\sigma =0$ (equivalently $0<\delta <2$), it is possible for the bound in part (a) to be sharper than that in part (b) or vice versa. Indeed, it is easy to construct a Lévy measure $\nu$ such that $\delta \in (0,2)$ in Theorem 3.3 (b) satisfies $\lim _{u\downarrow 0}u^{\delta -2}\overline{\sigma }_{u}^{2} =\inf _{u \in (0,1]}u^{\delta -2}\overline{\sigma }_{u}^{2}=1$. Then the bound in (3.2) is a multiple of $t^{-1/2}\kappa ^{\delta /2}$ as $t,\kappa \to 0$, while that in (3.3) behaves as $t^{-2/(3\delta )}\kappa ^{2/3}\min \{1,t^{1/3}\kappa ^{-\delta /3}\}$. Hence one bound may be sharper than the other depending on the value of $\delta$, as $t$ and/or $\kappa$ tend to zero. In fact, we use the bound in part (b) only when the maximal $\delta$ satisfying the assumption of Theorem 3.3 (b) is smaller than $4/3$. In that case, the activity of the Lévy measure around 0 is bounded away from its maximal possible activity, which would correspond to $\delta$ being close to 2.

3.2 The bias of locally Lipschitz and discontinuous functions of $\underline{\chi }_{t}$ and the Kolmogorov distance between the vectors $\underline{\chi }_{t}$ and $\underline{\chi }_{t}^{(\kappa )}$

The main tool for studying the bias of locally Lipschitz and discontinuous payoff functions of $\underline{\chi }_{t}$ is the SBG coupling underpinning Theorem 3.4. The Lipschitz case follows trivially from Theorem 3.4. Indeed, for any $d\in \mathbb{N}$, let ${\mathrm{Lip}}_K({\mathbb{R}}^d)$ denote the space of real-valued Lipschitz functions on ${\mathbb{R}}^d$ (under the $\ell ^{1}$-norm given above (3.10)) with Lipschitz constant $K>0$ and note that the triangle inequality and Theorem 3.4 imply for any time horizon $T>0$ the bounds on the bias

$$\begin{array}{rl}|\mathbb{E}[f(X_T,{\underset{\_}{X}}_T)]-\mathbb{E}[f(X_T^{(\kappa )},{\underset{\_}{X}}_T^{(\kappa )})]|& \le 2K{\mu }_1(\kappa ,T),\\ |\mathbb{E}[g({\underset{\_}{\tau }}_T)]-\mathbb{E}[g({\underset{\_}{\tau }}_T(X^{(\kappa )}))\left]\right|& \le K^{\prime }{\mu }_{\ast }^{\tau }(\kappa ,T),\end{array}$$

(3.11)

where $f\in {\mathrm{Lip}}_K({\mathbb{R}}^2)$ satisfies $\mathbb{E}[|f(X_T,{\underset{\_}{X}}_T)|]<\mathrm{\infty }$ and $g\in {\mathrm{Lip}}_{K^{\prime }}(\mathbb{R})$.

In applications, the process $X$ is often used to model log-returns of a risky asset $(S_{0} e^{X_{t}})_{t\geq 0}$. It is thus important to understand the bias of a Monte Carlo estimator for the class ${\mathrm{locLip}}_K({\mathbb{R}}^2)$ of locally Lipschitz functions, with the defining property $f\in {\mathrm{locLip}}_K({\mathbb{R}}^2)$ if and only if

$$|f(x,y)-f(x^{\prime },y^{\prime })|\le K(|e^x-e^{x^{\prime }}|+|e^y-e^{y^{\prime }}|)\text{for any}x,x^{\prime },y,y^{\prime }\in \mathbb{R}$$

(equivalently $(x,y)\mapsto f(\log x,\log y)$ is in $\mathrm{Lip}_{K}((0,\infty )\times (0,\infty ))$). Such payoffs arise in risk management (e.g. absolute drawdown) and in the pricing of hindsight call, perpetual American call and lookback put options.

Proposition 3.7

Let $f\in {\mathrm{locLip}}_K({\mathbb{R}}^2)$ and assume $\int _{[1,\infty )}e^{2x}\nu (dx)<\infty$, where $\nu$ is the Lévy measure of $X$. For any $T>0$ and $\kappa \in (0,1]$ and $\mu _{2}(\kappa ,T)$ defined in (3.5), the SBG coupling satisfies

$$\mathbb{E}[|f(X_T,{\underset{\_}{X}}_T)-f(X_T^{(\kappa )},{\underset{\_}{X}}_T^{(\kappa )})|]\le 4K\mathbb{E}{[e^{2X_T}]}^{1/2}(1+e^{{\bar{\sigma }}_{\kappa }^{2}T}){\mu }_2(\kappa ,T).$$

The assumption $\int _{[1,\infty )}e^{2x}\nu (dx)<\infty$ is equivalent to $\mathbb{E}[e^{2X_T}]<\mathrm{\infty }$ (see Sato [62, Theorem 25.3]), which is a natural requirement as the asset price model $(S_{0} e^{X_{t}})_{t\geq 0}$ ought to have finite variance. Moreover, via the Lévy–Khintchine formula, an explicit bound on the expectation $\mathbb{E}[e^{2X_T}]$ (and hence the constant in the inequality of Proposition 3.7) in terms of the Lévy triplet of $X$ can be obtained.

The bound in Proposition 3.7 does not via duality imply an analogous bound involving a function of the supremum $\overline{X}_{T}$, since the assumption is not symmetric in the Lévy measure. However, for $f(X_{T},\overline{X}_{T})$ the proof of Proposition 3.7 in Sect. 7.3 yields

$$\mathbb{E}[|f(X_T,{\bar{X}}_T)-f(X_T^{(\kappa )},{\bar{X}}_T^{(\kappa )})|]\le 4K{(\mathbb{E}[exp(2{\bar{X}}_T)]+\mathbb{E}[exp(2{\bar{X}}_T^{(\kappa )})])}^{1/2}{\mu }_2(\kappa ,T),$$

where both expectations $\mathbb{E}[e^{2{\bar{X}}_T}]$ and $\mathbb{E}[e^{2{\bar{X}}_T^{(\kappa )}}]$ are finite under our natural assumption $\int _{[1,\infty )}e^{2x}\nu (dx)<\infty$ and can be bounded explicitly in terms of the Lévy triplet of $X$; see e.g. the proof of [35, Proposition 2]. Thus the bias for $f\in {\mathrm{locLip}}_K({\mathbb{R}}^2)$ (applied to either $(X_{T},\overline{X}_{T})$ or $(X_{T},\underline{X}_{T})$) is at most a multiple of $\kappa \log (1/\kappa )$, as is by (3.11) the case for $f\in {\mathrm{Lip}}_K({\mathbb{R}}^2)$; see the discussion after Theorem 3.4.

In financial markets, the class of barrier-type functions arises naturally. For constants $K,M\geq 0$, $y<0$, define

(3.12)

Note that lies in $\mathrm{BT}_{1}(y,0,1)$ and satisfies . Moreover, a down-and-out put option payoff , for some constants $y<0<k$, is in $\mathrm{BT}_{1}(y,e^{k},e^{k}-e^{y})$. Bounding the bias of the estimators for functions in $\mathrm{BT}_{1}(y,K,M)$ requires the following regularity of the distribution of $\underline{X}_{T}$ at $y$.

Assumption 3.8

Given $C,\gamma >0$ and $y<0$, we have the inequality

$$|\mathbb{P}[{\underset{\_}{X}}_T\le x+y]-\mathbb{P}[{\underset{\_}{X}}_T\le y]|\le C{|x|}^{\gamma }\mathit{\text{for all }}x\in \mathbb{R}.$$

Proposition 3.9

Let $f\in \mathrm{BT}_{1}(y,K,M)$ for some $K,M\geq 0$ and $y<0$. If $y$ and some $C,\gamma >0$ satisfy Assumption 3.8, then for any $T>0$ and $\kappa \in (0,1]$, the SBG coupling satisfies

$$\begin{array}{rl}& \mathbb{E}[|f(X_T,{\underset{\_}{X}}_T)-f(X_T^{(\kappa )},{\underset{\_}{X}}_T^{(\kappa )})|]\\ & \le K{\mu }_1(\kappa ,T)+M^{\prime }min\{{\mu }_1{(\kappa ,T)}^{\frac{\gamma }{1+\gamma }},{\mu }_2{(\kappa ,T)}^{\frac{2\gamma }{2+\gamma }}\},\end{array}$$

(3.13)

where $M' = M\max \{(1+1/\gamma )(2C\gamma )^{1/(1+\gamma )}, (1+2/\gamma )(C \gamma )^{2/(2+\gamma )}\}$.

Remark 3.10

Because we have $\mu _{1}(\kappa ,T)\to 0$ and $\mu _{2}(\kappa ,T)\to 0$ as $\kappa \to 0$ and $\gamma /(1+ \gamma )<2\gamma /(2+\gamma )$ for all $\gamma >0$, the bound in (3.13) is typically dominated by a multiple of $\mu _{1}(\kappa ,T)^{\gamma /(1+\gamma )}$, if $\sigma \ne 0$ and $\beta <2-\gamma$ (recall the definition of the BG index $\beta$ in (2.6)), or by $\mu _{2}(\kappa ,T)^{2\gamma /(1+\gamma )}$, otherwise. By Hölder’s inequality, $f$ in (3.13) need not be bounded if appropriate moments of $X$ exist.

The proof of Proposition 3.9 is in Sect. 7.3 below. Assumption 3.8 with $\gamma =1$ requires the distribution function of $\underline{X}_{T}$ to be locally Lipschitz at $y$. By the Lebesgue differentiation theorem (see Cohn [18, Theorem 6.3.3]), any distribution function is differentiable Lebesgue-a.e., implying that Assumption 3.8 holds for $\gamma =1$ and a.e. $y<0$. However, there indeed exist Lévy processes that do not satisfy Assumption 3.8 with $\gamma =1$ for countably many levels $y$; see the example in González Cázares et al. [35, App. B]. (In fact, that example shows that Assumption 3.8 may fail at countably many levels $y$ for any $\gamma \in (0,1]$.) Proposition 3.15 below provides simple sufficient conditions, in terms of the Lévy triplet of $X$, for Assumption 3.8 to hold with $\gamma =1$ for all $y<0$. In particular, this is the case if $\sigma \ne 0$.

The next class of payoffs arises in the analysis of the duration of a drawdown. For $K,M\ge 0$, $s\in (0,T)$, let

(3.14)

The biases of these functions clearly include $|\mathbb{P}[{\underset{\_}{\tau }}_T(X)>s]-\mathbb{P}[{\underset{\_}{\tau }}_T(X^{(\kappa )})>s]|$. Analogously to Proposition 3.9, we require the following regularity from the distribution function of $\underline{\tau }_{T}(X)$.

Assumption 3.11

Given $C,\gamma >0$ and $s\in (0,T)$, we have the inequality

$$|\mathbb{P}[{\underset{\_}{\tau }}_T(X)\le s]-\mathbb{P}[{\underset{\_}{\tau }}_T(X)\le s+t]|\le C{|t|}^{\gamma }\mathit{\text{for all }}t\in \mathbb{R}.$$

Proposition 3.12

Let Assumption 3.11hold for some $s\in (0,T)$ and $C,\gamma >0$. Let $f\in \mathrm{BT}_{2}(s,K,M)$ for some $K,M\ge 0$. Then for all $\kappa \in (0,1]$, the SBG coupling satisfies

$$\begin{array}{rl}\mathbb{E}[|f({\underset{\_}{\chi }}_T)-f({\underset{\_}{\chi }}_T^{(\kappa )})|]& \le 2K{\mu }_1(\kappa ,T)\\ & \phantom{=:}+M{(2C\gamma )}^{1/(1+\gamma )}(1+1/\gamma ){\mu }_{\ast }^{\tau }{(\kappa ,T)}^{\gamma /(1+\gamma )}.\end{array}$$

(3.15)

Remark 3.13

As in Remark 3.10, the bound in (3.15) is asymptotically proportional to $\mu ^{\tau}_{*}(\kappa ,T)^{\gamma /(1+\gamma )}$ as $\kappa \to 0$. The inequality (3.15) can be generalised to unbounded functions $f$ if appropriate moments of $X$ exist.

If $X$ is not a compound Poisson process, Assumption 3.11 holds with $\gamma =1$ for all $s\in (0,T)$ since by Lemma 7.7 below, $\underline{\tau }_{T}(X)$ has a locally bounded density, making the distribution function of $\underline{\tau }_{T}(X)$ locally Lipschitz on $(0,T)$. Assumption 3.11 is satisfied if either $\nu (\mathbb{R}\setminus \{0\})=\mathrm{\infty }$ or $\sigma \ne 0$. In particular, Assumption 3.2 implies Assumption 3.11. The proof of Proposition 3.12 is in Sect. 7.3 below.

The classes $\mathrm{BT}_{1}(y,K,M)$ and $\mathrm{BT}_{2}(s,K,M)$ of payoffs in (3.12) and (3.14), respectively, consist of bounded functions. We stress that boundedness of the payoffs is not essential in Propositions 3.9 and 3.12. It can be substituted by a combination of a local Lipschitz assumption and a moment bound on the tails of the Lévy measure (cf. Proposition 3.7), typically satisfied in applications. The crucial Lemma 7.5, applied in the proofs of Propositions 3.9 and 3.12, can be generalised to unbounded payoffs by substituting the almost sure bound on the payoff in its current proof (see (7.11) below) with a bound on its expected value via Hölder’s inequality. The details are omitted for ease of exposition.

As a consequence of Proposition 3.9 (resp. 3.12), if Assumption 3.8 (resp. 3.11) holds uniformly over $y$ for fixed $C,\gamma >0$, then $\underline{X}_{T}^{(\kappa )}$ (resp. $\underline{\tau }_{T}(X^{(\kappa )})$) converges to $\underline{X}_{T}$ (resp. $\underline{\tau }_{T}(X)$) in the Kolmogorov distance as $\kappa \to 0$.

Corollary 3.14

(a) Suppose $C,\gamma >0$ satisfy Assumption 3.8for all $y<0$. Then for $\kappa \in (0,1]$,

$$\underset{x\in \mathbb{R}}{sup}|\mathbb{P}[{\underset{\_}{X}}_T\le x]-\mathbb{P}[{\underset{\_}{X}}_T^{(\kappa )}\le x]|\le M^{\prime }min\{{\mu }_1{(\kappa ,T)}^{\frac{\gamma }{1+\gamma }},{\mu }_2{(\kappa ,T)}^{\frac{2\gamma }{2+\gamma }}\},$$

where $M' = \max \{(1+1/\gamma )(2C\gamma )^{1/(1+\gamma )}, (1+2/\gamma )(C \gamma )^{2/(2+\gamma )}\}$.

(b) Suppose $C,\gamma >0$ satisfy Assumption 3.11for all $s\in [0,T]$. Then for $\kappa \in (0,1]$, we have

$$\underset{x\in \mathbb{R}}{sup}|\mathbb{P}[{\underset{\_}{\tau }}_T(X)\le x]-\mathbb{P}[{\underset{\_}{\tau }}_T(X^{(\kappa )})\le x]|\le {(2C\gamma )}^{\frac{1}{1+\gamma }}(1+1/\gamma ){\mu }_{\ast }^{\tau }{(\kappa ,T)}^{\frac{\gamma }{1+\gamma }}.$$

Proposition 3.15 gives sufficient conditions (in terms of the triplet $(\sigma ^{2},\nu ,b)$) for Assumptions 3.8 and 3.11 to hold for all $y<0$ and $s\in [0,T]$, respectively. Recall that a function $f(x)$ is said to be regularly varying with index $r$ as $x\to 0$ if $\lim _{x\to 0}f(\lambda x)/f(x)=\lambda ^{r}$ for every $\lambda >0$.

Proposition 3.15

Let $\overline{\nu }_{+}(x):=\nu ([x,\infty ))$ and $\overline{\nu }_{-}(x):=\nu ((-\infty ,-x])$ for $x>0$ and let $\beta$ be the BG index of $X$ defined in (2.6). Suppose that either (I) $\sigma > 0$ or (II) the Lévy measure $\nu$ satisfies the following conditions: $\overline{\nu }_{+}(x)$ is regularly varying with index $-\beta$ as $x\to 0$ and either

• $\beta =2$ and $\liminf _{x\to 0}\overline{\nu }_{+}(x)/\overline{\nu }_{-}(x)>0$, or

• $\beta \in (1,2)$ and $\lim _{x\to 0}\overline{\nu }_{+}(x)/\overline{\nu }_{-}(x)\in (0, \infty ]$.

Then there exist constants $\gamma >0$ and $C$ such that Assumption 3.11holds with $\gamma ,C$ for all $s\in [0,T]$. Moreover, for any compact $I\subseteq (-\infty ,0)$, Assumption 3.8holds with $\gamma =1$ and some constant $C_{I}$ for all $y\in I$.

Note that Proposition 3.15 holds if the roles of $\overline{\nu }_{+}$ and $\overline{\nu }_{-}$ are interchanged, i.e., $\overline{\nu }_{-}(x)$ is regularly varying and the limit conditions are satisfied by the quotients $\overline{\nu }_{-}(x)/\overline{\nu }_{+}(x)$. The assumptions of Proposition 3.15 are satisfied by most models used in practice that have infinite variation, including tempered stable and subordinated Brownian motion processes.

Proposition 3.15 is a consequence of a more general result, Proposition 7.9 below, stating that Assumptions 3.11 and 3.8 hold uniformly and locally uniformly, respectively, if over short time horizons, $X$ is “attracted to” an $\alpha$-stable process with non-monotone paths; see Sect. 7.3 below for details. In this case, $\rho :={lim}_{t\to 0}\mathbb{P}[X_t>0]$ exists in $(0,1)$, and $\gamma$ in the conclusion of Proposition 3.15, satisfying Assumption 3.11 on $[0,T]$, can be arbitrarily chosen in $(0,\min \{\rho ,1-\rho \})$. In contrast to Assumption 3.11, a simple sufficient condition for the uniform version of Assumption 3.8, required in Corollary 3.14(a), remains elusive beyond special cases such as stable or tempered stable processes with $\gamma$ in the interval $(0,\alpha (1-\rho ))$, where $\alpha$ is the stability parameter and $\rho$ is as above.

The reasoning in the previous paragraph does not apply if $X$ is attracted to a linear drift, since the paths of the limit are monotone, implying $\rho \in \{0,1\}$. This occurs if $X$ is of finite variation with $b\ne \int _{(-1,1)}x\nu (dx)$ or if $X$ is of infinite variation with $\beta =1$ (see Ivanovs [38, Theorem 2] for details). In these cases, the uniform convergence in Corollary 3.14 may fail due to an atom in the limit.

4 Simulation and the computational complexity of MC and MLMC

In this section, we describe a method using MC or MLMC for simulating the vector $\underline{\chi }_{T}^{(\kappa )}=(X_{T}^{(\kappa )},\underline{X}_{T}^{( \kappa )},\underline{\tau }_{T}(X^{(\kappa )}))$ (SBG-Alg in Sect. 4.1) and analyse the computational complexities for various locally Lipschitz and discontinuous functions of $\underline{\chi }_{T}^{(\kappa )}$ (Sect. 4.2). The numerical performance of SBG-Alg, which is based on the SB representation in (2.1), (2.2) of $\underline{\chi }_{T}^{(\kappa )}$, is far superior to that of the “obvious” algorithm for jump-diffusions (see Algorithm 2 below), particularly when the jump intensity is large (cf. Sects. 4.1.2 and 4.1.3). Moreover, SBG-Alg is designed with MLMC in mind, which turns out not to be feasible in general for the “obvious” algorithm (see Sect. 4.1.2).

Algorithm 2

Simulation of the law $\underline{\Pi }_{t}^{\kappa _{1},\kappa _{2}}$

Algorithm 3

(SBG-Alg) Simulation of the coupling $(\underline{\chi }^{(\kappa _{1})}_{T},\underline{\chi }^{(\kappa _{2})}_{T})$ with law $\underline{\Pi }_{n,T}^{\kappa _{1},\kappa _{2}}$

4.1 Simulation of $\underline{\chi }_{T}^{(\kappa )}$

The main aim of the subsection is to develop a simulation algorithm for the pair of vectors $(\underline{\chi }_{T}^{(\kappa )},\underline{\chi }_{T}^{(\kappa ')})$ at levels $\kappa ,\kappa '\in (0,1]$ over a time horizon $[0,T]$ such that the $L^{2}$-distance between $\underline{\chi }_{T}^{(\kappa )}$ and $\underline{\chi }_{T}^{(\kappa ')}$ tends to zero as $\kappa ,\kappa '\to 0$. SBG-Alg below, based on the SB representation in (2.2), achieves this aim; it applies Algorithm 1 for the increments over the stick-breaking lengths that arise in (2.2) and Algorithm 2 for the “error term” over the time horizon $[0,L_{n}]$. By Theorem 7.10 below, the $L^{2}$-distance for the coupling given in SBG-Alg decays to zero, ensuring the feasibility of MLMC (see Theorem 7.17 for the computational complexity of MLMC).

4.1.1 Simulation of $(X^{(\kappa _{1})}_{t},X^{(\kappa _{2})}_{t} )$

A simulation algorithm for a coupling $(X^{(\kappa _{1})}_{t},X^{(\kappa _{2})}_{t} )$ of Gaussian approximations (at levels $1\geq \kappa _{1}>\kappa _{2}>0$) of $X_{t}$ at an arbitrary time $t>0$ is based on the following observation. The compound Poisson processes $J^{2,\kappa _{1}}$ and $J^{2,\kappa _{2}}$ in the Lévy–Itô decomposition in (2.4) can be simulated jointly, as the jumps of $J^{2,\kappa _{1}}$ are precisely those of $J^{2,\kappa _{2}}$ with modulus of at least $\kappa _{1}$. By choosing the same Brownian motion $W$ in the representation (2.5) of $X^{(\kappa _{1})}_{t}$ and $X^{(\kappa _{2})}_{t}$, we obtain the coupling $(X^{(\kappa _{1})}_{t},X^{(\kappa _{2})}_{t} )$ with law $\Pi _{t}^{\kappa _{1},\kappa _{2}}$ given in Algorithm 1.

Since $Z^{(\kappa _{i})}_{t}\overset {d}{=}X^{(\kappa _{i})}_{t}$, $i\in \{1,2\}$, the definition in (3.10) and Proposition 7.11(a) below imply that the coupling $\Pi _{t}^{\kappa _{1},\kappa _{2}}$ provides the bound

$${\mathcal{W}}_2(X_t^{({\kappa }_1)},X_t^{({\kappa }_2)})\le \mathbb{E}{[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^2]}^{1/2}\le {(2t({\bar{\sigma }}_{{\kappa }_1}^2-{\bar{\sigma }}_{{\kappa }_2}^2))}^{1/2}.$$

(4.1)

This bound is not optimal since the sum of the jumps $J^{2,\kappa _{2}}_{t}-J^{2,\kappa _{1}}_{t}$ of magnitude in the interval $(\kappa _{2},\kappa _{1}]$ and the normal random variable $W_{t}$ constructed in Algorithm 1, which appear in the difference $Z^{(\kappa _{1})}_{t}-Z^{(\kappa _{2})}_{t}$, are independent. The minimal transport coupling, with the $L^{2}$-distance equal to $\mathcal{W}_{2} (X^{(\kappa _{1})}_{t},X^{(\kappa _{2})}_{t} )$, is not accessible via simulation.

An important open problem in this context is to find an algorithm that samples $Z^{(\kappa _{2})}_{t}$ as in Algorithm 1 and constructs

$$ Z^{(\kappa _{1})}_{t}= b_{\kappa _{1}}t + {\textstyle \sqrt {\sigma ^{2}+\overline {\sigma}^{2}_{\kappa _{2}}}}W_{t} + {\textstyle \sqrt {\overline {\sigma}^{2}_{\kappa _{1}}-\overline {\sigma}^{2}_{\kappa _{2}}}}W'_{t} +J^{2,\kappa _{2}}_{t},$$

where $W'_{t}$ is a normal variable with mean zero and variance $t$, independent of $W_{t}$ and $J^{2,\kappa _{2}}_{t}$, but coupled with the difference $J^{2,\kappa _{2}}_{t}-J^{2,\kappa _{1}}_{t}$ in a way that reduces the second moment $\mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^2]$ asymptotically as $\kappa _{1}\to 0$. Such an improvement in the bound in (4.1) on the $L^{2}$-Wasserstein distance would make the level variances in the MLMC estimator in (4.3), based on SBG-Alg, decay at a faster rate (because the increments in the SB representation in (2.2), and thus Algorithm 1, account for most of the output). Note, however, that sampling $W'_{t}$ independently of $J^{2,\kappa _{2}}_{t}-J^{2,\kappa _{1}}_{t}$ would increase the second moment $\mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^2]$ compared to the output of Algorithm 1, which uses a single normal random variable in both coordinates.

Since the law $\mathrm{Poi}(\overline{\nu }(\kappa _{2})t)$ of the variable $N_{t}$ in line 2 of Algorithm 1 is Poisson with mean $\overline{\nu }(\kappa _{2})t$, the expected number of steps of Algorithm 1 is bounded by a constant multiple of $1+\overline{\nu }(\kappa _{2})t$, which is in turn bounded by a negative power of $\kappa _{2}$ by (2.7). Since the computational complexity of sampling the law of $X^{(\kappa _{2})}_{t}$ is of the same order as that of the law $\Pi _{t}^{\kappa _{1},\kappa _{2}}$, in the complexity analysis of SBG-Alg below, we may apply Algorithm 1 with $\Pi _{t}^{1,\kappa}$ to sample $X^{(\kappa )}_{t}$ for any $\kappa \in (0,1]$.

4.1.2 Direct simulation of $(\underline{\chi }_{t}^{(\kappa _{1})},\underline{\chi }_{t}^{(\kappa _{2})})$

Algorithm 2 samples from the law $\underline{\Pi }_{t}^{\kappa _{1},\kappa _{2}}$ of a coupling $(\underline{\chi }_{t}^{(\kappa _{1})},\underline{\chi }_{t}^{( \kappa _{2})})$ for levels $0<\kappa _{2}<\kappa _{1}\leq 1$ and any $t>0$. In particular, it requires the sampler from Devroye [23, Alg. MAXLOCATION] for the law $\Phi _{t}(v,\mu )$ of $({\hat{B}}_{t},\underline{\hat{B}}_{t},\tau _{t}({\hat{B}}))$, where the process $({\hat{B}}_{s})_{s\ge 0}=(v B_{s}+\mu s)_{s\ge 0}$ is a Brownian motion with drift $\mu \in \mathbb{R}$ and volatility $v>0$.

Algorithm 2 samples the jump times and sizes of the compound Poisson process $J^{2,\kappa _{2}}$ on the interval $(0,t)$ and prunes the jumps to get $J^{2,\kappa _{1}}$. Then it samples the increment, infimum and the time the infimum is attained for the Brownian motion with drift on each interval between the jumps of $J^{2,\kappa _{2}}$. The pair $(\underline{\zeta }^{(\kappa _{1})},\underline{\zeta }^{(\kappa _{2})})$ clearly satisfies $\underline{\zeta }^{(\kappa _{i})}\overset {d}{=}\underline{\chi }_{t}^{( \kappa _{i})}$, $i\in \{1,2\}$. Since [23, Alg. MAXLOCATION] samples the law $\Phi _{t}(v,\mu )$ with expected runtime uniformly bounded over the choice of parameters $\mu$, $v$ and $t$, the computational cost of sampling the pair of vectors $(\underline{\chi }_{t}^{(\kappa _{1})},\underline{\chi }_{t}^{( \kappa _{2})})$ using Algorithm 2 is proportional to the cost of sampling $X^{(\kappa )}_{t}$ via Algorithm 1.

In principle, Algorithm 2 is an exact algorithm for the simulation of a coupling $(\underline{\chi }_{t}^{(\kappa _{1})},\underline{\chi }_{t}^{( \kappa _{2})})$. However, as explained in Remark 4.1 below, it cannot be applied within an MLMC simulation scheme for a function of $\underline{\chi }_{T}^{(\kappa )}$ at a fixed time horizon $T$. SBG-Alg below circumvents this issue via the SB representation in (2.2), which also makes SBG-Alg parallelisable and thus much faster in practice even in the context of MC simulation (see the discussion after Corollary 7.14 below).

Remark 4.1

To the best of our knowledge, there is no simulation algorithm for the increment, the infima and the times the infima are attained of a Brownian motion under different drifts, i.e., of the vector

$$\big(B_{t},\underline{B}^{(c_{1})}_{t},\underline{\tau }_{t}(B^{(c_{1})}), \underline{B}^{(c_{2})}_{t},\underline{\tau }_{t}(B^{(c_{2})})\big), \enskip \text{where}\enskip c_{1}\neq c_{2} \enskip \text{and}\enskip B_{s}^{(c)}=B_{s}+cs, \enskip s\ge 0. $$

Thus in line 7 of Algorithm 2, we are forced to take independent samples from $\Phi _{\delta _{k}}(\upsilon _{\kappa _{1}},b_{\kappa _{1}})$ and $\Phi _{\delta _{k}}(\upsilon _{\kappa _{2}},b_{\kappa _{2}})$ at each step $k$. In particular, the coupling of the marginals $X_{t}^{(\kappa _{1})}$ and $X_{t}^{(\kappa _{2})}$ of $\underline{\Pi }_{t}^{\kappa _{1},\kappa _{2}}$ given in line 16 of Algorithm 2 amounts to taking two independent Brownian motions in the respective representations in (2.5) of $X_{t}^{(\kappa _{1})}$ and $X_{t}^{(\kappa _{2})}$. Thus unlike the coupling defined in Algorithm 1, here, by Proposition 7.11 (b), the squared $L^{2}$-norm satisfies $\mathbb{E}[{(X_t^{({\kappa }_1)}-X_t^{({\kappa }_2)})}^2]\ge 2t{\sigma }^2$ for all levels $1\geq \kappa _{1}>\kappa _{2}>0$, where $\sigma ^{2}$ is the Gaussian component of $X$. Hence for a fixed time horizon, the coupling $\underline{\Pi }_{t}^{\kappa _{1},\kappa _{2}}$ of $\underline{\chi }_{t}^{(\kappa _{1})}$ and $\underline{\chi }_{t}^{(\kappa _{2})}$ is not sufficiently strong for an MLMC scheme to be feasible if $X$ has a Gaussian component, because the level variances do not decay to zero. However, by Proposition 7.11 (b), the $L^{2}$-distance between $\underline{\zeta }^{(\kappa _{1})}$ and $\underline{\zeta }^{(\kappa _{2})}$ constructed in Algorithm 2 does tend to zero with $t\to 0$. Thus SBG-Alg below, which applies Algorithm 2 over the time interval $[0,L_{n}]$ (recall $\mathbb{E}[L_n]=T/2^n$ from the SB representation (2.2)), circumvents this issue.

4.1.3 The SBG sampler

For a time horizon $T$, we can now define the coupling $\underline{\Pi }_{n,T}^{\kappa _{1},\kappa _{2}}$ of the vectors $\underline{\chi }^{(\kappa _{1})}_{T}$ and $\underline{\chi }^{(\kappa _{2})}_{T}$ via the following algorithm.

By the SB representation (2.2), the law $\underline{\Pi }_{n,T}^{\kappa _{1},\kappa _{2}}$ is indeed a coupling of the vectors $\underline{\chi }^{(\kappa _{1})}_{T}$ and $\underline{\chi }^{(\kappa _{2})}_{T}$ for any $n\in \mathbb{N}\cup \{0\}$. Note that if $n$ equals zero, the set $\{1,\ldots ,n\}$ in lines 1 and 2 of the algorithm is empty and the laws $\underline{\Pi }_{0,T}^{\kappa _{1},\kappa _{2}}$ and $\underline{\Pi }_{T}^{\kappa _{1},\kappa _{2}}$ coincide, implying that SBG-Alg may be viewed as a generalisation of Algorithm 2. The main advantage of SBG-Alg over Algorithm 2 is that it samples $n$ increments of the Gaussian approximation over the interval $[L_{n},T]$ using the fast Algorithm 1, with the “error term” contribution $\underline{\xi }_{i}$ being geometrically small in the number of sticks $n$.

The computational complexity of SBG-Alg and Algorithms 1 and 2 is simple to analyse. Assume throughout that all mathematical operations (addition, multiplication, exponentiation, etc.), as well as the evaluation of $\overline{\nu }(\kappa )$ and $\overline{\sigma }^{2}_{\kappa}$ for all $\kappa \in (0,1]$ have constant computational cost. Moreover, assume that the simulation of any of the following random variables has constant expected cost: standard normal ${\mathcal{N}}(0,1)$, uniform $\mathrm{U}(0,1)$, Poisson random variable (independently of its mean) and any jump with distribution $\nu {|}_{\mathbb{R}\setminus (-\kappa ,\kappa )}/\bar{\nu }(\kappa )$ (independently of the cutoff level $\kappa \in (0,1]$). Recall that [23, Alg. MAXLOCATION] samples the law $\Phi _{t}(v,\mu )$ with uniformly bounded expected cost for all values of the parameters $\mu \in \mathbb{R}$, $v>0$ and $t>0$. The next statement follows directly from the algorithms.

Corollary 4.2

Under the assumptions above, there exists a positive constant $C_{1}$ (resp. $C_{2}$; $C_{3}$), independent of $\kappa _{1},\kappa _{2}\in (0,1]$, $n\in \mathbb{N}$ and time horizon $t>0$, such that the expected computational complexity of Algorithm 1 (resp. Algorithm 2; SBG-Alg) is bounded by $C_{1}(1+\overline{\nu }(\kappa _{2})t)$ (resp. $C_{2}(1+\overline{\nu }(\kappa _{2})t)$; $C_{3}(n+\overline{\nu }(\kappa _{2})t)$).

Up to a multiplicative constant, Algorithms 1 and 2 have the same expected computational complexity. However, Algorithm 2 requires not only the additional simulation of the jump times of $X^{(\kappa _{2})}$ and a sample from $\Phi _{t}(v,\mu )$ using the sampler [23, Alg. MAXLOCATION] between any two consecutive jumps, but also a sequential computation of the output (the “for-loop” in lines 5–15) due to the condition in line 9 of Algorithm 2. This makes it hard to parallelise Algorithm 2. SBG-Alg avoids this issue by using the fast Algorithm 1 over the stick lengths in the SB representation (2.2) and calling Algorithm 2 only over the short time interval $[0,L_{n}]$, during which very few (if any) jumps of $X^{(\kappa _{2})}$ occur. Moreover, SBG-Alg consists of several conditionally independent evaluations of Algorithm 1, which is parallelisable, leading to additional numerical benefits (see Sect. 6.2 below).

Remark 4.3

Line 2 of SBG-Alg contains the only call of Algorithm 2, which samples the coupling $(\underline{\xi }_{1},\underline{\xi }_{2})$ of the “error terms” in the SB representation (2.2) over the geometrically small time interval $[0,L_{n}]$. There are two natural modifications of SBG-Alg that avoid Algorithm 2 altogether, but retain the asymptotic properties (up to logarithmic factors) of the bias and level variances: (I) set $(\underline{\xi }_{1},\underline{\xi }_{2})=0$ or (II) apply SBA introduced in González Cázares et al. [35] to approximate $\underline{\chi }^{(\kappa _{1})}_{L_{m}}$ and $\underline{\chi }^{(\kappa _{2})}_{L_{n}}$ as a function of the output of Algorithm 1 with $t=L_{n}$. Both of these choices would increase bias and level variance because unlike SBG-Alg, they are sampling from approximations to the laws of $\underline{\chi }^{(\kappa _{1})}_{L_{n}}$ and $\underline{\chi }^{(\kappa _{2})}_{L_{n}}$. This makes them slightly simpler to implement, but theoretically less attractive. Moreover, in order to match the asymptotic properties of the bias under SBG-Alg, the number of sticks $n$ in algorithms (I) and (II) would have to grow as a function of the decaying cutoff level $\kappa$.

4.2 MC and MLMC estimator based on SBG-Alg

This subsection gives an overview of the bounds on the computational complexity of the MC and MLMC estimators defined respectively in (4.2) and (4.3) below. Corollary 7.14 (for MC) and Theorem 7.17 (for MLMC) in Sect. 7.5 give the full analysis.

We suppose throughout the subsection that Assumption 3.2 holds with some $\delta \in (0,2]$. As discussed in Sect. 3.1 above, we take $\delta$ as large as possible. In particular, if $\sigma \neq 0$ then $\delta =2$. Let $q\in (0,2]$ be as in (2.7) and thus $q\ge \delta$ if $\sigma =0$. We take $q$ as small as possible. For processes used in practice with $\sigma =0$, we may typically take $\delta =q=\beta$, where $\beta$ is the BG index defined in (2.6). Assumption 3.11, required for the analysis of the class $\mathrm{BT}_{2}$ in (3.14) of discontinuous functions of $\underline{\tau }_{T}(X)$, holds with $\gamma =1$ as Assumption 3.2 is satisfied (see the discussion following Proposition 3.12). When analysing the class of discontinuous functions $\mathrm{BT}_{1}$ in (3.12), we suppose that Assumption 3.8 holds throughout with some $\gamma >0$.

4.2.1 Monte Carlo

Pick $\kappa \in (0,1]$ and let the sequence $\underline{\chi }_{T}^{\kappa ,i}$, $i\in \mathbb{N}$, be i.i.d. (with the same distribution as $\underline{\chi }_{T}^{(\kappa )}$) simulated by SBG-Alg with $n\in \mathbb{N}\cup \{0\}$ sticks. The MC estimator based on $N\in \mathbb{N}$ independent samples is given by

$$ \Upsilon _{\mathrm{MC}}:=\frac{1}{N}\sum _{i=1}^{N} f ( \underline{\chi }_{T}^{\kappa ,i} ). $$

(4.2)

The MC estimator is $L^{2}$-accurate at level $\epsilon >0$ if its bias is smaller than $\epsilon /\sqrt{2}$ and the number $N$ of independent samples is proportional to $\epsilon ^{-2}$; see Appendix A.1. Table 1 contains a summary of the values $\kappa$, as a function of $\epsilon$, such that the bias of the estimator in (4.2) is at most $\epsilon /\sqrt{2}$, and of the associated Monte Carlo cost $\mathcal{C}_{\mathrm{MC}}(\epsilon )$ (up to a constant) for various classes of functions of $\underline{\chi }_{T}$ analysed in Sect. 3.2. Corollary 7.14 below contains the full details of the analysis.

The number $n\in \mathbb{N}\cup \{0\}$ of sticks in SBG-Alg affects neither the law of $\underline{\chi }_{T}^{(\kappa )}$ nor the asymptotic behaviour as $\epsilon \searrow 0$ of the computational complexity $\mathcal{C}_{\mathrm{MC}}(\epsilon )$. It only impacts the MC estimator in (4.2) through numerical stability and the reduction of the simulation cost by a constant factor. It is hard to determine the optimal choice for $n$. Clearly, the choice $n=0$ (i.e., Algorithm 2) is not a good one as discussed in Sect. 4.1.3. A balance needs to be struck between (i) having a vanishingly small number of jumps in the time interval $[0,L_{n}]$, so that Algorithm 2 behaves in a numerically stable way, and (ii) not having too many sticks so that line 2 of SBG-Alg does not execute redundant computation of many geometrically small increments of $X^{(\kappa )}$, which are not detected in the final output. A good rule of thumb is $n=n_{0} + \lceil{\log ^{2}(1+\overline{\nu }(\kappa )T)} \rceil$, where $\lceil x\rceil :=inf\{j\in \mathbb{Z}:j\ge x\}$, $x\in \mathbb{R}$, and the initial value $n_{0}$ is chosen so that some sticks are present if for large $\kappa$, the total expected number $\overline{\nu }(\kappa )T$ of jumps is small (e.g. $n_{0}=5$ works well in Sect. 6.2 for jump-diffusions with low activity; see Figs. 7 and 6), ensuring that the expected number of jumps in $[0,L_{n}]$ vanishes as $\epsilon \to 0$ (and hence $\kappa \to 0$). This choice keeps the complexity of the simulation nearly constant for varying values of $\kappa$ when the increments of $X^{(\kappa )}$ can be sampled efficiently. Moreover, it typically satisfies the asymptotic assumptions of Theorem 7.17.

4.2.2 Multilevel Monte Carlo

The key ingredient of any MLMC estimator is the coupling between two consecutive levels of approximation that can be sampled efficiently. SBG-Alg is constructed with this in mind, returning a sample from a joint law for two different cutoff levels. (Note that the coupling constructed in SBG-Alg is different from the SBG coupling between $\underline{\chi }_{T}$ and its Gaussian approximation $\underline{\chi }_{T}^{(\kappa )}$, used in Sect. 3 to control the distances between the two laws.) More precisely, the MLMC estimator in (4.3), based on the coupling in SBG-Alg, is given as follows. Let ${({\kappa }_j)}_{j\in \mathbb{N}}$ (resp. ${(n_j)}_{j\in \mathbb{N}\cup \{0\}}$) be a decreasing (resp. increasing) sequence in $(0,1]$ (resp. ℕ) satisfying $\lim _{j\to \infty}\kappa _{j}=0$. Let $\underline{\chi }^{0,i}\overset {d}{=}\underline{\chi }_{T}^{(\kappa _{1})}$ and $(\underline{\chi }^{j,i}_{1},\underline{\chi }^{j,i}_{2})\sim \underline{\Pi }_{n_{j},T}^{\kappa _{j},\kappa _{j+1}}$, $i,j\in \mathbb{N}$, be independent draws constructed by SBG-Alg. Recall that the sequence $(n_{j})$ appears as a parameter in the coupling $\underline{\Pi}^{\kappa _{j},\kappa _{j+1}}_{n_{j},T}$ (which is the law that the pair of vectors $(\underline{\chi}_{1}^{j,i},\underline{\chi}_{2}^{j,i})$ follow). The number $n_{j}$ specifies the number $n$ of sticks used in SBG-Alg for the level $j$. Then for the parameters $m,N_0,\dots ,N_m\in \mathbb{N}$, the MLMC estimator takes the form

$$ \Upsilon _{\mathrm{ML}}:=\sum _{j=0}^{m}\frac{1}{N_{j}}\sum _{i=1}^{N_{j}}D_{j}^{i}, \quad \text{where}\quad D_{j}^{i}:=\textstyle\begin{cases} f (\underline{\chi }^{j,i}_{2} )-f (\underline{\chi }^{j,i}_{1} ),& \quad j\geq 1, \\ f (\underline{\chi }^{0,i} ),&\quad j=0. \end{cases} $$

(4.3)

Given a coupling between consecutive levels, the integer parameters $m,N_{0},\ldots ,N_{m}$ in the estimator $\Upsilon _{\mathrm{ML}}$ are chosen in a well-known optimal way; see Appendix A.2 for details. Table 2 summarises the resulting MLMC complexity up to logarithmic factors, with complete results available in Theorem 7.17 below.

There are two key ingredients in the proof of Theorem 7.17: (I) the bounds in Theorem 7.10 on the $L^{2}$-distance (i.e., the level variance, see Appendix A.2) between the functions of the marginals of the coupling $\underline{\Pi }_{n_{j},T}^{\kappa _{j},\kappa _{j+1}}$ constructed by SBG-Alg; (II) the bounds on the bias of various functions in Sect. 3. The number $m$ of levels in the MLMC estimator in (4.3) is chosen to ensure that its bias, equal to the bias of $\underline{\chi }_{T}^{(\kappa _{m})}$ at the top cutoff level $\kappa _{m}$, is bounded by $\epsilon /\sqrt{2}$. Thus the value of $m$ can be expressed in terms of $\epsilon$ using Table 1 and the explicit formula for the cutoff $\kappa _{j}$, given in the caption of Table 2. The formula for $\kappa _{j}$ at level $j$ in the MLMC estimator in (4.3) is established in the proof of Theorem 7.17 by minimising the multiplicative constant in the computational complexity $\mathcal{C}_{\mathrm{ML}}(\epsilon )$ over all possible rates of the geometric decay of the sequence ${({\kappa }_j)}_{j\in \mathbb{N}}$.

We stress that the analysis of the level variances for the various payoff functions of the coupling $\underline{\Pi }_{n_{j},T}^{\kappa _{j},\kappa _{j+1}}$ in Theorem 7.10 is carried out directly for locally Lipschitz payoffs; see Propositions 7.11. However, in the case of the discontinuous payoffs in $\mathrm{BT}_{1}$ (see (3.12)) and $\mathrm{BT}_{2}$ (see (3.14)), the analysis requires a certain regularity (uniformly in the cutoff levels) of the coupling $(\underline{\chi }_{T}^{(\kappa _{j})},\underline{\chi }_{T}^{( \kappa _{j+1})})$. This leads to a construction of a further coupling $(\underline{\chi }_{T}^{(\kappa _{j})},\underline{\chi }_{T}^{( \kappa _{j+1})}, \underline{\chi }_{T})$ where the components of $(\underline{\chi }_{T}^{(\kappa _{j})},\underline{\chi }_{T}^{( \kappa _{j+1})})$ can be compared to the limiting object $\underline{\chi }_{T}$, which can be shown to possess the necessary regularity (see Proposition 7.13 below for details).

5 Comparison with the literature

Approximations of the pair $(X_{T},\overline{X}_{T})$ abound. They include the random walk approximation, a Wiener–Hopf based approximation (Kuznetsov et al. [46], Ferreiro-Castilla et al. [25]), the jump-adapted Gaussian (JAG) approximation (Dereich and Heidenreich [22, 21]) and more recently, the SB approximation (González Cázares et al. [35]). The SB approximation converges the fastest as its bias decays geometrically in its computational cost. However, the JAG approximation is the only method known to us that does not require the ability to simulate the increments of the Lévy process $X$. Indeed, the JAG approximation simulates all jumps above a cutoff level, together with their jump times, and then samples the transitions of the Brownian motion from the Gaussian approximation on a random grid containing all the jump times. In contrast, in the present paper, we approximate the vector ${\overline{\chi }_{T}=(X_{T},\overline{X}_{T},\overline{\tau }_{T}(X))}$ with an exact sample from the law of the Gaussian approximation $\overline{\chi }_{T}^{(\kappa )} = (X_{T}^{(\kappa )},\overline{X}_{T}^{( \kappa )},\overline{\tau }_{T}(X^{(\kappa )}))$.

The JAG approximation has been analysed for Lipschitz payoffs applied to the pair $(X_{T},\overline{X}_{T})$ in Dereich and Heidenreich [22], Dereich [21]. The discontinuous and locally Lipschitz payoffs arising in applications and considered in this paper (see Fig. 1) have, to the best of our knowledge, not been analysed for the JAG approximation, nor have the payoffs involving the time $\overline{\tau }_{T}(X)$ at which the supremum is attained. Within the class of Lipschitz payoffs of $(X_{T},\overline{X}_{T})$, the computational complexities of the MC and MLMC estimators based on SBG-Alg are asymptotically smaller than those based on the JAG approximation; see Fig. 3. In fact, SBG-Alg applied to discontinuous payoffs outperforms the JAG approximation applied to Lipschitz payoffs by up to an order of magnitude in computational complexity; cf. Figs. 1(A), (B) and 3.

Fig. 3

Dashed (resp. solid) lines represent the power of $\epsilon ^{-1}$ in the computational complexity of the MC (resp. MLMC) estimator for the expectation of a Lipschitz functional $f(X_{T},\overline{X}_{T})$, plotted as a function of the BG index $\beta$ defined in (2.6). The SBG plots are based on Tables 1 and 2. The JAG plots are based on Dereich [21, Corollary 3.2] for the MC cost, and on [21, Corollary 1.2] if $\beta \geq 1$ (resp. Dereich and Heidenreich [22, Corollary 1] if $\beta <1$) for the MLMC cost

In order to understand where the differences in Fig. 3 come from, we summarise in Table 3 the bias and level variance for SBG-Alg and the JAG approximation as a function of the cutoff level $\kappa \in (0,1]$ in the Gaussian approximation; cf. (2.5).

Table 3 The rates (as $\kappa \to 0$) of decay of bias and level variance for Lipschitz payoffs of $(X_{T},\overline{X}_{T})$ under the JAG approximation are based on Dereich [21, Corollary 3.2] and Dereich and Heidenreich [22, Theorem 2], respectively. The rates on the bias and level variance for the SBG-Alg are given in Theorems 3.4 and 7.10

Table 3 shows that both bias and level variance decay at least as fast (and typically faster) for SBG-Alg than for the JAG approximation. The large improvement in the computational complexity of the MC estimator in Fig. 3 is due to the faster decay of the bias under SBG-Alg. Put differently, the SBG coupling constructed in the present paper controls the Wasserstein distance much better than the KMT-based coupling in Dereich [21]. For a BG index $\beta >1$, the improvement in the computational complexity of the MLMC estimator is mostly due to a faster bias decay. For $\beta <1$, Fig. 3 (A) suggests that the computational complexity of the MLMC estimator under both algorithms is optimal. However, in this case, Table 3 and the equality in (A.3) imply that the MLMC estimator based on the JAG approximation has a computational complexity proportional to $\epsilon ^{-2}\log ^{3}(1/\epsilon )$, while that of SBG-Alg is proportional to $\epsilon ^{-2}$. This improvement is due solely to the faster decay of level variance under SBG-Alg. The numerical experiments in Sect. 6.1 suggest that our bounds for Lipschitz and locally Lipschitz functions are sharp; see the graphs (A) and (C) in Figs. 4 and 5.

Fig. 4

Gaussian approximation of a tempered stable process: log–log plot of the bias and level variance for various payoffs as a function of $\log \kappa _{j}$. Circle (∘) and plus (+) correspond to $log|\mathbb{E}[D_j^1]|$ and $log\mathbb{V}[D_j^1]$, respectively, where $D_{j}^{1}$ is given in (4.3) with $\kappa _{j}=\exp (-r(j-1))$ for $r=1/2$. The dashed lines in all the graphs plot the rates of the theoretical bounds in Sect. 3.2 (blue for the bias) and Theorem 7.10 (red for level variances). In plots (A)–(D), the initial value of the risky asset is normalised to $S_{0}=1$ and the time horizon is set to $T=1/6$. In plot (B), we set $K=1$ and $M=1.2$. The model parameters are given in Table 4 below

Fig. 5

Gaussian approximation of a Watanabe process: log–log plot of the bias and level variance for various payoffs as a function of $\log \kappa _{j}$. Circle (∘) and plus (+) correspond to $log|\mathbb{E}[D_j^1]|$ and $log\mathbb{V}[D_j^1]$, respectively, where $D_{j}^{1}$ is given in (4.3) with $\kappa _{j}=\exp (-r(j-1))$ for $r=1$. The dashed lines in graphs (A) and (C) plot the rates of the theoretical bounds in Sect. 3.2 (blue for the bias) and Theorem 7.10 (red for level variances). In plots (A)–(D), the initial value of the risky asset is normalised to $S_{0}=1$ and the time horizon is set to $T=1$. The model parameters are given by $a=2$, $c_{+}=c_{-}=1$

To the best of our knowledge, there are no directly comparable results in the literature to either Theorem 3.4 or Proposition 3.12. Partial results in the direction of Theorem 3.4 are given in Dia [24], Mariucci and Reiß[50], Carpentier et al. [12]. Improvements in our Theorems 3.1 and 3.3 on the existing bounds on the distance between the marginals $X_{t}$ and $X^{(\kappa )}_{t}$ have been discussed in detail in Sect. 3.1.1. The rate of the bound in [24, Theorem 2] on the Wasserstein distance between the suprema $\overline{X}_{t}$ and $\overline{X}^{(\kappa )}_{t}$ is worse than that implied by the bound in Corollary 3.5 on the Wasserstein distance between the joint laws of $(X_{t},\overline{X}_{t})$ and $(X^{(\kappa )}_{t},\overline{X}^{(\kappa )}_{t})$. Proposition 3.7 bounds the bias of locally Lipschitz functions, generalising [24, Proposition 9] and providing a faster decay rate. Proposition 3.9 and Corollary 3.14 (a) cover a class of discontinuous payoffs, including the up-and-out digital option considered in [24, Proposition 10 (part 3)], and provide a faster rate of decay as $\kappa \to 0$ if either $X$ has a Gaussian component or a BG index $\beta >2/3$.

6 Numerical examples

In this section, we study numerically the performance of SBG-Alg. All the results are based on the code available in the repository [31]. In Sect. 6.1, we apply SBG-Alg to two families of Lévy models (tempered stable and Watanabe processes) and verify numerically the decay of the bias (established in Sect. 3.2) and level variance (see Theorem 7.10 below) of the Gaussian approximations. In Sect. 6.2, we study numerically the cost reduction of SBG-Alg, when compared to Algorithm 2, for the simulation of the vector $\underline{\chi }_{T}^{(\kappa )}$. In Sect. 6.3, we numerically demonstrate the stability and effectiveness of SBG-Alg for the Monte Carlo estimation of Delta and Gamma of barrier options under Lévy models.

6.1 Numerical performance of SBG-Alg for tempered stable and Watanabe models

To illustrate numerically our results, we consider two classes of exponential Lévy models $S=S_{0}e^{X}$. The first is the tempered stable class, containing the CGMY (or KoBoL) model, a process widely used for modelling risky assets in financial mathematics (see e.g. Cont and Tankov [20, Remarks 4.3 and 4.4] and the references therein), which satisfies the regularity assumptions from Sect. 3.2. The second is the Watanabe class, which has diffuse but singular transition laws (Sato [62, Theorem 27.19]), making it a good candidate to stress test our results.

We numerically study the decay of the bias and level variance of the MLMC estimator in (4.3) for the prices of a lookback put $\mathbb{E}[{\bar{S}}_T-S_T]$ and an up-and-out call as well as the values of the ulcer index (UI) given by $100\mathbb{E}{[{(S_T/{\bar{S}}_T-1)}^2]}^{1/2}$ (see Martin and McCann [51, Sect. 6.2]) and a modified ulcer index (MUI) defined by . The first three quantities are commonplace in applications; see Cont and Tankov [20, Sect. 11.3] and Martin and McCann [51, Sect. 6.2]. The MUI refines the UI by incorporating the information on the drawdown duration, and weights trends more heavily than short-time fluctuations.

In Sects. 6.1.1 and 6.1.2, we use $N=10^{5}$ independent samples to estimate the means and variances of the variables $D^{1}_{j}$ in (4.3) (with $\underline{\chi }_{T}^{(\kappa _{j})}$ substituted by $\overline{\chi }_{T}^{(\kappa _{j})}$), where the choice of the parameters $n_{j}= \lceil{\max \{j,\log ^{2}(1+\overline{\nu }(\kappa _{j+1}))\}} \rceil$ and $\kappa _{j}=e^{-r(j-1)}$, $j\in \mathbb{N}$, is discussed in Sect. 7.5 below.

6.1.1 Tempered stable model

The characteristic triplet $(\sigma ^{2},\nu ,b)$ of the tempered stable Lévy process $X$ is given by $\sigma =0$, drift $b\in \mathbb{R}$ and Lévy measure $\nu (dx)=|x|^{-1-\alpha _{\mathrm{sgn}(x)}}c_{\mathrm{sgn}(x)} e^{- \lambda _{\mathrm{sgn}(x)}|x|}dx$, where $\alpha _{\pm}\in [0,2)$, $c_{\pm}\ge 0$ and $\lambda _{\pm}>0$; cf. (2.3). Exact simulation of increments is currently out of reach if either $\alpha _{+}>1$ or $\alpha _{-}>1$ (see e.g. Grabchak [36]) and requires the Gaussian approximation.

Figure 4 suggests that our bounds are close to the exhibited numerical behaviour for continuous payoff functions. In the discontinuous case, $\overline{\chi }_{T}^{(\kappa _{j})}$ appears to be much closer to $\overline{\chi }_{T}$ (resp. $\overline{\chi }_{T}^{(\kappa _{j+1})}$), than predicted by Propositions 3.9 and 3.12 (resp. Theorem 7.10 (b) and (d)).

6.1.2 Watanabe model

The characteristic triplet $(\sigma ,\nu ,b)$ of the Watanabe process is given by $\sigma =0$, the Lévy measure $\nu$ equals ${\sum }_{n\in \mathbb{N}}(c_{+}{\delta }_{a^{-n}}+c_{-}{\delta }_{-a^{-n}})$, where $a\in \mathbb{N}\setminus \{1\}$ and $\delta _{x}$ is the Dirac measure at $x$, and the drift $b\in \mathbb{R}$ is arbitrary. The increments of the Watanabe process are diffuse, but have no density (see Sato [62, Theorem 27.19]). Since the process has very little jump activity, the bound in Proposition 3.12 (see also (3.6)) is non-vanishing and the bounds in Theorem 7.10 (c) and (d) are not applicable, meaning that we have no theoretical control on the approximation of $\overline{\tau }_{T}(S)$. This is not surprising as such acute lack of jump activity makes the Gaussian approximation unsuitable (cf. Asmussen and Rosiński [2, Proposition 2.2]).

The pictures in Fig. 5 (A) and (C) suggest that our bounds on the bias and level variance in Sect. 3.2 and Theorem 7.10 are robust for continuous payoff functions even if the underlying Lévy process has no transition densities. There are no dashed lines in Fig. 5 (B) and (D) as there are no results for discontinuous functions of $\overline{\tau }_{T}(S)$ in this case. In fact, Fig. 5 (B) suggests that the decay rate of the bias and level variance for functions of $\overline{\tau }_{T}(S)$ can be arbitrarily slow if the process does not have sufficient activity. Figure 5 (D), however, suggests that this decay is still fast if the underlying finite variation process $X$ has a nonzero natural drift (see also Remark 3.6).

6.2 The cost reduction of SBG-Alg over Algorithm 2

Recall that Algorithm 2 and SBG-Alg both draw exact samples of a Gaussian approximation $\underline{\chi }_{T}^{(\kappa )}$. However, in practice, SBG-Alg may be many times faster than Algorithm 2; Fig. 6 plots the speedup factor in the case of a tempered stable process, defined in Sect. 6.1.1, as a function of $\kappa$. In conclusion, one should use SBG-Alg instead of Algorithm 2 for the MC estimator in (4.2). Even though the efficiency of SBG-Alg over Algorithm 2 for $\kappa >0.1$ is not as drastic, one should still use SBG-Alg because Algorithm 2 is neither parallelisable nor suitable for MLMC, as discussed in Sect. 4.1.2.

Fig. 6

The pictures show the ratio of the cost of Algorithm 2 over the cost of SBG-Alg (both in seconds) for the Gaussian approximations of a tempered stable process as a function of the cutoff level $\kappa$. The parameters used are $\lambda _{\pm}=5$, $c_{\pm}=2$. The number of sticks $n$ in SBG-Alg varies between 5 and 20. The ratio for $n=20$ is 57.8 (resp. 61.7) in the case $\alpha _{\pm}=1.2$ (resp. $\alpha _{\pm}=1.4$) for $\kappa =2^{-16}$ (resp. $\kappa =2^{-14}$)

If the Lévy process $X$ is a jump-diffusion, i.e., $\nu (\mathbb{R}\setminus \{0\})<\mathrm{\infty }$, we may apply Algorithms 1 and 2 and SBG-Alg with $\kappa _{1}=\kappa _{2}=0$. In that case, SBG-Alg still outperforms Algorithm 2 by a constant factor, with computational benefits being more pronounced when the total expected number of jumps $\lambda :=\nu (\mathbb{R}\setminus \{0\})T$ is large; see Fig. 7. The cost reduction is most drastic when $\lambda$ is large, but the improvement is already significant for $\lambda =2$; see Fig. 7.

Fig. 7

The pictures show, for multiple number of sticks $n$, the ratio of the cost of Algorithm 2 over the cost of SBG-Alg (both in seconds) for jump-diffusions as a function of the mean number of jumps $\lambda =\nu (\mathbb{R}\setminus \{0\})T$. The ratio for $n=15$ is 11.8 (resp. 10.8) in Merton’s (resp. Kou’s) model when $\lambda =10$, see Merton [52] and Kou [44]

6.3 Estimating Greeks: Delta and Gamma for barrier options in Lévy models

A fundamental problem in mathematical finance is to compute the sensitivity of the price of a derivative security to the various underlying parameters in order to construct appropriate hedging strategies. These sensitivities are known as the Greeks and are in practice given by the partial derivatives of the option price $e^{-rT}\mathbb{E}[P]$ (where $r$ is the discount rate over the time horizon $T$ and $P$ is a random payoff). The most common of the Greeks are Delta and Gamma, given by the first and second derivatives of the price $e^{-rT}\mathbb{E}[P]$ with respect to the spot $S_{0}$.

If the risk-neutral dynamics of the risky asset is described by an exponential Lévy model $S=S_{0}e^{X}$, SBG-Alg provides a simple procedure for the Monte Carlo estimation of Delta and Gamma for any payoff $P=g(\overline{\chi }_{T})$ (where we recall that the derivatives $f'(x)$ and $f''(x)$ of a function $f(x)$ are approximated by the quotients $(f(x+h)-f(x-h))/(2h)$ and $(f(x+h)-2f(x)+f(x-h))/h^{2}$, respectively, for a small $h>0$). This approach, widely used in practice, requires a Monte Carlo evaluation using SBG-Alg of $e^{-rT}\mathbb{E}[g({\bar{\chi }}_T)]$ on a grid of current spot prices $S_{0}$, where the simulated stick-breaking sequence and the corresponding increments of $X^{(\kappa )}$ can be re-used over the grid points of $S_{0}$.

6.3.1 Delta and Gamma for up-and-out call in a tempered stable (CGMY) model

We demonstrate the numerical stability of SBG-Alg in this context by computing Delta and Gamma for the up-and-out call payoff considered in Sect. 6.1.1; the model parameters, calibrated from USD/JPY foreign exchange options data, are given as parameter set 1 in Table 4, with strike $K=1$, barrier level $M=1.2$ and interest rate $r=0.05$. To stress test the model, we increased the activity index by taking $\alpha _{\pm}=1.16$ instead of 0.66. Figure 8 reports the results of the Monte Carlo estimation of the up-and-out call option price, together with its Delta and Gamma, with the spot ranging over the interval $S_{0}\in [0.95,1.2)$ for the maturities of 1 month, 1 week and 1 day. The grid spacing in the interval $[0.95,1.2)$ was set at $h=0.001$ with jump cutoff $\kappa =0.001$. We used $n=10$ sticks and $N=10^{7}$ samples, which resulted in a total simulation time¹ of 12 minutes for all spot values $S_{0}$ on the grid and all maturities.

Fig. 8

Monte Carlo estimation of the price, Delta and Gamma for the up-and-out call option with payoff (see the first paragraph of Sect. 6.3.1 for parameter values) based on SBG-Alg. Solid lines (resp. dashed lines; dotted lines) correspond to the option maturity of one month (resp. one week; one day). Since the orders of magnitude (close to the barrier) of the Deltas and Gammas vary significantly with the maturity and all the Greeks in this example take both positive and negative values, we plot in graphs (B) and (C) $F(\mathrm{Delta})$ and $F(\mathrm{Gamma})$, where $F(x):=\mathrm{sgn}(x)\log (1+|x|)$, $x\in \mathbb{R}$, is a bijection on ℝ preserving the sign of $x$ but reducing its magnitude to logarithmic scale

Table 4 The parameters used for Fig. 4. The first set of parameters corresponds to the risk-neutral calibration to vanilla options on the USD/JPY exchange rate; see Andersen and Lipton [1, Table 3]. The second set is the maximum likelihood estimate based on the real-world S&P stock prices; see Kim et al. [40, Table 1]

We note that the option price, Delta and Gamma in Fig. 8 look remarkably smooth as functions of the spot $S_{0}$, given that all the values in the three graphs are obtained using Monte Carlo simulation. We further note that the spot grid spacing $h=10^{-3}$ should be small, but $h^{2}N=10$ should not be, which is consistent with the similar problem of density estimation via Monte Carlo (see e.g. Ben Abdellah et al. [6]). Having $h^{2}N$ of moderate size ensures that the discontinuities of the function do not dominate in the estimation of the Greeks. For each realisation of $X$, this function has a single discontinuity at the random level $I=\exp (-\overline{X}_{T})M$ with size of constant order. Every discontinuity of the Monte Carlo estimator will thus be of order $1/N$. The estimators of Delta and Gamma take a linear combination of such averages at different spot levels $S_{0}$ and divide by $h$ and $h^{2}$, respectively, resulting in discontinuities (as a function of $S_{0}$) of orders $1/(hN)$ and $1/(h^{2}N)$ for the Delta and Gamma, respectively. Hence $h$ should be chosen to make $h^{2}N$ of moderate size to keep these discontinuities from dominating in the estimation. The apparent smoothness of both Greeks further confirms our choice of $h$ to be reasonable.

There is an inflection point (a switch from concavity to convexity) for our approximation of the Delta near the barrier, visible in Fig. 8 for the 1 day maturity; it corresponds to a local minimum of Gamma at $S_{0}=1.1971$. For the larger maturities, this inflection point is much closer to the barrier and is not visible in the graph, but can be observed in the figures coming out of the simulation. This inflection point close to the barrier was a persistent feature of our numerical scheme, observed after repeating the simulation with different random seeds a number of times. In contrast to the diffusion setting in Mijatović [53], we are not aware of any theoretical or empirical studies documenting such phenomena for barrier options under models with jumps. Put differently, while our Monte Carlo method suggests that the approximation of the Delta exhibits inflection near the barrier, it is neither clear that inflection persists in the limit as the spacing tends to zero (i.e., $h\to 0$), nor that it is a genuine feature of the actual Delta in the model.

In order to understand the dependence on the jump cutoff $\kappa$, we compare the numerical results in Fig. 8 (where $\kappa =10^{-3}$) with an identical Monte Carlo algorithm based on SBG-Alg, but with $\kappa =0.1$. In Fig. 9, we plot the difference between Delta and Gamma produced by two different values of $\kappa$. There is little difference between the cutoff levels away from the barrier, meaning that the Monte Carlo estimator based on SBG-Alg for Delta and Gamma is robust in the value of the cutoff $\kappa$. This is surprising because we are using a naive (i.e., not based on Malliavin calculus) Monte Carlo estimator to compute derivatives of an expectation with respect to the starting point. The difference of the estimates for Delta and Gamma, corresponding to the different cutoffs, increases close to the barrier. In the regime when $S_{0}$ tends to the barrier level $M$, it is hard to give an intuitive explanation for the difference between the approximations of the first and second derivatives of the price.

Fig. 9

Modulus of the difference between the estimates for Delta and Gamma for an up-and-out call option using a Monte Carlo algorithm based on SBG-Alg, where the difference reflects the improved accuracy of using the cutoff $\kappa =0.001$ over the cutoff $\kappa =0.1$. Away from the barrier, the numerical values for both cutoff levels are close to each other. As expected, the gap widens close to the barrier. Since the order of magnitude (close to the barrier) of the differences between Deltas and Gammas for the two cutoffs varies significantly, we plot in both graphs $F(\mathrm{difference})$, where $F(x):=\mathrm{sgn}(x)\log (1+|x|)$, $x\in \mathbb{R}$, is a bijection on ℝ preserving the sign of $x$ but reducing its magnitude to logarithmic scale. A positive value of $F(\mathrm{difference})$ indicates that the estimate of the Greek based on the cutoff $\kappa =0.001$ is larger than the one for $\kappa =0.1$

6.3.2 Comparison with an analytically tractable pricing formula

We are not aware of an analytically tractable approximation for the price of an up-and-out call option studied in Sect. 6.3.1 under a Lévy model with jumps of infinite activity (i.e., with Lévy measure of infinite total mass), much less of its sensitivities. In order to test numerically the performance of SBG-Alg against a tractable formula, we compute Delta and Gamma of an up-and-out digital option with barrier $M$ and payoff under an exponential Lévy model with analytically tractable Delta and Gamma. Let $X$ be an $\alpha$-stable process of infinite variation without positive jumps. The strong Markov property of $X$ at the first crossing time $\tau _{x}:=\inf \{t\geq 0:X_{t}>x\}$ yields

$$\mathbb{P}[X_T>x]={\int }_{[0,T)}\mathbb{P}[X_{T-t}>0]\mathbb{P}[{\tau }_x\in dt]=\mathbb{P}[X_T>0]\mathbb{P}[{\bar{X}}_T>x]$$

for any $x>0$, since the scaling property of $X$ implies $\mathbb{P}[X_t>0]=\mathbb{P}[X_T>0]$ for all $t>0$, and the absence of positive jumps yields $X_{\tau _{x}}=x$ a.s. for any $x>0$ and $\{\tau _{x}< T\}=\{\overline{X}_{T}>x\}$ a.s. In turn, the formula above implies that $\overline{X}_{T}$ has the same law as $X_{T}$ conditioned to be positive. The option price is thus given as function of the spot by

$$S_0\mapsto e^{-rT}\mathbb{E}[g({\bar{\chi }}_T)]=e^{-rT}\mathbb{P}[X_T\le log(M/S_0)]/\mathbb{P}[X_T>0].$$

(6.1)

The corresponding Delta and Gamma, equal to the first and second derivatives of this function, can be expressed as a geometrically converging power series (see Uchaikin and Zolotarev [66, Chap. 4]) and computed numerically without the use of Monte Carlo.

The parameters for this test were chosen as follows: $X$ has unit scale (in Zolotarev’s (C) parametrisation; see Uchaikin and Zolotarev [66, Sect. 3.6]) and the stability parameter $\alpha =1.7$, while the market data is $r=0.05$, $T=1/12$, $M=1$ and $S_{0}\in [0.85,1)$. To highlight the importance of the cutoff level $\kappa$, we compare $\kappa =0.1$ with $\kappa =0.001$. We used $n=25$ sticks, $N=10^{7}$ samples and grid size $h=0.005$. This resulted in a total simulation time of 12 minutes. The estimation of Delta and Gamma is accurate and numerically stable.

Surprisingly, the error in Delta – see graph (B) in Fig. 10 – remains bounded all the way to the barrier $M$ for both values of $\kappa$. The error for $\kappa =0.001$ is smaller than the one for $\kappa =0.1$, but comes at a significant increase in cost due to the Blumenthal–Getoor index of $X$ being equal to 1.7 (and in particular much greater than one).

Fig. 10

Monte Carlo estimation of Delta and Gamma for the up-and-out digital option with payoff under an $\alpha$-stable model with no positive jumps; see the second paragraph of Sect. 6.3.2 for the values of the model and market parameters. Dashed lines (resp. dotted lines) correspond to the output based on Monte Carlo estimation using SBG-Alg for $\kappa =0.1$ (resp. $\kappa =0.001$). Figures (A) and (C) contain a solid line corresponding to the true values of Delta and Gamma, computed using a geometrically convergent power series in Uchaikin and Zolotarev [66, Chap. 4] for the value function in (6.1)

7 Proofs

In the remainder of the paper, we use the notation $\underline{\tau }_{t}:=\underline{\tau }_{t}(X)$, $\underline{\tau }_{t}^{(\kappa )}:=\underline{\tau }_{t}(X^{( \kappa )})$ for all $t>0$.

7.1 Proof of Theorems 3.1 and 3.3

In this subsection, we establish bounds on the Wasserstein and Kolmogorov distances between the increment $X_{t}$ and its Gaussian approximation $X^{(\kappa )}_{t}$ in (2.5).

Proof of Theorem 3.1

Recall the Lévy–Itô decomposition of $X$ at level $\kappa$ in (2.4) and the martingale $M^{(\kappa )} =\sigma B + J^{1,\kappa}$. Set $Z:=X-M^{(\kappa )}$ and note that we have $X^{(\kappa )}= Z+\sqrt{\overline{\sigma }_{\kappa}^{2}+\sigma ^{2}}\,W$, where $W$ is a standard Brownian motion in (2.5), independent of $Z$. Hence any coupling $(W_{t}, M^{(\kappa )}_{t})$ yields a coupling of $(X_{t},X^{(\kappa )}_{t})$ satisfying

$$\mathbb{E}[{|X_t-X_t^{(\kappa )}|}^p]=\mathbb{E}\left[{|M_t^{(\kappa )}-\sqrt{{\bar{\sigma }}_{\kappa }^2+{\sigma }^2}{W}_t|}^p\right].$$

Setting $W:=B$, which amounts to the independence coupling $(W,J^{1,\kappa})$, and applying Jensen’s inequality for $p\in [1,2]$ yields

$$\mathbb{E}{[{|X_t-X_t^{(\kappa )}|}^p]}^{2/p}\le \mathbb{E}\left[{|J_t^{1,\kappa }-(\sqrt{{\bar{\sigma }}_{\kappa }^2+{\sigma }^2}-\sigma \left)W_t\right|}^2\right]\le 2t{\bar{\sigma }}_{\kappa }^2.$$

For any $m\in \mathbb{N}$, we have $M_{t}^{(\kappa )}\overset {d}{=}\sum _{i=1}^{m} \xi _{i}$, where $\xi _{1},\ldots ,\xi _{m}$ are i.i.d. with $\xi _{1}\overset {d}{=}M^{( \kappa )}_{t/m}$. Hence Petrov [57, Theorem 16] and Rio [60, Theorem 4.1] imply the existence of universal constants $K_{p}$, $p\in [1,2]$, with $K_{1}=1/2$, satisfying

$$\begin{array}{rl}{\mathcal{W}}_p^p(M_t^{(\kappa )},\sqrt{{\bar{\sigma }}_{\kappa }^2+{\sigma }^2}{W}_t)& \le K_p^p\frac{{(t({\bar{\sigma }}_{\kappa }^2+{\sigma }^2))}^{p/2}\mathbb{E}[{|{\xi }_1|}^{p+2}]}{m^{p/2}\mathbb{E}{[{\xi }_1^2]}^{(p+2)/2}}\\ & =K_p^p\frac{(m/t)\mathbb{E}[{|M_{t/m}^{(\kappa )}|}^{p+2}]}{{\bar{\sigma }}_{\kappa }^2+{\sigma }^2}\end{array}$$

for all $m\in \mathbb{N}$. According to Figueroa-López [26, Theorem 1.1], the limit as $m\to \infty$ of the right-hand side of the display above equals

$$ K_{p}^{p}\int _{(-\kappa ,\kappa )}|x|^{p+2}\nu (dx) /( \overline{\sigma }_{\kappa}^{2}+\sigma ^{2}) \le K_{p}^{p}\kappa ^{p} \varphi _{\kappa}^{2}, $$

implying the claim in the theorem. □

Proof of Theorem 3.3

(a) Set $d_{\kappa }:={sup}_{x\in \mathbb{R}}|\mathbb{P}[M_t^{(\kappa )}\le x]-\mathbb{P}[\sqrt{{\bar{\sigma }}_{\kappa }^2+{\sigma }^2}{W}_t\le x]|$ and note that

$$\begin{array}{rl}& |\mathbb{P}[X_t\le x]-\mathbb{P}[X_t^{(\kappa )}\le x]|\\ & =\left|\mathbb{E}\right[\mathbb{P}[M_t^{(\kappa )}\le x-Z_t|Z_t]-\mathbb{P}[\sqrt{{\bar{\sigma }}_{\kappa }^2+{\sigma }^2}{W}_t\le x-Z_t|Z_t]\left]\right|\le d_{\kappa },\end{array}$$

where the processes $Z$ and $M^{(\kappa )}$ are as in the proof of Theorem 3.1. Since $M^{(\kappa )}$ is a Lévy process, for any $m\in \mathbb{N}$, we have $M_{t}^{(\kappa )}\overset {d}{=}\sum _{i=1}^{m} \xi _{i}$, where $\xi _{1},\ldots ,\xi _{m}$ are i.i.d. with $\xi _{1}\overset {d}{=}M^{(\kappa )}_{t/m}$. By the Berry–Esseen inequality, see Korolev and Shevtsova [42, Theorem 1], there exists a constant $C_{\mathrm{BE}}\in (0,\frac{1}{2})$ such that

$$d_{\kappa }\le \frac{C_{\mathrm{BE}}\mathbb{E}[{|{\xi }_1|}^3]}{\sqrt{m}\mathbb{E}{[{\xi }_1^2]}^{3/2}}=\frac{C_{\mathrm{BE}}t}{m\sqrt{m}}\frac{(m/t)\mathbb{E}[{|M_{t/m}^{(\kappa )}|}^3]}{{(t/m)}^{3/2}{({\bar{\sigma }}_{\kappa }^2+{\sigma }^2)}^{3/2}}=C_{\mathrm{BE}}\frac{(m/t)\mathbb{E}[{|M_{t/m}^{(\kappa )}|}^3]}{\sqrt{t}{({\bar{\sigma }}_{\kappa }^2+{\sigma }^2)}^{3/2}}$$

for all $m\in \mathbb{N}$. Taking $m\to \infty$ yields (a) since according to Figueroa-López [26, Theorem 1.1], the limit of the right-hand side of the display above equals

$$ C_{\mathrm{BE}}\int _{(-\kappa ,\kappa )}|x|^{3}\nu (dx) /\big(\sqrt{t}( \overline{\sigma }_{\kappa}^{2}+\sigma ^{2})^{3/2}\big) \le C_{ \mathrm{BE}}(\kappa /\overline{\sigma }_{\kappa})\varphi _{\kappa}^{3}/ \sqrt{t}. $$

(b) By Picard [58, Theorem 3.1(a)], $X_{t}$ has a smooth density $f_{t}$, and given $T>0$, the constant $C^{\prime }={sup}_{(t,x)\in (0,T]\times \mathbb{R}}{t}^{1/\delta }{f}_t(x)$ is finite. Applying (3.1) and (7.10) in Lemma 7.5 with $p=2$ gives (3.3). □

7.2 Proof of Theorem 3.4

We recall an elementary result for stick-breaking processes.

Lemma 7.1

Let ${({\varpi }_n)}_{n\in \mathbb{N}}$ be a stick-breaking process on $[0,1]$ based on the uniform law. For any measurable function $\phi \ge 0$, we have

$$\sum _{n\in \mathbb{N}}\mathbb{E}[\varphi ({\varpi }_n)]={\int }_0^1\frac{\varphi (x)}{x}dx.$$

In particular, for any $a_{1},a_{2}>0$ and $b_{1}< b_{2}$ with $b_{2}>0$, we have

$$\begin{array}{rl}& \sum _{n\in \mathbb{N}}\mathbb{E}[min\{a_1{\varpi }_n^{b_1},a_2{\varpi }_n^{b_2}\}]\\ & =\{\begin{array}{cc}\frac{a_2}{b_2}min{\{1,\frac{a_1}{a_2}\}}^{b_2/(b_2-b_1)}+\frac{a_1}{b_1}(1-min{\{1,\frac{a_1}{a_2}\}}^{b_1/(b_2-b_1)}),\hfill & b_1\ne 0,\hfill \\ b_2^{-1}min\{a_2,a_1\}(1+{log}^{+}\frac{a_2}{a_1}),\hfill & b_1=0.\hfill \end{array}\end{array}$$

Proof

The law of $-\log \varpi _{n}$ is gamma with shape $n$ and scale 1. Applying Fubini’s theorem implies

$$\sum _{n\in \mathbb{N}}\mathbb{E}[\varphi ({\varpi }_n)]=\sum _{n\in \mathbb{N}}{\int }_0^{\mathrm{\infty }}\frac{x^{n-1}}{(n-1)!}{e}^{-x}\varphi (e^{-x})dx={\int }_0^{\mathrm{\infty }}\varphi (e^{-x})dx={\int }_0^1\frac{\varphi (x)}{x}dx.$$

The formula for $\phi (x):=\min \{a_{1}x^{b_{1}},a_{2}x^{b_{2}}\}$ follows by a direct calculation. □

The $L^{p}$-Wasserstein distance, defined in (3.10), satisfies

$$ \mathcal{W}_{p}^{p}(\xi ,\xi _{*})=\int _{0}^{1} |F^{-1}(u)-F_{*}^{-1}(u)|^{p} du, $$

where $F^{-1}$ (resp. $F_{*}^{-1}$) is the right inverse of the distribution function $F$ (resp. $F_{\ast}$) of the real-valued random variable $\xi$ (resp. $\xi _{*}$) (see Bobkov and Ledoux [10, Theorem 2.10]). Thus the comonotonic (or minimal transport) coupling defined by

$$ (\xi ,\xi _{*}):=\big(F^{-1}(U),F_{*}^{-1}(U)\big) \qquad \text{for some }U\sim \mathrm{U}(0,1) $$

(7.1)

attains the infimum in definition (3.10).

Lemma 7.2

If $\xi$ and $\xi _{*}$ are real-valued and comonotonically coupled, then

Proof

Suppose $(\xi ,\xi _{*})=(F^{-1}(U),F_{*}^{-1}(U))$ for some $U\sim \mathrm{U}(0,1)$, where $F$ and $F_{*}$ are the distribution functions of $\xi$ and $\xi _{*}$. Suppose $y:=F(x)\le F_{*}(x)=:y_{*}$. Since $F^{-1}$ and $F_{*}^{-1}$ are monotonic functions, it follows that a.s. since this difference equals 0 or −1 according to whether $U\in (0,1)\setminus (y,y_{*}]$ or $U\in (y,y_{*}]$, respectively. If $y\ge y_{*}$, we have a.s. In either case, the result follows. □

For any $t>0$, let $G_{t}^{\kappa}$ denote the joint law of the comonotonic coupling of $X_{t}$ and $X_{t}^{(\kappa )}$ defined in (7.1). Note that a coupling $(X_{t},X_{t}^{(\kappa )})$ with law $G_{t}^{\kappa}$ satisfies the inequality in Theorem 3.1. The following lemma is crucial in the proof of Theorem 3.4.

Lemma 7.3

Let $\ell ={({\ell }_n)}_{n\in \mathbb{N}}$ be a stick-breaking process on $[0,t]$ and $(\xi _{n},\xi _{n}^{(\kappa )})$, $n\in \mathbb{N}$, a sequence of random vectors that conditionally on $\ell$ are independent and satisfy $(\xi _{n},\xi _{n}^{(\kappa )})\sim G_{\ell _{n}}^{\kappa}$ for all $n\in \mathbb{N}$. Then for any $p\in [1,2]$ and $x\in \mathbb{R}$, we have

$$\mathbb{E}{\left[{(\sum _{n=1}^{\mathrm{\infty }}|{\xi }_n-{\xi }_n^{(\kappa )}|)}^p\right]}^{\frac{1}{p}}\le {\mu }_p(\kappa ,t),$$

(7.2)

(7.3)

where $\mu _{p}$ and $\mu _{0}^{\tau}$ are defined in (3.5) and (3.6), respectively. Moreover, if Assumption 3.2holds, then for every $T>0$, there exists a constant $C>0$, dependent only on $(T,\delta ,\sigma ,\nu )$, such that for all $t\in [0,T]$, $\kappa \in (0,1]$ and $x\in \mathbb{R}$, we have

(7.4)

where $\mu _{\delta}^{\tau}$ is defined in (3.8).

Proof

Note that $\mu _{p}(\kappa ,t)=\mu _{2}(\kappa ,t)$ for all $p\in (1,2]$. Hence by Jensen’s inequality, in (7.3), we need only consider $p\in \{1,2\}$. Pick $n\in \mathbb{N}$ and set $\kappa _{p}:=K_{p}^{p}\kappa ^{p}\varphi _{\kappa}^{2}$, $p\in \{1,2\}$, where $K_{p}$ and $\varphi _{\kappa}$ are as in the statement of Theorem 3.1. Condition on $\ell _{n}$ and apply the bound in (3.1) to obtain

$$\mathbb{E}\left[{|{\xi }_n^{(\kappa )}-{\xi }_n|}^p\right|{\ell }_n]\le min\{2^{p/2}{\bar{\sigma }}_{\kappa }^p{\ell }_n^{p/2},{\kappa }_p\},p\in \{1,2\}.$$

(7.5)

Applying (7.5) and Lemma 7.1 yields (7.2) for $p=1$; indeed,

$$\begin{array}{rl}\sum _{n=1}^{\mathrm{\infty }}\mathbb{E}[|{\xi }_n-{\xi }_n^{(\kappa )}|]& \le \sum _{n=1}^{\mathrm{\infty }}\mathbb{E}[min\{\sqrt{2{\ell }_n}{\bar{\sigma }}_{\kappa },{\kappa }_1\}]\\ & =2min\{\sqrt{2t}{\bar{\sigma }}_{\kappa },{\kappa }_1\}(1+{log}^{+}(\sqrt{2t}{\bar{\sigma }}_{\kappa }/{\kappa }_1)).\end{array}$$

Now consider the case $p=2$. A simple expansion yields

$$\mathbb{E}\left[{\left(\sum _{n=1}^{\mathrm{\infty }}\right|{\xi }_n-{\xi }_n^{(\kappa )}\left|\right)}^2\right]=\sum _{n=1}^{\mathrm{\infty }}\mathbb{E}[{({\xi }_n-{\xi }_n^{(\kappa )})}^2]+2\sum _{n=1}^{\mathrm{\infty }}\sum _{m=n+1}^{\mathrm{\infty }}\mathbb{E}[|{\xi }_n-{\xi }_n^{(\kappa )}||{\xi }_m-{\xi }_m^{(\kappa )}|].$$

We proceed to bound both sums. Inequality (7.5) for $p=2$ and Lemma 7.1 imply

$$\begin{array}{rl}\sum _{n=1}^{\mathrm{\infty }}\mathbb{E}[{({\xi }_n-{\xi }_n^{(\kappa )})}^2]& \le \sum _{n=1}^{\mathrm{\infty }}\mathbb{E}[min\{2{\bar{\sigma }}_{\kappa }^2{\ell }_n,{\kappa }_2\}]\\ & =min\{2t{\bar{\sigma }}_{\kappa }^2,{\kappa }_2\}(1+2{log}^{+}(\sqrt{2t}{\bar{\sigma }}_{\kappa }/\sqrt{{\kappa }_2})).\end{array}$$

Define the $\sigma$-algebra $\mathcal{F}_{n} :=\sigma (\ell _{1},\ldots ,\ell _{n})$ and use the conditional independence to obtain

$$\mathbb{E}[|{\xi }_n-{\xi }_n^{(\kappa )}||{\xi }_m-{\xi }_m^{(\kappa )}||{\mathcal{F}}_m]\le min\{\sqrt{2{\ell }_n}{\bar{\sigma }}_{\kappa },{\kappa }_1\}min\{\sqrt{2{\ell }_m}{\bar{\sigma }}_{\kappa },{\kappa }_1\},n<m.$$

Note that $(\ell _{m}/L_{n})_{m=n+1}^{\infty}$ is a stick-breaking process on $[0,1]$ independent of $\mathcal{F}_{n}$. Use the tower property and apply (3.1) and Lemma 7.1 to get

$$\begin{array}{rl}& \sum _{m=n+1}^{\mathrm{\infty }}\mathbb{E}[|{\xi }_n-{\xi }_n^{(\kappa )}||{\xi }_m-{\xi }_m^{(\kappa )}||{\mathcal{F}}_n]\\ & \le min\{\sqrt{2{\ell }_n}{\bar{\sigma }}_{\kappa },{\kappa }_1\}\sum _{m=n+1}^{\mathrm{\infty }}\mathbb{E}[min\{\sqrt{2{\ell }_m}{\bar{\sigma }}_{\kappa },{\kappa }_1\}|{\mathcal{F}}_n]\\ & =2min\{\sqrt{2{\ell }_n}{\bar{\sigma }}_{\kappa },{\kappa }_1\}min\{\sqrt{2L_n}{\bar{\sigma }}_{\kappa },{\kappa }_1\}(1+{log}^{+}\frac{\sqrt{2L_n}{\bar{\sigma }}_{\kappa }}{{\kappa }_1})\\ & \le 2min\{2L_{n-1}{\bar{\sigma }}_{\kappa }^2,{\kappa }_1^2\}(1+{log}^{+}(\sqrt{2t}{\bar{\sigma }}_{\kappa }/{\kappa }_1)),\end{array}$$

where $\max \{L_{n},\ell _{n}\}\le L_{n-1}\le t$ is used in the last step. Since $\ell _{n}\overset {d}{=}L_{n}$, $n\in \mathbb{N}$, Lemma 7.1 yields

$$\begin{array}{rl}& 2\sum _{n=1}^{\mathrm{\infty }}\sum _{m=n+1}^{\mathrm{\infty }}\mathbb{E}[|{\xi }_n-{\xi }_n^{(\kappa )}||{\xi }_m-{\xi }_m^{(\kappa )}|]\\ & \le 4\sum _{n=1}^{\mathrm{\infty }}\mathbb{E}[min\{2L_{n-1}{\bar{\sigma }}_{\kappa }^2,{\kappa }_1^2\}](1+{log}^{+}(\sqrt{2t}{\bar{\sigma }}_{\kappa }/{\kappa }_1))=2{\mu }_1{(\kappa ,t)}^2.\end{array}$$

Putting everything together yields (7.2) for $p=2$.

Next we prove (7.3). By Lemma 7.2, we have

(7.6)

By (3.2) in Theorem 3.3 (a), ${\ell }_n|\mathbb{P}[X_{{\ell }_n}\le x|{\ell }_n]-\mathbb{P}[X_{{\ell }_n}^{(\kappa )}\le x|{\ell }_n]|\le \frac{1}{2}(\kappa /{\bar{\sigma }}_{\kappa }){\phi }_{\kappa }^3{\ell }_n^{1/2}$. By Fubini’s theorem, conditioning in each summand on $\ell _{n}$, using (7.6) and Lemma 7.1, we have

Let $\delta \in (0,2]$ satisfy $\inf _{u\in (0,1]}u^{\delta -2}(\overline{\sigma }_{u}^{2}+\sigma ^{2})>0$. By (3.3) in Theorem 3.3 (b), we get ${\ell }_n|\mathbb{P}[X_{{\ell }_n}\le x|{\ell }_n]-\mathbb{P}[X_{{\ell }_n}^{(\kappa )}\le x|{\ell }_n]|\le {\psi }_{\kappa }^{2/3}{\ell }_n^{1-2/(3\delta )}$, where $\psi _{\kappa }= C\kappa \varphi _{\kappa}$ as defined in (3.7). Moreover, ${\ell }_n|\mathbb{P}[X_{{\ell }_n}\le x|{\ell }_n]-\mathbb{P}[X_{{\ell }_n}^{(\kappa )}\le x|{\ell }_n]|\le {\ell }_n$. Hence by (7.6) and Lemma 7.1, we obtain

completing the proof. □

Proof of Theorem 3.4

Let $\ell ={({\ell }_n)}_{n\in \mathbb{N}}$ and $(\xi _{n},\xi _{n}^{(\kappa )})$, $n\in \mathbb{N}$, be as in Lemma 7.3. Define the vector

By (2.1) and (7.1), we have $(\zeta _{1},\zeta _{2},\zeta _{3})\overset {d}{=}\underline{\chi }_{t}$ and $(\zeta ^{(\kappa )}_{1},\zeta ^{(\kappa )}_{2},\zeta ^{(\kappa )}_{3}) \overset {d}{=}\underline{\chi }_{t}^{(\kappa )}$. Hence it suffices to show that these vectors satisfy (3.4), (3.6) and (3.7). Since the function $x\mapsto \min \{x,0\}$ is in ${\mathrm{Lip}}_1(\mathbb{R})$, the inequalities

follow from the triangle inequality. The theorem follows from Lemma 7.3. □

Remark 7.4

Let $C_{t}$ and $C_{t}^{(\kappa )}$ denote the convex minorants of $X$ and $X^{(\kappa )}$ on $[0,t]$, respectively. Couple $X$ and $X^{(\kappa )}$ in such a way that the stick-breaking processes describing the lengths of the faces of their convex minorants (see González Cázares and Mijatović [32, Theorem 11] and González Cázares et al. [35, Sect. 4.1]) coincide. (The Skorokhod space $\mathcal{D}[0,t]$ and the space of sequences on ℝ are both Borel spaces by Kallenberg [39, Theorems A1.1, A1.2 and A2.2]; so the existence of such a coupling is guaranteed by [39, Theorem 6.10].) By conditioning further, we may assume the increments $(\xi _{n},\xi ^{(\kappa )}_{n})$, $n\in \mathbb{N}$, are coupled as in Lemma 7.3, yielding an SBG coupling of the pair $(X,X^{(\kappa )})$ on the interval $[0,t]$.

Geometric arguments similar to González Cázares et al. [34, Sect. 5.1] show that the sequences of heights of the faces of the convex minorants ${({\xi }_n)}_{n\in \mathbb{N}}$ and ${({\xi }_n^{(\kappa )})}_{n\in \mathbb{N}}$ satisfy

Hence the inequalities in (7.3) and (7.4) yield the same bounds as in Theorem 3.4, but in a stronger metric (namely, the distance between the convex minorants in the supremum norm), while retaining the control on the time of the infimum.

7.3 The proofs of Propositions 3.7, 3.9, 3.12 and 3.15

The Lévy–Khintchine formula for $X_{t}$ in (2.3), the definition of $X^{(\kappa )}_{t}$ in (2.5) and the inequality $e^{z}\geq 1+z$ (for all $z\in \mathbb{R}$) imply for any $u\in \mathbb{R}$, $t>0$ and $\kappa \in (0,1]$ that

(7.7)

Thus $\mathbb{E}[exp(u{X}_t^{(\kappa )})]\le \mathbb{E}[exp(u{X}_t)]exp({\bar{\sigma }}_{\kappa }^2{u}^{2}t/2)$, and in particular, the Gaussian approximation $X^{(\kappa )}$ has as many exponential moments as the Lévy process $X$.

Proof of Proposition 3.7

By Villani [68, Theorem 6.16], there exists a coupling between $(\xi ,\zeta )\overset {d}{=}(X_{T},\underline{X}_{T})$ and $(\xi ',\zeta ')\overset {d}{=}(X^{(\kappa )}_{T},\underline{X}^{(\kappa )}_{T})$ such that

$$\mathbb{E}{[{(|\xi -{\xi }^{\prime }|+|\zeta -{\zeta }^{\prime }|)}^2]}^{1/2}={\mathcal{W}}_2((X_T,{\underset{\_}{X}}_T),(X_T^{(\kappa )},{\underset{\_}{X}}_T^{(\kappa )})).$$

The identity $e^{b}-e^{a}=\int _{a}^{b} e^{z}dz$ implies that for $x\ge y$ and $x'\ge y'$, we have

$$\begin{aligned} |f(x,y)-f(x',y')| &\leq K(|e^{x}-e^{x'}|+|e^{y}-e^{y'}|) \\ &\leq K(|x-x'|+|y-y'|)e^{\max \{x,x'\}}. \end{aligned}$$

(7.8)

Apply this inequality, the Cauchy–Schwarz inequality, the elementary inequalities $(a+b)^{2}\le 2(a^{2}+b^{2})$ and $(a+b)^{1/2}\le a^{1/2}+b^{1/2}$, which hold for all $a,b\geq 0$, and the bound in (7.7) to obtain

$$\begin{array}{rl}\mathbb{E}[|f(\xi ,\zeta )-f({\xi }^{\prime },{\zeta }^{\prime })|]& \le K\mathbb{E}{[{(|\xi -{\xi }^{\prime }|+|\zeta -{\zeta }^{\prime }|)}^2]}^{1/2}\mathbb{E}{[{(e^{\xi }+e^{{\xi }^{\prime }})}^2]}^{1/2}\\ & \le 2^{1/2}K{\mathcal{W}}_2((X_T,{\underset{\_}{X}}_T),(X_T^{(\kappa )},{\underset{\_}{X}}_T^{(\kappa )}))\mathbb{E}{[e^{2\xi }+e^{2{\xi }^{\prime }}]}^{1/2}\\ & \le 2K{\mathcal{W}}_2((X_T,{\underset{\_}{X}}_T),(X_T^{(\kappa )},{\underset{\_}{X}}_T^{(\kappa )}))\mathbb{E}{[e^{2X_T}]}^{1/2}(1+e^{{\bar{\sigma }}_{\kappa }^{2}T}).\end{array}$$

Applying Corollary 3.5 gives the desired inequality, concluding the proof of the proposition. □

We now introduce a tool that uses the $L^{p}$-distance $\mathbb{E}{[{|\zeta -{\zeta }^{\prime }|}^p]}^{1/p}$ between random variables $\zeta$ and $\zeta '$ to bound the $L^{1}$-distance between the indicators.

Lemma 7.5

Let $(\xi ,\zeta )$ and $(\xi ',\zeta ')$ be random vectors in ${\mathbb{R}}^n\times \mathbb{R}$. Fix $y\in \mathbb{R}$ and let $h\in {\mathrm{Lip}}_K({\mathbb{R}}^n)$ satisfy $0\le h\le M$ for some constants $K,M\geq 0$. Denote . Then for any $p,r>0$, we have

$$\begin{array}{rl}\mathbb{E}[|f(\xi ,\zeta )-f({\xi }^{\prime },{\zeta }^{\prime })|]& \le K\mathbb{E}[|\xi -{\xi }^{\prime }|]+M\mathbb{P}[|\zeta -y|\le r]\\ & \phantom{=:}+M{r}^{-p}\mathbb{E}[{|\zeta -{\zeta }^{\prime }|}^p].\end{array}$$

(7.9)

In particular, if $|\mathbb{P}[\zeta \le y]-\mathbb{P}[\zeta \le y+r]|\le C{|r|}^{\gamma }$ for some $C,\gamma >0$ and all $r\in \mathbb{R}$, then

$$\begin{array}{rl}\mathbb{E}[|f(\xi ,\zeta )-f({\xi }^{\prime },{\zeta }^{\prime })|]& \le K\mathbb{E}[|\xi -{\xi }^{\prime }|]\\ & \phantom{=:}+M{\left(2C\frac{\gamma }{p}\right)}^{\frac{p}{p+\gamma }}(1+\frac{p}{\gamma })\mathbb{E}{[{|\zeta -{\zeta }^{\prime }|}^p]}^{\frac{\gamma }{p+\gamma }}.\end{array}$$

(7.10)

Remark 7.6

An analogous bound to the one in (7.9) holds for the indicator . Moreover, it follows from the proof below that the boundedness of the function $h$ in Lemma 7.5 may be replaced with a moment assumption $\xi ,\xi '\in L^{q}$ for some $q>1$. In that case, Hölder’s inequality could be invoked to obtain an analogue to (7.11) below. Similar arguments may be used to simultaneously handle multiple indicators.

Proof of Lemma 7.5

Applying the local $\gamma$-Hölder-continuity of the distribution function of $\zeta$ to (7.9) and optimising over $r>0$ yields (7.10). Thus it remains to establish (7.9).

Elementary set manipulation yields

Hence the triangle inequality and the Lipschitz property give

(7.11)

Taking expectations and using Markov’s inequality $\mathbb{P}[|\zeta -{\zeta }^{\prime }|>r]\le r^{-p}\mathbb{E}[{|\zeta -{\zeta }^{\prime }|}^p]$ yields (7.9). □

Proof of Proposition 3.9

Theorem 3.4 and (7.10) in Lemma 7.5 (with $C$ and $\gamma$ given in Assumption 3.8 and $p=2$) applied to $(X_{T},\underline{X}_{T})$ and $(X^{(\kappa )}_{T},\underline{X}^{(\kappa )}_{T})$ under the SBG coupling give the claim. □

Proof of Proposition 3.12

Analogously to the proof of Proposition 3.9, applying Theorem 3.4 and (7.10) in Lemma 7.5 (with $C$ and $\gamma$ given in Assumption 3.11 and $p=1$) gives the result. □

Lemma 7.7

Suppose $X$ is not a compound Poisson process. Then the law of $\underline{\tau }_{T}$ is absolutely continuous on $(0,T)$ and its density is bounded on compact subsets of $(0,T)$.

Proof

If $X$ or $-X$ is a subordinator, then $\underline{\tau }_{T}$ is a.s. 0 or $T$, respectively. In either case, the result follows immediately. Suppose now that neither $X$ nor $-X$ is a subordinator. Denote by $\overline{n}(\zeta >\cdot \,)$ (resp. $\underline{n}(\zeta >\cdot \,)$) the intensity measures of the lengths $\zeta$ of the excursions away from 0 of the Markov process $\overline{X}-X$ (resp. $X-\underline{X}$). Then by Chaumont [16, Theorem 6], the law of $\underline{\tau }_{T}$ can only have atoms at 0 or $T$, is absolutely continuous on $(0,T)$ and its density is given by $s\mapsto \underline{n}(\zeta >s)\overline{n}(\zeta >T-s)$, $s\in (0,T)$. The maps $s\mapsto \underline{n}(\zeta >s)$ and $s\mapsto \overline{n}(\zeta >s)$ are nonincreasing, and so the density is bounded on any compact subset of $(0,T)$, completing the proof. □

In preparation for the next result, we introduce the following assumption.

Assumption 7.8

There exists some function $a:(0,\infty )\to (0,\infty )$ such that $X_{t}/a(t)$ converges in distribution to an $\alpha$-stable law as $t\to 0$.

Proposition 7.9

Let Assumption 7.8hold for some $\alpha \in (0,2]$.

(a) If $\alpha >1$, then Assumption 3.8holds uniformly on compact subsets of $(-\infty ,0)$ with $\gamma =1$.

(b) Suppose $\rho :={lim}_{t\to 0}\mathbb{P}[X_t>0]\in (0,1)$. Then for any $\gamma \in (0,\min \{\rho ,1-\rho \})$, there exists a constant $C>0$ such that Assumption 3.11holds for all $s\in [0,T]$.

Note that $\rho$ is well defined under Assumption 7.8 and that $X_{t}/a(t)$ can only have a nonzero weak limit as $t\to 0$ if the limit is $\alpha$-stable. Moreover, in that case, $a$ is necessarily regularly varying at 0 with index $1/\alpha$, and $\alpha$ is given in terms of the Lévy triplet $(\sigma ^{2},\nu ,b)$ of $X$ by

$$ \alpha :=\textstyle\begin{cases} 2, &\quad \sigma \ne 0, \\ 1, &\quad \beta \in (0,1)\text{ and }b\ne \int _{(-1,1)}x\nu (dx), \\ \beta , &\quad \text{otherwise}, \end{cases} $$

where $\beta$ is the BG index introduced in (2.6). In fact, the assumptions of Proposition 3.15 imply Assumption 7.8 for $\alpha >1$ by Bisewski and Ivanovs [8, Proposition 2.3], so that Proposition 7.9 generalises Proposition 3.15. We refer the reader to Ivanovs [38, Sects. 3 and 4] for conditions that are equivalent to Assumption 7.8.

Assumption 7.8 allows the cases $\rho =0$ or $\rho =1$ when $\alpha \le 1$, which correspond to the stable limit being a.s. negative or a.s. positive, respectively. In these cases, the distribution of $\overline{\tau }_{T}(X)$ may have an atom at 0 or $T$, while the law of $\overline{\tau }_{T}(X^{(\kappa )})$ is absolutely continuous, making the convergence in the Kolmogorov distance impossible. This is the reason for excluding $\rho \in \{0,1\}$ in Proposition 7.9.

Proof of Proposition 7.9

By [8, Lemma 5.7], under the assumptions in part (a) of the proposition, $\underline{X}_{T}$ has a continuous density on $(-\infty ,0)$, implying the conclusion in (a).

Since $\rho ={lim}_{t\to 0}\mathbb{P}[X_t>0]\in (0,1)$, 0 is regular for both half-lines by Rogozin’s criterion; see Sato [62, Theorem 47.2]. Chaumont [16, Theorem 6] then asserts that the law of $\underline{\tau }_{T}$ is absolutely continuous with density given by $s\mapsto \underline{n}(\zeta {>}s)\overline{n}(\zeta {>}T{-}s)$, $s\in (0,T)$. The maps $s\mapsto \underline{n}(\zeta >s)$ and $s\mapsto \overline{n}(\zeta >s)$ are nonincreasing and by [8, Proposition 3.5] regularly varying with indices $\rho -1$ and $-\rho$, respectively. Thus for any $\gamma \in (0,\min \{\rho ,1-\rho \})$, there exists some constant $C>0$ such that the inequality $\underline{n}(\zeta >s)\overline{n}(\zeta >T-s) \le Cs^{\gamma -1}(T-s)^{ \gamma -1}$ holds for all $s\in (0,T)$. Thus for any $s,t\in [0,T/2]$ with $t\ge s$, we have

$$\begin{array}{rl}\mathbb{P}[{\underset{\_}{\tau }}_T\le t]-\mathbb{P}[{\underset{\_}{\tau }}_T\le s]& \le {\int }_s^{t}C{u}^{\gamma -1}{(T-u)}^{\gamma -1}du\le C{\int }_s^t{u}^{\gamma -1}{(T/2)}^{\gamma -1}du\\ & \le C{\gamma }^{-1}{(T/2)}^{\gamma -1}(t^{\gamma }-s^{\gamma })\le C{\gamma }^{-1}{(T/2)}^{\gamma -1}{(t-s)}^{\gamma },\end{array}$$

since the map $x\mapsto x^{\gamma}$ is concave. A similar bound holds for $s,t\in [T/2,T]$. Moreover, when $s\in [0,T/2]$ and $t\in [T/2,T]$, we have

$$\begin{array}{rl}\mathbb{P}[{\underset{\_}{\tau }}_T\le t]-\mathbb{P}[{\underset{\_}{\tau }}_T\le s]& \le \mathbb{P}[{\underset{\_}{\tau }}_T\le t]-\mathbb{P}[{\underset{\_}{\tau }}_T\le T/2]+\mathbb{P}[{\underset{\_}{\tau }}_T\le T/2]-\mathbb{P}[{\underset{\_}{\tau }}_T\le s]\\ & \le C{\gamma }^{-1}{(T/2)}^{\gamma -1}({(T/2-s)}^{\gamma }+{(t-T/2)}^{\gamma })\\ & \le C{\gamma }^{-1}{(T/2)}^{2\gamma -2}{(t-s)}^{\gamma }.\end{array}$$

This gives part (b) of the proposition. □

7.4 Level variances under SBG-Alg

In the present subsection, we establish bounds on the level variances under the coupling $\underline{\Pi }_{n,T}^{\kappa _{1},\kappa _{2}}$ (constructed in SBG-Alg) for Lipschitz, locally Lipschitz and discontinuous payoff functions (see $\mathrm{BT}_{1}$ in (3.12) and $\mathrm{BT}_{2}$ in (3.14)) of $\underline{\chi }_{T}$.

Theorem 7.10

Fix $T>0$, $n\in \mathbb{N}$ and $1\geq \kappa _{1}>\kappa _{2}>0$. Let $(Z_{n,T}^{(\kappa _{i})},\underline{Z}_{n,T}^{(\kappa _{i})}, \underline{\tau }_{n,T}^{(\kappa _{i})})$ denote the vector $\underline{\chi }_{n,T}^{(\kappa _{i})}$, $i\in \{1,2\}$, where the vector $(\underline{\chi }_{n,T}^{(\kappa _{1})},\underline{\chi }_{n,T}^{( \kappa _{2})} )$ constructed in SBG-Alg follows the law $\underline{\Pi }_{n,T}^{\kappa _{1},\kappa _{2}}$.

(a) For any Lipschitz function $f\in {\mathrm{Lip}}_K({\mathbb{R}}^2)$, $K>0$, we have

$$\mathbb{E}\left[{(f(Z_{n,T}^{({\kappa }_2)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_2)})-f(Z_{n,T}^{({\kappa }_1)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_1)}))}^2\right]\le K^{2}T(27{\sigma }^2{2}^{-n}+40{\bar{\sigma }}_{{\kappa }_1}^2).$$

(7.12)

For $f\in {\mathrm{locLip}}_K({\mathbb{R}}^2)$ as defined in Sect. 3.2, if $\int _{[1,\infty )}e^{4x}\nu (dx)<\infty$, then there exists a constant $C>0$ independent of $(n,\kappa _{1},\kappa _{2})$ such that

(7.13)

(b) Suppose Assumption 3.8is satisfied by some $y<0$ and $C,\gamma >0$. Then for any $f\in \mathrm{BT}_{1}(y,K,M)$, $K,M\ge 0$, there exists some $K'>0$ independent of $(n,\kappa _{1},\kappa _{2})$ such that

$$\mathbb{E}\left[{(f(Z_{n,T}^{({\kappa }_2)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_2)})-f(Z_{n,T}^{({\kappa }_1)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_1)}))}^2\right]\le K^{\prime }{({\sigma }^2{2}^{-n}+{\bar{\sigma }}_{{\kappa }_1}^2)}^{\frac{\gamma }{2+\gamma }}.$$

(c) If $\delta \in (0,2]$ satisfies Assumption 3.2, then there exists some $C>0$ such that for any $K>0$, $f\in {\mathrm{Lip}}_K(\mathbb{R})$, $n\in \mathbb{N}$, $\kappa _{1}>\kappa _{2}$ and $p\in \{1,2\}$, we have

(7.14)

(d) Fix $s\in (0,T)$ and let Assumption 3.2hold for some $\delta \in (0,2]$. Then for any $f\in \mathrm{BT}_{2}(s,K,M)$, $K,M\ge 0$, there exists a constant $C>0$ such that for any $n\in \mathbb{N}$, $p\in \{1,2\}$ and $\kappa _{1}>\kappa _{2}$, we have

The synchronous coupling of the large jumps of the Gaussian approximations implicit in SBG-Alg ensures that no moment assumption on the large jumps of $X$ is necessary for (7.12) to hold. For locally Lipschitz payoffs, however, the function may magnify the distance when a large jump occurs. This leads to the moment assumption $\int _{[1,\infty )}e^{4x}\nu (dx)<\infty$ for $f\in {\mathrm{locLip}}_K({\mathbb{R}}^2)$.

The proof of Theorem 7.10 requires bounds on certain moments of the differences of the components of the output of Algorithms 1 and 2 and SBG-Alg. They are given in Proposition 7.11.

Proposition 7.11

For any $1\geq \kappa _{1}>\kappa _{2}>0$, $t>0$ and $n\in \mathbb{N}$, the following statements hold:

(a) The pair $(Z_{t}^{(\kappa _{1})},Z_{t}^{(\kappa _{2})} ) \sim \Pi _{t}^{ \kappa _{1},\kappa _{2}}$ constructed in Algorithm 1satisfies the inequalities

$$\begin{array}{rl}\mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^2]& \le 2({\bar{\sigma }}_{{\kappa }_1}^2-{\bar{\sigma }}_{{\kappa }_2}^2)t,\\ \mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^4]& \le 12{({\bar{\sigma }}_{{\kappa }_1}^2-{\bar{\sigma }}_{{\kappa }_2}^2)}^2{t}^2+({\bar{\sigma }}_{{\kappa }_1}^2-{\bar{\sigma }}_{{\kappa }_2}^2){\kappa }_1^{2}t.\end{array}$$

Moreover, we have $\mathbb{E}[{({\underset{\_}{Z}}_t^{({\kappa }_1)}-{\underset{\_}{Z}}_t^{({\kappa }_2)})}^{2p}]\le 4\mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^{2p}]$ for $p\in \{1,2\}$.

(b) The vector $(Z^{(\kappa _{1})}_{t},\underline{Z}^{(\kappa _{1})}_{t}, \underline{\tau }_{t}^{(\kappa _{1})}, Z_{t}^{(\kappa _{2})}, \underline{Z}_{t}^{(\kappa _{2})},\underline{\tau }_{t}^{(\kappa _{2})} ) \sim \underline{\Pi }_{t}^{\kappa _{1},\kappa _{2}}$ constructed in Algorithm 2satisfies the inequalities

$$\begin{array}{rl}\mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^2]& =2({\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2)t,\\ \mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^4]& \le 12{({\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2)}^2{t}^2+({\bar{\sigma }}_{{\kappa }_1}^2-{\bar{\sigma }}_{{\kappa }_2}^2){\kappa }_1^{2}t.\end{array}$$

Moreover, we have $\mathbb{E}[{({\underset{\_}{Z}}_t^{({\kappa }_1)}-{\underset{\_}{Z}}_t^{({\kappa }_2)})}^{2p}]\le 4\mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^{2p}]$ for $p\in \{1,2\}$.

(c) The coupling $(\underline{\chi }^{(\kappa _{1})}_{n,t},\underline{\chi }^{( \kappa _{2})}_{n,t} ) \sim \underline{\Pi }_{n,t}^{\kappa _{1}, \kappa _{2}}$ constructed in SBG-Alg with components $\underline{\chi }_{n,t}^{(\kappa _{i})}=(Z_{n,t}^{(\kappa _{i})}, \underline{Z}_{n,t}^{(\kappa _{i})},\underline{\tau }_{n,t}^{(\kappa _{i})})$, $i\in \{1,2\}$, satisfies the inequalities

$$\mathbb{E}[{(Z_{n,t}^{({\kappa }_1)}-Z_{n,t}^{({\kappa }_2)})}^2]\le 2({\sigma }^2{2}^{-n}+{\bar{\sigma }}_{{\kappa }_1}^2)t,$$

(7.15)

$$\mathbb{E}[{(Z_{n,t}^{({\kappa }_1)}-Z_{n,t}^{({\kappa }_2)})}^4]\le (25{\bar{\sigma }}_{{\kappa }_1}^4+24{\sigma }^4{3}^{-n})t^2+{\bar{\sigma }}_{{\kappa }_1}^2{\kappa }_1^{2}t,$$

(7.16)

$$\mathbb{E}[{({\underset{\_}{Z}}_{n,t}^{({\kappa }_1)}-{\underset{\_}{Z}}_{n,t}^{({\kappa }_2)})}^2]\le (2+3\pi )({\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2)2^{-n}t+(2+5\pi ){\bar{\sigma }}_{{\kappa }_1}^{2}t,$$

(7.17)

$$\begin{array}{rl}\mathbb{E}[{({\underset{\_}{Z}}_{n,t}^{({\kappa }_1)}-{\underset{\_}{Z}}_{n,t}^{({\kappa }_2)})}^4]& \le 2\times {10}^3({({\sigma }^2+{\bar{\sigma }}_{{\kappa }_1})}^2{3}^{-n}+{\bar{\sigma }}_{{\kappa }_1}^4)t^2\\ & \phantom{=:}+2\pi {\bar{\sigma }}_{{\kappa }_1}^{5/2}{\kappa }_1^{3/2}{t}^{5/4}+4{\bar{\sigma }}_{{\kappa }_1}^2{\kappa }_1^{2}t.\end{array}$$

(7.18)

Remark 7.12

(i) Applying Proposition 7.11, we see that the $L^{2}$-norms of the differences $Z^{(\kappa _{1})}_{n,t}-Z^{(\kappa _{2})}_{n,t}$ and $\underline{Z}^{(\kappa _{1})}_{n,t}-\underline{Z}^{(\kappa _{2})}_{n,t}$ of the components of $(\underline{\chi }_{n,t}^{(\kappa _{1})},\underline{\chi }_{n,t}^{( \kappa _{2})})$ constructed in SBG-Alg decay at the same rate as the $L^{2}$-norm of $Z_{t}^{(\kappa _{1})}-Z_{t}^{(\kappa _{2})}$ constructed in Algorithm 1. Indeed, assume that $\kappa _{1}=c\kappa _{2}$ for some $c>1$, $\kappa _{2}\to 0$ and for some $c',r>0$ and all $x>0$, we have $\bar{\nu }(x)=\nu (\mathbb{R}\setminus (-x,x))\ge c^{\prime }{x}^{-r}$. Then for $n= \lceil{\log ^{2}(1+\overline{\nu }(\kappa _{2}))} \rceil$, we have $2^{-n}\le \overline{\sigma }_{\kappa _{1}}^{2}$ for all sufficiently small $\kappa _{1}$, implying the claim by Proposition 7.11 (a) and (c). Moreover, by Corollary 4.2, the corresponding expected computational complexities of Algorithm 1 and SBG-Alg are proportional as $\kappa _{2}\to 0$. Furthermore, since the decay of the bias of SBG-Alg is by Theorem 3.4 at most a logarithmic factor away from that of Algorithm 1, the MLMC estimator based on Algorithm 1 for $\mathbb{E}[f(X_t)]$ has the same computational complexity (up to logarithmic factors) as the MLMC estimator for $\mathbb{E}[f(X_t,{\underset{\_}{X}}_t)]$ based on SBG-Alg (see Table 2 for the complexity of the latter).

(ii) The proof of Proposition 7.11 implies that an improvement in Algorithm 1 (i.e., a simulation procedure for a coupling with a smaller $L^{2}$-norm of $Z_{t}^{(\kappa _{1})}-Z_{t}^{(\kappa _{2})}$) would result in an improvement in SBG-Alg for the simulation of a coupling $(\underline{\chi }_{t}^{(\kappa _{1})},\underline{\chi }_{t}^{( \kappa _{2})})$. Interestingly, this holds in spite of the fact that SBG-Alg calls Algorithm 2 whose coupling $\underline{\Pi }_{t}^{\kappa _{1},\kappa _{2}}$ is inefficient in terms of the $L^{2}$-distance, but is applied over the short interval $[0,L_{n}]$.

(iii) A nontrivial bound on the moments of the difference $\underline{\tau }_{t}^{(\kappa _{1})}-\underline{\tau }_{t}^{( \kappa _{2})}$ under the coupling of Algorithm 2, which would complete the statement in Proposition 7.11 (b), appears to be out of reach. By the SB representation in (2.2), such a bound is not necessary for our purposes. The corresponding bound on the moments of the difference $\underline{\tau }_{n,t}^{(\kappa _{1})}-\underline{\tau }_{n,t}^{( \kappa _{2})}$ constructed in SBG-Alg follows from Proposition 7.13 below; see (7.24).

(iv) The bounds on the fourth moments in (7.16) and (7.18) are required to control the level variances of the MLMC estimator in the case of locally Lipschitz payoff functions and are applied in the proof of Theorem 7.10 (a).

Proof of Proposition 7.11

(a) The difference $Z^{(\kappa _{1})}_{t}-Z^{(\kappa _{2})}_{t}$ constructed by Algorithm 1 equals by (2.5) a sum of the two independent martingales

$$ \big((\overline{\sigma }_{\kappa _{1}}^{2}+\sigma ^{2})^{1/2} -( \overline{\sigma }_{\kappa _{2}}^{2}+\sigma ^{2})^{1/2}\big)W_{t}, \qquad J_{t}^{2,\kappa _{1}}-J_{t}^{2,\kappa _{2}} + (b_{\kappa _{1}}-b_{ \kappa _{2}})t. $$

Thus we obtain the identity

$$\mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^2]=({(\sqrt{{\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2}-\sqrt{{\sigma }^2+{\bar{\sigma }}_{{\kappa }_2}^2})}^2+{\bar{\sigma }}_{{\kappa }_1}^2-{\bar{\sigma }}_{{\kappa }_2}^2)t.$$

The first inequality follows since $0<(\sigma ^{2}+\overline{\sigma }^{2}_{\kappa _{1}})^{1/2} -(\sigma ^{2}+ \overline{\sigma }^{2}_{\kappa _{2}})^{1/2} \le (\overline{\sigma }^{2}_{ \kappa _{1}}-\overline{\sigma }^{2}_{\kappa _{2}})^{1/2}$. Since $Z^{(\kappa _{1})}_{t}-Z^{(\kappa _{2})}_{t}$ is a Lévy process, differentiating its Lévy–Khintchine formula in (2.3) yields the identity

$$\begin{array}{rl}\mathbb{E}[{(Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)})}^4]& =3{({(\sqrt{{\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2}-\sqrt{{\sigma }^2+{\bar{\sigma }}_{{\kappa }_2}^2})}^2+{\bar{\sigma }}_{{\kappa }_1}^2-{\bar{\sigma }}_{{\kappa }_2}^2)}^2{t}^2\\ & \phantom{=:}+t{\int }_{(-{\kappa }_1,{\kappa }_1)\setminus (-{\kappa }_2,{\kappa }_2)}{x}^4\nu (dx),\end{array}$$

implying the second inequality. Since $|\underline{Z}_{t}^{(\kappa _{1})}-\underline{Z}_{t}^{(\kappa _{2})}| \le \sup _{s\in [0,t]}|Z_{s}^{(\kappa _{1})}-Z_{s}^{(\kappa _{2})}|$, Doob’s maximal martingale inequality applied to the martingale $(Z_{s}^{(\kappa _{1})}-Z_{s}^{(\kappa _{2})})_{s\in [0,t]}$ yields

$$\mathbb{E}[{|{\underset{\_}{Z}}_t^{({\kappa }_1)}-{\underset{\_}{Z}}_t^{({\kappa }_2)}|}^p]\le {(1-1/p)}^{-p}\mathbb{E}[{|Z_t^{({\kappa }_1)}-Z_t^{({\kappa }_2)}|}^p],p>1.$$

The corresponding inequalities follow because $(p/(p-1))^{p}\le 4$ for $p\in \{2,4\}$.

(b) Analogously to part (a), the difference $Z_{t}^{(\kappa _{1})}-Z_{t}^{(\kappa _{2})}$ constructed in Algorithm 2 is a sum of two independent martingales $(\overline{\sigma }_{\kappa _{1}}^{2}+\sigma ^{2})^{1/2}B_{t} -( \overline{\sigma }_{\kappa _{2}}^{2}+\sigma ^{2})^{1/2}W_{t}$ and $J_{t}^{2,\kappa _{1}}-J_{t}^{2,\kappa _{2}} + (b_{\kappa _{1}}-b_{ \kappa _{2}})t$, where $B$ and $W$ are independent standard Brownian motions. Thus the statements follow as in part (a).

(c) Let $(\xi _{1,k},\xi _{2,k})\sim \Pi _{\ell _{k}}^{\kappa _{1},\kappa _{2}}$, $k\in \{1,\ldots ,n\}$, and $(\underline{\zeta }_{1},\underline{\zeta }_{2})\sim \underline{\Pi }_{L_{n}}^{ \kappa _{1},\kappa _{2}}$ be independent draws as in line 2 of SBG-Alg. Denote by $(\xi _{i,n+1},\underline{\xi }_{i,n+1})$ the first two coordinates of $\underline{\zeta }_{i}$, $i\in \{1,2\}$. Since the variables $\xi _{1,k}-\xi _{2,k}$, $k=1, \dots , n+1$, have zero mean and are uncorrelated, by conditioning on $\ell _{k}$, $k=1, \dots , n$, and $L_{n}$ and applying parts (a) and (b), we obtain

$$\begin{array}{rl}\mathbb{E}[{(Z_{n,t}^{({\kappa }_1)}-Z_{n,t}^{({\kappa }_2)})}^2]& =\mathbb{V}[Z_{n,t}^{({\kappa }_1)}-Z_{n,t}^{({\kappa }_2)}]\\ & =\mathbb{V}[{\xi }_{1,n+1}-{\xi }_{2,n+1}]+\sum _{k=1}^n\mathbb{V}[{\xi }_{1,k}-{\xi }_{2,k}]\\ & \le 2({\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2)\mathbb{E}[L_n]+2{\bar{\sigma }}_{{\kappa }_1}^2\sum _{k=1}^n\mathbb{E}[{\ell }_k]\\ & =2({\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2)2^{-n}t+2{\bar{\sigma }}_{{\kappa }_1}^2(1-2^{-n})t,\end{array}$$

implying (7.15). Similarly, by conditioning on $\ell _{k}$, $k=1, \dots , n$, and $L_{n}$, we deduce that the expectations of

$$ (\xi _{1,k_{1}}-\xi _{2,k_{1}})^{3}(\xi _{1,k_{2}}-\xi _{2,k_{2}}), \quad (\xi _{1,k_{1}}-\xi _{2,k_{1}})^{2}\prod _{i=2}^{3} (\xi _{1,k_{i}}- \xi _{2,k_{i}}), \quad \prod _{i=1}^{4} (\xi _{1,k_{i}}-\xi _{2,k_{i}}) $$

vanish for any distinct $k_{1},k_{2},k_{3},k_{4}\in \{1,\ldots ,n+1\}$. Thus expanding yields

$$\begin{array}{rl}\mathbb{E}[{(Z_{n,t}^{({\kappa }_1)}-Z_{n,t}^{({\kappa }_2)})}^4]& =\sum _{k=1}^{n+1}\mathbb{E}[{({\xi }_{1,k}-{\xi }_{2,k})}^4]\\ & +6\sum _{m=1}^n\sum _{k=m+1}^{n+1}\mathbb{E}[{({\xi }_{1,m}-{\xi }_{2,m})}^2{({\xi }_{1,k}-{\xi }_{2,k})}^2].\end{array}$$

The summands in the first sum are easily bounded by parts (a) and (b). To bound the summands of the second sum, condition on $\ell _{k}$, $k=1, \dots , n$, and $L_{n}$ and apply parts (a) and (b) to get

$$\mathbb{E}[{({\xi }_{1,k}-{\xi }_{2,k})}^2{({\xi }_{1,m}-{\xi }_{2,m})}^2]\le \{\begin{array}{cc}4{\bar{\sigma }}_{{\kappa }_1}^4\mathbb{E}[{\ell }_m{\ell }_k],\hfill & m<k\le n,\hfill \\ 4({\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2){\bar{\sigma }}_{{\kappa }_1}^2\mathbb{E}[{\ell }_m{L}_n],\hfill & m<k=n+1.\hfill \end{array}$$

Inequality (7.16) follows since $\mathbb{E}[{\ell }_m{\ell }_k]=3^{-m}{2}^{m-k-1}{t}^2$, $\mathbb{E}[{\ell }_k{L}_n]=3^{-k}{2}^{k-n-1}{t}^2$ for $m< k\le n$ and $\sigma ^{2}2^{-n}\overline{\sigma }_{\kappa}^{2} \le \sigma ^{2}3^{-n/2} \overline{\sigma }_{\kappa}^{2} \le (\sigma ^{4} 3^{-n}+ \overline{\sigma }_{\kappa}^{4})/2$.

The representation in line 3 of SBG-Alg and an appeal to the elementary inequality $|a-b|\ge |\min \{a,0\}-\min \{b,0\}|$ (for all $a,b\in \mathbb{R}$) imply

$$\begin{array}{rl}\mathbb{E}[{({\underset{\_}{Z}}_{n,t}^{({\kappa }_1)}-{\underset{\_}{Z}}_{n,t}^{({\kappa }_2)})}^2]& \le \mathbb{E}[{({\underset{\_}{\xi }}_{1,n+1}-{\underset{\_}{\xi }}_{2,n+1})}^2+\sum _{k=1}^n{({\xi }_{1,k}-{\xi }_{2,k})}^2]\\ & \phantom{=:}+2\mathbb{E}[\sum _{k=1}^n|{\underset{\_}{\xi }}_{1,n+1}-{\underset{\_}{\xi }}_{2,n+1}||{\xi }_{1,k}-{\xi }_{2,k}|\\ & \phantom{=:}+\sum _{m=1}^{n-1}\sum _{k=m+1}^n|{\xi }_{1,m}-{\xi }_{2,m}||{\xi }_{1,k}-{\xi }_{2,k}|].\end{array}$$

(7.19)

The first term on the right-hand side of this inequality is easily bounded via the inequalities in parts (a) and (b). To bound the second term, condition on $\ell _{k}$, $k=1, \dots ,n$, and $L_{n}$, apply the Cauchy–Schwarz inequality, denote $\upsilon :=\sqrt{\sigma ^{2}+\overline{\sigma }_{\kappa _{1}}^{2}}$ and observe that for $m< k\le n$, we get

$$\begin{array}{rl}\mathbb{E}[|{\underset{\_}{\xi }}_{1,n+1}-{\underset{\_}{\xi }}_{2,n+1}||{\xi }_{1,k}-{\xi }_{2,k}|]& \le \mathbb{E}\left[\sqrt{16({\sigma }^2+{\bar{\sigma }}_{{\kappa }_1}^2){\bar{\sigma }}_{{\kappa }_1}^2{\ell }_k{L}_n}\right]\\ & =\pi \upsilon {\bar{\sigma }}_{{\kappa }_1}{\left(\frac{2}{3}\right)}^n{\left(\frac{3}{4}\right)}^{k}t,\\ \mathbb{E}[|{\xi }_{1,m}-{\xi }_{2,m}||{\xi }_{1,k}-{\xi }_{2,k}|]& \le \mathbb{E}\left[\sqrt{4{\bar{\sigma }}_{{\kappa }_1}^4{\ell }_m{\ell }_k}\right]=\pi {\bar{\sigma }}_{{\kappa }_1}^2{(1/2)}^{m+1}{(2/3)}^{k-m}t,\end{array}$$

where the equalities follow from the definition of the stick-breaking process (see Sect. 2.1). By (7.19), we have

$$\begin{array}{rl}\mathbb{E}[{({\underset{\_}{Z}}_{n,t}^{({\kappa }_1)}-{\underset{\_}{Z}}_{n,t}^{({\kappa }_2)})}^2]& \le {\upsilon }^2{2}^{1-n}t+2{\bar{\sigma }}_{{\kappa }_1}^{2}t\sum _{k=1}^{\mathrm{\infty }}{2}^{-k}+2\pi \upsilon {\bar{\sigma }}_{{\kappa }_1}{\left(\frac{2}{3}\right)}^{n}t\sum _{k=1}^{\mathrm{\infty }}{\left(\frac{3}{4}\right)}^k\\ & \phantom{=:}+\pi {\bar{\sigma }}_{{\kappa }_1}^{2}t\sum _{m=1}^{\mathrm{\infty }}\sum _{k=1}^{\mathrm{\infty }}{2}^{-m}{\left(\frac{2}{3}\right)}^k.\end{array}$$

So (7.17) follows from the inequalities $v(2/3)^{n}\overline{\sigma }_{\kappa }\le \upsilon 2^{-n/2} \overline{\sigma }_{\kappa }\le (\upsilon ^{2} 2^{-n}+ \overline{\sigma }_{\kappa}^{2})/2$.

As before, $|\min \{a,0\}-\min \{b,0\}|\leq |a-b|$ for $a,b\in \mathbb{R}$ yields the inequality

$$\mathbb{E}[{({\underset{\_}{Z}}_{n,t}^{({\kappa }_1)}-{\underset{\_}{Z}}_{n,t}^{({\kappa }_2)})}^4]\le \mathbb{E}\left[{(|{\underset{\_}{\xi }}_{1,n+1}-{\underset{\_}{\xi }}_{2,n+1}|+\sum _{k=1}^n|{\xi }_{1,k}-{\xi }_{2,k}|)}^4\right].$$

(7.20)

By Jensen’s inequality, $\mathbb{E}[{|\vartheta |}^3]\le \mathbb{E}{[{\vartheta }^4]}^{3/4}$ and $\mathbb{E}[\vartheta ]\le \sqrt{\mathbb{E}[{\vartheta }^2]}$ for any random variable $\vartheta$. Hence we may bound the first and third conditional moments of the differences $|\xi _{1,k}-\xi _{2,k}|$ and $|\underline{\xi }_{1,n+1}-\underline{\xi }_{2,n+1}|$ given $\ell _{k}$, $k=1, \dots ,n$, and $L_{n}$. Thus by expanding (7.20), conditioning on $\ell _{k}$, $k=1, \dots ,n$, and $L_{n}$ and using elementary estimates as in all the previously developed bounds, we obtain (7.18). □

In order to control the level variances of the MLMC estimator in (4.3) for discontinuous payoffs of $\underline{\chi }_{t}$ and functions of $\underline{\tau }_{t}$, we should need to apply Lemma 7.5 to the components of $(\underline{\chi }^{(\kappa _{1})}_{n,t},\underline{\chi }^{( \kappa _{2})}_{n,t} )$ constructed in SBG-Alg. In particular, the assumption in Lemma 7.5 requires a control on the constants in the local Lipschitz property of the distribution functions of the various components of $(\underline{\chi }^{(\kappa _{1})}_{n,t},\underline{\chi }^{( \kappa _{2})}_{n,t} )$ in terms of the cutoff levels $\kappa _{1}$ and $\kappa _{2}$. As such a uniform bound in the cutoff level appears to be out of reach, we establish Proposition 7.13 which allows us to compare the sampled quantities $\underline{\chi }^{(\kappa _{1})}_{n,t}$ and $\underline{\chi }^{(\kappa _{2})}_{n,t}$ with their limit $\underline{\chi }_{t}$ (as $\kappa _{1},\kappa _{2}\to 0$). Since under mild assumptions, the distribution functions of the components of the limit $\underline{\chi }_{t}$ possess the necessary regularity and do not depend on the cutoff level, the application of Lemma 7.5 in the proof of Theorem 7.10 becomes feasible by using Proposition 7.13.

Proposition 7.13

There exists a coupling between the vector $\underline{\chi }_{t}=(X_{t},\underline{X}_{t},\underline{\tau }_{t})$ and the pair of vectors $(\underline{\chi }^{(\kappa _{1})}_{n,t},\underline{\chi }^{( \kappa _{2})}_{n,t} ) \sim \underline{\Pi }_{n,t}^{\kappa _{1}, \kappa _{2}}$ such that for $i\in \{1,2\}$ and any $p\ge 1$, the vector $(Z_{n,t}^{(\kappa _{i})}, \underline{Z}_{n,t}^{(\kappa _{i})}, \underline{\tau }_{n,t}^{(\kappa _{i})}) =\underline{\chi }_{n,t}^{( \kappa _{i})}$ satisfies

(7.21)

(7.22)

Moreover, if $\delta \in (0,2]$ satisfies Assumption 3.2, we have

$$\mathbb{E}[{|{\underset{\_}{\tau }}_t-{\underset{\_}{\tau }}_{n,t}^{({\kappa }_i)}|}^p]\le 2^{-n}{t}^p+t^{p-1}\theta (t,{\kappa }_i),$$

(7.23)

where given $T\ge t$, there exists a constant $C>0$ dependent only on $(T,\sigma ^{2},\nu ,b)$ such that for all $\kappa \in (0,1]$, the function $\theta (t,\kappa )$ is defined as

$$ \theta (t,\kappa ) :=\textstyle\begin{cases} \min \{1,\sqrt{C\overline{\sigma }_{\kappa}}\}t, &\quad \delta =2, \\ \min \{t,(C\overline{\sigma }_{\kappa})^{\frac{2\delta}{2-\delta}}\} \\ \quad +\frac{4\delta }{5\delta -2}\sqrt{C\overline{\sigma }_{\kappa}} (t^{ \frac{5\delta -2}{4\delta}} -\min \{t,(C\overline{\sigma }_{\kappa})^{ \frac{4\delta}{4-2\delta}}\} ^{\frac{5\delta -2}{4\delta}} ), &\quad \delta \in (0,2) \setminus \{\frac{2}{5}\}, \\ \min \{t,\sqrt{C\overline{\sigma }_{\kappa}}\}+\sqrt{C \overline{\sigma }_{\kappa}} \log ^{+} (t/\sqrt{C\overline{\sigma }_{ \kappa}} ), &\quad \delta =\frac{2}{5}. \end{cases} $$

A simple consequence of (7.23) (with $p=1$) in Proposition 7.13 and the elementary inequality $|\underline{\tau }^{(\kappa _{1})}_{n,t} -\underline{\tau }^{( \kappa _{2})}_{n,t}|\le t$ is that the coupling in SBG-Alg satisfies

$$\mathbb{E}[{|{\underset{\_}{\tau }}_{n,t}^{({\kappa }_1)}-{\underset{\_}{\tau }}_{n,t}^{({\kappa }_2)}|}^p]\le 2^{1-n}{t}^p+2t^{p-1}\theta (t,{\kappa }_1)\text{for any }p\ge 1.$$

(7.24)

The bounds in (7.21) and (7.22) of Proposition 7.13 imply the inequalities in (7.15) and (7.17) of Proposition 7.11 (c) with slightly worse constants.

Proof

The proof and construction of the random variables is analogous to that of Proposition 7.11 (c) where for $i\in \{1,2\}$, we compare the increment $Z_{s}^{(\kappa _{i})}$ defined in Algorithm 1 with the Lévy–Itô decomposition $X_{s} = bs+\sigma W_{s} + J^{1,\kappa _{i}}_{s} + J^{2,\kappa _{i}}_{s}$ ($W$ is as in Algorithm 1, independent of $J^{1,\kappa _{i}}$ and $J^{2,\kappa _{i}}$) over the time horizons $s\in \{\ell _{1},\ldots ,\ell _{n-1}\}$. Similarly, we compare the pair of vectors $(\underline{\chi }_{s}^{(\kappa _{1})},\underline{\chi }_{s}^{( \kappa _{2})})$ produced by Algorithm 2 with $\underline{\chi }_{s}$ for $s=L_{n}$, where we assume that the (standardised) Brownian component of $X$ equals that of $\underline{\chi }_{s}^{(\kappa _{2})}$ (and is thus independent of the one in $\underline{\chi }_{s}^{(\kappa _{1})}$) and all jumps in $J^{2,\kappa _{2}}$ are synchronously coupled.

Denote the first and fourth components of the vector $(\underline{\chi }_{s}^{(\kappa _{1})},\underline{\chi }_{s}^{( \kappa _{2})})$ by $Z_{s}^{(\kappa _{1})}$ and $Z_{s}^{(\kappa _{2})}$, respectively. Hence it is enough to obtain the analogous bounds and identities to those presented in parts (a) and (b) for the expectations $\mathbb{E}[{(X_t-Z_t^{({\kappa }_i)})}^2]$, $i\in \{1,2\}$, under both couplings $\Pi _{t}^{\kappa _{1},\kappa _{2}}$ and $\underline{\Pi }_{t}^{\kappa _{1},\kappa _{2}}$. Such bounds may be obtained by using the proofs of parts (a) and (b), resulting in the following estimates: for $i\in \{1,2\}$, we have

(7.25)

Thus Doob’s martingale inequality and elementary inequalities give (7.21), (7.22).

By the construction of the law $\underline{\Pi }_{n,t}^{\kappa _{1},\kappa _{2}}$ in SBG-Alg, there exist random variables $\xi '_{k}$, $k=1, \dots ,n$, such that for $k\in \{1,\ldots ,n\}$, conditionally on $\ell _{k}=s$ and independently of $\ell _{j}$, $j\ne k$, the distributional equality $(\xi '_{k},\xi _{1,k},\xi _{2,k}) \overset {d}{=}(X_{s},Z_{s}^{(\kappa _{1})},Z_{s}^{( \kappa _{2})})$ holds, where $(Z_{t}^{(\kappa _{1})},Z_{t}^{(\kappa _{2})})\sim \Pi ^{\kappa _{1}, \kappa _{2}}_{t}$ and $W$ in Algorithm 1 equals the Brownian component of $X$ in (2.4). Note that by (2.2), we have

(7.26)

Let $\delta \in (0,2]$ be as in the statement of the proposition. By Picard [58, Theorem 3.1 (a)], as in the proof of Theorem 3.4, we know that the density $f_{t}$ of $X_{t}$ exists, is smooth and given $T>0$, the constant $C^{\prime }:=2^{3/2}{sup}_{(s,x)\in (0,T]\times \mathbb{R}}{s}^{1/\delta }{f}_s(x)$ is finite. Thus (7.10) in Lemma 7.5 (with constants $\gamma =1$, $C=2^{-3/2}\ell _{k}^{-1/\delta}C'$ and $M=1$, $K=0$, $p=1$) gives

for $i\in \{1,2\}$ and any $k\in \{1,\ldots ,n\}$, where the second inequality follows from Jensen’s inequality and (7.25). Hence elementary inequalities, (7.26) and Lemma 7.1 imply that for $i\in \{1,2\}$,

For $p>1$, the result follows from the case $p=1$ and by using the inequality $|\underline{\tau }_{t}-\underline{\tau }_{n,t}^{(\kappa _{i})}|^{p} \le t^{p-1}|\underline{\tau }_{t}-\underline{\tau }_{n,t}^{(\kappa _{i})}|$. □

Proof of Theorem 7.10

(a) Proposition 7.11 (c) and elementary inequalities yield (7.12). So it remains to consider the case $f\in {\mathrm{locLip}}_K({\mathbb{R}}^2)$. As in the proof of Proposition 3.7, by the inequality in (7.8) and the Cauchy–Schwarz inequality, we have

$$\begin{array}{rl}& \mathbb{E}{\left[{(f(Z_{n,T}^{({\kappa }_1)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_1)})-f(Z_{n,T}^{({\kappa }_2)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_2)}))}^2\right]}^2\\ & \le K^4{K}^{\prime }\mathbb{E}[{(|Z_{n,T}^{({\kappa }_1)}-Z_{n,T}^{({\kappa }_2)}|+|{\underset{\_}{Z}}_{n,T}^{({\kappa }_1)}-{\underset{\_}{Z}}_{n,T}^{({\kappa }_2)}|)}^4],\end{array}$$

where $K^{\prime }:=\mathbb{E}[{(exp(Z_{n,T}^{({\kappa }_1)})+exp(Z_{n,T}^{({\kappa }_2)}))}^4]\le 8\mathbb{E}[exp(4X_T^{({\kappa }_1)})+exp(4X_T^{({\kappa }_2)})]$. Applying (7.7), we get $\mathbb{E}[exp(4X_T^{({\kappa }_i)})]\le \mathbb{E}[exp(4X_T)]exp(4T{\bar{\sigma }}_{{\kappa }_i}^2)$ and $\overline{\sigma }^{2}_{\kappa _{i}}\le \overline{\sigma }^{2}_{1}$, $i\in \{1,2\}$, where $\mathbb{E}[exp(4X_T)]$ is finite since $\int _{[1,\infty )}e^{4x}\nu (dx)<\infty$. The concavity of $x\mapsto \sqrt{x}$ and the inequalities (7.16) and (7.18) in Proposition 7.11 (c) imply the existence of a constant $C>0$ satisfying

$$\begin{array}{rl}& \sqrt{\mathbb{E}[{(|Z_{n,T}^{({\kappa }_1)}-Z_{n,T}^{({\kappa }_2)}|+|{\underset{\_}{Z}}_{n,T}^{({\kappa }_1)}-{\underset{\_}{Z}}_{n,T}^{({\kappa }_2)}|)}^4]}\\ & \le C{(2/3)}^{n/2}+11T{\bar{\sigma }}_{{\kappa }_1}^2+\sqrt{2\pi }{T}^{5/8}{\bar{\sigma }}_{{\kappa }_1}^{5/4}{\kappa }_1^{3/4}+\sqrt{5T}{\bar{\sigma }}_{{\kappa }_1}{\kappa }_1.\end{array}$$

The inequality (7.13) then follows since $\overline{\sigma }_{\kappa _{1}}^{1/4}\kappa _{1}^{3/4} \le \max \{ \overline{\sigma }_{\kappa _{1}},\kappa _{1}\} \le \overline{\sigma }_{ \kappa _{1}}+\kappa _{1}$.

(b) Let $(\underline{\chi }_{T},\underline{\chi }_{n,T}^{(\kappa _{1})}, \underline{\chi }_{n,T}^{(\kappa _{2})})$ be as in Proposition 7.13, where $\underline{\chi }_{T}=(X_{T},\underline{X}_{T},\underline{\tau }_{T})$ and $\underline{\chi }_{n,T}^{(\kappa _{i})}=(Z_{n,T}^{(\kappa _{i})}, \underline{Z}_{n,T}^{(\kappa _{i})},\underline{\tau }_{n,T}^{(\kappa _{i})})$, $i\in \{1,2\}$. The triangle inequality and the inequalities $0\leq f\leq M$ give

$$\begin{array}{rl}& \mathbb{E}\left[{(f(Z_{n,T}^{({\kappa }_1)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_1)})-f(Z_{n,T}^{({\kappa }_2)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_2)}))}^2\right]\\ & \le M\mathbb{E}[|f(Z_{n,T}^{({\kappa }_1)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_1)})-f(Z_{n,T}^{({\kappa }_2)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_2)})|]\\ & \le M\sum _{i=1}^2\mathbb{E}[|f(Z_{n,T}^{({\kappa }_i)},{\underset{\_}{Z}}_{n,T}^{({\kappa }_i)})-f(X_T,{\underset{\_}{X}}_T)|].\end{array}$$

Apply (7.10) in Lemma 7.5 with $C$ and $\gamma$ from Assumption 3.8 to $(X_{T},\underline{X}_{T})$ and $(Z^{(\kappa _{i})}_{n,T},\underline{Z}^{(\kappa _{i})}_{n,T} )$ to get

for $i\in \{1,2\}$, where $K'':=M(1+2/\gamma ) (48C^{2}\gamma ^{2}T^{\gamma})^{1/(2+ \gamma )}$. In the second inequality, we used the bounds (7.21) and (7.22). Since $\overline{\sigma }_{\kappa _{1}}\ge \overline{\sigma }_{\kappa _{2}}$, the result follows.

(c) Recall that (7.24) follows from (7.23). The inequality (7.14) in the proposition is a direct consequence of the Lipschitz property and (7.24).

(d) The proof follows along the same lines as in part (b): apply (7.10) in Lemma 7.5 with $C$ and $\gamma$ from Assumption 3.11 and the bounds (7.21)–(7.23) from Proposition 7.13. □

7.5 Computational complexity of the MC and MLMC estimators

In this subsection, we address the application of our previous results to estimate the expectation $\mathbb{E}[f({\underset{\_}{\chi }}_T)]$ for various real-valued functions $f$ satisfying $\mathbb{E}[f{({\underset{\_}{\chi }}_T)}^2]<\mathrm{\infty }$. By definition, an estimator $\Upsilon$ of $\mathbb{E}[f({\underset{\_}{\chi }}_T)]$ has $L^{2}$-accuracy of level $\epsilon >0$ if it satisfies $\mathbb{E}[{(\mathrm{\Upsilon }-\mathbb{E}[f({\underset{\_}{\chi }}_T)])}^2]<{ϵ}^2$. We assume in this subsection that $X$ has jumps of infinite activity, i.e., $\nu (\mathbb{R}\setminus \{0\})=\mathrm{\infty }$. If the jumps of $X$ are of finite activity, both Algorithm 2 and SBG-Alg are exact with the latter outperforming the former in practice by a constant factor, which is a function of the total number of jumps, $T\nu (\mathbb{R}\setminus \{0\})<\mathrm{\infty }$; see Sect. 6.2 for a numerical example.

7.5.1 MC complexity

As above, for any $\kappa \in (0,1]$, let the sequence $\underline{\chi }_{T}^{\kappa ,i}$, $i\in \mathbb{N}$, be i.i.d. with the same distribution as $\underline{\chi }_{T}^{(\kappa )}$ simulated by SBG-Alg with $n\in \mathbb{N}\cup \{0\}$ sticks. Recall that the MC estimator in (4.2), based on $N\in \mathbb{N}$ independent samples, is given by

$$ \Upsilon _{\mathrm{MC}}=\frac{1}{N}\sum _{i=1}^{N} f ( \underline{\chi }_{T}^{\kappa ,i} ). $$

The requirements on the bias and variance of the estimator $\Upsilon _{\mathrm{MC}}$ (see Appendix A.1), together with Theorem 3.4 and the bounds in (3.11) as well as Propositions 3.7, 3.9 and 3.12, imply Corollary 7.14. By expressing $\kappa$ in terms of $\epsilon$ via Corollary 7.14 and (3.5), (3.8), (3.9), the formulae for the expected computational complexity $\mathcal{C}_{\mathrm{MC}}(\epsilon )$ in Table 1 (see Sect. 4.2) follow.

Corollary 7.14

For any $\epsilon \in (0,1)$, define first $\kappa$ for given $f$ as in one of (a)–(d) below and then $N:=\lceil 2{ϵ}^{-2}\mathbb{V}[f({\underset{\_}{\chi }}_T^{(\kappa )})]\rceil$ as in Appendix A.1. Then the MC estimator $\Upsilon _{\mathrm{MC}}$ of $\mathbb{E}[f({\underset{\_}{\chi }}_T)]$ has $L^{2}$-accuracy of level $\epsilon$ and expected cost $\mathcal{C}_{\mathrm{MC}}(\epsilon )$ bounded by a constant multiple of $(1+\overline{\nu }(\kappa )T)N$.

(a) For any $K>0$, $g\in {\mathrm{Lip}}_K({\mathbb{R}}^2)$ (resp. $g\in {\mathrm{locLip}}_K({\mathbb{R}}^2)$) and the function $f:(x,z,t)\mapsto g(x,z)$, set

$$\begin{array}{rl}\kappa & :=sup\{{\kappa }^{\prime }\in (0,1]:2{\mu }_1({\kappa }^{\prime },T)<ϵ/\sqrt{2}\}\\ (\mathit{\text{resp. }}\kappa & :=sup\{{\kappa }^{\prime }\in (0,1]:8K^2{\mu }_2({\kappa }^{\prime },T)(1+exp(2T{\bar{\sigma }}_{{\kappa }^{\prime }}^2))\\ & \times \mathbb{E}[exp(2X_T)]<{ϵ}^2/2\left\}\right).\end{array}$$

(b) Pick $y<0$ and let Assumption 3.8hold for some $C,\gamma >0$. Suppose that $f:{\mathbb{R}}^3\to \mathbb{R}$ is given by , where $h\in {\mathrm{Lip}}_K(\mathbb{R})$ and ${0\le h\le M}$ for some $K,M>0$. Then

$$\begin{aligned} \kappa :=\sup \bigg\{ \kappa '\in (0,1] &: M(C\gamma )^{2/(2+ \gamma )}\bigg(1+\frac{2}{\gamma}\bigg) \mu _{2}(\kappa ',T)^{2 \gamma /(2+\gamma )} \\ & \phantom{=} + K\mu _{1}(\kappa ',T)< \epsilon /\sqrt{2}\bigg\} . \end{aligned}$$

(c) Let $\delta \in (0,2]$ satisfy Assumption 3.2. Let $f(x,z,t)= g(t)$, $g\in {\mathrm{Lip}}_K(\mathbb{R})$, $K>0$. Then

$$\kappa :=\sup \{\kappa '\in (0,1]:K\mu ^{\tau}_{*}(\kappa ',T)< \epsilon /\sqrt{2}\}. $$

(d) Fix $s\in (0,T)$ and let $\delta \in (0,2]$ satisfy Assumption 3.2. Then there exists a constant $C>0$ such that for $f\in \mathrm{BT}_{2}(s,K,M)$, $K,M>0$, we have

$$ \kappa :=\sup \{\kappa '\in (0,1]: C\sqrt{K\mu ^{\tau}_{*}( \kappa ',T)}< \epsilon /\sqrt{2}\}. $$

The constant $C$ in Corollary 7.14 (d) depends on a value of the density of $\underline{\tau}_{t}$ at $s$ which is not known a priori. The purpose of Corollary 7.14 (d) is to specify the dependence of $\kappa$ on $\epsilon$ up to the constant $C$ for all considered payoffs. In practice, $\kappa$ is determined adaptively from some initial preliminary samples, and Corollary 7.14 (d) only serves as a theoretical guarantee (see e.g. Giles [29, Sect. 2.1]).

7.5.2 MLMC complexity

Let ${({\kappa }_j)}_{j\in \mathbb{N}}$ (resp. ${(n_j)}_{j\in \mathbb{N}\cup \{0\}}$) be a decreasing (resp. increasing) sequence in $(0,1]$ (resp. ℕ) such that $\lim _{j\to \infty}\kappa _{j}=0$. Let $\underline{\chi }^{0,i}\overset {d}{=}\underline{\chi }_{T}^{(\kappa _{1})}$ and $(\underline{\chi }^{j,i}_{1},\underline{\chi }^{j,i}_{2})\sim \underline{\Pi }_{n_{j},T}^{\kappa _{j},\kappa _{j+1}}$, $i,j\in \mathbb{N}$, be independent draws constructed by SBG-Alg. As in Sect. 4.2.2, recall that the sequence $(n_{j})$ appears as a parameter in the coupling $\underline{\Pi}^{\kappa _{j},\kappa _{j+1}}_{n_{j},T}$ (which is the law that the pair of vectors $(\underline{\chi}_{1}^{j,i},\underline{\chi}_{2}^{j,i})$ follow). The number $n_{j}$ specifies the number $n$ of sticks used in SBG-Alg for the level $j$. Recall that for the parameters $m,N_0,\dots ,N_m\in \mathbb{N}$, the MLMC estimator in (4.3) takes the form

$$ \Upsilon _{\mathrm{ML}}= \sum _{j=0}^{m}\frac{1}{N_{j}}\sum _{i=1}^{N_{j}}D_{j}^{i}, \qquad \text{where } D_{j}^{i}:=\textstyle\begin{cases} f (\underline{\chi }^{j,i}_{2} )-f (\underline{\chi }^{j,i}_{1} ),& \quad j\geq 1, \\ f (\underline{\chi }^{0,i} ),&\quad j=0. \end{cases} $$

The bias of the MLMC estimator is equal to that of the MC estimator in (4.2) with $\kappa =\kappa _{m}$. Given the sequences ${(n_j)}_{j\in \mathbb{N}\cup \{0\}}$ and ${({\kappa }_j)}_{j\in \mathbb{N}}$ which determine the simulation algorithms used in the estimator (4.3), Appendix A.2 derives the asymptotically optimal (as $\epsilon \searrow 0$) values for the integers $m$ and $(N_{j})_{j=0}^{m}$ minimising the expected computational complexity of (4.3) under the constraint that the $L^{2}$-accuracy of $\Upsilon _{\mathrm{ML}}$ is of level $\epsilon$. The key quantities are the bounds $B(j)$, $V(j)$ and $C(j)$ on the bias, level variance and the computational complexity of SBG-Alg at level $j$ (i.e., run with parameters $\kappa _{j}$ and $n_{j}$). The number $m$ of levels in (4.3) is determined by the bound on the bias $B(j)$, while the number $N_{j}$ of samples used at level $j$ is given by the bounds on the complexity and level variances; see the formulas in (A.1), (A.2) below. Proposition 7.15, which is a consequence of Theorem 3.4 and Propositions 3.7, 3.9 and 3.12 (for the bias), Theorem 7.10 (for the level variance) and Corollary 4.2 (for the complexity), summarise the relevant bounds $B(j)$, $V(j)$ and $C(j)$ established in this paper (suppressing the unknown constants as we are only interested in the asymptotic behaviour as $\epsilon \searrow 0$).

Proposition 7.15

Given sequences ${({\kappa }_j)}_{j\in \mathbb{N}}$ and ${(n_j)}_{j\in \mathbb{N}\cup \{0\}}$ as above, we define $C(j):=n_{j}+\overline{\nu }(\kappa _{j+1})T$. Then the following choices of functions $B$ and $V$ ensure that for any $\epsilon >0$, the MLMC estimator $\Upsilon _{\mathrm{ML}}$, with integers $m$ and $N_{j}$, $j=0, \dots , m$, given by (A.1)–(A.2), has $L^{2}$-accuracy of level $\epsilon$ with complexity asymptotically proportional to $\mathcal{C}_{\mathrm{ML}}(\epsilon ) =2\epsilon ^{-2} (\sum _{j=0}^{m} \sqrt{C(j)V(j)} )^{2}$.

(a) If $K>0$, $g\in {\mathrm{Lip}}_K({\mathbb{R}}^2)$ (resp. $g\in {\mathrm{locLip}}_K({\mathbb{R}}^2)$) and $f (x,z,t) = g(x,z)$, then for any $j\in \mathbb{N}$,

(b) Pick $y<0$ and suppose that Assumption 3.8holds for some $C,\gamma >0$. If $f\in \mathrm{BT}_{1}(y,K,M)$, $K,M>0$, then for any $j\in \mathbb{N}$,

$$ B(j) :=\min \big\{ \mu _{1}(\kappa _{j},T)^{ \frac{\gamma}{1+\gamma}}, \mu _{2}(\kappa _{j},T)^{ \frac{2\gamma}{2+\gamma}}\big\} \quad \textit{and}\quad V(j) :=\sigma ^{\frac{2\gamma}{2+\gamma}} 2^{-\frac{n_{j}\gamma}{2+\gamma}} + \overline{\sigma }^{\frac{2\gamma}{2+\gamma}}_{\kappa _{j}}. $$

(c) Let Assumption 3.2hold for some $\delta \in (0,2]$ and $f (x,z,t)= g(t)$ for some $g\in {\mathrm{Lip}}_K(\mathbb{R})$, $K>0$. Then for any $j\in \mathbb{N}$,

(d) Let $f\in \mathrm{BT}_{2}(s,K,M)$ for some $s\in (0,T)$ and $K,M\ge 0$. If $\delta \in (0,2]$ satisfies Assumption 3.2, then for any $j\in \mathbb{N}$,

Remark 7.16

By (3.5) and (A.2), we note that $\kappa _{m}$ in Proposition 7.15 (a) is bounded by (and typically proportional to) $C_{0} \epsilon /|\log \epsilon |$. Moreover, if $\kappa _{m}=e^{-r(m-1)}$ for some $r>0$, then the constant $C_{0}$ does not depend on the rate $r$. A similar statement holds for (b), (c) and (d); see Table 1 in Sect. 4.2.

It remains to choose the parameters ${(n_j)}_{j\in \mathbb{N}\cup \{0\}}$ and ${({\kappa }_j)}_{j\in \mathbb{N}}$ for the estimator in (4.3). Since we require the bias to vanish geometrically fast, we set $\kappa _{j}=e^{-r(j-1)}$ for $j\in \mathbb{N}$ and some $r>0$. The value of the rate $r$ in Theorem 7.17 below is obtained by minimising the multiplicative constant in the complexity $\mathcal{C}_{\mathrm{ML}}(\epsilon )$. Note that $n_{j}$ does not affect the bias (nor the bound $B(j)$) of $\Upsilon _{\mathrm{ML}}$. By Proposition 7.15, $n_{j}$ may be as small as a multiple of $\log (1/\overline{\sigma }_{\kappa _{j}}^{2})$ without affecting the asymptotic behaviour of the level variances $V(j)$, and as large as $\overline{\nu }(\kappa _{j+1})$ without increasing the asymptotic behaviour of the cost $C(j)$ of each level. Moreover, to ensure that the term $\sigma ^{2}2^{-n_{j}}$ in the level variances (see Theorem 7.10) decays geometrically, it suffices to let $n_{j}$ grow at least linearly in $j$. In short, there is a large interval within which we may choose $n_{j}$ without it having any effect on the asymptotic performance of the MLMC estimation (see Theorem 7.17 below). The choice $n_{j}=n_{0}+ \lceil{\max \{j,\log ^{2}(1+\overline{\nu }(\kappa _{j+1})T) \}} \rceil$ for $j\in \mathbb{N}$ in the numerical examples of Sect. 6 falls within this interval.

Theorem 7.17

Suppose $q\in (0,2]$ and $c>0$ satisfy $\overline{\nu }(\kappa ) \le c\kappa ^{-q}$ and $\overline{\sigma }^{2}_{\kappa}\le c\kappa ^{2-q}$ for all $\kappa \in (0,1]$. Pick $r>0$, set $\kappa _{j}:=e^{-r(j-1)}$ and assume that for some $C>0$ and all sufficiently large $j\in \mathbb{N}$, we have $\max \{j,\log _{2/3}(\overline{\sigma }_{\kappa _{j}}^{4})\}\le n_{j} \le C\overline{\nu }(\kappa _{j+1})$. Then in the cases (a)–(d) below, there exists a constant $C_{r}$ such that for $\epsilon \in (0,1)$, the MLMC estimator $\Upsilon _{\mathrm{ML}}$ defined in (4.3), with parameters given by (A.1), (A.2) below, is $L^{2}$-accurate at level $\epsilon$ with the stated expected computational complexity $\mathcal{C}_{\mathrm{ML}}(\epsilon )$. Moreover, $C_{r}$ is minimal for , with $a\in \mathbb{R}$ given explicitly in each case (a)–(d).

(a) Let $g\in {\mathrm{Lip}}_K({\mathbb{R}}^2)\cup {\mathrm{locLip}}_K({\mathbb{R}}^2)$ for $K>0$ and $f (x,z,t)= g(x,z)$. Define

and $a:=2(q-1)$. Then

(b) Let $f (x,z,t)= g(x,z)$, where $g\in \mathrm{BT}_{1}(y,K,M)$ for some $y<0\le K,M$, such that Assumption 3.8is satisfied by $y$ and some $C,\gamma >0$. Define

and $a:=2\frac{q(1+\gamma )-\gamma}{2+\gamma} \in (- \frac{2\gamma}{2+\gamma},2]$. Then

(c) Let $f (x,z,t)= g(t)$, $g\in {\mathrm{Lip}}_K(\mathbb{R})$, $K>0$, and let Assumption 3.2hold for some $\delta \in (0,2]$. Set $a:=q-(1-\frac{q}{2})\min \{\frac{1}{2}, \frac{2\delta}{2-\delta}\}$ and $b:=\min \{2/\delta ,\max \{3/2,1/\delta \}\}$. Then

(d) Fix $s\in (0,T)$ and let $\delta \in (0,2]$ satisfy Assumption 3.2. Define the constants $a:=q-(1-\frac{q}{2})\min \{\frac{1}{4}, \frac{\delta}{2-\delta}\}$ and $b:=\min \{4/\delta ,\max \{3,2/\delta \}\}$. Then for $K,M\ge 0$ and $f\in \mathrm{BT}_{2}(s,K,M)$,

Remark 7.18

For most models, either $\beta =\delta$ or $\sigma >0$, implying $a^{+}b\in [0,2]$ in parts (a) and (c), $a^{+}b\in [0,2(1/2+1/\gamma )]$ in part (b) (with $\gamma$ typically equal to 1) and $a^{+}b\in [0,4]$ in part (d).

Proof of Theorem 7.17

Note that $\kappa _{1}=1$ by definition independently of $r>0$, thus making both the variance $\mathbb{V}[D_0^i]$ and the cost of sampling of $D_{0}^{i}$ independent of $r$. We may thus ignore the 0th term in the bound $\epsilon ^{-2} (\sum _{j=0}^{m}\sqrt{V(j)C(j)})^{2}$ on the complexity $\mathcal{C}_{\mathrm{ML}}(\epsilon )$ derived in Appendix A.2. Since $m$ is given by (A.1) below, by Table 1 and Remark 7.16, the function $\overline{m}:(0,1)\to (0,\infty )$ given by

$$ \overline{m}(\epsilon ) :=\textstyle\begin{cases} (b|\log \epsilon |+c\log |\log \epsilon |)/r &\quad \text{in (a) and (b) and}, \\ &\qquad \text{if $\delta =\frac{2}{3}$, in (c) and (d)}, \\ b|\log \epsilon |/r &\quad \text{in (c) and (d) if $\delta \ne \frac{2}{3}$}, \end{cases} $$

(7.27)

where

$$ c= \textstyle\begin{cases} 1 &\quad \text{in (a) and (c)}, \\ 1/2 &\quad \text{in (b) and (d)}, \end{cases} $$

satisfies $m\le \overline{m}(\epsilon )+C'/r$ for all $\epsilon \in (0,1)$ and $r>0$, where the constant $C'>0$ is independent of $r>0$. Thus we need only study the growth rate of

$$ \phi (\epsilon ) :=\sum _{j=1}^{\left \lceil{\overline{m}( \epsilon )}\right \rceil }\sqrt{C(j)V(j)} =\sum _{j=1}^{\left \lceil{ \overline{m}(\epsilon )}\right \rceil } \sqrt{\big(n_{j}+ \overline{\nu }(\kappa _{j+1})T\big)V(j)} \qquad \text{as }\epsilon \to 0, $$

because $\mathcal{C}_{\mathrm{ML}}(\epsilon )$ is bounded by a constant multiple of $\epsilon ^{-2}\phi (\epsilon )^{2}$. In the cases where $V(j)$ contains a term of the form $e^{-sn_{j}}$ for some $s>0$ (only possible if $\sigma \neq 0$), the product $n_{j}e^{-sn_{j}}\le e^{-sn_{j}/2}$ vanishes geometrically fast since $n_{j}\ge j$ for all large $j$. Thus the corresponding component in $\phi (\epsilon )$ is bounded as $\epsilon \to 0$ and may thus be ignored. By Proposition 7.15, we may assume in all cases that $V(j)$ is bounded by a multiple of a power of $\overline{\sigma }_{\kappa _{j}}^{2}$ and $C(j)$ is dominated by a multiple of $\overline{\nu }(\kappa _{j+1})$.

Since $\overline{\nu }(\kappa )\le c\kappa ^{-q}$ and $\overline{\sigma }^{2}_{\kappa}\le c\kappa ^{2-q}$ for $\kappa \in (0,1]$, Proposition 7.15 yields

for some constant $K_{*}>0$ independent of $r$ and all $\epsilon \in (0,1)$, where we used in part (a) the fact that $\overline{\sigma }_{\kappa}\kappa \le \sqrt{c}\kappa ^{2-q/2}$ for all $\kappa \in (0,1]$.

(a) Recall that $\kappa _{j}=e^{-r(j-1)}$ and $\kappa _{j+1}=e^{-r(j-1)-r}$, implying

$${\kappa }_{j+1}^{-q}{\kappa }_j^{2-q}=e^{rq}{e}^{ar(j-1)}\mathrm{\text{for all }}j\in \mathbb{N}\mathrm{\text{, where }}a=2(q-1).$$

(7.28)

Suppose first $a<0$, implying $q\in (0,1)$. By (7.28), the sequence ${({\kappa }_{j+1}^{-q}{\kappa }_j^{2-q})}_{j\in \mathbb{N}}$ decays geometrically fast. This implies that $\lim _{\epsilon \downarrow 0}\phi (\epsilon )<\infty$ and gives the desired result. Moreover, the leading constant $C_{r}$, as a function of $r$, is proportional to $e^{rq}/(1-e^{ar/2})^{2}$ as $\epsilon \downarrow 0$. Since $a\ne 0$ for $q\in (0,1)$, the minimal value of $C_{r}$ is attained when $r=(2/|a|)\log (1+|a|/q)$.

If $a=0$, hence $q=1$, we have $\phi (\epsilon )\le K_{*}e^{r/2} (b|\log \epsilon |+\log |\log \epsilon |)/r$ by (7.28) and (7.27), giving the desired result. As before, the leading constant $C_{r}$, as a function of $r$, is proportional to $e^{r}/r^{2}$ as $\epsilon \to 0$, attaining its minimum at $r=2$.

Finally, suppose $a>0$, implying $q\in (1,2]$. By (7.28) and (7.27), it follows that

$$ \phi (\epsilon )^{2} \le \frac{K_{*}^{2}e^{rq}}{(e^{ar/2}-1)^{2}}e^{a (b| \log \epsilon |+\log |\log \epsilon |)} = \frac{K_{*}^{2}e^{rq}}{(e^{ar/2}-1)^{2}}\epsilon ^{-ab}|\log \epsilon |^{a}. $$

The corresponding result follows easily, where the leading constant $C_{r}$, as a function of $r$, is proportional to $e^{rq}/(e^{ar/2}-1)^{2}$ as $\epsilon \downarrow 0$ and attains its minimum at $r=(2/a)\log (1+a/q)$, concluding the proof of (a).

(b) As before, we have

$${\kappa }_{j+1}^{-q}{\kappa }_j^{(2-q)\gamma /(2+\gamma )}=e^{rq}{e}^{ar(j-1)}\mathrm{\text{for }}j\in \mathbb{N}\mathrm{\text{, with }}a=2\frac{q(1+\gamma )-\gamma }{2+\gamma }.$$

(7.29)

Suppose $a<0$, implying $q<\gamma /(1+\gamma )$. Then $\lim _{\epsilon \downarrow 0}\phi (\epsilon )<\infty$ by (7.29), implying the claim. Moreover, $C_{r}$ is minimal for $r=(2/|a|)\log (1+|a|/q)$ as in part (a).

Now suppose $a=0$, implying $q=\gamma /(1+\gamma )$. Then

$$ \phi (\epsilon )^{2} \le K_{*}^{2}r^{-2}e^{rq}(b|\log \epsilon |+ \log |\log \epsilon |/2)^{2}, $$

and the leading constant is minimised when $r=2/q=2+2/\gamma$.

Finally, suppose $a>0$, implying $q>\gamma /(1+\gamma )$. By (7.29), we have

$$ \phi (\epsilon )^{2} \le \frac{K_{*}^{2}e^{rq}}{(e^{ar/2}-1)^{2}} e^{a(b| \log \epsilon |+\log |\log \epsilon |/2)} = \frac{K_{*}^{2}e^{rq}}{(e^{ar/2}-1)^{2}}\epsilon ^{-ab} |\log \epsilon |^{a/2}, $$

and the leading constant is minimal for $r=(2/a)\log (1+a/q)$.

In parts (c) and (d), note that $a<0$ if and only if $\delta =2$ (i.e., $\sigma \ne 0$). Analogous arguments as in (a) and (b) complete the proof of the theorem. □

Appendix: MC and MLMC estimators

1.1 A.1 Monte Carlo estimator

Consider square-integrable random variables $P,P_{1},P_{2},\ldots$ Let ${(P_k^i)}_{k,i\in \mathbb{N}}$ be independent with $P_{k}^{i}\overset {d}{=}P_{k}$ for $k,i\in \mathbb{N}$. Suppose $|\mathbb{E}[P]-\mathbb{E}[P_k]|\le B(k)$ for all $k\in \mathbb{N}$ and assume that $C(n)$ bounds the expected computational cost of simulating a single value of $P_{n}$. Pick arbitrary $\epsilon >0$ and define $m:=inf\{k\in \mathbb{N}:B(k)<ϵ/\sqrt{2}\}$, $N:=\lceil 2\mathbb{V}[P_m]/{ϵ}^2\rceil$. Then the Monte Carlo estimator

$$\hat{P}:=\frac{1}{N}\sum _{i=1}^N{P}_m^i\mathrm{\text{of }}\mathbb{E}[P]\mathrm{\text{is }}{L}^2\mathrm{\text{-accurate at level }}ϵ\mathrm{\text{, i.e., }}\mathbb{E}{\left[{(\hat{P}-\mathbb{E}[P])}^2\right]}^{1/2}<ϵ\text{,}$$

since $\mathbb{E}[{(\hat{P}-\mathbb{E}[P])}^2]=\mathbb{V}[\hat{P}]+{(\mathbb{E}[P_m]-\mathbb{E}[P])}^2$ and $\mathbb{V}[\hat{P}]<{ϵ}^2/2$ by the definition of $N$, while ${(\mathbb{E}[P_m]-\mathbb{E}[P])}^2<{ϵ}^2/2$ by the definition of $m$. Thus if the bound $B(m)$ on the bias is asymptotically sharp, the formulae for the integers $m,N\in \mathbb{N}$ above result in the computational complexity given by the formula

$${\mathcal{C}}_{\mathrm{MC}}(ϵ)=NC(m)=\lceil 2\mathbb{V}[P_m]/{ϵ}^2\rceil C(m).$$

Although in practice one does not have access to the variance $\mathbb{V}[P_m]$, it is typically close to $\mathbb{V}[P]$ (which often has an a priori bound) or can be estimated via simulation.

1.2 A.2 Multilevel Monte Carlo estimator

This section is based on the works of Heinrich and Giles [37] and Giles [28]. Let $P,P_{1},P_{2},\ldots$ be square-integrable random variables and set $P_{0}:=0$. Suppose that the array of independent random variables ${(D_k^i)}_{k\in \mathbb{N}\cup \{0\},i\in \mathbb{N}}$ satisfies $D_{k}^{i}\overset {d}{=}D_{k}^{1}$ and $\mathbb{E}[D_k^i]=\mathbb{E}[P_{k+1}-P_k]$ for $k\in \mathbb{N}\cup \{0\}$ and $i\in \mathbb{N}$. For $k\in \mathbb{N}\cup \{0\}$, assume that the bias and level variance satisfy the inequalities $B(k)\ge |\mathbb{E}[P]-\mathbb{E}[P_k]|$ and $V(k)\ge \mathbb{V}[D_k^1]$ for some functions $k\mapsto B(k)$ and $k\mapsto V(k)$, respectively, and let $C(k)$ bound the expected computational complexity of simulating a single value of $D_{k}^{1}$. For $m\in \mathbb{N}\cup \{0\}$ and $N_0,\dots ,N_m\in \mathbb{N}$, the MLMC estimator

$$\hat{P} :=\sum _{k=0}^{m} \frac{1}{N_{k}} \sum _{i=1}^{N_{k}}D_{k}^{i} $$

satisfies $\mathbb{E}[{(\hat{P}-\mathbb{E}[P])}^2]=\mathbb{V}[\hat{P}]+{(\mathbb{E}[P_m]-\mathbb{E}[P])}^2$, since $\mathbb{E}[\hat{P}]=\mathbb{E}[P_m]$. Thus for any $\epsilon >0$, the inequality $\mathbb{E}[{(\hat{P}-\mathbb{E}[P])}^2]<{ϵ}^2$ holds if the number of levels in $\hat{P}$ equals

$$m:=inf\{k\in \mathbb{N}\cup \{0\}:B(k)<ϵ/\sqrt{2}\},$$

(A.1)

and the variance is bounded by $\mathbb{V}[\hat{P}]={\sum }_{k=0}^m\mathbb{V}[D_k^1]/N_k\le {\sum }_{k=0}^{m}V(k)/N_k\le {ϵ}^2/2$. Since the computational complexity of $\hat{P}$, $\mathcal{C}_{\mathrm{ML}}(\epsilon )=\sum _{k=0}^{m} C(k)N_{k}$, is linear in the number of samples $N_{k}$ on each level $k$, we only require that the variance $\mathbb{V}[\hat{P}]$ be of the same order as $\epsilon ^{2}/2=\sum _{k=0}^{m}V(k)/N_{k}$. Then by the Cauchy–Schwarz inequality, we have

$$ \mathcal{C}_{\mathrm{ML}}(\epsilon ) \epsilon ^{2}/2 =\bigg(\sum _{k=1}^{m} C(k) N_{k}\bigg) \bigg(\sum _{k=0}^{m}\frac{V(k)}{N_{k}}\bigg) \geq \bigg(\sum _{k=0}^{m}\sqrt{C(k)V(k)}\bigg)^{2}, $$

where the lower bound does not depend on $N_{0},\ldots ,N_{m}$ and is attained if and only if

$$ N_{k} :=\bigg\lceil 2\epsilon ^{-2} \sqrt{\frac{V(k)}{C(k)}} \sum _{j=0}^{m}\sqrt{C(j)V(j)}\bigg\rceil \qquad \text{for }k\in \{0, \ldots ,n\}, $$

(A.2)

ensuring that the expected cost is a multiple of

$$ \mathcal{C}_{\mathrm{ML}}(\epsilon ) =2\epsilon ^{-2}\bigg(\sum _{k=0}^{m} \sqrt{C(k)V(k)}\bigg)^{2}. $$

(A.3)

Moreover, if $B$, $V$ and $C$ are asymptotically sharp, the formulae in (A.2), up to constants, minimise the expected computational complexity. Consequently, the computational complexity analysis of the MLMC estimator is reduced to the analysis of the behaviour of $\sum _{j=0}^{m}\sqrt{C(j)V(j)}$ as $\epsilon \downarrow 0$.