The self-financing equation in limit order book markets

Abstract

The goal of this paper is to present a mathematical framework for trading on a limit order book, including its associated transaction costs, and to propose continuous-time equations which generalise the self-financing relationships of frictionless markets. These equations naturally differentiate between trading via limit and via market orders, as they include a price impact or adverse selection constraint. We briefly mention several possible applications, including hedging European options with limit orders, to illustrate their impact and how they can be used to the benefit of low-frequency traders. Two appendices include empirical evidence for facts which are not universally recognised in the current literature on the subject.

Appendices

Appendix A: Empirical evidence from high-frequency data

We present here the empirical evidence which led us to formulate our self-financing condition. We report numerical results for a particular example (intraday trading of Intel stock on April 18, 2013), and we refer to the exhaustive empirical analysis conducted in [6] for ample evidence that the features identified here for the purpose of illustration are typical, and not merely anecdotal.

We work with NASDAQ’s ITCH data files. They include all visible limit and market orders. We pre-processed the data to remove the special deals, trades that happen within the bid–ask spread, and market orders that execute hidden liquidity. This leaves us with only visible market orders hitting visible limit orders at the best bid or ask price.

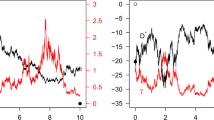
Because the identities of the traders are typically not part of the ITCH format, we work with a representative liquidity provider by aggregating all the executions against limit orders to construct the market maker portfolio. Figure 5 gives the plot of the quantities of interest in this appendix.

Fig. 5

Intel (INTC) stock on 18/04/13. Inventory, cash and wealth are those of the aggregate liquidity provider

The left panel of Fig. 6 gives the plot of the empirical quadratic covariation between the aggregate liquidity provider’s inventory and the price process. It shows that this quadratic covariation is negative and decreasing. So, if one wishes to model the price as a diffusion process, we need the aggregate inventory to have a non-trivial Brownian component. This issue is tackled in Appendix B. In practice, both processes are actually pure point processes, and the diffusion limit is only an approximation resulting from the aggregation of very many small jumps.

Fig. 6

(Left panel) Quadratic covariation between inventory and price path. (Right panel) Plots of the actual wealth of the aggregate liquidity provider (as in Fig. 5) together with the wealth computed from the three self-financing conditions. Red is the frictionless case. Green corresponds to (A.2). The actual wealth and the wealth computed from our self-financing condition (A.3) are indistinguishable on the graph

In [6], we propose a statistical test based on the assumption that price and inventory satisfy

$$ \left \{ \textstyle\begin{array}{rl} dp_{t} = \mu _{t} \,dt + \sigma _{t} \,dW_{t},\\ dL_{t} = \ell _{t} \,dt + \eta _{t} \,dW'_{t}, \end{array}\displaystyle \right . $$

with instantaneous correlation $\rho _{t}$. In this context, adverse selection means that $\rho _{t} \le 0$, that is, the changes of the liquidity provider’s inventory are always negatively correlated to the price returns. For statistical purposes, the goal is to reject the null hypothesis

$$ H_{0}:\quad \text{There exists } t \in [0,1] \text{ such that }\rho _{t} >0. $$

If we then denote by $p^{N}$ and $L^{N}$ the subsampling of the diffusion processes $p$ and $L$ on the uniform grid $\{1/N, 2/N, \dots , 1\}$ and if we define

$$ \left \{ \textstyle\begin{array}{rl} C^{N}_{t} &= \displaystyle \sum _{n=1}^{\lfloor Nt\rfloor -1} \Delta _{n} p^{N} \Delta _{n} L^{N},\\ V^{N}_{t} &= \displaystyle N \sum _{n=1}^{\lfloor Nt\rfloor -2} \big( (\Delta _{n} p^{N} \Delta _{n+1} L^{N})^{2} + \Delta _{n} p^{N} \Delta _{n} L^{N} \Delta _{n+1} p ^{N} \Delta _{n+1} L^{N} \big), \end{array}\displaystyle \right . $$

then the functional central limit theorem of [1, Theorem 6.4] states that

$$ \mathcal{L}\,\bigg( \frac{C^{N}_{t} - [p,L]_{t}}{\sqrt{N^{-1} |V ^{N}_{t}|}} \bigg) \longrightarrow N(0,1), $$

(A.1)

which suggests a practical computation of the rejection probabilities of the null hypothesis in buckets of $M$ trades if we assume that $\rho _{t}$, $\sigma _{t}$ and $\eta _{t}$ are constant over these buckets. We can then multiply these rejection probabilities to obtain the overall rejection probability for the null hypothesis $H_{0}$. We chose $M$ such that the trading day was divided into 8 buckets. We obtain a rejection probability of 0.98443 for our null hypothesis.

A final argument in favour of our form of the self-financing condition is given by the right panel of Fig. 6 which compares the actual wealth of the aggregate liquidity provider, as given by the NASDAQ trade data, to the wealth obtained from the price and the aggregate liquidity provider inventory using different forms of the self-financing condition. One can appreciate the significant gap between the different equations for wealth and the true wealth. We compare four quantities:

• 1. the actual wealth;

• 2. the wealth computed from the standard self-financing equation

  $$ \Delta _{n} X = L_{n} \Delta _{n} p $$

  used in the classical Black–Scholes option pricing and Merton portfolio theories;

• 3. the wealth computed from the standard self-financing condition

  $$ \Delta _{n} X = L_{n} \Delta _{n} p + \frac{s_{n}}{2} |\Delta _{n} L| $$

  (A.2)

  advocated to include transaction costs in Merton’s theory of optimal portfolio choice; and finally,

• 4. the wealth computed from our self-financing condition

  $$ \Delta _{n} X = L_{n} \Delta _{n} p + \frac{s_{n}}{2} |\Delta _{n} L| + \Delta _{n} p \Delta _{n} L. $$

  (A.3)

Clearly, the plot illustrates the fact that our form of the self-financing condition is perfectly satisfied.

Appendix B: Quadratic variation of inventory processes

Appendix A reported on some of the empirical results of the study [6] conducted on the ITCH data from the NASDAQ stock exchange. While a very small percentage of the messages do carry a field called MPID for market participant ID, the vast majority of the messages do not, and we had to aggregate the activities of the participants in what we called a representative liquidity provider by using all the executions against limit orders to construct the market maker portfolio to test for adverse selection and check the validity of our self-financing condition.

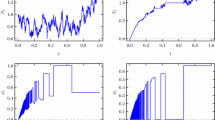
Here we provide evidence backing our assumption that the traders’ inventories have a non-trivial quadratic variation component, a fact which cannot be attributed to the aggregation used to process the NASDAQ data. We use trade and quotes (TAQ) data purchased from the Toronto Stock Exchange (TSX). While the TAQ format is standard, the trade files of the TSX include for each trade the identities of the buyer and the seller involved in the trade. So for each stock, for each trading day and for each market participant (we identified 92 of them during the period covered by our data), we can track the evolution of the inventory in the stock accumulated by a particular market participant over that day.

For the purpose of illustration, we choose a stock which was actively traded during the period covered by our data, for example Blackberry, we choose a trading day, say “06/04/2014”, and the three most active Blackberry traders on that day, CIBC World Markets Inc. (an investment banking subsidiary of the Canadian Imperial Bank of Commerce), Royal Bank of Canada (RBC) Capital Markets and TD Securities Inc. Figure 7 shows the time evolution of their inventories throughout the day. Among other things, it highlights a special feature of TSX data. While we know the identities of the agents (buyers and sellers) involved in each trade, we do not know if they act on behalf of a client to accumulate or liquidate a position in the stock, or if they act on their own behalf, or if they act as market makers (liquidity providers). For example, we suspect that the top panel of Fig. 7 indicates that CIBC was acting as a market maker on that day, while RBC (resp. TD Securities) were trading to acquire a long (resp. short) position in Blackberry, whether it was on behalf of a client or for their own account.

Fig. 7

Plot of the CIBC, RBC Capital Markets and TD Securities Inc. inventories in Blackberry on June 4, 2014

More generally, if one uses the asymptotic result (A.1) of Ait-Sahalia and Jacod to test the null hypothesis that the quadratic variation of the inventory process is 0, the asymptotic $p$-value of the test on that day is $10^{-68}$! Systematic use of this test on different days and other actively traded stocks give systematic rejections of this null hypothesis, with a $p$-value never greater than $10^{-5}$.