Chebyshev interpolation for parametric option pricing

Abstract

Recurrent tasks such as pricing, calibration and risk assessment need to be executed accurately and in real time. We concentrate on parametric option pricing (POP) as a generic instance of parametric conditional expectations and show that polynomial interpolation in the parameter space promises to considerably reduce run-times while maintaining accuracy. The attractive properties of Chebyshev interpolation and its tensorized extension enable us to identify broadly applicable criteria for (sub)exponential convergence and explicit error bounds. The method is most promising when the computation of the prices is most challenging. We therefore investigate its combination with Monte Carlo simulation and analyze the effect of (stochastic) approximations of the interpolation. For a wide and important range of problems, the Chebyshev method turns out to be more efficient than parametric multilevel Monte Carlo. We conclude with a numerical efficiency study.

1 Introduction

The development of fast and accurate computational methods for parametric models is one of the central issues in computational finance. Financial institutions dedicated to the trading or assessment of financial derivatives have to cope with the daily tasks of computing numerous characteristic financial quantities. Examples of interest include prices, sensitivities and risk measures for products in different models and for varying parameter constellations. With regard to the ever growing market activities, more and more of these evaluations need to be delivered in real time. In addition, we face constantly rising model sophistication since the original work of [1] and [33]. From the early 1990s onwards, stochastic volatility and Lévy models, as well as models based on further classes of stochastic processes, have been developed to reflect the observed market data in a more appropriate way. For asset models, see e.g. [8, 10, 12, 25], and for the case of fixed income models, see e.g. [13, 15, 26]. Moreover, the aftermath of the 2007–2009 financial crisis has led to a new generation of more complex models, for instance, by incorporating more risk factors. The usefulness of a pricing model critically depends on how well its numerical implementation captures the relevant aspects of market reality. Exploiting new ways to deal with the rising computational complexity therefore supports the evolution of pricing models and touches a core concern of present-day mathematical finance.

A large body of computational tasks in finance needs to be repeatedly performed in real time for a varying set of parameters. Prominent examples include option pricing and hedging of different option sensitivities, e.g. delta and vega, that also need to be calculated in real time. In particular, for optimization routines arising in model calibration, large parameter sets come into play. Further examples arise in the context of risk control and assessment, such as for the quantification and monitoring of risk measures. The following question serves as a starting point for our investigations: How can we systemically exploit the recurrent nature of parametric computational problems in finance with the objective of gaining efficiency? Looking for answers to this question, we focus in the sequel on parametric option pricing (POP) that we identify as a generic instance.

In the present literature on computational methods in finance, complexity reduction for parametric problems has largely been addressed by applying Fourier techniques following the seminal works of [6] and [39]; see also the monograph [2]. Research in this area concentrates on adopting fast Fourier transform (FFT) methods and variants for option pricing. Lee [30] accurately describes pricing European options with FFT. Further developments are, for instance, provided by [31] for early exercise options and by [14] and [28] for barrier options. Another path towards efficiently handling large parameter sets that has been pursued in finance relies on reduced basis methods. These are techniques for solving parametrized partial differential equations. The authors of [4, 7, 21, 36, 41] applied this approach to price European and American plain vanilla options and European baskets. On the one hand, FFT methods can be highly beneficial when the prices are required in a large number of Fourier variables, e.g. for a large set of strikes of European plain vanillas. A method that tailors Fourier pricing to the whole parametric family of integrands has recently been developed in [17]. On the other hand, numerical experiments have shown a promising gain in efficiency of reduced basis methods when an accurate PDE solver is readily available. In essence, all these approaches reveal an immense potential of complexity reduction by targeting parameter dependence. To do this, they exploit the functional architecture of the underlying pricing technique for varying parameters.

Financial institutions have to deal simultaneously with a diversity of models, a multitude of option types, and—as a consequence—a wide variety of underlying pricing techniques. It is therefore worthwhile to explore the possibility of a generic complexity reduction method that is independent of the specific pricing technique. To do so, we focus on the set of option prices and the set of parameters of interest, deliberately disregard the pricing technology, and view the option price as a function of the parameters. The core idea is now to introduce interpolation of option prices in the parameter space as a complexity reduction technique for POP.

The resulting procedure naturally splits into two phases: pre-computation and real-time evaluation. The first one is also called the offline phase, while the second is also called the online phase. In the pre-computation phase, the interpolation is made available. In the case of polynomial interpolation, this steps amounts to the computation of the coefficients for the basis functions. The actual procedure depends on the choice of the interpolation method. In all cases, however, the prices have to be computed for some fixed parameter configurations. Here, any appropriate pricing method—for instance, based on Fourier, PDE or even Monte Carlo techniques—can be chosen. The real-time evaluation phase then consists in evaluating the interpolation. Provided that the evaluation of the interpolation is faster than the benchmark tool, the scheme permits a gain in efficiency in all cases where accuracy can be maintained. Then we distinguish several cases:

• In comparison to the benchmark pricing routine, the fast evaluation of the interpolation will eventually outweigh the expensive pre-computation phase if pricing is a task which is repeatedly employed. Optimization procedures are an obvious instance where this feature becomes advantageous.

• The interpolation can simultaneously deliver a multitude of outputs. For instance, as we shall see in the sequel, the interpolation can be set up such that it delivers sensitivities as well.

• Even if the number of price computations is limited, we can still benefit from separating the procedure into its two phases. In this way, e.g. idle times in the financial industry can be put to good use by preparing the interpolation for whenever real-time pricing is needed during business activities.

The question arising at this stage is: Under what circumstances can we hope to find an interpolation method that delivers both reliable results and a considerable gain in efficiency?

One could now be tempted to proceed in a naive manner and first define an equidistant grid and then interpolate piecewise linearly in the parameter space. Numerical experiments for Black–Scholes call prices as function of the volatility, for instance, would then provide convincing evidence that the number of nodes needed for a given accuracy is quite high. Increasing the polynomial degree might lead to better results. However, convergence might not be guaranteed. Runge [40] showed that polynomial interpolation on equispaced grids may diverge, even for analytic functions. Second, the evaluation of the polynomial interpolants may be numerically problematic, as it is shown in [40] that “the interpolation problem for polynomial interpolation on an equidistant grid is exponentially ill-conditioned”, a formulation we borrow from [45]. For these reasons, we refrain from polynomial interpolation with equidistant grids. Rather, we take a step back and ask: Which methods of interpolating prices as functions of model and payoff parameters are numerically promising in terms of convergence, stability and implementational ease?

Regarding this research question, we need to take into consideration both the set of interpolation methods and the specific features of the functions we investigate. It is well known that the efficiency of interpolation methods critically depends on the degree of regularity of the approximated function. For the core problem of our study—European (basket) options—we investigate the regularity of the option prices as functions of the parameters. We find that these functions are indeed analytic for a large set of option types, models and parameters. Taking the perspective of approximation theory, this inspires the hope that suitable interpolation methods can be found. In particular, it is well known that orthogonal polynomial interpolation in this case yields exponential convergence for univariate and subexponential convergence for multivariate interpolation. We call this (sub)exponential convergence in the sequel.

In this article, we propose and investigate the interpolation of financial quantities in the parameter space by Chebyshev polynomials. This has various reasons. We empirically observe that parameters of interest often range within bounded intervals, and Chebyshev polynomial interpolation is well known for its excellent numerical properties in approximating analytic functions on bounded intervals. The following key properties of Chebyshev interpolation are of particular interest for our purposes:

• For univariate functions that are several times differentiable, the method converges polynomially, and for univariate analytic functions, convergence is exponential—in stark contrast to polynomial interpolation on equally spaced nodal points. Even more, Chebyshev polynomials appear as an optimal choice when minimizing the error in a certain way among the nodal polynomial interpolations; see Appendix A.

• The method can be implemented in a numerically stable way. This is crucial for its actual performance.

• The interpolation nodes are explicitly available, and thus the coefficients are explicitly given as a linear transformation of the function values at the nodal points. On the one hand, this makes the implementation straightforward, a feature that is valuable both for the application of the method in complex IT infrastructures of the financial industry and for further developments of the method. On the other hand, since the interpolation nodes are explicitly given, we can avoid a significant approximation step, typically a regression, and therewith a major source of inaccuracy.

• The derivatives are trivial for the interpolation and known to converge as well with a rate that is determined by the regularity of the function that is interpolated. Thus sensitivities are additional outputs of high accuracy.

• Chebyshev interpolation can be easily concatenated yielding Chebyshev-spline approximation, which is extremely appealing when the function, for instance, exhibits discontinuities.

• Chebyshev interpolation can be highly efficiently extended to higher dimensionality, for instance, by low-rank tensor and sparse grid techniques.

In a remarkable monograph [46], Trefethen gives a comprehensive review of Chebyshev interpolation. Its appealing theoretical properties are indeed of practical use as the software tool Chebfun¹ demonstrates. In this implementation, Platte and Trefethen [38] aim “to combine the feel of symbolics with the speed of numerics”. Exploring the potential of interpolation methods for more than one single free parameter, we choose a tensorized version of Chebyshev interpolation as follows. For parameters $p\in[-1,1]^{D}$, where $D\in \mathbb {N}$ denotes the dimensionality of the parameter space, the price $\mathrm {Price}^{p}$ is approximated by tensorized Chebyshev polynomials $T_{j}$ with pre-computed coefficients $c_{j}$, $j\in J$, as

$$ \mathrm {Price}^{p} \approx\sum_{j\in J}c_{j} T_{j}(p). $$

Chebyshev interpolation is a standard numerical method that has proved to be extremely useful for applications in such diverse fields as physics, engineering, statistics and economics. Nevertheless, for pricing tasks in mathematical finance, Chebyshev interpolation still seems to be rarely used and its potential is yet to be unfolded. Pistorius and Stolte [37] use Chebyshev interpolation of Black–Scholes prices in the volatility as an intermediate step to derive a pricing methodology for a time-changed model. Independently from the present article, Pachon [35] recently proposed Chebyshev interpolation as a quadrature rule for the computation of option prices with a Fourier-type representation, which is comparable to the cosine method.

Our main results are the following:

• Proposition 2.1 refines the known result that analyticity guarantees an asymptotic error decay of order $O\big(\varrho^{-\sqrt[D]{N}}\big)$ in the total number $N$ of interpolation nodes, where $\varrho>1$ is given by the domain of analyticity and $D$ is the number of varying parameters. In our article, we allow an anisotropic analyticity domain and a different number of nodal points in each dimension.

• Propositions 2.3 and 2.4 show convergence results for the related sensitivities.

The method promises the highest gain in efficiency for the most challenging and therefore most computationally extensive problems. In these cases, the computation of the values at the nodal points cannot be delivered at machine precision, but is affected by an approximation error. This approximation error in turn affects the accuracy of the interpolation.

• Theorem 2.5 therefore provides an error bound including distortions of the nodal points. We consider two types of distortions, those bounded by a common deterministic threshold and those that are normally distributed. The first case is tailored to an underlying pricing method that is accurate up to a pre-specified deterministic accuracy, the latter to the computation of the values at the nodal points by Monte Carlo.

Qualitatively, we illustrate the relation to advanced Monte Carlo techniques and compare our approach with the parametric multilevel Monte Carlo approach of [22] and [24]. We derive a theoretical result of the “offline efficiency”, i.e., the asymptotic rate of convergence in terms of the offline cost. This is a measure for the accuracy versus the offline cost:

• In Theorem 2.6, we show that for each $\beta >D/2$, there exist constants $\bar{c}_{1},\bar{c}_{2}>0$ such that the offline cost is bounded by $\bar{c}_{1}\mathcal{M}$ and the expected error of the Chebyshev method is bounded by $\bar {c}_{2}(\log\mathcal{M})^{\beta}\mathcal{M}^{-1/2}$, where ℳ is the number of nodal points times the number of Monte Carlo simulations.

In Sect. 3, we introduce the general framework of POP (parametric option pricing).

• Theorem 3.2 provides accessible sufficient conditions on options and models that guarantee analyticity in the parameters. Moreover, it establishes a method to access the domain of analyticity. In combination with Proposition 2.1, this allows us to deduce a (sub)exponential convergence rate, as well as to access the constants in the exact error bound.

The advantageous convergence properties motivate us to further explore the potential of the Chebyshev method for multivariate options. Here we deliberately go beyond the scope of our theoretical results and consider additional features like path-dependence. We present empirical results demonstrating the efficiency of the Chebyshev method:

• The explicit gains in efficiency in comparison to standard Monte Carlo methods are shown in Sect. 4.2, taking multivariate lookback options in the Heston model as examples.

The remainder of the article is organized as follows. In Sect. 2, we introduce Chebyshev interpolation in detail and establish the general error estimates and convergence results. Section 3 presents a convergence analysis of Chebyshev interpolation for POP. The numerical experiments in Sect. 4 confirm these findings using Fourier techniques. The gain in efficiency when pricing basket options is numerically investigated. Experiments based on Monte Carlo and finite differences moreover suggest to further explore the potential of the approach beyond the scope of the theoretical investigations from the previous sections. We conclude the section with complexity considerations and by discussing the relation to advanced Monte Carlo techniques. The resulting conclusion and outlook are presented in Sect. 5. Finally, the appendix provides the proof of the multivariate convergence result.

2 Chebyshev polynomial interpolation

Let us introduce the notation for Chebyshev interpolation along with its tensor-based extension to the multivariate case; see e.g. [42, Definition 7.1.17]. In order to obtain convenient notation, consider the interpolation of prices

$$ p \mapsto \mathrm {Price}^{p},\qquad p\in[-1,1]^{D}.$$

For a more general hyperrectangular parameter space $\mathcal{P}=[\underline{p}_{1},\overline{p}_{1}]\times\cdots \times[\underline{p}_{D},\overline{p}_{D}]$, appropriate linear transformations need to be applied. Let $\overline{N}:=(N_{1},\ldots,N_{D})$ with $N_{i} \in \mathbb {N}_{0}$ for $i=1,\ldots,D$. The interpolation, which has $\prod_{i=1}^{D} (N_{i}+1)$ summands, is given by

$$ I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p) := \sum_{j\in J} c_{j}T_{j}(p), $$

(2.1)

where the summation index $j$ is a multi-index ranging over

$$J:=\{(j_{1},\dots, j_{D})\in \mathbb {N}_{0}^{D}: j_{i}\le N_{i}\ \mbox{for}\ i=1,\ldots ,D\}, $$

the basis functions are

$$ T_{j}(p_{1},\dots,p_{D}) = \prod_{i=1}^{D} T_{j_{i}}(p_{i}), \qquad T_{j_{i}}(p_{i}) := \cos (j_{i} \arccos p_{i}), $$

the coefficients are

(2.2)

where $\sum{}^{''}$ indicates that the first and last summands are halved, and the Chebyshev nodes $p^{k}$ for the multi-index $k=(k_{1},\dots ,k_{D})\in J$ are given by

$$ p^{k} = (p_{k_{1}},\dots,p_{k_{D}}),\qquad p_{k_{i}}=\cos\left(\pi\frac {k_{i}}{N_{i}}\right). $$

At the $N_{i}+1$ points $p_{k_{i}}$, the Chebyshev polynomial $T_{N_{i}}(x)$ reaches its extreme values. These points are also referred to as Chebyshev–Lobatto points, Chebyshev extreme points, or Chebyshev points of the second kind, and they satisfy a discrete orthogonality property; see (B.4).²

2.1 Exponential convergence

In the univariate case, it is well known that the error of approximation with Chebyshev polynomials decays polynomially for differentiable functions and exponentially for analytic functions; see, for instance, [46, Theorems 7.2 and 8.2]. We provide a multivariate version of the latter result. In order to state our result, we need to introduce the appropriate domain of analyticity. A Bernstein ellipse $B([-1,1],\varrho)$ with parameter $\varrho>1$ is defined as the open region in the complex plane bounded by the ellipse with foci $\pm1$ and semiminor and semimajor axis lengths summing to $\varrho$. We define the $D$-variate and transformed analogue of a Bernstein ellipse around the hyperrectangle $\mathcal{P}$ with parameter vector $\varrho\in (1,\infty)^{D}$ as

$$\begin{aligned} B(\mathcal{P},\varrho):=B([\underline{p}_{1},\overline{p}_{1}],\varrho _{1})\times\cdots \times B([\underline{p}_{D},\overline{p}_{D}],\varrho_{D} ) \end{aligned}$$

with $B([\underline{p},\overline{p}],\varrho):=\tau_{[\underline {p},\overline{p}]}( B([-1,1],\varrho))$, where for $p\in \mathbb {C}$, we have the transform $\tau_{[\underline {p},\overline{p}]}(\Re(p)) :=\overline{p} + \frac{\underline{p}-\overline{p}}{2}(1-\Re(p))$ and $\tau_{[\underline{p},\overline{p}]}(\Im(p)):= \frac{\overline {p}-\underline{p}}{2}\Im(p)$. We call $B(\mathcal{P},\varrho)$ a generalized Bernstein ellipse if the sets $B([-1,1],\varrho_{i})$ are Bernstein ellipses for $i=1,\ldots,D$.

The following proposition is a slight improvement of [42, Lemma 7.3.3]. More precisely, the error bound is given in terms of the constants $\varrho_{1},\ldots,\varrho_{D}$ rather than by $\underline{\varrho}:=\min_{i=1,\dots,D}\varrho_{i}$. For our purpose, it is worth to provide this generalization since the domain of analyticity is typically anisotropic; see, for instance, Condition 3.1 in Sect. 3 below. This allows us to derive sharper error bounds and improved assertions on the convergence rates.

Proposition 1

Let $\mathcal{P}\ni p\mapsto \mathrm {Price}^{p}$ be a real-valued function that has an analytic extension to some generalized Bernstein ellipse $B(\mathcal{P},\varrho)$ for some parameter vector $\varrho\in (1,\infty)^{D}$, and suppose that $\sup_{p\in B(\mathcal{P},\varrho )}|\mathrm {Price}^{p}|\le V$. Then

$$\begin{aligned} \max_{p\in\mathcal{P}}|\mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p)| \le2^{\frac{D}{2}+1} V \bigg(\sum_{i=1}^{D}\varrho_{i}^{-2N_{i}}\prod _{j=1}^{D}\frac{1}{1-\varrho_{j}^{-2}}\bigg)^{\frac{1}{2}}. \end{aligned}$$

The proof of the proposition is provided in Appendix B and is based on the proof of [42, Lemma 7.3.3]. A further improved error bound for tensorized Chebyshev interpolation is presented in [20]. Sharper error bounds reduce the computational cost because they allow us to use fewer nodal points to achieve a given accuracy.

Corollary 2

Under the assumptions of Proposition 2.1, there exists a constant $C>0$ such that

$$\begin{aligned} \max_{p\in\mathcal{P}}|\mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p)| \le C\underline{\varrho}^{-\underline{N}}, \end{aligned}$$

(2.3)

where $\underline{\varrho} = \min\limits_{1\le i\le D}\varrho_{i}$ and $\underline{N} = \min\limits_{1\le i\le D} N_{i}$.

In particular, under the assumptions of Proposition 2.1, if $N=\prod_{i=1}^{D} (N_{i}+1)$ denotes the total number of nodes, Corollary 2.2 shows that the error decay has (sub)exponential order $O(\varrho^{-\sqrt[D]{N}})$ for some $\varrho>1$.

2.2 Convergence of the sensitivities

The sensitivities play a crucial role in financial applications. We therefore state convergence results for the partial derivatives as well. The one-dimensional result is shown in [44] and a multivariate result is derived in [5] for functions in Sobolev spaces. These results allow us to obtain the Chebyshev approximation of derivatives at no additional cost. To state the corresponding convergence results, we follow the approach of [5] and introduce the weighted Sobolev spaces for $\sigma\in \mathbb {N}$ as

$$W_{2}^{\sigma,\omega}(\mathcal{P}) = \big\{ \phi\in L^{2}(\mathcal {P}): \Vert\phi\Vert_{W_{2}^{\sigma,\omega}(\mathcal{P})}< \infty \big\} , $$

with norm

$$ \Vert\phi\Vert_{W_{2}^{\sigma,\omega}(\mathcal{P})}^{2}=\sum_{\vert \alpha\vert\le\sigma} \int_{\mathcal{P}}\vert\partial^{\alpha }\phi(p)\vert^{2} \omega(p) \operatorname{d}\!p, $$

where $\alpha=(\alpha_{1},\dots,\alpha_{D})\in \mathbb {N}_{0}^{D}$ is a multi-index, $\partial^{\alpha}= \partial^{\alpha_{1}} \cdots\partial ^{\alpha_{D}}$, and the weight function $\omega$ on $\mathcal{P}$ is given by

$$ \omega(x):=\prod_{j=1}^{D} \omega\Big(\tau^{-1}_{[\underline {p}_{j},\overline{p}_{j}]}(x_{j})\Big),\qquad\omega\Big(\tau ^{-1}_{[\underline{p}_{j},\overline{p}_{j}]}(x_{j})\Big):=\Big(1-\tau ^{-1}_{[\underline{p}_{j},\overline{p}_{j}]}(x_{j})^{2}\Big)^{-\frac{1}{2}}, $$

with $\tau_{[\underline{p}_{j},\overline{p}_{j}]}(p)=\overline{p}_{j} + \frac{\underline{p}_{j}-\overline{p}_{j}}{2}(1-p)$. We are now in a position to present the following result.

Proposition 3

Let $\mathcal{P}\ni p\mapsto \mathrm {Price}^{p}\in W_{2}^{\sigma,\omega }(\mathcal{P})$ and set $N_{i}=N,\ i=1,\ldots,D$, i.e., we take the same number of nodal points in each dimension. Then for any $\frac{D}{2}<\sigma\in \mathbb {N}$ and any $\sigma\geq\mu\in \mathbb {N}_{0}$, there exists a constant $C>0$ such that

$$\begin{aligned} \Vert \mathrm {Price}^{(\cdot)} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(\cdot )\Vert_{W_{2}^{\mu,\omega}(\mathcal{P})}\le C N^{2\mu-\sigma}\Vert \mathrm {Price}^{(\cdot)}\Vert_{W_{2}^{\sigma,\omega}(\mathcal{P})}. \end{aligned}$$

The proof of the proposition is provided in Appendix C and applies [5, Theorem 3.1] together with the transformation $\tau$.

The result in Proposition 2.3 is given in terms of weighted Sobolev norms. In the following proposition, we relate the approximation error in the weighted Sobolev norm to the $C^{\ell}(\mathcal{P})$-norm, where $C^{\ell}(\mathcal{P})$ is the Banach space of all functions $u$ in $\mathcal{P}$ such that $u$ and $\partial^{\alpha}u$ with $|\alpha|\leq\ell$ are uniformly continuous on $\mathcal{P}$ and the norm

$$ \lVert u \rVert_{C^{\ell}(\mathcal{P})} = \max_{|\alpha|\leq\ell }\max\limits_{p\in\mathcal{P}}|\partial^{\alpha}u(p)| $$

is finite.

Proposition 4

Let $\mathcal{P}\ni p\mapsto \mathrm {Price}^{p}\in W_{2}^{\sigma,\omega }(\mathcal{P})$ and set $N_{i}=N,\ i=1,\ldots,D$, i.e., we take the same number of nodal points in each dimension. Then for any $\frac{D}{2}<\sigma\in \mathbb {N}$ and any $\sigma\geq\mu\in \mathbb {N}_{0}$ and $\ell\in \mathbb {N}_{0}$ with $\mu -\ell>\frac{D}{2}$, there exists a constant $\bar{C}(\sigma)>0$ depending on $\sigma$ such that

$$\begin{aligned} \Vert \mathrm {Price}^{(\cdot)} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(\cdot )\Vert_{C^{\ell}(\mathcal{P})}\le\bar{C}(\sigma) N^{2\mu-\sigma }\max_{\vert\alpha\vert\le\sigma}\sup_{p\in\mathcal{P}}\vert \partial^{\alpha} \mathrm {Price}^{p}\vert. \end{aligned}$$

The proof of the proposition is elementary and combines [5, Theorem 3.1] and [47, Corollary 6.2].

2.3 Interaction of approximation errors at nodal points and interpolation errors

The Chebyshev method is most promising for cases where computationally intensive pricing methods are required. In such cases, the issue of distorted prices and their consequences arises naturally when computing the prices at the Chebyshev nodes. The observed noisy prices at the Chebyshev nodes are

$$\begin{aligned} \mathrm {Price}_{\varepsilon}^{p^{(k_{1},\dots,k_{D})}}=\mathrm {Price}^{p^{(k_{1},\dots ,k_{D})}} + \varepsilon^{p^{(k_{1},\dots,k_{D})}}, \end{aligned}$$

where $\varepsilon^{p^{(k_{1},\dots,k_{D})}}$ is the approximation error introduced by the underlying numerical technique at the Chebyshev nodes. By linearity, the resulting interpolation has the form

$$ I_{\overline{N}}(\mathrm {Price}_{\varepsilon}^{(\cdot)})(p) = I_{\overline {N}}(\mathrm {Price}^{(\cdot)})(p)+I_{\overline{N}}(\varepsilon^{(\cdot )})(\cdot) $$

with error function

$$ \varepsilon^{(p)}=\sum_{j_{D}=0}^{N_{D}}\cdots\sum _{j_{1}=0}^{N_{1}}c_{j_{1},\ldots,j_{D}}^{\varepsilon}T_{j_{1},\ldots,j_{D}}(p), $$

where the coefficients $c^{\varepsilon}_{j}$ for $j=(j_{1},\dots, j_{D})\in J$ are given by

In the sequel, we are interested in two types of distortions $\varepsilon^{p^{j}}$ for the multi-indices $j= (k_{1},\dots ,k_{D})\in J$. First, analyzing the case that all distortions are bounded by a fixed constant $\overline{\varepsilon}$ will give a stability result. Second, when computing the values at the nodal points independently with a crude Monte Carlo method, the distortions will be i.i.d. and asymptotically normally distributed, $\varepsilon^{p^{j}} \mathop{\sim}\limits^{\rm approx} \mathcal{N}(0,\sigma_{M})$ with $\sigma_{M}=\sigma/\sqrt{M}$. Third, in practice, it often turns out to be considerably more efficient to compute the values at the nodal points in the offline phase in a stochastically dependent way. For instance, it is often advantageous to sample the driving stochastic process once and re-use it for the whole set of parameters $p^{j}$.

Formally, we distinguish the following cases:

• (i) $|\varepsilon^{p^{j}}|\le\overline{\varepsilon}$ for all $j\in J$.

• (ii) $\varepsilon^{p^{j}}$ is normally distributed with distribution $\mathcal{N}(0,\sigma_{j,M})$ for all multi-indices $j\in J$ (not necessarily independent).

In order to express the error bounds for these different cases, let

$$ \varepsilon^{\ast}(N_{1},\ldots,N_{D}) := \textstyle\begin{cases} \overline{\varepsilon} & \qquad \text{in case (i)}, \\ \sqrt{2 \log(2\prod_{i=1}^{D} (N_{i}+1))} \max_{j\in J} \sigma_{j,M} & \qquad \text{in case (ii)}. \end{cases} $$

Theorem 5

Let $\mathcal{P}\ni p\mapsto \mathrm {Price}^{p}$ be given as in Proposition 2.1 and assume one of the conditions (i) or (ii) for the distortions $\varepsilon^{p^{j}}$, $j\in J$. Then the interpolation $I_{\overline{N}}(\mathrm {Price}^{(\cdot)}_{\varepsilon})$ including the distortions satisfies

$$\begin{aligned} E\Big[ \max_{p\in\mathcal{P}}|\mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)}_{\varepsilon})(p)|\Big] &\le2^{\frac{D}{2}+1} V \bigg(\sum_{i=1}^{D}\varrho_{i}^{-2N_{i}}\prod _{j=1}^{D}\frac{1}{1-\varrho_{j}^{-2}}\bigg)^{\frac{1}{2}} \\* &\phantom{=:} + \Lambda_{\overline{N}} \varepsilon^{\ast}(N_{1},\ldots ,N_{D}) , \end{aligned}$$

(2.4)

where the Lebesgue constant $\Lambda_{\overline{N}}$ is bounded by $\Lambda_{\overline{N}}\le\prod_{i=1}^{D}(\frac{2}{\pi}\log(N_{i}+1)+1)$.

Proof

In order to derive a significant estimate, we rewrite the interpolation in Lagrangian form, i.e.,

$$ I_{\overline{N}}(f)(p) = \sum_{k_{1}=0}^{N_{1}}\cdots\sum_{k_{D}=0}^{N_{D}} f(p^{(k_{1},\dots,k_{D})})\lambda^{(k_{1},\dots,k_{D})}(p) $$

with $\lambda^{(k_{1},\dots,k_{D})}(p) =\prod_{i=1}^{D} \ell_{k_{i}}(\tau^{-1}_{[\underline{p}_{i},\overline {p}_{i}]}(p_{i}))$, where $\ell_{k_{i}}(x)=\prod_{j\in\{1,\ldots,D\}\setminus\{i\}}\frac {x-x_{k_{i}}}{x_{k_{j}}-x_{k_{i}}}$. From Proposition 2.1, we deduce

$$\begin{aligned} &E\Big[ \max_{p\in\mathcal{P}}|\mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)}_{\varepsilon})(p)|\Big] \\ &\le c (\overline{N})+ E\bigg[ \max_{p\in\mathcal{P}} \sum _{k_{1}=0}^{N_{1}}\cdots\sum_{k_{D}=0}^{N_{D}} \vert\varepsilon ^{p^{(k_{1},\dots,k_{D})}}\vert\vert\lambda^{(k_{1},\dots,k_{D})}(p)\vert \bigg] \end{aligned}$$

with $c (\overline{N})$ defined as the term on the first line of the right-hand side of the inequality (2.4). Next, we estimate the Lebesgue constant

$$\begin{aligned} \Lambda_{\overline{N}} &:= \max_{p\in\mathcal{P}}\sum_{k_{1}=0}^{N_{1}}\cdots\sum _{k_{D}=0}^{N_{D}}|\lambda^{(k_{1},\dots,k_{D})}(p)|\\ &\phantom{:}= \max_{p\in\mathcal{P}}\sum_{k_{1}=0}^{N_{1}}\cdots\sum _{k_{D}=0}^{N_{D}}\prod_{i=1}^{D} |\ell_{k_{i}}(p_{i})|\\ &\phantom{:}= \prod_{i=1}^{D} \max_{p_{i}\in[\underline{p}_{i},\overline {p}_{i}]} \sum_{k_{i}=0}^{N_{i}} \big|\ell_{k_{i}}\big(\tau^{-1}_{[\underline{p}_{i},\overline {p}_{i}]}(p_{i})\big)\big|. \end{aligned}$$

Since $\max_{p\in[\underline{p},\overline{p}]}\sum_{k=0}^{N} |\ell _{k}(\tau^{-1}_{[\underline{p},\overline{p}]} (p))|= \max_{p\in[-1,1]}\sum_{k=0}^{N} |\ell_{k}(p)| =\Lambda_{N}$, which is the Lebesgue constant of the univariate Chebyshev interpolation, invoking its well-known estimate $\Lambda_{N} \le\frac{2}{\pi} \log(N+1)+1$ (see, for instance, [46, Theorem 15.2]) yields the result for case (i).

Under (ii), for arbitrary $t>0$, we use Jensen’s inequality and the symmetry of the centered normal distribution to estimate

$$\begin{aligned} \operatorname {e}^{t E [\max_{j\in J} |\varepsilon^{p^{j}}|]}\leq E[\operatorname {e}^{t \max _{j\in J} |\varepsilon^{p^{j}}|} ] & = E \Big[\max_{j\in J} \operatorname {e}^{t |\varepsilon^{p^{j}}|}\Big] \\* & \leq\sum_{j\in J} E[\operatorname {e}^{ t |\varepsilon^{p^{j}}|}] \leq2 \sum _{j\in J} E[\operatorname {e}^{ t \varepsilon^{p^{j}}}]. \end{aligned}$$

Inserting the normal moment-generating function and setting $n:=\prod_{i=1}^{D} (N_{i}+1)$ and $\overline{\sigma}:=\max_{j\in J}\sigma_{j,M}$, we obtain $E [\max_{j\in J} |p^{j}|] \le\log(2n)/t + \overline{\sigma}^{2} t/2$. Finally, minimizing over $t>0$ yields

$$ E \Big[\max_{j\in J} |p^{j}|\Big] < \sqrt{2 \log(2n)}\, \overline {\sigma}. $$

 □

2.4 Relation to parametric multilevel Monte Carlo

There is an interesting relation between our proposed Chebyshev interpolation approach and the parametric multilevel Monte Carlo method suggested by Heinrich in [22] and [24]. To be more precise, as concisely explained in [23, Sect. 2.1], the starting point of [22] is the interpolation of the function $p^{1}\mapsto E[f^{p^{1}}(X)]$ and the computation of $E[f^{p_{k}}(X)]$ at the nodes $p_{k}$ with Monte Carlo. Note that in this setting, the random variable $X$ is not parametric. Next, the multilevel Monte Carlo method is introduced. This is a hierarchical procedure based on nested grids. In each step, the estimator of the coarser grid serves as a control variate. The grids then are chosen optimally to balance cost and accuracy. Heinrich and Sindambiwe [24] show that the resulting algorithm is optimal for a certain class of problems. This class of problems is characterized by the regularity of the function

$$(p^{1},x)\mapsto f^{p^{1}}(x), $$

namely that it belongs to a Sobolev space of a certain order $r$. The order $r$ for which partial derivatives in $(p^{1},x)$ are assumed is the determining factor for the efficiency. In particular, the weak partial derivatives in both the parameters $p^{1}\in \mathbb {R}^{D}$ and in $x\in \mathbb {R}^{d}$ need to exist in order to apply the approach of [24].

In contrast, our error analysis is based on the regularity of the mapping

$$ (p^{1},p^{2})\mapsto E[f^{p^{1}}(X^{p^{2}})]. $$

Under appropriate integrability assumptions, the resulting problem class is significantly larger than the setting of [22] and [24]. This is essential for applications in finance, as the examples of a European call and digital option illustrate. The payoff function of a European call has a kink. According to the ansatz of [22], this yields a very poor convergence rate. The call option prices as a function of the parameters, however, are in many cases even analytic, as we prove in the following Sect. 3. The situation is even more severe for digital options, whose payoffs are not even weakly differentiable. Here, the approach of [22] does not even yield convergence. The Chebyshev method as proposed in this article, however, can be shown to converge with an exponential rate for a wide range of applications. We again refer to Sect. 3.

We relate the error analysis presented in Sect. 2.3 with the results of [24] where a bound of the expected error in the $L^{2}$-norm is presented as a function of the cost to obtain an asymptotic analysis of the efficiency. In [23], it is shown that there exist constants $c_{1}$ and $c_{2}$ such that for each integer $M$, the cost of the parametric Monte Carlo method is bounded by $c_{1}M$ and the error is bounded by $c_{2}M^{-\alpha}$, where $\alpha\in(0,\frac{1}{2})$ depends on the dimension of the parameter space and the Sobolev order of the function space to which $f$ belongs.

To present an error analysis in the same spirit, we observe that the cost for estimating $\mathrm {Price}^{(p)}$ for a fixed $p$ is bounded by $\bar{c}_{1} M$ for $M$ Monte Carlo simulations with a constant $\bar{c}_{1}>0$. It follows directly that the cost of deriving the interpolation $I_{\overline{N}}(\mathrm {Price}^{(\cdot)}_{\varepsilon})$ is bounded by $\bar{c}_{1}\mathcal{M:}=\bar{c}_{1}\prod_{i=1}^{D}(N_{i}+1)M$, where $N_{i}$ is the number of nodal points in dimension $i$ and $M$ is the number of sample paths at each nodal point. In this setting, according to the central limit theorem, the errors $\varepsilon^{p^{j}}$ are asymptotically normally distributed with variance $\sigma_{j,M}=\sigma_{j}/\sqrt{M}$. This motivates the choice of $\sigma_{j,M}$ in the following theorem.

Departing from the framework of [23], we estimate the expectation of the $L^{\infty}$-norm of the error instead of the weaker $L^{2}$-norm. The maximum norm is more suitable for quantifying mispricing, and it is available without additional cost, since the Chebyshev interpolation is tailored to minimize the maximum error.

Theorem 6

Let the assumptions of Theorem 2.5 with condition (ii) on the distortions hold, and suppose $\sigma_{j,M}=\sigma_{j}/\sqrt {M}$. For each $\beta>D/2$, there exist constants $\bar{c}_{1},\bar{c}_{2}>0$ such that for each integer $\mathcal{M}>1$, there is a choice of $M,N$ such that the offline cost of the Chebyshev method is bounded by $\bar {c}_{1}\mathcal{M}$ and

$$\begin{aligned} E\Big[ \max_{p\in\mathcal{P}}|\mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)}_{\varepsilon})(p)|\Big]\le\bar{c}_{2}(\log\mathcal {M})^{\beta}\mathcal{M}^{-1/2}. \end{aligned}$$

Proof

Combining (2.4) and Corollary 2.3 results in

$$\begin{aligned} E\Big[ \max_{p\in\mathcal{P}}|\mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)}_{\varepsilon})(p)|\Big]\le C_{1} \underline{\varrho }^{-\underline{N}} +\Lambda_{\overline{N}} \varepsilon^{\ast}(N_{1},\ldots,N_{D}) , \end{aligned}$$

where $\underline{\varrho} = \min\limits_{1\le i\le D}\varrho_{i}$ and $\underline{N} = \min\limits_{1\le i\le D} N_{i}$. Setting $N_{i}(M)=N(M)=\alpha\log M$ for some $\alpha>1/(2\log\underline{\varrho})$ and $\mathcal{M}=cN(M)^{D}M$ to determine $M$, the result follows from elementary estimations. □

Remark 7

In Theorem 2.6, the error of the resulting Chebyshev interpolation is put in relation to the cost of the offline phase. This is in the spirit of [23]. The following two observations show that our approach is in this regard competitive:

(i) In contrast to [23, Theorem 1], the payoff function $(p^{1},x)\mapsto f^{p^{1}}(x)$ is not required to be weakly differentiable to a specific order. Moreover, Theorem 2.6 allows a parametrized random variable $X^{p^{2}}$.

(ii) The error of the multilevel Monte Carlo estimate of [23, Theorem 1] decays with $\sqrt{\mathcal{M}}$ if the function $f$ is of high regularity. This is the only case in which the asymptotic order of convergence in [23, Theorem 1] is slightly better than the rate of Theorem 2.6, where an additional logarithmic term appears. Note, however, that the error in Theorem 2.6 is measured in the stronger $L^{\infty}$-norm.

We emphasize that the analysis according to [23] considers efficiency in terms of accuracy versus the cost of the offline phase and ignores the online phase. From an application point of view, however, the cost of the online phase is crucial. This is especially the case where real-time evaluation is required. In some applications, it is even rather the offline cost that can be disregarded. This is for instance the case if the offline phase can be executed in idle times.

To make the implications clear, let us consider a concrete example. Following the reasoning of efficiency as accuracy versus “offline cost”, the number of nodal points of the interpolation is of minor importance. So is the choice of the interpolation method. This is in line with [24] choosing piecewise linear interpolation to illustrate the multilevel Monte Carlo method that they originally described for an arbitrary nodal interpolation. Whereas this choice of interpolation can be appropriate for a one-dimensional parameter space, a simple calculation makes clear how crucial it becomes for multivariate parameter spaces to require as few nodal points as possible to achieve a pre-specified accuracy. For instance, when interpolating piecewise linearly on an equidistant grid in the multilevel Monte Carlo method of [23] with $L$ levels, $2^{L}$ nodal points in each direction are applied. For a $D$-dimensional parameter space, this results in $2^{LD}$ nodal points, which for $L=10$ and $D=2$ means more than 1 million nodal points. In this case, the “online cost” is in the range of the cost of a Monte Carlo simulation, which makes the interpolation redundant. Applying Chebyshev polynomial interpolation, a small number of nodal points such as 7, as shown in Sect. 4.2 below, suffices for the Chebyshev interpolation method to obtain an appropriate accuracy. In this case, the total number of nodes is 49 for the tensorized Chebyshev interpolation in two dimensions. Thus the online cost outperforms Monte Carlo significantly. This highlights the fact that the choice of the interpolation method is crucial.

Remark 8

The online cost is proportional to the number of nodal points. If the highest priority is given to the efficiency of the online phase, one can proceed as follows to achieve a pre-specified accuracy $\varepsilon$. First, choose the number of nodal points such that the first summand of the error bound in (2.4) is smaller than $\varepsilon/2$. Then choose the number of samples $M$ of the selected Monte Carlo technique such that also the second summand of the error bound in (2.4) is smaller than $\varepsilon/2$.

3 Exponential convergence of Chebyshev interpolation for POP

In this section, we embed the multivariate Chebyshev interpolation into the option pricing framework. We provide sufficient conditions under which option prices depend analytically on their parameters. We keep the option pricing framework sufficiently abstract so that it also comprises various different applications such as the computation of risk quantities on the basis of parametric random variables.

Let us first observe that an analysis along the lines of [22] and [24] would start from the regularity of the function $p^{1}\mapsto f^{p^{1}}(X)$. But basic functions such as the payoff of a plain vanilla option or a digital option which also underlies the computation of the quantile function and thus, for instance, the VaR are not differentiable and not even continuous. We therefore conclude that the approach of [22] and [24] is too restrictive for financial applications.

Invoking the fact that although the payoff of a plain vanilla option has a kink, its price function is smooth in virtually all models, we exploit the smoothing property of the distribution in order to derive analyticity of the price as function of its parameters. For linear problems, this can conveniently be studied in terms of Fourier transforms. First, Fourier representations of option prices are explicitly available for a large class of option types and asset models. Second, Fourier transformation unveils the analytic properties of both the payoff structure and the distribution of the underlying stochastic quantity in a beautiful way. The Fourier transform of the damped call or digital payoff function, for instance, is evidently analytic in the strike.

To introduce a general option pricing framework, we consider option prices of the form

$$\begin{aligned} \mathrm {Price}^{p=(p^{1},p^{2})}=E[f^{p^{1}}(X^{p^{2}})], \end{aligned}$$

(3.1)

where $f^{p^{1}}:\mathbb {R}^{d}\rightarrow \mathbb {R}_{+}$ is a parametrized family of measurable payoff functions with payoff parameters $p^{1}\in\mathcal {P}^{1}$ and $X^{p^{2}}$ is a family of $\mathbb {R}^{d}$-valued random variables with model parameters $p^{2}\in\mathcal{P}^{2}$. The parameter set

$$\begin{aligned} p=(p^{1},p^{2})\in\mathcal{P}=\mathcal{P}^{1}\times\mathcal {P}^{2}\subseteq \mathbb {R}^{D} \end{aligned}$$

(3.2)

is again of hyperrectangular structure, i.e.,

$$\mathcal{P}^{1}=[\underline{p}_{1},\overline{p}_{1}]\times\cdots\times [\underline{p}_{m},\overline{p}_{m}]\,\text{ and }\mathcal {P}^{2}=[\underline{p}_{m+1},\overline{p}_{m+1}]\times\cdots\times [\underline{p}_{D},\overline{p}_{D}] $$

for some $1\le m \le D$ and real $\underline{p}_{i}\le\overline{p}_{i}$ for $i=1,\ldots,D$.

Typically, we are given a parametrized $\mathbb {R}^{d}$-valued driving stochastic process $H^{p'}$, where the vector of asset price processes $S^{p'}$ is modeled as an exponential of $H^{p'}$, i.e.,

$$\begin{aligned} S^{p',i}_{t}=S^{p',i}_{0}\exp(H^{p',i}_{t}), \qquad0\leq t\leq T, 1\le i\le d, \end{aligned}$$

and $X^{p^{2}}$ is an $\mathcal {F}_{T}$-measurable $\mathbb {R}^{d}$-valued random variable, possibly depending on the history of the $d$ driving processes, i.e., $p^{2}=(T,p')$ and

$$\begin{aligned} X^{p^{2}}:= \Psi(H_{t}^{p'},\,0\le t\le T), \end{aligned}$$

where $\Psi$ is an $\mathbb {R}^{d}$-valued measurable functional.

We now focus on the case where the price (3.1) is given in terms of Fourier transforms. This enables us to provide sufficient conditions under which the parametrized prices have an analytic extension to an appropriate generalized Bernstein ellipse. For most relevant options, the payoff profile $f^{p^{1}}$ is not integrable and its Fourier transform over the real axis is not well defined. Instead, there exists an exponential damping factor $\eta\in \mathbb {R}^{d}$ such that $\operatorname{e}^{\langle\eta,\cdot\rangle}\!f^{p^{1}}\! \in L^{1}(\mathbb {R}^{d})$. We therefore introduce exponential weights in our set of conditions and denote the Fourier transform of $g\in L^{1}(\mathbb {R}^{d})$ by

$$\begin{aligned} \hat{g}(z):= \int_{\mathbb {R}^{d}} \operatorname{e}^{i\langle z, x\rangle } \!g(x) \operatorname{d} \!x \end{aligned}$$

and the Fourier transform of $\operatorname{e}^{\langle\eta,\cdot \rangle}\!f\in L^{1}(\mathbb {R}^{d})$ by $\hat{f}(\cdot-i\eta)$. The exponential weight of the payoff will be compensated by exponentially weighting the distribution of $X^{p^{2}}$, and that weight reappears in the argument of $\varphi^{p^{2}}$, the characteristic function of $X^{p^{2}}$.

Condition 1

Let $\mathcal{P}=\mathcal{P}^{1}\times\mathcal{P}^{2}\subseteq \mathbb {R}^{D}$ be a parameter set with hyperrectangular structure as in (3.2). Let $\varrho\in(1,\infty)^{D}$, denote $\varrho ^{1}:=(\varrho_{1},\ldots,\varrho_{m})$ and $\varrho^{2}:=(\varrho _{m+1},\ldots,\varrho_{D})$ and consider a weight $\eta\in \mathbb {R}^{d}$.

• (A1) For every $p^{1}\in\mathcal{P}^{1}$, the mapping $x\mapsto\operatorname{e}^{\langle \eta,x \rangle }\!f^{p^{1}}(x)$ is in $L^{1}(\mathbb {R}^{d})$.

• (A2) For every $z\in \mathbb {R}^{d}$, the mapping $p^{1}\mapsto \widehat{f^{p^{1}}}(z-i\eta)$ is analytic in the generalized Bernstein ellipse $B(\mathcal{P}^{1},\varrho^{1})$, and moreover, there exist constants $c_{1},c_{2}>0$ such that $\sup_{p^{1}\in B(\mathcal{P}^{1},\varrho^{1})}|\widehat{f^{p^{1}}}(-z-i\eta)|\le c_{1}e^{c_{2}|z|}$ for all $z\in \mathbb {R}^{d}$.

• (A3) For every $p^{2}\in\mathcal{P}^{2}$, the exponential moment condition $E[\operatorname{e}^{-\langle\eta,X^{p^{2}}\rangle}]<\infty$ holds.

• (A4) For every $z\in \mathbb {R}^{d}$, the mapping $p^{2}\mapsto \varphi^{p^{2}}(z+i\eta)$ is analytic in the generalized Bernstein ellipse $B(\mathcal{P}^{2},\varrho^{2})$, and there are constants $\alpha\in(1,2]$ and $c_{1},c_{2}>0$ such that $\sup_{p^{2} \in B(\mathcal{P}^{2},\varrho^{2})}|\varphi^{p^{2}}(z+i\eta)|\le c_{1}\operatorname{e}^{-c_{2} |z|^{\alpha}}$ for all $z\in \mathbb {R}^{d}$.

Conditions (A1)–(A4) are satisfied for a large class of payoff functions and asset models; see [16].

Theorem 2

Let $\varrho\in(1,\infty)^{D}$ and consider a weight $\eta\in \mathbb {R}^{d}$. Under conditions (A1)–(A4), $\mathcal{P}\ni p\mapsto \mathrm {Price}^{p}$ has an analytic extension to the generalized Bernstein ellipse $B(\mathcal {P},\varrho)$ and $\sup_{p\in B(\mathcal{P},\varrho)}|\mathrm {Price}^{p}|\le V$, and therefore,

$$\begin{aligned} \max_{p\in\mathcal{P}}|\mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p)| \le2^{\frac{D}{2}+1} V \bigg(\sum_{i=1}^{D}\varrho_{i}^{-2N_{i}}\prod _{j=1}^{D}\frac{1}{1-\varrho_{j}^{-2}}\bigg)^{\frac{1}{2}}. \end{aligned}$$

Proof

Thanks to (A2) and (A4), the mapping $z\mapsto\widehat{f^{p^{1}}}(-z-i\eta) \varphi^{p^{2}}(z+i\eta)$ belongs to $L^{1}(\mathbb {R}^{d})$ for every $p=(p^{1},p^{2})\in\mathcal{P}$. Together with (A1) and (A3), we can therefore apply [11, Theorem 3.2]. This gives for the option prices the Fourier representation

$$\begin{aligned} \mathrm {Price}^{p}=\frac{1}{(2\pi)^{d}} \int_{\mathbb {R}^{d}+ i\eta} \widehat {f^{p^{1}}}(-z) \varphi^{p^{2}}(z) \operatorname{d}\! z. \end{aligned}$$

By (A2) and (A4), the mapping $p=(p^{1},p^{2})\mapsto\widehat{f^{p^{1}}}(-z) \varphi^{p^{2}}(z)$ has an analytic extension to $B(\mathcal{P},\varrho)$.

Let $\gamma$ be the contour of a compact triangle in the interior of $B([\underline{p}_{i},\overline{p}_{i}],\varrho_{i})$ for arbitrary $i=1,\ldots,D$. Then by (A2) and (A4), we may apply Fubini’s theorem to obtain

$$\begin{aligned} \int_{\gamma} \mathrm {Price}^{(p_{1},\ldots,p_{D})}(z)\operatorname{d}\! p_{i} &= \frac{1}{(2\pi)^{d}} \int_{\gamma}\int_{\mathbb {R}^{d}+ i\eta} \widehat {f^{p^{1}}}(-z) \varphi^{p^{2}}(z) \operatorname{d}\! z \operatorname {d}\! p_{i}\\* & = \frac{1}{(2\pi)^{d}} \int_{\mathbb {R}^{d}+ i\eta} \int_{\gamma}\widehat {f^{p^{1}}}(-z) \varphi^{p^{2}}(z) \operatorname{d} \!p_{i} \operatorname {d}\! z=0. \end{aligned}$$

Moreover, thanks to (A2) and (A4), dominated convergence shows continuity of $p\mapsto \mathrm {Price}^{p}$ in $B(\mathcal{P},\varrho)$, which yields the analyticity of $p\mapsto \mathrm {Price}^{p}$ in $B(\mathcal{P},\varrho)$ thanks to a version of Morera’s theorem provided in [43, Theorem 5.1]. □

Similarly to Proposition 2.3, if Condition 3.1 is satisfied, the Chebyshev interpolation also allows the corresponding derivatives to be well approximated. One very interesting application of this result in finance is the computation of sensitivities like delta or vega of an option price for risk assessment purposes. Theorem 3.2 together with Proposition 2.3 yields the following corollary.

Corollary 3

Set $N_{i}=N,\ i=1,\ldots,D$, i.e., we take the same number of nodal points in each dimension. Under Condition 3.1, $\mathcal{P}\ni p\mapsto \mathrm {Price}^{p}\in W_{2}^{\sigma,\omega}(\mathcal{P})$ for all $\sigma\in \mathbb {N}$, and therefore for all $\ell\in\mathbb {N}$, $\mu$ and $\sigma$ with $\sigma>\frac{D}{2}$, $0\le\mu\le\sigma$ and $\mu-\ell>\frac{D}{2}$, there exists a constant $C$ such that

$$\begin{aligned} \Vert \mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p)\Vert _{C^{\ell}(\mathcal{P})}\le C N^{2\mu-\sigma}\Vert \mathrm {Price}^{p}\Vert _{W_{2}^{\sigma}(\mathcal{P})}. \end{aligned}$$

4 Numerical experiments

In this section, we use the Chebyshev method to price basket and path-dependent options. First, we apply the method to interpolate Monte Carlo estimates of prices of financial products and check the resulting accuracy. To this end, we choose example basket, barrier and lookback options in 5-dimensional Black–Scholes, Heston and Merton models. Second, we combine the Chebyshev method with a Crank–Nicolson finite difference solver using the Brennan–Schwartz approximation, see [3], in order to price a univariate American put option in the Black–Scholes model.

In our Monte Carlo simulation, we use $10^{6}$ sample paths, antithetic variates as a variance reduction technique, and 400 time steps per year. The error of the Monte Carlo method cannot be computed directly. We thus turn to statistical error analysis and use the width of the 95% confidence intervals to determine the accuracy. We refer to this width as confidence bounds. These bounds are derived from the assumption of a normally distributed Monte Carlo estimator with mean equal to the estimator’s value and variance equal to the empirical variance of the payoff on the Monte Carlo samples. The confidence bounds then yield a range around the mean that includes the true price with approximately 95% probability. We pick two free parameters $p_{i_{1}},\ p_{i_{2}}$ out of (3.2), $1\leq i_{1}< i_{2}\leq D$, in each model setup and fix all other parameters at reasonable constant values. In this section, we define the discrete parameter grid $\overline {\mathcal{P}} \subseteq[\underline{p}_{i_{1}},\overline{p}_{i_{1}}]\times [\underline{p}_{i_{2}},\overline{p}_{i_{2}}]$ by

$$ \begin{aligned} \overline{\mathcal{P}} =&\ \left\{\left (p_{i_{1}}^{k_{i_{1}}},p_{i_{2}}^{k_{i_{2}}}\right),\ {k_{i_{1}}},{k_{i_{2}}}\in\{ 0,\dots,40\}\right\},\\ p_{i_{j}}^{k_{i_{j}}} =&\ \underline{p}_{i_{j}} + \frac{k_{i_{j}}}{40}( \overline{p}_{i_{j}}- \underline{p}_{i_{j}}),\quad k_{i_{j}}\in\{0,\dots ,40\}, j\in\{1,2\}, \end{aligned} $$

(4.1)

and call $\overline{\mathcal{P}}$ the test grid. On this test grid, the largest confidence bound is 0.025, and is less than 0.013 on average. For the finite difference method, we find that the absolute error between the numerical approximation and the option price is below 0.005 on all computed parameter tuples in $\overline{\mathcal{P}}$. This error bound was computed by comparing each approximation to the limit of the sequence of finite difference approximations as the grid size is increased. In our calculations, we work with a grid size in time as well as in space (log-moneyness) of $50\max\{1,T\}$, and we compare the result to the prices obtained using grid sizes of $1000\max \{1,T\}$. This grid size was determined to be sufficient for approximating the limit, since it was observed that a grid size of $500\max\{1,T\}$ produces nearly identical prices.

Here, our main concern is the accuracy of the Chebyshev interpolation as we vary the strike and maturity parameters of each option analogously to the previous section. For $N\in\{5,10,30\}$, we precompute the Chebyshev coefficients defined in (2.2) with $D=2$ while always keeping $N_{1}=N_{2}=N$. An overview of the fixed and free parameters in our model selection is given in Table 1. Since in our implementation neither the correlations nor the marginal distributions affect the computational complexity, we assume that the underlyings are i.i.d. for ease of implementation.

Table 1 Parametrization of models, basket and path-dependent options. The model parameters are given for $j=1,\ldots,d=5$ to reflect the multivariate setting with free parameters given by the strike $K$ and the maturity $T$

Let us briefly define the payoffs of the multivariate basket and path-dependent options. The payoff profile of a basket option for $d$ underlyings is given as

$$f^{K}(S^{1}_{T},\ldots,S^{d}_{T})=\bigg(\frac{1}{d}\sum_{j=1}^{d} S^{j}_{T} -K\bigg)^{+}. $$

We write $S_{t}=(S^{1}_{t},\ldots,S^{d}_{t})$, $\underline{S}^{j}_{T}:=\min_{0\le t\le T}S^{j}_{t}$ and $\overline{S}^{j}_{T}:=\max_{0\le t\le T}S^{j}_{t}$. A lookback option for $d$ underlyings is defined as

$$f^{K}(\overline{S}^{1}_{T},\ldots,\overline{S}^{d}_{T})=\bigg(\frac {1}{d}\sum_{j=1}^{d} \overline{S}^{j}_{T}-K\bigg)^{+}. $$

As an example of a multivariate barrier option on $d$ underlyings, we define the payoff

4.1 Accuracy study

We now turn to the results of our numerical experiments. In order to evaluate the accuracy of the Chebyshev interpolation, we investigate the worst-case error $\varepsilon_{L^{\infty}}$. The absolute error of the Chebyshev interpolation method can be directly computed by comparing the interpolated option prices with those obtained by the reference numerical algorithm, i.e., either the Monte Carlo or the finite difference method. Since the Chebyshev interpolation matches the reference method on the Chebyshev nodes, we use the out-of-sample test grid as in (4.1). Table 2 shows the numerical results for the basket and path-dependent options for $N=5$, Table 3 shows $N=10$, and Table 4 shows $N=30$. In addition to the $L^{\infty}$-errors, the tables display the Monte Carlo (MC) prices, the Monte Carlo confidence bounds, and the Chebyshev interpolation (CI) prices for the parameters at which the $L^{\infty}$-error is realized.

Table 2 Interpolation of exotic options with Chebyshev interpolation. $N=5$ and $d=5$ in all cases. In addition to the $L^{\infty}$-errors, the table displays the Monte Carlo (MC) prices, the Monte Carlo confidence bounds, and the Chebyshev interpolation (CI) prices for the parameters at which the $L^{\infty}$-error is realized

Table 3 Interpolation of exotic options with Chebyshev interpolation. $N=10$ and $d=5$ in all cases. In addition to the $L^{\infty}$-errors, the table displays the Monte Carlo (MC) prices, the Monte Carlo confidence bounds, and the Chebyshev interpolation (CI) prices for the parameters at which the $L^{\infty}$-error is realized

Table 4 Interpolation of exotic options with Chebyshev interpolation. $N=30$ and $d=5$ in all cases. In addition to the $L^{\infty}$-errors, the table displays the Monte Carlo (MC) prices, the Monte Carlo confidence bounds, and the Chebyshev interpolation (CI) prices for the parameters at which the $L^{\infty}$-error is realized

The results show that for $N=30$, the accuracy of all option prices is $10^{-3}$. We see that the Chebyshev interpolation error is dominated by the Monte Carlo confidence bounds to the extent that the interpolation error becomes negligible when comparing the two. For basket and barrier options, the $L^{\infty}$-error already reaches satisfactory levels of order $10^{-3}$ at $N=10$. Again, the Chebyshev approximation falls within the confidence bounds of the Monte Carlo approximation. Thus, Chebyshev interpolation with only $121=(10+1)^{2}$ nodes suffices to mimic the Monte Carlo pricing results. This statement does not hold for lookback options, where the $L^{\infty}$-error still differs noticeably when comparing $N=10$ to $N=30$. As can be seen from Table 2, Chebyshev interpolation with $N=5$ may yield unreliable pricing results. For lookback options in the Heston model, we even observe negative prices in individual cases.

We conclude that the Chebyshev interpolation is highly promising for the valuation of multivariate basket and path-dependent options. However, the accuracy of the interpolation critically depends on the accuracy of the reference method at the nodal points, which motivates further analysis that we perform in the next subsection.

4.2 Study of the gain in efficiency

We compute the results on a standard PC with an Intel i5 CPU, 2.50 GHz with cache size of 3 MB. In Sect. 4.2, we used a PC with Intel Xeon CPU with 3.10 GHz with 20 MB SmartCache. All codes are written in Matlab R2014a. In this section, we choose a multivariate lookback option in the Heston model, based on $d=5$ underlyings, as an example. For the efficiency study, we first vary one parameter, then we vary two.

Variation of two model parameters

We choose $\rho_{j}=\rho$, $j=1,\ldots,5$, and vary

$$ \begin{aligned} \rho&\in[\rho_{\text{min}}, \rho_{\text{max}}],&\qquad\rho_{\text{min}}&=-1, \rho_{\text{max}}=1,\\ \sigma&\in[\sigma_{\text{min}}, \sigma_{\text{max}}],&\qquad\sigma _{\text{min}}&=0.1, \sigma_{\text{max}}=0.5, \end{aligned} $$

fixing all other parameters to the values of Table 1. In order to guarantee a roughly comparable accuracy between the Chebyshev interpolation method and the benchmark Monte Carlo pricing, we use the test grid $\overline{\mathcal{P}} \subseteq[\sigma_{\text{min}},\sigma_{\text{max}}]\times[\rho_{\text{min}},\rho_{\text{max}}]$ given by

$$ \begin{aligned} \overline{\mathcal{P}} =&\ \big\{ (\sigma^{k_{1}},\rho^{k_{2}}), {k_{1}},{k_{2}}\in\{0,\dots,20\}\big\} ,\\ \sigma^{k_{1}} =&\ \sigma_{\text{min}} + \frac{k_{1}}{20}\left( \sigma_{\text{max}}- \sigma_{\text{min}}\right),\quad k_{1}\in\{ 0,\dots,20\},\\ \rho^{k_{2}} =&\ \rho_{\text{min}} + \frac{k_{2}}{20}\left( \rho _{\text{max}}- \rho_{\text{min}}\right),\quad k_{2}\in\{0,\dots,20\}. \end{aligned} $$

In Table 5, we present the accuracy for the Chebyshev interpolation with $N=6$ based on the enriched Monte Carlo setting. Comparing the benchmark Monte Carlo setting and the enriched Monte Carlo setting on this test grid, we observe that the maximal absolute error is $2.791\times10^{-2}$ and the confidence bounds of the benchmark Monte Carlo setting do not exceed $6.783\times10^{-2}$.

Table 5 Interpolation of multivariate lookback options in the Heston model with Chebyshev interpolation for $N=6$ based on an enriched Monte Carlo setting with $5\times10^{6}$ sample paths, antithetic variates, and 400 time steps per year. In addition to the $L^{\infty}$-error on the test grid, we also report the Monte Carlo (MC) price, the Monte Carlo confidence bound, and the Chebyshev interpolation (CI) price for the parameters at which the $L^{\infty}$-error is realized. We observe that the accuracy of the Chebyshev interpolation $N=6$ is roughly in the same range as the accuracy of the benchmark Monte Carlo setting (worst-case confidence bound of $6.783\times10^{-2}$ and worst-case error of $2.791\times10^{-2}$)

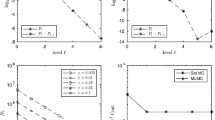
To compare the run-times, we show the run-times necessary to compute the prices for $M^{2}$ parameter tuples for different values of $M$. For the Monte Carlo estimates, the results for $M = 1$ were empirically measured; all others were extrapolated from that since the same amount of computation time would have had to be invested for each parameter set. Table 6 presents the results. In Fig. 1, for each $M=1,\ldots,100$, the run-times of the Chebyshev interpolation method, including the offline phase, are presented and compared to the Monte Carlo method. We observe that for $M=15$, both lines intersect and for $M>15$, the Chebyshev method outperforms its benchmark.

Fig. 1

Efficiency study for a multivariate lookback option in the Heston model based on $d=5$ underlyings, varying the two model parameters $\sigma$ and $\rho$. Comparison of run-times for Monte Carlo pricing and Chebyshev pricing including the offline phase. Both methods have been set up to deliver comparable accuracies. We observe that the Monte Carlo and the Chebyshev curves intersect at roughly $M=15$

Table 6 Efficiency study for a multivariate lookback option in the Heston model based on $d=5$ underlyings. Here, we vary two model parameters and compare the Chebyshev results to Monte Carlo. Both methods have been set up to deliver comparable accuracies. As the number of computed prices increases, the Chebyshev algorithm increasingly profits from the initial investment of the offline phase

Additionally, Table 6 highlights that in the case of a total number of $50^{2}$ parameter tuples, the Chebyshev method exhibits a significant decrease in (total) pricing run-times. For the maximal number of $100^{2}$ parameter tuples that we investigated, pricing resulted in more than 97% of run-time savings in our implementation. While computing $100^{2}$ Heston prices using the Monte Carlo method requires up to 39 days, the Chebyshev method computes the very same prices in 23 hours only. Note that only 7 seconds of this time span are consumed by actual pricing during the online phase.

5 Conclusion and outlook

This article introduces the famous Chebyshev interpolation method to the problem of parametric option pricing and more generally of parametric conditional expectations. The introduction explains the advantage of tackling the complexity by Chebyshev interpolation in this context. We analysed the resulting online–offline numerical scheme. The main convergence results are established in Sect. 2, and special care is taken of the error resulting from deriving the prices at the nodal point by Monte Carlo simulation. A comparison of the efficiency in terms of accuracy versus offline costs shows significant improvement over the existing approaches in the literature. We emphasize again that this type of efficiency needs to be accomplished by efficiency as online cost versus accuracy. The “online efficiency” is more significant than the “offline scheme” in many situations, although typically the “offline efficiency” still matters on a lower scale. In a numerical case study, we investigated the gain in “online efficiency”. The results reveal that the method has a high potential for a variety of applications and further developments.

The most urgent and challenging problems in finance are of high dimensionality. For multivariate polynomial interpolation, the introduction of sparsity techniques promises higher efficiency, for instance, by using compression techniques for tensors as reviewed by [27]. The high potential of low-rank tensor methods is illustrated in an online available numerical example for evaluating spread options in the bivariate Black–Scholes model; see [19]. These types of techniques have to beat the curse of dimensionality for both the online as well as the offline complexity.

Addressing further the offline complexity, we note that up to this point, we have compared the Chebyshev interpolation method with a standard Monte Carlo technique. Since the invention of Monte Carlo methods in the 1940s, see [34], Monte Carlo techniques have been further developed. In particular, quasi Monte Carlo and multilevel Monte Carlo methods have proved to be significantly more efficient in a variety of examples in mathematical finance; see [18, 29]. Thus by employing these techniques in the offline phase, the Chebyshev interpolation method can be enhanced. In terms of efficiency, we expect Fig. 1 to change only by rescaling the time axis, meaning that the run-time for the computation of the Monte Carlo prices on the test grid is reduced proportionally. Obviously, the offline phase of the Chebyshev interpolation scales in the same way. As a first improvement of our implementation of the offline phase, in which we produce a new independent set of samples for each nodal point, one can re-use a once drawn sample set to compute the prices at all nodal points. Furthermore, the run-time of the offline phase can be reduced significantly by parallelization and computations with the help of technical devices such as graphics processing units.

Appendices

Appendix A: Remark on Chebyshev polynomials

Following [9, Chap. 3.3], Chebyshev interpolation appears as a natural choice among the nodal polynomial interpolations. Namely, let $f$ be a function that is $n$ times continuously differentiable on $[-1,1]$ and for which $f^{(n+1)}$ exists and is bounded on $(-1,1)$. Let $p_{n}$ be a polynomial that coincides with $f$ at the nodal points $x_{0},\ldots,x_{n}$. Then there exists $\zeta\in(-1,1)$ such that

$$\begin{aligned} |f(x)-p_{n}(x)|&=\left|\frac{\prod_{i=0}^{n} (x-x_{i})}{(n+1)!}f^{(n+1)}(\zeta)\right| \le\frac{\prod_{i=0}^{n} |x-x_{i}|}{(n+1)!}\sup_{z\in(-1,1)}|f^{(n+1)}(z)|. \end{aligned}$$

The nodal points $x_{0},\dots,x_{N}$ that minimize the maximum over $x$ of the right-hand side above turn out to be the Chebyshev points of the first kind, and the corresponding Chebyshev polynomial interpolation is the resulting minimizing polynomial $p_{n}$. We point out that we decide to implement the Chebyshev points of the second kind, which are the extrema of the Chebyshev polynomials. The advantage of this choice becomes clear when generalizing the method presented in this article to the case of piecewise polynomial interpolation: The Chebyshev points of the second kind contain the two end points of the interval, and thus it is straightforward to concatenate interpolations on adjacent intervals.

Appendix B: Proof of Proposition 2.1

The basic structure of the proof is the same as in [42, Proof of Lemma 7.3.3]. To provide a complete, understandable proof, we first show the same steps as in [42, Proof of Lemma 7.3.3] and state explicitly at which point the proof changes.

Proof

In [42, Proof of Lemma 7.3.3], the proof is given for the error bound

$$\begin{aligned} \max_{p\in\mathcal{P}}\big|f(p ) - I_{\overline{N}}\big(f(\cdot )\big)(p)\big| \le\sqrt{D}2^{\frac{D}{2}+1}V\varrho_{\min}^{-N}(1-\varrho_{\min }^{-2})^{-\frac{D}{2}}, \end{aligned}$$

where $N$ is the number of interpolation points in each of the $D$ dimensions, we set $\varrho_{\min}:=\min_{i=1, \dots,D}\varrho_{i}$, and $V$ is the bound of $f$ on $B(\mathcal{P},\varrho)$ with $\mathcal{P} = [-1,1]^{D}$. We now extend [42, Proof of Lemma 7.3.3] by incorporating the different values of $N_{i}$, $i=1,\ldots,D$, as well as expressing the error bound with the different $\varrho_{i}$, $i=1,\ldots,D$.

In general, we work with parameter spaces $\mathcal{P}=[\underline{p}_{1},\overline{p}_{1}]\times\cdots\times [\underline{p}_{D},\overline{p}_{D}]$ that are of hyperrectangular structure. The linear transformation introduced in Sect. 2 gives a transformation $\tau _{\mathcal{P}}:[-1,1]^{D}\rightarrow\mathcal{P}$ defined by

$$\begin{aligned} \tau_{\mathcal{P}}(p)=\left(\overline{p}_{i}+\frac{\underline {p}_{i}-\overline{p}_{i}}{2}(1-p)\right)_{i=1,\dots,D}. \end{aligned}$$

Let $p\mapsto \mathrm {Price}^{p}$ be a function on $\mathcal{P}$. We set $\widehat{\mathrm {Price}}^{p}=(\mathrm {Price}\circ\tau_{\mathcal{P}})(p)$. Furthermore, let $\widehat{I}_{\overline{N}}(\widehat{\mathrm {Price}}^{(\cdot)})(p)$ be the Chebyshev interpolation of $\widehat{\mathrm {Price}}^{p}$ on $[-1,1]^{D}$. Then it holds that

$$\begin{aligned} I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p)=\big(\widehat{I}_{\overline {N}}(\widehat{\mathrm {Price}}^{(\cdot)})(\cdot)\circ\tau^{-1}_{\mathcal {P}}\big)(p). \end{aligned}$$

From this, it directly follows that

$$\begin{aligned} \mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p)=\Big(\big(\widehat{\mathrm {Price}}^{(\cdot)} -\widehat{I}_{\overline{N}}(\widehat {\mathrm {Price}}^{(\cdot)})(\cdot) \big)\circ\tau^{-1}_{\mathcal{P}}\Big)(p). \end{aligned}$$

Applying the error estimate from [42, Lemma 7.3.3] results in

$$\begin{aligned} |\mathrm {Price}- I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(\cdot)|_{C^{0}(\mathcal{P})} &= \big|\big(\widehat{\mathrm {Price}}^{(\cdot)}-\widehat{I}_{\overline{N}}(\widehat {\mathrm {Price}}^{(\cdot)})(\cdot)\big) \circ\tau^{-1}_{\mathcal{P}}(p)\big|_{C^{0}([-1,1]^{D})}\\ &\le\sqrt{D}2^{\frac{D}{2}+1}\widehat{V}\varrho_{\min }^{-N}(1-\varrho_{\min}^{-2})^{-\frac{D}{2}}, \end{aligned}$$

where $\widehat{V}:=\sup_{p\in B([-1,1]^{D},\varrho)}\widehat{\mathrm {Price}}^{p}$. Inserting that $\widehat{V}=V:=\sup_{p\in B(\mathcal{P},\varrho)}\mathrm {Price}^{p}$ shows that we obtain the same error bound as for the original domain $[-1,1]^{D}$. Therefore, in the following, it suffices to show the proof for $\mathcal{P}=[-1,1]^{D}$. Note that the rest of our proof differs from [43, Proof of Lemma 7.3.3] in that we allow an anisotropic analyticity domain and different numbers of Chebyshev nodes in each direction.

As in [42, Proof of Lemma 7.3.3], we introduce the scalar product

$$\begin{aligned} \langle f,g\rangle_{\varrho}:=\int_{B(\mathcal{P},\varrho)}\frac {f(z)\overline{g(z)}}{\prod_{i=1}^{D}\sqrt{|1-z_{i}^{2}|}}\operatorname {d}\!z \end{aligned}$$

and the Hilbert space

$$\begin{aligned} L^{2}\big(B(\mathcal{P},\varrho)\big):=\{f: f\text{ is analytic in }B(\mathcal{P},\varrho)\text{ and }\Vert f\Vert^{2}_{\varrho }:=\langle f,f\rangle_{\varrho}< \infty\}. \end{aligned}$$

Following the approach in [42, Proof of Lemma 7.3.3], we define a complete orthonormal system for the space $L^{2}(B(\mathcal{P},\varrho))$ with respect to the scalar product $\langle \cdot,\cdot\rangle_{\varrho}$ by the scaled Chebyshev polynomials

$$\begin{aligned} \tilde{T}_{\mu}(z):=c_{\mu}T_{\mu}(z)\quad \text{ with } c_{\mu }:=\left(\frac{2}{\pi}\right)^{\frac{D}{2}}\prod_{i=1}^{D}(\varrho _{i}^{2\mu_{i}}+\varrho_{i}^{-2\mu_{i}})^{-\frac{1}{2}}\quad\text{ for all } \mu\in\mathbb{N}_{0}^{D}. \end{aligned}$$

Then for any bounded linear functional $H$ on $L^{2}(B(\mathcal {P},\varrho))$, we have

$$\begin{aligned} \vert H(f)\vert\le\Vert H\Vert_{\varrho}\Vert f\Vert_{\varrho }, \end{aligned}$$

(B.1)

where $\Vert H\Vert_{\varrho}$ denotes the operator norm. By the orthonormality of $(\tilde{T}_{\mu})_{\mu\in\mathbb{N}_{0}^{D}}$, it follows that

$$\begin{aligned} \Vert H \Vert_{\varrho}=\sup_{f\in L^{2}(B(\mathcal{P},\varrho ))\setminus\{0\}}\frac{\vert H(f)\vert}{\Vert f\Vert_{\varrho }}=\sqrt{\sum_{\mu\in\mathbb{N}_{0}^{D}}\vert H(\tilde{T}_{\mu })\vert^{2}}. \end{aligned}$$

In the following, let $H$ be the error of the Chebyshev polynomial interpolation at a fixed $p\in\mathcal{P}$,

$$\begin{aligned} H(f):=f(p)- I_{\overline{N}}\big(f{(\cdot)}\big)(p). \end{aligned}$$

We recall at this point the notation ${\overline{N}} := (N_{1},\dots ,N_{D})$ with possibly different values for $N_{j}$ for $j = 1,\dots,D$. Starting with (B.1), we first focus on $\Vert H\Vert_{\varrho}$ and compute

$$\begin{aligned} \Vert H \Vert^{2}_{\varrho}=\sum_{\mu\in\mathbb{N}_{0}^{D}}\vert H(\tilde{T}_{\mu})\vert^{2}=\sum_{\mu\in\mathbb{N}_{0}^{D}} c^{2}_{\mu }\vert H(T_{\mu})\vert^{2}. \end{aligned}$$

From now on, the proof differs from [42, Proof of Lemma 7.3.3] since we use the values of $N_{i}$, $i=1,\ldots ,D$, and $\varrho_{i}$, $i=1,\ldots,D$. Since we chose Chebyshev points of the second instead of the first kind in the Chebyshev interpolation, we cannot apply [42, Corollary 7.3.1], but adjust this in Lemma B.1 below to the Chebyshev points of the second kind. We now apply Lemma B.1 to obtain

$$\begin{aligned} \sum_{\mu\in\mathbb{N}_{0}^{D}} c^{2}_{\mu}\vert H(T_{\mu})\vert ^{2}=\sum_{\mu\in\mathbb{N}_{0}^{D}, \exists i:\mu_{i}>N_{i}} c^{2}_{\mu }\vert H(T_{\mu})\vert^{2}\le\sum_{\mu\in\mathbb{N}_{0}^{D}, \exists i:\mu_{i}>N_{i}} 4c^{2}_{\mu}. \end{aligned}$$

Overall, using $(\prod_{j=1}^{D}\varrho_{j}^{2\mu_{j}}+x)^{-1}\le(\prod _{j=1}^{D}\varrho_{j}^{2\mu_{j}})^{-1}=\prod_{j=1}^{D}\varrho_{j}^{-2\mu_{j}}$ for $x>0$, $\mu_{j}\in\mathbb{N}_{0}$ and $j=1,\ldots,D$, this leads to

$$\begin{aligned} \Vert H \Vert^{2}_{\varrho}&\le4 \sum_{\mu\in\mathbb{N}_{0}^{D}, \exists i:\mu_{i}>N_{i}}c_{\mu}^{2} \\ &\le4\left(\frac{2}{\pi}\right)^{D}\sum_{i=1}^{D}\bigg( \sum_{\mu \in\mathbb{N}_{0}^{D}, \mu_{i}>N_{i}}\prod_{j=1}^{D}\varrho^{-2\mu _{j}}_{j}\bigg)\\ &\le4\left(\frac{2}{\pi}\right)^{D} \sum_{i=1}^{D}\varrho _{i}^{-2N_{i}}\bigg( \sum_{\mu\in\mathbb{N}_{0}^{D},\mu_{i}>N_{i}}\varrho _{i}^{-2(\mu_{i}-N_{i})}\prod_{j=1,j\neq i}^{D}\varrho^{-2\mu_{j}}_{j}\bigg)\\ &\le4\left(\frac{2}{\pi}\right)^{D} \sum_{i=1}^{D}\varrho _{i}^{-2N_{i}}\bigg( \sum_{\mu\in\mathbb{N}_{0}^{D}}\prod_{j=1}^{D}\varrho ^{-2\mu_{j}}_{j}\bigg). \end{aligned}$$

From this point on, since $\vert\varrho_{j}^{-2}\vert<1$ for $j=1,\ldots,D$, we use the convergence of the geometric series to obtain

$$\begin{aligned} \Vert H \Vert^{2}_{\varrho}&\le4\left(\frac{2}{\pi}\right)^{D} \sum _{i=1}^{D}\varrho_{i}^{-2N_{i}} \left( \sum_{\mu_{1}=0}^{\infty}\cdots\sum_{\mu_{D}=0}^{\infty}\prod _{j=1}^{D}\varrho^{-2\mu_{j}}_{j}\right)\\ &=4\left(\frac{2}{\pi}\right)^{D} \sum_{i=1}^{D}\varrho _{i}^{-2N_{i}}\prod_{j=1}^{D}\frac{1}{1-\varrho^{-2}_{j}}. \end{aligned}$$

Recalling (B.1), we have to estimate $\Vert f\Vert _{\varrho}$, for which we get

$$\begin{aligned} \Vert f\Vert_{\varrho}^{2}=\int_{B(\mathcal{P},\varrho)}\frac {f(z)\overline{f(z)}}{\prod_{i=1}^{D}\sqrt{|1-z_{i}^{2}|}}\operatorname {d}\!z\le\bigg(\sup_{z\in B(\mathcal{P},\varrho)}\vert f(z)\vert\bigg)^{2}\Vert 1\Vert_{\varrho}^{2}. \end{aligned}$$

From $\pi^{\frac{D}{2}}\tilde{T}_{0}=1$, it directly follows that $\Vert1\Vert_{\varrho}^{2}=(\pi^{\frac{D}{2}})^{2}\Vert\tilde {T}_{0}\Vert_{\varrho}^{2}=\pi^{D}$ and hence

$$\begin{aligned} \Vert f\Vert_{\varrho}^{2}\le\pi^{D} V^{2}. \end{aligned}$$

Combining the results leads to

$$\begin{aligned} \vert H(f)\vert=\big|f(p)- I_{\overline{N}}\big(f{(\cdot)}\big)(p)\big|&\le\bigg(\pi^{D} V^{2} 4\Big(\frac{2}{\pi}\Big)^{D} \sum _{i=1}^{D}\varrho_{i}^{-2N_{i}}\prod_{j=1}^{D}\frac{1}{1-\varrho ^{-2}_{j}}\bigg)^{\frac{1}{2}}\\ &= 2^{\frac{D}{2}+1}V\bigg( \sum_{i=1}^{D}\varrho_{i}^{-2N_{i}}\prod _{j=1}^{D}\frac{1}{1-\varrho^{-2}_{j}}\bigg)^{\frac{1}{2}}. \end{aligned}$$

 □

The following lemma shows that the Chebyshev interpolation of a polynomial with a degree at most as high as the degree of the interpolating Chebyshev polynomial is exact and furthermore determines an upper bound for interpolating Chebyshev polynomials with higher degrees.

Lemma B.1

For $x\in[-1,1]^{D}$, it holds that

$$\begin{aligned} &\big|T_{\mu}(x)-I_{\overline{N}}\big(T_{\mu}{(\cdot)}\big)(x)\big|=0,\qquad \forall\mu\in\mathbb{N}_{0}^{D}:\mu_{i}\le N_{i},i=1,\ldots,D, \end{aligned}$$

(B.2)

$$\begin{aligned} &\big|T_{\mu}(x)-I_{\overline{N}}\big(T_{\mu}{(\cdot)}\big)(x)\big|\le2,\qquad \forall\mu\in\mathbb{N}_{0}^{D}:\exists i\in\{ 1,\ldots,D\}:\mu_{i}>N_{i} . \end{aligned}$$

(B.3)

Proof

The uniqueness properties of the Chebyshev interpolation directly imply (B.2). The proof of (B.3) is similar to [42, Proof of Corollary 7.3.1], where the zeros of the Chebyshev polynomial are used as nodal points. Since we use the extreme points of the Chebyshev polynomials instead, we need to adapt the proof by applying the appropriate orthogonality property. We first focus on the one-dimensional case. Recalling (2.1), the Chebyshev interpolation of $T_{\mu}$, $\mu>N$, is given as

where $x_{k}$ denotes the $k$th extremum of $T_{N}$. The following orthogonality relation holds:

$$\begin{aligned} \begin{aligned} \sum_{k=0}^{N}{}^{''}T_{\mu}(x_{k})T_{j}(x_{k}) = \textstyle\begin{cases} 0, & (\mu+j)\text{ mod }2N \neq0 \text{ and } \vert\mu-j\vert \text{ mod } 2N\neq0,\\ N, & (\mu+j)\text{ mod }2N = 0 \text{ and } \vert\mu-j\vert\text{ mod }2N = 0, \\ \frac{N}{2}, &(\mu+j)\text{ mod }2N = 0 \text{ and } \vert\mu -j\vert\text{ mod }2N \neq0,\\ \frac{N}{2}, &(\mu+j)\text{ mod }2N \neq0 \text{ and }\vert\mu -j\vert\text{ mod }2N = 0. \end{cases}\displaystyle \end{aligned} \qquad \end{aligned}$$

(B.4)

For $\mu,j\le N,$ the identity is shown in [32, (4.46)], and for $\mu>N$, it follows along the same lines. Then (B.4) yields for $\mu>N$ the existence of $\gamma\le N$ such that

$$I_{N}(T_{\mu}) = T_{\gamma}, $$

from which we deduce $|I_{N}(T_{\mu})|=1$ and hence

$$\vert T_{\mu} - I_{N}(T_{\mu})\vert\le\vert T_{\mu}\vert+ \vert I_{N}(T_{\mu})\vert\le2. $$

Thus (B.3) holds in the one-dimensional case. Finally, considering the $D$-dimensional case, we observe that it is elementary to verify

$$I_{\overline{N}}(T_{\mu}) = \prod_{i=1}^{D} I_{N_{i}}(T_{\mu_{i}}). $$

Thus we have

$$ \bigg\vert \prod_{i=1}^{D} T_{\mu_{i}} - \prod_{i=1}^{D} I_{N_{i}}(T_{\mu _{i}})\bigg\vert \le\bigg\vert \prod_{i=1}^{D} T_{\mu_{i}}\bigg\vert + \bigg\vert \prod_{i=1}^{D} I_{N_{i}}(T_{\mu_{i}})\bigg\vert = \prod _{i=1}^{D} \vert T_{\mu_{i}}\vert + \prod_{i=1}^{D} \vert I_{N_{i}}(T_{\mu_{i}})\vert, $$

by the triangle inequality. Inserting $\vert T_{\mu_{i}}\vert=1$ and $\vert I_{N_{i}}(T_{i,\mu_{i}})\vert=1$ shows (B.3). □

Appendix C: Proof of Proposition 2.3

Proof

Before we apply [5, Theorem 3.1], which assumes $\mathcal{P}=[-1,1]^{D}$, we investigate how the linear transformation $\tau_{\mathcal{P}}$ from the proof of Proposition 2.1 influences the derivatives. Let $p\mapsto \mathrm {Price}^{p}$ be a function on $\mathcal{P}$. We set $\widehat{h}(p)=(\mathrm {Price}\circ\tau_{\mathcal{P}})(p)$. Furthermore, let $\widehat{I}_{\overline{N}}(\widehat{h})(p)$ be the Chebyshev interpolation of $\widehat{h}(p)$ on $[-1,1]^{D}$. Then it directly follows that

$$\begin{aligned} \mathrm {Price}^{p} - I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p)=\Big(\big(\widehat{h}(\cdot) -\widehat{I}_{\overline{N}}(\widehat{h})(\cdot ) \big)\circ\tau^{-1}_{\mathcal{P}}\Big)(p). \end{aligned}$$

First, let us assume $D=1$, i.e., $\mathcal{P}=[\underline {p},\overline{p}]$, and let $\alpha\in\mathbb{N}_{0}$. For the partial derivatives, it holds that

$$\begin{aligned} \partial^{\alpha} \mathrm {Price}^{p} - \partial^{\alpha}I_{\overline {N}}(\mathrm {Price}^{(\cdot)})(p)&=\partial^{\alpha}\big(\mathrm {Price}^{p} -I_{\overline{N}}(\mathrm {Price}^{(\cdot)})(p)\big)\\ &=\partial^{\alpha}\bigg(\Big( \big(\widehat{h}(\cdot) -\widehat {I}_{\overline{N}}(\widehat{h})(\cdot) \big)\circ\tau ^{-1}_{\mathcal{P}}\Big)(p)\bigg)\\ &=\partial^{\alpha-1}\frac{2}{\overline{p}-\underline{p}}\Big((\partial^{1}\widehat{h})\big(\tau^{-1}_{\mathcal{P}}(p)\big) \\ &\phantom{=:\partial^{\alpha-1}\frac{2}{\overline{p}-\underline {p}}\Big(} -\big(\partial^{1}\widehat{I}_{\overline{N}}(\widehat {h}^{(\cdot)})\big)\big(\tau^{-1}_{\mathcal{P}}(p)\big) \Big). \end{aligned}$$

Repeating this step iteratively yields

$$\begin{aligned} \partial^{\alpha} \mathrm {Price}^{p} - \partial^{\alpha}I_{\overline {N}}(\mathrm {Price}^{(\cdot)})(p) & =\frac{2^{\alpha}}{(\overline{p}-\underline{p})^{\alpha}}\Big((\partial^{\alpha}\widehat{h})\big(\tau^{-1}_{\mathcal {P}}(p)\big) \\ &\phantom{=:\frac{2^{\alpha}}{(\overline{p}-\underline{p})^{\alpha }}\Big(}-\big(\partial^{\alpha}\widehat{I}_{\overline {N}}(\widehat{h}^{(\cdot)})\big)\big(\tau^{-1}_{\mathcal {P}}(p)\big) \Big). \end{aligned}$$

This scales the error in $[-1,1]$ by a factor $\frac{2^{\alpha }}{(\overline{p}-\underline{p})^{\alpha}}$.

Extending this to the $D$-variate case where $\alpha=(\alpha_{1},\dots ,\alpha_{D})\in \mathbb {N}_{0}^{D}$ is a multi-index and $\partial^{\alpha}= \partial^{\alpha_{1}} \cdots\partial^{\alpha_{D}}$ results in

$$\begin{aligned} \partial^{\alpha} \mathrm {Price}^{p} - \partial^{\alpha}I_{\overline {N}}(\mathrm {Price}^{(\cdot)})(p) &= \prod_{i=1}^{D}\frac{2^{\alpha_{i}}}{(\overline{p}_{i}-\underline {p}_{i})^{\alpha_{i}}}\Big((\partial^{\alpha}\widehat{h})\big(\tau ^{-1}_{\mathcal{P}}(p)\big) \\ &\phantom{=:\prod_{i=1}^{D}\frac{2^{\alpha_{i}}}{(\overline {p}_{i}-\underline{p}_{i})^{\alpha_{i}}}\Big(}-\big(\partial^{\alpha }\widehat{I}_{\overline{N}}(\widehat{h}^{(\cdot)})\big)\big(\tau ^{-1}_{\mathcal{P}}(p)\big) \Big). \end{aligned}$$

From Theorem 3.1 in [5], the assertion follows directly for $\widehat{h}(\cdot)\text{ on }\mathcal{P}=[-1,1]^{D}$, i.e., for any $\frac{D}{2}<\sigma\in \mathbb {N}$ and any $\sigma\geq\mu\in \mathbb {N}_{0}$, there exists a constant $\tilde{C}>0$ such that

$$\begin{aligned} \Vert\widehat{h}(\cdot) -\widehat{I}_{\overline{N}}(\widehat {h})(\cdot) \Vert_{W_{2}^{\mu,\omega}(\mathcal{P})}\le\tilde{C} N^{2\mu-\sigma}\Vert\widehat{h}(\cdot)\Vert_{W_{2}^{\sigma,\omega }(\mathcal{P})}. \end{aligned}$$

(C.1)

For arbitrary $\mathcal{P}$, the constant from (C.1) has to be multiplied with the corresponding factor resulting from the linear transformation $\tau_{\mathcal{P}}$. □