1 Introduction

Increasing CO2 emissions over the years plays an important role in climate change. Recently, each sector has started to take some actions to reduce CO2 emission levels. The shipping industry, whose share is around 3% of global CO2 emission [1], is one of the main industries looking for a solution to reduce CO2 emission. Since the International Maritime Organization (IMO) declared that the CO2 emission level should be reduced by 50% in 2050 compared to CO2 emission levels in 2008 [2], studies related to the decarbonization of the shipping industry gained momentum.

The aim of reducing CO2 emission level by 50% requires many efforts including the design of engines, the type of fuels, the design of hull and propeller, the optimization of route, and introducing innovative technologies. Soft sails, fixed sails, rotor sails, kites, and wind turbines use wind energy, which is a renewable and clean energy source, to create additional thrust forces [3]. In addition, there are some conceptual studies to replace diesel engines with electric power systems using solar and wind power [4]. Controllable pitch propellers are also promising to achieve a reduction in power consumption. Gypa et al. proposed using a controllable-pitch propeller together with a wind sail system to achieve a larger amount of reduction in power consumption [5]. Among the diverse options, wind power is one of the promising solutions due to the availability of strong winds in the open sea, being free to use, and having a high thrust power generation capacity as a clean source of energy. Therefore, some ships installing wind-assisted devices such as rigid wind sails and rotor sails, as shown in Fig. 1, were being developed.

Fig. 1
figure 1

Wind assisted ships equipped with rigid wind sails [6], and rotor sails [7]

Full size image

Previous studies about sailing systems were mostly focused on rigid wind sails and rotor sails. Tillig and Ringsberg conducted a comprehensive study to understand how different configurations of rotor sails affect the performance of a RoRo and tanker by using a 4 degrees-of-freedom model under steady-state conditions [8]. Thies and Ringsberg investigated the effects of the Flettner rotor and suction wing of different sizes on a ferry considering steady-state characteristics [9]. Fujiwara et al. implemented a sail system on the MMG model and investigated the steady sailing performance of a bulk carrier [10]. Vilenova et al. conducted a comparative study between rotor sails, rigid wind sails, and DynaRigs based on steady-state solutions. It was concluded that rotor sails performed best in terms of power saving per unit area [11]. In another study, Lu and Ringsberg compared the Flettner rotor, rigid wing sail, and DynaRig. Rotor sail contributed more than other sails and further investigations were conducted. It was revealed that reducing speed is as effective as implementing a sailing system and the performance of a sailing system depends on ship type, size, route, and weather conditions [12]. Viola et al. considered implementing a 2-piece wing sail on KVLCC2 ship and the effect of the number, aspect ratio and area of sails, and ship speed on the power reduction was examined [13]. Ouchi et al. conducted CFD (computational fluid dynamics) and FEM (finite element method) analyses to understand the aerodynamics of sails and evaluate the structural performance of rigid wind sails [14]. Wang et al. used a grid system to find energy-efficient routes by determining wind sail angle, ship speed, and position in a collaborative way using particle swarm optimization [15]. Although many studies were conducted to predict the effect of wind sails on performance, they mostly focused on steady-state solutions. In the present study, we proposed using a ship dynamics model with controllers of rudder angle and propeller speed to maintain ship course and speed due to generated thrust and side forces by wind sails. Thus, the time responses of each component and their interactions with each other will be understood clearly.

Although different wind sails were proposed and implemented on ships, there is a requirement to understand how a sailing system affects the ship dynamics and energy consumption depending on the design of the ship, the sailing system, and environmental factors. The MMG model, which allows us to examine ship dynamics by considering all these effects, forms the basis of this study due to the suitability to investigate different ship types, wind, and wave. The MMG model was used to investigate the maneuverability of different ships with very good accuracy [16]. Each subsystem, such as propeller, hull resistance, etc., is modeled and the equation of motion under different conditions can be tested. Yasukawa et al. investigated the maneuverability of KVLCC2 ship under adverse weather conditions by considering the effects of wind and waves on the hull [17]. In the present study, the MMG model was extended by considering a wind sailing system and controllers for propeller speed, rudder angle, and operational parameters of the sailing system. Apart from previous studies, the angle of attack of wind sails, and the spin ratio of rotor sails were optimized at each time step to maximize thrust depending on environmental conditions.

In the present study, the performance of wind-assistance systems was investigated using a model-based design approach. In the proposed method, the MMG model was used to investigate ship dynamics under the environmental effects of wind and waves. Each source of force; hull resistance in the water, propeller, rudder, wind sail, hull-wind interaction, and hull-wave interaction, were modeled. Controllers for rudder angle and propeller speed were implemented to follow a track in a given time. Then, propeller power with and without wind assistive devices and power consumption by wind assistive devices were obtained. The reduction of total energy consumption under different conditions was investigated. Finally, the effects of route optimization on the performance of windsails were discussed.

2 Methods

2.1 Standard MMG model

The target ship chosen for the implementation of wind assistive is KVLCC2 [18] due to extensive research and availability of data about it. Ship dynamics of KVLCC2 were investigated using 3 degrees-of-freedom: surge, sway, and yaw based on the previous work, conducted by Yasukawa and Yoshimura [16]. Two coordinate systems were defined: global fixed coordinate system (\({x}_{0}-{y}_{0}-{z}_{0}\)) and moving ship coordinate system (\(x-y-z\)) as shown in Fig. 2. (\(x-y-z\)) coordinate system is fixed at mid-ship position, \(x\) and \(y\) axes are through the bow and starboard of the ship. The velocity components at the center of mass were denoted as \(u\) and \(v\) in forward and starboard directions. Since the (\(x-y-z\)) coordinate system is shifted from center of gravity to mid-ship (\({x}_{G},\mathrm{0,0})\), the velocity component at mid-ship position in y-direction, \({v}_{m}\), was found as given in Eq. 1. The resultant speed, \(U\), and drift angle, \(\beta\), were defined by \(U=\sqrt{{u}^{2}+{v}_{m}^{2}}\) and \(\beta ={\text{atan}}(-{v}_{m}/u)\).

Fig. 2
figure 2

Definition of coordinate systems

Full size image
$${v}_{m}=v-{x}_{G}r$$
(1)

The equation of motion is given in Eq. 2. \(m\) and \({I}_{zG}\) are the mass and inertia of the ship around the center of gravity. \({x}_{G}\) is the position of the center of mass according to the mid-ship coordinates. \({m}_{x}\), \({m}_{y}\) and \({J}_{z}\) are added mass and inertia terms. \(X\), \(Y\), and \({N}_{m}\) are the resultant forces and moment in \(x\), \(y\), and \(r\) directions.

$$\begin{array}{c}\left(m+{m}_{x}\right)\dot{u}-\left(m+{m}_{y}\right){v}_{m}r-{x}_{G}m{r}^{2}=X\\ \left(m+{m}_{y}\right)\dot{{v}_{m}}+\left(m+{m}_{x}\right)ur+{x}_{G}m\dot{r}=Y\\ \left({I}_{zG}+{x}_{G}^{2}m+{J}_{z}\right)\dot{r}+{x}_{G}m\left(\dot{{v}_{m}}+ur\right)={N}_{m}\end{array}$$
(2)

The resultant forces acting on the ship were obtained by the summation of the hull, propeller, rudder forces and hull-wind interaction, hull-wave interaction, and wind-assisted system generated force as shown in Eq. 3.

$$\begin{aligned} X = & & X_{H} + X_{P} + X_{R} + X_{{{\text{Hull}} - {\text{Wind}}}} + X_{{{\text{Hull}} - {\text{Wave}}}} + X_{{{\text{WAD}}}} \\ Y = & & Y_{H} + Y_{P} + Y_{R} + Y_{{{\text{Hull}} - {\text{Wind}}}} + Y_{{{\text{Hull}} - {\text{Wave}}}} + Y_{{{\text{WAD}}}} \\ N_{m} = & N_{H} + N_{P} + N_{R} + N_{{{\text{Hull}} - {\text{Wind}}}} + N_{{{\text{Hull}} - {\text{Wave}}}} + N_{{{\text{WAD}}}} \\ \end{aligned}$$
(3)

Hydrodynamic forces acting on the ship hull were calculated by using Eq. 4. Here, \(v_{m}^{\prime }\) and \(r^{\prime }\) are nondimensional speeds and were defined by \(v_{m}^{\prime } = v_{m} /U\) and \(r^{\prime } = rL_{pp} /U\). Nondimensional hydrodynamic resistance on the hull was expressed by using polynomial functions as given by Eq. 5. Hydrodynamic coefficients for maneuvering simulation of KVLCC2 were obtained based on the previous work by Yasukawa and Yoshimura [16].

$$\begin{array}{*{20}c} {X_{H} = \,\left( {1/2} \right)\rho L_{pp} dU^{2} X_{{H\left( {v_{m}^{\prime } ,r^{\prime } } \right)}}^{\prime } } \\ {Y_{H} = \,\left( {1/2} \right)\rho L_{pp} dU^{2} Y_{{H\left( {v_{m}^{\prime } ,r^{\prime } } \right)}}^{\prime } } \\ {N_{H} = \,\left( {1/2} \right)\rho L_{pp}^{2} dU^{2} N_{{H\left( {v_{m}^{\prime } ,r^{\prime } } \right)}}^{\prime } } \\ \end{array}$$
(4)
$$\begin{aligned} X_{{H\left( {v_{m}^{\prime } ,r^{\prime } } \right)}}^{\prime } = & \, - R_{0}^{\prime } + X_{{{\text{vv}}}}^{\prime } \left( {v_{m}^{\prime } } \right)^{2} + X_{{{\text{vr}}}}^{\prime } v_{m}^{\prime } r^{\prime } + X_{{{\text{rr}}}}^{\prime } \left( {r^{\prime } } \right)^{2} + X_{{{\text{vvvv}}}}^{\prime } \left( {v_{m}^{\prime } } \right)^{4} \\ Y_{{H\left( {v_{m}^{\prime } ,r^{\prime } } \right)}}^{\prime } = & \,Y_{v}^{\prime } v_{m}^{\prime } + Y_{r}^{\prime } r^{\prime } + Y_{{{\text{vvv}}}}^{\prime } \left( {v_{m}^{\prime } } \right)^{3} + Y_{{{\text{vvr}}}}^{\prime } \left( {v_{m}^{\prime } } \right)^{2} r^{\prime } + Y_{{{\text{vrr}}}}^{\prime } v_{m}^{\prime } \left( {r^{\prime } } \right)^{2} + Y_{{{\text{rrr}}}}^{\prime } \left( {r^{\prime } } \right)^{3} \\ N_{{H\left( {v_{m}^{\prime } ,r^{\prime } } \right)}}^{\prime } = & \,Y_{v}^{\prime } v_{m}^{\prime } + Y_{r}^{\prime } r^{\prime } + Y_{{{\text{vvv}}}}^{\prime } \left( {v_{m}^{\prime } } \right)^{3} + Y_{{{\text{vvr}}}}^{\prime } \left( {v_{m}^{\prime } } \right)^{2} r^{\prime } + Y_{{{\text{vrr}}}}^{\prime } v_{m}^{\prime } \left( {r^{\prime } } \right)^{2} + Y_{{{\text{rrr}}}}^{\prime } \left( {r^{\prime } } \right)^{3} \\ \end{aligned}$$
(5)

Propeller generates thrust only in the \(x\) direction as given in Eq. 6 where \({t}_{P}\) is the thrust deduction factor, \({n}_{P}\) is the rotational speed of propeller, \({D}_{P}\) is the diameter of the propeller, and \({K}_{T}\) is propeller thrust which depends on the advance ratio of the propeller, \({J}_{P}\).

$$\begin{aligned} X_{P} = & \left( {1 - t_{P} } \right)\rho n_{P}^{2} D_{P}^{4} K_{{T(J_{p} )}} \\ Y_{P} =\, &0 \\ N_{P} =\, &0 \\ \end{aligned}$$
(6)

The relation between \({K}_{T}\) and \({J}_{P}\) was defined by a second-order polynomial as shown in Eq. 7. Advance ratio of the propeller can be found by using Eq. 8. Wake coefficient,\({w}_{P}\), depends on maneuvering motion and wake coefficient at straight moving,\({w}_{P0}\), as given in Eq. 9. Geometric inflow angle,\({\beta }_{P}\), was defined as \(\beta_{P} = \beta - x_{P}^{\prime } r^{\prime }\).

$${K}_{T}={k}_{0}+{k}_{1}{J}_{P}+{k}_{2}{J}_{P}^{2}$$
(7)
$${J}_{P}=\frac{u\left(1-{w}_{P}\right)}{{n}_{P}{D}_{P}}$$
(8)
$$\left(1-{w}_{P}\right)/\left(1-{w}_{P0}\right)=1+\left\{1-{\text{exp}}\left(-{C}_{1}\left|{\beta }_{P}\right|\right)\right\}\left({C}_{2}-1\right)$$
(9)

The definition of rudder forces was given in Eq. 10. The coefficients of \({t}_{R}\), \({a}_{H}\) and \({x}_{H}\) are related to the interaction between hull and rudder. \({F}_{N}\) is the normal force created by the rudder and given in Eq. 11. The resultant inflow speed and angle were defined in Eqs. 12 and 13.

$$\begin{aligned} X_{R} = & - \left( {1 - t_{R} } \right)F_{N} \sin \delta \\ Y_{R} = & - \left( {1 + a_{H} } \right)F_{N} \cos \delta \\ N_{R} = & - \left( {x_{R} + a_{H} x_{H} } \right)F_{N} \cos \delta \\ \end{aligned}$$
(10)
$${F}_{N}=(1/2)\rho {A}_{R}{U}_{R}^{2}{f}_{\alpha }{\text{sin}}{\alpha }_{R}$$
(11)
$${U}_{R}=\sqrt{{u}_{R}^{2}+{v}_{R}^{2}}$$
(12)
$${\alpha }_{R}=\delta -{\text{atan}}({v}_{R}/{u}_{R})$$
(13)

Longitudinal and lateral velocity components, \({u}_{R}\) and \({v}_{R}\), around the rudder are required to calculate rudder forces as shown in Eqs. 14 and 15.

$$u_{R} = {\varepsilon}{\rm{u}}\left( {1 - w_{P} } \right)\sqrt {\eta \left\{ {1 + \kappa \left( {\sqrt {1 + \frac{{8K_{T} }}{{\pi J_{P}^{2} }}} - 1} \right)} \right\}^{2} + \left( {1 + \eta } \right)}$$
(14)
$$v_{R} = U\gamma_{R} \left( {\beta - l_{R}^{{^{\prime } }} r^{\prime } } \right)$$
(15)

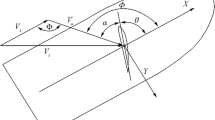
Environmental factors, like wind and waves, also affect the motion of ships. Therefore, the interaction between the ship and the environment was also considered. The effect of wind on the hull was defined according to Fig. 3 using the density of air, \({\rho }_{{\text{air}}}\), frontal and lateral area, \({A}_{F}\) and \({A}_{L}\), apparent wind speed, \({V}_{A}\), and force coefficients as given Eq. 16. Wind force coefficients, \({C}_{{\text{XA}}}\), \({C}_{{\text{YA}}}\), and \({C}_{{\text{NA}}}\), at different apparent wind direction, \({\theta }_{A}\), were obtained based on the previous study by Yasukawa et al. [17].

$$\begin{aligned} X_{{{\text{Hull}} - {\text{Wind}}}} = & \,\left( {1/2} \right)\rho_{{{\text{air}}}} A_{F} V_{A}^{2} C_{{{\text{XA}}\left( {\theta_{A} } \right)}} \\ Y_{{{\text{Hull}} - {\text{Wind}}}} = & \,\left( {1/2} \right)\rho_{{{\text{air}}}} A_{L} V_{A}^{2} C_{{{\text{YA}}\left( {\theta_{A} } \right)}} \\ N_{{{\text{Hull}} - {\text{Wind}}}} = & \,\left( {1/2} \right)\rho_{{{\text{air}}}} A_{L} L_{{{\text{pp}}}} V_{A}^{2} C_{{{\text{NA}}\left( {\theta_{A} } \right)}} \\ \end{aligned}$$
(16)
Fig. 3
figure 3

Definition of true and apparent wind speed directions

Full size image

Wave-induced steady forces were defined using water density, \(\rho ,\) gravitational acceleration, \(g\), significant wave height, \({H}_{1/3},\) length of the ship, \({L}_{{\text{pp}}},\) and resistance coefficients, \(\overline{{C_{{{\text{XW}}}} }}\), \(\overline{{C_{{{\text{YW}}}} }}\), and \(\overline{{C_{{{\text{NW}}}} }}\) as given in Eq. 17. Wave resistance coefficients, which depend on the resultant ship speed, \(U\), wave period, \({T}_{v}\), and relative wave direction, \({\chi }_{0}\), were obtained by previous work of Yasukawa et al. [17].

$$\begin{aligned} X_{{{\text{Hull}} - {\text{Wave}}}} = \, & \rho gH_{1/3}^{2} L_{{{\text{pp}}}} \overline{{C_{{{\text{XW}}}} }}_{{\left( {U,T_{v} ,\chi_{0} } \right)}} \\ Y_{{{\text{Hull}} - {\text{Wave}}}} = \, & \rho gH_{1/3}^{2} L_{{{\text{pp}}}} \overline{{C_{{{\text{YW}}}} }}_{{\left( {T_{v} ,\chi_{0} } \right)}} \\ N_{{{\text{Hull}} - {\text{Wave}}}} = \, & \rho gH_{1/3}^{2} L_{{{\text{pp}}}}^{2} \overline{{C_{{{\text{NW}}}} }}_{{\left( {T_{v} ,\chi_{0} } \right)}} \\ \end{aligned}$$
(17)

Principal particulars, hydrodynamic coefficients, interaction coefficients, propeller, and rudder characteristics used in the simulation were given in Table 1.

Table 1 Ship particular, hydrodynamic coefficients, propeller and rudder characteristics
Full size table

2.2 Characteristics of wind sail systems

In the present study, a rigid wind sail and a rotor sail were considered to reduce energy consumption. Rigid wind sails produce lift and drag forces by adjusting the angle of attack to maximize thrust generated by sail systems. The airfoil shape considered in this study is NACA0015. Lift and drag characteristics of NACA0015 airfoil between 0 and 90 degree was used for Reynolds number of 10 million [19]. The height and width of the wind-assisted device were assumed to be 50 m and 30 m.

Rotor sails are another type of wind assistance propulsion system investigated in the present study. Unlike rigid wind sails, rotor sails consume additional power through rotating. Lift and drag characteristics of the rotor sails depend on the ratio of the rotational speed of the rotor sail and apparent wind speed. The generated forces and power consumption by rotor sails were obtained based on the results in [8]. Since coefficients were valid for rotor sails having an aspect ratio of 6 and disc diameter twice the diameter of the rotor, the dimensions of rotor sails were determined as a diameter of 5 m and a height of 30 m. The lift and drag coefficients used in simulations for rigid wind sails and rotor sails were shown in Fig. 4.

Fig. 4
figure 4

Lift and drag coefficients for rigid wind sails [19] and rotor sails [8]

Full size image

Lift and drag forces generated by different sail systems were calculated as given in Eqs. 18 and 19 where lift and drag coefficients are \({c}_{L}\) and \({c}_{D}\), apparent wind speed and angle are \({V}_{A}\) and \({\theta }_{A}\), angle of attack is \({\alpha }_{A}\), and the spin ratio is \({\text{SR}}\). Then, the forces and moment acting on the ship were obtained using Eq. 20 where \({x}_{{\text{Sail}}}\) is the position of the wind-assisted device along the \(x\)-axis of the ship coordinate system.

$$\begin{array}{c}{L}_{{\text{rigid}}}=\left(1/2\right){\rho }_{{\text{air}}}{V}_{A}^{2}A{{c}_{L}}_{\left({\alpha }_{A}\right)}\\ {D}_{{\text{rigid}}}=\left(1/2\right){\rho }_{{\text{air}}}{V}_{A}^{2}A{{c}_{D}}_{\left({\alpha }_{A}\right)}\end{array}$$
(18)
$$\begin{array}{c}{L}_{{\text{rotor}}}=\left(1/2\right){\rho }_{{\text{air}}}{V}_{A}^{2}A{{c}_{L}}_{\left(SR\right)}\\ {D}_{{\text{rotor}}}=\left(1/2\right){\rho }_{{\text{air}}}{V}_{A}^{2}A{{c}_{D}}_{\left(SR\right)}\end{array}$$
(19)
$$\begin{aligned} X_{{{\text{WAD}}}} = \, & D\cos \left( {\theta_{A} } \right) - L\sin \left( {\theta_{A} } \right) \\ {\text{Y}}_{{{\text{WAD}}}} = \, & D\sin \left( {\theta_{A} } \right) + L\cos \left( {\theta_{A} } \right) \\ N_{{{\text{WAD}}}} = \, & Y_{{{\text{WAD}}}} \times x_{{{\text{Sail}}}} \\ \end{aligned}$$
(20)

2.3 Controllers

To investigate the performance of wind assistive systems at different sea and weather conditions, rudder angle, propeller speed, angle of attack of the rigid wind sail, and spin ratio of the rotor sail need to be controlled. In the present study, we assumed that the planned ship trajectory is straight, and wind and wave are subject to change. Thus, the same trajectory is followed under different conditions of wind, wave, and cruising speed of the ship.

Reference position and heading of the ship were defined as the position and heading of the ship after \({T}_{{\text{ref}}}\) seconds later, which is acquired based on the route information as shown in Fig. 5. The definition of ship heading error and ship speed error was given in Eqs. 21 and 22. After calculating the heading error, a proportional controller was used to determine the rudder angle.

Fig. 5
figure 5

The definition of heading and speed error

Full size image

The propeller speed rate was also controlled to consider the effect of different sails under different environments. When external forces acting on a ship change due to wind and waves, propeller speed should be controlled to reach the destination point at the desired time. The reference ship speed was calculated at each time step and PID (proportional-integral-derivative) controller was designed to determine the propeller speed rate. Then, propeller speed was obtained by integrating the propeller speed rate. Through control of the rudder and propeller, the same conditions were obtained for ship with and without wind-assistive systems.

$${\psi }_{e}={\psi }_{{\text{actual}}}-{\text{atan}}\left(\frac{{y}_{{\text{ref}}}-y}{{x}_{{\text{ref}}}-x}\right)$$
(21)
$${u}_{e}=\frac{\sqrt{{\left({y}_{{\text{ref}}}-y\right)}^{2}+ \text{ } {\left({x}_{{\text{ref}}}-x\right)}^{2}}}{{T}_{{\text{ref}}}}-u$$
(22)

Wind assistance systems also require a controller to maximize the thrust under different external conditions. Since rigid wind sails require power mainly to adjust angle of attack, operating steady power of rigid wind sails is negligible. Angle of attack of rigid wind sails was determined to maximize thrust between \(-90\) and \(90\) degrees. The angle of attack was determined by maximizing the \({f}_{{\text{Rigid}}}\) function, which is given in Eq. 23, in each time step. When it comes to rotor sails, they require external power input to rotate the sail at a certain rotational speed. Therefore, the spin ratio of rotor sails was determined between ± 5 SR to maximize average power reduction, \({f}_{{\text{Rotor}}}\), which is given in Eq. 24. Average power reduction was predicted as the difference between the approximate reduction of power created by rotor sail and power consumption of rotor sail, \({P}_{{\text{WAD}}}\). The approximate reduction of power was assumed to be the multiplication of thrust force generated, \({X}_{{\text{WAD}}}\), and surge speed, \(u\). It should be noted that functions to determine operational condition of rigid wind sails and rotor sails, \({f}_{{\text{Rigid}}}\) and \({f}_{{\text{Rotor}}}\), have different dimensions, because rotor sails should be operated considering power required to rotate rotor sails and generated thrust power, but rigid wind sails should be operated considering thrust force and resultant force.

$${f}_{{\text{Rigid}}}={X}_{{\text{WAD}}}\times \left({X}_{{\text{WAD}}}^{2}+{Y}_{{\text{WAD}}}^{2}\right)$$
(23)
$${f}_{{\text{Rotor}}}={X}_{{\text{WAD}}}\times u-{P}_{{\text{WAD}}}$$
(24)

2.4 MATLAB/Simulink integration

Wind-assisted ship dynamics model was built using MATLAB R2022b/Simulink as shown in Fig. 6. Each source of force, propeller, rudder, hull resistance, added mass and inertia, wind sails, hull-wind interaction, and hull-wave interaction, was considered separately. Control models for propeller speed and rudder angle were considered autopilot. Then, wind sail controllers were designed to determine the angle of attack and the spin ratio.

Fig. 6
figure 6

An integrative model of each subsystem using Simulink

Full size image

2.5 Performance investigation index

The performance of different sailing systems was predicted by considering many parameters including environmental conditions during the route. To evaluate the effect of the sailing system, the target ship followed a straight line under different environmental conditions by using a controller. A scenario database, consisting of different environmental conditions and the probability of each, was created. The overall performance function was evaluated based on the total energy consumption and the probabilities as given in Eq. 25 where \(P\) is the probability which depends on ship speed, \({u}_{i}\), true wind speed, \({V}_{{\text{true}},{\text{j}}}\), and true wind direction, \({\theta }_{{\text{true}},{\text{k}}}\). To compare ship with and without wind sailing system, energy consumptions of both ships were calculated considering energy consumption of propeller and rotor sail between two points along straight route considering same true wind speed, true wind direction, and ship speed. Then, \({\epsilon }_{i,j,k}\) is calculated as the percent reduction in the total energy consumption to maintain the ship speed constant.

$${f}_{{\text{WAD}}}={\sum }_{i}{\sum }_{j}{\sum }_{k}P\left({u}_{i},{V}_{{\text{true}},j},{\theta }_{{\text{true}},k}\right)\times {\epsilon }_{i,j,k}$$
(25)

2.6 Route optimization

The performance of wind sails depends on environmental conditions significantly and this makes which direction to follow to harvest the maximum amount of power from the wind quite important. An optimization problem was defined to understand how route optimization and simultaneous control of sailing system control variables (angle of attack or spin ratio) affect power consumption. Route control points, \({x}_{i}\), were defined as deviations from the straight path from the start point to the end point of the route as shown in Fig. 7. The length of the route was assumed to be 105 m and the upper and lower bounds of design variables, \({x}_{i}\), were assumed to be ± 105 m. Wind and wave conditions were assumed to be constant during simulations. The formulation of the optimization problem was given in Eq. 26

$$\begin{array}{*{20}c} {\mathop {\min }\limits_{{\mathbf{x}}} f_{{\left( {\varvec{x}} \right)}} = \int\limits_{0}^{{T_{{{\text{final}}}} }} {\left( {P_{{{\text{Propeller(}}t,x{)}}} + P_{{{\text{WAD(}}t,x{)}}} \,} \right)dt} } \\ {{\text{ subject to}} - 10^{5} \le x_{i} \le 10^{5} {\text{where i}} = 1,{ }2,{ }3} \\ \end{array}$$
(26)
Fig. 7
figure 7

Design variables of the route optimization problem

Full size image

3 Results

In the present study, the dynamics of wind-assisted ships were investigated by using a system modeling approach in MATLAB R2022b/Simulink. First, the controller parameter, \({T}_{{\text{ref}}}\), and coefficients of PID controllers were tuned to ensure that the ship follows the given trajectory. Different \({T}_{{\text{ref}}}\) values were tested on the given route and trajectory following performances were investigated as given in Fig. 8. When \({T}_{{\text{ref}}}\) is low, the ship leaves the route for some time and balances itself again. On the other hand, high \({T}_{{\text{ref}}}\) caused the ship to have a larger error around control points. It was found that tracking performance was the best at \(T_{{{\text{ref}}}} = 100 s.\)

Fig. 8
figure 8

The effect of different \({T}_{{\text{ref}}}\) values on the trajectory following performance

Full size image

Then, each component that generates force was considered separately, and interactions between environmental effects and each component were examined. First, a constant wind condition, so that true wind speed is 15 m/s and true wind direction is 90 degrees, was created for the ship traveling along a straight line at 7 m/s. Responses of propeller speed, rudder angle, ship speed, and wind assistance systems were given in Figs. 9 and 10. The initial propeller speed was specified considering the case without wind, wave, and sailing system. When the wind comes at 90 degrees, the required thrust by the propeller decreases and propeller speed reduces slightly. The existence of a rigid wind sail or rotor sail creates propulsive power and reduces the thrust demand of the propeller. On the other hand, wind generates forces also along sway direction, and lateral forces are larger if wind assistance systems were used. The rudder angle is controlled to overcome lateral force. Thus, it is ensured that the ship follows a straight course at a constant speed. During the course of the ship, rigid wind sails and rotor sails adjust the angle of attack and spin ratio to maximize the thrust.

Fig. 9
figure 9

Propeller, rudder, ship speed, and wind sail response at the true wind speed of 15 m/s and true wind direction of 90 degrees with and without rigid wind sail

Full size image
Fig. 10
figure 10

Propeller, rudder, ship speed, and wind sail response at the true wind speed of 15 m/s and true wind direction of 90 degrees with and without rotor sail

Full size image

To understand how wind sails behave at different true wind speeds and directions, the percent reduction of energy consumption was obtained for ship speed of 7 m/s and true wind speeds of 5, 10, and 15 m/s between 0 and 360 degrees as given in Fig. 11. Whereas rigid wind sail gives maximum reduction around true wind direction of 80 degrees, rotor sail gives maximum reduction around true wind direction of 110 degrees. Although the rotor sail has one-tenth projected area of the rigid wind sail, the amount of energy consumption reduction was similar to that of rigid wind sails. On the other hand, the rigid wind sail system provided a reduction in energy consumption for a larger range of wind direction compared to the rotor sail. Rigid wind sails used backwind as thrust power in a more efficient way than rotor sails due to having a larger surface area.

Fig. 11
figure 11

The percent reduction of energy consumption at different true wind speeds and directions

Full size image

The position of the wind-assisted systems on ships may also affect the reduction of propeller power consumption. For this purpose, the performance of wind-assisted ships where rigid wind sails were mounted at front (\(x_{{{\text{Sail}}}}^{\prime } = 0.4\)), middle (\(x_{{{\text{Sail}}}}^{\prime } = 0\)), and back (\(x_{{{\text{Sail}}}}^{\prime } = - 0.4\)) were investigated. The percent reduction of energy consumption was calculated for the true wind speed of 10 m/s and wind angles between 0 and 360 degrees as given in Fig. 12. It was that the position of sailing systems did not affect the amount of energy consumption significantly in any wind direction.

Fig. 12
figure 12

The effect of positions of rigid wind sails on the performance

Full size image

The amount of force generated by sailing systems depends on the apparent wind speed and apparent wind direction. Ship speed is therefore important as much as true wind speed and direction. The percent reduction of energy consumption was obtained for ship speeds of 5 and 7 m/s as given in Fig. 13. It can be clearly said that speed reduction significantly reduces total energy consumption. The effect of speed reduction from 7 m/s to 5 m/s was almost the same as adding one more sailing.

Fig. 13
figure 13

The effect of ship speed on the percent reduction of energy consumption

Full size image

In addition to the wind, waves also have a significant effect on the performance of ship propulsion. Therefore, the percent reduction in energy consumption including both wave and wind effects was compared to performance evaluation considering only the effect of wind. True wind speed, significant wave height, and wave period were determined based on the Beaufort scale as shown in Table 2. Wind and wave direction was assumed to be the same, and the propeller power was obtained between 0 and 360 degrees of true wind direction. The percent reduction in energy consumption considering both wind and wave effects and considering only wind effect were given in Fig. 14. According to Fig. 14, the percent reduction of energy consumption was found to be quite similar in both cases. However, the effect of wave increases at higher Beaufort scale values.

Table 2 Wind speed, wave height, and wave period at Beaufort scales of 4, 5, and 6
Full size table
Fig. 14
figure 14

The effect of considering forces related to wave at different Beaufort scales

Full size image

The overall performance of wind-assisted ships was predicted based on probabilistic way. The scenario database contains various ship speeds, true wind speeds, and directions as given in Table 3. The probability of true wind speed, true wind direction, and ship speed for the ship route was assumed as given in Fig. 15.

Table 3 The scenarios that consider different ship speeds, wind speeds and wind directions
Full size table
Fig. 15
figure 15

The probability of wind speed, wind direction, and ship speed

Full size image

The overall reductions of energy consumption generated by a single rigid wind sail and rotor sail were found as 3.07% and 1.97% respectively, based on the probability given in Fig. 15. To achieve a higher reduction in energy consumption, the number of sails can be increased. For this purpose, the overall reduction of energy consumption was obtained for different numbers of sails as shown in Fig. 16. It can be said that the reduction of energy consumption can reach 20% on average when the number of sails were increased to 10. It should be noted that the relation between the number of sails and percent reduction in energy consumption is not linearly increasing.

Fig. 16
figure 16

The effect of increasing the number of sails on the reduction of energy consumption

Full size image

In addition to the investigation of sailing performance during a straight path, it is also important to predict how routing can improve the reduction of energy consumption further. Although sail systems reduce energy consumption in general, total energy consumption may increase depending on the environmental conditions. For example, when a ship encounters an upwind condition, sails cannot generate any thrust force and causes additional resistive forces. For this purpose, a scenario having an upwind condition at 20 m/s was created to find optimal routing for rigid wind sail and rotor sail considering the ship dynamics including resistance during maneuvering. Ship speed was fixed at 6 m/s, and 4 rotor sails (height of 30 m and diameter of 5 m) and 4 rigid wind sails (height of 50 m and width of 30 m) were considered as wind assistance systems. Then, optimal routes were found for both sailing systems as shown in Fig. 17. Ship which is equipped rigid sails deviated from straight route more than the ship having rotor sails. Compared to a ship without any sailing system, rotor sails and rigid wind sails increased the total energy consumption by 6.8% and 0.6% under upwind condition. When the route was optimized, the performances of both wind sails were improved. The amount of increase in energy consumption was reduced from 6.8% to 3.1% for a ship having rotor sails under upwind condition whereas the ship having rigid wing sails caused a 15.9% decrease in energy consumption compared to the ship having no sails. Although a significant amount of power reduction was achieved in the case of rigid wind sails, the voyage time was increased significantly due to increasing traveled distance. During the simulations, the angle of attack and the spin ratio of sailing systems were optimized at each time step to maximize the thrust generation.

Fig. 17
figure 17

a Optimal routes and b, c power consumption of ship with rigid wind sail and rotor sail. d, e variation of the angle of attack and the spin ratio through route

Full size image

4 Discussion

Wind sails are one of the promising solutions to reduce the CO2 emission of ships. In the present study, the performances of rigid wind sails and rotor sails were investigated under different environmental conditions. Each component that generates forces was modeled based on a system modeling approach to predict the performance of different sail systems. Through a system model of ship dynamics in 3 degrees-of-freedom, the interactions between propeller, rudder, hull dynamics, and wind-assisted device were investigated.

Wind-assisted ship system was modeled based on model-based design approach, as shown in Fig. 6. First, each component of the system, such as propeller, sailing system, etc. was created and combined to investigate the overall ship system performance. Then, rudder and propeller speed rate controllers were designed to follow given route. In addition to motion controllers, sailing system controllers were created to provide the maximum performance from sails. The reason why model-based design approach was adopted is to consider the interaction between components and obtaining overall system response depending on the component design parameters. In addition, the model-based design of wind-assisted ship system forms a general design platform for future studies to optimize the performance of subsystems and overall ship system through combining high fidelity subsystem models and overall ship system model.

In the present study, the performance of wind-assisted ships was investigated using time domain solutions unlike previous studies which focus on solving equilibrium equations [10, 20]. The main reason why time domain solutions were chosen is that subsystems and controllers interact dynamically with each other under disturbance of wind and wave. Time domain analysis of ship system provides a transient response of each subsystem, allows to build controllers to follow given trajectory which is necessary to conduct a fair comparison of different sailing systems, and gives more accurate results by including acceleration terms especially during route optimization. Besides, the fluctuation of wind and wave, which will be considered in future studies, leads to fluctuations in other subsystems and it makes time domain solutions necessary to evaluate the performance of ship for real case conditions.

To conduct a fair comparison among wind sail systems, controllers were designed to follow straight route under different environmental conditions. The value of \({T}_{{\text{ref}}}\) was used to determine the reference position and it affected the performance of tracking significantly as shown in Fig. 8. Low \({T}_{{\text{ref}}}\) values make speed error more sensitive and cause instability. On the other hand, high \({T}_{{\text{ref}}}\) values resulted in large errors around the corners due to a larger distance between the reference ship and the actual ship. Whereas the rudder angle controller adjusted the position of the ship to follow the path under the external effects of wind and waves acting on the ship and sailing system, the propeller speed controller adjusted the thrust force required to keep ship speed constant as shown in Figs. 9 and 10. Thus, the conditions with and without wind assistance were compared fairly and the reduction in propeller power generated by wind assistance was obtained.

The performances of rigid wind sail and rotor sail showed different characteristics depending on the true wind angle according to Fig. 11. The maximum percent reduction in energy consumption was achieved at around 80 degrees in rigid sail and 100 degrees in rotor sail. The force generation capacity of sailing systems depends on apparent wind speed and lift/drag coefficients. Although the apparent wind speed is lower around 100 degrees, rotor sails produce larger thrust forces due to having a larger range of lift coefficient depending on the spin ratio. Thus, rotor sails can generate maximum thrust force around 100 degrees by increasing the lift coefficient significantly although apparent wind speed drops. On the other hand, rigid wind sails have a smaller range of lift coefficient, and the maximum percent reduction was obtained where the apparent wind speed is higher. Another different behavior was observed when the wind is coming from the back. Due to having a larger surface area, rigid wind sails produce larger thrust forces. Moreover, the disadvantage of having a larger surface area under opposite wind condition can be reduced using a retractable design.

The position where the wind-assisted device was mounted was found to have a negligible effect on the reduction of energy consumption according to Fig. 12. When wind conditions were considered the same over the ship, mounting sails away from the mid-ship causes an additional yaw moment and rudder angle is adjusted to follow the route. Therefore, the resistive forces generated by the rudder change, and only small variations in energy consumption occur.

In addition to sailing system parameters, ship speed also significantly affects the energy consumption of ships. According to Fig. 13, the amount of reduction in energy consumption significantly increases when ship speed is reduced from 7 m/s to 5 m/s. Because, when ship speed was reduced, the amount of required thrust dropped, and propeller power diminished. Besides, the ratio of thrust obtained by wind sails to the total required thrust increased. Thus, propeller speed and energy consumption were reduced significantly.

The effect of waves on the performance of wind-assisted ships was investigated by comparing the percent reduction in energy consumption of propeller. It appeared that the effect of considering forces related to waves was not significant for environmental conditions at lower Beaufort scales. However, it becomes clearer starting from the Beaufort-7 scale according to Fig. 14. If the existence of strong wind and higher waves shows a correlation, it is necessary to consider the wave effect through the optimization process of route of wind-assisted ships. Also, since the effect of waves increases significantly at higher Beaufort scales, strong winds are not desirable always and there will be an optimal wind speed that different sailing systems perform best. In the present study, the directions of wind and wave were assumed to be the same, but there might be some differences in fact.

According to Fig. 16, the reductions in energy consumption of propeller of ships equipped with single rigid wind sail and rotor sail were found as 3.07% and 1.97%, respectively. Compared to the previous studies, the amount of reduction in energy consumption was lower due to the ratio of ship size and sail size. Ouchi et al. investigated the effect of using 9 rigid wind sails, each having a sail area of 1000 m2, on a bulk carrier with 180,000 DWT and reached 22% power reduction on Great Circle when ship speed is constant [14]. Kramer and Steen investigated different design and control alternatives for wind-assisted ship having 5000 DWT and fuel saving was predicted between 17 and 65% with varying speeds between 8 and 12 knots and varying wind sail area between 784 m2 and 3920 m2 [19]. Viola et al. considered implementing a multi-element rigid wind sail on KVLCC2M ship and the effects of the number of sails, ship speed, and wind speed were considered. It was concluded that an approximately 10% reduction in propeller thrust was achieved at a slower speed and higher sail area [13]. Tilling and Ringsberg found that six rotor sails can provide up to 30% reduction for a tanker having 50,600 DWT on the Pacific Ocean route [8]. It can be concluded that the amount of reduction in energy consumption depends on many factors based on the results obtained in the present study and previous works. In addition to the design and control of wind sails, the size and speed of ship affect the reduction of energy consumption. Therefore, the design of ship and sailing system should be considered together to use wind power more efficiently.

The effect of increasing the number of sails was handled by increasing the wing area without considering the interaction between sails. According to Fig. 16, when the number of sails increased, the percent reduction of energy consumption also increased but at a lower rate than the number of sails due to propeller characteristics and nonlinear hydrodynamic resistance. It was found that the amount of energy consumed by propeller reduction reaches 22.8% and 16.03% for 10 rigid wind sails and rotor sails, respectively. However, there are geometrical limits and larger interaction effects to build many rigid wind sails or rotor sails. It can be said that there is a need to optimize the shape of wind sails or rotor sails to achieve a higher reduction in energy consumption, especially for larger ships.

The average performances of wind sails were predicted by assuming different scenarios and the probability of each. The change in the route affects the probability of each scenario and the performance of wind sails can be further improved. Unlike conventional ships, wind-assisted ships should adjust their route where higher wind power can be harvested. Therefore, it is necessary to consider route optimization conducted for specific to wind-assisted ships. Route optimization improved the performance of sailing systems under upwind conditions, according to Fig. 17. The ship having rigid wind sails showed a large deviation from a straight path to minimize the energy consumption and voyage time increased. On the other hand, ships having rotor sails showed less deviation. Considering the rotor sails performance in head wind conditions, the result is seemingly contradictory because ships having rotor sails should deviate much larger than ships with rigid wind sails to reduce power. However, the obtained result oppositely showed less deviation through the integral evaluation of the voyage time and the total energy consumption. In both sailing systems, a lot of effort is required to understand the potential of route optimization under different conditions. The scope of the study will be extended to route optimization to harvest the wind power efficiently depending on sailing systems and different weather conditions.

In the present study, different aspects of rigid wind sails and rotor sails were investigated. However, the performance of sailing systems also depends on the ship. Through updating ship and sail parameters, the performance of different sailing systems on different ships can be obtained to understand how much a sailing system can contribute to reduction in energy consumption. Moreover, the performance of sailing systems can be further increased by optimizing the route of ship and the design of the sailing system. Besides, there are some limitations of the existing model. For example, when a tower-like sailing system was mounted on the ship, forces in surge and sway direction will generate a considerable amount of moment in roll and pitch direction. In future studies, the existing model should be extended to six degrees-of-freedom model to consider roll, pitch, and heave motions as well. Also, the inertial effects of sailing systems and interaction between sails were not taken into account.

5 Conclusion

The present study investigates the effect of wind sail systems on ship dynamics and propeller power consumption using the model-based design approach. The interaction between each subsystem was considered, and controllers for propeller speed and rudder angle were designed to compare wind-assisted ships and conventional ships. We have conducted several simulations to understand the effect of wind speed, wind angle, wave, ship speed, and the type and position of wind sails. It was found that rigid wind sails and rotor sails have different characteristics at different wind angles. Both sailing systems generated a higher reduction in energy consumption of propeller when wind speed increased. On the other hand, the existence of strong wind shows some correlation with higher waves, which increases energy consumption. Therefore, it is quite necessary to conduct route optimization specific to wind-assisted ships to determine how the ship route changes depending on the conditions of wind and waves. The overall performances of using a single rigid sail and single rotor sail were found as 3.07% and 1.97% based on the different scenarios and their probabilities. When the number of sails was increased to 10, the reduction in energy consumption of propeller was 22.8% and 16.03% for rigid wind sails and rotor sails, respectively. It was concluded that the optimization of the shape of the sail system is necessary to achieve higher reduction of energy consumed by propeller.