Effect of Engine Output on Maneuverability of a VLCC in Still Water and Adverse Weather Conditions

Abstract

In this study, an MMG-based maneuvering simulation method (Yasukawa and Yoshimura, J Mar Sci Technol 20(1):37–52, 1) was used to investigate the maneuverability of a VLCC in still water and adverse weather conditions. Specifically, the investigation involved a situation where the engine output of a VLCC was significantly reduced owing to advances in energy-saving technology. First, a VLCC with 30% reduced Energy Efficiency Design Index (EEDI) (IMO MEPC 63/23, Annex 8, Resolution MEPC.212(63), 2012 guidelines on the method of calculation on the attained EEDI for New Ships, 2) (Step3) is actually planned to the conventional VLCC (Step0) by adoption of energy efficiency devices, a large-diameter and low-revolution propeller, etc. Next, maneuvering simulations of two ships (Step0 and Step3) were performed in still water and adverse weather conditions. It was observed that Step3 satisfied IMO maneuvering criteria in the still water condition. However, the maneuverability of Step3 was worse than that of Step0 since the rudder force was reduced owing to the low propeller load, which resulted from the small engine output. Additionally, steady-state sailing performance of Step3 in adverse weather conditions, such as check helm, hull drift angle, and speed drop, generally worsened when compared with those of Step0. Furthermore, course changing ability also deteriorated in the case of Step3. However, the difference between the trajectories of Step0 and Step3 reduced with respect to the large Beaufort scale since the difference in the rudder force became less noticeable owing to the presence of large external lateral forces caused by strong winds and waves.

1 Introduction

Advances in energy savings with respect to ships have led to expectations involving the evolution of ships with a small main engine. Small engine output generally results in a power margin loss relative to external disturbances such as wind and waves. Additionally, small engine output leads to a low propeller load and thereby reduces the rudder force. Therefore, an excessive reduction in the engine output will result in a potentially unexpected unsafe situation wherein a helms man may not be able to maneuver the ship well in adverse weather conditions [1, 2].

Hirano et al. [3] investigated ship maneuverability in regular waves by the simple prediction method where only wave-induced steady forces are considered as the wave effect to a time domain simulation method. Yasukawa et al. [4] presented a practical integrated motion simulation method which can calculate both maneuvering and wave-induced motions and to verify the calculation accuracy, the simulation results were compared with the model test results for a S175 container ship model in regular waves. Yoshimura et al. [5] and Hasegawa et al. [6] investigated maneuverability of a Pure Car Carrier in wind by a time domain simulation method. Nagarajan et al. [7] investigated maneuverability of a large tanker with the Mariner Schilling Rudder in strong wind. However, they never mentioned the engine output effect on the ship maneuverability in adverse weather conditions.

Takahashi and Asai [8] investigated maneuverability in severe weather conditions for a full hull ship with a length of 300 m while varying the design speed as 16, 13, and 10 knots in conjunction with appropriate reductions in the engine output. The results indicated that a lower powered ship has larger speed loss and poorer course keeping ability when compared with a higher powered ship in stormy conditions. Although the results of the aforementioned study are useful, the fundamental precondition of the study in question is different from that of the present study. The present study involves a case in which engine output is reduced owing to advances in energy-savings given the same design speed. Conversely, Takahashi and Asai examined a case in which engine output was reduced with decreases in the design speed. Additionally, the study by Takahashi and Asai did not consider the impact of specific maneuvering motions such as turning and zig-zag maneuvers.

This study examined a situation in which the engine output of a VLCC was reduced due to the progress of the energy-saving and used an MMG-based maneuvering simulation method [1] to investigate the maneuverability of the VLCC in still water and adverse weather conditions. It may be noted that the prediction accuracy of the simulation method was sufficient for practical use [1, 9]. First, a VLCC with 30% reduced Energy Efficiency Design Index (EEDI) [2] was proposed instead of a conventional VLCC by employing energy efficiency devices, a large-diameter and low-revolution propeller. In the study, the VLCC with 30% reduced EEDI is referred to as Step3, and the conventional VLCC is referred to as Step0. The engine output of Step3 was inevitably smaller than that of Step0. Next, maneuvering simulations for Step0 and Ship3 in still water and adverse weather conditions were performed. The effect of the engine output on maneuverability was discussed based on the calculation results from a navigation safety viewpoint.

2 Studied ship

2.1 Principal particulars of a target ship

In this study, the target ship was a VLCC titled KVLCC2 [10] for which hull form data were previously published. Table 1 shows the principal particulars, and Fig. 1 illustrates the body plan. In the table, L denotes length between perpendiculars, $L_{wl}$ denotes the length waterline, B denotes the breadth, D denotes the depth, d denotes the draft, $\nabla$ denotes the displacement volume, S denotes the wetted surface area, $x_{G}$ denotes the longitudinal position of center of gravity (fore position from the midship was positive), and $C_{b}$ denotes the block coefficient. The load condition involved a full load even keel.

Table 1 Principal particulars of a target ship (KVLCC2)

Fig. 1

Body plan of a target ship (KVLCC2)

The ship possessed a Mariner rudder. Table 2 shows the principal particulars of the rudder. In the table, $H_{R}$ denotes span of the rudder, $B_{R}$ denotes the averaged chord of the rudder including horn, $A_{R}$ denotes the rudder area of the movable part, and $\Lambda$ denotes the aspect ratio.

Table 2 Principal particulars of the rudder

Figure 2 shows the side and front views including the super-structure of the target ship. The configuration and arrangement of the super-structure was estimated based on an existing VLCC tanker with a similar size since no actual fullscale ship corresponding to KVLCC2 was available. The front wind pressure area $A_{X}$ corresponds to 1161 m$^2$, and the profile wind pressure area corresponds to $A_{Y}$ 4258 m$^2$.

Fig. 2

Side and front views of a VLCC

2.2 Initial design for improving the propulsive performance

An improvement of the EEDI (or the propulsive performance) was performed based on the KVLCC2 by employing the following technologies:

• a low-revolution engine and large-diameter propeller,

• a low-output engine with electronic control,

• energy-saving devices, such as Pre-Swirl Fin and Rudder Bulb Fin, to improve self-propulsion factors, and

• low frictional resistance paint and air lubrication technology to reduce hull frictional resistance.

Further, it was assumed that there were no changes in the main particulars and the hull form of the ship except for the propeller characteristics.

Table 3 shows a summary of EEDI, the main engine output, the propeller revolution, and other details for Step0 and Step3. In the study, Step0 corresponds to a conventional VLCC that was the base ship and Step3 corresponds to a VLCC with 30% reduced EEDI.

Table 3 Summary of the basic concept involved in reducing EEDI

Table 4 shows the estimated self-propulsion factors and roughness allowance $\Delta C_{f}$ in addition to the designed propeller particulars. In the table, $D_{P}$ denotes the propeller diameter, p denotes the propeller pitch ratio, $A_e/A_{d}$ denotes the expanded area ratio, Z denotes the number of blades, $t_{P}$ denotes the thrust deduction factor, $w_{P}$ denotes the wake fraction, and $\eta _{R}$ denotes the relative rotative efficiency. The propeller was designed such that it could achieve a ship speed of 15.5 knots in the normal output (NOR) with 15% sea margin based on the existing propeller diagram. Changes in the self-propulsion factors due to the installation of energy-saving devices were determined based on prior experience of the authors of the present study. Moreover, $\Delta C_{f}$ was reduced to account for the reduction in hull frictional resistance due to air bubbles.

Table 4 Designed propeller particulars, estimated self-propulsion factors, and $\Delta C_{f}$

Figure 3 shows a wave-making resistance coefficient curve ($C_{ws}$) based on wetted surface area. The horizontal axis corresponds to the Froude number $F_{nwl}$ based on the length waterline $L_{wl}$. The Hughes formula was used to predict the frictional resistance coefficient, and the form factor K was assumed as 0.40. Thus, the wave resistance coefficient and the form factor were same for Step0 and Step3 given that the hull form was the same.

Fig. 3

Wake-making resistance coefficient curve

Figure 4 shows the BHP curves of Step0 and Step3 versus the ship speed. The transmission efficiency was assumed as 0.97. A significant reduction in the engine output of Step3 was observed due to the improvements in the EEDI. In the study, ship maneuverability was investigated for two ships with Step0 and Step3.

Fig. 4

Estimated BHP curves

3 Outline of the maneuvering simulation method

The MMG-based time domain simulation method [1, 9] is used for the investigation. The outline of the simulation method is described in this section.

3.1 Coordinate systems

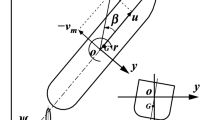
Figure 5 shows the coordinate systems used in this study. Specifically, the space-fixed coordinate system was denoted as $o_0-x_0y_0z_0$, where the $x_0-y_0$ plane coincided with the still water surface, and the $z_0$-axis pointed vertically downward. The moving ship-fixed coordinate system was denoted as $o-xyz$ in which o was considered on the midship of the ship, and x, y, and z-axes pointed toward the ship’s bow, i.e., toward the starboard and vertically downward, respectively. The heading angle $\psi$ was defined as the angle between the $x_0$ and x-axes. Furthermore, $\delta$ denoted the rudder angle, and r denoted the yaw rate. Additionally, u and $v_{m}$ denoted the velocity components in x and y directions, respectively, and the drift angle at the midship position was defined by $\beta (= \tan ^{-1}(-v_{m}/u))$. The total velocity corresponded to U($=\sqrt{u^2+v_{m}^2}$).

The main wave propagation direction is denoted as $\chi$ as shown in Fig. 5. Then, relative wave direction $\chi _0$ is defined as $\chi _0 \equiv \chi -\psi$. The head wave of the ship is defined as $\chi _0=0^{\circ }$, the beam wave as $\chi _0=90^{\circ }$, and the following wave as $\chi _0=180^{\circ }$. The wind direction $\theta _W$ is assumed to be same as the wave direction $\chi$.

Fig. 5

Coordinate systems

3.2 Motion equations

The motion equations with respect to surge, sway, and yaw are expressed as follows [1]:

$$\left.\begin{aligned}(m+m_{x})\dot{u} - (m+m_{y})v_{m}r -x_{G}mr^2 = X \\ (m+m_{y})\dot{v}_{m} + (m+m_{x})ur + x_{G}m\dot{r} = Y \\ (I_{{zG}}+x_{G}^2m+J_{{z}})\dot{r} + x_{G}m(\dot{v}_{m}+ur)= N \end{aligned} \right\} $$

(1)

where m denotes ship’s mass, $I_{zG}$ denotes the moment of inertia around center of gravity, $m_{x}$ and $m_{y}$ denote the added masses of x-axis direction and y-axis direction, respectively, and $J_{z}$ denotes the added moment of inertia. Equation (1) denotes the equations of motion to be solved. The unknown variables corresponded to u, $v_{m}$, and r. Additionally, X, Y, and N in the right-hand side of Eq. (1) denote the surge force, lateral force, and yaw moment around midship except added mass components, respectively, and are expressed as follows:

$$\begin{aligned} \left. \begin{array}{lll} X&{}=&{} X_{H} + X_{R} + X_{P} +X_{W} + X_A\\ Y&{}=&{} Y_{H }+ Y_{R} +Y_{W} + Y_A \\ N&{}=&{} N_{H} + N_{R} +N_{W} + N_{A} \end{array} \right\} \end{aligned}$$

(2)

Here, subscripts H, R, and P denote hull, rudder, and propeller, respectively. The forces with subscripts H, R, and P could be predicted using the MMG standard method [1].The subscript W denotes the wave-induced steady forces in irregular waves, and A denotes the wind forces. By solving the equation of motion, i.e., Eq. (1), it was numerically possible to determine the maneuvering motions of the ship.

3.3 Wave-induced steady forces

The wave-induced steady forces in irregular waves ($X_{W}, Y_{W}, N_{W}$) are expressed as follows:

$$\begin{aligned} \left. \begin{array}{lll} X_{W} &{}=&{} \rho gH_{1/3}^2L\, \overline{C_{{XW}}}(U, T_{v}, \chi _0) \\ Y_{W} &{}=&{} \rho gH_{1/3}^2L\, \overline{C_{{YW}}}(T_{v}, \chi _0) \\ N_{W }&{}=&{} \rho gH_{1/3}^2L^2\, \overline{C_{{NW}}}(T_{v}, \chi _0) \end{array} \right\} \end{aligned}$$

(3)

where $\rho$ denotes water density, $H_{1/3}$ denotes the significant wave height, and g denotes the gravity acceleration. The averaged wave-induced added resistance coefficient in irregular waves ($\overline{C_{{XW}}}$) is expressed as a function of ship speed (denoted as U), averaged wave period (denoted as $T_{v}$), and relative wave direction (denoted as $\chi _0$). The speed effect on $\overline{C_{{XW}}}$ cannot be neglected. In contrast, the speed effect on the averaged wave-induced steady lateral force and yaw moment coefficients in irregular waves ($\overline{C_{{YW}}}$, $\overline{C_{{NW}}}$) is assumed as negligible [11]. Then, $\overline{C_{{YW}}}$ and $\overline{C_{{NW}}}$ are expressed as a function of $T_{v}$ and $\chi _0$. The averaged value of wave-induced steady force coefficients in irregular waves are calculated by applying the short-term prediction technique based on the wave-induced steady force coefficients in regular waves as follows:

$$\begin{aligned} \left. \begin{array}{lll} \overline{C_{{XW}}}(U, T_{v}, \chi _0) &{}=&{} 2{\displaystyle \int _{-\pi }^{\pi }}G(\theta )\text {d}\theta {\displaystyle \int _{0}^{\infty }}C_{{XW}}(U, \omega , \chi _0)\dfrac{S_{\zeta \zeta }(\omega )}{H_{1/3}^2}\text {d}\omega \\ \overline{C_{{YW}}}(T_{v}, \chi _0) &{}=&{} 2{\displaystyle \int _{-\pi }^{\pi }}G(\theta )\text {d}\theta {\displaystyle \int _{0}^{\infty }}C_{{YW}}(\omega , \chi _0)\dfrac{S_{\zeta \zeta }(\omega )}{H_{1/3}^2}\text {d}\omega \\ \overline{C_{{NW}}}(T_{v}, \chi _0) &{}=&{} 2{\displaystyle \int _{-\pi }^{\pi }}G(\theta )\text {d}\theta {\displaystyle \int _{0}^{\infty }}C_{{NW}}(\omega , \chi _0)\dfrac{S_{\zeta \zeta }(\omega )}{H_{1/3}^2}\text {d}\omega \end{array} \right\} \end{aligned}$$

(4)

where $S_{\zeta \zeta }(\omega )$ denotes the wave spectrum, and $G(\theta )$ denotes the wave direction distribution function. $C_{{XW}}$, $C_{{YW}}$, and $C_{{NW}}$ denote the wave-induced steady force coefficients in regular waves, and $C_{{XW}}$ and $C_{{YW}}$ are non-dimensionalized through the division by $\rho gh_a^2L$ where $h_a$ denotes amplitude of incident waves, and $C_{{NW}}$ is non-dimensionalized through the division $\rho gh_a^2L^2$.

The following procedure was employed in the actual simulations: prior to the simulations, a database of wave-induced steady force coefficients in irregular waves ($\overline{C_{{XW}}}$, $\overline{C_{{YW}}}$, $\overline{C_{{NW}}})$) was provided as the functions of U, $T_{v}$, and $\chi _0$. The steady forces at the moment of the maneuvering motion were estimated in the time domain by an interpolation technique based on the database [9].

3.4 Wind forces

Based on the assumption of steady and constant wind, the surge force, lateral force, and yaw moment due to the wind ($X_{A}, Y_{A}, N_{A}$) are expressed as follows:

$$\begin{aligned} \left. \begin{array}{lll} X_{A} &{}=&{} (1/2)\rho _{a} A_{X }V^2_{A}\, C_{{XA}}(\theta _{A}) \\ Y_{A }&{}=&{} (1/2)\rho _{a} A_{Y} V^2_{A}\, C_{{YA}}(\theta _{A}) \\ N_{A }&{}=&{} (1/2)\rho _{a }A_{Y}L\, V^2_{A}\, C_{{NA}}(\theta _{A}) \end{array} \right\} \end{aligned}$$

(5)

where

$$\begin{aligned} \theta _{A }= & {} \tan ^{-1} (v_{A }/u_{A }) \end{aligned}$$

(6)

$$\begin{aligned} V_{A}= & {} \sqrt{u^2_{A } + v^2_{A }} \end{aligned}$$

(7)

$$\begin{aligned} u_{A }= & {} u+U_{W }\cos (\theta _{W}- \psi ) \end{aligned}$$

(8)

$$\begin{aligned} v_{A }= & {} v_{m}+U_W \sin (\theta _{W}- \psi ) \end{aligned}$$

(9)

Here, $\rho _{a}$ denotes air density, $V_{A}$ denotes the relative wind speed, $U_{W}$ denotes the absolute wind speed, $\theta _{A}$ denotes the relative wind direction, and $\theta _W$ denotes the absolute wind direction. $C_{{XA}}$, $C_{{YA}}$, and $C_{{NA}}$ denote the aerodynamic force coefficients expressed as a function of the relative wind direction (denoted by $\theta _{A}$).

3.5 Torque limit line

A large load could act on the main engine in a severe sea. To avoid an undesirable situation, the propeller revolution was controlled such that it did not exceed a propeller torque limit. In accordance with a previous study Ref. [12], the limit line is expressed as follows:

$$\begin{aligned} P_{B}= & {} \min (P_{\text {BMEP}}, P_{\text {BOLP}}) \end{aligned}$$

(10)

where $P_{B}$ denotes the main engine output. Averaged effective pressure limit $P_{\mathrm{BMEP}}$ is expressed as follows:

$$\begin{aligned} P_{\text {BMEP}}= & {} \mathrm{MCR}\frac{N_{E}}{N_{\text {MCR}}} \end{aligned}$$

(11)

where $N_{E}$ denotes the engine revolution. Overload protection limit $P_{\mathrm{BOLP}}$ is expressed as follows:

$$\begin{aligned} P_{\mathrm{BOLP}}= & {} \alpha ^{1-\Gamma }\mathrm{MCR}\left( \frac{N_{E}}{N_{\mathrm{MCR}}}\right) ^{\Gamma } \end{aligned}$$

(12)

Here, $\alpha =0.967$ and $\Gamma =2$ were used. Figure 6 shows the torque limit lines for Step0 and Step3, which were obtained by the present model.

Fig. 6

Torque limit lines

4 Maneuvering in still water

The hydrodynamic force coefficients on maneuvering examined in a previous study Ref. [1] were used to conduct maneuvering simulations for both Step0 and Step3.

4.1 Turning

Figure 7 shows a comparison of turning trajectories between Step0 and Step3 given a rudder angle of $\pm 35{^{\circ }}$. The approach speed $U_0$ corresponded to 15.5 knots. Table 5 shows a comparison of turning indexes, advances ($A_{d}$), and tactical diameters ($D_{t}$). The turning radius increases in Step3 when compared with that of Step0, and $A_{d}$ and $D_{t}$ increased 14 and 12%, respectively, as averaged value of port and starboard turning. The reduction in the rudder normal force ($F_{N}$) is the reason for the deterioration in the turning performance. Figure 8 shows a comparison of the time histories of the rudder normal force during turning. The time history of $F_{N}$ in Step3 was smaller than that in Step0 at the peak that appeared immediately after steering and the steady turning condition. This was due to the low propeller load that resulted from the small engine output. Although the turning performance worsened in Step3, the turning indexes ($A_{d}$, $D_{t}$) still satisfied the IMO maneuvering criteria [13] as shown in Table 5. The turning performance of Step3 was not at a potentially problematic level.

Fig. 7

A comparison of the turning trajectories in still water ($\delta$=±35 deg)

Table 5 A comparison of turning indexes

Fig. 8

Comparison of time histories of rudder normal force during turning in still water ($\delta =35{^{\circ }}$)

4.2 Zig-zag maneuvers

Figure 9 shows the time histories of heading angle $\psi$ and rudder angle $\delta$ in 10 / 10 and $-10/-10$ zig-zag maneuvers in calm water. Additionally, Figure 10 shows the time histories of $\psi$ and $\delta$ during 20 / 20 and $-20/-20$ zig-zag maneuvers. The steering timing of Step3 was slower than that of Step0, and this implied that the response of Step3 had worsened. Tables 6 and 7 show the comparison of overshoot angle (OSA) during the zig-zag maneuvers. The OSA of Step3 was larger than that of Step0, and the course stability evidently worsened. Averaged value of the 1st OSA in the port and starboard side increased by 23 % in Step3, and the averaged value of 2nd OSA also increased by 43%. However, the zig-zag maneuvering performance was not at a potentially problematic level since the IMO maneuvering criterion [13] was fulfilled in Step3.

Fig. 9

Comparison of time histories of the heading angle ($\psi$) and rudder angle ($\delta$) in still water (left 10/10 zig-zag, right $-10/\!\!-\!\!10$ zig-zag)

Fig. 10

Comparison of time histories of the heading angle ($\psi$) and rudder angle ($\delta$) in still water (left 20/20 zig-zag, right $-20/\!\!-\!\!20$ zig-zag)

Table 6 Comparison of the overshoot angle of 10/10 and $-10/-10$ zig-zag maneuvers in still water

Table 7 Comparison of the overshoot angle of 20/20 and $-20/\!\!-\!\!20$ zig-zag maneuvers in still water

5 Maneuvering in adverse conditions

This was followed by performing maneuvering simulations in adverse weather conditions.

5.1 Data related to wind and waves

5.1.1 Wave-induced steady force coefficients in irregular waves

A theoretical method based on potential theory was used to predict the wave-induced steady force coefficients in regular waves, i.e., $C_{{XW}}$, $C_{{YW}}$, and $C_{{NW}}$. With respect to the zero speed case, $C_{{XW}}$, $C_{{YW}}$, and $C_{{NW}}$ were predicted by a 3D panel method [14]. A method based on strip theory [15] was used to consider the speed effect on the added resistance coefficients (denoted as $C_{{XW}}$). In strip theory framework, Maruo’s far field theory [16] was applied for added resistance prediction with the empirical correction of the added resistance in short wavelength proposed by Tsujimoto et al. [12]. As shown in Fig. 11, a database was made based on the results for the interpolation in the maneuvering simulations.

Figure 11 shows $\overline{C_{{XW}}}$ with different Froude numbers, i.e., $F_{n}=0.15$ and 0.0, and $\overline{C_{{YW}}}$ and $\overline{C_{{NW}}}$. In the calculations, the ITTC spectrum was used as the wave spectrum $S_{\zeta \zeta }$. The $\cos ^2$-function was used as the wave direction distribution function $G(\theta )$.

Fig. 11

Averaged wave-induced steady force coefficients in irregular waves

5.1.2 Aerodynamic force coefficients

Aerodynamic force coefficients $C_{{XA}}$, $C_{{YA}}$, and $C_{{NA}}$ were predicted using a method proposed by Fujiwara [17]. Figure 12 shows the coefficients of the target ship versus those of the relative wind direction $\theta _{A}$.

Fig. 12

Aerodynamic force coefficients

5.1.3 Wind and wave conditions: Beaufort scale

Based on the wind power class of the Beaufort scale (BF), the absolute wind speed (denoted as $U_{W}$), the significant wave height (denoted as $H_{1/3}$) and the averaged wave period (denoted as $T_{v}$) were determined as shown in Table 8. The wind and waves were assumed be constant with respect to time, and the wind direction ($\theta _{W}$) was same as the wave direction ($\chi$).

Table 8 Wind and wave conditions in the simulations

5.2 Steady-state sailing conditions

A ship traveling with a propeller revolution in the design speed under wind and waves was considered using the auto-pilot. In the auto-pilot, the PD control was applied with a proportional gain corresponding to 3.0 and a differential gain corresponding to 30.0 s. The ship course was set to be $\psi =0{^{\circ }}$. Figure 13 shows the longitudinal component of the ship speed (denoted as u), hull drift angle (denoted as $\beta$), and check helm (denoted as $\delta$) in the steady-state sailing condition under wind and waves. In the figure, for purposes of distinction, additional lines were placed to connect the calculation results. As expected, a significant decrease in speed occurred with the increase in the BF scale. The speed decrease for Step3 was slightly larger than that for Step0 with respect to head waves. With respect to the head waves of BF9, u was less than 8 knots in both Step0 and Step3, and the propeller revolution ($N_{P}$) decreased due to the restriction placed by the torque limit as shown in Fig. 6. Thus, the torque limit line model employed in this study worked well with the propeller revolution control. The $\beta$ and absolute value of $\delta$ increased with the increase in the BF scale. With respect to BF9, the maximum $\beta$ was approximately 2.9${^{\circ }}$ in Step0 and approximately 3.2${^{\circ }}$ in Step3, and the minimum $\delta$ was approximately $-7.3{^{\circ }}$ in Step0 and approximately $-10.6{^{\circ }}$ in Step3. The maximum $\beta$ and the absolute value of minimum $\delta$ were slightly larger in Step3. The largest $\beta$ occurred at approximately $\chi =75{^{\circ }}$, and the smallest $\delta$ occurred at approximately $\chi =90{^{\circ }}$. This tendency was the same for both Step0 and Step3. The drift angle and check helm were not very large in both Step0 and Step3, and the ship speeds reached approximately 6 knots in head wind and waves until BF9, even though the torque rich occurs (Fig. 14).

Fig. 13

Comparison of ship speed (u), drift angle ($\beta$) and check helm ($\delta$) in wind and waves

Fig. 14

Comparison of propeller revolution ($N_{P}$) in wind and waves

5.3 Course changing ability

Course changing simulations were performed by steering the rudder angle, $\delta =20{^{\circ }}$, in wind and waves. Figure15 shows a comparison of ship trajectories in BF7 and BF9. The direction of the wind and waves changed to $\chi =0{^{\circ }}$, 30${^{\circ }}$ and 60${^{\circ }}$. The steady-state speed shown in Fig. 13 was used as an approach speed in the simulation. A course change with a significant speed decrease was observed in BF9 since the situations involved the bow wind and waves. Figure 16 shows a comparison of the non-dimensional values of advance $A_{d}$ and transfer $T_{r}$ in the course changing with respect to the BF scale for the three different wave (wind) directions. It should be noted that “SW” shown in the horizontal axis of the figure denotes the still water. The results of $A_{d}$ and $T_{r}$ were smaller in Step0 when compared to those in Step3. Thus, Step0 indicated better maneuverability than Step3. This was because Step0 had a better turning performance in still water when compared with that of Step3 as discussed in Sect. 4.1. However, the difference between the trajectories (or $A_{d}$ and $T_{r}$) for Step0 and Step3 clearly decreased when the BF scale was large.

Fig. 15

Comparison of ship trajectories for course changing in wind and waves

Fig. 16

Comparison of $A_{d}$ and $T_{r}$ in wind and waves ($\delta =20{^{\circ }}$ deg)

Thus, time histories of the rudder normal force ($F_{N}$), the lateral force acting on the ship by the wind and waves ($Y_{A}+Y_{W}$), and the ratio ($F_{N}/(Y_{A} + Y_{W})$) during course changing in BF7 and BF9 were checked as shown in Fig. 17. Specifically, $F_{N}/(Y_{A}+Y_{W})$ denotes a ratio of the rudder normal force to the lateral force acting on the ship hull due to external disturbances such as wind and waves. A greater value of $F_{N}/(Y_{A}+Y_{W})$ indicates higher rudder effectiveness with respect to external disturbances. Additionally, $F_{N}$ of Step0 exceeded that of Step3 for both BF7 and BF9, and this tendency was the same as the result in still water as shown in Fig. 8. The difference of $Y_{A}+Y_{W}$ between Step0 and Step3 was small since the wind forces and the wave-induced steady forces were the same for both Step0 and Step3 in principle. As a result, $F_{N}/(Y_{A}+Y_{W})$ of Step0 exceeded that of Step3, and this tendency became significant in BF7. In contrast, with respect to BF9, the difference of $F_{N}/(Y_{A}+Y_{W})$ between Step0 and Step3 decreased. This was because $Y_{A}+Y_{W}$ showed a more significant increase in BF9 than BF7. Thus, it could be interpreted that the difference in the rudder force between Step0 and Step3 decreased due to the presence of large external lateral forces in terms of the strong wind and waves such as BF9. Thus, the course changing performance of Step3 became similar to that of Step0 with respect to strong external disturbances, although the turning performance of Step3 was worse in still water.

Fig. 17

A comparison of the rudder normal force ($F_{N}$), lateral force due to wind and waves ($Y_{A} + Y_{W}$), and ratio of $F_{N}$ to $Y_{A} + Y_{W}$ during course changing ($\chi =0$, $\delta =20{^{\circ }}$)

6 Concluding remarks

In this study, an MMG-based maneuvering simulation method [1] was used to investigate the maneuverability of a VLCC in still water and adverse weather conditions. Specifically, a situation was considered wherein there was a significant reduction in the engine output of the VLCC due to advances in energy-saving technology. First, a VLCC with 30% reduced EEDI (Energy Efficiency Design Index) [2] was proposed to replace a conventional VLCC by employing energy efficiency devices and a propeller with a large diameter and low revolution. The engine output of the VLCC with 30% reduced EEDI (Step3) evidently reduced when compared with that of a conventional VLCC (Step0). This was followed by performing maneuvering simulations of the ships in still water and adverse weather conditions. The effect of the engine output on the maneuverability was discussed based on the calculated results with respect to a navigation safety viewpoint. In summary, the study revealed the following findings:

• Maneuverability in still water: in Step3, both the turning radius and the overshoot angles of the zig-zag maneuver increased with improved EEDI when compared with those of Step0. This was because the rudder force reduced due to the low propeller load that was a result of the small engine output. Although the maneuverability worsened in Step3, the turning indexes and the overshoot angles satisfied the IMO maneuvering criteria [13]. The maneuverability of Step3 was not at a potentially problematic level.

• Maneuverability in adverse weather conditions: generally, the steady-state sailing performance of Step3 was worse than that of Step0. Specifically, speed drop, hull drift angle, and check helm of Step3 were slightly large. The course changing ability of Step3 also worsened in adverse weather conditions. However, the difference in the trajectories of Step0 and Step3 clearly reduced when the BF scale was large. This was because the difference of the rudder force between Step0 and Step3 decreased due to the presence of large external lateral forces in the strong wind and waves. Hence, the course changing performance of Step3 was at a similar level to that of Step0 in the presence of strong external disturbances.

In the simulations in the present study, problems that not comply with the IMO maneuvering criteria did not occur even though the engine output was reduced in Step3. This was because the subject ship (Step0) initially possessed good maneuverability, and there was a sufficient margin for the IMO criteria. Accordingly, if the main engine output was reduced (due to advances in energy-saving technology) based on a situation wherein a ship faced limitation in terms of the IMO criteria, there could be a possibility in which the maneuverability worsened until an unacceptable level was reached in terms of navigational safety by reducing the rudder force as described in this study. In this case, measures are required to ensure that the maneuverability does not worsen given further advances in energy savings. For example, additional care should be taken to increase the rudder area relative to that in a conventional case.

In this study, all investigations were conducted with respect to the VLCC. Thus, it may not be possible to directly apply the findings of this study to studies involving other types of ships with different sizes. Hence, investigations involving other types of ships could be a topic for future research.