Simulation study of the effect of loading condition changes on the maneuverability of a container ship

Abstract

Ships are operated under various loading conditions with changes in the draft or trim. Therefore, it is necessary to understand how changes in the loading conditions affect ship maneuvering from the viewpoint of navigation safety. For this, five loading conditions with different values of draft and trim based on the full-load even-keel condition were set for a container ship, and maneuvering simulations were performed using the MMG-method (Yasukawa and Yoshimura, J Marine Sci Technol 20(1):37–52, 2015; Yasukawa et al. J Marine Sci Technol 24(4):1280–1296, 2019). The hydrodynamic force characteristics required for the simulations were obtained by conducting captive model tests. The simulation results were compared with the free-running model test results for validation. After confirming the validity, simulations of 35$^\circ$ rudder angle turning and 10$^\circ$/10$^\circ$ zig-zag maneuvers were performed for a full-scale ship (ship length: 230 m, ship speed: approximately 24 kn). The results showed that a deeper draft or bow trim worsens the zig-zag maneuver performance to the extent that the overshoot angles do not meet the IMO maneuverability criteria.

Appendices

Appendix

Maneuvering simulation method based on the MMG-model

The maneuvering simulations were performed using a method called the MMG-model [8] [9]. The detail of the method is shown below.

2.1 Motion equations

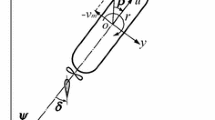
The motion equations with respect to the surge, sway, yaw, and roll are expressed as follows:

$$\begin{aligned} \left. \begin{array}{lll} (m + m_x){\dot{u}} - (m + m_y)v_mr - mx_Gr^2 + mz_Gr{\dot{\phi }} &{}=&{} X \\ (m + m_y){\dot{v}}_m + (m + m_x)ur + x_Gm{\dot{r}} - (m_y\alpha _z + mz_G)\ddot{\phi } &{}=&{} Y \\ (I_{zz} + J_{zz} + m{x_G}^2){\dot{r}} + mx_G({\dot{v}}_m - z_G\ddot{\phi } +ur) &{}=&{} N \\ (I_{xx} +J_{xx} + m{z_G}^2)\ddot{\phi } - (m_y\alpha _z + mz_G){\dot{v}}_m - mz_G(x_G{\dot{r}} + ur) &{}=&{} K \end{array} \right\} \end{aligned}$$

(9)

Here, m is the ship mass, and $I_{xx}$ and $I_{zz}$ are the moments of inertia for the roll and yaw, respectively. In addition, $m_x$, $m_y$, $J_{zz}$, and $J_{xx}$ denote the added mass for surge, added mass for sway, added moment of inertia for yaw, and added moment of inertia for roll, respectively. Moreover, $\alpha _z$ is the vertical acting point of the lateral added mass component $m_y$, X is the surge force, excluding the added mass component. Y is the lateral force, excluding the added mass component. N is the yaw moment around the midship excluding the added moment of the inertia component, and K is the roll moment around the x-axis, excluding the added moment of the inertia component. In the equations, the dot notation indicates the ordinary differential with respect to time t. The unknown variables in the motion equations are the longitudinal velocity component u, lateral velocity component $v_m$, yaw rate r, and roll angle $\phi$. These motion equations are the base equations to be solved.

2.2 Expression of hydrodynamic forces

Here, X, Y, N, and K are expressed as follows:

$$\begin{aligned} \left. \begin{array}{lll} X &{}=&{} X_H + X_R + X_P \\ Y &{}=&{} Y_H + Y_R \\ N &{}=&{} N_H + N_R \\ K &{}=&{} K_H - Y_Rz_R - mg{\overline{GM}}\phi + K_{{\dot{\phi }}}{{\dot{\phi }}} + K_{{\dot{\phi }}{\dot{\phi }}}{{\dot{\phi }}}|{{\dot{\phi }}}| \end{array} \right\} \end{aligned}$$

(10)

The subscripts H, P, and R on the right-hand side of Eq. 10 denote the hull, propeller, and rudder, respectively. $z_R$ denotes the vertical acting point of the lateral force by steering. $K_{{\dot{\phi }}}$ and $K_{{\dot{\phi }}{\dot{\phi }}}$ are the roll damping coefficients.

2.2.1 Hull forces

The hydrodynamic forces acting on the ship hull ($X_H$, $Y_H$, $N_H$) are expressed as follows:

$$\begin{aligned} \left. \begin{array}{lll} X_H &{}=&{} (1/2)\rho Ld_mU^2\ X_H'(v_m',r',\phi ) \\ Y_H &{}=&{} (1/2)\rho Ld_mU^2\ Y_H'(v_m',r',\phi ) \\ N_H &{}=&{} (1/2)\rho L^2d_mU^2\ N_H'(v_m',r',\phi ) \\ \end{array} \right\} \end{aligned}$$

(11)

where $\rho$ is the water density, $v_m'$ is the nondimensional lateral velocity ($=v_m/U$), and $r'$ is the nondimensional yaw rate ($=rL/U$). $X_H'$, $Y_H'$, and $N_H'$ are expressed as follows:

$$\left. {\begin{array}{*{20}{l}} {{X_{H}'}({v_{m}'},r',\phi ) = - {R_{0}'} + {X_{vv}'}v_{m}'^2 + {X_{vr}'}{v_{m}'}r' + {X_{rr}'}{{r'}^2} + {X_{vvvv}'}v_{m}'^4 + {X_{v\phi}'}{v_{m}'}\phi} \\ {\quad + {X_{r\phi}'}r'\phi + {X_{\phi\phi}'}{\phi ^2}} \\ {{Y_{H}'}({v_{m}'},r',\phi ) = {Y_{v}'}{v_{m}'} + {Y_{r}'}r' + {Y_{vvv}'}v_{m}'^3 + {Y_{vvr}'}v_{m}'^2r' + {Y_{vrr}'}{v_{m}'}{{r'}^2} + {Y_{rrr}'}{{r'}^3}} \\ {\quad + {Y_{\phi}'}\phi + {Y_{vv\phi}'}v_{m}'^2\phi + {Y_{rr\phi}'}{{r'}^2}\phi + {Y_{v\phi\phi}'}{v_{m}'}{\phi ^2} + {Y_{r\phi\phi}'}r'{\phi ^2}} \\ {{N_{H}'}({v_{m}'},r',\phi ) = {N_{v}'}{v_{m}'} + {N_{r}'}r' + {N_{vvv}'}v_{m}'^3 + {N_{vvr}'}v_{m}'^2r' + {N_{vrr}'}{v_{m}'}{{r'}^2} + {N_{rrr}'}{{r'}^3}} \\ {\quad + {N_{\phi }'}\phi + {N_{vv\phi}'}v_{m}'^2\phi + {N_{rr\phi}'}{{r'}^2}\phi + {N_{v\phi\phi}'}{v_{m}'}{\phi ^2} + {N_{r\phi\phi}'}r'{\phi ^2}} \end{array}} \right\}$$

(12)

Here, $X_{vv}'$, $Y_v'$, $N_v'$, and so on are called the hydrodynamic derivatives on maneuvering. $X_H'$ is expressed as a second-order polynomial function of $v_m'$, $r'$, and $\phi$ except for the $X_{vvvv}'$-term, and $Y_H'$ and $N_H'$ are expressed as the first- and third-order polynomial functions of $v_m'$, $r'$, and $\phi$. $R_0$ denotes the hull resistance in a straight motion.

$K_H$ is expressed as

$$\begin{aligned} K_H = -Y_Hz_H \end{aligned}$$

(13)

where $z_H$ is the vertical acting point of hull lateral force.

2.2.2 Propeller force

The effective propeller force $X_P$ is expressed as

$$\begin{aligned} X_P = (1-t_P)T_P \end{aligned}$$

(14)

where $t_P$ denotes the thrust deduction factor. Then, the propeller thrust $T_P$ is expressed as:

$$\begin{aligned} T_P= \, & {} \rho n_P^2 D_P^4 \ K_T(J_P) \end{aligned}$$

(15)

where $n_P$ is the propeller revolution and $D_P$ is the propeller diameter. Propeller thrust open water characteristic $K_T$ is expressed as follows:

$$\begin{aligned} K_T(J_P)= \, & {} k_0 +k_1J_P +k_2J_P^2 \end{aligned}$$

(16)

where $k_2$, $k_1$, and $k_0$ are coefficients that represent $K_T$. $J_P$ is the propeller advance ratio, which is expressed as follows:

$$\begin{aligned} J_P= \, & {} \frac{u(1-w_P)}{n_P D_P} \end{aligned}$$

(17)

where $w_P$ is the wake fraction at the propeller position and is expressed as a function of the geometrical inflow angle to the propeller $\beta _P$ as follows:

$$\begin{aligned} w_P = w_{P0}\exp \left( -C_0{{\beta }_P}^2\right) \end{aligned}$$

(18)

Here, $\beta _P$ is defined as $\beta _P \equiv \beta -l_P'r'+ z_P' \dot{\phi '}$, where $l_P'$ is the nondimensional longitudinal coordinate of the propeller position, and $z_P'$ is the nondimensional vertical coordinate of the propeller position. $w_{P0}$ is the wake fraction at the propeller position in a straight motion, and $C_0$ is an experimental constant that represents the characteristics of the wake behavior versus $\beta _P$.

2.2.3 Rudder forces

The effective rudder forces ($X_R$, $Y_R$, $N_R$) are expressed as follows:

$$\left. {\begin{array}{*{20}{l}} {{X_R} = - (1 - {t_R}){F_N}\sin \delta \cos \phi } \\ {{Y_R} = - (1 + {a_H}){F_N}\cos \delta \cos \phi } \\ {{N_R} = - ({x_R} + {a_H}{x_H}){F_N}\cos \delta \cos \phi } \end{array}} \right\}$$

(19)

where $t_R$, $a_H$, and $x_H'$ are the hull rudder interaction coefficients. Then, $F_N$ is expressed as follows:

$$\begin{aligned} F_N= \, & {} (1/2)\rho A_R\ f_{\alpha } \ U_R^2 \ \sin \alpha _R \end{aligned}$$

(20)

where $A_R$ is the rudder area and $f_\alpha$ is the rudder lift gradient coefficient. In addition, $U_R$ is the inflow velocity to the rudder, and $\alpha _R$ is the inflow angle to the rudder and is expressed as follows:

$$\begin{aligned} U_R= \, & {} \sqrt{u_R^2 + v_R^2} \end{aligned}$$

(21)

$$\begin{aligned} \alpha _R= \, & {} \delta - \tan ^{-1}(v_R/u_R) \end{aligned}$$

(22)

$u_R$ and $v_R$ are the longitudinal and lateral inflow velocity components, respectively. The value of $v_R$ is expressed as a formula that introduces a flow straightening coefficient $\gamma _R$ to a geometrical inflow angle to the rudder in maneuvering motions $\beta _R$ as follows:

$$\begin{aligned} v_R= \, & {} U\ \gamma _R\ \beta _R \end{aligned}$$

(23)

Here, $\beta _R$ is defined as $\beta -l'_Rr'+z'_R{\dot{\phi }}'$, where $l_R$ is the effective longitudinal coordinate of the rudder position. The value of $u_R$ is expressed as follows:

$$\begin{aligned} u_R= \, & {} \varepsilon \ u(1-w_P) \sqrt{ \eta \left\{ 1+\kappa \left( \sqrt{1+\frac{8K_T}{\pi J_P^2}}-1 \right) \right\} ^2 +(1-\eta ) } \end{aligned}$$

(24)

Here, $\varepsilon$ is the ratio of the wake fraction at the propeller and rudder positions, $\kappa$ is an experimental constant for expressing $u_R$, and $\eta$ is the ratio of the propeller diameter to the rudder span ($=D_P/H_R$).