1 Introduction

Parametric roll is known as a roll motion of a ship that is excited by a roll restoring moment that varies because of a periodic variation of the underwater hull geometry. Accidents due to this phenomenon are now being reported because of the increasing size and specialization of ships. Fine ships (e.g., container ships or pure car and truck carriers) are particularly susceptible to this phenomenon. In 1998, a C11-class post-Panamax container ship encountered a violent storm in the North Pacific Ocean. A roll motion of the ship was induced in head waves, with the maximum roll angle reaching 40°. On that occasion, 400 containers were lost and another 400 were damaged [1]. This indicates that the existing intact stability criteria, which are based on statistical data of previous accidents, are insufficient for evaluating the stability of every ship. In 2002, accidents due to parametric roll, including the aforementioned one, forced the International Maritime Organization (IMO) into considering physics-based intact stability criteria, which are still under development. The new criteria will comprise level 1 and level 2 vulnerability criteria and a direct stability assessment as level 3.

In the early stages of the study of parametric roll of ships, the Mathieu equation was used to examine whether the upright condition was stable against parametric roll. The IMO agreed to use this technique as the level 1 vulnerability criteria, which are simple enough to be calculated by hand. However, the Mathieu equation cannot be used to estimate the amplitude of steady-state parametric roll.

To obtain finite parametric roll amplitudes from the uncoupled roll equation, the nonlinearity of the restoring and/or damping moment should be taken into account. Here we treat the restoring moment as the sum of a wave-induced variation of the metacentric height (GM) and an Nth order approximation of the calm-water restoring arm (GZ) curve, where N is a natural number. These approximations for the restoring moment make it possible to obtain analytical solutions for the parametric roll amplitude [2,3,4,5,6,7]. A harmonic-balance method [2], a multiple-scales method [3], and an averaging method [4,5,6] were used for obtaining analytical solutions in previous studies.

Another way to obtain solutions of the uncoupled or coupled nonlinear roll equation is numerical simulation, such as the widely used Runge–Kutta method. Indeed, because restoring moments are not always well approximated even with higher order polynomials, there is a view that numerical solutions of the uncoupled roll equation with a hydrostatically calculated calm-water GZ curve should be directly used as the level 2 vulnerability criteria [8]. However, the use of numerical simulation in the time domain as regulatory stability criteria would raise non-straightforward outcomes because the resulting time series could differ from typical parametric roll or even be chaotic [5, 9, 10]. Hence, it is unrealistic to expect administrators and ship masters, most of whom are not experts in nonlinear dynamics, to evaluate such outcomes correctly.

Consequently, analytical approaches are more suitable for the level 2 vulnerability criteria because they straightforwardly quantify danger of parametric roll. In the present study, to overcome the aforementioned difficulties with analytical solutions, we newly apply an averaging method to the uncoupled roll equation without fitting a polynomial to the calm-water GZ curve.

To improve the estimation accuracy, we change the form of solutions assumed in the averaging method. Originally, this was expressed using only one frequency component, which was one of the reasons for discrepancies between the analytical and numerical solutions. Instead, we assume a form of solutions that includes an additional superharmonic component.

The level 2 vulnerability criteria involve the probability of dangerous wave conditions occurring in the North Atlantic Ocean that would make a ship vulnerable to parametric roll. According to the draft criteria, seven running conditions (stationary and 50, 86.6, and 100% of the ship’s service speed in either following or heading waves) should be used in the calculations. However, using such specific ship speeds, the critical ship speed might be overlooked. To address this issue, we propose a method to obtain the critical ship speed associated with the largest amplitude of parametric roll using an averaging method.

If a ship fails the level 2 vulnerability criteria, the stability is evaluated generally by the direct stability assessment. To avoid this time-consuming assessment, the ship must be operated in compliance with an operational guidance. It is necessary to estimate the parametric roll amplitude in oblique waves because both the ship’s speed and course are essential operational parameters for ship masters. Analytical solutions of the uncoupled roll equation in oblique waves are necessary for the same reason as the level 2 vulnerability criteria. However, despite there being some studies of this problem in the literature [11, 12], their findings are not sufficiently accessible to the public and so they have not been incorporated into the IMO regulations thus far. Thus, we propose two more-accessible estimation methods for obtaining the amplitude of parametric roll in oblique waves using an averaging method.

In the final stage of this study, we confirm that the amplitudes estimated by all our proposed methods agree well with numerical time-domain solutions of the uncoupled roll equation with appropriate initial values, and that they assess the model experiment as being within the margins of safety.

2 Mathematical model

The uncoupled roll equations with and without the polynomial approximation are described, respectively, by following equations [5]:

$$ \begin{aligned} {\ddot{\phi }} + 2\alpha \dot{\phi } + \gamma \dot{\phi }^{3} + \omega_{\phi }^{2} \left( {\frac{{{\text{GM}}_{\text{mean}} }}{\text{GM}} + \frac{{{\text{GM}}_{\text{amp}} }}{\text{GM}}\cos \omega_{\text{e}} t} \right)\left\{ {\phi - \left( {1/\pi^{2} } \right)\phi^{3} } \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,&\quad + \omega_{\phi }^{2} \frac{{{\text{GZ}}_{\text{calm}} (\phi )}}{\text{GM}} = \zeta_{a} \,r\,k\,\omega_{\phi }^{2} \,\sin \chi \,\sin \omega_{e} t\,, \hfill \\ \end{aligned} $$
(1)
$$ \begin{aligned} {\ddot{\phi }} + 2\alpha \dot{\phi } + \gamma \dot{\phi }^{3} + \omega_{\phi }^{2} \left( {\frac{{{\text{GM}}_{\text{mean}} }}{\text{GM}} + \frac{{{\text{GM}}_{\text{amp}} }}{\text{GM}}\cos \omega_{\text{e}} t} \right)\left\{ {\phi - \left( {1/\pi^{2} } \right)\phi^{3} } \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,&\quad + \omega_{\phi }^{2} \left( {\phi + l_{3} \phi^{3} + l_{5} \phi^{5} } \right) = \zeta_{a} \,r\,k\,\omega_{\phi }^{2} \,\sin \chi \,\sin \omega_{e} t\,. \hfill \\ \end{aligned} $$
(2)

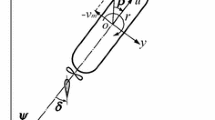
Here, α and γ are the roll damping coefficients estimated by Ikeda’s simplified method [13] with the lift component of Ikeda’s original method [14]. The term \( \omega_{\phi } \) is the natural roll frequency, and GMmean and GMamp are the mean and amplitude of the wave-induced GM variation, respectively. The term \( \omega_{\text{e}} \) is the wave-encounter frequency, \( {\text{GZ}}_{\text{calm}} (\phi ) \) is the hydrostatically calculated calm-water GZ curve, and l 3 and l 5 are the cubic and quintic coefficients, respectively, of the approximated calm-water GZ curve divided by GM. The term ζ a is the wave amplitude, r is the effective wave-slope coefficient (here, we use r = 0.8), k is the wave number, and χ is the heading angle relative to the wave direction. In the calculation of the instantaneous GM in waves, the wave crest should be located amidships, at 0.1λ, 0.2λ, 0.3λ, 0.4λ, and 0.5λ forward, and at 0.1λ, 0.2λ, 0.3λ, and 0.4λ aft, where λ is the wavelength [15]. The value of GMamp is half the difference between the maximum and minimum values of the GM in the presence of waves, and GMmean is the difference between the mean value of the two and the calm-water GM. This method can be applied only to the case of a longitudinal wave. Hence, we represent an oblique wave as the equivalent longitudinal wave estimated by the extended Grim’s effective wave concept [16]. The length of this equivalent wave is the ship length between perpendiculars L pp, and the equivalent amplitude ζ ae is calculated as follows:

$$ \zeta_{\text{ae}} = \zeta_{\text{a}} \sqrt {\frac{{2\pi \,\frac{{L_{\text{pp}} }}{\lambda }\,\cos (\chi )\,\sin \left( {\pi \,\frac{{L_{\text{pp}} }}{\lambda }\,\cos (\chi )} \right)}}{{\pi^{2} - \left( {\pi \,\frac{{L_{\text{pp}} }}{\lambda }\,\cos (\chi )} \right)^{2} }}} \,, $$
(3)

where λ is the wavelength and ζ a is the wave amplitude.

3 Averaging method

3.1 General explanation of averaging method

An averaging method is an analytical way to obtain approximate periodic orbits by assuming that the amplitude and phase both vary slowly [17, 18].

3.2 Averaging uncoupled roll model without polynomial approximation

We introduce an application of an averaging method to an uncoupled roll model without polynomial approximation, Eq. 1. A form of periodic solutions is assumed as follows:

$$ \begin{aligned} \phi = A\cos \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } t - \varepsilon } \right)\,, \hfill \\ \dot{\phi } = - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } A\sin \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } t - \varepsilon } \right)\,. \hfill \\ \end{aligned} $$
(4)

Here, A and ε are the parametric roll amplitude and phase difference from the GM variation, respectively, and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } \) is the parametric roll frequency, which is equal to half the wave-encounter frequency. The time derivatives of these parameters are obtained as follows:

$$ \begin{aligned} \dot{A} = \frac{{\dot{\phi }}}{{\hat{\omega }^{2} A}}\left( {{\ddot{\phi }} + \hat{\omega }^{2} \phi } \right)\,, \hfill \\ \dot{\varepsilon } = \frac{\phi }{{\hat{\omega }A^{2} }}\left( {{\ddot{\phi }} + \hat{\omega }^{2} \phi } \right)\,. \hfill \\ \end{aligned} $$
(5)

Assuming that A and ε vary slowly with time, the time derivatives can be represented by time averages over one period \( {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }}} \right. \kern-0pt} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }} \):

$$ \dot{A} = - \alpha A - \frac{3}{8}\gamma \hat{\omega }^{2} A^{3} - \frac{1}{4}\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}MA\left( {1 - \frac{1}{{2\pi^{2} }}A^{2} } \right)\sin 2\varepsilon \,, $$
(6)
$$ \begin{aligned} \dot{\varepsilon } &= \frac{1}{2}\hat{\omega } - \frac{1}{2}\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}F\left( {1 - \frac{3}{{4\pi^{2} }}A^{2} } \right) \hfill \\ & \quad\, - \frac{1}{4}\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}M\left( {1 - \frac{1}{{\pi^{2} }}A^{2} } \right)\cos 2\varepsilon \hfill \\ & \quad \, - \frac{{\omega_{\phi }^{2} }}{2\pi \,GM\,A}\int_{0}^{{\frac{2\pi }{{\hat{\omega }}}}} {{\text{GZ}}_{\text{calm}} \left( {A\cos \left( {\hat{\omega }t - \varepsilon } \right)} \right)\cos \left( {\hat{\omega }t - \varepsilon } \right)} {\text{d}}t\,, \hfill \\ \end{aligned} $$
(7)

where

$$ F = \frac{{{\text{GM}}_{\text{mean}} }}{\text{GM}}\,,\,\,\,\,\,M = \frac{{{\text{GM}}_{\text{amp}} }}{\text{GM}}\,. $$
(8)

Equations (6) and (7) are called averaging equations. The steady-state parametric roll amplitude and phase difference can be obtained by setting the averaged time derivatives to zero. There is still an integration term left so that it is impossible to obtain analytical solutions of the amplitude and phase difference. In this study, we use the Newton method to obtain solutions from initial values that are obtained analytically from existing averaging equations proposed by Maki et al. [19] according to Eq. 2.

3.3 Averaging method with superharmonics

We introduce an application of an averaging method to an uncoupled roll model, Eq. 2 with taking into account superharmonics. The existing averaging method assuming the form of solutions given in Eq. 4 sometimes fails to provide sufficient accuracy because of superharmonics. Thus, we assume the following periodic form of solutions that includes a superharmonic component:

$$ \begin{aligned} \phi &= A_{1} \cos \left( {\hat{\omega }t - \varepsilon_{1} } \right) + A_{3} \cos \left( {3\hat{\omega }t - \varepsilon_{3} } \right)\,, \hfill \\ &\dot{\phi } = - \hat{\omega }A_{1} \sin \left( {\hat{\omega }t - \varepsilon_{1} } \right) - 3\hat{\omega }A_{3} \sin \left( {3\hat{\omega }t - \varepsilon_{3} } \right)\,. \hfill \\ \end{aligned} $$
(9)

These include the amplitudes and phase differences of both a harmonic and superharmonic component. The time derivatives of these four parameters are obtained using the same procedure as in Sect. 3.2:

$$ \begin{aligned} \dot{A}_{1} &= - \alpha \,A_{1} - \frac{3}{8}\gamma \,\hat{\omega }^{2} \,A_{1}^{3} - \frac{27}{4}\gamma \,\hat{\omega }^{2} \,A_{1} \,A_{3}^{2} \hfill \\ &\quad + M\,\sin \left( {2\varepsilon_{1} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left( {\frac{1}{{8\pi^{2} }}A_{1}^{3} + \frac{3}{{8\pi^{2} }}A_{1} A_{3}^{2} - \frac{1}{4}A_{1} } \right) \hfill \\ &\quad + M\,\sin \left( {\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left( {\frac{3}{{16\pi^{2} }}A_{1}^{2} \,A_{3} + \frac{3}{{16\pi^{2} }}A_{3}^{3} - \frac{1}{4}A_{3} } \right) \hfill \\ &\quad + \sin \left( {3\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left( { - \frac{3}{8}l_{3} \,A_{1}^{2} \,A_{3} - \frac{15}{32}l_{5} \,A_{1}^{4} \,A_{3} } \right.\left. { - \frac{15}{16}l_{5} \,A_{1}^{2} \,A_{3}^{3} } \right) \hfill \\ &\quad + \cos \left( {3\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{9}{8}\gamma \,\hat{\omega }^{2} \,A_{1}^{2} \,A_{3} } \right)\,, \hfill \\ \end{aligned} $$
(10)
$$ \begin{aligned} \dot{\varepsilon }_{1} &= \frac{1}{{2\hat{\omega }}}\left( {\hat{\omega }^{2} - \omega_{\phi }^{2} - \omega_{\phi }^{2} \,F} \right)\,A_{1} + \frac{3}{8}\left( {\frac{F}{{\pi^{2} }} - l_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{1}^{3} \hfill \\ &\quad - \frac{5}{16}l_{5} \,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{1}^{5} - \frac{15}{16}l_{5} \,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{1} \,A_{3}^{4} \hfill \\ &\quad+\, \frac{3}{4}\left( {\frac{F}{{\pi^{2} }} - l_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)A_{1} \,A_{3}^{2} - \frac{15}{8}l_{5} \,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{1}^{3} \,A_{3}^{2} \hfill \\ &\quad + \, M\cos \left( {2\varepsilon_{1} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\left( {\frac{1}{{4\,\pi^{2} }}A_{1}^{3} + \frac{3}{{8\,\pi^{2} }}A_{1} \,A_{3}^{2} - \frac{1}{4}A_{1} } \right) \hfill \\ &\quad+ \, M\cos \left( {\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\left( {\frac{9}{{16\pi^{2} }}A_{1}^{2} \,A_{3} + \frac{3}{{16\pi^{2} }}A_{3}^{3} - \frac{1}{4}A_{3} } \right) \hfill \\ &\quad+ \, \cos \left( {3\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left\{ { - \frac{25}{32}l_{5} \,A_{1}^{4} \,A_{3} - \frac{15}{16}l_{5} \,A_{1}^{2} \,A_{3}^{3} } \right. + \left. {\frac{3}{8}\left( {\frac{F}{{\pi^{2} }} - l_{3} } \right)A_{1}^{2} \,A_{3} } \right\} \hfill \\ &\quad + \, \sin (3\varepsilon_{1} - \varepsilon_{3} )\left( { - \frac{9}{8}\gamma \hat{\omega }^{2} A_{1}^{2} A_{3} } \right)\,, \hfill \\ \end{aligned} $$
(11)
$$ \begin{aligned} \dot{A}_{3} &= - \alpha \,A_{3} - \frac{27}{8}\gamma \,\hat{\omega }\,A_{3}^{3} - \frac{3}{4}\gamma \,\hat{\omega }\,A_{1}^{2} \,A_{3} \hfill \\ &\quad + M\,\sin \left( {\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left( { - \frac{1}{{16\pi^{2} }}A_{1}^{3} - \frac{3}{{16\pi^{2} }}A_{1} \,A_{3}^{3} + \frac{1}{12}A_{1} } \right) \hfill \\ &\quad + \sin \,\left( {3\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left\{ {\frac{5}{96}l_{5} \,A_{1}^{5} + \frac{5}{48}l_{5} \,A_{1}^{3} \,A_{3}^{2} } \right. \hfill \\ &\quad\left. { - \frac{1}{24}\left( {\frac{F}{{\pi^{2} }} - l_{3} } \right)A_{1}^{3} } \right\} \hfill \\ &\quad + \cos \left( {3\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{1}{24}\gamma \,\hat{\omega }^{2} \,A_{1}^{3} } \right)\,, \hfill \\ \end{aligned} $$
(12)

and

$$ \begin{aligned} \dot{\varepsilon }_{3} &= \frac{1}{{6\hat{\omega }}}\left( {9\hat{\omega }^{2} - \omega_{\phi }^{2} - \omega_{\phi }^{2} \,F} \right)\,A_{3} - \frac{15}{16}l_{5} \,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{1}^{4} \,A_{3} \hfill \\ &\quad - \frac{5}{8}l_{5} \,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{1}^{2} \,A_{3}^{3} - \frac{5}{48}l_{5} \,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{3}^{5} \hfill \\ &\quad + \frac{1}{4}\left( {\frac{F}{{\pi^{2} }} - l_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{1}^{2} \,A_{3} + \frac{1}{8}\left( {\frac{F}{{\pi^{2} }} - l_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,A_{3}^{3} \hfill \\ &\quad + \sin \left( {3\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{1}{24}\gamma \hat{\omega }^{2} A_{1}^{3} } \right) \hfill \\ &\quad + M\cos \left( {2\varepsilon_{1} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left( {\frac{1}{{8\pi^{2} }}A_{1}^{2} A_{3} } \right) \hfill \\ &\quad + \, M\cos \left( {\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left( {\frac{1}{{16\pi^{2} }}A_{1}^{3} + \frac{3}{{16\pi^{2} }}A_{1} \,A_{3}^{2} - \frac{1}{12}A_{1} } \right) \hfill \\ &\quad + \cos \left( {3\varepsilon_{1} - \varepsilon_{3} } \right)\,\left( {\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}} \right)\,\left\{ { - \frac{5}{96}l_{5} \,A_{1}^{5} - \frac{5}{16}l_{5} \,A_{1}^{3} \,A_{3}^{2} \left. { + \frac{1}{24}\left( {\frac{F}{{\pi^{2} }} - l_{3} } \right)\,A_{1}^{3} } \right\}\,\,.} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{aligned} $$
(13)

Because it is difficult to solve these averaging equations analytically, we used the Newton method instead.

3.4 Critical speed for parametric roll

Maki et al. applied an averaging method to Eq. 2 and showed that the parametric roll amplitude A can be expressed by the following algebraic equation [19]:

$$ \sum\limits_{k = 0}^{12} {\left( {a_{k} \,A^{k} } \right)} = 0\,. $$
(14)

Here, the coefficients a k are given in Appendix A [see electronic supplementary material (ESM)]. By differentiating Eq. 14 partially with respect to the ship speed U, an equation for the ship speed at which the parametric roll amplitude becomes a maximum can be obtained:

$$ \sum\limits_{k = 0}^{12} {\left( {\frac{{\partial a_{k} }}{\partial U}\,A^{k} } \right)} + \frac{\partial A}{\partial U}\,\sum\limits_{k = 0}^{12} {\left( {a_{k} \,k\,A^{k - 1} } \right)} = 0. $$
(15)

The requirement for the critical speed (i.e., that the partial derivative of A with respect to the ship speed is zero) can then be expressed as

$$ \sum\limits_{k = 0}^{12} {\left( {\frac{{\partial a_{k} }}{\partial U}\,A^{k} } \right)} = 0\,. $$
(16)

The only coefficients in Eq. 2 that depend on the ship speed are the linear damping coefficient and the wave-encounter frequency. The partial derivatives of a k with respect to the ship speed are given in Appendix A (see EMS). Solving Eqs. 14 and 16 simultaneously gives the critical ship speed.

3.5 Parametric roll in oblique waves

In a previous study, we applied an averaging method to Eq. 2 to evaluate parametric roll in oblique waves [20]. The conventional form of solutions, Eq. 4, does not express motion with a frequency that is equal to the wave-encounter one. This is forced by the direct wave-excitation moment, which is given on the right-hand side of Eq. 2. Here, Eq. 2 can be regarded as follows:

$$ {\ddot{\phi }} + \hat{\omega }^{2} \,\phi = \varepsilon \,f\left( {\phi ,\dot{\phi },t} \right) + E\,\sin \left( {\omega_{e} \,t} \right)\,, $$
(17)

where

$$ E = \zeta_{a} \,r\,k\,\omega_{\phi }^{2} \,\sin \chi \,. $$
(18)

Here, ε is a small parameter. Generally, the form of solutions used in an averaging method is determined by the general solution when ε is equal to zero. The form of solutions is assumed as follows:

$$ \begin{aligned} \phi = A\cos (\hat{\omega }t - \xi ) + B\sin (\omega_{e} t - \eta )\,, \hfill \\ \dot{\phi } = - \hat{\omega }A\sin (\hat{\omega }t - \xi ) + \omega_{e} B\cos (\omega_{e} t - \eta )\,. \hfill \\ \end{aligned} $$
(19)

We propose two methods of applying an averaging method. In the first method, the second term in Eq. 19 is regarded as the particular solution of Eq. 17 with ε = 0, and an averaging method is applied to the rest. In the second method, the first and second terms are determined by an averaging method. The averaging equations of the first method are as follows:

$$ \begin{aligned} \dot{A} &= \left( { - \alpha \,A - 3\gamma \,\hat{\omega }^{2} \,B^{2} \,A - \frac{3}{8}\gamma \,\hat{\omega }^{{^{2} }} 2\,A^{3} } \right) \hfill \\ &\quad- \frac{1}{4}\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}M\,A\,\left( {1 - \frac{3}{{4\pi^{2} }}B^{2} - \frac{1}{{2\pi^{2} }}A^{2} } \right)\,\sin \left( {2\xi } \right) \hfill \\ \quad + \frac{5}{8}\frac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}l_{5} \,B^{2} \,A^{3} \,\cos \left( {2\xi } \right)\,\sin \left( {2\xi } \right)\,, \hfill \\ \end{aligned} $$
(20)
$$ \begin{aligned} \dot{\xi } &= \tfrac{{\hat{\omega }}}{2} - \tfrac{1}{2}\tfrac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}\left\{ {1 + F\,\left( {1 - \tfrac{3}{{4\pi^{2} }}A^{2} } \right) + \tfrac{3}{4}l_{3} \,A^{2} } \right. \hfill \\ \quad \left. { + \tfrac{5}{8}l_{5} \,A^{4} + \tfrac{15}{8}l_{5} \,B^{4} + \tfrac{15}{4}l_{5} \,B^{2} \,A^{2} + \tfrac{3}{2}\left( {l_{3} - \tfrac{F}{{\pi^{2} }}} \right)\,B^{2} } \right\} \hfill \\ \quad - \tfrac{1}{4}\tfrac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}\,M\,\left( {1 - \tfrac{3}{{4\pi^{2} }}B^{2} - \tfrac{1}{{\pi^{2} }}A^{2} } \right)\cos \left( {2\xi } \right) \hfill \\ \quad + \tfrac{5}{16}\tfrac{{\omega_{\phi }^{2} }}{{\hat{\omega }}}l_{5} \,B^{2} \,A^{2} \left( {\cos^{2} \left( {2\xi } \right) - \sin^{2} \left( {2\xi } \right)} \right)\,, \hfill \\ \end{aligned} $$
(21)

where

$$ B = - \frac{E}{{3\hat{\omega }^{2} }}\,,\,\,\,\,\,\eta = 0\,. $$
(22)

By solving Eqs. 20 and 21 by setting the time derivatives to zero, the parameters in Eq. 19 can be determined. The equations are given in Appendix B (see ESM).

Equation 2 contains a term related to the GM variation, which is expressed as a sinusoidal function with the wave-encounter frequency. Multiplying this term by the second term of Eq. 19 generates a constant term. Then, for the second method, we add a constant term to the assumed form of solutions as follows:

$$ \begin{aligned} \phi = A\cos (\hat{\omega }t - \xi ) + B\sin (\omega_{e} t - \eta ) + C\,, \hfill \\ \dot{\phi } = - \hat{\omega }A\sin (\hat{\omega }t - \xi ) + \omega_{\text{e}} B\cos (\omega_{\text{e}} t - \eta )\,. \hfill \\ \end{aligned} $$
(23)

Equation 23 is the solution of Eq. 2, so the sum of the constant terms must be zero when Eq. 23 is substituted into Eq. 2. From this requirement, the following equation is obtained:

$$ \begin{aligned} &\left( {\omega_{\phi }^{2} \,l_{5} } \right)\,C^{5} + \left( {5\omega_{\phi }^{2} \,l_{5} } \right)\,B^{2} \,C^{3} + \left( {\tfrac{15}{8}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{4} \,C \hfill \\ &\quad + \left( {5\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,C^{3} + \left( {\tfrac{15}{8}\omega_{\phi }^{2} \,l_{5} } \right)\,B^{4} \,C \hfill \\ &\quad + \left( {\tfrac{15}{2}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B^{2} \,C + \left( {\omega_{\phi }^{2} \,l_{3} - \frac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F} \right)\,C^{3}\hfill \\ &\quad + \tfrac{3}{2}\left( {\omega_{\phi }^{2} \,l_{3} - \frac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F} \right)\,A^{2} \,C + \tfrac{3}{2}\left( {\omega_{\phi }^{2} \,l_{3} - \frac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F} \right)\,B^{2} \,C\hfill \\ &\quad + \left( {\omega_{\phi }^{2} + \omega_{\phi }^{2} \,F} \right)\,C + {\text{sin}}\left( {2\xi - \eta } \right)\,\left\{ {\left( { - \tfrac{15}{2}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B\,C^{2} } \right. \hfill \\ &\quad + \left( { - \tfrac{5}{4}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{4} \,B + \left( { - \tfrac{15}{8}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B^{3} \hfill \\ & \quad \left. { - \tfrac{3}{4}\left( {\omega_{\phi }^{2} \,l_{3} - \frac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F} \right)\,A^{2} \,B} \right\} + {\text{cos}}\left( {2\xi - \eta } \right)\,\left\{ {\left( {\tfrac{3}{2}\gamma \,\hat{\omega }^{3} } \right)\,A^{2} \,B} \right\}\hfill \\ &\quad + {\text{sin}}\left( \eta \right)\,\left\{ {\left( {\frac{3}{{4\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,A^{2} \,B + \left( {\frac{3}{{8\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B^{3} } \right.\hfill \\ &\quad \left. {+ \left( {\frac{3}{{2\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B\,C^{2} + \left( { - \tfrac{1}{2}\omega_{\phi }^{2} \,M} \right)\,B} \right\}\hfill \\ &\quad + {\text{cos}}\left( {2\xi } \right)\,\left\{ {\left( {\frac{3}{{4\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,A^{2} \,C} \right\} = 0. \hfill \\ \end{aligned} $$
(24)

The averaging equations of the second method can be presented as follows:

$$ \begin{aligned} \dot{A} &= \left\{ {\left( { - \tfrac{3}{8}\gamma \,\hat{\omega }^{3} } \right)\,A^{2} + \left( { - 3\gamma \,\hat{\omega }^{3} } \right)\,B^{2} + \left( { - \alpha \,\hat{\omega }} \right)} \right\} \hfill \\ &\quad + \sin \left( {2\xi } \right)\,\left\{ {\left( { - \tfrac{1}{{8\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,A^{2} + \left( { - \tfrac{3}{{8\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B^{2} } \right. \hfill \\ & \quad \left. { + \left( { - \tfrac{3}{{4\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,C^{2} + \left( {\tfrac{1}{4}\omega_{\phi }^{2} \,M} \right)} \right\} \hfill \\ &\quad + \cos \left( {2\xi - \eta } \right)\,\left\{ {\left( { - \tfrac{5}{2}\omega_{\phi }^{2} l_{5} } \right)\,A^{2} \,B\,C + \left( { - \tfrac{15}{4}\omega_{\phi }^{2} l_{5} } \right)\,B^{3} \,C} \right.\hfill \\ &\quad \left. { \, + \left( { - 5\omega_{\phi }^{2} \,l_{5} } \right)\,B\,C^{3} + \tfrac{3}{2}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} l_{3} } \right)\,B\,C} \right\} \hfill \\ &\quad + \sin \left( {2\xi - 2\eta } \right)\,\left\{ {\left( {\tfrac{3}{{16\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B^{2} } \right\} \hfill \\ &\quad + \sin \left( {4\xi - 2\eta } \right)\,\left\{ {\left( {\tfrac{5}{16}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B^{2} } \right\}\,, \hfill \\ \end{aligned} $$
(25)
$$ \begin{aligned} \dot{\xi } = \left\{ {\left( { - \tfrac{5}{16}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{4} + \left( { - \tfrac{15}{8}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B^{2} + \left( { - \tfrac{15}{16}\omega_{\phi }^{2} \,l_{5} } \right)\,B^{4} } \right.\hfill \\ &\quad \left. { \, + \left( { - \tfrac{15}{4}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,C^{2} } \right\} + \left( { - \tfrac{15}{2}\omega_{\phi }^{2} \,l_{5} } \right)\,B^{2} \,C^{2} + \left( { - \tfrac{5}{2}\omega_{\phi }^{2} \,l_{5} } \right)\,C^{4} \hfill \\ &\quad + \tfrac{3}{8}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,A^{2} + \tfrac{3}{2}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,B^{2}\hfill \\ &\quad \left. { \, + \tfrac{1}{2}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,C^{2} + \tfrac{1}{2}\left( {\hat{\omega }^{2} - \omega_{\phi }^{2} - \omega_{\phi }^{2} \,F} \right)} \right\} \hfill \\ &\quad + {\text{cos}}\left( {2\xi } \right)\,\left\{ {\left( { - \tfrac{1}{{4\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,A^{2} + \left( { - \tfrac{3}{{8\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B^{2} } \right. \hfill \\ & \quad \left. { + \left( { - \tfrac{3}{{4\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,C^{2} + \left( {\tfrac{1}{4}\omega_{\phi }^{2} \,M} \right)} \right\} \hfill \\ &\quad + {\text{sin}}\left( {2\xi - \eta } \right)\,\left\{ {\left( {5\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B\,C + \left( {\tfrac{15}{4}\omega_{\phi }^{2} \,l_{5} } \right)\,B^{3} \,C} \right. \hfill \\ & \quad \left. { + \left( {5\omega_{\phi }^{2} \,l_{5} } \right)\,B\,C^{3} - \tfrac{3}{2}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,B\,C} \right\} \hfill \\ &\quad + {\text{cos}}\left( {2\xi - 2\eta } \right)\,\left\{ {\left( {\tfrac{3}{{16\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B^{2} } \right\} \hfill \\ &\quad + {\text{cos}}\left( {4\xi - 2\eta } \right)\,\left\{ {\left( {\tfrac{5}{16}\omega_{\phi }^{2} \,l_{5} } \right)A^{2} \,B^{2} } \right\} \hfill \\ &\quad + {\text{sin}}\left( \eta \right)\,\left\{ {\left( { - \tfrac{3}{{2\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B\,C} \right\}\,, \hfill \\ \end{aligned} $$
(26)
$$ \begin{aligned} \dot{B} &= \left\{ {\left( { - 3\gamma \,\hat{\omega }^{3} } \right)\,A^{2} \,B + \left( { - 6\gamma \,\hat{\omega }^{3} } \right)\,B^{3} + \left( { - 4\alpha \,\hat{\omega }} \right)\,B} \right\} \hfill \\ &\quad + {\text{cos}}\left( \eta \right)\left\{ {\left( {\tfrac{3}{{2\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,A^{2} \,C + \left( {\tfrac{3}{{4\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B^{2} \,C} \right.\hfill \\ &\quad \left. { \, + \left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,C^{3} + \left( { - \omega_{\phi }^{2} \,M} \right)\,C} \right\} \hfill \\ &\quad + {\text{sin}}\left( \eta \right)\,\left\{ {\left( E \right)} \right\} + {\text{cos}}\left( {2\xi - \eta } \right)\,\left\{ {\left( {\tfrac{5}{2}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{4} \,C} \right. \hfill \\ &\quad + \left( {\tfrac{15}{4}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B^{2} \,C + \left( {5\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,C^{3}\hfill \\ &\quad \left. { \, - \tfrac{3}{2}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,A^{2} \,C} \right\} \hfill \\ &\quad + {\text{sin}}\left( {2\xi - 2\eta } \right)\,\left\{ {\left( { - \tfrac{3}{{8\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,A^{2} \,B} \right\} \hfill \\ &\quad + {\text{sin}}\left( {4\xi - 2\eta } \right)\,\left\{ {\left( { - \tfrac{5}{16}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{4} \,B} \right\}\,, \hfill \\ \end{aligned} $$
(27)
$$ \begin{aligned} \dot{\eta } &= \left\{ {\left( { - \tfrac{15}{16}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{4} \,B + \left( { - \tfrac{15}{8}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B^{3} + \left( { - \tfrac{15}{2}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B\,C^{2} } \right. \hfill \\ &\quad + \left( { - \tfrac{5}{16}\omega_{\phi }^{2} \,l_{5} } \right)\,B^{5} + \left( { - \tfrac{15}{4}\omega_{\phi }^{2} \,l_{5} } \right)\,B^{3} \,C^{2} + \left( { - \tfrac{5}{2}\omega_{\phi }^{2} \,l_{5} } \right)\,B\,C^{4} \hfill \\ &\quad + \tfrac{3}{4}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,A^{2} \,B + \tfrac{3}{2}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,B\,C^{2}\hfill \\ &\quad \left. { \, + \tfrac{3}{8}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,B^{3} + \tfrac{1}{2}\left( {4\hat{\omega }^{2} - \omega_{\phi }^{2} - \omega_{\phi }^{2} \,F} \right)\,B} \right\} \hfill \\ &\quad + {\text{sin}}\left( \eta \right)\,\left\{ {\left( { - \tfrac{9}{{8\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,B^{2} \,C + \left( { - \tfrac{3}{{4\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,A^{2} \,C} \right. \hfill \\ &\quad \left. { + \left( { - \tfrac{1}{{2\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,C^{3} + \left( {\tfrac{1}{2}\omega_{\phi }^{2} \,M} \right)\,C} \right\} \hfill \\ &\quad + {\text{cos}}\left( \eta \right)\,\left\{ {\left( {\tfrac{1}{2}E} \right)} \right\} + {\text{sin}}\left( {2\xi - \eta } \right)\,\left\{ {\left( {\tfrac{5}{4}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{4} \,C} \right. \hfill \\ &\quad + \left( {\tfrac{45}{8}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B^{2} \,C + \left( {\tfrac{5}{2}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,C^{3}\hfill \\ &\quad \left. { \, - \tfrac{3}{4}\left( {\tfrac{1}{{\pi^{2} }}\omega_{\phi }^{2} \,F - \omega_{\phi }^{2} \,l_{3} } \right)\,A^{2} \,C} \right\} \hfill \\ &\quad + {\text{cos}}\left( {2\xi - 2\eta } \right)\,\left\{ {\left( {\tfrac{3}{{16\pi^{2} }}\omega_{\phi }^{2} \,M} \right)\,A^{2} \,B} \right\} \hfill \\ &\quad + {\text{cos}}\left( {4\xi - 2\eta } \right)\,\left\{ {\left( {\tfrac{3}{16}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{4} \,B} \right\} \hfill \\ &\quad + {\text{cos}}\left( {2\xi } \right)\,\left\{ {\left( {\tfrac{5}{32}\omega_{\phi }^{2} \,l_{5} } \right)\,A^{2} \,B} \right\}\,. \hfill \\ \end{aligned} $$
(28)

By solving the above five equations numerically with the time derivatives set to zero, all the parameters in Eq. 23 can be determined.

4 Experiment

To validate the above methods, we used existing results from towing-model experiments with a C11-class post-Panamax container ship [21] and free-running model experiments with an ITTC A-1 container ship [22] and the ONR Flare topside vessel [23], of which the experimental procedure was based on the ITTC recommended procedures for intact stability model tests, 7.5-02-07-04.1. The principal particulars are listed in Table 1, and the wave and running conditions of the experiments are listed in Tables 2, 3, and 4. Here, the 0° course is defined as the condition in which the ship runs in following waves. The relevant hydrostatically calculated calm-water GZ curves and quintic approximations are shown in Fig. 1. These were calculated with a heel angle of 0°–50° in steps of 1°, and the least-squares method was used to obtain l 3 and l 5 in Eq. 2. The quintic approximations provide satisfactory results for the ONR Flare topside vessel and the C11-class post-Panamax container ship, but less so for the ITTC A-1 container ship. The detailed hull forms of these ships are accessible without commercial secret, and parametric roll has previously been observed in model experiments with these ships.

Table 1 Principal particulars of the subject ships at full scale
Full size table
Table 2 Wave and running conditions of the experiments with the ONR Flare topside vessel
Full size table
Table 3 Wave and towing conditions of the experiments with the C11-class post-Panamax container ship
Full size table
Table 4 Wave and running conditions of the experiments with the ITTC A-1 container ship
Full size table
Fig. 1
figure 1

Hydrostatically calculated calm-water GZ curves and their quintic approximations: a ONR Flare topside vessel; b C11-class post-Panamax container ship; c ITTC A-1 container ship

Full size image

5 Results and discussion

The four methods newly proposed in this study are compared with the results of analytical or numerical calculations and model experiments. The abbreviations used in this section are given in Table 5.

Table 5 Explanations of abbreviations
Full size table

Firstly, the averaging method without the polynomial approximation of the calm-water GZ curve (ave_GZ) is compared with the averaging method with the polynomial approximation (the existing averaging method, ave_exg), numerical solutions of the uncoupled roll equation without the polynomial approximation (sim_1), and experiments (exp), as shown in Fig. 2. Throughout this paper, positive and negative Froude numbers indicate that the ship runs in following and heading waves, respectively. All methods here are conservatively able to predict the results of the experiments. This is because we neglect heaving and pitching effect on a roll restoring moment and assume that the GZ variation can be represented by the GM variation [24]. The ave_GZ gives almost the same results as those of both ave_exg and sim_1 for the ONR Flare topside vessel and the C11-class post-Panamax container ship. However, this is not so for the ITTC A-1 container ship; the ave_GZ well agree only with sim_1 in that case. This is because the accuracy of the approximate GZ curves is unsatisfactory only for the ITTC A-1 container ship, as shown in Fig. 1. Hence, the method using the more accurate GZ curves can be recommended for applying an averaging method.

Fig. 2
figure 2

Comparison of parametric roll amplitudes from the averaging methods with and without the polynomial approximation of the calm-water GZ curves in longitudinal waves: a ONR flare topside vessel with a wave steepness of 0.04; b C11-class post-Panamax container ship with a wave steepness of 0.01; c C11-class post-Panamax container ship with a wave steepness of 0.02; d C11-class post-Panamax container ship with a wave steepness of 0.03; e ITTC A-1 container ship with a wave steepness of 0.03

Full size image

Secondly, the averaging equations with superharmonics taken into account (ave_3ω) are compared with the existing averaging equations (ave_exg), the numerical solutions of the uncoupled roll equation with the polynomial approximation (sim_2), and the model experiments (exp), as shown in Fig. 3. All these methods can conservatively predict the experimental results as mentioned before. The accuracy of the estimation with the averaging method was drastically improved, especially if the parametric roll amplitudes were relatively large. This is because the superharmonic component, whose frequency is three times the fundamental parametric roll frequency (i.e., 3\(\hat{\omega}\)) is not negligibly small in the Fourier series expansion of a numerical solution of Eq. 2, as shown in Fig. 4.

Fig. 3
figure 3

Comparison of parametric roll amplitudes from the averaging methods with and without the 3ω superharmonics taken into account in longitudinal waves: a ONR flare topside vessel with a wave steepness of 0.04; b C11-class post-Panamax container ship with a wave steepness of 0.01; c C11-class post-Panamax container ship with a wave steepness of 0.02; d C11-class post-Panamax container ship with a wave steepness of 0.03; e ITTC A-1 container ship with a wave steepness of 0.03

Full size image
Fig. 4
figure 4

Amplitude ratio of each frequency component of parametric roll for the C11-class post-Panamax container ship with a Froude number of 0.015, a wavelength-to-ship length ratio of 1.0, and a wave steepness of 0.03

Full size image

Thirdly, the critical speed for parametric roll (Fn_cr) is also shown in Fig. 3. Each calculated critical speed is the relevant peak value of the existing averaging method, so the critical speed is not overlooked using this method.

Fourthly, two types of averaging equations that can estimate parametric roll in oblique waves (ave_O1 and ave_O2) are compared with the numerical solutions of Eq. 2 (sim_2) and the model experiments (exp) as shown in Fig. 5. Here, the ship’s forward speed in the analytical/numerical calculations was set as the mean value of the ship’s mean speed along the ship trajectory as measured in the eight runs shown in the bottom line of Table 2, with a Froude number of 0.0364. The roll motions shown in Fig. 5 do not disappear even when the heading angle is very large. This is because the ship is also forced to roll by the direct wave-excitation moment, which is given on the right-hand side of Eq. 2. In contrast, at the right-hand ends of the curves of the two averaging methods, the parametric roll amplitude [A in Eqs. 19 and 23] becomes zero. The averaging methods agree well with the numerical solutions and the experiments: ave_O2 is more accurate than ave_O1, especially around the heading of − 40°. There are some discrepancies between the averaging methods and the numerical simulation after parametric roll vanishes at a heading of roughly − 50°. Hence, any future modeling of the restoring variation in beam seas should be reconsidered.

Fig. 5
figure 5

Maximum and minimum roll angles of the ONR Flare topside vessel in oblique following waves whose length is 1.25 times longer than the ship length, and a wave steepness of 0.03

Full size image

6 Conclusions

Four new estimation methods concerning parametric roll were proposed. Firstly, an averaging method without using a polynomial approximation for the calm-water GZ curve can overcome the drawback of using an inaccurate polynomial approximation of the GZ curve. Secondly, an averaging method with superharmonics taken into account improves the estimation accuracy of the parametric roll amplitude. Thirdly, the critical speed for parametric roll can be estimated directly by using an averaging method. Fourthly, two estimation methods for parametric roll in oblique waves were proposed based on the concept of an averaging method. Finally, they were validated against numerical simulations and existing model experiments.