Introduction

The mean mass concentration of total particulate matter for gases in industrial plants is not determined in an ideal manner, that is, strictly in accordance with its definition for which the continuous distributions of total particulate matter concentration and gas velocity have to be known in the measurement plane of the installation. For technical reasons, the distribution of particulate matter concentration has not been identified in routine industrial measurements so far. The velocity distribution of gas is usually known approximately and discretely. Making it continuous would not be essentially an issue, although it would definitely extend the duration of field measuring sessions and would enlarge the handling of measurement results. For these reasons, the standard practice is that an approximate mean particulate matter concentration in the conduit is measured (i.e. duct or stack) based on gas sampling using the standard manual gravimetric method.

Manual gravimetric measurements of the mean mass concentration of particulate matter in waste gases are performed very often. They serve as the following: (1) a component of risk assessment for clean air from stationary sources of dust emissions, (2) the basis for the calibration of non-manual (automated) dust monitors, (3) a way to determine dust discharge in technological processes, and (4) a way to determine the efficiency of dust-removing devices. In the relevant international [1,2,3] and national standards (e.g. in Poland: [4] and Polish language versions of [1, 2]), for particulate pollutant emissions from stationary sources, there is a description of how to conduct these measurements by the gravimetric method and how to process their results. They also include general recommendations as to ways to estimate the uncertainty of the final measurement result obtained by applying the method. The necessity of reporting the uncertainty of the final result in measurement reports and—as a consequence—of taking it into account in exceeded emissions assessments is imposed by specific provisions, for example, in Poland, in the form of ministerial regulations [5, 6].

The measurements under discussion are complex by their nature, both because of the non-ideally stable functioning conditions of industrial plants, and because of the specific procedure for the averaged sampling of dust-laden gas, during which many physical quantities are measured and complex measuring systems are applied.

According to the procedure described in these standards, the measurement plane is located in the appropriate place in the industrial waste gas plant, and it coincides with the cross section of the conduit. At predetermined measurement (or sampling) points, the sample is collected sequentially and cumulatively so that, in relation to particulate matter concentration, it is representative for the entire section as much as possible; that is, the total particulate matter concentration in the sample is possibly closest to the true/accurate mean concentration of total particulate matter in the cross section. This is a key assumption of the gravimetric method. The concentration measured in the sample is considered to be the mean concentration in the conduit within an approximation regarded as sufficient. The mean concentration that actually occurs in the cross section depends, according to its definition, on the particulate matter concentration profile and velocity profile of the gas throughout the entire section. Naturally, the concentration in the sample depends on the level of the sample representativeness; therefore, there is some discrepancy between the concentration in the sample and the accurate mean concentration in the conduit. There are two aspects of representativeness. One is spatial representativeness, i.e. the extent to which the averaged sample represents the actual, continuous distribution of concentration. The other is local representativeness, which is representing the accuracy of the separate sampling of different dust particle sizes in gas from the sampling point.

When it comes to the local accuracy of sampling, the foremost requirements are isokinetic sampling conditions within the predetermined, acceptable limits. The influence of the acceptable anisokinetic sampling on the value of the total particulate matter concentration in the sample can be quantified in two ways, depending on the available data on the particle size distribution, gas parameters, and sampling conditions (e.g. the sampling characteristic of the entry nozzle, the precision of isoaxial position of the nozzle, or the turbulence of the duct gas flow), namely either by correcting the measured total concentration or by entering the appropriate component of measurement uncertainty. Some factors like turbulence that can affect the pressure difference measured by a Pitot tube as well as its calibration constant itself (both having an repercussion for maintaining isokinetic rate) or can influence the phenomenon of sampling the individual dust fractions, are in principle omitted (because of the lack of data or consciousness, or the insufficient state of today’s knowledge, regulations, or measuring instruments).

When it comes to the quantitative inclusion of spatial representativeness of the sample, applying a correction to the measured concentration value is impossible, since, at this point, the deviation has not been determined, and it is not recommended to adopt a given deviation in respect to the level of this type of representativeness. Moreover, its value is variable, depending on the specific continuous profiles of particulate matter concentration and gas velocity. Thus, what remains is the inclusion of the measurement uncertainty component. The evaluation of this component in the budget of overall particulate matter concentration uncertainty in the conduit is difficult. The VDI guidelines that have been discontinued [7] indicated the need of expertise for the measuring team necessary to make this assessment. Consequently, in practice, this uncertainty component is not estimated nor is it taken into account. If the value of the uncertainty component was known, it would function as a feature of the gravimetric method in the balance sheet of the uncertainty of a single mean concentration measurement, which is a balance sheet based on type B evaluation [8] and resulting from the broadest possible knowledge of the essence of the measurement method itself. The complementary issue of this problem is not discussed here, namely performing a series of several, repeated individual measurements, and determining uncertainty for them reflecting statistical dispersion of the results. Since the significance of gas velocity distribution was mentioned earlier, it should be noted as an aside that this distribution significantly influences the level of accuracy of another parameter, which is always of interest in gravimetric measurements of dust emissions, i.e. the mean gas velocity in the conduit (as in the case at issue in this article, also this influence is unfortunately overlooked in the analysis of measurement accuracy in mass flow rate of emitted dust, and it turns out that it is considerable [9]).

Thus, it was undertaken to find out whether omitting the uncertainty component of a single gravimetric measurement of mean particulate matter concentration (resulting from the presence of transverse distributions of particulate matter concentration and gas velocity in measurement plane) is justified, or, on the contrary, whether it should be included in the budget uncertainty along with other components. For this purpose, the task of developing a convenient way of estimating this uncertainty was undertaken. This article describes simulation calculations—with assumptions concerning conduits and flows—performed to determine the unavoidable measurement deviation of the mean concentration made in the binding gravimetric reference method that results from the multi-point sampling of gas. Based on the obtained possible values of this deviation, the uncertainty component was derived for the measured total particulate matter concentration throughout the entire section, reflecting the spatial representativeness of the sample.

It is worth realizing the level of this discussed uncertainty contribution of the spatial representativeness of the sample taken against the background of the other uncertainty components assigned to different phenomena, operations, properties, etc. influencing the measured particulate matter concentration. Among them, the most important are the following: an extensive group of factors deciding the already aforementioned local accuracy of sampling; the weighing, conditioning, handling, transportation, etc. of the filter; the determination of the aspirated gas sample volume (here: the influence of gas temperature, pressure and chemical composition measurements); the potential losses of the dust particles inside the sampling train (upstream of the filter); the filter separation efficiency; determining the oxygen concentration in context of possible particulate matter concentration conversion to the reference oxygen content; and finally, the also aforementioned statistical dispersion in the series of a few obtained particulate matter concentration measurement results, ensuing primarily from the non-ideal industrial measurement conditions.

The quantitative description of spatial representativeness of a sample

The flow of dust-laden gas and sampling it in the measurement plane of the waste gas plant is illustrated by Fig. 1 (for a rectangular section). Assuming steady conditions in the measurement plane with area F, there is a continuous distribution of total particulate matter concentration s(X, Y) and a continuous gas velocity distribution w(X, Y). X and Y are absolute coordinates in the measurement plane (further on, respective relative coordinates will be introduced). The global flow of the two-phase system (which is the dust-laden gas) through the measurement plane is described by two parameters: the particulate (total) mass flow rate M F (total dust mass flowing across the measurement plane area in a time unit) and gas volumetric flow rate Q F (gas volume flowing across the measurement plane area in a time unit). With that in mind, one can characterize the flowing dust-laden gas by means of a true, global particulate matter concentration, s av, being by its nature a space average concentration, given by Eq. 1. The connection between s av, s(X, Y) and w(X, Y) is presented in point (i), subpoint (a) of the Electronic Supplementary Material (ESM).

$$s_{{\text{av}}} \mathop = \limits^{{\text{def}}} \frac{{M_{\text{F}} }}{{Q_{\text{F}} }}$$
(1)
Fig. 1
figure 1

The quantities related to the flow and collection of a sample of dust-laden gas in the measurement plane against the background of the occurrence of spatial distributions of total particulate matter concentration s(X, Y) and gas velocity w(X, Y) (symbols are explained in the text of the article.)

Full size image

In the gravimetric measurement of the mean total particulate matter concentration, the sampling of aerosol takes place in the specified P i measurement points, in the component fields, CF, at N number of times (see “The idea for solving the task” section for details on the shape and number of component fields). All of the component fields that the measurement plane is divided into have the same area of F 0. The sampling nozzle, SN, remains at each point P i for the same duration of Δτ s; the inlet tip is round and has an area of F s (small in relation to the area of the measurement plane). The nozzle is moved to the consecutive points. The sampling is cumulative in character: The mass m s of the dust collected in a sample is the sum—for the total duration of sample collection throughout the entire measuring section—of all dust masses collected in the consecutive points, and the volume of gas in the sample (or: sample volume) V s is the sum—for the same total duration—of all volumes of suctioned gas in consecutive samplings. The total particulate matter concentration in the sample, i.e. the measured concentration, s m is according to [1, 3], the quotient of mass m s and volume V s:

$$s_{\text{m}} = \frac{{m_{\text{s}} }}{{V_{\text{s}} }}$$
(2)

Using Eq. 2, the s m is calculated and as such, it is adopted as the final result of the entire measurement. Both m s and V s values are determined in accordance with the standard sampling procedure (using the specified apparatus) and with common laboratory practice; both values are measured. It can be proved [see point (i), subpoint (b) of ESM] that the following relationship is true:

$$s_{\text{m}} = \frac{{\sum\nolimits_{i = 1}^{N} {s_{i} \,w_{i} } }}{{\sum\nolimits_{i = 1}^{N} {w_{i} } }}$$
(3)

where w i is the local gas velocity and s i is the local particulate matter concentration in the conduit at a given ith measurement point.

The gravimetric method assumes the following approximation of the spatial representativeness of a sample (which is precisely what is assessed in this paper): (1) point concentration s i at an ith sampling point P i in a given ith component field is approximately equivalent to the mean concentration for this component field, marked in Fig. 1 as \(\bar{s}_{i}\) and (2) point velocity w i at an ith measurement point P i in a given ith component field is approximately equivalent to the mean velocity for this component field, marked in Fig. 1 as \(\bar{w}_{i}\). In other words, the particulate mass flow rate flowing through an ith component field that is equal to exactly, according to its definition, \(M_{i} = \bar{s}_{i} \,\bar{w}_{i} \,F_{0}\), is assumed approximately as

$$M_{i} \approx s_{i} \,w_{i} \,F_{0}$$
(4)

As a result of this approximation, Eq. 3 for s m concentration, after multiplying the numerator and denominator by F 0, can be further formulated as

$$s_{\text{m}} = \frac{{\sum\nolimits_{i = 1}^{N} {s_{i} \,w_{i} \,F_{0} } }}{{\sum\nolimits_{i = 1}^{N} {w_{i} \,F_{0} } }} \approx \frac{{\sum\nolimits_{i = 1}^{N} {M_{i} } }}{{\sum\nolimits_{i = 1}^{N} {Q_{i} } }} = \frac{{M_{\text{F}} }}{{Q_{\text{F}} }}$$
(5)

where Q i , equal to the product of w i  F 0, constitutes volumetric flow rate of gas flowing through an ith component field.

Equations 5 and 1 indicate that the measurement quantity of s m, appropriate for a collected, almost representative sample, is an approximation of the true concentration s av: s m ≈ s av. These relationships are correct when one sampling nozzle is used for the entire measurement plane and also when several sampling nozzles are used (when the velocity profile is substantially non-uniform).

The discrepancy between the measured s m value from Eq. 2 and the searched true s av value is, in fact, a deviation of the gravimetric mean total concentration measurement.

The above quantitative formulation (complemented with details in ESM) has been adapted for the simulated flows (“The key calculated value: the deviation of total particulate matter concentration” section).

The flows of dust-laden waste gases in industrial plants

The starting point for the simulation studies was determining certain data concerning the actual flows of dust-laden gases in dust-removing plants, which would then be appropriately presented. A reliable and practical source of information about the actual flows of gas phase can be only found in the results of specific anemometric industrial measurements (in situ). The information can be gathered from reports of measurements conducted by different measurement teams for the standard auditing of compliance with emission level limits (although they are usually hard to obtain), or from reports on industrial plant research for scientific purposes (unfortunately rare, and some of them are out-of-date). The spatial profiles of gas velocity in the measurement planes have diversely non-uniform shapes. This non-uniformity depends on the shape of the installation, on the location of the measurement plane, and on the boundary conditions at the outlet of the dust collector or the dust generating process (the author’s article [9] and other sources cited there). When it comes to particulate matter concentration distributions across conduits in different places, their prediction by simple theoretical calculation of the transport of solids for industrial conditions solely based on certain models and the approximate knowledge of gas velocity does not give satisfactory results. It is because there are too many phenomena and data in such systems that are difficult to quantify and that play a role (sometimes a stochastic one) in the movement of dust particles inside the conduit [10, 11]. These include the non-homogeneity of particle sizes and their spatial distribution, sometimes a variation in dust density, the concentration field at the outlet of the dust removal device, or the dust generating source (often unknown). Other phenomena include the following: (a) turbulent diffusion; (b) inertial precipitation of dust on the walls of the conduit as a result of local high gas velocities in different locations of ducts; (c) dust retention on the walls due to low near-wall velocities; (d) collisions among dust particles, forces of adhesion and cohesion, and a resulting variable particle agglomeration; (e) re-entrainment of dust from the laminar sublayer; and (f) thermal phenomena. Practice shows that sedimentation deposition of dust in the ducts and the re-entrainment of such sediment escapes engineering and design criteria and is a common (and often dangerous) phenomenon. All these aspects make it difficult to predict the relationship between the gas velocity profile and the particulate matter concentration profile in the industrial flow conduit. For example, one cannot risk a claim that in the uniform flow of the gas phase the uniform dust flow definitely occurs. Moreover, sources with particulate matter concentration distribution measurement data are unfortunately very rare. Such measurements are not normally performed in industrial measurements, because they are not required by the regulations. Overall, when considering real (existing in industrial plants) gas velocity distributions and especially particulate matter concentration ones, one can only speak from a basis of very limited information (for example [2, 9, 12,13,14,15,16]). In studies related to spatial distribution of particulate matter concentration of dust removal plants, for example, those concerning its impact on the operation of dust collectors, approximate distributions are met as a result of CFD simulations [17, 18]. They can be used to approximate the recognition of possible flow-through situations in these plants. Some useful information can be found in the reports on dust-laden, process gases in industrial plants [19] or on flows in heavily dust-laden air in slightly different situations, i.e. in ventilated longitudinal spaces like roadways [20].

The relevant description, from the point of view of the planned simulation here of the actual streams of dust-laden gases, for which gravimetric measurements are made, can be summed up in the following statements:

  1. (1)

    Inevitably, the locations in the industrial plants that disturb the flow in the conduits cause, at different distances from these places, the local gas velocities within a given section (excluding zero velocity on the walls of the conduits) can differ by several folds, and velocity profiles are jagged, with a large number of local extrema in the entire cross section of the conduit.

  2. (2)

    Maintaining the condition for at least a few hydraulic diameters in a straight conduit before and after the measurement plane and applying appropriate elements of the ductwork limit the cases of non-uniform gas velocity profiles in a section where the ratio of highest to lowest local gas velocity measured at sampling points α w is less than 3:1, which is also a standard requirement [1,2,3]. The best uniformity of the flow of dust-laden gas is also manifest in the co-axial local flows in relation to the conduit walls and consequently to the axis of the sampling probe head, with acceptable small deviations from their directions. (This is one of the conditions for the possibly highest point-related representativeness for the collection of individual particulate fractions.)

  3. (3)

    There is often no simple, evident, and predictable correlation between the gas velocity profile and the particulate matter concentration profile within the measurement plane. In principle, one can only talk about the different associations of velocity and concentration profiles.

  4. (4)

    The local particulate matter concentrations within the cross section of the conduit can vary several folds, which can be translated into the relevant ratio value of the greatest to the smallest concentration α s.

The idea for solving the task

The task of estimating the uncertainty for a single gravimetric measurement of mean particulate matter concentration resulting from the point penetration of cross-sectional distributions of particulate matter concentration and gas velocity in the measurement plane (that is, in the cross section of the conduit) was solved through the simulation of the measurement situations.

For the analysis, typical rectangular cross sections were assumed, i.e. with the ratio of the sides no more than 2:1. According to the standards [1,2,3], in these sections with an area between 0.10 m2 and 1.00 m2, the minimum number of sampling points in the direction of one side N 0 is, depending on the standard, either 2 (EN) or 3 (ISO). This gives the number of measurement points in the entire section N between 4 and 9. For very small cross sections, with an area less than 0.1 m2, there is one measurement point approved (in the cross-sectional centre), but this situation carries the expected large errors and moreover is rare in industrial plants; thus, they were not taken into account in this paper. For cross sections greater than 1 m2, the minimum number of points N increases; for example, for 4 m2 the number of points is 16. In the study, the recommendations of both EN standards presented in Table 1 were assumed as the basis for calculations. The data contained in the table reflect the view that, in larger conduit cross sections, the profiles of particulate matter concentration will be well represented by sampling, if, for each square metre of the section, the number of points will be at least 4. In every day practice, the most common case is N = 4 (N 0 = 2). The situation where N > 4 is less common and appears for special measurements with an expected higher accuracy (that is, the spatial representativeness). In these studies, the focus was on cross sections with the area more than about 1 m2.

Table 1 The minimum number of measurement points in a gravimetric measurement of particulate matter concentration in the conduit. (Adapted from the standards [1, 2])
Full size table

Considering the significance of Table 1, the following notion is suggested. The measurement plane can be roughly divided into modular, elementary rectangles, termed “base planes”, with the length of the sides’ ratio of L to M (in an absolute coordinate system 0XY) not more than 2:1 and the area of about 1 m2 (e.g. 0.7 m × 1.3 m, 0.9 m × 1.2 m, 1.1 m × 1.1 m). This feature is typical for a large number of conduits. The base plane contains measurement points P i , with each representing one rectangular component field CF i . The number of measurement points and thus component fields in a base plane equal n (i = 1, …, n). This number is at least 4; the number of measurement points along a given side, designated n 0, is, therefore, at least 2. The case of n = 4 (n 0 = 2) was adopted as the basic case, and Fig. 2 serves as an illustration. One can also imagine that the base plane consists of, for example, n = 6 points (along one side n 0 = 2, along the other n 0 = 3) or n = 9 points (for each side n 0 = 3), when a greater measurement accuracy is desired. For the base plane, a relative coordinate system 0xy was introduced where x = X/L and y = Y/M. The length of both sides of the base plane in this case equals 1. The relative distances of individual measurement points from the edge of the base plane were marked as x k and y k , where k = 1, …, n 0.

Fig. 2
figure 2

An illustration of the assumptions for the base planes (in this case, when n 0 = 2, n = 4). CF denotes a component field and P a measurement point. a Measurement plane with base planes and b base plane

Full size image

In the base plane, different base profiles of particulate matter concentration and gas velocity are simulated, between which there is no clear correlation. There can be various combinations of velocity and concentration profiles, and these combinations are equally probable. Using simulation profiles, a calculation is performed for the base plane for a given combination of particulate matter concentration and gas velocity profiles of an accurate mean total particulate matter concentration, and the total particulate matter concentration in the sample and, as a result, the divergence between these concentrations, namely the measurement deviation of total concentration. Based on the set of simulated values of possible measurement deviations, the end-result measurement uncertainty of concentration in the base plane is determined, and the uncertainty of this is attributed to the whole measurement plane (composed of base planes).

The simulation calculation of the total concentration deviation

Base simulation distributions

In the base profile, there are artificially generated, continuous, spatial base distributions that are irregular (the profiles) with the relative particulate matter concentration c and relative gas velocity v that is co-axial in relation to the walls of the conduit, which are described by a polynomial function of two variables x and y. A simplifying assumption was adopted that these are profiles that do not have values equal to or approximating zero, i.e. those that only occur on and next to the walls of the conduit, namely in a microscopically small portion of the profile in the entire cross section of the conduit.

Nine simulation base profiles of the concentration c(x, y) were adopted, indicated with the letter C, and thus symbols C1, C2,…, C9, described by the ratio, where the highest to lowest value of c in the profile α c = c max/c min is between 1.5 and 5. Three profiles have α c approximately equal to 1.5, three are approximately equal to 3, and three are approximately equal to 5. The general mathematical form of the profiles is provided in Eq. 6, and the coefficients are in Table E1 in point (ii), subpoint (a) of ESM.

$$c\left( {x, y} \right) = \beta_{1} x^{3} y^{2} + \beta_{2} x^{3} y + \beta_{3} x^{3} + \gamma_{1} x^{2} y^{2} + \gamma_{2} x^{2} y + \gamma_{3} x^{2} + \varepsilon_{1} xy^{2} + \varepsilon_{2} xy + \varepsilon_{3} x + \zeta_{1} y^{2} + \zeta_{2} y + \zeta_{3}$$
(6)

In addition to the non-uniformity index α c (which can be also termed the span of the concentration profile), the shape of each C1–C9 function is described by the following feature: In every plane along the x direction, there are at most two local extrema, and in the y direction, there is at most one extremum. This is illustrated (for the C3 function, α c = 1.49) in Fig. 3.

Fig. 3
figure 3

An example of a spatial representation of the simulated base distribution of the relative particulate matter concentration c(x, y): profile C3, α c = c max/c min = 1.49

Full size image

Nine simulation velocity base profiles v(x, y) were adopted, indicated by a V, thus having V1, V2, …, V9 symbols, characterized by the ratio between the greatest and the smallest value of v in the profile α v = v max/v min, which is between 1.5 and 3. Three profiles have α v approximately equal to 1.5, three are approximately equal to 2, and three are approximately equal to 3. The general mathematical form of the profiles is provided in Eq. 7, while the coefficients are in Table E2 in point (ii), subpoint (a) of ESM.

$$v\left( {x, y} \right) = \eta_{1} x^{3} y^{2} + \eta_{2} x^{3} y + \eta_{3} x^{3} + \theta_{1} x^{2} y^{2} + \theta_{2} x^{2} y + \theta_{3} x^{2} + \kappa_{1} xy^{2} + \kappa_{2} xy + \kappa_{3} x + \lambda_{1} y^{2} + \lambda_{2} y + \lambda_{3}$$
(7)

Apart from the non-uniformity index α v (which can be termed as the span of the velocity profile), the shape of each of V1–V9 functions is described by the following feature: in every plane, along x, there are at most two local extrema, and no more than one extremum along y. A base velocity profile (for the function V4, α v = 2.07) is illustrated in Fig. 4.

Fig. 4
figure 4

An example of a spatial representation of the simulated base distribution of the relative gas velocity v(x, y): profile V4, α v = v max/v min = 2.07

Full size image

Additionally, in comparative calculations, an ideally uniform velocity profile was used V0: w(x, y) = 1 (naturally, with the index: α v = 1).

More definite data on the construction of profiles c(x, y) and v(x, y) are presented in point (ii), subpoint (b) of ESM.

Evaluation of the adopted simplification

The simplification consisting in the omission of values that are near or are equal to zero in the base profiles c(x, y) and v(x, y) is equivalent to a broader simplifying assumption, namely the non-inclusion in this study of these extremely low values specific for the direct proximity of the conduit walls in the entire cross section of the conduit. Although it is well known that this particular fragment of the section right next to the walls with practically zero velocities is very small, this broader simplification was subjected to quantitative evaluation.

To that end, a certain test calculation was carried out for a sample, straightforward in-duct flow situation. The description of the test is found in point (iii) of ESM. For a typical uniform, turbulent, co-axial gas flow in a circular cross section conduit, it was demonstrated that excluding the laminar sublayer results in the reduction in volumetric flow rate in different cases of at most 0.3 %. Such minimally reduced flow may be treated within an excellent approximation as attributed to the whole conduit interior.

The test result constitutes the rationale for the general assumptions carried out in the simulation, i.e. to remove from each total conduit flow the laminar sublayer and consequently to construct the total velocity profile from base profiles in which there are only velocities that are characteristic for the internal, non-uniform turbulent flow (i.e. from the core and partly from the buffer layer). This simplification allowed for an easy modelling of the non-uniform base velocity profile using one function with two variables (for a given cross section) without taking up additional flow modelling in the laminar sublayer.

Similarly to the gas velocity distribution, the distribution of particulate matter concentration also results from the shape of the installation, not to mention the fact that it can be additionally associated with a specific size of dust particles. In the light of these estimates, a hypothesis was put forward that the omission of the very thin layer right next to the wall will result in a similarly negligible error when it comes to particulate matter concentration distribution in the entire section. Therefore, in the base profile simulations for particulate matter concentration, there are only those values that belong to the principal non-uniform profile for the concentration inside the conduit. The benefit of this simplification of particulate matter concentration distribution is the same as for gas velocity.

The key calculated value: the deviation of total particulate matter concentration

All combinations of particulate matter concentration profiles C1–C9 and gas velocity profiles V0–V9 were taken into account in base planes—a total of 90 cases. For the base plane, the same assumptions were adopted, for which Eqs. 1–5 and Eqs. E1–E2 (from ESM) are true for the entire actual measurement plane, and Eq. 3 and Eq. E1 (from ESM) were adopted for the base plane with a pair of simulation fields of c(x, y) and v(x, y). Following are the calculations done for each given pair.

A true and accurate mean relative particulate matter concentration occurring in a given base plane c av was calculated by a suitable integration using the continuous functions c(x, y) and v(x, y), as described in point (iv), subpoint (a) of ESM.

Sampling was simulated in the same base plane at n points (along the side, at n 0 points). The primary variant adopted for calculation, corresponding to the least number of points required by the standards, is n = 4 (n 0 = 2). Moreover, one real-life surplus variant was adopted for n = 9 (n 0 = 3) and, practically hardly ever used, two surplus variants for n = 16 (n 0 = 4) and n = 36 (n 0 = 6). These latter two have been introduced for a more certain understanding of the expected regularities in the changeable concentration results in the simulation sample.

At the (x k , y k ) coordinate points [see point (iv), subpoint (b) of ESM for details], the following ith values were calculated for c(x, y) and v(x, y) polynomials: c i and v i . These values were inserted into Eq. 8, which is analogous to Eq. 3, thus providing the relative particulate matter concentration in the simulation sample c m. This value is not burdened with any error in this method.

$$c_{\text{m}} = \frac{{\sum\nolimits_{i = 1}^{n} {c_{i} \,v_{i} } }}{{\sum\nolimits_{i = 1}^{n} {v_{i} } }}$$
(8)

The relative deviation δ for the measured concentration c m was calculated in reference to the value of the measured concentration as the following:

$$\delta = \frac{{\mathop c\nolimits_{\text{m}} - \mathop c\nolimits_{{\text{av}}} }}{{\mathop c\nolimits_{\text{m}} }} = 1 - \frac{{\mathop c\nolimits_{{\text{av}}} }}{{\mathop c\nolimits_{\text{m}} }}$$
(9)

The deviation defined in this way allows one to determine, based on its distribution, the relative uncertainty of measured concentrations c m in relation to the c m value. Only the deviation constructed in this way may have a practical application.

Calculation results

The results of the calculations in the deviation in measured particulate matter concentration δ according to Eq. 9 {using Eq. E3 [see ESM, point (iv), subpoint (a)] and Eq. 8} were gathered in the form of four tabular listings, each for a given value of number of measurement points n. The exemplary data, namely covering the most important case n = 4, are placed in Table E3 in point (v) of ESM. The table contains δ values for 90 combinations of particulate matter concentration profiles (with a division of α c = 1.5, 3, and 5) and gas velocity profiles (with a division of α v = 1, 1.5, 2, and 3). Such a tabular listing allows identifying which combination of two profiles C + V yields what value of particulate matter concentration measurement deviation δ, whereas what makes the variation of δ values together with α c, α v and n possible to be observed and statistically analysed is the suitable graphical representation of δ values. For the mentioned, sample case n = 4, such graphical representation is shown in Fig. 5. The sets of calculated deviations δ obtained for all remaining cases of n: 9, 16, and 36 are presented graphically in Figs. E1–E3 in point (v) of ESM.

Fig. 5
figure 5

The deviation of mean particulate matter concentration in the base plane δ, depending on the index of non-uniformity of particulate matter concentration profile α c and depending on the index of the non-uniformity of gas velocity profile α v—for the number of measurement points n = 4. a α v = 1, b α v = 1.5, c α v = 2, and d α v = 3

Full size image

Determining the uncertainty of total particulate matter concentration

Let us consider the illustration of particulate matter concentration deviation values in the exemplary Fig. 5. In the four graphs a, b, c, and d, the layout of the deviation values δ clearly indicates that, within individual sets of δ values (i.e. roughly in the vertical sets of points marked by empty circles) assigned to the subsequent values of α c, approximated to 1.5, 3, and 5, there are no regular distributions of the deviation. In the position of these sets, against the backdrop of the variable α c index, there is no manifest existence of a systematic component, for example, permanent excess or a permanent deficit of c m in relation to c av. The δ deviation for a given value of α c has a rectangular distribution, because all error-causing simulated flow situations (namely c(x, y) and v(x, y) combinations) are equally probable. Thus, the maximum deviation is sought (or boundary deviation) δ max. The δ values are within a field delimited by envelopes: positive (top) and negative (bottom), representing, respectively, an extreme positive deviation equal to δ max, and an extreme negative deviation, equal to −δ max. Moreover, among the a, b, c, and d charts, there are no significant differences that might indicate an influence of non-uniformity index for velocity profile α v on δ and consequently on δ max. Therefore, for a given number of n points, the same pair of envelopes was adopted for all α v values together, which by definition crosses point (1, 0). The same regularities as described above appear in all other cases of n, i.e. in Figs. E1–E3 in point (v) of ESM. The envelopes for all n values were found to be logarithmic functions—as purely approximation, “tool” functions δ max(α c)—that best fulfil the following conditions: (1) in the space of a given n, the top and bottom envelopes have to be symmetric (theoretically infinitive number of positive and negative δ values would fill a symmetric area); (2) function δ max(α c) must be monotonically increasing, without local extrema, because the following expected influence of α c is intended to be reflected: the more non-uniformity of local particulate matter concentration distribution the higher possible non-representativeness of discrete sampling; (3) the pair of envelopes δ max(α c) and −δ max(α c) should embody all calculated δ values while passing as precisely as possible through the edge ones. This does not mean that, for a given n, the envelope is to pass through each edge δ value, since the calculation cases are not here all possible ones (which, in reality, occur in infinite number); (4) the envelope δ max(α c) must pass through point (1; 0). For an idealized, absolutely flat profile of particulate matter concentration, the concentration in the sample of dust-laden gas will always be, regardless of the number of sampling points for this sample, equal to the concentration in the conduit. Sampling deviation (identical to δ max) will then be zero. For this profile, α c coefficient is naturally equal to 1; and (5) the mathematical, approximation model of envelope δ max(α c) must be the same for each n (4, 9, 16 and 36) so that this function could be parameterized by n.

The logarithmic description of the shape of the positive envelopes δ max = f(α c) was proposed as the most accurate and practical in use both for the case n = 4 (as presented in Fig. 5) and for all remaining cases of n values. All the relationships δ max = f(α c) were generalized as one function δ max = f(n, α c). The details are accessible in point (vi) of ESM.

Since the width of a rectangular distribution, which is here equal to the maximum (positive) deviation δ max, divided by the square root of 3 yields the standard uncertainty u [8, 21], there is the following relationship \(u = {{\mathop \delta \nolimits_{\hbox{max} } } \mathord{\left/ {\vphantom {{\mathop \delta \nolimits_{\hbox{max} } } {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}\) and, in consequence, standard uncertainty u as a function of two variables n and α c, derived based on the obtained generalized function δ max = f(n, α c), is the following:

$$u = 0.18475\,n^{{{-}1.12}} \,{ \ln }\,a_{\text{c}}$$
(10)

The level of u value according to Eq. 10 is sufficiently greater than the described earlier uncertainty in the applied method (estimated at <0.1 %) that it will be omitted here for convenience. Including it according to the formula \(\sqrt {\left( {0.18475\,n^{ - 1.12} \,{ \ln }\,\alpha_{\text{c}} } \right)^{2} + 0.001^{2} }\) would introduce an insignificant correction.

Discussion

The found uncertainty corresponds with the relative c and v modelled profiles. If we imagine the profile of particulate matter concentration in absolute values in the base plane, with specified units (e.g. mg/m3) and, similarly, the velocity profile of gas in absolute values, with specified units (e.g. m/s), then the established deviation δ max as well as uncertainty u (Eq. 10) will be the same for these absolute profiles and for the relative profiles. The index for the relative concentration, α c = c max/c min, will be equal to absolute concentration index, α s = s max/s min.

In the classical approach to determine the expanded (formerly overall) uncertainty, individual standard uncertainties (obtained by Type A and B evaluations) are compiled first, then the combined standard uncertainty is calculated, and finally it is multiplied by a coverage factor, usually adopted as equal to 2 to ensure a confidence level of roughly 95 %, also for rectangular distribution [8, 21, 22]. In practice, it is a frequent approach where the needed uncertainty components are available in the form of the uncertainties valid for the above-mentioned confidence level. They are twice as large in relation to the standard uncertainty components. Therefore, the relative, and corresponding to a confidence level of approx. 95 %, uncertainty component for the gravimetric measurement of the mean concentration of particulate matter responsible for one source of possible measurement deviation considered here, namely caused by particulate matter concentration absolute profile and gas velocity absolute profile in the base plane, marked here with U, was introduced and is expressed with sufficient accuracy by the following equation, valid at least for the modelled cases of said distributions:

$$U = 0.37\,n^{{{-}1.12}} \,{ \ln }\,a_{\text{s}}$$
(11)

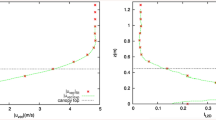
The span of gas velocity profile, which is the ratio of the highest to lowest velocity value, does not affect the measurement uncertainty of mean particulate matter concentration in the base plane; the α w value, as shown, does not appear in Eq. 11. The factors that do have influence include the span of particulate matter concentration profile (the ratio of the highest to lowest concentration value) and the number of sampling points in the base plane. A graphic representation of the function from Eq. 11 for selected values of α s is shown in Fig. 6. Equation 11 is correct for α s in the range between 1 and 5, and for n in the range between 4 and 36. The U values are highlighted that were calculated using Eq. 11 for the most common variant n = 4 (black circles) and for one surplus variant n = 9 (empty circles).

Fig. 6
figure 6

The relative uncertainty component of the mean particulate matter concentration measurement U, at a confidence level of approx. 95 %, caused by a several-point sample collection depending on the index of the non-uniformity of particulate matter concentration profile α s and the number of points in the base plane n as a function described by Eq. 11. The points ● and ○ are the calculated values of the function (suggested for the inclusion in the uncertainty budget): ● refers to the basic, most common variant n = 4, ○ to the surplus variant n = 9

Full size image

Let us, in turn, pass on to some more general aspect. As indicated in “The flows of dust-laden waste gases in industrial plants” section, one can agree that the real non-uniformity of particulate matter concentration and gas velocity profiles may be expressed by some well-approximated parameters (maximum α w and α s, and the occurrence of local extrema). The simulated profiles fulfil those parameters; therefore, they may be treated as at least partial representation of real cases. In this connection, the obtained simulated uncertainty may be considered as that giving the imagination of anyway not less level of actual (if determinable at all) uncertainty. It is proposed, by way of a good approximation, to use this fixed uncertainty for estimating the influence of “measurement sampling discretization” under not precisely identified continuous distributions of particulate matter concentrations and gas velocity in industrial conditions.

The relationship shown in Eq. 11 can have a practical application for adopting the uncertainty under consideration in relation to the mean particulate matter concentration measurement in the conduit in the way presented through the examples placed in point (vii) of ESM.

Conclusion

The calculations conducted in this study for simulated profiles of particulate matter concentration and gas velocity in dust-laden flue gas conduits show that the difference between total particulate matter concentration measured by the gravimetric method (which is ascribed to the sample of dust-laden gas) and the actual mean concentration in the entire stream flowing in the conduit resulting from multi-point sampling can be significant. The relative deviation of the measured total particulate matter concentration very clearly depends on the number of sampling points and the shape of particulate matter concentration profile in the conduit. There is also a weak dependence related to the shape of the gas velocity profile. The value of this deviation for the adopted simulation profiles reaches the level of 8–10 % in extreme conditions. Simulations were performed for the typical rectangular channels where the ratio of the sides’ lengths is less than 2:1.

Since the distributions of concentration are not well known in the measurement practice, relationships were developed (Eq. 11 or Fig. 6) that reflect the uncertainty component of gravimetric, reference measurement of mean particulate matter concentration. For practical application purposes of this calculation tool in specific sampling of dust-laden gas in a measurement plane, it is crucial to be able to most reliably estimate the span of particulate matter concentration profile in this plane α s, namely the ratio of the highest to the lowest concentration value, in modular, component fragments of the entire section (called here the base planes) with an area of about 1 m2, that can notionally constitute the entire section. Another necessary known value is the number of sampling points n applied in a given measurement per one square metre, as a consequence of applying the standard regulations. The suggested Eq. 11 (and Fig. 6) shows that, for the basic standard-imposed number of measurement points n equal to 4, the measurement uncertainty component of the mean particulate matter concentration (at a confidence level of approx. 95 %), due to the existence of the distribution of local concentrations, is, for example, from about 3 % to about 5.5 %, for α s from 1.5 to 2. Naturally, increasing the number of measurement points decreases uncertainty, e.g. for n = 9 an analogous uncertainty is between 1.3 % and 2.2 %. Conversely, in distributions with greater spans α s, greater uncertainty is to be expected, for example, with n = 4 and α s = 3, the uncertainty will be over 8.5 %. The span of the gas velocity profile (the ratio of maximum to minimum velocity) does not affect this uncertainty.

The cited several per cent levels of the uncertainty component of the mean particulate matter concentration must be considered high, and they are not to be omitted in the budget of the expanded uncertainty of this concentration. The presented results of simulation calculations can be considered as a quantitatively recognized new element of metrological description of a common measuring procedure that constitutes the gravimetric method within this simulation. Like many other estimates of uncertainty, the one proposed here also depends on the assumptions and methodology. However, it definitely provides the view of the importance of issues that has been overlooked so far and of the need to include it in the analysis of the measurements. Naturally, estimating the required index of the non-uniformity of the base concentration profile α s can sometimes be difficult, especially in absence of advanced experience of the measuring team. However, this should not be an excuse for the total exclusion of the uncertainty component considered here.