1 Introduction

The growth of financial markets has led to the same set of institutional investors, such as Vanguard, BlackRock, State Street, and Fidelity, holding substantial shares in major listed firms that compete in the same industries.Footnote 1 If these firms are concerned about the interests of these common owners, then they are indirectly concerned about other firms’ profits. This means that these firms’ payoffs are dependent on each other. Hence, they may deviate from profit-maximizing behavior. In addition, several firms in the same industry hold minor shares in each other (cross-shareholding).Footnote 2 This common, or overlapping, ownership among competing firms may affect their behavior and yield anti-competitive outcomes. Common ownership has become a central issue in recent debates on antitrust policies, and some empirical studies show that it has a substantial effect on the strategic behavior of firms held by institutional stockholders.Footnote 3 Azar et al. (2018) study common ownership in the US airline industry and find that ticket prices are higher under common ownership. Azar et al. (2019) provide evidence that common ownership and cross-ownership increase monopsony power in the banking industry.

On one hand, common ownership restricts competition in product or service markets and raises prices. On the other hand, partial ownership by common owners in the same industries may internalize industry-wide externalities and improve welfare. López and Vives (2019) point out that common ownership internalizes the spillover effect of R &D and may accelerate welfare-improving R &D. Sato and Matsumura (2020) show that common ownership internalizes the business-stealing effect in free-entry markets and moderate common ownership may improve welfare.Footnote 4

In this study, we discuss how common ownership affects firms’ locations and welfare. We introduce common ownership in the standard two-stage delivered pricing model formulated by Hurter and Lederer (1985).Footnote 5 In the model, two firms choose their locations on the Hotelling line (Hotelling 1929) and then compete in prices. The firms deliver their products from their locations to consumers and determine delivered prices at each market point. A continuum of consumers is uniformly distributed in the interval [0, 1] and each of them purchases one unit of goods from the firm offering a lower price. As expected, common ownership restricts competition and directly raises prices, given the locations. However, under our assumption of inelastic total demand (each consumer purchases one unit of the product), the high prices do not yield a welfare loss. Nevertheless, we show that common ownership harms welfare because it distorts the locations. Although how common ownership affects the location choice of each firm depends on the degree of common ownership and asymmetry in transport costs between the two firms, an increase in the degree of common ownership always induces excessive dispersion of firms’ locations, which harms welfare. In other words, we show another unknown channel for welfare loss due to common ownership.

We then endogenize transport costs in the delivered pricing model. Firms engage in transport cost-reducing investments and then play a location-price game. We show that equilibrium investments are excessive for welfare, and common ownership promotes investments. In other words, common ownership accelerates welfare loss because of excessive investments. This also creates an unknown channel for welfare loss caused by common ownership.

In a spatial price discrimination model, we can interpret "space" as product varieties and each firm’s location as its most efficient sector. We can also interpret distant locations as a firm’s inefficient sectors. For example, in the automobile industry, "space" represents car size, for instance, and a firm’s location indicates that the firm produces small cars efficiently but large cars inefficiently.Footnote 6 Following this interpretation, our result suggests that common ownership may yield excessive technology differentiation among firms.Footnote 7

This interpretation of space is similar to that of Anderson and de Palma (1988), Eaton and Schmitt (1994), and Norman and Thisse (1999). To explain flexible manufacturing systems (FMSs), they use spatial price discrimination models. They interpret that the location of a firm corresponds to their "base product," each of the other points corresponds to a "customized product", and the transport cost corresponds to the cost of customization. Following this interpretation, our result suggests that common ownership may yield excessive differentiation of basic products among firms, and accelerates excessive flexibility in FMS when the degree of common ownership is large. We believe that our analysis is also applicable to nonspatial contexts.

Our analysis also relates to a string of literature on cooperation. Cyert and DeGroot (1973) discussed the possibility of firms maximizing a linear combination of their profits and those of their rivals by introducing the concept of coefficient of cooperation. In their model, learning behaviors make this collaboration possible. Escrihuela-Villar (2015) showed the same result can be achieved by the conjectural variation approach. In addition to learning behavior and conjectural variation approach, common ownership can be considered as another way to rationalize why firms take into account the profits of their rivals when maximizing profits. Moreover, another group of studies is about cross-ownership between public and private firms. Jain and Pal (2012), Cai and Karasawa-Ohtashiro (2015). These papers are focused on mixed oligopoly and analyze the impact of the presence of cross-ownership on privatization policies. The most recent work, Heywood and Wang (2020), also discussed the possibility of cooperation on transport costs between firms that have a competitive relationship. They demonstrate that firms may collude to increase transport costs under repeated games. Whereas in our study, even without repeated games, the presence of common ownership distorts the equilibrium locations and leads to excessive investment in reducing transport costs.

The remainder of the paper is organized as follows. Section 2 formulates a model. Section 3 presents an analysis of equilibrium prices and locations. Section 4 discusses welfare implications. Section 5 endogenizes transport costs and presents another distortion of common ownership. Section 6 concludes. All proofs of propositions are relegated to the Appendix.

2 Model

We consider a two-stage location-price model in a linear space [0, 1], in which two firms produce a homogeneous product. We investigate a shipping model in which firms deliver their products from their locations to consumers and determine delivered prices at each market point.

A continuum of consumers is uniformly distributed in the interval [0, 1] and each of them purchases one unit of goods from the firm offering a lower price. The utility level of a consumer at location x is given by \(u(x)=U-p(x)\), where U is a sufficiently large positive constant, and p(x) is the price at location \(x \in [0,1]\). We assume that U is sufficiently large that the constraint \(p(x) \le U\) is not binding.

The two-stage game runs as follows. In the first stage, each firm i chooses its location \(x_i \in [0,1]\) \((i =1,2)\) independently. Without loss of generality, we assume that \(x_1 \le x_2.\) Each firm i pays the transportation cost \(t_i|x-x_i|\) to ship one unit of product from its own location to a consumer at point x, where \(t_i\) is a positive constant. Without loss of generality, we assume \(t_1 \le t_2\). We also assume that the common marginal production costs are constant and normalized to zero.

In the second stage, after observing the firms’ locations, each firm i simultaneously chooses \(p_i(x) \in [0, \infty )\) for \(x \in [0,1].\) Firms are able to discriminate among consumers since they control transportation. Consumer arbitrage is assumed to be prohibitively expensive. These are standard assumptions in the literature (Hurter and Lederer 1985; Lederer and Hurter 1986; Hamilton et al. 1989).

Following the recent theoretical literature on common ownership (López and Vives 2019), we assume that each firm i has the following objective function

$$\begin{aligned} \psi _i=\Pi _i+\lambda _i \Pi _j, \end{aligned}$$

where \(\Pi _i\) is firm i’s profit, \(\Pi _j\) is its rival’s profit, and \(\lambda _i\) is the shareholding of firm i in firm j. Furthermore, to ensure the independence of the two firms, we investigate the case where \(\lambda _i \in [0,1/2]\) in following context, implying that neither firm has a controlling interest in the rival’s firm. To guarantee an interior solution (\(0< x_1^L, x_2^L < 1\) ), we need additional assumptions about the parameters as follows:

$$\begin{aligned} \frac{2(1-\lambda _1)\lambda _2}{(1+\lambda _1 \lambda _2)(1-\lambda _2)} \le \frac{t_1}{t_2} \le \frac{(1-\lambda _1 \lambda _2)(1-\lambda _1)(1+\lambda _2)-2(1-\lambda _2)^2\lambda _1}{2(1-\lambda _2)^2\lambda _1}. \end{aligned}$$

We adopt the subgame perfect Nash equilibrium as the equilibrium concept, and, thus, we solve the game by backward induction.

3 Equilibrium

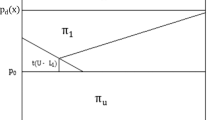
First, we discuss the second-stage price competition. Let \(\bar{x}\) be the point where both firms’ transport costs are the same (i.e., \(t_1(\bar{x}-x_1)=t_2(x_2-\bar{x})\)). It is well-known that in a general delivered pricing model, the firm with the lower cost obtains the market at x and the equilibrium price is equal to the price that the rival names. Firm 1 obtains market \(x \in [0, \bar{x}]\), and firm 2 obtains market \(x \in (\bar{x},1].\)

Suppose that \(\lambda _i=0 (i=1,2)\). For market \(x \in [0, \bar{x}]\), the equilibrium price is equal to firm 2’s marginal cost, \(t_2(x_2-x)\). When the price is \(t_2(x_2-x)\), firm 2 is indifferent to obtaining the market at the price or not obtaining the market. Thus, firm 2 has no incentive to undercut this price, and thus, it is the Bertrand equilibrium price (the thick line in Fig.1 ).

Fig. 1
figure 1

Price schedule when \(\lambda _1=\lambda _2=0\)

Full size image

Suppose that \(\lambda _i>0\ (i=1,2)\). Firm 2 gains a positive payoff \(\lambda _2 (p(x)-t_1|x-x_1|)\) at market \(x \le \bar{x}\), even when it does not serve. Its payoff at market x is \(p(x)-t_2(x_2-x)\) when it serves. Therefore, the indifferent price level for firm 2 will be

$$\begin{aligned} p(x)=\frac{t_2\vert x-x_1\vert -\lambda _2 t_1\vert x-x_2 \vert }{1-\lambda _2}, \end{aligned}$$

and it is the equilibrium price.Footnote 8

When \(\lambda _i=0\), the equilibrium prices in the markets that firm 1 serves depend only on firm 2’s marginal costs. By contrast, under common ownership, they also depend on firm 1’s marginal cost. A decrease in firm 1’s cost at market x increases firm 1’s profit in market x and reduces firm 2’s incentive for undercutting, which leads to this property. Let the superscript ’P’ denote the second-stage equilibrium (’price’ competition game given firms’ locations). In summary, firm 1 (2) serves the market where \(x \le \bar{x}\) (\(x>\bar{x}\)), and the price at each x is given by (the thick line in Fig. 2)

$$\begin{aligned} p^P(x;\,x_1,x_2) = \left\{ \begin{array}{ll} \frac{t_2\vert x-x_2\vert -\lambda _2 t_1\vert x-x_1\vert }{1-\lambda _2} &{} \text{ if } \ x \le \bar{x}, \\ \frac{t_1\vert x-x_1\vert -\lambda _1 t_2\vert x-x_2\vert }{1-\lambda _1} &{} \text{ if } \ x > \bar{x}. \end{array} \right. \end{aligned}$$
Fig. 2
figure 2

Price schedule when \(\lambda _1=\lambda _2>0\)

Full size image

Second, we discuss the location choice. In the first stage, each firm i chooses its location \(x_i\) to maximize its payoff \(\psi _i(x_i,x_j)=\Pi _i+\lambda _i \Pi _j\) \((i,j =1,2, \ i \ne j)\). The objective functions are given by

$$\begin{aligned} \psi _1(x_1,x_2)= & {} \int _0^{\bar{x}} \left[ \frac{t_2\vert x-x_2\vert -\lambda _2 t_1\vert x-x_1\vert }{1-\lambda _2}-t_1\vert x-x_1\vert \right] dx \\{} & {} + \lambda _1 \int _{\bar{x}}^1 \left[ \frac{t_1\vert x-x_1\vert - \lambda _1 t_2\vert x-x_2\vert }{1-\lambda _1}-t_2\vert x-x_2\vert \right] dx, \\ \psi _2(x_1,x_2)= & {} \lambda _2 \int _0^{\bar{x}} \left[ \frac{t_2\vert x-x_2\vert -\lambda _2 t_1\vert x-x_1\vert }{1-\lambda _2}-t_1\vert x-x_1\vert \right] dx \\{} & {} +\int _{\bar{x}}^1 \left[ \frac{t_1\vert x-x_1\vert - \lambda _1 t_2\vert x-x_2\vert }{1-\lambda _1}-t_2\vert x-x_2\vert \right] dx. \end{aligned}$$

The first-order conditions of firms 1 and 2 are, respectively,

$$\begin{aligned}{} & {} \big (\frac{1}{1-\lambda _2}+\frac{\lambda _1}{1-\lambda _1}\big )\frac{t_1x_1+t_2 x_2}{t_1+t_2}-\frac{2x_1}{1-\lambda _2} -\frac{\lambda _1}{1-\lambda _1} =0, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \quad \big (\frac{1}{1-\lambda _1}+\frac{\lambda _2}{1-\lambda _2}\big )\frac{t_1x_1+t_2 x_2}{t_1+t_2}-\frac{2x_2}{1-\lambda _1} +\frac{1}{1-\lambda _1} =0. \end{aligned}$$
(2)

The second-order conditions

$$\begin{aligned} \frac{1}{1-\lambda _j} \Big ( \frac{t_i}{t_1+t_2} \frac{1-\lambda _1 \lambda _2}{1-\lambda _i}-2 \Big )<0 \ (i,j=1,2) \end{aligned}$$

are satisfied. Let the superscript ’L’ denote the equilibrium outcome in the first-stage game (the game including the ’location’ choices). From (1) and (2), we obtain

$$\begin{aligned} \ x_1^L= & {} \frac{(1-\lambda _1\lambda _2)(1-\lambda _1)(1+\lambda _2)t_2-2\lambda _1(1-\lambda _2)^2(t_1+t_2)}{2(1-\lambda _1)(1-\lambda _2 )(t_1+t_2)-2\lambda _1(1-\lambda _2)^2t_1-2\lambda _2(1-\lambda _1)^2t_2}, \end{aligned}$$
(3)
$$\begin{aligned} \ x_2^L= & {} 1-\frac{(1-\lambda _1\lambda _2)(1-\lambda _1)(1+\lambda _2)t_1-2\lambda _2(1-\lambda _1)^2(t_1+t_2)}{2(1-\lambda _1)(1-\lambda _2 )(t_1+t_2)-2\lambda _1(1-\lambda _2)^2t_1-2\lambda _2(1-\lambda _1)^2t_2} \end{aligned}$$
(4)

We now present the results of the relationship between \(\lambda _i\ (i=1,2)\) and \(x_1^L\).

Proposition 1

(i) \(x_1^L\) is decreasing in \(\lambda _1\) and (ii) increasing in \(\lambda _2\).

Proof

See Appendix.

Proposition 1(i) states that an increased share of rival firm’s profit in the firms objective function gives the firm an incentive to locate away from the rival. Proposition 1(ii) states that an increase in the shareholding of the rival firm in its own gives a firm an incentive to locate toward the center. The increase in \(\lambda _1\) makes firm 1 more concerned with firm 2’s profits, and a decrease in \(x_1^L\) improves firm 2’s profit by raising the price at the market firm 2 serves. By contrast, when firm 2 moves toward the endpoint due to an increased \(\lambda _2\), firm 1 gets more market thus motivating it to move to the center to reduce its transport costs.

Then, naturally we want to discuss which effect dominates if \(\lambda _1\) and \(\lambda _2\) increase simultaneously. However, there are no clearcut results under \(\lambda _1 \ne \lambda _2\), so the rest of the analysis is limited to the case where \(\lambda =\lambda _1=\lambda _2\). Although this assumption would prevent us from knowing how the difference in the shareholding in the rival firm affects the equilibrium outcomes, we can still draw conclusions about our main research problem. As a result, the previously mentioned interior solution (\(0< x_1^L, x_2^L < 1\)) conditions will become

$$\begin{aligned} \lambda \le \lambda ^I = \frac{t_2-\sqrt{(t_2+t_1)(t_2-t_1)}}{t_1}, \end{aligned}$$

and we can show that \(x_1 \in (0,1)\) for \(\lambda \in [0,1)\) and that \(x_2 \in (0,1)\) for \(\lambda \in [0, \lambda ^I)\). \(\square\)

We now present the results of the relationship between the degree of common ownership and the equilibrium locations.

Proposition 2

  1. (i)

    \(x_1^L\) is decreasing in \(\lambda\) if and only if \(\lambda \in [0, \bar{\lambda }),\) where

    $$\begin{aligned} \bar{\lambda }= \frac{t_2-\sqrt{2t_2(t_2-t_1)}}{t_2} \le \lambda ^I \end{aligned}$$

    and \(\bar{\lambda }=\lambda ^I\) if and only if \(t_1=t_2\).

  2. (ii)

    \(x_2^L\) is increasing in \(\lambda\) for \(\lambda \in [0, \lambda ^I)\).

Proof

See Appendix.

Proposition 2(ii) states that the firm’s location with a higher transport cost (\(x_2^L\)) moves toward the endpoint (point one) when \(\lambda\) becomes larger, as long as the solution is interior (i.e., \(x_2 <1\)). According to Proposition 2(i), the firm’s movement with a lower transport cost (\(x_1^L\)) is nonmonotonic to \(\lambda\). The relationship between \(x_1^L\) and \(\lambda\) is U-shaped. When \(\lambda\) is smaller, firm 1 moves toward the endpoint (point zero) when \(\lambda\) becomes larger. But when \(\lambda\) increases to exceed a threshold (\(\bar{\lambda }\)), as \(\lambda\) becomes larger, firm 1 moves toward the rival.

Combining this with the explanation of Proposition 1, we could infer that firms always move away from their rivals when there is no difference in the shareholding in the rival firm. An increase in \(\lambda\) increases the weight of the rival firm’s profit in the firm’s objective. IncreaseS in \(x_2\) (a decrease in \(x_1\)) raise the market price for which firm 1 (2) serves and increase firm 1’s (2’s) profits. As a result, when \(\lambda\) is greater, each firm has an incentive to increase its distance from the rival.

However, under asymmetric transport costs, a relatively high \(\lambda\) means that the two firms are nearly a cartel, and from the perspective of joint profit maximization, it is cost-saving for the more efficient firm to locate near the center to supply a bigger market. Therefore, \(x_1^L\) can be nonmonotonic with respect to \(\lambda\). By contrast, the market share of the less efficient firm (firm 2) should shrink from the viewpoint of joint profit maximization. Therefore, \(x_2^L\) is monotone (it is always increasing in \(\lambda\)).Footnote 9

Because \(x_1^L\) is nonmonotonic with respect to \(\lambda\), we cannot determine whether an increase in \(\lambda\) promotes or restricts firm location dispersion from Proposition 2. However, the following proposition states that an increase in \(\lambda\) always promotes the dispersion of firms’ locations. \(\square\)

Proposition 3

\(x_2^L-x_1^L\) is increasing in \(\lambda\).

Proof

See Appendix.

Proposition 3 states that even when \(x_1^L\) is increasing in \(\lambda\), an increase in \(\lambda\) affects \(x_2\) more strongly than it affects \(x_1\). As discussed above, an increase in \(\lambda\) increases the incentive to reduce \(x_1\) because a decrease in \(x_1\) increases firm 2’s profit. However, an increase in \(\lambda\) moves firms’ objectives toward joint profit maximization, and firm 1 has an incentive to increase \(x_1\). Thus, the two effects have opposite directions, and these effects are partially canceled out. Thus, the resulting effect is weak. By contrast, for firm 2, both effects increase \(x_2\). Therefore, an increase in \(\lambda\) affects \(x_2^L\) more strongly than it affects \(x_1^L\), which yields Proposition 3.

4 Welfare

We now discuss the welfare implications of common ownership. Social welfare W comprises consumer surplus and producer surplus. The consumer surplus is

$$\begin{aligned} CS^L&=U-\int _0^1 p^L(x) dx \\&= U-\frac{(1+\lambda )^2}{2(1-\lambda )^3(t_1+t_2)}\Big [\frac{(t_2-\lambda t_1)^2}{1+\lambda }-\frac{\lambda t_1(t_1-\lambda t_2)^2+\lambda t_2(t_2 -\lambda t_1)^2}{2(t_1+t_2)}\\&\quad\ -t_1(1-\lambda )(t_1-\lambda t_2) \Big ] +\frac{\lambda (t_1+t_2)}{4(1-\lambda )}, \end{aligned}$$

where \(p^L(x)\) is derived by substituting \((x_1,x_2)=(x_1^L,x_2^L)\) into \(p^P(x).\) Producer surplus \(\Pi _1^L+\Pi _2^L\) is

$$\begin{aligned} PS^L=\int _0^{\bar{x}^L}\pi _1^Ldx+\int _{\bar{x}^L}^{1}\pi _2^Ldx=\frac{t_2+2\lambda t_1}{(1-\lambda )^2} +\frac{t_1-t_2}{2(1-\lambda )}-\frac{(1+\lambda )^2t_1t_2}{(1-\lambda )(t_1+t_2)}\Bigl (\frac{1}{4}+\frac{1}{1-\lambda }\Bigr ). \end{aligned}$$

\(W^L=CS^L+PS^L\). We now show that the profits of the two firms are increasing in \(\lambda\).

Lemma 1

\(PS^L\) is increasing in \(\lambda\).

Proof

See Appendix.

This result is intuitive. Common ownership restricts competition and increases firms’ profits. We naturally expect that this is harmful to consumers and may be harmful even for welfare.Footnote 10\(\square\)

Proposition 4

\(p^L(x)\) is increasing in \(\lambda\) for all \(x \in [0,1]\). (ii) \(W^L\) is decreasing in \(\lambda\).

Proof

See Appendix.

Proposition 4(i) implies that common ownership is always harmful for all consumers. An increase in \(\lambda\) raises the prices directly given firms’ locations. In addition, an increase in \(\lambda\) increases the distance between the firms, which further softens the competition. These two effects raise the prices and thus reduce the consumer surplus. For the same reason, an increase in \(\lambda\) increases the joint profit (Lemma 1). And for the social welfare, notice that price changes simply shift surplus around between consumers and producers when the demand is inelastic, thus, the welfare loss arises from the relocation. When \(\lambda =0\), the equilibrium locations maximize welfare (Lederer and Hurter 1986). An increase in \(\lambda\) distorts the location and harms the welfare, and the welfare loss is increasing in \(\lambda\). \(\square\)

Finally, we show how relocation from the equilibrium locations affects welfare.

Proposition 5

At \((x_1,x_2)=(x_1^L,x_2^L)\), (i) \(\partial PS^L/\partial x_1<0\) if and only if \(\lambda <t_1/t_2\). (ii) \(\partial PS^L/\partial x_2>0.\) (iii) \(\partial PS^L/\partial x_1-\partial PS^L/\partial x_2<0.\) (iv) \(\partial CS^L/\partial x_1>0\) and \(\partial CS^L/\partial x_2<0\). (v) \(\partial W^L/\partial x_1>0\) and \(\partial W^L/\partial x_2<0.\)

Proof

See Appendix.

An increase in \(x_2\) increases PS (Proposition 5(ii)) and reduces CS and W (Proposition 5(iv,v)). In other words, the equilibrium distance is too far for social welfare and consumer surplus, but too close for joint-profit maximization. Similarly, an increase in \(x_1\) increases CS and W (Proposition 5 (iv,v)). As we stated after Proposition 1, an increase in \(x_1\) may increase PS when both \(\lambda\) and \(t_2/t_1\) are large (Proposition 5(i)). However, simultaneous relocation by both firms that equally reduces the distance between them reduces PS (Proposition 5(iii)). This suggests that the equilibrium distance between the two firms is too small for joint profit maximization.Footnote 11\(\square\)

5 Endogenous transport costs

In this section, we consider a model in which each firm i chooses \(t_i\). As discussed in the Introduction, we can interpret \(t_i\) as a measure of flexibility in the FMS (the lower \(t_i\) is, the more flexible firm i’s manufacturing system will be). Thus, we can interpret the model of this section as a discussion of endogenous flexibility in FMS.Footnote 12

We assume that at the beginning of the game two firms are symmetric, and focus the symmetric equilibrium on the equilibrium path. The game runs as follows: In the first stage, each firm i simultaneously chooses \(t_i \in [0, \bar{t}]\), with the investment cost \(I(t_i)\) where \(I(\bar{t})=0\), \(I'<0\), \(I''>0\) and \(\lim _{t \rightarrow 0}I(t)=\infty .\) Then, firms play the location-price game discussed in Sections 2 and 3.

In the first stage, the first-order condition for firm 1 is

$$\begin{aligned} \frac{1}{2(1-\lambda )^3(t_1+t_2)^3}&\Big [\lambda (1+\lambda )(t_1+t_2)(t_1-\lambda t_2)^2-(1+\lambda )^3(1-\lambda )t_2^2(t_2-\lambda t_1)\nonumber \\&-\frac{1}{2}(t_1+t_2)[(t_2-\lambda t_1)-\lambda (t_1-\lambda t_2)]^2\Big ]-I'(t_1)=0. \end{aligned}$$
(5)

We assume that \(I''\) is sufficiently large that the second-order condition is satisfied. Let the superscript ‘I’ denote the equilibrium outcome in the game (‘I’ means ‘investment’ stage). Substituting \(t_1=t_2\) into (5) yields the equilibrium investment level, \(I^T\). We obtain \(f_F(\lambda )=-I'(t^I)\), where

$$\begin{aligned} f_F(\lambda ):=\frac{2-\lambda +2\lambda ^2+\lambda ^3}{16(1-\lambda )} \end{aligned}$$

is each firm’s marginal benefit of the investment (i.e., private marginal gain of investment).

Now, we consider the situation in which the social planner chooses the symmetric investment level \(I=I_1=I_2\) to maximize welfare. We consider the second-best problem in the sense that the social planner chooses the investment level only (i.e., the planner does not control for locations and prices). Let \(I^*=I_1^*=I_2^*\) be the solution of this problem. Because the demand is inelastic, welfare is maximized when the sum of transport and investment costs is minimized. Because of symmetric transport costs, locations, and pricing, firm 1’s total transport cost is \(t/8+t x_1^2-tx_1/2\).

Substituting \(t_1=t_2=t\) into (4), we obtain \(x_1=1/2-(1+\lambda )/4\). Substituting this into the expression for total transport cost of each firm, we obtain each firm’s total transport cost:

$$\begin{aligned} \frac{t}{16}(1+\lambda ^2). \end{aligned}$$

Therefore, \(I^*\) is derived from \(f_S(\lambda )=-I'(t^I)\), where

$$\begin{aligned} f_S(\lambda ):=\frac{1+\lambda ^2}{16} \end{aligned}$$

is the social marginal benefit of the investment.

\(f_F-f_S\) is the difference between private and social marginal gains from the investment. If \(f_F-f_S\) is positive (negative), the equilibrium investment level is excessive (insufficient) for social welfare. Proposition 5 states that common ownership accelerates excessive cost-reducing investments and, thus, is harmful for welfare.

Proposition 6

(i) Both \(f_F\) and \(f_S\) (and thus \(I^I\) and \(I^*\)) are increasing in \(\lambda\). (ii) \(f_F-f_S>0\) (and thus \(I^I-I^*>0\)) for \(\lambda \in [0,1)\).

Proof

See Appendix.

Proposition 6(i) states that both private and social incentives for investment are increasing in \(\lambda\). Therefore, both \(I^I\) and \(I^*\) are increasing in \(\lambda\). An increase in \(\lambda\) distort firms’ location choices (too large locational dispersion), which in turn increases total transport costs. Thus, both private and social marginal gains from the reduction of the unit transport cost increases as \(\lambda\) increases.

Proposition 6(ii) states that regardless of \(\lambda\), the equilibrium incentive for each firm’s investment is excessive for welfare, and thus \(I^I>I^*\). This is true even when \(\lambda =0\). We explain the intuition as follows. Suppose that \(\lambda =0\). A decrease in \(t_1\) (i) reduces firm 1’s cost at the markets for which firm 1 supplies and (ii) increases \(x_2\), which raises the prices for which firm 1 supplies. The effect in (i) increases the total social surplus, whereas the effect in (ii) does not. Thus, a profit-maximizing investment level exceeds the welfare-maximizing investment level (over-investment for welfare).

Suppose that \(\lambda >0\). In addition to the above two effects, given \(x_2\), a decrease in \(t_1\) (iii) raises the prices for which firm 1 supplies, and (iv) reduces the prices for which firm 2 supplies, which reduces firm 1’s payoff. When \(\lambda\) is positive, the third and fourth effects appear, and both effects are stronger when \(\lambda\) is larger. Proposition 6(ii) states that the second and third effects dominate the fourth effect, and thus, \(I^I>I^*\) holds. This is a natural result. The effect in its own profit (the third effect) affects its payoff more strongly than the effect in the rival’s profit does because \(\lambda <1\).

Proposition 6(ii) states that the equilibrium investment level is always excessive for welfare. That is, a marginal increase in I always reduces welfare. Proposition 6(i) states that a marginal increase in \(\lambda\) increases \(I^I\), which yields a negative effect to welfare.

In the model, the effect of a marginal increase in welfare is decomposed into two effects, the location effect and the investment effect. Both effects are negative, and thus, an increase in \(\lambda\) always harms welfare. Proposition 6 states this point formally. \(\square\)

Proposition 7

The equilibrium welfare \(W^I\) is decreasing in \(\lambda\).

Proof

See Appendix. \(\square\)

6 Concluding remarks

In this study, we identify two possible sources of welfare loss caused by common ownership, from the distortion of firms’ location and investment choices.

First, we analyze how common ownership affects equilibrium prices and locations in a delivered pricing duopoly model. We find that common ownership raises the prices directly given particular locations and further raises them through location changes. This location change harms welfare. From a welfare perspective, firms locate too far away, and the higher the degree of common ownership, the farther the two firms are. We also find that the location of a more efficient firm is nonmonotonic with respect to the degree of common ownership, whereas that of a less efficient firm is monotone.

Next, we endogenize the transport costs. We find that the equilibrium level of transport cost-reducing investments is higher than the social optimum level, and the welfare loss of over-investment increases with the degree of common ownership.

These findings suggest that the antitrust department should be concerned about the detrimental impacts of common ownership, as well as the departments in charge of location and industrial policy, as common ownership not only leads in skyrocketing prices but also location distortion.

In this study, industry demand is assumed to be inelastic; thus, the total consumption level does not depend on common ownership. This property simplifies the analysis greatly, and we obtain some clear results. Introducing elastic demands in this framework makes the analysis intractable. However, if the demand is elastic, common ownership reduces the equilibrium total consumption level, which yields additional welfare loss. Future research could extend our analysis in this direction.

In this study, we use a price competition (Bertrand competition) model. As pointed out by Hamilton et al. (1989) and Anderson and Neven (1991), a striking feature of price-setting spatial models is that firms’ spatial markets never overlap. Because the product is homogeneous, it is only supplied by the lower cost firm in each local market. By contrast, if we adopt a quantity competition model, market overlap appears, and the properties may be different from those of a price competition model. In our framework, introducing quantity competition makes the analysis intractable. However, it may be possible under a more simplified spatial structure. This could also be explored in future research.