Introduction

Mechanical twins are the most conspicuous deformation features in calcite deformed at low temperatures (T < 300 °C) or at high strain rates (e.g. 10−4 s−1 at 700 °C) (Barber and Wenk 1979; Schmid et al. 1980; Burkhard 1993; Lacombe 2010). Three types of deformation twins occur in calcite (Paterson and Turner 1970; Barber and Wenk 1979). For the most common, the so called e-twins, the misorientation between twin and host corresponds to a rotation of 180 ° about the pole of an e\( \left\{01\overline{1}8\right\} \)-plane, resulting in slip along a \( \left\langle 40\overline{4}1\right\rangle \) direction, where the twin and the host share the e-plane as their common boundary. The other two known mechanical twins in calcite are the r- and f-twins, which show a misorientation between twin and host corresponding to a rotation of 180 ° about an r\( \left\{10\overline{1}4\right\} \) and f\( \left\{01\overline{1}2\right\} \) plane pole, respectively, resulting in slip along a \( \left\langle \overline{2}021\right\rangle \) and a \( \left\langle \overline{1}01\overline{1}\right\rangle \) direction, respectively, where the r- and f-planes constitute the respective twin boundaries. Due to the trigonal symmetry of calcite three symmetrically equivalent twins occur for e-, r- and f- twins (Fig. 1).

Fig. 1
figure 1

Stereographic projection of calcite marked with the plane poles relevant for twinning in calcite. In addition, plane poles and directions relevant for deformation lamellae observed in this study are marked as well. The grid spacing is 15 °. Modified after Fig. 1 in Schuster et al. (2017)

Full size image

Mechanical e-twins are common in naturally deformed rocks and can also be produced in experiments (Turner et al. 1954) even by simple means such as by pushing a knife edge into a calcite single crystal (Baumhauer 1879). The e-twins show characteristic morphologies and frequencies (#/mm) depending on deformation conditions such as stress, strain and temperature (Burkhard 1993; Ferrill et al. 2004). Many of the pioneering studies on mechanical twinning focused on the symmetry relations and dislocation mechanisms of deformation twins in calcite (see review by Duparc 2017). More recent studies addressed the relationships between deformation conditions and the morphology (Burkhard 1993; Ferrill et al. 2004; Rybacki et al. 2013; Covey-Crump et al. 2017) and frequency (Jamison and Spang 1976; Rowe and Rutter 1990; Lacombe 2007) of e-twins. The morphology and characteristic size of mechanical calcite twins were calibrated as geothermometers and were used for extracting information on deformation conditions in naturally deformed carbonate rocks (Burkhard 1993; Ferrill et al. 2004; Lacombe 2010).

Burkhard (1993) and Ferrill et al. (2004) established a scheme for relating four characteristic e-twin morphologies to specific deformation conditions. Thin (<1 μm) and straight twins are referred to as ``type I″ twins, which are characteristic for deformation at T < 200 °C; wider twins (> > 1 μm) with a moderate lensoid shape constitute ``type II” twins, which occur at temperatures between 150 and 300 °C; wide (> > 1 μm) and curved twins, which taper out towards grain boundaries, are termed ``type III” twins and form at T > 200 °C; they are produced during high-strain deformation by dislocation creep; ``type IV” twins form thick lamellae with irregular and sutured grain boundaries and may be disrupted by the host, giving rise to trails of small twin grains with low aspect ratios. Type IV twins commonly occur in rocks that were deformed to high strain at temperatures above 250 °C and are associated with significant twin boundary recrystallization.

The influence of temperature and applied strain on the morphology of mechanical twins is due to the mechanism of twin propagation. Mechanical twins grow by the movement of partial dislocations that may be generated by dissociation from full dislocations (Hirth and Lothe 1982). Lamellae of mechanical twins in calcite may grow in length by glide of partial dislocations on the twin plane, where the Burgers vectors are oriented parallel to the shear direction of the twin.

The broadening of twins, however, requires that dislocations move out of the glide plane. For dislocations with edge character this can only occur by climb, which is a thermally activated process. The broadening of twin lamellae is thus also regarded as a thermally activated process, which gives rise to the relationship between twin-thickness/morphology and deformation temperature providing the basis for twin morphology geothermometers. Boundary migration, which leads to lamellae with irregular shapes, is driven by the heterogeneity of the lattice defect energy associated with dislocations and vacancies in twin and host grains and is also a thermally activated process (Urai et al. 1986). In contrast to the deformation temperature, the influence of the confining pressure on deformation mechanisms and in particular on twinning in calcite is usually assumed to be negligible (De Bresser 2002). However, since high confining pressures during deformation suppress both macroscopic brittle failure as well as recovery, the lattice defect energies produced during deformation increase with higher pressures and thus influence intragranular deformation mechanisms.

In this communication we report on the influence of high confining pressures on the mechanisms of intragranular deformation in polycrystalline calcite deformed to high strains at room temperature. We employed high-pressure torsion (HPT) to perform deformation experiments under confining pressures between 1 and 4 GPa to shear strains of up to about 100. The high confining pressures suppress crack formation and propagation and allow to perform experiments to high shear strains without brittle sample failure, which occurred at previous low temperature deformation experiments at confining pressures up to 300 MPa (Barnhoorn et al. 2004). Deformation under confining pressures above 1 GPa facilitated the activation of alternative deformation mechanisms leading to previously unreported microstructural elements. Schaebitz et al. (2015) reported evidence for internal pressures of up to 4 GPa in nanocrystalline calcite deformed at near ambient conditions in landslides, illustrating the importance to investigate the deformation mechanisms of calcite during low temperature and high pressure deformation.

The microstructures of HPT deformed samples were analyzed by electron backscatter diffraction (EBSD) in a scanning electron microscope (SEM). This contribution complements earlier studies by Schuster et al. (2017), where the deformation mechanisms in calcite deformed by HPT were analyzed by means of X-ray line profile analysis (XPA) and Schuster et al. (2019), which investigated the microstructural and textural evolution of calcite deformed by HPT at elevated temperatures by means of EBSD.

Materials and methods

Sample preparation and description

Sample preparation, HPT-deformation experiments, and microstructure analysis by SEM followed the same procedures as laid out in the previous study on HPT deformation of calcite at elevated temperatures (Schuster et al. 2019). Therefore, only a brief description of the methods is given here. The powder samples for the HPT deformation were prepared by crushing a block of Carrara marble of high purity and sieving the resulting powder to obtain the 63–100 μm particle size fraction. To obtain specimens with the necessary dimensions for HPT processing 110 and 170 mg, respectively, of the calcite powder were cold pressed into cylindrical discs with 8 and 10 mm diameter, respectively, which corresponds to a sample height of 0.8 mm for samples with no porosity.

The Carrara marble block exhibits a microstructure of equidimensional grains, with a grain size of several 10 μm to a few 100 μm (Fig. 2a). Some grains show a single e\( \left\{01\overline{1}8\right\} \) twin, where the twin width is significantly smaller than the grain diameter. The cold pressed powder exhibits a porous agglomeration of calcite grains with their grain sizes corresponding to the particle size fraction of the powder (Fig. 2b). Cold pressed power material largely did not display evidence of twinning in FSD images, although a few grains showed several straight twins of up to about 1 μm width (Fig. 2c).

Fig. 2
figure 2

Sample microstructure before and after HPT processing. a Transmitted cross-polarized light microscope image of Carrara marble before crushing b Reflected light microscope image of cold pressed powder before HPT-processing. c EBSD orientation deviation map (see section Data Treatment) of a twinned grain in the cold pressed powder showing the largest twin thickness observed before HPT processing d Reflected light microscope image of the central region of sample ‘C-3-rt-1’ deformed for one rotation at 3 GPa pressure. The image was taken at a distance of 1 mm from the sample center corresponding to γ ≈ 10 and \( \dot{\upgamma} \) ≈ 3.5 × 10−3 s−1. e Color code for the orientation deviation maps. The internal reflections in (b) correspond to surface roughness and internal porosity of the pressed powder sample which was fully eliminated during HPT treatment (d)

Full size image

Deformation experiments

The HPT experiments were performed using the HPT device at the Faculty of Physics, University of Vienna. The samples investigated in this study were deformed at room temperature at a twist rate of 0.02 rotations per minute (RPM). The confining pressure was varied between 1 and 4 GPa. The sample diameter was 8 mm for deformation experiments with confining pressures of at least 1.75 GPa and 10 mm for deformation at lower pressures. The sample thickness was 0.6 mm after deformation. The local shear strain γ in the sample increases with increasing radial distance from the rotation axis:

$$ \gamma =\frac{2\pi nr}{t} $$
(1)

where n is the number of rotations, r is the distance from the rotation axis, and t is the thickness of the sample. The maximum shear strain rate at the sample rim was therefore 1.7 × 10−2 s−1 in the 10 mm case and 1.4 × 10−2 s−1 in the 8 mm case. Torsion experiments, where markers on the bottom and top surfaces of the pellets were used to test for slip at the sample-anvil interface, revealed that no such slip occurred and that the applied torsion was entirely accommodated by deformation within the specimen.

Specimen preparation for EBSD

After the deformation experiments the samples were embedded in epoxy resin. Most samples were analyzed on sections normal to the rotation axis (parallel to the sample’s basal plane). A selection of samples was cut normal to the basal plane through the sample center and subsequently investigated along this section to obtain access to the grain morphology parallel to the rotation axis.

The embedded samples were ground and polished with silicon carbide, diamond- and aluminum oxide-suspensions down to a particle size of 0.05 μm to obtain the surface quality required for EBSD analysis. Despite the sophisticated polishing technique, the surface quality was not sufficient for EBSD analysis of the fine-grained regions between the porphyroclasts. Thus, the EBSD results only refer to the porphyroclasts and their relatively coarse-grained derivatives. To reduce charging effects during the SEM measurements the samples and epoxy mount were coated with a thin layer of amorphous carbon. In some cases the epoxy mount was painted with a layer of graphite paste to further decrease sample charging during EBSD data collection.

EBSD and texture measurements

The EBSD analyses were carried out on the FEI QuantaTM 3D FEG scanning electron microscope at the Laboratory for Scanning Electron Microscopy and Focused Ion Beam Applications of the Faculty of Geosciences, Geography and Astronomy at the University of Vienna. The EBSD data were collected using an EDAX Digiview IV EBSD camera installed at an elevation angle of 5 ° in the microscope applying the software TSL OIM Data Collection 6.2. The acceleration voltage of the electron beam was at 15 kV. The sample surface was positioned at a working distance of 14 mm, with a 20 ° angle to the beam incidence direction. An EBSD camera binning of 4 × 4 was used, while Hough settings of a 140 pixels binned pattern size, a θ step size of 1 °, and a 9 × 9 convolution mask were employed. To index the data, the lattice parameters of calcite were defined as a = 4.99 Å and c = 17.064 Å using the hexagonal unit cell. The maps were collected on a hexagonal grid using step sizes between 80 and 600 nm. The texture of cold-pressed pellets not yet subjected to HPT deformation was measured using an AXS BRUKER D8 diffractometer at the Faculty of Physics University of Vienna utilizing Cu Kα1 radiation with a spot size of 0.5 mm.

Data treatment

The crystal orientation data derived from EBSD analyses were processed using the EDAX OIM analysis software version 7. Before data evaluation, the EBSD raw data were subjected to the clean-up procedures implemented in the EDAX OIM analysis software. After a grain confidence index (CI) standardization procedure, where the CI of equally oriented data points inside an identified grain are changed to the maximum CI value inside that grain, one step of the Neighbor Orientation Correlation procedure was applied. Finally one step of Grain Dilation was used in order to minimize mis- or non-indexed data points, which mainly occur at grain boundaries due to mixed EBSD signals from the two neighbor crystals. This ensured that neighboring grains are in direct contact with one another. After the cleanup procedure, data points with a CI smaller than 0.05 and grains consisting of only a single data point were excluded from the data evaluation, so that only grains with a diameter larger than the step size are considered. Grains were defined as domains with a misorientation angle >15 ° to neighboring domains.

The EBSD scans are presented as orientation deviation maps, where the deviation of the local orientation from a reference orientation of the associated host crystal is represented by a greyscale color code, where black corresponds to 0 ° deviation and white to 110 ° deviation from the host orientation (Fig. 2e). Only in Fig. 9 the color code ranges from 0 ° (black) to 20 ° misorientation (white). The color coding of twin and deformation lamella boundaries in the orientation deviation maps was defined by the misorientation relationship between the twin or lamella and the host.

The twin misorientations were defined by a 180 ° rotation about the respective pole of the twinning plane. The tolerance angle for the misorientation relationships was set to 10 °. The relatively high tolerance angle is required to include most relevant boundary segments, as the high lattice strain in the porphyroclasts leads to a significant deviation from the ideal misorientation relationships, in particular in the case of early twins, which are exposed to high shear strains after their formation. In addition, since mechanical twins in calcite are coherent twins, i.e. the boundary plane coincides with the twin plane, the orientation of the twin plane traces in both the host and twin were manually compared to the orientation of the boundary trace. General grain boundaries are plotted as thin yellow lines (Fig. 4). Boundaries with misorientations corresponding to e-, r-, and f-twins are plotted as thick lines colored red, green and blue, respectively. Specific misorientations between deformation lamellae and host are plotted as thick lines and colored purple for misorientations corresponding to a rotation of 35 ° about an a-axis, and cyan for misorientations corresponding to a rotation of 76 ° about an f-plane pole. In maps where the color coding deviates from this scheme, the change is described in the corresponding figure caption. The data presented as orientation deviation maps are also shown in the supplementary as inverse pole figure maps generated using the Matlab toolbox MTEX 5.1 (Bachmann et al. 2010). The orientation color code for the IPF maps after Nolze and Hilscher (2016) was applied with respect to the sample normal direction, i.e. normal to the pellet surface.

Results

The room temperature HPT deformation experiments of the compacted calcite powder produced solid pellets. No traces of any CaCO3 polymorph other than calcite could be detected by ex-situ X-ray and electron diffraction analysis. Optical and scanning electron microscopy of the post-deformation microstructures reveals evidence of both, cataclastic and crystal-plastic deformation. The samples are pervaded by numerous inter- and intragranular cracks (Figs. 2d and 3). The cracks supposedly result from both brittle deformation during HPT-processing as well as from fracturing during unloading after the HPT experiments. The microstructures are characterized by the presence of larger porphyroclasts of similar size as the initial grain size surrounded by smaller porphyroclast remnants. The boundaries between neighboring porphyroclast remnants are constituted either by twin boundaries or cracks. The sample volume between the porphyroclasts is comprised of a fine-grained matrix (Figs. 3 and 5). The samples do not exhibit any significant bulk texture.

Fig. 3
figure 3

Cross polarized light microscope images a,b and secondary electron image taken with an Everhart-Thornley SED c showing a region near the rim of sample ‘C-4-RT-1q’. The dark grain in the center of (a) is a porphyroclast, which is shown in a close-up in (b) Abundant inter- and intragranular cracks, deformation lamellae and undulous extinction in the porphyroclasts are present in all samples investigated in this study. The bright regions in (c) are due to charging effects around cracks. The sample ‘C-4-RT-1q’ was deformed under 4 GPa for 1 rotation and the images were taken at a distance of 3 mm from the sample center, corresponding to γ ≈ 31 and \( \dot{\upgamma} \) ≈ 1 × 10−2 s−1

Full size image

The EBSD analysis reveals a high density of e-, r-, and f-twins and deformation lamellae in the porphyroclasts (Figs. 4, 5 and 6). The deformation lamellae show characteristic shape orientations and lattice misorientations with the host that are related to the crystallographic orientation relationships of mechanical twins. At low shear strains (< 10), the twins and lamellae in 2D sections have high aspect ratios and straight twin boundary segments. With increasing strain the twin and lamella boundaries tend to become sutured and the twins and lamellae either exhibit irregular shapes, or are disrupted so that trails of small, irregularly shaped crystals with twin orientation relationships to the host form (Fig. 7).

Fig. 4
figure 4

EBSD orientation deviation map of sample ‘C-4-RT-1q’ showing predominant e-twinning a. The sample was deformed for 1 rotation at 4 GPa. The EBSD map was taken at a distance of 1 mm from the sample center corresponding to γ ≈ 10 and \( \dot{\upgamma} \) ≈ 3.5 × 10−3 s−1. b is a close-up of (a) showing the features associated with twin boundary migration in detail. c shows the boundary color coding. The EBSD scan step size was 120 nm. For the definition of twin and lamella boundaries see section Data Treatment

Full size image
Fig. 5
figure 5

EBSD orientation deviation map (color coding as in Fig. 2e) a and two close-ups b, c of sample ‘8IIb’ deformed under 4 GPa for 0.25 rotations at a distance of 1 mm from the sample center, corresponding to γ ≈ 2.5 and \( \dot{\upgamma} \) ≈ 3.5 × 10−3 s−1. (b) Close-up marked in (a) showing the boundary types between a- and f-type lamellae. (c) Close-up marked in (a) showing the boundary between parallel a- and f-type lamellae split into two r-twin boundaries. In addition to the boundary color coding described in the section data treatment, the boundaries between the a- and f-type lamellae (see text) corresponding to a rotation of 52 ° about an {2\( \overline{11}3 \)} pole and 83 ° about an {11\( \overline{2} \)6} pole are colored orange and brown, respectively. The EBSD scan step size was 160 nm

Full size image
Fig. 6
figure 6

EBSD orientation deviation map (color coding as in Fig. 2e) of sample ‘8IIb’ a, and a close-up b showing the high density of twins and deformation lamellae in a porphyroclast. (b) Shows a-type boundaries split into r- and f-twin boundaries and the interference of a- and f - type lamellae. The sample was deformed under 4 GPa for 0.25 rotations. The map was taken at 3 mm distance from the sample center, corresponding to γ ≈ 8 and \( \dot{\upgamma} \) ≈ 1 × 10−2 s−1. In addition to the boundary color coding described in the section data treatment, the boundaries between a- and f-type lamellae (see text) with a misorientation corresponding to a rotation of 52 ° about an \( \left\{2\overline{11}3\right\} \) pole are colored orange. The EBSD scan step size was 110 nm

Full size image
Fig. 7
figure 7

EBSD orientation deviation maps (color coding as in Fig. 2e) showing boundary splitting and evidence of boundary migration in a-type lamellae in sample ‘C-4-rt-1-q’ (4 GPa confining pressure, one rotation, section normal to the basal plane through the sample center) a-c, and sample ‘C-2.5-rt-1’ (2.5 GPa confining pressure, one rotation, section perpendicular to the rotation axis) d. Maps (a) and (b) were taken at 2 mm distance from the rotation axis (γ ≈ 21 and \( \dot{\upgamma} \) ≈ 7 × 10−3 s−1). Map (c) was taken at 3 mm distance from the rotation axis (γ ≈ 31 and \( \dot{\upgamma} \) ≈ 1 × 10−2 s−1). Map (d) was taken at 1 mm distance from the rotation axis (γ ≈ 10 and \( \dot{\upgamma} \) ≈ 3.5 × 10−3 s−1). The EBSD scan step size for was 120 nm for (a-c) and 100 nm for (d)

Full size image

The type and the density of twins and deformation lamellae in a porphyroclast depend on the crystallographic orientation of the porphyroclast relative to the local orientation of the shear stress. Porphyroclasts oriented favorably for e-twinning are characterized by significant primary and secondary e-twins and exhibit only a low density of other twins or lamellae (Fig. 4). The primary e-twins have rather straight twin boundaries and are several μm wide. The secondary twins, present within both, the host and the primary twins, are thinner and exhibit sutured boundaries or consist of trails of smaller grains, particularly within the host. These characteristics point to the activity of twin boundary migration. The primary twins show clear signs of broadening and subsequent merging of neighboring twins, where the former boundary between the two twin individuals can often be traced by low-angle boundaries or “terminal points” of secondary twins inside the primary twins. However, continued deformation may also lead to the elimination of earlier twins by twin boundary migration. Figure 4b shows the remnant of such a primary twin with a broad internal secondary twin consumed by the host through grain boundary migration. In addition to e-twins, trails of r-twin grains are found in the primary twins (running W to E on the left hand side of Fig. 4a).

Porphyroclasts oriented unfavorably for e-twinning exhibit complex microstructures comprising r- and f-twins and two types of deformation lamellae (Figs. 5 and 6). The two types of deformation lamellae have a fixed crystallographic orientation relationship with the host and constitute a prominent feature of the microstructures investigated in this study (see also Fig. 7). The lamellae running SE to NW in Fig. 6b are characterized by a misorientation with respect to the host, which corresponds to a rotation of about 30–40 ° about an a-axis. They are referred to as a-type lamellae. Such a-type lamellae were observed in more than 50% of the porphyroclasts investigated in this study. The misorientation of the a-type lamellae with respect to the host does not correspond to any of the known twin laws in calcite and neither can it be described in terms of a single 180 ° rotation about a plane pole or direction in calcite with reasonably low Miller indices (<30). The observed misorientation of the a-type lamellae can, however, be constructed by successively applying the rotations corresponding to the misorientations of either specific e- and r-twin boundaries or f- and r-twin boundaries. In particular, two successive rotations of 180 ° about an e- and an r-plane pole, which both lie on a great circle with the c-axis in the stereographic projection lead to a rotation of 141.8 ° about the negative a-axis that is normal to the plane defined by the specific e- and r-plane poles (Fig. 8a).

Fig. 8
figure 8

a-c Misorientation relationships between host and a-type (a,b) and f-type (c) lamellae shown in upper hemisphere stereographic projections using antipodal symmetry of one a-axis and the c-axis. The original positions of the c and a3 axes are marked in grey. The color scheme follows the boundary coloring in the IPF maps: r-, f- and e-plane poles and rotations are colored in green, blue, and red, respectively. The small symbols trace the rotations in 20 ° intervals and the arrows show the sense of rotation. Rotation axes are marked with the symbol ×. The symbol ` next to the rotated a- and c-axes marks the number of rotations performed. The grid spacing is 15 °. (a) Successive rotations of 180 ° about e\( \left(\overline{1}018\right) \) and r\( \left(10\overline{1}4\right) \) leading to a rotation of 141.8 ° about a\( \left[1\overline{2}10\right] \). (b) Successive rotations of 180 ° about r\( \left(10\overline{1}4\right) \) and f\( \left(\overline{1}012\right) \) leading to a rotation of 144.5 ° about a\( \left[1\overline{2}10\right] \). (c) Successive rotations of 180 ° about f\( \left(01\overline{1}2\right) \)and r\( \left(10\overline{1}4\right) \) leading to a rotation of 101.2 ° about \( \left[\overline{2}021\right] \). d Schematic sketch of an a-type lamella and corresponding sub-lamellae using the same color scheme as in (a-c). The lamella interior color code indicates the misorientation with regard to the host and follows the color code used for grain boundaries

Full size image

Since the a-axes are 2-fold rotation axes this rotation is symmetrically equivalent to a rotation of 38.2 ° about the positive a-axis. The misorientation of the a-type lamellae can thus be produced by the combination of one e- and one r-twin boundary. Three combinations of e- and r-twin boundaries are conceivable, namely e\( \left(01\overline{1}8\right) \) and r\( \left(0\overline{1}14\right) \), e\( \left(1\overline{1}08\right) \) and r\( \left(\overline{1}104\right) \) as well as e\( \left(\overline{1}018\right) \) and r\( \left(10\overline{1}4\right) \) (Fig. 1). However, the misorientation between the a-type lamellae and the host can also be constructed by successive rotations of 180 ° about an r- and an f-plane pole, which both lie on a great circle together with the c-axis in the stereographic projection (Fig. 8b). The combination of these two rotations leads to a rotation of 144.5 ° about the negative a-axis normal to the plane defined by the specific r- and f-plane poles. This rotation therefore produces a misorientation of 35.5 ° about the corresponding positive a-axis. Accordingly, three combinations of r- and f-twin boundaries can produce the observed lamella misorientation: f\( \left(01\overline{1}2\right) \) and r\( \left(0\overline{1}14\right) \), f\( \left(1\overline{1}02\right) \) and r\( \left(0\overline{1}14\right) \) as well as f\( \left(\overline{1}012\right) \) and r\( \left(10\overline{1}4\right) \).The successive application of the reverse order of the twinning rotations (i.e. first 180 ° about r followed by 180 ° about e and first 180 ° about f followed by 180 ° about r) leads to the inverse misorientations: 38.2 ° and 35.5 °, respectively, about the negative a-axis.

The shape orientation of the lamellae is controlled by the crystallographic orientation of the host. The boundary plane traces of a-type lamellae in the EBSD maps always lie normal to the a\( \left\{2\overline{11}0\right\} \) plane orientation that is common to both the lamellae and the host (i.e. parallel to the projection of the a-axis that serves as the rotation axis of the lamella host misorientation), both in EBSD sections normal to the HPT rotation axis as well as in sections normal to the sample’s basal plane.

Occasionally, segments of the boundaries between a-type lamellae and the host porphyroclast split up into two spatially separated boundaries, thus creating sub-lamellae between the host and the a-type lamellae. Both new boundary segments of the sub-lamellae correspond to specific misorientations with respect to the host and the a-type lamellae (Figs. 6 and 7). The misorientation across one of the new boundary segments corresponds to the misorientation of an r-twin and the misorientation across the other boundary segment corresponds consequently either to the misorientation of an e- or an f-twin, resulting in the same combined misorientation between lamella and porphyroclast host across the split boundary segments as in the unsplit a-type boundary segments. Some a-type lamellae exhibit both a split into r- and f-, and into r- and e- boundaries (Fig. 7b). The sequence of split boundaries is not random. In the case where the a-type boundary splits into r- and f-twin boundaries, the r-twin boundary separates the a-type lamella from the sub-lamella and the f-twin boundary separates the sub-lamella from the host. When the a-type boundary splits into r- and e-twin boundaries, the r-twin boundary separates the sub-lamella from the host and the e-twin boundary separates the sub-lamella from the a-type lamella (Figs. 6 and 7). However, unlike the boundaries of regular mechanical e-, r-, and f-twins, the boundary segment traces of split deformation lamellae do not follow the respective twin planes and thus the twin boundaries constitute incoherent twin boundaries.

Though in many cases a-type boundary segments split into two parallel twin boundaries, they may also have differently orientated traces. So may a-type lamellae be cross cut by r-twin boundaries, which produce lamella sections with f-twin misorientation relative to the host between two a-type lamella sections (Fig. 6). The f-twin lamellae sections extend parallel to the a-type lamellae sections and may occur repeatedly along one a-type lamella. In the case of more irregular grain shapes, one or both of the split a-type boundaries may show highly curved, irregular trace geometry in the 2D section. Occasionally, the boundary segments appear to be highly mobile, in particular in regions deformed to high shear strains (Fig. 7b,c).

Often deformation lamellae or trails of small grains with misorientations corresponding to r- or f-twins extend parallel to a-type lamellae. Similarly, lamellae that show predominantly twin misorientations with respect to the host, but also comprise a-type sub-lamellae can be aligned with a-type lamellae (Figs. 5 and 7a,d). However, the boundary trace orientations of these incoherent twins differ from those of regular calcite twins. The incoherence of the apparent r- or f-twins with the host indicates that the deformation lamellae with twin misorientation with the host do not develop as regular mechanical twins, but originate from precursor a-type lamellae.

Due to the defined sequence and spatial arrangement of split boundaries (r inside and f outside for r-f splits and e inside and r outside for r-e splits), the split character determines, which type of incoherent twin can form from an a-type lamella. The combination of two 180 ° rotations about the same or antiparallel axis leads to the original orientation. Hence, the movement of the inner twin boundaries within a lamella may lead to partial or complete annihilation of those boundaries, resulting in twin lamellae corresponding to the outer twin type. Accordingly, r-f splits lead to incoherent f-twins and r-e splits lead to incoherent r-twins (Fig. 7a,d). One apparent contradiction to this rule is the set of incoherent r-twins in the central and left parts of Fig. 6a resulting from r-f splits. There, the dark gray domain originated from a-type lamellae (visible in Fig. 6b), which largely consumed the host (black) presumably by grain boundary migration. Therefore, the remaining incoherent twins in this domain are r- instead of f-twins.

The second and less common type of deformation lamellae observed in this study exhibits a misorientation with respect to the host that corresponds to a rotation of 76 ° about an f-plane pole (Fig. 6b). The lamellae are referred to as f-type lamellae, accordingly. As in the case of a-type boundaries, this misorientation can be obtained by the successive application of two mechanical twins. The misorientation across an f-type lamella boundary is the result of the successive rotations associated with one f- and one r-twin operation. In contrast to the a-type boundaries, the corresponding r- and f-plane poles do not lie on the same great circle as the c-axis in the stereographic projection (Fig. 1). For example, the successive rotations of 180 ° about f\( \left(1\overline{1}02\right) \) and r\( \left(0\overline{11}4\right) \) result in a rotation of 101.2 ° about \( \left[0\overline{2}2\overline{1}\right] \), which is symmetrically equivalent to a rotation of 76 ° about f\( \left(\overline{1}012\right) \) (Fig. 8c). The misorientation of 76 ° about an f-plane pole can be produced by rotating first about the r- and subsequently about the f-plane pole or vice versa. In the case where the r-twin operation is applied first, the misorientation axis of the f-type lamella is identical or antiparallel to the rotation axis of the subsequent f-twin. The axes are parallel, when a rotation about r\( \left(\overline{1}104\right) \) is followed by a rotation about f\( \left(01\overline{1}2\right) \), a rotation about r\( \left(0\overline{1}14\right) \) is followed by a rotation about f\( \left(\overline{1}012\right) \), or a rotation about r\( \left(10\overline{1}4\right) \) is followed by a rotation about f\( \left(1\overline{1}02\right) \). The axes are antiparallel, when a rotation about r\( \left(\overline{1}104\right) \) is followed by a rotation about f\( \left(\overline{1}012\right) \), a rotation about r\( \left(0\overline{1}14\right) \)is followed by a rotation about f\( \left(1\overline{1}02\right) \), or a rotation about r\( \left(10\overline{1}4\right) \) is followed by a rotation about f\( \left(01\overline{1}2\right) \). When the f-twin operation is applied first, the misorientation axis is identical or antiparallel to the f-plane pole that is not the rotation axis of the f-twin operation and also does not lie on a great circle with the c-axis and the rotation axis of the corresponding r-twin operation. So is the misorientation axis for an f\( \left(01\overline{1}2\right) \)/r\( \left(10\overline{1}4\right) \) lamella f\( \left(1\overline{1}02\right) \), while for an f\( \left(01\overline{1}2\right) \)/r\( \left(\overline{1}104\right) \) lamella it is\( \left(10\overline{12}\right) \).

As in the case of a-type lamellae, the shape preferred orientation of the f-type lamellae is controlled by the crystallographic orientation of the host. For f-type lamellae, the boundary traces lie parallel to one f-plane in both the host and the lamella as in the case of a coherent f-twin.

Similar to the a-type boundary segments, f-type boundary segments occasionally split into two spatially separated boundaries, where, analogous to the a-type boundaries, the misorientation of one boundary segment amounts to the misorientation of one f-twin boundary and the other segment to a corresponding r-twin boundary (Fig. 5c). Two a- and f-type lamellae may be adjoined, so that they share a common boundary (Figs. 5 and 6). We observed two different types of boundaries between the lamellae in this study, depending on the angle at which the lamellae connect.

Considering that the shape orientation of an a-type lamella is normal to one of the a-planes both in the host and the lamella, and the boundary of an f-type lamella coincides with an f-plane shared by host and lamella, f- and a-type lamellae may be parallel in a host, since every a-plane pole is perpendicular to one f-plane pole (e.g. a\( \left(2\overline{11}0\right) \) is normal to f\( \left(01\overline{1}2\right) \)). In fact composite lamellae that consist of a- and f-type lamellae may be oriented parallel and joined along the lamellae tips (Figs. 5c and 7d). The boundary between the two lamellae is then characterized by a misorientation resulting in a rotation of 83 ° about a \( \left\{11\overline{2}6\right\} \) pole. This misorientation corresponds to the misorientation resulting from the combination of two twin boundaries, namely two different r-twin boundaries (e.g. one r\( \left(10\overline{1}4\right) \) and one r\( \left(0\overline{1}14\right) \) twin boundary). This boundary may also split into the two constituent r-twin boundaries (Fig. 5c). The domain between these different incoherent r-twin boundaries corresponds to a coherent f-twin with regard to the host.

When the a- and f-type lamellae connect at a high angle, the misorientation between the lamellae corresponds to a rotation of 52 ° about a \( \left\{2\overline{11}3\right\} \) pole (Figs. 5b and 6). This misorientation is produced by the combination of one f- and one e-twin boundary, where the corresponding poles do not lie on the same great circle as the c-axis (e.g. f\( \left(01\overline{1}2\right) \) and e\( \left(\overline{1}018\right) \)). Figure 5 features one f-type lamella that is connected to two a-type lamellae at two different angles. The misorientation between the two a-type lamellae is 64 ° about an \( \left\{0\ 10\ \overline{10}\ 7\right\} \) pole. This misorientation can therefore be constructed by combining the misorientation of two a-type boundaries rotated about different a-axes or the two types of boundaries between a- and f-type domains. The successive application of rotations corresponding to r\( \left(0\overline{1}14\right) \)-, r\( \left(10\overline{1}4\right) \)-, e\( \left(01\overline{1}8\right) \)- and f\( \left(1\overline{1}02\right) \)-twin boundaries then leads to the required misorientation. Most porphyroclasts contain only relatively few low-angle grain boundaries and no subgrains, though the lattice is severely strained. The lattice strain is evident from the high lattice misorientation in the porphyroclast hosts and in the deformation lamellae and twins. The lattice strain in porphyroclasts may lead to a cumulative misorientation of more than 1 ° per μm over distances >10 μm, without the formation of low-angle boundaries. Porphyroclasts with low densities of twins and deformation lamellae may, however, exhibit long and straight low-angle grain boundaries with misorientation angles typically below 5 ° (Fig. 9a). These low-angle boundaries become patchier at higher strain, but still largely retain their straight traces (Fig. 9b). Grains with unfavorable crystallographic orientation for twinning in regions deformed to high shear strains may show irregularly arranged low-angle grain boundaries with constant misorientation angles (Fig. 5).

Fig. 9
figure 9

EBSD orientation deviation maps showing low angle grain boundaries in porphyroclasts with low twin and lamella densities at low a and high shear strain b. (a) IPF map of sample ‘C-1-RT-1b’ deformed under 1 GPa for 1 rotation. EBSD map taken at a distance of 2 mm from the sample center, corresponding to γ ≈ 20 and \( \dot{\upgamma} \) ≈ 7 × 10−3 s−1. (b) IPF map of sample ‘C-4-RT-1q’ deformed under 4 GPa for 1 rotation. EBSD map taken at a distance of 3 mm from the sample center, corresponding to γ ≈ 30 and \( \dot{\upgamma} \) ≈ 1 × 10−2 s−1. Low angle grain boundaries are colored yellow (2–5 °) and red (5–15 °). The orientation color key (Fig. 2e) ranges from 0 to 20 °

Full size image

Discussion

Effect of pressure on the microstructural evolution

The apparent high-temperature twin morphology and the observation of previously unreported deformation lamellae in calcite deformed to high strains by HPT demonstrate that employing a high confining pressure in the GPa range has a significant effect on the deformation behavior of calcite at room temperature. Through the application of confining pressures in excess of 1 GPa macroscopic brittle failure of the sample during deformation at room temperature is prevented even at shear strains exceeding 40. The formation and propagation of cracks during deformation is largely suppressed, because the excess volume associated with defects must be generated against the high hydrostatic pressure (Poirier 1985; Zehetbauer et al. 2003). Thus, HPT allows to perform deformation experiments to much higher strains at low temperatures than would be possible by torsional deformation of calcite at confining pressures of 300 MPa, where sample failure occurs at shear strains of 13 or less even at 500 °C (Barnhoorn et al. 2004). Therefore, a markedly higher fraction of the applied strain is accommodated by an increase in lattice strain at confining pressures in the GPa range. This leads to the activation of alternative deformation mechanisms compared to experiments performed at lower confining pressures.

On the microscopic level, high confining pressures reduce the mobility of point defects. Therefore, the activity of recovery and dynamic recrystallization, which requires dislocation climb, is greatly diminished at pressures in the GPa range as compared to deformation at ambient or low confining pressures. While this effect leads to apparent low temperature characteristics of the microstructures in calcite deformed at elevated temperatures (Schuster et al. 2019), the effect is negligible at room temperature, since the mobility of point defects is already limited at the low homologous temperatures of 0.16–0.18 at pressures between 1 and 4 GPa (Suito et al. 2001). The additional effect of high confining pressures on the mobility of point defects is minute. In contrast to HPT experiments performed at 235 and 450 °C, where the variation of the confining pressure between 1 and 4 GPa significantly affects microstructural parameters such as the morphology of mechanical twins (Schuster et al. 2019), we could not observe significant changes in the microstructural evolution during deformation, when the confining pressure is increased beyond 1 GPa at room temperature.

At room temperature, calcite transforms to CaCO3-II at 1.7 GPa with further transformations to CaCO3-IIIb at 1.9 GPa and to CaCO3-III at 3.3 GPa (Bridgman 1938; Merrill and Bassett 1975; Merlini et al. 2012). The absence of a significant effect of pressure variations between 1 and 4 GPa on the microstructural evolution shows that the stability fields of high pressure polymorphs, do not have any discernible effect on the nucleation and propagation of mechanical twins and the a- and f-type lamellae. Since the presence of a- and f-type boundaries as well as the branching into the constituent twin boundaries, are observed at pressures above and below the transition between calcite and CaCO3-II, their occurrence cannot be explained by effects of different crystal structures during deformation or the back transformation of the high pressure polymorphs to calcite after the pressure release.

Morphology of e-twins

Our findings on the morphology of mechanical e-twins differ from those reported in earlier studies on both naturally and experimentally deformed calcite rocks. The twins conform to morphologies typical for substantially higher deformation temperatures according to the twin morphology geothermometer introduced by Ferrill (1991), Burkhard (1993) and Ferrill et al. (2004), where only thin twins (<1 μm) should occur in calcite deformed at room temperature and increased shear strain should lead to the nucleation of new twins instead of broadening of existing twins, resulting in a high density of thin twins (Ferrill et al. 2004). The primary e-twins in HPT deformed calcite are significantly thicker than 1 μm and have a moderate lensoid shape, which indicates some boundary mobility (Fig. 4). These e-twins are classified as type II twins in the scheme of Burkhard (1993), which are expected to occur only at deformation temperatures above 150 °C. For producing thick, lens-shaped deformation twins, it is necessary that the glissile partial dislocations that propagate the twin can move out of their glide plane by climb or cross-slip (Hirth and Lothe 1982) (Fig. 10). In particular, the climb of edge dislocations requires that point defects are appreciably mobile. Motohashi et al. (1976) found that edge e\( \left\{01\overline{1}8\right\}\left\langle 0\overline{4}41\right\rangle \) twin dislocations have lower line energies than the corresponding screw dislocations. A prevalence of edge twin dislocations compared to screw dislocations was also observed in TEM investigations on deformed calcite (Braillon and Serughetti 1976). Our results indicate that even though it is a thermally activated process necessitating dislocation climb, substantial twin broadening occurs during deformation at room-temperature, if confining pressures in excess of 1 GPa are applied. This suggests that particularly high lattice strain produced during the deformation provides a sufficiently strong driving force that can overcome the sluggish twin boundary motion kinetics and leads to twin broadening even at room temperature.

Fig. 10
figure 10

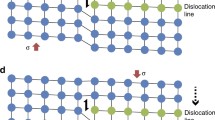
Twin formation and propagation by glide of partial dislocations with their Burgers vector parallel to the shear direction (sd) of the twin. The twin plane is the glide plane of the dislocations. Twin broadening occurs by climb of the partial dislocations. Modified after Hirth and Lothe (1982)

Full size image

The strongly sutured boundaries of secondary twins inside both the host and the primary twins demonstrate significant recrystallization by twin boundary migration, where the secondary twins are consumed by the host and by the primary twins, respectively. In the scheme of Burkhard (1993), such twins are classified as type IV twins, which occur at deformation temperatures exceeding 250 °C. However, a study by Kennedy and White (2001) on twin microstructures in carbonate rocks deformed at low-grade conditions demonstrated that migration and bulging of calcite e-twin boundaries may already occur at temperatures between 150 and 250 °C. The authors suggested that twin boundary migration recrystallization was driven by the high lattice strain arising from dislocation pileups at twin boundaries. Heterogeneously distributed lattice strain is the most significant driving force for grain boundary migration in heavily deformed materials (Urai et al. 1986). Our results indicate, that very high lattice strain, which is inferred from the intense intragranular fracturing during decompression after the HPT experiments and by dislocation densities of 1–2 × 1015 m−2 (Schuster et al. 2017) can induce twin boundary migration recrystallization in calcite even at room temperature. In this manner, apparent high temperature twin morphologies showing significant twin broadening and twin boundary migration may be generated at room temperature and the influence of high confining pressures cannot be neglected when twin morphologies are used as a geothermometer for naturally deformed calcite bearing rocks.

Though thin primary e-twins (type I) were not observed in our study, we cannot exclude the formation of such twins during the initial stages of deformation, since we observed the annihilation of twin lamellae of several μm thickness through twin boundary migration (Fig. 4b). The stability of twin and lamella boundaries varies with the boundary type. The effects of recrystallization on the shape of grain boundaries is usually much more pronounced in the case of r-twins, both coherent and incoherent, than for e- or f-twins or for a-type boundaries.

Deformation lamellae

The prevalence and apparent stability of a-type boundaries in the microstructures investigated in this study point to a low-energy grain boundary structure, which may have general relevance for microstructures of deformed calcite. In fact, several studies on both experimentally and naturally deformed calcite rocks reported a significant number of grain boundaries with a-type misorientation or misorientations about an a-axis with a misorientation angle of up to about 40 ° as a result of different recrystallization mechanisms (Bestmann and Prior 2003; Rogowitz et al. 2014; Schuster et al. 2019).

In Schuster et al. (2019), this boundary misorientation angle was found between isometric grains formed by subgrain rotation recrystallization in samples deformed by HPT at 450 °C. Although most boundaries between recrystallized grains show random misorientations, the a-type boundaries constitute a marked accumulation in misorientation space. Even though remnants of e- and r-twins, obliterated by recrystallization, can be observed in the vicinity of the a-type boundaries, there is no evidence for the twin boundary splitting observed in the current study.

Rogowitz et al. (2014) found evidence for dynamic recrystallization of calcite in natural ultramylonitic shear zones in Syros, Greece, where recrystallization occurs by grain boundary bulging and subsequent overprinting by dislocation glide and grain boundary sliding. The recrystallized shear zones exhibit a-type grain boundaries with a significantly higher frequency than in a random misorientation distribution, where the relative frequency of these boundaries increases with the strain rate (A. Rogowitz, personal communication, March 8, 2017).

Bestmann and Prior (2003) studied recrystallization mechanisms in a natural shear zone within calcite marble rocks on Thassos Island, Greece. They reported the formation of recrystallized grains and subgrains by dislocation creep and subgrain rotation recrystallization in twinned porphyroclasts. In one of the microstructures they found that intragranular deformation and nucleation of grains and subgrains proceeds, apart from e-twinning, by lattice rotations about an a-axis, where the rotation angles are concentrated at low angles. Some more heavily deformed domains show misorientation angles of >30 °, which conform to the misorientations of the a-type boundaries found in the current study.

The examples of a-type boundaries occurring under a wide range of deformation conditions in calcite demonstrate that they can be produced by different deformation and recrystallization mechanisms. The apparent stability and frequency of these grain boundaries may therefore influence the texture and microstructure development during deformation in a range of deformation conditions in both natural and experimental settings.

Conclusions

HPT-processing of compacted calcite powder at room temperature under confining pressures between 1 and 4 GPa produces solid cylindrical pellets that show microstructures associated with cataclastic deformation and extensive twinning as well as the accumulation of substantial lattice strain in the porphyroclasts. The resulting microstructures are characterized by large porphyroclast remnants with pervasive mechanical twins and deformation lamellae.

Results from electron backscatter diffraction indicate the activity of twin boundary migration, a phenomenon that was previously observed only at markedly higher deformation temperatures in calcite. We infer that the high lattice strain accumulated during HPT deformation at confining pressures in the GPa range provides a sufficiently strong driving force that can overcome the sluggish low-temperature kinetics of twin boundary migration. Furthermore, the primary twins are significantly broader than the twins observed after room temperature deformation at sub-GPa confining pressures in the studies that were used to calibrate calcite twin morphology geothermometers. Thus, high confining pressures cannot be neglected when calcite twin morphologies are used as geothermometers.

In addition to pronounced mechanical twinning on e- and to lesser degree on r- and f-planes, a substantial quantity of two distinct types of deformation lamellae form during high-pressure torsion processing. These a- and f-type lamellae have specific crystallographic orientation relationships with the host. The misorientation of these lamellae with the host results from the combination of two different twin operations. The correlation between deformation lamellae and related twin boundaries manifests itself in the frequently observed separation of lamella boundary sections into the two corresponding twin boundaries.

The deformation lamella boundaries and their split boundary segments appear to be highly mobile, leading to irregular grain morphologies. The combined effects of lamella boundary separation and boundary mobility can lead to trails of incoherent apparent f- or r-twins.

The new experimental dataset extends the knowledge on intragranular deformation mechanisms in calcite to deformation to high shear strains at room temperature and high confining pressure. The effect of confining pressures above 1 GPa on the microstructural evolution of calcite during deformation to high shear strains supposes that high confining pressure could significantly contribute to the deformation behavior of carbonate rocks.