1 Introduction

Contact problems play an important role in mechanics because of their wide application to many engineering problems, such as foundations, pavements in roads and runways, railway ballast, brake disks, and gas turbines. Due to their advanced mechanical properties, functionally graded materials (FGMs) have been widely used in various engineering practices. The usage of FGMs as a coating layer or an interfacial material reduces mismatching stresses, increases the bonding strength, improves surface properties, and provides protection against adverse thermal or chemical environments [1, 2]. Some of the applications of FGMs are cylinder linings, brake disks and other automotive components for the purpose of improving the wear resistance of abradable seal design in stationary gas turbines [3]. Numerous studies on FGMs have been conducted recently. For example, Draiche et al. [4] developed an integral shear and normal deformation theory for functionally graded (FG) sandwich curved beams. Free vibration analysis of FG sandwich beams, and two-dimensional FG structures with an exponential material gradation were presented by Yang, Lam et al. and Yang, Kou et al. respectively [5, 6]. A formulation for analyzing FG sandwich structures was presented by Rezaiee-Pajand et al. [7] who developed a mixed interpolated formulation for nonlinear analysis of plates and shells. Xu and Meng [8] presented beam models for FGMs with regular polygonal cross sections, while Chikh [9] presented an analytical solution to a problem of isotropic homogeneous beams based on an elastic foundation.

Among the contact problems, the moving punch problem has a separate and important place. Since, if the speed of the rigid body relative to the elastic one is small enough, then the dynamic character of the phenomenon could be neglected. However, there are problems that arise in practice in which the speed of one body relative to the other is quite large, and, therefore, we need to investigate whether it is necessary to take the dynamic character of the problem into account [10]. Some studies on the moving contact problem are as follows:

Balcı and Dag [11,12,13,14] reduced moving contact problems to singular integral equations and presented a detailed mechanical analysis. Chen and Chen [2] considered a thermoelastic contact model sliding at a speed V on a finite graded layer in which the determination of stress intensity factors (SIFs) and contact stresses were given. A frictional moving punch problem for orthotropic materials was presented for different punch cases by Zhou et al. [15], the study leading to the explanation of the surface damage mechanism of orthotropic materials. The exact solution of moving triangular or parabolic punch problems was presented by Zhou et al. [16]. Meanwhile, Zhou and Lee [17] presented an eigenvalues analysis for a moving frictional punch problem and Çömez [18, 19] considered frictionless and frictional moving contact problems, respectively. The obtained singular integral equations were solved by Gauss–Chebyshev and Gauss–Jacobi integration formulas, respectively. Güler [20] considered a frictional moving contact problem in which a rigid cylindrical punch was assumed to slide at a constant velocity on an orthotropic layer attached to an isotropic half-plane. A singular integral equation was obtained with the help of the Fourier transform technique and Galilean transformation. Numerical results were obtained with the help of the Gauss–Jacobi method. Çömez [21] also applied the singular integral equation technique to a sliding moving contact problem in which the FG layer was bonded to an isotropic homogeneous layer. Zhou and Kim [22] employed the Galilean transformation and Fourier transforms to a frictional moving contact problem of piezomagnetic materials to obtain Cauchy integral equations. Numerical analysis revealed the effects of the friction coefficient and the moving speed of the punch.

In the application of contact mechanics, material properties have great importance. The materials can be classified as isotropic and anisotropic. While isotropic materials have the same properties in all directions, anisotropic materials have different properties in different directions. In particular, the mechanics of anisotropy are of interest when increasing the usage of anisotropic materials such as composites. Among the anisotropic materials, orthotropic materials, in which their mechanical and thermal properties are unique and independent in three mutually perpendicular directions, have been used in many applications, such as fiber-reinforced plates and shells, thin films, and coatings. Bagheri et al. [23] and Bagheri and Hosseini [24] considered multiple moving crack problems in a non-homogeneous orthotropic strip and a non-homogeneous orthotropic plane, respectively. Numerical results were presented for material properties. Hashemi and Ayatollahi [25] examined the transient behavior of an orthotropic layer in multiple crack problems while another multiple crack problem in an orthotropic non-homogeneous plane was studied by Mottale et al. in [26]. Lobatto-Chebyshev method was applied to present the material orthotropy on SIFs. Lei et al. [27] applied the generalized finite difference method to crack problems for anisotropic materials, the numerical results given for orthotropic materials. Yusufoglu and Turhan [28, 29] solved an orthotropic strip problem using different methods for thick and thin strips, respectively Erbaş et al. [30] considered an orthotropic strip problem and solved it with an iterative solution technique and a direct asymptotic procedure for thick and thin strip cases, respectively. Rodriguez-Tembleque and Abascal [31] presented a new methodology for 3D frictional contact problems, while Pozharskii [32] approached a 3D contact problem in orthotropic half-space numerically and analytically. An orthotropic plane problem with a slit was considered by Hakobyan and Dashtoyan [33] and an exact solution presented. Shavlakadze et al. [34] used the methods of the theory of analytic function to reduce the contact problem for a piecewise homogeneous orthotropic plate to a system of singular integro-differential equations, Hou et al. [35] proposed a method based on the Green's function for the orthotropic coating-substrate system and Ustinov and Idrisov [36] calculated two modes of SIFs for the problem of two strips of different degenerate and non-degenerate orthotropic materials. Finally, Cao et al. [37] examined the effect of the material orthotrophy in a frictional receding contact problem.

Although there are many studies in the literature where the punch is static, the number of studies involving the moving contact problem is relatively very few. On the other hand, moving contact studies involving FG half-planes and layers are fewer than homogeneous studies. More specifically, there are no studies on the moving contact problems of an FG orthotropic layer bonded to a homogeneous isotropic half-plane. To fill this gap in the literature, the moving punch problem is modeled with the help of elasticity theory and boundary conditions of the problem in the view of the basics of elasticity theory. This study consists of six sections. The second section defines the boundary conditions and formulation of the problem. In the third section, the singular integral equation is derived, the fourth section is devoted to the numerical solution of singular integral equations and the fifth section is devoted to the numerical results and mechanical interpretation. Finally, the last section is the conclusion.

2 Problem statement and formulation

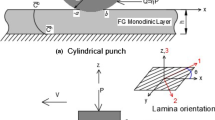
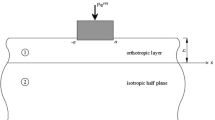
This section presents the formulation of a frictional moving contact problem of an FG orthotropic layer bonded to a homogeneous isotropic half-plane (see Fig. 1). It is assumed that the thickness of the FG orthotropic layer is h and the punch profile is cylindrical. The rigid punch with a radius R moves frictionally at a constant velocity V in the negative direction of the \(- x\) axis. The rectangular coordinates \((X,Z)\) are fixed in the layer and the translating coordinates \((x,z)\) are attached to the moving punch. It is modeled that the punch and layer are in relative motion, that is, \(Q = \eta P\). Where \(\eta\) is the coefficient of friction, P and Q are the resultant normal and tangential forces, respectively.

Fig. 1
figure 1

Geometry of frictional moving contact problem

Full size image

The boundary conditions of the problem can be defined as:

$$ \sigma_{z1} (x,0) = \left\{ {\begin{array}{*{20}l} { - p(x)} \hfill & { - a < x < - b} \hfill \\ 0 \hfill & {x \le a,\;x \ge b} \hfill \\ \end{array} } \right. $$
(1a)
$$ \tau_{xz1} (x,0) = \left\{ {\begin{array}{*{20}c} { - \eta {\kern 1pt} p(x)} & { - a < x - b} \\ 0 & {x \le a,\;x \ge b} \\ \end{array} } \right. $$
(1b)
$$ u_{1} (x, - h) = u_{2} (x, - h) $$
(1c)
$$ w_{1} (x, - h) = w_{2} (x, - h) $$
(1d)
$$ \sigma_{z1} (x, - h) = \sigma_{z2} (x, - h) $$
(1e)
$$ \tau_{xz1} (x, - h) = \tau_{xz2} (x, - h) $$
(1f)

where \(\sigma_{zi} \, \left( {i = 1,2} \right)\) and \(\tau_{xzi} \, \left( {i = 1,2} \right)\) are stress components; \(u_{i} \, \left( {i = 1,2} \right)\) and \(w_{i} \, \left( {i = 1,2} \right)\) are displacement components, \(p(x)\) and \(\eta\) are the contact stress under the rigid punch on the contact area \(( - a,b)\) and the friction coefficient, respectively.

Now, we will give some basic equations of elasticity theory. Motion equations without body forces can be written as

$$ \frac{{\partial \sigma_{xi} }}{\partial X} + \frac{{\partial \tau_{xzi} }}{\partial Z} = \rho_{i} (z)\frac{{\partial^{2} u_{i} }}{{\partial t^{2} }} $$
(2a)
$$ \frac{{\partial \tau_{xzi} }}{\partial X} + \frac{{\partial \sigma_{zi} }}{\partial Z} = \rho_{i} (z)\frac{{\partial^{2} w_{i} }}{{\partial t^{2} }} $$
(2b)

where \(\sigma_{xi}\), \(u_{i}\), \(w_{i}\), \(t\) and \(\rho\) denote the \(X -\) components of the stress, \(X -\) and \(Z -\) components of the displacement vector, time variable and density, respectively.

The generalized Hooke’s law for an FG orthotropic material in a state of plane strain can be written as follows.

$$ \sigma_{x1} = C_{11} (z)\frac{{\partial u_{1} }}{\partial X} + C_{13} (z)\frac{{\partial w_{1} }}{\partial Z} $$
(3a)
$$ \sigma_{z1} = C_{13} (z)\frac{{\partial u_{1} }}{\partial X} + C_{33} (z)\frac{{\partial w_{1} }}{\partial Z} $$
(3b)
$$ \tau_{xz1} = C_{55} (z)\left( {\frac{{\partial u_{1} }}{\partial Z} + \frac{{\partial w_{1} }}{\partial X}} \right) $$
(3c)

where \(C_{ij} (z)\) are the elastic stiffness constants and their continuous variation is modeled by an exponential function in the following form:

$$ C_{ij} (z) = C_{ij}^{0} e^{\gamma z} ,\;\;\gamma h = - Log{\kern 1pt} \,\Gamma ,\;\;\Gamma = C_{ij}^{h} /C_{ij}^{0} $$
(4)

where \(\gamma\) and \(\Gamma\) denote the inhomogeneity constant and the ratio of material constants on the top and bottom surfaces of the FG orthotropic layer, respectively. It is assumed that the variation of the Poisson’s ratio is constant.

The following Galilean transformation is suitable to use for the constant speed:

$$ x = X - Vt,\;\;z = Z $$
(5)

Substitution of the generalized Hooke’s laws (3) and Galilean transformation (5) into motion Eq. (2) yields the steady-state governing equations in the coordinate system \((x,z)\).

$$ C_{11}^{0} \frac{{\partial^{2} u{}_{1}}}{{\partial x^{2} }} + C_{55}^{0} \frac{{\partial^{2} u_{1} }}{{\partial z^{2} }} + \left( {C_{13}^{0} + C_{55}^{0} } \right)\frac{{\partial^{2} w_{1} }}{\partial x\partial z} + \gamma C_{55}^{0} \left( {\frac{{\partial u_{1} }}{\partial z} + \frac{{\partial w_{1} }}{\partial x}} \right) = c_{1}^{2} C_{55}^{0} \frac{{\partial^{2} u_{1} }}{{\partial x^{2} }} $$
(6a)
$$ \left( {C_{13}^{0} + C_{55}^{0} } \right)\frac{{\partial^{2} u}}{\partial x\partial z} + C_{55}^{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} + C_{33}^{0} \frac{{\partial^{2} w}}{{\partial z^{2} }} + \gamma \left( {C_{33}^{0} \frac{\partial w}{{\partial z}} + C_{13}^{0} \frac{\partial u}{{\partial x}}} \right) = c_{1}^{2} C_{55}^{0} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} $$
(6b)

where \(c_{1}^{2} = V^{*} = V^{2} /(C_{55}^{0} /\rho_{10} )\).

Let us rewrite the displacement vectors \(u_{1} (x,z)\) and \(w_{1} (x,z)\;\) using Fourier integral transforms as follows:

$$ u_{1} (x,z) = \int\limits_{ - \infty }^{\infty } {\tilde{u}_{1} (\alpha ,z)e^{ - I\alpha x} } {\text{d}}\alpha $$
(7a)
$$ w_{1} (x,z) = \int\limits_{ - \infty }^{\infty } {\tilde{w}_{1} (\alpha ,z)e^{ - I\alpha x} {\text{d}}\alpha } $$
(7b)

where \(\tilde{u}_{1} (\alpha ,z)\) and \(\tilde{w}_{1} (\alpha ,z)\;\) are the inverse Fourier transforms of the displacement vectors, \(\alpha\) and \(I\) denote the transform variables and the imaginary unit, respectively.

Inserting Eq. (7) into the governing Eq. (6) and applying inverse Fourier transform gives rise to a system of ordinary differential equations

$$ C_{55}^{0} \frac{{{\text{d}}^{2} \tilde{u}_{1} }}{{{\text{d}}z^{2} }} + \gamma C_{55}^{0} \frac{{{\text{d}}\tilde{u}_{1} }}{{{\text{d}}z}} + \alpha^{2} ( - C_{11}^{0} + c_{1}^{2} )\tilde{u}_{1} - I\alpha (C_{13}^{0} + C_{55}^{0} )\frac{{{\text{d}}\tilde{w}_{1} }}{{{\text{d}}z}} - I\alpha \gamma C_{55}^{0} \tilde{w}_{1} = 0 $$
(8a)
$$ - I\alpha (C_{13}^{0} + C_{55}^{0} )\frac{{{\text{d}}\tilde{u}_{1} }}{{{\text{d}}z}} - I\gamma \alpha C_{13}^{0} \tilde{u}_{1} + C_{33}^{0} \frac{{{\text{d}}^{2} \tilde{w}_{1} }}{{{\text{d}}z^{2} }} + \gamma C_{33}^{0} \frac{{{\text{d}}\tilde{w}_{1} }}{{{\text{d}}z}} + \alpha^{2} ( - 1 + c_{1}^{2} )C_{55}^{0} \tilde{w}_{1} = 0 $$
(8b)

The characteristic polynomial of the ordinary differential Eq. (8) is as

$$ n^{4} + L_{1} n^{3} + L_{2} n^{2} + L_{3} n + L_{4} = 0 $$
(9)

where

$$ L_{1} = 2\gamma $$
(10a)
$$ L_{2} = \frac{{\left( {(C_{13}^{0} )^{2} - C_{11}^{0} C_{33}^{0} + 2C_{13}^{0} C_{55}^{0} } \right)\alpha^{2} + C_{55}^{0} \left( {c_{1}^{2} (C_{33}^{0} + C_{55}^{0} )\alpha^{2} + C_{33}^{0} \gamma^{2} } \right)}}{{C_{33}^{0} C_{55}^{0} }} $$
(10b)
$$ L_{3} = \frac{{\left( {(C_{13}^{0} )^{2} - C_{11}^{0} C_{33}^{0} + 2C_{13}^{0} C_{55}^{0} + c_{1}^{2} C_{55}^{0} (C_{33}^{0} + C_{55}^{0} )} \right)\alpha^{2} \gamma }}{{C_{33}^{0} C_{55}^{0} }} $$
(10c)
$$ L_{4} = \frac{{\alpha^{2} \left( {( - 1 + c_{1}^{2} )\left( { - C_{11}^{0} \alpha^{2} + c_{1}^{2} C_{55}^{0} \alpha^{2} } \right) + C_{13}^{0} \gamma^{2} } \right)}}{{C_{33}^{0} }} $$
(10d)

So, the solution of the system of ordinary differential Eq. (8) leads to the following transformed displacement expressions \(\tilde{u}_{1}\) and \(\tilde{w}_{1}\):

$$ \tilde{u}_{1} (\alpha ,z) = \sum\limits_{j = 1}^{4} {A_{j} } \,e^{{n_{j} {\kern 1pt} {\kern 1pt} z}} ,\;\tilde{w}_{1} (\alpha ,z) = I\sum\limits_{j = 1}^{4} {m_{j} A_{j} } \,e^{{n_{j} {\kern 1pt} {\kern 1pt} z}} $$
(11)

where \(n_{j}\) \((j = 1,2,...4)\) are the roots of the characteristic polynomial (9), \(A_{j}\) \((j = 1,2...4)\) are the unknown functions which will be determined by the boundary conditions of the moving contact problem and \(m_{j}\) is found as

$$ m_{j} = - \frac{{I\alpha (C_{55}^{0} n_{j} + C_{13}^{0} (n_{j} + \gamma ))}}{{( - 1 + c_{1}^{2} )C_{55}^{0} \alpha^{2} + C_{33}^{0} n_{j} (n_{j} + \gamma )}} $$
(12)

Now, the stress expressions for the FG orthotropic layer can be rewritten by substituting Eq. (11) into Eq. (3):

$$ \sigma_{x1} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\sum\limits_{j = 1}^{4} {\left[ {A_{j} (C_{13} m_{j} n_{j} - I\alpha C_{11} )\,e^{{n_{j} {\kern 1pt} {\kern 1pt} z}} } \right]} } \,e^{{ - I{\kern 1pt} \alpha {\kern 1pt} x}} {\text{d}}\alpha $$
(13a)
$$ \sigma_{z1} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\sum\limits_{j = 1}^{4} {\left[ {A_{j} (C_{33} m_{j} n_{j} - I\alpha C_{13} )\,e^{{n_{j} {\kern 1pt} {\kern 1pt} z}} } \right]} } \,e^{{ - I{\kern 1pt} \alpha {\kern 1pt} x}} {\text{d}}\alpha $$
(13b)
$$ \tau_{xz1} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\sum\limits_{j = 1}^{4} {\left[ {A_{j} C_{55} (n_{j} - I\alpha m_{j} )\,e^{{n_{j} {\kern 1pt} {\kern 1pt} z}} } \right]} } \,e^{{ - I{\kern 1pt} \alpha {\kern 1pt} x}} {\text{d}}\alpha $$
(13c)

Note that, by setting \(C_{11}^{0} = C_{33}^{0} = \mu_{2} \frac{{\kappa_{2} + 1}}{{\kappa_{2} - 1}}\), \(C_{13}^{0} = \mu_{2} \frac{{3 - \kappa_{2} }}{{\kappa_{2} - 1}}\), \(C_{55}^{0} = \mu_{2}\), \(\gamma = 0\) and \(h \to \infty\) the FG orthotropic layer becomes an homogeneous isotropic half plane. So, for isotropic half plane, the displacement and stress components can be given as [10]:

$$ u_{2} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\sum\limits_{j = 1}^{2} {\left[ {B_{j} e^{{n_{2j} \alpha z}} } \right]} } \,e^{ - I\alpha x} {\text{d}}\alpha $$
(14a)
$$ w_{2} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {I\left[ {B_{1} {\kern 1pt} \frac{1}{{n_{21} }}e^{{n_{21} \alpha z}} + B_{2} n_{22} {\kern 1pt} e^{{n_{22} \alpha z}} } \right]} \,e^{ - I\alpha x} {\text{d}}\alpha $$
(14b)
$$ \sigma_{x2} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } { - I\mu_{2} \alpha } \left[ {2B_{1} e^{{n_{21} \alpha z}} + B_{2} \frac{{(1 + n_{22}^{2} ( - 3 + \kappa_{2} ) + \kappa_{2} )}}{{ - 1 + \kappa_{2} }}e^{{n_{22} \alpha z}} } \right]e^{ - I\alpha x} {\text{d}}\alpha $$
(14c)
$$ \sigma_{z2} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {I\mu_{2} \alpha } \left[ {2B_{1} e^{{n_{21} \alpha z}} + B_{2} \frac{{( - 3 + n_{22}^{2} (1 + \kappa_{2} ) + \kappa_{2} )}}{{ - 1 + \kappa_{2} }}e^{{n_{22} \alpha z}} } \right]e^{ - I\alpha x} {\text{d}}\alpha $$
(14d)
$$ \tau_{xz2} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\mu_{2} \alpha } \left[ {\frac{{1 + n_{21}^{2} }}{{n_{21} }}B_{1} e^{{n_{21} \alpha z}} + 2n_{22} B_{2} e^{{n_{22} \alpha z}} } \right]e^{ - I\alpha x} {\text{d}}\alpha $$
(14e)

where \(\kappa_{2} = 3 - 4v_{2}\). Also \(\mu_{2}\) is the shear modulus and \(v_{2}\) is the Poisson’s ratio of the isotropic half plane, respectively. \(B_{j}\) \((j = 1,2)\) are the unknowns which will be determined from the boundary conditions of the problem. \(n_{2j}\) \((j = 1,2)\) is defined as

$$ n_{21} = \sqrt {1 - c_{2}^{2} } ,\;\;n_{22} = \sqrt {1 - c_{2}^{2} \frac{{( - 1 + \kappa_{2} )}}{{(1 + \kappa_{2} )}}} $$
(15)

where \(c_{2} = V/\sqrt {\mu_{2} /\rho_{2} }\).

Note that, in a translating coordinate system, the unknowns \(A_{j}\) \((j = 1,2...4)\), \(B_{1}\) and \(B_{2}\) will be determined with the help of boundary and continuity conditions (1).

3 Derivation of singular integral equation

In this section, we will use the basic equations of elasticity theory and boundary conditions (1) to derive the singular integral equation. Using Eqs. (13)–(14) in the boundary conditions (1) and applying inverse Fourier transform, six linear algebraic equations are obtained. By solving the obtained system of linear algebraic equations, the coefficients \(A_{j}\) and \(B_{j}\) can be obtained depending on the unknown contact stress \(p(x)\) as the following form

$$ A_{j} = \int\limits_{ - a}^{b} {p(\xi )} e^{I\alpha \xi } (A_{j}^{p} + \eta \,A_{j}^{q} ){\text{d}}\xi \;\;j = 1,2 \ldots 4 $$
(16a)
$$ B_{j} = \int\limits_{ - a}^{b} {p(\xi )} e^{I\alpha \xi } (B_{j}^{p} + \eta \,B_{j}^{q} ){\text{d}}\xi \;\;j = 1,2 $$
(16b)

The following mixed condition will be used to find the unknown contact stress \(p(x)\)

$$ \frac{{\partial w_{1} (x,0)}}{\partial x} = \frac{x}{R} $$
(17)

Using the unknowns \(A_{j}\) in the mixed condition (17) and considering the asymptotic behavior of the kernels for \(\left| \alpha \right| \to \infty\) yields the following second kind of singular integral equation of Cauchy type:

$$ \eta \phi_{2} p(x) + \frac{1}{\pi }\int\limits_{ - a}^{b} {p(\xi )} \left[ {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right.\frac{{\phi_{1} }}{\xi - x} + K_{1} (x,\xi ) + \eta \,K_{2} (x,\xi )\left. {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right]{\text{d}}\xi = \frac{x}{R}\;\;( - a < x < b) $$
(18)

where

$$ K_{1} (x,\xi ) = \int\limits_{0}^{\infty } {(\;S_{1} } (\alpha ) - \phi_{1} )\sin \alpha (\xi - x){\text{d}}\alpha $$
(19a)
$$ K_{2} (x,\xi ) = \int\limits_{0}^{\infty } {(S_{2} } (\alpha ) - \phi_{2} )\cos \alpha (\xi - x){\text{d}}\alpha $$
(19b)
$$ S_{1} (\alpha ) = \alpha \sum\limits_{j = 1}^{4} {A_{j}^{p} } m_{j} ,\;\;S_{2} (\alpha ) = - I\alpha \sum\limits_{j = 1}^{4} {A_{j}^{q} } m_{j} $$
(19c)
$$ \phi_{1} = \mathop {\lim }\limits_{\alpha \to \infty } \;S_{1} (\alpha ),\;\;\phi_{2} = \mathop {\lim }\limits_{\alpha \to \infty } \;S_{2} (\alpha ) $$
(19d)

Note that, the contact widths must satisfy the following equilibrium condition

$$ \int\limits_{ - \infty }^{\infty } {\sigma_{z1} (x,0){\text{d}}x} = - \int\limits_{ - a}^{b} {p(\xi ){\text{d}}\xi } = - P $$
(20)

4 Numerical solution of the singular integral equation

This section presents the numerical solution of the singular integral Eq. (18). Here, it is aimed to convert the solution of singular integral equation to the solution of system of algebraic equations. Gauss–Jacobi integration formulas are used to approach the numerical solution. So, first, the singular integral equation should be converted to the dimensionless form by using following normalization procedure:

$$ \xi = \frac{a + b}{2}r + \frac{b - a}{2},\;\;\;\;x = \frac{a + b}{2}s + \frac{b - a}{2} $$
(21)

Hence, the integral Eq. (18) can be rewritten as

$$ \eta \phi_{2} p(s) + \frac{1}{\pi }\int\limits_{ - 1}^{1} {p(r)} \left[ {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right.\frac{{\phi_{2} }}{r - s} + K_{1}^{*} (s,r) + \eta \,K_{2}^{*} (s,r)\left. {\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right]{\text{d}}r = f\left( s \right) $$
(22)

where

$$ K_{1}^{*} (s,r) = \frac{a + b}{2}K_{1} (x,\xi ),\;\;K_{2}^{*} (s,r) = \frac{a + b}{2}K_{2} (x,\xi ),\;\;f\left( s \right) = \frac{1}{R}\left( {\frac{a + b}{2}s + \frac{b - a}{2}} \right) $$
(23)

By applying the same variable transform (21) to the equilibrium condition (20), the following integral equation can be obtained:

$$ \frac{a + b}{2}\int\limits_{ - 1}^{1} {p(r){\text{d}}r} = P $$
(24)

Since the punch profile is cylindrical, smooth contact occurs at the end points of the contact \(x = - a\) and \(x = b\). Therefore, the index of the integral Eq. (18) is taken \(- 1\).

Now, let us seek the solution of the singular integral Eq. (22) as

$$ p(r) = g(r)(1 - r)^{{\beta_{1} }} (1 + r)^{{\beta_{2} }} $$
(25)

where \(g(r)\) is an unknown bounded function and

$$ \beta_{1} = \frac{1}{2\pi I}\ln \left[ {\frac{{\eta \,\phi_{2} /\phi_{1} - I}}{{\eta \,\phi_{2} /\phi_{1} + I}}} \right] $$
(26a)
$$ \beta_{2} = - \frac{1}{2\pi I}\ln \left[ {\frac{{\eta \,\phi_{2} /\phi_{1} - I}}{{\eta \,\phi_{2} /\phi_{1} + I}}} \right] + 1 $$
(26b)

By applying Gauss–Jacobi integration formulas [38] to the singular integral Eq. (22) and equilibrium condition (24), the following system of algebraic equations is obtained:

$$ \sum\limits_{i = 1}^{N} {W_{i}^{N} } g(r_{i} )\left[ {\frac{1}{{r_{i} - s_{k} }} + K_{1}^{*} (s_{k} ,r_{i} ) + \eta \,K_{2}^{*} (s_{k} ,r_{i} )} \right] = f\left( {s_{k} } \right)\;\;\;k = 1,2,...,N + 1 $$
(27)
$$ \frac{b + a}{2}\sum\limits_{i = 1}^{N} {W_{i}^{N} } g(r_{i} ) = \frac{P}{\pi } $$
(28)

where \(r_{i}\) and \(s_{k}\) are the roots of Jacobi polynomials defined as

$$ P_{N}^{(\alpha ,\beta )} (r_{i} ) = 0\;\;\;i = 1,2,...,N $$
(29a)
$$ P_{N + 1}^{( - \alpha , - \beta )} (s_{k} ) = 0\;\;\;\;\;k = 1,2,...,N + 1 $$
(29b)

and \(W_{i}^{N}\) is the weighting constant given as follows:

$$ W_{i}^{N} = - \frac{1}{\pi }\frac{2N + \alpha + \beta }{{(N + 1)!}}\frac{\Gamma (N + \alpha + 1)\Gamma (N + \alpha + 1)}{{\Gamma (N + \alpha + \beta + 1)}}\frac{{2^{(\alpha + \beta )} }}{{P_{N}^{{(\alpha ,\beta ){\prime} }} (r_{i} )P_{N + 1}^{(\alpha ,\beta )} (r_{i} )}} $$
(29c)

As is seen from Eqs. (27) and (28), there are \(N + 2\) equations which have \(N + 2\) unknowns. The unknowns are \(g(r_{i} )\) \((i = 1,2....N)\) and contact widths \(a\) and \(b\). Since the contact widths \(a\) and \(b\) are initially unknown, the system of equations is non-linear, and, therefore, an iterative procedure is applied to determine the contact widths. In the iterative algorithm the initial values of the \(a\) and \(b\) are chosen and \(N\) unknowns \(g(r_{i} )\) are determined from the linear algebraic equations in (27). Then, the subtracted equation in (27), i.e. the consistency condition and the equilibrium condition (25) are checked. If the selected accuracy is not achieved, new values of \(a\) and \(b\) are selected. The selection of new values of \(a\) and \(b\) will continue until \(a\) and \(b\) achieve the desired accuracy.

In mechanics, the analysis of in-plane stress is also an important subject. The in-plane stress at the surface of FG orthotropic layer \(\sigma_{x1} (x,0)\) can be determined by the relation below:

$$ \sigma_{x1} (x,0) = \left\{ {\begin{array}{*{20}c} {\phi_{3} p(x) + H(x),} & { - a < x < b} \\ {H(x),} & {x \le - a,\;\;x \ge b} \\ \end{array} } \right\} $$
(30)

where

$$ H(x) = \frac{1}{\pi }\int\limits_{ - a}^{b} {p(\xi )} \left[ {\phi_{4} \frac{\eta }{\xi - x} + K_{3} (x,\xi ) + \eta \,K_{4} (x,\xi )} \right]{\text{d}}\xi $$
(31a)
$$ K_{3} (x,\xi ) = \int\limits_{0}^{\infty } {(S_{3} } (\alpha ) - \phi_{3} )\cos \alpha (\xi - x){\text{d}}\alpha $$
(31b)
$$ K_{4} (x,\xi ) = \int\limits_{0}^{\infty } {(\;S_{4} } (\alpha ) - \phi_{4} )\sin \alpha (\xi - x){\text{d}}\alpha $$
(31c)
$$ S_{3} (\alpha ) = \sum\limits_{j = 1}^{4} {\left[ {A_{j}^{p} (C_{13} m_{j} n_{j} - I\alpha C_{11} )\,} \right]} $$
(31d)
$$ S_{4} (\alpha ) = I\sum\limits_{j = 1}^{4} {\left[ {A_{j}^{q} (C_{13} m_{j} n_{j} - I\alpha C_{11} )\,} \right]} $$
(31e)
$$ \phi_{3} = \mathop {\lim }\limits_{\alpha \to \infty } \;S_{3} (\alpha ),\;\;\phi_{4} = \mathop {\lim }\limits_{\alpha \to \infty } \;S_{4} (\alpha ) $$
(31f)

5 Numerical results

This section presents the effect of the dimensionless quantities such as moving velocity \(V^{*} = V/\sqrt {C_{55}^{0} /\rho_{10} }\), inhomogeneity parameter \(\Gamma = C_{h} /C_{0}\), friction coefficient \(\eta\), shear modulus of the half plane \(\mu_{2}^{*} = \mu_{2} /C_{55}^{0}\), density of the half plane \(\rho_{2}^{*} = \rho_{2} /\rho_{10}\) and indentation load \(P^{*} = P/(C_{55}^{0} h)\), on the dimensionless contact stress \(p(x)/C_{55}^{0}\) and in-plane stress \(\sigma_{x1} (x,0)/C_{55}^{0}\) are given. During the analysis, it is assumed that the FG orthotropic layer is made of glass/epoxy (Gl/Ep). The material properties of glass/epoxy are listed in Table 1.

Table 1 Material properties of glass/epoxy [39]
Full size table

By setting \(\Gamma = C_{h} /C_{0} = 1\) the FG orthotropic layer becomes a homogeneous orthotropic layer. So, it gives a chance to validate the present results with the numerical results obtained in [20]. As a result of comparison of the results of the limiting case by [20], a very good agreement was obtained as depicted in Fig. 2.

Fig. 2
figure 2

Comparison of the contact stress and in-plane stress with those from [20]. \((V^{*} = 0.4,\eta = 0.4,\;P/(C_{550} h) = 0.01,\Gamma = C_{h} /C_{0} = 1,\rho_{2} /\rho_{10} = 1,\mu_{2} /C_{550} = 2)\)

Full size image

Variation of the contact width with moving velocity \(V^{*}\) and indentation load \(P^{*}\) is given in Fig. 3. It is seen in the figure that the punch becomes more embedded in the layer with increasing load. On the other hand, increasing the movement speed at small load values affects the contact width less than at large load values.

Fig. 3
figure 3

Variation of the contact width \((a + b)/h\) with moving velocity \(V^{*}\) and indentation load \(P^{*}\). \((\eta = 0.4,R/h = 100,\;\Gamma = C_{h} /C_{0} = 2,\rho_{2} /\rho_{10} = 1.5,\mu_{2} /C_{550} = 2)\)

Full size image

Variation of the contact width with the shear modulus of the half-plane and \(\Gamma\) inhomogeneity parameter is shown in Fig. 4. The stiffness of the functionally graded orthotropic layer changes exponentially depending on the \(\Gamma\) inhomogeneity parameter, starting from the bottom surface of the layer. Increasing the \(\Gamma\) parameter increases the stiffness of the FG layer while decreasing the \(\Gamma\) parameter reduces the stiffness of the FG layer. The situation where \(\Gamma\) is equal to one corresponds to the homogeneous layer particular case. When the layer become soft, the penetration between the punch and the layer increases, and, accordingly, the contact width between the FG layer and the punch increases. At values of the \(\Gamma\) inhomogeneity parameter close to zero, there is a tendency for contact widths to approach infinity. On the other hand, as the dimensionless shear modulus ratio of the half-plane decreases, the contact widths under the punch increase as the half-plane becomes flexible. Especially if this ratio is equal to 0.5, contact widths increase significantly.

Fig. 4
figure 4

Variation of the contact width \((a + b)/h\) with shear modulus of half plane \(\mu_{2}^{*}\) and inhomogeneity parameter \(\Gamma\). \((\eta = 0.4,R/h = 200,\;P/(C_{550} h) = 0.02,\rho_{2} /\rho_{10} = 2,V^{*} = 0.2)\)

Full size image

Figure 5 shows the variation of the contact width with the friction coefficient \(\eta\) and dimensionless density of the half-plane \(\rho_{2}^{*}\). It can be concluded from the figure that changes in density ratio and friction coefficient do not much affect the contact width. On the other hand, since it creates resistance forces that prevent separation between the FG layer and the punch due to the friction forces, it causes a slight decrease in the contact widths between the punch and the FG layer. Moreover, according to Newton's law of motion, as the mass density increases, the dynamic forces acting on the system due to the speed of the punch also increase. Therefore, as the density ratio \(\rho_{2}^{*}\) increases, the contact lengths under the punch increase slightly.

Fig. 5
figure 5

Variation of the contact width \((a + b)/h\) with friction coefficient \(\eta\) and density of half plane \(\rho_{2}^{*}\). \((R/h = 200,\;P/(C_{550} h) = 0.02,\Gamma = C_{h} /C_{0} = 2,V^{*} = 0.2,\mu_{2} /C_{550} = 2)\)

Full size image

Figure 6 presents the variation of the dimensionless contact stress and in-plane stress versus different moving velocity values. The regions where tensile stress occurs in the \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane stress distribution under the punch are the regions where contact damage and crack formation are likely. Surface cracks may subsequently cause fatigue cracks to form and propagate. For this reason, the dimensionless \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane stress distribution under the punch was evaluated based on the behavior of tensile stresses. As can be seen from the figure, because of the increase in the moving speed of the punch, the peak value of the tensile stresses in the \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane stress distribution decreases. In addition, it leads to smaller contact pressure associated with a larger contact zone when the punch slides faster.

Fig. 6
figure 6

Variations of the contact stress, \(p(x)\), in-plane stress, \(\sigma_{x1} (x,0)\), versus moving velocity, \(V^{*}\). \((R/h = 200,\;P/(C_{550} h) = 0.02,\Gamma = C_{h} /C_{0} = 2,\rho_{2} /\rho_{10} = 2,\mu_{2} /C_{550} = 2)\)

Full size image

Variations of the contact stress \(p(x)/C_{55}^{0}\) and in-plane stress \(\sigma_{x1} (x,0)/C_{55}^{0}\) versus inhomogeneity parameter \(\Gamma\) are illustrated in Fig. 7. As can be seen from the figure, as the \(\Gamma\) inhomogeneity parameter increases, the FG layer will become stiffer and the dimensionless contact widths under the punch decrease. Since the stresses will disperse over a smaller area, the maximum value of the contact stresses under the punch increases. Although the \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane stresses under the punch are not significantly affected by the increase in this \(\Gamma\) inhomogeneity parameter, the peak value of the tensile stresses at the trailing edge decreases slightly.

Fig. 7
figure 7

Variations of the contact stress, \(p(x)\), in-plane stress, \(\sigma_{x1} (x,0)\),versus inhomogeneity parameter, \(\Gamma\). \((\eta = 0.4,R/h = 200,\;P/(C_{550} h) = 0.02,\rho_{2} /\rho_{10} = 2,V^{*} = 0.4,\mu_{2} /C_{550} = 2)\)

Full size image

Figure 8 presents variations of contact stress \(p(x)/C_{55}^{0}\) and in-plane stress \(\sigma_{x1} (x,0)/C_{55}^{0}\) versus friction coefficient \(\eta\). The distribution of dimensionless contact stresses under the punch is symmetrical in the case of frictionless contact (\(\eta = 0\)) and takes its largest value on the z-axis. This symmetry disappears when friction forces are influential (\(\eta \ne 0\)). However, as the friction forces increase, the values of the tensile stresses at the right end of the distribution of dimensionless \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane normal stresses increase significantly. Therefore, it should be taken into consideration that increased friction effects may cause damage and crack formation on the contact surfaces. To prevent such damage, a small coefficient of friction should be selected.

Fig. 8
figure 8

Variations of the contact stress, \(p(x)\), in-plane stress, \(\sigma_{x1} (x,0)\), versus friction coefficient, \(\eta\). \((R/h = 200,\;P/(C_{550} h) = 0.02,\Gamma = C_{h} /C_{0} = 2,\rho_{2} /\rho_{10} = 2,V^{*} = 0.4,\mu_{2} /C_{550} = 2)\)

Full size image

Figure 9 illustrates variations of contact stress \(p(x)/C_{55}^{0}\) and in-plane stress \(\sigma_{x1} (x,0)/C_{55}^{0}\) versus the dimensionless shear modulus of the half-plane \(\mu_{2}^{*}\). Since the rigidity of the system increases with bigger values of \(\mu_{2}^{*}\) ratio, the contact width under the punch decreases. Additionally, the maximum values ​​of tensile stresses in the \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane stress distribution increase with the increase in the shear modulus of the half-plane \(\mu_{2}^{*}\).

Fig. 9
figure 9

Variations of the contact stress, \(p(x)\), in-plane stress, \(\sigma_{x1} (x,0)\), versus shear modulus of half plane, \(\mu_{2}^{*}\). \((\eta = 0.4,R/h = 200,\;P/(C_{550} h) = 0.02,\Gamma = C_{h} /C_{0} = 2,\rho_{2} /\rho_{10} = 2,V^{*} = 0.2)\)

Full size image

Variations of the contact stress \(p(x)/C_{55}^{0}\) and in-plane stress \(\sigma_{x1} (x,0)/C_{55}^{0}\) versus indentation load \(P^{*}\) and dimensionless density of the half-plane \(\rho_{2}^{*}\) are shown in Fig. 10 and Fig. 11. In contrast to the other parameters, an increase in load increases both contact widths and contact stresses together. The peak values of tensile stresses in the \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane stress distribution under the punch also increase significantly with this increase. Although the change in the dimensionless density values of the half-plane \(\rho_{2}^{*}\) does not have a significant effect, the peak values of the contact stress under the punch and the \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane tensile stresses decrease slightly as this value increases.

Fig. 10
figure 10

Variations of the contact stress, \(p(x)\), in-plane stress, \(\sigma_{x1} (x,0)\), versus indentation load, \(P^{*}\). \((\eta = 0.4,R/h = 200,\;\Gamma = C_{h} /C_{0} = 2,\rho_{2} /\rho_{10} = 2,V^{*} = 0.4,\mu_{2} /C_{550} = 2)\)

Full size image
Fig. 11
figure 11

Variations of the contact stress, \(p(x)\), in-plane stress, \(\sigma_{x1} (x,0)\), versus density of half plane, \(\rho_{2}^{*}\).\((\eta = 0.4,R/h = 200,\;P/(C_{550} h) = 0.02,\Gamma = C_{h} /C_{0} = 2,V^{*} = 0.2,\mu_{2} /C_{550} = 2)\)

Full size image

Figures 12 and 13 show the effect of \(C_{330}\) and \(C_{110}\) orthotropy constants on the distribution of \(p(x)\) contact stress and \(\sigma_{x1} (x,0)\) in-plane stress. Since increasing the \(C_{330}\) orthotropy constant will increase the material rigidity in the direction of the force, the contact length under the punch decreases, and the peak value of contact stress increases for increasing the \(C_{330}\) orthotropy constant value. In the \(\sigma_{x1} (x,0)\) in-plane stresses under the punch, as the \(C_{330}\) orthotropy constant increases, the maximum value of the tensile stress, which can trigger crack formation and surface damage, also increases. The change of the \(C_{110}\) orthotropy constant is not related to the change of material stiffness in the force direction. However, since the increase in the \(C_{110}\) orthotropy constant will increase the layer stiffness, the contact lengths under the punch decrease slightly. Additionally, with the increase of the \(C_{110}\) orthotropy constant, the maximum value of in-plane \(\sigma_{x1} (x,0)\) tensile stress under the punch increases significantly.

Fig. 12
figure 12

Variations of the contact stress, \(p(x)\), in-plane stress, \(\sigma_{x1} (x,0)\), versus orthotropy constant \(C_{330}\). \((\eta = 0.4,R/h = 200,\;P/(C_{550} h) = 0.01,\Gamma = C_{h} /C_{0} = 2,\rho_{2} /\rho_{10} = 1,V^{*} = 0.4,\mu_{2} /C_{550} = 2)\)

Full size image
Fig. 13
figure 13

Variations of the contact stress, \(p(x)\), in-plane stress, \(\sigma_{x1} (x,0)\), versus orthotropy constant \(C_{110}\). \((\eta = 0.4,R/h = 200,\;P/(C_{550} h) = 0.01,\Gamma = C_{h} /C_{0} = 2,\rho_{2} /\rho_{10} = 1,V^{*} = 0,\mu_{2} /C_{550} = 2)\)

Full size image

6 Conclusions

This study investigated the moving contact problem of a functionally graded orthotropic-coated half-plane. Numerical results for dimensionless contact widths, contact pressures and in-plane stress distributions under the punch were obtained for different values of moving velocity, indentation loads, inhomogeneity parameter, the density of the half-plane, shear modulus of the half-plane and friction coefficient. The outcomes of the study can be summarized as given as follows.

  • Dimensionless contact widths under the punch vary directly proportional to the moving velocity, indentation load, and orthotropy constant \(C_{330}\), and inversely proportional to the values of the inhomogeneity parameter and the dimensionless shear modulus of the half plane. The size of the contact area under the punch is not much affected by the change in the friction coefficient, the dimensionless density ratio of the half plane and orthotropy constant \(C_{110}\).

  • The regions where tensile stress occurs at the in-plane stress distribution under the punch are the regions where contact damage and crack formation are likely. Surface cracks may subsequently cause fatigue cracks to form and propagate. In the \(\sigma_{x1} (x,0)/C_{55}^{0}\) in-plane stress distribution, the peak values ​​of tensile stresses increase significantly with the increase in the friction coefficient, dimensionless shear modulus of the half-plane, indentation load values, orthotropy constants \(C_{110}\) and \(C_{330}\). On the other hand, increasing the moving velocity of the punch causes the peak values ​​of tensile stresses to decrease. The change in the density ratio of the half-plane and the \(\Gamma\) inhomogeneity parameter values ​​does not have much effect on the peak values ​​of tensile stresses.