Abstract
This paper investigates the vibration characteristics of a sandwich nanosensor plate composed of piezoelectric materials, specifically barium and cobalt, in the upper and lower layers, and a core material consisting of either ceramic (silicon nitride) or metal (stainless steel) foams reinforced with graphene (GPRL). The study utilized the novel sinosoidal higher-order deformation theory and nonlocal strain gradient elasticity theory. The equations of motion for nanosensor sandwich graphene were derived using Hamilton's principle, considering the thermal, electroelastic, and magnetostrictive characteristics of the piezomagnetic surface plates. These equations were then solved using the Navier method. The core element of the sandwich nanosensor plate can be represented using three distinct foam variants: a uniform foam model, as well as two symmetric foam models. The investigation focused on analyzing the dimensionless fundamental natural frequencies of the sandwich nanosensor plate. This analysis considered the influence of three distinct foam types, the volumetric graphene ratio, temperature variation, nonlocal parameters, porosity ratio, electric and magnetic potential, as well as spring and shear viscoelastic support. Furthermore, an analysis was conducted on the impact of the metal and ceramic composition of the central section of the sandwich nanosensor plate on its dimensionless fundamental natural frequencies. In this context, the use of ceramic as the central material results in a mean enhancement of 33% in the fundamental natural frequencies. In contrast, the incorporation of graphene into the core material results in an average enhancement of 27%. The thermomechanical vibration behavior of the nanosensor plate reveals that the presence of graphene-supported foam and a viscoelastic support structure in the core layer leads to an increase in thermal resistance. This increase is dependent on factors such as the ratio of graphene, porosity ratio of the foam, and parameters of the viscoelastic support. Metal foam or ceramic foam has been found to enhance thermal resistance when compared to solid metal or ceramic core materials. The analysis results showed that it is important to take into account the temperature-dependent thermal properties of barium and cobalt, which are piezo-electromagnetic materials, and the core layer materials ceramics and metal, as well as the graphene used to strengthen the core. The research is anticipated to generate valuable findings regarding the advancement and utilization of nanosensors, transducers, and nano-electromechanical systems engineered for operation in high-temperature environments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Magneto–electroelastic smart plates are a type of composite material that exhibit magneto–electric coupling behavior, meaning they can respond to both magnetic and electric fields. These plates are composed of layers of different materials, such as ferromagnetic and ferroelectric materials, which allow for the coupling of electric and magnetic fields [1]. Research has been conducted on various aspects of magneto–electroelastic plates. Bhangale and Ganesan studied the static analysis of simply supported functionally graded and layered magneto–electroelastic plates. They used a semi-analytical finite element method to analyze the behavior of these plates. They also investigated the free vibration of non-homogeneous transversely isotropic magneto–electroelastic plates [1]. The finite element method is a technique employed for achieving great computational accuracy and analyzing static measurement data [2, 3]. Hong et al. developed a magneto–electroelastic functionally graded Timoshenko microbeam model. The extended modified couple stress theory was employed to account for the influence of microstructure. The model allowed for the analysis of the bending and vibration behavior of functionally graded magneto–electroelastic microbeams [4]. Surface effects on magneto–electroelastic structures have also been investigated. The investigation conducted by Wu et al. focused on examining the influence of surface factors on the propagation of anti-plane shear waves in magneto–electroelastic nanoplates. They developed a surface magneto–electroelasticity theory to describe the motion of the material surface. The study showed that the material surface can have a significant effect on the mechanical behavior of magneto–electroelastic structures at the nanoscale [5].
In addition to the above studies, there have been investigations into the wave propagation, surface wave speed, and magneto–electric coupling properties of magneto–electroelastic materials [6]. To analyze FG-MEE plates and shells statically and dynamically, Zhang et al. [7] created a FE model containing magneto–electroelastic fields. These studies have contributed to a better understanding of the behavior and potential applications of magneto–electroelastic smart plates. Overall, research on magneto–electroelastic smart plates has focused on various aspects such as static analysis, free vibration, surface effects, and wave propagation. These studies have provided valuable insights into the behavior and potential applications of these composite materials.
Foam core sandwich plates are composite structures consisting of two face sheets bonded to a lightweight foam core. These plates have been extensively studied in various fields, including blast loading, impact resistance, vibration analysis, and energy absorption. Radford et al. conducted experiments to measure the dynamic response of clamped circular monolithic and sandwich plates with metallic foam cores to simulated blast loading. The sandwich plates consisted of AISI 304 stainless steel face sheets and aluminum alloy metal foam cores. The study quantified the resistance to shock loading and evaluated the permanent transverse deformation of the plates [8]. The study conducted by Mcshane et al. focused on examining the reaction of clamped sandwich plates containing lattice cores when subjected to shock loading. The sandwich plates were constructed with face sheets made of AISI 304 stainless steel, accompanied by either pyramidal cores made of AL-6XN stainless steel or lattice cores made of AISI steel. The study measured the dynamic response of the plates when loaded at mid-span with metal foam projectiles [9]. Al-Waily et al. studied the free vibration analysis of sandwich plates with reinforced foam cores using micro-aluminum powder. The study evaluated the stiffness characteristics of the foam–aluminum core and found that the use of microspherical powder foam in the vacant spherical gaps of the foam core improved the free vibration and static behavior of the sandwich plates [10]. The study conducted by Civalek et al. investigated the impact of deformable border and porosity on the free vibration parameters of metal foam functionally graded restricted Rayleigh microbeams [11]. The study conducted by Babaei et al. focused on investigating the characteristics of small and large amplitude free vibrations in a composite beam composed of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) [12]. The study conducted by Borojeni et al. examined the impact of temperature and magnetoelastic stress on the free vibration characteristics of an elastomer sandwich beam inside a high temperature [13]. Zhao et al. conducted experimental and numerical investigations on the anti-penetration performance of metallic sandwich plates with aluminum foam cores for marine applications. The study evaluated the ballistic limit of the sandwich plates and analyzed the effects of impact velocity, facesheet thickness, and foam core density on the anti-penetration performance [14]. The study conducted by Ren et al. included an analysis of the dynamic failure behavior shown by sandwich constructions composed of carbon fiber-reinforced plastics with polyvinyl chloride (PVC) foam cores when exposed to impact stress. The study investigated the influence of core density and thickness on the impact resistance of the composite sandwich plates [15]. The objective of Sun et al.'s study was to enhance the structural integrity of foam core sandwich structures through the incorporation of carbon fiber/epoxy stitched reinforcements, which were carefully selected based on their fiber volume fraction [16]. The function of low-density structural polymeric foams filling the interstices of the cores of metal sandwich plates was investigated by Vaziri et al. The research investigated the structural properties of square honeycomb and folded plate steel cores that were filled with two different densities of structural foams. The objective was to determine the extent to which these cores could be reinforced and how they may improve the performance of the plates when subjected to crushing and impulsive loads [17]. The sandwich panel developed by Boztoprak et al. exhibits characteristics of sound absorption and low sound transmission [18]. Bakir et al. investigated the impact energy absorption of aromatic thermosetting copolyester (ATSP) foam core and aluminum foam face three-layer sandwich composites. The study concluded that the interfacial bonding between the ATSP foam core and high-performance aluminum and titanium alloys, stainless steel, and high-temperature polymer composite laminate enhanced the impact energy absorption of the sandwich composite structure [19]. Mocian et al. assessed the energy absorption of foam core sandwich panels under low-velocity impact. The study examined the response to low-velocity impact and the damage processes of foam core sandwich panels. Different foam core materials, such as polyurethane and polystyrene, were used in combination with aluminum facesheets [20]. The study conducted by Kaboglu et al. aimed to examine the impact of core density on the quasi-static flexural and ballistic characteristics of fiber–composite skin/foam core sandwich constructions. The study manufactured various sandwich structures using glass-fiber-reinforced polymer skins and polymeric foam cores. The core density was varied to analyze its influence on the flexural and ballistic performance of the sandwich structures [21]. These studies provide valuable insights into the behavior and performance of foam core sandwich plates in different loading conditions, including blast loading, impact resistance, vibration analysis, and energy absorption. The findings contribute to the understanding and design of lightweight and high-performance composite structures for various applications.
Micromechanics and nonlocality of nanoplates have been extensively studied in the literature. Several research papers have investigated various aspects of the behavior and properties of nanoplates, including buckling analysis, vibration analysis, and the effects of different factors on their mechanical response. The buckling analysis of nanoscale magneto–electroelastic plates was accomplished by Park and Han, using the nonlocal elasticity theory. The study focused on the higher-order shear deformation theory and investigated the buckling behavior of nonlocal magneto–electroelastic nanoplates. The in-plane magnetic and electric fields were considered negligible for these plates [22]. The buckling study of nanocomposite sandwich plates with piezoelectric face sheets was conducted by Amir et al., using the principles of flexoelectricity and the first-order shear deformation theory. The study examined the effects of flexoelectricity on the critical buckling load of the sandwich plates and discussed the implications for the design and control of similar systems [23]. Monaco et al. investigated the critical temperatures associated with vibrations and buckling in magneto–electroelastic nonlocal strain gradient plates. The research focused on the vibrations and buckling behavior of magneto–electroelastic plates at the nanoscale, considering the effects of hygro-thermal loads. The study provided insights into the critical temperatures for vibrations and buckling of these plates [24]. Boyina et al. [25] proposed a nonlocal strain gradient model to analyze the buckling of functionally graded Euler–Bernoulli beams subjected to thermomechanical stresses. Woo et al. [26] presented an analytical method to investigate the post-buckling behavior of plates and shallow cylindrical shells composed of functionally graded materials subjected to edge pressure loads and temperature variations. Quan et al. [27] presented analytical solutions for analyzing the static buckling and vibration phenomena in nanocomposite multilayer perovskite solar cells. The study conducted by Arefi et al. focused on the examination of free vibrations in a three-layered nano-/microplate with piezomagnetic face sheets. The plate was graded exponentially in terms of its size and was supported by Pasternak's foundation. The researchers used the modified couple stress theory for their analysis. The study employed the Mindlin's plate theory and the modified couple stress theory to analyze the static bending and forced vibration of the nano-/microplate. The effects of size dependency and the foundation on the vibration behavior were considered [28]. Yan et al. [29] utilized nonlocal continuum mechanics in order to obtain precise and asymptotic expressions for infinite higher-order governing differential equations pertaining to nanobeam and nanoplate models. Naghinejad and Ovesy studied the free vibration characteristics of nonlocal viscoelastic nanoscaled plates with rectangular cutouts and surface effects. The research focused on the nonlocal effects on the mechanical properties of small-sized plates and investigated the influence of surface effects on the free vibration behavior of the plates [30]. The vibration characteristics of orthotropic circular and elliptical nanoplates, which are immersed in an elastic mediums, were examined by Anjomshoa and Tahani. This analysis was conducted by using the nonlocal Mindlin plate theory and utilizing the Galerkin technique. The study investigated the vibration behavior of nanoplates with different geometries and materials, considering the nonlocal effects and the interaction with the surrounding elastic medium [31]. The study conducted by Wu et al. focused on examining the influence of surface factors on the propagation of anti-plane shear waves in magneto–electroelastic nanoplates. The study developed a surface magneto–electroelasticity theory to describe the motion of the material surface of magneto–electroelastic structures at the nanoscale. The effects of the material surface on the mechanical behavior of these structures were analyzed [5]. Wang et al. [32] measured the inherent vibrations of nonlinear vehicle platoons that oscillate due to external influences. Zhang et al. [33] explored sandwich microshell dynamics. In a microscale size-dependent framework, Hamilton's principle derives basic governing equations. Bai et al. [34] used strain energy theory to simulate cracks and examined how crack lengths affected operation. Some studies have studied the development of vibration isolation and energy harvesting [35, 36]. Additionally, some studies [37,38,39,40,41] applying carbon-coated porous aluminum, directed energy deposition-arc, infrared detectors cooling, welding residual stress measurement, and static homotopy response analysis are interesting.
1.1 The novelty of this paper
The nonlocal elasticity theory only considers the inter-atomic long-range force. Similar to classical elasticity theory, nonlocal elasticity theory treats particles as mass points without considering microstructure deformation [42]. The growing prevalence of nanotechnology has resulted in the extensive utilization of nanosensors and comparable nano-electromechanical systems in high-temperature applications. Hence, there is a must for novel designs or arrangements, such as the sandwich structure, to guarantee precise measurement and functioning of these systems. There is a lack of literature on this subject, so it is necessary to include unique contributions through the present study. This work aims to analyze the thermomechanical vibration behavior of sandwich nanosensor plates in order to meet the previously specified criteria. The plates consisted of a top layer that was enhanced with metal or ceramic graphene and a core layer made of solid or foam material. The work seeks to provide a valuable contribution to the development and examination of nanosensor plates specifically designed for use in high-temperature situations. These plates are designed to conduct gas, temperature, and acceleration measurements under such conditions. Furthermore, it can be employed for the transportation of nanomaterials in high-temperature settings, as well as for sampling and analysis reasons, medical surgical procedures, the delivery of nanomedicine, and the collection of nanofragrances. Moreover, this substance exhibits promising potential for use as a nanotransducer/actuator in nanorobotic systems and as a radar-absorbent surface coating for vehicles in the defense and aviation industries. These investigations offer vital insights into the intricate physics and nonlocal behavior of nanoscale plates. Their contribution is in enhancing the comprehension of the behavior and characteristics of nanosensor plates when subjected to diverse loading situations, encompassing buckling, vibration, and the influence of elements such as flexoelectricity, surface effects, and material size dependency.
2 Mathematical modeling of the sandwich nanosensor plate
The mathematical model in this study is based on Hamilton's technique to create the equations of motion for magneto–electroelastic face plates with functionally graded nanosensor plates. This lets the nanosensor plate's dynamic behavior and responsiveness to thermal stresses, magneto–electroelastic coupling, external electric and magnetic fields, nonlocal features, porosity volume fraction, and thickness porosity variation be examined. The model takes into consideration the nanosensor plate's component materials' many properties and their thermomechanical effects.
2.1 General acceptances
It is assumed that the layers of sandwich plates are perfectly bonded to each other. It is accepted that the middle geometric surface and neutral surface of the sandwich plate coincide in all models. The materials of the layers are modeled with their variable properties depending on temperature, and the necessary formulas or references related to material mixtures are explained where necessary.
2.2 Effective material properties of nanosensor plate
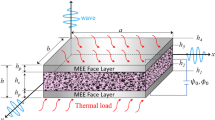
The figure illustrates a three-layer rectangular plate positioned on a Cartesian coordinate system (x, y, z). The plate has dimensions a and b in the x and y directions, respectively (refer to Fig. 1). The total thickness of the plate, denoted as Ht, is determined by the sum of the core layer (h) and twice the thickness of the surface layers (hs), expressed as \({H}_{\rm{t}}=h+2{h}_{\rm{s}}\). Ω represents the central plane of the plate in its original, undeformed state. The tensor Ω x represents the boundary of the plate's entire domain, which is situated between the lower surface \(\left(z={-h}_{\rm{s}}-h/2\right)\) and the upper surface \(\left(z={h}_{\rm{s}}+h/2\right)\), as well as the edge \(\overline{\Gamma }\). The curved surface Γ is described by the tensor \(\Gamma x(-{h}_{\rm{s}}-h/2, h/2+{h}_{\rm{s}})\). It possesses an outward normal \(\widehat{n}\), which can be expressed as \(\widehat{n}={n}_{x}{\widehat{e}}_{x}+{n}_{y}{\widehat{e}}_{y}\), where \({n}_{x}\) and \({n}_{y}\) represent the direction cosines of the unit normal.
Configuration of sandwich nanosensor plate with top and bottom layers of piezo material and core layer of graphene-reinforced metal/ceramic
For uniform graphene distribution by using Halpin–Tsai micromechanics model [43, 44], the elastic modulus of non-porous graphene platelets (GPLs)-reinforced metal matrix can be determined:
where
The dimensions of GPLs are represented by WGPL, lGPL, and tGPL, which correspond to width, length, and thickness, respectively. Em and EGPL represent the Young's modulus of the metal matrix and the graphene platelets (GPLs), respectively. The rule of mixture [44, 45] provides expressions for the Poisson's ratio and mass density of non-porous GPLs-reinforced metal matrix.
The equation above utilizes subscript symbols GPL and m to represent GPLs and metal, respectively. Additionally, Vm is defined as (1 − VGPL).
Figure 1a, b depicts the geometric configuration of the sandwich beam investigated in this study. The beam consists of a functionally graded metal/ceramic foam core. The dimensions of the plate along the x, y, and z axes are represented by a, b, and h, respectively. The Young's modulus E and density ρ of the metal foam core at any height z can be found in references [43, 46,47,48]. Type I foam, as shown in Fig. 2a.
Three models of foam distributions a Type I; edge-focused pattern b Type II; core-focused pattern c Type III; uniform-focused pattern
Type II foam (Fig. 2b):
Type III foam (Fig. 3c):
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the temperature difference \(\Delta T\) and four volumetric graphene ratio VG = 0, 0.05, 0.15, 0.25 for \(\alpha =0\) and \(\alpha =0.4\) a PMGP b PMGFP c PCGP d PCGFP
E1 and ρ1 represent the Young's modulus and density of metal foam, respectively. The foam coefficients (κo, κo*, ψ) and (κd, κd∗, ψ*) represent the Young's modulus and density for Type I, II, and III foams, respectively. The coefficients are typically represented as the ratio of foam density to the density of the solid material comprising the foam. The factor denoted as E1 within the bracket corresponds to the porosity of foam [49]. Reference [49] established a correlation between density and Young's modulus for open-cell metal foams.
The equations below demonstrate the correlation between the coefficients of mass density and Young's modulus (Table 1).
To facilitate comparison, we assume that the masses of all three types of foams remain constant. The values for κo* and ψ can be determined by the following relationship, given a specific value of κo [47]:
Chen et al. [50] and Wang and Zhao [47] proposed κo values ∈ [0, 0.6] using Eq. (8). Table 2 lists foam coefficients.
Temperature impacts are considered necessary for accurate prediction of structural behavior. The temperature-dependent characteristics of the material include the elastic modulus Eef, effective Poisson's ratio νef, conductivity coefficients ψef, thermal expansion κef, and Eef. These properties can be described by a nonlinear function of temperature [51].
In this context, the variable P is used to denote a temperature-dependent ingredient, while P0 represents the corresponding material. Table 2 displays the P−1, P1, P2, and P3 values corresponding to temperature T, with orders ranging from − 1 to 3. The mass density ρ(z) primarily depends on z and is moderately influenced by variations in temperature, as indicated by the effective material properties.
2.3 The nonlinear temperature change
This section presents the equations for uniform temperature rise (UTR), linear temperature rise (LTR), and nonlinear temperature rise (NLTR) across the thickness of the nanosensor plate. The nanoplate's entire body, initially at a temperature of T0 = 300 K, is uniformly heated to its final temperature T. This process occurs under stress-free conditions and involves a uniform temperature rise (UTR), as described by the following equation.
The temperature distribution in a plane along the z-direction can be determined using the equation. This equation considers the temperatures of the top and bottom surfaces, Tt and Tb, respectively. It assumes a linear temperature rise from Tb to Tt across the thickness of the plane [52]:
For nonlinear temperature rises (NLTR) across the thickness of a nanoplate, the determination of the top surface temperature (Tt) and bottom surface temperature (Tb) can be achieved by solving the steady-state one-dimensional heat transfer equation. This equation incorporates known temperature boundary conditions [53].
Thus, the temperature at any given z within the thickness can be determined based on the specified boundary condition.
2.4 Introduction of the nonlocal strain gradient theory (NSGT) for the magneto–electroelastic smart material
Eringen's study [54] assumes that the stress at a specific point in a continuum body is dependent on the stresses at all other locations. This hypothesis proposes that the stiffness of the structure is influenced by the intensity of nonlocal and material scale effects. The structure exhibits smoother behavior compared to classical forms, depending on the magnitude of the nonlocal influence. The strain gradient hypothesis solely accounts for the material scale effect by enhancing the stiffness of the structure. The nonlocal elasticity theory and Eringen's strain gradient theory differentiate between distinct physical phenomena. The NSGT considers both factors simultaneously to incorporate nonlocality [55, 56]. The σ and \({\sigma }^{(h)}\) stress tensors in NSGT are represented by the following equations [55].
The impact of surface bulk has been simulated in the literature through the use of non-classical continuum mechanics [57]. The classical kernel and higher-order nonlocal functions \({\alpha }_{0}\) and \({\alpha }_{1}\) are located in different positions. The Laplacian operator \(\left(\nabla =\partial /\partial x +\partial /\partial y)\right.\) and the fourth-order material coefficient are represented by the symbols ∇ and C, respectively. The terms ∇ε and ε refer to the classical strain tensors and the strain gradient. In addition, the nonlocality constants \({e}_{0}a\) and \({e}_{1}a\) are associated with the material coefficients \({e}_{1}\) and \({e}_{0}\), while a represents the geometric characteristics of atomic bonds. The \({l}_{{\text{m}}}\) parameter represents the size of the material, while the colon symbol ":" denotes the double-dot product of the tensor. The stress tensor derived from the NSGT can be represented as [55, 58, 59].
Assuming that the notions of \({{\alpha }_{1}({\varvec{x}}}^{{{\prime}}},{\varvec{x}},{e}_{1}a)\) and \({{\alpha }_{0}({\varvec{x}}}^{{{\prime}}},{\varvec{x}},{e}_{0}a)\) are compatible with the Ref. [60] and that \({e}_{0}={e}_{1}{=e}_{0}a\), we can use the linear differentiation operator on Eq. (4) to obtain the following result.
Equations (4–6) can be utilized to calculate the total stress as follows:
The stress–strain relations of the plate are determined by references [55, 56]:
The symbols \({\sigma }_{xx}\), \({\sigma }_{yy},\) \({\varepsilon }_{xx}\), and \({\varepsilon }_{yy}\) represent the conventional stresses and strains in the x and y directions, respectively. Furthermore, the shear stresses and strains in the xz and yz planes can be denoted as \({\sigma }_{xz}\), \({\sigma }_{yz}\), and \({\gamma }_{xz}\), \({\gamma }_{yz}\). E(z) and G(z) represent the elasticity and shear modulus, respectively. When the values of the \({l}_{{\text{m}}}\) and \({e}_{0}a\) in Eq. (11) are both set to zero, the stress–strain relations of the classical continuum theory can be determined [60]. The constitutive equations of the NGST microplate under thermal loads can be established by considering the magneto–electroelastic characteristics. The structure of these equations is as follows.
2.5 Displacement fields and strains
The SHSDT is a sinusoidal higher-order shear deformation theory used for analyzing three-layer rectangular plates. It is based on the following assumptions [61]:
-
1.
The displacements in relation to the plate's thickness are negligible, resulting in infinitesimally small stresses.
-
2.
The plane displacements u and v consist of the components u0 for extension, ws for shear, and w0 for bending.
-
3.
The transverse displacement w is modified to account for the bending w0, shear ws, and stretching wst components of the transverse stresses (σxz, σyz, σzz) and strains (εxz, εyz, εzz).
-
4.
The inclusion of shear components (ws in u, v in-plane and w transverse displacements) leads to an increase in the trigonometric variation of shear stresses (σxz, σyz) and strains (εxz, εyz) across the thickness of the plate. Consequently, the top and bottom faces of the plate experience no shear stresses (σxz, σyz).
Based on the aforementioned assumptions regarding the full form of the SHSDT, the displacement field of the nanoplate can be expressed as follows:
Let us define the functions f(z), wst and g(z) as follows:
The variables u, v, and w in the displacement equations represent the overall displacements of a point within an unaltered body. The symbols u0, v0, and w0 represent the in-plane and transverse displacements of a point on the undeformed plate's midplane (x, y, 0) at time t. The plate's u and v displacements are associated with its extensional deformation, while the w displacement represents its bending deflection. The strain–displacement interactions related to the displacement field in Eq. (13) can be expressed in the following general form.
The strain components are as follows:
2.6 Constitutive equations
The study examines a nanoplate with a linear elastic behavior. The nanoplate consists of an isotropic core (n) that is surrounded by top and bottom surface layers (l). Functional grading of barium–titanate and cobalt–ferrite elements was employed for the organization of the nanoplate's core, while the surface layers were created using pure or homogeneous mixes of these materials. The constitutive relations of the isotropic core plate can be defined using the differential version of Eringen's constitutive relations Eq. (13).
The stiffness coefficients, denoted as \({C}_{ij}^{n}\), represent the coefficients that determine the stiffness of a given system.
The stiffness coefficients λ(z) and μ(z) represent the Lamé constants in the context of elasticity. Specifically, λ(z) is calculated as \(\left(\lambda \left(z\right)=\frac{vE(z)}{(1+v)(1-2v)}\right)\), while μ(z) is determined by \(\mu \left(z\right)=\frac{E(z)}{2(1+v)}\). Furthermore, it is assumed that the Poisson's ratio remains constant, while the Young's modulus varies across the thickness (h) of the core plate within the range of \((-h/2\le z\le h/2)\), following a power-law relationship as defined in [62].
The constitutive relations of the surface layers are described using the nonlocal and strain gradient differential operators [63]. The expressions \(\mathcal{L}\left(*\right)\) and \(\Gamma \left(*\right)\) can be defined as follows: \(\mathcal{L}\left(*\right)\equiv 1-{{(e}_{0}a)}^{2}{\nabla }^{2}\) and \(\Gamma \left(*\right)\equiv 1-{{(l}_{\rm{m}})}^{2}{\nabla }^{2}\).
The establishment of electric \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varphi }\) and magnetic potentials \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\psi }\) allows for the complete definition of constitutive relations. The electric field components Ei and magnetic field components Hi can be represented using three-dimensional potentials.
The potential distributions for a nanoplate activated with initial external electric potential φ0 and magnetic potential ψ0 can be described using a combination of linear and cosine functions, as stated in [64, 65] based on Maxwell's equations.
The functions \(\varphi \)(x, y, t) and ψ(x, y, t) correspond to the time-varying electric and magnetic potential distributions in a two-dimensional plane. The \(\widehat{z}\) variable represents the thickness of the surface layers, denoted as \(\left(\widehat{z}=z\pm h/2\pm {h}_{\rm{s}}/2\right)\). The top layer of the plate is defined by the equation \(\widehat{z}\equiv {z}_{1}=z-h/2-{h}_{\rm{s}}/2\), while the bottom layer is defined by \(\widehat{z}\equiv {z}_{2}=z+h/2+{h}_{\rm{s}}/2\). Please note that the variable z is only applicable within the range of \(\left(h/2\le z\le h/2+{h}_{\rm{s}}/2\right)\) and \(\left(-h/2-{h}_{\rm{s}}/2\le z\le -h/2\right)\).
2.7 Motion equations
The virtual displacements can be employed to modify Hamilton's principle for the motion equations of a three-layered rectangular nanosensor plate [66]:
\(\delta \mathcal{U}, \delta \mathcal{K}\), and \(\delta \mathcal{V}\) represent the virtual counterparts of strain energy, kinetic energy, and work performed by external forces, respectively. \(\delta \mathcal{E}\) and \(\delta \mathcal{M}\) represent the virtual contributions of the electric and magnetic fields. The virtual strain energy, denoted as \(\delta \mathcal{U}\), is defined as follows.
Moreover, the contributions of the electric \(\delta \mathcal{E}\) and magnetic \(\delta \mathcal{M}\) fields can be expressed as:
The contribution of kinetic energy can be summarized as follows:
The symbols ρp(z) and ρn(z) represent the mass densities of the surface layers and core of the nanosensor plate, respectively. These densities are defined by a power-law equation.
The values \({\rho }_{\rm{t}}^{c}\) and \({\rho }_{b}^{c}\) represent the mass densities of the superior and inferior core surfaces, respectively. Furthermore, the time derivative of a variable is denoted by a dot superscript, as seen in the equation \(\dot{u}=\partial u/\partial t\). In-plane external pressures significantly impact the virtual work.
The subscripts \(0,\mathcal{E},\) and \(\mathcal{M}\) denote the in-plane compressive mechanical, electrical, and magnetic forces. The equations Nxx0 = Px0 and Nyy0 = Py0 represent compressive mechanical forces. Similarly, \({N}_{xx\mathcal{M}}={P}_{q31}\) and \({N}_{yy\mathcal{M}}={P}_{q32}\) denote magnetic forces originating from magnetic potential. Additionally, \({N}_{xx\mathcal{E}}={P}_{e31}\) and \({N}_{yy\mathcal{E}}={P}_{e32}\) represent electric forces resulting from external electric voltage. The virtual work equation in this study focuses solely on the free vibration and buckling responses of MEE nanoplates, thus disregarding the mechanical forces exerted on the top and lower surfaces. Assume the plate exhibits cylindrical bending behavior upon the application of an external force along its midplane. In this case, only the bending component (w0) of the deflection is influenced by the externally applied axial forces. Furthermore, the plate's behavior is affected by its shear deflection (ws) and stretch deflection (wst). The forces and moments associated with thickness can be expressed as follows:
The virtual strain energy can be expressed as follows:
The electric \({\overline{D} }_{i} \left(i=x,y,z\right)\) and magnetic \({\overline{B} }_{i} \left(i=x,y,z\right)\)) coefficients related to thickness are provided.
The virtual contribution of the electric and magnetic fields can be simplified.
The variation of kinetic energy, which is determined by the mass inertias (mi), can be expressed as:
The differentiation of variables with respect to time is denoted by the dot superscript. The mass inertias, denoted as \({m}_{i}\) (where i = 0, 1, 2), are defined as.
The latest form of virtual work resulting from in-plane external forces is expressed as:
The analyses assume that the in-plane mechanical compression forces are equal to px0 = N0 and py0 = γN0, where \(\gamma \) represents the ratio of \({p}_{x0}\) to \({p}_{y0}\). The in-plane electric forces, denoted as \({p}_{e3i}\), and magnetic forces, denoted as \({p}_{q3i}\) (where i = 1, 2), are characterized.
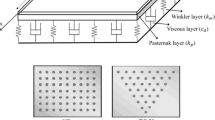
The external force exerted on the nanoplate can be effectively described by incorporating the Pasternak foundation [67].
The variable q represents the external load distributed over a unit area. \({k}_{w}\) and \({k}_{p}\) denote the spring and shear foundation, correspondingly.
The final seven motion Eqs. (38a–g) for a macro-rectangular plate, based on the sinusoidal higher-order shear deformation theory, can be derived by substituting the energy variation equations δ\(\mathcal{U}\), δ\(\mathcal{E}\), δ\(\mathcal{M}\), δ\(\mathcal{K}\), and δ\(\mathcal{V}\) from Eqs. (30) and (32)–(34) and (36) into Eq. (22). Partial integration is then performed to obtain the complete differentiations of generalized virtual translations with respect to x, y, and t.
The boundary conditions of the nanosensor plate are expressed in the following format:
The thermal load is presented here.
The moments and stresses resulting from thermal loading can be characterized by the equations \({M}_{x}^{bT}={M}_{y}^{bT}\), \({M}_{x}^{sT}={M}_{y}^{sT}\), and \({N}_{x}^{T}={N}_{y}^{T}\).
The variables \({E\left(\mathcal{Z}\right)}^{\left(n\right)}\) and \({\alpha }^{\left(n\right)}(Z)\) denote the effective modulus of elasticity and thermal expansion coefficient, respectively, for each layer (n) of the sandwich nanosensor plate.
The nonlocal and strain gradient differential operators can be defined as \(\mathcal{L}\left(*\right)\equiv 1-{{(e}_{0}a)}^{2}{\nabla }^{2}\) and \(\Gamma \left(*\right)\equiv 1-{{(l}_{\rm{m}})}^{2}{\nabla }^{2}\). By substituting Eqs. (13), (17)–(19), (22), (29), and (31) into Eq. (38), we can derive a set of equilibrium equations (Eq. 40a–g) that describe the displacements and magneto–electroelastic coefficients of a rectangular nanosensor plate. These equations can be expressed as follows:
The definitions of the magneto–electroelastic coefficients are given in Appendix A1–A3.
The remaining variables, \(\overline{u}\), \(\overline{v}\), \({\overline{w}}_{0}\), \({\overline{w}}_{\rm{s}}\), \(\overline{\phi }\), \(\overline{\varphi }\), and \(\overline{\psi }\) represent the maximum values of displacement, electric potential, and magnetic potential, respectively. Here, it represents the natural frequency. These seven variables can be represented as vectors for convenience.
2.8 Solution method
The research successfully obtained precise analytical solutions for a simply supported (SS) three-layered rectangular nanoplate by employing Navier's solution approach. The double trigonometric series expansion is employed to determine the values of the seven unknowns in the following manner.
The governing equations are expressed in the following form using the stiffness [K] and inertia [M] matrices, as well as the load vector {F}.
The load vector, which is negligible in free vibration and buckling analysis, is as follows:
For free vibration analysis, the governing equation system of the nanoplate under in-plane static forces is defined as follows.
For the buckling analysis of nanoplates, the governing equations are:
The Appendix A4–A5 section provides the elements of the symmetric stiffness matrix [K] (where Kij = Kij) and the symmetric inertia matrix (where Mij = Mij).
2.9 Validation
Tables 3 and 4 present a comparison between the dimensionless maximum deflections obtained from three nonlocal plate theories and the results of the current investigation. The comparison is based on different nonlocal parameter and thickness values for square and rectangular plates subjected to uniformly distributed and point loads. The assessments showed that the present research findings were similar to studies using first- and third-order theories. Moreover, the nonlocal theory yielded better predictions for larger displacements. Furthermore, the first and third-order theories produced similar results across all nonlocal effect values. Tables 5 and 6 compare the computed natural frequencies of third-order nonlocal plate theories, considering different nonlocal parameters and aspect ratio values. The equations employed for comparing the maximum non-dimensional deflection and natural frequencies are as follows:
Q0 and q0 represent the sizes of the point and uniform loads, while a, E, v, and represent the length, elastic modulus, Poisson's ratio, and density of the plate, respectively.
Table 6 presents a comparison of the deflections computed for an isotropic plate with a support, where the parameters used are a = 10, v = 0.3 for the Poisson ratio, and E = 300 × 106 for the elastic modulus. These deflections are determined by applying a single load of q0 = 1N. Table 6 presents the deflections of a supported, isotropic plate with specific parameters. The plate has a length-to-thickness ratio of 10, a Poisson ratio of 0.3, and an elastic modulus of 300 × 106. These deflections are computed under the influence of a uniform load of Q0 = 1 N/m, using a 100 term series. Table 7 presents a comparison between different investigations that have utilized various theories from the literature. The focus of this comparison is on the non-dimensional first mode frequency \({\overline{\omega }}_{11}\) of an isotropic plate that is supported. The plate has specific parameters, namely a = 10, Poisson ratio v = 0.3, and modulus of elasticity E = 300 × 106. Table 8 presents a comparison between different investigations that have utilized various theories from the literature. The focus of the comparison is on the computed non-dimensional higher-order frequencies (represented as \(\overline{\omega }\)) of a simply supported isotropic plate. The plate has specific dimensions, with a value of 10 for parameter a, a ratio of 1 for a/b, a ratio of 100 for a/h, a Poisson ratio of 0.3, and a modulus of elasticity of 300 × 106.
Here, due to the nanosize, the external electric and magnetic potentials Vm and Hm are non-dimensionalized using the following relations;
The non-dimensional foundations parameters \({K}_{1}\), \({K}_{2}\) are also defined by:
The non-dimensional frequency parameters \(\lambda_{mn}\) are defined by:
Here, \({\rho }_{\rm{m}}=4512\) kg/m3 and \({E}_{\rm{m}}=105.7 \)GPa are the mass density and elasticity modulus of metal (Ti6Al4V) in room temperature.
3 Numerical results
In this study, the sandwich nanosensor plate is composed of barium and cobalt materials in the upper and lower layers, which are known to be piezo-compatible materials. As seen in Fig. 1, the core of the nanosensor plate is made of either metal or ceramic and can potentially be strengthened with graphene. Furthermore, the central component is represented by three distinct foam types: one uniform and two symmetrical variants. Figure 3 presents an investigation of sandwich nanosensor plates composed of PMGFP and PCGFP. In this context, the following abbreviations are used: P for piezo, M for metal, C for ceramic, G for graphene, and F for foam. For instance, in Fig. 3a, the sandwich nanosensor plate comprises piezoelectric layer material in its upper and lower sections, with the core section consisting of metal material reinforced with graphene. The metallic material employed in this context is Ti6Al4V, while the ceramic material utilized is Si3N4. In this paper, the figures illustrate a sandwich nanosensor plate characterized by an upper thickness of hp = 0.1 h and a lower thickness of hp = 0.8 h. The nanosensor plate's core is characterized by a thickness of hc, which is equal to 0.8 times the height h.
3.1 Effect of volumetric graphene ratio
Figure 3 examines the impact of the volumetric graphene ratio on the fundamental natural frequencies of the sandwich nanosensor plate. The graph presents a comprehensive analysis of the temperature difference across four distinct volumetric graphene ratios, denoted as VG = 0, 0.05, 0.15, and 0.25. The temperature range considered in this analysis spans from ΔT = 0 to 2500 K. Upon examining Fig. 3a, it can be observed that the dimensionless natural frequency of the sandwich nanosensor plate with a metal core decreases as the temperature difference increases. Conversely, the natural frequencies increase due to the reinforced provided by graphene. In the case where the temperature difference is ΔT = 0, the natural frequency of the sandwich nanosensor plate is λ = 2.03 for VG = 0, and λ = 2.92 when VG = 0.25.
With the augmentation of graphene content, the natural frequency exhibited a rise of approximately 43.8%. Furthermore, it is evident that the fundamental natural frequency of the nanosensor plate composed of a sandwich structure exhibits buckling behavior, reaching a minimum value of zero when the volumetric graphene ratio is subjected to a temperature difference ΔT = 1900. Upon closer examination, it becomes evident that the metal nanosensor plate, which incorporates graphene reinforced within its core, exhibits early buckling. Figure 3b presents an analysis of a foam material that has a uniform distribution and has a porosity ratio of α = 0.4. The core of this material is reinforced with graphene and metal. In the given graph, buckling is observed as the temperature rises proportionally and reaches a value of ΔT = 1920. Simultaneously, the fundamental natural frequency of the sandwich nanosensor plate experiences a reduction of approximately 16.25%, resulting in a value of λ = 1.7 at VG = 0 and a temperature difference of ΔT = 0 due to the presence of uniform foam. Concisely, the foam effect caused a decrease in natural frequencies, whereas the buckling temperature experienced a slight increase. Figure 3c presents the natural frequency graph of the nanosensor plate with a silicon nitride core, illustrating the variations in temperature difference and graphene ratio. The dimensionless natural frequency value at ΔT = 0 increased by approximately 40.6% when comparing the ceramic core to the metal core. This increase resulted in a value of λ = 2.84 for VG = 0. Furthermore, it can be observed that with an increase in temperature, there is a significant decrease in the natural frequency, leading to the occurrence of buckling at a critical temperature difference of ΔT = 2350. Essentially, when the central component is made of ceramic material, there is a significant increase in the buckling temperature. Regarding Fig. 3d, the central component comprises ceramic and uniform foam material. The graph illustrates a decrease in both the natural frequency and buckling temperature as a result of the foam effect. In the graph depicting the composition of metal and foam in the core region, there was an observed increase in the buckling temperature. However, in the current graph, it is evident that there has been a partial decrease in the buckling temperature. Another distinction lies in the relationship between the graphene ratio and the buckling temperature of the sandwich nanosensor plate, which features a ceramic core. As the graphene ratio increases, so does the buckling temperature.
Figure 4 depicts the variation in the fundamental natural frequency of the sandwich nanosensor plate, comprising a metal core reinforced with graphene, as a function of the volumetric graphene ratio (VG) ranging from 0 to 0.25. Additionally, two distinct porosity ratios (α) are considered: α = 0 and α = 0.4. In this study, we consider the use of uniform foam, specifically the foam III model. Furthermore, the study considered four distinct temperature differences, denoted as ΔT = 0, 300, 600, and 1000. It was observed that as the temperature difference increases, the fundamental natural frequencies decrease. Conversely, an increase in the volumetric graphene ratio leads to an increase in the fundamental natural frequencies. In the given scenario, as depicted in Fig. 4a, when the temperature difference (ΔT) is zero and the VG is also zero, the value of λ is measured to be 2.03. However, when VG is increased to 0.25, the fundamental natural frequency of the sandwich nanosensor plate (λ) is found to be 2.92. In addition, when the change in temperature (ΔT) is equal to 1000 and the VG is equal to 0, the natural frequency (λ) is equal to 1.54. As the volumetric ratio of graphene increased, the dimensionless fundamental natural frequency exhibited a 43.8% increase, whereas an increase in temperature difference resulted in a decrease of 24.1%. In Fig. 4b, the consideration of the porosity ratio α = 0.4 is applied to foam III type. The natural frequency was fundamentally decreased by increasing the porosity ratio. In Fig. 4c, it is observed that when the temperature difference is ΔT = 600, the λ is 1.77 at α = 0 and VG = 0, whereas λ is 1.48 at α = 0.4 and VG = 0. In this particular scenario, it can be observed that an increase in the porosity ratio resulted in a corresponding decrease in the natural frequency value, specifically by 16.4%. The study investigates the impact of the volumetric ratio of graphene and temperature difference on the fundamental natural frequencies of a sandwich nanosensor plate. The nanosensor plate's core is composed of ceramic material. This analysis is presented in Fig. 5. The graph yields comparable findings, albeit with a notable discrepancy in the natural frequency values, which are approximately 40% greater as a result of the ceramic composition of the core component.
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the volumetric graphene ratio VG and four distinct temperature difference ΔT for\(\alpha =0-0.4\), hp = 0.1 h, hc = 0.8 h and Br = 0.5, Co = 0.5 a PMGFP, \(\alpha =0\) b PMGFP, \(\alpha =0.4\) c PMGFP, ΔT = 0
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the volumetric graphene ratio VG and four distinct temperature difference ΔT for \(\alpha =0-0.4\), hp = 0.1 h, hc = 0.8 h and Br = 0.5, Co = 0.5 a PCGFP, \(\alpha =0\) b PCGFP, \(\alpha =0.4\) c PCGFP, ΔT = 0
3.2 Effect of foam distributions
The study investigated three distinct foam types, including one uniform foam and two symmetrical foams, for the core component of the sandwich nanosensor plate, as depicted in Fig. 2. The analysis in Figs. 6 and 7 considered four distinct temperature differences, denoted as ΔT = 0, 300, 600, and 1000, along with a range of α values from 0 to 0.6. Furthermore, the influence of graphene was disregarded, and the central region of the nanosensor plate was assumed to be composed of either metal or ceramic materials. Upon examining Fig. 6, it can be observed that the dimensionless natural frequency of the sandwich nanosensor plate experiences a decrease as the porosity ratio increases for foam I and foam III. Conversely, for foam II, an increase in the porosity ratio leads to an increase in the dimensionless natural frequency. Moreover, augmenting the temperature disparity diminishes the natural frequencies for every foam type. In Fig. 6a, the dimensionless natural frequency was observed to be λ = 2.03 at ΔT = 0. However, it exhibited a decrease of 23% to λ = 1.54 when ΔT = 1000. In a similar vein, Fig. 6c demonstrates a correlation between the decrease in natural frequencies and the increase in temperature difference for foam III. Meanwhile, Fig. 6b indicates a decrease of approximately 9% in natural frequencies for foam II. Furthermore, in contrast to the remaining graphs depicted in Fig. 6b, the natural frequency of the sandwich nanosensor plate exhibits an upward trend with increasing porosity ratio. Figure 6d depicts the alterations in the inherent frequencies of the sandwich nanosensor plate in relation to the porosity ratio, while considering a temperature difference ΔT = 600 across three distinct foam varieties. As depicted in the graph, the natural frequencies exhibit an upward trend with the increase in porosity ratio for foam II, whereas they demonstrate a downward trend for foam I and foam III.
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the porosity ratio \(\alpha \) and three foam distribution type for \(\alpha =0\) and \(\alpha =0.4\). a PMFP, Foam I b PMFP, Foam II c PMFP, Foam III d PMFP, ΔT = 600
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the porosity ratio \(\alpha \) and three foam distribution type for \(\alpha =0\) and \(\alpha =0.4\). a PCFP, Foam I b PCFP, Foam II c PCFP, Foam III d PCFP, ΔT = 600
Figure 7 presents the relationship between the fundamental natural frequency of the sandwich nanosensor plate, composed of a silicon nitride core, and the porosity ratio. This relationship is examined under four distinct temperature differences. Based on the graphical representations, it can be observed that the natural frequency of the sandwich nanosensor plate decreases with an increase in both the porosity ratio and temperature difference for foam I and foam III. In Fig. 7a, it is observed that the dimensionless fundamental natural frequency (λ) of the sandwich nanosensor plate is 2.84 when the porosity ratio (α) is 0 and the temperature difference (ΔT) is 0. Conversely, when α is 0.6, λ is found to be 2.36. In this instance, with an increase in the porosity ratio, there was an observed decrease in the natural frequency by approximately 17%. Furthermore, in the case where the porosity ratio is α = 0 and the temperature difference is ΔT = 1000, it can be observed that the natural frequency decreases to λ = 2.59. Here, it is acknowledged that augmenting the temperature gradient in sandwich nanosensor plates featuring a ceramic core leads to a reduction in the fundamental natural frequency by approximately 8.8%. In the previous graph, the analysis involving a metal core exhibited a reduction in the natural frequency of approximately 23%. Consequently, it is comprehended that metals are significantly influenced by variations in temperature.
3.3 Effect of electric and magnetic fields
Figures 8 and 9 present the variations in the fundamental natural frequency of the sandwich nanosensor plate, taking into account four distinct factors: electric potential, magnetic field, and temperature difference. The graphics depict a sandwich nanosensor plate with an upper thickness of hp = 0.4 h and a lower thickness of hp = 0.4 h. The core part of the nanosensor plate has a thickness of hc = 0.2 h. Moreover, in the context of electric potential effect, both the upper and lower layers are composed entirely of barium. Conversely, in the context of magnetic field effect, the composition solely comprises cobalt. Upon examination of Fig. 8, it is observed that the natural frequency of the sandwich nanosensor plate exhibits a decrease with an increase in the electric potential effect, as well as a decrease with an increase in the temperature difference. In the given scenario depicted in Fig. 8a, where the core component consists solely of metal without any graphene contribution, the natural frequency value is denoted as λ = 4.56 when Vm = 0 and ΔT = 0. However, this value decreases to λ = 3.94 when Vm = 2. In Fig. 8b, when the core material of the sandwich nanosensor plate is ceramic, the natural frequency of the nanosensor plate is λ = 3.45 for Vm = 0 and ΔT = 0. Given the composition of ceramic as the primary constituent in this scenario, a reduction of 24.3% in the frequency value was observed. In Fig. 8c, for a sandwich nanosensor plate with a metal core and a volumetric graphene ratio of VG = 0.2, the natural frequency is λ = 4.62 when Vm = 0 and ΔT = 0. To clarify, when the core component is composed of metal, augmenting the volume of graphene results in a just 1.3% increment in the natural frequency of the nanosensor plate sandwich structure. In a similar vein, when the central component comprises of graphene ceramic that has been reinforced, there is a partial increase in the natural frequency. Furthermore, with an increase in temperature, the fundamental natural frequency of the sandwich nanosensor plate decreases to zero, leading to the occurrence of buckling. Figure 8 demonstrates a negative correlation between the electric potential effect and the critical temperature difference for buckling.
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the temperature difference ΔT and four electric potential Vm for \(\alpha =0\), \({V}_{G}=0-0.2\), hp = 0.4 h, hc = 0.2 h and Br = 1, Co = 0 a PMGP, VG = 0 b PCGP, VG = 0 c PMGP, VG = 0.2 d PCGP, VG = 0.2
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the temperature difference ΔT and four magnetic potential Hm for \(\alpha =0\), \({V}_{G}=0-0.2\), hp = 0.4 h, hc = 0.2 h and Br = 1, Co = 0 a PMGP, VG = 0 b PCGP, VG = 0 c PMGP, VG = 0.2 d PCGP, VG = 0.2
Figure 9 presents the variations in the natural frequency of the sandwich nanosensor plate, considering the influence of four distinct magnetic field phenomena Hm and temperature gradients ΔT. Upon examination of these graphs, similar to the previous graph, it can be observed that the natural frequencies exhibit a rapid decrease as the temperature difference increases. Nevertheless, with an increase in the magnetic field, there is a corresponding increase in the natural frequencies and buckling temperature. In Fig. 9a, the magnetic field effect is observed at Hm values of 0, 0.2, 0.4, and 0.6, resulting in temperature changes of ΔT = 2017, 2132, 2237, and 2332 K, respectively.
3.4 Effect of nonlocal elasticity and material size factor
The study in Fig. 10 investigates the impact of altering the temperature difference on the fundamental natural frequency of the sandwich nanosensor plate. This is accomplished by analyzing four distinct nonlocal parameters, denoted as e0a = 0, 1, 2, and 4. Based on the graphical representations, it can be observed that an increase in the nonlocal parameter and temperature difference leads to a decrease in the natural frequency. Furthermore, it is noteworthy that even at a temperature difference of ΔT = 1920, buckling is observed in the sandwich nanosensor plate with a metal core. In Fig. 10b, the temperature difference (ΔT) is 1905 K for the metal nanosensor plate with a graphene-reinforced core, 2350 K for the ceramic nanosensor plate, and 2368 K for the graphene-reinforced nanosensor plate. Put simply, if the core material is ceramic, the temperature threshold for buckling is raised. Moreover, the incorporation of graphene as a reinforced material leads to a reduction in the buckling temperature of the metal core, while simultaneously causing an increase in the buckling temperature of the ceramic core. Upon examination of Fig. 10a, it is observed that as the nonlocal parameter for ΔT = 0 is increased from e0a = 0 to e0a = 4 nm2, there is a decrease in the natural frequency by 8.87% from λ = 2.03 to λ = 1.85. In Fig. 10b, considering a graphene-reinforced metal core, the natural frequency (λ) of the sandwich nanosensor plate is found to be 2.72, with a nonlocal parameter (e0a) of 0 and a temperature difference (ΔT) of 0. In similar instances, in Fig. 10c, d, the fundamental natural frequency of the sandwich nanosensor plate is denoted as λ = 2.84 and λ = 3.43, correspondingly. It can be inferred that the utilization of ceramic as the core material leads to an average increase of 33% in the fundamental natural frequencies. Conversely, when the core material is reinforced with graphene, the average increase amounts to 27%.
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the temperature difference ΔT and four nonlocal parameters e0a for \(\alpha =0\), \({l}_{\rm{m}}=0\), hp = 0.1 h, hc = 0.8 h and Br = 0.5, Co = 0.5 a PMGP, VG = 0 b PMGP, VG = 0.2 c PCGP, VG = 0 d PCGP, VG = 0.2
The alteration in the fundamental natural frequencies of the sandwich nanosensor plate, as depicted in Fig. 11, is determined by considering four distinct material size factors (lm = 0, 1, 2, and 4) and the temperature difference. Upon examination of the figures, it becomes evident that the material size factor exerts a significant influence on the natural frequencies. In the given illustration, denoted as Fig. 11a, the sandwich nanosensor plate featuring a metal core exhibits distinct natural frequency values. Specifically, when the parameters lm = 0 and ΔT = 0, the natural frequency is determined to be λ = 2.03. However, when lm is altered to 4 nm2, the natural frequency increases to λ = 7.92. Notably, as the material size factor is progressively enhanced, the natural frequency value experiences an almost fourfold amplification. In a similar manner, the natural frequencies of the sandwich nanosensor plate with a ceramic core are observed to increase when the material size factor is increased, as depicted in Fig. 11c, d. It is important to observe that the buckling formation temperature increases with an increase in the material size factor when the core part is composed of metal. Conversely, when the core part is made of ceramic, the buckling temperature decreases. The fundamental natural frequency values of the sandwich nanosensor plate exhibit an increase when graphene reinforced is applied, as depicted in the provided graphs.
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the temperature difference ΔT and four material size factors \({l}_{\rm{m}}\) for \(\alpha =0\), e0a = 0, hp = 0.1 h, hc = 0.8 h and Br = 0.5, Co = 0.5 a PMGP, VG = 0 b PMGP, VG = 0.2 c PCGP, VG = 0 d PCGP, VG = 0.2
3.5 Effect of viscoelastic foundation
Figures 12 and 13 investigate the effects of spring and shear foundation considering the temperature differential. Figure 12 illustrates the inverse relationship between the temperature difference and the natural frequencies of the sandwich nanosensor plate. As the temperature difference increases, the natural frequencies decrease, leading to buckling phenomena. As the spring foundation's magnitude increases, the buckling temperature also increases. In the provided figure (Fig. 12a), it is evident that buckling takes place as the value of K1 varies from 0 to 20. The buckling phenomenon is observed as the parameter λ decreases to 0 at specific values of ΔT, namely 1920, 2056, 2182, and 2412, corresponding to K1 values of 0, 5, 10, and 20, respectively. In Fig. 12b, buckling is observed at four distinct points: ΔT = 2350, 2388, 2424, and 2492. Hence, when the core component comprises ceramic material and the spring foundation exhibits coefficient values such as K1 = 0.5, there is a notable augmentation in the temperature at which buckling occurs. Furthermore, it is observed that the incorporation of a ceramic core enhances the inherent frequencies of the nanosensor plate sandwich structure. Figure 13 investigates the impact of four distinct shear foundation K2 = 0, 0.02, 0.04, 0.08 coefficients on the alteration of the natural frequency. The graph exhibits analogous characteristics to those observed in the spring foundation.
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the temperature difference ΔT and four distinct spring foundation K1 for \(\alpha =0\), lm = 0, hp = 0.1 h, hc = 0.8 h and Br = 0.5, Co = 0.5 a PMP b PCP
Variation of the dimensionless frequencies \({\lambda }_{(1,1)}\) depending on the temperature difference ΔT and four distinct spring foundation K2 for \(\alpha =0\), lm = 0, hp = 0.1 h, hc = 0.8 h and Br = 0.5, Co = 0.5 a PMP b PCP
4 Result and discussion
In this study, volumetric ratio, temperature difference, foam type, porosity ratio, electric and magnetic fields, nonlocal and material size parameters, and foundation were examined to see how they affect graphene qualities. Graphene exhibited a significant 43.8% increase in its natural frequency as a result of volume augmentation. Moreover, the nanosensor plate, which is constructed in a sandwich configuration, exhibits buckling phenomena when subjected to its inherent frequency. This behavior occurs when the graphene volume ratio reaches a temperature difference of ΔT = 1900, resulting in a minimum value of zero. The natural frequency of the sandwich nanosensor plate decreases as the porosity ratio increases for foam I and foam III. In foam II, increasing porosity increases the natural frequency. The sandwich nanosensor plate's natural frequency decreases with higher porosity ratio and temperature difference for foam I and foam III. In a sandwich nanosensor plate with a metal core and a graphene ratio of VG = 0.2, the natural frequency is λ = 4.62 when Vm = 0 and ΔT = 0. Increasing the amount of graphene in the metal core component only results in a 1.3% increase in the natural frequency of the nanosensor plate sandwich configuration. Increasing the nonlocal parameter and temperature difference decreases the natural frequency. Additionally, buckling occurs in the sandwich nanosensor plate with a metal core even at a temperature difference of ΔT = 1920 K. In Fig. 8b, the temperature differences (ΔT) are as follows: 1905 K for the metal nanosensor plate with a graphene-reinforced core, 2350 K for the ceramic nanosensor plate, and 2368 K for the graphene-reinforced nanosensor plate. The material size factor affects the natural frequencies. Figure 9a shows a sandwich nanosensor plate with a metal core and noticeable natural frequency values. When lm = 0 and ΔT = 0, the natural frequency is λ = 2.03. When lm is changed to 4 nm2, the natural frequency increases to λ = 7.92. As the volume of graphene increased, the natural frequency increased by 43.8%. However, a higher temperature difference caused a decrease of 24.1%. When exploring foundation parameters, we can observe that changes in temperature difference may have an impact on natural frequencies. Specifically, an increase in temperature difference seems to be associated with a decrease in natural frequencies. This decrease in natural frequencies, in turn, may potentially lead to the occurrence of buckling phenomena.
5 Conclusion
This study aims to examine the buckling properties of a sandwich nanosensor plate consisting of piezoelectric materials on its top and bottom surfaces, with a metal or ceramic core that might potentially be strengthened by integrating graphene. Moreover, an inquiry was carried out about the modeling of the central component in three separate structures, specifically Foam I, Foam II, and Foam III. The thermal buckling properties of sandwich nanosensor plates are calculated by employing trigonometric functions to solve the sinusoidal higher-order shear deformation theory.
References
Bhangale, R.K., Ganesan, N.: Static analysis of simply supported functionally graded and layered magneto–electro-elastic plates. Int. J. Solids Struct. (2006). https://doi.org/10.1016/j.ijsolstr.2005.05.030
Wu, Z., Huang, B., Fan, J., Chen, H.: Homotopy based stochastic finite element model updating with correlated static measurement data. Measurement 210, 112512 (2023). https://doi.org/10.1016/j.measurement.2023.112512
Li, J., Liu, Y., Lin, G.: Computers and Geotechnics Implementation of a coupled FEM-SBFEM for soil-structure interaction analysis of large-scale 3D base-isolated nuclear structures. Comput. Geotech. 162, 105669 (2023). https://doi.org/10.1016/j.compgeo.2023.105669
Hong, J.S., Wang, S., Gao, X.-L., Mi, C.: On the bending and vibration analysis of functionally graded magneto–electro-elastic Timoshenko microbeams. Crystals (2021). https://doi.org/10.3390/cryst11101206
Wu, B., Zhang, C., Chen, W., Zhang, C.: Surface effects on anti-plane shear waves propagating in magneto–electro-elastic nanoplates. Smart Mater. Struct. (2015). https://doi.org/10.1088/0964-1726/24/9/095017
Li, L., Wei, P.J.: Surface wave speed of functionally graded magneto–electro-elastic materials with initial stresses. J. Theor. Appl. Mech. (2014). https://doi.org/10.2478/jtam-2014-0016
Zhang, S.Q., Zhao, Y.F., Wang, X., Chen, M., Schmidt, R.: Static and dynamic analysis of functionally graded magneto–electro-elastic plates and shells. Compos. Struct. (2022). https://doi.org/10.1016/j.compstruct.2021.114950
Radford, D.C., McShane, G.J., Deshpande, V., Fleck, N.A.: The response of clamped sandwich plates with metallic foam cores to simulated blast loading. Int. J. Solids Struct. (2006). https://doi.org/10.1016/j.ijsolstr.2005.07.006
McShane, G.J., Radford, D.D., Deshpande, V., Fleck, N.A.: The response of clamped sandwich plates with lattice cores subjected to shock loading. Eur. J. Mech. A/Solids (2006). https://doi.org/10.1016/j.euromechsol.2005.08.001
Al-Waily, M., Raad, H., Njim, E.K.: Free vibration analysis of sandwich plate-reinforced foam core adopting micro aluminum powder. Phys. Chem. Solid State 23, 659–668 (2022). https://doi.org/10.15330/pcss.23.4.659-668
Civalek, Ö., Ersoy, H., Uzun, B., Yaylı, M.Ö.: Dynamics of a FG porous microbeam with metal foam under deformable boundaries. Acta Mech. (2023). https://doi.org/10.1007/s00707-023-03663-7
Babaei, H., Kiani, Y., Eslami, M.R.: Vibrational behavior of thermally pre-/post-buckled FG-CNTRC beams on a nonlinear elastic foundation: a two-step perturbation technique. Acta Mech. 232, 3897–3915 (2021). https://doi.org/10.1007/s00707-021-03027-z
Mirzavand Borojeni, B., Shams, S., Kazemi, M.R., Rokn-Abadi, M.: Effect of temperature and magnetoelastic loads on the free vibration of a sandwich beam with magnetorheological core and functionally graded material constraining layer. Acta Mech. 233, 4939–4959 (2022). https://doi.org/10.1007/s00707-022-03316-1
Zhao, N., Ye, R., Tian, A., Cui, J., Ren, P., Wang, M.: Experimental and numerical ınvestigation on the anti-penetration performance of metallic sandwich plates for marine applications. J. Sandw. Struct. Mater. 22, 494–522 (2019). https://doi.org/10.1177/1099636219855335
Ren, P., Yin, L., Tao, Q., Guo, Z., Zhang, W.: Dynamic failure of carbon fiber-reinforced plastics sandwich structures with polyvinyl chloride foam cores subjected to ımpact loading. J. Sandw. Struct. Mater. 23, 2375–2398 (2020). https://doi.org/10.1177/1099636220909948
Sun, C., Albustani, H., Phadnis, V.A., Nasr, M., Cantwell, W.J., Guan, Z.: Improving the structural integrity of foam-core sandwich composites using continuous carbon fiber stitching. Compos. Struct. 324, 117509 (2023). https://doi.org/10.1016/j.compstruct.2023.117509
Vaziri, A., Xue, Z., Hutchinson, J.W.: Metal sandwich plates with polymer foam-filled cores. J. Mech. Mater. Struct. (2006). https://doi.org/10.2140/jomms.2006.1.97
Boztoprak, Y., Ünal, M., Özada, Ç., Kuzu, E., Özer, H., Ergin, F., et al.: Sound insulation performance of honeycomb core aluminum sandwich panels with flexible epoxy-based foam infill. Compos. Struct. 319, 117149 (2023). https://doi.org/10.1016/j.compstruct.2023.117149
Bakir, M., Jasiuk, I., Meyer, J.D., Economy, J., Jasiuk, I.: Aromatic thermosetting copolyester foam core and aluminum foam face three-layer sandwich composite for impact energy absorption. Mater. Lett. (2017). https://doi.org/10.1016/j.matlet.2017.03.116
Mocian, O., Constantinescu, D.M., Indreş, A.: Assessment on energy absorption of foam core sandwich panels under low velocity impact. Macromol. Symp. (2021). https://doi.org/10.1002/masy.202000300
Kaboglu, C., Yu, L., Mohagheghian, I., Blackman, B.R.K., Kinloch, A.J., Dear, J.P.: Effects of the core density on the quasi-static flexural and ballistic performance of fibre-composite skin/foam-core sandwich structures. J. Mater. Sci. (2018). https://doi.org/10.1007/s10853-018-2799-x
Park, W.-T., Han, S.-C.: Buckling analysis of nano-scale magneto–electro-elastic plates using the nonlocal elasticity theory. Adv. Mech. Eng. (2018). https://doi.org/10.1177/1687814018793335
Amir, S., Khorasani, M.T., BabaAkbar-Zarei, H.: Buckling analysis of nanocomposite sandwich plates with piezoelectric face sheets based on flexoelectricity and first-order shear deformation theory. J. Sandw. Struct. Mater. 22, 2186–2209 (2018). https://doi.org/10.1177/1099636218795385
Monaco, G.T., Fantuzzi, N., Fabbrocino, F., Luciano, R.: Critical temperatures for vibrations and buckling of magneto–electro-elastic nonlocal strain gradient plates. Nanomaterials 11, 1–18 (2021). https://doi.org/10.3390/nano11010087
Boyina, K., Piska, R., Natarajan, S.: Nonlocal strain gradient model for thermal buckling analysis of functionally graded nanobeams. Acta Mech. (2023). https://doi.org/10.1007/s00707-023-03637-9
Woo, J., Meguid, S.A., Liew, K.M.: Thermomechanical postbuckling analysis of functionally graded plates and shallow cylindrical shells. Acta Mech. 165, 99–115 (2003). https://doi.org/10.1007/s00707-003-0035-4
Quan, T.Q., Dat, N.D., Duc, N.D.: Static buckling, vibration analysis and optimization of nanocomposite multilayer perovskite solar cell. Acta Mech. 234, 3893–3915 (2023). https://doi.org/10.1007/s00707-023-03588-1
Arefi, M., Kiani, M., Zenkour, A.M.: Size-dependent free vibration analysis of a three-layered exponentially graded nano-/micro-plate with piezomagnetic face sheets resting on Pasternak’s foundation via McSt. J. Sandw. Struct. Mater. 22, 55–86 (2017). https://doi.org/10.1177/1099636217734279
Yan, J.W., Tong, L.H., Li, C., Zhu, Y., Wang, Z.W.: Exact solutions of bending deflections for nano-beams and nano-plates based on nonlocal elasticity theory. Compos. Struct. 125, 304–313 (2015). https://doi.org/10.1016/j.compstruct.2015.02.017
Naghinejad, M., Ovesy, H.R.: Free vibration characteristics of nonlocal viscoelastic nano-scaled plates with rectangular cutout and surface effects. Zamm. J. Appl. Math. Mech./Zeitschrift Für Angew. Math. Und. Mech. (2020). https://doi.org/10.1002/zamm.201900294
Anjomshoa, A., Tahani, M.: Vibration analysis of orthotropic circular and elliptical nano-plates embedded in elastic medium based on nonlocal Mindlin plate theory and using galerkin method. J. Mech. Sci. Technol. (2016). https://doi.org/10.1007/s12206-016-0506-x
Wang, P., Wu, X., He, X.: Vibration-theoretic approach to vulnerability analysis of nonlinear vehicle platoons. IEEE Trans. Intell. Transp. Syst. 24, 11334–11344 (2023). https://doi.org/10.1109/TITS.2023.3278574
Zhang, M., Jiang, X., Arefi, M.: Dynamic formulation of a sandwich microshell considering modified couple stress and thickness-stretching. Eur. Phys. J. Plus (2023). https://doi.org/10.1140/epjp/s13360-023-03753-4
Bai, X., Zhang, Z., Shi, H., Luo, Z.: Identification of subsurface mesoscale crack in full ceramic ball bearings based on strain energy theory. Appl. Sci. 13, 7783 (2023)
Lu, Z., Wu, D., Ding, H., Chen, L.: Vibration isolation and energy harvesting integrated in a Stewart platform with high static and low dynamic stiffness. Appl. Math. Model. 89, 249–267 (2021). https://doi.org/10.1016/j.apm.2020.07.060
Lu, Z., Zhao, L., Ding, H., Chen, L.: A dual-functional metamaterial for integrated vibration isolation and energy harvesting. J. Sound Vib. (2021). https://doi.org/10.1016/j.jsv.2021.116251
Tong, X., Zhang, F., Ji, B., Sheng, M., Tang, Y.: Carbon-coated porous aluminum foil anode for high-rate long-term cycling stability and high energy density dual-ion batteries. Adv. Mater. (2016). https://doi.org/10.1002/adma.201603735
Yan, Z., Hu, Q., Jiang, F., Lin, S., Li, R., Chen, S.: Mechanism and technology evaluation of a novel alternating-arc-based directed energy deposition method through polarity-switching self-adaptive shunt. Addit. Manuf. 67, 103504 (2023). https://doi.org/10.1016/j.addma.2023.103504
Zhou, L., Meng, F., Sun, Y.: Numerical study on infrared detectors cooling by multi-stage thermoelectric cooler combined with microchannel heat sink. Appl. Therm. Eng. 236, 121788 (2024). https://doi.org/10.1016/j.applthermaleng.2023.121788
Zhu, Q., Chen, J., Gou, G., Chen, H., Li, P.: Ameliorated longitudinal critically refracted—attenuation velocity method for welding residual stress measurement. J. Mater. Process. Technol. 246, 267–275 (2017). https://doi.org/10.1016/j.jmatprotec.2017.03.022
Zhang, H., Xiang, X., Huang, B., Wu, Z., Chen, H.: Static homotopy response analysis of structure with random variables of arbitrary distributions by minimizing stochastic residual error. Comput. Struct. 288, 107153 (2023). https://doi.org/10.1016/j.compstruc.2023.107153
Li, L., Hu, Y.: Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 107, 77–97 (2016). https://doi.org/10.1016/j.ijengsci.2016.07.011
Yang, J., Chen, D., Kitipornchai, S.: Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev–Ritz method. Compos. Struct. 193, 281–294 (2018). https://doi.org/10.1016/j.compstruct.2018.03.090
Tran, H.Q., Vu, V.T., Tran, M.T.: Free vibration analysis of piezoelectric functionally graded porous plates with graphene platelets reinforcement by pb-2 Ritz method. Compos. Struct. 305, 116535 (2023). https://doi.org/10.1016/j.compstruct.2022.116535
Nakamura, T., Wang, T., Sampath, S.: Determination of properties of graded materials by inverse analysis and instrumented indentation. Acta Mater. 48, 4293–4306 (2000). https://doi.org/10.1016/S1359-6454(00)00217-2
Chen, D., Yang, J., Kitipornchai, S.: Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 133, 54–61 (2015). https://doi.org/10.1016/j.compstruct.2015.07.052
Wang, Y.Q., Zhao, H.L.: Free vibration analysis of metal foam core sandwich beams on elastic foundation using Chebyshev collocation method. Arch. Appl. Mech. 89, 2335–2349 (2019). https://doi.org/10.1007/s00419-019-01579-0
Garg, A., Chalak, H.D., Li, L., Belarbi, M.O., Sahoo, R., Mukhopadhyay, T.: Vibration and buckling analyses of sandwich plates containing functionally graded metal foam core. Acta Mech. Solida Sin. 35, 1–16 (2022). https://doi.org/10.1007/s10338-021-00295-z
Gibson, I.J., Ashby, M.F.: The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 382, 43–59 (1982). https://doi.org/10.1098/rspa.1982.0088
Chen, D., Yang, J., Kitipornchai, S.: Free and forced vibrations of shear deformable functionally graded porous beams. Int. J. Mech. Sci. 108–109, 14–22 (2016). https://doi.org/10.1016/j.ijmecsci.2016.01.025
Touloukian, Y.S.: Thermophysical Properties of High Temperature Solid Materials. Macmillan, New York (1967)
Kiani, Y., Eslami, M.R.R.: An exact solution for thermal buckling of annular FGM plates on an elastic medium. Compos. Part B Eng. 45, 101–110 (2013). https://doi.org/10.1016/j.compositesb.2012.09.034
Zhang, D.G.: Thermal post-buckling and nonlinear vibration analysis of FGM beams based on physical neutral surface and high order shear deformation theory. Meccanica 49, 283–293 (2014). https://doi.org/10.1007/s11012-013-9793-9
Eringen, A.C.: Theories of nonlocal plasticity. Int. J. Eng. Sci. 21, 741–751 (1983). https://doi.org/10.1016/0020-7225(83)90058-7
Lim, C.W., Zhang, G., Reddy, J.N.: A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 78, 298–313 (2015). https://doi.org/10.1016/j.jmps.2015.02.001
Li, L., Li, X., Hu, Y.: Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 102, 77–92 (2016). https://doi.org/10.1016/j.ijengsci.2016.02.010
Li, L., Lin, R., Ng, T.Y.: Contribution of nonlocality to surface elasticity. Int. J. Eng. Sci. (2020). https://doi.org/10.1016/j.ijengsci.2020.103311
Farajpour, A., Rastgoo, A.: Influence of carbon nanotubes on the buckling of microtubule bundles in viscoelastic cytoplasm using nonlocal strain gradient theory. Results Phys. 7, 1367–1375 (2017). https://doi.org/10.1016/j.rinp.2017.03.038
Jiang, Y., Li, L., Hu, Y.: A physically-based nonlocal strain gradient theory for crosslinked polymers. Int. J. Mech. Sci. (2023). https://doi.org/10.1016/j.ijmecsci.2022.108094
Eringen, A.C.: On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54, 4703–4710 (1983). https://doi.org/10.1063/1.332803
Żur, K.K., Arefi, M., Kim, J., Reddy, J.N.: Free vibration and buckling analyses of magneto–electro-elastic FGM nanoplates based on nonlocal modified higher-order sinusoidal shear deformation theory. Compos. Part B Eng. (2020). https://doi.org/10.1016/j.compositesb.2019.107601
Reddy, J.N., Wang, C.M., Kitipornchai, S.: Axisymmetric bending of functionally graded circular and annular plates. Eur. J. Mech. A/Solids (1999). https://doi.org/10.1016/S0997-7538(99)80011-4
Pan, E., Heyliger, P.R.: Free vibrations of simply supported and multilayered magneto–electro-elastic plates. J. Sound Vib. (2002). https://doi.org/10.1006/jsvi.2001.3693
Arefi, M., Zenkour, A.M.: A simplified shear and normal deformations nonlocal theory for bending of functionally graded piezomagnetic sandwich nanobeams in magneto-thermo-electric environment. J. Sandw. Struct. Mater. (2016). https://doi.org/10.1177/1099636216652581
Arefi, M., Zenkour, A.M.: Free vibration analysis of a three-layered microbeam based on strain gradient theory and three-unknown shear and normal deformation theory. Steel Compos. Struct. (2018). https://doi.org/10.12989/scs.2018.26.4.421
Reddy, J.N.: Energy Principles and Variational Methods. Theory Anal. Elastic Plates Shells (2020). https://doi.org/10.1201/9780849384165-6
Mekerbi, M., Benyoucef, S., Mahmoudi, A., Tounsi, A., Bousahla, A.A., Mahmoud, S.R.: Thermodynamic behavior of functionally graded sandwich plates resting on different elastic foundation and with various boundary conditions. J. Sandw. Struct. Mater. 23, 1028–1057 (2021). https://doi.org/10.1177/1099636219851281
Reddy, J.N., Chin, C.D.: Thermomechanical analysis of functionally graded cylinders and plates. J Therm Stress 21, 593–626 (1998). https://doi.org/10.1080/01495739808956165
Aghababaei, R., Reddy, J.N.: Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 326, 277–289 (2009). https://doi.org/10.1016/j.jsv.2009.04.044
Koç, M.A., Esen, İ, Eroğlu, M.: Thermomechanical vibration response of nanoplates with magneto–electro-elastic face layers and functionally graded porous core using nonlocal strain gradient elasticity. Mech. Adv. Mater. Struct. (2023). https://doi.org/10.1080/15376494.2023.2199412
Funding
Open access funding provided by the Scientific and Technological Research Council of Türkiye (TÜBİTAK). No funding was received for conducting this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eroğlu, M., Esen, İ. & Koç, M.A. The effect of the viscoelastic support and GRPL-reinforced foam material on the thermomechanical vibration response of piezomagnetic sandwich nanosensor plates. Acta Mech 235, 2415–2453 (2024). https://doi.org/10.1007/s00707-023-03843-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-023-03843-5